SCAMPI: A scalable statistical framework for genome-wide interaction testing harnessing cross-trait correlations

Abstract

Family-based heritability estimates of complex traits are often considerably larger than their single-nucleotide polymorphism (SNP) heritability estimates. This discrepancy may be due to non-additive effects of genetic variation, including variation that interacts with other genes or environmental factors to influence the trait. Variance-based procedures provide a computationally efficient strategy to screen for SNPs with potential interaction effects without requiring the specification of the interacting variable. While valuable, such variance-based tests consider only a single trait and ignore likely pleiotropy among related traits that, if present, could improve power to detect such interaction effects. To fill this gap, we propose SCAMPI (Scalable Cauchy Aggregate test using Multiple Phenotypes to test Interactions), which screens for variants with interaction effects across multiple traits. SCAMPI is motivated by the observation that SNPs with pleiotropic interaction effects induce genotypic differences in the patterns of correlation among traits. By studying such patterns across genotype categories among multiple traits, we show that SCAMPI has improved performance over traditional univariate variance-based methods. Like those traditional variance-based tests, SCAMPI permits the screening of interaction effects without requiring the specification of the interaction variable and is further computationally scalable to biobank data. We employed SCAMPI to screen for interacting SNPs associated with four lipid-related traits in the UK Biobank and identified multiple gene regions missed by existing univariate variance-based tests. SCAMPI is implemented in software for public use.

Introduction

Genome-wide association studies (GWAS) have successfully improved our understanding of the role of common single-nucleotide polymorphisms (SNPs) on many complex human traits and diseases. Researchers can further use SNP data from a GWAS study to estimate a trait’s narrow-sense heritability (proportion of trait variance due to additive genetic effects) using statistical techniques like GCTA and LD Score Regression (LDSC).^{1; 2} Interestingly, SNP-based heritability estimates of a complex trait are routinely smaller than the corresponding family-based estimates of narrow-sense heritability based on kinship. For instance, studies have reported SNP-based estimates of narrow-sense heritability for body mass index (BMI) to be 0.3, which is considerably less than the narrow-sense heritability estimates of 0.47–0.90 for BMI reported in twin studies.^{3; 4} For Alzheimer’s Disease (AD), family-based heritability estimates of the disease range from 0.60–0.80, whereas the latest population-based AD GWAS meta-analyses estimated the narrow-sense heritability from SNP data to be between 0.06–0.41.^5–13 Likewise, a GWAS analysis of Amyotrophic Lateral Sclerosis (ALS) estimated SNP-based heritability of approximately 0.21, which is significantly less than the estimates of 0.38–0.85 observed in twin studies.¹⁴

The gap between family-based estimates of narrow-sense heritability and corresponding SNP-based estimates may be due to several factors, including rare causal variation poorly tagged by common SNPs as well as shared familial environmental effects ignored in traditional family-based heritability estimation.^{15; 16} Here, we focus on another possible explanation for this gap - the presence of non-additive effects (including higher-order genetic interactions) on complex traits and diseases. As noted in the Supplemental Materials (S1), we can show that higher-order interactions of a complex trait inflate narrow-sense heritability estimates more among close relatives (traditionally used for family-based estimates of heritability) than distantly related individuals (traditionally used to estimate GWAS heritability via LDSC/GCTA).¹⁷ Thus, higher-order interactions can explain the discrepancy between family-based and SNP-based heritability estimates observed for many complex human traits. This motivates the search for genetic variants in large-scale genetic studies that demonstrate non-additive effects, including gene-gene and gene-environment interactions.

While studies have identified SNPs demonstrating interaction effects on complex traits,^18-23 genome-wide investigation of non-additive effects is inherently challenging.^{24; 25} Comprehensive genome-wide testing of SNP-SNP (epistatic) interactions is computationally intractable as 10 million SNPs can lead to approximately 5 × 10¹³ potential interaction tests. Even if such analyses were tractable, the resulting multiple-testing adjustment cripples the power to detect epistatic effects. Gene-environment interaction analyses require fewer tests and are more computationally feasible, but measuring the right environmental determinants can be difficult and is often unknown.^26–29 To circumvent uncertainty about the right environmental factor yet still test for evidence of interaction, Paré et al. proposed an efficient variance-based method for a quantitative trait that screens for SNPs with possible interactive effects without requiring specification of the interacting factor.³⁰ Recognizing that a SNP with an interaction effect on a trait induces trait variance that differs by genotype (see Supplemental Figure S1), Paré screened for SNPs with potential interaction effects by testing for equality of variances across genotype categories using Levene’s test.³¹ Researchers have successfully applied this type of variance-based approach within the UK Biobank to identify genetic variants with interaction effects on obesity phenotypes and cardiometabolic serum biomarkers.^{32; 33}

The variance-based test of Paré is a univariate test that considers whether a SNP has an interactive effect with a single phenotype. However, biobanks routinely collect detailed information on a large collection of related phenotypes with shared genetic effects. Many recent methods of gene mapping illustrate the appeal of leveraging the ubiquitous phenomenon of pleiotropy across related traits when present.^34–37 Consequently, if pleiotropic genetic variants with interactive effects exist, we expect a multi-trait statistical method that leverages this information will have improved performance over existing univariate variance-based interaction procedures. Bass et al. recently showed that a SNP with an interaction effect induces not only variance but also covariance patterns between traits that differ by genotype (which we illustrate in Supplemental Figure S2).³⁸ Based on this observation, the authors developed a kernel framework for interaction testing that assessed where similarity in variance/covariance patterns among a group of modeled traits correlated with genotypic similarity at a test SNP. While more powerful than standard variance-based testing, the kernel framework of Bass lacks practical features for genetic analysis such as the inability to identify the specific phenotypes (among those modeled) that demonstrate interaction effects with the test SNP. Identifying these specific phenotypes are of substantial value for further downstream analyses.

To this end, we propose here an efficient screening method SCAMPI (Scalable Cauchy Aggregate test using Multiple Phenotypes to test Interactions) for identifying potential SNPs with interaction effects using multiple phenotypes. SCAMPI fits simple regression models relating SNP genotype to (standardized) cross products of all pairwise combinations of traits under consideration and then aggregates the correlated p-values from these separate regression tests together into an omnibus test using the Cauchy Combination Test.^{39; 40} Similar to variance-based interaction tests, SCAMPI does not require specification of the factor that interacts with the SNP of interest, thereby reducing the computational and testing burden and enabling the scaling of the method to biobank-size datasets. Moreover, SCAMPI scales to handle many related phenotypes and can identify the specific phenotype(s) that have interaction effects among those modeled. Using simulations, we show that SCAMPI can detect interactions under various scenarios and has improved performance over univariate variance-based interaction procedures. We also applied SCAMPI to lipid panel data (an indicator of risk of heart disease and stroke) in the UK Biobank (UKBB) and identified several genes with putative interaction effects that were missed by standard univariate variance-based procedures. For public use, SCAMPI is implemented as an R package.

Materials and Methods

Motivation:

We first show that a SNP with a pleiotropic interaction effect yields trait correlation patterns that differ by genotype category. We could analogously show that a SNP with a pleiotropic interaction trait effect influences the covariance patterns between traits but chose to focus on correlation due to the scale-free nature of the latter measure. For subject $i$, define ${\mathit{G}}_i$ as the subject’s genotype at a test SNP and define $W_i$ as some factor (either genetic or environmental) that interacts with the SNP to influence multiple traits. Suppose subject $i$ possesses two correlated traits $Y_{i,1}$ and $Y_{i,2}$ that are generated under the relationships:

$$Y_{i,2}={\alpha }_1+{\beta }_1{G}_i+{\gamma }_1{W}_i+{\delta }_1{G}_i{W}_i+{ϵ}_{i,1};Y_{i,2}={\alpha }_2+{\beta }_2{G}_i+{\gamma }_2{W}_i+{\delta }_2{G}_i{W}_i+{ϵ}_{i,2}.$$

Here, ${\beta }_j$, ${\gamma }_j$, ${\delta }_j$ denote the main effect of genotype, the main effect of the factor, and two-way interaction effect between genotype and factor, respectively, on trait $J(J=1,2)$. We further assume each of the error terms ${ϵ}_{i,1}$ and ${ϵ}_{i,2}$ has a standard normal distribution ${ϵ}_{i,1}$, ${ϵ}_{i,2}~N(0,1)$. Without loss of generality, further assume $W_i$ is distributed as $W_i~N(0,1)$ and is independent of $G_i$.

Based on the trait models listed above, Paré previously showed that that variance of $Y_1(Y_2)$ differs by $G$ when the genotype has an interaction effect on trait 1 (trait 2), respectively.³⁰ Additionally, when pleiotropic interaction effects exist, we can show the correlation of traits 1 and 2 also differ by genotype. In Supplementary Materials S2, we derive the correlation between $Y_{i,1}$ and $Y_{i,2}$ conditional on genotype $G_i$ as:

$$cor(Y_{i,1},Y_{i,2}|G_i=g_i)=\frac{{\gamma }_1{\gamma }_2+({\delta }_1{\gamma }_2+{\delta }_2{\gamma }_1)g_i+{\delta }_1{\delta }_2{g}_i^2}{\sqrt{{({\gamma }_1+{\delta }_1{g}_i)}^2+1}\times \sqrt{{({\gamma }_2+{\delta }_2{g}_i)}^2+1}}$$ (1)

Equation (1) shows that the correlation between two traits differs by genotype when either a) the genotype interacts with the factor on both phenotypes or b) the genotype interacts with the factor on at least one of the phenotypes, provided the factor has a main effect on the other phenotype. We can see that if the SNP has no interaction effect on either phenotype $({\delta }_1={\delta }_2=0)$, the phenotypic correlation will not differ by genotype even when main effects for the factor exist $({\gamma }_1\ne 0,{\gamma }_2\ne 0)$.

The above result suggests an efficient strategy for screening SNPs with potential interaction effects. Instead of performing traditional interaction analyses, which mandates defining potential interacting factors $W_i$, we can instead screen for SNPs with interaction effects without having to specify $W_i$ by examining whether the correlation between traits changes as a function of the linear and quadratic effects of genotype. Such modeling provides a workaround in situations where interacting covariates are uncollected or inaccurately recorded. The screening procedure further provides an efficient alternative strategy for genome-wide epistatic analysis in that it does not require direct modeling of the interacting genetic factor, which substantially reduces the number of tests to be considered. If we are analyzing $M$ SNPs, SCAMPI requires only $M$ tests whereas comprehensive epistatic analysis requires $\left(\begin{array}{c}M\\ 2\end{array}\right)$ tests. Thus, when $M=200\text{K}\left(M=2\text{M}\right)$, SCAMPI reduces the number of tests required by approximately 5 (6) orders of magnitude.

Rather than model trait correlation as a function of linear and quadratic effects of genotype mentioned above, we note that we can alternatively parameterize this relationship using a general genotype model that allows for separate effects of each genotype relative to a baseline category. That is, for some outcome $Y^{*}$, the coefficient estimates of ${\widehat{\alpha }}_1$, ${\widehat{\alpha }}_2$ and ${\widehat{\alpha }}_3$ in the regression model $Y^{*}={\alpha }_1+{\alpha }_{2}G+{\alpha }_3{G}^2+{ϵ}^{*}$ can be directly mapped to coefficient estimates ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$ and ${\widehat{\beta }}_3$ in a model $Y^{*}={\beta }_1+{\beta }_2{G}_1+{\beta }_3{G}_2+ϵ$, where $G_1$ and $G_2$ are genotype indicators for those with 1 and 2 copies of the reference allele, respectively (those with 0 copies are treated as baseline). Given the familiarity of this general genotype model in GWAS, ^41–44 we chose to use this alternative parameterization in our method moving forward.

Notation and Trait Standardization:

Assume a sample of $N$ unrelated subjects that possess $J$ continuous phenotypes. Let ${\mathit{Y}}_j={(Y_{1,j},Y_{2,j},\dots ,Y_{N,j})}^T$ denote the $N\times 1$ vector of observations for trait $j(j=1,\hspace{0.5em}\dots ,J)$. Define $\mathit{G}={(G_1,G_2,\dots ,G_N)}^T$ as an $N\times 1$ vector of genotypes for one test SNP, where $G_1$ represents $\left[0,1,2\right]$ copies of the minor allele that subject $i$ possesses at the site. As noted in the previous section, we are interested in applying a general genotype model for interaction testing as it naturally captures the linear and quadratic effects of genotype shown in equation (1). Consequently, further define $G_i^{(1)}=I[G_i=1]$ and $G_i^{(2)}=I[G_i=2]$ as indicator variables for genotype categories 1 and 2, respectively (we treat genotype category 0 as baseline). Finally, let $\mathit{Z}$ be an $N\times K$ matrix of confounding variables. These confounding variables can be a mixture of continuous or categorical features. Common confounder examples include age, biological sex, batch ID, and principal components of ancestry to deal with population stratification.

Our goal is to detect a SNP with an interaction effect that yields correlation patterns that differ by genotype. Such trait pattern differences can erroneously arise if the main effect of the genotype, as well as main and variance effects of confounders (such as population structure), are unaccounted for prior to analysis.^{45; 46} To avoid this issue, we first standardize and adjust each ${\mathit{Y}}_j(j=1,\dots ,J)$ prior to analysis using a double generalized linear model (DGLM) that corrects for the mean effects of the test SNP and confounders, as well as the potential variance effects of confounders.^47,48

DGLM is composed of two sub-models, where the first sub-model controls population mean, and the second sub-model controls population variance. For our work, the first sub-model adjusts ${\mathit{Y}}_j$ for the mean effects of ${\mathit{G}}^{(1)}\hspace{0.5em}\&\hspace{0.5em}{\mathit{G}}^{(2)}$ and confounders $\mathit{Z}$ using the following framework:

$${\mathit{Y}}_j=[\mathbf{1}{\mathit{G}}^{(\text{1})}{\mathit{G}}^{(\text{2})}\mathit{Z}\text{]}\left[\begin{array}{c}{\beta }_{j,0}\\ {\beta }_{j,G^{(1)}}\\ {\beta }_{j,G^{(2)}}\\ {\mathbf{\beta }}_{j,z}\end{array}\right]+{\mathit{\epsilon }}_j$$

where ${\beta }_{j,0}$ is the intercept associated with the $j^{th}$ trait. ${\beta }_{j,G^{(1)}}$ and ${\beta }_{j,G^{(2)}}$ are the regression coefficient for ${\mathit{G}}^{(1)}$ and ${\mathit{G}}^{(2)}$ respectively, and ${\mathit{\beta }}_{j,z}$ is a $K\times 1$ vector of regression coefficients for confounders $\mathit{Z}$. Finally, ${\mathit{\epsilon }}_j$ is a $N\times 1$ vector of residual errors that follow

$${\mathit{\epsilon }}_j~\mathit{MVN}\left({\mathit{\mu }}_{{\epsilon }_{\text{j}}}={\mathbf{0}}_{\mathit{Nx}\mathbf{1}}\text{,}{\mathbf{\sum }}_{{\epsilon }_{\text{j}}}=\left[\begin{array}{ccc}{\sigma }_{{\epsilon }_{1,j}}^2& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sigma }_{{\epsilon }_{1,j}}^2\end{array}\right]\right)$$ (2)

The second sub-model of the DGLM then models ${\mathit{\epsilon }}_j$ in (2) as a function of confounders $\mathit{Z}$ using the following framework using the log link function:

$$\log \left(E\left(diag\left({\mathit{\sum }}_{{\epsilon }_j}\right)\right)\right)={\mathit{\phi }}_j=\left[\mathbf{1}\mathit{Z}\right]\left[\begin{array}{c}{\gamma }_0\\ {\mathit{\gamma }}_Z\end{array}\right]$$

where ${\mathit{\phi }}_j$ is the $N\hspace{0.5em}x\hspace{0.5em}1$ column vector representing the expected residual variance of the $j^{th}$ observed trait. Here, ${\gamma }_0$ is the intercept while ${\mathit{\gamma }}_Z$ represents the $K\times 1$ column vector of confounder effects on the variance. The error distribution to be used in the two sub-models is Gaussian.

We fit the above DGLM using the R package “dglm”. Let ${\tilde{\mathit{Y}}}_{\text{j}}(j=1,\dots ,J)$ denote the adjusted and standardized form for trait $j$ produced from the DGLM model fit. We subsequently use ${\tilde{\mathit{Y}}}_{\text{j}}(j=1,\dots ,J)$ to construct appropriate measures for our downstream screening analyses for interaction effects.

Analysis Strategy:

For $J=2$ traits, we show in Supplemental Materials (S3) that we can approximate the sample Pearson correlation coefficient of traits ${\mathit{Y}}_1$ and ${\mathit{Y}}_2$ as the average of the $N\times 1$ vector of cross products of the traits after standardization,${\tilde{\mathit{Y}}}_1$ and ${\tilde{\mathit{Y}}}_2$. That is, we estimate the Pearson correlation between ${\mathit{Y}}_1$ and ${\mathit{Y}}_2$ as the sample average of

$${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_2={\left({\tilde{Y}}_{1,1}\cdot {\tilde{Y}}_{1,2},{\tilde{Y}}_{2,1}\cdot {\tilde{Y}}_{2,2},\dots ,{\tilde{Y}}_{N,1}\cdot {\tilde{Y}}_{N,2}\right)}^{\text{T}}$$

where $\odot$ denotes the row-wise product operator of two vectors. Similarly, we can estimate the variance of ${\mathit{Y}}_1$ and ${\mathit{Y}}_2$ by ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_1$ and ${\tilde{\mathit{Y}}}_2\odot {\tilde{\mathit{Y}}}_2$, respectively.

Using these estimates, we construct a screening procedure to identify a SNP with an interaction effect on trait ${\mathit{Y}}_1$ and/or ${\mathit{Y}}_2$ by assessing whether SNP genotype $\mathit{G}$ is associated with either ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_1,{\tilde{\mathit{Y}}}_2\odot {\tilde{\mathit{Y}}}_2$, or ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_2$. Examination of the relationship of $\mathit{G}$ with ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_1,(\text{or}{\tilde{\mathit{Y}}}_2\odot {\tilde{\mathit{Y}}}_2)$ is similar to assessing whether trait variance differs by genotype (which Paré³⁰ investigated using Levene’s test) while the study of $\mathit{G}$ with ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_2$ leverages additional information on interactions based on differences in trait correlations. To implement our procedure, we fit 3 separate linear regression models; each model treating one of ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_1,{\tilde{\mathit{Y}}}_2\odot {\tilde{\mathit{Y}}}_2$, or ${\tilde{\mathit{Y}}}_1\odot {\tilde{\mathit{Y}}}_2$ as outcome with SNP genotype ${\mathit{G}}^{(1)}$ and ${\mathit{G}}^{(2)}$ as predictors. Each regression models produces a p-value based on a two-degree-of-freedom test. Since the resulting 3 p-values from these regression tests are correlated, we can then combine them into an omnibus p-value (described in the next section) to assess whether the SNP has an interaction effect on at least one of the two traits under study.

The above example considered two traits under study. However, the strategy easily extends to the study of $J>2$ correlated traits as well. Assuming $J$ traits, we fit $J$ regression models that regress ${\tilde{\mathit{Y}}}_j\odot {\tilde{\mathit{Y}}}_j$ on ${\mathit{G}}^{(1)}$ and ${\mathit{G}}^{(2)}(j=1,\dots ,J)$ and further fit $\left(\begin{array}{c}J\\ 2\end{array}\right)$ additional regression models that regress ${\tilde{\mathit{Y}}}_j\odot {\tilde{\mathit{Y}}}_l=(j,l=1,\dots ,J;j\ne l)$ on ${\mathit{G}}^{(1)}$ and ${\mathit{G}}^{(2)}$. We then can combine the $J_c=\left(J+\left(\begin{array}{c}J\\ 2\end{array}\right)\right)$ p-values from these tests together to assess whether the SNP has an interaction effect on at least one of the $J$ traits under study.

Cauchy Combination Test (CCT):

After obtaining the $J_c$ p-values above, we create a final omnibus test for whether the test SNP has an interactive effect on any of the traits under consideration using the Cauchy Combination Test (CCT),^{39; 40} which is a popular technique for aggregating many potentially dependent tests of high dimension together into an omnibus framework. CCT has provable type I error rate control for genome wide significance thresholds even when p-values are dependent. CCT is especially useful when an SNP signal is sparse and only affects a subset of the traits under consideration. The test statistics of CCT is a weighted sum of the Cauchy transformation of individual p-values in SCAMPI. Let $p_r$ to denote the dependent individual p-value from the $r^{th}$ regression test $\left(r=1,2,\dots ,J_c\right)$. The CCT statistic is defined as

$$T={\sum }_{r=1}^{J_c}\frac{1}{J_c}\tan \left\{\left(0.5-p_r\right)\pi \right\}$$ (3)

Under the null hypothesis of no SNP interactive effect with any of the traits under consideration, $T$ in (3) follows a standard Cauchy Distribution, i.e., $T~Cauchy(X_0=0,\gamma =J_c)$. This derived p-value is the SCAMPI p-value at the given genotype $\mathit{G}$.

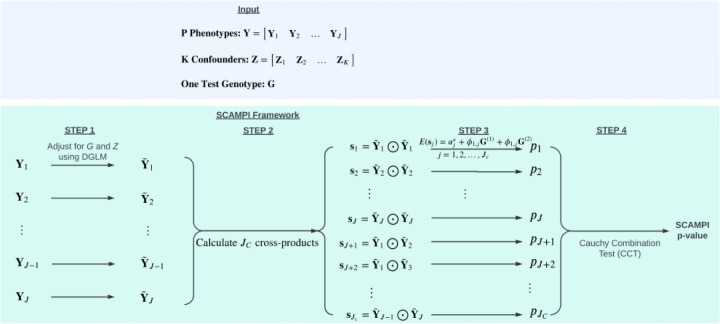
Overview of the SCAMPI Framework:

Our SCAMPI framework aggregates the regression tests outlined earlier with the CCT to produce an omnibus p-value for testing whether the SNP has an interactive effect with at least one of the traits under study. SCAMPI, which is implemented in a public R package of the same name, requires the following inputs:

1. Multiple target traits are denoted as $\mathit{Y}$. Should these traits not follow a normal distribution, users can apply a rank-based Inverse Normal Transformation to normalize the traits, if desired.

2. The confounding variables, represented by $\mathit{Z}$;

3. One test SNP, represented by $\mathit{G}$ and coded as ${\mathit{G}}^{(1)}$ and ${\mathit{G}}^{(2)}$.

SCAMPI then follows the workflow depicted in Figure 1.

Figure 1. Illustration of the SCAMPI framework.

The SCAMPI framework involves a four-step process that consists of 1) adjustment of phenotypes for genotype and confounders, 2) calculation of cross products from adjusted phenotypes, 3) derivation of p-values from regression tests of cross products on test genotype, and 4) aggregating all p-values using the Cauchy Combination Test (CCT) to derive the final SCAMPI p-value to determine overall significance.

Application to UK Biobank Data:

We applied SCAMPI to identify SNPs with potential interaction effects on lipid measures within the UK Biobank (application ID 42223). We focused attention on four lipid-related measures: high-density lipoprotein cholesterol (HDL-C), low-density lipoproteins cholesterol (LDL-C), triglycerides (TGs), and Body Mass Index (BMI). Both the sample and SNP QC procedures are in accordance with Marderstein et al.⁴⁹ Similar QC procedures were also carried out in multiple studies.⁵⁰ From the cohort, we excluded individuals who either (1) had missing heterozygosity information, (2) were outliers in terms of heterozygosity or had missing genotype rates greater than 0.02, (3) had over 10 putative third-degree relatives in the kinship table, (4) were omitted from the kinship inference procedure, or (5) were either self-reported as anything other than ‘White British’ or did not show similar genetic ancestry to this group based on a principal components analysis of the genotypes. After performing this quality control, 337,422 independent subjects remained (N_Female= 181,203; N_Male= 156,219). Moreover, the UKB employed two genotyping arrays. In this post-QC sample, we have the UK Biobank Axiom array (N_UKBB= 300,345) and the UK BiLEVE array (N_UKBL= 37,077). For the SNP QC, genotypes were discarded if they had an INFO score < 0.8, MAF < 0.05 and HWE p-value < 10^-10. After SNP QC procedures, 288,910 SNPs were retained. Finally, 277,653 SNPs were included for analysis using SCAMPI after applying a 10% missing rate threshold.

We first adjusted the four lipid-related traits for confounders, including the first six genetic principal components, biological sex, age, age squared (age^²), and the type of genotyping array, before applying SCAMPI to these traits. Notably, the first six principal components effectively captured population structure at subcontinental geographic scales.^51,52 Of the initial set of 337,422 independent subjects, 288,709 possessed complete information on all traits and confounders and were considered moving forward. We first transformed the four traits using the inverse normal transformation (INT) to align the traits, which is a common practice to ensure the residual of traits is normally distributed In a regression model such as DGLM.^53–56 The distribution of the four traits, both pre and post-INT, can be found in Supplemental Figure S3 (a) - (d). Correlation between post-INT traits was 0.1246 for HDL-C and LDL-C, −0.4938 for HDL-C and TG, −0.3809 for HDL-C and BMI, 0.2797 for LDL-C and TG, 0.0394 for LDL-C and BMI, and 0.3708 for TG and BMI.

Simulations:

We conducted comprehensive simulations to evaluate the type-I error rate of SCAMPI under a variety of scenarios. For each scenario, we simulated a sample size of 300,000 to reflect biobank-scale datasets. Each scenario is analyzed based on 100,000 simulations. We assumed $J=2,4,8$ traits and simulated the trait values for the $i^{th}$ individual based on the multivariate normal distribution illustrated below:

$$\left(\begin{array}{l}{Y}_{i,1}\\ ⋮\\ Y_{i,J}\end{array}\right)~MNV\left(\mathit{\mu }=\left[\begin{array}{l}{\alpha }_1+{\beta }_1{G}_i+{\gamma }_1{W}_i\\ ⋮\\ {\alpha }_J+{\beta }_J{G}_i+{\gamma }_J{W}_i\end{array}\right],\sum =\left[\begin{array}{l}1\cdots {\sigma }^2\\ ⋮\ddots ⋮\\ {\sigma }^2\cdots 1\end{array}\right]\right)$$ (4)

For predictors, we generated the test SNP genotype $G_i$ under Hardy-Weinberg equilibrium, assuming the SNP had a minor-allele frequency of either 0.05 or 0.25. We further generated a factor $W_i$ that followed a standard normal distribution. For the choice of parameters in the equation, we simulated the intercept ${\alpha }_j$ from $N(0,5)$, the genotype main effect ${\beta }_j$ from $Unif(0,0.2)$, and the factor main effect ${\gamma }_j$ from $Unif(0,0.3)(j=1,\dots ,J)$. In the covariance matrix $\Sigma$ in (4), the off-diagonal covariance elements are assigned as ${\sigma }^2$. We performed different simulations assuming ${\sigma }^2=0.01$ (negligibly correlated traits), 0.25 (moderately correlated traits), and 0.5 (strongly correlated traits). For $J=4$ traits, we conducted additional simulations where we considered a specific covariance matrix that mirrored the observed covariance structure of the lipid-related traits that we studied in the UKBB dataset. Finally, we conducted additional type-I error simulations based directly on our UKBB sample. Specifically, we randomly permuted the UKBB phenotype data (consisting of our four trait outcomes and confounding variables) across subjects and then re-ran SCAMPI on the genome-wide data. We repeated the permutation process four times, which resulted in a total of >1M SCAMPI p-values under the null hypothesis.

For power simulations, we implemented a similar simulation design as for our type-I error simulations but introduced additional parameters to model the effect of the interaction between SNP and the factor on the simulated traits. Specifically, we generated $J$ traits based on the multivariate normal distribution as presented in Eq. (5):

$$\left(\begin{array}{l}{Y}_{i,1}\\ ⋮\\ Y_{i,J}\end{array}\right)~MNV\left(\mathit{\mu }=\left[\begin{array}{l}{\alpha }_1+{\beta }_1{G}_i+{\gamma }_1{W}_i+{\delta }_i{G}_i{W}_i\\ ⋮\\ {\alpha }_J+{\beta }_J{G}_i+{\gamma }_J{W}_i+{\delta }_J{G}_i{W}_i\end{array}\right],\sum =\left[\begin{array}{l}1\cdots {\sigma }^2\\ ⋮\ddots ⋮\\ {\sigma }^2\cdots 1\end{array}\right]\right)$$ (5)

${\delta }_j(j=1,\dots ,J)$ in equation (5) represents the interaction effect of the SNP and factor on trait $j$. For a given simulation scenario, we vary the percentage of traits that possess such an interaction (i.e. the sparsity of the interaction signal) among the values 25%, 50%, 75%, and 100%. For those traits with an interaction effect, we vary the value of ${\delta }_j$ across a range of values from 0.01 to 0.50 to study how the power trends change as ${\delta }_j$ increases for each scenario. The settings for the number of traits, MAF, ${\alpha }_j,{\beta }_j$ align with those in the Type I error simulations. However, ${\gamma }_j$ is held at fixed values for all traits instead of being simulated from a distribution. Without loss of generality, this approach eliminates the potential for power fluctuations arising from the randomness in ${\gamma }_j$. We simulated the results for various combinations under different parameter sets. To illustrate the overall pattern of the power simulation, we selected the simulation with $\gamma =0.05$ and $0.25$, and $\sigma =0.1,0.3$ and $0.5$. For each simulation scenario, we assumed a sample size of 20K and generated 10K replicates for inference.

We chose to benchmark SCAMPI against an enhanced multi-phenotype version of Levene’s test that was originally restricted to a single phenotype.³⁰ This enhanced version is termed as the multivariate Levene’s test in our context. The multivariate Levene’s test applies Levene’s test (described in Supplemental Materials S4) to each trait separately, resulting in $J$ p-values. These $J$ p-values are then aggregated together into an omnibus test using the CCT methodology detailed in the prior section (see Supplemental Figure S4 for an outline of the framework). While this benchmark examines how variances vary by genotype across different traits, it does not consider difference in correlation patterns among traits that SCAMPI integrates within its framework.

Results

Simulation Studies:

Table 1 provides empirical type 1 error rates for SCAMPI summarized at a nominal rate $\alpha$ of 10⁻² and 10⁻³ across varying numbers of phenotypes, MAF and $\sum$ when $\gamma$ is simulated from $Unif(0,0.3)$. As described in Supplemental S5, we focused primarily on studying the empirical type-I error rate at 10⁻³ based on the number of simulations performed and observed that SCAMPI was well calibrated at such a threshold. To examine whether SCAMPI was well calibrated at more stringent thresholds, we studied type-I error rates based on permutation of the UKBB data, which yielded > 1M tests under the null hypothesis. For these null simulations, we observed the type I error rates of SCAMPI to be 1.08 × 10⁻², 1.06 × 10⁻³ and 9.81 × 10⁻⁵ at $\alpha$ of 10⁻², 10⁻³ and 10⁻⁴, respectively. SCAMPI p-values generally followed the same pattern as p-values of other statistical methodology that employs CCT.^{39; 57–59}

Table 1. Nominal rate of empirical type 1 error rates for SCAMPI.

The empirical type I error rates for SCAMPI at nominal rates $\alpha$ of 10⁻² and 10⁻³ in 100,000 simulations with 300,000 observations. The result is presented across a range of conditions including varying Minor Allele Frequencies (MAF), numbers of phenotypes $\left(J\right)$, and covariance of the phenotypes $\Sigma$ when $\gamma$ is simulated from a uniform distribution between 0 and 0.3. The value presented in the ‘LEQ 0.01’ and ‘LEQ 0.001’ columns reflect the pre-specified nominal error rates.

N	MAF	$\sum$	$J$	LEQ 0.01	LEQ 0.001
3.00E+05	0.05	0.01	2	9.56E-03	1.01E-03
			4	1.00E-02	1.18E-03
			8	1.05E-02	1.13E-03
3.00E+05	0.05	0.25	2	9.96E-03	1.09E-03
			4	1.09E-02	9.30E-04
			8	1.12E-02	1.01E-03
3.00E+05	0.05	0.5	2	1.05E-02	1.16E-03
			4	1.16E-02	1.02E-03
			8	1.26E-02	1.23E-03
3.00E+05	0.25	0.01	2	9.51E-03	1.17E-03
			4	1.03E-02	1.13E-03
			8	1.00E-02	1.14E-03
3.00E+05	0.25	0.25	2	1.01E-02	1.12E-03
			4	1.09E-02	1.06E-03
			8	1.09E-02	9.40E-04
3.00E+05	0.25	0.5	2	1.03E-02	9.80E-04
			4	1.09E-02	1.03E-03
			8	1.28E-02	1.09E-03

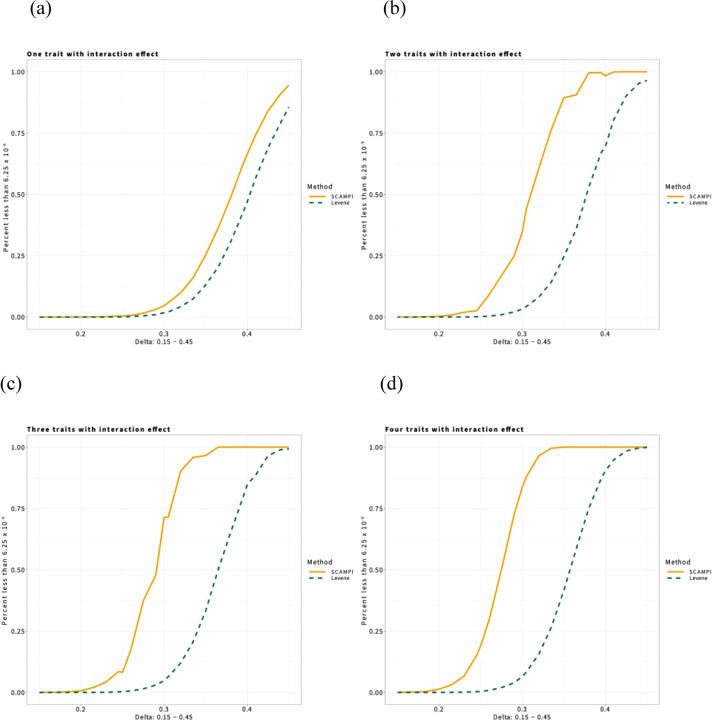
We assessed the power of SCAMPI in different scenarios. Figure 2 provides representative power results at a genome-wide significance threshold of 6.25 × 10⁻⁸ (based on a multiple-testing correction for the total number of ~800,000 SNPs in the UKBB) assuming $J=4$ traits and a correlation matrix that mirrored the observed correlation structure of the lipid-related traits that we studied in the UKBB dataset. Figure 2 is comprised of four sub-figures, with each sub-figure presenting simulation results and assuming a different level of sparsity for the interaction effect among the traits modeled. For example, Figure 2a assumes the test SNP has an interaction effect with only one of the four traits, while Figure 2d assumes the test SNP has an interaction effect on all four traits. Within each sub-figure, the yellow solid line represents the power of SCAMPI while the dashed green line represents the power of Multivariate Levene’s test. Within each sub-figure, results show, as expected, that the power of both SCAMPI and Multivariate Levene’s test increases as the magnitude of the interaction effect increases. Further, the power of each method increases as the number of traits the SNP has an interaction effect with increases (or, similarly, the sparsity of the interaction effect decreases). However, across all four sub-figures, SCAMPI consistently shows improved power over Multivariate Levene’s test. We note that such improved power of SCAMPI over Multivariate Levene’s test holds even when the SNP has an interaction effect on only one of the traits under study (Figure 2a), which suggests that the inclusion of traits with no interaction effects still contributes valuable information to the SCAMPI test via their correlation with the trait that does have an interaction effect. We do see that, in Figure 2b and Figure 2c, SCAMPI experiences a pattern at $\text{δ}=0.4$ and $\text{δ}=0.25$, respectively, where power dips slightly at the parameter value; this pattern emerges under conditions where interaction effects are present in multiple, but not all, traits. It results from randomly assigning interaction effects to a subset of traits, provided that the pairwise correlation among the traits are distinct. While the Multivariate Levene’s test does not exhibit this behavior (since it only considers the variance of the traits under study), we find that SCAMPI is still more powerful in these situations. We also overlay the power curve of SCAMPI and Multivariate Levene’s test with varying sparsity for better visualization in the same plot in Supplemental Figure S5.

Figure 2. UKBB-inspired power simulation of SCAMPI for four traits.

Power of SCAMPI at $\alpha =6.25\times {10}^{-\mathbf{8}}$ for four traits at a sample size of 20,000 with MAF=0.05 and $\gamma =0.05$. The correlation among the four traits is inspired by correlation among lipid traits considered in our applied UKBB analysis. Yellow solid line represents power of SCAMPI, while dashed green line denotes power of the benchmark Multivariate Levene’s test. Sub-figures (a) – (d) examines power when interaction effects exist for one trait, two traits, three traits and four traits, respectively. We analyzed 10,000 replicates under each model.

In addition to the power simulations inspired by the UKBB, Supplemental Figure S6 provides power results for SCAMPI and multivariate Levene’s test under a broader range of models that vary the number of traits considered, the sparsity of the interaction effect, the correlation among traits, and the main effect of the variable interacting with genotype. Overall, we find the power of SCAMPI increases with a decrease in the sparsity of the interaction effect, a decrease in the trait correlation, and an increase in the effect size of the interaction variable. Assuming these three inputs are fixed, we find that the power of SCAMPI increases as the number of traits modeled increases. Regarding the power comparisons between SCAMPI and the Multivariate Levene’s test under this broader range of models, Supplemental Figure S6 also reaffirms the trends observed in our UKBB-inspired power simulations. Across the spectrum of scenarios tested, SCAMPI consistently exhibited superior performance when compared to the Multivariate Levene’s test, largely because the former method accounts for correlation among traits that the latter method ignores.

Application to UKBB:

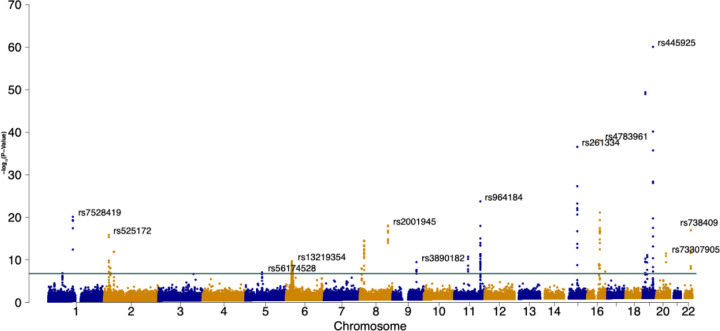
Figure 3 provides the Manhattan plot of SCAMPI results for detecting interaction effects on four lipid-related traits. SCAMPI identified 210 SNPs across 68 genes and intergenic regions at a study-wide significance level ($\alpha =1.67\times {10}^{-7}$, i.e., multiple comparison correction for 300,000 SNPs). Table 2 highlights the SNPs with the smallest SCAMPI p-value on each chromosome from the 210 SNPs. A comprehensive list of the 210 SNPs is available in the Supplemental Table S1. The Q-Q plot for SCAMPI (Supplemental Figure S7) shows no evidence of inflation. SCAMPI is an omnibus test that, by aggregating p-values (outputs of Step 3 in Figure 1) from association tests of trait correlation, pinpoints the specific traits that influence the overall signal. Thus, for every lead SNP in Table 2, we examined the p-values linked to each trait variance and cross-trait correlation at a genome-wide significance threshold of 1.67 × 10⁷. Significant variance and correlation terms among traits are noted in the “Significant Variance/Correlation Components” column of the Table. For example, SNP rs7528419 on CELSR2 is significantly associated with the correlation of triglycerides and LDL, as well as the variance of LDL alone, suggesting the SNP may have an interaction effect with other genetic or environmental factors on these two specific traits that merit further investigation.

Figure 3. Genome-wide results on lipid traits in UKBB using SCAMPI.

SCAMPI results for detecting latent interaction effects on high-density lipoprotein cholesterol (HDL-C), low-density lipoproteins cholesterol (LDL-C), triglycerides (TGs), and Body Mass Index (BMI). After SNP QC, 288,910 SNPs are included in the analysis with their MAF ≥ 0.05. SCAMPI successfully identified 210 SNPs from 68 genes and intergenic regions at the pre-specified study-wide significance $(\alpha =1.67\times {10}^{-7})$ represented by the green solid horizontal line. The SNP with the smallest SCAMPI p-value is rs445925 located on ApoC1.

Table 2. The lead SNPs, identified by SCAMPI within each chromosome, implies interaction effects for the four lipid traits in UKBB.

SCAMPI identified 12 lead SNPs from 12 chromosomes. The position of the SNPs is based on the Genome Reference Consortium Human Build 37 (GRCh37). Column “Gene” indicates the gene where the SNP locates. Column “SCAMPI P-value” shows the SCAMPI p-value. Column “Significant Variance/Correlation Components” indicates the variance or the correlation components of the four lipids that are significantly associated with the corresponding SNP at the pre-specified study-wide significance $(\alpha =1.67\times {10}^{-7})$. Column “PheWAS” lists the traits involved in the significant variance and correlation components as noted in column “Significant Variance/Correlation Components”, and these traits are also identified to be significant in PheWAS results, which is cross-referenced based on the GWAS Catalog or UK Biobank from the Open Targets Platform.

Chr	Pos	Alt	Ref	RS #	Gene	SCAMPI P-value	Significant Variance/Correlation Components	PheWAS
1	109817192	G	A	rs7528419	CELSR2	7.33E-21	Corr(TRIG, LDL), Var(LDL)	TRIG, LDL
2	21382976	G	T	rs525172	Intergenic	1.33E-16	Corr(TRIG, HDL), Var(LDL)	TRIG, LDL
5	74400516	C	G	rs56174528	ANKRD31	8.26E-08	Var(LDL)	LDL
6	27185664	C	T	rs13219354	PRSS16	1.83E-10	Var(BMI)	BMI
8	126477978	C	G	rs2001945	(TRIB1)	8.34E-19	Var(LDL)	LDL
9	107647655	A	G	rs3890182	ABCA1	3.34E-10	Var(HDL)	HDL
11	116648917	C	G	rs964184	ZPR1	1.73E-24	Corr(TRIG, LDL), Corr(TRIG, HDL), Corr(LDL, HDL), Corr(LDL, BMI), Var(Trig), Var(LDL)	TRIG, LDL, HDL
15	58726744	C	G	rs261334	LIPC; LIPC-AS1	2.63E-37	Corr(HDL, BMI), Var(TRIG)	TRIG, HDL
16	56994894	A	G	rs4783961	CETP	7.61E-39	Var(HDL)	HDL
19	45415640	A	G	rs445925	APOC1	8.10E-61	Corr(TRIG, LDL), Corr(TRIG, HDL), Corr(LDL, HDL), Corr(LDL, BMI), Var(Trig), Var(LDL), Var(HDL)	TRIG, LDL, HDL
20	44545773	C	A	rs73307905	(PLTP)	2.90E-12	Var(HDL)	HDL
22	44324727	G	C	rs738409	PNPLA3	1.07E-17	Corr(TRIG, BMI), Var(TRIG)	BMI

We also cross-referenced our findings in Table 2 with PheWAS results based on the GWAS Catalog or UK Biobank from the Open Targets Platform (v22.10), which confirmed many of our initial findings.⁶⁰ For instance, SNP rs738409 in PNPLA3 (which SCAMPI identified to be associated with the correlation of triglycerides and BMI as well as triglyceride variance) is reported by Open Targets Platform to be significantly linked with BMI. These results of the lead SNPs are cross listed in the “PheWAS” column of Table 2. Beyond the lead SNPs, Supplemental Table S2 includes the p-values for all correlation components related to the 210 SNPs.

Overall, SCAMPI identified several established lipid- and BMI-related genes that also demonstrate potential interaction effects. For example, APOC1, which contained the smallest SCAMPI p-value (p= 8.1 × 10⁻⁶¹ ), has pleiotropic effects on lipid metabolism, influencing various processes through its actions on lipoprotein receptors and enzyme activity modulation. By controlling the lipids plasma level, the influence of APOC1 spans several disease areas, including cardiovascular physiology, inflammation, immunity, sepsis, diabetes, cancer, viral infectivity, and cognition.⁶¹ Furthermore, CETP, which contained a SNP demonstrating a possible interaction effect with HDL (p=7.61 × 10⁻³⁹), may prevent plaque buildup and protect from atherosclerotic cardiovascular disease.⁶² There are also mixed results regarding the modifying effects of CETP on cardiovascular events.^63–65 Another top gene identified by SCAMPI was LIPC. Evidence suggests the LIPC promoter polymorphism (T-514C) affects the activity of Hepatic lipase (HL) and, in concert with other factors, modifies the therapeutic response in coronary artery disease (CAD) patients, with those having the CC genotype benefiting the most from intensive lipid-lowering treatments due to their predisposition to high HL activity and smaller, denser LDL particles.⁶⁶ SCAMPI also identified SNPs in CELSR2 with interaction effects predominantly on lipids. Research has shown CELSR2 deficiency impacts intracellular Ca²⁺ levels, possibly due to compromised endoplasmic reticulum (ER) function and unfolded protein response (UPR). The depletion of CELSR2 affects the expression of UPR sensors and the splicing of XBP-1, a critical transcription factor for hepatic lipogenesis, as demonstrated by reactions to various cellular stresses.⁶⁷

Interestingly, SCAMPI identified several SNPs (shown in Supplemental Table S3) exclusively through the correlation among traits (such that they were not detected by the multivariate Levene’s test that only considered variance terms). Noteworthy among these are rs2228603 (NCAN), rs58542926 (TM6SF2), and rs10415849 (GATAD2A). For each of these three SNPs, SCAMPI detected a significant effect exclusively via the correlation of BMI and triglycerides (each p <10⁻⁸); the SNP was not significantly associated with the variance of either trait and, as such, was not picked up by Levene’s test. Prior PheWAS studies show an association between these SNPs and triglycerides.^68–71 A similar pattern is observed for three SNPs in NECTIN2; each SNP is associated with the correlation of LDL and HDL (each p <10⁻⁸) but not with the variance of either trait. PheWAS analysis previously demonstrated the association of these SNPs with LDL. Beyond PheWAS, we also want to highlight that the SNPs identified by SCAMPI have been implicated in other studies of lipid traits and BMI. For example, numerous studies suggest that rs2228603 and rs58542926 are risk alleles associated with an increased likelihood of liver inflammation and fibrosis that is closely associated with weight change, indeed impacting BMI.^72–74 rs10415849 is significantly associated with $\alpha$-Tocopherol (one type of vitamin E), which interacts with biological sex to modify BMI.⁷⁵ The two SNPs rs519113 and rs6859, which are BCL3-PVRL2-TOMM40 SNPs, imply gene-gene and gene-environment interactions on dyslipidemia, which pathophysiology is characterized by reverse cholesterol transport in HDL metabolism.^{76; 77} Even though there are not many direct studies showing the association between rs3852860 and HDL, rs3852860 is a well-known predictor in Alzheimer’s disease, and Alzheimer’s disease progressed with HDL change.^78–80

SCAMPI Analysis in UKBB Adjusting for APOE:

In our applied analyses of lipid traits and BMI in the UKBB, the strongest signal detected by SCAMPI was located within APOC1, which is in close physical proximity to APOE, a gene with established relevance to the lipid traits we examined. Given APOE’s prominence as a biomarker in lipid panels,⁸¹ we determined whether the signals we observed at APOC1 were independent of those at APOE. To assess this, we repeated our SCAMPI analyses conditioning on the main and variance effects of APOE SNPs. Specifically, we selected all SNPs on APOE, located within 45,409,113 and 45,412,532 on chromosome 19, based on the Genome Reference Consortium Human Build 37 (GRCh37). Five SNPs (rs440446, rs769449, rs769450, rs429358, and rs7412) within this region passed the SNP level QC. We adjusted for the effects of the five APOE SNPs on the phenotypic outcomes’ mean and variance and then reapplied the SCAMPI methodology. We note that the sample size for our adjusted SCAMPI analysis dropped from 288,709 samples to 241,167 samples due to missing genotypes at the five APOE SNPs.

We provide the Manhattan and Q-Q plots for the APOE-adjusted SCAMPI analyses in Supplemental Figure S8. Overall, SCAMPI identified 150 SNPs (see Supplemental Table S4) that remained significant after adjusting for APOE genotypes. Our original top hits in APOC1 remain significant after adjusting for APOE genotypes (minimum p = 3.35 × 10⁻³⁸), which suggests an independent relationship between this gene and lipid traits. This underscores the potential for APOC1 to be a locus of interest in interaction analyses, with implications for lipid metabolism and associated phenotypes. We note that the initial UKBB analysis identified APOC1 as the top gene and LDLR as the second top gene on Chromosome 19. Upon adjusting for APOE, we note that the rankings of the two genes switch; the SNP with the lowest SCAMPI p-value is now rs55791371 (p = 4.11 × 10⁻⁴⁸), located in an intergenic region near LDLR.

Computational Performance:

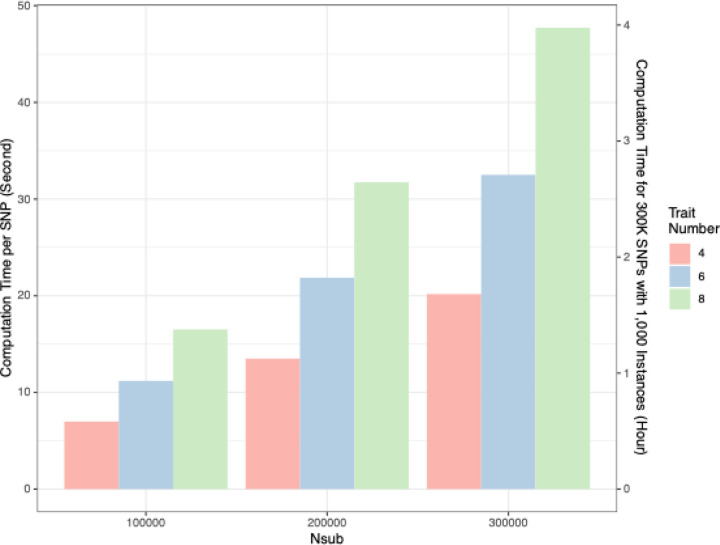
We benchmarked the computational performance of SCAMPI across varying sample sizes and numbers of traits for analyzing a single genotype using the High-Performance Computing (HPC) cluster hosted by Emory University Rollins School of Public Health (RSPH), whose infrastructure consists of 25 nodes: twenty-four equipped with 32 compute cores and 192GB of RAM, and one outlier with 1.5TB of RAM. We provide average computational run times per genotype in Figure 4. For instance, in our applied analysis of UKB data, SCAMPI processed a single genotype in an average of 20.17 seconds for four lipid-related traits with 300,000 participants. In general, computational run time of SCAMPI increased linearly with sample size and exhibited quadratic growth with the number of traits. While using SCAMPI on the RSPH HPC, we distribute the computational workload into one job array with 1,000 simultaneous job instances (1,000 job instances are the maximum allowance per job array on RSPH cluster), which effectively partitions the analysis of 300,000 SNPs into 1000 instances of 300 SNPs each. Figure 4 also depicts the number of hours required to complete analyses under various sample sizes and trait quantities by assigning 1,000 job instances on RSPH HPC. Notably, our computational configuration can complete the UKB analysis in approximately 1.68 hours. The figure also shows that processing times grow only modestly with the expansion of the dataset; for instance, a dataset featuring 8 traits and 300,000 samples is estimated to take about 3.98 hours, underscoring SCAMPI’s effectiveness for large-scale genetic analyses. Moreover, for the users who are interested in applying SCAMPI to analyze the UKB imputed dataset of over 90 million SNPs, which has approximately 6,000,000 SNPs after QC using the same QC procedure we have discussed in the previous session,⁴⁹ supplemental Figure S9 depicts the number of hours required to complete analyses of 6,000,000 SNPs under various sample sizes and trait quantities by assigning 1,000 job instances on RSPH HPC. Notably, our computational workload configuration can complete the UKBB analysis in approximately 33.62 hours for 6,000,000 SNPs.

Figure 4. Computational performance of SCAMPI.

Computational run time of SCAMPI for different sample sizes and number of traits using High-Performance Computing (HPC) cluster hosted by Emory University Rollins School of Public Health (RSPH). Computational run time is based on average of 1,000 simulations for different scenarios with varying trait number and sample size. The first y-axis in Figure 4 displays the time in seconds to complete SCAMPI for one SNP at different configurations. The second y-axis shows the hours required to complete analyses assuming 1,000 job instances on a high-performance cluster.

It should be noted that optimizing the HPC system with a more powerful processing configuration could significantly decrease computational time. Enhancements such as increasing CPU count and expanding storage and memory would contribute to this efficiency. Our evaluation of SCAMPI’s computational performance on a single genotype, across various sample sizes and trait numbers, also utilized a MacBook Pro with an Apple M1 chip. This analysis, detailed in Supplemental Figure S10 (a)-(b), mirrors the one in Figure 4 and Figure S9, where SCAMPI processed a single SNP for four lipid-related traits among 300,000 participants in an average of 8.65 seconds. An HPC system powered with the M1 chip could presumably and feasibly complete our UKBB analysis, involving 300,000 samples and 4 traits, in just about 0.72 hours. Moreover, it will take 14.41 hours to analyze 6,000,000 SNPs.

Discussion

The observation that narrow-sense heritability estimates of complex traits are often considerably larger when estimated from close relatives than distant relatives points to a potential role of variants with interactive effects on such traits. In this work, we develop our method SCAMPI to help screen for such variants that can then be prioritized for subsequent interaction analyses using standard tools. By studying correlation patterns among multiple traits, we showed using simulated data that SCAMPI has improved power relative to univariate variance-based screening procedures. Like variance-based procedures, SCAMPI does not require the specification of the factor that interacts with the variant to influence the traits under study. This means that users do not need prior knowledge of potential interacting factors, which can often be overlooked, unavailable, or difficult to collect. Furthermore, while SCAMPI produces an omnibus test to assess whether a SNP has an interactive effect on at least one of the traits under study, the method allows a user to identify the specific traits that are driving the signal by inspection of the individual cross-product p-values that are aggregated to form the omnibus test. The method, implemented in R code, is scalable to biobank-scale data and can handle many phenotypes.

While we developed SCAMPI with the intent of identifying variants harboring interaction effects with other genetic variants or environments, the method generally detects any variants with non-additive effects, which can also include dominance effects or parent-of-origin effects. To help delineate dominance effects from potential gene-gene or gene-environment effects, one can rerun SCAMPI regressing out the dominance effect of the variant in the DGLM model prior to analysis and observing whether the original interaction signal remains. For parent-of-origin testing, one can recode the SCAMPI regression framework to assess whether the trait correlation among heterozygotes is significantly different from the two homozygote categories.⁸² We note that the appearance of a variant with a possible interaction effect can also arise if the variant is in linkage disequilibrium (LD) with a nearby variant that has a marginal effect on the traits under study.³² In this situation, we suggest identifying such variants with marginal effects in LD with the test variant prior to analysis and regressing the effects of such variants out of the DGLM mean model prior to analysis using SCAMPI.

SCAMPI makes a few modeling assumptions that warrant further discussion. By implementing a DGLM model that assumes a Gaussian distribution to standardize traits, the SCAMPI framework inherently assumes the trait values under study follow a multivariate normal distribution. To meet this assumption in the main analysis, we transform the traits to normality using a non-parametric rank-based method, the Inverse Normal Transformation (INT), prior to SCAMPI analysis. We also explored whether transforming the traits before residualizing on the main effects of genotype and confounders (which we refer to as Direct INT or D-INT) led to different inference from transforming after residualizing (which we refer to as Indirect INT or I-INT) ⁵³ and found no marked difference in results (see Tables S5-S7). Rather than conducting a rank-based inverse normal transformation, we could also explore trait standardization on the original scale using a different form of a DGLM that assumes the trait outcome follows a gamma distribution. An additional SCAMPI assumption is that the sample size is large enough and the minor allele frequency of the tested variant common enough to enable p-value derivation of the cross-product regression test using asymptotic theory. For SCAMPI analysis of less-common variants in modest sample sizes, we recommend deriving the p-values of the cross-product regression tests using resampling procedures (which randomly shuffle genotypes across subjects) rather than relying on asymptotic theory to ensure valid inference.

Our SCAMPI framework complements a recent kernel-based method Latent Interaction Testing (LIT) for interaction testing that used kernel distance covariance techniques to test whether similarity of sample trait correlation patterns correlate with genotype similarity at a test SNP.³⁸ SCAMPI has practical features that LIT lacks, including the ability to directly assess which phenotypes among those modeled demonstrate interaction effects (as illustrated in Table 2 and Supplemental Table S3). Additionally, because SCAMPI is based on aggregating results across multiple cross-trait regression tests, it can handle missing data more efficiently than LIT (which requires complete information on all traits for inference). To illustrate, suppose we have a sample where N subjects possess information on two phenotypes while only half of these subjects further possess additional information on a third phenotype. For joint analysis of all 3 phenotypes, LIT only considers the N/2 subjects with complete trait data for inference. SCAMPI, on the other hand, can incorporate the remaining N/2 subjects that have only information on phenotypes 1 and 2 within its cross-trait statistic. The flexible regression framework that forms the backbone of SCAMPI also enables extensions to perform interaction screening for a variety of other study designs used in genetic projects, including longitudinal and family-based designs. Moreover, SCAMPI can be extended to meta-analysis settings where individual-level data cannot be shared across studies. We will explore these SCAMPI extensions in future work.

SCAMPI R Package is available for installation on GitHub: https://github.com/epstein-software/SCAMPI

Funding Statement

This work was supported by NIH grants R01 AG071170 (AJB, SB, DJC, MPE) and R01 AG075827 (TSW and APW).