Clinical translation of noninvasive intracranial pressure sensing with diffuse correlation spectroscopy

Abstract

OBJECTIVE

Intracranial pressure (ICP) is an important therapeutic target in many critical neuropathologies. The current tools for ICP measurements are invasive; hence, these are only selectively applied in critical cases where the benefits surpass the risks. To address the need for low-risk ICP monitoring, the authors developed a noninvasive alternative.

METHODS

The authors recently demonstrated noninvasive quantification of ICP in an animal model by using morphological analysis of microvascular cerebral blood flow (CBF) measured with diffuse correlation spectroscopy (DCS). The current prospective observational study expanded on this preclinical study by translating the method to pediatric patients. Here, the CBF features, along with mean arterial pressure (MAP) and heart rate (HR) data, were used to build a random decision forest, machine learning model for estimation of ICP; the results of this model were compared with those of invasive monitoring.

RESULTS

Fifteen patients (mean age ± SD [range] 9.8 ± 5.1 [0.3–17.5] years; median age [interquartile range] 11 [7.4] years; 10 males and 5 females) who underwent invasive neuromonitoring for any purpose were enrolled. Estimated ICP (ICP_est) very closely matched invasive ICP (ICP_inv), with a root mean square error (RMSE) of 1.01 mm Hg and 95% limit of agreement of ≤ 1.99 mm Hg for ICP_inv 0.01–41.25 mm Hg. When the ICP range (ICP_inv 0.01–29.05 mm Hg) was narrowed on the basis of the sample population, both RMSE and limit of agreement improved to 0.81 mm Hg and ≤ 1.6 mm Hg, respectively. In addition, 0.3% of the test samples for ICP_inv ≤ 20 mm Hg and 5.4% of the test samples for ICP_inv > 20 mm Hg had a limit of agreement > 5 mm Hg, which may be considered the acceptable limit of agreement for clinical validity of ICP sensing. For the narrower case, 0.1% of test samples for ICP_inv ≤ 20 mm Hg and 1.1% of the test samples for ICP_inv > 20 mm Hg had a limit of agreement > 5 mm Hg. Although the CBF features were crucial, the best prediction accuracy was achieved when these features were combined with MAP and HR data. Lastly, preliminary leave-one-out analysis showed model accuracy with an RMSE of 6 mm Hg and limit of agreement of ≤ 7 mm Hg.

CONCLUSIONS

The authors have shown that DCS may enable ICP monitoring with additional clinical validation. The lower risk of such monitoring would allow ICP to be estimated for a wide spectrum of indications, thereby both reducing the use of invasive monitors and increasing the types of patients who may benefit from ICP-directed therapies.

Intracranial pressure (ICP) is defined as the pressure within the craniospinal compartment, a closed system that comprises a fixed total volume of neural tissue, cerebral blood, and cerebrospinal fluid (CSF).¹ Within the rigid skull, any increase in one volume compartment needs to be matched by an equal decrease in another or ICP will rise, as illustrated by the Monro-Kellie doctrine.^2,3 Although the CSF and the blood compartments provide some buffering of increasing volume, once the compensatory capacity is exhausted, further increases in volume lead to a rise in ICP, as routinely observed in patients with many neuropathologies.^2,4–7 Thus, ICP is an important biomarker in the care of patients with these critical diseases.^8–13

The techniques currently used in the clinic for ICP measurements are invasive, requiring pressure transducers to be placed into the parenchyma⁸ or the ventricular system.¹⁴ Due to the invasive nature of these procedures, there are associated risks that include infection and hemorrhagic complications.¹⁵ Hence, ICP monitoring is typically only recommended in critical cases where the benefits exceed the procedural risks.¹⁶ There is a need for a noninvasive alternative that minimizes the risk of complications and at the same time allows accurate ICP monitoring for a broader set of indications.

Over the past years, a variety of noninvasive approaches have been proposed for ICP measurement, including transcranial Doppler (TCD) ultrasonography and several diffuse optical techniques.^17–23 Although TCD is considered promising and is being used in some regions of the world, factors such as operator dependence, motion sensitivity, and lack of ease for long-term bedside measurements limit its widespread clinical applicability.^24,25 The measurement of optic nerve sheath diameter (ONSD), which increases with ICP, with standard intracranial imaging or more recently with ultrasound have also shown the promise of clinical utility.^26,27 However, ONSD measurement is limited in that it is susceptible to inaccuracy due to differences in baseline ONSD between individuals, can only delineate between normal and elevated ICP, does not provide continuous monitoring, and presents additional shortcomings such as patient discomfort.^26,27

In an attempt to derive absolute ICP values noninvasively, our prior work utilizing diffuse correlation spectroscopy (DCS) estimated ICP with an accuracy of < 4 mm Hg in a nonhuman primate model.²⁸ DCS is an emerging diffuse optical technique that measures microvascular cerebral blood flow (CBF) noninvasively and continuously.^29,30 DCS can resolve the cardiac pulsatility in CBF,³¹ and we have previously shown that the shape of the CBF cardiac pulse waveforms changes with baseline ICP; this association was previously explored and tested with TCD.^32,33 Because DCS directly measures CBF instead of blood flow velocity, and also because the small cortical vessels probed with DCS are more susceptible to transmural pressure changes than the large vessels probed with TCD, DCS may be a superior option for noninvasive ICP measurement.³⁴

This work specifically expanded on our preclinical study by translating the method to pediatric patients. First, we provide details on strategic and technical optimizations implemented in this work, including DCS data processing and machine learning tools. Then, we present data from 15 pediatric intensive care unit (PICU) patients and show estimation of ICP from the pulse morphological features of CBF with and without other physiological signals, e.g., mean arterial pressure (MAP) and heart rate (HR), by using a random forest regressor model.

Methods

To briefly summarize the methodology, pediatric patients were evaluated with DCS to extract CBF data. Next, morphological features were extracted from the CBF pulses, in addition to MAP and HR data, by using signal processing to train a machine learning model. Lastly, ICP estimated by the model was validated against invasively measured ICP.

Clinical Pediatric Population

The study was conducted at the PICU of the University of Pittsburgh Medical Center Children’s Hospital of Pittsburgh, Pittsburgh, Pennsylvania. The study protocol was approved by the University of Pittsburgh and Carnegie Mellon University Institutional Review Board.

Children between 1 month and under 18 years of age who underwent placement of an external ventricular drain (EVD) or a parenchymal pressure monitor for ICP monitoring as a part of their routine clinical care were eligible for enrollment. Written informed consent was provided by the legal guardian. Noninvasive monitoring was not performed in settings where it may have impeded patient care. For this study, a total of 18 patients were recorded and data from 3 patients were excluded. Two of these patients had a low signal-to-noise ratio (SNR), and 1 had a technical error resulting in incorrect synching of invasive and noninvasive data.

The mean ± SD (range) age of the population was 9.8 ± 5.1 (0.3–17.5) years, median age (interquartile range) was 11 (7.4) years, and 10 males and 5 females were included (Table 1). Optical measurement was taken on the left or right forehead, and the ICP sensor was surgically inserted at Kocher’s, Keen’s, and Frasier’s points as dictated by clinical necessity (Fig. 1). Each DCS measurement session spanned approximately 1 hour, with repeated measurements not exceeding a total of 6 hours/day for 7 consecutive days. During measurement, the patient was either supine or seated, as well as sedated or awake, depending on the clinical condition. Of 15 patients, 1 had a parenchymal pressure monitor for continuous ICP recording (Table 1). In patients with an EVD, a 3-way stopcock valve was turned to switch from draining CSF to recording ICP inside the closed catheter. Synched noninvasive recording was performed during the periods of time in which the EVD was clamped for clinical purposes.

TABLE 1.

Overview of the pediatric patient population, including measurement details

Patient No.	Age (yrs)/Sex	Medical Diagnosis	Sensor Type	Location ICP	Location DCS	Value*
1	11/M	Tumor	EVD	Lt	Not documented	1 (1.9, 287)
2	8.1/F	Possible hydrocephalus, unresponsiveness	EVD	Rt	Lt	2 (6.7, 4311)
3	4/M	TBI	ICP monitor	Rt	Lt	1 (3, 1254)
4	15/M	TBI	EVD	Rt	Lt	1 (2.6, 863)
5	14.4/F	Tumor	EVD	Rt	Rt	1 (0.17, 60)
6	13/F	Tumor	EVD	Rt	Rt	3 (1.83, 556)
7	14.3/M	Abscess/meningitis	EVD	Lt	Rt	2 (1.6, 702)
8	0.3/M	Shunt infection	EVD	Rt	Rt	2 (7.5, 3023)
9	12.1/M	TBI	EVD	Rt	Lt	2 (8.1, 5089)
10	5/M	Intraventricular hemorrhage	EVD	Lt	Rt	1 (0.7, 188)
11	13.2/F	Obstructive hydrocephalus	EVD	Lt	Not documented	1 (1.9, 803)
12	17.5/M	Abscess/meningitis	EVD	Rt	Not documented	1 (0.8, 329)
13	7.7/M	Abscess/meningitis	EVD	Rt	Lt	2 (0.2, 79)
14	2.3/M	Shunt infection	EVD	Rt	Lt/Rt	3 (1.8, 1264)
15	9/F	Tumor	EVD	Rt	Rt	1 (0.6, 211)

Location DCS = location of DCS probe on the forehead; Location ICP = location of invasive ICP sensor in the frontal lobe; TBI = traumatic brain injury.

^*Shown as days measured (hours analyzed, number of pulse averages).

FIG. 1.

Details of DCS instrumentation and measurement setup. A–B: Probe secured on the left forehead with the adjustable headband. C: Probe placement on the right forehead of a patient, where the ICP monitor is surgically inserted in the left frontal lobe. D: Hospital cart with instruments placed. E: Custom-made DCS device. F: Custom-made DCS optical probe. The green regions refer to the DCS source and detector.

Signal Acquisition

DCS provides a measure of CBF in the microvasculature.^29,35 A custom-built DCS device, which is not approved by the US Food and Drug Administration (FDA), was used (Fig. 1).²⁸ DCS is similar to near-infrared spectroscopy, and some devices used for clinical purposes have been FDA approved and are often considered to have minimum risk. The device contained an auxiliary port to receive time markers used to time synchronize CBF with the signals obtained from the patient monitor. In addition to invasive ICP (ICP_inv), electrocardiography (EKG) was performed and MAP was measured with the hospital bedside monitor (General Electric Solar 8000M, GE Healthcare). Although ICP and EKG data were measured continuously, MAP was measured sporadically, approximately every 30 minutes via a blood pressure cuff, or continuously measured with an arterial line. The optical probe was secured on the forehead with sports tape or a padded adjustable headband (Fig. 1A–B). More details on the DCS methodology can be found in the Supplemental Materials and Methods, Section 1.

Signal Processing

Signal processing was performed using MATLAB R2019b (The MathWorks Inc.). A total of 18 patients were recorded; however, 3 were excluded owing to poor SNRs or errors in patient monitoring data. Among the 15 included patients, the DCS sessions with poor SNRs (SNR < 4.8, empirically determined) were also removed. Movement, routine ICU procedures, room light, poor tissue contact, and poor probe placement were some of the probable reasons behind a poor SNR.

For each DCS measurement session, the CBF time series was preprocessed to remove noise such as respiration and time aligned with the signals from the patient monitor. Figure 2A shows example time traces of CBF and ICP from a representative patient, where the dashed vertical lines represent the R-peaks within the QRS complex of the EKG signal. The next step in data processing was to segment each individual CBF pulse from its time series, and an average of 100 consecutive pulses (150 for patients with an average SNR < 7) generated an average CBF cardiac pulse. The process was repeated, after the average window was shifted by 10% of the window length, to generate a series of average CBF pulses from the CBF time trace (Fig. 2B).

FIG. 2.

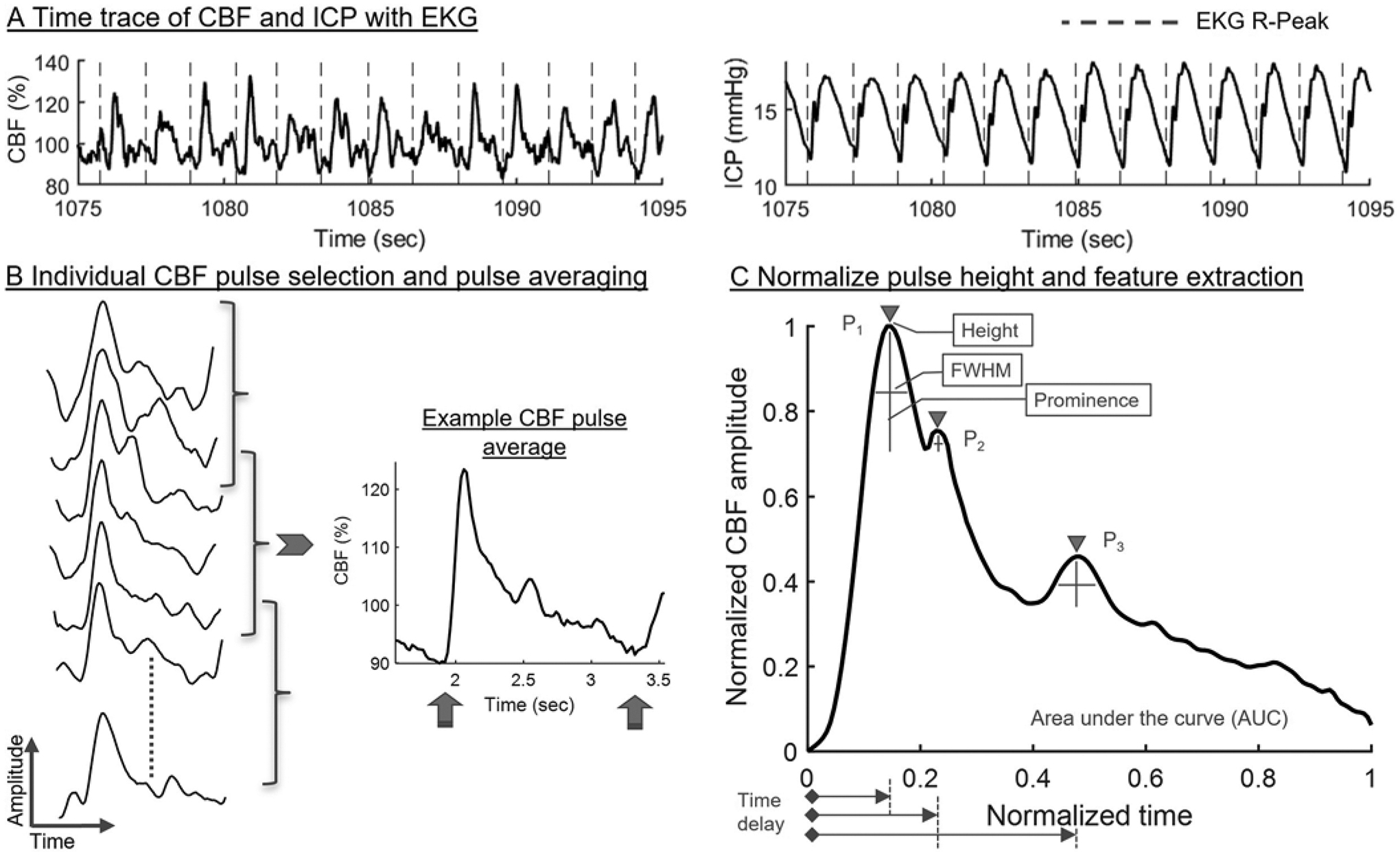
A: Example time traces of CBF and ICP from a representative patient, where the dashed vertical lines represent the R-peaks within the QRS complex of the EKG signal. B: Segmented CBF pulses on the left side, and an example CBF pulse average on the right side. The upward arrows indicate the two diastolic points utilized for pulse normalization in time. C: CBF pulse average normalized in amplitude and in time. The features extracted from the pulse average are described in the Regression Learner section of the Methods. FWHM = full width at half maximum.

Following that, the CBF pulse averages were normalized between 0 and 1 in time (x-axis) and amplitude (y-axis) (Fig. 2C) to achieve comparability across patients. At this step, ICP_inv and MAP were averaged over the time span of CBF pulse averages to obtain average values. Additionally, the difference between the R-peaks within the QRS complex of the EKG signal was used to generate an HR value. Thus, at the end of signal processing, each CBF pulse average waveform was associated with a set of ICP_inv, MAP, and HR values. The last column in Table 1 shows the number of days each patient was evaluated, the number of hours of the CBF time series that were analyzed, and the number of CBF pulse averages finally used for feature extraction. Altogether, a total of 19,019 pulse averages were extracted from 15 patients with an ICP_inv range of 0.01–41.25 mm Hg.

Next, the morphological features of 3 different waveform peaks (P_1–3) were extracted from the CBF pulse average (Fig. 2C). To describe the individual peaks, peak height (pk), prominence (p), full width at half maximum (w), and time point of the peak relative to the prior diastolic minimum (pos) were extracted. Area under the curve (AUC) was also acquired. Features were further obtained by quantifying the differences in pk, p, w, and pos between P₁ and P₂, as well as between P₂ and P₃. This resulted in a set of 21 features from each CBF pulse average for use in supervised machine learning. See the Supplemental Materials and Methods, Section 2, for further details on determining SNR, noise filtration, pulse averaging, normalization, and feature extraction.

Regression Learner

In this step, the entire data set of CBF pulses was randomly split, with 80% of the data used for training the model and 20% was held out from the training process for testing. The data points were randomly sampled in time. The model was optimized compared with our previous work in animals (Supplemental Materials and Methods, Section 3).²⁸

Figure 3 describes the main aspects of the training and testing steps. The CBF features, MAP, HR, and ICP_inv from the training set (total 15,215) were used to build and train a random decision forest with a bagged ensemble of 200 individual decision tree regressors. Each tree estimator was randomly assigned 60% of the training samples and 80% of the features (total 23) to reduce variance and limit overfitting.³⁶ After training, the CBF features along with the corresponding MAP and HR data from the testing set were fed into each tree regressor to extract an estimated ICP. Lastly, the outputs of the 200 trees were averaged to obtain the estimated ICP value (ICP_est). More details on the regression learner can be found in the Supplemental Materials and Methods, Section 3.

FIG. 3.

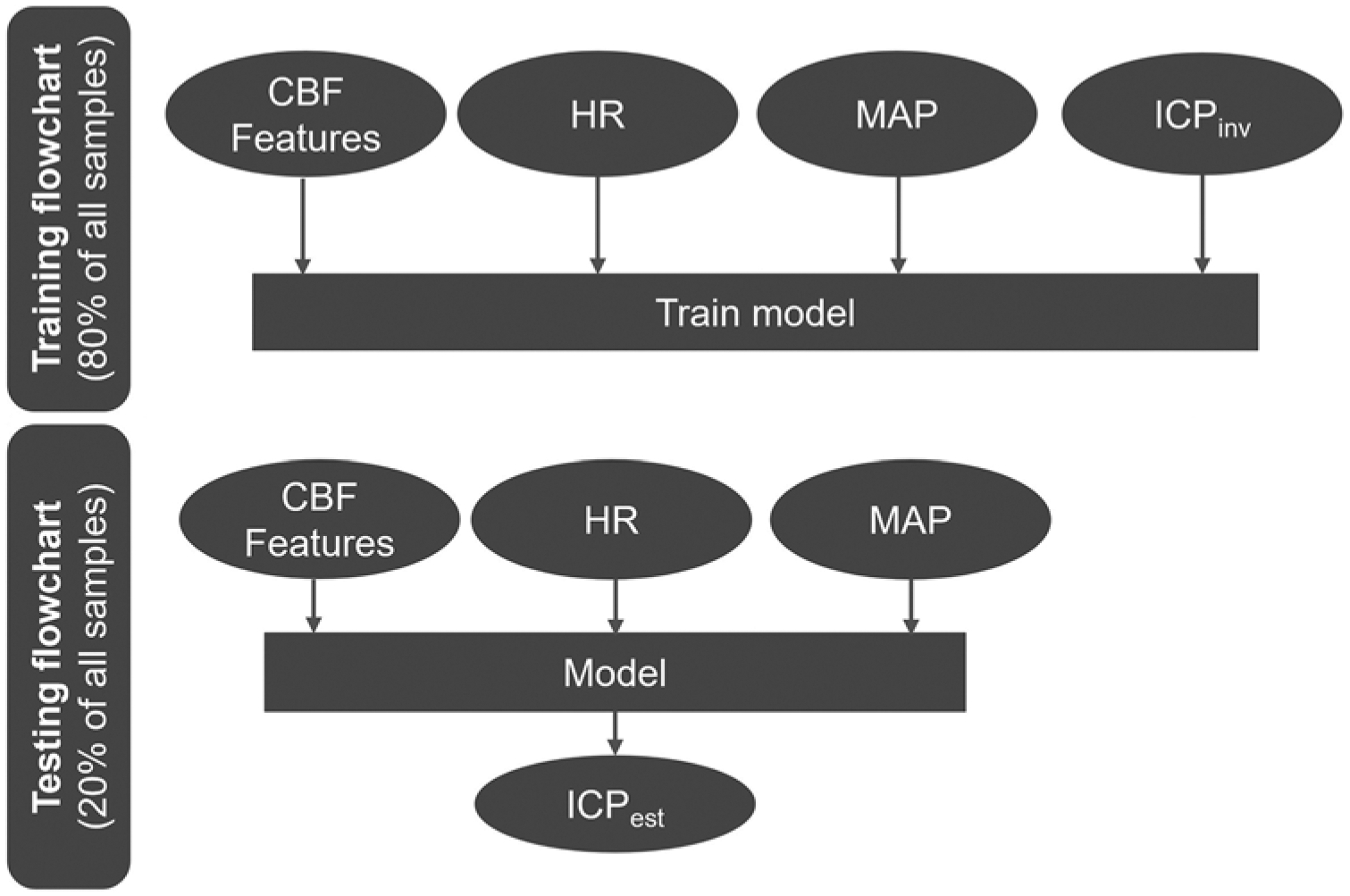
Algorithm flowchart of the machine learning model. A train/test split ratio of 80%/20% was used. Upper: The CBF morphological features and MAP, HR, and ICP_inv values were used to train a random decision forest. Lower: During testing, the CBF features and MAP and HR values were fed into the model as input to obtain an estimated ICP.

Statistical Analysis

Statistical analyses were conducted using MATLAB R2019b (The MathWorks Inc.). For the statistical analyses, results from only the testing set were reported. The goodness of fit between ICP_inv and ICP_est was calculated using the coefficient of determination metric (R²) and root mean squared error (RMSE). Bland-Altman analysis was also conducted to determine the mean bias and 95% limit of agreement between the two methods. A discrepancy of 5 mm Hg between invasive and noninvasive monitoring was defined as the maximum difference that would justify use of DCS as, at minimum, a clinically useful screening adjunct.

Results

Random Decision Forest Regression Learner

The withheld testing data demonstrated that ICP_est very closely matched ICP_inv, with an R² value of 0.97 and an RMSE error of 1.01 mm Hg (Fig. 4A); however, the sample population was not consistent across ICP_inv values, as shown in the inset histogram. Noticeably, the size of the sample population was reduced drastically at high ICP_inv values, which would subsequently reduce the sample size of the training set at these values. Because a small training set population is known to affect model performance,³⁷ a new analysis was conducted with only ICP_inv, for which the sample population matched or surpassed a certain threshold (as shown with the horizontal dotted line in the histogram shown Fig. 4A). This threshold represented 5% of the largest sample population. This masking based on the sample population narrowed down ICP_inv to the range of 0.01–29.05 mm Hg. By using this narrower ICP range and by retraining the algorithm (Fig. 4B), we determined that the narrower ICP_inv range improved both the R² value and RMSE error to 0.98 and 0.81 mm Hg, respectively. The inset image shows a histogram of the sample population for the narrower ICP_inv.

FIG. 4.

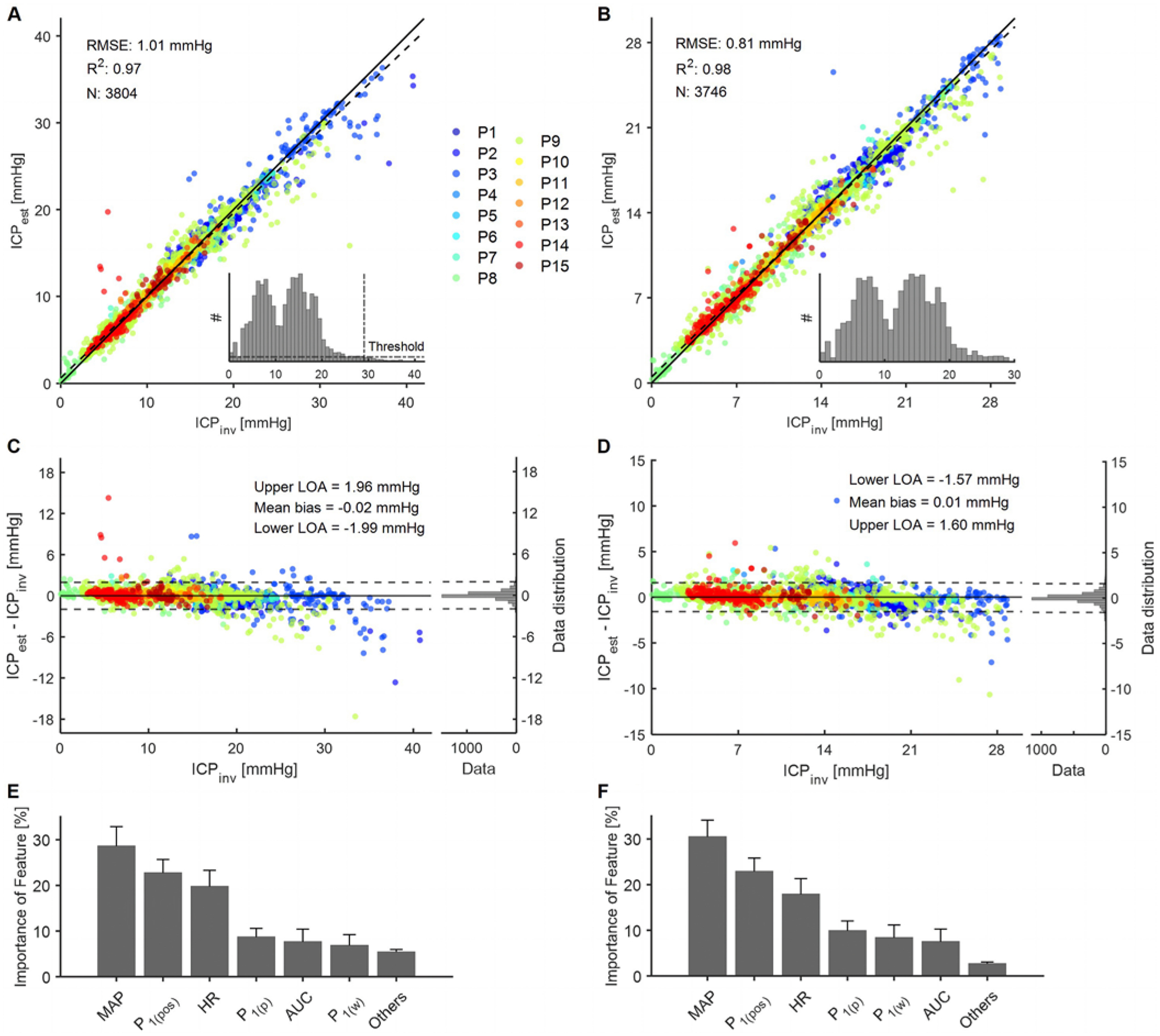
Results of the regression forest machine learning model for the entire range of ICP_inv (0.01–41.25 mm Hg) and a narrower range of ICP_inv (0.01–29.05 mm Hg). The data points are color coded according to patient identification. A–B: Performance of the regression forest. The solid line shows the ideal fit between ICP_inv and ICP_est, whereas the dashed line shows the linear fit. R² represents goodness of fit, and N represents the sample size of the testing set. The inset images show histograms of ICP_inv of the entire sample population before splitting into the train/test sets. A bin width of 0.83 mm Hg was used in the histogram. C–D: The Bland-Altman plot shows the difference between the two methods with respect to ICP_inv. The solid line represents mean bias and the dashed lines represent the upper and lower 95% LOA. The histogram plots on the right side of each panel display the distributions of the differences. E–F: Distribution of features used in the regression forest model as a percentage of all chosen features of all decision criteria generated. The standard deviation across 200 individual trees is shown as error bars. Others refers to all other features apart from the ones shown in the plot. For nomenclature, please see the Signal Processing section of the Methods and Fig. 2C. LOA = limit of agreement.

Further evidence of goodness of fit for both ICP_inv ranges was provided by the Bland-Altman plots shown in Fig. 4C and D, where the difference between ICP_est and ICP_inv was plotted against ICP_inv. Negligible bias was observed for both the entire and narrower ICP_inv ranges. The narrower ICP_inv range also slightly improved the upper and lower limits of the agreement values and demonstrated that 95% of the testing data points were within ± 1.6 mm Hg of the corresponding ICP_inv. Because 5 mm Hg was considered the acceptable limit of agreement for clinical validity of ICP sensing, we explored what percentage of the testing samples, less than and greater than 20 mm Hg, was outside the limit of agreement of 5 mm Hg. To summarize, for the entire ICP range, 0.3% of the test samples for ICP_inv ≤ 20 mm Hg and 5.4% of the test samples for ICP_inv > 20 mm Hg were outside the limit of agreement of 5 mm Hg. For an ICP range of 0.01–29.05 mm Hg, only 0.1% of data points for ICP_inv ≤ 20 mm Hg and 1.1% of data points for ICP_inv > 20 mm Hg were outside the limit of agreement of 5 mm Hg.

To further delve into the model, the importance of the features was analyzed for both ICP_inv ranges (Fig. 4E and F). The order of features in terms of importance was consistent between the entire and narrower ICP_inv ranges. MAP was the most widely used, as observed in our previous work.²⁸ HR was also promising and turned out to be the third strongest predictor. Among the CBF features, the features related to the P₁ peak were found to be the most useful compared with the other two peaks. For example, P1_(pos) was the second strongest feature and P_1(p) was the fourth strongest feature. P_1(w) and AUC were interchangeably the fifth and sixth best features.

Leave-one-out analysis was also conducted, during which data points from 1 patient were used in the testing set and data points from the other 14 patients were used in the training set. This analysis mimics how well the algorithm would work for a new patient who was not a part of the training set. The process was repeated for each patient. When averaged over all 15 patients, an RMSE of 6.1 mm Hg and limit of agreement ≤ 7.4 mm Hg was observed for the entire ICP range, and an RMSE of 6 mm Hg and limit of agreement ≤ 7 mm Hg were observed for the narrower ICP range.

Dependence of Learner Performance on Model Parameters

Because learner performance can depend on the model parameters, several model parameters were tested against learner outputs; the results are shown in Table 2. All analyses were conducted for the narrow ICP_inv range of 0.01–29.05 mm Hg. We investigated train/test split ratios of 80%/20%, 70%/30%, 60%/40%, and 50%/50%. The results showed that R² changed slightly; however, both RMSE and limit of agreement values increased by as much as approximately 32% because the training population size was reduced from 80% to 50% of the train/test ratio.

TABLE 2.

Dependence of learner performance on algorithm parameters

Analysis of Model Variables		Stationary Model Variables	Accuracy		Bland-Altman Analysis
			RMSE (mm Hg)	R2	Mean (mm Hg)	Upper LOA (mm Hg) Lower LOA (mm Hg)
Train/test split ratio	80%/20%	Random forest, CBF, MAP, & HR	0.81	0.98	0.01	1.6	−1.57
	70%/30%		0.86	0.98	0.03	1.71	−1.66
	60%/40%		0.98	0.97	−0.02	1.9	−1.93
	50%/50%		1.06	0.97	−0.0	2.07	−2.08
Regressor type	Random forest	80%/20% split, CBF, MAP, & HR	0.81	0.98	0.01	1.6	−1.57
	Bagging		0.94	0.97	0.01	1.85	−1.84
Feature performance	CBF, MAP, & HR	Random forest & 80%/20% split	0.81	0.98	0.01	1.6	−1.57
	CBF & MAP		1.03	0.97	−0.03	1.99	−2.05
	CBF & HR		1.77	0.91	0.02	3.49	−3.44
	CBF features only		2.38	0.82	−0.03	4.64	−4.69
	MAP & HR only		2.79	0.76	0.04	5.51	−5.43

LOA = limit of agreement.

Because our previous work in animals used a different type of decision forest classifier called the bagging regressor, we also compared the bagging and random forest regressors.³⁸ The parameters for the bagging regressor were kept as previously used,²⁸ except the number of trees was kept at 200 for an even comparison. To summarize, although R² showed only a slight improvement, the bagging regressor underperformed because it increased both the RMSE and limit of agreement values by approximately 17% (Table 2).

Lastly, features were tested to find the optimum feature set for the most accurate learner prediction. Because MAP and HR were among the top three important features in this analysis (Fig. 4E and F), either one or both features were excluded from the feature set to investigate how that could affect model performance. The results showed that truncating one or both features increased both RMSE and limit of agreement values by as much as approximately 200% compared with CBF, MAP, and HR (Table 2). However, when the same analysis was conducted with only MAP and HR as features (i.e., no CBF features), RMSE and the limit of agreement increased by approximately 246% compared with CBF, MAP, and HR. This confirmed that although MAP and HR were important features, the CBF features played a very important role in learner performance, and the best performance was achieved when MAP and HR were added to the model with CBF features.

Discussion

In this work, we have demonstrated the clinical translation of our previously developed, noninvasive DCS-based ICP estimation method to pediatric patients admitted to the PICU. We found that the waveform features in CBF measured in the cerebral microvasculature are influenced by ICP. These CBF features, along with HR and MAP data, were used to train a random forest regressor for mapping CBF onto ICP.²⁸ To summarize the results, strong similarity between estimates of ICP and the invasive measurements (R² = 0.97, RMSE = 1.01 mm Hg) were obtained with a limit of agreement ≤ 1.99 mm Hg. Model performance was improved for a narrower ICP_inv range of 0.01–29.05 mm Hg, with RMSE reduced to 0.81 mm Hg and the limit of agreement reduced to ≤ 1.6 mm Hg. For this ICP range, only 0.1% of data points for ICP_inv ≤ 20 mm Hg and 1.1% for ICP_inv > 20 mm Hg were found with the limit of agreement > 5 mm Hg. These results show the potential of DCS as a valid screening tool for ICP.

More accurate ICP extraction was possible when evaluating a narrower ICP_inv range of 0.01–29.05 mm Hg compared with the data set that included ICP > 30 mm Hg. The increase in estimation error likely stems from the lack of data at higher ICP and not the model inaccuracy. We believe that, with the addition of more data at higher ICP values, the model could be trained across a wider ICP range and thus improve overall model accuracy even at ICP > 30 mm Hg. Our results suggest that absolute ICP estimation based on noninvasive measurements of CBF cardiac waveforms is possible, with further enhanced performance with concurrent MAP and HR data. Although we used EKG signals to obtain HR, other means such as a wrist-worn wearable device should suffice.³⁹ The invasively measured ICP used as the reference/gold standard was certainly not free from measurement error. The combined mean (95% CI) difference between invasive ICP probes, reportedly 1.6 (1.3–1.9) mm Hg in the literature,⁴⁰ was comparable to the noninvasive limit of agreement values calculated in this study.

Machine learning approaches such as regression forests provide information about feature importance in terms of how often a feature was used for ICP splits at split nodes.²⁸ This information could be used to improve algorithm performance in the future by optimizing good features and rejecting bad ones. In this work, MAP and HR were among the topmost features, as both signals were strongly related to the cardiac cycle. Among the CBF features, P₁ peak was the most useful compared with the P₂ and P₃ features, which is consistent with our previous preclinical work. AUC was found to be the fifth or sixth best feature, which implies that changes in P₁ peak features (pos, p, and w) were more significant than the overall broadening of the CBF pulse in contributing to change in AUC. Most notably, in contrast to the preclinical results, none of the differences in peak features between P₁ and P₂, or between P₂ and P₃, were found to be useful.

Because MAP and HR turned out to be among the top three features, analyses were conducted to explore how the model performed without these features. Truncating MAP and HR data from the feature set increased both RMSE and limit of agreement values by approximately 200%, but using only these two features in the feature set affected the algorithm outcome even more by raising the percentage error to approximately 246% compared with that of the feature set that also included CBF. This indicated that although MAP and HR were valuable components to the model, the CBF features were crucial, thus offering the best prediction accuracy when combined. In the comparison of regressor types, the random forest regressor performed slightly better than the bagging regressor, and we assume this was a result of the additional subsampling of the features (80%) and samples (60%) assigned to each tree during training; this an important attribute of the random forest regressor known to curb overfitting.³⁶ The leave-one-out analysis showed an RMSE ≤ 6.1 mm Hg and a limit of agreement ≤ 7.4 mm Hg. Although this suggests that the model loses accuracy when validated against unknown data, we believe this is avoidable by increasing the number of patients and thus the training set population.³⁷ With additional refinement, a noninvasive model capable of consistently predicting a limit of agreement < 5 mm Hg will have clinically meaningful applications. Invasive monitors could be then applied in the setting of equipoise, such as a result of ≥ 20 mm Hg. In our current model, we used 100–150 consecutive pulses to estimate 1 ICP value, corresponding to a readout of 1–2 per minute. Although the data were downsampled by averaging multiple waveforms, a readout of every pulsation should be feasible when SNR is high, producing real-time or near real-time ICP estimation.

Depth of measurement inside the brain varied due to differences in patient age, scalp thickness, and head size.⁴¹ Although different brain volumes were measured between patients, SNR was not age dependent (data not shown). Our previous animal study was conducted directly on the skull to avoid the effect of the scalp on DCS measurements. Although the clinical measurements in this work were taken with the scalp in place, we did not see an effect on data quality or model performance. This implies that the implementation of this technology is feasible across a wide span of pediatric and adult patients.

Our work compares favorably to other noninvasive ICP monitors that use TCD, which have shown an overall accuracy of ± 12 mm Hg,²⁵ and acoustic signals propagating through the cranium within an accuracy of ≤ 7.38 mm Hg.⁴² In terms of methodology, a close similarity can be drawn to Fischer et al., who applied a neural network model with solely CBF time traces from DCS without using MAP or HR data.⁴³ Although the accuracy of ICP estimation was comparable to the results shown here, we believe the added benefit of our approach is the interpretability of the features found. Given that the same importance of peak features was found between our animal studies and human data, we believe that the presented model can be generalized to different diseases, ages, and patient populations.

The current study was limited to its demonstration of potential efficacy in pediatric populations, although older patients in the cohort may be physiologically comparable to some adult populations. To show generalization, the next steps will involve recruiting a larger cohort of patients with various ages and conditions. We anticipate several challenges in translation to an adult population, e.g., increased scalp thickness and vascular stiffness. The increase in central arterial stiffening due to aging may alter MAP.⁴⁴ However, we believe that the proposed method will remain highly accurate in the adult population because it performed well as MAP changed in children and adolescents.⁴⁵

With decreasing risk of harm to patients, the possibility of new applications for ICP measurement may arise for traditional pathologies such as hydrocephalus and shunt malfunction, but also for novel ones such as concussion, intraoperative monitoring, and Chiari malformation. It is our hope, with time, that ICP will transition to becoming the next commonly used vital sign for patients with neurological disease and allow for a greater understanding of normal and abnormal ICP across a wide spectrum of patients.

Conclusions

DCS-based sensing of ICP showed a high level of similarity with invasive measurements. CBF waveforms were used for ICP estimation, but inclusion of MAP and HR data improved accuracy. Our preliminary leave-one-out analysis showed that the algorithm could be applied to a new patient not included in the training set, but accuracy of prediction requires a larger data set, particularly at high ICP. Further work is needed to streamline and automate the entire process of DCS measurement and ICP estimation. We believe that our method made promising advancements in the translation of DCS-based ICP estimation to humans. The wide availability of noninvasive ICP measurement technology would minimize procedural risk and at the same time expand ICP monitoring to a wide array of clinical circumstances.

ABBREVIATIONS

AUC

area under the curve

CBF

cerebral blood flow

CSF

cerebrospinal fluid

DCS

diffuse correlation spectroscopy

EKG

electrocardiography

EVD

external ventricular drain

FDA

US Food and Drug Administration

HR

heart rate

ICP

intracranial pressure

ICP_est

estimated ICP

ICP_inv

invasive ICP

MAP

mean arterial pressure

ONSD

optic nerve sheath diameter

p

prominence

PICU

pediatric intensive care unit

pk

peak height

pos

time point of the peak relative to the prior diastolic minimum

P₁

waveform peak

RMSE

root mean square error

SNR

signal-to-noise ratio

TCD

transcranial Doppler

w

full width at half maximum