Monte Carlo sensitivity analysis for unmeasured confounding in dynamic treatment regimes

Abstract

Data-driven methods for personalizing treatment assignment have garnered much attention from clinicians and researchers. Dynamic treatment regimes formalize this through a sequence of decision rules that map individual patient characteristics to a recommended treatment. Observational studies are commonly used for estimating dynamic treatment regimes due to the potentially prohibitive costs of conducting sequential multiple assignment randomized trials. However, estimating a dynamic treatment regime from observational data can lead to bias in the estimated regime due to unmeasured confounding. Sensitivity analyses are useful for assessing how robust the conclusions of the study are to a potential unmeasured confounder. A Monte Carlo sensitivity analysis is a probabilistic approach that involves positing and sampling from distributions for the parameters governing the bias. We propose a method for performing a Monte Carlo sensitivity analysis of the bias due to unmeasured confounding in the estimation of dynamic treatment regimes. We demonstrate the performance of the proposed procedure with a simulation study and apply it to an observational study examining tailoring the use of antidepressant medication for reducing symptoms of depression using data from Kaiser Permanente Washington.

1 |. INTRODUCTION

Precision medicine focuses on data-driven methods for personalizing treatment assignment to improve health care. Dynamic treatment regimes (DTRs) operationalize clinical decision-making through a sequence of functions that map individual patient characteristics to a recommended treatment (Chakraborty and Moodie, 2013; Tsiatis et al., 2019). An optimal DTR is one that maximizes the mean of some desirable measure of clinical outcome when applied to select treatment for all patients in the population of interest (Murphy, 2003; Robins, 2004). Optimal DTRs have been estimated to improve care for many different medical conditions including HIV (Cain et al., 2010; van der Laan et al., 2005), bipolar disorder (Wu et al., 2015; Zhang et al., 2018), diabetes (Ertefaie and Strawderman, 2018; Luckett et al., 2018), and cancer (Murray et al., 2018; Thall et al., 2000).

Data for estimating an optimal DTR are ideally collected through the use of a sequential multiple assignment randomized trial (SMART) (Lavori and Dawson, 2000, 2004; Murphy, 2005). However, longitudinal observational studies are frequently used due to the availability of data collected from electronic health records (EHRs) and the potentially prohibitive cost of conducting an SMART. These analyses rely on assuming that there is no unmeasured confounding; this assumption is not verifiable from the observed data. Not adjusting for all of the confounding variables can result in a biased estimate of the optimal DTR.

Sensitivity analyses have been used as a way to assess how the estimated effect would change if there was an unmeasured confounder. There has been much work on conducting sensitivity analyses for unmeasured confounding when estimating average causal effects from observational data beginning with Cornfield et al. (1959), in which they studied whether the causal link found between smoking and lung cancer could be due to unmeasured confounding. A wide array of different approaches have been proposed since. Rosenbaum and Rubin (1983) proposed a method for examining how sensitive the conclusions of a study with a binary outcome are to a binary unmeasured confounder by assessing what odds ratios between the unmeasured confounder and each of the treatment and the outcome would cause the effect to be no longer significant. Lin et al. (1998) proposed positing a regression model for the outcome containing the effect of the unmeasured confounder and probability distributions for the unmeasured confounder in each treatment group. Under certain assumptions, this allows for simple expressions of the bias in the treatment effect that can then be used to calculate treatment effects for a wide range of different effect sizes of the unmeasured confounder on the outcome and exposure.

An alternative to formulaic approaches are probabilistic sensitivity analyses, which posit probability distributions for the bias parameters and average over the distributions to obtain bias-adjusted estimates. There are two different existing approaches to implementing a probabilistic sensitivity analysis, Bayesian sensitivity analysis, and Monte Carlo sensitivity analysis (McCandless and Gustafson, 2017). A Bayesian sensitivity analysis (McCandless et al., 2007) works by positing prior distributions for the bias parameters and uses Bayes theorem to generate a posterior distribution for the causal effect that accounts for the uncertainty due to the unmeasured confounder. In a Monte Carlo sensitivity analysis (Greenland, 2005; Phillips, 2003; Steenland and Greenland, 2004), we posit prior distributions for the bias parameters in the same way and then draw values from the prior distributions and calculate a bias-adjusted estimate for the parameter of interest for each Monte Carlo repetition. This allows for a straightforward implementation that corrects bias while incorporating uncertainty due to the unmeasured confounding within a frequentist framework.

There has been some work on estimating DTRs in the presence of unmeasured confounding. This has mainly focused on using instrumental variables to estimate an optimal DTR (Chen and Zhang, 2021; Cui and Tchetgen Tchetgen, 2021; Liao et al., 2021; Qiu et al., 2021). An instrumental variable is a pretreatment variable that is correlated with treatment, independent of all unmeasured confounders, and has no direct effect on the outcome of interest. In some applications, there is not an obvious choice for an instrumental variable based on domain knowledge and it is impossible to empirically check whether a variable satisfies the assumptions for being an instrumental variable (Hernan and Robins, 2006). Zhang et al. (2021) proposed a method for ranking individualized treatment rules when there is unmeasured confounding by creating a partial order under the framework proposed by Rosenbaum (1987). Kallus and Zhou (2019) examined estimating a DTR that maximizes the value for the worst-case scenario of an uncertainty set that quantifies the degree of confounding that is unmeasured.

We propose using a Monte Carlo sensitivity analysis for the estimation of DTRs. Section 2 details setup and notation. In Section 3, we provide an overview of our proposed sensitivity analysis procedure. In Section 4, we examine the performance of our proposed method using a simulation study. Section 5 demonstrates applying the proposed procedure to EHRs when estimating DTRs to reduce symptoms of depression using data from Kaiser Permanente Washington (KPWA). A discussion of the proposed procedure is contained in Section 6.

2 |. SETUP AND NOTATION

Suppose we have data from an observational study in which patients are treated throughout the course of $K$ stages. We collect data of the form ${\mathcal{D}}_n={\left\{\left({\mathit{X}}_{1,i},A_{1,i},\dots ,{\mathit{X}}_{K,i},A_{K,i},Y_i\right)\right\}}_{i=1}^n$, which consists of $n$ i.i.d. replicates of $\left({\mathit{X}}_1,A_1,\dots ,{\mathit{X}}_K,A_K,Y\right)$ such that ${\mathit{X}}_1\in {ℝ}^{p_1}$ denotes baseline patient characteristics, $A_k\in \{0,1\}$ denotes the treatment assigned at stage $k$ for $k=1,\dots ,K,{\mathit{X}}_k\in {ℝ}^{p_k}$ for $k=2,\dots ,K$ denotes patient information recorded during the course of the ${(k-1)}^{\text{st}}$ treatment, and $Y\in ℝ$ denotes the continuous patient outcome coded such that higher values are better. We let $U$ denote an unmeasured time-fixed confounding variable that can be continuous or binary. This unmeasured confounder is measured at baseline and does not change over time, but influences treatment choices at any of the $K$ stages as well as the outcome $Y$. Let ${\mathit{H}}_1={\mathit{X}}_1$ and ${\mathit{H}}_k=\left({\mathit{X}}_1,A_1,\dots ,A_{k-1},{\mathit{X}}_k\right)$ for $k=2,\dots ,K$ denote the history of a patient such that ${\mathit{H}}_k$ is all of the information available to a clinical decision maker at stage $k$. Let $\mathit{d}=\left(d_1,\dots ,d_K\right)$ denote a DTR such that $d_k:\text{dom}{\mathit{H}}_k\to \text{dom}{A}_k$ for $k=1,\dots ,K$ is a function that maps a patient’s history to a recommended treatment, where dom indicates the domain or set of possible treatments. Therefore, DTR $\mathit{d}$ would recommend treatment $d_k\left({\mathit{h}}_k\right)$ at stage $k$ for a patient with history ${\mathit{H}}_k={\mathit{h}}_k$.

To allow us to reference components of the history and regimes, we will use overbar notation to indicate up to stage $k$ such that ${\overline{\mathit{x}}}_k=\left({\mathit{x}}_1,\dots ,{\mathit{x}}_k\right),{\overline{\mathit{a}}}_k=\left(a_1,\dots ,a_k\right)$, and ${\overline{\mathit{d}}}_k=\left(d_1,\dots ,d_k\right)$. We will suppress the subscript when denoting the entire sequence, for example, $\overline{\mathit{x}}={\overline{\mathit{x}}}_K$. Similarly, we will use an underbar to denote treatments, covariates, and regimes after and including stage $k$ such that ${\underset{\_}{\mathit{x}}}_k=\left({\mathit{x}}_k,\dots ,{\mathit{x}}_K\right)$ and likewise for ${\underset{\_}{\mathit{a}}}_k$ and ${\underset{\_}{\mathit{d}}}_k$.

We will use the potential outcomes framework to define an optimal DTR (Rubin, 1978). Let $Y^{\ast }(\overline{\mathit{a}})$ denote the potential outcome under the treatment sequence $\overline{\mathit{A}}=\overline{\mathit{a}}$ and ${\mathit{H}}_k^{\ast }\left({\overline{\mathit{a}}}_{k-1}\right)$ denote the potential history at stage $k$ under treatments ${\overline{\mathit{A}}}_{k-1}={\overline{\mathit{a}}}_{k-1}$. Denote the set of all potential outcomes as ${\mathcal{O}}^{\ast }=\{{\mathit{H}}_2^{\ast }\left(a_1\right)$, ${\mathit{H}}_3^{\ast }\left({\overline{\mathit{a}}}_2\right),\dots$, ${\mathit{H}}_K^{\ast }\left({\overline{\mathit{a}}}_{K-1}\right)$, $Y^{\ast }(\overline{\mathit{a}}):\overline{\mathit{a}}\in {\{0,1\}}^K\}$. The potential outcome of a DTR, $\mathit{d}$, is then defined as.

$$Y^{\ast }(\mathit{d})=\sum _{\overline{\mathit{a}}\in {\{0,1\}}^K}{Y}^{\ast }(\overline{\mathit{a}})𝕀\left\{d_1\left({\mathit{h}}_1\right)=a_1\right\}\prod _{k=2}^K𝕀\left[d_k\left\{{\mathit{H}}_k^{\ast }\left(a_{k-1}\right)\right\}=a_k\right],$$

where 𝕀 is the indicator function (Murphy, 2003). Define the value of a DTR by $V(\mathit{d})=\text{E}\left\{Y^{\ast }(\mathit{d})\right\}$. An optimal regime, ${\mathit{d}}^{opt}$, is defined as a regime that satisfies $V\left({\mathit{d}}^{opt}\right)\ge V(\mathit{d})$ for all regimes $\mathit{d}$.

When estimating DTRs, it is standard to make the following causal assumptions (Robins, 2004): (i) the stable unit treatment value assumption (SUTVA), $Y=Y^{\ast }(\overline{\mathit{A}})$ and ${\mathit{H}}_k={\mathit{H}}_k^{\ast }\left({\overline{\mathit{A}}}_{k-1}\right)$ for $k=2,\dots ,K$ (ii) positivity, $\text{P}\left(A_k=a_k\mid {\mathit{H}}_k={\mathit{h}}_k\right)>0$ with probability one for each $a_k\in \{0,1\}$ for $k=1,\dots ,K$; and (iii) sequential ignorability, ${\mathcal{O}}^{\ast }\perp A_k\mid {\mathit{H}}_k$ for $k=1,\dots ,K$. We will assume SUTVA and positivity holds, but sequential ignorability does not hold because we have an unmeasured confounder, $U$. This is a key assumption and if it is violated, standard methods for estimating DTRs will lead to biased estimates of the optimal DTR. In addition, sequential ignorability is unverifiable from data and requires domain expertise to assess whether it is a reasonable assumption. Our proposed Monte Carlo sensitivity analysis requires making the following additional assumptions. We will assume that $U$ is the only unmeasured confounder and ${\mathcal{O}}^{\ast }\perp A_k\mid U,{\mathit{H}}_k$ for $k=1,\dots ,K$. We will also assume that the unmeasured confounder has an additive effect on the outcome $Y$ and is conditionally independent of later-stage covariates, so we have that ${\mathit{X}}_k\perp U\mid {\mathit{H}}_{k-1},A_{k-1}$ for $k=2,\dots ,K$. These last two assumptions can be relaxed, though that would require more complex assumptions about the distribution and effect of the unmeasured confounder as well as a more complex expression for the bias.

2.1 |. Dynamic weighted ordinary least squares

Dynamic weighted ordinary least squares (dWOLS) is a regression-based method for estimating DTRs (Wallace and Moodie, 2015). This method estimates an optimal DTR by estimating a contrast function that represents the difference in expected outcome of receiving a given treatment at stage $k$ when compared to the reference treatment, which we take to be treatment $A_k=0$, assuming that treatment is assigned optimally after stage $k$. This contrast function is referred to as the optimal blip-to-zero function, $\gamma \left({\mathit{h}}_k,a_k\right)$, and is defined as

$$\begin{array}{l}{\gamma }_K\left({\mathit{h}}_K,a_K\right)=\text{E}\left\{Y^{\ast }\left({\overline{\mathit{a}}}_{K-1},a_K\right)-Y^{\ast }\left({\overline{\mathit{a}}}_{K-1},0\right)|{\mathit{H}}_K={\mathit{h}}_K\right\},\\ {\gamma }_k\left({\mathit{h}}_k,a_k\right)=\text{E}\left\{Y^{\ast }\left({\overline{\mathit{a}}}_{k-1},a_k,{\underset{\_}{\mathit{d}}}_{k+1}^{opt}\right)-Y^{\ast }\left({\overline{\mathit{a}}}_{k-1},0,{\underset{\_}{\mathit{d}}}_{k+1}^{opt}\right)\mid {\mathit{H}}_k={\mathit{h}}_k\right\}\text{for}k=2,\dots ,K-1,\\ {\gamma }_1\left({\mathit{h}}_1,a_1\right)=\text{E}\left\{Y^{\ast }\left(a_1,{\underset{\_}{\mathit{d}}}_2^{opt}\right)-Y^{\ast }\left(0,{\underset{\_}{\mathit{d}}}_2^{opt}\right)\mid {\mathit{H}}_1={\mathit{h}}_1\right\}.\end{array}$$

The optimal blip-to-zero function characterizes the optimal DTR (Robins, 2004). The optimal treatment rule at stage $k$ is given by recommend treatment $A_k=1$ if ${\gamma }_k\left({\mathit{h}}_k,1\right)>0$, otherwise recommend $A_k=0$. In general, when considering more than two treatment options, the optimal DTR at stage $k$ is given by $d_k^{\text{opt}}\left({\mathit{h}}_k\right)=\arg {\max }_{a_k}{\gamma }_k\left({\mathit{h}}_k,a_k\right)$. dWOLS estimates an optimal DTR by positing models for the blip functions and estimating their parameters through a series of weighted ordinary least squares regressions. Let ${\gamma }_k\left({\mathit{h}}_k,a_k;{\psi }_k\right)$ denote our posited model for the blip function. We will assume that the blip-to-zero function is correctly specified, so we have that ${\gamma }_k\left({\mathit{h}}_k,a_k;{\psi }_k^{\ast }\right)={\gamma }_k\left({\mathit{h}}_k,a_k\right)$ for all $k$. The estimated optimal DTR is then given by ${\widehat{\mathit{d}}}^{\text{opt}}=\left({\widehat{d}}_1^{\text{opt}},\dots ,{\widehat{d}}_K^{\text{opt}}\right)$ such that ${\widehat{d}}_k^{\text{opt}}\left({\mathit{h}}_k\right)=\arg {\max }_{a_k}{\gamma }_k\left({\mathit{h}}_k,a_k;{\widehat{\psi }}_k\right)$.

Denote the treatment-free outcome at stage $k$ by $G_k\left({\underset{\_}{\psi }}_k\right)$ that represents a patient’s observed outcome adjusted by the expected difference in a patient’s outcome had they received treatment 0 at stage $k$ and then treated optimally via the blip models with parameters ${\underset{\_}{\psi }}_k$ after stage $k$. Therefore, $G_k\left({\underset{\_}{\psi }}_k\right)=Y-{\gamma }_k\left({\mathit{h}}_k,a_k;{\psi }_k\right)+{\sum }_{j=k+1}^K[{\gamma }_j\left\{{\mathit{h}}_j,d_j^{\text{opt}}\left({\mathit{h}}_j\right);{\psi }_j\right\}-{\gamma }_j\left({\mathit{h}}_j,a_j;{\psi }_j\right)]$. We posit a model for the treatment-free outcome which we denote by $g_k\left({\mathit{h}}_k,a_k;{\beta }_k\right)$. We assume linear models for the treatment-free and blip models, so a model for the outcome at stage $K$ is given by

$$\begin{array}{c}\text{E}\left(Y\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K;{\beta }_K,{\psi }_K\right)=g_K\left({\mathit{h}}_K,a_K;{\beta }_K\right)+{\gamma }_K\left({\mathit{h}}_K,a_K;{\psi }_K\right)\\ ={\mathit{h}}_{K,\beta }^T{\beta }_K+a_K{\mathit{h}}_{K,\psi }^T{\psi }_K,\end{array}$$

where ${\mathit{h}}_{K,\beta }$ and ${\mathit{h}}_{K,\psi }$ are components of ${\mathit{h}}_K$ with a leading one for the intercept and ${\mathit{h}}_{K,\psi }\subset {\mathit{h}}_{K,\beta }$. We also model the propensity score, ${\pi }_k\left({\mathit{h}}_k\right)=\text{E}\left(A_k\mid {\mathit{H}}_k={\mathit{h}}_k\right)$, which we denote by ${\pi }_k\left({\mathit{h}}_k;{\alpha }_k\right)$ for $k=1,\dots ,K$. We estimate the blip model parameters using weighted ordinary least squares using weights $w_k\left(a_k,{\mathit{h}}_k;{\alpha }_k\right)$ that satisfy ${\pi }_k\left({\mathit{h}}_k;{\alpha }_k\right)w_k\left(1,{\mathit{h}}_k;{\alpha }_k\right)=\{1-{\pi }_k\left({\mathit{h}}_k;{\alpha }_k\right)\}{w}_k\left(0,{\mathit{h}}_k;{\alpha }_k\right)$. Examples of weights that satisfy this equality are given by the inverse probability of treatment weights (IPTWs), $a_k{\left\{\pi \left({\mathit{h}}_k;{\alpha }_k\right)\right\}}^{-1}+\left(1-a_k\right){\left\{1-\pi \left({\mathit{h}}_k;{\alpha }_k\right)\right\}}^{-1}$ and overlap weights, $\left|a_k-\pi \left({\mathit{h}}_k;{\alpha }_k\right)\right|$. First, we estimate the blip parameters for the final stage $K$ using our posited model for the outcome. Then, form the pseudo-outcome which we define as

$${\tilde{Y}}_k=Y+\sum _{j=k+1}^K\left[{\gamma }_j\left\{{\mathbf{h}}_j,{\widehat{d}}_j^{\text{opt}}\left({\mathbf{h}}_j\right);{\widehat{\psi }}_j\right\}-{\gamma }_j\left({\mathbf{h}}_j,a_j;{\widehat{\psi }}_j\right)\right].$$

At each stage starting with $k=K-1$ and moving backwards, we model the pseudo-outcome by

$$\text{E}\left({\tilde{Y}}_k\mid {\mathit{H}}_k={\mathit{h}}_k,A_k=a_k;{\beta }_k,{\psi }_k\right)=g_k\left({\mathit{h}}_k,a_k;{\beta }_k\right)+{\gamma }_k\left({\mathit{h}}_k,a_k;{\psi }_k\right)$$

and fit the model using weighted least squares. The resulting estimate of $\psi$ is consistent as long as the blip model is correctly specified and at least one of the treatment free and propensity score models is correctly specified. When we have an unmeasured confounder, $U$, both the treatment free and propensity score model will be misspecified leading to bias in the estimator of $\psi$.

3 |. MONTE CARLO SENSITIVITY ANALYSIS

A Monte Carlo sensitivity analysis is a probabilistic approach to sensitivity analysis in which probability distributions are posited for the parameters governing the bias due to the unmeasured confounder. The posited probability distributions are repeatedly sampled from and used to calculate a series of bias corrected effect estimates (Greenland, 2005; McCandless and Gustafson, 2017). In what follows, we detail a Monte Carlo approach that seeks to posit models (and associated parameters) to describe the confounding due to the unmeasured variable $U$ through its relationship to the outcome, the treatment, and other covariates, and to use that to impute the unmeasured confounder and hence assess and correct bias. Ideally, a secondary data set that contains data on the unmeasured confounder as well as the confounders, treatment, and outcomes measured in the current study with the potential unmeasured confounding is used to learn about the probability distributions for the bias parameters that must be posited. This allows us to fit the postulated unmeasured confounder models to the data from the secondary study and use the estimated parameters and standard errors to posit distributions that capture the uncertainty related to the unmeasured confounder. These data could be historical data or gathered from a concurrent or follow-up study and can be significantly smaller than the full study. If a secondary data set is unavailable, we can instead use subject matter expertise to posit probability distributions for the bias parameters with wide distributions to capture the additional uncertainty. For example, if we only know that the unmeasured confounder is positively associated with the outcome, we could posit a uniform distribution from 0 to a conservative estimate of the maximum for the presumed effect of the unmeasured confounder on the outcome. If there are bias parameters for which we have no information, we could posit a uniform distribution that is centered at 0 with conservative estimates for the bounds of the distribution. When noninformative distributions for the bias parameters are used, the bias-adjusted point estimate of the parameters indexing the optimal regime will be closer to the unadjusted estimate, but the confidence intervals will still capture the uncertainty in the optimal regime due to both sampling variability and unmeasured confounding.

Alternative approaches to sensitivity analyses for unmeasured confounding typically make assumptions about the association between the unmeasured confounder and treatment as well as the unmeasured confounder and outcome, often capturing these by a single sensitivity parameter (Groenwold et al., 2010; Hernan and Robins, 2020; Lash et al., 2009). When the bias due to unmeasured confounding is controlled by one or two parameters, a conditional analysis in which we examine the estimated effect for a fixed value of the bias parameters is appropriate. This type of analysis then allows for examining what values of the bias parameters would significantly change the conclusions of the study (Rosenbaum & Rubin, 1983). For the estimation of DTRs, we are interested in treatment interaction effects in addition to the main effect of treatment. To better quantify the bias in the interaction effects, we make additional assumptions about the association between the unmeasured confounder and the measured covariates. These assumptions lead to the bias being dictated by many more parameters. The additional parameters make it very difficult to succinctly describe the potential bounds of the bias parameters with a conditional analysis, as the regions for which the results would be consistent could be very complex in addition to being multidimensional. By instead positing distributions for the bias parameters, we can quantify the uncertainty in the estimated DTR while accounting for the uncertainty in the posited models for the unmeasured confounder and can integrate over the posited distributions to calculate a bias-adjusted estimate.

Recall that we assume that the unmeasured confounder has an additive effect on the outcome $Y$ in addition to linear models for the treatment-free and blip models. Therefore, a model for the outcome $Y$ is given by

$$\text{E}\left(Y\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K,U=u;{\beta }_K,{\psi }_K,{\beta }_u\right)={\mathit{h}}_{K,\beta }^T{\beta }_K+{\beta }_{u}u+a_K{\mathit{h}}_{K,\psi }^T{\psi }_K.$$

We will also posit a model for the conditional mean of the unmeasured confounder given by $\text{E}\left(U\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K;\zeta \right)$ such that $\zeta$ denotes the parameters of the model. This will typically be given by a linear or logistic regression model depending on whether $U$ is continuous or binary, but there are no restrictions on the form of this model. We then have that ${\beta }_u$ and $\zeta$ are the parameters that dictate the bias due to the unmeasured confounding with $\zeta$ indexing the model for the conditional mean of $U$, and ${\beta }_u$ controlling the effect of the unmeasured confounder on the outcome $Y$.

Let ${\mathit{B}}_k={\left({\mathit{H}}_{k,\beta }^T,A_k{\mathit{H}}_{k,\psi }^T\right)}^T$ and ${\widehat{w}}_k=w_k\left(A_k,{\mathit{H}}_k;{\widehat{\alpha }}_k\right)$ for $k=1,\dots ,K$. If the unmeasured confounder $U$ is not included in the regression, and then the estimated coefficients are given by

$$(\begin{array}{c}{\widehat{\beta }}_K\\ {\widehat{\psi }}_K\end{array})={\left\{{\mathbb{P}}_n\left({\widehat{w}}_K{\mathit{B}}_K{\mathit{B}}_K^T\right)\right\}}^{-1}{\mathbb{P}}_n\left({\widehat{w}}_K{\mathit{B}}_{K}Y\right)$$

such that ${\mathbb{P}}_n$ denotes the empirical expectation. Recall we assume that the unmeasured confounder, $U$, has an additive effect on the outcome and let ${\beta }_u$ denote the coefficient for the unmeasured confounder. In Section A of the Supporting Information, we show that the bias is given by

$$\begin{array}{l}\text{bias}\left({\widehat{\psi }}_K\right)=\text{E}\left({\widehat{\psi }}_K\right)-{\psi }_K\\ =[-\text{E}\left({\widehat{w}}_K{A}_K{\mathit{H}}_{K,\psi }{\mathit{H}}_{K,\beta }^T\right){\left\{\text{E}\left({\widehat{w}}_K{\mathit{H}}_{K,\beta }{\mathit{H}}_{K,\beta }^T\right)\right\}}^{-1}\text{E}\left({\widehat{w}}_K{A}_K{\mathit{H}}_{K,\beta }{\mathit{H}}_{K,\psi }^T\right)\\ {+\text{E}\left({\widehat{w}}_K{A}_K{\mathit{H}}_{K,\psi }{\mathit{H}}_{K,\psi }^T\right)]}^{-1}[\text{E}\left({\widehat{w}}_K{A}_K{\mathit{H}}_{K,\psi }{\beta }_{u}U\right)\\ -\text{E}\left({\widehat{w}}_K{A}_K{\mathit{H}}_{K,\psi }{\mathit{H}}_{K,\beta }^T\right){\left\{\text{E}\left({\widehat{w}}_K{\mathit{H}}_{K,\beta }{\mathit{H}}_{K,\beta }^T\right)\right\}}^{-1}\text{E}\left({\widehat{w}}_K{\mathit{H}}_{K,\beta }{\beta }_{u}U\right)].\end{array}$$ (1)

We can estimate the bias in finite samples by replacing the expectations with empirical expectations and imputing an estimate of $\text{E}\left(U\mid {\mathit{H}}_K,A_K\right)$ for $U$ which we will denote by $\widehat{\text{bias}}\left({\widehat{\psi }}_K\right)$. Note that this is then a function of the data and the parameters of the unmeasured confounder models.

If we proceeded with dWOLS, the bias in the blip parameters would bias the pseudo-outcome given by ${\tilde{Y}}_{K-1}=Y+{\gamma }_K\left\{{\mathit{h}}_K,{\widehat{d}}_K^{\text{opt}}\left({\mathit{h}}_K\right);{\widehat{\psi }}_K\right\}-{\gamma }_K\left({\mathit{h}}_K,a_K;{\widehat{\psi }}_K\right)$. Additionally, estimating the blip model at stage $K-1$ without accounting for the unmeasured confounder would introduce additional bias that further compounds as we move backward through the stages. We can use the bias-corrected estimate of $\psi$ to calculate the pseudo-outcome and, if we assume that ${\mathit{X}}_k\perp U\mid {\mathit{H}}_{k-1},A_{k-1}$ for $k=2,\dots ,K$, we have that Equation (1) for $k=K$ holds for $k=1,\dots ,K$. This assumption can be relaxed at the expense of additional assumptions about the effect of $U$ on ${\mathit{X}}_k$ and a more complex expression for the bias. Being able to accurately posit models and parameter distributions for $U$ when a more complex relationship exists could be potentially difficult without data. Therefore, a different approach to sensitivity analysis may be more appropriate when secondary data are unavailable if this assumption is unreasonable.

ALGORITHM 1.

Monte Carlo sensitivity analysis

1:	Posit a model for $\text{E}\left(U\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K\right)$ given by $\text{E}(U\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K;\zeta )$
2:	Posit distributions $f(\zeta )$ and $f\left({\beta }_u\right)$ for the bias parameters $\zeta$ and ${\beta }_u$
3:	for $b\in \{1,\dots ,B\}$ Monte Carlo/bootstrap repetitions do
4:	Draw a bootstrap sample from ${\mathcal{D}}_n$
5:	Sample ${\zeta }^{(b)}$, ${\beta }_u^{(b)}$ from the distributions posited in step 2
6:	Impute ${\widehat{U}}^{(b)}$ from $\text{E}(U\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K;{\zeta }^{(b)})$
7:	Estimate ${\widehat{\alpha }}_K^{(b)}$ with the propensity score model and calculate weights ${\widehat{w}}_K^{(b)}$
8:	Estimate ${\widehat{\psi }}_K^{(b)}$ using weighted least squares, i.e. perform a dWOLS estimation using the bootstrap sample
9:	Calculate bias in ${\widehat{\psi }}_K^{(b)}$ with equation 1 using ${\widehat{U}}^{(b)}$ and ${\beta }_u^{(b)}$ as estimates for $U$ and ${\beta }_u$
10:	Calculate bias-adjusted estimate ${\widehat{\psi }}_K^{\text{adj},(b)}={\widehat{\psi }}_K^{(b)}-\widehat{\text{bias}}\left({\widehat{\psi }}_K^{(b)}\right)$
11:	for $k=K-1,\dots ,1$ do
12:	Calculate pseudo-outcome
	${\tilde{Y}}_k^{(b)}=Y+\sum _{j=k+1}^K\left[{\gamma }_j\left\{{\mathit{h}}_j,{\widehat{d}}_j^{\text{opt}}\left({\mathit{h}}_j\right);{\widehat{\psi }}_j^{\text{adj},(b)}\right\}-{\gamma }_j\left({\mathit{h}}_j,a_j;{\widehat{\psi }}_j^{\text{adj},(b)}\right)\right]$
13:	Estimate ${\widehat{\alpha }}_k^{(b)}$ with the propensity score model and calculate weights ${\widehat{w}}_k^{(b)}$
14:	Estimate ${\widehat{\psi }}_K^{(b)}$ using weighted least squares
15:	Calculate bias in ${\widehat{\psi }}_K^{(b)}$ with equation 1 using ${\widehat{U}}^{(b)}$ and ${\beta }_u^{(b)}$ as estimates for $U$ and ${\beta }_u$
16:	Calculate bias-adjusted estimate ${\widehat{\psi }}_k^{\text{adj},(b)}={\widehat{\psi }}_k^{(b)}-\widehat{\text{bias}}\left({\widehat{\psi }}_k^{(b)}\right)$
17:	end for
18:	end for
19:	Calculate bias-adjusted estimate ${\widehat{\psi }}_k^{\text{adj}}=B^{-1}{\sum }_{b=1}^B{\widehat{\psi }}_k^{\text{adj},(b)}$ for $k=1,\dots ,K$

The primary objective of conducting sensitivity analyses in this context is to quantify the uncertainty in the estimated DTR when there is bias due to unmeasured confounding. If we generated confidence intervals for the bias by taking the percentiles of our adjusted results across the Monte Carlo samples, these interval estimates would only capture the variability due to the uncertainty in our bias parameters and would not account for the uncertainty in our estimate of the parameters of interest. Therefore, we take a bootstrap sample for each Monte Carlo repetition and confidence intervals are formed by taking percentiles of the bias-adjusted values of $\psi$. To account for nonregularity in estimators resulting from the nonsmoothness in the pseudo-outcome when estimating a multistage DTR, we will adapt the $m\text{-out-of-}n$ bootstrap (Chakraborty et al., 2013).

We perform a Monte Carlo sensitivity analysis by first positing a model for the conditional mean of the unmeasured confounder given by $\text{E}\left(U\mid {\mathit{H}}_K={\mathit{h}}_K,A_K=a_K;\zeta \right)$. We also posit distributions $f(\zeta )$ and $f\left({\beta }_u\right)$ for the bias parameters $\zeta$ and ${\beta }_u$. We then draw $B$ bootstrap samples which we will denote by ${\mathcal{D}}_n^{(b)}$ for $b=1,\dots ,B$. For each bootstrap sample, we sample ${\zeta }^{(b)}$ and ${\beta }_u^{(b)}$ from the posited distributions, $f(\zeta )$ and $f\left({\beta }_u\right)$. We use the sampled value of ${\zeta }^{(b)}$ and the bootstrap data to impute values for the unmeasured confounder, $U$, which we denote by ${\widehat{U}}^{(b)}$. Then use the bootstrap data, the sampled bias parameter ${\beta }_u^{(b)}$, and the imputed values of $U$ to calculate a bias-adjusted estimate of ${\psi }^{(b)}$ which we will denote by ${\widehat{\psi }}^{\text{adj},(b)}$. This is done by implementing dWOLS to estimate ${\widehat{\psi }}_K^{(b)}$ and then using Equation (1) to calculate a bias-adjusted estimate, ${\widehat{\psi }}_K^{\text{adj},(b)}$. This bias-adjusted estimate is then used to calculate the pseudo-outcome ${\tilde{Y}}_{K-1}^{(b)}$. We continue implementing dWOLS to estimate ${\widehat{\psi }}_K^{\text{adj},(b)}$ at each stage by estimating ${\widehat{\psi }}_K^{(b)}$ and using Equation (1) to adjust for the bias due to the unmeasured confounder. A bias-adjusted estimate for ${\psi }_k$ is then given by ${\widehat{\psi }}_k^{\text{adj}}=B^{-1}{\sum }_{b=1}^B{\widehat{\psi }}_k^{\text{adj},(b)}$ for $k=1,\dots ,K$. A step-by-step procedure for generating bias-adjusted estimates for the parameters indexing the optimal regime, $\psi$, is given in Algorithm 1.

To construct a confidence interval for $\psi$ for a single-stage DTR, we calculate the percentiles of the bias-adjusted estimates from each bootstrap sample. When the number of stages is greater than 1, we have that the pseudo-outcome is a nonsmooth function of the generative model, and therefore, the estimator for ${\psi }_k$ for $k<K$ is nonregular (Laber et al., 2014; Moodie and Richardson, 2009; Robins, 2004). Therefore, we adapt the $m\text{-out-of-}n$ bootstrap that is a method for producing confidence intervals for nonsmooth functionals in which we take bootstrap samples with a smaller resample size of $m<n$ (Bickel et al., 1997; Dumbgen, 1993; Shao, 1994; Swanepoel, 1986). Chakraborty et al. (2013) proposed using a resample size of $m=n^{\frac{1+\kappa (1-p)}{1+\kappa }}$ such that $\kappa$ is a tuning parameter and $p=P\left({\mathit{H}}_2^T{\psi }_2=0\right)$ to construct a confidence interval for ${\psi }_1$ when $K=2$. The tuning parameter controls the minimum resample size because, for a fixed $n$, the resample size takes values within the interval $\left[n^{\frac{1}{1+x}},n\right]$. Chakraborty et al. (2013) proposed using a double bootstrap procedure to choose the tuning parameter $\kappa$. The nonsmoothness in the pseudo-outcome occurs at and near the point(s) where ${\mathit{H}}_2^T{\psi }_2=0$, so large values of $p$ indicate a high degree of nonregularity. They propose using a plug-in estimator for $p$ given by

$$\widehat{p}={\mathbb{P}}_n𝕀\left\{n{\left({\mathit{H}}_{2,\psi }^T{\widehat{\psi }}_2\right)}^2\le {\mathit{H}}_{2,\psi }^T{\widehat{\text{Σ}}}_{{\psi }_2}{\mathit{H}}_{2,\psi }{\chi }_{1,1-\nu }^2\right\},$$

where ${\widehat{\text{Σ}}}_{{\psi }_2}$ denotes an estimate of $n\text{Cov}\left({\widehat{\psi }}_2,{\widehat{\psi }}_2\right)$ and ${\chi }_{1,1-v}^2$ denotes the $(1-\nu )\times 100$ percentile of a chi-squared distribution with 1 degree of freedom. To generalize this to $K>2$ stages, we define $p_k=P\left({\mathit{H}}_k^T{\psi }_k=0\right)$ and construct an estimate, ${\widehat{p}}_k$, for each stage (Rose et al., 2022). We first calculate a resample size ${\widehat{m}}_K=n^{\frac{1+\kappa \left(1-{\widehat{p}}_K\right)}{1+\kappa }}$ such that

$${\widehat{p}}_K={\mathbb{P}}_n𝕀\left\{n{\left({\mathit{H}}_{K,\psi }^T{\widehat{\psi }}_K^{\text{adj}}\right)}^2\le {\mathit{H}}_{K,\psi }^T{\widehat{\text{Σ}}}_{{\psi }_K}{\mathit{H}}_{K,\psi }{\chi }_{1,1-\nu }^2\right\}.$$

We then take bootstrap samples of size ${\widehat{m}}_K$ to construct a confidence interval for ${\mathit{h}}_{K-1,\psi }^T{\psi }_{K-1}^{\text{adj}}$ for each ${\mathit{H}}_{K-1,\psi }={\mathit{h}}_{K-1,\psi }$ in the sample. This confidence interval is created by estimating ${\widehat{\psi }}_{K-1,{\widehat{m}}_{K-1}}^{\text{adj},(b)}$ for each bootstrap sample by drawing from the posited distributions for the bias parameters and adjusting the estimated parameters using Equation (1) as before. This allows us to obtain an estimate, ${\widehat{p}}_{K-1}$, of $p_{K-1}=P\left({\mathit{H}}_{K-1}^T{\psi }_{K-1}=0\right)$ by calculating the proportion of individuals in the study for which the confidence interval for ${\mathit{h}}_{K-1,\psi }^T{\psi }_{K-1}^{\text{adj}}$ contains zero. This procedure is repeated for $k=K-2,\dots ,1$. We then calculate $\widehat{p}={\max }_k{\widehat{p}}_k$ and the corresponding resample size $\widehat{m}=n^{\frac{1+\kappa (1-\widehat{p})}{1+k}}$. Finally, we take $B$ bootstrap samples of size $\widehat{m}$ and estimate ${\widehat{\psi }}_{k,\widehat{m}}^{\text{adj,}(b)}$ for each bootstrap sample by again sampling from the posited distributions for the bias parameters, ${\beta }_u$ and $\zeta$, and adjusting for the bias using Equation (1). To construct a $\left(1-{\vartheta }_k\right)\times 100\text{\%}$ confidence region for ${\psi }_k$, calculate ${\vartheta }_k/2\times 100$ and $\left(1-{\vartheta }_k/2\right)\times 100$ percentiles of $\sqrt{\widehat{m}}\left({\widehat{\psi }}_{k,\widehat{m}}^{\text{adj},(b)}-{\widehat{\psi }}_k^{\text{adj}}\right)$, denoted as ${\widehat{l}}_k$ and ${\widehat{u}}_k$, respectively, for $k=1,\dots ,K$. A $\left(1-{\vartheta }_k\right)\times \mathrm{100\%}$ confidence region for ${\psi }_k$ is then given by $\left({\widehat{\psi }}_k^{\text{adj}}-{\widehat{u}}_k/\sqrt{\widehat{m}},{\widehat{\psi }}_k^{\text{adj}}+{\widehat{l}}_k/\sqrt{\widehat{m}}\right)$ for $k=1,\dots ,K$. A step-by-step procedure for constructing a confidence interval for $\psi$ that accounts for uncertainty in the unmeasured confounder and random sampling variability is outlined in Algorithm 2.

4 |. SIMULATION EXPERIMENTS

We conducted a series of simulation experiments to evaluate the effectiveness of the proposed method. We applied the proposed method to two different data-generating models, the first being a one-stage study and the second a two-stage study. Additional simulations are contained in Sections B and C of the Supporting Information with B containing simulations with a binary unmeasured confounder and C containing a different generative model in which the bias does not meaningfully affect the performance of the estimated regime. The data-generating model for the one-stage study was given by:

$$\begin{array}{ll}U\sim N\left(0,{\sigma }_u^2\right),\hfill & \hfill \\ X_1={\varphi }_{10}+{\varphi }_{11}U+{ϵ}_{x_1},\hfill & {ϵ}_{x_1}\sim N\left(0,{\sigma }_{x_1}^2\right),\hfill \\ X_2={\varphi }_{20}+{\varphi }_{21}U+{ϵ}_{x_2},\hfill & {ϵ}_{x_2}\sim N\left(0,{\sigma }_{x_2}^2\right),\hfill \\ \text{P}\left(A_1=1\mid \mathit{X}=\mathit{x},U=u\right)={\left[1+\exp \left\{-\left({\alpha }_0+{\alpha }_1{x}_1+{\alpha }_2{x}_2+{\alpha }_{3}u\right)\right\}\right]}^{-1},\hfill & \hfill \\ Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_{u}U+A_1\left({\psi }_0+{\psi }_1{X}_1+{\psi }_2{X}_2\right)+{ϵ}_y,\hfill & {ϵ}_y\sim N\left(0,{\sigma }_y^2\right).\hfill \end{array}$$

ALGORITHM 2.

Monte Carlo sensitivity analysis: confidence intervals

1:	Calculate ${\widehat{p}}_K={\mathbb{P}}_n𝕀\left\{n{\left({\mathit{H}}_{K,\psi }^T{\widehat{\psi }}_K^{\text{adj}}\right)}^2\le {\mathit{H}}_{K,\psi }^T{\widehat{\text{Σ}}}_{{\psi }_K}{\mathit{H}}_{K,\psi }{\chi }_{1,1-\nu }^2\right\}$ where ${\widehat{\text{Σ}}}_{{\psi }_K}$ denotes an estimate of $n\text{Cov}\left({\widehat{\psi }}_K,{\widehat{\psi }}_K\right)$
2:	Calculate resample size ${\widehat{m}}_K=n^{\frac{1+\kappa \left(1-{\widehat{p}}_K\right)}{1+\kappa }}$
3:	for $k=K-1,\dots ,1$ do
4:	Draw $B$ bootstrap samples of size ${\widehat{m}}_k$
5:	Estimate ${\widehat{\psi }}_{k,{\widehat{m}}_k}^{\text{adj},(b)}$ for $b=1,\dots ,B$
6:	For each given ${\mathit{H}}_{k,\psi }={\mathit{h}}_{k,\psi }$, construct a confidence interval for ${\mathit{h}}_{k,\psi }^T{\psi }_k^{\text{adj}}$
7:	Calculate ${\widehat{p}}_k$ by the proportion of confidence intervals for ${\mathit{h}}_{k,\psi }^T{\psi }_k^{\text{adj}}$ that contain zero
8:	Calculate the resample size ${\widehat{m}}_k=n^{\frac{1+\kappa \left(1-p_k\right)}{1+\kappa }}$
9:	end for
10:	Calculate $\widehat{p}={\max }_k{\widehat{p}}_k$ and $\widehat{m}=n^{\frac{1+\kappa (1-p)}{1+\kappa }}$
11:	Draw $B$ bootstrap sample of size $\widehat{m}$
12:	Estimate ${\widehat{\psi }}_{k,\widehat{m}}^{\text{adj},(b)}$ for $k=K,\dots ,1$, $b=1,\dots ,B$
13:	Calculate ${\vartheta }_k/2\times 100$ and $\left(1-{\vartheta }_k/2\right)\times 100$ percentiles of $\sqrt{\widehat{m}}\left({\widehat{\psi }}_{k,\widehat{m}}^{\text{adj},(b)}-{\widehat{\psi }}_k^{\text{adj}}\right)$ which we denote by ${\widehat{l}}_k$ and ${\widehat{u}}_k$ respectively for $k=1,\dots ,K$
14:	Calculate a confidence interval for ${\psi }_k$ by $\left({\widehat{\psi }}_k^{\text{adj}}-{\widehat{u}}_k/\sqrt{\widehat{m}},{\widehat{\psi }}_k^{\text{adj}}+{\widehat{l}}_k/\sqrt{\widehat{m}}\right)$ for $k=K,\dots ,1$

We conducted 1000 repetitions for the simulation study. We let the sample size be given by $n=1000$ and conducted $B=500$ Monte Carlo repetitions for the sensitivity analysis. The parameter values were given by:

$$\begin{array}{ll}\psi =\left({\psi }_0,{\psi }_1,{\psi }_2\right)=(-1,0.5,0.5),\hfill & \alpha =\left({\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3\right)=(0,1,1,2),\hfill \\ {\varphi }_1=\left({\varphi }_{10},{\varphi }_{11}\right)=(0,1),\hfill & \beta =\left({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_u\right)=(1,1,1,2),\hfill \\ {\varphi }_2=\left({\varphi }_{20},{\varphi }_{21}\right)=(0,-1),\hfill & {\sigma }_u^2={\sigma }_{x_1}^2={\sigma }_{x_2}^2={\sigma }_y^2=1.\hfill \end{array}$$

We posited four different sets of distributions for the parameters in the unmeasured confounder models. This allowed us to assess how sensitive our proposed method is to bias in the distributions for these parameters. The four different simulation scenarios were given by: (i) narrow normal, centered properly; (ii) wide normal, centered properly; (iii) narrow normal, off-center; (iv) wide normal, off-center. For scenario (i), we posited models given by ${\beta }_u^{(b)}\sim N\left({\beta }_u,0.1\right)$ and ${\zeta }_j^{(b)}\sim N\left({\zeta }_j^{\ast },0.1\right)$ for $j=0,\dots ,3$ such that ${\zeta }^{\ast }={\min }_{\zeta }\text{E}\left\{{\left(U-{\zeta }_0-{\zeta }_1{X}_1-{\zeta }_2{X}_2-{\zeta }_3{A}_1\right)}^2\right\}$. For the wide distribution settings, the variance was increased to 0.5 and for the off-center scenarios, the distribution was centered at the true mean plus 0.1.

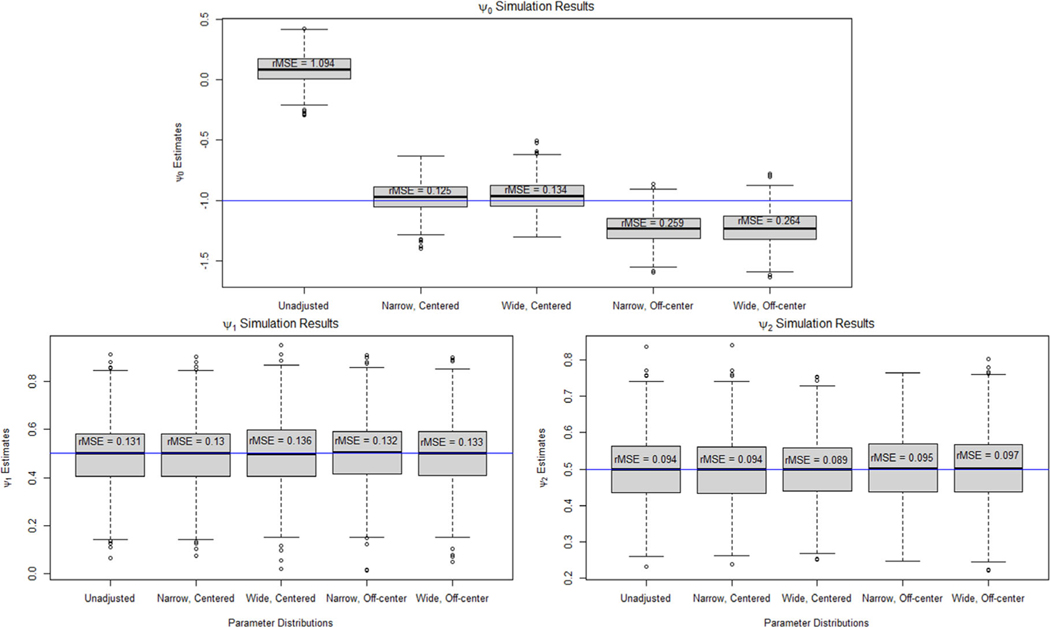
Figure 1 shows boxplots of the point estimates of ${\psi }_0$, ${\psi }_1$, and ${\psi }_2$ across 1000 repetitions when not adjusting and adjusting for the unmeasured confounder using a Monte Carlo sensitivity analysis with different distributions for the bias parameters. We can see that when we did not adjust for bias due to the unmeasured confounder, the estimate of ${\psi }_0$ is biased with a root mean squared error (rMSE) of 1.094. When the parameter distributions were centered on the true value, the adjusted estimate of ${\psi }_0$ was unbiased. There was some bias in the adjusted values of ${\psi }_0$ when the distribution is off-center as expected. We can see that for the narrow distribution, the rMSE increased from 0.125 to 0.259 and for the wide distribution, rMSE increased from 0.134 to 0.264. The unmeasured confounder did not cause bias in the estimation of ${\psi }_1$ and ${\psi }_2$, so the adjusted estimates using a Monte Carlo sensitivity analysis were very similar to the unadjusted results.

FIGURE 1.

Boxplots of the point estimates for $\psi$ under an unadjusted model and when using Monte Carlo sensitivity analysis to adjust for bias due to unmeasured confounding for the one-stage data-generating model.

Bias in the blip model parameters that index the optimal DTR can cause the estimated regime to differ from the true optimal regime. For each repetition of the simulation study, we simulated 10,000 new patients and assessed what proportion of the patients’ treatment would match the recommended treatment of the true optimal DTR when following each one of the adjusted and unadjusted estimates of the optimal regime. Table 1 displays the proportion of patients who would receive the treatment recommend by the true optimal regime across all 1000 repetitions of the simulation study. We can see that the bias in ${\psi }_0$ causes the treatment recommended by the estimated regime to match the optimal regime 52.8% of the time. When adjusting for the unmeasured confounder, this increased to 95.6% in the ideal scenario of a narrow, centered parameter distribution and to 95.8% when we used a wide, off-centered parameter distributions.

TABLE 1.

Proportion of patients whose recommended treatment when following each of the estimated regime matches the recommendation of the true optimal regime for the one-stage data-generating model.

Parameter Distr.	Proportion optimal
Unadjusted	0.528
Narrow, Centered	0.956
Wide, Centered	0.953
Narrow, Off-center	0.959
Wide, Off-center	0.958

In practice, if we do not have external data to help posit the mean model for the unmeasured confounder and distributions for the parameters, we will have less belief that the bias-adjusted DTR is close to the true optimal regime. The proposed method should be used to examine confidence intervals to assess whether the unmeasured confounder could be introducing bias to our estimated regimes. Table 2 displays the coverage and width of 95% confidence intervals generated using a Monte Carlo sensitivity analysis and from the unadjusted analysis that assumes no unmeasured confounding. For the unadjusted analysis, the empirical coverage of the confidence interval for ${\psi }_0$ was 0%. Even for ${\psi }_1$ and ${\psi }_2$, which did not appear to have any bias in the estimation, the coverage was still below the nominal rate of 95%. For all of the different posited parameter distributions, Monte Carlo sensitivity analysis produced confidence intervals that attained or were close to the nominal coverage probability. The width of the confidence intervals for ${\psi }_0$ increased significantly when conducting sensitivity analysis, indicating that this parameter is sensitive to the unmeasured confounding. Note that the width of the confidence intervals increased when the variability in the parameter distributions was increased.

TABLE 2.

Coverage (Cvr.) and average width (Wth.) of the 95% confidence intervals for $\psi$ for the unadjusted analysis and sensitivity analysis under each of the posited parameter distributions for the one-stage data-generating model.

Parameter Distr.	Cvr. (Wth.) ${\psi }_0$	Cvr. (Wth.) ${\psi }_1$	Cvr. (Wth.) ${\psi }_2$
Unadjusted	0.000* (0.359)	0.897* (0.426)	0.887* (0.300)
Narrow, Centered	1.000* (2.628)	0.946 (0.520)	0.947 (0.365)
Wide, Centered	1.000* (6.212)	0.954 (0.520)	0.959 (0.365)
Narrow, Off-center	1.000* (2.764)	0.950 (0.519)	0.951 (0.366)
Wide, Off-center	1.000* (6.495)	0.955 (0.519)	0.936* (0.367)

^*indicates coverages that are significantly different than 95%.

To compare our proposed procedure to an alternative method for sensitivity analysis, we conducted a simulation study for estimating an optimal DTR with G-estimation using the same single-stage generative model (Hernan and Robins, 2020; Robins et al., 1999). G-estimation for a single-stage study proceeds by defining $H(\psi )=Y-{\gamma }_1\left({\mathit{H}}_1,A_1;\psi \right)$ (Robins, 2004). $H(\psi )$ then represents a candidate potential outcome for $Y^{\ast }(0)$ for a given value of $\psi$. Consider the model

$$\text{logit}\left[\text{P}\left\{A_1=1\mid H(\psi ),{\mathit{H}}_1={\mathit{h}}_1\right\}\right]={\xi }_0+H(\psi )\left({\mathit{h}}_{1,\psi }^T{\xi }_1\right)+{\mathit{h}}_1^T{\xi }_2.$$ (2)

We assume sequential ignorabilty holds, which implies that ${\xi }_1=\mathbf{0}$ for the true value of $\psi$ where $\mathbf{0}$ denotes the zero vector. Therefore, to estimate the true value of $\psi$, we find the value of $\psi$ in $H(\psi )$ that results in ${\widehat{\xi }}_1=\mathbf{0}$ when fitting the logistic regression model in Equation (2). When there is unmeasured confounding, we have that ${\xi }_1\ne \mathbf{0}$. Therefore, we can conduct a sensitivity analysis by setting ${\xi }_1$ to a range of different fixed values and estimating $\psi$ for each to examine how sensitive the estimated DTR is to an unmeasured confounder.

This approach leads to bias parameters that are far more difficult to interpret than the bias parameters in our proposed Monte Carlo sensitivity analysis. A sensitivity analysis could conclude that a given value of ${\xi }_1$ would significantly alter the conclusions of the study, but it is unclear what degree of confounding would result in that value of ${\xi }_1$. To avoid this problem, we can use a similar approach to our proposed Monte Carlo sensitivity analysis by collecting data from a small, secondary study that includes the unmeasured confounder to learn about the true value of the bias parameters ${\xi }_1$. First, we use the secondary study to estimate $\widehat{\psi }$ using G-estimation with the unmeasured confounder included in the logistic regression model given in Equation (2). We refit the logistic regression model with $H(\widehat{\psi })$ included and the unmeasured confounder removed to estimate ${\xi }_1$. We then proceed in the same manner as the proposed Monte Carlo procedure. We posit distributions for ${\xi }_1$ using the point estimate and standard error from the model fit to the secondary study. We then use the bootstrap, sample ${\xi }_1$ from the posited distribution for each repetition, and calculate a bias-adjusted estimate of $\psi$ for each Monte Carlo repetition. We then take the mean of the estimates for $\psi$ to get a point estimate and take percentiles to construct a confidence interval.

We conducted a simulation study of this procedure using comparable distributions for the bias parameters to those used for the previous simulations. For this generative model, ${\xi }_1=\left({\xi }_{10},{\xi }_{11},{\xi }_{12}\right)$ is given by (0.52, 0, 0). For the simulation study, we will assume ${\xi }_{11}=0$ and ${\xi }_{12}=0$ and only posit a distribution for ${\xi }_{10}$. The four different simulation settings will again be given by (i) narrow normal, centered properly; (ii) wide normal, centered properly; (iii) narrow normal, off-center; and (iv) wide normal, off-center. For scenario (i), we posited a distribution for ${\xi }_{10}$ given by ${\xi }_{10}^{(b)}\sim N\left({\xi }_{10},0.1\right)$. For the wide distributions settings, we increased the variance to 0.5, and for the off-center simulations, we centered the distribution at the true value of ${\xi }_{10}$ plus 0.1.

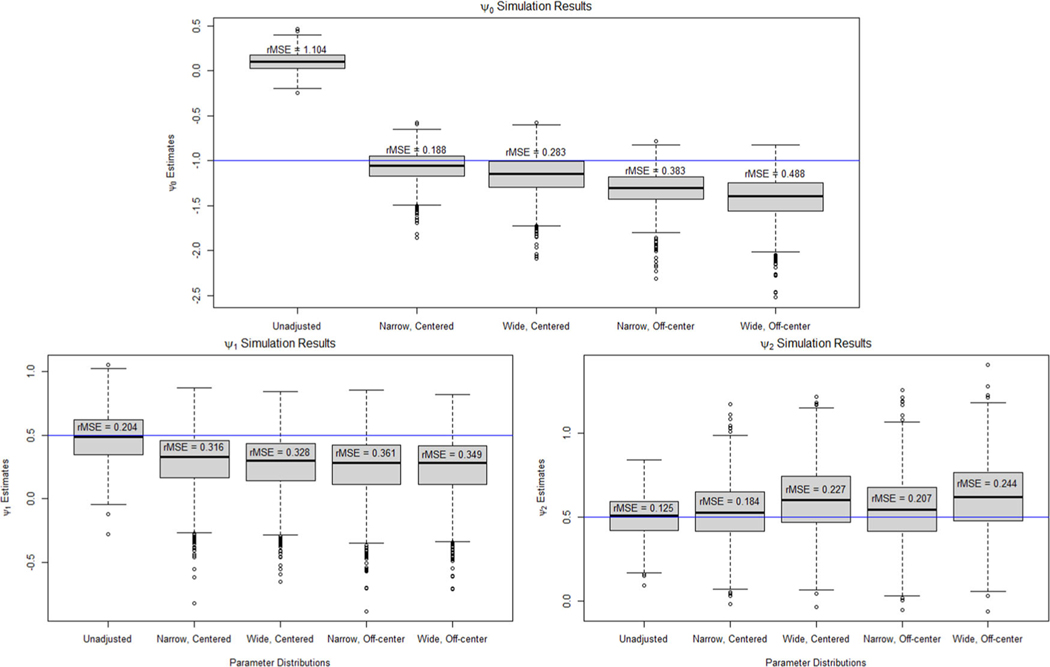
Figure 2 shows boxplots of the point estimates of $\psi$ across the 1000 repetitions. For ${\psi }_0$, adjusting for the unmeasured confounder using the narrow, correctly centered distribution reduced the rMSE from 1.104 to 0.188. This was worse than our proposed procedure that reduced the rMSE to 0.125. The G-estimation sensitivity analysis was also more sensitive to misspecification of the bias parameter distribution with the incorrectly centered distribution resulting in an rMSE of 0.383 and 0.488 for the narrow and wide distributions, respectively. For the interaction effect parameters, ${\psi }_1$ and ${\psi }_2$, the bias-adjusted estimates had a greater rMSE than the unadjusted estimates with the narrow, correctly centered bias distribution increasing the rMSE from 0.204 to 0.316 for ${\psi }_1$ and from 0.125 to 0.184 for ${\psi }_2$. Section D of the Supporting Information contains additional results on the coverage of confidence intervals and the proportion of new patients whose recommended treatment from the estimated regimes matched the optimal DTR for this simulation study. Section D also contains an additional simulation study in which we do not assume ${\xi }_{11}=0$ and ${\xi }_{12}=0$. The results for this were very poor with all four of the posited bias parameter distributions resulting in an increase in the rMSE in the estimates of ${\psi }_0$, ${\psi }_1$, and ${\psi }_2$. These simulation results demonstrate how simpler sensitivity analysis methods that avoid positing a model for the relationship between the unmeasured confounder and the other covariates can reduce the number of models and bias parameters distributions that need to be posited, but can produce considerably less reliable results about the effect of the unmeasured confounding on the estimated DTR.

FIGURE 2.

Boxplots of the point estimates for $\psi$ under an unadjusted model and when using G-estimation sensitivity analysis to adjust for bias due to unmeasured confounding for the one-stage data-generating model when we assume we know ${\xi }_{11}$ and ${\xi }_{12}$.

We conducted a similar simulation study with a two-stage study to assess the effectiveness of a Monte Carlo sensitivity analysis for the estimation of multistage DTRs. We let the data-generating model be given by:

$$\begin{gathered} \begin{array}{ll}U\sim N\left(0,{\sigma }_u^2\right),\hfill & \hfill \\ X_{11}={\varphi }_{10}+{\varphi }_{11}U+{ϵ}_{x_{11}},\hfill & {ϵ}_{x_{11}}\sim N\left(0,{\sigma }_{x_{11}}^2\right),\hfill \\ X_{12}={\varphi }_{20}+{\varphi }_{21}U+{ϵ}_{x_{12}},\hfill & {ϵ}_{x_{12}}\sim N\left(0,{\sigma }_{x_{12}}^2\right),\hfill \\ X_2={\varpi }_0+{\varpi }_1{X}_{11}+{\varpi }_2{X}_{12}+{ϵ}_{x_2},\hfill & {ϵ}_{x_2}\sim N\left(0,{\sigma }_{x_2}^2\right),\hfill \end{array} \\ \text{P}\left(A_1=1\mid {\mathit{H}}_1={\mathit{h}}_1,U=u\right)={\left[1+\exp \left\{-\left({\alpha }_{10}+{\alpha }_{11}{x}_{11}+{\alpha }_{12}{x}_{12}+{\alpha }_{13}u\right)\right\}\right]}^{-1}, \\ \text{P}\left(A_2=1\mid {\mathit{H}}_2={\mathit{h}}_2,U=u\right)={\left[1+\exp \left\{-\left({\alpha }_{20}+{\alpha }_{21}{x}_{11}+{\alpha }_{22}{x}_{12}+{\alpha }_{23}{a}_1+{\alpha }_{24}{x}_2+{\alpha }_{25}u\right)\right\}\right]}^{-1}, \\ Y={\beta }_{20}+{\beta }_{21}{X}_{11}+{\beta }_{22}{X}_{12}+{\beta }_{23}{A}_1+{\beta }_{24}{A}_1{X}_{11}+{\beta }_{25}{A}_1{X}_{12} \\ +{\beta }_{26}{X}_2+{\beta }_{u}U+A_2\left({\psi }_{20}+{\psi }_{21}{X}_{11}+{\psi }_{22}{X}_{12}+{\psi }_{23}{X}_2\right)+{ϵ}_y,{ϵ}_y\sim N\left(0,{\sigma }_y^2\right). \end{gathered}$$

As before, we conducted 1000 repetitions for the simulation study, set the sample size to $n=1000$, and conducted the sensitivity analysis using $B=500$ Monte Carlo repetitions. The parameter values for this data-generating process were given by:

$$\begin{gathered} {\beta }_2=\left({\beta }_{20},{\beta }_{21},{\beta }_{22},{\beta }_{23},{\beta }_{24},{\beta }_{25},{\beta }_{26},{\beta }_u\right)=(1,-1,1,-1,1,1,1,2), \\ \begin{array}{ll}{\psi }_2=\left({\psi }_{20},{\psi }_{21},{\psi }_{22},{\psi }_{23}\right)=(-1,0.5,0.5,0.5),\hfill & \hfill \\ {\alpha }_1=\left({\alpha }_{10},{\alpha }_{11},{\alpha }_{12},{\alpha }_{13}\right)=(0,1,1,2),\hfill & {\varphi }_1=\left({\varphi }_{10},{\varphi }_{11}\right)=(0,1),\hfill \\ {\alpha }_2=\left({\alpha }_{20},{\alpha }_{21},{\alpha }_{22},{\alpha }_{23},{\alpha }_{24},{\alpha }_{25}\right)=(0,1,1,1,1,3),\hfill & {\varphi }_2=\left({\varphi }_{10},{\varphi }_{11}\right)=(0,-1),\hfill \\ {\sigma }_u^2={\sigma }_{x_{11}}^2={\sigma }_{x_{12}}^2={\sigma }_{x_2}^2={\sigma }_y^2=1,\hfill & \varpi =\left({\varpi }_0,{\varpi }_1,{\varpi }_2\right)=(0,1,1).\hfill \end{array} \end{gathered}$$

We again varied the posited distributions for the parameters of the unmeasured confounder model and the effect of the unmeasured confounder using the same posited distributions as the single-stage simulation study.

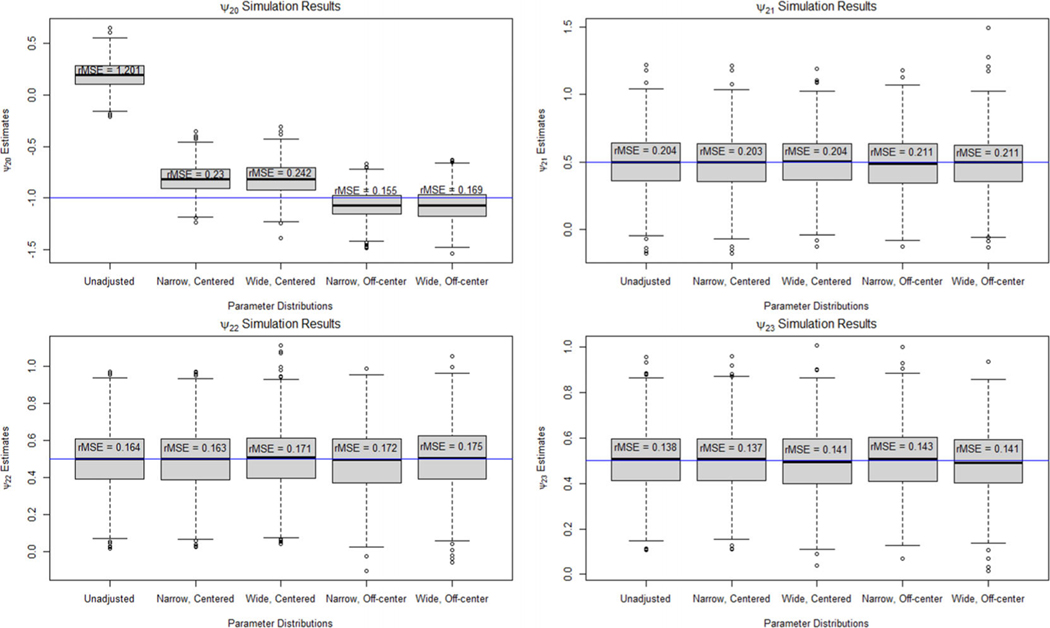
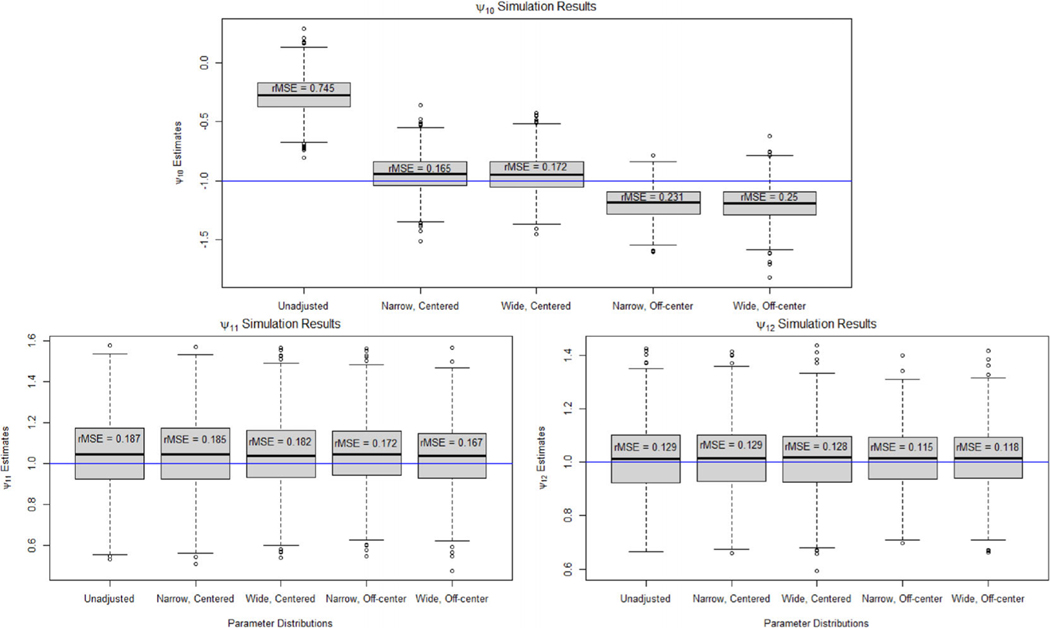
Figures 3 and 4 show boxplots of the point estimates for ${\psi }_2$ and ${\psi }_1$, respectively, across the 1000 repetitions. The results for the two-stage study were very similar to the one-stage results. In the second-stage models, the unmeasured confounder caused significant bias in ${\psi }_{20}$ in the unadjusted analysis leading to an rMSE of 1.201. Applying our Monte Carlo sensitivity analysis reduced the bias significantly with all scenarios having an rMSE of 0.242 or less. We found that the unmeasured confounder did not cause bias in the estimates of ${\psi }_{21}$, ${\psi }_{22}$, and ${\psi }_{23}$, leading to similar results between the unadjusted and adjusted estimates. There was significant bias in the unadjusted estimate of ${\psi }_{10}$ for the first-stage blip model. The rMSE of the unadjusted estimate is 0.745, whereas the rMSE of the bias-adjusted estimate under the narrow, centered parameter distribution is 0.165. The rMSE increased to 0.25 when using a wide parameter distribution that is not centered on the true parameter value.

FIGURE 3.

Boxplots of the point estimates for ${\psi }_2$ under an unadjusted model and when using Monte Carlo sensitivity analysis to adjust for bias due to unmeasured confounding for the two-stage data-generating model.

FIGURE 4.

Boxplots of the point estimates for ${\psi }_1$ under an unadjusted model and when using Monte Carlo sensitivity analysis to adjust for bias due to unmeasured confounding for the two-stage data-generating model.

As before, we simulated 10,000 additional patients and assessed whether the treatment recommended by each of the estimated regimes matched the recommendation of the true optimal regime for each of the 1000 repetitions. Table 3 displays the proportion of patients who were recommended the same treatment as the true optimal regime when following each of the different estimated regimes. The bias from the unmeasured confounder caused the unadjusted estimated regime to recommend the same treatment as the true optimal regime 81.4% of the time at the first stage and 70.2% of the at the second stage. After performing Monte Carlo sensitivity analysis using the narrow, centered posited distribution, the proportion increased to 95.1% at the first stage and 93.7% at the second stage. The alternative parameter distributions produced similar results.

TABLE 3.

Proportion of patients whose recommended treatment when following each of the estimated regime matches the recommendation of the true optimal regime at each stage for the two-stage data-generating model.

Parameter Distr.	Stage 1	Stage 2
Unadjusted	0.814	0.702
Narrow, Centered	0.951	0.937
Wide, Centered	0.949	0.936
Narrow, Off-center	0.951	0.948
Wide, Off-center	0.948	0.947

We also examined the coverage and width of the confidence intervals generated using a Monte Carlo sensitivity analysis for the two-stage study. Table 4 contains the empirical coverage and width of 95% confidence intervals for the parameters of the second-stage blip model. The empirical coverage of ${\psi }_{20}$ for the unadjusted analysis was 0% as it was significantly biased by the unmeasured confounder. Monte Carlo sensitivity analysis produced intervals for ${\psi }_{20}$ with 100% coverage for all of the simulation scenarios at the expense of being much wider. The remaining second-stage blip parameters, ${\psi }_{21}$, ${\psi }_{22}$, and ${\psi }_{23}$, were not biased in the unadjusted analysis, but the unmeasured confounder led to confidence intervals that did not achieve the nominal coverage probability. Monte Carlo sensitivity analysis produced confidence intervals that achieved the nominal coverage for all sets of posited parameter distributions.

TABLE 4.

Coverage (Cvr.) and average width (Wth.) of the 95% confidence intervals for ${\psi }_2$ for the unadjusted analysis and sensitivity analysis under each of the posited parameter distributions for the two-stage data-generating model.

Parameter Distr.	Cvr. (Wth.) ${\psi }_{20}$	Cvr. (Wth.) ${\psi }_{21}$	Cvr. (Wth.) ${\psi }_{22}$	Cvr. (Wth.) ${\psi }_{23}$
Unadjusted	0.000* (0.339)	0.810* (0.529)	0.810* (0.435)	0.801* (0.359)
Narrow, Centered	1.000* (2.634)	0.948 (0.803)	0.953 (0.658)	0.943 (0.541)
Wide, Centered	1.000* (6.208)	0.948 (0.804)	0.951 (0.654)	0.941 (0.537)
Narrow, Off-center	1.000* (2.775)	0.932* (0.803)	0.949 (0.657)	0.936* (0.542)
Wide, Off-center	1.000* (6.483)	0.934* (0.805)	0.937 (0.659)	0.941 (0.540)

^*indicates coverages that are significantly different than 95%.

Table 5 contains the empirical coverage and average width of 95% confidence intervals for the parameters of the first-stage blip model. The unadjusted confidence interval for ${\psi }_{10}$ had a coverage of only 0.1%, whereas the sensitivity analysis resulted in conservative confidence intervals that had coverage of 100%. For ${\psi }_{11}$ and ${\psi }_{12}$, the unadjusted analysis resulted in confidence intervals that did not attain nominal coverage with empirical coverages of 86.1% and 86.8%, respectively, despite the unmeasured confounder not resulting in bias in the parameters estimation. The sensitivity analysis intervals were instead conservative with coverages of 100% and 98.9% for ${\psi }_{11}$ and ${\psi }_{12}$, respectively, for the narrow, centered parameter distributions. The confidence intervals resulting from the sensitivity analysis for the first-stage blip model were considerably wider than those for the second-stage blip model parameters.

TABLE 5.

Coverage (Cvr.) and average width (Wth.) of the 95% confidence intervals for ${\psi }_1$ for the unadjusted analysis and sensitivity analysis under each of the posited parameter distributions for the two-stage data-generating model.

Parameter Distr.	Cvr. (Wth.) ${\psi }_{10}$	Cvr. (Wth.) ${\psi }_{11}$	Cvr. (Wth.) ${\psi }_{12}$
Unadjusted	0.001* (0.456)	0.861* (0.542)	0.868* (0.382)
Narrow, Centered	1.000* (4.236)	1.000* (2.609)	0.989* (2.439)
Wide, Centered	1.000* (7.362)	1.000* (2.828)	1.000* (2.590)
Narrow, Off-center	1.000* (4.607)	1.000* (2.833)	0.995* (2.663)
Wide, Off-center	1.000* (7.857)	1.000* (3.081)	1.000* (2.840)

^*indicates coverages that are significantly different than 95%.

5 |. ILLUSTRATION USING KPWA EHR DATA

We applied the proposed method to data from EHRs. KPWA is a health system that provides heath care and insurance to its members. This study used data from EHRs and health insurance claims for all KPWA clients to study the use of antidepressants for treating depression. The data include information on demographics, prescription fills, and depressive symptom severity for 82,691 patients with depression who received antidepressant medication from 2008 through 2018. Severity of depression symptoms was assessed through the use of the Patient Health Questionnaire-8 (PHQ) (Kroenke et al., 2001). This is a self-report questionnaire that produces a score ranging from 0 to 24, such that higher values indicate more severe symptoms of depression. The inclusion criteria for the study were that patients must have been 13 years or older, have been enrolled in KPWA insurance for at least a year, have been diagnosed with a depressive disorder in the year before or 15 days after treatment initiation, had no prescription fills for antidepressant medications in the past year, and had no diagnosis for personality, bipolar, or psychotic disorders in the past year. We additionally required, for this analysis, that patients did not have missing information on obesity, baseline PHQ, or follow-up PHQ at 1 year after baseline. Our analysis focuses on demonstrating the impact of our sensitivity analysis but does not adjust for missing information; therefore, the estimated DTRs must be interpreted as potentially biased; any clinical findings should be viewed in this light.

Research has suggested that obesity increases the risk of depression (Luppino et al., 2010). Weight gain has been found to be a side effect of taking antidepressants (Fava, 2000), with different classes of antidepressants affecting weight differently; treatment guidelines for clinicians recommend using the current weight of a patient as a consideration when prescribing antidepressants (Santasieri and Schwartz, 2015). Obesity is therefore a potentially important confounder that, if unmeasured, could lead to bias in observational studies of their effects, whether average or individualized. We considered a patient to be obese if they had a body mass index (BMI) of 30 or larger. We used this data in two different ways. We assumed that obesity was unavailable and estimated a DTR to minimize depression symptoms without adjusting for obesity in the analysis. We then applied the proposed procedure to assess how sensitive the estimated regime was to obesity being unmeasured and compared this to the estimated regime with obesity measured. We also conducted a plasmode simulation study in which we used the real data with simulated obesity and patient outcomes. This allowed us to know the true optimal DTR and distribution of obesity.

5.1 |. Application to the study of first-line choice of antidepressant

Our outcome is the negative of the PHQ score after 1 year so that higher values correspond with better patient outcomes. Equally, we could use the PHQ score and find the regime that minimizes instead of maximizes the mean outcome. The PHQ score after 1 year was given by the PHQ score recorded between 305 and 425 days after initiating treatment that was measured closest to 365 days after medication initiation. Patients were treated with 1 of 17 different antidepressants initially. Selective serotonin reuptake inhibitors (SSRIs) are a class of antidepressants that increase serotonin levels in the brain by decreasing reabsorption by nerve cells and are commonly prescribed due to having generally milder side effects. We classified the initial treatment received as an antidepressant from either the SSRI class or an alternative class of antidepressants.

We let $Y$ denote the negative of the PHQ score after 1 year. We denote treatment by $A$, such that $A=1$ if assigned an SSRI and $A=0$ if assigned a non-SSRI. We considered sex, age, baseline PHQ, and obesity as confounders and examined the bias that occurs if obesity was unmeasured. We centered the age variable to make the intercept more interpretable. Our outcome model was given by:

$$\begin{gathered} \text{E}(Y\mid \mathit{X},A;\beta ,\psi )={\beta }_0+{\beta }_1\text{SEX}+{\beta }_2\text{AGE}+{\beta }_3\text{PHQ}+{\beta }_u\text{OBESE} \\ +A\left({\psi }_0+{\psi }_1\text{SEX}+{\psi }_2\text{AGE}+{\psi }_3\text{PHQ}\right) \end{gathered}$$ (3)

such that the optimal DTR is then given by recommend an SSRI if (${\psi }_0+{\psi }_1\text{SEX}+{\psi }_2\text{AGE}+{\psi }_3\text{PHQ}$) is greater than zero.

To posit the models for the unmeasured confounder and the distributions for the bias parameters in practice, we would ideally conduct a small, secondary study. To replicate this process for this example, we took a random subsample of 250 patients from our data and treated this as a secondary data set. We found that obesity was correlated with age, baseline PHQ, race, census block education level (EDU), and diagnosis of an anxiety disorder in the prior year (ANX). Race was categorized as Asian, Black or African American, Hispanic, Native Hawaiian/Pacific Islander, American Indian/Native Alaskan, White, other, or unknown and was coded using dummy coding with Asian as the reference group. EDU was given by an indicator for whether less than 25% of people living in the patient’s census block had a college degree. Therefore, to conduct a Monte Carlo sensitivity analysis for the bias if obesity is unmeasured, we posited a model for obesity given by:

$$\begin{array}{c}\text{P}(\text{OBESE}=1\mid \mathit{X};\zeta )=[1+\exp \{-({\zeta }_0+{\zeta }_1\text{AGE}+{\zeta }_2\text{PHQ}+{\zeta }_3^T\text{RACE}\\ {+{\zeta }_4\text{EDU}+{\zeta }_5\text{ANX}+{\zeta }_{6}A)\}]}^{-1}.\end{array}$$ (4)

We first estimated ${\beta }_u$ and $\zeta$ using the secondary data set. We then posited normal distributions for ${\beta }_u$ and $\zeta$ that were centered at the estimated values of the parameters with standard deviations equal to the estimated standard errors.

We also examined using our proposed procedure when we do not have a secondary data set to help specify distributions for the bias parameters and instead need to use subject matter expertise. Recall that research has found that obesity increases the risk of depression that implies that obesity is negatively correlated with the negative of the PHQ score. Therefore, we will let the distribution for ${\beta }_u$ be given by a uniform distribution from −2 to 0. Since we centered the age variable, expit(${\zeta }_0$) can be interpreted as the probability of being obese, given that an individual is 45 years old, Asian, has a baseline PHQ score of 0, has no diagnosis of an anxiety disorder, is not from a low education census block, and who received a non-SSRI. We used the overall prevalence of obesity in Asian people over 18 years old in the United States obtained from the 2017 National Health Interview Survey to center the distribution for ${\zeta }_0$ (Blackwell and Villarroel, 2018). Since the overall prevalence was given by 0.119, the distribution for ${\zeta }_0$ was selected to be a uniform distribution with support [$\text{logit}(0.119)-0.5$, $\text{logit}(0.119)+0.5$]. We chose to use a uniform distribution as using the prevalence in the entire Asian population in the United States as a surrogate for the conditional probability given by expit(${\zeta }_0$) is an imperfect approach. We chose the distributions for each component of ${\zeta }_3$ in the same manner with a uniform distribution centered using the overall prevalence in the United States by race with a width of 1. The remaining parameters in $\zeta$ were given by a uniform distribution from −1 to 1 because we are unsure of how they are related to obesity.

Table 6 contains estimates and confidence intervals for $\psi$ from the full model, the model with obesity unmeasured, and after adjusting for the bias with and without a secondary data set to posit the bias parameter distributions. The adjusted estimates of $\psi$ using the secondary data set with obesity unmeasured were close to the estimates from the full model with obesity included; however, uncertainty was increased reflecting the lack of information available on the unmeasured confounder. The adjusted estimates using uniform distributions posited with subject matter expertise resulted in estimates close to the unadjusted estimate as expected. Both sensitivity analyses also produced confidence intervals that were wider for the parameters that were biased due to the unmeasured confounding. Section E of the Supporting Information contains a similar sensitivity analysis in which we used the full data set with obesity included to posit distributions for the bias parameters.

TABLE 6.

Estimates and 95% confidence intervals for treatment decision rule parameters $\psi$ from models with and without obesity and adjusted estimates from the sensitivity analysis for unmeasured confounding of obesity.

Covariate	Full model	Obesity unmeasured	Adjusted Est. secondary data	Adjusted est. subject expertise
$A$	−1.56 (−3.11, 0.00)	−1.46 (−3.02, 0.10)	−1.60 (−3.37, 0.12)	−1.48 (−3.13, 0.42)
$A\times \text{SEX}$	0.72 (−0.34, 1.79)	0.69 (−0.38, 1.76)	0.73 (−0.58, 2.05)	0.69 (−0.70, 1.98)
$A\times \text{AGE}$	0.00 (−0.03, 0.03)	0.00 (−0.03, 0.03)	0.00 (−0.04, 0.04)	0.00 (−0.04, 0.04)
$A\times \text{PHQ}$	0.12 (0.02, 0.22)	0.12 (0.02, 0.22)	0.12 (0.00, 0.25)	0.12 (−0.01, 0.24)

5.2 |. Plasmode simulations

We also conducted a plasmode simulation study in which we used the real data with simulated obesity and patient outcomes. This allowed us to know the true optimal DTR and unmeasured confounder distribution. The data were simulated using models 3 and 4 that we used for the real data analysis with the outcome having a random error given by $ϵ\sim N(0,1)$.

We let the value of $\beta$, $\psi$, and $\zeta$ be given by the estimated values from the data that can be found in Section F of the Supporting Information. For conducting the sensitivity analysis, we posited the same normal distributions for ${\beta }_u$ and $\zeta$ that were posited using the small, secondary study for the empirical evaluation in addition to the uniform distributions posited using subject matter expertise. We simulated 1000 data sets and estimated the adjusted parameter estimates for each data set. Table 7 contains the estimates of $\psi$ averaged over the 1000 simulated data sets in addition to the empirical coverage and average width of 95% confidence intervals for $\psi$. The unadjusted estimate for ${\psi }_0$ was biased with an average estimate of −1.432 as opposed to the true value of −1.556. Adjusting for obesity using a secondary study reduced the bias and resulted in an estimate of −1.538. Positing the bias parameter distributions with subject matter expertise resulted in an estimate of −1.446 that was closer to the unadjusted estimate than the true value. The 95% confidence intervals from the unadjusted analysis did not achieve the nominal rate for any of the parameters. Monte Carlo sensitivity analysis resulted in slightly wider intervals that had the correct coverage when we posited the bias parameter distributions using a secondary data set or subject matter expertise.

TABLE 7.

Estimates (Est.), coverage (Cvr.), and average width (Wth.) of 95% confidence intervals for treatment decision rule parameters $\psi$ after adjusting for the unmeasured confounder obesity averaged over 1000 plasmode data sets using data from KPWA.

	Est. ${\psi }_0$	Est. ${\psi }_1$	Est. ${\psi }_2$	Est. ${\psi }_3$
True Value	−1.556	0.724	0.001	0.119
Unadjusted	−1.432	0.714	0.001	0.118
Adjusted—Secondary Data	−1.538	0.721	0.001	0.119
Adjusted—Subject Expertise	−1.446	0.715	0.001	0.119
	Cvr. (Wth.) ${\psi }_0$	Cvr. (Wth.) ${\psi }_1$	Cvr. (Wth.) ${\psi }_2$	Cvr. (Wth.) ${\psi }_3$
Unadjusted	0.822* (0.665)	0.880* (0.455)	0.870* (0.012)	0.880* (0.042)
Adjusted—Secondary Data	0.975* (0.958)	0.949 (0.586)	0.958 (0.016)	0.959 (0.054)
Adjusted—Subject Expertise	0.940 (0.889)	0.953 (0.588)	0.975* (0.018)	0.981* (0.057)

^*indicates coverages that are significantly different than 95%.

6 |. DISCUSSION

We proposed a method for conducting sensitivity analysis for bias due to unmeasured confounding in the estimation of DTRs. We used a Monte Carlo sensitivity analysis to estimate a bias-adjusted DTR and construct confidence intervals for the parameters indexing the optimal regime that account for the uncertainty due to unmeasured confounding. This procedure is straightforward to implement and can be used for continuous or binary unmeasured confounders. This approach was found to perform well for both simulated and real data.

This method requires positing parametric models for the relationship between the unmeasured confounder(s) and the outcome, treatment, and measured confounders. Moreover, the model for the conditional mean of the unmeasured confounder needs to be of high quality, which can be challenging without external data or domain expertise. We also must posit probability distributions for the parameters indexing these models. These distributions do not need to be centered on the true value of the parameter to construct confidence intervals, and they only need the true value to not be in the tails of the distribution. If there are high levels of uncertainty about these parameters, wider distributions can be posited resulting in wider confidence intervals for the parameters indexing the estimated optimal DTR. We posited normal distributions for these parameters, but any probability distribution can be used that accurately reflect the prior information about the true value of these parameters. Here, we focused on DTRs that are estimated using dWOLS, though this approach can be applied to any regression-based method of estimation. Direct-search or value-search estimators are an alternative approach to estimating DTRs that our proposed method could not be directly applied to (Laber and Zhao, 2015; Orellana et al., 2010). We leave extensions to direct-search estimators as future work.

DATA AVAILABILITY STATEMENT

Research data are not shared.