Abstract
Measurements of cell size dynamics have revealed phenomenological principles by which individual cells control their size across diverse organisms. One of the emerging paradigms of cell size homeostasis is the adder, where the cell cycle duration is established such that the cell size increase from birth to division is independent of the newborn cell size. We provide a mechanistic formulation of the adder considering that cell size follows any arbitrary non-exponential growth law. Our results show that the main requirement to obtain an adder regardless of the growth law (the time derivative of cell size) is that cell cycle regulators are produced at a rate proportional to the growth law and cell division is triggered when these molecules reach a prescribed threshold level. Among the implications of this generalized adder, we investigate fluctuations in the proliferation of single-cell derived colonies. Considering exponential cell size growth, random fluctuations in clonal size show a transient increase and then eventually decay to zero over time (i.e., clonal populations become asymptotically more similar). In contrast, several forms of non-exponential cell size dynamics (with adder-based cell size control) yield qualitatively different results: clonal size fluctuations monotonically increase over time reaching a non-zero value. These results characterize the interplay between cell size homeostasis at the single-cell level and clonal proliferation at the population level, explaining the broad fluctuations in clonal sizes seen in barcoded human cell lines.
Introduction
The size of cells critically impacts all aspects of their physiology regulating essential processes including gene expression regulation, nutrient metabolism and proliferation [1–7]. The factors determining cell size, and its maintenance around a desired setpoint specific to a cell type are fundamental questions that have long fascinated biologists. To achieve size homeostasis, cells must synchronize multiple processes such as chromosome replication [8], growth rate [9], cell membrane synthesis [10], organelle duplication [11], and divisome formation [12]. Remarkably, recent findings in bacterial, fungi, animal, and plant cells have uncovered common principles by which aberrations in cell size are corrected through size-dependent duration of cell -cycle stages [13–19].
One such phenomenological principle of cell size homeostasis is the adder, where for an isogenic cell population under stable growth conditions, the size added (or increment) from cell birth to division is uncorrelated with newborn size (Figure 1). Thus, regardless of how large or small a cell is born, the division timing is set to add, on average, a fixed cell size [20, 21]. This constant size increment itself depends on growth conditions and can vary considerably across cell types. For an exponential increase in cell size, an adder implies an inverse correlation between the cell cycle duration and the newborn cell size [22].
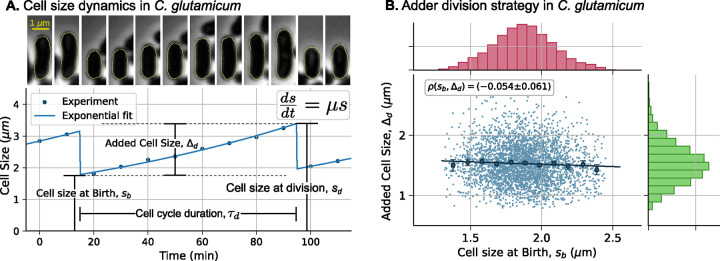
Figure 1: Cell size homeostasis in C. glutamicum occurs via the adder mechanism.
(A) Top: Timelapse of a C. glutamicum cell undergoing division, with one of the newborns randomly chosen for cell size tracking. Bottom: The cell size (quantified by cell length) over time (dots) fits relatively well with exponential growth in cell size (solid line). Key cell cycle variables are illustrated on the plot: the growth law , cell size at birth , cell size at division , added cell size from birth to division (), and cell cycle duration (). (B) Data reveals adder-based cell size control, where is uncorrelated to across C. glutamicum cell cycles. The marginal plots show histograms of cell size at birth (red) and added cell size (green). Data are taken from [34], and we refer readers to this source for experimental details and image segmentation for cell size measurements. The circles on the plot correspond to the mean added size for binned newborn sizes (11 bins), with error bars representing the 95% confidence interval of the mean for each bin. The line represents the linear fit and is the correlation coefficient between and , with the 95% confidence interval obtained using bootstrapping.
The adder was discovered with the development of microfluidic imaging in evolutionary divergent bacteria such as E. coli, B. subtilis [23], C. crescentus [24], and P. aeruginosa [25]. Cell size analysis for organisms more complex than rod-shaped bacteria presents difficulties that have been recently solved. For example, the variable morphology of mammalian cells complicates the estimation of cell size. With advances in methods that combine measurements of cell size and cell mass, it has been observed that the adder principle is prevalent even in different human cell lines [26]. Some of these cell lines exhibit nonexponential growth [26, 27], which poses challenges to existing models that mainly account for the adder in exponentially growing cells [12, 28]. The adder principle has also been observed in different species, including budding yeast [29], Dictyostelium amoebas [30], bacterial strains that exceed exponential growth rates [31], and even flatworms that consistently increase their body area from the head after transverse splitting [32].
In this study, we investigate the minimal theoretical requirements to achieve an adder in cell size dynamics under any arbitrary growth law (the time derivative of cell size). We propose a phenomenological approach that employs a size-dependent division rate that results in an adder with an arbitrary added-size distribution. We compare this approach with an equivalent mechanistic model that involves a cell cycle regulator expressed at a rate proportional to the growth law, with cell division triggered when the regulator reaches a critical threshold level [33]. We show that, under these conditions, stochastically formulated models result in an adder, where the size added from cell birth to division is statistically independent of the initial size.
Recent studies have shown that adder-based cell size homeostasis significantly influences the stochastic dynamics of clonal populations. Specifically, clonal expansion models based on the adder principle produce qualitatively different predictions compared to classical time-based division models [34, 35]. Mathematical predictions and experimental observations indicate that exponentially growing cells exhibit a high degree of clonal size regulation (low stochastic fluctuations) when following the adder mechanism [34]. Motivated by these findings, we investigate how cell proliferation statistics change when cells adhere to growth laws other than exponential cell size dynamics.
Our findings indicate that exponentially growing cells that implement the adder exhibit clonal size fluctuations with a transient increase until the first generation, followed by a decay to zero over time. This means that cell colonies become asymptotically more homogeneous relative to each other in terms of their population size. In contrast, for non-exponential cell size dynamics, clonal size fluctuations increase monotonically over time, leading to greater heterogeneity in clone sizes as they grow. These insights are crucial for understanding noise mechanisms affecting cell lineage expansion, with significant implications for diverse fields such as cancer biology [36], embryogenesis, mutant fixation [37], and microbial ecology [38].
Results
A generalized adder mechanism
In this section, we present a generalized formalism to achieve an adder strategy for cell size regulation. We begin by introducing the main cell cycle variables. Figure 1 illustrates the cell size dynamics during one cell cycle of the gram-positive, rod-shaped bacterium C. glutamicum. Cell cycle begins with the division of the parent cell into two newborn descendants. We randomly select one of these newborns and track its size , over time until its division. For each cell cycle, we measure the cell size at birth and at division , the cell cycle duration , and the size added from birth to division . The relationships between these variables are fundamental for characterizing cell size homeostasis mechanisms. For instance, Figure 1B illustrates the adder mechanism, where the size added from birth to division is uncorrelated with the newborn size.
We assume that the cell is born at time with size . Then, its cell size evolves according to the time-varying ordinary differential equation:
| (1) |
where is a timekeeper variable measuring the time spent within the cell cycle since birth. The function is referred to as the growth law and is allowed to be an arbitrary function of the cell size and timer. Given an initial size at birth , the growth law is assumed to take a form that results in a unique solution for all . The positivity of the growth law ensures a strictly monotonic increase in cell size over time until the cell undergoes division. We define another monotonically increasing function:
| (2) |
that is the size added at time after cell birth with . Considering as the cell cycle duration, a random variable, one can define the added size from cell birth to division as:
| (3) |
Note that since both and are random variables, is also a random variable, having different values for different cell cycles (Figure 1B). Our aim is to define a propensity for cell division that ensures two properties:
An adder for any growth law where the added size becomes independent of the newborn size . Note that while experimentally an adder is often characterized by being uncorrelated to (as in Figure 1B), here we impose a stricter condition of statistical independence.
The added size follows an arbitrary given probability density function (pdf) , i.e, the probability that the added size is in the interval , follows the equation:
| (4) |
Our key result is as follows: given and at any time instant in the cell cycle, a cell division event occurs with propensity , i.e., the probability of division in the next infinitesimal time interval is , where is an arbitrary positively valued function of the added size. Referring the reader to supplementary section S1 for a detailed proof, with the chosen division propensity, becomes independent of with pdf satisfying
| (5) |
Conversely, it can be shown that choosing
| (6) |
implements an adder for any arbitrary . Thus, irrespective of newborn size and growth law, the cell cycle timing is set such that the added size is an independent and identically distributed random variable with pdf . As a simple example, the division propensity for a constant results in being an exponentially-distributed random variable with mean . Here, we use the notation to denote the operation of expected value. Similarly, for this example, the randomness of , quantified by the squared coefficient of variability
| (7) |
satisfies .
Upon cell divsion, the size and timer are reset as
| (8) |
which correspond to selection of one of the daughters for further size tracking. In addition, is an independent and identically distributed random variable. For symmetric division in which mother cell size is approximated halved between daughters, the mean value of is , and its squared coefficient of variation quantifies the error in size partitioning between daughters [39]. In general, it is possible to consider any arbitrary mean for non-symmetric cell size partitioning, as occurs in the case of budding yeast [40]. For , the newborn cell size statistics (mean and coefficient of variation squared, respectively) are given by [39, 41, 42]
| (9a) |
| (9b) |
Note from (9b) that the noise in the newborn size is much more sensitive to errors in cell size partitioning than the noise in added size . This point is more clearly seen in the limit when (9b) simplifies to
| (10) |
which means that contributes approximately of its noise to the newborn cell size variability while contributes only of its noise.
Mechanistic implementation of the adder
In order to have a biological interpretation for the division propensity, we provide a mechanistic framework for implementing the adder size control. Consider a timekeeping regulator that accumulates from zero molecules at the time of cell birth. The molecules of this regulator are assumed to be stable with a long half-life and synthesized according to a Poisson process with a rate proportional to the growth law. A special case of this is the exponential growth law , where the division regulator is produced at a rate proportional to cell size [12, 28]. The theoretical foundation of this mechanism has been investigated in several previous works [25, 43, 44]. The number of molecules of our regulator is a random process with integer values, with transitions from to molecules occurring stochastically with propensity (Figure 2A). From a biological perspective, the rate of change in cell size corresponds to the global protein production rate. Therefore, the synthesis rate can be naturally interpreted as indicating that there is a fraction of proteome synthesis allocated to the expression of cell cycle regulators [45]. A cell division event is triggered when the cell cycle regulator accumulates to a threshold of molecules, and the regulator is subsequently degraded during cytokinesis so that newborns restart the cycle with zero molecules.
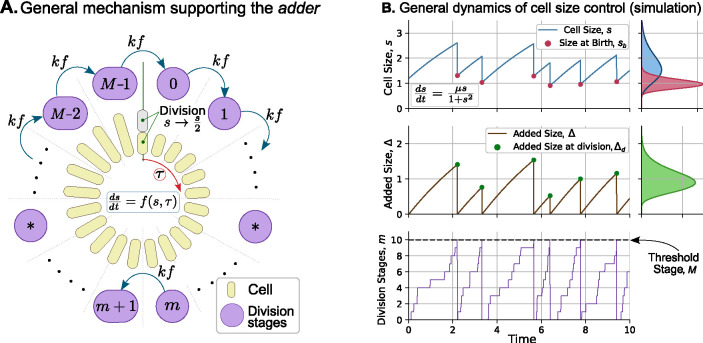
Figure 2: A general mechanism implementing adder based cell size homeostasis.
(A) The cell size grows according to (1) with an arbitrary growth law . During the cell cycle, cell performs transitions between different stages at a rate proportional to the growth law, . Upon reaching the M-th stage, the cell divides, and the newborns restart the cell cycle from stage . Alternatively, can be interpreted as the number of molecules of a stable cell cycle regulator expressed at a rate , with cell division triggered upon reaching a critical threshold of molecules. (B) Simulation of cell size over time for a general non-exponential growth law. Top: Cell size over time (solid line) showing different values of size at birth (red dots). The marginal plot shows their respective steady-state distribution. Middle: Added cell size as a function of time (solid line) showing different values of added size at division (green dots). The marginal plot shows the distribution of added size from cell birth to division. Bottom: Crossing of division stages over time. Once the cell reaches stage (threshold stage), it undergoes cell division, and the stage is reset to . Simulation parameters: , . The resets in cell size upon division were modeled as per (8) with with probability one.
Alternatively, can be interpreted as the number of stages a cell must pass through from birth until division. Newborns start with , and the transition between stages occurs stochastically with propensity . In each transition from to , the added cell size is an exponentially distributed random variable with a mean of . Since there are such transitions to reach the division threshold, the total added size during the cell cycle follows an Erlang distribution with a mean of and a squared coefficient of variation (Figure 2B):
| (11) |
To connect this interpretation with our general theory, we observe that it is possible to obtain an associated propensity by estimating using the Erlang distribution as in (6). This mechanistic interpretation of the generalized adder has recently been applied in the analysis of cancer cells that were characterized by their higher [36] compared to healthy ones.
This multi-step framework can be extended to different scenarios leading to an adder but with higher stochasticity in the added size. These scenarios include:
The rates of transition from to can be generalized to be , . In that case, the added size is a sum of independent exponential random variables, each with mean [41].
As previously done for the case of exponential growth [28], the expression of the regulator can occur in bursts, where bursts arrive as a non-homogeneous Poisson process with rate , and each burst creates several molecules that are itself drawn from a size-invariant distribution.
Finally, there could be statistical fluctuations in parameters and across cell cycles that correspond to some form of extrinsic noise in combination with the intrinsic noise of the regulator copy numbers.
Our proposed generalized model, while ensuring an adder regardless of the growth rate specifics, can be modified to capture other paradigms of cell size homeostasis, such as timer (cell cycle duration is independent of newborn size) or sizer (division size is independent of newborn size) [20, 46]. Such cases often result in an added size becoming correlated with the size at birth. For example, an adder-sizer combination would result in a negative correlation between and as in fission yeast [47] and slow-growing E. Coli cells [48]. This adder-sizer can be predicted by modifications to this mechanism, such as reversible steps in the stage-crossing process related to degradation of the division regulator [12, 48, 49]. Alternatively, this adder-sizer can also be modeled by accumlation of the regulator with a rate corresponding to size-dependent proteome allocation to regulator synthesis [46, 48, 50]. Here captures the negative (positive) correlations between the added size and newborn size. Finally, the description of the division process using propensities has opened new perspectives in the characterization, not only of division strategies, but also of cell size dynamics across multiple cell species [46, 51, 52].
In summary, we have described both a phenomenological approach and a mechanistic approach implementing cell size homeostasis as per the adder principle irrespective of the growth law, and this approach can be easily generalized to other forms of cell size control.
Clonal proliferation dynamics for different adders depends on the growth law
Next, we explore how cell size regulation at the single-cell level propagates across generations to affect the colony population. Can different types of growth laws yield qualitatively different fluctuations in clonal size, even though cell size control remains an adder? To illustrate this, consider a cell colony that begins with a newborn cell (the progenitor) of size . Given that division events occur stochastically, the number of descendant cells from the single progenitor is a stochastic process. To characterize the random variability of the colony population size, we use its statistical moments: the mean number of cells in the colony and the population noise quantified by , the squared coefficient of variation of . We are specifically interested in connecting the transient dynamics of to the growth law in (1) for an adder with given statistical properties of .
Modeling approach for computing
Statistical moments of can be approximated analytically [35] or numerically [53] in particular cases. To have a more accurate approach, in this article, we use individual-based simulation algorithms to simulate clonal expansion [34]. The stochastic timing of division is set by the requirement of the added size to division for each newborn cell to follow a prescribed distribution , and each division event results in addition of two newborns to the population. To better illustrate the effect of the growth law on , we simplify the approach by considering that all clonal replicas start with a single newborn with the same size, all cells follow the same growth law (i.e., no intercellular differences in growth rate). We further assume the added size to follow a gamma distribution with mean (arbitrary units) and noise in added size . Note from (9a) that this choice of fixes the average size of the newborn cell to always be . In this scenario, stochasticity in the added size is the only source of noise impacting clonal size dynamics and we modulate this noise level by considering two cases: a high noise and a low noise in .
Referring the reader to supplementary section S2 for details on our simulation algorithm, we present sample trajectories of cell size, clonal population size, and total biomass (sum of cell sizes of all descendant cells at a given time point) in Figure 3 for exponential (top panel) and non-exponential growth in cell size (bottom panel).
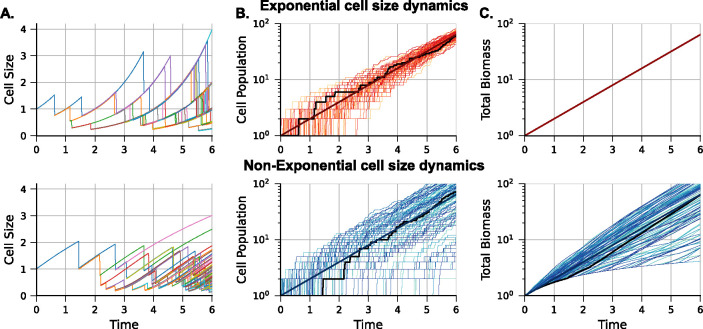
Figure 3: Illustration of sample trajectories for cell size, clonal population size, and total biomass for exponential and non-exponential cell size dynamics, with cell division timing set according to the adder.
(A) (top panel) Cell size dynamics for exponentially and (bottom panel) non-exponentially growing cells within a proliferating colony. Different colors represent different descendants of the colony progenitor. In both cases, size control follows the adder model, where the size added () in each cell cycle is an independent and identically distributed random variable following an exponential distribution with and . (B) Examples of clonal population size over time for simulated colonies. Each colony starts with a newborn progenitor cell with size a.u. The black line represents the colony in (A), and the dark red line is the mean population number. The y-axis is on a logarithmic scale. (C) Total colony biomass, defined as the sum of the cell sizes of all descendant cells at a given time. When all colonies start with the same-sized progenitor, the biomass is given by (13). For the exponential case (top panel), the total biomass does not vary across colony replicas, while for the nonexponential case (bottom panel), biomass shows considerable inter-colony differences.
As an example of non-exponential growth law, we use
| (12) |
that was previously reported based on experiments measuring the proliferation potential of cell size-sorted human and Drosophila cells [54, 55].
Exponential cell size dynamics
Our results show that for exponential cell size dynamics with in (1), increases from zero reaching its maximum around the first division and then decreases monotonically to zero over time (Figure 4A). Thus, as the average clonal size expands exponentially (Figure 3B top), the interclonal population size differences asymptotically vanish. The difference between low-noise () and high-noise () in added size is the transient behavior of , with exhibiting a lower peak value of and oscillatory dynamics (Figure 4A).
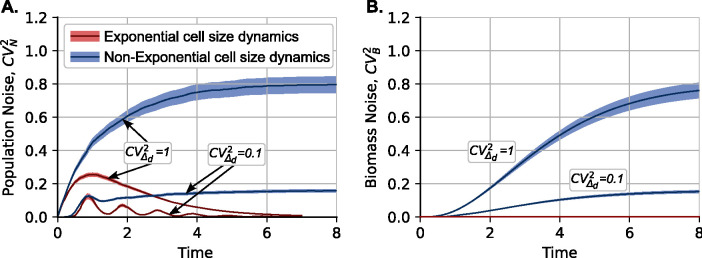
Figure 4: Cell size dynamics qualitatively impact the stochastic dynamics of clonal population size.
(A) Plot of the squared coefficient of variation of clonal size () over time for cell size dynamics following exponential and non-exponential growth laws as described in Figure 3. In all cases, cell size homeostasis occurs according to the adder model, with following a gamma distribution with and two values of corresponding to high noise and low noise . For exponential cell size dynamics, exhibits a transient peak and then approaches zero as . In stark contrast, increases over time to asymptotically approach a non-zero value for non-exponential cell size dynamics. Lowering the noise in the added size results in lower values of . (B) Plot of the squared coefficient of variation of total biomass, i.e., the aggregated size of all cells in a colony. For the exponential case, due to (13), while monotonically increases over time in the non-exponential case, exhibiting similar asymptotic values to . All coefficients of variation are computed based on 5000 colony replicas, with colored regions representing the 95% confidence interval obtained using bootstrapping.
To intuitively understand why as it might be useful to consider the net biomass of the colony which is the aggregate size of all cells in a colony at a given time. For exponential cell size dynamics, the total biomass follows the simple expression
| (13) |
where is the cell size of the progenitor cell that is assumed to be the same across colony replicas. Thus, despite the fact that the number of cells is variable from colony to colony, the total biomass is fixed between colonies at any time with the coefficient of variation . When the number of cells in the colony is very large (each having random differences in cell size), by the central limit theorem one could approximate , where is the average steady-state cell size. From this approximation, it can be seen that
| (14) |
Note that for (14) to hold, the noise in cell size has to be bounded . This property is ensured by cell size homeostasis mechanisms. A particular case where (14) does not hold is the timer-based cell division. In this mechanism, cell cycle duration is a size-independent random variable. Such timer-based are known to be non-homeostatic with variance in cell size increasing unboundedly over time [56].
Non-exponential cell size dynamics
Interestingly, a qualitatively different result emerges when cell size dynamics follow non-exponential dynamics. This stark contrast is illustrated in Figure 3C. Unlike the exponential case, where biomass is given by (13) with no interclonal variability , the non-exponential case shows biomass differences between clones due to the history of cell division events in the colony . The variability in biomass across colony replicas is quantified in Figure 4B, where the biomass coefficient of variation increases monotonically over time, eventually reaching a positive value. Tighter cell size regulation results in lower values ( compared to ). Consequently, as indicated by (14), since , the population noise does not decay to zero but instead reaches a positive value after several generations (Figure 4A). Although and are both zero at the start of clonal expansion, simulations confirm that . However, as shown in Figure 4, the transient profiles of these noises and differ. Additional examples of the effect of non-linearity in the growth law on clonal size noise are provided in the supplementary section S3.
Discussion
An important contribution of this article is to formulate a systems-level stochastic model implementing adder-based cell size homeostasis for any arbitrary cell size dynamics. This is achieved by appropriately defining a stochastic propensity of cell division events that ensures that the added size from cell birth to division is a random variable independent of newborn size and follows a given distribution . At any instant in the cell cycle, this propensity is given as the product of two functions: the growth law in (1); and a function defined in (6) of the added size since birth to that cell cycle time instant. We also proposed a mechanistic implementation of this scheme, which consists of a cell division regulator synthesized at a rate proportional to the cell size growth law, and division is triggered upon reaching a prescribed threshold level (Figure 2). In the context of bacteria, a potential regulator could be the FtsZ protein that polymerizes to form a ring (Z-ring) defining the site of division and recruiting other division proteins to the site [12]. The generalization of the adder presented here is particularly relevant given recent findings of an adder in several human cell lines [26, 57] despite exhibiting non-exponential cell size dynamics (see Figure 4 in [26]).
We connect adder-based cell size control at the single-cell level to variations in clonal size at the population level, as quantified by the coefficient of variation of cell number across colony replicates. The main finding is that despite having exactly similar adder mechanisms, the growth law qualitatively changes the stochastic dynamics of clonal population expansion. For exponential cell size dynamics, our results show a transient peak in that decays to zero over time (Figure 4A), while for the non-exponential case, increases over time to reach a positive steady-state limit (Figure 4B). These qualitative differences can be explained by looking at the dynamics of the total colony biomass. Exponentially growing cells show smooth exponential growth of biomass that increases as in (13) and is invariant of the timing specifics of individual division events. In contrast, cells with non-exponential growth yield a colony biomass that depends on the history of division events (Figure 3C). The latter non-exponential scenario results in colony-to-colony biomass fluctuations that increase over time (Figure 4B), resulting in higher levels of approaching a non-zero steady state value as per (14).
An important limitation of the results presented in Figures 3–4 is that we considered the timing of cell division events as the only source of noise in the colony expansion process. Several biologically realistic factors, such as variability in the size of the initial progenitor cell and growth rate fluctuations, were ignored. In supplementary section S4, we repeated simulations of clonal expansion with these additional noise sources and, as expected, we observe that they amplify both and (Figure S2).
These findings have important implications for understanding the clonal expansion of cancer cells, for example, measured through barcoding technologies. More specifically, each cell receives a unique barcode at an initial time, and after several generations of clonal expansion, the number of cells in each barcode (or clone) is determined. Taking data from a recent publication on a melanoma cell line [58], we find a large variability in clonal population size at the endpoint (). Given that many human cell lines exhibit non-exponential cell size dynamics [26], this value is consistent with our results in Figure 4, where approaches a positive steady state. However, given the large variability seen in the data, it may be necessary to include other noise mechanisms (such as differences in the growth rate of single cancer cells within the same isogenic population) to capture the experimentally observed . In contrast, cells with tighter cell size regulation and exponential growth, as seen with some bacterial species, yield lesser inter-clonal population size fluctuations [34]. Our study motivates time-resolved measurements of to systematically discern the noise sources driving clonal expansion differences, and such differences have important medical consequences driving single-cell heterogeneity in response to targeted cancer drug therapy [58–62].
Supplementary Material
Acknowledgments
AS acknowledges the support of NIH-NIGMS via grant R35GM148351.
Footnotes
Competing interests
The authors have no conflict of interest to declare.
Artificial intelligence
The authors declare that they did not use generative AI and AI-assisted technologies in the writing process.
Data accessibility statement
The simulation code used for these plots is publicly available at https://doi.org/10.5281/zenodo.13251255 [63].
References
- [1].Marshall Wallace F, Young Kevin D, Swaffer Matthew, Wood Elizabeth, Nurse Paul, Kimura Akatsuki, Frankel Joseph, Wallingford John, Walbot Virginia, Qu Xian, et al. What determines cell size? BMC Biology, 10:1–22, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Ginzberg Miriam B, Kafri Ran, and Kirschner Marc. On being the right (cell) size. Science, 348(6236):1245075, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Lloyd Alison C. The regulation of cell size. Cell, 154(6):1194–1205, 2013. [DOI] [PubMed] [Google Scholar]
- [4].Chadha Yagya, Khurana Arohi, and Schmoller Kurt M. Eukaryotic cell size regulation and its implications for cellular function and dysfunction. Physiological Reviews, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Guillemin Anissa and Stumpf Michael PH. Noise and the molecular processes underlying cell fate decision-making. Physical Biology, 18(1):011002, 2020. [DOI] [PubMed] [Google Scholar]
- [6].Schwabe A, Dobrzyński M, Rybakova K, Verschure P, and Bruggeman FJ. Origins of stochastic intracellular processes and consequences for cell-to-cell variability and cellular survival strategies. In Methods in enzymology, volume 500, pages 597–625. Elsevier, 2011. [DOI] [PubMed] [Google Scholar]
- [7].Robinson Dana O, Coate Jeremy E, Singh Abhyudai, Hong Lilan, Bush Max, Doyle Jeff J, and Roeder Adrienne HK. Ploidy and size at multiple scales in the Arabidopsis sepal. The Plant Cell, 30(10):2308–2329, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Wallden Mats, Fange David, Lundius Ebba Gregorsson, Baltekin Özden, and Elf Johan. The synchronization of replication and division cycles in individual E. coli cells. Cell, 166(3):729–739, 2016. [DOI] [PubMed] [Google Scholar]
- [9].Xie Shicong and Skotheim Jan M. A G1 sizer coordinates growth and division in the mouse epidermis. Current Biology, 30(5):916–924, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Opalko Hannah E, Miller Kristi E, Kim Hyun-Soo, Vargas-Garcia Cesar Augusto, Singh Abhyudai, Keogh Michael-Christopher, and Moseley James B. Arf6 anchors cdr2 nodes at the cell cortex to control cell size at division. Journal of Cell Biology, 221(2):e202109152, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Costello Rona, Emms David M, and Kelly Steven. Gene duplication accelerates the pace of protein gain and loss from plant organelles. Molecular Biology and Evolution, 37(4):969–981, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Si Fangwei, Treut Guillaume Le, Sauls John T, Vadia Stephen, Levin Petra Anne, and Jun Suckjoon. Mechanistic origin of cell-size control and homeostasis in bacteria. Current Biology, 29(11):1760–1770, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Zatulovskiy Evgeny and Skotheim Jan M. On the molecular mechanisms regulating animal cell size homeostasis. Trends in Genetics, 36(5):360–372, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Willis Lisa, Refahi Yassin, Wightman Raymond, Landrein Benoit, Teles José, Huang Kerwyn Casey, Meyerowitz Elliot M, and Jönsson Henrik. Cell size and growth regulation in the Arabidopsis thaliana apical stem cell niche. Proceedings of the National Academy of Sciences, 113(51):E8238–E8246, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Liu Shixuan, Ginzberg Miriam Bracha, Patel Nish, Hild Marc, Leung Bosco, Li Zhengda, Chen Yen-Chi, Chang Nancy, Wang Yuan, Tan Ceryl, et al. Size uniformity of animal cells is actively maintained by a p38 gabifcmacedo -dependent regulation of G1-length. Elife, 7:e26947, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Schmoller Kurt M., Turner J. J., Koivomagi M., and Skotheim Jan M.. Dilution of the cell cycle inhibitor Whi5 controls budding-yeast cell size. Nature, 526:268–272, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Amir Ariel. Cell size regulation in bacteria. Physical Review Letters, 112:208102, 2014. [Google Scholar]
- [18].Garmendia-Torres Cecilia, Tassy Olivier, Matifas Audrey, Molina Nacho, and Charvin Gilles. Multiple inputs ensure yeast cell size homeostasis during cell cycle progression. Elife, 7:e34025, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Rhind N.. Cell-size control. Current Biology, 31(21):R1414–R1420, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Sauls John T, Li Dongyang, and Jun Suckjoon. Adder and a coarse-grained approach to cell size homeostasis in bacteria. Current Opinion in Cell Biology, 38:38–44, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Campos Manuel, Surovtsev Ivan V, Kato Setsu, Paintdakhi Ahmad, Beltran Bruno, Ebmeier Sarah E, and Jacobs-Wagner Christine. A constant size extension drives bacterial cell size homeostasis. Cell, 159(6):1433–1446, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Vargas-Garcia Cesar A, Ghusinga Khem Raj, and Singh Abhyudai. Cell size control and gene expression homeostasis in single-cells. Current Opinion in Systems Biology, 8:109–116, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Taheri-Araghi Sattar, Bradde Serena, Sauls John T, Hill Norbert S, Levin Petra Anne, Paulsson Johan, Vergassola Massimo, and Jun Suckjoon. Cell-size control and homeostasis in bacteria. Current Biology, 25(3):385–391, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Iyer-Biswas Srividya, Wright Charles S, Henry Jonathan T, Lo Klevin, Burov Stanislav, Lin Yihan, Crooks Gavin E, Crosson Sean, Dinner Aaron R, and Scherer Norbert F. Scaling laws governing stochastic growth and division of single bacterial cells. Proceedings of the National Academy of Sciences, 111(45):15912–15917, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Deforet Maxime, Van Ditmarsch Dave, and Xavier Joao B. Cell-size homeostasis and the incremental rule in a bacterial pathogen. Biophysical Journal, 109(3):521–528, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Liu Xili, Yan Jiawei, and Kirschner Marc W. Cell size homeostasis is tightly controlled throughout the cell cycle. PLoS Biology, 22(1):e3002453, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Sung Yongjin, Tzur Amit, Oh Seungeun, Choi Wonshik, Li Victor, Dasari Ramachandra R, Yaqoob Zahid, and Kirschner Marc W. Size homeostasis in adherent cells studied by synthetic phase microscopy. Proceedings of the National Academy of Sciences, 110(41):16687–16692, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Ghusinga Khem Raj, Vargas-Garcia Cesar A, and Singh Abhyudai. A mechanistic stochastic framework for regulating bacterial cell division. Scientific Reports, 6:30229, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Chandler-Brown Devon, Schmoller Kurt M, Winetraub Yonatan, and Skotheim Jan M. The adder phenomenon emerges from independent control of pre-and post-start phases of the budding yeast cell cycle. Current Biology, 27(18):2774–2783, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Tanaka Masahito, Kitanishi-Yumura Toshiko, and Yumura Shigehiko. A ‘dynamic adder model’for cell size homeostasis in Dictyostelium cells. Scientific Reports, 11(1):13742, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Cylke Arianna and Banerjee Shiladitya. Super-exponential growth and stochastic size dynamics in rod-like bacteria. Biophysical Journal, 122(7):1254–1267, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Carter Jason A, Lind Christine H, Truong M Phuong, and Collins Eva-Maria S. To each his own: reproductive strategies and success of three common planarian species: Schmidtea mediterranea, dugesia japonica, and dugesia tigrina. Journal of Statistical Physics, 161:250–272, 2015. [Google Scholar]
- [33].Panlilio Mia, Grilli Jacopo, Tallarico Giorgio, Iuliani Ilaria, Sclavi Bianca, Cicuta Pietro, and Lagomarsino Marco Cosentino. Threshold accumulation of a constitutive protein explains e. coli cell-division behavior in nutrient up-shifts. Proceedings of the National Academy of Sciences, 118(18):e2016391118, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nieto César, Täuber Sarah, Blöbaum Luisa, Vahdat Zahra, Grünberger Alexander, and Singh Abhyudai. Coupling cell size regulation and proliferation dynamics of C. glutamicum reveals cell division based on surface area. bioRxiv, 2023. [Google Scholar]
- [35].Jones Eric W, Derrick Joshua, Nisbet Roger M, Ludington William B, and Sivak David A. First-passage-time statistics of growing microbial populations carry an imprint of initial conditions. Scientific Reports, 13(1):21340, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Jones Ian, Dent Lucas, Higo Tomoaki, Roumeliotis Theodoros, Garcia Maria Arias, Shree Hansa, Choudhary Jyoti, Pedersen Malin, and Bakal Chris. Characterization of proteome-size scaling by integrative omics reveals mechanisms of proliferation control in cancer. Science Advances, 9(4):eadd0636, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Muñoz-Gómez Sergio A, Bilolikar Gaurav, Wideman Jeremy G, and Geiler-Samerotte Kerry. Constructive neutral evolution 20 years later. Journal of Molecular Evolution, 89(3):172–182, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Sen Rishika, Nayak Losiana, and De Rajat Kumar. A review on host–pathogen interactions: classification and prediction. European Journal of Clinical Microbiology & Infectious Diseases, 35(10):1581–1599, 2016. [DOI] [PubMed] [Google Scholar]
- [39].Modi Saurabh, Vargas-Garcia Cesar Augusto, Ghusinga Khem Raj, and Singh Abhyudai. Analysis of noise mechanisms in cell-size control. Biophysical Journal, 112(11):2408–2418, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Turner Jonathan J, Ewald Jennifer C, and Skotheim Jan M. Cell size control in yeast. Current Biology, 22(9):R350–R359, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Nieto César, Vargas-Garcia Cesar Augusto, and Singh Abhyudai. A moments-based analytical approach for cell size homeostasis. IEEE Control Systems Letters, 2024. [Google Scholar]
- [42].Thomas Philipp. Analysis of cell size homeostasis at the single-cell and population level. Frontiers in Physics, 6:64, 2018. [Google Scholar]
- [43].Basan Markus, Zhu Manlu, Dai Xiongfeng, Warren Mya, Sévin Daniel, Wang Yi-Ping, and Hwa Terence. Inflating bacterial cells by increased protein synthesis. Molecular Systems Biology, 11(10):836, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Nieto César, Blanco Sergio Camilo, Vargas-García César, Singh Abhyudai, and Manuel Pedraza Juan. PyEcoLib: a python library for simulating stochastic cell size dynamics. Physical Biology, 20(4):045006, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Bertaux François, Kügelgen Julius Von, Marguerat Samuel, and Shahrezaei Vahid. A bacterial size law revealed by a coarse-grained model of cell physiology. PLoS Computational Biology, 16(9):e1008245, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Nieto César, Arias-Castro Juan, Sánchez Carlos, Vargas-García César, and Pedraza Juan Manuel. Unification of cell division control strategies through continuous rate models. Physical Review E, 101(2):022401, 2020. [DOI] [PubMed] [Google Scholar]
- [47].Miller Kristi E, Vargas-Garcia Cesar, Singh Abhyudai, and Moseley James B. The fission yeast cell size control system integrates pathways measuring cell surface area, volume, and time. Current Biology, 33(16):3312–3324, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Nieto César, Augusto Vargas-García César, Pedraza Juan Manuel, and Singh Abhyudai. Mechanisms of cell size regulation in slow-growing escherichia coli cells: discriminating models beyond the adder. npj Systems Biology and Applications, 10(1):61, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].ElGamel Motasem and Mugler Andrew. Effects of molecular noise on cell size control. Physical Review Letters, 132(9):098403, 2024. [DOI] [PubMed] [Google Scholar]
- [50].Jia Chen, Singh Abhyudai, and Grima Ramon. Cell size distribution of lineage data: analytic results and parameter inference. Iscience, 24(3):102220, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Miotto Mattia, Scalise Simone, Leonetti Marco, Ruocco Giancarlo, Peruzzi Giovanna, and Gosti Giorgio. A size-dependent division strategy accounts for leukemia cell size heterogeneity. Communications Physics, 7(1):248, 2024. [Google Scholar]
- [52].Jia Chen, Singh Abhyudai, and Grima Ramon. Characterizing non-exponential growth and bimodal cell size distributions in fission yeast: An analytical approach. PLoS Computational Biology, 18(1):e1009793, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Nieto César, Vargas-García César, Pedraza Juan Manuel, and Singh Abhyudai. Cell size control shapes fluctuations in colony population. In 2022 IEEE 61st Conference on Decision and Control (CDC), pages 3219–3224. IEEE, 2022. [Google Scholar]
- [54].Miettinen Teemu P and Björklund Mikael. Cellular allometry of mitochondrial functionality establishes the optimal cell size. Developmental Cell, 39(3):370–382, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Vargas-Garcia Cesar A, Björklund Mikael, and Singh Abhyudai. Modeling homeostasis mechanisms that set the target cell size. Scientific Reports, 10(1):13963, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Vargas-García César Augusto,Soltani Mohammad, and Singh Abhyudai. Conditions for cell size homeostasis: A stochastic hybrid systems approach. IEEE Life Sciences Letters, 2:47–50, 2016. [Google Scholar]
- [57].Cadart Clotilde, Monnier Sylvain, Grilli Jacopo, Sáez Pablo J, Srivastava Nishit, Attia Rafaele, Terriac Emmanuel, Baum Buzz, Marco Cosentino-Lagomarsino, and Matthieu Piel. Size control in mammalian cells involves modulation of both growth rate and cell cycle duration. Nature Communications, 9(1):3275, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Harmange Guillaume, Hueros Raúl A Reyes, Schaff Dylan L, Emert Benjamin, Saint-Antoine Michael, Kim Laura C, Niu Zijian, Nellore Shivani, Fane Mitchell E, Alicea Gretchen M, et al. Disrupting cellular memory to overcome drug resistance. Nature Communications, 14(1):7130, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Shaffer Sydney M, Dunagin Margaret C, Torborg Stefan R, Torre Eduardo A, Emert Benjamin, Krepler Clemens, Beqiri Marilda, Sproesser Katrin, Brafford Patricia A, Xiao Min, et al. Rare cell variability and drug-induced reprogramming as a mode of cancer drug resistance. Nature, 546(7658):431–435, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Piho Paul and Thomas Philipp. Feedback between stochastic gene networks and population dynamics enables cellular decision-making. Science Advances, 10(21):eadl4895, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Chang Chewei Anderson, Jen Jayu, Jiang Shaowen, Sayad Azin, Mer Arvind Singh, Brown Kevin R, Nixon Allison ML, Dhabaria Avantika, Tang Kwan Ho, Venet David, et al. Ontogeny and vulnerabilities of drug-tolerant persisters in HER2+ breast cancer. Cancer discovery, 12(4):1022–1045, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Pu Yi, Li Lu, Peng Haoning, Liu Lunxu, Heymann Dominique, Robert Caroline, Vallette François, and Shen Shensi. Drug-tolerant persister cells in cancer: the cutting edges and future directions. Nature Reviews Clinical Oncology, 20(11):799–813, 2023. [DOI] [PubMed] [Google Scholar]
- [63].Cesar Nieto. Simulator for the article: “A generalized adder mechanism for cell size homeostasis: Implications for stochastic dynamics of clonal proliferation. Zenodo. 10.5281/zenodo.13251255“, August 2024. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The simulation code used for these plots is publicly available at https://doi.org/10.5281/zenodo.13251255 [63].