Interpretable machine learning for allergic rhinitis prediction among preschool children in Urumqi, China

Abstract

This study aimed to investigate the advantages and applications of machine learning models in predicting the risk of allergic rhinitis (AR) in children aged 2–8, compared to traditional logistic regression. The study analyzed questionnaire data from 7131 children aged 2–8, which was randomly divided into training, validation, and testing sets in a ratio of 55:15:30, repeated 100 times. Predictor variables included parental allergy, medical history during the child’s first year (cfy), and early life environmental factors. The time of first onset of AR was restricted to after the age of 1 year to establish a clear temporal relationship between the predictor variables and the outcome. Feature engineering utilized the chi-square test and the Boruta algorithm, refining the dataset for analysis. The construction utilized Logistic Regression (LR), Support Vector Machine (SVM), Random Forest (RF), and Extreme Gradient Boosting Tree (XGBoost) as the models. Model performance was evaluated using the area under the receiver operating characteristic curve (AUROC), and the optimal decision threshold was determined by weighing multiple metrics on the validation sets and reporting results on the testing set. Additionally, the strengths and limitations of the different models were comprehensively analyzed by stratifying gender, mode of birth, and age subgroups, as well as by varying the number of predictor variables. Furthermore, methods such as Shapley additive explanations (SHAP) and purity of node partition in Random Forest were employed to assess feature importance, along with exploring model stability through alterations in the number of features. In this study, 7131 children aged 2–8 were analyzed, with 524 (7.35%) diagnosed with AR, with an onset age ranging from 2 to 8 years. Optimal parameters were refined using the validation set, and a rigorous process of 100 random divisions and repeated training ensured robust evaluation of the models on the testing set. The model construction involved incorporating fourteen variables, including the history of allergy-related diseases during the child’s first year, familial genetic factors, and early-life indoor environmental factors. The performance of LR, SVM, RF, and XGBoost on the unstratified data test set was 0.715 (standard deviation = 0.023), 0.723 (0.022), 0.747 (0.015), and 0.733 (0.019), respectively; the performance of each model was stable on the stratified data, and the RF performance was significantly better than that of LR (paired samples t-test: p < 0.001). Different techniques for evaluating the importance of features showed that the top5 variables were father or mother with AR, having older siblings, history of food allergy and father’s educational level. Utilizing strategies like stratification and adjusting the number of features, this study constructed a random forest model that outperforms traditional logistic regression. Specifically designed to detect the occurrence of allergic rhinitis (AR) in children aged 2–8, the model incorporates parental allergic history and early life environmental factors. The selection of the optimal cut-off value was determined through a comprehensive evaluation strategy. Additionally, we identified the top 5 crucial features that greatly influence the model’s performance. This study serves as a valuable reference for implementing machine learning-based AR prediction in pediatric populations.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-73733-w.

Background

Allergic rhinitis (AR) is a chronic condition characterized by an IgE-mediated immune response to allergenic triggers, manifesting with symptoms like nasal itching, congestion, sneezing, and a runny nose¹. Globally, AR affects an estimated 1.4 billion individuals and its prevalence is on the rise². Predominantly observed in children and adolescents, AR affects around 12.5% of children aged 3–6 years³ and 35% of adolescents aged 13–14 years⁴, with a reported lifespan persistent AR prevalence of 19.93%. Symptoms such as nasal congestion, nasal leakage, and medication use impact sleep quality and mental well-being, leading to heightened sensitivity to triggers, reduced focus, emotional distress, and diminished quality of life in AR patients. AR also contribute to indirect losses later in life due to school or work absenteeism, medical consultations, diagnostics, treatments, and preventive measures, imposing a significant socio-economic burden^5–7. Furthermore, AR elevates the risk of various comorbidities, including asthma in children. Early prediction and identification of AR are crucial for exploring underlying pathologies and initiating prompt treatment^8,9. The development of AR is influenced by a combination of genetic and environmental factors¹⁰, with parental allergies and exposure to environmental risks playing pivotal roles. Therefore, predicting AR in preschoolers based on familial genetic and early-life environmental factors to enable screening and early intervention for high-risk populations represents a vital yet often overlooked research focus.

Machine learning (ML) in computer science aims to discern patterns in data to enhance performance, particularly in complex tasks¹¹. Recent years have seen a surge in interest and acknowledgment of machine learning among scientists, driven by advancements in statistical theory and computer technology. Innovative machine learning algorithms are extensively employed to develop disease prediction models, outperforming traditional approaches¹². Concurrently, the application of machine learning in advancing children’s health has grown, offering insights into identifying, predicting, and managing children’s health issues and related adverse outcomes¹³. For example, Sarabu C et al. used real-world survey data from a mobile research platform to predict the occurrence and severity of symptoms related to allergic rhinitis in middle-aged and elderly individuals¹⁴. In a different study, Yang J et al. employed a chain-integrated neural network model for multi-label prediction of characteristics of allergic rhinitis patients, serving as a valuable resource for diagnosing clinical rhinitis and guiding treatment¹⁵.

However, there is a lack of research on using interpretable machine learning algorithms for the prediction of allergic rhinitis in children .Therefore, the purpose of this study is to develop a machine learning model that predicts the risk of allergic rhinitis in children aged 2–8 years while ensuring the temporal relationship between predictors and allergic rhinitis. Additionally, the study aims to evaluate features using a model interpretability method, providing insights to support population-based healthcare practices for allergic rhinitis in children.

Method and material

Study population

In this study, data from the 2019 CCHH ( China, Children, Homes, Health) cross-sectional study in Urumqi City was utilized¹⁶. The study included six aspects in its questionnaire: demographic characteristics, children’s feeding status, AR illness in children and their family members, living environment, living habits, and dietary habits. A total of 60 kindergartens in six administrative districts were selected using a stratified random sampling strategy. The questionnaires were administered by trained teachers and completed by guardians within a week, then submitted to the Education Bureau. All respondents provided signed informed consent forms approved by the Ethics Committee. Questions to determine AR in children include “Has the child ever had sneezing, runny nose, or nasal congestion in the absence of a cold or flu”, “Has the child ever been diagnosed by a doctor with hay fever or allergic rhinitis”, and “If ‘yes’, at about what age was the child first diagnosed with hay fever or allergic rhinitis by a doctor”. We limited children AR to those with a definitive diagnosis by a physician and a first onset age of 2–8 years. We used inherent variables such as family history of AR and environmental factors in children aged 1 year or before as predictor variables for model construction, thus ensuring a clear time-series relationship between prediction and outcome to improve the interpretability of the model. The inclusion exclusion process for this study is shown in Fig. 1.

Fig. 1.

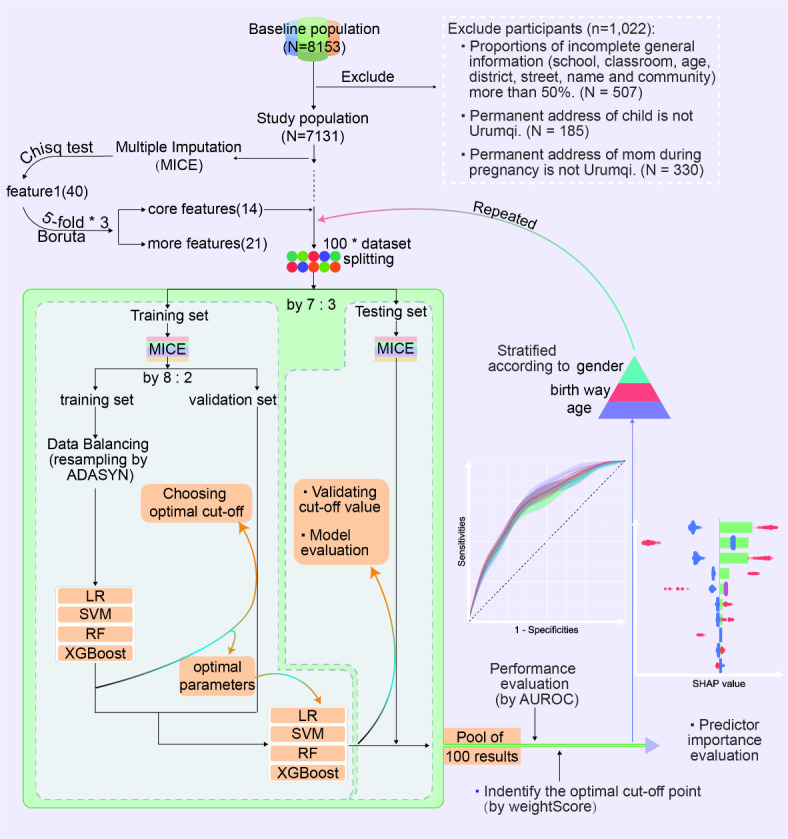
Flowchart for data inclusion exclusion, feature selection and model training. LR: Logistic Regression, SVM: Support Vector Machine, RF: Random Forest, XGBoost: Extreme Gradient Boost tree.

Features selection

In this study, we utilized a combination of univariate analysis and Boruta’s algorithm for feature selection. For multiple imputation of the data, we initially employed the chi-square test to screen variables with P < 0.05, resulting in 40 features (Table S1). Subsequently, Boruta’s algorithm¹⁷ was utilized for further screening. This is a feature selection method based on Random Forest classification. It aims to identify all relevant variables in a dataset, focusing on understanding underlying mechanisms rather than only predictive modeling. The Boruta’s algorithm extends the dataset with shuffled ‘shadow’ attributes as a reference for randomness. It then calculates the importance of each feature using Z-scores, considering features with higher Z-scores than the maximum Z-score among shadow attributes as potentially important. Finally, it categorizes features as confirmed (important), rejected (non-important), or tentative in each iteration. While confirmed features are undoubtedly the most relevant to AR, tentative features should also be considered to avoid loss of important information. We implemented a 5*3 strategy, randomly dividing the data into 5 folds and repeating the operation 3 times to return the final pool of confirmed and unrejected features. The number of features was constrained to the range of 10–15 for “core features” and 20–30 for “more features”. The term “core features” is used by default unless explicitly stated in the following text (Fig. 1).

Model construction

Under the premise of ensuring balanced and comparable outcomes across groups, we randomly divided the original data (with missing values) into ' Training’ and testing sets in a 70:30 ratio. Both sets underwent the Multiple Imputation by Chained Equations (MICE) method¹⁸ independently to fill in the missing values based on the overall data distribution. Since all variables in this study were categorical, the Random Forest method was utilized for 5 iterations and take the mode. The ‘Training set’ was further divided into a training set and a validation set at a 55:15 ratio to adjust hyperparameters on the validation set. To address class imbalance, a common issue in machine learning models, we employed the Adaptive Synthetic Sampling Technique (ADASYN)¹⁹ on the training set. ADASYN effectively mitigates class imbalance by generating synthetic samples for the minority class, ensuring a balance of 40% in the training set for this study.

Next, four models, Logistic Regression (LR), Support Vector Machine (SVM), Random Forest (RF), and Extreme Gradient Boosting tree (XGBoost) were constructed using the training set. Optimal cut-off values and hyperparameter tuning were conducted based on the validation set. Contrary to the conventional threshold selection method, we introduce WeightScore:

• WeightScore = 0.1 * Accuracy + 0.15 * F1 + 0.35 * YI + 0.3 * PPV + 0.1 * NPV.

Accuracy, F1, and YI emphasize model stability (60% weightage), while PPV and NPV focus on model benefits (40% weightage). Therefore, WeightScore is used for a more comprehensive evaluation of the model’s suitability compared to the traditional F1 value. Due to the limitation of 100 replications, parameter tuning was randomly performed on the validation sets across three samples and used the mode.

Based on the optimal hyperparameters, we trained the four models again using the ' Training’ set (a merger of the training and validation set), and the testing set was used to assess performance of models and optimal cut-off points. The results were finally pooled 100 times and the metrics were expressed using mean ± standard deviation. Figure 1 displays all the procedures of this study.

Stratification analysis and interpretability of models

To further explore potential variations in model performance based on gender, mode of birth and age, we conducted separate analyses for each of these variables. Our examination of gender and age groups (2–4, 5, and 6–8 years) provides insights into the model’s consistency across different demographics, thus enhancing the generalizability of our study results to a broader population. The importance of interpretability in machine learning models is a widely discussed issue that can impact their practical utility. To address this concern, we utilized SHAP value²⁰ and mean decreased Gini value²¹ to assess the “core features” comprehensively. SHAP, originally developed for competitive game theory, has shown promising results when applied to evaluating traditional complex black box models in recent years. The SHAP value evaluates the importance of features and determines the direction of predictor variables on the outcome, indicating the danger or protection effect based on positive and negative values. As the base learner of RF, the decision tree uses Mean Decreased Gini as a crucial criterion for node division, with a larger value indicating a more significant impact on the model’s performance and greater importance of the feature. However, this method is limited to reflecting only the magnitude of the feature’s importance.

Impact of feature number on model performance

The top 5 core features identified in the unstratified data feature importance assessment were categorized as “less features,” while the variables that Boruta algorithm did not exclude as “more features.” These features underwent 50 additional training iterations to assess the stability of model performance across varying numbers of features.

All analyses were done using R program [Version 4.3.0], and the packages used in this study included gmodels, Boruta, mice, UBL, caret, e1071, randomForest, xgboost, and ggplot2.All tests were two-sided, with P < 0.05 considered to be statistical significance. Based on python 3.11 program, we publicly deployed the optimal model incorporating the five variables via streamlit platform.

Result

Characteristics of the study population and feature engineering

In this study, a total of 7131 children aged 2–8 years participated, with 3653 (51.2%) boys and 3478 (48.8%) girls. The age distribution was as follows: 2680 (37.6%) children aged 2–4 years, 2303 (32.3%) children aged 5 years, and 2148 (30.1%) children aged 6–8 years. The univariate analysis revealed significant differences in distribution for 40 variables between the healthy control and AR groups. Table S1 displays the distribution of variables analyzed in the univariate comparisons between the control and case groups. Based on univariate analysis, the 5*3 Boruta algorithm identified 14 variables as “core features” with qualifying acceptor features repeated more than 3 times (see Table 1), and 21 features were identified with qualifying non-rejectors repeated more than 5 times (refer to Table S2). Beside, the feature engineering, data partitioning, and model tuning training process in this paper took approximately 50 h in total.

Table 1.

“Core features” by univariate analysis and 5*3 Boruta algorithm with qualifying acceptor features repeated more than 3 times.

Class	Variables
History of allergic disease	Successive bouts of rash more than 6 months during cfy, Child with food allergy
Hereditary factor	Father with AR, Mother with AR, Mother with AD, Siblings with AR,
Indoor environment	Father smoking during mp, Paternal grandfather smoking during mp, Feeding pats or growing plants during cfy, Father smoking during cfy, Flowers planting during cfy
Others	Father’s education, Have older siblings, Antibiotic therapy during cfy

Abbreviation: mp: maternal pregnancy, cfy: child first year, AD: atopic dermatitis.

Evaluation of model performance

Table 2. shows the optimal value and explanation for optimal hyperparameters of machine learning algorithms on the unstratified data with “core features”. Figure 2A displays the AUROC results (mean ± standard deviation) for the four models, LR, SVM, RF, and XGBoost, after 100 training sessions on the unstratified training and testing sets. The training set shows comparable performance among LR (0.763 ± 0.01), RF (0.769 ± 0.013), and XGBoost (0.769 ± 0.01), while SVM performs worse (0.741 ± 0.012). On the test set, RF (0.747 ± 0.015) performs the best, followed by XGBoost (0.733 ± 0.019) and SVM (0.723 ± 0.022), while LR performs poorly (0.715 ± 0.023). Besides, Fig. 2B illustrates the model’s performance on the stratified test set based on gender, mode of birth, and age after 100 training sessions. The performance of the four models remains relatively stable across the stratified test sets compared to random guessing (AUROC = 0.5). Overall, models for the boy population performed poorly compared to the unstratified dataset, while the 5-year-old group’s models performed relatively well. Additionally, RF consistently outperforms all other models across different strata, with LR generally weaker than the machine learning models. The differences between RF and LR are all statistically significant (paired samples t-test: p < 0.001). Refer to Table S4 for the hypothesis test details.

Table 2.

Optimal value and explanation for optimal hyperparameters of machine learning algorithms on the unstratified data with core features.

Model	Hyperparameter	Explanation	Value
RF	ntree	Number of trees to grow	625
	mtry	Number of variables randomly sampled as candidates at each split	1
	nodesize	Minimum size of terminal nodes, increasing the nodesize leads to the growth of smaller trees and reduces the time required to fit the model.	4
SVM	kernel	Kernel functions for model training and prediction, including linear and radial kernels.	linear
	cost	Cost of constraints violation	0.4
XGBoost	eta	The learning rate, a larger ‘eta’ value results in a more conservative boosting process, increasing the risk of underfitting, while a smaller value may lead to overfitting.	0.05
	max_depth	Maximum depth of individual learners (classification trees)	2
	subsample	The subsample proportion of the training instances, when set to 0.5 means half of the training samples are randomly selected for each learner, aiding in preventing overfitting.	0.5
	colsample_bytree	Percentage of columns selected when training individual learners	0.3
	gamma	Minimum loss required for further division of leaf nodes for an individual learner (classification tree)	10
	nrounds	Maximum number of boosting iterations	150

Fig. 2.

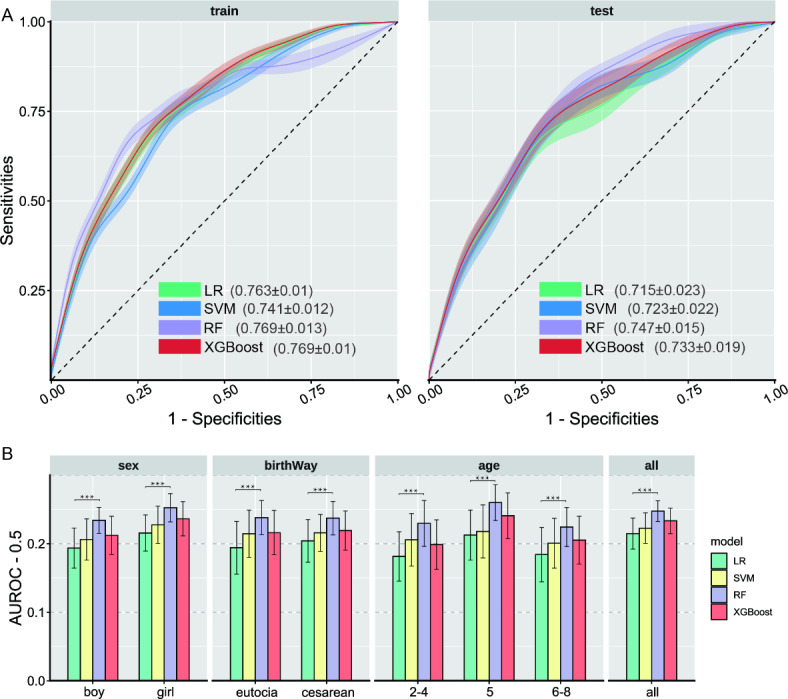
AUROC (mean ± standard deviation) of the four models on different sampled data sets. (A) Performance of the four models on the training and test sets of unstratified data. (B) Performance of the four models on the test set after stratification according to gender, mode of birth and age compared to randomized blind guessing (AUROC = 0.5), and paired samples t-test between RF and LR.

Selection of optimal cut-off value

In this study, we evaluate the reliability of WeightScore for optimal threshold value selection from multiple perspectives, including optimal threshold value determination and assessment for different models. Figure 3A displays the cut-off values determined from validation set across 100 training sessions. The WeightScore-based decision point selection shows relative stability across groups, with LR having an optimal threshold value around 0.5, XGBoost around 0.45, and SVM and RF close to 0.3. The WeightScore scores for each model are consistent across datasets, averaging around 0.35 (Table S3). Figure 3B and C depict the model performance for both unstratified data and the subgroup of 5-year-olds at the optimal cut-off value in Fig. 3A. The value intervals of the polar coordinates are determined by the minimum and maximum values of the metric across all models and sampled data sets at the optimal cut-off value. In general, the model excels in negative predictive value (NPV), accuracy, and specificity, but falls short in positive predictive value (PPV), F1 and sensitivity. Furthermore, the model’s stability metrics, including accuracy, F1, sensitivity, and specificity, exhibit significant fluctuations in their values, whereas the model’s benefits metrics, such as PPV and NPV, demonstrate more consistent values. When examining individual models, Support Vector Machine (SVM) tends to yield higher sensitivity values, while Random Forest (RF) tends to prioritize higher PPV values.

Fig. 3.

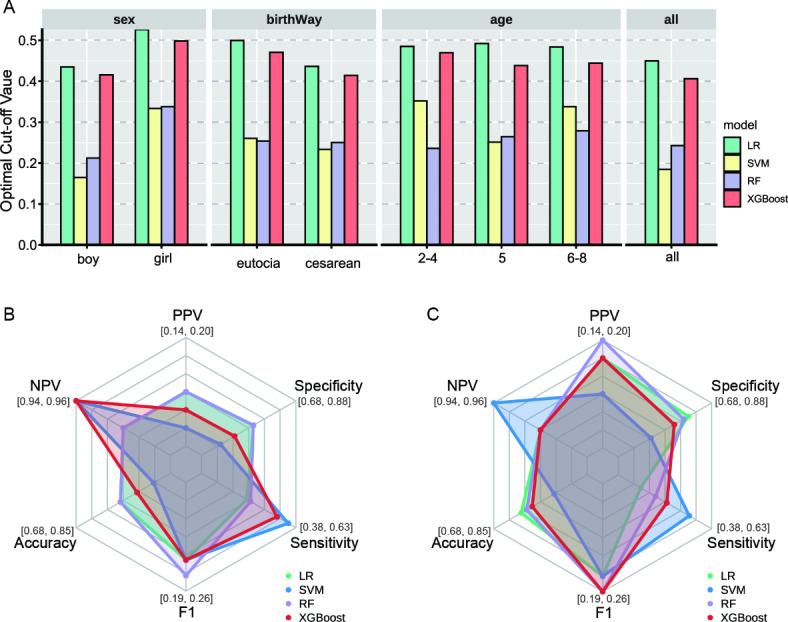
Comparison of the optimal cutoff points of the four models on different subgroups of data sets. (A) Optimal decision values determined by the four models based on different stratified data validation sets. (B,C) Comparison of the six metrics (PPV, NPV, Accuracy, F1, Sensitivity and Specificity) corresponding to the optimal cut-off value taken by the four models on the unstratified data (B) and the 5-year age subgroup of the population (C.) test sets.

Evaluation of features importance

Figure 4 displays the ranking of model feature importance based on SHAP values and mean decreased Gini values for unstratified data and the subgroup of children aged 5 years, presenting the top 10 variables. There is a high degree of consistency between the results of the two methods for evaluating feature importance. When combined with Fig. 4A and B, it is evident that in the unstratified data, the top 5 variables are mother with AR, father with AR, having older siblings, child with food allergy, and father’s education level. What’s more, in the 5-year age group population, the top 5 variables are mother with AR, father’s education level, father with AR, having older siblings, and child with food allergy.

Fig. 4.

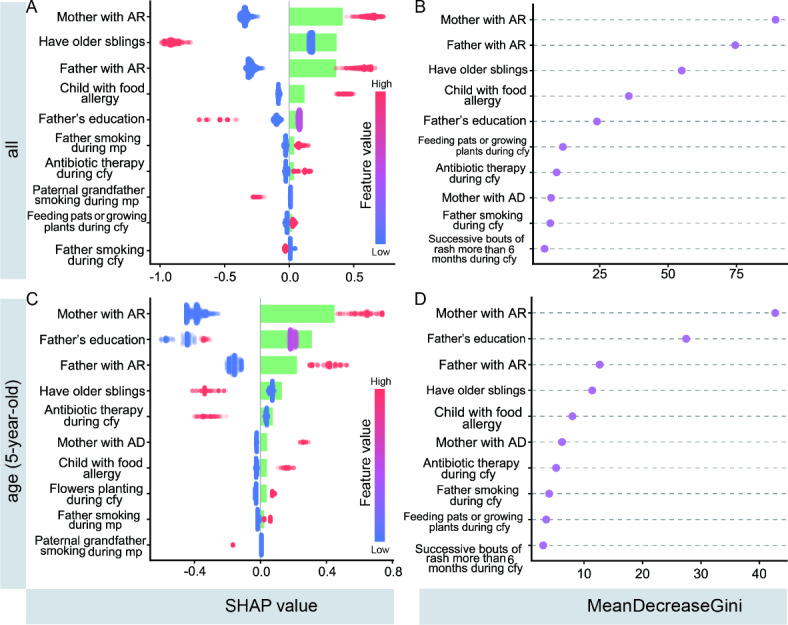
Model feature importance was assessed using SHAP values and mean decreased Gini for unstratified data and the 5-year-old subgroup of the population (top10). (A,C) The bars in the plot represent the absolute value of SHAP, reflecting the feature importance magnitude. The scatter points represent individual sample data, with point color indicating the variable value range, corresponding to the color bar ends for dichotomous variables, and to the respective color for multicategorical ordered variables. For instance, considering “Mother with AR,” a high variable value is associated with a positive SHAP value. That is, when the mother has a history of AR (coded as 1) compared to no history of AR (coded as 0), the child has a higher risk of developing AR between the ages of 2–8 years old. (B,D) Characteristic significance was determined based on MeanDecreaseGini, with the mean decrease Gini value is larger, the more important the feature is. Abbreviation: mp: maternal pregnancy, cfy: child first year, AD: atopic dermatitis.

Stability of model performance with different features

Figure 5 illustrates the performance and hypothesis testing of the four models on the unstratified data test set after varying the number of features. In general, increasing the number of less important features does not enhance model performance, while reducing or selecting optimal features tends to improve performance. Specifically, LR’s performance significantly decreases with increasing features (P < 0.05), SVM appears unaffected by feature number (P > 0.05), and for RF, reducing features significantly decreases performance. Conversely, XGBoost exhibits a similar trend to LR, with significantly improved performance when reducing features (P < 0.05). Refer to Table S5 for the hypothesis testing details. Considering the memory and time expenses of running the model, we deployed the random forest model on unstratified data for the five most important features, online (https://rhinitismodel-egfpa9aysjlgho8qsvlaw7.streamlit.app/).

Fig. 5.

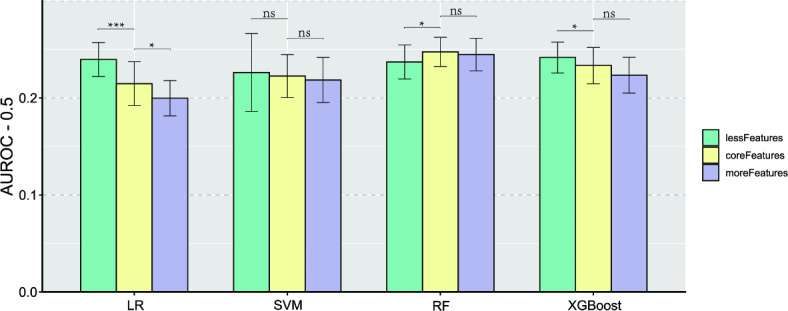
The impact of reducing or increasing the number of features on the model’s performance on an unstratified test set.

Discussion

Evaluation of predictive models

As a classical statistical algorithm, Logistic regression is a generalized linear regression variant based on the sigmoid function that maps any real input value to the interval [0, 1] for classification tasks. In particular, the coefficients of the independent variables intuitively reflect the impact of the variable on the outcome, making this method easy to be accepted. And the algorithm automatically adjusts for the potential role of confounding factors, and is thus a frequently used approach for analyzing the effects of potential risk factors²². When applied to prediction, the Logistic algorithm works well with data with few dimensions and small sample sizes, and visualizes the odds ratios of independent variables through nomogram, and the construction of tools for predicting disease risk. However, the method tends to underperform for complex data with many dimensions²³. Our results show that with the increase of relatively unimportant features, the performance of LR significantly decreases with the increase of data complexity (Fig. 5). Especially when including 14 features, LR performs worse than the RF model on both stratified and unstratified data testing sets.

The support vector machine (SVM) model aims to find a hyperplane to maximize the separation of sample categories in the feature space for efficient outcome division. By utilizing kernel functions, this method can effectively partition both linear and nonlinear feature spaces. SVM, as robust traditional machine learning models, held significant popularity and played essential roles in specific tasks prior to the emergence of more complex models like XGBoost²⁴. Our study revealed that the SVM model with a linear kernel function exhibits the least sensitivity to the number of features. This characteristic may stem from the algorithm’s similarity to data downscaling in finding the optimal hyperplane, indicating that increasing non-significant features does not enhance the model’s classification accuracy. This observation also implies the potential nonlinearity of the learning task in our study.

Random Forest (RF) is a bagging ensemble model based on parallel Classification And Regression Trees (CART)^25,26. Simple decision trees in early stages often suffer from excessive branching in complex data, leading to overfitting during training and suboptimal performance during testing. RF addresses this issue by employing bootstrap sampling to create a balanced training dataset, with the remaining samples used for testing model performance through out-of-bag estimation²⁶. Additionally, RF optimizes performance by using a subset of attributes, rather than the optimal one, during node partitioning to reduce time consumption per training iteration and prevent redundant attribute influence. This approach effectively combats overfitting by perturbing data samples and input attributes. Through strategies like the voting method, RF consolidates outcomes from multiple decision tree trainings, while also controlling overfitting by adjusting the random forest’s depth and maximal number of iterations. Furthermore, RF integrates many decision trees in parallel, and the Gini index, which reflects the dataset’s purity negatively, serves as the basis for optimal attribute selection and node partition of CART²⁷. The algorithm selects the attribute that yields the lowest Gini value for the child nodes, ensuring accurate completion of the classification regression task. Therefore, the mean decreased Gini value is an important index used by decision trees and RF to measure the importance of features. The RF model demonstrated consistent high performance across training and testing sets, in both stratified and unstratified data, irrespective of feature variations. Unlike the other models, RF maintains performance even with an increase in non-significant features, highlighting its robustness to redundant features. Considering RF’s interpretability, it emerges as a trustworthy option for predicting AR occurrence in children aged 2–8 based on early life factors.

The Extreme Gradient Boosting Tree (XGBoost) model employs decision trees as base learners as well, distinguishing from RF, however, XGBoost exhibits strong interdependencies among individual learners, which are sequentially generated in a serialized strategy. Following the training of each base learner, XGBoost adjusts the samples based on previous model discrepancies, prioritizing samples with prior errors in subsequent training iterations. This approach enhances base learner diversity by modifying sample distribution and increasing data perturbation. Ultimately, the model produces the final output by weighting the results of individual decision trees^25,28,29. Additionally, XGBoost can be viewed as iteratively optimizing the exponential loss function through an additive model, while the SHAP interpretability strategy relies on the additivity of the Shapley value and the treeSHAP method. The fusion of XGBoost and SHAP significantly enhances the former’s interpretability and generalization. In this research, XGBoost’s performance ranks second to RF and remains consistent across data subgroups. However, this correlation is not absolute, as reducing the number of features to the top five variables notably boosts model performance, approaching that of RF.

While ROC is commonly used for model selection as a comprehensive index for evaluating model performance, practical applications are more concerned with finding an optimal threshold to transform probability values from prediction models into binary outcomes to meet task requirements. Most studies base the selection of the optimal decision value on ROC analysis, often determining sensitivity equal to specificity as the optimal cut-off value³⁰. However, this approach represents a compromise, aiming for the model’s ability to correctly detect positives to be as close as possible to its ability to correctly exclude negative events. Yet, in real-world tasks, the costs of failing to diagnose a patient and misdiagnosing a healthy person are often unequal and can vary depending on the disease and application. Therefore, flexibility in selecting metrics to determine the optimal threshold value based on specific task requirements is necessary. Given the population-oriented nature of this study, we prioritized reliability and the method’s potential benefit to the population. Our findings revealed that although the performance of the four models varied significantly across the sampled datasets, there was always an optimal cut-off value resulting in similar overall scores for the models (Table S3), with RF emerging as the superior model. Furthermore, the substantial difference in the optimal threshold value among the four models may be linked to the models’ sensitivity to the class imbalance problem, their inherent characteristics (e.g., the boosting attribute of XGBoost), and the intrinsic pattern of the data samples.

Explanation of features importance

This study utilized SHAP values and mean decreased Gini values to identify the top 5 variables in the unstratified data: mother with AR, father with AR, having older siblings, child with food allergy, and father’s education level. Subsequent model evaluation revealed that a model based on these 5 variables performed comparably to the core features (Fig. 5), and notably, LR and XGBoost outperformed the ”core features”. This indicates that LR and XGBoost are more susceptible to the influence of non-important features than RF, underscoring the importance of feature selection as well. Additionally, it highlights the effectiveness of the feature evaluation strategy employed in this study.

Parental allergy history significantly increases offspring’s AR risk³¹, with parental AR potentially outweighing atopic dermatitis and asthma as a risk factor³². A birth cohort study of 2413 participants revealed a 120% increased AR risk in children of parents with hay fever compared to those without (OR = 2.2, 95% CI: 1.6–3.2). Notably, parental asthma or eczema history did not significantly impact the child’s AR risk, emphasizing the paramount role of parental AR as a genetic risk factor³³. Contrarily, the present study identified parental AR history as not only a crucial genetic risk factor but also stronger than known early life environmental factors. Additionally, debates persist regarding the significance of paternal or maternal rhinitis, which is difficult to determine. Evaluation of feature importance using unstratified and stratified data consistently indicated a stronger contribution of maternal AR to children’s AR compared to paternal AR.

The composition of siblings has garnered significant attention in examining the impact of early life factors on AR, particularly following the discovery of a negative correlation between the number of siblings and AR³⁴. Stracha et al. first proposed the “hygiene hypothesis”, suggesting that the immune response of the naive immune system to appropriate pathogenic microbial stimuli in early life contributes to immune system refinement and the establishment of a robust Th1-dominant immune tolerance microenvironment between Th1- and Th2-type immune cells, thereby preventing the development of allergic diseases^34,35. A recent meta-analysis of 76 studies involving a total population of 2 million revealed that second or later-born children are protective against both current (RR = 0.79, 95% CI: 0.73–0.86) and ever (RR = 0.77, 95% CI: 0.68–0.88) AR³⁶. The present study also identified a similar effect through the SHAP interpretable technique, indicating that children with older siblings have a reduced risk of later AR, with this variable contributing to AR risk second only to parental AR.

Cross-sectional and cohort studies have indicated a chronological progression of allergic diseases from atopic dermatitis and food allergy to allergic rhinitis and asthma, known as the “atopic march”³⁷. The exact mechanisms of this process remain incompletely understood, with genetic environment and age being known influences; for instance, the process is more likely to fully develop in childhood than in adulthood³⁸. Following a univariate analysis and Boruta’s algorithm for variable selection, food allergy and Successive bouts of rash more than 6 months during cfy were included in the model training. This suggests a strong association between food allergy and early-life eczema with the occurrence of allergic rhinitis (AR) between 2 and 8 years of age. Additionally, we observed that a history of food allergy is second in importance only to parental AR and the presence of older siblings in predicting AR, offering a new perspective on research into the atopic march.

Furthermore, we observed heterogeneity in the impact of father’s education level on children’s AR. Moderate education level was found to increase the risk of AR in children aged 2–8 years, while lower and higher education levels were associated with a decreased risk of AR. This variation can be attributed to several factors. Firstly, parental education level can influence the developmental trajectory of AR in children by affecting access to healthcare resources³⁹. Higher education levels provide access to specialized therapeutic knowledge, unlike moderate levels, potentially preventing early-onset AR. Additionally, parental education level may impact AR through economic status and hygiene practices, particularly in Chinese society where fathers are often primary breadwinners. When fathers have lower education levels, children may experience less hygienic environments compared to those with moderately educated fathers, leading to increased early exposure to pathogens in early life that can strengthen the child’s immune system and decrease the risk of AR later in life, according to hygiene hypothesis⁴⁰.

Moreover, the study revealed a correlation between early tobacco exposure and antibiotic use in children and the onset of AR among children aged 2 to 8. Exposure to air pollutants, particularly tobacco smoke, is a robust risk factor for rhinitis^41,42. A meta-analysis linking maternal tobacco exposure during pregnancy or postpartum to children’s AR demonstrated a significant increase in risk, with OR of 1.12 and 1.19, respectively⁴³. Concurrently, basic research indicates that tobacco’s toxic components, including tar, carbon monoxide, and nicotine, can lead to upper respiratory injuries via oxidative stress and inflammatory mechanisms⁴⁴. Consistent with these findings, our study identified paternal smoking during maternal pregnancy and during the child’s first year, as well as grandfather’s smoking during maternal pregnancy, as top10 risk factors for AR in children aged 2 to 8, according to univariate analysis, Boruta’s combined screening, and SHAP value analysis (Fig. 4A). Furthermore, excessive antibiotic use is a critical threat to children’s health⁴⁵. Observational studies indicate that early-life and lifespan antibiotic overuse heightens the likelihood of AR development^46,47. Unstratified data (Fig. 4A) showed that antibiotic use from ages 0 to 1 raised the risk of AR in children aged 2 to 8. astonishingly, in the 5-year age group (Fig. 4C), such use was linked to a reduced risk of AR, although the reasons remain unclear and may indicate that age is a key moderating factor in the long-term impact of antibiotic use on AR development.

Strengths and limitations

This study utilized interpretable machine learning techniques to predict AR in children aged 2–8 years, assessing model stability through stratification and varying feature counts. Together with the analysis of the top 5 features’ impact on AR stands out as a strength. However, contradictions and limitations exist. Hyperparameter tuning and determining the optimal cut-off value require dataset division into training, validation, and testing sets with 100 training repetitions for reliability. Yet, the challenge arises from individual feature selection on the full set rather than solely on the training set, leading to potential data leakage issues⁴⁸ and inflated model performance. Given the repeated model training, selecting optimal parameters for each training session is impractical. Instead, a viable approach involves aggregating optimal tuning results from three training sessions, different from data leakage risks, however, this may albeit potentially underestimating the model’s true performance. Despite these challenges and limitations, the study’s model performance remains reliable.

Conclusion

Leveraging an interpretable machine learning algorithm, we developed a robust model utilizing parental history of allergic diseases and early life factors to predict AR occurrence in preschoolers aged 2–8. The model outperformed traditional logistic regression and maintained stability across diverse stratifications and feature variations. Furthermore, the feature evaluation technique facilitated the identification of crucial features not easily detected by conventional methods, including older siblings, food allergy history, and father’s education level. Random Forest modeling proves to be a valuable asset in population-based preventive care practices for pediatric AR.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

Y.Y. and J.Y.W. designed experiments, J.Y.W. wrote the manuscript, X.L.G. conceived and supervised the project. J.Y.W. performed the experiments and analysed data, J.Y.W. and Y.Y. analysed data and completed manuscript editing.Ye Yang and Xueli Gong contributed equally to this work.

Funding

The work was supported by the Xinjiang Medical University Innovation Training Programme for Undergraduates (grant no.X202310760105), Xinjiang Outstanding Youth Science Fund Project (2023D01E04) ,State Key Laboratory of Pathogenesis, Prevention and Treatment of High Incidence Diseases in Central Asia (SKL-HIDCA-2022-DX3).

Data availability

The datasets generated and/or analyzed during the current study are not publicly available. However, they are available from the corresponding author upon reasonable request.The code used in this study has been uploaded to github (https://github.com/a-silliy-sheep/Interpretable-Machine-Learning-for-Allergic-Rhinitis-Prediction).

Declarations

Competing interests

The authors declare no competing interests.

Ethics approval and consent to participate

The study was conducted strictly in accordance with the Declaration of Helsinki and approved by the research ethics committee of Fudan University (protocol no. IRB00002408 & FWA00002399), all parents and class teachers of the children under investigation have signed written informed consent.