Abstract
In this paper, a flexural Mikaelian lens in thin plate is designed by using conformation transformation. The propagation characteristics of flexural waves in the lens are investigated through rays trajectory equation, simulation analyses, and experimental tests, confirming the self-focusing properties of the Mikaelian lens. Additionally, the study explores the Talbot effect for flexural waves, revealing through simulation studies that the Talbot effect within the Mikaelian lens exhibits nearly diffraction-free properties. Building on the non-diffractive nature of the Talbot effect within the Mikaelian lens, we explore the potential for encoding flexural waves using active interference sources. The simulation and experiment results demonstrate the good performance of the designed active encoding system. This work opens up new avenues for the encoding of flexural waves, presenting promising implications for applications in communication such as structural health monitoring, wireless communication in solid media and data transmission in robotics and other areas related to flexural wave technology.
Subject terms: Physics, Mechanical engineering
Introduction
Metamaterials have showcased significant advantages and vast potential in the domain of subwavelength control1–5. Leveraging these materials alongside foundational theories such as transformation theory and the generalized Snell’s law6–9 has led to the successful development of functional devices. These include acoustic and optical cloaking devices10–12, metasurfaces13–15, and high-performance lenses16–18, thereby enriching device functionality and broadening their applicability.
While metamaterial devices offer groundbreaking potential, they often face limitations such as singular functionality, constraints to specific environments, and static operational frequency ranges. The development of programmable and reconfigurable metamaterial devices emerges as a solution to these challenges, significantly expanding the versatility and adaptability of these devices across various applications19–22. This advancement marks a pivotal shift towards creating more dynamic and flexible metamaterial systems. Lau et al proposed a reconfigurable electromagnetic metasurface arrays to archieve omni directional phase coverage23. Cui et al develped the concepts of digital metamaterials inspired by the binary representation of digital circuits24. By integrating a two-phase composite approach, combining hydrogel-based fillers with auxetic lattices, the research offers a programmable method for creating materials with custom mechanical properties, including temperature-responsive behavior for dynamic adaptability25. Tian and colleagues proposed a programmable acoustic metasurface based on Helmholtz resonators and straight channels, utilizing a fluid system to regulate the resonators’ equivalent mass, thereby achieving multifunctional manipulation of the phase and amplitude of sound waves26. By carefully designing rotating supports within each unit and employing 3D printing to craft a base with periodic holes, Chen presented a reconfigurable hexagonal Helmholtz resonator, which enables easy rotation and adjustment of the acoustic metamaterial chamber to different configurations without the need for reprinting or redesigning the entire structure, allowing for efficient control over ventilation and insertion loss27.
The control of flexural waves in thin plates also deserves in-depth study and attention28–32, since it holds crucial significance in vibration and elastic wave control. Similarly, programmable and reconfigurable devices for flexural waves have also experienced rapid development. Xu et al proposed an alternative method for beam splitting of flexural waves based on the generalized Snell’s law, utilizing a coding meta-slab composed of two logical units, “0” and “1,” which has been experimentally verified to effectively split incident flexural waves across a broadband frequency range33. Yaw et al proposed a functionally switchable 3-bit active coding elastic metasurface, utilizing stacked piezoelectric patches and connected negative capacitance circuitry to achieve omnidirectional frequency control of elastic longitudinal waves, covering the entire phase range and demonstrating a wide range of manipulation capabilities and high transmittance34. Li et al. introduced the concept of binary metasurfaces into the field of elastic waves, proposing a strategy for designing coding units through topology optimization. They successfully constructed a structured binary elastic metasurface, achieving accurate guidance and focusing of flexural waves, along with demonstrating an efficient energy harvesting system35. Yuan et al. have designed and implemented a broadband reconfigurable metasurface using a “screw-and-nut” operating mechanism, achieving active control of the wavefront of flexural waves36. Wu et al introduced a linear active metalayer, achieving independent frequency conversion of flexural waves in elastic beams and plates, opening up new possibilities for comprehensive control of time-domain signals and wave energy37.
Recently, the regulation of flexural waves by Mikaelian lenses has attracted the attention and research of researchers38–40. Mikaelian lens, with hyperbolic secant refractive index, enables self-focusing, facilitating phenomena including point-to-point imaging, aberration-free spherical surfaces, enhanced convergence, effective waveguiding, and Talbot effects without diffraction, illustrating their broad utility in wave controlling. Zhao et al designed and experimental demonstrated a Mikaelian lens with large refraction to realize broadband sub-diffraction focusing without introducing evanescent waves38. Then a flexural wave Mikaelian lens was designed and fabricated by conformal transformation, successfully achieving achromatic subwavelength focusing (FWHM approximately ) and a beam-scanning angle of up to in the frequency ranges from 30 to 180 kHz. These work indicate significant potential applications of the Mikaelian lens in high-resolution medical imaging and flexural wave communication40. However, compared to its optical41–43 and acoustical counterparts9,44, research reports on flexural wave Mikaelian lenses are still relatively limited. Therefore, the research on flexural wave Mikaelian lenses has important application value in designing and opening programmable and reconfigurable flexural wave devices based on Mikaelian lenses.
In this work, we design a flexural wave Mikaelian lens using conformal transformation, and study the propagation properties of flexural wave in the designed Mikaelian lens. The designed Mikaelian lens has a width of mm, a self-focusing period of mm, and a lens length of , that is, of the self-focusing period. A piezoelectric sheet line array was arranged at the incident end of the lens as interference sources. The flexural wave Talbot effect generated by the interference sources are studied, and the non-diffraction characteristics of the Talbot effect in the Mikaelian lens are verified with simulation. Furthermore, we develop an active encoding system based on the designed lens to achieve flexural non-diffraction Talbot communication. Based on the self-focusing effect of the Mikaelian lens, the image converges at one quarter of the period, and reappears as an inverted image near one half of the period. Therefore, if the channel state of the piezoelectric sheet is regarded as 1 in the binary code, and the open one as 0 in the binary code, then the incident signal can be regarded as being encrypted near the quarter period of the lens, and it is decoded again at the half of the period. Simulation and experimental results indicate that the designed system has excellent performance in actively encoding flexural waves. This study focuses on the development and demonstration of a non-diffractive Talbot effect using a Mikaelian lens, with multifunctional capabilities in flexural wave manipulation. It shows significant potential for enhancing high-resolution imaging and communications through flexural waves, offering new avenues for technological advancements in these fields.
Theory and design
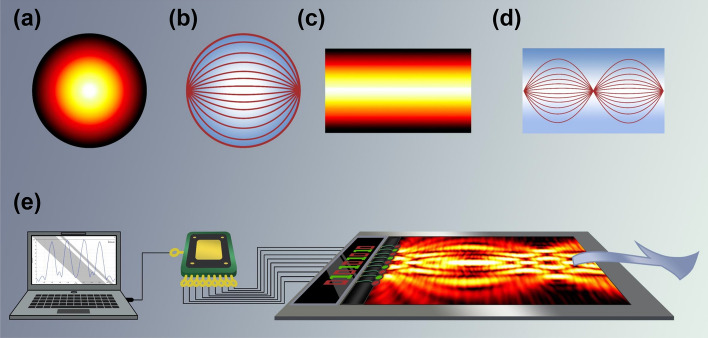
The Mikaelian lens is a self-focusing lens designed by A.L. Mikaelian in 195145, which has a hyperbolic cosine inverse distribution of refractive indices. Recent research indicates that the Maxwell’s fish-eye lens and the Mikaelian lens can establish a mapping relationship through conformal transformations, as demonstrated below41,44:
| 1 |
where and are the refractive index distributions in virtual space (Maxwell’s fish-eye) and physical space (Mikaelian lens), respectively, as shown in Fig. 1a–d. The refractive index distribution for the Maxwell fisheye lens is:
| 2 |
where and R denote the refractive index on the lens boundary and the radius of the lens, respectively, and r is the distance to the center of the lens, as shown in Fig. 1a. The wave rays emanate from the left end of Maxwell’s fish-eye lens and will then propagate along a circular arc and converge at the far right end of the lens, as shown in Fig. 1b. Performing an exponential conformal transformation on the Maxwell fish-eye lens yields a physical spatial refractive index distribution is:
| 3 |
Equation (3) represents the refractive index distribution of the Mikaelian lens. In Eq. (3), is the length coefficient controlling the Mikaelian lens, represents the width of the lens, and is the period of the Mikaelian lens. And is the maximum refractive index along the lens’s central axis, defined as . The refractive index distribution of the lens, as shown in Fig. 1c, clearly indicates a gradual increase in refractive index from both sides of the lens towards its central axis. The self-focusing effect of the Mikaelian lens can be reflected through ray trajectories, as illustrated in Fig. 1d. In this work, we use Mikaelian lens to modulate the flexural wave and implement a kind of coding for flexural wave, where the schematic is shown in Fig. 1e.
Fig. 1.
Theoretical design and communication encoding technique schematics of the conformal mapping Mikaelian lens. (a) Refractive index distribution of the Maxwell’s fish-eye lens. (b) The rays trajectories in the Maxwell’s fish-eye lens. (c) Refractive index distribution of conformal Mikaelian lens. (d) Self-focusing phenomenon of the Mikaelian lens. (e) Schematic representation of active encoding of flexural waves by the Mikaelian lens.
The two-dimensional motion equation for flexural wave in a thin plate with variable local thickness is:
| 4 |
In Eq. (4), indicates the flexural rigidity, w represents the transverse displacement of the plate, and are the Young’s modulus, mass density, Poisson’s ratio, angular frequency, longitudinal displacement of the plate correspondingly. The solution of Eq. (4) is given as:
| 5 |
where and are the wave amplitude and cumulative phase at the view point . Thus, the velocity c of flexural wave in a Mikaelian lens is expressed as:
| 6 |
The refractive index of the lens is controlled by the thickness of the localization39:
| 7 |
As a result, the thickness distribution of the flexural wave Mikaelian lens can be expressed as:
| 8 |
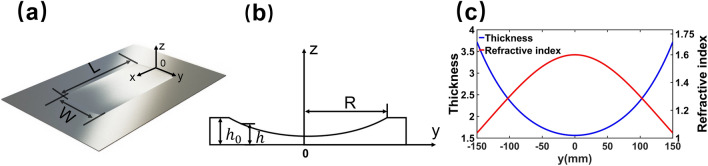
The designed Mikaelian lens is embedded in a stainless steel plate with a thickness of , Young’s modulus of , density of , and Poisson’s ratio of 0.29, as shown in Fig. 2a. To achieve impedance matching, an impedance matching gradient layer has been designed between the lens and the background plate. The cross-sectional view of the lens is illustrated in Fig. 2b, with the corresponding thickness and refractive index depicted in Fig. 2c.
Fig. 2.
(a) The model of the designed flexural wave Mikaelian lens. (b) Cross-sectional view of the lens with a thickness variation structure. (c) Relationship between thickness, refractive index, and distance from the lens center.
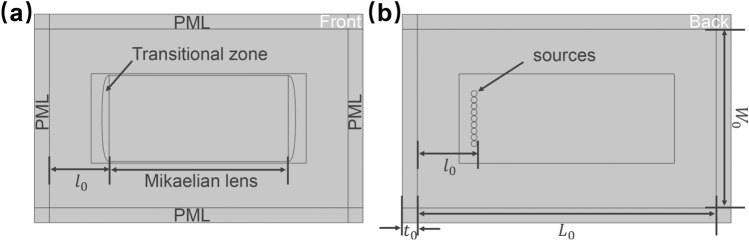
The simulation model is shown in Fig. 3a, in which a transitional zone has been added between the lens and the thin plate38 to achieve impedance matching. The designed simulation model has a width of , a length of , and the width of PML of . The distance from the piezoelectric element to the edge of the thin plate is .
Fig. 3.
Schematic of the simulation model: (a) Schematic of the relative positioning of the Mikaelian lens on the stainless steel thin plate (front side). (b) Schematic of circular piezoelectric sheet array element (back side).
The flexural wave is generated by an array of circular piezoelectric elements46, shown as the circles in Fig. 3b, where the produced flexural wave is determined by the following equation:
| 9 |
with and as the radius and amplitude of a circular source,correspondingly. In addition, Perfect Matched Layer (PML) are imposed to minimize the reflections. Therefore, the superposition of N sources on a point outside the plane can be explained as:
| 10 |
where is the initial phase of each element, represents the distance from the nth element to the observation point. And the distance from the nth element to the first element is with d as the distance between two adjacent sources. Therefore, in the Eq. (10) can be replaced by , and can be replaced by , which can be rewritten as:
| 11 |
where is the phase difference between adjacent elements. By substituting , into the Eq. (11), it can be obtained that:
| 12 |
with considering that the initial phases of the sources are all the same in our research, leading . According to Eq. (12), the modulation of the flexural wave propagation can be realized by adjusting multiple piezoelectric sheet array element circles.
The equation for the trajectory of the rays inside a Mikaelian lens can be determined by the transverse components of the wave vector being equal to each other9:
| 13 |
Here, represents the entry position on the y-axis to the left of the lens, and is the angle of incidence. The refractive index distribution of the Mikaelian lens mentioned above is given by Eq. (3), thus the equation of the trajectory of the ray in the lens is given by Refs.47–49:
| 14 |
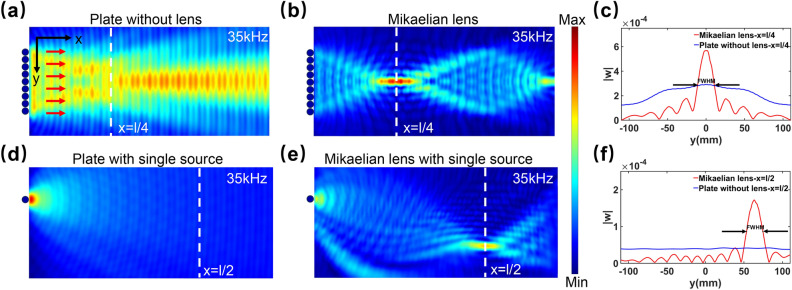
According to Eq. (14), y becomes to zero at and at in the case of plane wave normally incident to the lens, which indicates the properties of self-focusing. Figure 4 illustrates the flexural wave produced by the circle sources propagating in the thin plate and the designed Mikaelian lens. In Fig. 4a, it can be seen that the wave produced by the source array exhibits nearly as plane wave. However, in the Mikaelian, the wave focuses at and then transforms to plane wave at , as described by Eq. (14), implying the self-focusing of the designed lens, as illustrated Fig. 4b. Figure 4c shows the distributions of the displacements along the line at in thin plate (blue curve) and Mikaelian lens (red curve). It can observed that there is an obvious shark peak with a FWHM of in the red curve, while the blue cure tend to be more flat. This further verifies the focusing of the Mikaelian lens. Figure 4d demonstrates the simulation results for the wave from point source propagating in the ordinary thin plate, indicating that the flexural wave gradually spreads as it propagates. However, when the flexural wave from a single source is incident to the Mikaelian lens, due to the self-focusing of the Mikaelian lens, the wave propagates along a curve and forms a iverted image at , as shown in Fig. 4e. Figure 4f presents the displacements along the line in thin plate (red curve) and Mikaelian lens (blue curve), correspondingly. It can be seen a very obvious peak at mm, with the FWHM of , in the displacements distribution of the Mikaelian lens, while the blue curve is almost a straight line. Since the source is at , this further proves the good performance of the inverting focusing of the designed lens.
Fig. 4.
Simulation results of displacement of plane wave in a thin plate (a) and in the designed Mikaelian lens (b). (c) Distributions of the displacements along . Simulation results of the flexural wave excited by a single piezoelectric sheet propagating in a thin plate (d) and in the designed Mikaelian lens (e). (f) Distributions of the displacements along .
Non-diffractive Talbot effect and its encoding in flexural wave Mikaelian lens
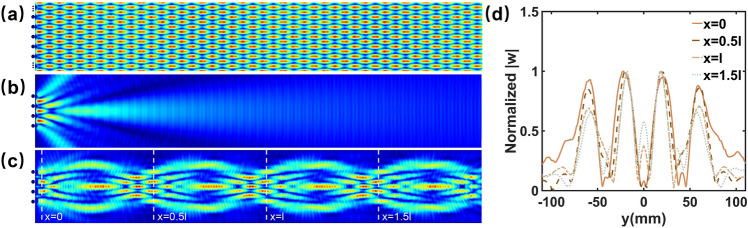
The Talbot effect was firstly discovered by Talbot in optics50, and has practical applications in optical fields for beam collimation tests and precise lens focal length measurements51. Considering the similarity between optical wave and elastic wave, the Talbot effect should also appear in flexural wave. Since the phenomena of diffraction and interference are all produced by the wave’s superposition, the periodic interference sources can also generate the Talbot effects. Figure 5 shows the Talbot effects in different situations. In Fig. 5a, it presents the interference field produced by the infinite periodic sources with a period of , where is the radius of the source. It can be observed that periodic sources repeat along the propagation direction at integer multiples of the main Talbot length and are equally spaced in the transverse direction. This has the same phenomena of Talbot effect produced by infinite periodic diffraction gratings41. However, in practical systems, the array cannot be infinitely large, hence the Talbot spots are limited into near fields. For instance, Fig. 5b displays the simulated results of the ordinary Talbot effect for finite-period sources. Clearly, due to the diffraction, the Talbot effect can only be maintained over relatively short distances in finite-period systems. Consequently, it is not possible to achieve long-distance propagation of the sources’ modes through the Talbot effect in thin plate. Since the Mikaelian lens has a self-focusing effect, it can achieve a non-diffractive Talbot effect. Theoritically, the non-diffractive Talbot effect of the Mikaelian lens can propagate the modes of the interference sources over a considerable distance. Figure 5c shows the simulation results of the Talbot effect propagating in the Mikaelian lens, which is excited by four adjacent piezoelectric plates with a spacing of . It can be observed that the Talbot diverge at a quarter of the period but reimage at half the period. According to Eq. (14), the image at should be antisymmetric to the input signals about the lens axis. Since the input signals are symmetric, thus the image at are the same with the input signals. This mode periodically repeat as the propagation distance increases. Figure 5d presents the fields distributions at (orange curve), (dashed curve), (dot dashed curve) and (dot curve). It can be seen that there are four peaks in the curves, which actually presents the Talbot spots. The peaks in the curves locate at the same positions correspondingly, which further more verify the repetitive imaging of the Talbot effects in the Mikaelian lens.
Fig. 5.
The Talbot effects generated by (a) infinite and (b) finite periodic interference sources in thin plate and (c) generated by finite periodic sources in the designed Mikaelian lens. (d) The Talbot spots located at (orange curve), (dashed curve), (dot dashed curve) and (dot curve).
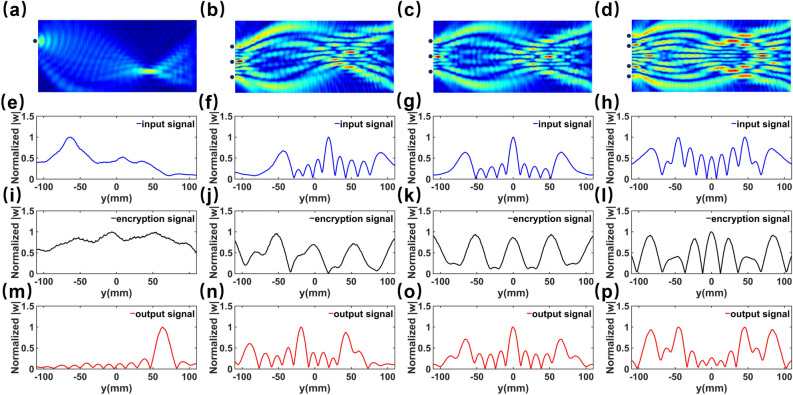
The research above demonstrates that the Talbot effect produced by finite-period interference sources in the Mikaelian lens possesses non-diffractive properties and can reform the image of the interference source at the half-period position. This feature can be used to achieve communication encoding for flexural waves. To further investigate the potential of using the non-diffractive Talbot effect of flexural waves in the Mikaelian lens for communication encoding, simulations are conducted using the commercial software COMSOL Multiphysics. In the simulations, we utilized a proprietary tetrahedral mesh to partition the model, while simultaneously setting the maximum element size to 1/6 of the wavelength and the minimum element size to 1/12 of the wavelength. The simulations are performed at 35 kHz with the specified displacements applied at the incident end of the Mikaelian lens model (Fig. 3b sources position), and the displacement field was observed both on the thin plate and the back of the lens. By adjusting whether the actively controlled piezoelectric elements were excited, encoding was performed using for no excitation and for excitation. The simulation results are shown in Fig. 6, where Fig. 6a–d represent the displacement fields of flexural waves for various encoding sequences of 01000000, 001001001, 010010010, and 101000101, respectively. The input signal (blue solid line) is obtained near the left end of the Mikaelian lens. The encrypted result (black solid line) is at the (focusing plane). The final output result (red solid line) is obtained at . It can be observed that the four sequences are transmitted and focused over long distances in the lens. Figure 6e shows the normalized displacement distribution of the input signal when exciting a single piezoelectric element, where there is only one peak located at , indicating the 9-bits binary code of 010000000, while Fig. 6i shows the normalized displacement distribution of the encrypted result. In Fig. 6m, there is an obviously peak appearing at the location of (0.5l, 63.2), implying a 9-bits binary code of 000000010. The source creates an inverted image at half period, making the encoding at antisymmetric to the incoming signal, as discussed in the previous parts. Consequently, by applying a reverse transformation-converting the output signal 000000010 to its reverse 010000000-we can accurately reconstruct the original incident signal as 010000000. Figure 6f,j,n,g,k,o,h,l,p correspond to different encoding sequences. The simulation results show that the designed system has a good performance for non-diffractive Talbot effect encoding.
Fig. 6.
Simulation results of the displacement field for a single interference source (a), sources of 001001001 (b), sources of 010010010 (c) and sources of 101000101 (d). Normalized displacement distribution of the input signals (e–h), encryption signals (i–l) and output signals (m–p), corresponding to (a–d), respectively.
Experimental results
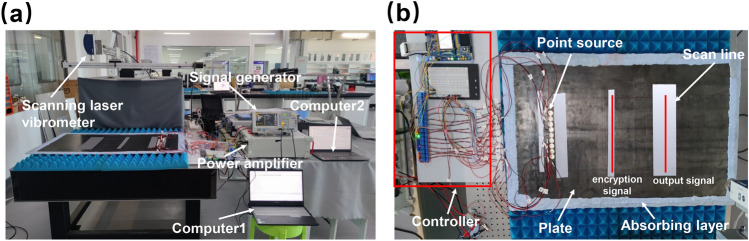
The performance of the designed lens is further verified by experiments. The experimental setup, as shown in Fig. 7, consists of the flexural wave Mikaelian lens, a signal generator, an array of piezoelectric elements with a radius of , a controller comprising a Stm32 microcontroller and relays, a laser scanner, and other components. The designed Mikaelian lens is fabricated by the precision mechanical machining technology on a CK6160 CNC lathe, as shown in Fig. 7a. This approach allows to efficiently realize the design with precision and speed. Blu-tack is adhesive to the edges of the lens to absorb the reflected waves, and the lens lies on the sound-absorbing wedge made up of sponge. This will result in a slight deviation between the experimental and simulation results, but this deviation can be ignored as it is sufficiently small. And placing the lens in this way would be more convenient for experiments. Nine circular piezoelectric elements are attached to the back of the lens and are located at the incident end of the lens to generate incident flexural waves. The incident wave signal applied to the piezoelectric elements is generated by a signal generator and amplified by a power amplifier. The displacements are scanned and recorded by a laser vibrometer.
Fig. 7.
(a) Experimental setup. (b) The wave source is mounted on the backside of the sample, and the displacement normalized distribution of the lens’s focusing and imaging positions is measured using a laser vibrometer.
The controller has multiple channels to independently control their different element of the line array. The open and closed circuit states represent the binary codes of 0 and 1, respectively. A signal generator is used to excite the circular piezoelectric elements.
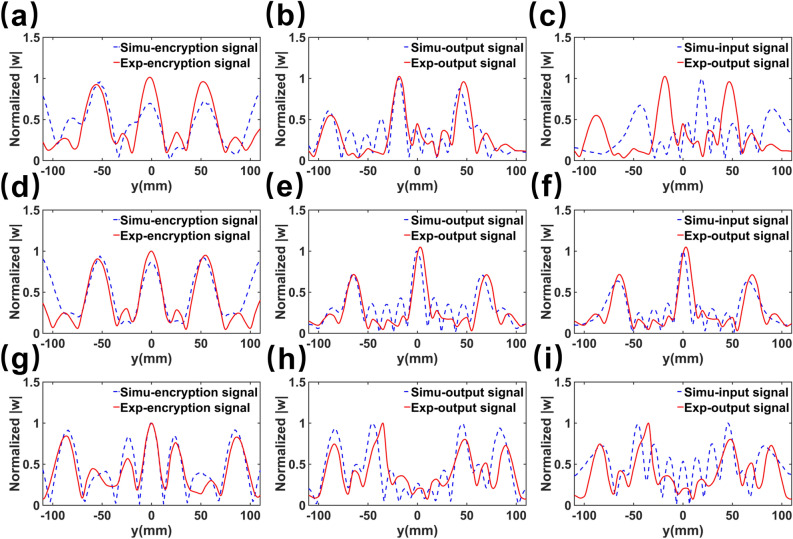
Figure 8 shows the simulated and experimental results of the non-diffractive encoding, where three different 9bits codes, i.e. 001001001, 010010010 and 101000101, are employed to verify the encoding capacities. Figure 8a–c are the cases of 001001001, where in Fig. 8a the dashed and solid lines represent the displacement distribution of the simulation and experiment at , respectively. It can be seen that the simulated results match with the experiments well. The output signals are shown in Fig. 8b, where the simulated and experiment result have a high consistency. Since the input and output signals are near the left end and half of the period of the Mikaelian lens correspondingly, they are anti-symmetric about . This can be further proved in Fig. 8c, where the dashed and solid curves are the input and the output signals, respectively. It can be seen that there are 3 peaks both in the input and output signals. Furthermore, the y coordinates of the 3 input peaks are and 91.08 respectively, while the peaks of the output signals are at and 46.80 correspondingly. Given that the spacing between two adjacent binary codes is approximately or 20 mm, the input signal encodes a 9-bit binary sequence of 001001001. Conversely, the corresponding output signal reflects an inverted pattern, represented by 100100100. Therefore, by inverting themselves, the output signals are transformed into the same as the input signals, achieving the reconstruction of the input signal. According to Fig. 8a–c, it is obvious that the system works well for the encoding of 001001001. Figure 8d–f and h–i are the experiment results of the cases of 010010010 and 101000101, respectively.
Fig. 8.
The simulations (dashed blue curves) and experiments (solid red curves) of the non-diffractive encodings of 001001001 (a–c), 010010010 (d–f) and 101000101 (g–i), respectively.
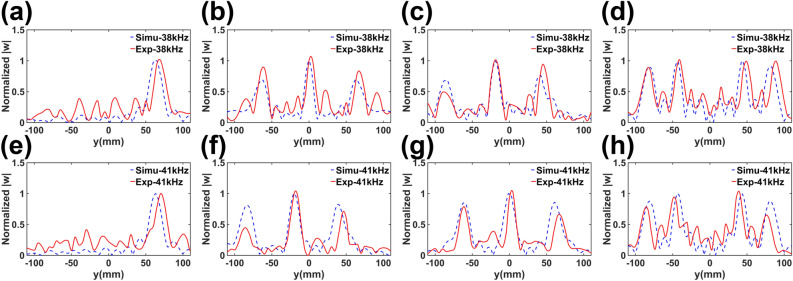
Since the encoding process is based on the active interference sources, the system works in a broadband frequency range. This is further proved by the experiments, as shown in Fig. 9, where the simulated and experimental displacements at output ends are represented by the dashed and solid curves correspondingly. Figure 9a shows the displacements at the output ends produced by a single source at , where there can be found the good matching between the simulations and experiment. And Fig. 9b to d are the cases of the coding sequences of 001001001,010010010 and 101000101 at respectively, in which the simulations matches the experiments well. Figure 9e–h present the counterparts of the scenarios in Fig. 9a–d. Additionally, it is noteworthy that the performance remains robust at , as indicated by the close agreement between simulations and experiments in Fig. 9e–h.
Fig. 9.
Simulation and experimental results of the output binary sequences of (a) 001001001, (b) 010010010, (c) 101000101 at 38 kHz, correspondingly. (e–h) The counterpart of subfigures (a–c) at 41kHz.
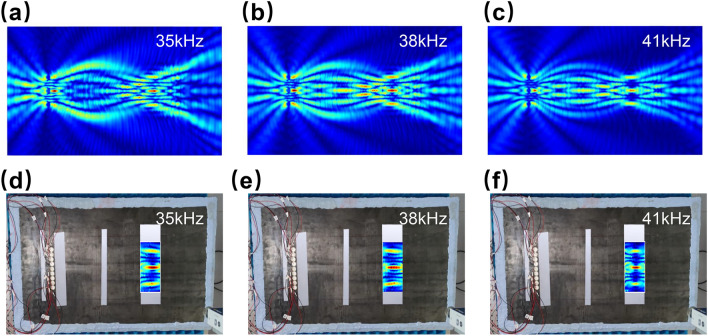
In addition, we conduct a field scan of the output displacements of the system at 35 kHz, 38 kHz, and 41 kHz to visually illustrate the alignment between simulations and experiments, as depicted in Fig. 10. Specifically, Fig. 10a–c represent the simulated displacement fields for the coding sequence 010010010 at , , and , respectively. It is evident that the Talbot effect can be generated through the interference sources, and a reconstructed image of the source is formed at l/2 after convergence at the coding output end. Corresponding experimental results are shown in Fig. 10d–f, where the displacement field was measured in an area near the output end with a width of 80 mm and a length of 200 mm, with a scanning step size of 5 mm. The high consistency between experimental and simulated results confirms the broad-frequency effectiveness of the designed system.
Fig. 10.
The simulated displacements of the coding sequences of 010010010 at (a) , (b) and (c) . The experimental displacements of the coding sequences of 010010010 at (d) , (e) and (f) .
Conclusions
In conclusion, we design a Mikaelian lens, with a length of about half a period, for manipulating flexural waves with conformal transformation theory. The properties of the designed lens are studied with simulations, which show that the flexural wave propagating in the lens exhibits behaviors of self-focusing as well as non-diffraction Talbot effects. Based on these properties, an active encoding system is proposed to encoding the fleuxral wave effectively. In the proposed system, 9 adjacent piezoelectric pieces are placed at the incident end of the lens to provide the incident binary signals, where the open and closed states of the piezoelectric pieces represent 0 and 1 in the binary, respectively. The output end is at the right end of the lens, which means the distance between the input and the output signals is as far as half of the lens period, leading to antisymmetry of the signals. According to the properties of the designed Mikaelian lens, the input signals and the output signals are antisymmetric about the main axis of the lens. Therefore, the input coding sequences can be reconstructed by inverting the binary sequences of the output signals. Moreover, the piezoelectric pieces are connected to a programmable switch controller, which enables active control of both closed and open circuits, resulting in flexible active encoding. The results from simulations, corroborated by experimental evidence, substantiate the efficiency of active encoding in this study, indicating promising avenues for its application in the realms of flexural wave communication and detection, such as structural health monitoring, wireless communication in solid media and data transmission in robotics.
Acknowledgements
The authors sincerely acknowledge the financial support of BIGC Projects (Grant Nos. BIGC Ed202206, 27170123007), the Project of Construction and Support for high-level Innovative Teams of Beijing Municipal Institutions(Grant No. BPHR20220107), the financial support of Anhui Provincial Natural Science Foundation (Grant No. JZ2023AKZR0583).
Author contributions
Z.Li wrote the main manuscript text; Z. Li, K. Liu and C. Li finished the experiments; Y. Liu, T. Li and Y. Du contributed to the methodology; Z. Sun, L. Zhao and J. Yang developed the idea and concept,guiding the researching process All authors reviewed the manuscript.
Data availability
The datasets analyzed during the current study are available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Zhaoyong Sun, Email: sunzhaoyong@bigc.edu.cn.
Liuxian Zhao, Email: lxzhao@hfut.edu.cn.
Jun Yang, Email: jyang@mail.ioa.ac.cn.
References
- 1.Kadic, M., Milton, G. W., Van Hecke, M. & Wegener, M. 3d metamaterials. Nat. Rev. Phys.1, 198–210. 10.1038/s42254-018-0018-y (2019). [Google Scholar]
- 2.Gao, N. et al. Acoustic metamaterials for noise reduction: A review. Adv. Mater. Technol. 10.1002/admt.202100698 (2022).35668819 [Google Scholar]
- 3.Padilla, W. J. & Averitt, R. D. Imaging with metamaterials. Nat. Rev. Phys.4, 85–100. 10.1038/s42254-021-00394-3 (2021). [Google Scholar]
- 4.Dong, E. et al. Underwater acoustic metamaterials. Natl. Sci. Rev. 10.1093/nsr/nwac246 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang, Z. et al. Diffusion metamaterials. Nat. Rev. Phys.5, 218–235. 10.1038/s42254-023-00565-4 (2023). [Google Scholar]
- 6.Pendry, J. B. Controlling electromagnetic fields. Science312, 1780–1782. 10.1126/science.1125907 (2006). [DOI] [PubMed] [Google Scholar]
- 7.Leonhardt, U. Notes on conformal invisibility devices. New J. Phys.8, 118–118. 10.1088/1367-2630/8/7/118 (2006). [Google Scholar]
- 8.Yu, N. et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science334, 333–337. 10.1126/science.1210713 (2011). [DOI] [PubMed] [Google Scholar]
- 9.Sun, Z., Zhao, L. & Yang, J. Underwater acoustic self-focusing and bending in conformal mikaelian lens by pentamode metafluid. J. Phys. D Appl. Phys.56, 505304. 10.1088/1361-6463/acf869 (2023). [Google Scholar]
- 10.Liu, R. et al. Broadband ground-plane cloak. Science323, 366–369. 10.1126/science.1166949 (2009). [DOI] [PubMed] [Google Scholar]
- 11.Chen, Y. et al. Broadband solid cloak for underwater acoustics. Phys. Rev. B95, 180104. 10.1103/PhysRevB.95.180104 (2017). [Google Scholar]
- 12.Sun, Z., Sun, X., Jia, H., Bi, Y. & Yang, J. Quasi-isotropic underwater acoustic carpet cloak based on latticed pentamode metafluid. Appl. Phys. Lett.114, 094101. 10.1063/1.5085568 (2019). [Google Scholar]
- 13.Jiang, Z. H., Kang, L. & Werner, D. H. Conformal metasurface-coated dielectric waveguides for highly confined broadband optical activity with simultaneous low-visibility and reduced crosstalk. Nat. Commun. 10.1038/s41467-017-00391-0 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Arbabi, E. et al. Mems-tunable dielectric metasurface lens. Nat. Commun.9, 812. 10.1038/s41467-018-03155-6 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ren, H. et al. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 10.1038/s41565-020-0768-4 (2020). [DOI] [PubMed] [Google Scholar]
- 16.Lemoult, F., Lerosey, G., de Rosny, J. & Fink, M. Resonant metalenses for breaking the diffraction barrier. Phys. Rev. Lett. 10.1103/PhysRevLett.104.203901 (2010). [DOI] [PubMed] [Google Scholar]
- 17.Kaina, N., Lemoult, F., Fink, M. & Lerosey, G. Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials. Nature525, 77–81. 10.1038/nature14678 (2015). [DOI] [PubMed] [Google Scholar]
- 18.Walker, E. L., Jin, Y., Reyes, D. & Neogi, A. Sub-wavelength lateral detection of tissue-approximating masses using an ultrasonic metamaterial lens. Nat. Commun.11, 5967. 10.1038/s41467-020-19591-2 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen, Al., Tang, Q., Wang, H., Zhao, S. & Wang, Y. Multifunction switching by a flat structurally tunable acoustic metasurface for transmitted waves. Sci. China Phys. Mech. Astron.63, 244611. 10.1007/s11433-019-1498-2 (2020). [Google Scholar]
- 20.Hu, Z. et al. Engineering zero modes in transformable mechanical metamaterials. Nat. Commun.14, 1266. 10.1038/s41467-023-36975-2 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wei, Z., Hu, Z., Zhu, R., Chen, Y. & Hu, G. A transformable anisotropic 3d penta-mode metamaterial. Mater. Des.234, 112306. 10.1016/j.matdes.2023.112306 (2023). [Google Scholar]
- 22.Zabihi, A., Ellouzi, C. & Shen, C. Tunable, reconfigurable, and programmable acoustic metasurfaces: A review. Front. Mater.10, 1132585. 10.3389/fmats.2023.1132585 (2023). [Google Scholar]
- 23.Lau, J. Reconfigurable transmitarray design approaches for beamforming applications. IEEE Trans. Antennas Propag.60, 5679–5689 (2012). [Google Scholar]
- 24.Cui, T. Coding metamaterials, digital metamaterials and programmable metamaterials. Light-Sci. Appl.3, e218–e218 (2014). [Google Scholar]
- 25.Du, L. et al. Mechanically programmable composite metamaterials with switchable positive/negative Poisson’s ratio. Adv. Funct. Mater.[SPACE]10.1002/adfm.202314123 (2024).39071865 [Google Scholar]
- 26.Tian, Z. et al. Programmable acoustic metasurfaces. Adv. Funct. Mater.29, 1808489. 10.1002/adfm.201808489 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen, Z., Chong, Y. B., Lim, K. M. & Lee, H. P. Reconfigurable 3d printed acoustic metamaterial chamber for sound insulation. Int. J. Mech. Sci.266, 108978. 10.1016/j.ijmecsci.2024.108978 (2024). [Google Scholar]
- 28.Zhang, M., Hu, C., Yin, C., Qin, Q.-H. & Wang, J. Design of elastic metamaterials with ultra-wide low-frequency stopbands via quantitative local resonance analysis. Thin-Walled Struct.165, 107969. 10.1016/j.tws.2021.107969 (2021). [Google Scholar]
- 29.Ma, F., Liu, C., Li, Y. & Wu, J. H. A thin-walled mesoscopic hybrid slit-resonator metamaterial absorber. Thin-Walled Struct.193, 111226. 10.1016/j.tws.2023.111226 (2023). [Google Scholar]
- 30.Li, K. et al. Mechanical properties of re-entrant anti-chiral auxetic metamaterial under the in-plane compression. Thin-Walled Struct.184, 110465. 10.1016/j.tws.2022.110465 (2023). [Google Scholar]
- 31.Wang, L., Chen, Z. & Cheng, L. A metamaterial plate with magnetorheological elastomers and gradient resonators for tuneable, low-frequency and broadband flexural wave manipulation. Thin-Walled Struct.184, 110521. 10.1016/j.tws.2022.110521 (2023). [Google Scholar]
- 32.Zhu, S., Wang, J., Chen, L., Liu, T. & Li, W. Negative stiffness metamaterial with directional stability in uniform fields. Thin-Walled Struct.194, 111302. 10.1016/j.tws.2023.111302 (2024). [Google Scholar]
- 33.Xu, Y. et al. Beam splitting of flexural waves with a coding meta-slab. Appl. Phys. Express12, 097002. 10.7567/1882-0786/ab36bd (2019). [Google Scholar]
- 34.Yaw, Z., Zhou, W., Chen, Z. & Lim, C. Stiffness tuning of a functional-switchable active coding elastic metasurface. Int. J. Mech. Sci.207, 106654. 10.1016/j.ijmecsci.2021.106654 (2021). [Google Scholar]
- 35.Li, X.-S., Wang, Y.-F. & Wang, Y.-S. Sparse binary metasurfaces for steering the flexural waves. Extreme Mech. Lett.52, 101675. 10.1016/j.eml.2022.101675 (2022). [Google Scholar]
- 36.Yuan, S.-M. et al. Reconfigurable flexural waves manipulation by broadband elastic metasurface. Mech. Syst. Signal Process.179, 109371. 10.1016/j.ymssp.2022.109371 (2022). [Google Scholar]
- 37.Wu, Q., Zhang, X., Shivashankar, P., Chen, Y. & Huang, G. Independent flexural wave frequency conversion by a linear active metalayer. Phys. Rev. Lett.128, 244301. 10.1103/PhysRevLett.128.244301 (2022). [DOI] [PubMed] [Google Scholar]
- 38.Zhao, J. et al. Broadband sub-diffraction and ultra-high energy density focusing of elastic waves in planar gradient-index lenses. J. Mech. Phys. Solids150, 104357. 10.1016/j.jmps.2021.104357 (2021). [Google Scholar]
- 39.Chen, J., He, X., Chen, M. & Liu, Y. Broadband achromatic flexural wave mikaelian lens for high resolution focusing. J. Phys. D Appl. Phys.55, 335502. 10.1088/1361-6463/ac72d1 (2022). [Google Scholar]
- 40.Chen, J. et al. Ultrabroadband and multifunctional achromatic mikaelian lens on an elastic plate. Phys. Rev. Appl.18, 064047. 10.1103/PhysRevApplied.18.064047 (2022). [Google Scholar]
- 41.Wang, X. et al. Self-focusing and the Talbot effect in conformal transformation optics. Phys. Rev. Lett. 10.1103/PhysRevLett.119.033902 (2017). [DOI] [PubMed] [Google Scholar]
- 42.Chen, J. et al. Conformally mapped Mikaelian lens for broadband achromatic high resolution focusing. Laser Photonics Rev.15, 2000564. 10.1002/lpor.202000564 (2021). [Google Scholar]
- 43.Zhou, Y. & Chen, H. Near-field multiple super-resolution imaging from Mikaelian lens to generalized Maxwell’s fish-eye lens. Chin. Phys. B31, 104205. 10.1088/1674-1056/ac5d34 (2022). [Google Scholar]
- 44.Gao, H. et al. Conformally mapped multifunctional acoustic metamaterial lens for spectral sound guiding and Talbot effect. Research2019, 1–10. 10.34133/2019/1748537 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mikaelian, A. & Prokhorov, A. V. Self-focusing media with variable index of refraction. Progr. Opt.17, 279–345. 10.1016/S0079-6638(08)70241-5 (1980). [Google Scholar]
- 46.Liao, Q. et al. Solid-phase sintering and vapor-liquid-solid growth of bp@mgo quantum dot crystals with a high piezoelectric response. J. Adv. Ceram.11, 1725–1734. 10.1007/s40145-022-0643-x (2022). [Google Scholar]
- 47.Su, X., Norris, A. N., Cushing, C. W., Haberman, M. R. & Wilson, P. S. Broadband focusing of underwater sound using a transparent pentamode lens. J. Acoust. Soc. Am.141, 4408–4417. 10.1121/1.4985195 (2017). [DOI] [PubMed] [Google Scholar]
- 48.Lin, S.-C.S., Huang, T. J., Sun, J.-H. & Wu, T.-T. Gradient-index phononic crystals. Phys. Rev. B79, 094302. 10.1103/PhysRevB.79.094302 (2009). [Google Scholar]
- 49.Zigoneanu, L., Popa, B.-I. & Cummer, S. A. Design and measurements of a broadband two-dimensional acoustic lens. Phys. Rev. B10.1103/PhysRevB.84.024305 (2011). [Google Scholar]
- 50.Talbot, H. F. Facts relating to optical science. Philos. Mag.9, 401–407 (1836). [Google Scholar]
- 51.Wen, J., Zhang, Y. & Xiao, M. The talbot effect: Recent advances in classical optics, nonlinear optics, and quantum optics. Adv. Opt. Photonics5, 83. 10.1364/AOP.5.000083 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets analyzed during the current study are available from the corresponding author on reasonable request.