Abstract
With increasing accessibility to geographic information systems (GIS) software, statisticians and data analysts routinely encounter scientific data sets with geocoded locations. This has generated considerable interest in statistical modeling for location-referenced spatial data. In public health, spatial data routinely arise as aggregates over regions, such as counts or rates over counties, census tracts, or some other administrative delineation. Such data are often referred to as areal data. This review article provides a brief overview of statistical models that account for spatial dependence in areal data. It does so in the context of two applications: disease mapping and spatial survival analysis. Disease maps are used to highlight geographic areas with high and low prevalence, incidence, or mortality rates of a specific disease and the variability of such rates over a spatial domain. They can also be used to detect hot spots or spatial clusters that may arise owing to common environmental, demographic, or cultural effects shared by neighboring regions. Spatial survival analysis refers to the modeling and analysis for geographically referenced time-to-event data, where a subject is followed up to an event (e.g., death or onset of a disease) or is censored, whichever comes first. Spatial survival analysis is used to analyze clustered survival data when the clustering arises from geographical regions or strata. Illustrations are provided in these application domains.
Keywords: Bayesian hierarchical modeling, conditional autoregressive (CAR) models, cure rate models, disease mapping, multivariate CAR models, multivariate disease mapping, spatial survival analysis
INTRODUCTION
The emergence of highly efficient geographical information systems (GIS) databases and associated computational resources has transformed the way spatial or geographical data are collected, stored, managed, and analyzed. Researchers in diverse disciplines within the physical, social, and environmental sciences and in public health are increasingly faced with the task of analyzing data that are geographically referenced and often presented as maps. Consequently, the past decade has seen significant development in statistical modeling of complex spatial data; for a variety of methods and applications, see the texts by Cressie (16), Webster & Oliver (41), Cromley & McLafferty (18), Møller (32), Schabenberger & Gotway (37), Waller & Gotway (40), Cressie & Wikle (17), and Banerjee et al. (5), among others.
Following convention, spatial data are often classified into one of three basic types: point-referenced data, point pattern data, and areal data. Point-referenced data sets consist of variables (e.g., outcomes and predictors) that are linked to a specific point location, customarily referenced by a coordinate system (e.g., longitude-latitude, easting-northing). Point-referenced data sets are not uncommon in environmental monitoring for public health, where pollutants are often measured at spatial fixed locations or monitoring stations. The spatial locations are considered fixed, and investigators are usually interested in the spatial distribution of the measurements and in predicting their levels at new spatial locations. Point pattern data refer to situations where the spatial locations themselves correspond to random events. Examples include locations being reported as sites of the occurrence of a particular disease. Areal data consist of variables that are aggregated over regions as counts or rates. Areal data are more common in public health applications, where geospatial referencing is not performed at very fine scales, such as GPS locations of households or small neighborhoods, to protect the privacy of human subjects.
The Annual Review of Public Health has published two excellent reviews on spatial analytic methods by Rushton (36) and Auchincloss et al. (1). This review differs from the previous ARPH articles because of its emphasis on the advances made in formal statistical modeling and inference for spatial data. It is beyond the scope of a single article to review all such methods. The aforementioned texts offer more comprehensive coverage. This review focuses primarily on areal data analysis because areal data are most conspicuous in public health. In fact, point patterns are often reported as areal aggregates, i.e., counts, rates of other summaries over well-delineated spatial regions such as counties or census tracts or zip codes, and subsequently modeled as areal data. Within this context, the review briefly discusses disease mapping for single diseases and for multiple diseases that may be associated with each other, as well as modeling of areally referenced survival data.
SPATIAL MODELS FOR DISEASE MAPPING
In the fields of medicine and public health, researchers often seek a better understanding of regional patterns of disease. In the United States, publicly available data on precise locations of disease cases are fairly uncommon owing to strict confidentiality regulations. Summaries of disease at a regional level, however, are often relatively easy to obtain. Disease mapping is an epidemiological technique used to highlight geographic areas with high and low incidence or mortality rates of a specific disease and to map how such rates vary over the study region. Disease maps are often used to detect spatial clusters, which may generate hypotheses regarding common underlying environmental, demographical, or cultural factors shared by neighboring regions.
Although one could easily map the crude incidence and mortality rates, such maps can lead to spurious conclusions when the population sizes for some of the areal regions are small. Sparse populations usually result in large variability in the estimated rates and impair our ability to distinguish chance variability from genuine differences. Statistical models that allow a more accurate depiction of true disease rates by borrowing information from neighboring regions will help mitigate the effects of sparsely populated regions and deliver better inference.
Perhaps the most conspicuous manner of modeling spatial dependence is to introduce spatially associated random effects within a Bayesian hierarchical setting [see, for example, Banerjee et al. (5)]. The Bayesian modeling and inferential framework is flexible and extremely rich in its capabilities to accommodate various scientific hypotheses and assumptions. In particular, it provides a cohesive framework for combining complex data models and external knowledge or expert opinion. This review discusses spatial modeling within a Bayesian context. The models and illustrations that follow are produced using Markov chain Monte Carlo (MCMC) simulation methods. Again, it is beyond the scope of this review to discuss MCMC algorithms. Details on established MCMC and other computational algorithms for spatial data can be found in the books by Møller (32), Gelman et al. (22), and Robert & Casella (35).
Spatial Modeling of a Single Disease: A Brief Review
A popular class of models for areal data come from Markov random fields (MRF). These models are based on a Markov property, where the conditional distribution of the health outcome from a region, given the observations from all the other regions, depends only on the observations in the neighborhood. Here, we define the neighborhood by area adjacency, such that two regions are neighbors if they share a common boundary (or perhaps even meet at a point). Other definitions are sometimes used (e.g., regions with centroids within a given fixed distance).
Let be the observed number of cases of a certain disease in region , and let be the expected number of cases in this same region. A popular likelihood for mapping a single disease is
| 1. |
where represents the log-relative risk expressed in terms of departures of the observed from expected counts, each is a vector of explanatory variables or covariates associated with region having parameter coefficient , and are spatially correlated random effects. We place a form of Gaussian MRF model, commonly referred to as the conditionally autoregressive (CAR) prior, on the random effects , i.e.,
| 2. |
where denotes the -dimensional normal distribution, is an diagonal matrix with diagonal elements that denote the number of neighbors of region , and is the adjacency matrix of the map (i.e., , and if is adjacent to and 0 otherwise). In Equation 2, is the spatial dispersion parameter, and is the spatial autocorrelation parameter. The CAR prior corresponds to the following conditional distribution of :
| 3. |
where denotes that region is a neighbor of region . The CAR structure (2) reduces to the well-known intrinsic conditionally autoregressive (ICAR) model [described in Besag et al. (10)] if or an independence model if . The ICAR model induces local smoothing by borrowing strength from the neighbors, whereas the independence model assumes independence of spatial rates and induces global smoothing. The smoothing parameter in the CAR prior (2) controls the strength of spatial dependence among regions, though it has long been appreciated that a fairly large may be required to deliver significant spatial correlation [see Wall (39) for details on this]. Other variants of CAR models have been developed and applied to public health problems by Leroux et al. (30) and Dean et al. (19).
Spatial Modeling of Multiple Diseases
Turning to multiple diseases, let be the observed number of cases of disease in region , , and let be the expected number of cases for the same disease in this same region. As in the previous section above, the are thought of as random variables, whereas the are thought of as fixed and known. For the first level of the hierarchical model, conditional on the random effects , we assume the are independent of each other such that
| 4. |
where each is a vector of region-specific explanatory variables for disease having (possibly region-specific) parameter coefficients . The key problem here is to specify rich and flexible spatial distributions for the .
Carlin & Banerjee (11) and Gelfand & Vounatsou (21) generalized the univariate CAR (2) to a joint model for the random effects , which permits modeling of correlation among the diseases while maintaining spatial dependence for each of the diseases. These models were subsequently subsumed by more general, and flexible, Bayesian hierarchical frameworks developed and implemented by Jin et al.(27, 28).
The idea in Jin et al. (28) is best expounded with diseases. Let be the vector of spatial random effects for the first disease, and let be the same for the second disease. Jin et al. (28) specify a joint spatial model for and by specifying a conditional distribution of given and a marginal distribution for . To achieve spatial smoothing, we assume that both these distributions are CARs. More precisely, we write the joint density as
| 5. |
where and are the bridging parameters associating the spatial effect for disease 1 in region with disease 2 in region . With disease 2 in a neighboring region, and are smoothing parameters associated with the conditional distribution of and the marginal distribution of respectively, and and scale the precision of and , respectively. The model in Equation 5 yields a legitimate probability density as long as the two CAR distributions on the right-hand side are valid, which means that the two dispersion matrices for and must be positive definite. Jin et al. (28) provide conditions for these matrices to be positive definite.
Models where the spatial random effects are shown as in Equation 5 are known as generalized multivariate conditionally autoregressive (GMCAR) models. The specification in Equation 5 subsumes several special cases in the multivariate disease mapping literature. Setting and produces a model showing that the association between the two diseases remains the same across the regions. If we assume and , then we ignore dependence between the multivariate components, and the model turns out to be equivalent to fitting two separate univariate CAR models. Finally, if we assume , and , then the model becomes a simple bivariate normal model with no spatial association.
The above approach is appealing for two diseases, or perhaps at most for three diseases, but using it to model several diseases at once has its limitations. An inherent problem with these methods is that their conditional specification imposes a potentially arbitrary order on the variables being modeled, as they lead to different marginal distributions depending on the conditioning sequence [i.e., whether to model and then , or and then ]. This problem is somewhat mitigated in certain (e.g., medical and environmental) contexts where a natural order is reasonable, but in many disease mapping contexts this is not the case.
To obviate the ordering issue, Jin et al. (27) developed an order-free, joint framework for multivariate areal modeling that allows versatile spatial structures, yet is computationally feasible for many outcomes. These are called coregionalized MCAR models, named after linear models of coregionalization in multivariate geostatistics [see, e.g., Wackernagel (38)]. The underlying idea here is to develop richer spatial association models using linear transformations of much simpler spatial distributions. The objective is to allow explicit smoothing of cross-covariances without being hampered by conditional ordering. In particular, suppose we assume a common proximity specification for each component of the random effects vector, . Then, we could write , where , the component of , is a univariate intrinsic CAR with precision parameter and each of the component CAR models are independent. The matrix represents the linear transformation that maps independent CAR effects for each disease to correlated CAR (or multivariate CAR) effects for the diseases.
MCAR models are not the only available option for analyzing multivariate areal data. Zhang et al. (43) have developed an arguably simpler approach by adapting smoothed ANOVA (SANOVA) models (24) for areal data. The underlying idea is to extend SANOVA to cases in which one factor is a spatial map, which is smoothed using a CAR model, and a second factor is, for example, a type of disease. Data sets routinely lack enough information to identify the additional structure of MCAR. SANOVA offers a simpler and more intelligible structure than MCAR while performing equally well. Nevertheless, the MCAR and more general CAR-based models offer a rich inferential framework for capturing complex spatial associations. We focus on MCAR models and their variants within the disease mapping context in the remainder of this article.
Illustration
We illustrate with a brief example from Jin et al. (28), who modeled the numbers of deaths due to cancers of the lung and esophagus between 1991 and 1998 across the 87 counties in Minnesota. The county-level maps of the raw standardized mortality ratios (i.e., ) shown in Figure 1 exhibit evidence of correlation both across space and between cancers, motivating use of our proposed GMCAR models. The bottom row shows the smoothed maps obtained from the GMCAR model specified using a CAR prior for the conditional distribution [lung|esophagus] and another CAR for the marginal distribution [esophagus].
Figure 1.
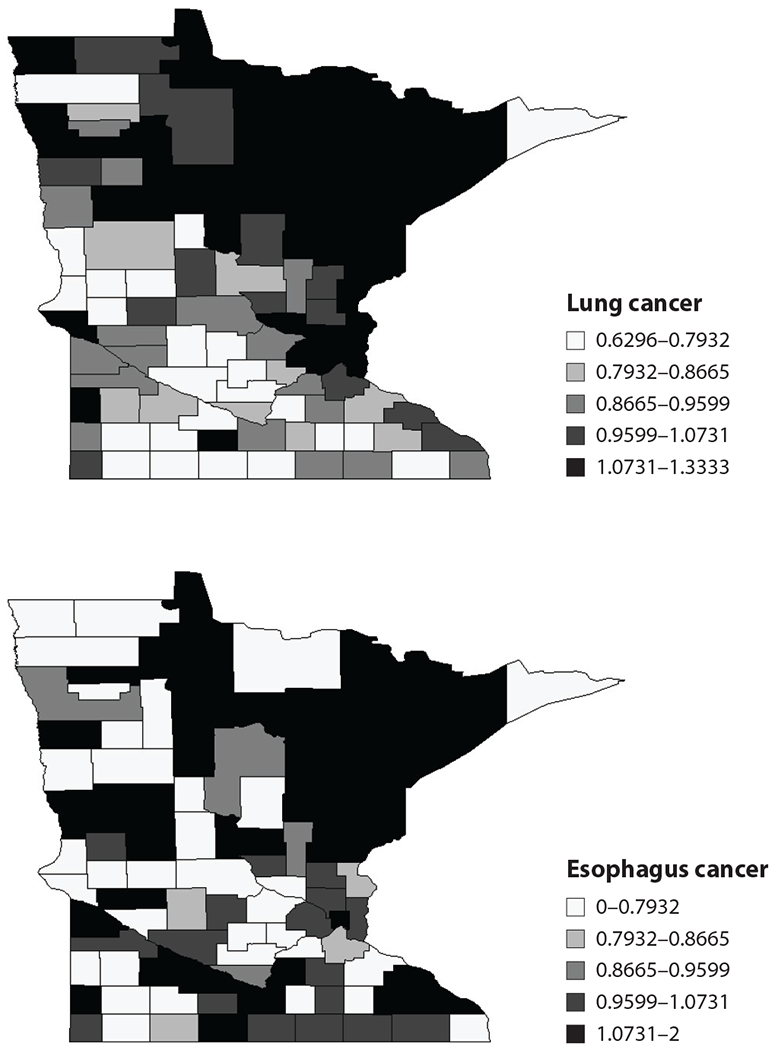
Maps of raw standard mortality ratios (SMRs) of lung and esophagus cancer in Minnesota between 1991 and 1998.
We fit the model Banerjee & Carlin (4) to this data set. To determine , we account for each county’s age distribution by calculating the expected age-adjusted number of deaths due to cancer in county as for and , where is the age-specific death rate for cancer and age group over all Minnesota counties, is the number of deaths in age group for county and cancer , and is the total population at risk in age group for county . Jin et al. (28) conducted exploratory analysis on the basis of least-squares estimation as well as formal Bayesian model comparison methods to show that a GMCAR model specified using CAR distributions for [lung|esophagus] and [esophagus] was preferable to modeling [esophagus|lung]. The GMCAR models are easily implemented in the Bayesian modeling language BUGS (see http://www.biostat.umn.edu/~brad/software.html for the code and the data). Figure 2 presents maps of the smoothed standardized mortality ratios (SMRs) for lung and esophagus cancer in Minnesota from the GMCAR.
Figure 2.
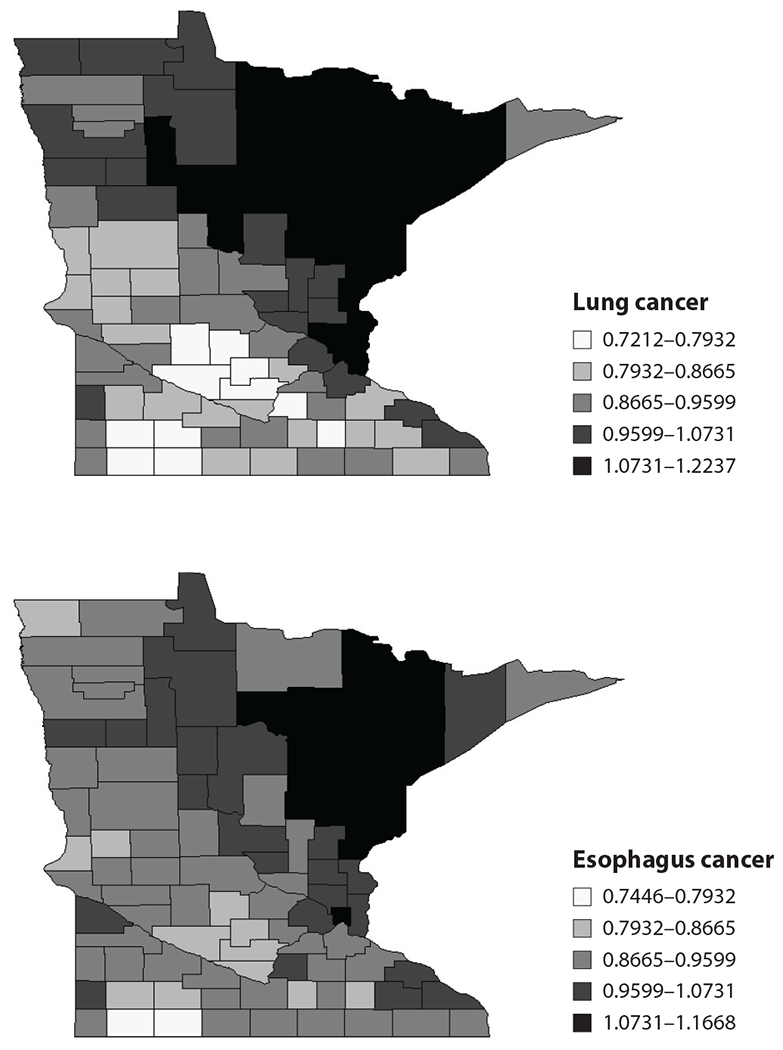
Maps of posterior means of standardized mortality ratios (SMRs) of lung and esophagus cancer in Minnesota between 1991 and 1998 from the generalized multivariate conditionally autoregressive (GMCAR) model with conditioning order [lung|esophagus].
Jin et al. (28) also reported that the estimate of the parameter was statistically significant for the GMCAR with [lung|esophagus] and not significant in the reverse order. We also saw that the posterior distribution of the linking parameters and had mostly positive support, meaning that the two cancers had positive spatial correlation. This is also evident from the maps of the posterior means of the SMRs for the two cancers under the full model shown in Figure 2. Incidence of the two cancers is clearly strongly correlated, with higher fitted ratios extending from the Twin Cities metro area (eastern side, about one-third of the way up) to the mining and tourism-oriented north and northeast, regions where conventional wisdom suggests that cigarette smoking may be more common.
The GMCAR delivered point and 95% equal-tail interval estimates of 0.602 and (0.0267, 0.979) for , and 0.699 and (0.0802, 0.973) for . These are spatial parameters, but while their values are between 0 and 1 they are not “correlations” in the usual sense; the moderate point estimates and wide confidence intervals suggest a relatively modest degree of spatial association in the random effects. Note also that in this setup, measures spatial association in the esophagus random effects , whereas measures spatial association in the lung random effects given the esophagus random effects . Turning to and , under the GMCAR we obtained 32.65 (16.98, 66.71) and 13.73 (4.73, 38.05) as our point and interval estimates, respectively. Because these parameters measure spatial precision for each disease, they suggest slightly more variability in the esophagus random effects, although again comparison is difficult here because is a marginal precision for whereas is a conditional precision for given .
SPATIAL SURVIVAL ANALYSIS
Survival models, such as in Cox & Oakes (15), are widely used in biostatistics and epidemiology for analyzing time-to-event data, where a subject is followed up to an event (e.g., death or onset of a disease) or is “censored,” whichever comes first. Right censoring refers to situations where the event does not occur for a subject during the period of the study and the subject’s time to event is censored at the study end point. Certain study designs can produce left-censored or interval-censored data, defined analogously. As opposed to modeling disease incidence and mortality, survival models focus on how many are expected to survive after a certain period of time and the rate of failure, as well as to ascertain which underlying factors (e.g., gender, race, age, type of cancer, treatment obtained, and access to health care facilities) generate shortened or prolonged survival.
The past decade has seen much demand for the analysis of spatially referenced survival data. When each subject can be referenced with respect to a clinical site or geographical region, we might suspect that random effects corresponding to proximate regions will be similar in magnitude. Models for spatially arranged survival data customarily introduce spatial frailties, such as in Banerjee et al. (7). How these spatial frailties are introduced in survival models depends on the specific model. We briefly discuss a few alternate spatial survival models. Apart from the spatial distribution for the frailties, one needs to model a spatial hazard function with the understanding that expected survival times (or hazard rates) will be more similar in neighboring regions, owing to underlying factors (access to care, willingness of the population to seek care, etc.) that vary spatially. This expectation is in contrast to the similarity observed among survival times from subjects in proximate regions, which is not necessarily implied by spatially associated frailties.
Survival Models with Spatial Frailties
Let be the waiting time for a subject to experience an event (e.g., disease onset, relapse, death). The subject’s survival function is defined as and the hazard function as , where is the probability density function of . Let index the -th subject in region and let be observations from subjects in a study, where indicates the time at which either subject experienced the event or the subject was censored. Associated with each is an event indicator, , where if the event occurred before the termination of the study and if the subject was censored. For right-censored data, we have the likelihood
| 6. |
If , then subject contributes to the likelihood, whereas if , then it contributes to the likelihood. Cox & Oakes (15) provide the corresponding expressions for left-censored and interval-censored data.
Let be a vector of observed explanatory variables associated with subject . To account for heterogeneity in the population, most survival models will introduce these explanatory variables in Equation 6 in the hazard function. For example, the proportional hazards model stipulates that
| 7. |
where is a baseline hazard function affected only multiplicatively by the exponential term involving the explanatory variables. Another option is a “proportional odds” model (9), which requires the survival function for subject to satisfy
| 8. |
Yet another alternative is the accelerated failure time model. Here, the survival function for subject is , where is any parametric survival function and . The corresponding hazard function for subject is , where is the hazard derived from . In each of the above situations, the hazard function can be modeled using parametric or nonparametric statistical methods. The data-analytic settings where the above specifications are appropriate, or not, have been comprehensively explored and documented in the survival analysis literature. For example, the proportional odds model posits that the hazard ratio approaches unity over time, i.e., the covariate effects on the hazards disappear over time, which is clearly distinct from the proportional hazards model. The interpretation of the regression component significantly differs. The term in the proportional odds model reflects the change in the odds of survival (or failure, depending on the parameterization) given the observed covariates or risk factors.
Li & Ryan (31) provided the basis for legitimate likelihood-based inference from semiparametric spatial survival models. They proposed modeling the hazard function nonparametrically and the spatially correlated frailties using different spatial covariance functions. These models were applied to the East Boston Asthma Study to detect prognostic factors leading to childhood asthma. Henderson et al. (23) proposed using multivariate Gamma distributions to investigate spatial association and variation in the survival of acute myeloid leukemia patients in northern England. Banerjee et al. (7) proposed a Bayesian hierarchical framework to introduce spatially correlated frailties and compared performances between frailties modeled using Markov random field and geostatistical covariance functions. Data from a large infant mortality study in the state of Minnesota were analyzed. Subsequent papers explored Bayesian semiparametric modeling (2), spatiotemporal modeling (3, 8), semiparametric proportional odds models with spatial frailties (6), joint survival and longitudinal modeling with frailties (44), and parametric accelerated failure time models (42). Finally, we refer the reader to Lawson et al. (29) for spatial survival models that do not deploy spatial frailties.
Spatial Cure Rate Models
In light of significant progress in medical and health sciences, scientists and health professionals increasingly encounter data sets in which patients are expected to be cured. Models accounting for cure are important for understanding prognosis in potentially terminal diseases. Traditional parametric survival models such as Weibull or Gamma [see, e.g., Cox & Oakes (15)] do not account for cure, assuming instead that individuals who do not experience the event are censored. The subtle distinction between censoring and cure is worth noting: A subject who does not fail within the time window of the experiment is considered censored, whereas a subject is cured if he will never relapse. The latter is clearly a more abstract concept because we are never able to observe a cure, yet there is interest in estimating the probability of such an outcome, especially in various disease-relapse settings.
Cure models, such as survival models, also enjoy a rich literature too vast to be comprehensively reviewed here. The reader should see Ibrahim et al. (26) for a methodological introduction, whereas Othus et al. (34) offer a more recent review and practical introduction. Cooner et al. (14) build on their previously proposed flexible framework [13; also see Hurtado Rúa & Dey (25)] to introduce spatial frailties in cure models for geographically referenced data. Banerjee & Carlin (4) propose a spatial extension of earlier work by Chen et al. (12), which assumes that some latent biological process is generating the observed data. Suppose that subject has potential latent (unobserved) risk factors, the presence of any of which (i.e., ) will ultimately manifest the event. Chen et al. (12) consider the case of multiple latent factors, assuming that the are distributed as independent Poisson random variables with mean , i.e., is . For example, in cancer settings, these factors may correspond to metastasis-competent tumor cells within the individual. Subjects who do not experience the event during the observation period are considered censored. Thus, if is the time to an event arising from the -th latent factor for subject , the observed time to event for an uncensored individual is generated by .
Given , the are independent with survival function and corresponding density function . The parameter is a collection of all the parameters (including possible regression parameters) that may be involved in a parametric specification for the survival function . In this section, we work with a two-parameter Weibull distribution specification for the density function , where we allow the Weibull scale parameter to vary across the regions, and , which may serve as a link to covariates in a regression setup, to vary across individuals. Therefore, .
Banerjee & Carlin (4) analyze smoking cessation data using interval-censored spatial cure rate models. The outcome of interest is the time for a subject to relapse into smoking. Here, we observe only a time interval () within which the event (smoking relapse) is known to have occurred. For patients who did not resume smoking prior to the end of the study, we have , yielding the case of right-censoring at time point . Thus we now set if subject is interval-censored (i.e., the subject has experienced the event) and if the subject is right-censored.
Following Finkelstein (20), the general interval-censored cure rate likelihood is given by
If , then the marginal likelihood obtained by summing over the is and can be written as
| 9. |
As with the covariates, we introduce the frailties through the Weibull link as intercept terms in the log-relative risk; that is, we set . Here we allow the to be spatially correlated across the regions; similarly we would like to permit the Weibull baseline hazard parameters, , to be spatially correlated. A natural approach in both cases is to use a univariate CAR prior. Although one may certainly employ separate, independent CAR priors on and , another option is to use a bivariate CAR model for the . For further details, see Banerjee & Carlin (4).
Illustration
We present part of a more elaborate data analysis as part of a smoking cessation study reported by Murray et al. (33), which is of particular relevance to studies of lung health and primary cancer control. For our illustration here, we restrict attention to 223 subjects from 54 zip codes in southeastern Minnesota. These subjects were all smokers at study entry and were randomized into either a smoking intervention (SI) group or a usual care (UC) group, which received no antismoking intervention. On the basis of a consecutive five-year monitoring period between 1994 and 1998, each of these subjects were known to have quit smoking at least once during these five years. The event of interest is whether they relapse into smoking (resume smoking). The raw data revealed that 29.7% resumed smoking, producing an empirical cure fraction of 0.703. Additional information available for each subject includes sex, years as a smoker, and the average number of cigarettes smoked per day prior to the quit attempt.
As is not unusual in spatial data sets, the 54 zip codes that contributed the data were not contiguous, which made it difficult to fit neighborhood-based models. Banerjee & Carlin (4) considered 81 contiguous zip codes shown in Figure 3, which included the 54 dark-shaded regions that had patients in the data set; the 27 regions that did not contribute patients were treated as if the data were missing.
Figure 3.
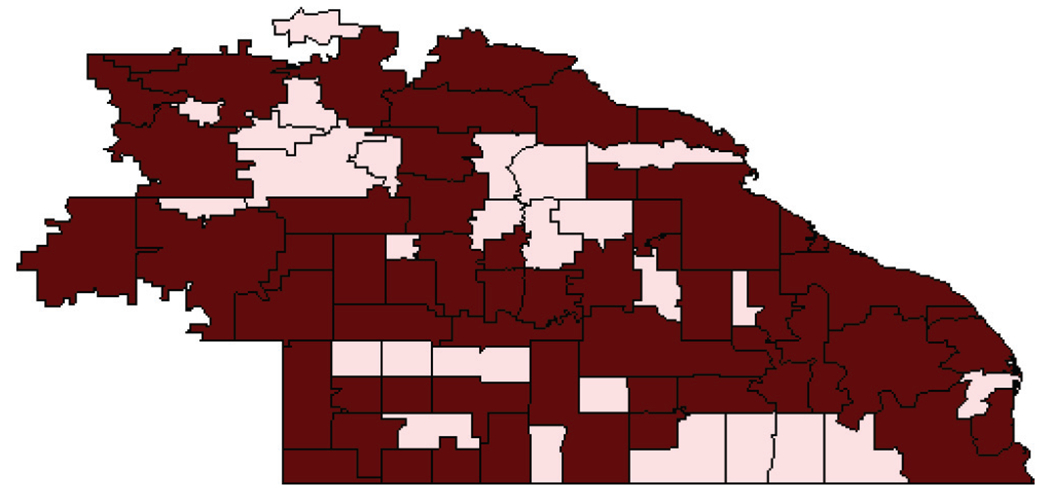
Map showing a missingness pattern for the smoking cessation data between 1994 and 1998 from 54 zip codes in southeastern Minnesota: Lightly shaded regions are those having no responses.
Table 1 presents estimated posterior quantiles for the fixed effects , cure fraction , and hyperparameters. Smoking intervention, expectedly, produces a significant decrease in the log relative risk of relapse. Women seem to be more likely to relapse than men. This result is often attributed to the (real or perceived) risk of weight gain following smoking cessation. The number of cigarettes smoked per day seems to be less significant; however, what is perhaps somewhat counterintuitive is that shorter-term smokers relapse sooner, perhaps attributable to subjects being better able to quit smoking as they age.
Table 1.
Posterior quantiles, full model, interval-censored case
| Parameter | Median | (2.5%, 97.5%) |
|---|---|---|
| Intercept | −2.720 | (−4.803, −0.648) |
| Sex (male = 0) | 0.291 | (−0.173, 0.754) |
| Duration as smoker | −0.025 | (−0.059, 0.009) |
| SI/UC (usual care = 0) | −0.355 | (−0.856, 0.146) |
| Cigarettes smoked per day | 0.010 | (−0.010, 0.030) |
| (cure fraction) | 0.694 | (0.602, 0.782) |
| 0.912 | (0.869, 0.988) | |
| 0.927 | (0.906, 0.982) | |
| Spatial variance component for | 0.005 | (0.001, 0.029) |
| Spatial variance component for | 0.007 | (0.002, 0.043) |
Abbreviations: SI, smoking intervention; UC, usual care.
CONCLUDING REMARKS
This article has provided a glimpse of the different types of statistical spatial models available for analyzing regionally aggregated data (or areal data) and the type of statistical inference that is obtained from such models. Although the illustrations provided here aggregated the data over a number of years and did not attempt to model associations across time, such associations can also be modeled by allowing the spatial random effects to vary across time. Also, this review has restricted attention to the CAR models, which are especially congruous with Bayesian statistical inference. Other types of spatial dependence structures, such as simultaneous autoregressive (SAR) models, are very popular, and perhaps better suited, for maximum-likelihood-based inference. Comparisons between these models can be found in Wall (39). Several other variants of such models, including spatiotemporal extensions, can be found in Banerjee et al. (5) and references therein.
SUMMARY POINTS.
Statistical modeling and scientific inference using spatially referenced data sets are becoming increasingly common in public health research. Examples include disease mapping and spatial survival analysis.
Researchers are formulating more complex spatially oriented hypotheses that require formal model-based testing and inference.
Statistical models for spatial data introduce dependence on the basis of whether the data are point referenced or areally referenced. The latter, which are usually presented as aggregates or summaries over regions, are more common in public health research and practice because they protect patients’ privacy.
Much of the statistical research over the past decade has focused on stochastic models for spatial dependence and how they can be introduced as random effects within Bayesian hierarchical models. These models are estimated using computationally intensive MCMC methods and have been applied to diverse data-analytic settings, including multiple disease mapping and spatial survival analysis.
FUTURE ISSUES.
As the accessibility to GIS and related computational resources continues to expand, spatial statisticians are encountering increasingly complex data sets with more demanding research questions. The scope for spatial modeling and analysis within public health will continue to expand, ushering in new domains of application.
A large part of methodological research will be devoted to the development of probability models, estimation methods, and computational algorithms for analyzing such data sets.
Statistical methods for analyzing spatially referenced data sets are computationally expensive and become unfeasible for large data sets. As spatial data sets become larger, statisticians start encountering the so-called “big data” problems in geostatistics. This area has started to garner much attention over the past five years or so and is seeing increasing research activity with regard to statistical models, methods, and algorithms for massive spatial data sets.
Footnotes
DISCLOSURE STATEMENT
The author is not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
The Annual Review of Public Health is online at publhealth.annualreviews.org
LITERATURE CITED
- 1.Auchincloss AH, Gebreab SY, Mair C, Diez Roux AV. 2012. A review of spatial methods in epidemiology, 2000–2010. Annu. Rev. Public Health 33:107–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Banerjee S, Carlin B. 2002. Spatial semiparametric proportional hazards models for analyzing infant mortality rates in Minnesota counties. In Case Studies in Bayesian Statistics, Vol. VI, ed. Gatsonis C, Kass R, Carriquiry A, Gelman A, Higdon D, et al. , pp. 137–52. New York: Springer [Google Scholar]
- 3.Banerjee S, Carlin B. 2003. Semiparametric spatiotemporal frailty modeling. Environmetrics 14:523–35 [Google Scholar]
- 4.Banerjee S, Carlin B. 2004. Parametric spatial cure rate models for interval-censored time-to-relapse data. Biometrics 60:268–75 [DOI] [PubMed] [Google Scholar]
- 5.Banerjee S, Carlin B, Gelfand A. 2014. Hierarchical Modeling and Analysis for Spatial Data. Boca Raton, FL: Chapman and Hall/CRC Press. 2nd ed. [Google Scholar]
- 6.Banerjee S, Dey D. 2005. Semiparametric proportional odds model for spatially correlated survival data. Lifetime Data Anal. 11:175–91 [DOI] [PubMed] [Google Scholar]
- 7.Banerjee S, Wall M, Carlin B. 2003. Frailty modelling for spatially correlated survival data with application to infant mortality in Minnesota. Biostatistics 4:123–42 [DOI] [PubMed] [Google Scholar]
- 8.Bastos L, Gamerman D. 2006. Dynamical survival models with spatial frailty. Lifetime Data Anal. 12:441–60 [DOI] [PubMed] [Google Scholar]
- 9.Bennett S. 1983. Analysis of survival data by the proportional odds model. Stat. Med 2:273–77 [DOI] [PubMed] [Google Scholar]
- 10.Besag J, York J, Mollié A. 1991. Bayesian image restoration, with two applications in spatial statistics (with discussion). Ann. Inst. Stat. Math 43:1–59 [Google Scholar]
- 11.Carlin B, Banerjee S. 2003. Hierarchical multivariate CAR models for spatio-temporally correlated survival data (with discussion). In Bayesian Statistics 7, ed. Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, et al. , pp. 45–64. Oxford, UK: Oxford Univ. Press [Google Scholar]
- 12.Chen M-H, Ibrahim JG, Sinha D. 1999. A new Bayesian model for survival data with a surviving fraction. J. Am. Stat. Assoc 94:909–19 [Google Scholar]
- 13.Cooner F, Banerjee S, Carlin B, Sinha D. 2007. Flexible cure rate modeling under latent activation schemes. J. Am. Stat. Assoc 102:560–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cooner F, Banerjee S, McBean A. 2006. Modelling geographically referenced survival data with a cure fraction. Stat. Methods Med. Res 15:307–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cox D, Oakes D. 1984. Analysis of Survival Data. London: Chapman and Hall [Google Scholar]
- 16.Cressie N. 1993. Statistics for Spatial Data. New York: Wiley. 2nd ed. [Google Scholar]
- 17.Cressie N, Wikle C. 2011. Statistics for Spatio-Temporal Data. New York: Wiley. 1st ed. [Google Scholar]
- 18.Cromley E, McLafferty S. 2002. GIS and Public Health. New York: Guilford [Google Scholar]
- 19.Dean CB, Ugarte MD, Militino AF. 2001. Detecting interaction between random region and fixed age effects in disease mapping. Biometrics 57:197–202 [DOI] [PubMed] [Google Scholar]
- 20.Finkelstein D. 1986. A proportional hazards model for interval-censored failure time data. Biometrics 42:845–54 [PubMed] [Google Scholar]
- 21.Gelfand A, Vounatsou P. 2003. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics 4:11–25 [DOI] [PubMed] [Google Scholar]
- 22.Gelman A, Carlin J, Stern H, Dunson D, Vehtari A, Rubin D. 2013. Bayesian Data Analysis. Boca Raton, FL: Chapman and Hall/CRC Press. 3rd ed. [Google Scholar]
- 23.Henderson R, Shikamura S, Gorst D. 2002. Modeling spatial variation in leukemia survival data. J. Am. Stat. Assoc 97:965–72 [Google Scholar]
- 24.Hodges JS, Cui Y, Sargent DJ, Carlin BP. 2007. Smoothing balanced single-error-term analysis of variance. Technometrics 49:12–25 [Google Scholar]
- 25.Hurtado Rúa SM, Dey D. 2012. A transformation class for spatio-temporal survival data with a cure fraction. Stat. Methods Med. Res doi: 10.1177/0962280212445658 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ibrahim J, Chen MH, Sinha D. 2001. Bayesian Survival Analysis. New York: Springer-Verlag [Google Scholar]
- 27.Jin X, Banerjee S, Carlin B. 2007. Order-free coregionalized lattice models with application to multiple disease mapping. J. R. Stat. Soc. B 69:817–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jin X, Carlin B, Banerjee S. 2005. Generalized hierarchical multivariate CAR models for areal data. Biometrics 61:950–61 [DOI] [PubMed] [Google Scholar]
- 29.Lawson A, Choi J, Zhang J. 2014. Prior choice in discrete latent modeling of spatially referenced cancer survival. Stat. Methods Med. Res 23:183–200 [DOI] [PubMed] [Google Scholar]
- 30.Leroux B, Lei X, Breslow N. 1999. Estimation of disease rates in small areas: a new mixed model for spatial dependence. In Statistical Models in Epidemiology, the Environment, and Clinical Trials, ed. Halloran ME, Berry D, pp. 135–78. New York: Springer [Google Scholar]
- 31.Li Y, Ryan L. 2002. Modeling spatial survival data using semiparametric frailty models. Biometrics 58:287–97 [DOI] [PubMed] [Google Scholar]
- 32.Møller J, ed. 2003. Spatial Statistics and Computational Methods. New York: Springer [Google Scholar]
- 33.Murray R, Anthonisen N, Connett J, Wise R, Lindgren P, et al. 1998. Effects of multiple attempts to quit smoking and relapses to smoking on pulmonary function. Lung Health Study Research Group. J. Clin. Epidemiol 51:1317–26 [DOI] [PubMed] [Google Scholar]
- 34.Othus M, Barlogie B, LeBlanc M, Crowley J. 2012. Cure models as a useful statistical tool for analyzing survival. Clin. Cancer Res 18:3731–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Robert C, Casella G. 2005. Monte Carlo Statistical Methods. New York: Springer [Google Scholar]
- 36.Rushton G. 2003. Public health, GIS, and spatial analytic tools. Annu. Rev. Public Health 24:43–56 [DOI] [PubMed] [Google Scholar]
- 37.Schabenberger O, Gotway C. 2004. Statistical Methods for Spatial Data Analysis. Boca Raton, FL: Chapman and Hall/CRC [Google Scholar]
- 38.Wackernagel H. 2003. Multivariate Geostatistics: An Introduction With Applications. New York: Springer. 3rd ed. [Google Scholar]
- 39.Wall M. 2004. A close look at the spatial structure implied by the CAR and SAR models. J. Stat. Plann. Inference 121:311–24 [Google Scholar]
- 40.Waller L, Gotway C. 2004. Applied Spatial Statistics for Public Health Data. New York: Wiley [Google Scholar]
- 41.Webster R, Oliver M. 2001. Geostatistics for Environmental Scientists. New York: Wiley [Google Scholar]
- 42.Zhang J, Lawson AB. 2011. Bayesian parametric accelerated failure time spatial model and its application to prostate cancer. J. Appl. Stat 38:591–603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang Y, Hodges J, Banerjee S. 2009. Smoothed ANOVA with spatial effects as a competitor to MCAR in multivariate spatial smoothing. Ann. Appl. Stat 3:1805–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zhou H, Lawson AB, Hebert J, Slate E, Hill E. 2008. Joint spatial survival modelling for the date of diagnosis and the vital outcome for prostate cancer. Stat. Med 27:3612–28 [DOI] [PMC free article] [PubMed] [Google Scholar]


