Abstract
Understanding the interplay between individual magnetic impurities and superconductivity is crucial for bottom-up construction of novel phases of matter. Sub-gap bound states that are used in this endeavor are typically considered as independent entities that each result from the exchange scattering between the respective impurity orbitals and electrons of the superconducting condensate. Here we present experimental evidence of individual multi-spin impurities where the sub-gap states are not independent. Specifically, we find that by tuning the energy of the state closest to zero through zero, all other sub-gap states change particle-hole asymmetry as well. We show that this can be understood by including Hund’s coupling, which favors high-spin configurations, into a multi-orbital Anderson model. Unlike for the case of independent spins, the transition we observe signals the simultaneous departure of more than one quasiparticle from the impurity, while the parity of the ground state may remain unchanged. Our results show that Hund’s coupling is not only crucial in generating high-spin impurities, but also to understand the transition between two distinct ground states, and should therefore be taken into account for e.g. impurity-based band-structure engineering.
Subject terms: Superconducting properties and materials, Phase transitions and critical phenomena
Sub-gap states generated by single spins in a superconductor can be used as building blocks for quantum devices. In this work, it is shown that the sub-gap states of multi-spin impurities are intimately linked, leading to unexpected behavior.
Introduction
The exchange interaction between a localized magnetic moment and the electron pair condensate of a superconductor can change the ground state of the system as a function of the value of the spin, Si, of the local moment and the strength of the interaction1. As originally pointed out for classical spins2, this transition corresponds to a change of in the total spin (from Si to for an anti-ferromagnetic interaction), which occurs for a critical value of the exchange interaction. In a singlet superconductor the two ground states physically correspond to an unscreened and (for , partially) screened magnetic moment of the impurity. Spectroscopically, this quantum phase transition (QPT) has a distinct signature: the local in-gap excitation originating from the interference of the quasi-particles scattered by the impurity crosses zero energy3–8.
An ideal tool to investigate quantum phase transitions at the atomic scale with high energy and spatial resolution is scanning tunneling microscopy and spectroscopy. Single spins can be introduced to a superconductor by placing a magnetic impurity on top of a superconducting substrate3–5,9–13. Interestingly, it has been shown that the energy of sub-gap states the impurities generate, which are usually called Yu-Shiba-Rusinov (YSR) states14–16, can strongly depend on the absorption site4,5, and can even be tuned by changing the tip-impurity distance6. In general, magnetic adatoms on a superconducting substrate, such as Mn or Fe, are in the high-spin configuration as the Hund’s coupling overcomes the crystal field splitting. The exchange coupling of each singly occupied d-orbital of the impurity with the condensate results in multiple sub-gap states, as readily observed in experiment4,9,12,17. Imaging of these states furthermore revealed the d-character of the orbitals of the impurity12,17 and suggests that each bound state can be treated independently while the effect of Hund’s coupling is only coded in the total spin, Si. A key question is whether the inter-orbital interaction responsible for the high spin configuration leads to any other distinct phenomenology that cannot be accounted for using independent scattering channels. Specifically, will the states, regardless of the Hund’s coupling, all have separate QPTs, or can they respond collectively, leading to a single QPT for all states? Physically, this question boils down to whether or not the total spin can only change by at the QPT, or if larger changes are possible. In this work, we show that large changes in occupation (and thus spin) are indeed possible due to strong Hund’s coupling.
Results
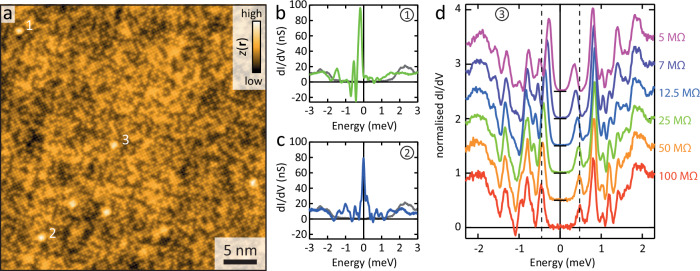
To search for tunable, interacting in-gap states, we studied excess Fe atoms at the surface of superconducting FeSe0.45Te0.55, whose in-gap states were recently shown to be sensitive to the tip-sample distance8. Fe(Se,Te) thus combines the ability to tune the sub-gap excitation energies, with the high-spin configuration of an interstitial Fe impurity resulting from Hund’s coupling of electrons in the d-orbitals. Figure 1a shows a typical constant current image of cleaved Fe1+xSe0.45Te0.55 containing several excess Fe impurities recognizable as bright protrusions among the mixture of respectively bright and dark Te and Se atoms. The excess Fe concentration (x ~ 0.05%) is chosen to be high enough to have ample choice of local interstitial Fe environments, yet still low enough to only minimally introduce signal inside the gap in between the impurities. Contrary to previous reports18,19, all of the up to 100 excess Fe we probed show multiple in-gap peaks. The energy of the in-gap peaks varies for different impurities, highlighting the variation in coupling parameters with local environment of e.g. Se and Te mixture. Differential conductance spectra taken at the center of two different Fe impurities are shown in Fig. 1b, c. Interestingly, not only peaks are observed, but well over 50% of excess Fe also displays negative differential conductance (NDC) at one or more energies. Whereas NDC is common for superconducting tips3–6,8,9,12,13,20, for the normal metal tip we use here (see Supplementary Note 4) the only possibility for NDC to occur inside the superconducting gap is through interactions between the different sub-gap states21. Last but not least, by changing the tip-sample distance all excitation energies can be shifted as shown in Fig. 1d.
Fig. 1. Tunable multi-orbital YSR in Fe(Se,Te).
a Constant current image of Fe(Se,Te) with several interstitial excess Fe atoms (bright protrusions). Vset = 5 mV, Iset = 100 pA. b, c Differential conductance spectra taken at the excess Fe impurities marked 1 and 2 in panel a, respectively (setup resistance = 100 MΩ). Both show a multitude of peaks highlighting the multi-orbital nature of the Fe sites. The appearance of negative differential conductance in both spectra reflects interactions between sub-gap states. The gray spectrum is taken in between impurities 1 and 3 for comparison. d Junction resistance dependence of differential conductance on the Fe impurity marked 3 in panel a (dashed lines are guides to the eye). Upon lowering the setup resistance, the peaks shift closer to zero. Source data are provided as a Source Data file.
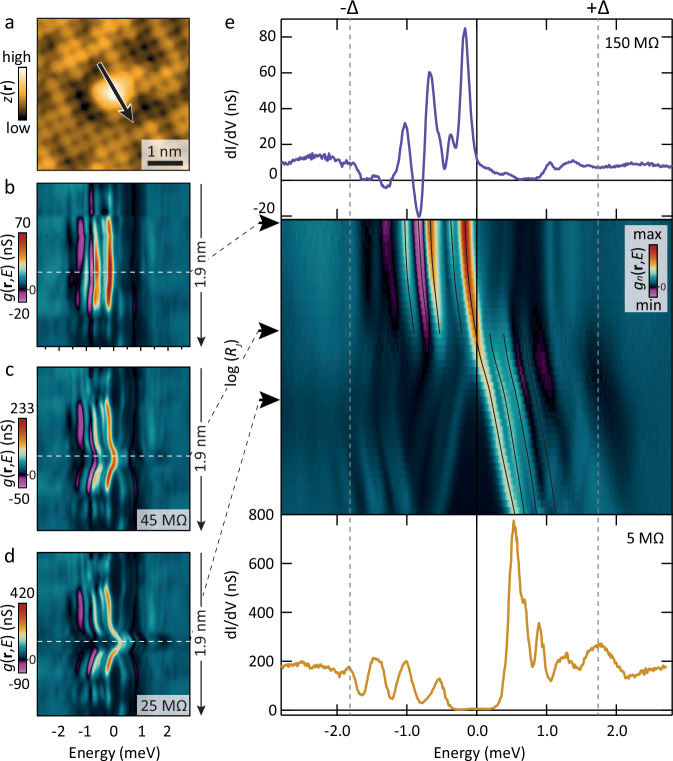
Having identified controllable, multiple in-gap states, we can next use the tip-impurity distance to shift low-lying states through zero and track their evolution. To determine the lateral range of the tip-induced shifts, and to find the location with the most dramatic shift, we first take a line cut across the excess Fe atom in Fig. 2a at different junction resistances. As Fig. 2b shows, at high junction resistance (large tip-sample distance), the in-gap states hardly shift as function of position. Upon nearing the tip to the surface, however, the states move towards zero energy (Fig. 2c), and the first one eventually crosses when the tip is directly above the Fe impurity and at a sufficiently low junction resistance (Fig. 2d). To analyze the crossing more precisely, we perform a detailed junction resistance dependence on top of the Fe impurity, see Fig. 2e, using resistances ranging from 150 MΩ (Fig. 2e, top) to 5 MΩ (Fig. 2e, bottom). Since the electric field that likely drives the level shifts (see ref. 8 and Supplementary Note 4) is linearly proportional to the tip-sample distance, and the current (and thus resistance) depends exponentially on the distance, we furthermore use a logarithmic scale for the resistance to enhance visibility of the crossing. For large tip-sample distance, the in-gap state closest to zero energy is strongest in intensity at negative bias, and is followed by additional peaks and a relatively prominent negative differential conductance dip (similar to the Fe in Fig. 1b). Importantly, the intensity of all peaks is stronger at negative bias than at positive bias. For lower setup resistances, all features shift closer to zero bias. Then, as soon as the first peak crosses zero bias, all other peaks switch polarity (their intensity becomes dominant at positive bias instead of negative bias), while the NDC disappears. Additionally, whereas the peak that crossed continues to shift to higher energy, the others never cross, but instead an ever increasing gap is formed after the crossing point. For independent in-gap states this would not have been possible: higher-energy states would simply have continued shifting until they also would have crossed zero.
Fig. 2. Crossing zero energy.
a Constant current image of FeSe0.45Te0.55 with an excess Fe atom in the middle. b–d Differential conductance taken along the line in panel a for 150 MΩ, 45 MΩ and 25 MΩ, respectively. Directly on top of the Fe impurity the in-gap states shift most dramatically and cross zero. e Junction resistance dependence (middle) of the normalized differential conductance directly above the Fe impurity (white dashed lines in b–d) ranging from 150 MΩ (top) to 5 MΩ (bottom), the dashed gray lines mark the gap edges. The step size in resistance uses a logarithmic scale, the black lines are guides to the eye. As soon as the first state crosses zero, the intensity of all others is affected. We note that since the spectra are normalized outside the gap and since there is no dramatic change in intensity without a crossing (Fig. 1d) or of the state crossing zero, the intensity switch of the other states is not an artifact of normalization. The disappearance of NDC (purple, zero dI/dV is black and marked in the color legends) can moreover not be due to normalization, and un-normalized spectra in panel d also clearly show the switch. Source data are provided as a Source Data file.
To understand the observed behavior, we focus on two key observations: (1) the simultaneous switch of the in-gap states from hole-like (dominant intensity at E < 0) to electron-like (dominant intensity at energy E > 0), and (2) the appearance of negative differential conductance. We stress that whereas NDC3–6,8,9,12,13,20, and switching of particle-hole asymmetry of a sub-gap state with junction resistance20 are not unusual for measurements with a superconducting tip, the mechanisms underlying these two features do not apply to the normal metal tip we use in this work. Furthermore, the observation of NDC, even though the experiment is well within the tunneling regime, implies that the tunneling current cannot be described by the single-particle density of states: the impurity must involve at least two states with variable electron occupation, which allows the blocking of tunneling current (and hence negative conductance) through one state due to interactions with electrons present in the other state21. Therefore, the impurity cannot be treated as a purely spin variable, regardless of whether this is a classical or quantum spin17,22–24, since this would not produce states with a variable occupation required for NDC to occur.
To understand these data, we consider the general multi-orbital Anderson impurity model coupled to a superconducting bath. To capture the main features, we restrict ourselves to only two orbitals. As we concentrate exclusively on in-gap states, we simplify the problem by treating the substrate as an s-wave superconductor with zero-bandwidth25–27, where the BCS density of states is replaced by two quasi-particle states at energy Δ. This is the main limitation of our treatment, although this approximation has been successfully compared with more elaborate methods such as NRG for the Anderson model28 and is also known to perform very well for in-gap bound states of spin impurities24,29,30. To address the necessary interactions, we take each orbital as characterized by the impurity energy level εα = a, b, and intra-orbital Coulomb energy Uα = a, b ≡ U, and we assume they are each coupled to a different site of the superconducting bath i = A, B via tunneling rates ΓA,a, ΓB,b > Δ2. The combination of site and orbital (i, α) = (A, a) or (B, b) is referred to as a channel, since the i state is a scattering channel in the superconductor that best couples with the orbital α. The key interaction that couples the orbitals can be represented as the Hund’s coupling31,
| 1 |
with Sα = a, b the spin operator for each orbital (see Fig. 3a and Methods). To favor higher-spin configurations typical of transition-element impurities, we set the phenomenological parameters as
| 2 |
In previous work on molecules4–6, the presence of the tip was assumed to modify the hybridization of the impurity with the surrounding substrate7. A recent study on sub-surface impurities in FeTe0.55Se0.45, however, indicates that the impurity states can be affected by the electric field of the tip8, likely due to only partial screening associated to a low super-fluid density32. In such a scenario, one can expect that the impurity energy levels vary with the tip-sample distance, which is linearly proportional to the electric field8. Importantly, the excess Fe atoms we study are on top of the Se/Te surface layer and therefore expected to be even more susceptible to the electric field since they are closer to the tip. Here, we, therefore, assume that the average impurity energy level controls the energy of the sub-gap excitations and represents the key experimentally tunable parameter. However, in Supplementary Note 5 we demonstrate that choosing the hybridization as the driving parameter will lead to the same phenomenology. Lastly, we assume for simplicity that the difference between energy levels δε remains constant, as it does not change the phenomenology as long as Eq. (2) holds.
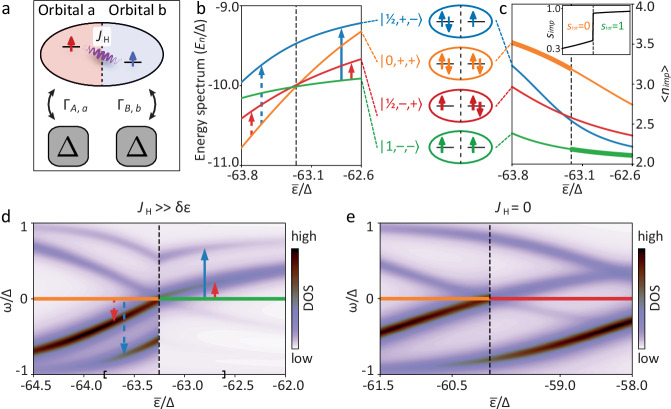
Fig. 3. Theoretical description of a multi-channel QPT.
a Sketch of the model Hamiltonian. The ellipse represents an impurity with two orbitals interacting via a Hund’s coupling JH, while squares represent the two scattering channels of the superconductor coupled to the orbitals, each channel modeled by a superconducting site. b Evolution of the energy of the four lowest-lying many-body states for increasing average orbital energy driven by the STM tip electric field. The vertical arrows indicate the STM-accessible excitations before and after the MCQPT. All the energy curves were shifted by to improve readability. c Evolution of the average total electron occupation on the impurity for all four many-body states (same coloring as in panel b). The thick line marks the ground state for the given value of . The inset shows the spin of the impurity simp and the total spin stot of the ground state in the same range. d Simulated in-gap LDOS at the impurity site as a function of . Vertical arrows same as panel b, where now the direction marks the dominant electron- or hole-nature. The region of shown in b and c is delimited by the square brackets on the horizontal axis. e Simulated in-gap LDOS for the transition in case of absence of Hund’s coupling, JH = 0. The color-coding of the horizontal line at ω = 0 in panels (d, e) represents the ground state (colors from panels b, c). The vertical dashed lines in panels b-e mark the quantum phase transition. Calculation parameters in (b, c, d): JH = 30Δ, U = 60Δ, ΓA,a = ΓB,b = 5Δ2, δε = −6Δ. Same for panel e except JH = 0 and δε = −3Δ. Phenomenological broadening in (d, e) is η = 0.075Δ. Source data for panels d and e are provided as a Source Data file.
In this model, we discover a multi-channel quantum phase transition (MCQPT) in the evolution of the four lowest-lying many-body eigenstates. We can label the eigenstates as , due to the conserved total-spin stot, and conserved electron-number parity pi,α of channels (i, α) (see “Methods”). The four states are , , , , with ± denoting even and odd parity, respectively. The evolution of the energies of the four states with is shown in Fig. 3b. The phase transition occurs as the state exchanges places with the state . Hence, at the transition, both channels are involved, and both undergo a parity flip so that the total parity does not change. This property is in stark contrast with the generic spin-impurity model quantum phase transition (e.g. associated to the YSR model), but is actually not the universal signature of our MCQPT, since the parity may switch in presence of more than two orbitals (see Supplementary Note 6). The essential property of our MCQPT is the large change of the average orbital occupation, 〈nimp〉, from nearly 4 (both orbitals fully occupied) to nearly 2 (both singly occupied) as changes, see Fig. 3c. The distinctive switch of all in-gap excitations from hole-like to electron-like is due to the depletion of the average electron occupation of the impurity orbitals. It is the strong Hund’s coupling that determines the MCQPT to be from fully occupied orbitals and a low-spin state (total spin of system stot = 0) into singly occupied orbitals and a high-spin state (total spin of system stot = 1). This mechanism is allowed by a reasonable assumption that the impurity is in a mixed-valence state, i.e., the energy cost of the change of orbital occupation can be compensated by the gain of Hund’s energy, leading to the requirement
| 3 |
in addition to Eq. (2). Within this hierarchy, for our parameters we find a crossing for an average level energy , which is similar to the value employed for modeling an iron impurity on FeSe in previous works33. To address the STM observations, we calculate the total local density of states (LDOS) of the impurity orbitals (see “Methods”). Since we consider single-particle excitations, only transitions from the many-body ground state to states with opposite total parity can have a non-zero spectral weight. To demonstrate the phenomenology of the MCQPT we focus on the two lowest in-gap excitations which result from the four lowest many-body eigenstates described above (see arrows in Fig. 3b, d). To be precise, before the MCQPT, the in-gap excitations correspond to excitations from to and to ; there is a + → − parity flip in channels (A, a) or (B, b), respectively. After the MCQPT, they correspond to excitations from to and . Panel Fig. 3d shows clear agreement with the STM results (Fig. 2e), where the MCQPT is signaled by the lowest excitation crossing zero energy, and there is a concurrent change of spectral weight in the higher excitation. We emphasize that the fundamental ingredients underlying the occurrence of the MCQPT are (i) the inter-orbital interaction (Hund’s coupling) favoring a high-spin configuration and (ii) the impurity being in a mixed-valence state. Therefore, the simultaneous change of spectral weight of the in-gap states as the lowest excitation crosses zero energy is also recovered by continuously tuning the impurity-substrate coupling (ΓA,a, ΓB,b), provided conditions (i) and (ii) are fulfilled (see Supplementary Note 5). Further, the two constraints on the parameters of our minimal model that follow from (i) and (ii) [i.e., Eqs. (2) and (3), respectively], are independent from each other, meaning that the modeling does not impose any fine-tuning on the specific U/JH ratio (see Supplementary Note 7).
Another key feature of our model is that the single-particle excitations appearing in the in-gap LDOS result from different eigenstates before and after the MCQPT. Therefore, in general there is a discontinuity of slope of the in-gap state energy at the point it crosses zero-bias with changing (see Fig. 3d and Fig. S2a, c in Supplementary Note 1). Indeed, this property is a common feature for the experimentally measured Fe impurities where a MCQPT occurs (see Supplementary Note 1), further supporting our interpretation. Note that the discontinuity of the slope at the MCQPT is a priori independent of the precise functional dependence of on the electric field.
Importantly, the phenomenology discussed above is not fine-tuned, but is present for a range of values of parameters as long as we stay in the regime given by Eqs. (2), (3), as we show through a systematic study in Supplementary Note 1. In Supplementary Note 2 we also relate the excitation spectrum to a transport calculation to demonstrate that, without changing any of the above conclusions, negative differential conductance can occur for a reasonable range of asymmetry in tunneling between the tip and the different wave functions of the bound states as is known in the case of tunneling through a quantum dot with multiple interacting levels21. To confirm our interpretation and the significance of multi-orbital interactions, we present the calculated LDOS with the Hund’s coupling switched off (JH = 0) in panel Fig. 3e, where obviously the experimental phenomenology is not captured. We note that the JH = 0 model completely decouples the two orbitals, hence in accord with intuition the spectral weight of the excitation in one channel is not affected by the transition in the other channel (see Supplementary Note 3). The same negative outcome is obtained for independent Kondo channels or independent YSR channels.
Discussion
Multiple in-gap excitations may appear through various mechanisms in impurity models, e.g., due to a higher impurity spin (classical17,22,23 or quantum24), splitting by anisotropy5,34, and in e.g., Fe(Se, Te) due to multiple superconducting gaps35. Notably among these, in a model of a quantum higher spin on the impurity, there may be total-parity-conserving QPT in which two channels undergo a screening transition simultaneously, either due to anisotropy or due to symmetry-protected degeneracy of some impurity-substrate couplings. In such a transition, the spectral weights of some in-gap states may shift between hole- and electron-like. However, such a model could never reproduce negative differential conductance.
A realistic description of a Fe impurity obviously demands a larger number of orbitals, which in turn would yield a larger number of in-gap states; however, the two-orbital model discussed here contains minimal ingredients to capture the distinctive feature of the MCQPT. Secondly, our model, with its single-site single-gap s-wave superconductor, clearly cannot address the spatial dependence of impurity-bound states. Nevertheless, the fact that the key features in the experiment, for impurities that show a quantum phase transition, are found at various distances from the impurity in both horizontal and vertical movement indicates that we are observing universal characteristics.
The experimental observation of interacting sub-gap states in superconducting Fe(Se, Te) shows that multi-orbital models that take inter-orbital interactions (i.e. the Hund’s interaction) accurately into account are essential. While the rich physics of multiple in-gap states and of impurity QPT are each well recognized, here we emphasize the importance of exploring the physics of QPTs of multiple interacting states, which reveals the true nature of the underlying physics. Specifically, the MCQPT we observe does not at all fit the paradigm of a transition due to screening of impurity by substrate, but instead is characterized by a simultaneous change of impurity occupation and total spin driven by Hund’s interaction. Given the prevalence of studies on multi-orbital transition-element atoms and their use in bottom-up construction of devices3,36–38, our findings likely hold for numerous systems and could perhaps be experimentally exploited to generate previously unanticipated phenomena as exemplified by the multi-orbital quantum phase transition.
Methods
Tip and sample preparation
Fe(Se,Te) single crystals were grown using the self-flux method. As-grown samples with a superconducting transition temperature of 14.5 K were used throughout this work. The crystals were mechanically cleaved in a cryogenic vacuum at T ~ 20 K and directly inserted into the STM head at 4.2 K. An etched atomically sharp and stable tungsten tip was used for all measurements. Differential conductance measurements were performed by numerical derivation as well as with a standard lock-in amplifier operating at 429.7 Hz. All measurements were recorded at the base temperature of T = 0.3 K (electron temperature of 0.4 K).
Theory
The total Hamiltonian reads
| 4 |
with
| 5 |
| 6 |
| 7 |
where the operators create a spin-σ electron in impurity orbital α = a, b, each coupled to a superconducting site i = A, B, respectively, on which the electron creation operator is . The represents the particle-number operator on the impurity (not a conserved quantity), while the impurity spin operator reads
| 8 |
The operators for total spin, channel-1 parity, and channel-2 parity, all conserved quantities introduced to label the eigenstates, read
| 9 |
| 10 |
| 11 |
where . Owing to the Hamiltonian’s full spin-rotation symmetry, eigenstates can also be labeled according to the z component of the total spin m, but we dropped this label to lighten the notation in the main text. Note that eigenstates , , , are indeed zero-, two-, two- and three-fold degenerate, respectively. Further, the total Fermion parity operator P = PA,a ⋅ PB,b also commutes with the total Hamiltonian.
The LDOS on the impurity site reads
| 12 |
where the retarded Green function can be expressed through the Lehmann representation at T = 0,
| 13 |
with dGS the degeneracy of the ground state. The experimental temperature is low, namely, the smallest energy scale in our problem, kBT ≪ Δ. In this case, the contributions to the LDOS from transitions between excited states are exponentially small, and they would only induce a slight broadening at the level crossings. Hence, in the modeling, we assume T = 0. The tunneling rate introduced in the main text is related to the tunneling amplitude as .
Supplementary information
Source data
Acknowledgements
We thank G. Zaránd, C. Pepin and Q. Si for useful discussions. M.U., A.M. and P.S. acknowledge the support of the French Agence Nationale de la Recherche (ANR), under grant number ANR-22-CE30-0037. The work at BNL was supported by the US Department of Energy, office of Basic Energy Sciences, contract no. DOE-sc0012704. FM would like to acknowledge funding from the ANR (ANR-21-CE30-0017-01).
Author contributions
F.M., A.M., and P.S. supervised the project. F.M. conceived and performed the experiment and analyzed the data. M.U. performed the theoretical study with A.M. and P.S. M.A., and A.P.M. contributed to the interpretation of the results. G.D.G synthesized samples. M.U., A.M., M.A., P.S., and F.M. wrote the manuscript.
Peer review
Peer review information
Nature Communications thanks Lucas Schneider, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Data availability
Source data are provided in this paper.
Code availability
The code used in this work is available upon reasonable request to the authors.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-52847-9.
References
- 1.Balatsky, A. V., Vekhter, I. & Zhu, J.-X. Impurity-induced states in conventional and unconventional superconductors. Rev. Mod. Phys.78, 373–433 (2006). [Google Scholar]
- 2.Sakurai, A. Comments on superconductors with magnetic impurities. Prog. Theor. Phys.44, 1472–1476 (1970). [Google Scholar]
- 3.Heinrich, B. W., Pascual, J. I. & Franke, K. J. Single magnetic adsorbates on s-wave superconductors. Prog. Surf. Sci.93, 1–19 (2018). [Google Scholar]
- 4.Franke, K. J., Schulze, G. & Pascual, J. I. Competition of superconducting phenomena and Kondo screening at the nanoscale. Science332, 940–944 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Hatter, N., Heinrich, B. W., Ruby, M., Pascual, J. I. & Franke, K. J. Magnetic anisotropy in Shiba bound states across a quantum phase transition. Nat. Commun.6, 8988 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Farinacci, L. et al. Tuning the coupling of an individual magnetic impurity to a superconductor: quantum phase transition and transport. Phys. Rev. Lett.121, 196803 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Huang, H. et al. Quantum phase transitions and the role of impurity-substrate hybridization in Yu-Shiba-Rusinov states. Commun. Phys.3, 199 (2020). [Google Scholar]
- 8.Chatzopoulos, D. et al. Spatially dispersing Yu-Shiba-Rusinov states in the unconventional superconductor FeTe0.55Se0.45. Nat. Commun.12, 298 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ji, S. H. et al. High-resolution scanning tunneling spectroscopy of magnetic impurity induced bound states in the superconducting gap of Pb thin films. Phys. Rev. Lett.100, 226801 (2008). [DOI] [PubMed] [Google Scholar]
- 10.Yazdani, A., Jones, B. A., Lutz, C. P., Crommie, M. F. & Eigler, D. M. Probing the local effects of magnetic impurities on superconductivity. Science275, 1767 (1997). [DOI] [PubMed] [Google Scholar]
- 11.Ménard, G. C. et al. Coherent long-range magnetic bound states in a superconductor. Nat. Phys.11, 1013–1016 (2015). [Google Scholar]
- 12.Choi, D. J. et al. Mapping the orbital structure of impurity bound states in a superconductor. Nat. Commun.8, 15175 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang, H. et al. Tunnelling dynamics between superconducting bound states at the atomic limit. Nat. Phys.16, 1227–1231 (2020). [Google Scholar]
- 14.Yu, L. Bound state in superconductors with paramagnetic impurities. Acta Phys. Sin.21, 75–91 (1965). [Google Scholar]
- 15.Shiba, H. Classical spins in superconductors. Prog. Theor. Phys.40, 435–451 (1968). [Google Scholar]
- 16.Rusinov, A. I. Superconductivity near a paramagnetic impurity. Pis.’ma Zh. Eksp. Teor. Fiz.9, 146–149 (1968). [Google Scholar]
- 17.Ruby, M., Peng, Y., von Oppen, F., Heinrich, B. W. & Franke, K. J. Orbital picture of Yu-Shiba-Rusinov multiplets. Phys. Rev. Lett.117, 186801 (2016). [DOI] [PubMed] [Google Scholar]
- 18.Yin, J. X. et al. Observation of a robust zero-energy bound state in iron-based superconductor Fe(Te,Se). Nat. Phys.11, 543–546 (2015). [Google Scholar]
- 19.Wang, Z. et al. Evidence for dispersing 1D Majorana channels in an iron-based superconductor. Science367, 104–108 (2020). [DOI] [PubMed] [Google Scholar]
- 20.Ruby, M. et al. Tunneling processes into localized subgap states in superconductors. Phys. Rev. Lett.115, 087001 (2015). [DOI] [PubMed] [Google Scholar]
- 21.Thielmann, A., Hettler, M. H., König, J. & Schön, G. Super-Poissonian noise, negative differential conductance, and relaxation effects in transport through molecules, quantum dots, and nanotubes. Phys. Rev. B71, 045341 (2005). [Google Scholar]
- 22.Arrachea, L. Yu-Shiba-Rusinov multiplets and clusters of multiorbital adatoms in superconducting substrates: subgap Green’s function approach. Phys. Rev. B104, 134515 (2021). [Google Scholar]
- 23.Moca, C. P., Demler, E., Jankó, B. & Zaránd, G. Spin-resolved spectra of Shiba multiplets from Mn impurities in MgB2. Phys. Rev. B77, 174516 (2008). [Google Scholar]
- 24.von Oppen, F. & Franke, K. J. Yu-Shiba-Rusinov states in real metals. Phys. Rev. B103, 205424 (2021). [Google Scholar]
- 25.Rozhkov, A. V. & Arovas, D. P. Interacting-impurity Josephson junction: variational wave functions and slave-boson mean-field theory. Phys. Rev. B62, 6687 (2000). [Google Scholar]
- 26.Vecino, E., Martín-Rodero, A. & Levy Yeyati, A. Josephson current through a correlated quantum level: Andreev states and π junction behavior. Phys. Rev. B68, 035105 (2003). [Google Scholar]
- 27.Meng, T., Florens, S. & Simon, P. Self-consistent description of Andreev bound states in Josephson quantum dot devices. Phys. Rev. B79, 224521 (2009). [Google Scholar]
- 28.Bergeret, F. S., Levy Yeyati, A. & Martín-Rodero, A. Josephson effect through a quantum dot array. Phys. Rev. B76, 174510 (2007). [Google Scholar]
- 29.Trivini, S. et al. Cooper pair excitation mediated by a molecular quantum spin on a superconducting proximitized gold film. Phys. Rev. Lett.130, 136004 (2023). [DOI] [PubMed] [Google Scholar]
- 30.Skurativska, A., Ortuzar, J., Bercioux, D., Bergeret, F. S. & Cazalilla, M. A. Robust spin polarization of Yu-Shiba-Rusinov states in superconductor/ferromagnetic insulator heterostructures. Phys. Rev. B107, 224507 (2023). [Google Scholar]
- 31.Rubio-Verdú, C., Zaldívar, J., žitko, R. & Pascual, J. I. Coupled Yu-Shiba-Rusinov states induced by a many-body molecular spin on a superconductor. Phys. Rev. Let.126, 017001 (2021). [DOI] [PubMed] [Google Scholar]
- 32.Homes, C. C., Dai, Y. M., Wen, J. S., Xu, Z. J. & Gu, G. D. FeTe0.55Se0.45: a multiband superconductor in the clean and dirty limit. Phys. Rev. B91, 144503 (2015). [Google Scholar]
- 33.Martiny, J. H. J., Kreisel, A. & Andersen, B. M. Theoretical study of impurity-induced magnetism in FeSe. Phys. Rev. B99, 014509 (2019). [Google Scholar]
- 34.Žitko, R., Bodensiek, O. & Pruschke, T. Effects of magnetic anisotropy on the subgap excitations induced by quantum impurities in a superconducting host. Phys. Rev. B83, 054512 (2011). [Google Scholar]
- 35.Li, J. & Wang, Y. Magnetic impurities in the two-band s±-wave superconductors. EPL88, 17009 (2009). [Google Scholar]
- 36.Khajetoorians, A. A., Wegner, D., Otte, A. F. & Swart, I. Creating designer quantum states of matter atom-by-atom. Nat. Rev. Phys.1, 703–715 (2019). [Google Scholar]
- 37.Kim, H. et al. Toward tailoring Majorana bound states in artificially constructed magnetic atom chains on elemental superconductors. Sci. Adv.4, eaar5251 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Beck, P. et al. Spin-orbit coupling induced splitting of Yu-Shiba-Rusinov states in antiferromagnetic dimers. Nat. Commun.12, 2040 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source data are provided in this paper.
The code used in this work is available upon reasonable request to the authors.