Comparison of DNA methylation based classification models for precision diagnostics of central nervous system tumors

Abstract

As part of the advancement in therapeutic decision-making for brain tumor patients at St. Jude Children’s Research Hospital (SJCRH), we developed three robust classifiers, a deep learning neural network (NN), k-nearest neighbor (kNN), and random forest (RF), trained on a reference series DNA-methylation profiles to classify central nervous system (CNS) tumor types. The models’ performance was rigorously validated against 2054 samples from two independent cohorts. In addition to classic metrics of model performance, we compared the robustness of the three models to reduced tumor purity, a critical consideration in the clinical utility of such classifiers. Our findings revealed that the NN model exhibited the highest accuracy and maintained a balance between precision and recall. The NN model was the most resistant to drops in performance associated with a reduction in tumor purity, showing good performance until the purity fell below 50%. Through rigorous validation, our study emphasizes the potential of DNA-methylation-based deep learning methods to improve precision medicine for brain tumor classification in the clinical setting.

Introduction

DNA methylation is an epigenetic mechanism in which a methyl group is added to the 5-carbon position of cytosine, creating a 5-methyl-cytosine (5^meC) base within a cytosine-phosphate-guanine (CpG) dinucleotide. This modification can regulate gene expression without altering the DNA sequence, serving as a crucial process in normal development and tissue specification^1,2. Within cells, DNA methylation regulates critical functions such as transcription factor binding, gene silencing, X-chromosome inactivation, imprinting, and the preservation of chromosome stability^1,3,4. The DNA methylation patterns can be transmitted to the daughter cell upon replication through the activity of DNA methyltransferase-1 (DNMT1)⁵.

Both normal and neoplastic tissues have an inherent epigenetic signature encoded in their methylome^6–9. This DNA methylation signature is considered a combined representation of the cell of origin and, in the case of tumors, the genomic driver abnormality. It is retained even after tumor recurrence or passage of tumors as an orthotopic xenograft^10–12. Because DNA methylation patterns are reconstituted in the dividing cell, the pattern of CpG methylation across the genome has been established as a stable and reliable biomarker^6,13.

A powerful tool for exploring DNA methylation landscapes across the genome is a methylation array. Methylation arrays are high-throughput techniques that quantify DNA methylation levels across the genome at specific loci^14,15. These arrays rely on bisulfite conversion of DNA, wherein unmethylated cytosines are converted to uracil, but methylated cytosines remain unchanged, followed by hybridizing the converted DNA to specific probes on the array. This technology has enabled large-scale epigenome-wide association studies, providing comprehensive insights into epigenetic modifications across different biological conditions and diseases^14,15. Methylation arrays have become invaluable in epigenetics research, offering a balance between throughput, resolution, and cost, making them particularly suitable for studies aiming to understand the complex relationship between DNA methylation, gene expression, and disease phenotypes.

Historically, brain tumor classification relied on morphologic examination of tumor specimens under a light microscopy¹⁶. Refinement of the process has occurred through the recognition of additional tumor-specific histologic patterns and by integrating testing modalities such as cytogenetics, immunohistochemistry, and nucleic acid sequencing findings into the classification schemes. Histologically defined tumor types often include heterogeneous molecular subtypes with distinct biological and clinical behaviors^17,18. The adoption of high-density methylation arrays (Illumina Infinium 450 K and 850 K EPIC arrays) has allowed for genome-wide evaluation of DNA methylation from large cohorts of human tumors. These arrays have favorable characteristics, including, streamlined workflows, comparable performance on fresh or formalin-fixed and paraffin-embedded (FFPE) tissues, and stability of the methylation mark even in material stored for multiple decades¹⁹. The ability to assay FFPE has facilitated the accumulation of large tumor cohorts and allows easy integration into standard clinical workflows^9,13,20. While initial utility of methylation profiling to refine the classification of brain tumors relied on unsupervised analyses comparing specific tumor cohorts of interest to reference brain tumor types^9,20–22, the introduction of supervised models to classify tumors utilizing methylation data has been a critical advance in clinical diagnostics.

Several supervised classification models utilizing simple and advanced machine-learning techniques have been proposed and utilized for biomedical applications^23–26. Models using DNA-methylation profiles for brain tumor classification, such as random forest (RF) and deep-learning frameworks^27–29, have been widely researched. On the other hand, in the clinical environment, DNA methylation-based classifiers for central nervous system (CNS) tumors have relied on the RF models³⁰. The most widely adopted RF classifier for brain tumors was developed by Capper et al. ¹³. This model was trained on a reference cohort containing all tumor entities represented in the 2016 WHO Classification of Tumors of the Central Nervous System³¹. An alternative RF clinical classifier for CNS tumors was developed and validated by Northwestern Medicine³². These models show good accuracy for tumors in the reference dataset, but a relatively high proportion of subthreshold classification scores has been observed upon implementation, creating clinical ambiguity.

In this study, we focused on developing a robust model for clinical use. Specifically, we evaluated multiple machine learning approaches to find a model with improved performance in outputting clinically confident results. Because methylation arrays have been prone to changes in probe composition, we were also interested in the ability of different models to handle data sparsity and robustness against random probe dropout. As a comparison to the more traditional RF model (RFmod)¹³, we constructed a neural network model (NNmod) and an exact bootstrap version of kNN (kNNmod), which efficiently simulates the bootstrap distribution without the need for actual resampling, thereby saving significant computing resources and time. Neural networks are well-known to provide both high accuracy and robustness to noise. An exact bootstrap kNN³³ was chosen because it theoretically allows for more robustness to probe loss, normal tissue contamination, and improved prediction accuracy in clinical settings where such data challenges are prevalent.

We validated the performance of these two models and the RFmod with two independent brain tumor cohorts consisting of 1104 samples from GSE109379 and 950 samples from the St. Jude Children’s Research Hospital. Our results showed that although all models performed robustly to missing data, the deep NN model had the highest CNS classification accuracy and the most favorable performance characteristics, especially in minimizing the proportion of subthreshold scores during testing and validation. Average precision and recall of the NNmod started reducing to similar levels of kNNmod and RFmod when tumor purity was less than 50%. This suggests that a deep NN model can be implemented in clinical laboratories as a reliable and essential diagnostic tool to assist in precision therapy for brain tumors.

Results

Model performance on train and test set

We developed three models, i.e., a k-nearest neighbors model (kNNmod), a random forest model (RFmod), and a multilayer perceptron neural network model (NNmod) (Supplementary Fig. 1), to classify human CNS tumors based on methylation signatures of the comprehensive reference set (GSE90496, n = 2801). This set comprises 91 methylation classes grouped into 75 methylation class families based on their histological and biological closeness¹³. The RF model represented a recapitulation of the previous random forest produced by Capper et al. representing the best in the current model. Here, we compared the performance of kNNmod and NNmod to the RFmod. The three models were evaluated with 1000 leave-out-25% cross-validations in predicting methylation classes and families (Supplementary Fig. 2). All models produced accuracies above 0.95 for class and family prediction (Table 1). Among the three models, classification accuracy and its Kappa statistic were highest in NNmod (above 0.98) and lowest in kNNmod (0.90 and 0.95 for class and family prediction) (Table 1). These accuracies were statistically significantly different from the null accuracy, i.e., the accuracy could be achieved by predicting the most frequent class (McNeMar’s p-values < 10⁻¹⁶). These results suggested that all models produced useful predictions with high accuracy. F1-scores were also calculated to evaluate the balance between precision and recall, especially in the presence of class imbalances. Similarly, NNmod achieved the highest F1-score both in class and family prediction (0.99 for family prediction) compared to kNNmod (0.90 for family prediction) and RF mod (0.98 for family prediction) (Table 1). Achieving the highest F1-score suggested that the NNmod not only balanced the rates of false positives and negatives but also managed the trade-off between capturing true cases and avoiding false detections.

Table 1.

Overall performance of leave-out-25% train-test process for each classifier on the GSE90496

	RF		kNN		NN
	Class	Family	Class	Family	Class	Family
Accuracy	0.98	0.99	0.95	0.96	0.99	0.99
Accuracy null	0.05	0.11	0.06	0.11	0.06	0.12
Kappa	0.96	0.99	0.90	0.95	0.98	0.99
F1-score	0.97	0.98	0.88	0.90	0.98	0.99
Recall	0.97	0.98	0.86	0.88	0.98	0.99
Precision	0.96	0.985	0.90	0.92	0.98	0.995
Specificity	0.99	0.99	0.99	0.99	0.99	0.99

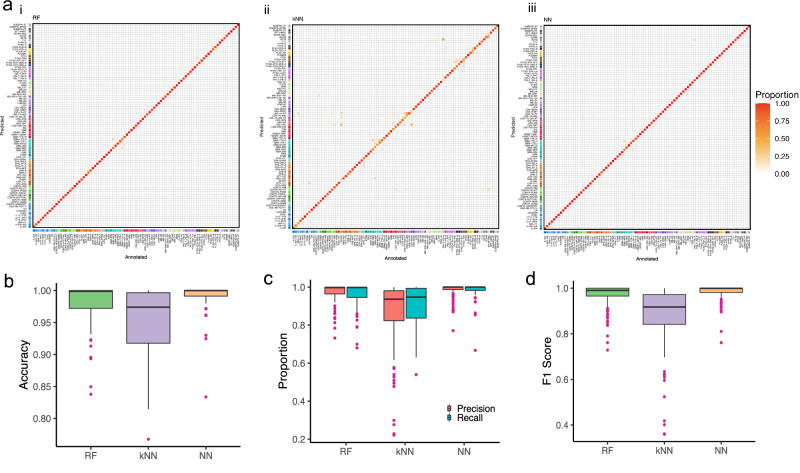
Cross-validation misclassifications by RFmod and NNmod focused on a few methylation classes while miss-classifications by kNNmod spread into many classes. Cross-validation of RFmod, kNNmod, and NNmod resulted in an average accuracy of 98%, 95%, and 99% for class prediction, respectively (Table 1). Notably, NNmod produced the best accuracy in predicting methylation class in all 1000 cross-validation rounds (Supplementary Table 1). kNNmod, compared to RFmod and NNmod, had the lowest precision (90% vs. 96% and 98%, respectively) and recall (86% vs. 97% and 98%). All models had comparable specificity (around 99%). Most miss-classifications among the three models occurred within the six histologically and biologically closely related tumor classes (ie. subclasses of pituitary adenomas) (Fig. 1a). However, kNNmod misclassification expanded to other methylation subclasses such as the subclasses of ependymomas (EPN), low-grade gliomas (LGG), melanocytic neoplasms (MELAN and MELCYT), and plexus tumors (PLEX). Some misclassifications of the KNNmod had important clinical implications such as confusing glioblastoma classes with low-grade glioma classes. (Fig. 1aii). On the other hand, NNmod had the narrowest ranges in accuracy, precision, and recall of predicting 91 subclasses with a median value around 0.98 for each metric (Fig. 1b, c and Supplementary Table 1). Minimal F1 scores for RFmod, kNNmod, and NNmod were 0.729, 0.359, and 0.761, respectively (Fig. 1d and Supplementary Data 1), suggesting NNmod had the best balance between precision and recall.

Fig. 1. Leave-out-25% testing results for each methylation class.

a Heat map showing results of methylation class prediction after 1000 stratified random samplings of i RF, ii kNN, and iii NN classifier incorporating information of n = 2801 reference tumor samples allocated to 91 methylation classes (GSE90496). Deviations from the bisecting line represent misclassification errors (using the maximum calibrated score for class prediction). Boxplots showing (b) the accuracy, (c) precision and recall, and (d) F1-score for each classifier with outliers.

All models, in general, performed better at predicting methylation families. The classification metrics of these 75 methylation families are shown in Table 1 and Supplementary Figure 3. The cross-validation accuracies for the clinically relevant groupings were improved in all models. Compared to kNNmod, NNmod showed higher accuracy (99% vs 96%), precision (99% vs 88%), and recall (99.5% vs 93%). Compared to RFmod, the NNmod showed higher recall (99% vs. 98%) and comparable accuracy (~99%), precision (~98%), and specificity (~99.9%) (Table 1). Among the 1000 cross-validation rounds in predicting methylation family, NNmod produced the best accuracy 604 times, while RFmod produced the best accuracy 280 times. The rest of the cross-validation rounds, NNmod and RFmod had the same accuracy that was higher than kNNmod (Supplementary Data 2). The misclassification of RFmod and NNmod among the CNS tumor classes shown in Fig. 1a appeared to be dissolved but retained in kNNmod (Supplementary Fig. 3a). Although accuracy was improved for all models, the gap between precision (88%) and recall (93%) for kNNmod (Supplementary Fig. 3b–d and Supplementary Data 1) remained the same in predicting methylation families. Minimal F1 scores for RFmod and NNmod were increased to 0.878 and 0.883, while this score was reduced to 0.318 by kNNmod (Supplementary Data 2). In conclusion, these results indicated that although RFmod and NNmod had very comparable performance, NNmod still had the highest accuracy and the best balance between precision and recall among the three models, suggesting that it had the highest discriminating power for both methylation class and family.

Model performance on two independent validation sets

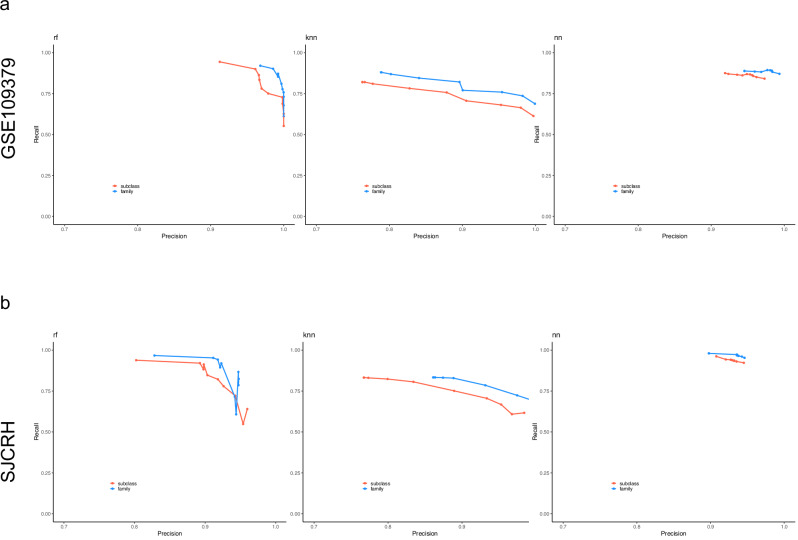
The classification performance of the three models was additionally tested on two independent data sets (GSE 109379) and the SJCRH data sets. To objectively assign each independent test sample to the reference methylation class group, we performed a semi-supervised learning approach³⁴ to assign labels to the two validation data sets. The 1,104 samples were assigned to 65 methylation classes and 50 families (Supplementary Data 3), while the 950 SJCRH samples were grouped into 49 methylation classes (Supplementary Data 4). This result was then used as the ground truth to measure the accuracy of the prediction results from our classifiers. We evaluated the performance of each classifier at multiple probabilistic prediction cutoffs ranging from 0 to 0.9 with a 0.1 increment. Figure 2 shows the overall average precision and recall at each cutoff for each classifier when validating on GSE109379 and SJCRH data sets. Although all models had their prediction precision increase as the threshold increased for both class (red line) and family (blue line) prediction, the recalls that met the cutoff dropped quickly to around 65% in RFmod and kNNmod, but it stayed above 0.75 in NNmod (Fig. 2 and Supplementary Data 5–8). For application to diagnostic tumor samples, an optimal calibrated score threshold of ≥ 0.9 was selected¹³. For subclasses within methylation class families, a threshold value of ≥ 0.5 was defined as sufficient for a valid prediction if all family member scores add up to a total score of ≥ 0.9. Single-class specificity and sensitivity are provided in Supplemental Table 5–8. At the 0.9 thresholds, all three models achieved a balanced accuracy of 99% with at least 95% precision when predicting methylation class and family in both GSE109379 and SJCRH (Table 2). However, recall produced by RFmod and kNNmod dropped below 65% while NNmod still maintained good recalls (>84% for class and > 87% for family) in GSE109379 (Fig. 2a and Table 2). When predicting SJCRH at the 0.9 thresholds, NNmod achieved a 92% and 95% recall for methylation class and family, respectively, with a 95% precision. Meanwhile, recalls in RFmod reduced to 55% and 60% for predicting methylation class and family, respectively (Fig. 2b). Similarly, kNNmod only achieved a recall of 62% for predicting methylation class and 66% for predicting methylation family (Fig. 2b and Table 2). These results suggested that NNmod could identify the most positive calls with higher accuracy and precision.

Fig. 2. Precision and recall above a classification probabilistic threshold for methylation class and family of each classifier.

a Precision and recall when predicting samples in GSE109379. b Precision and recall when predicting SJCRH samples. Validation results for subclass calls are in red. Validation results for family calls are in blue. Each point shows the precision and proportion of calls at each classification probabilistic threshold ranging from 0 to 0.9 with 0.1 increments.

Table 2.

Performance of each classifier when predicting methylation class in the independent test sets at 0.9 threshold

Data set	RF			kNN			NN
	Precision	Recall	Accuracy	Precision	Recall	Accuracy	Precision	Recall	Accuracy
GSE109379	0.97	0.72	0.99	0.73	0.64	0.99	0.91	0.82	0.97
SJCRH	0.92	0.87	0.93	0.8	0.7	0.84	0.96	0.89	0.94

Model robustness

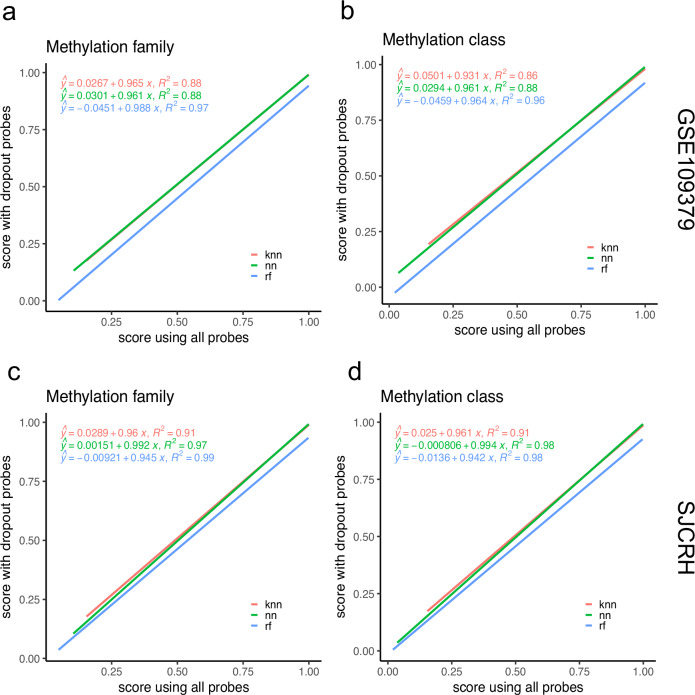
CNS tumor classification of our classifiers is based on features that measure DNA methylation at different CpG sites in the human genome using probes on Illumina BeadChip arrays. This microarray technology is easy to use, time-efficient, and cost-effective. However, it keeps evolving, and in each new release, more probes are printed to cover more diverse genomic regions, and some probes are purposely removed for efficiency. Other potential applications, such as detection of tumors by cell-free DNA testing, may also have uneven or missing values. Because the missing probes could differentially affect model performance, we investigated whether the performance of the three classifiers was robust in producing consistent outputs in class labels and their corresponding prediction scores even when a proportion of input probes were not present. We performed an experiment in which we randomly dropped 10% of the probes in the independent test data sets GSE109379 and SJCRH. We repeated this process 10 times to create 10 different missing probes scenarios. The robustness of each classifier was assessed based on the Theil’s U uncertainty coefficients between the two sets of predicted labels and Spearman’s correlation coefficients between prediction scores with and without missing probes. Table 3 shows that RFmod and NNmod have Theil’s U uncertainty coefficients greater than 0.94, suggesting that the predicted labels by RFmod and NNmod before probe drop-out were as similar as those produced after probe drop-out. In contrast, kNNmod has the lowest uncertainty coefficient among the three classifiers with Theil’s U ranging from 0.889 to 0.908 for methylation family and class prediction. These results indicate that the two sets of predicted labels are strongly associated. All models have Pearson correlation coefficients > 0.928 with p-values < 2.2e⁻¹⁶, suggesting a strong and statistically significant linear correlation between prediction scores produced when 10% of probes were missing and when there were no missing probes (Table 4). Figure 3 shows the regression analysis of the two sets of classification scores. Scores produced by NNmod and kNNmod with drop-out data set were generally higher than those that were output using all probes as indicated with positive y-intercepts (Fig. 3). RFmod, when using data with missing probes, produced lower classification scores (negative y-intercepts). All models had the goodness-of-fit R-squared of at least 86%, indicating a strong correlation between the two sets of prediction scores (Fig. 3). These results suggest that missing probes do not affect the prediction outcomes of any classifiers.

Table 3.

Theil’s U uncertainty coefficient with a 95% confidence interval of each classifier with and without dropping 10% of probes in the GSE109379 and SJCRH independent test sets

Data set	RFmod		kNNmod		NNmod
	Class	Family	Class	Family	Class	Family
GSE109379	0.969 (0.967, 0.972)	0.974 (0.970, 0.978)	0.892 (0.887, 0.898)	0.908 (0.902, 0.914)	0.973 (0.970, 0.9796)	0.980 (0.976, 0.983)
SJCRH	0.945 (0.940, 0.949)	0.964 (0.960, 0.968)	0.889 (0.883, 0.894)	0.899 (0.894, 0.905)	0.970 (0.966, 0.974)	0.979 (0.975, 0.982)

Table 4.

Pearson’s correlation coefficients of prediction scores with and without 10% missing probes

Data set	RFmod		kNNmod		NNmod
	Class	Family	Class	Family	Class	Family
GSE109379	0.98	0.99	0.93	0.94	0.94	0.94
SJCRH	0.99	0.99	0.95	0.96	0.99	0.99

Fig. 3. RFmod, kNNmod, and NNmod classification scores when predicting independent testing samples having all the probes versus samples having 10% of probes randomly dropped.

Line plots showing prediction scores for (a) methylation family and (b) methylation class of GSE109379 data set. Line plots showing (c) methylation family prediction scores and (d) methylation class prediction scores of SJCRH data set. Linear regression lines and the R-squared goodness-of-fit measures were estimated using the scores produced from kNNmod (red), NNmod (green), and RFmod (blue).

Model assessment based on sample purity

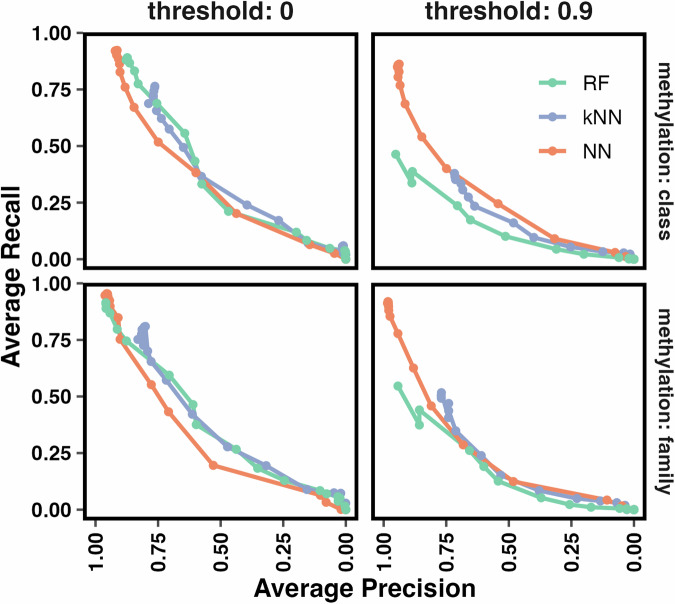
Infiltrating of normal cells such as epithelial, stromal, and immune cells in tumor tissue can perturb the tumor signal in molecular studies. In our application, this contamination can affect the methylation level measured by microarray chips, leading to possible degradation in the performance of a classifier. Therefore, we developed an in-silico experiment in which different fractions of the normal control cells were mixed with the tumor tissue to answer these questions: (1) whether a classifier produces unexpected methylation class/family prediction (2) if yes, would the prediction have a suprathreshold score, and (3) approximately at what percentage of control contamination, the classification accuracy starts to degrade. We first observed the overall performance of the three classifiers based on their average recall and precision for methylation class and family prediction at different thresholds and purity fractions (Fig. 4). NNmod started to perform the best, as seen in previous sections. RFmod degraded at a comparable rate with kNNmod after the sample purity was less than 65%. As the purity of tumor samples was less than 40%, NNmod started to yield lower precision and recall compared to the other two classifiers (Fig. 4, threshold = 0). At the 0.9 clinical threshold and 0.95 purity, NNmod had twice the average recalls and a much higher average precision than RFmod and kNNmod. The performance of NNmod did not start to degrade at a similar rate to RFmod and kNNmod until the purity of tumor samples was less than 50%. As the contamination increased, RFmod had the lowest performance among the three classifiers (Fig. 4, threshold = 0.9). NNmod maintained the highest average precision and recall among the three classifiers. Its performance reduced to a comparable level with RFmod and kNNmod only when the tumor purity was less than 50%.

Fig. 4. Average precision and recall of each classifier at different purity fractions per 0 and 0.9 threshold.

Tumor samples from GSE109379 were mixed with control samples (as indicated in Supplemental Table 2) to create different fractions of normal vs tumor mixture. The average precision and recall for predicting methylation classes and families by RFmod (green), kNNmod (purple), and NNmod (orange) were computed for different mixed fractions of GSE109379 (0 to 0.95 purity—points on the lines) at 0 and 0.9 threshold.

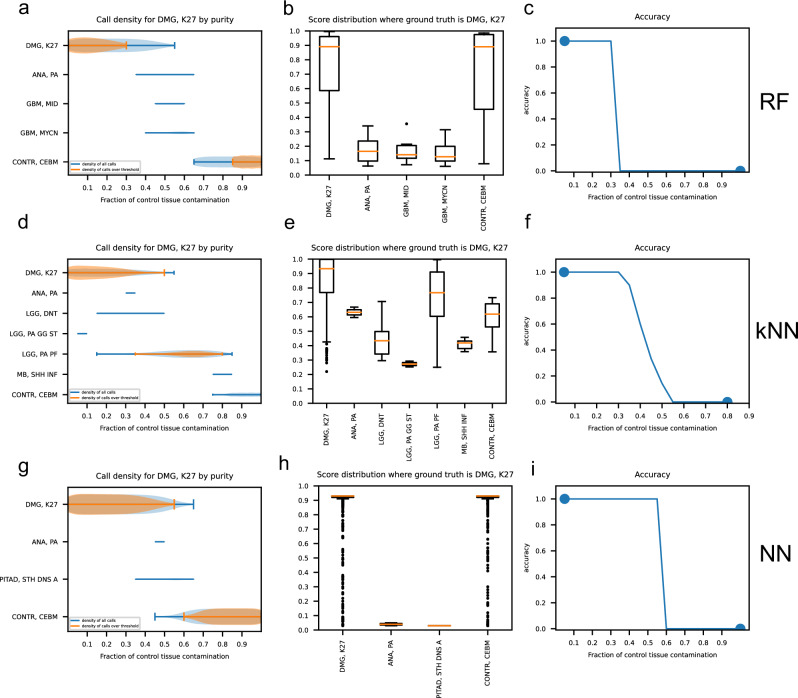
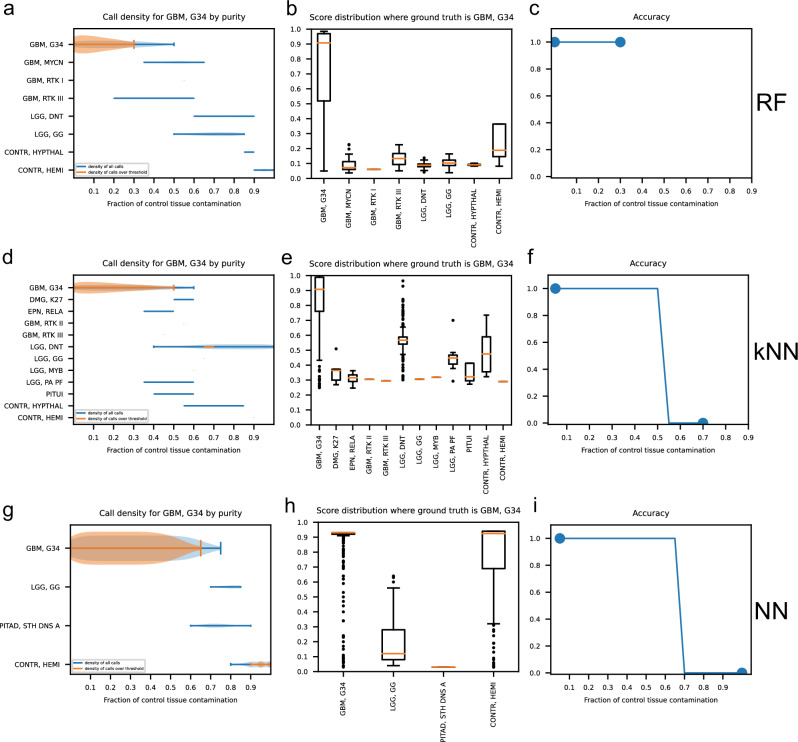
Next, we observed the prediction results of each classifier for each methylation class and family. Figures 5 and 6 show the performance of RFmod, kNNmod, and NNmod at different control fractions in the tumor sample for methylation class diffuse midline glioma H3 K-27 mutant (DMG, K27) and glioblastoma, IDH wildtype, H3.3 G34 mutant (GBM, G34), respectively. When the high-grade DMG, K27 tumors got contaminated with control, RFmod and NNmod did not produce unexpected methylation classes besides DMG, K27 and its corresponding mixed control cerebellar hemisphere (CONTR, CEBM) class (Fig. 5a, b, g, and h) or family (Supplementary Fig. 4a, c, d, and f). On the other hand, kNNmod unexpectedly predicted selected high-grade glioma samples to be low-grade pilocytic astrocytoma (LGG, PA PF) with scores above the clinical threshold (0.9) (Fig. 5d, e and Supplementary Fig. 4b, e). kNNmod and RFmod could not accurately predict the methylation class of the DMG, K27 tumors if the purity of these samples was less than 70% (Fig. 5c, f and Supplementary Fig. 4g, h). Meanwhile, NNmod was able to maintain its prediction accuracy for DMG, K27 samples until the sample purity dropped below 40% (Fig. 6i). Figure 6 shows that when predicting the GBM, G34 methylation class, RFmod did not provide any suprathreshold results if greater than 30% of control tissue were present in the mixture (Fig. 6a–c). On the contrary, kNNmod accurately predicted these samples until the contamination was up to 60%. At this fraction, kNNmod unexpectedly classified these grade 4 tumors as grade I dysembryoplastic neuroepithelial tumors (LGG, DNT) (Fig. 6d–f). NNmod did not provide any suprathreshold classification scores for alternative classes to GBM, G34 except for the corresponding normal hemispheric cortex (CONTR, HEMI) starting at 70% contamination (Fig. 6g–i). Similar results were shown in Supplementary Fig. 5 for GBM, G34 samples at the methylation family.

Fig. 5. Classification results of RF, kNN, and NN model for high-grade diffused midline glioblastoma with K-27 mutant (DMG, K27) methylation class at different contamination levels.

a, d, g Density plots of all calls (blue curve) and calls over the 0.9 clinical threshold (orange curve) at each possible methylation family predicted by RF, kNN, and NN when the ground truth is DMG, K27 at different fractions of control tissue contamination. b, e, h Box plots show the score distribution for each methylation family predicted by RF, kNN, and NN models. c, f, i Prediction accuracy of each classifier at each purity level.

Fig. 6. Classification results of RF, kNN, and NN model for grade 4 glioblastoma, IDH wildtype, H3.3 G34 mutant (GBM, G34) methylation class at different contamination levels.

a, d, g Density plots of all calls (blue curve) and calls over the 0.9 clinical threshold (orange curve) at each possible methylation family predicted by RF, kNN, and NN when the ground truth is GBM, G34 at different fractions of control tissue contamination. b, e, h Box plots show the score distribution for each methylation family predicted by RF, kNN, and NN models. c, f, i Prediction accuracy of each classifier at each purity level.

The results of our in silico mixing were validated using a small independent validation cohort of samples with known variant allele frequency for IDH1 mutations or H3F3A p.K27M mutations. Similar to the in silico findings, the NNmod maintained correct suprathreshold classification within the range of estimated tumor fraction of 38–76% for IDH1 mutant tumors (19–38% variant allele fraction) and 46–98% for H3F3A p.K28M mutant tumors (23–48% variant allele fraction). In contrast, the RFmod and kNNmod failed to classify these samples reliably across the range of variant allele fractions, yielding either subthreshold scores or misclassing scores in some instances (Supplementary Table 2).

Discussion

We developed a deep neural network model to predict CNS tumor classification based on a large DNA-methylation data set from 2801 patients of 82 distinct CNS tumors and 9 controls. Our multilayer perceptron neural network classifier achieved high performance, as demonstrated in 3 different evaluation settings. Compared with RFmod, a current-state-of-the-art CNS tumor classifier based on DNA-methylation, our NNmod showed higher overall accuracy (99% vs. 98%), precision (98% vs. 97%) and recall (98% vs. 96%) and comparable specificity (~99%) in methylation class prediction (Table 1). Among the three developed models, the kNN model produced the lowest accuracy (95%), precision (86%), and sensitivity (90%) (Table 1). In addition, we showed that our DNN model is highly robust and generalizable as evaluated in an independent testing dataset of 1104 GSE109379 samples (65 tumor classes) and 700 classifiable SJCRH samples (45 tumor classes), with an overall accuracy of 91% and 94%. Among these results, NNmod showed the highest accuracy and the best balance between precision and recall compared to RFmod and kNNmod (Table 1, Figs. 1–2). All classifiers were trained on the reference data (GSE90496) generated from the Illumina Human Methylation 450 K chips. These chips featured 485,577 CpG sites throughout the human genome, but they became obsolete and have been replaced by the Illumina HumanMehtylationEPIC BeadChip (EPIC). EPIC measures methylation at > 850,000 CpG sites and covers approximately 90% of the same sites represented on the 450 K chip. EPIC eliminates sites reported to be poorly performed³⁵ and features more CpGs that cover more regulatory elements. When using classifiers trained on data produced by 450 K chips to predict samples ran on EPIC chips, it is possible that some probes used for prediction are no longer present on EPIC chips and could hinder the classifier performance. As such, we performed a random probes drop-out experiment to evaluate the classification performance of RFmod, kNNmod, and NNmod (Tables 3 and 4). Although having the probes dropped out randomly may be adequate, it would be additionally useful to know in the future whether dropping all the poorly performed probes in the 450 K training data set would enhance the performance and increase the robustness of all classifiers.

Neural networks (NNs), k-nearest neighbors (kNN), and random forests (RF) serve as fundamental machine learning models with distinct operational principles. The NNs’ architecture is inspired from the human brain, featuring layers of interconnected nodes that simulate neurons. This architecture enables NNs to capture complex, non-linear relationships through weighted inputs and outputs optimized during training, making them particularly suited for tasks like image and speech recognition³⁶. On the simpler end, kNN operates on the premise that similar data points are found in proximity, as such classification of a new point is based on its nearest neighbors. This model is intuitive and straightforward but may falter in high-dimensional spaces³⁷. Meanwhile, RFs enhance decision tree models by creating an ensemble of trees from random subsets of the dataset, thereby reducing overfitting and improving prediction accuracy³⁸. This method balances the simplicity of decision trees and the robustness required for complex data analysis.

The performance comparison among the DNN, RF, and kNN models in classifying CNS tumors based on DNA methylation data highlights several key insights. The NN model outperforms the other two, particularly in handling the complex and high-dimensional DNA methylation data sets, achieving the best combination of precision, recall, and robustness to probe dropout. Improved precision in the random forest and k-nearest neighbor classifiers comes at the expense of drastically reduced recall. In the clinical settings, increased recall, i.e., rate of positive samples correctly classified above clinical reporting threshold, is extremely desirable because correctly diagnosing all actual positive cases can effectively improve patient safety, treatment efficacy, and overall health outcomes. Additionally, the generalizability of the NN is demonstrated through its consistent performance across independent testing data sets, indicating its practical applicability in clinical settings. Comparatively, the RF model, while efficient and generally accurate, may not capture as complex interactions among features as effectively as neural networks. On the other hand, the lower performance in kNNmod was likely due to the lack of explicit data structure making it inefficient in dealing with high-dimensional DNA methylation data. The DNN’s adaptive learning capabilities and its potential for feature learning and architectural flexibility enable it to outperform RF and kNN, making DNN a promising candidate for clinical applications. Another advantage of NN model was its high recall compared to kNNmod and RFmod, especially when dealing with imbalanced classes within the data set. The distribution of classes in the datasets can significantly impact recall. The SJCRH data set contained mostly pediatric tumor types, while the GSE109379 had more representation of adult tumors. Some of these adult tumor types, including specific molecular classes of glioblastoma, are closely related and difficult to classify above the threshold. As such, NNmod and RFmod had equivalent recalls when dealing with SJCRH. However, the sensitivity of NNmod was more robust and remained high compared to that of RFmod when dealing with closely related adult tumors in GSE109379.

The primary aim of our study was to optimize a classification model for clinical use, addressing challenges such as the occasional changes in probe representation on Illumina arrays. These changes can necessitate time-consuming retraining and revalidation of models, although our findings suggest that some models are robust enough to withstand a significant reduction of probes without requiring retraining. This resilience is particularly relevant as methylation profiling, especially in cell-free DNA (cfDNA) testing like cell-free cerebral spinal fluid, where probe dropout is likely due to low DNA content. Additionally, while imputation methods are commonly used in research settings^39–41, they may not be suitable for clinical scenarios where patient data is unique and not necessarily reflective of broader cohort characteristics. However, in serial clinical monitoring, where the primary tumor’s DNA characteristics are known, imputation from the primary tumor might be feasible and safe. Our approach leverages a neural network and an exact bootstrap version of kNN, which efficiently simulates the bootstrap distribution without the need for actual resampling, thereby saving significant computing resources and time.

Some limitations of our study included probe selection and the NN architecture. Firstly, the probe selection was constrained to a smaller subset overlapping between the 450 K and EPIC methylation arrays. This restriction potentially impacts the coverage breadth of our genomic data, which could limit the generalizability of our findings. To overcome this limitation, future work could explore the use of the covariance structure of the probes for imputation purposes replication of the reference series with more comprehensive arrays^39–41, or DNA methylation sequencing. An additional limitation is that the neural network’s architecture in our study, consisting of 11 layers, may be overly complex, raising concerns about overfitting. This complexity could hinder the model’s ability to generalize to new, unseen data. Future improvements could focus on simplifying the neural network by reducing the number of layers. Employing methods such as pruning or parameter optimization through cross-validation could help in creating a more efficient and robust model.

Despite these potential limitations, our results from two independent cohorts from different institutions have shown minimal signs of overfitting. This observation was supported by results from dropout tests (Fig. 3 and Table 4) and analysis of tumor purity levels (Fig. 4), which indicated that the models was robust across different data sets and probe missing scenarios. Further optimization of the model architecture could enhance the utility and reliability of the model in the clinical setting. Diagnosis of CNS tumors is a complex multiclass classification problem as the number of diagnostic classes in which patients are stratified is not limited to a few selected classes but rather to a very high list of entities represented in the 5th edition of the WHO Classification of CNS Tumors¹³. It has been shown that diagnostic accuracy can be improved by utilizing a robust machine-learning classification algorithm based on DNA-methylation profiles obtained from formalin-fixed, paraffin-embedded (FFPE), or frozen tissue samples¹³. The preparation of FFPE samples is one of the most widely used procedures to preserve and archive specimens in clinical oncology. This workflow requires an invasive tissue biopsy to be performed on patients. Recently, liquid biopsies, a less invasive method for cancer detection, have rapidly gained prominence⁴². Particularly, plasma cell-free DNA methylation profiles have been shown to be highly sensitive, cost-effective, and accurate in early tumor detection for cancer interception, and for multi-cancer classification^43,44. Our study demonstrated that NNmod was the top stand-alone classifier among the three developed classifiers using DNA-methylation signatures from FFPE samples. The 11-layer perceptron NNmod maintained high recalls (>82% for GSE109379 and > 90% for SJCRH) above a 0.9 clinical threshold with > 0.92 precision when validated with two independent data sets (Fig. 2 and Supplementary Data 5–8). With these improvements over RFmod, NNmod represents a viable method that could be used in conjunction with clinical, histopathologic, and molecular data to aid in the diagnosis and classification of CNS tumors. Future studies would be to apply this machine learning modeling with the DNA-methylation profiles from plasma cell-free DNA obtained through the less invasive liquid biopsy procedure.

Methods

Patient material

FFPE or frozen tumor samples representing pediatric patient samples encountered on the typical pathology service were evaluated. The samples represented 650 samples expected to be present in the reference series and 300, true negative samples representative of non-brain solid tumors known to be absent from the reference series (Supplementary Data 9). All experimental protocols were approved by the St. Jude Children’s Research Hospital Institutional Review Board (#XPD17-163) and performed in accordance with the Declaration of Helsinki. Informed consent was not required under the Office for Human Research Protections (OHRP) guidelines regarding the disposition of deidentified human tissues for human subjects research and was waived by the St. Jude Children’s Research Hospital Institutional Review Board.

Training and independent testing data sets

All supervised models were trained on the genome-wide DNA methylation profiles from the CNS tumor reference cohort (GSE90496), consisting of 2801 samples from 91 methylation classes¹³. All classifiers were independently validated with two methylation data sets, including the 950 CNS tumor samples from the St. Jude Children’s Research Hospital (SJCRH) and 1104 CNS tumor samples from GSE109379¹³.

Data generation and methylation array processing

We analyzed the 950 independent test samples using Illumina Methylation BeadChip (EPIC) arrays according to the manufacturer’s instructions. In summary, DNA was isolated from formalin-fixed paraffin-embedded (FFPE) tumor tissue using the Maxwell® Clinical Sample Concentrator system (Promega, Madison, WI). Following extraction, DNA was quantified using a Qubit fluorometer and quantitation reagents (Thermo Fisher Scientific, Waltham, MA), and bisulfite converted using the Zymo EZ DNA methylation kit (Zymo Research, Irvine, CA). The overall DNA input amount was approximately 250 ng. DNA methylation profiling was carried out with the Infinium HumanMethylationEPIC BeadChip (850 K) array (Illumina Inc., San Diego, CA) on the Illumina iScan platform.

All methylation data analyses, including those from GSE90496 and GSE109379, were performed in R (http://www.r-project.org, version 3.5.3), using several packages from Bioconductor and other repositories. Specifically, array data were preprocessed using the minfi package (v.1.28.4)⁴⁵. Background correction with dye-bias normalization was performed for all samples using noob (normal-exponential out-of-band) with the “single” dye method⁴⁶. Batch effects such as hybridization time and other technical variables were removed using removeBatchEffect from the limma package (v.3.38.3)⁴⁷. Probe filtering was performed after normalization. Specifically, we removed probes located on sex chromosomes, probes containing nucleotide polymorphism (dbSNP132 Common) within five base pairs, including the targeted CpG-site, or mapping to multiple sites on hg19 (allowing for one mismatch), as well as cross-reactive probes.

Semi-supervised analysis

We developed a combination approach including a self-training with editing using a support vector machine (SETRED-SVM) as the base learner model with an L2-penalized, multinomial logistic regression model to obtain high confidence labels from a few reference instances³⁴. We applied this approach on GSE109379 and the SJ samples to get labels for the independent validation purpose of the supervised models. The ssc R package (v2.1-0) was used to build and train the SETRED-SMV semi-supervised model. First, the standard deviation for each probe across all 2801 samples from GSE90496 was calculated. Input features for SSL models were the 5072 probes with a standard deviation greater than 0.3 across all 2801 samples. We used the best SETRED-SVM model to predict the methylation class for 1104 GSE109379 and 950 SJ samples. The SSL scores were calibrated with an L2-penalized, multinomial logistic regression. Scores above the 0.8 threshold were considered correctly classifiable³⁴.

The random forest algorithm and development

The random forest algorithm was reconstructed from Capper’s algorithm¹³ using the randomForest R package (v.4.6-14)^48–50. This model was trained based on the 408,862 overlapping probes of the 450 K and 850 K array probes. First, the 10,000 features (or probes) with the highest importance scores were selected by splitting the 408,862 intersecting probes into 43 sets of ~9500 probes. Next, one hundred trees were fitted for each set using 639 randomly sampled candidate features at each split (mtry = square root of 408,862). The subclass labels, stratified subsampling methods, and the number of trees in the forest were followed as in ref. ¹³. This framework can produce a model that either predicts the methylation class or the methylation “family” scores¹³ that represent clinically equivalent families on which Capper et al. witnessed their best error rates. Next, a multinomial logistic regression was used to calibrate the prediction scores from all cross-validation splits as previously described¹³. The family scores were then generated as the sum of all methylation class scores from the trained random forest.

The k-nearest neighbor algorithm and development (kNNmod)

An exact bootstrap k-nearest neighbor model (kNNmod) was built as described in ref. ³³. The model was trained on score vectors constructed based on the difference in median beta values of the top 100 hyper- and hypo-methylated probes. Each set of 100 top probes was selected based on the mean ß values in a methylation group and the absolute z-scores computed by taking the differences between mean beta values of two CNS methylation groups divided by the square root of the sum of the variance in each group. Hence, each methylation group had a list of 200 probes that were either most hypo- or hypermethylated based on the absolute z-scores. Each sample had a vector of scores, i.e., one score per methylation group. Each score was computed by taking the median ß values of the top 100 hypermethylated probes and subtracting that from the top 100 hypomethylated probes. Euclidean distance on these vectors was used to measure the distance between each pair of samples. The entire Euclidean distance matrix on the methylation group score vectors was computed for all pairwise samples.

To classify a new sample, kNNMod ordered all other samples by their distance from the new observation and derived the probability that those neighbors would be included among the k nearest neighbors in the binomial distribution. We used k = 5 neighbors for classification because some subgroups were very rare. For each new sample, the exact bootstrap probability of assignment to each methylation group can be conditionally computed on the training data set and the resulting probe selection and group score definition.

The multilayer sparse perceptron architecture and development (NNmod)

The overarching design principle of the NNmod was to generate a simple neural network using brute-force hyperparameter optimization. The model and the training data were chosen to be as large as possible, subject to the memory constraints of the available computing machinery (NVIDIA P100 GPUs with 16G of on-chip memory). Internally, buffer and array sizes for model parameters were determined to be powers of 2 to use computer memory as efficiently as possible. The design of the multilayer sparse perceptron is shown in Supplemental Fig. 1. This design is based on two primary assumptions: (i) the methylation data from central nervous system tumors and normal brain is embedded in low dimensional space, and (ii) random combinations of important probes can predict methylation class. The first assumption is typical of high dimensional data and is supported by examining the singular value decomposition of previously published reference data¹³ (data not shown). In addition, the ability of combined methylation probes to predict methylation class is supported by previous implementations of random forest classifiers¹³.

We constructed an 11-layer perceptron neural net. The input dimension was 51,108, composed of roughly 1/8th of probes, selected with feature extraction described in the network training section (below). The neural network architecture began with a large sparse layer that maximized output dimensions while remaining within 16GB GPU memory constraints. This ensured the subsequent dense layers had adequate memory space during training. Specifically, a sparse matrix of dimensions (51,108, 139,264) with 256 nonzero entries per column was chosen. The number of nonzero entries was optimized by searching powers of two from 64 through 512 for each nonzero entry size with a dense layer with 91 outputs followed by a softmax appended, and the model was trained and evaluated for bulk precision at full recall.

The 7 dense layers that follow the sparse layer were determined by a process that iteratively added dense layers between the sparse layer and the final output layer. The iteration ceased when the performance improvement due to an added layer diminished below a threshold of 1e-3. The final dense layer serves as the output layer, linked to a softmax function.

For optimizing the Stochastic Gradient Descent (SGD) parameters, we began by setting momentum to 0 and weight decay to 0. The learning rate was then optimized by searching through an exponential space of values, starting from 1e-2 down to 1e-5, to select the rate that yields the highest precision. Once the optimal learning rate was established, momentum was optimized by exploring values from 1e-1 to 1e-4, selecting the value that maximizes precision. Finally, with both the learning rate and momentum fixed, the weight decay was fine-tuned by testing values ranging from 1e-9 to 1e-1, selecting the decay that further enhanced precision.

Stochastic gradient descent was performed with a batch size of 32 and minimizing negative log-likelihood loss of output scores from the network using a learning rate of 0.001. The batch size parameter was obtained by searching the parameter space from 128 to 8 in powers of 2. Using the evaluation partitions from the cross-validation splits, model calibration was performed with a multinomial logistic regressor. The final model was trained on the complete 2801 samples using identical parameters following cross-validation.

Classifier cross-validation

To reduce the overfitting problem when training classifiers on high-dimensional data, all classifiers were cross-validated based on 1000 leave-out-25% cross-validations. We randomly selected 75% of the data used to train the classifiers (GSE90496), while the remaining 25% of the data were used for predictions. Stratified random sampling was performed for each methylation class or family to ensure the number of categories remained the same in each iteration. This validation process was repeated 1000 times (Supplemental Fig. 2).

Model calibration

Calibration of machine learning methods may be necessary because the scores output by the classifier may have different scales when broken down by class, even when the scores are normalized so that they sum to 1. This poses problems for comparing the uncertainty in class or family calls between cases or even in the same case. Thus, the scores must be rescaled to form a well-calibrated multinomial distribution with minimal differences between expected values and variances between the class call groups.

Both RF and NN models were calibrated with the same multinomial logistic regression approach described by Capper et al.¹³. The glmnet package (v-4.1-3)⁵¹ was used with R bindings for the random forest and python bindings for the neural net.

Model robustness

To test whether missing methylation probes (features) affect our machine learning models, we randomly dropped 10% of the probes from the testing data (GSE109379 and SJCRH) and calculated the accuracy. The same probes at each round were used for all models. This process was repeated ten times to create 10 different missing sets of probes. Pearson’s correlation and Theil’s U uncertainty coefficients were computed using the ggpubr R package (v.0.4.0) and the DescTools R package (v.99.44), respectively. Pearson’s correlation coefficients with p-values were calculated to examine the linear relationship between the two sets of prediction scores (with and without missing probes). Theil’s U uncertainty coefficients were calculated to measure the nominal association between the two sets of labels predicted by the three classifiers on samples of GSE109379 and SJCRH data with and without missing probes.

Purity analysis

We performed an in silico simulated impurity experiment using different fractions of control and positive samples in GSE109379 and SJCRH test sets. The experiment was performed based on m-values. The in silico mixed m-values (m_mixed) for each positive sample were computed as follows

$$m_{\mathrm{mixed}}=(1-p)m_{\mathrm{test}}+p{m}_{\mathrm{control}}$$ 1

where $m_{\mathrm{test}}$ is the input m-value from the positive samples, and $m_{\mathrm{control}}$ is the average m-values of up to 19 appropriate control (i.e., normal) tissue samples in the test sets, p is the proportion of normal control tissues contaminated in a tumor sample (ranging from 0 to 1 with 0.05 increment). The control samples were selected based on their control methylation class corresponding to the methylation class tumor as described in Supplementary Table 1. The final measurement of the mixed sample was then converted back to beta values for classifier inputs.

Model performance metrics

All models were evaluated based on accuracy, precision, specificity, recall, and F1 score. Classification accuracy is the number of correct predictions (true positives and true negatives) divided by the total number of predictions. Precision is the ratio of true positives to all the total positives predicted by a classifier. Specificity measures the proportion of true negatives correctly identified by a classification model. Recall or sensitivity is the ratio of true positives to all the ground truth positives. The F1-score is the harmonic mean of precision and recall and a good metric to measure the results in imbalanced classification problems. The higher the F1 score, the better the performance of a model. All measurements were computed using the caret R package (v.6.0-90).

Author contributions

A.B. developed the MLPNet framework and implemented the RF model. Q.T.T. modified and maintained the models, analyzed the data and interpreted the results, produced figures and tables, and drafted the manuscript. B.A.O. conceptualized the project, interpreted the results, and drafted the manuscript. T.L. and S.P. implemented the KNN model. R.T., S.J.A. extracted the DNA and produced methylation data. M.C., L.V.F., G.R., P.N., A.G., E.A., S.S., and D.W.E. provided samples and interpreted the results. M.C., D.H., and T.M. modified and maintained the MLPNet. All authors reviewed and edited the manuscript.

Data availability

In this study, we used the following datasets: (i) GSE90496, GSE109379¹³, and GSE276299 available from the National Center for Biotechnology Information (NCBI https://www.ncbi.nlm.nih.gov). The SJCRH samples were collected de-identified based on tumors that were evaluated at our center. They were collected to be representative of broad tumor types seen in the general clinical practice. They were not selected by any demographic features, only on diagnosis and availability of material.

Code availability

The generated code is available from the corresponding authors upon reasonable request for non-commercial use.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41698-024-00718-3.