Abstract
Power flow (PF) analysis is a foundational computational method to study the flow of power in an electrical network. This analysis involves solving a set of non-linear and non-convex differential-algebraic equations. State-of-the-art solvers for PF analysis, therefore, face challenges with scalability and convergence, specifically for large-scale and/or ill-conditioned cases characterized by high penetration of renewable energy sources, among others. The adiabatic quantum computing paradigm has been proven to efficiently find solutions for combinatorial problems in the noisy intermediate-scale quantum (NISQ) era, and it can potentially address the limitations posed by state-of-the-art PF solvers. For the first time, we propose a novel adiabatic quantum computing approach for efficient PF analysis. Our key contributions are (i) a combinatorial PF algorithm and a modified version that aligns with the principles of PF analysis, termed the adiabatic quantum PF algorithm (AQPF), both of which use Quadratic Unconstrained Binary Optimization (QUBO) and Ising model formulations; (ii) a scalability study of the AQPF algorithm; and (iii) an extension of the AQPF algorithm to handle larger problem sizes using a partitioned approach. Numerical experiments are conducted using different test system sizes on D-Wave’s Advantage™ quantum annealer, Fujitsu’s digital annealer V3, D-Wave’s quantum-classical hybrid annealer, and two simulated annealers running on classical computer hardware. The reported results demonstrate the effectiveness and high accuracy of the proposed AQPF algorithm and its potential to speed up the PF analysis process while handling ill-conditioned cases using quantum and quantum-inspired algorithms.
Keywords: Combinatorial power flow analysis, Quantum annealing, QUBO, Hubo, Power systems
Subject terms: Energy grids and networks, Power distribution, Applied mathematics, Computational science, Electrical and electronic engineering
Introduction
Power flow (PF) analysis aims to calculate the complex voltage, i.e., the voltage magnitude and phase angle, of all buses in power systems for given loads, generations, and network topologies. The calculated voltage magnitudes and phase angles are subsequently used to estimate the power and current line flows and, eventually, facilitate the operation and planning of power systems. PF analysis involves solving a set of equations that relate the complex voltage and (active/reactive) power at each bus. From this perspective, a state-space representation of the power system that includes a set of differential-algebraic equations is used. These equations describe the active and reactive power balance at all the buses, as well as the voltage magnitude drop at all lines due to the power losses. The alternating current (AC) PF equations are examples of such equations and can be written as a set of nonlinear and non-convex equations in polar or rectangular coordinates, representing Kirchhoff’s laws1.
The AC PF equations are non-linear and non-convex, which rules out their exact analytical solution. Hence, the state-space representation of the power system is conventionally solved using iterative numerical methods, such as the Gauss-Seidel (GS) and Newton-Raphson (NR) methods2. These methods can provide steady-state solutions, i.e., voltages for all buses within specified accuracy boundaries3,4. However, the use of conventional PF analysis methods can cause convergence problems in large-scale modern power systems and is very time-consuming. For instance, GS has limitations regarding its dependence on the initial guess solution, accuracy level, ability to handle small network sizes, and difficulty converging for certain system conditions. Similarly, NR is limited by its inability to converge when the Jacobian matrix is singular, computational expense, and poor performance for ill-conditioned cases, such as highly unbalanced operation 5,6. Therefore, conventional PF analysis approaches are becoming ineffective at supporting modern power system operation and planning 7–9. From this perspective, inadequate PF analysis potentially leads to safety risks due to the inability of PF to accurately handle power generation from large numbers of distributed energy resources 10, as well as to predict blackouts. Hence, it is crucial to develop computationally efficient and numerically stable PF algorithms that can effectively handle the unique challenges of modern power systems11.
Several advanced algorithms have been developed in the literature to address the challenges faced by PF analysis, including scalability12–16 and the management of ill-conditioned cases17–23. These studies mostly focus on the advancement of programming techniques and the formulation of mathematical models grounded in classical computation principles. Efforts to address the scalability concern focus on reducing the computational challenges for PF analysis of large-scale modern power systems. For example, Lopez et al.12 developed an extended dynamic programming approach based on the optimality principle of the recursive Hamilton-Jacobi-Bellman equations for electrical distribution systems. The scalability of the proposed approach was demonstrated through experimentation with large-scale power systems and benchmarking against commercial programming solvers. Goncalves et al.13 formulated a mixed integer linear programming model for the operation planning problem of electrical distribution systems. The proposed formulation leverages linear expressions to model steady-state operation and hence ensures convergence toward the optimal solution for large-scale power systems. Dai et al.14 proposed a scalable algorithm employing a reduced modeling technique for solving the AC PF problem. Reformulating this problem as a zero-residual least-squares problem with consensus constraints, the authors used a Gauss-Newton-based inexact algorithm to improve scalability. Idema et al.15 presented iterative linear solvers, which offer enhanced scalability, thus rendering them suitable for the evolving modern power systems. In16, the authors proposed modifications to NR to address sparsity in large power systems. Specifically, they introduced a sparse PF and integrated parallelization and vectorization techniques to accelerate computations.
With respect to the management of ill-conditioned cases, conventional PF solvers, such as NR, often encounter numerical stability issues during convergence. Consequently, the literature offers robust alternatives to mitigate these challenges. For example, Tostado-Veliz et al.17, introduced a novel robust PF technique using the current injection form of the PF equations. Similarly, Tripathy20 applied K.M. Brown’s method to solve the PF. This method is a variation of NR that incorporates Gaussian elimination and ensures the utilization of the most recent information at each iteration. The method is particularly effective for solving ill-conditioned non-linear algebraic equations. Tostado-Veliz et al.21 also presented a four-stage algorithm to address ill-conditioned cases. The algorithm was integrated with an efficient paradigm and is particularly useful in solving systems with reactive constraints of generators. Liu et al.22, on the other hand, took a different approach where the PF model is transformed into a hypothetical dynamic system by introducing a differential equation on the loading parameter. This innovation enables a non-iterative method based on differential transformation to solve the dynamic system effectively. Iwamoto23 devise a PF calculation method, characterized by its simplicity, absence of mathematical approximations, and minimal additional computational overhead when incorporated into NR. The method, therefore, offers a pragmatic solution to address ill-conditioned cases.
Despite the significant progress made in PF analysis algorithms, there remains a critical need for scalable, computationally efficient, and numerically stable PF analysis algorithms to meet the growing requirements of modern power systems. In particular, high levels of distributed energy resources, variable loads, and bidirectional power flows require more precise and efficient PF analysis approaches. In addition, the increasing deployment of advanced control and optimization techniques, such as real-time monitoring and control, demand response, and distributed energy resource management, necessitates the development of more sophisticated PF analysis algorithms. Therefore, although state-of-the-art methods have shown improvements, they are not enough to address the needs of modern power systems11,24. Considering the next example, the use of NR in the Power Grid Model environment (https://github.com/PowerGridModel) for a 369-node network necessitates approximately 10 seconds to solve a scenario with a specific computer architecture. For a thousand scenarios, the time required would be 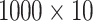 seconds, or more than 2.7 hours, using the same computer architecture. This duration is not feasible for specific applications, such as stochastic optimal power flow25, where a large number of calculations should be completed within a few minutes. Consequently, the power systems community is increasingly interested in exploring novel approaches, including quantum computing26–28, which have shown promising results in various applications and are, therefore, expected to revolutionize the field of PF analysis in the near future29.
seconds, or more than 2.7 hours, using the same computer architecture. This duration is not feasible for specific applications, such as stochastic optimal power flow25, where a large number of calculations should be completed within a few minutes. Consequently, the power systems community is increasingly interested in exploring novel approaches, including quantum computing26–28, which have shown promising results in various applications and are, therefore, expected to revolutionize the field of PF analysis in the near future29.
Quantum computing models can be categorized into two key paradigms: (i) the gate-based quantum computing model (GQC) and (ii) the adiabatic quantum computing model (AQC). Optimism for a quantum speedup stems from the potential of quantum algorithms to take advantage of unique properties, e.g., superposition and entanglement, which allows computations with fewer operations than classical algorithms. An increasing number of studies, therefore, explore how quantum computing can address the complexities of modern power systems. Most studies implement the GQC paradigm, which can simulate specific computations using quantum gates and discrete time steps30,31. GQC offers flexibility in algorithm design and potential quantum speedup for specific problem instances, such as linear system solving. However, GQC algorithms, e.g., the Harrow-Hassidim-Lloyd (HHL) algorithm, demand a large number of qubits and quantum gates even for small-scale problems, which makes them susceptible to noise inherent in current quantum computers. This noise, along with challenges related to the condition number of the system and readout requirements, can significantly limit the expected quantum speedup in power flow problems32,33.
On the other hand, a few studies focus on the AQC paradigm34,35. AQC is similar to GQC in terms of computational power, but it operates in an analog manner, i.e., without quantum gates or discrete time steps36,37. The continuous evolution of AQC from an initial ground state to a final ground state of a problem Hamiltonian makes it more robust to certain types of noise and, therefore, potentially offers a more practical approach to solving complex optimization problems in the near term38. For example, a comparative study between a GQC algorithm, i.e., Quantum Alternating Operator Ansatz (QAOA), and an AQC algorithm demonstrated that AQC outperformed GQC on specific hardware platforms39. D-Wave’s quantum processing units (QPUs) powering the current generation of Advantage™ systems, as an AQC hardware example, serve as specialized accelerators for solving NP-hard optimization problems through a solution method called quantum annealing. These QPUs must be supercooled to temperatures close to absolute zero to maintain the quantum properties essential for computation. However, the key feature that enables efficient computation is their ability to control quantum mechanical effects for solving specific types of optimization problems36. Note that QPUs facilitate heuristic approaches to finding approximate solutions rather than solving NP-hard problems directly, and they do not guarantee a solution to all NP-hard problems.
The present work uses the AQC paradigm to address PF analysis. A combinatorial PF algorithm and an adiabatic quantum PF (AQPF) algorithm are developed and numerically justified. For the first time, two formulations are implemented based on the Quadratic Unconstrained Binary Optimization (QUBO) and the Ising model formulations for PF analysis. The scalability of the AQPF algorithm and of a partitioned variant is demonstrated numerically by applying them to various power system benchmarks. Experiments are performed for 4-bus, 9-bus, and 14-bus test systems on D-Wave’s quantum annealer and Fujitsu’s digital annealer, and two simulated annealers running on classical hardware. The results show the effectiveness and the significant potential of the AQPF algorithm in the NISQ and FTQ era. In addition, the proposed partitioned algorithm is introduced for the first time in the literature to the best of the authors’ knowledge, which can speed up PF analysis in two different aspects: by leveraging quantum hardware and reducing the number of operations needed for a given test system.
Results
Power flow equations
For all buses i of a power system, the mismatch between the given active and reactive power consumption/injection at buses i, 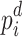 and
and 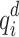 , and their net counterparts,
, and their net counterparts, 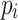 and
and 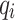 , can be written as
, can be written as
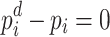 |
1 |
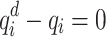 |
2 |
with
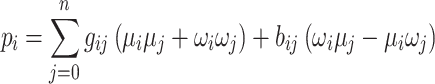 |
3 |
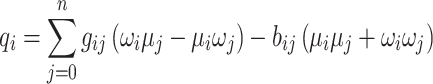 |
4 |
where 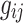 and
and 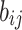 are the known real and imaginary parts of the elements in the bus admittance matrix Y, respectively, and
are the known real and imaginary parts of the elements in the bus admittance matrix Y, respectively, and 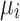 and
and 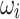 are the real and imaginary parts of the complex voltages to be determined such that Eqs. (1)–(2) hold with equality for all buses i. To transform the problem at hand into a form that can be solved by a quantum or digital annealer, Eqs. (3)–(4) are expanded into
are the real and imaginary parts of the complex voltages to be determined such that Eqs. (1)–(2) hold with equality for all buses i. To transform the problem at hand into a form that can be solved by a quantum or digital annealer, Eqs. (3)–(4) are expanded into
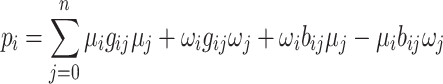 |
5 |
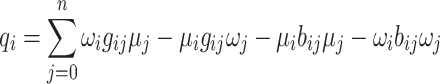 |
6 |
Here, 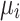 ,
, 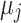 ,
, 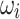 , and
, and 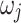 are real-valued variables that need to be discretized in order to obtain a binary problem, i.e., a discrete combinatorial optimization problem. This work implements two different formulations, i.e., Quadratic Unconstrained Binary Optimization (QUBO) formulation and Ising model formulation, to solve such combinatorial PF.
are real-valued variables that need to be discretized in order to obtain a binary problem, i.e., a discrete combinatorial optimization problem. This work implements two different formulations, i.e., Quadratic Unconstrained Binary Optimization (QUBO) formulation and Ising model formulation, to solve such combinatorial PF.
Combinatorial power flow—QUBO formulation
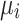 and
and 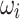 can be written using a straightforward discretization of the form
can be written using a straightforward discretization of the form
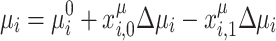 |
7 |
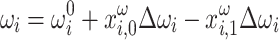 |
8 |
where 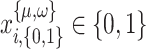 are binary decision variables whose value decides whether the base values
are binary decision variables whose value decides whether the base values 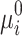 and
and 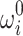 are increased (
are increased (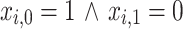 ), decreased (
), decreased (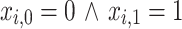 ), or kept at their current value (
), or kept at their current value (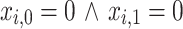 or
or 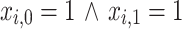 ). The last case allows for an ambiguous solution, but at the same time, it ensures that all four combinations – 00, 01, 10, 11 – of the two binary variables
). The last case allows for an ambiguous solution, but at the same time, it ensures that all four combinations – 00, 01, 10, 11 – of the two binary variables 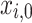 and
and 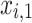 are valid bitstrings. In contrast to the often-used one-hot encoding, the above approach does not involve any constraints to rule out invalid bitstrings, which makes it particularly attractive for practical implementation on quantum and digital annealers. Nevertheless, a minor downside of the discretization of Eqs. (7)–(8) is that only three options (‘increase’, ‘decrease’, ‘keep’) are considered at a time, thereby not fully exploiting the full capability of two decision variables. Furthermore, the convergence of the iterative approach to be presented below can be slow if the increments
are valid bitstrings. In contrast to the often-used one-hot encoding, the above approach does not involve any constraints to rule out invalid bitstrings, which makes it particularly attractive for practical implementation on quantum and digital annealers. Nevertheless, a minor downside of the discretization of Eqs. (7)–(8) is that only three options (‘increase’, ‘decrease’, ‘keep’) are considered at a time, thereby not fully exploiting the full capability of two decision variables. Furthermore, the convergence of the iterative approach to be presented below can be slow if the increments 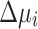 and
and 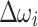 are chosen to be too small and/or if the base values
are chosen to be too small and/or if the base values 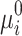 and
and 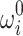 are far away from the values that satisfy Eqs. (1)–(2). This might be partly mitigated by choosing
are far away from the values that satisfy Eqs. (1)–(2). This might be partly mitigated by choosing 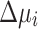 and
and 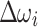 adaptively, i.e., updating their values in each iteration loop and, potentially, even choosing individual values for each bus i. For net active power injection, substitution of Eqs. (7)–(8) into Eq. (5) yields
adaptively, i.e., updating their values in each iteration loop and, potentially, even choosing individual values for each bus i. For net active power injection, substitution of Eqs. (7)–(8) into Eq. (5) yields
 |
9 |
where the terms in the equation can be categorized as follows: constant terms, which do not contain any binary variables, e.g., 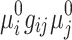 ; linear terms, which include a single binary variable per term, e.g.,
; linear terms, which include a single binary variable per term, e.g., 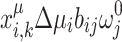 ; and quadratic terms, which involve two binary variables per term, e.g.,
; and quadratic terms, which involve two binary variables per term, e.g., 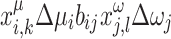 . Details on how deriving the equations are provided in the “Supplementary information”. A similar expression can be derived for the net reactive power injection by substituting Eqs. (7)–(8) into Eq. (6)
. Details on how deriving the equations are provided in the “Supplementary information”. A similar expression can be derived for the net reactive power injection by substituting Eqs. (7)–(8) into Eq. (6)
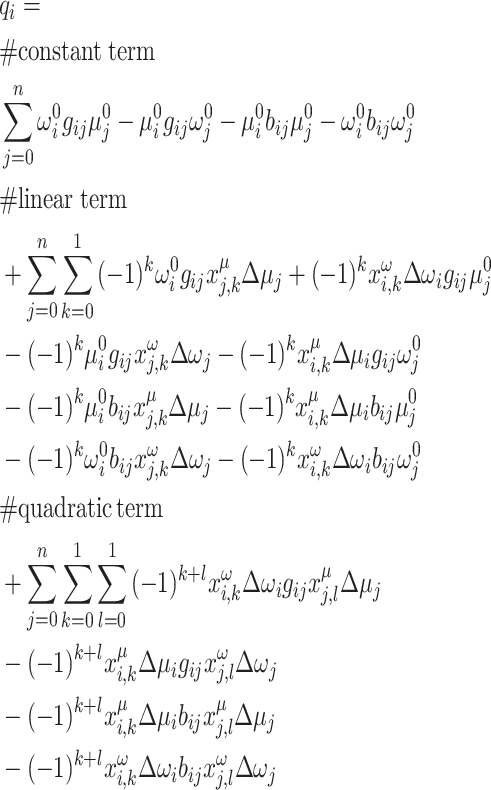 |
10 |
Combinatorial power flow— Ising model formulation
As an alternative to the above QUBO formulation, 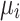 and
and 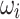 can be represented using an alternative discretization of the form
can be represented using an alternative discretization of the form
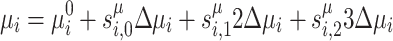 |
11 |
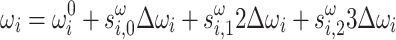 |
12 |
where 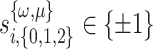 are spin variables. As for the binary variables in Eqs. (7)–(8), any combination of spin-variable values yields an admissible solution in the range
are spin variables. As for the binary variables in Eqs. (7)–(8), any combination of spin-variable values yields an admissible solution in the range 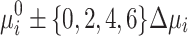 and
and 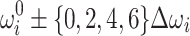 , which allows for more fine-grained control of the increment/decrement at the cost of just two additional variables per bus i. To prevent any confusion, we would like to note that the resulting Ising model is not equivalent to the previous QUBO formulation but an algorithmic alternative with different properties. In particular, adding an increment or decrement in the QUBO formulation requires introducing two additional binary variables, with one variable representing an increment and the other a decrement. In contrast, the Ising model inherently includes both positive and negative values in its spin variables and hence, needs only one spin variable to represent an increment or a decrement. Based on a sensitivity analysis performed in this work, it is recommended to rescale
, which allows for more fine-grained control of the increment/decrement at the cost of just two additional variables per bus i. To prevent any confusion, we would like to note that the resulting Ising model is not equivalent to the previous QUBO formulation but an algorithmic alternative with different properties. In particular, adding an increment or decrement in the QUBO formulation requires introducing two additional binary variables, with one variable representing an increment and the other a decrement. In contrast, the Ising model inherently includes both positive and negative values in its spin variables and hence, needs only one spin variable to represent an increment or a decrement. Based on a sensitivity analysis performed in this work, it is recommended to rescale 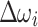 and
and 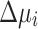 by a factor of 3. For net active power injection, substitution of Eqs. (11)–(12) into Eq. (5) yields
by a factor of 3. For net active power injection, substitution of Eqs. (11)–(12) into Eq. (5) yields
 |
13 |
where the three clauses represent constant, linear, and quadratic terms, respectively. A similar expression can be derived for net reactive power injection by substituting Eqs. (11)–(12) into Eq. (6)
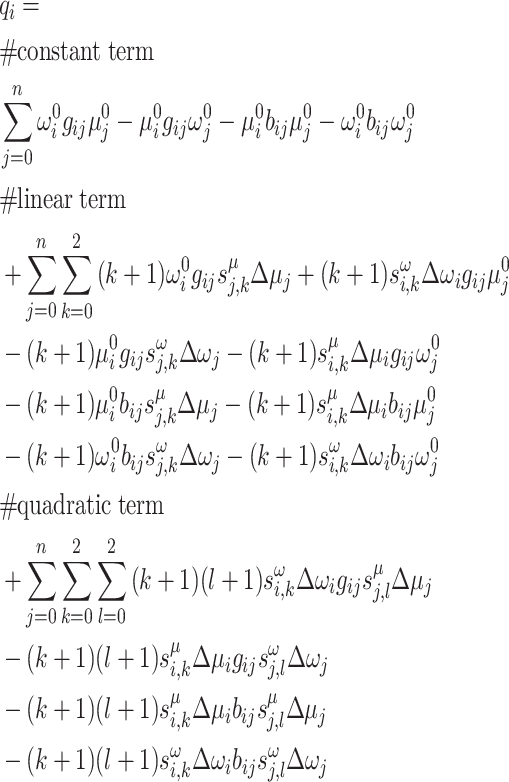 |
14 |
Numerical justification of combinatorial power flow
Solving Eqs. (1)–(2) with the aid of a simulated, digital, or quantum annealer amounts to minimizing the sum of all the terms squared, i.e., the Hamiltonian 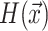 and
and 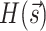
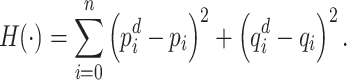 |
15 |
Here, 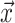 and
and 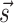 represent vectors of binary and spin variables, respectively. Working out all the terms yields a fourth-order polynomial for the binary/spin variables. The solvers are D-Wave’s simulated annealer Neal (https://docs.ocean.dwavesys.com/en/latest/docs_neal/sdk_index.html) (
represent vectors of binary and spin variables, respectively. Working out all the terms yields a fourth-order polynomial for the binary/spin variables. The solvers are D-Wave’s simulated annealer Neal (https://docs.ocean.dwavesys.com/en/latest/docs_neal/sdk_index.html) ( ), D-Wave’s quantum-classical hybrid annealer (https://docs.dwavesys.com/docs/latest/doc_leap_hybrid.html) (HA), D-Wave’s Advantage™ system (www.dwavesys.com/learn/quantum-computing) (QA), Fujitsu’s classical simulated annealer (
), D-Wave’s quantum-classical hybrid annealer (https://docs.dwavesys.com/docs/latest/doc_leap_hybrid.html) (HA), D-Wave’s Advantage™ system (www.dwavesys.com/learn/quantum-computing) (QA), Fujitsu’s classical simulated annealer (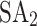 ), and Fujitsu’s digital annealer V3 (www.fujitsu.com/global/services/business-services/digital-annealer) (DA). Since all solvers can handle only quadratic terms, higher-order terms need to be reduced by introducing auxiliary variables. The Python packages PyQUBO (https://pyqubo.readthedocs.io) and DADK are used to develop the QUBO and Ising model based on the Hamiltonian (15), which can perform the reduction of higher-order terms through the functions H.compile().to_qubo() and BinPol.reduce_higher_degree_to_qubo(H), respectively. PyQUBO is used when the solver is
), and Fujitsu’s digital annealer V3 (www.fujitsu.com/global/services/business-services/digital-annealer) (DA). Since all solvers can handle only quadratic terms, higher-order terms need to be reduced by introducing auxiliary variables. The Python packages PyQUBO (https://pyqubo.readthedocs.io) and DADK are used to develop the QUBO and Ising model based on the Hamiltonian (15), which can perform the reduction of higher-order terms through the functions H.compile().to_qubo() and BinPol.reduce_higher_degree_to_qubo(H), respectively. PyQUBO is used when the solver is 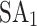 , HA, and QA, while DADK is used in combination with
, HA, and QA, while DADK is used in combination with 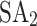 and DA to reduce higher-order terms.
and DA to reduce higher-order terms.
We observe differences between the two implementations, PyQUBO and DADK, in terms of the number of auxiliary variables required to encode the same problem sizes, with the DADK package often proving more efficient by requiring fewer auxiliary variables. However, in both implementations, we ensure that the order reduction process accurately preserves the optimal solutions and retains the same variable assignments for the lowest energy solutions. When performing order reduction, it is crucial to consider the specific objectives. In some scenarios, maintaining the entire energy spectrum ordering is important, especially when relative energy differences between states are significant. However, in many practical applications, including this study, the primary goal is to ensure that the optimal solutions remain unchanged after order reduction. References40,41 provide a broader perspective on various order reduction techniques.
For all solvers, the number of readouts is the same and ranges from 2000 to 100,000, depending on the size of the test system. 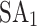 approaches equilibrium by updating at decreasing temperatures until reaching the target temperature, that is 1/kT, where T is the temperature in kelvin and k is Boltzmann’s constant. Spins are updated once per point per temperature using the Metropolis-Hastings algorithm. At low temperatures, the distribution focuses on the ground states, and long, smooth temperature schedules ensure that samples match the equilibrium distribution. For HA, the time limit parameter was set to 10 seconds. The chip ID of QA is Advantage_system5.4. The minor embedding method is used to map the problem onto the QA. Chain strength is determined by the square of the power consumption variables
approaches equilibrium by updating at decreasing temperatures until reaching the target temperature, that is 1/kT, where T is the temperature in kelvin and k is Boltzmann’s constant. Spins are updated once per point per temperature using the Metropolis-Hastings algorithm. At low temperatures, the distribution focuses on the ground states, and long, smooth temperature schedules ensure that samples match the equilibrium distribution. For HA, the time limit parameter was set to 10 seconds. The chip ID of QA is Advantage_system5.4. The minor embedding method is used to map the problem onto the QA. Chain strength is determined by the square of the power consumption variables 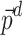 and
and 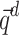 , as well as the line properties of the test systems, i.e., the admittance matrix Y. This ensures that the chain strength is sufficiently large to prevent chain breaks while remaining small enough to maintain the significance of the QUBO terms. The target graph for the embedding is sparse, reflecting the nature of the power test systems, which are not fully connected.
, as well as the line properties of the test systems, i.e., the admittance matrix Y. This ensures that the chain strength is sufficiently large to prevent chain breaks while remaining small enough to maintain the significance of the QUBO terms. The target graph for the embedding is sparse, reflecting the nature of the power test systems, which are not fully connected.
For 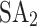 and DA, the time limit is 10 seconds, the scaling bit precision is 64, and the overall timeout is 3,600 seconds. In addition to simulated annealing, DA supports parallel tempering as an alternative optimization algorithm. Parallel tempering runs multiple replicas of the optimization process at different temperatures simultaneously. These replicas can exchange their temperatures with neighboring replicas based on a Metropolis criterion, which, in turn, facilitates a global search for the optimum.
and DA, the time limit is 10 seconds, the scaling bit precision is 64, and the overall timeout is 3,600 seconds. In addition to simulated annealing, DA supports parallel tempering as an alternative optimization algorithm. Parallel tempering runs multiple replicas of the optimization process at different temperatures simultaneously. These replicas can exchange their temperatures with neighboring replicas based on a Metropolis criterion, which, in turn, facilitates a global search for the optimum. 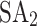 and DA initiate optimization from a random state in each run, aiming to reach a configuration with the optimal energy value within the decision variable space.
and DA initiate optimization from a random state in each run, aiming to reach a configuration with the optimal energy value within the decision variable space.
Algorithm 1 represents the pseudo-code of the combinatorial PF algorithm. Initially, the vectors 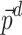 and
and 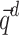 , respectively, representing the active and reactive power demands, and the admittance matrix Y are assigned based on the given test system power consumption and topology (lines 1-3). The increments/decrements
, respectively, representing the active and reactive power demands, and the admittance matrix Y are assigned based on the given test system power consumption and topology (lines 1-3). The increments/decrements 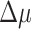 and
and 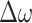 , as well as the real and imaginary voltage vectors
, as well as the real and imaginary voltage vectors 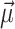 and
and 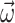 , are initialized with user-specified values (lines 4–7), based on which the initial active and reactive power vectors
, are initialized with user-specified values (lines 4–7), based on which the initial active and reactive power vectors 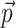 and
and 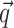 are calculated (lines 8-9). Subsequently, the initial Hamiltonian
are calculated (lines 8-9). Subsequently, the initial Hamiltonian 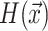 or
or 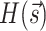 (cf. Eq. (15)) is calculated (line 10), providing an approximate solution based on the initial voltage estimates. The residual threshold
(cf. Eq. (15)) is calculated (line 10), providing an approximate solution based on the initial voltage estimates. The residual threshold 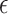 is set in line 11, and the iteration counter it is initialized to zero before starting the loop.
is set in line 11, and the iteration counter it is initialized to zero before starting the loop.
Once the minimization problem with the Hamiltonian (15) has been solved (line 14), the resulting vectors 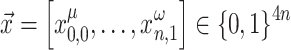 for the QUBO formulation, and
for the QUBO formulation, and 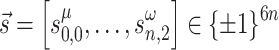 for the Ising model formulation can be used to update the real and imaginary parts of the voltages
for the Ising model formulation can be used to update the real and imaginary parts of the voltages 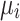 and
and 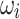 according to Eqs. (7)–(8), and (11)–(12), respectively (lines 15 and 16). Note that auxiliary variables stemming from the conversion of higher-order terms into quadratic ones are neglected for the voltage updates. If the values of
according to Eqs. (7)–(8), and (11)–(12), respectively (lines 15 and 16). Note that auxiliary variables stemming from the conversion of higher-order terms into quadratic ones are neglected for the voltage updates. If the values of 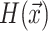 or
or 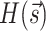 drop below a certain user-defined threshold
drop below a certain user-defined threshold 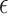 , the so-computed complex voltages (
, the so-computed complex voltages (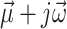 ) are accepted as solution values. Otherwise, the complex voltage base values
) are accepted as solution values. Otherwise, the complex voltage base values 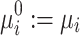 and
and 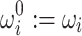 are redefined, and the minimization problem is solved with the updated Hamiltonian (15) until convergence is reached. A secondary stopping criterion of the iteration schemes is when all
are redefined, and the minimization problem is solved with the updated Hamiltonian (15) until convergence is reached. A secondary stopping criterion of the iteration schemes is when all 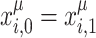 and
and 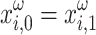 for the QUBO formulation, and
for the QUBO formulation, and 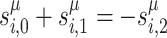 and
and 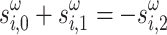 for the Ising model formulation, meaning that none of the base values
for the Ising model formulation, meaning that none of the base values 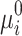 and
and 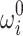 are updated and the iteration stalls. Note that this is very unlikely to happen in practice. Sporadic qubit flips most likely trigger at least some updates. Once convergence is reached,
are updated and the iteration stalls. Note that this is very unlikely to happen in practice. Sporadic qubit flips most likely trigger at least some updates. Once convergence is reached, 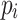 and
and 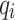 are calculated for all buses i via Eqs. (3)–(4). Note that the iterative process in Algorithm 1 is essential for refining the solution to the power flow problem, as the initial solution may not meet the desired accuracy or might be a local minimum.
are calculated for all buses i via Eqs. (3)–(4). Note that the iterative process in Algorithm 1 is essential for refining the solution to the power flow problem, as the initial solution may not meet the desired accuracy or might be a local minimum.
Algorithm 1.
Combinatorial power flow algorithm.
Five different annealers, i.e., 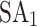 , HA, QA,
, HA, QA, 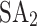 , and DA, are used to minimize the QUBO/Ising model for which the computational details are presented in Table 1. Experiments are performed on a 4-bus test system with known
, and DA, are used to minimize the QUBO/Ising model for which the computational details are presented in Table 1. Experiments are performed on a 4-bus test system with known 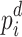 and
and 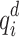 and unknown
and unknown 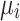 and
and 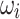 for all buses i. This implementation results in 136 binary and 300 spin variables for the QUBO and Ising model formulations, respectively, using PyQUBO, and 104 binary and 236 spin variables for the QUBO and Ising model formulations, respectively, using DADK. The difference in variables stems from the fact that the two Python packages implement different strategies to convert higher-order terms into quadratic terms, with DADK adopting a more efficient approach. In the QUBO formulation, QA requires the most iterations to reach the defined threshold
for all buses i. This implementation results in 136 binary and 300 spin variables for the QUBO and Ising model formulations, respectively, using PyQUBO, and 104 binary and 236 spin variables for the QUBO and Ising model formulations, respectively, using DADK. The difference in variables stems from the fact that the two Python packages implement different strategies to convert higher-order terms into quadratic terms, with DADK adopting a more efficient approach. In the QUBO formulation, QA requires the most iterations to reach the defined threshold 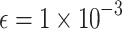 , while
, while 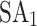 takes the most iterations in the Ising model formulation. DA achieves
takes the most iterations in the Ising model formulation. DA achieves 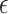 with the fewest iterations in both the QUBO and Ising model formulations. The Ising model with QA is the most time-consuming per iteration due to the high communication time, including QPU access, delay, programming, readout, and sampling time. It is also important to note that different annealers reach different minimal energies with the same defined
with the fewest iterations in both the QUBO and Ising model formulations. The Ising model with QA is the most time-consuming per iteration due to the high communication time, including QPU access, delay, programming, readout, and sampling time. It is also important to note that different annealers reach different minimal energies with the same defined 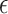 , as shown in Table 1.
, as shown in Table 1.
Table 1.
Computational details for the combinatorial power flow algorithm with the QUBO and Ising model formulations based on the 4-bus test system.
| Formulation | Compiler | # of variables 
|
Compile time [s] | Annealer | # of iterations 
|
Time per iteration [s] | Hamiltonian 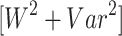
|
|---|---|---|---|---|---|---|---|
| QUBO | PyQUBO | 136 | 0.08 | 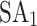 |
35 | 0.677 | 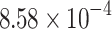 |
| PyQUBO | 136 | 0.08 | HA | 35 | 9.718 | 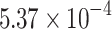 |
|
| PyQUBO | 136 | 0.08 | QA | 98 | 58.598 | 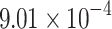 |
|
| DADK | 104 | 0.14 | 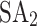 |
34 | 0.16 | 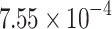 |
|
| DADK | 104 | 8.66 | DA | 24 | 8.12 | 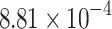 |
|
| Ising | PyQUBO | 300 | 1.88 | 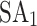 |
69 | 1.942 | 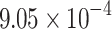 |
| PyQUBO | 300 | 1.88 | HA | 52 | 10.602 | 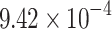 |
|
| PyQUBO | 300 | 1.88 | QA | 44 | 230.2 | 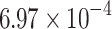 |
|
| DADK | 236 | 1.03 |  |
52 | 1.06 | 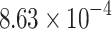 |
|
| DADK | 236 | 9.12 | DA | 23 | 9.38 | 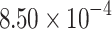 |
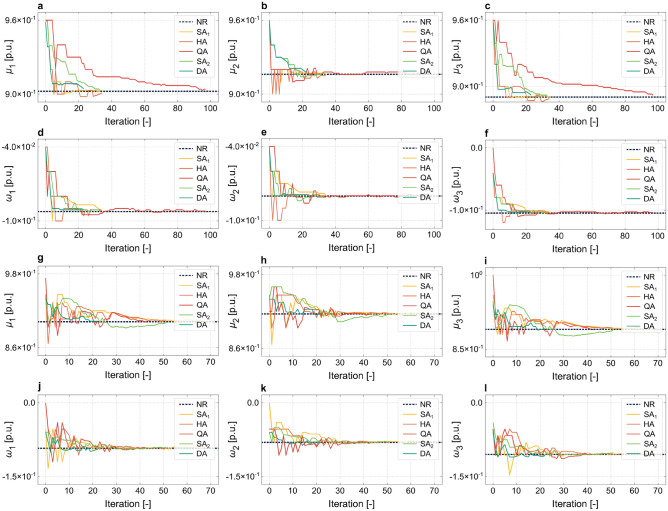
Figure 1 illustrates 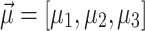 and
and 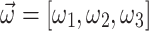 achieved by five annealers using the combinatorial PF algorithm for the 4-bus test system over iterations. Graphs (a-f) show results for the QUBO formulation, while graphs (g-l) depict results for the Ising model formulation. Note that the values of
achieved by five annealers using the combinatorial PF algorithm for the 4-bus test system over iterations. Graphs (a-f) show results for the QUBO formulation, while graphs (g-l) depict results for the Ising model formulation. Note that the values of 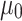 and
and 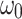 are already known for the reference bus, set, respectively, to 1 and 0, and hence are not shown in the graphs. The
are already known for the reference bus, set, respectively, to 1 and 0, and hence are not shown in the graphs. The 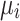 and
and 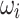 obtained from the Newton-Raphson classical solver (NR) are also included in the graphs. Figure 1a–c presents the convergence of
obtained from the Newton-Raphson classical solver (NR) are also included in the graphs. Figure 1a–c presents the convergence of 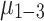 using the QUBO formulation. It is observed that
using the QUBO formulation. It is observed that 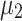 converges more rapidly than
converges more rapidly than 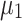 and
and 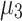 , with the primary delay in the convergence of
, with the primary delay in the convergence of 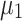 and
and 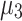 being attributed to the slow convergence of QA. QA, in particular, exhibits slower convergence compared to the other annealers. Interestingly, although QA struggles with convergence speed, the values of
being attributed to the slow convergence of QA. QA, in particular, exhibits slower convergence compared to the other annealers. Interestingly, although QA struggles with convergence speed, the values of 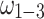 generated by QA oscillate around the corresponding values obtained by NR. This suggests that while QA may eventually approach the correct solution, its path to convergence is less direct, particularly in the QUBO formulation. The slower convergence of
generated by QA oscillate around the corresponding values obtained by NR. This suggests that while QA may eventually approach the correct solution, its path to convergence is less direct, particularly in the QUBO formulation. The slower convergence of 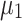 and
and 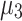 in the QUBO formulation, therefore, can be directly linked to the performance of QA. On the other hand, the Ising model formulation, depicted in Fig. 1g–l, shows a different trend. Here,
in the QUBO formulation, therefore, can be directly linked to the performance of QA. On the other hand, the Ising model formulation, depicted in Fig. 1g–l, shows a different trend. Here, 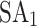 is the slowest to converge, as corroborated by Table 1. However, the convergence behavior in the Ising model is more uniform across
is the slowest to converge, as corroborated by Table 1. However, the convergence behavior in the Ising model is more uniform across 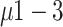 and
and 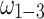 . Therefore, the annealers, when working with the Ising model, exhibit a smoother and more consistent convergence trajectory due to the more fine-grained updates allowed by this formulation.
. Therefore, the annealers, when working with the Ising model, exhibit a smoother and more consistent convergence trajectory due to the more fine-grained updates allowed by this formulation.
Figure 1.
Representation of 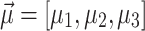 and
and 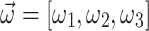 obtained by the combinatorial power flow algorithm. Experiments are performed using D-Wave’s classical simulated annealer Neal (
obtained by the combinatorial power flow algorithm. Experiments are performed using D-Wave’s classical simulated annealer Neal ( ), D-Wave’s quantum-classical hybrid annealer (HA), D-Wave’s Advantage™ system (QA), Fujitsu’s classical simulated annealer (
), D-Wave’s quantum-classical hybrid annealer (HA), D-Wave’s Advantage™ system (QA), Fujitsu’s classical simulated annealer ( ), and Fujitsu’s digital annealer V3 (DA) using both (a–f) QUBO and (g–l) Ising model formulations for the 4-bus test system. The reference bus
), and Fujitsu’s digital annealer V3 (DA) using both (a–f) QUBO and (g–l) Ising model formulations for the 4-bus test system. The reference bus 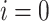 is not shown. The graphs include
is not shown. The graphs include 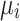 and
and 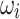 obtained from the Newton-Raphson classical solver (NR).
obtained from the Newton-Raphson classical solver (NR).
Numerical justification of adiabatic quantum power flow
In the combinatorial PF algorithm, we assume that the active and reactive powers are available for all buses 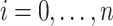 , which is inconsistent with the principles of PF analysis. For example, active and reactive powers at the reference bus are unknown, while the complex voltage
, which is inconsistent with the principles of PF analysis. For example, active and reactive powers at the reference bus are unknown, while the complex voltage 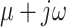 is known. To address this discrepancy, adjustments are necessary to Algorithm 1. Algorithm 2 represents the pseudo-code of the modified algorithm that aligns with the principles of PF analysis. Specifically, for a power system with one reference bus, the active and reactive power values for the reference bus
is known. To address this discrepancy, adjustments are necessary to Algorithm 1. Algorithm 2 represents the pseudo-code of the modified algorithm that aligns with the principles of PF analysis. Specifically, for a power system with one reference bus, the active and reactive power values for the reference bus 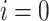 are excluded from the respective vectors
are excluded from the respective vectors 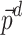 and
and 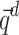 , resulting in
, resulting in 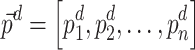 and
and 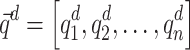 (lines 1 and 2). In addition,
(lines 1 and 2). In addition, 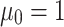 and
and 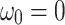 are assigned to the reference bus
are assigned to the reference bus 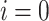 before the loop starts, ensuring they are not updated during the loop (lines 4 and 5). The remaining of the algorithm is the same as Algorithm 1.
before the loop starts, ensuring they are not updated during the loop (lines 4 and 5). The remaining of the algorithm is the same as Algorithm 1.
Algorithm 2.
Adiabatic power flow algorithm.
D-Wave’s Advantage™ system (QA) and Fujitsu’s digital annealer V3 (DA) are used to minimize the QUBO/Ising model developed based on the Hamiltonian at each iteration until convergence is reached. Experiments are performed for the 4-bus test system with known 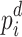 and
and 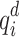 and unknown
and unknown 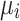 and
and 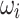 for all load buses
for all load buses 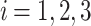 , while
, while 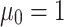 and
and 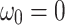 are known and
are known and 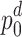 and
and 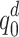 are unknown for the reference bus
are unknown for the reference bus 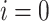 . Note that for the AQPF algorithm, the number of binary and spin variables is the same as in the combinatorial PF algorithm. The effectiveness of the AQPF algorithm is justified by comparing
. Note that for the AQPF algorithm, the number of binary and spin variables is the same as in the combinatorial PF algorithm. The effectiveness of the AQPF algorithm is justified by comparing 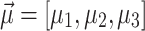 and
and 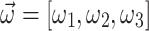 obtained by QA and DA with those obtained from NR for the 4-bus test system. The results are detailed in Table 2. It is observed that the Ising model formulation with QA achieves results closest to those derived from NR, followed by the QUBO formulation with QA, for
obtained by QA and DA with those obtained from NR for the 4-bus test system. The results are detailed in Table 2. It is observed that the Ising model formulation with QA achieves results closest to those derived from NR, followed by the QUBO formulation with QA, for 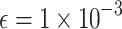 . A systematic comparison between the performance of the AQPF algorithm and NR over iterations is provided in the “Supplementary information”.
. A systematic comparison between the performance of the AQPF algorithm and NR over iterations is provided in the “Supplementary information”.
Table 2.
Performance comparison of D-Wave’s Advantage™ system (QA) and Fujitsu’s digital annealer V3 (DA) with the Newton-Raphson classical solver (NR).
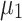 |
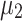 |
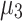 |
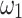 |
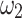 |
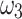 |
|
|---|---|---|---|---|---|---|
| NR | 0.902 | 0.916 | 0.890 | − 0.092 | − 0.080 | − 0.104 |
| QA (QUBO) | 0.904 | 0.917 | 0.892 | − 0.092 | − 0.079 | − 0.104 |
| DA (QUBO) | 0.904 | 0.918 | 0.895 | − 0.091 | − 0.079 | − 0.103 |
| QA (Ising) | 0.902 | 0.916 | 0.891 | − 0.092 | − 0.081 | − 0.104 |
| DA (Ising) | 0.903 | 0.917 | 0.891 | − 0.094 | − 0.080 | − 0.107 |
The AQPF algorithm is implemented using the QUBO and Ising model formulations for the 4-bus test system. The reference bus 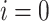 with known values of
with known values of 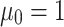 and
and 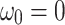 is not shown.
is not shown.
Numerical justification of scalability of AQPF
The scalability of the AQPF algorithm, defined as the ability to handle a larger number of binary/spin variables, is justified through experiments conducted on a larger power system, specifically a 9-bus test system, using the same five annealers as before. In this implementation, PyQUBO generates 666 binary and 1485 spin variables for the QUBO and Ising model, respectively, while DADK generates 249 binary and 900 spin variables for the QUBO and Ising model, respectively. The threshold value for considering the iteration process converged is set to 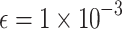 .
.
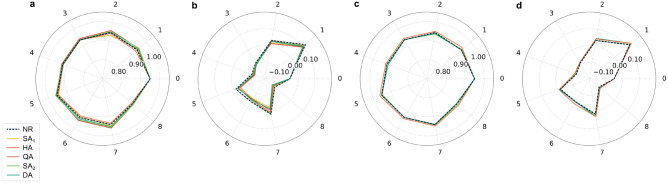
Figure 2 illustrates the vectors 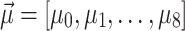 and
and 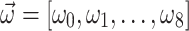 obtained from
obtained from  , HA, QA,
, HA, QA,  , and DA using both the (a and b) QUBO and (c and d) Ising model formulations. Additionally, the graphs include
, and DA using both the (a and b) QUBO and (c and d) Ising model formulations. Additionally, the graphs include 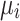 and
and 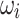 obtained from the Newton-Raphson classical solver (NR). Accordingly, the AQPF algorithm shows scalability, yet using the Ising model with it for the 9-bus test system requires managing more variables than does the use of the QUBO formulation. This presents challenges for embedding in QA due to the partial connectivity of qubits in D-Wave’s Advantage™ system. In addition,
obtained from the Newton-Raphson classical solver (NR). Accordingly, the AQPF algorithm shows scalability, yet using the Ising model with it for the 9-bus test system requires managing more variables than does the use of the QUBO formulation. This presents challenges for embedding in QA due to the partial connectivity of qubits in D-Wave’s Advantage™ system. In addition, 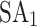 fails to converge for the Ising model formulation. However, HA,
fails to converge for the Ising model formulation. However, HA, 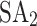 , and DA effectively manage the increased number of spin variables for the 9-bus test system. Note that the computational time per iteration on the quantum hardware, independent of the communication overhead, is substantially less than the microsecond scale. This observation indicates the prospective capability of the AQPF algorithm to address PF challenges, i.e., scalability and handling ill-conditioned cases, in large power systems within a microsecond timeframe, provided that quantum hardware accessibility resembles that of today’s classical hardware. However, realizing this potential is impeded by the constraints inherent to current quantum hardware implementations.
, and DA effectively manage the increased number of spin variables for the 9-bus test system. Note that the computational time per iteration on the quantum hardware, independent of the communication overhead, is substantially less than the microsecond scale. This observation indicates the prospective capability of the AQPF algorithm to address PF challenges, i.e., scalability and handling ill-conditioned cases, in large power systems within a microsecond timeframe, provided that quantum hardware accessibility resembles that of today’s classical hardware. However, realizing this potential is impeded by the constraints inherent to current quantum hardware implementations.
Fig. 2.
Representation of (a and c) 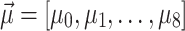 and (b and d)
and (b and d) 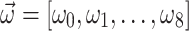 obtained by the AQPF algorithm. Experiments are performed using D-Wave’s classical simulated annealer (
obtained by the AQPF algorithm. Experiments are performed using D-Wave’s classical simulated annealer ( ), D-Wave’s quantum-classical hybrid annealer (HA), D-Wave’s Advantage™ system (QA), Fujitsu’s classical simulated annealer (
), D-Wave’s quantum-classical hybrid annealer (HA), D-Wave’s Advantage™ system (QA), Fujitsu’s classical simulated annealer ( ), and Fujitsu’s digital annealer V3 (DA) using both (a and b) QUBO and (c and d) Ising model formulations for the 9-bus test system. The graphs include
), and Fujitsu’s digital annealer V3 (DA) using both (a and b) QUBO and (c and d) Ising model formulations for the 9-bus test system. The graphs include 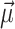 and
and 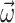 obtained from the Newton-Raphson classical solver (NR).
obtained from the Newton-Raphson classical solver (NR).
Numerical justification of a partitioned AQPF
A heuristic search algorithm is developed and integrated into the AQPF algorithm to provide valid solutions for specific parts of the QUBO/Ising model formulation by excluding one or more buses from the formulations. This is especially important for large power systems as increasing the number of buses exponentially increases the number of binary/spin variables in the QUBO/Ising model formulation. The heuristic search algorithm is employed before using the resulting bitstring 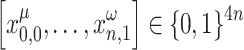 for the QUBO formulation, and
for the QUBO formulation, and 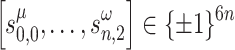 for the Ising model formulation to update the real and imaginary parts of the complex voltages, i.e.,
for the Ising model formulation to update the real and imaginary parts of the complex voltages, i.e., 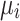 and
and 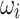 . The proposed heuristic search algorithm randomly flips one or more bits of the bitstring multiple times to prevent convergence to local optima and ensure a heuristic search of the solution space. The partitioned AQPF algorithm, therefore, offers a distinctive advantage by enabling PF analysis in cases where data is incomplete or inaccurate or computational resources are inadequate.
. The proposed heuristic search algorithm randomly flips one or more bits of the bitstring multiple times to prevent convergence to local optima and ensure a heuristic search of the solution space. The partitioned AQPF algorithm, therefore, offers a distinctive advantage by enabling PF analysis in cases where data is incomplete or inaccurate or computational resources are inadequate.
The algorithm is explored and justified using 4-bus and 14-bus test systems. The experiments are conducted using DA. For the 4-bus test system, bus 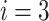 is left out of Hamiltonian (15) based on the QUBO formulation (9)–(10), i.e.,
is left out of Hamiltonian (15) based on the QUBO formulation (9)–(10), i.e.,
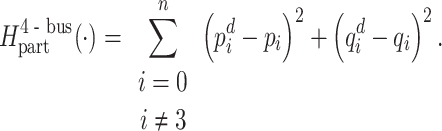 |
16 |
The resulting values with 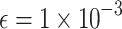 are
are 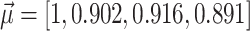 and
and 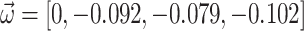 . Note that by excluding bus
. Note that by excluding bus 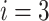 , the number of binary variables decreases by up to 44%, generating only 58 binary variables using DADK. For the 14-bus test system, three buses, namely,
, the number of binary variables decreases by up to 44%, generating only 58 binary variables using DADK. For the 14-bus test system, three buses, namely, 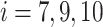 are left out of Hamiltonian (15) leading to
are left out of Hamiltonian (15) leading to
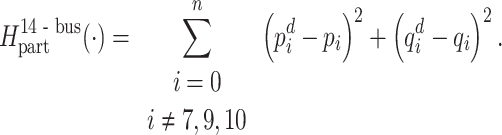 |
17 |
This implementation results in a total of 392 binary variables, reducing their count by 102 (up to 20%) compared to the AQPF algorithm. For the 14-bus test system, the mean difference between 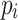 obtained from the partitioned AQPF algorithm and
obtained from the partitioned AQPF algorithm and 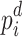 obtained from NR is
obtained from NR is 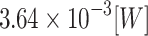 , with a standard deviation of
, with a standard deviation of 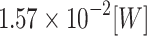 . Similarly, the mean difference between
. Similarly, the mean difference between 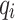 obtained from the partitioned AQPF algorithm and
obtained from the partitioned AQPF algorithm and 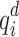 obtained from NR is
obtained from NR is 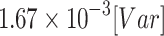 , with a standard deviation of
, with a standard deviation of 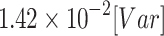 . Details on the results obtained by the 14-bus test system are provided in the “Supplementary information”.
. Details on the results obtained by the 14-bus test system are provided in the “Supplementary information”.
Discussion
This work introduces adiabatic quantum power flow (AQPF) for the first time in the literature, which leverages reliable quantum annealers42–44. Hence, the AQPF algorithm proposed is appropriate for noisy-intermediate-scale quantum (NISQ) and fault-tolerant quantum (FTQ) hardware as the adiabatic quantum computing model offers more fault tolerance than does the gate-based quantum computing model (GQC) in the NISQ era36. Fujitsu’s Digital Annealer, with the capacity to handle up to 100,000 decision variables, can test larger power systems compared to state-of-the-art (gate-based) quantum algorithms for power flow (PF) analysis, which can hardly handle test systems with more than five buses for the time being.
The AQPF algorithm adheres to the principles of the adiabatic quantum computing model (AQC), where the system evolves slowly enough to remain in its ground state throughout the computation. This gradual evolution mirrors how the AQPF algorithm iteratively refines voltage estimates to reduce the PF mismatch and ensure steady convergence to the optimal solution. It is important to note that while AQC offers a promising alternative to GQC for certain applications, it also has limitations, particularly in the context of PF analysis. AQC is inherently more suited for discrete optimization problems, whereas PF analysis is a continuous problem. Additionally, the performance of AQC can be highly dependent on problem encoding and the specific characteristics of the quantum hardware. Therefore, further research is needed to identify scenarios where AQC can provide a practical quantum advantage in PF analysis.
An effective partitioned AQPF algorithm is also proposed, which is capable of reducing the number of required (coherent) qubits for a given test system. This advantage is especially very important for performing computations on D-Wave’s Advantage™ system. The partitioned AQPF algorithm, when used on various power test systems, shows remarkable capability. It can solve a partitioned formulation, which is a significant achievement, and enables PF analysis even when data is incomplete or inaccurate or when computational resources are insufficient. However, this reduction leads to an increased number of iterations needed to reach a defined threshold compared to the standard AQPF algorithm. Nevertheless, in the short term, this trade-off is beneficial as many NISQ architectures can quickly repeat executions45.
The proposed AQPF algorithm is a valuable contribution to the literature and holds promise as a pivotal bridge toward harnessing adiabatic quantum capabilities for enhancing PF analysis. It is also noteworthy that the (partitioned) AQPF algorithm can link up with a classical Newton-Raphson (NR) solver. This combination can be applied with a large defined threshold to serve as a warm start for managing ill-conditioned cases. There are several questions that persist in the study of AQPF. These include broadening the scope of the algorithm to incorporate PV buses, devising a systematic approach for independently updating complex voltages for each bus in every iteration, exploring efficient order reduction techniques specifically developed for PF analysis, and eventually implementing the algorithm in real-world power systems.
Methods
Quantum annealing
(QA) is one of the two paradigms encountered in quantum computing. While gate-based quantum computing follows the principles of digital computing, that is, the data stored in the quantum registers is nuancedly controlled by applying a sequence of gates — the quantum program —, quantum annealing can be seen as an analog computing approach tailored toward solving unconstrained optimization problems given in Ising model formulation
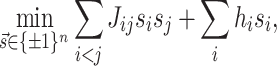 |
18 |
with interaction terms 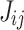 and external magnetic field terms
and external magnetic field terms 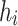 . Starting from a superposition of all possible states, the system evolves following the time-dependent Schrödinger equation into a state of minimal energy—the ground state of the Hamiltonian. The results reported in this paper have been obtained on D-Wave’s Advantage™ system which provides more than 5000 qubits and 35,000 couplers between them responsible for imprinting the problem Hamiltonian. Simply said, a positive weight,
. Starting from a superposition of all possible states, the system evolves following the time-dependent Schrödinger equation into a state of minimal energy—the ground state of the Hamiltonian. The results reported in this paper have been obtained on D-Wave’s Advantage™ system which provides more than 5000 qubits and 35,000 couplers between them responsible for imprinting the problem Hamiltonian. Simply said, a positive weight, 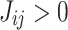 , stimulates the opposite orientation of the spin qubits
, stimulates the opposite orientation of the spin qubits 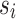 and
and 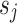 , whereas a negative weight,
, whereas a negative weight, 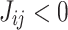 , stimulates
, stimulates 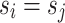 .
.
The main challenges in practical QA are as follows: (i) since physical qubits are not all-to-all connected the graph of the problem Hamiltonian needs to be ‘embedded’ into the hardware graph, which, in general, is an NP-hard problem; (ii) the number of couplers per qubit is limited (degree 15 for the Advantage™ system) so that a qubit, say, 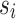 with a lot of non-zero
with a lot of non-zero 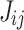 s needs to be expanded into a chain of qubits that are forced to attain the same value via sufficiently larger coupler values; and (iii) the value range of the hardware is limited meaning that J and h are rescaled to
s needs to be expanded into a chain of qubits that are forced to attain the same value via sufficiently larger coupler values; and (iii) the value range of the hardware is limited meaning that J and h are rescaled to 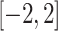 thereby possibly suppressing values that are small in magnitude. While (iii) leads to inaccurate results, (i) and (ii) are a severe problem for scalability since larger problem instances can no longer be embedded and, hence, cannot be solved with QA, cf. Fig. 2.
thereby possibly suppressing values that are small in magnitude. While (iii) leads to inaccurate results, (i) and (ii) are a severe problem for scalability since larger problem instances can no longer be embedded and, hence, cannot be solved with QA, cf. Fig. 2.
Digital annealing
(DA) mimics the annealing process on application-specific CMOS hardware that solves many Markov-Chain Monte-Carlo instances in parallel. Fujitsu’s DA offers up to 100000 qubits organized in units of 8,192 fully-connected qubits and 64-bit precision. In contrast to D-Wave’s QA, Fujitsu’s DA accepts problems in QUBO form, which can be obtained from Eq. (18) by setting 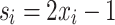 and converting J and h into a symmetric matrix Q. For the problem sizes studied in this paper, a single unit of 8192 qubits suffices, so that embedding is not a problem.
and converting J and h into a symmetric matrix Q. For the problem sizes studied in this paper, a single unit of 8192 qubits suffices, so that embedding is not a problem.
Reduction of higher-order terms
is necessary to convert the fourth-order polynomial of the Hamiltonian (15) into a quadratic polynomial that can be directly solved on D-Wave’s QA and Fujitsu’s DA. A possible approach is to introduce auxiliary variables of the form 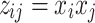 and replace triplet interactions by
and replace triplet interactions by
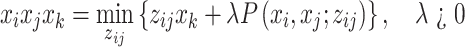 |
19 |
with the penalty term P defined as follows
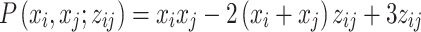 |
20 |
Likewise, expressions with four binary variables can be replaced by
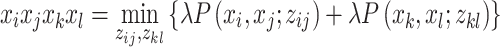 |
21 |
A comprehensive overview of so-called quadratization techniques is given in46.
Heuristic search
Algorithm 3 presents the heuristic search approach adopted in this work to avoid getting stuck in local minima and enable a partitioned AQPF algorithm.
Algorithm 3.
Heuristic search approach.
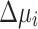 and
and 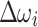 update.
update. 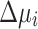 and
and 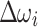 are updated as a function of the number of iterations. In the beginning, i.e.,
are updated as a function of the number of iterations. In the beginning, i.e., 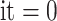 , the increment/decrement is large, i.e.,
, the increment/decrement is large, i.e., 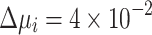 and
and 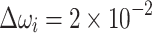 , and as the number of iterations increases, it becomes increasingly smaller to refine the values, e.g.,
, and as the number of iterations increases, it becomes increasingly smaller to refine the values, e.g., 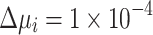 and
and 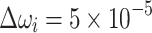 for
for 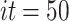 . In this work, the same
. In this work, the same 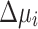 and
and 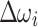 are used for all the buses i.
are used for all the buses i.
Supplementary Information
Acknowledgements
This work is part of the DATALESs project, with project number 482.20.602, jointly financed by the Netherlands Organization for Scientific Research (NWO) and the National Natural Science Foundation of China (NSFC). This work used the Dutch national e-infrastructure with the support of the SURF Cooperative using grant number EINF-6569. The authors gratefully acknowledge the Jülich Supercomputing Centre (https://www.fzjuelich.de/ias/jsc) for funding this project by providing computing time on the D-Wave Advantage™ System JUPSI through the Jülich UNified Infrastructure for Quantum computing (JUNIQ). The research received support from the Center of Excellence RAISE, which receives funding from the European Union’s Horizon 2020 - Research and Innovation Framework Programme H2020-INFRAEDI-2019-1 under grant agreement no. 951733. We would furthermore like to thank Fujitsu Technology Solutions for providing access to the Fujitsu Digital Annealer V3 and, in particular, to Markus Kirsch for his support and custom extensions of the DADK python package.
Author contributions
This work was initiated in discussions with all the authors. Z.K. and M.M. conceived the experiments, analyzed the results, and contributed to writing the manuscript. Z.K. developed the code, conducted the experiments, and created the display items. Z.K., M.M., and P.P.V. reviewed the manuscript.
Data availability
The data that support the plots within this article and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code for this article is available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-73512-7.
References
- 1.Saadat, H. Power System Analysis (McGraw Hill, 1999). [Google Scholar]
- 2.Arrillaga, J. & Smith, B. AC-DC Power System Analysis (Institution of Electrical Engineers, 1998). [Google Scholar]
- 3.Schavemaker, P. & van der Sluis, L. Electrical Power System Essentials 2nd edn. (Wiley, 2017). [Google Scholar]
- 4.Bienstock, D. & Verma, A. Strong NP-hardness of AC power flows feasibility. Oper. Res. Lett.47, 494–501. 10.1016/j.orl.2019.08.009 (2019). [Google Scholar]
- 5.Al-Jaafreh, M. A. & Mokryani, G. Planning and operation of LV distribution networks: A comprehensive review. IET Energy Syst. Integr.1, 133–146. 10.1049/iet-esi.2019.0013 (2019). [Google Scholar]
- 6.Mokryani, G., Majumdar, A. & Pal, B. C. Probabilistic method for the operation of three-phase unbalanced active distribution networks. IET Renew. Power Gener.10, 944–954. 10.1049/iet-rpg.2015.0334 (2016). [Google Scholar]
- 7.Sexauer, J., Javanbakht, P. & Mohagheghi, S. Phasor measurement units for the distribution grid: Necessity and benefits. In 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT) 1–6 10.1109/ISGT.2013.6497828 (IEEE, 2013).
- 8.Guttromson, R. Modeling distributed energy resource dynamics on the transmission system. IEEE Trans. Power Syst.17, 1148–1153. 10.1109/TPWRS.2002.804957 (2002). [Google Scholar]
- 9.Hu, X., Hu, H., Verma, S. & Zhang, Z.-L. Physics-guided deep neural networks for power flow analysis. IEEE Trans. Power Syst.36, 2082–2092. 10.1109/TPWRS.2020.3029557 (2021). [Google Scholar]
- 10.Sharma, N. et al. Major blackouts of the decade: Underlying causes, recommendations and arising challenges. In 2021 9th IEEE International Conference on Power Systems (ICPS) 1–6 10.1109/ICPS52420.2021.9670166 (IEEE, 2021).
- 11.Giraldo, J. S., Montoya, O. D., Vergara, P. P. & Milano, F. A fixed-point current injection power flow for electric distribution systems using Laurent series. Electr. Power Syst. Res.211, 108326. 10.1016/j.epsr.2022.108326 (2022). [Google Scholar]
- 12.Lopez, J. C., Vergara, P. P., Lyra, C., Rider, M. J. & da Silva, L. C. P. Optimal operation of radial distribution systems using extended dynamic programming. IEEE Trans. Power Syst.33, 1352–1363. 10.1109/TPWRS.2017.2722399 (2018). [Google Scholar]
- 13.Gonçalves, R. R., Alves, R. P., Franco, J. F. & Rider, M. J. Operation planning of electrical distribution systems using a mixed integer linear model. J. Control Autom. Electr. Syst.24, 668–679. 10.1007/s40313-013-0055-9 (2013). [Google Scholar]
- 14.Dai, X., Cai, Y., Jiang, Y. & Hagenmeyer, V. Rapid scalable distributed power flow with open-source implementation. IFAC-PapersOnLine55, 145–150. 10.1016/j.ifacol.2022.07.250 (2022). [Google Scholar]
- 15.Idema, R., Lahaye, D. J. P., Vuik, C. & van der Sluis, L. Scalable Newton–Krylov solver for very large power flow problems. IEEE Trans. Power Syst.27, 390–396. 10.1109/TPWRS.2011.2165860 (2012). [Google Scholar]
- 16.Zeng, L., Alawneh, S. G. & Arefifar, S. A. GPU-based sparse power flow studies with modified newton’s method. IEEE Access9, 153226–153239. 10.1109/ACCESS.2021.3127393 (2021). [Google Scholar]
- 17.Tostado-Véliz, M., Kamel, S. & Jurado, F. Power flow solution of Ill-conditioned systems using current injection formulation: Analysis and a novel method. Int. J. Electr. Power Energy Syst.127, 106669. 10.1016/j.ijepes.2020.106669 (2021). [Google Scholar]
- 18.Yang, X. & Zhou, X. Application of asymptotic numerical method with homotopy techniques to power flow problems. Int. J. Electr. Power Energy Syst.57, 375–383. 10.1016/j.ijepes.2013.12.014 (2014). [Google Scholar]
- 19.Sheng, H. & Chiang, H.-D. CDFLOW: A practical tool for tracing stationary behaviors of general distribution networks. IEEE Trans. Power Syst.29, 1365–1371. 10.1109/TPWRS.2013.2289917 (2014). [Google Scholar]
- 20.Tripathy, S., Prasad, G., Malik, O. & Hope, G. Load-flow solutions for Ill-conditioned power systems by a Newton-like method. IEEE Trans. Power Appar. Syst.PAS–101, 3648–3657. 10.1109/TPAS.1982.317050 (1982). [Google Scholar]
- 21.Tostado-Veliz, M. et al. Mann-iteration process for power flow calculation of large-scale Ill-conditioned systems: Theoretical analysis and numerical results. IEEE Access9, 132255–132266. 10.1109/ACCESS.2021.3114969 (2021). [Google Scholar]
- 22.Liu, Y., Sun, K. & Dong, J. A dynamized power flow method based on differential transformation. IEEE Access8, 182441–182450. 10.1109/ACCESS.2020.3028060 (2020). [Google Scholar]
- 23.Iwamoto, S. & Tamura, Y. A load flow calculation method for Ill-conditioned power systems. IEEE Trans. Power Appar. Syst.PAS–100, 1736–1743. 10.1109/TPAS.1981.316511 (1981). [Google Scholar]
- 24.Baker, K. Solutions of DC OPF are Never AC Feasible. arXiv (2019).
- 25.Duque, E. M. S. et al. Risk-aware operating regions for PV-rich distribution networks considering irradiance variability. IEEE Trans. Sustain. Energy14, 2092–2108. 10.1109/TSTE.2023.3281890 (2023). [Google Scholar]
- 26.Leipold, H. & Spedalieri, F. M. Quantum annealing with special drivers for circuit fault diagnostics. Sci. Rep.12, 11691. 10.1038/s41598-022-14804-8 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jing, H., Wang, Y. & Li, Y. Data-driven quantum approximate optimization algorithm for power systems. Commun. Eng.2, 12. 10.1038/s44172-023-00061-8 (2023). [Google Scholar]
- 28.Silva, F. F. C., Carvalho, P. M. S. & Ferreira, L. A. F. M. A quantum computing approach for minimum loss problems in electrical distribution networks. Sci. Rep.13, 10777. 10.1038/s41598-023-37293-9 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Golestan, S. et al. Quantum computation in power systems. Energy Rep.9, 584–596. 10.1016/j.egyr.2022.11.185 (2023). [Google Scholar]
- 30.Feng, F., Zhou, Y. & Zhang, P. Quantum power flow. IEEE Trans. Power Syst.36, 3810–3812. 10.1109/TPWRS.2021.3077382 (2021). [Google Scholar]
- 31.Feng, F., Zhou, Y.-F. & Zhang, P. Noise-resilient quantum power flow. iEnergy2, 63–70. 10.23919/IEN.2023.0008 (2023). [Google Scholar]
- 32.Pareek, P., Jayakumar, A., Coffrin, C. & Misra, S. Demystifying quantum power flow: Unveiling the limits of practical quantum advantage. Tech. Rep.
- 33.Kaseb, Z., Möller, M., Balducci, G. T., Palensky, P. & Vergara, P. P. Quantum neural networks for power flow analysis. Electr. Power Syst. Res.235, 110677. 10.1016/j.epsr.2024.110677 (2024). [Google Scholar]
- 34.Halffmann, P., Holzer, P., Plociennik, K. & Trebing, M. A Quantum Computing Approach for the Unit Commitment Problem. 113–120, 10.1007/978-3-031-24907-5_14 (2023).
- 35.Morstyn, T. Annealing-based quantum computing for combinatorial optimal power flow. IEEE Trans. Smart Grid14, 1093–1102. 10.1109/TSG.2022.3200590 (2023). [Google Scholar]
- 36.McGeoch, C. C. Adiabatic Quantum Computation and Quantum Annealing Theory and Practice (Springer, 2014). [Google Scholar]
- 37.Beer, K. et al. Training deep quantum neural networks. Nat. Commun.11, 808. 10.1038/s41467-020-14454-2 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cao, C., Xue, J., Shannon, N. & Joynt, R. Speedup of the quantum adiabatic algorithm using delocalization catalysis. Phys. Rev. Res.3, 013092. 10.1103/PhysRevResearch.3.013092 (2021). [Google Scholar]
- 39.Pelofske, E., Bärtschi, A. & Eidenbenz, S. Short-depth QAOA circuits and quantum annealing on higher-order ising models. npj Quantum Inf.10, 30. 10.1038/s41534-024-00825-w (2024). [Google Scholar]
- 40.Bian, Z. et al. Discrete optimization using quantum annealing on sparse Ising models. Front. Phys.2, 56. 10.3389/fphy.2014.00056 (2014). [Google Scholar]
- 41.De Simone, C. et al. Exact ground states of Ising spin glasses: New experimental results with a branch-and-cut algorithm. J. Stat. Phys.80, 487–496. 10.1007/BF02178370 (1995). [Google Scholar]
- 42.Asaoka, H. & Kudo, K. Nonnegative/Binary matrix factorization for image classification using quantum annealing. Sci. Rep.13, 16527. 10.1038/s41598-023-43729-z (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Date, P., Arthur, D. & Pusey-Nazzaro, L. QUBO formulations for training machine learning models. Sci. Rep.11, 10029. 10.1038/s41598-021-89461-4 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Date, P. & Potok, T. Adiabatic quantum linear regression. Sci. Rep.11, 21905. 10.1038/s41598-021-01445-6 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature574, 505–510. 10.1038/s41586-019-1666-5 (2019). [DOI] [PubMed] [Google Scholar]
- 46.Dattani, N. Quadratization in discrete optimization and quantum mechanics. arXiv (2019).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the plots within this article and other findings of this study are available from the corresponding author upon reasonable request.
The code for this article is available from the corresponding author upon reasonable request.