Direct observation of ion cyclotron damping of turbulence in Earth’s magnetosheath plasma

Abstract

Plasma turbulence plays a key role in space and astrophysical plasma systems, enabling the energy of magnetic fields and plasma flows to be transported to particle kinetic scales at which the turbulence dissipates and heats the plasma. Identifying the physical mechanisms responsible for the dissipation of the turbulent energy is a critical step in developing the predictive capability for the turbulent heating needed by global models. In this work, spacecraft measurements of the electromagnetic fields and ion velocity distributions by the Magnetospheric Multiscale (MMS) mission are used to generate velocity-space signatures that identify ion cyclotron damping in Earth’s turbulent magnetosheath, in agreement with analytical modeling. Furthermore, the rate of ion energization is directly quantified and combined with a previous analysis of the electron energization to identify the dominant channels of turbulent dissipation and determine the partitioning of energy among species in this interval.

Most space plasmas are in turbulent state and turbulence plays an essential role in transferring energy from large to small scales. Here, the authors show direct measurements of ion cyclotron damping in the Earth’s turbulent magnetosheath plasma and the resulting ion and electron energization rates.

Introduction

Turbulence plays an essential role in space and astrophysical plasmas by mediating the transport of the energy in large-scale magnetic fields and plasma flows down to smaller scales, where poorly constrained physical mechanisms damp the turbulent fluctuations and thereby energize the plasma particles, yielding either heating of the plasma species or acceleration of particles¹. Predicting the heating or acceleration of the different plasma species by turbulence, based on the observable turbulence and plasma parameters at large scales, is recognized as a grand challenge problem in heliophysics², critical to ongoing efforts to globally model^3–5 the flow of energy from the Sun through the interplanetary medium to the Earth, other planets, and on to the boundary of the heliosphere with the surrounding interstellar medium⁶. Such predictive models of turbulent plasma heating^7,8 are also critical for the interpretation of remote astronomical observations of emissions from black hole accretion disks, such as the ground-breaking observations by the Event Horizon Telescope of the supermassive black holes at the center of M87⁹ and at Sagittarius A^* in the Milky Way¹⁰, where alternative turbulent heating prescriptions yield drastically different predictions for the emitted radiation¹¹.

Identifying the physical mechanisms governing the dissipation of the turbulence and quantifying the resulting partitioning of energy among the plasma species are two essential steps in achieving the long-term goal of developing a predictive capability for plasma turbulence. Physical mechanisms proposed to govern the dissipation of turbulence in weakly collisional space plasmas include resonant wave-particle interactions (e.g., Landau damping^12,13, transit-time damping¹⁴, cyclotron damping¹⁵), non-resonant wave-particle interactions (e.g., stochastic ion heating^16–18, magnetic pumping¹⁹,"viscous” heating mediated by temperature anisotropy instabilities²⁰), and dissipation in coherent structures (e.g., magnetic reconnection in current sheets^21–24).

Previous studies have used proton and helium temperature anisotropy measurements in the solar wind as a function of the plasma parameters and the differential ion flow to argue indirectly that ion cyclotron damping leads to enhanced perpendicular ion temperatures in the inner heliosphere^25,26, though an alternative analysis suggests that ion stochastic heating may also lead to similar observational signatures¹⁶. Another study used the Flux Angle operation mode on the Solar Probe Cup²⁷ of the Parker Solar Probe (PSP)^28,29 to measure the correlation between fluctuations of the perpendicular electric field and the fluctuations within a narrow range of the proton velocity distribution³⁰, showing evidence of energy transfer between ion cyclotron waves (ICWs) and the protons. More recently, PSP observations in the inner heliosphere at 30 solar radii showed ion velocity distributions elongated anisotropically in the direction perpendicular to the magnetic field, with contours consistent with the expectations for quasilinear diffusion due to a spectrum of parallel ICWs; using the observed spectrum of left-handed fluctuations, an ion cyclotron heating rate was estimated by applying the quasilinear diffusion operator to the measured velocity distribution³¹.

Here we apply the field-particle correlation (FPC) technique^32–35 to spacecraft observations from the Magnetospheric Multiscale (MMS) mission³⁶ to provide direct measurements of ion cyclotron damping in the Earth’s turbulent magnetosheath plasma and to determine the resulting rate of ion energization. By combining perpendicular electric field and ion velocity distribution measurements from the MMS spacecraft, we generate velocity-space signatures that identify ion cyclotron damping of the ICWs observed within the turbulent spectrum. Furthermore, these measurements enable us to compute the rate of work done by the perpendicular electric field on the ions. In combination with a previous analysis of electron Landau damping during the same interval³⁷, we show that we have identified all significant channels of turbulent energy dissipation at small scales, observationally quantifying the partitioning of turbulent energy between ions and electrons.

Results

Event overview and evidence of ion cyclotron waves

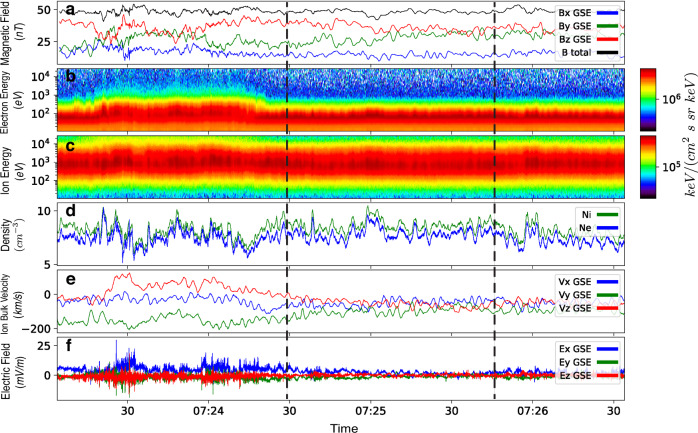
We analyze a 77-second interval of burst-mode data from the MMS1 spacecraft starting at 07:24:28 on 12 January 2016. At this time, the spacecraft probed the Earth’s magnetosheath—the region of shocked solar wind bounded by the bow shock and the magnetopause—at a position near the dawnward side of the sub-solar point close to the magnetopause, where the turbulent cascade is generally found to be well developed³⁸. Previous examination of this interval in Afshari et al. (Interval 02 of that study) identified that electron Landau damping accounted for approximately 7.5% of the dissipation of the estimated turbulent cascade rate³⁷.

Here we use magnetic field data sampled at 128 Hz from the Fluxgate Magnetometers (FGM)³⁹, electric field data sampled at 8192 Hz from the Electric Field Double Probes (EDP)^40,41, and full sky measurements of the ion velocity distribution functions (iVDFs) at a cadence of 150 ms from the Fast Plasma Investigation (FPI) Dual Ion Spectrometers (DIS)⁴². This event was selected due to having relatively constant plasma parameters over the duration of the interval: magnetic field magnitude ∣B₀∣ = 48  ± 5 nT, ion number density n_i = 8.6  ± 0.6 cm⁻³, perpendicular and parallel ion temperatures T_⊥i = 614 ± 30 eV and T_∥i = 253 ± 14 eV yielding an effective isotropic ion temperature T_i = (2T_⊥i + T_∥i)/3 = 494  ± 22 eV, perpendicular and parallel electron temperatures T_⊥e = 36 ± 2 eV and T_∥e = 37 ± 4 eV yielding an effective isotropic electron temperature T_e = (2T_⊥e + T_∥e)/3 = 37  ± 2 eV, perpendicular and parallel ion thermal speed $v_{\perp ti}={\left(2T_{\perp i}/m_i\right)}^{1/2}=$ 343  ± 8 km/s and $v_{\parallel ti}={\left(2T_{\parallel i}/m_i\right)}^{1/2}=$ 220  ± 6 km/s, Alfvén speed $v_A=B_0/{\left({\mu }_0{m}_i{n}_i\right)}^{1/2}=$ 355  ± 21 km/s, parallel ion plasma beta ${\beta }_{\parallel i}=v_{\parallel ti}^2/v_A^2=2{\mu }_0{n}_i{T}_i/B^2=$ 0.383  ± 0.058, linear ion (proton) cyclotron frequency f_ci = q_iB₀/(2πm_i) = 0.73  ± 0.02 Hz, and ion bulk flow speed ∣U_0i∣ = 122  ± 38 km/s. Here the standard deviation quantifies the variation in the parameters; the parallel and perpendicular directions are with respect to the mean magnetic field B₀. The relevant wave forms are shown in Fig. 1, with the 77-second interval denoted by the dashed vertical lines.

Fig. 1. MMS observations of magnetosheath turbulence.

Burst-mode data from MMS1 on 12 January 2016 starting at 07:23:04. a Magnetic field, (b) ion and (c) electron energy spectra, (d) ion and electron densities, (e) ion bulk velocity, and (f) electric field measurements. Dashed vertical lines delimit the 77 s interval analyzed here. Source data are provided as a Source Data file.

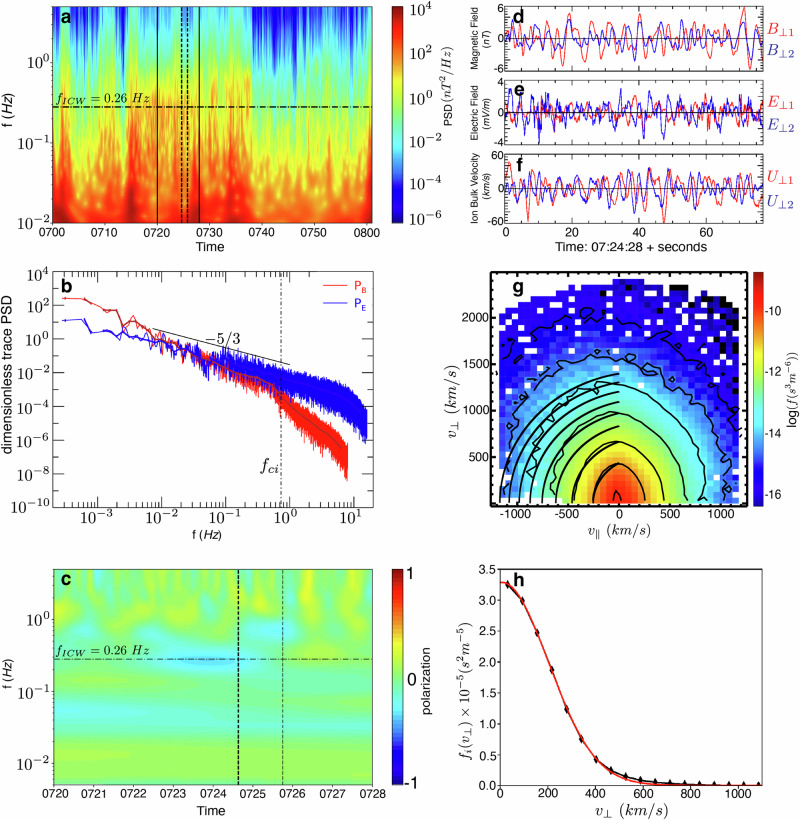
The magnetic field energy spectrum over 07:00–08:00, calculated using a Morlet wavelet transform^43,44 and shown in Fig. 2a, exhibits excess power predominantly in the time range 07:15–07:38, over the frequency range 0.2Hz ≲ f ≲ 0.5 Hz. The dimensionless trace magnetic and electric spectra, shown in Fig. 2b, exhibit a spectral index of approximately—5/3 at f ≲ 0.5 Hz, in agreement with expectations for the turbulent inertial range at k_⊥ ρ_i < 1 from modern theories for anisotropic plasma turbulence^45,46. Analysis of the magnetic field polarization, calculated using the cross-coherence of the Morlet wavelet transform^43,44 and shown in Fig. 2c, shows a significant left-hand polarization at f_ICW ≃ 0.26 Hz (yielding an ICW period T_ICW = 3.85 s), consistent with the properties of ICWs. To highlight these left-hand polarized fluctuations, in Fig. 2d–f we plot the perpendicular components of the magnetic field B_⊥(t), electric field E_⊥(t), and ion bulk flow velocity U_⊥i(t) over the 77 s interval in a magnetic field-aligned coordinate (FAC) system in the reference frame of the mean ion bulk flow velocity (see Methods). We have also high-pass filtered the measurements at f_cut = 0.1 Hz to eliminate the larger amplitude, lower frequency fluctuations. The sense of left-handed polarization is most apparent in the π/2 phase shift between U_⊥1 and U_⊥2, Fig. 2e. Together this analysis supports a significant presence of ICWs in the turbulent fluctuations of this interval. The origin of these ICWs is unknown, and our direct measurements below show that they are damping in this interval; we speculate that the ICWs were generated upstream via the Alfvén/ion cyclotron instablity⁴⁷ driven by the ion temperature anisotropy T_⊥i/T_∥i > 1 (see Supplementary Information (SI) Sec. S2), perhaps due to compression within a quasiperpendicular region of the bow shock, but analysis of the conditions upstream of the bow shock is inconclusive (see SI Sec. S4).

Fig. 2. Evidence of ion cyclotron waves and ion distribution response.

a Magnetic field energy spectrum from MMS1 over 07:00–08:00 on 12 January 2016. Solid vertical lines indicate the 8 minute interval shown in c, dashed vertical lines indicate the 77 s burst-mode interval analyzed in this work, horizontal dashed-dotted line indicates the ion cyclotron wave frequency. b Dimensionless trace PSD of magnetic field (P_B, red) and electric field (P_E, blue) with spectral index of −5/3 (black) shown, vertical dashed-dotted line indicates the ion cyclotron frequency. c Magnetic field polarization from 07:20–07:28, where dashed vertical lines indicate the 77 s burst-mode interval; significant left-hand polarization is observed at frequency f_ICW ≃ 0.26 Hz (horizontal dashed-dotted line). Perpendicular components of (d) the magnetic field, (e) electric field, and (f) ion bulk velocity, all high-pass filtered at f_cut = 0.1 Hz. g Background ion distribution f_0i(v_⊥, v_∥) for the 77 s interval, with contours of constant energy (solid black) in the wave frame centered at v_ph = 0.7v_A. h Reduced perpendicular ion distribution f_0i(v_⊥) (black) with an overplotted Gaussian fit (red). Source data are provided as a Source Data file.

Furthermore, the time-averaged iVDF f_0i(v_∥, v_⊥) is shown in Fig. 2g with circular contours of constant energy (solid black lines) plotted at v_∥ < 0 in the frame of reference of an ICW with a parallel phase velocity of v_ph = 0.7v_A, chosen to best fit the contours in the core of the iVDF. These contours serve as a qualitative guide along which the iVDF appears to be flattened, which is an indication of ICWs pitch-angle scattering the iVDF through cyclotron resonance^31,48. In Fig. 2h, we show the reduced perpendicular iVDF f_0i(v_⊥) (black), where we have integrated over the parallel velocity coordinate v_∥, with a Gaussian (red) plotted for comparison. A lack of flattening in the core at v_⊥ < v_⊥ti compared to the Gaussian argues against the possibility that stochastic ion heating is involved in damping the turbulent fluctuations^49,50.

Velocity-space signatures of ion cyclotron damping

To determine whether ion cyclotron damping plays a role in the damping of the turbulent fluctuations in this interval, we apply the FPC technique^32–35 to determine the velocity-space signature of the ion energization using the perpendicular field-particle correlation $C_{E_{\perp }}\left(\mathbf{v},t;\tau \right)$ and to compute the rate of energy transfer to the ions. The FPC technique uses single-point measurements of the electric field and particle velocity distributions to determine the energy transfer to particles as a function of the particle velocity which can be used to identify the nature of the wave-particle interactions involved (see Methods for the detailed analysis procedure).

In our application of the FPC technique, we first determine the mean magnetic field B₀ and mean ion bulk flow velocity U_0i over the full correlation interval τ = 77 s, then Lorentz transform the fields E(t) and B(t) and iVDF f_i(v, t) to the mean ion bulk flow frame, and rotate these measurements into a magnetic FAC system. Next we compute the instantaneous alternative field-particle correlation $C_{E_j}^{\prime }\left(\mathbf{v},t;\tau =0\right)=q_i{v}_j{E}_j\left(t\right)f_i\left(\mathbf{v},t\right)$ where j indicates the vector component in the magnetic FAC system and the electric field E_j has been high-pass filtered at f_cut = 0.1 Hz (to eliminate oscillatory energy transfer^32–34). These $C_{E_j}^{\prime }\left(\mathbf{v},t;\tau =0\right)$ measurements are summed in Cartesian velocity bins, then the velocity-space derivatives are taken for each field component using (6) and combined to yield the perpendicular field-particle correlation $C_{E_{\perp }}\left(\mathbf{v},t;\tau \right)$ in three-dimensional (3V) velocity space. Time-averages are computed by averaging the $C_{E_{\perp }}\left(\mathbf{v},t;\tau \right)$ values in each velocity bin over the correlation interval τ.

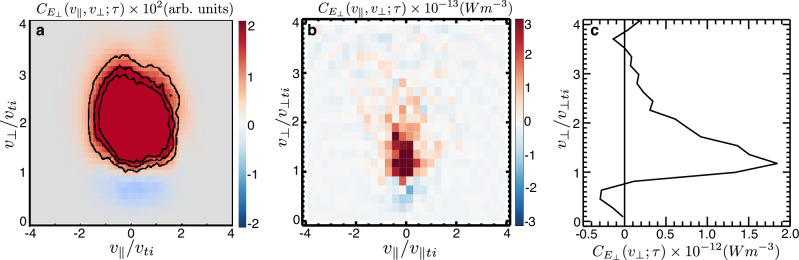
The velocity-space signature of ion cyclotron damping in 2V gyrotropic space (v_∥, v_⊥) was found previously in numerical simulations^35,49,51, with an example reproduced in Fig. 3a. In Fig. 3b, we present the 2V gyrotropic correlation $C_{E_{\perp }}\left(v_{\parallel },v_{\perp };\tau \right)$ from this magnetosheath interval using a correlation interval equal to the full burst-mode interval, τ = 77 s. This observed velocity-space signature shows a loss of phase-space energy density (blue) at v_⊥ /v_⊥ti ≲ 1 and a gain (red) over 1 ≲ v_⊥ /v_⊥ti ≲ 3. This pattern of energization in gyrotropic velocity-space in Fig. 3b agrees qualitatively with that found in Fig. 3a. Integrating over v_∥ yields the curve $C_{E_{\perp }}\left(v_{\perp };\tau \right)$ in Fig. 3c, showing clearly that ions are gaining energy from the perpendicular electric field in the region where $C_{E_{\perp }}\left(v_{\perp };\tau \right)>0$ for v_⊥ /v_⊥ti ≳ 1, consistent with ion cyclotron damping.

Fig. 3. Gyrotropic velocity-space signature of ion cyclotron damping.

The gyrotropic velocity-space signature of ion cyclotron damping $C_{E_{\perp }}\left(v_{\parallel },v_{\perp };\tau \right)$ from (a) a hybrid Vlasov–Maxwell (HVM) simulation of Alfvén-ion cyclotron turbulence³⁵ and from (b) the MMS data for a correlation interval τ = 77 s. c Reduced correlation $C_{E_{\perp }}\left(v_{\perp };\tau \right)$ for same interval of MMS data. Source data are provided as a Source Data file.

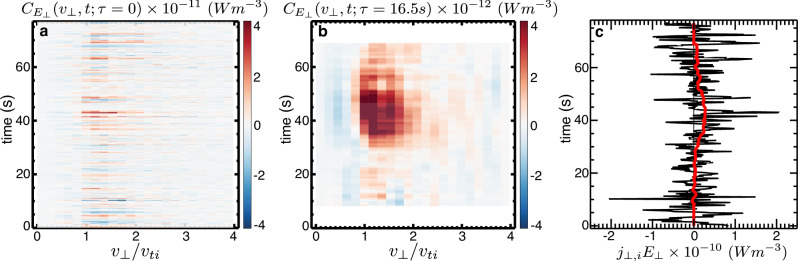
To assess whether the ion cyclotron damping is persistent in time over our correlation interval, in Fig. 4a we present a timestack plot of the instantaneous perpendicular correlation $C_{E_{\perp }}\left(v_{\perp },t;\tau =0\right)$, and in Fig. 4b the timestack plot of the time-averaged correlation $C_{E_{\perp }}\left(v_{\perp },t;\tau =16.5s\right)$ with τ ≈ 4T_ICW (corresponding to 110 iVDFs from the FPI DIS instrument). The instantaneous correlation $C_{E_{\perp }}\left(v_{\perp },t;\tau =0\right)$ includes a large oscillatory component of the energy transfer which obscures the net energization rate of ions. This oscillatory component is removed through time-averaging, and the persistent energization of ions is apparent in the time-averaged correlation $C_{E_{\perp }}\left(v_{\perp },t;\tau =16.5s\right)$, Fig. 4b, in velocity-space over 1 ≲ v_⊥ /v_⊥ti ≲ 3 lasting over the time range 30s ≲ t ≲ 70 s. In Fig. 4c, the correlations are integrated over v_⊥, yielding the instantaneous $\int d{v}_{\perp }{C}_{E_{\perp }}\left(v_{\perp },t;\tau =0\right)={\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }$ (black) and the time-averaged ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }$ (red) rates of ion energization. While the net energization is difficult to assess in the instantaneous j_⊥,i ⋅ E_⊥ (black), the time-averaged ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }$ (red) unequivocally exposes net positive energization rates for the ions. Thus, the ion cyclotron damping is persistent in time and lasts more than 10 times as long as the ICW period. Furthermore, this energization appears to coincide in time with the disappearance of the ICW, as seen in Fig. 2c. Therefore, this FPC analysis presents the velocity-space signature of ion cyclotron damping as evidence of the damping of ICWs measured in the turbulent magnetosheath plasma, directly measuring the work done on the ions by the perpendicular electric field.

Fig. 4. Timestack plot of ion cyclotron damping.

Timestack plots of the perpendicular correlation $C_{E_{\perp }}\left(v_{\perp },t;\tau \right)$ using both (a) instantaneous values (τ = 0) and (b) a correlation interval τ = 16.5 s. c The rate of ion energization by the perpendicular electric field ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }$, computed both instantaneously with τ = 0 (black) and time-averaged over τ = 16.5 s (red). Source data are provided as a Source Data file.

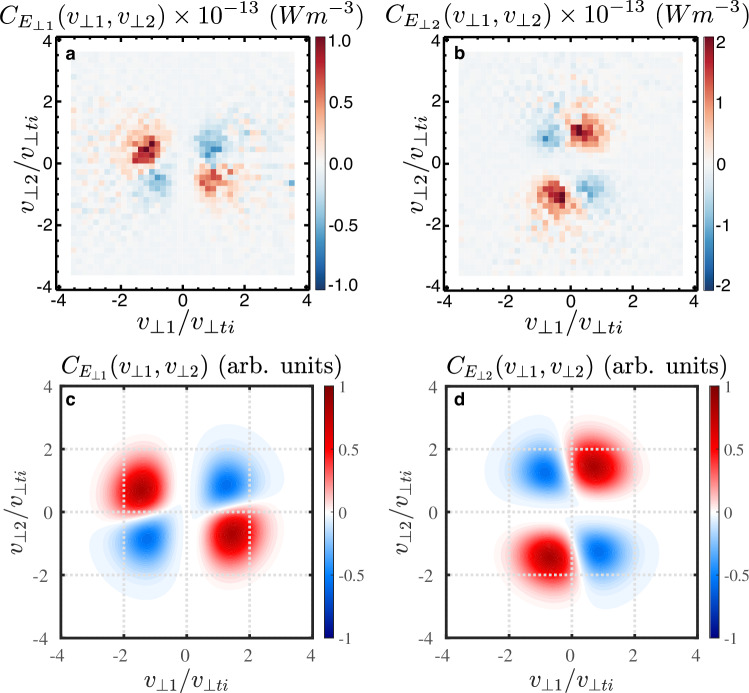
To demonstrate conclusively that ion cyclotron damping is playing a role in the dissipation of the fluctuations in magnetosheath turbulence, we integrate over v_∥ and plot the energization by both components of the perpendicular electric field in perpendicular velocity-space (v_⊥1, v_⊥2), shown in Fig. 5a $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2};\tau \right)$ and Fig. 5b $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2};\tau \right)$ correlated over the full interval τ = 77 s (see Methods for definition of (v_⊥1, v_⊥2)). The quadrupolar velocity-space signatures presented in Fig. 5a, b are characteristic of ion cyclotron damping (as discussed in detail for a fiducial case of ion cyclotron damping in the SI Sec. S1, with results for the plasma conditions of this magnetosheath interval shown in the next section), providing a new means to identify ion cyclotron damping using single-point spacecraft measurements.

Fig. 5. Perpendicular velocity-space signatures of ion cyclotron damping.

From the MMS measurements, the perpendicular velocity-space signatures (a) $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2};\tau \right)$ and (b) $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2};\tau \right)$ over correlation interval τ = 77 s. Analytical model prediction using the eigenfunction solutions of the Vlasov–Maxwell dispersion relation of the perpendicular velocity-space signatures of ion cyclotron damping, (c) $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2}\right)$ and (d) $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2}\right)$ averaged over one wave period, showing a qualitatively similar pattern as the MMS measurements. Source data are provided as a Source Data file.

Analytical model of ion cyclotron damping

To interpret the perpendicular velocity-space signatures $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2}\right)$ and $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2}\right)$ shown in Fig. 5a, b, we use solutions of the linear Vlasov–Maxwell dispersion relation for the Alfvén/ion cyclotron wave to generate a simple analytical prediction for comparison. First, we use the PLUME linear dispersion relation solver⁵² to calculate the linear ICW frequency and damping rate for a fully ionized, hydrogenic plasma with bi-Maxwellian equilibrium velocity distributions with parameters based on the observed MMS interval: β_∥i = 0.383, T_∥i/T_∥e = 6.84, T_⊥i/T_∥i = 2.43, T_⊥e/T_∥e = 0.973, and v_∥ti/c = 7.34 × 10⁻⁴. The ion temperature anisotropy leads to the unstable growth of wave modes with 0.3 ≲ k_∥ρ_⊥i ≲ 1.0 and k_⊥ < k_∥ through the proton cyclotron instability^47,52, where ρ_⊥i = v_⊥ti/Ω_i (see SI Fig. S5). Based on these estimates, we choose to model ICWs as a function of k_∥d_i with k_⊥d_i = 0.016 (note that the ion cyclotron damping rate is dominant and unchanged for all perpendicular wavenumbers k_⊥d_i ≲ 0.5), where the ion inertial length is defined by $d_i=v_A/{\mathrm{\Omega }}_i={\rho }_{\perp i}{\left(T_{\parallel i}/T_{\perp i}\right)}^{1/2}{\beta }_{\parallel i}^{-1/2}$. Since our direct measurements in Fig. 4c unequivocally show damping of the measured ion cyclotron waves rather than unstable growth, we also calculate the eigenfunction for all of the same parameters but with an isotropic ion velocity distribution with T_⊥i/T_∥i = 1.0. There are a couple of possible explanations why we observe wave damping rather than growth in the observed interval (see SI Sec. S2): (i) the clear presence of perpendicular wave motions can lead to an elevated perpendicular “apparent temperature”⁵³ in the measurements of the ion velocity distribution (see SI Fig. S6); and (ii) the fluctuation frequencies in the turbulence are faster than the predicted unstable wave growth rate, meaning that the instability is growing on a time-dependent background, so the linear dispersion relation predictions, which assume static background conditions, may not accurately predict the damping or growth rates of ICWs in this interval.

In Fig. 6a we plot the normalized wave frequency ω/Ω_i vs. k_∥d_i for both cases T_⊥i/T_∥i = 1.0 (dotted) and T_⊥i/T_∥i = 2.43 (dashed) and Fig. 6b the normalized damping or growth rates ∣γ∣/ω. We find damping with γ < 0 at all values of k_∥d_i for the isotropic case (dotted), but unstable growth with γ > 0 (red dashed) over 0.3≤k_∥d_i≤0.9 for the anisotropic ion temperature case. For the isotropic case T_⊥i/T_∥i = 1.0, in Fig. 6c, we decompose the total collisionless damping rate into the contributions from different collisionless damping mechanisms. We find that ion Landau damping (red short-dashed) and ion transit-time damping (red long-dashed) are very weak for this ICW mode, as well as all collisionless damping mechanisms with electrons (blue). Ion cyclotron damping (green dashed) dominates the damping for k_∥d_i > 0.3, with significant damping rates of  −γ/ω > 0.1 at parallel wavenumbers k_∥d_i > 0.6. For the anisotropic (k_⊥ ≫ k_∥) fluctuations of the large-scale turbulent cascade, the ion damping at k_⊥d_i ~ 1 via the Landau resonance for these parameters is expected to be very weak, with  −γ/ω ≲ 4 × 10⁻³ (see SI Sec. S6 and Fig. S9).

Fig. 6. Vlasov–Maxwell frequencies and damping/growth rates.

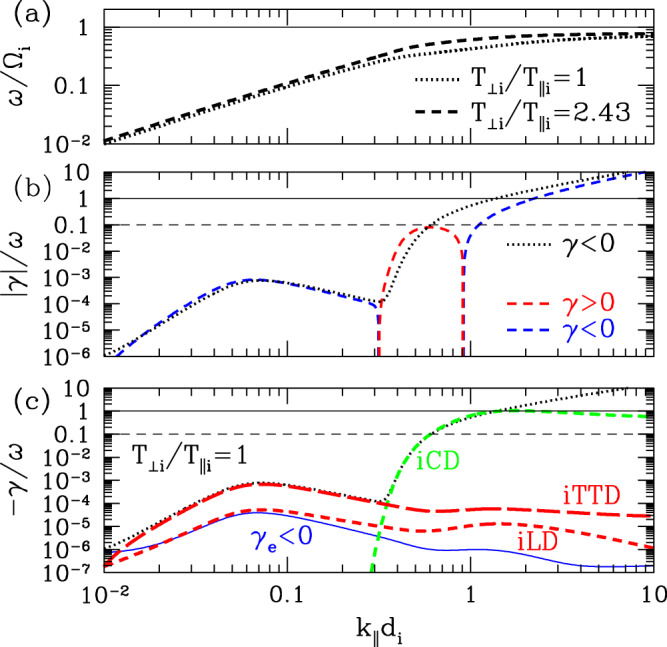
a Normalized wave frequency ω/Ω_i for T_⊥i/T_∥i = 1.0 (dotted) and T_⊥i/T_∥i = 2.43 (dashed) vs. normalized parallel wavenumber k_∥d_i with fixed k_⊥d_i = 0.016. b For T_⊥i/T_∥i = 1.0, damping γ < 0 (black dotted) occurs for all k_∥d_i, but for T_⊥i/T_∥i = 2.43, unstable growth with γ > 0 (red dashed) occurs over 0.3≤k_∥d_i≤0.9, with damping γ < 0 (blue dashed) outside that range. c For T_⊥i/T_∥i = 1.0, decomposition of the total damping rate (black dotted): total electron damping γ_e (blue), ion Landau damping (iLD, red short-dashed), ion transit-time damping (iTTD, red long-dashed), and ion cyclotron damping (iCD, green dashed). Source data are provided as a Source Data file.

Using the measured magnetic field direction and ion bulk flow velocity, we estimate the parallel wavenumber of the ICW to fall within the range 0.5 ≲ k_∥d_i ≲ 1.5 (see SI Sec. S3), which is consistent with the linear dispersion relation solutions in Fig. 6c showing significant ion cyclotron damping rates at k_∥d_i ≳ 0.6. Note that an increasing value of k_∥d_i yields a stronger damping rate due the perpendicular ion bulk flow and electric field fluctuations becoming increasingly more in phase, which leads to a skew in the quadrupolar signatures in the perpendicular plane (v_⊥1, v_⊥2) (see SI Sec. S1 and Fig. S2 for examples). For the measured plasma parameters, but with T_⊥i/T_∥i = 1.0 to yield damping as observed, we choose a value k_∥d_i = 0.8 with k_⊥d_i = 0.016 (to satisfy the condition k_∥/k_⊥ ≫ 1 for waves driven unstable by ion temperature anisotropy, see SI Sec. S2 and Fig. S5) which appears to produce the best agreement with the observations. Choosing a value of E_⊥1/B₀v_A = 0.15 to match the observational amplitude of the ICW, the PLUME eigenfunction calculation yields values for the analytical model (see Methods) of E_⊥2/B₀v_A = 0.15, ϕ = −π/2, U_⊥1/v_A = U_⊥2/v_A = 0.62, and δ₁ = δ₂ = −0.44π. Using these parameters and averaging the velocity-space signatures over one ICW period yields the perpendicular velocity-space signatures in Fig. 5c $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2}\right)$ and Fig. 5d $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2}\right)$.

These analytically predicted quadrupolar perpendicular velocity-space signatures in Fig. 5c and d show excellent qualitative agreement with the observed signatures presented in Fig. 5a and b, including the sight skew of the red regions across v_⊥2 = 0 in $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2}\right)$ and across v_⊥1 = 0 in $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2}\right)$. Note that the quadrupolar appearance is a consequence of the phase relations between the perpendicular electric field and ion bulk velocity components (as illustrated in SI Fig. S3). Furthermore, the sum of these quadrupolar signatures, $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2}\right)+C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2}\right)$, yields energization of ions from v_⊥ < v_⊥ti to v_⊥ > v_⊥ti, consistent with the intuitive expectation of perpendicular energization of the ions by ion cyclotron damping (see SI Fig. S4). It is important to note that, once the plasma parameters and wavevector of the ICW have been specified, the only free parameter left in determining these velocity space signatures is the overall wave amplitude, characterized by the parameter E_⊥1/B₀v_A; the quadrupolar appearance is a consequence of the self-consistently determined phase and amplitude relationships among the perpendicular electric field and ion bulk velocity components. Thus, this analytical prediction demonstrates that these two quadrupolar signatures in the (v_⊥1, v_⊥2) plane represent the perpendicular velocity-space signature of ion cyclotron damping. Along with the signature in gyrotropic velocity-space (v_∥, v_⊥) shown in Fig. 3b, these velocity-space signatures enable us to identify definitively ion cyclotron damping of the turbulent fluctuations in space plasmas using single-point spacecraft measurements.

Discussion

We can use these results to distinguish and identify mechanisms of turbulent dissipation. Direct in situ measurements of the electric field and ion current density in a turbulent space plasma can be used to determine the net rate of work done on the ions by the electric field; in Fig. 4c, we have shown significant perpendicular energization of the ions, j_⊥,i ⋅ E_⊥ > 0. But both ion cyclotron damping¹⁵ and stochastic ion heating^17,49,51,54 are potential mechanisms that can damp the turbulent fluctuations at the scale of the ion Larmor radius and energize ions via the perpendicular component of the electric field. The FPC technique provides a practical means for distinguishing different physical mechanisms of particle energization through the features of their velocity-space signatures, such as electron Landau damping^13,37,55 or ion cyclotron damping³⁵.

Several lines of evidence enable us to rule out a significant contribution by stochastic ion heating in this magnetosheath interval. First, theoretical considerations suggest that stochastic ion heating largely energizes ions in the core of the velocity distribution at v_⊥/v_⊥ti < 1^17,50, flattening the core of the iVDF relative to a Maxwellian; evidence from hybrid numerical simulations supports this hypothesis^49,51. The reduced perpendicular iVDF in Fig. 2h shows no evidence for this predicted impact of stochastic ion heating. Second, the gyrotropic velocity-space signature $C_{E_{\perp }}\left(v_{\parallel },v_{\perp };\tau \right)$ in Fig. 3b instead shows ion energization over the range 1 ≲ v_⊥/v_⊥ti ≲ 3, inconsistent with the expectation for stochastic ion heating but consistent with the expectation for ion cyclotron damping from numerical simulations, as shown in Fig. 3a³⁵. Finally, the predictions for the stochastic ion heating rate (see next section) are also much smaller than the ion energization rate measured in the interval presented here.

A key result of this study is the observational determination of the velocity-space signature of ion cyclotron damping with these distinguishing features: (i) in the gyrotropic velocity-space signature $C_{E_{\perp }}\left(v_{\parallel },v_{\perp };\tau \right)$ in Fig. 3b, a pattern showing the loss of phase-space energy density at v_⊥/v_ti ≲ 1 (blue) and gain at 1 ≲ v_⊥/v_ti ≲ 3 (red); and (ii) in the perpendicular velocity-space signatures $C_{E_{\perp 1}}\left(v_{\perp 1},v_{\perp 2};\tau \right)$ and $C_{E_{\perp 2}}\left(v_{\perp 1},v_{\perp 2};\tau \right)$ in Fig. 5a,b, the appearance of quadrupolar signatures showing ion energization in opposite quadrants for E_⊥1 and E_⊥2, in agreement with analytical predictions for ion cyclotron damping of ICWs using a Vlasov–Maxwell linear dispersion relation solver, as shown in Fig. 5c,d. These velocity-space signatures uniquely identify that ion cyclotron damping is acting to dissipate the fluctuations in the turbulent magnetosheath plasma during this MMS observation, establishing a critical foundation for distinguishing different physical mechanisms of ion energization. The timestack plot $C_{E_{\perp }}\left(v_{\perp },t;\tau \right)$ in Fig. 4b, averaged over a correlation interval τ ≈ 4T_ICW, shows clearly that there is persistent perpendicular energization of the ions over an extended duration, lasting approximately ten times the measured ICW period of T_ICW = 3.85 s. Together, these lines of evidence constitute the first measurement of ion cyclotron damping in a turbulent space plasma through a direct determination of the work done by the perpendicular electric field on the ions.

With the ability to identify different mechanisms of particle energization, we are able to quantify the different channels of turbulent energy dissipation. In order to develop predictive models of plasma turbulent heating and the resulting partitioning of energy among the plasma species, a critical first step is to identify the different mechanisms of energization responsible for damping the turbulence as a function of the plasma and turbulence parameters. Applying the FPC technique to spacecraft observations provides a viable means to achieve the identification of all physical mechanisms that contribute to damping the turbulence and to compute the resulting particle energization rates by species. Here we propose a working definition of the turbulence as all of the physical mechanisms that serve to mediate the conversion of the energy of large-scale plasma flows and electromagnetic fields into heat of the plasma species, including both the local energy transfer by the turbulent cascade and any nonlocal energy transfer via kinetic instabilities. We adopt this definition because, in a practical sense, it is not generally possible to separate observationally whether the measured turbulent fluctuations were driven by local or nonlocal energy transfer. Our estimate of the cascade rate ϵ is based on the measured turbulent amplitudes that includes fluctuations from both sources, so the observed dissipation rate may be compared to this turbulent cascade rate.

In Afshari et al., twenty MMS burst-mode intervals of magnetosheath turbulence were analyzed, finding the velocity-space signature of electron Landau damping in nineteen of the twenty intervals³⁷. The electron energization rates due to the parallel component of the electric field were plotted against the estimated turbulent energy cascade rate ϵ (computed using (7), see Methods), as shown in Fig. 7, where the open diamonds correspond to each of these measurements. The blue diamond denotes the electron energization rate due to Landau damping ${⟨j_{\parallel ,e}{E}_{\parallel }⟩}_{\tau }=1.7\times 10^{-12}$ W m⁻³ for Interval 02 in that study, the same interval analyzed here, and the estimated cascade rate for this interval³⁷ is ϵ = 23 × 10⁻¹² W m⁻³. Since the calculation of the turbulent cascade rate—based on a cascade model of critically balanced, anisotropic plasma turbulence^56,57—is simply an order-of-magnitude estimate, any points falling within the diagonal dotted lines (factors of three above or below the predicted ϵ) represent significant dissipation rates of the same order as the turbulent cascade rate. The interval-averaged rate of ion energization by the dissipation of the turbulent fluctuations via ion cyclotron damping computed here yields ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }=9.1\times 10^{-12}$ W m⁻³ (red diamond), and the sum of the electron Landau damping and ion cyclotron damping yields 10.8 × 10⁻¹² W m⁻³ (black diamond), agreeing to order of magnitude with the estimated turbulent cascade rate ϵ.

Fig. 7. The particle energization rate versus the theoretical cascade rate ϵ.

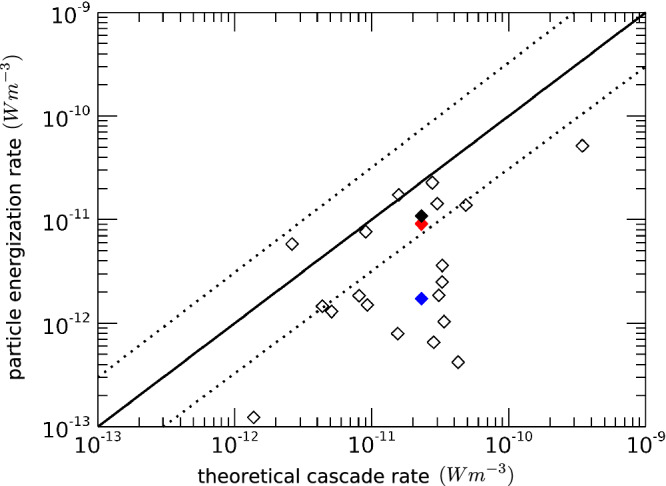
The solid line represents particle energization rates equal to the estimated turbulent cascade rate ϵ, with the dotted lines indicating the range of the order-of-magnitude estimate of ϵ. We plot the parallel electron energization rates ${⟨j_{\parallel ,e}{E}_{\parallel }⟩}_{\tau }$ from twenty intervals in Afshari et al. (open diamonds), highlighting ${⟨j_{\parallel ,e}{E}_{\parallel }⟩}_{\tau }$ from the interval analyzed here (their Interval 02, blue diamond)³⁷. The perpendicular ion energization ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }$ (red diamond) by ion cyclotron damping is plotted along with the sum of ion and electron energization rates (black diamond). Source data are provided as a Source Data file.

For context, let us determine the potential contributions from other proposed mechanisms of turbulent dissipation. Using a procedure analogous to Chen et al.¹³ to analyze the parallel energization of the ions via Landau damping, we obtain a rate ${⟨j_{\parallel ,i}{E}_{\parallel }⟩}_{\tau }~10^{-14}$ W m⁻³, which is below the estimated noise floor for these measurements (see Fig. 8 in the Methods section). This result indicates negligible ion Landau damping, consistent with the linear collisionless damping rate prediction with  −γ/ω ≲ 4 × 10⁻³ for the anisotropic turbulent fluctuations with k_⊥ ≫ k_∥ from the large-scale cascade in this interval (see SI Sec. S6 and Fig. S9). In principle, we could use the FPC technique to estimate the electron cyclotron damping of turbulent fluctuations via E_⊥ using $C_{E_{\perp },e}$, but we do not attempt this determination for two reasons: (i) the Nyquist frequency of the sampling interval for the electron velocity distribution, f_Ny ≃ 16 Hz, is much less than the electron cyclotron frequency, f_ce = 1.34 kHz, so the measurement cadence is much too small to obtain reliable results⁵⁸; and (ii) the observed energy in turbulent fluctuations with f ~ f_ce is about two orders of magnitude lower than the energy at f < 100 Hz, so theoretical arguments suggest that turbulent dissipation by electron cyclotron damping is negligible. We can estimate the rate of stochastic ion heating using

$$Q_{\perp ,stoch}=n_i{m}_i\frac{c_1{\left(\delta v_i\right)}^3}{{\rho }_i}{e}^{-c_2/{ϵ}_i}$$ 1

from Bourouaine and Chandran⁵⁹, where c₁ = 0.75, c₂ = 0.34, δv_i = 30 km/s is the amplitude of the ion velocity fluctuations at the scale of the ion Larmor radius ρ_i = 75 km from Fig. 2f, and ϵ_i = δv_i/v_⊥ti = 0.087. The resulting value Q_⊥,stoch = 8.0 × 10⁻¹⁴W m⁻³ is negligible compared to the measured ion energization rates, providing a strong argument that stochastic ion heating plays no role. It has been recently shown that, in β ≫ 1 plasmas, kinetic temperature instabilities can generate an enhanced effective collisionality that leads to anisotropic “viscous” heating of large-scale turbulent fluctuations²⁰, but that mechanism does not apply to our comparison to the turbulent cascade rate for two reasons: (i) our parallel ion plasma beta β_∥i = 0.383 is too low for this mechanism to be effective; and (ii) we estimate the turbulent cascade rate at f = 0.2 Hz³⁷ at the end of the inertial range, so any energy removed by large-scale viscous heating would not appear in our estimate turbulent cascade rate.

Fig. 8. Ion energization rate as a function of cut-off frequency.

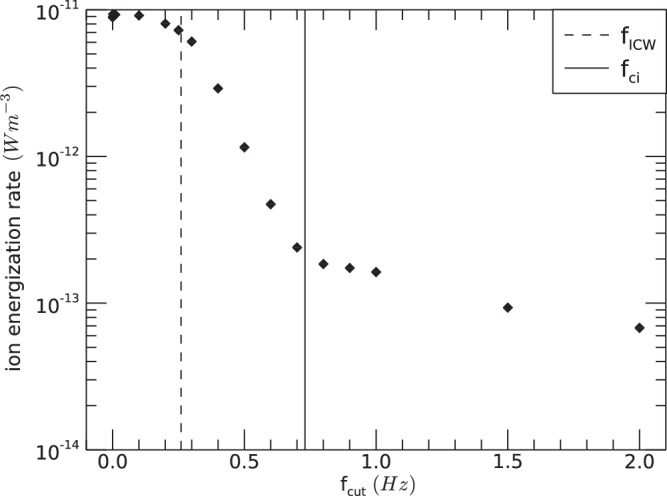
Time-averaged rate of work done on the ions by the perpendicular electric field ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }$ vs. the high-pass cut off frequency f_cut. Source data are provided as a Source Data file.

In summary, application of the FPC technique to this MMS interval produces unique velocity-space signatures, enabling us to identify ion cyclotron damping and electron Landau damping as the dominant physical mechanisms removing energy from the turbulence. In addition to providing the first direct measurement of ion cyclotron damping of turbulence in a space plasma, we have shown that the resulting ion and electron energization rates from these mechanisms sum to yield order-of-magnitude agreement with the predicted turbulent cascade rate. Thus, we have identified the key channels of turbulent dissipation and particle energization, as well as directly measured the partitioning of dissipated turbulent energy between the ions and electrons. Application of the FPC analysis to a larger statistical sample of spacecraft measurements provides a viable means to identify the dominant dissipation mechanisms and to characterize the partitioning of energy among species as a function of the plasma and turbulence parameters, a critical step in the development of a predictive theory of turbulent dissipation and plasma heating in space and astrophysical plasmas.

Methods

Field-particle correlation technique

The field-particle correlation (FPC) technique combines the electromagnetic fields and particle velocity distributions measured at a single point in space to determine a velocity-space signature the can be used to identify the mechanism of particle energization and to determine the rate of collisionless energy transfer between the fields and particles^32–35. The technique has been applied to explore the collisionless damping of plasma waves^1,32,33, the damping of kinetic plasma turbulence in numerical simulations^34,35,55,60 and spacecraft observations^13,37, the acceleration of particles in numerical simulations of collisionless shocks^61,62, the acceleration of auroral electrons by Alfvén waves in laboratory experiments⁶³, and electron heating in collisionless magnetic reconnection⁶⁴.

Multiplying the Vlasov equation by m_sv²/2, we obtain an equation

$$\frac{\partial w_s}{\partial t}=-\mathbf{v}\cdot \nabla w_s-q_s\frac{v^2}{2}\mathbf{E}\cdot \frac{\partial f_s}{\partial \mathbf{v}}-q_s\frac{v^2}{2}\mathbf{v}\times \mathbf{B}\cdot \frac{\partial f_s}{\partial \mathbf{v}}$$ 2

that dictates the rate of change of the 3D-3V phase-space energy density of species s, w_s(r, v, t) ≡ m_sv²f_s(r, v, t)/2, where f_s(r, v, t) is velocity distribution function for species s, q_s and m_s are the charge and mass, r is the spatial position, v is the velocity coordinate, and E(r, t) and B(r, t) are the electric and magnetic fields, respectively. Only the electric field term (middle term on the right-hand side of (2)) leads to a net change in the energy of species s^32–34.

Therefore, in a magnetic field aligned coordinate (FAC) system (see below) with unit vectors $\left({\widehat{\mathbf{e}}}_{\parallel },{\widehat{\mathbf{e}}}_{\perp 1},{\widehat{\mathbf{e}}}_{\perp 2}\right)$, we define the FPC with each component j = 1, 2 of the perpendicular electric field $C_{E_{\perp j},s}$ over a correlation interval τ at a single position r₀ by

$$C_{E_{\perp j},s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)=\frac{1}{\tau }{\int }_{t-\tau /2}^{t+\tau /2}d{t}^{\prime }\frac{-q_s}{2}{v}_{\perp j}^2\frac{\partial f_s\left({\mathbf{r}}_0,\mathbf{v},t^{\prime }\right)}{\partial v_{\perp j}}{E}_{\perp j}\left({\mathbf{r}}_0,t^{\prime }\right),$$ 3

where the total energization by the perpendicular components of the electric field is given by $C_{E_{\perp },s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)=C_{E_{\perp 1},s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)+C_{E_{\perp 2},s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)$.

The integration of $C_{E_{\perp },s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)$ over 3V velocity space yields

$$\int d^3\mathbf{v}{C}_{E_{\perp },s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)={⟨{\mathbf{j}}_{\perp ,s}\left({\mathbf{r}}_0,t\right)\cdot {\mathbf{E}}_{\perp }\left({\mathbf{r}}_0,t\right)⟩}_{\tau },$$ 4

the rate of work done on species s by the perpendicular electric field at position r₀ averaged over the correlation interval τ. Note that the replacement of v² in the electric field term of (2) by $v_{\perp j}^2$ in (3) does not change the net velocity-integrated rate of energy transfer, but does help to highlight the regions in velocity space that govern the net energization of the particles⁶¹.

At position r₀, $C_{E_{\perp },s}\left({\mathbf{r}}_0,\mathbf{v},t;\tau \right)$ is a four-dimensional function in 3V velocity space v and time t, so reduction to fewer dimensions is beneficial for visualization and analysis. Converting to a cylindrical FAC system with $v_{\perp }=\sqrt{v_{\perp 1}^2+v_{\perp 2}^2}$, and integrating over the gyrophase angle about the mean magnetic field B₀, we obtain a gyrotropic velocity-space signature, $C_{E_{\perp },s}\left(v_{\parallel },v_{\perp };\tau \right)$, where we have suppressed spatial position dependence and taken the correlation interval to be the full burst-mode interval τ = 77 s. We can further integrate over v_∥ to obtain $C_{E_{\perp },s}\left(v_{\perp };\tau \right)$. Alternatively, we can instead correlate over sub-intervals τ ≪ 77 s, and integrate over gyrophase angle and v_∥ to obtain a timestack plot, $C_{E_{\perp },s}\left(v_{\perp },t;\tau \right)$, to assess the particle energization by E_⊥ as a function of v_⊥ over time. Finally, we can return to the Cartesian FAC system $\left({\widehat{\mathbf{e}}}_{\parallel },{\widehat{\mathbf{e}}}_{\perp 1},{\widehat{\mathbf{e}}}_{\perp 2}\right)$, correlate over the full interval τ = 77 s, and integrate over v_∥ to obtain the perpendicular velocity-space signature, $C_{E_{\perp },s}\left(v_{\perp 1},v_{\perp 2};\tau \right)$, which is essential in positively identifying ion cyclotron damping in the analysis here.

FPC implementation using spacecraft measurements

For the 77 s burst-mode interval, we time-average the instantaneous magnetic field measurements in GSE coordinates by the FGM instrument³⁹ to determine a mean magnetic field direction B₀ = 〈B(t)〉_τ, where angle brackets 〈…〉_τ denote an average over the full time interval τ = 77 s. Similarly, we compute the mean ion bulk flow velocity by ${\mathbf{U}}_{0i}={⟨{\mathbf{U}}_i\left(t\right)⟩}_{\tau }$. We then define a local FAC system by $\left({\widehat{\mathbf{e}}}_{\parallel },{\widehat{\mathbf{e}}}_{\perp 1},{\widehat{\mathbf{e}}}_{\perp 2}\right)$, where ${\widehat{\mathbf{e}}}_{\parallel }={\mathbf{B}}_0/\mid {\mathbf{B}}_0\mid$, and ${\widehat{\mathbf{e}}}_{\perp 1}=\left({\mathbf{B}}_0\times {\mathbf{U}}_{0i}\right)\times {\mathbf{B}}_0/\mid \left({\mathbf{B}}_0\times {\mathbf{U}}_{0i}\right)\times {\mathbf{B}}_0\mid$, and ${\widehat{\mathbf{e}}}_{\perp 2}={\mathbf{B}}_0\times {\mathbf{U}}_{0i}/\mid {\mathbf{B}}_0\times {\mathbf{U}}_{0i}\mid$.

The electric field is measured at 8192 Hz in GSE coordinates by the EDP instrument suite^40,41,65. The electric field measurements in the spacecraft frame (primed), ${\mathbf{E}}^{\prime }$(t), are Lorentz transformed^66,67 to the mean ion bulk flow frame (unprimed), E(t) $={\mathbf{E}}^{\prime }\left(t\right)+{\mathbf{U}}_{0i}\times \mathbf{B}$(t). The E(t) is down-sampled (by averaging) to 150 ms to match the cadence of FPI Dual Ion Spectrometer (DIS)⁴², and rotated into the FAC system to obtain E_⊥1(t) and E_⊥2(t). The iVDF measurements f_i(v, t) are likewise transformed to the mean ion bulk flow frame and rotated into the FAC system. To remove the large-amplitude signal of oscillatory energy transfer by large-scale, low-frequency electric fields^32–34, we high-pass filter our time series E(t) at f_cut = 0.1 Hz using a 5th-order Butterworth filter.

Next, for each DIS measurement interval, we compute the alternative field-particle correlation^33,68 with τ = 0 for each electric field component E_j(t) in the FAC system, given by

$$C_{E_j}^{\prime }\left(\mathbf{v},t;\tau =0\right)=q_i{v}_j{E}_j\left(t\right)f_i\left(\mathbf{v},t\right),$$ 5

where q_i is the ion charge (assumed to be protons), and v_j is each velocity coordinate in the FAC system. To convert from the alternative FPC $C_{E_j}^{\prime }\left(\mathbf{v},t;\tau =0\right)$ to the standard FPC $C_{E_j}\left(\mathbf{v},t;\tau \right)$, we first create a Cartesian grid of bins in FAC velocity-space (v_∥, v_⊥1, v_⊥2) with bin width Δv/v_ti = 0.2. At each DIS measurement time t, the instantaneous $C_{E_j}^{\prime }\left(\mathbf{v},t;\tau =0\right)$ values falling within each velocity bin are summed. We use finite differencing between velocity bins to compute the derivatives¹³ for each component E_j,

$$C_{E_j}\left(\mathbf{v},t;\tau \right)=-\frac{v_j}{2}\frac{\partial C_{E_j}^{\prime }\left(\mathbf{v},t;\tau \right)}{\partial v_j}+\frac{C_{E_j}^{\prime }\left(\mathbf{v},t;\tau \right)}{2}.$$ 6

To obtain the final perpendicular FPC given by (3), we sum the two perpendicular components $C_{E_{\perp }}\left(\mathbf{v},t;\tau \right)=C_{E_{\perp 1}}\left(\mathbf{v},t;\tau \right)+C_{E_{\perp 2}}\left(\mathbf{v},t;\tau \right)$. Subsequently, to obtain a time-averaged $C_{E_j}\left(\mathbf{v};\tau \right)$, the values of $C_{E_j}\left(\mathbf{v};\tau \right)$ in each velocity bin are time-averaged over any chosen interval of length τ.

As a consistency check that the rate of ion energization by E_⊥ computed here is indeed due to ion cyclotron damping, we adjust the cut-off frequency f_cut of the high-pass filtered electric field and compute the resulting averaged rate of ion energization ${⟨{\mathbf{j}}_{\perp ,i}\cdot {\mathbf{E}}_{\perp }⟩}_{\tau }$ for τ = 77 s, shown in Fig. 8. These results clearly show that nearly all the energy is lost over the frequency range f_ICW ≤ f ≤ f_ci, as expected for ion cyclotron damping. Furthermore, when the electric field is high-pass filtered at f_cut > f_ci in Fig. 8, the ion energization rate levels out at approximately 10⁻¹³ W m⁻³, which we take to be the noise floor of energization rate calculations using the FPC technique.

Turbulent energy cascade model

Using a cascade model for turbulence^56,57, we estimate the turbulent energy cascade rate ϵ in the inertial range given by³⁷

$$ϵ~\frac{\text{Energy Density}}{\text{Cascade Time}}=\frac{n_0{m}_p{U}_{\perp }^2}{1/\left(k_{\perp }{U}_{\perp }\right)}=n_0{m}_p\left(\frac{2\pi f}{v_{\perp ,sc}}\right)\frac{{\left[\delta {\widehat{B}}_{\perp }\left(f\right)\right]}^3}{{\left({\mu }_0{n}_0{m}_p\right)}^{3/2}}$$ 7

where n₀ is the ion number density, m_p is the proton mass, f = 0.2 Hz is the frequency within the inertial range, $\delta {\widehat{B}}_{\perp }\left(f\right)$ is the amplitude of the magnetic field fluctuations computed at a frequency f using an increment with lag t = 5 s. The turbulent energy density includes both kinetic and magnetic contributions, which are assumed equal for Alfvénic turbulence, and the cascade time is calculated within the turbulent inertial range at f ≃ 0.2 Hz.

Analytical model

Here we develop an analytical model that uses the phase and amplitude eigenfunction relations between the perpendicular electric field components E_⊥1 and E_⊥2 and the perpendicular ion bulk velocity components U_⊥1,i and U_⊥2,i to generate a prediction of the velocity-space signature in the (v_⊥1, v_⊥2) plane. First, we define a local magnetic FAC system $\left({\widehat{\mathbf{e}}}_{\parallel },{\widehat{\mathbf{e}}}_{\perp 1},{\widehat{\mathbf{e}}}_{\perp 2}\right)$. The components of the electric field and ion fluid velocity in the $\left({\widehat{\mathbf{e}}}_{\perp 1},{\widehat{\mathbf{e}}}_{\perp 2}\right)$ plane can be specified by

$$E_{\perp 1}=E_1\cos \left(\omega t\right);E_{\perp 2}=E_2\cos \left(\omega t-\varphi \right),$$ 8

$$U_{\perp 1,i}=U_1\cos \left(\omega t-{\delta }_1\right);U_{\perp 2,i}=U_2\cos \left(\omega t-\varphi -{\delta }_2\right).$$ 9

Given the amplitude E₁, the eigenfunction from the Vlasov–Maxwell linear dispersion relation specifies: (i) the wave frequency ω, (ii) the amplitudes of the other components E₂, U₁, and U₂, (iii) ϕ the phase shift between E_⊥1 and E_⊥2, and (iv) the δ_j is the phase shift between E_⊥j and U_⊥j. The rate of ion energization by the perpendicular components of the electric field is given by j_⊥,i ⋅ E_⊥ = q_iU_⊥1,iE_⊥1 + q_iU_⊥2,iE_⊥2, where the right-hand side shows the separate contributions from the two components. To generate predicted velocity-space signatures using the FPC technique, the iVDF is taken to be a shifted Maxwellian with a characteristic perpendicular thermal velocity v_⊥ti and a perpendicular ion bulk velocity given by the self-consistent PLUME⁵² eigenfunction for U_⊥,i.

For this model, a left-hand circularly polarized wave has E₁ = E₂ and ϕ = −π/2. In the low-frequency limit ω ≪ Ω_i, the ion fluid velocity is given by the E × B velocity, such that U_⊥1,i = E_⊥2 /B and U_⊥2,i = −E_⊥1/B, which yields δ₁ = δ₂ = −π/2. In this case, the rate of ion energization integrated over a full wave period T = 2π/ω is zero, because the relative phase shifts δ₁ = δ₂ = −π/2 dictate that the perpendicular ion current is always  −π/2 out of phase with the perpendicular electric field.

As the frequency increases towards the ion cyclotron frequency ω/Ω_i → 1, the self-consistent ion response to the electric field fluctuations is calculated by the PLUME Vlasov–Maxwell linear dispersion relation solver⁵². In the case of ion cyclotron damping, the phase of the jth component of the perpendicular ion bulk velocity U_⊥j,i increases relative to the jth component of the perpendicular electric field E_⊥j into the range −π/2 < δ_j < 0, so that the two fields gain an in-phase component; in this case, there is net positive work j_⊥,i ⋅ E_⊥ done on the ions by the perpendicular electric field, leading to damping of the ion cyclotron wave.

Author contributions

A.S.A. performed the scientific analysis and wrote the initial manuscript text. G.G.H. contributed to the development of the analysis method, interpretation of the results, modeling of the results, and the manuscript text. J.R.S. provided insight and input into the analysis of the data. K.G.K. contributed to the development of the analysis method, interpretation of the results, numerical simulations, and linear wave analysis. D.M. contributed to the data analysis. M.M.M. contributed the wave analysis. S.A.B. provided details for the data processing and wave analysis. C.R.B. and R.H. contributed to the development of the model. D.P.H. contributed to the data analysis. C.A.K. assisted with the interpretation of the results.

Peer review

Peer review information

Nature Communications thanks Alfred Mallet, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data used in this research is available to the public via the MMS Science Data Center (https://lasp.colorado.edu/mms/sdc/public/) or from the corresponding author upon request. Source data are provided with this paper (10.5281/zenodo.13207412).

Code availability

The code used in this research is written in the proprietary Interactive Data Language (IDL) and is available upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-52125-8.