Hippocampal representations of alternative possibilities are flexibly generated to meet cognitive demands

Abstract

The cognitive ability to go beyond the present to consider alternative possibilities, including potential futures and counterfactual pasts, can support adaptive decision making. Complex and changing real-world environments, however, have many possible alternatives. Whether and how the brain can select among them to represent alternatives that meet current cognitive needs remains unknown. We therefore examined neural representations of alternative spatial locations in the rat hippocampus during navigation in a complex patch foraging environment with changing reward probabilities. We found representations of multiple alternatives along paths ahead and behind the animal, including in distant alternative patches. Critically, these representations were modulated in distinct patterns across successive trials: alternative paths were represented proportionate to their evolving relative value and predicted subsequent decisions, whereas distant alternatives were prevalent during value updating. These results demonstrate that the brain modulates the generation of alternative possibilities in patterns that meet changing cognitive needs for adaptive behavior.

Introduction

Animals are continually faced with decisions about what to do and where to go next. In the context of behavioral tasks, a long tradition of animal experiments and behavioral models suggest that the brain can make adaptive decisions by comparing the expected values of available options, which are learned through experience. As an example, in spatial settings, an animal may compare the expected values of different rewarded locations and associated paths. After making a choice, a rewarding outcome would lead to an update that increases the stored value of the rewarded location and the path taken to get there, enabling subsequent adaptive decisions even as outcomes change^1–4.

While the idea of retrieving and updating expected values of possible options seems relatively simple, in real-world situations like navigation, choices often lead to outcomes that are distant in space or time. This poses a challenge: the brain must go beyond current experience to decide among or learn about alternative “non-local” possibilities. For instance, when making a choice among nearby routes, the brain may retrieve values related to their ultimate destinations. Further, in complex structured scenarios, rewards received in one location can imply information about the availability of rewards in other places, as in zero-sum situations or multi-step planning tasks. In such cases, the brain may take advantage of learned structure to make inferences across space, and update not only the value of the current location but also the values of alternative locations and paths^5–8. Additionally, unlike many laboratory tasks, naturalistic scenarios can have many alternatives available at once^9–14. This indicates a need to prioritize¹⁵; when deciding among or updating different possibilities, some judicious mechanism is required to consider the most relevant non-local alternatives to meet current demands.

The neural mechanisms that enable such prioritized computations about relevant non-local possibilities during complex behavior are not understood. Existing data indicate the hippocampus and its representations of space as a starting point. First, the hippocampus is critical for rapid learning and performance of spatial tasks where animals must learn the locations of and routes among rewarded locations^16–23. Second, the hippocampus is well known for spatially tuned “place cells” whose activity typically signals the actual location of the animal²⁴. These cells are often described as the substrate for a cognitive map, or an internal model of the world, that encodes the relationships among both locations and experiences more broadly^25–27. Critically, while place cells are best known for coding an animal’s actual position, they are also capable of expressing non-local representations of alternative locations at a sub-second timescale^8,28–34. Finally, natural behavior often involves experience-guided decision making during active navigation, and hippocampal non-local representations can be regularly expressed during movement^35,36. Thus, during active behavior, generating a non-local representation corresponding to a particular alternative location could serve to retrieve or update information associated with that location, including its value.

Non-local representations have been linked to cognitive processes for both decision making and learning during navigation. These population-level representations are most often associated with the sequential firing of place cells corresponding to a trajectory through locations behind, at, and ahead of the animal’s actual location^{28,37,29,38,39}. In the context of decision making, as animals approach a choice point, these representations can sweep along future paths ahead, which is evocative of a role in retrieving at least immediately upcoming options^{10,35,40–46}. These sequences also engage place cell activity on timescales consistent with synaptic plasticity, suggesting a role in learning^{28,29,47–51}, and potentially updating internal representations based on experience.

Yet, whether or how the brain generates representations of different alternatives as cognitive demands change throughout experience-guided decision making and learning remains unclear. We therefore combined approaches typically used to separately study decision making and reinforcement learning, or experience-guided navigation. We developed a dynamic patch-foraging task where changing reward probabilities across six locations challenged animals to continually update their internal models to make experience-guided choices about where to go for reward. By leveraging a computational model, we estimated internal cognitive variables from animal behavior related to both value-guided decision making and value updating. As these cognitive variables evolved across successive trials of experience, we monitored hippocampal neural activity to identify non-local representations expressed during active navigation. We observed a range of representations of alternatives, corresponding to potential paths not only ahead of, but also behind the animal, including along counterfactuals, and to distant locations in remote foraging patches. We further found that these representations were modulated across successive trials in two distinct patterns, one for representational content and the other for spatial extent, each of which was related to distinctly evolving cognitive variables. These findings demonstrate that mechanisms exist that regulate the expression of distinct non-local possibilities in conjunction with cognitive needs.

Results

Rats make experience-guided decisions in the Spatial Bandit task

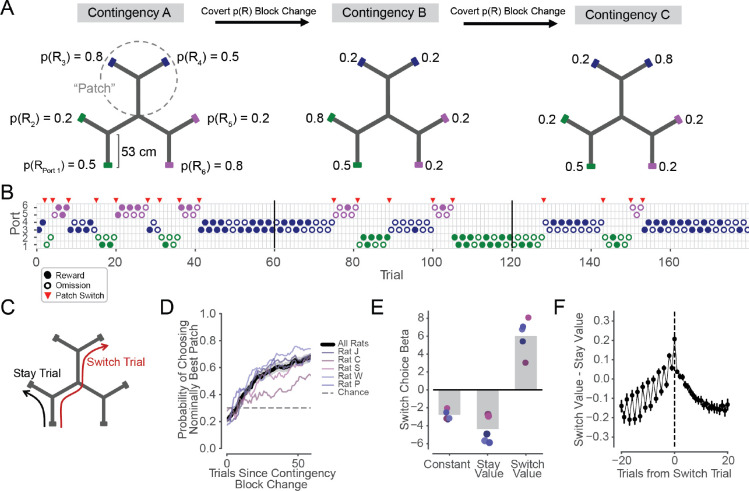
We developed a dynamic foraging task where performance could benefit from representing alternative possibilities, both for deliberating among alternatives and for updating information about alternatives. This “spatial bandit” task combined features of spatial memory and decision-making paradigms (Fig. 1A). First, as in classic spatial memory behaviors, rats (n=5) navigated a maze based on prior experience to reach reward locations. The track was made up of three Y shaped “foraging patches” radiating from the center of the maze, and each patch contained two reward ports at the ends of the linear segments (Fig. 1A, left). The multiple bifurcations and reward locations provided many opportunities for deliberation among alternative options and reward-based updating. Second, as in classic decision-making tasks, we introduced uncertainty by dispensing rewards probabilistically. Each port was assigned a nominal probability of reward, p(R), of 0.2, 0.5, or 0.8 (Fig. 1A), and one of the three patches had a greater average p(R) than the other two. On any visit to a port the rats either did or did not receive reward, determined by the p(R), and consecutive visits to the same port were never rewarded. Thus, animals could only accurately infer each port’s hidden reward probability state through experiences across multiple visits and multiple port locations.

Figure 1. Rats make experience-guided decisions in the Spatial Bandit task.

(A) Track schematic with example reward Contingencies A-C from one behavioral epoch. The track contains three Y-shaped “patches,” each with 2 reward ports located at the ends of linear segments. Probability of reward at each of 6 identical reward ports is indicated as p(R_1–6). Ports are colored by patch for figure visualization only. Uncued reward contingency changes occur every 60 trials.

(B) Example sequence of choices from one behavioral session. Vertical black lines indicate contingency changes shown in A. Circles indicate chosen port on each trial and are colored by patch. Filled circles represent rewarded trials, empty circles represent unrewarded trials. Red triangles indicate a patch Switch.

(C) Schematic of example Stay (black) and Switch (red) trial trajectories.

(D) Proportion of trials in which the animal chose a port in the patch with the highest average nominal reward probabilities, as a function of trial number within the contingency block. Black line and grey shading indicate average across rats and 95% CI on the mean. Distribution on 60th trial of blocks is significantly different from chance level of 1/3 in each animal (n=168, 87, 78, 131, 87 blocks for animals J, C, S, W, and P, respectively, p=2.7e-22, 8.7e-5, 6.4e-10, 2.5e-21, 6.1e-11, binomial test), and distribution on 60th trial is also significantly different from values on first trials of blocks (p=9.6e-20, 3.9e-4, 2.5e-9, 3.2e-18, 1.5e-11, Z test for proportions)

(E) Regression coefficients on model-estimated values of Stay locations and Switch locations for the prediction of Stay or Switch choice on each trial. All individual coefficients are significantly different than zero, indicating that rats rely on reward history from both current “Stay” patch and alternative “Switch” patches to make Stay or Switch choices (for each animal, p_Constant=3.8e-25, 1.6e-111, 5. 6e-98, 1.5e-39, 8.2e-40, p_Stay=5.6e-17, 7.3e-24, 3.8e-47, 1.5e-39, 8.2e-40, p_Switch=1.2e-23, 8.6e-9, 8.9e-30, 4.9e-25, 1.6e-22, from n = 5416, 8572, 9608, 7450, 4732 Stay trials and n = 344, 398, 583, 467, 488 Switch trials). Grey bars indicate averages and coefficient points are colored by subject per legend in D.

(F) Relative value of Switching versus Staying increases across trials leading up to patch Switch choices, peaks on Switch trials, and decreases following patch Switch trials. Switch trial values are distinct from Stay trial values in the 20 trials before (p=4.3e-61, 2.1e-44, 4.5e-134, 6.6e-126, 4.3e-113, Wilcoxon rank sum test) and after (p=8.4e-81, 5.3e-63, 8.5e-162, 4.0e-149, 1.4e-132) Switch trials in each animal. Individual animal data in Fig. S5C.

During run sessions, reward probabilities around the track covertly changed in blocks (as in Fig. 1A,B) every 60 (n=4 animals) or 80 (n=1 animal) trials. Each day of task experience consisted of up to 8 run sessions, separated by rest sessions in a rest box, and each run session consisted of 180 (n=4 animals) or 160 (n=1 animal) trials. A trial was defined as the period between a departure from one port to a departure at another port, and animals individually completed 5760, 8970, 10191, 7917, and 5220 trials, providing a large dataset compatible with behavioral and neural analyses. Importantly, the reward contingency block transitions were uncued and changed which patch was associated with the highest overall nominal probability of reward. These reward probability transitions thereby encouraged experience-based, adaptive decision making.

Animals exhibited choice behavior akin to patch foraging⁵² (Fig. 1B). They began by serially exploring the ports in the three patches, often making repeated choices to alternate between ports within a patch (Stay trials) and occasionally making flexible choices to navigate to an alternative patch (Switch trials) (Fig. 1B,C, Fig. S1A). Animals adapted their choices based on their dynamic reward experiences across reward ports, trials, and contingencies (as in Fig. 1B). As a result, animals generally learned and remained within the patch with the highest nominal reward probabilities by the end of each block (Fig. 1D).

The patterns of these Stay and Switch choices indicated a decision strategy that used reward history information, including reward history related to both the current patch and to distant alternative patches. To understand how reward information related to animals’ choices at a single-trial level, we fit a behavioral learning model to each animal’s sequence of port choices and reward outcomes (see Methods). We estimated weights related to the expected values of the animal’s two potential options on each trial: Staying within the current patch or Switching between patches. Logistic regressions predicting Stay or Switch choices revealed significant effects of not only the Stay value (measured as the value of the upcoming port in the current patch) but also the Switch value (measured as the value of the more valuable unoccupied patch) in each animal (Fig. 1E). The coefficients were negative for Stay values, indicating that animals were less likely to make Switch choices as the value of Staying increased (Fig. 1E). In contrast, the coefficients were positive for Switch values, indicating that animals were more likely to choose to Switch as the value of Switching increased (Fig. 1E). Thus, animals’ behavior depended on previous reward experiences both from nearby Stay locations and more spatially distant Switch locations across the maze (Fig. 1E, Fig. S5A,B).

Since Switch choices were value-guided and punctuated often longer, stable bouts of Stay choices (Fig. 1B,C, Fig. S1A), we anchored further analyses around these self-paced patch changes. Here, a central decision variable is the relative value between these two options on each trial: Switch value - Stay value (Fig. 1F). This relative value was low during trials far from a Switch and on average increased over the course of the Stay trials leading up to a Switch choice. On the Switch trial, relative value was highest, and then decreased again across trials after the Switch (Fig. 1F). Note that these relative values do not incorporate the bias to Stay (or cost to Switch) as illustrated by the negative constants in Fig. 1E. We also note the relative value fluctuations on alternating trials before a Switch, which are consistent with animals tending to Switch after visiting the higher value port within a patch (Fig. 1F). Importantly, the increasing and decreasing relative value pattern around Switches reflects a gradual updating of values over successive trial outcomes. This suggests that animals may similarly access internal estimates of values associated with Switch and Stay options when deciding whether to leave the current patch and, after Switching, whether to remain in the new patch or again navigate elsewhere.

Taken together, these findings provide evidence that animals learn from their changing reward experiences across the maze, and leverage this experience to make value-guided decisions among alternative paths. Furthermore, they suggest that seemingly isolated and behaviorally overt Switch choices occur in the context of gradually changing covert reward expectancies that place evolving cognitive demands on the animal across successive trials.

Representations of alternative paths ahead of the animal

Given these behavioral results, we then asked whether the content of hippocampal representations of alternative paths was also modulated around Switch choices. As previous work has identified non-local representations consistent with possible future locations^35,40–43, we began by examining non-local representations extending ahead of the animal’s actual position that occurred while the animal was in the first segment of each trial. In this period, the animal approached the first choice point, which is associated with the choice to Stay or Switch. We used an established state space decoding algorithm^53,54 (2 cm spatial bins, 2 ms temporal bins, see Methods) to assess the instantaneous hippocampal representation of space^55–57 during navigation (animal speed > 10 cm/s) across all five rats, each implanted with tetrode microdrives targeting the CA1 region of the hippocampus (Fig. S1). We limited our analyses of non-local representations to periods with high confidence that the decoded hippocampal representation was in a non-local track segment, defined as a segment distinct from the one corresponding to the rat’s actual location (Fig. 2A, see Methods).

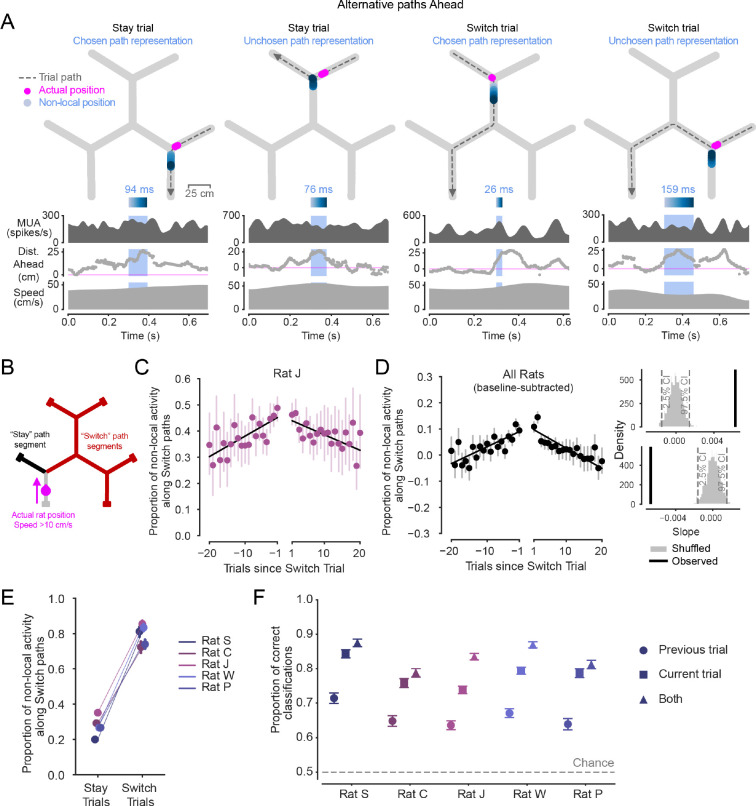
Figure 2. Non-local representations of alternative paths Ahead are enriched across trials before and after patch Switching.

(A) Examples of non-local representations of alternative paths ahead on Stay and Switch trials. As the animal approaches the choice point, the hippocampus can represent the Stay or Switch path ahead. Top: Animal’s actual position (magenta) and decoded position from hippocampal spiking (blue, shaded by time) during the light blue-highlighted period (below) are plotted on the track. Dashed grey line with arrow indicates animal’s path and direction on the current trial. Highlighted non-local duration is labeled above blue time-shaded heatmap. Top-middle: multiunit spike rate from hippocampal tetrodes before, during, and after highlighted non-local representation. Bottom-middle: Distance from actual position to decoded position, with positive values corresponding to in front of the animal’s heading, and negative numbers corresponding to behind the animal’s heading. Note that blue non-local periods are required to have representations in a different track segment from the animal’s actual position. Bottom: Animal speed.

(B) Schematic defining Stay and Switch non-local activity ahead, analyzed in C-F. Non-local activity was analyzed from times in which the animal was running >10 cm/s from the reward port to the first choice point in the trial (magenta) by assessing the per-trial proportion of time in which non-local activity extended along the path ahead consistent with Switching (red) out of all non-local activity times along both the Stay (black) and Switch (red) paths.

(C) Proportion of all non-local activity that represents paths consistent with Switching during the approach of the first choice point across Stay trials preceding and following Switch trials in one rat. Left and right x axes separated to reflect patch change. Error bars are 95% CIs on the mean. Linear regressions show increasing and decreasing proportions across trials before and after patch Switch trials.

(D) Left: Proportion of all non-local activity that represents paths consistent with Switching during the approach of the first choice point across all animals (n=5 rats), normalized per animal by subtracting off the average baseline proportion on Stay trials. Error bars are 95% CIs on the mean. Pre- and post-Switch linear regressions overlaid. Upper right: observed slope of pre-Switch regression (black) is significantly different from 0 (p<0.002) based on 1000 shuffles of the underlying data (grey). Lower right: observed slope of post-Switch regression (black) is significantly different from 0 (p<0.002) based on 1000 shuffles of the underlying data (grey). Both slopes were individually significant in all five animals (Fig. S2A).

(E) Proportion of all non-local activity that represents paths consistent with Switching during the approach of the first choice point in each animal on Stay trials and Switch trials. Error bars are 95% CIs on the mean. The proportion on Switch trials is greater than on Stay trials for all animals (p=2.7e-192, 4.2e-108, 1.0e-100, 2.1e-315, 1.6e-201, Wilcoxon rank sum test, for n=313, 335, 523, 422, 452 Switch trials, and n=3349, 3803, 5600, 5028, 3294 Stay trials).

(F) Cross-validated accuracy of logistic regressions that predicted Stay or Switch choices based on the proportion of all non-local activity that represents paths consistent with Switching during the approach of the first choice point. Neural data from each of three trial types: previous trial (circle marker), current trial (square marker), or both (triangle marker). Error bars are 95% CIs on the proportion. Training data were balanced, so chance level was 0.5. Accuracy of model using previous trial neural data is significantly greater than chance level in all animals (p=3.2e-63, 1.1e-43, 4.0e-133, 9.7e-131, 3.3e-60, Z test for proportions), accuracy from model using current trial neural data is greater than accuracy from model using previous trial neural data (p=2.3e-39, 7.0e-27, 6.0e-33, 2.8e-46, 6.3e-43), and accuracy of model based on both trials is greater than accuracy of current trial model (p=1.1e-4, 1.2e-3, 4.3e-39, 4.9e-26, 5.6e-3).

We observed non-local representations that reflected locations along either of the two paths ahead of the choice point (Fig. 2A). We also verified the expected organization of these non-local representations of paths ahead based on the phase of the hippocampal theta rhythm^{28,29,37,58,59} (Fig. S2C). On each trial, we then classified non-local representations as reflecting paths that, if physically traversed, would either lead the animal to Stay in the patch or to Switch between patches (Fig. 2B). We began by examining the Stay trials leading up to and following Switch choices. Critically, this enabled us to assess the content of non-local representations as the relative value of Stay and Switch paths changed (Fig. 1F), while the behavioral choice to Stay remained constant.

Strikingly, the relative representation of Switch and Stay paths mirrored their evolving relative value. Across trials preceding a patch Switch, non-local representations of Switch paths ahead became increasingly prevalent relative to Stay paths (Fig. 2C,D). All animals exhibited this pattern, showing an approximately 1.3–1.5 fold increase in the likelihood of non-local representations consistent with the unchosen Switch versus the chosen Stay paths over the 20 trials before a Switch choice (Fig. 2C,D, Fig. S2A). This culminated in a ratio approaching equal (0.5) representation of each path ahead on the trial before a Switch trial (Fig. 2C, Fig. S2A). Additionally, on Stay trials after the animal arrived in a different patch following a Switch, non-local representations were again enriched for the unchosen Switch path. Then, the longer the animal chose to Stay, the less the non-local representations reflected the Switch path (Fig. 2C,D, Fig. S2A). These increases and decreases in the proportion of Switch path representations were driven largely by changes in the amount of time spent representing the Switch path, while the level of Stay path representation remained, on average, relatively stable across successive Stay trials (Fig. S3A). We also confirmed that the approximately symmetrical increasing and decreasing pattern around a Switch was not driven by periods when the animal and decoded non-local spatial representation were very close by, as is possible near choice points, by requiring representations to extend at least 10 cm from the animal (Fig. S3C). Additionally, this pattern was not driven only by short Stay bouts, but was also seen when analyses were restricted to long bouts (Fig. S3F).

Notably, the modulation of non-local representations of paths ahead of the animal before and after Switch trials resembles the changes in relative value between the Switch and Stay options (Fig. 1F). That is, trials with a higher relative value of Switching were associated with greater relative representation of Switch paths. This same relationship could also explain differences in non-local representations across Stay and Switch trials. Stay trials were on average associated with approximately 20–30% non-local representation of paths consistent with Switching, whereas the complementary bias was seen on Switch trials, in which 70–80% of the alternative representations were of the Switch path (Fig. 2E).

These findings indicate that the hippocampus continually tunes the retrieval of spatial alternatives in a pattern related to their evolving relative value. In the context of experience-guided decision making, our results are consistent with an across-trial process where internal sampling of alternatives is biased by relative expected value, such that as these estimated values become more similar—and the cognitive demand for distinguishing between them potentially greater—the options are sampled more equally. Recruiting representations of relevant paths based on their viability for making the best choice, in turn, could enable more accurate comparisons of the values⁶⁰.

The possibility that non-local representations are engaged across trials in an internal sampling process led us to ask whether the proportion of non-local representation of the Switch path was predictive of the future choice to Stay or Switch. We reasoned that proportionally more representation of the Switch option on the Stay trial an entire trial in advance of the Switch could provide samples of the relatively high value Switch option (Fig. 1F) that in turn could influence the decision on the next trial. To investigate this at the level of single trials, we used a cross-validated logistic regression to predict whether an animal would choose to Stay or Switch on each trial based on the proportion of non-local representation corresponding to Switch paths as the animal approached the first choice point of each trial (using the same metric as in Figs. 2C–E). Training data were balanced such that chance level was 0.5.

We found evidence that non-local representations could be used in an across-trial decision process. Non-local representations occurring on the previous trial predicted the subsequent trial’s Stay or Switch choice better than chance. This indicates that the increased alternative representation on the Stay trial before a Switch trial was predictive of a future Switch choice an entire trial in advance, even when the immediately upcoming choice on the current trial was still to Stay (Fig. 2F). This choice prediction was even more accurate when considering only the non-local representations that occurred during the approach of the choice point on the current trial (Fig. 2F), which is expected from Fig. 2E. Strikingly, including non-local representations on both the previous trial and the current trial led to an even better prediction of the choice the animal would make on the current trial (Fig. 2F). While Fig. 2C–E indicate a ramping process on average across bouts of Stay trials before patch Switches, this regression result extends the observation of an across-trial modulation to the level of individual choices within bouts.

Representations of alternative paths behind the animal

The idea that representations of alternatives may be flexibly generated to meet decision-making needs across trials, rather than only for the immediate future choice, led us to ask next whether non-local representations of alternatives could be expressed at times when there was no immediately upcoming choice point. Here we focused on periods when the animal was traversing the final track segment of a trial and approaching a reward port. During this period, we found that non-local representations not only corresponded to the path the animal recently traversed, but also the unchosen Stay or Switch path that the animal could have come from or gone to but did not. This is consistent with the representation of counterfactuals (Fig. 3A,B).

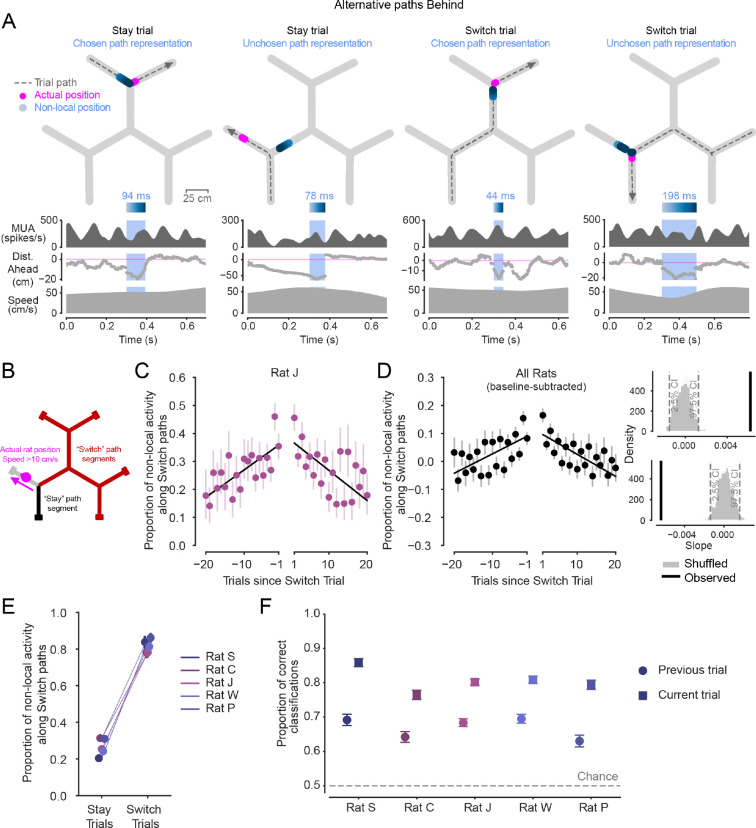
Figure 3. Non-local representations of alternative paths Behind are also enriched across trials before and after patch Switching.

(A) Examples of non-local representations of paths behind in Stay and Switch trials. Top: Animal’s actual position (magenta) and decoded position from hippocampal spiking (blue, shaded by time) during the blue-highlighted period (below) are plotted on the track. Dashed grey line with arrow indicates animal’s path and direction on the current trial. Highlighted non-local duration is labeled above blue time-shaded heatmap. Top-middle: multiunit spike rate from hippocampal tetrodes before, during, and after highlighted non-local representation. Bottom-middle: Distance from actual position to decoded position, with positive values corresponding to in front of the animal’s heading, and negative numbers corresponding to behind the animal’s heading. Bottom: Animal speed. Note that periods outside the blue shaded region where the distance behind is large (e.g., second example) correspond to representations that are in the same track segment as the animal at that time rather than an alternative non-local segment.

(B) Schematic defining Stay and Switch non-local activity behind, analyzed in C-F.

(C) Proportion of all non-local activity that represents paths consistent with Switching during the approach of the reward port across Stay trials preceding and following Switch trials in one rat. Left and right x axes separated to reflect patch change. Error bars are 95% CIs on the mean. Linear regression lines show increasing and decreasing proportions before and after patch Switch trials occur. Individual data for all rats shown in Fig. S2B.

(D) Left: Proportion of all non-local activity that represents paths consistent with Switching during the approach of the reward port across all animals (n=5 rats), normalized per animal by subtracting off the average baseline proportion on Stay trials. Error bars are 95% CIs on the mean. Pre- and post-Switch linear regressions overlaid. Upper right: observed slope of pre-Switch regression (black) is significantly different from 0 (p<0.002) based on 1000 shuffles of the underlying data (grey). Lower right: observed slope of post-Switch regression (black) is significantly different from 0 (p<0.002) based on 1000 shuffles of the underlying data (grey). Both slopes were individually significant in all five animals (Fig. S2B).

(E) Proportion of all non-local activity that represents paths consistent with Switching during the approach of the reward port in each animal on Stay trials and Switch trials. Error bars are 95% CIs on the mean. Switch trial distributions are significantly greater than in Stay trials for all animals (p=5.6e-264, 1.1e-155, 3.2e-300, 1.0e-100, 1.1e-277, Wilcoxon rank sum test, for n=292, 344, 525, 424, 443 Switch trials and n=3079, 3660, 6582, 4924, 3001 Stay trials).

(F) Accuracy of logistic regressions predicting Stay or Switch choices based on proportion of all non-local activity that represents paths consistent with Switching during the approach of the reward port. Neural data from two trial types: previous trial (circle marker), or current trial (square marker). Error bars are 95% CIs on the proportion. Training data were balanced, so chance level was 0.5. Accuracy of model using previous trial neural data is significantly greater than chance in all animals (p=2.4e-58, 7.1e-32, 1.2e-56, 1.3e-40, 3.1e-48, Z test for proportions), and current trial model accuracy is greater than previous trial model accuracy (p=2.4e-58, 7.1e-32, 1.2e-56, 1.3e-40, 3.1e-48 ).

These non-local representations of Stay or Switch paths behind the animal (Fig. 3C,D) showed a very similar pattern of modulation around Switch choices as did non-local representations of paths ahead of the animal (Fig. 2C,D). Even though the representations behind were expressed after the animal had behaviorally indicated a choice on the current trial (Fig. 3B), the relative representation of the counterfactual Switch path ramped up across Stay trials before a Switch and ramped down across the subsequent Stay trials after arriving in a different patch (Fig. 3B–D, Fig. S2B). Again, this increasing and decreasing pattern was roughly symmetric on average around the Switch trial. Furthermore, just as for representations ahead (Fig. 2E), representations behind the animal were biased on average to represent locations along the actual path taken on the current Stay or Switch trial (Fig. 3E). Thus, the non-local representations behind the animal were systematically modulated with the evolving relative values of the options (Fig. 1F).

As with non-local representations extending ahead of the animal, the dynamic generation of representations of alternatives behind the animal was primarily driven by changing levels of Switch path representation (Fig. S3B). This is consistent with an increasing relative representation of the unchosen alternative path leading up to and following a choice to Switch. These results were also consistent when analyses were limited to representations extending at least 10 cm behind the animal (Fig. S3D), as well as in bouts within a patch lasting at least 10 Stay trials (Fig. S3G). Further, these non-local representations behind were concentrated in early phases of the theta rhythm, as expected from previous work^28,29,37,58 (Fig. S2D).

Representations behind the animal could also predict future behavior, consistent with an across-trial decision process. The relative representation of non-local paths behind the animal on the previous trial were predictive of whether the animal chose to Stay or Switch on the entirely subsequent trial (Fig. 3F). These predictions were, as expected (Fig. 3E), not as accurate as those from non-local representations occurring as the animal traversed the final segments of trials, after the animal had already behaviorally expressed a choice to Stay or Switch (Fig. 3F). Nonetheless, previous trial non-local representations predicted subsequent choice well above chance. Thus, the proportion of non-local representation of the Switch path behind the animal on a given trial could predict what the animal would do several seconds later following traversal down the track segment to the reward port and back up the track segment to the choice point.

Together with the results from representations ahead of the animal (Fig. 2), these findings indicate that animals can progressively engage non-local representations associated with a progressively more valuable unchosen alternative (here Switching) both before and after the choice point leading to that option on each trial. These findings provide further support that the hippocampus dynamically samples alternative options, and can do so across successive trials with varying cognitive demands throughout flexible decision making.

Representations of remote alternatives

Beyond retrieving information from an internal model related to an ongoing decision-making process, non-local information could be useful for additional purposes, including relating experiences or making inferences across space. In this task, where reward ports are distributed far across the maze, representing distant locations^{38,43,61–63}, including those in alternative patches, could support relating reward experiences across space or updating values of distant locations based on local reward experiences. We therefore asked whether there was evidence for representations of distant locations across the maze, and whether these representations were specifically generated in relation to patch Switching, as animals learned from dynamic reward experiences.

In addition to non-local representations corresponding to track segments neighboring the animal’s actual location (Fig. 2A,3A; Fig. 4A left), we also observed non-local representations corresponding to alternative patches, closer to other reward ports (Fig. 4A). Alternative patches were represented on 10–20% of trials with any non-local representation (Fig. S4C). To quantify the extent of non-local representations, we then measured the maximal distance in centimeters between the animal’s actual position and the most likely decoded position represented by the hippocampus on each trial, during running at least 10 cm/s (Fig. 4B). Given our previous observation of representations of paths both ahead (Fig. 2) and behind (Fig. 3), we investigated non-local distance both as animals approached the first choice point and after the animal passed the final choice point in each trial (Fig. 4B).

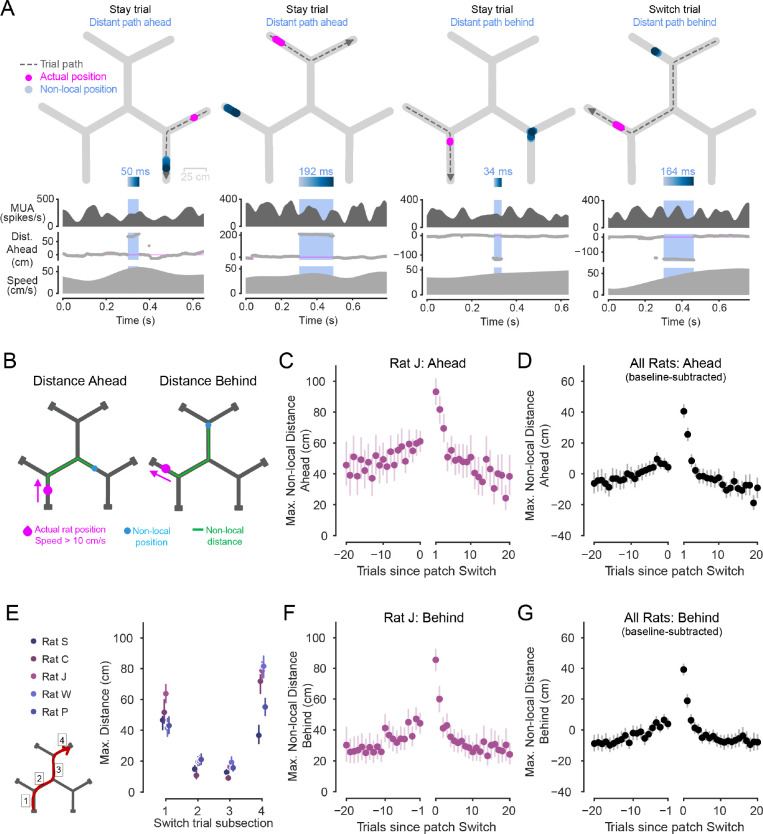
Figure 4. Non-local representations extend further early in patch experience.

(A) Examples of distant non-local representations of paths ahead or behind, in track segments distinct from the animal’s current segment. Top: Animal’s actual position (magenta) and decoded position from hippocampal spiking (blue, shaded by time) during the blue-highlighted period (below) plotted on the track. Dashed grey line with arrow indicates animal’s path and direction on the current trial. Highlighted non-local duration is labeled above blue time-shaded heatmap. Top-middle: multiunit spike rate from hippocampal tetrodes before, during, and after highlighted non-local representation. Bottom-middle: Distance from actual position to decoded position, with positive values corresponding to in front of the animal’s heading, and negative numbers corresponding to behind the animal’s heading. Bottom: Animal speed. Representations can correspond to distant locations within the current patch (left example) as well as in alternative, unoccupied patches (right three examples).

(B) Schematic showing non-local distance, defined as distance in centimeters of the path along the track (green) from the animal’s actual position (magenta) to the peak of the decoded posterior (blue). Example schematics correspond to representations of locations an example distance ahead of (left) or behind (right) the animal’s actual position.

(C) Maximum non-local distances represented on trials leading up to and following patch Switches for one animal. Data taken from during the period of each trial in which the animal approached the first choice point (as in B, left). Left and right x axes separated to reflect patch change. Error bars are 95% CIs on the mean. Individual animals shown in Fig. S4A. Exponential regression intercepts a and rate constants b are significantly larger magnitude for post-patch-change than pre-patch-change data in all individual animals except one (p_a = 1.3e-4, 4.6e-9, 1.1e-11, 3.1e-6, 0.8, p_b = 2.3e-4, 1.1e-8, 3.2e-10, 3.3e-6, 0.9, Z test).

(D) Maximum non-local distance ahead represented on trials leading up to and following patch Switches, across all animals. Data taken from first segment of trials and normalized per animal by subtracting off the average across trials. Error bars are 95% CIs on the mean.

(E) Maximum non-local distance represented for each animal while traversing each of the four segments of a Switch trial (segments 1–4 schematized in lower left). Error bars are 95% CIs on the mean. Non-local distance is significantly greater when each animal is in the first segment than the second (p=4.7e-52, 1.0e-55, 6.4e-59, 8.5e-24, 2.1e-42, Wilcoxon rank sum test), and is also significantly greater in the final segment than the third segment for each animal (p=2.3e-49, 2.4e-56, 3.3e-69, 1.5e-49, 3.0e-70).

(F) Maximum non-local distance represented on trials leading up to and following patch Switches for one animal. Data taken from final segment of each trial, during approach of the reward port (as in B, right). Left and right x axes separated to reflect patch change. Error bars show 95% CIs on the mean. Individual animals shown in Fig. S4B. Exponential regression intercepts a and rate constants b are significantly larger magnitude for post-patch-change than pre-patch-change data in all five animals individually (p_a =8.8e-9, 2.9e-9, 1.4e-7, 3.2e-7, 9.2e-4, p_b =5.7e-6, 3.0e-7, 2.3e-5, 4.0e-5, 3.6e-2, Z test).

(G) Maximum non-local distance behind represented on trials leading up to and following patch Switches, across all animals. Data taken from final segment of trials and normalized per animal by subtracting off the average across trials. Error bars are 95% CIs on the mean.

We found that non-local distance ahead was strongly modulated (Fig. 4C,D) in a pattern surprisingly distinct from the modulation of non-local content (Fig. 2C,D). The maximum non-local distance gradually ramped up across Stay trials and the first segment of Switch trials (Fig. 4C,D). The extent was then greatly elevated once the animal arrived in a new patch, and then decreased rapidly across the subsequent few Stay trials (Fig. 4C,D). This is in marked contrast to the modulation of non-local content, which increased and decreased in a roughly symmetrical manner. The maximum non-local distances could reach an average of approximately 90 cm from the animal (Fig. 4C, Fig. S4A), and, across animals, increased by approximately 40 cm from baseline (Fig. 4D) on the Stay trial following a Switch. This asymmetric pattern of non-local extent around Switch trials suggests a second kind of modulation of the generation of non-local representations across successive trials by the hippocampus during experience-guided decision making.

We then examined how these distances changed throughout the Switch trials themselves (Fig. 4E). Here we considered maximally distant representations both ahead and behind the animal during traversal of each of the four track segments of Switch trials. We found that while on average non-local representations extended as far as 40–60 cm from the animal on the first segment, this distance dropped to approximately 20 cm on both the second and third segment. Then, interestingly, the maximum distances rose again to approximately 40–80 cm as the animal traversed the final track segment of the trial and approached the reward port in the new patch.

The extent of non-local representations behind the animal also showed an asymmetric pattern of across-trial modulation around Switches (Fig. 4F,G, Fig. S4B). That is, the maximum distance of non-local representations behind the animal on the final segment of trials was also elevated upon Switching patches, and then decreased back to baseline over subsequent Stay trials (Fig. 4F,G). Thus, the extent both ahead and behind showed a modulation pattern around Switch trials that was distinct from the modulation of Switch versus Stay path content (Fig. 2,3).

We next asked whether non-local representations that corresponded to alternative, unoccupied patches were predictive of past or future patch choices. We found no evidence for such a relationship. Representations of specific alternative patches were neither biased to represent the patch the animal just arrived from nor predictive of the patch the animal would visit next (Fig. S4D). And, while in some animals these alternative patch representations did tend to overrepresent the track segments containing reward ports, rather than the central three track segments, this effect was not consistently observed across animals (Fig. S4E). These results indicate that representations of specific distant spatial alternatives in other patches are not directly reflective of specific prior or upcoming Switch choices.

Together, these patterns indicate that non-local extent is modulated above and beyond distance to a goal⁴³ or choice point³⁸. These findings also raise the possibility that more distant representations are involved in computations particularly required upon patch switching, including the initial approach of the first reward port in the new patch. This is a period in which the animal has the opportunity to learn about the reward values in the new patch, and potentially how they relate to values across the maze. Importantly, the reduced maximum distances observed in the third segment of Switch trials (Fig. 4E) indicates that the relative novelty or time since last visit for each track segment cannot be the main driver of the elevated distances observed after a patch Switch (Fig. 4D,G). This is because the third segment has a very similar level of relative novelty to the final segment, but the expression of non-local representations was very different.

Non-local distance is enhanced during learning opportunities

The observation that the extent of non-local representations was greatly elevated on the final segment of a Switch trial and for a few trials thereafter, after entering the new patch, suggested that representing distant locations might be particularly useful at those times. Specifically, we hypothesized that these representations might support computations that enable inference and updating related to alternative options across the environment. We then returned to our computational model of choice behavior, which suggested why this might be the case.

This model is an abstract statistical learning model that captures what a rational observer would expect about the probability of reward at each port given the animal’s actual history of reward experiences, which themselves occurred across different ports. Additionally, we fit the parameters of a choice model, similar to logistic regression, to estimate how this value information was used in relation to choice behavior. These analyses provided the opportunity to ask when information about the values of distant ports around the maze are most likely to be updated in relation to behavior at the level of trials.

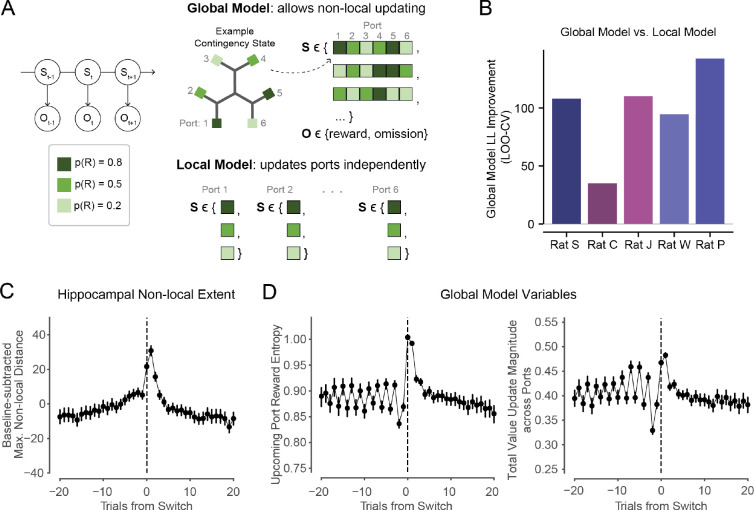
Our model choice was guided by the blocked reward contingency structure in this task, in which high reward probabilities tend to be mutually exclusive across patches at any given time. For example, the presence of a highly rewarding patch indicates that the other patches are less rewarding, and vice versa. An animal could account for this structure by estimating value jointly across ports rather than separately. Accordingly, the model estimates the expected value of each port on each trial by inferring the underlying contingency state across the entire maze. Specifically, the learning model is a hidden Markov model (HMM) whose hidden states are the sets of reward probabilities across all six ports (Fig. 5A, left and upper right, see Methods). This “global” model enables non-local value updating, where a reward outcome at one port can impact the expected values of other ports across the maze by providing evidence for specific contingency states.

Figure 5. Behavioral modeling captures enhanced learning opportunities in early patch experience.

(A) Left: schematic of Hidden Markov Model with hidden state S and observation O on each trial t. Colors correspond to potential nominal reward probabilities. Upper right: schematic of Global Model, showing example contingency states S with specific values for each port, and the two potential observations O of reward outcomes on each trial at the chosen port. Lower right: Example states S in Local Model, in which each port’s value is estimated independently. The Global and Local models had matched reward distributions, though here we visualize unique example states.

(B) Leave-one-out cross-validated log-likelihood improvement (higher is better) of Global Model versus Local Model. Global Model better fit behavior in all animals (p=.0035, .0285, .0006, .0013, .0104, t-test on cross-validated log-likelihoods per day).

(C) All animals’ normalized maximum hippocampal non-local distance represented on trials leading up to and following Switch trials, for non-local representations both ahead and behind (as in Fig. 4D,G). Trial-level quantification, rather than sub-trial-level quantification, shown here to match trial-level resolution of behavioral model. Error bars are 95% CIs on the mean.

(D) Global Model variables related to learning opportunities in new patch and associated value updating across the maze are enhanced upon patch Switching. Left: Entropy over reward states at upcoming reward port shows asymmetrical pattern around Switch trials, becoming elevated on and after Switch trials, and decreasing across trials thereafter. Patterns were consistent across animals, shown individually in Fig. S5D. Right: Absolute value update resulting from each trial’s reward outcome, summed across all ports in maze. Degree of value updating is elevated upon patch Switching, and decreases across trials the longer the animal Stays within a patch. Patterns are similar for updates both within the current patch and across unoccupied patches (shown individually in Fig. S5). Error bars are 95% CIs on the mean. Patterns were consistent across animals, shown individually in Fig. S5E.

We first asked whether this non-local updating was important to model animal behavior in this task. If so, then a model that included this feature should fit the data better than an otherwise closely matched model that does not allow for non-local updating. We therefore implemented a second “local” model that inferred the value state of each port independently, as separate HMMs (Fig. 5A, lower right) that were otherwise identical to the initial “global” model (see Methods).

The global model that allowed for non-local inference across ports significantly improved the fit to behavior in all animals (Fig. 5B). This suggests that animals did not learn port values independently, and instead adopted a non-local learning strategy in which outcomes at one port informed reward estimates at other ports, across the maze.

We then asked whether the dynamics of variables related to value updating in the model corresponded to the dynamics of non-local representation distance in the neural data (Fig. 5C, Fig. 4C–G). Importantly, in this model, the degree of updating is not required to be uniform for every trial’s experienced reward outcome. Instead, as is typical in Bayesian statistical learning, an outcome drives greater learning when its reward probability is more uncertain. We therefore quantified both outcome uncertainty as well as global value updating using the model (Fig. 5D). We first assessed outcome uncertainty, defined as the entropy over the value state of the upcoming port.

As with non-local extent, this outcome uncertainty was, on average, relatively stable in trials before animals Switched, increased substantially on Switch trials, and then decayed rapidly back to baseline (Fig. 5D left, Fig. S5D). Higher values upon Switching patches reflect the lack of recent information about likely outcomes at the locations in the new patch, which, in turn, could drive stronger value updating. The asymmetric pattern of outcome uncertainty around Switch trials is similar to that of the hippocampal extent results (Fig. 5C), potentially reflecting preferential updating or propagation of value information to internally represented distant non-local places during these uncertain periods.

We next aimed to specifically capture this global value updating process using the model. To do so, we quantified the total change in the estimated values across all ports, including both the local (occupied) and non-local (unoccupied) patches in the maze from trial to trial (Fig. 5D right, Fig. S5E). This revealed that value updating at locations across the maze was also asymmetric around patch Switch trials, with higher degrees of updating on and after the Switch, and a rapid decay thereafter (Fig. 5D, right), again akin to the pattern of hippocampal extent (Fig. 5C). Taken together, these results are consistent with the idea that the hippocampus preferentially samples more distant locations across the environment when expected values are uncertain, and new reward outcome information must be integrated into the animal’s internal model across the environment.

Discussion

Our findings demonstrate the distinct modulation of the content and spatial extent of non-local representations of alternatives in the hippocampus, in patterns that are well-matched to the animals’ evolving cognitive needs throughout flexible decision making. The task structure encouraged animals to continually update their estimates of the values of different options based on experience and to use those values to decide whether to Stay in the current patch or Switch to a different patch. Moment-by-moment decoding of hippocampal spatial representations during navigation, in combination with behavioral modeling, revealed two distinct patterns of modulation: (1) non-local representations of alternatives were expressed in relation to their relative expected values, with the higher value alternative making up the greater fraction, and (2) non-local representations extended further from the animal at times where our model suggested that non-local learning was most prevalent. These patterns of modulation spanned successive trials and engaged non-local representations of locations not only ahead of, but also behind the animal. Further, the representations included locations that were not only close to, but also very distant from the animal. These findings reveal the broad representational capacity of the hippocampus during locomotion and indicate that this representational capacity is specifically engaged in patterns appropriate to subserve cognitive demands for both making decisions among and updating internal representations of alternatives.

Our behavioral model provided a framework for understanding these contrasting patterns between non-local content corresponding to alternatives (Fig. 2,3, which are approximately symmetric around Switch trials) and non-local extent (Fig. 4, which is asymmetric). In the trials leading up to a patch Switch, the hippocampus tended to reflect locations at distances within the neighboring track segments (Fig. 4), along either the Stay or Switch path (Fig. 2,3), rather than at the remote port locations where reward was previously obtained. This is consistent with a key idea of many reinforcement learning models—that choices are guided by a learned representation of the long-term reward consequences of some local action. In this framework, an animal would evaluate Stay or Switch options leading up to a Switch choice by retrieving the up-to-date values associated with the neighboring paths nearby rather than their ultimate remote destinations. The observation that non-local representations extend further during greater non-local value updating, particularly after Switching, is further consistent with the idea that non-local updating of locations across the maze could help to propagate value information from those distal reward port targets to proximal choice points. Thus, whereas the elevated extent of non-local representations after Switches may reflect a non-local updating process (Fig. 5D), the representation of alternative Stay and Switch paths may reflect judicious retrieval of nearby segments when they are relevant to an ongoing choice between alternatives (Fig. 1F).

Modulation of non-local representations with relative choice value

Previous work on non-local representations and cognitive functions during locomotion has often focused on representations ahead of the animal and identified a variety of relationships between the alternatives represented and current trial behavior. These results included an association between alternative representation content and head-scanning behavior⁴⁴, although non-local representations are also observed in the absence of this behavioral signature^35,64. These results also included reports that representations of specific alternatives either did^41,43,45 or did not^35,40,42 predictably relate to the upcoming choice on the current trial.

Our results provide a potentially unifying framework to explain these previous observations. We identified a modulation of non-local representational content with relative value across successive trials. Specifically, when the difference between the values of the Stay and Switch options was large, the higher value alternative dominated non-local representations. When the differences were smaller, the relative proportion of non-local representation of each was more similar. These findings suggest that the expected values of options or related decision variables influence the extent to which those options are expressed in the context of non-local activity. This provides a potential prioritization of options to be considered, as the hippocampus would be most likely to represent the best, most viable options. Similar prioritization, in which the most promising options are internally sampled most extensively, also arises in rational computational analyses of choice under uncertainty⁶⁰.

Thus, when the preferred choice is clear, the hippocampus primarily represents that path, but nevertheless samples occasionally from the alternative, potentially to retrieve information about the path not taken. In conditions where the preferred choice becomes less clear, the hippocampus generates progressively more balanced representations of the two options. Critically, therefore, hippocampal non-local representations are neither constantly predicting the planned choice, nor strictly providing a menu that evenly represents all potential options—rather, representations can be more or less predictive of behavior depending on the current decision-making demands.

At the same time, relative value-related modulation of non-local representations suggests that the mechanisms selecting non-local representations already have an estimated value of the alternatives. If so, then why would it be useful to generate a non-local representation? We suggest that non-local representations activate place and associated value representations on the actual path toward possible goals. This sampling of place and value could progressively refine and provide a more accurate estimate of the value, and thus serve to better inform decision processes^10,46. This is consistent with our observation that the proportion of representation of the Switch path ahead was predictive of choice on even the next trial, and that similar patterns of non-local content extending behind the animal also related to upcoming choice, well in advance of physically approaching the next choice point.

Modulation of non-local extent during periods of updating

Our results also suggest that non-local representations of distant locations may particularly be recruited to support updating an internal model. Behavior in the Spatial Bandit task was better fit by a model that included non-local value updates wherein experiences at one reward port could alter the values at other ports. The pattern of model-estimated updates around Switch trials was similar to the measured extent of non-local representations on these trials, with the largest updates and the most distant representations preferentially expressed after the Switch decision was made and on subsequent trials in the new patch.

One way to understand why value updating is associated with the representation of more distant locations is that it may enable more proximal value retrieval at the time of later choices. In the context of a choice to Switch patches, we found that animal behavior was driven in part by the reward value experienced at remote destination ports. Yet, the non-local representations in trials immediately preceding a patch Switch largely sampled paths along the neighboring track segments, rather than sampling distal reward port locations. This is consistent with the widespread idea that the brain learns a value function, mapping locations near each choice point to the rewards to which the paths ultimately lead⁶. Thus, when outcomes are experienced at reward ports, the hippocampus may support non-locally updating information at distant locations across the maze in part to simplify later retrieval when that up-to-date information is needed for evaluating nearby choices.

While the potential mechanisms by which non-local representations during navigation could support updating merit further investigation, some initial points can be made. First, the extent of non-local representations was low as animals traversed the central segments on a Switch trial but increased substantially in the final segment; that is, non-local extent increased immediately before rather than only after the first outcome in the new patch was revealed. This suggests that the role of these remote representations is not dependent on having just experienced an outcome at a reward port. Instead, the hippocampus may facilitate post-outcome updating by activating representations of distant alternatives that should be subsequently updated after new outcomes are observed in the chosen patch. One possibility is that activation during running could promote reactivation during subsequent replay events at the reward port⁶⁵, and thus link the outcome of the current trial to representations of distant places. Second, prior work has demonstrated that non-local representations during navigation are strongly associated with the theta rhythm, and sequences along the theta rhythm are thought to support learning by binding together elements of experience at a compressed timescale through plasticity mechanisms^{38,48,58,66,67}. Thus, this system could be used to learn relationships between current experience and unchosen alternatives within theta cycles (or other organizing codes⁶⁸), in support of updating knowledge of remote alternatives during active navigation.

These possibilities are consistent with prior work showing that animals make internal model-based choices that rely on structural knowledge^6,7,69–73 rather than just stimulus-response associations. Internal model maintenance and updating is particularly beneficial for flexible decision making to keep up with changing environments. However, previous neurophysiological and computational work on how non-local representations in the hippocampus may support value updating has primarily focused on replay during “offline” rest^8,74–83, rather than active locomotion^84,85. Thus, our findings suggest that “online” movement-associated non-local representations in the hippocampus also have the potential to contribute to this learning.

A broad range of alternatives are flexibly engaged

Our results also establish that a diverse range of alternatives are expressed by hippocampal non-local representations during active navigation. In the context of a specific decision among options, previous work has often focused on representations that corresponded to possible future locations on the current trial^40,42,43. Our findings show that representations of alternative paths not only ahead of the animal but also behind the animal—even when moving away from the associated choice point—are flexibly engaged across trials associated with decision-making and learning processes. We also found that this engagement included non-local representations of very remote locations, including representations that occasionally jump far across the maze rather than sweep ahead at a constant rate.

The dynamic engagement of a broad range of alternative possibilities by the hippocampus³⁵ during locomotion is consistent with the idea that non-local population representations can support a range of cognitive functions that involve computations about alternatives^86–89. In particular, the dynamic engagement of representations behind the animal³⁸ during navigation raises the possibility that the hippocampus supports computations about actual and counterfactual⁹⁰ past paths during navigation, not only during rest. Moreover, the relative prevalence of representations behind the animal predicted behavior on the subsequent trial, indicating that representations of alternatives behind the animal need not be strictly retrospective, but could also support future decision making.

Additional observations from prior studies exemplify that hippocampal activity during locomotion can correspond to various correlates, including representations of opposite directions³⁵, forward and reverse sequences⁹¹, distant locations^43,61, alternative environmental contexts⁶², and different spatial reference frames⁶³; our results are consistent with the idea that any of these representations of alternatives may be differentially engaged and specifically curated across trials depending on the cognitive computations needed for the task at hand.

Non-local computations in immediate and long-term adaptive behavior

Retrieving information about alternative options related to making a specific upcoming decision and retrieving information about alternatives in service of updating an internal model are both computations that inform inference across space (“non-local inference”). In the former case, representations of alternatives may support non-local inference of which alternative has the greater expected value based on prior experience. And, in the latter, representations of alternatives may support non-local inference about how the expected value of remote alternatives should be altered based on outcomes observed elsewhere. This possibility is consistent with prior work indicating that the hippocampus is important for inference^7,75,92–99, and relational thinking more broadly^26,100–104.

The prolonged relationship across trials of non-local representations to Switching behavior serves as a reminder that the behavioral benefit of non-local inference need not be immediate. While we observed that non-local representations can predict immediate future and past Stay or Switch choices, we also found that representations of alternatives ramped across many trials before and after Switch choices, that they predicted choices an entire trial in advance, and that remote representations in alternative patches did not predict prior or subsequent patch choices. Thus, while non-local representations can have immediate behavioral benefit by supporting the immediately upcoming choice, they may also support decision making over the longer term, perhaps by integrating and accumulating^105,106 retrieved information across trials. This is consistent with the idea that inferring structure in an environment and relations between experiences may occur in the background of behavior¹⁰⁷, particularly as new information needs to be incorporated into an internal model, even if an animal does not yet know if or when it will later need to draw on that knowledge to support adaptive choices. This is thought to be especially important in complex and dynamic environments to enable flexible decision making when confronted with new or unexpected circumstances.

While the circuit-level mechanisms that determine the flexible generation of representations of alternatives remain largely unstudied, our observations of modulation with respect to relative values and the need to learn them implicates brain regions like the prefrontal cortex as possible drivers^108–116. Consistent with this possibility, activity in the medial prefrontal cortex (mPFC) and the hippocampus can be precisely coordinated^42,117–119 and mPFC spiking can predict the future engagement of non-local hippocampal spiking⁶¹. Further, observations of coordination of hippocampal representations and peripheral sensory-motor processes¹²⁰ suggest broad engagement of many brain areas at times when hippocampal non-local activity may be important for ongoing behavioral computations. The specific generation of non-local hippocampal activity patterns and associated representations of alternative possibilities could engage widely distributed computations to enable learning and adaptive decision making in a complex and dynamic world.

Methods

Subjects

All animal procedures were approved by the Institutional Animal Care and use Committee at University of California, San Francisco. Five adult male Long-Evans rats (Charles River Laboratories, 450–650g) were each pair housed in a temperature-and humidity-controlled environment on a 12-hour light-dark cycle with lights on 6 AM - 6 PM. Rats had ad libitum access to standard rat chow and water. Prior to behavioral training, rats were transitioned to single housing and food restricted to 85% of their baseline weight.

Behavioral pre-training

All behavioral tasks were controlled via custom code written in Python and Statescript in combination with an Environmental Control Unit (Spikegadgets). Animals were pre-trained to run back and forth on a linear track with walls for liquid food reward (Carnation evaporated milk sweetened with 5% sucrose) from reward ports fixed at each end of the track. Upon entry of a reward port, 100 μL reward was delivered by syringe pump immediately and automatically, gated by an infrared beam. Animals learned to alternate between and obtain rewards from the two ports across two 40-minute and one 25-minute sessions. To familiarize animals with navigating an elevated maze, animals then performed the same task on an elevated linear track (1.1 m long, 84 cm high) until they performed at least 30 rewards in a 15-minute session. Pretraining took place in an environment with distal spatial cues on the walls. The pretraining environments were fully separate from the Spatial Bandit Task environment. Animals were subsequently returned to ad libitum food access prior to surgical implantation.

Neural implant

Custom hybrid microdrives contained 24 independently movable 12.5 μm diameter nichrome tetrodes (California Fine Wire and Kanthal). The drive body was 3D printed (PolyJet HD, Stratasys) and funneled tetrodes into two cannulae to target 12 tetrodes to each hemisphere. Tetrodes were gold plated to reduce impedance to ~250 kOhms. Implants also contained a custom headstage (Spikegadgets) that coupled with a stacking set of up to four custom 128-channel polymer probes¹²¹ (Lawrence Livermore National Labs) per animal. Implant was housed in a custom 3D-printed enclosure with removable cap. Drive was sterilized before surgical implantation.

Custom hybrid microdrives were implanted stereotaxically under sterile conditions. In anesthetized animals, cannulae were implanted above dHC (+/−2.6–2.8 ML, −3.7–3.8 AP relative to skull Bregma) and polymer probes were implanted in mPFC and OFC. A stainless-steel ground screw was implanted over the cerebellum to serve as a global reference. Titanium screws were placed in the skull to help anchor the implant, which was secured with Metabond (Parkell, Inc) and dental cement (Henry Schein).

After surgery, tetrodes were advanced deeper into the brain daily over ~3–4 weeks. One tetrode per hemisphere was advanced to corpus callosum as a local reference and all other tetrodes were advanced to dorsal hippocampus CA1 stratum pyramidale, guided by physiological signatures of spiking activity and the local field potential.

After full recovery from surgery, animals were food deprived to 85% of their baseline weight and reintroduced to the elevated linear track, as described above. Animals reached criterion again over several days to refamiliarize them with obtaining reward on a track and to familiarize them with running with their implant. Two rats had additional experience on a fork maze¹²². Re-training animals to run after surgery recovery ensured that the animals were motivated enough to begin the main experiment.

Data collection: Spatial Bandit task

The Spatial Bandit task took place on a maze with three radially arranged Y-shaped foraging “patches” each containing a central hallway that bifurcated into two hallways that each terminated in a photogated reward port, resulting in two ports per patch and six total reward ports. Each port had a separate automated pump, as described above. Hallways were 6.5 cm wide and linear track segments were each 53 cm long. All hallways intersected at 120 degrees, such that the track had three-fold symmetry. The track was made of black acrylic (TAP Plastics) with walls that were 3 cm high, enabling animals to see distal spatial cues.

The behavior took place in a dimly lit room (2.4 m by 2.9 m) with black distal spatial cues on the white walls and a plastic black curtain separating the maze from the experimenter, rig, and computer. A ceiling-mounted camera (Allied Vision) centered over the maze recorded animal behavior at 30 frames/second and was synchronized with all other data via Precision Time Protocol. Before behavior began each day, a ring of red and green LEDs was mounted atop the implant to enable online head position and direction tracking via SpikeGadgets Trodes software.

Animals began the task only once tetrodes had reached stratum pyramidale. Neural data was recorded from the animals’ first experience of the Spatial Bandit maze and environment. The general structure of each day of recording began by moving rats from their home cage into a rest box in the same room as the Spatial Bandit maze. Run sessions were interleaved with rest sessions throughout the day; rats typically completed 7 or 8 ~20-minute run sessions per day, interleaved with rest sessions of at least 30 minutes each. Rest sessions helped to maintain stable motivation by providing breaks throughout each day. Each day also started and ended with a rest session. These behavioral data were collected over 8–17 days per animal.

During each run session, an animal was first placed in the center of the track facing the same wall each time, and then navigated freely in the environment, which was otherwise fully automated by Trodes (SpikeGadgets) software and custom behavioral control scripts written in Statescript (SpikeGadgets) and Python. At a high level, each individual run session contained multiple reward contingency blocks. Each contingency defined the reward probability p(R) assigned to each of the six reward ports. Contingency blocks covertly changed when an animal completed a certain number of trials, or hit a 20-minute time limit per contingency, whichever came first. Contingency changes almost always occurred based on the trial limit, very rarely changed based on the time limit, and did not depend on any other performance metric. A trial was defined as the period from exiting one photogated reward port to exiting a different port. Therefore, each trial contained both the run between two ports and an outcome (100 μL reward or omission) at the chosen port. Reward was only available probabilistically if an animal poked into a distinct port; consecutive pokes at the same port were never rewarded.

Each animal’s first run session began with reward probability p(R) of 1 at all reward ports for 100 trials, followed by an uncued contingency change to p(R) of 0.5 at all ports for the next 100 trials. This first session exposed the animal to the environment, encouraged the animal to visit all reward ports, and introduced probabilistic rewards. After this session, run sessions were each 180 trials long and contained three reward contingencies that each lasted 60 trials for four animals. One animal had 160 trial sessions each containing two contingencies of 80 trials.

From the second run session onward, each reward contingency defined a p(R) of 0.2, 0.5, and 0.8 per port, such that each contingency had a best patch on average. Both ports within a patch could have the same or different reward probabilities, but the best patch combination was 0.5 and 0.8 (not 0.8 and 0.8) across the two ports in a patch. By having ports of two different values within a patch, animals were encouraged to spend some trials not only at high-value but also at nearby lower-value locations, enabling us to sample neural data as animals visited ports of a full range of values. Contingencies were pseudorandomized to counterbalance which patch was best, whether the left or right port within each patch was best, and whether the best, medium, and worst patch followed a clockwise or counterclockwise order around the track. Contingency changes and reward port values were never cued, so that animals had to make navigational choices based on memory of their prior experiences across the maze.

Continuous neural data, as well as digital inputs and outputs associated with beam breaks and reward pumps, were recorded during each rest and run session at 30 kHz in four animals and 20 kHz in one animal using Trodes version 1.8.2 (SpikeGadgets).

Histology

At the conclusion of behavioral experiments, animals were anesthetized with isoflurane, and small electrolytic lesions were made. One day later, animals were anesthetized and transcardially perfused with 4% paraformaldehyde. Brains were fixed in situ overnight, after which tetrodes were retracted from the tissue and brains were extracted from the skull. Brain fixation continued for two days. After cryoprotection by 30% sucrose for 5–7 days, brains were blocked and sectioned with a cryostat into 50–100 μm sections. Nissl labeling enabled identification of tetrode tracks and localization of tetrode tips at the sites of electrolytic lesions (Fig. S1B).

Data processing and analyses

All data processing and analyses were carried out using Python and Julia using Spyglass¹²³.

Behavioral analysis

Trials were parsed based on behavioral Statescript log files (SpikeGadgets). A trial was defined as the final exit from one port to the final exit from another port, and therefore included both the run from one port to the next as well as the entry into and outcome at the chosen port. Stay trials were defined as starting and ending within the same track patch, while Switch trials were defined by starting and ending in distinct track patches. The nominal reward probabilities assigned to each port and reward delivery times were also tracked by parsing log files. The nominal best patch on each trial was defined as the patch with the highest average of the nominal reward probabilities of the two ports within the patch (Fig. 1D). These reward probabilities are referred to as nominal because they are assigned by the reward contingency. Importantly, an animal’s experienced reward values at each port at any time in behavior are related to but not necessarily identical to the location’s nominal reward probability, given the self-paced nature of the task and stochasticity of the rewards in the environment.

Behavioral Hidden Markov Model

To estimate the rats’ expected belief about the value of each of the six ports, we used a Hidden Markov Model (HMM), which tracks belief across a discrete set of states of the world via a forward model of expected reward outcomes. The rationale for this modeling approach is to abstract away many under-constrained implementational decisions in a more mechanistic model, and instead take as a starting point the question of what inferences would be drawn by an ideal statistical observer experienced with the task environment’s structure. More specifically, the HMM is capable of modeling the true dynamics of how rewards change during the experiment by having states of the HMM directly map onto the joint reward probabilities across the six reward ports, allowing it, for example, to capture the intuition that a change of reward probability at one patch should indicate to the animal that rewards have likewise changed at the other two patches, an inference that is not feasible with traditional Q-learning models. That said, we expect that a more mechanistic implementation would approximate the HMM computations by augmenting a Q-learning style model with non-local activations and updates^74,124.

Here, state is an assignment of expected reward probability to each of the six ports, and whose dynamics directly capture the ideal estimation strategy of an agent aware of the true underlying task structure, but without explicit knowledge of the precise timing of state changes. Notably, unlike traditional Q-learning models, the HMM captures the high-level idea that state configurations jointly change across each session, and that each trial can be viewed as evidence of which among these possible state configurations the rat is currently experiencing.

The HMM tracks value of reward ports by assigning a probability, or belief, to each possible state configuration of the six reward ports, alongside dynamics to update these beliefs via per-trial outcomes. Here, we considered a state to be a particular assignment of reward probabilities to each of the 6 reward ports, such as:

$${\varphi }_i=\left[p_1=0.2,p_2=0.2,p_3=0.5,p_4=0.2,p_5=0.8,p_6=0.5\right]$$

Each trial can be viewed as evidence of which among these possible state configurations the rat is currently experiencing, allowing trial-by-trial state inference and thus value estimations of each of the reward ports.

Reward port value estimation

In the HMM, we are modeling belief about which of $n$ discrete states the rat is currently in. These states correspond to the contingencies that define reward probabilities for the rats. For computational convenience, and motivated by the informed ideal observer perspective, our set of contingencies, $\varphi$, was the subset of the $n=72$ most frequently occurring of these possible contingencies in the actual experimental design, though we found our results to be relatively insensitive to the exact choice of contingencies.

Our belief state, $\alpha$, is a probability distribution over these 72 contingencies such that $\sum {\alpha }_i=1$. On any given trial, we can combine our belief state $\alpha$ with the set of contingencies $\varphi$ to find an estimate of reward $Q$ at each of the six ports that minimizes the MSE:

$$\mathit{Q}=\left[Q_1,Q_2,Q_3,Q_4,Q_5,Q_6\right]=\sum _{i=1}^n{\alpha }_i{\varphi }_i$$

Patch value estimation

Patch values were derived from the reward port estimates as follows: As the rat approaches a bifurcation and must choose between the upcoming port within a patch or the ports within the other patches, $Q_{\mathit{patch}}$ for the current patch was defined as the Q-value of the upcoming reward port as estimated by the HMM. For the other two patches, it was assumed that their value was an average of their two reward ports as estimated by the HMM, or $Q_{\mathit{patch}}=\left(Q_a+Q_b\right)/2$, where $a$ and $b$ were the two reward ports of the respective patch.

Behavioral model state updates

We assumed that any contingency could transition to any other contingency with a fixed probability, or hazard rate $h$, which is the probability of transitioning to any new contingency, and $1-h$ is the probability of remaining in the current contingency. This hazard rate was assumed to be identical among all state transitions, and was a free parameter inferred via fitting.

At each timestep, beliefs were updated via $\mathit{\varphi }\leftarrow \mathit{T}\mathit{\varphi }$, where $\mathit{T}$ was an $n\times n$ matrix whose diagonal entries were $1-h$ and all other entries were $h/(n-1)$. This essentially results in a small diffusion of all reward port values around the maze towards baseline.

To incorporate observations (here, whether a port was rewarded), at the end of each trial we updated each entry of $\alpha$ based on the probability of the observed outcome for each respective contingency. If the outcome was positive, the probability given by a contingency was the value of $\varphi$ for that contingency and port, and so ${\alpha }_i\leftarrow {\alpha }_i{\varphi }_{ij}$ for contingency $i$ and port $j$. If the outcome was negative, this became ${\alpha }_i\leftarrow {\alpha }_i\left(1-{\varphi }_{ij}\right)$. This update was performed for all contingencies.

Behavioral choice model

To connect this learning model to choices and assess our ability to capture animal behavior, we computed the likelihood of choice of patch on every trial as the softmax of the three patch values, given by:

$$p_{{\mathit{patch}}_i}=\frac{e^{V_{{\mathit{patch}}_i}}}{e^{V_{{\mathit{patch}}_1}+V_{{\mathit{patch}}_2}+V_{{\mathit{patch}}_3}}}$$

The value at the current patch was given by:

$$V_{{\mathit{patch}}_i}={\beta }_{\mathit{stay}}{Q}_{{\mathit{patch}}_i}+b_{\mathit{stay}}$$

For the patch clockwise from the current patch, value was given by:

$$V_{{\mathit{patch}}_i}={\beta }_{go}{Q}_{{\mathit{patch}}_i}+b_{\mathit{turn}}$$

The value of the remaining patch was given by:

$$V_{{\mathit{patch}}_i}={\beta }_{\mathit{go}}{Q}_{{\mathit{patch}}_i}$$

where $Q_{{\mathit{patch}}_i}$ was either an individual port estimate or average of ports as described above.

The inverse temperature parameters, ${\beta }_{\mathit{go}}$ and ${\beta }_{\mathit{stay}}$, determined how sensitive choice behavior was to differences in expected reward – high temperatures indicate high sensitivity to reward, while low temperatures indicate insensitivity. To allow for differential sensitivity to reward estimates at the current patch versus alternate patches, we fit two independent softmax temperatures, ${\beta }_{\mathit{stay}}$ for the current patch, and ${\beta }_{go}$ for the two alternative patches.

The term $b_{\mathit{stay}}$ reflected a fixed cost to changing patches due to the time and distance to reach a new patch (as opposed to the reward sensitivity fit by ${\beta }_{\mathit{stay}}$), and was added to the valuation of the current patch.

To incorporate tendencies of the animals to prefer to turn in certain directions when changing patches, we included a turn bias $b_{\mathit{turn}}$, an offset which was consistently applied to the patch to the left of the animal’s current position. If the rat was in patch 1, this was added to patch 2. If the rat was in patch 2, this was added to patch 3, and if the rat was in patch 3, this was added to patch 1.

On trials where the animal switched patches, likelihood of port choice was modeled as a subsequent softmax between the two ports, with a separate softmax temperature ${\beta }_{\mathit{port}}$ applied to the per-port reward estimates:

$$p_{{\mathit{port}}_{L/R}}=\frac{e^{V_{{\mathit{port}}_{L/R}}}}{e^{V_{{\mathit{port}}_L}+V_{{\mathit{port}}_R}}}$$

The value of the left port was given by:

$$V_{{\mathit{port}}_L}={\beta }_{\mathit{port}}{Q}_{{\mathit{port}}_L}+b_{{\mathit{portbias}}_i}$$

where $b_{{\mathit{portbias}}_i}$ was fit independently for each of the three patches, reflecting biases in which reward port each rat tended to enter when switching to each of the three patches.

The value of the right port was given by:

$$V_{{\mathit{port}}_R}={\beta }_{\mathit{port}}{Q}_{{\mathit{port}}_R}$$

Local behavioral model

To test whether animal behavior reflected a belief that the outcomes at the six reward ports were linked, a core assumption of our Global behavioral model, or whether the animals instead estimated the value of the six reward ports independently from one another, we considered an alternate model in which we estimated animal behavior via a set of six independent HMMs, one for each of the six reward ports (Fig. 5A,B). Each HMM individually contained the same distribution of rewards as in the distribution in our joint HMM model, as well as a belief distribution over those rewards. However, the belief distributions at the six reward ports were independent – while volatility would be modeled for all six reward ports after each trial, only the belief distribution of the visited reward port would be updated from observation via the forward model on each trial – the other five belief distributions would not incorporate this reward information. Importantly, the comparison between these two models (rather than, for instance, between the HMM and a local Q learning model) most directly isolates the question of local versus non-local updating, since the models are identical in all other features.

To compare the independent Local model with the original joint Global model, we computed a cross-validated approximation to the negative log marginal likelihood for each day. Specifically, we used leave-one-session-out cross validation for the population-level prior parameters and a Laplace approximation for the per-day parameters: for each day, we refit the population-level model omitting that day, then conditional on that prior, we computed a Laplace approximation to that day’s log marginal likelihood. We aggregated these per-day scores to obtain a total score for each rat and model. Finally, we use paired tests on these scores across rats, between both models, to formally test whether either model fit consistently better over the population of rats (Fig. 5B).

Global model reward sensitivity

To confirm that the HMM’s behavioral predictions were driven by its reward estimates, and that incorporating these estimates improved its performance, we compared our Global behavioral model against two nested models, one model where ${\beta }_{go}$ was fixed to 0 (such that choice predictions ignored the estimate of the current patch value) and one model where ${\beta }_{\mathit{stay}}$ was fixed to zero (such that choice predictions ignored the estimate of alternative patch values). These two alternative models were compared against the full model (Fig. S5A,B) with an identical procedure to the Local model comparison (see above).

Behavioral model fitting procedure

For our HMM, we optimized the free parameters of the model by embedding each of them within a hierarchical model to allow parameters to vary from day-to-day. Day-level parameters were themselves modeled as arising from a population-level Gaussian distribution over days, separately for each rat. We estimated the model for each rat to obtain best fitting day- and rat-level parameters to minimize the negative log likelihood of the data using an expectation-maximization algorithm with a Laplace approximation to the day-level marginal likelihoods in the M step¹²⁵.

Behavioral model variables

In subsequent analyses, we characterized value-guided Stay and Switch choices at the level of trials using variables estimated through the HMM, including the values associated with each port on each trial. We built a binomial family generalized linear model (Logit link function) for each animal to predict Stay or Switch choices from estimated expected values associated with the choice to Stay or to Switch (Fig. 1E). The value of Staying was defined as the model-estimated value of the upcoming port within the patch on the current trial, and the value of Switching was defined as the greater of the average port values in the two alternative unoccupied patches into which the animal had the option to Switch on the current trial. The difference between the Switch and Stay values on each trial, without accounting for the cost of Switching or other biases, defined the relative value of Switching and Staying on each trial (Fig. 1F). The entropy over the reward belief state of the upcoming port (Fig. 5D) was calculated on each trial as follows. Given a belief state $\mathrm{\alpha }$, and reward probabilities $\varphi$, each port $j$ had a marginal reward distribution $\left[p_{1,}{p}_2,p_3\right.$ ] where $p_1=p(r=0.2)$, $p_2=p(r=0.5)$, $p_3=p(r=0.8)$. For each port $j,rewardentrop{y}_j=-{\sum }_i{p}_i\mathrm{l}\mathrm{o}\mathrm{g}\left(p_i\right)$. The value update at each port on each trial was calculated as the difference between the port value before and after the outcome was observed on each trial, and absolute value updates across a patch, set of patches, or the entire maze, were summed across ports to determine the total update magnitude on each trial (Fig. 5D, Fig. S5).

Position

LEDs mounted on the front and back of the implant were tracked via overhead camera at 30 frames/second using Trodes software (SpikeGadgets). Positions were converted from pixels to centimeters, smoothed, interpolated and upsampled to 500 Hz to match neural decoding resolution. The front and back LEDs were used to calculate head orientation and angular velocity. The head position and head speed were calculated from the centroid of the font and back LEDs. To enable faster decoding, head position was linearized into one dimension by projecting the two-dimensional head position onto a graph representation of the track with nodes at the reward ports and track segment intersections, connected by edges. In between the track edges, which corresponded to the nine physical track segments, we introduced 15 cm gaps in 1D space to avoid inappropriate smoothing across adjacent linear positions that were not adjacent in physical space (Fig. S1).

Spatial decoding

To decode spatial position from hippocampal spiking at high spatial and temporal resolution, we used a previously established clusterless state space algorithm^{53,54,126,127,82,128,120} from Denovellis et al., 2021⁵³. Briefly, for each session, we built an encoding model to relate spike waveform features to the animal’s linearized head position in 2 ms bins using data from the beginning of the first trial to the end of the final trial of the session. The peak amplitude of each spike on each dCA1 tetrode channel served as spike waveform features. Spikes were detected by a 100 μV threshold on the recorded neural signal filtered 600–6000 Hz. To remove potential artifacts, a 1 ms window around times in which at least 75% of channels had an amplitude of 2000 μV or greater was excluded.

For each session, we then decoded spatial position from this hippocampal population spiking in 2 cm linear position bins and 2 ms temporal bins (Fig. S1). The state space decoding model⁵³ had two states, spatially continuous and spatially fragmented, to capture smooth and discontinuous movement dynamics, respectively, of the hippocampal representation through the maze. The fragmented state was modelled by a uniform transition matrix and the continuous state was modelled by a random-walk transition matrix with a 6 cm movement variance. The probability of staying in the current state in the discrete transition matrix was 0.98. The initial conditions were set to be uniform across states and uniform across positions, as we did not have prior information about the most likely initial conditions. The model used kernel density estimators with a 24 μV bandwidth for waveform features and a 6 cm bandwidth for position to estimate the likelihood of a spike waveform feature predicting a position.

The model output the posterior probability of position across the two movement dynamic states. We marginalized the joint probability over the two states, and then determined the most likely decoded position in each 2 ms bin as the peak of the posterior probability distribution.

We assessed decoding quality based on the concentration of the posterior probability, and only included times that were decoded with high confidence in subsequent analyses, by requiring the highest 50% of the posterior probability values to be concentrated within 50 cm of the track, as has been done previously¹²⁰. We further note that this decoding approach was conservative in the sense that we decoded using the same data used to build the encoding model. In contrast, a cross-validated approach would instead decode periods distinct from those used to encode, and thereby exclude the place cell spikes predominantly associated with the animal’s actual current position during the decoded moments.

We measured the distance between the animal’s actual position to the most likely decoded position as the shortest path distance in linear space along the track in each 2 ms bin based on Dijkstra’s¹²⁹ algorithm, with the rat and most likely decoded position as nodes on the track graph. We also classified the animal position and most likely decoded position into one of nine track graph segments in each 2 ms bin. For visualization, we projected linearized position back to the 2D track graph (Figs. 2A, 3A, 4A).

Non-local representation of Stay and Switch paths

Non-local representation times were identified as times in which the most likely decoded position (hereafter “decoded position”) was in a track segment distinct to the animal’s actual position. We analyzed valid times of high speed (>10 cm/s) in order to limit our analyses to locomotor periods in which theta power is high and associated theta sequences are known to occur ^29,36,59,130, and thereby excluded stationary rest periods in which sharp wave ripple replay events occur^1,8,34.

To analyze the content of non-local representations occurring as the animal approached the first choice point on each trial (Fig. 2), we first identified which track segment the animal began in on each trial and used data from the time at which the animal exited the reward port to the first time at which the animal’s position exited that initial track segment. During this period, the animal approached the first choice point in the trial (Fig. 2B). Out of this period, we limited analysis to only the times that satisfied the decoding confidence and speed thresholds described above. For these valid times, we then quantified the total duration of non-local representation. We also quantified the duration of representation of the single segment ahead consistent with a subsequent Stay path and the duration of representation of any of the other segments ahead consistent with a subsequent Switch path, as in Fig. 2B. This enabled us to then calculate the proportion of the total valid non-local representation duration that was consistent with a non-local Switch path representation. The per-trial proportion was therefore calculated as: valid non-local Switch representation duration, divided by the sum of the valid non-local Switch representation duration and the valid non-local Stay representation duration.

A very similar approach was used to analyze the content of non-local representations occurring as the animal traversed the final track segment of each trial (Fig. 3). Here, we identified which track segment the animal ended in on each trial and used data from the final time at which the animal crossed from another segment into this final segment to the time at which the animal entered the chosen reward port. During this period, the animal approached the reward port, rather than a bifurcation (Fig. 3B). Again, we limited analysis to only the times that satisfied the decoding confidence and speed thresholds described above. For these valid times, we then quantified the total duration of non-local representation, and what proportion of that total non-local duration corresponded to a non-local representation consistent with a Switch path behind the animal (rather than the neighboring Stay path within the patch), as in Fig. 3B.

Peri-Switch linear regressions and shuffles

Ordinary least squares linear regressions were fit to Stay trial data for trials before or after Switch trials (Fig. 2C,D, Fig. 3C,D, Fig. S2A,B). Shuffled distributions were obtained within animal by randomly shifting trial labels 1000 times, where the label is the number of trials from either the prior or next Switch trial.

Predicting Stay and Switch choices from non-local representations

Generalized linear models with a logit link function (Fig. 2F, Fig. 3F) were used to predict Stay or Switch choices from the proportion of valid non-local representation corresponding to Switch paths. Models were fit separately per animal. Each model had one predictor, corresponding to the proportion of Switch path representation occurring while the animal occupied either the first or final segment of a trial t, the trial before t-1, or the average across the two trials t and t-1. Models were five-fold cross validated, and training data were balanced by resampling Switch trials. Predictions were binarized with a threshold of 0.5 and total accuracy was calculated across folds.

Theta phase

Neural data from a reference electrode in corpus callosum was filtered 0–400 Hz and downsampled to 1 kHz. This local field potential signal was then further filtered in the theta band from 5–11 Hz. The analytic signal was calculated with a Hilbert transform. The instantaneous phases for all valid local and non-local decoded run times were assessed separately for periods in which the animal was approaching the first choice point in each Stay or Switch trial, or after crossing the final choice point in each Stay or Switch trial (Fig. S2C,D). Phase convention refers to descending phases of corpus callosum theta as early phases, 0 to π, and ascending phases as late phases, π to 2π. Data were binned for visualization only. Full theta phase distributions for local and non-local times were compared with Kuiper’s non-parametric test for continuous circular data for each animal.

Non-local distance

Non-local distance was calculated as the distance between the animal’s actual position and the most likely decoded position in each 2 ms bin (see spatial decoding methods). Using only high-quality valid running times, as described above, we identified the maximum absolute actual-to-decoded distance that occurred during the animal’s approach to the first choice point on a trial (Fig. 4C,D) or during the animal’s traversal of the final segment of a trial (Fig. 4F,G). Data in Fig. 4C,D,F,G were calculated based only on representations that occurred in non-local, unoccupied, track segments to limit representations to those either ahead of (Fig. 4C,D) or behind (Fig. 4F,G) the animal’s trajectory. To compare the non-local distance dynamics before and after Switches for each animal, we log-transformed the model $y=a{e}^{bx}$ into linear form and applied ordinary least squares regression to estimate $\mathrm{l}\mathrm{o}\mathrm{g}\left(a\right)$ and $b$, for both pre- and post-Switch data. Z tests were used to statistically compare the pre- and post-Switch parameters (Fig. 4C,D,F,G). Fig. 4E maximum distances were not required to be in a distinct non-local track segment to the animal’s actual position. Data occurring while the animal occupied the middle two segments of Switch trials (Fig. 4E) were calculated based on Switch trials in which exactly four segments were occupied. Wilcoxon rank sum tests were used for each animal to statistically compare distances observed between different segments.

Confidence intervals and statistics

Error bars, unless otherwise stated, correspond to 95% confidence intervals on the mean. To take a nonparametric approach to determining the statistic, we randomly resampled with replacement from the underlying data distribution 1000 times and calculated the statistic’s bootstrap distribution. Statistical tests are stated throughout the figure legends and text with sample sizes and p values.

Data and code availability

Data and code will be shared publicly via the Distributed Archives for Neurophysiology Data Integration (DANDI) Archive and a repository at https://github.com/LorenFrankLab. Further information necessary for analysis of this dataset is available upon request from the Lead Contact.