Facet‐Dependent Surface Charge and Hydration of Semiconducting Nanoparticles at Variable pH

Abstract

Understanding structure and function of solid–liquid interfaces is essential for the development of nanomaterials for various applications including heterogeneous catalysis in liquid phase processes and water splitting for storage of renewable electricity. The characteristic anisotropy of crystalline nanoparticles is believed to be essential for their performance but remains poorly understood and difficult to characterize. Dual scale atomic force microscopy is used to measure electrostatic and hydration forces of faceted semiconducting SrTiO₃ nanoparticles in aqueous electrolyte at variable pH. The following are demonstrated: the ability to quantify strongly facet‐dependent surface charges yielding isoelectric points of the dominant {100} and {110} facets that differ by as much as 2 pH units; facet‐dependent accumulation of oppositely charged (SiO₂) particles; and that atomic scale defects can be resolved but are in fact rare for the samples investigated. Atomically resolved images and facet‐dependent oscillatory hydration forces suggest a microscopic charge generation mechanism that explains colloidal scale electrostatic forces.

The surface properties of different facets of SrTiO₃ nanoparticles are investigated by atomic force microscopy. Facet‐specific forces, atomic‐level surface structure, defects, and charges are characterized in liquid environment. These measurements reveal substantial differences in isoelectric points and hydration between adjacent facets. These insights are important for the performance of anisotropic nanoparticles in (photoelectro‐)catalysis and for their colloidal self‐assembly.

1. Introduction

Anisotropy of shape and surface properties determine the functionality of faceted nanoparticles (NPs) in various contexts including crystal growth,^{[ 1 ]} biosensing,^{[ 2 ]} facet selective colloidal self‐assembly of complex materials,^{[ 3} , ^{4 ]} enhanced selective cellular uptake,^{[ 5 ]} and improved photo/electrocatalytic activity.^{[ 6} , ^{7 ]} In all cases, the interplay between the intrinsic anisotropy of the NPs and their interaction with the (usually aqueous) ambient environment gives rise to the anisotropic interaction forces that control the performance of the NPs. Specifically, in (photoelectro‐)catalysis with semiconducting NPs the anisotropy of surface charge has the important distinct functions of controlling the selective attraction or repulsion of reactants from the ambient solution outside the NP and generating an internal electric field inside the NP that separates photogenerated electrons and holes to different facets.^{[ 8 ]} This dual function is relevant both during operation and upfront during material synthesis, upon facet‐selective deposition of co‐catalysts (BiVO₄,^{[ 9 ]} TiO₂,^{[ 10 ]} SrTiO₃,^{[ 11} , ¹² , ^{13 ]} and others^{[ 14 ]}). A recent report indeed attributed the observed near‐100% internal quantum efficiency for water splitting by SrTiO₃ NPs to anisotropy‐induced internal electric fields.^{[ 12 ]} Yet, direct experimental confirmation of the potential differences and other microscopic facet properties is lacking. As a consequence, the relative importance of competing charge generation mechanisms such as (de)hydroxylation and ion adsorption/desorption equilibria,^{[ 8} , ¹⁵ , ¹⁶ , ^{17 ]} hydration,^{[ 18} , ^{19 ]} possible surface reconstructions,^{[ 20} , ^{21 ]} atomic scale defects,^{[ 22 ]} and metal–semiconductor contacts at co‐catalyst‐NP interfaces^{[ 23 ]} is poorly understood.

Currently, surface properties are largely inferred from averaging techniques applied either to macroscopic single crystalline surfaces in vacuum or to large ensembles of NPs. For instance, X‐ray photoelectron spectroscopy and scanning tunneling microscopy, in conjunction with detailed numerical simulations have revealed important aspects of the surface termination/reconstructions and surface energy of faceted SrTiO₃ NPs.^{[ 20} , ²¹ , ²⁴ , ^{25 ]} Yet, it is not clear to what extent these observations prevail when faceted NPs are immersed in electrolytes of variable composition. Likewise, electrokinetic measurements in ambient electrolyte often yield highly scattered results, e.g., with isoelectric points of SrTiO₃ and other materials varying by several pH^{[ 13} , ^{26 ]} units, presumably due to preparation‐dependent variations of surface properties. A detailed in situ characterization of NPs is therefore highly needed.

However, techniques to address this challenge with subparticle resolution are hard to implement and still in their infancy.^{[ 23} , ²⁷ , ^{28 ]} While in situ atomic force microscopy (AFM) and spectroscopy have revealed unprecedented insights into structure,^{[ 29 ]} hydration,^{[ 30} , ^{31 ]} interaction forces,^{[ 28} , ^{32 ]} and adsorption processes at solid–electrolyte interfaces^{[ 33} , ^{34 ]} in recent years, direct access to local electrical properties is severely compromised by the electrical conductivity of the background electrolyte.^{[ 35 ]} Moreover, techniques such as Kelvin probe microscopy and scanning capacitance AFM provide access to continuum scale electrostatic potentials but fail to resolve details of the atomic surface structure. In contrast, our recently developed approach of combining colloidal scale atomic force spectroscopy with atomic resolution AFM imaging provides access to both continuum and atomic scale information and thereby enables a detailed picture of charge generation at heterogeneous mineral–electrolyte interfaces and the structure of the electric double layer.^{[ 14} , ²⁸ , ^{33 ]}

Here, we apply this combination of dual scale AFM spectroscopy and imaging with adapted AFM tip sizes to individual faceted SrTiO₃ NPs in aqueous electrolyte. Per facet, we determine the isoelectric point, local surface charge densities as a function of pH, and establish a microscopic model of the charge generation and hydration for both the {100} and the {110} facet.

2. Results and Discussion

2.1. Facet‐Dependent Surface Charge Density Measurement

Faceted nanoparticles of strontium titanate (SrTiO₃) were synthesized by a solvothermal method.^{[ 36 ]} They display a truncated rhombic dodecahedral shape with six squared {100} facets surrounded by twelve hexagonal {110} facets (Figure  1a and Figures S1 and S2, Supporting Information). X‐ray diffraction confirms a high degree of crystallinity and phase purity (Figure S3, Supporting Information). The particles are immobilized on clean sapphire substrates by spontaneous adsorption from suspension and subsequently imaged in aqueous NaCl solutions (conc. 10 × 10⁻³ m) using dynamic noncontact AFM in a 3D force–volume acquisition mode (see the Experimental Section for details). Force gradient maps extracted from the raw data using standard procedures^{[ 28 ]} reveal that the sign of the tip–sample interaction force depends on the facet: hexagonally shaped {110} facets display repulsive forces; squared {100} facets display attractive forces (Figure 1b). As the AFM tips are made from silica, which is negatively charged for all pH values investigated here, the sign of the forces implies that the {110} facets of SrTiO₃ NPs carry a negative and the {100} facets a positive surface charge at pH 5.7. Forces are found to decay exponentially with a decay length of ≈2.6 nm for tip–sample separations of ≈1.5 nm and beyond, as expected for electric double layer forces (Figure 1c). At tip–sample separations below 1.5–2 nm the interactions are determined by the balance of van de Waals and short‐range hydration forces. While the sign of the force is consistent for each type of facet, the absolute forces depend somewhat on the orientation of the specific facet with respect to the surface normal (Figure S4, Supporting Information). For a quantitative analysis, we fit the force curves using Derjaguin‐Landau‐Verwey‐Overbeek (DLVO) theory using a Gouy‐Chapman model with linearized charge regulation boundary condition^{[ 28} , ³² , ^{37 ]} (see the Experimental Section and Note S1, Supporting Information, for details). For the two almost horizontally oriented facets in Figure 1b (see encircled regions), this results in averaged surface charge densities of σ_{100} = + 0.033 ± 0.008 e nm⁻² and σ_{110} = − 0.04 ± 0.01 e nm⁻², corresponding to surface potentials of +17 and −27 mV, respectively. Such values are rather common in colloid science. They reflect charge densities as experienced on a continuum colloidal scale of ≈1.5 nm from the surface and beyond. From an atomistic perspective, however, these values are very low with several tens of nm² per net elementary charge. Much higher charge densities as suggested, e.g., for ideal ${\mathrm{O}}_2^{4-}$‐ or SrTiO⁴⁺ ‐terminated configurations of SrTiO₃ {110} are thus never observed on the colloidal scale. If present, we conclude that such high charge densities are locally compensated by hydroxylation and/or adsorbing water ions (see below). Only within ≈1 nm of the surface, charged reactants may experience much stronger local charges, depending on the configuration of the surface involving, e.g., steps, defects, hydroxylation, and adsorbed ions.^{[ 33 ]}

Figure 1.

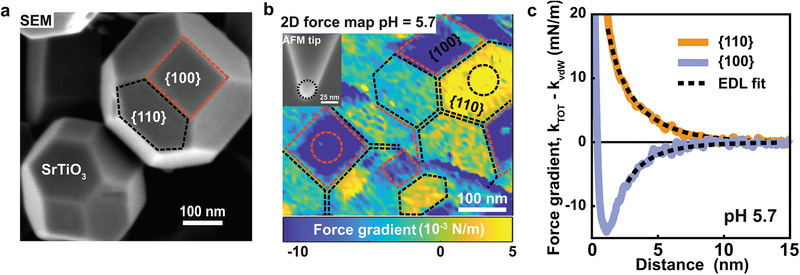
Atomic force microscopy (AFM) measurement on SrTiO₃ nanoparticles. a) SEM image of SrTiO₃ nanoparticles on a silicon wafer. Red square and black hexagonal shapes indicate the {100} and {110} facet, respectively. b) 2D force gradient (k _TOT) map shows tip–SrTiO₃ nanoparticle interactions in 10 × 10⁻³ m NaCl solution at pH = 5.7. The 2D map showing the force gradient at 2 nm away from the SrTiO₃ surface was extracted from 3D force versus distance (FD) volume plot. The 3D FD volume plot was obtained by measuring 80 × 80 tip‐SrTiO₃ interaction curves. The lateral distance between each force–distance curve is 6 nm. Color code: yellow indicates a repulsive interaction, whereas blue indicates an attractive interaction. Inset: SEM image of AFM tip after the experiment. (MikroMash NSC36/Cr‐Au back side coated tip, with parameters of the silicon cantilever: Q factor = 2.6; resonance frequency = 16.137 kHz; spring constant = 0.49 N m⁻¹; tip radius = 13.2 ± 2 nm). c) Average force gradient versus distance curves across a flat region at the center of {100} and {110} facets of SrTiO₃ particles (marked with black and red circles on the 2D maps in (b). Solid lines are experimental data after subtraction of van der Waals interaction (k _TOT−k _vdW) and dotted black lines are the theoretically fitted force curves using EDL theory, taking into account charge regulation. The resulting surface charge from fitting the experimental data are 0.033 and −0.04 e nm⁻² on {100} and {110} facets, respectively. The total interaction stiffness (k _TOT) and topography image corresponding to the force map is shown in Figure S1 (Supporting Information).

2.2. Facet‐Dependent Potential of Zero Charge

To explore the charging behavior of SrTiO₃ in more detail, we monitored two adjacent {100} and {110} facets on a single NP upon varying the pH between 3.5 and 11 (Figure  2 ). At pH 10.8, the forces are repulsive on both facets, implying negative surface charge densities. The DLVO analysis with charge regulation yields values of σ_{100} = − 0.052 e nm⁻² and σ_{110} = − 0.082 e nm⁻², respectively (Figure 2d,h). Upon decreasing the pH to 5.7 and further down to pH 4, the force on the {110} facet remained repulsive, whereas the force on the {100} facet became attractive indicating a charge reversal toward a positive charge density, in agreement with Figure 1. Upon reducing the pH even further to 3.5, both facets display attractive forces and hence carry a positive charge (Figure 2a,e). This result is confirmed for a series of NPs with diameters ranging from 100 to 250 nm (Figure  3a).

Figure 2.

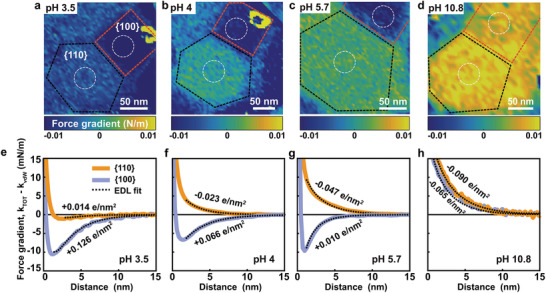
Atomic force microscopy (AFM) of SrTiO₃ nanoparticles. a–d) Color‐coded 2D force maps showing tip–sample interaction (k _TOT) forces on the SrTiO₃ nanoparticle facets in 10 × 10⁻³ m NaCl solution at a) pH 3.5, b) pH 4, c) pH 5.7, and d) pH 10.8 (blue: attractive force; yellow: repulsive force). Note: The maps are shown at 2 nm distance from the SrTiO₃ nanoparticle surface. All force maps are recorded on the same SrTiO₃ particle with the same probe (tip parameters: Q factor = 3.3; resonance frequency = 25.368 kHz; spring constant = 1.02 N m⁻¹; tip radius = 13.9 ± 2 nm; see the Experimental Section for details). Topography image corresponding to the force maps are shown in Figure S5 (Supporting Information). e‐h) The force gradient versus distance after subtraction of van der Waals force averaged over white encircled areas in (a)–(d). Solid lines: orange – center of on {110} facet; blue – center of {100} facet. Dotted black lines are the theoretically fitted force curves using EDL theory with charge regulation boundary condition. Orientations of the local surface normal on {100} and {110} are ≈10° and 30°, respectively. The total interaction stiffness and DVLO is shown in Figure S5 (Supporting Information).

Figure 3.

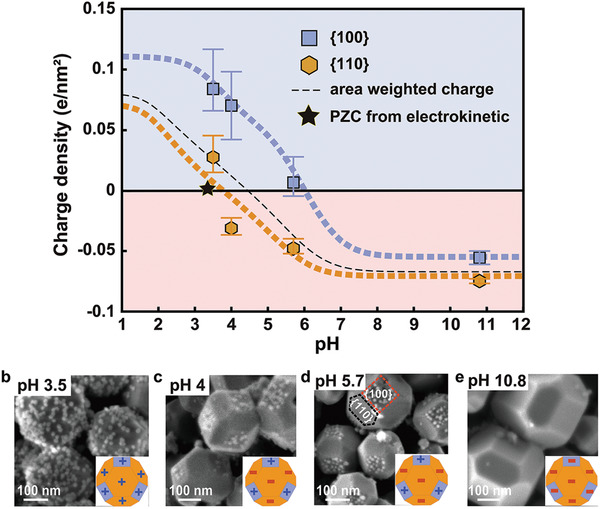
Electrical (charge) properties of {100} and {110} facets SrTiO₃ nanoparticles. a) Surface charge of {100} and {110} facets of SrTiO₃ nanoparticle as a function of pH in 10 × 10⁻³ m NaCl. The thick dashed blue and orange lines represent the best‐fit surface complexation model (see the Experimental Section for details). The thin black dotted line is the calculated particle charge accounting for particle {110} and {100} facets areas ({100}:{110} = 0.224:0.776). b–e) SEM images of SrTiO₃ nanoparticle after silica nanoparticles (12 nm) adsorption experiment at different pH. At pH 4 and 5.7 negatively charged SiO₂ nanoparticles are adsorbed only on positively charged squared {100} facets. At pH 3.5 both {100} and {110} facets of SrTiO₃ are positively charged and negatively charged SiO₂ are deposited on both facets. At pH 10.8 negatively charged facets and silica nanoparticles repel each other, thus no adsorption of SiO₂ particles is observed.

For all particles, both facets reverse their charge density from negative at high to positive at low pH. Yet, the isoelectric points (IEPs) of the two facets are two pH units apart: IEP_{100} ≈ 6 and IEP_{110} ≈ 4 (Figure 3a and Figure S6, Supporting Information). Within the rather wide range of 4 < pH < 6, the two facets thus carry an opposite surface charge, implying a very strong electric field within the particle.^{[ 8 ]} Yet, even for higher and lower pH, the potential of the {100} facet is always more positive than the one of the {110} facets (Figure S6, Supporting Information), implying that photogenerated electrons accumulate at the {100} and holes at the {110} facet. This observation is consistent with the reductive and oxidative photodeposition of co‐catalysts on the {100} and {110} facets of SrTiO₃.^{[ 11} , ^{12 ]}

Suspensions of our SrTiO₃ NPs display an (average) IEP of pH 3.5 in electrokinetic measurements of the ζ‐potential (black star in Figure 3a; Figure S7, Supporting Information). Comparison to the facet‐resolved AFM measurements (Figure 3a) thus clearly demonstrates that a vanishing electrokinetic mobility does not imply vanishing charge densities across the surface of faceted NPs. This observation has important consequences for the interaction of the NPs with charged solutes and other suspended particles. To illustrate this point, we analyzed mixed colloidal suspensions of faceted SrTiO₃ NPs and amorphous, silica NPs (diameter: 12 nm) with a homogeneous negative surface charge, Figure 3b–e and Figure S8 (Supporting Information). At high pH, the mixed suspension is stable and silica particles do not adsorb to any facet of the STO NPs. For intermediate pH values between 4 and 6, the silica particles selectively adsorb to the {100} facet, while the {110} facets remain silica‐free. At pH 3.5, below the IEP of both facets, indeed both facets are covered by silica particles. At even lower pH < 2, silica also becomes positively charged and hence adsorption is again suppressed for both facets (Figure S8, Supporting Information).

Based on these results, one might expect to find the minimum electrokinetic mobility at the pH where the facet area‐weighted total charge of the NPs vanishes—possibly with some minor corrections due to higher moments of charge distribution.^{[ 38 ]} Using the geometric ratio between {110} and {100} facets of ≈3.5:1 (Figure S2, Supporting Information), we find that the net charge switches sign at pH ≈ 4.5 (black dashed line in Figure 3a), i.e., at a substantially higher pH than extracted from the zeta potential measurements (black star in Figure 3a; see also Figure S7, Supporting Information). Remarkably, the measured average IEP is even lower than IEP_{110}.

2.3. Microscopic Charge Generation and Hydration Structure

To identify possible origins of this apparent discrepancy, we imaged the faceted SrTiO₃ NPs using at higher lateral resolution using ultrasharp AFM tips with a radius of 1–2 nm, Figure  4 . The resulting images confirm the overall dominance of hexagonal {110} and squared {100} facets on the NPs. Yet, they also display a transition region between neighboring facets that is smeared out over a width of 10–30 nm (Figure 4b and Figure S9, Supporting Information). Within this region, the surface is disordered with a typical corrugation of ≈ 300 pm, i.e., substantially more than on the adjacent atomically smooth {100} and {110} facets with a corrugation of 10–20 pm. The transition region contains steps and other structural defects that prevent detailed imaging of the atomic structure. This disorder also modifies the tip–sample interaction and gives rise to a distinct contrast in AFM phase images (Figure 4a,b and Figure S9, Supporting Information). From the AFM images, we estimate that the disordered regions make up 20–30% of the total surface area of the NPs. Using this value and assuming that the minimum of the electrokinetic mobility corresponds to zero total charge, we infer an average charge density of σ_edge = − 0.075 e nm⁻² of the disordered edge regions at pH 3.5. This value corresponds to a local potential of −45.2 mV, which has important effect on the electrostatic potential distribution at the NP surfaces and hence also within the particle.

Figure 4.

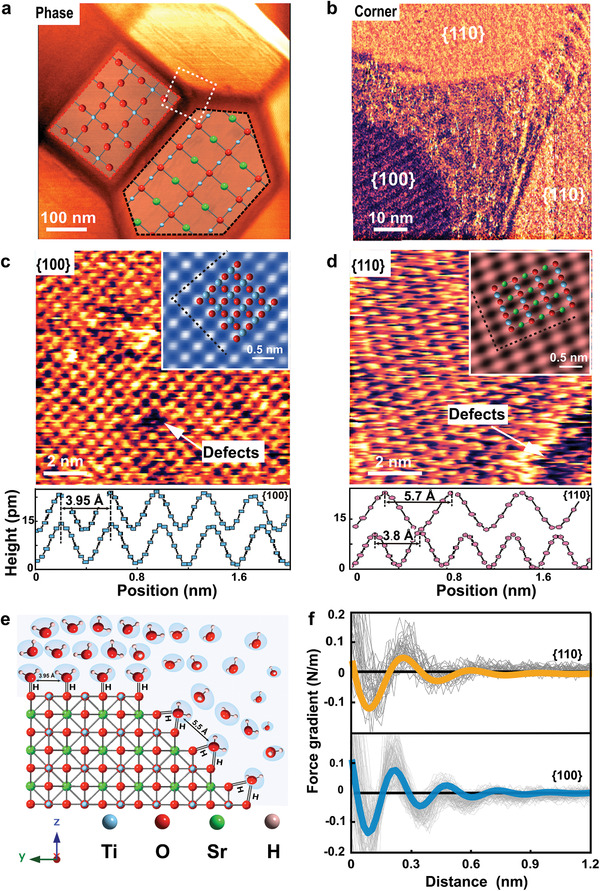
Hydration forces and atomic resolution images of {100} and {110} on SrTiO₃ nanoparticles measured using AM‐AFM. a) AFM phase image of SrTiO₃ nanoparticle superimposed with crystallographic lattice structure of {110} and {100} facets in ab planes. O, Sr, and Ti atoms are shown in red, green, and blue, respectively. b) High‐resolution phase image of edge and corner between several facets displaying some steps and regions with heterogeneous structure composed of domains of crystalline and disordered structure. c,d) Atomic resolution topography images on {100} and {110} of SrTiO₃ measured in 10 × 10⁻³ m NaCl at pH 6. It displays square lattice with lattice parameters a = 0.383 nm and b = 0.393 nm with a vacancy defect on {100} and rectangular structure on {110} of SrTiO₃ with lattice parameters a = 0.38 nm and b = 0.57 nm and a region with disordered nonperiodic structure on {110}. Top insets represent zoomed and Fourier‐filtered view of atomic scale images with superimposed X‐ray resolved structure of {100} and {110}. e) X‐ray crystal structure of SrTiO₃ displaying {110} and {100} planes with graphic representation of facets hydration structure. f) Averaged force gradient versus apparent tip–sample distance measured in 10 × 10⁻³ m NaCl with pH of 6. (Thick orange line for {110} and blue for {100} of SrTiO₃ nanoparticle, light gray: individual force curves on {100} and {110}.)

Having established the role of the transition regions for the total charge, we return to the mechanism of charge generation on the {100} and the {110} facet. The atomically resolved images of the {100} facets display a square symmetry with lattice parameters of 0.38 and 0.39 nm along the (001) and the (010) direction (X‐ray structure: 0.39 nm^{[ 25 ]}) (Figure 4c and Figure S10, Supporting Information). The {110} facets display periodicities of 0.38 nm along [101] and 0.57 nm along [010] (X‐ray: 0.39 and 0.56 nm^{[ 25 ]}) (Figure 4d and Figure S10, Supporting Information). Occasionally, atomic scale defects are observed on both facets and demonstrate the “true atomic resolution” character of the imaging process (Figure 4c,d). However, the density of such defects is very low, except upon approaching the disordered transition regions toward an adjacent facet.

Periodicity and symmetry of the patterns reflect a bulk‐terminated structure for both facets without indications of any surface reconstruction. This deviates from various reports on thermally annealed macroscopic single crystals that display various types of surface reconstructions for both types of facets.^{[ 20} , ²¹ , ^{39 ]} Apparently, such reconstructions do not occur for the present hydrothermal synthesis procedure of SrTiO₃ NPs in ambient electrolyte.^{[ 40 ]}

Bulk termination still offers two possible surface terminations for each facet. The {100} facets can display either TiO₂‐termination or SrO‐termination, both being intrinsically electrically neutral^{[ 25 ]} (Figure S10b,c, Supporting Information). Given the more ionic character of the SrO‐termination and the higher solubility of Sr²⁺, it is widely believed that TiO₂‐termination is more stable, in particular in ambient water.^{[ 41 ]} Given the positive and negative partial charges on the metal ions and the oxygen atoms, respectively, the two sites are likely to attract hydroxyl ions and protons from the ambient electrolyte, leading to an overall neutral hydroxylated surface. This hydroxylated surface offers many possible configurations for hydrogen bonding to the ambient water and hydronium and/or hydroxide ions, as observed in molecular simulations and XPS studies.^{[ 24} , ^{42 ]} A slight imbalance between protonation and hydroxyl ion adsorption appears to be responsible for the net average surface charge at high and low pH. To provide a qualitative description of this behavior, we introduce effective surface speciation reactions $\sim STi+{\text{OH}}^{-}\leftrightarrow \sim STiO{\mathrm{H}}^{-}$ and $\sim SO+{\mathrm{H}}^{+}\leftrightarrow \sim SO{\mathrm{H}}^{+}$with equilibrium constants $K_1^{\{100\}}$ and $K_2^{\{100\}}$. Fitting to the experimental data presented in Figure 3a (see the Experimental Section and Note S2, Supporting Information, for details) yields $p{K}_1^{\{100\}}=5.6$ and $p{K}_2^{\{100\}}=8.4$ (dashed blue lines in Figure 3a). The maximum charge densities shown in Figure 3a then correspond to a fraction of at most 1.4% of (de)protonated surface hydroxyl groups.

The {110} surface is more complex than the {100} surface. Based on the bulk structure, it is polar with two highly charged possible terminations, SrTiO⁴⁺ and (2O)⁴⁻ (Figure S10e,f, Supporting Information). In view of the very low surface charge densities on the colloidal scale, we conclude that this intrinsic charge is compensated at the interface by water ions. The very low isoelectric point of the {110} facet then suggests that the surface is oxygen terminated with near‐perfect charge compensation of protons from the ambient electrolyte. Like in the case of the {100} facet, we describe the amphoteric charging at low and high pH by (de)protonation reactions of the surface hydroxyl groups $\sim {\text{SO}}^{-}+{\mathrm{H}}^{+}\leftrightarrow \sim SOH$ and $\sim SOH+{\mathrm{H}}^{+}\leftrightarrow \sim SO{H}_2^{+}$. We find effective pK values of $p{K}_1^{\{110\}}=4.3$ and $p{K}_2^{\{110\}}=3.1$ (dashed orange lines in Figure 3a). Again, we emphasize that these reactions should be considered as an effective description of presumably more complex configurations of water molecules and ions that generate the net charge as experienced on a continuum scale.

Additional insight about the hydration structure arises from the periodicity observed of the atomic resolution images. The distance between adjacent protrusions along the [110] direction in Figure 4d is twice the distance between adjacent surface oxygen atoms. Considering that the contrast in atomic resolution images in ambient electrolyte is mediated by hydration water and typically shows the structure of the hydration water rather than the surface atoms,^{[ 30 ]} this suggests that two adjacent hydroxylated surface O atoms along the [110] direction both act as H‐donors in H‐bonds to the same water molecule (Figure 4e). The corrugation in the AFM images then reflects this first layer H₂O molecules, which are doubly H‐bonded to the substrate.^{[ 30 ]} This configuration has another important consequence: the rather large distance between adjacent hydration H₂O molecules along the [110] direction as well as their saturated H‐bonding capacity with the substrate reduce the strength of the H‐bonding network within the interfacial water layer as compared to the {100} surface, suggesting that the hydration structure away from the solid surface has to be less pronounced.^{[ 43 ]} This is indeed observed in AFM spectroscopy measurements with ultrasharp AFM tips (Figure 4e). While the averaged force curves on both facets display the expected oscillatory character corresponding to the diameter of H₂O molecules, both amplitude and range of these oscillations are clearly more pronounced on the {100} as compared to the {110} facet. According to simulations,^{[ 43 ]} a higher degree of organization of water within the hydration layers implies longer residence times for water molecules and higher diffusion barriers of solutes and particles.^{[ 4 ]} A recent study on H‐evolution from Pt electrodes demonstrated a strong correlation between hydration structure and electrocatalytic activity.^{[ 19 ]} Similarly, highly organized interfacial water layers with a high density of hydrogen bonds, are believed to stabilize reaction intermediates such as •OH and •OOH.^{[ 17} , ⁴³ , ^{44 ]}

3. Conclusion

Our results provide a consistent picture of both the charging behavior and hydration structure of faceted SrTiO₃ NPs in aqueous electrolyte. The AFM spectroscopy technique provides direct access to the facet‐dependent local surface charge density and potential drop across the diffuse part of the electric double layer and thereby to the potential of the solid–electrolyte interfaces at variable pH. In photocatalysis, this information is an essential boundary condition for understanding the distribution and dynamics of both charged reactants in the ambient solution and for photogenerated charge carriers within the NPs. Both situations can be studied in detail by extending the technique to situations under illumination and in the presence of co‐catalysts. Facet‐dependent hydration may provide additional clues to facet‐specific reactivity and—beyond photocatalysis—to a more quantitative understanding of self‐assembly processes such as oriented attachment in crystal growth.

4. Experimental Section

Sample Preparation

SrTiO₃ nanoparticles with anisotropic facets were synthesized as described in detail by Dong et al.^{[ 36 ]} A suspension of the powder (≈0.1 mg mL⁻¹) was prepared using deionized water (Millipore Inc.). A 100 µL aliquot of this suspension was drop‐cast onto freshly cleaned 12 mm × 12 mm sapphire substrates. After a residence time of 5 min at 120 °C, the sample was rinsed with deionized water to remove loosely bounded particles and blown dry.

Adsorption of SiO₂ Nanoparticles onto SrTiO₃

100 µL of commercial SiO₂ nanoparticles (LUDOX AS‐30) dispersed in water with average diameter of 12 nm were mixed with 2 mg of SrTiO₃ nanoparticles in 20 mL of 10 × 10⁻³ m NaCl solution (99% ACS reagent grade, Sigma Aldrich). Afterward, the pH of the solutions was adjusted to 1.7, 3.2, 4.5, 5.7, 7.7, and 10.8 by adding HCl (ACS reagent, 37%, Sigma Aldrich) or NaOH solutions (ACS reagent, ≥97.0%, pellets, Sigma Aldrich). All chemicals used were purchased from Sigma‐Aldrich. After 10 min the suspension was centrifuged (2000 rpm, for 15 min), and subsequently the solution was drop‐cast onto the substrate, blown dry and imaged using scanning electron microscopy (SEM).

Atomic Force Microscopy

Dynamic amplitude modulation (AM‐AFM) imaging and force spectroscopy measurements were performed with a commercial Asylum Research Cypher ES equipped with photo‐thermal excitation. First, the topography of the sample under liquid was taken, using AM‐AFM imaging. Next, small amplitude (A ≤ 1 nm) AM‐AFM force spectroscopy was performed on SrTiO₃ particles. Amplitude (A) and phase (φ) were measured as a function of tip–substrate distance either on a fixed point on the particle surface (≈200 approach curves) or on a 2D grid over the area of interest using the built‐in 3D force volume mapping of the Cypher AFM software. Tip–sample force gradient (interaction stiffness k _int) was calculated from the amplitude and phase shift versus distance curves using standard force inversion procedures as extensively described by Klaassen et al.^{[ 28} , ^{37 ]}

Force spectroscopy measurements were performed using rectangular silicon cantilevers with conical silicon probes tips (MikroMash NSC36/Cr‐Au BS, cone angle 40°) covered by a 1–2 nm thick native oxide layer. The cantilever stiffness k _c, quality factor Q, and resonance frequency f ₀ were extracted from the thermal noise spectrum of the free cantilever in liquid at a distance of h = 500 nm from the substrate. Typical values are k _c ≈ 0.5–1 N m⁻¹, f ₀ ≈ 22–25 kHz, Q ≈ 2.9. To measure the tip–sample interactions, the cantilever was driven at a fixed frequency (f ≈ 0.97∙f ₀) by an intensity‐modulated blue laser diode that was focused on the gold‐coated topside of the cantilever close to its base. To protect tip sharpness, the amplitude signal was not allowed to drop below 80% of its free oscillation amplitude (A ₀ < 1 nm). The radius of the tip was determined after AFM data collection, from SEM images. Prior to use, AFM tips and sapphire substrates were subsequently cleaned by rinsing with isopropanol, ethanol, water and exposed to oxygen plasma (PDC‐32G‐2, Harrick Plasma) for 15–30 min.

Atomic resolution imaging and measurements of short‐range hydration forces were performed with ultrasharp Arrow UHF‐AUD tips (Nanoworld, Neuchatel, Switzerland; k = 3.35 N m⁻¹, f ₀ = 600–1000 kHz, and Q = 11, tip radius ≈ 1–2 nm). The AM‐AFM mode was operated with a free amplitude A ₀ ≤ 0.3 nm, a high scan rate ≈12 Hz, and an amplitude set point as high as possible, typically A/A ₀ ≥ 0.9.^{[ 29 ]}

The experiments were performed in a closed cell that allows liquid exchange and temperature control, T = 22.7 ± 0.5 °C. The cantilever was immersed in a droplet of liquid (0.2 mL) that was sandwiched between the substrate (1.2 × 1.2 cm²) and the top of the cell. The liquid exchange was done by replacing at least 25 times the drop volume. Measurements were performed after an equilibration time of 15 min.

Surface Charge Determination from Force–Distance Curves

As described earlier,^{[ 28} , ^{32 ]} the measured force–distance curves were converted to surface charge using DLVO theory, taking into account charge regulation (see Note S1, Supporting Information, for details).

Surface Chemistry Modeling

For modeling the surface charge complexation of SrTiO₃ nanoparticles on the {100} and {110} facets, a multisite proton adsorption (MUSIC) model^{[ 45 ]} was used (see Note S2, Supporting Information, for details).

Conflict of Interest

The authors declare no conflict of interest.

Author Contributions

I.S., F.M., B.M., and G.M. conceived and designed the experiments. S.S. synthesized the particles. S.S. and I.S. carried out AFM experiments. I.S., F.M., B.M., and G.M. contributed to overall interpretation of data and their implications. S.S., I.S., and D.v.d.E. performed data analysis and theoretical calculations. S.S., I.S., B.M., and F.M. wrote the manuscript.

Supporting information

Supporting Information

Su S., Siretanu I., van den D. Ende, Mei B., Mul G., Mugele F., Facet‐Dependent Surface Charge and Hydration of Semiconducting Nanoparticles at Variable pH. Adv. Mater. 2021, 33, 2106229. 10.1002/adma.202106229

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.