Abstract
We propose a novel quantitative method to explore the forces affecting mitochondria within living cells in an almost non-invasive fashion. This new tool enables the detection of localized mechanical impulses on these organelles that occur amidst the stationary fluctuations caused by the thermal jittering in the cytoplasm. Recent experimental evidence shows that the action of mechanical forces has important effects on the dynamics, morphology and distribution of mitochondria in cells. In particular, their crosstalk with the cytoskeleton has been found to alter these organelles function; however, the mechanisms underlying this phenomenon are largely unknown. Our results highlight the different functions that cytoskeletal networks play in shaping mitochondrial dynamics. This work presents a novel technique to extend our knowledge of how the impact of mechanical cues can be quantified at the single organelle level. Moreover, this approach can be expanded to the study of other organelles or biopolymers.
Subject terms: Intracellular movement, Mitochondria, Cytoskeleton, Biological physics
Introduction
Mitochondria are essential organelles responsible for fulfilling vital functions that guarantee cell survival1. These organelles are particularly dynamic and flexible, being able to redistribute themselves in the cytoplasm and to adopt different morphologies in response to chemical or physical signals2,3. In recent years, there has been growing interest in understanding how mechanical forces impact on the morphological fluctuations and dynamics of mitochondria. In particular, the cytoskeleton has been identified as one of the mechano-regulatory agents of these organelles due to its close interaction with them2.
In the cell, mitochondria transport, organization, and morphodynamics strongly depend on the cytoskeletal networks4–8. Given their anchorage to cytoskeletal elements (i.e. microtubules, F-actin, and intermediates filaments), these organelles are consistently exposed to both compressive and tensile stresses within the cytoplasm9. Thus, their dynamics and function are affected by the mechanical impulses transmitted to them3,10–12. For instance, F-actin and microtubule-associated motor proteins (i.e. myosins and dynein/kinesin, respectively) produce piconewton forces13 that are transferred to mitochondria through adaptor complexes that tether mitochondria to cytoskeletal filaments14,15. These mechanical impulses are able to deform mitochondria membranes and induce fission16–18.
The metabolic activity of cells is closely linked to changes in mitochondrial morphology and their exposure to mechanical signals19. Modifications in the biophysical properties of these organelles lead to the reorganization of the cellular chondriome. The relationship between mitochondrial mechanics and metabolism is bidirectional, yet our understanding of how mitochondria adapt mechanically in response to metabolic cues remains limited.
Understanding the mechanobiology of mitochondria in their physiological environment is challenging2. In many cell types, they display elongated shapes20–22 and their mechanical behavior resembles that of semiflexible filaments7. The theory of flexible and semiflexible filaments has provided useful analytical tools to describe polymer dynamics in viscous and viscoelastic environments, which include: center of mass motion, amplitudes of flexural modes, curvature, end to end length and spatial and temporal correlations23–25. All these statistical quantities strongly depend on mechanical properties of the filament and the medium, as well as the presence of external active (e.g. molecular motors) or passive forces (e.g. thermal agitation or constraints). These models have been tested in many experimental systems, such as cilia and microtubules in living cells26–30. In particular, within this framework mitochondria apparent persistence length was estimated in m in Xenopus laevis melanocytes22, highlighting the bending plasticity of these organelles.
Inspired by these ideas, we present here a new methodology that allows determining the active and passive forces exerted on mitochondria within living cells. Additionally, we study the different transport regimes to explore whether these organelles are subjected to active motion, diffusive movement, and/or confinement. We used these tools to explore the mechanisms underlying the motion and deformation of mitochondria within Xenopus laevis melanocytes. Due to their large size (50 m) and relatively small thickness away from the perinuclear region ( 3 m)5 these cells behave as a 2D system in the periphery and so they represent an ideal model for live-cell confocal microscopy. In addition, most mitochondria display simple, i.e. non-branching, filamentous shapes7.
We assessed the influence of the cytoskeleton on mitochondrial motion by selectively disrupting cytoskeletal networks (i.e. microtubules, F-actin and vimentin filaments), as discussed in a previous work7. The cytoskeleton regulates cytoplasmic rheology and transmits mechanical impulses to mitochondria through molecular motors and crosslinkers6,15,31. Therefore, we hypothesized that these treatments would impair mitochondrial cytoskeleton-dependent confinement and mechanical jittering, allowing us to explore the mechanical crosstalk between them. Using the quantitative tools proposed in this work, our results shed new light on how the cytoskeleton-exerted forces modulate mitochondrial dynamics. We believe that this study presents a new approach to extend the knowledge of how the impact of mechanical cues can be quantified at the single organelle level.
Quantitative description of the motion of a filamentous mitochondrion
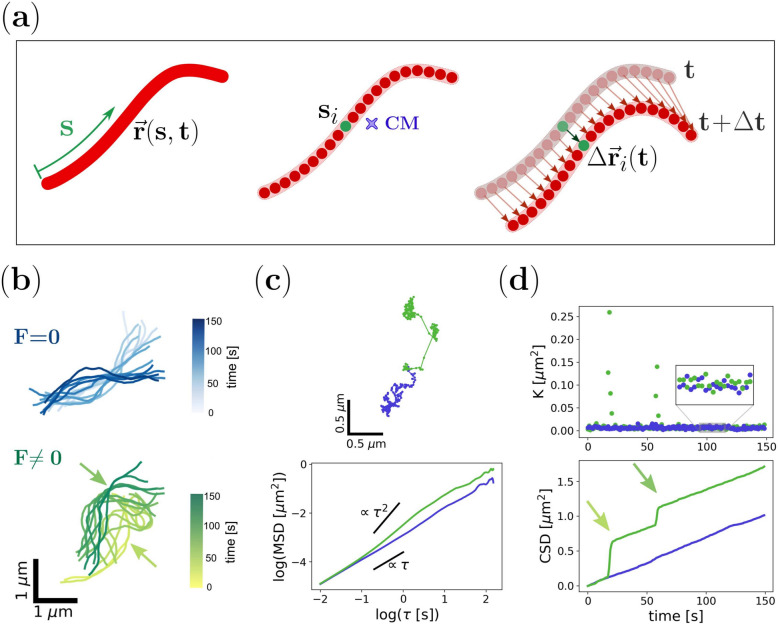
The motion and deformation of an elongated mitochondrion can be described through its curvilinear shape (Fig. 1). In this approximation, the shape of the filament and its evolution in time is characterized by the position of a material point s at time t, with , where L is the natural length. Ideally, s and t are continuous, but in experiments (or numerical simulations) the shape is described by a set of discrete material points (beads), tracked at discrete times , with the sampling time, as represented in Fig. 1a.
Fig. 1.
Physical modeling of mitochondria motion.(a) Representative scheme of a filamentous mitochondria characterized by its curvilinear shape. The organelle profile is described by the position () of a material point (s) registered at a certain time (t) at a distance s from its edge. Each discrete point or bead constituting the filament (, green) was tracked to determine the trajectory of the center of mass (CM) and the displacement after a time lag . (b) Temporal evolution of simulated semiflexible filaments in the absence (F=0, blue; top panel) or presence (F0, green; bottom panel) of active forces. The arrows indicate the points of force application at different times. (c) Trajectories of the CM corresponding to the filaments shown in (b) and dependence of the MSD with for each of them (top and bottom panel, respectively). (d) Temporal evolution of K values and the CSD obtained for the filaments indicated in (b). In the presence of active forces (green data set), K fluctuations over time exhibit outliers that correspond to the jumps (arrows) shown in the CSD graph coinciding with the time of force application.
To characterize the mechanics and motion of the filament, one of the most well-known quantities is the position of the center of mass (CM):
| 1 |
The trajectory of the center of mass contains important information about the overall motion of the filament and its interaction with the environment, which can be rendered by its Mean Square Displacement (MSD):
| 2 |
where is the time-lag,e.g. , and the brackets indicate an average on time t. Typically, the MSD as a function of time-lag is fitted by a power law32:
| 3 |
where and are the generalized diffusion coefficient and exponent, respectively.
While represents a rate of motility, the diffusion exponent constitutes a key global parameter that indicates the overall directionality of a trajectory. Moreover, it is related to the balance of active vs. passive forces acting on the organelle. In the absence of active processes, this exponent will take values smaller than 1 – a hallmark of sub-diffusion – like in ATP-depleted cells33 or in overcrowded environments34–36, reflecting the viscoelastic nature of the microenvironment. In contrast, organelles driven by active forces lead to super-diffusion, and, in these conditions, values ranging 1.2–1.5 have been determined in a wide variety of systems37–40. Yet, for a free filament in a viscous medium, subjected to thermal noise, a diffusive motion is expected . In this case, the diffusion coefficient depends inversely on the medium’s viscosity and the filament’s length23.
Nevertheless, a filament could deform in such a way that the center of mass remains still, but its shape is completely different after a certain time. Therefore, it is more informative to analyze the displacement of individual material points of a filament after a time lag (Fig. 1a, right panel):
| 4 |
This is a very fluctuating quantity, so different averages can be performed to extract relevant information. Here, we consider the average of the square displacements along the filament as a function of time:
| 5 |
This is related to the average area swept by each material point of the filament in a time interval . The greater the fluctuation of the filament’s shape due to stochastic thermal (and non-thermal) forces, the greater the value of K will be, regardless of the movement of the center of mass, which can eventually be still. In Eq. 5, we keep implicit the dependence of K and with , as it is typically the sampling time of the experiment.
For reasons that will become clear later, it is useful to also define the Cumulative Square Displacement (CSD) as:
| 6 |
Since the CSD is the sum of positive quantities, it grows monotonically with time.
In order to explore how these two magnitudes, the MSD and the CSD, can unveil aspects of the dynamics underlying the motion of elongated mitochondria, we performed numerical simulations of a simple model system. We adapted a Worm-Like Chain Model30,41 to describe the temporal evolution of a semiflexible filament immersed in a viscous medium. Briefly, we consider a filament composed of coupled beads immersed in a homogeneous viscous medium and subjected to thermal noise (see Methods and Supplementary Section 1 for details). Active forces are modeled as point-like impulses acting on individual beads following stochastic temporal dynamics. Figure 1b shows two representative filament configurations obtained from simulations in the absence or the presence of active forces.
First, we recovered the trajectories of the center of mass from the simulated shapes and computed the MSD, displayed in Fig. 1c. Normal diffusion behavior is recovered in the absence of active forces, while a super-diffusive regime is obtained in their presence, as predicted by previous studies23.
Then, we also calculated K and CSD from the filament coordinates, shown in Fig. 1d. Interestingly, the behavior of K for both simulations is very similar (i.e. their medians are not significantly different), except for the presence of a few outlier data points in the simulations with active forces. The effect of these extreme values is more evident in the CSD, where jumps are observed on top of a linear behavior obtained in the absence of active forces. Even more relevant, the occurrence of these events correlates with the periods when these forces are turned on, thus providing a potentially useful tool to uncover the temporal pattern of the active forces acting on the filament.
These results illustrate that both magnitudes, MSD and CSD, describe different but complementary aspects of the motion of a semiflexible filament in the presence of active forces. In the next sections, we will evaluate their performance with experimental data obtained from the tracking of mitochondria in living cells.
The Mean Square Displacement of the mitochondria center of mass reveals the coexistence of different motion regimes
The shapes of filamentous mitochondria were recovered from confocal microscopy images of X. laevis melanocytes, as explained in Methods. Briefly, the organelles were considered as curvilinear filaments and a set of discretized coordinates were obtained for each frame of the time-lapse using a tracking algorithm (Fig. 2a and Supplementary Video S1).
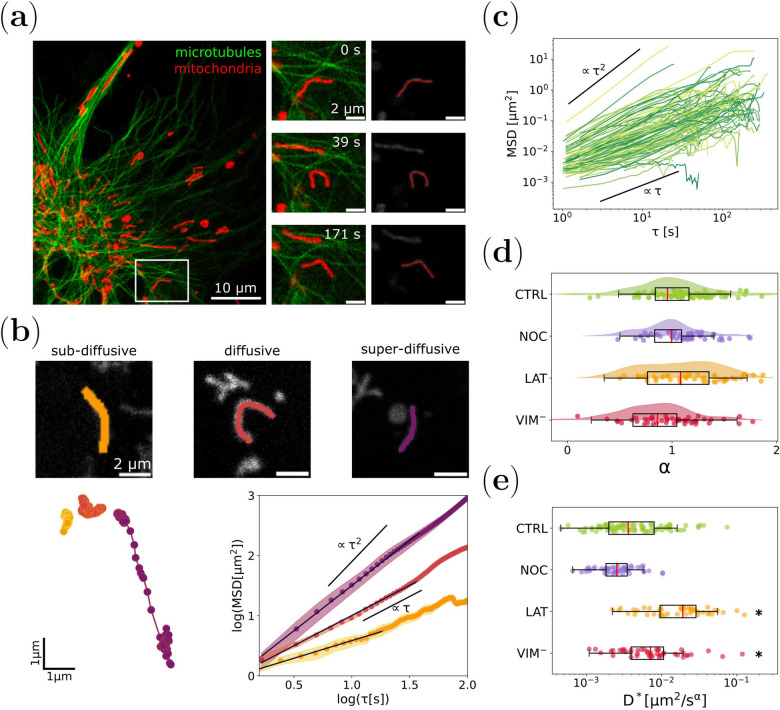
Fig. 2.
Mitochondrial motion regimes depend on cytoskeleton integrity. (a) Representative confocal image of a X. laevis melanophore cell expressing EGFP-XTP (green: microtubules) and incubated with MitoTracker Deep Red FM (red: mitochondria). Time-lapse images of a mitochondrion (white square, left panel) and its respective track are shown in the right panel and Supplementary Video S1. (b) Mitochondrial motion regimes. Tracking of three mitochondria experiencing sub-diffusive (orange, , Supplementary Video S2), diffusive (dark red, , Supplementary Video S3), and super-diffusive (purple, , Supplementary Video S4) behavior (top panel). The trajectories of the CM corresponding to these organelles and the MSD dependence with for each of them are shown at the bottom panel. (c) MSD curves obtained for mitochondria within melanocytes in control condition (CTRL, N=89). (d) Distribution of values registered for mitochondria in control cells (CTRL: green), cells treated with nocodazole (NOC: blue, partial depolymerization of microtubules, N=49) or latrunculin-B (LAT: orange, depolymerization of F-actin, N=48) and cells transfected with mCherry-vim(1-138) (: red, disruption of vimentin filaments, N=46). (e) Generalized diffusion coefficient () distribution obtained for each experimental condition. The asterisks denote significant differences (p-value < 0.05) with respect to CTRL.
Cells were treated with nocodazole (NOC) or latrunculin-B (LAT) to depolymerize microtubules or F-actin, respectively, or transiently transfected with a dominant negative vimentin mutant (mCherry-vim(1-138), ) that resulted in the depletion of this intermediate filaments network.
For each experimental condition, the trajectory of the center of mass of individual organelles was obtained, and the corresponding MSD was computed. An anomalous diffusion model (Eq. 3) was fitted to the MSD time courses, giving the parameters and . In all the evaluated experimental conditions, we identified mitochondria exhibiting super-diffusive (), diffusive (), and sub-diffusive () behaviors. Super- and sub-diffusive regimes could be explained by the presence of active forces23 and confinement of the organelles in the cytoplasm25, respectively. Figure 2b displays three representative examples of these cases (Supplementary Videos S2-S4), while Fig. 2c shows all the experimental MSD trajectories obtained for control condition (CTRL) to illustrate the wide dispersion of the observed different motion regimes.
Figure 2d shows that the distribution of obtained for control condition displays a more pronounced symmetry, in contrast to the results obtained for cells treated with latrunculin-B, which displayed a bimodal distribution (Supplementary Section 2). We found that this bi-modality is compatible with an enhancement of the super-diffusive population that could be attributed to an increase in the frequency and/or intensity of active forces that reach mitochondria in the absence of F-actin. On the contrary, disruption of the vimentin network reduced the directionality of mitochondria trajectories, i.e. values were lower than those observed in control cells, with a sub-diffusive behavior on average. This result could be interpreted considering that vimentin filaments may act as a physical network/mesh that confines organelles close to microtubules or F-actin. This proximity would increase the time mitochondria remain near those filaments, thus promoting motor binding and enhancing active transport38,42,43.
On the other hand, the generalized diffusion coefficients () displayed asymmetric distributions and heavy tails towards high values of (Fig. 2e). Mitochondria from cells with a partially depolymerized microtubule network presented less variability than those recorded in cells without F-actin, which exhibit greater dispersion. Interestingly, although non-significant differences were observed for the distributions of between NOC-treated and control cells (Fig. 2d), mitochondria values were significantly lower in that condition.
Nonetheless, we wanted to better explore the mechanisms underlying the differences in mitochondria motion, so we further analyzed the data displaying apparent normal diffusion regimes, i.e. . We compared the apparent diffusion coefficient values attained in the different experimental conditions (Supplementary Fig. S5 and Table S4) and found that microtubules and F-actin have contrary effects on mitochondria mobility, as previously reported7. The lower mobility observed when microtubules are partially depolymerized suggests a decrease in the active forces jittering mitochondria, supporting previous results showing that mechanical impulses are mainly transmitted to these organelles by the microtubule cytoskeleton4,6,11. In contrast, LAT-treated cells displayed larger diffusion coefficient values, which can be associated with an increase of the active forces and a reduction of the effective viscosity, suggesting that F-actin would confine mitochondria and shield them from mechanical stimuli.
The analysis of the Cumulative Square Displacement allows inferring the active forces temporal pattern acting on mitochondria.
Although the analysis of the MSD gives valuable information on the mitochondria global motion regimes, these results fall short of a complete characterization of the forces acting on the organelles. We propose the study of the Cumulative Square Displacement (CSD) (Eq. 6) as a complementary tool to the MSD.
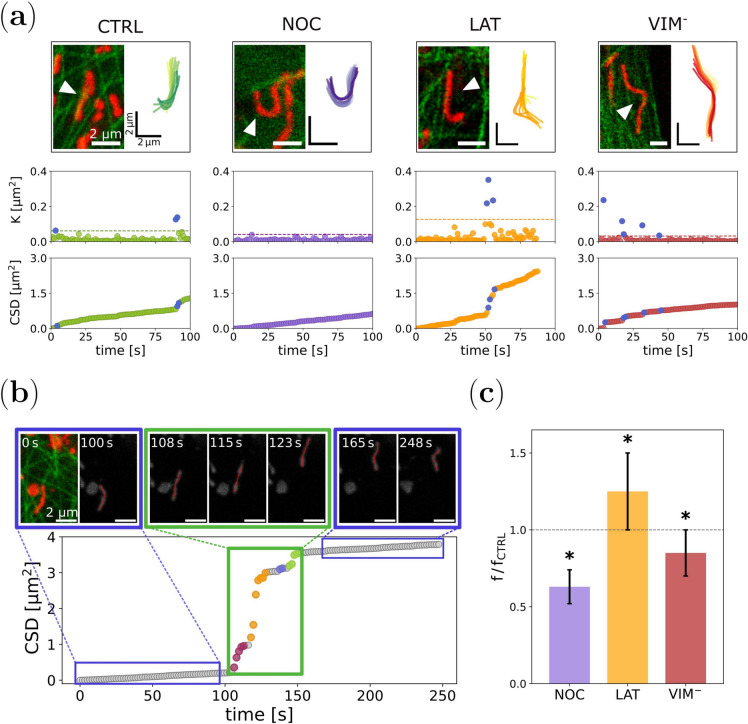
Figure 3a shows the time course of the square displacements K and the CSD of representative mitochondria corresponding to the four explored experimental conditions (see Supplementary Videos S5-S8). Similarly to what was observed in the numerical simulations, the K data points fluctuate around an average value, except for a few outliers. These extreme values are spotted as jumps in the CSD curves. Consistently with the results found in the numerical examples, we propose that these shifts are originated by large mechanical impulses, i.e. kicks, acting on the organelles.
Fig. 3.
Quantification of intracellular forces involved in mitochondrial dynamics. (a) Temporal evolution of the square displacements K and the CSD for mitochondria within X. laevis melanophore cells. For each experimental condition, mitochondria were tracked (top panels, Supplementary Videos S5-S8) to compute K values and the CSD dependence over time (bottom panels). The K outliers and the corresponding jumps at the CSD plots are shown in blue. (b) Correlation of the CSD jumps and the active forces exerted on mitochondria. Representative time-lapse images and tracking of a mitochondrion engaging in active transport (top panel, Supplementary Video S4). When the organelle undergoes a significant longitudinal displacement, a jump is recorded in the CSD graph (bottom panel). The color code at the jump indicates the number of different events detected by the algorithm. (c) Mean frequency of events obtained from the CSD analysis for each experimental condition relative to CTRL, calculated as explained in the text. Asterisks denote significant differences with CTRL.
To explore this possibility, and taking advantage that the used X. laevis cell line expresses fluorescent microtubules – EGFP-XTP44,45– we examined the movies of mitochondria and tried to identify moments when an organelle deforms considerably or is transported along these filaments. In most cases, these pushes correlate with jumps in the CSD curves. An example is shown in Fig. 3b and Supplementary Video S4. It is observed that for times t < 100 s, the mitochondrion slightly fluctuates, but around times 100 s and 150 s, rapid successive displacements of the organelle’s position occur, which is reflected in a vertical shift in the CSD curve. After that, the mitochondrion returns to a slow-motion regime. From the video, the origin of the driving force is not clear, but it might be caused by molecular motors driving the organelle. However, the push from the previous stationary motion is indisputable, highlighting the feasibility of using these events as force detectors.
To perform a systematic study of the data, an automated procedure was developed to detect outliers from the K distribution and group them into single events. The algorithm is based on a threshold criterion and was tested with numerical simulations to tune the threshold value that better reproduced the simulated force pattern (Methods, Supplementary Section 3, and Supplementary Figs. S7-S10). Although one could argue that the choice of this threshold is arbitrary, we will show that the procedure allowed us to compare the results in the treated cells with respect to the control condition., i.e. relative measurement.
We applied this routine to compute the number of events in the trajectories of mitochondria in X. laevis melanocytes, for each experimental condition. It is important to recall that K depends implicitly on , so both the stationary and outlier values of K, change if different time lags are considered. Therefore, to compare the results between different trajectories, it is crucial that they have very similar sampling times.
The average frequency of events was obtained as the quotient between the total number of events and the total tracking duration (Table 1). A bootstrapping procedure was applied to compute the confidence interval (see Methods). Since the number of detected events is sensitive to the data sampling time, as discussed above, Fig. 3c displays the mean frequency of each experimental condition relative to the control one obtained using the same sampling time.
Table 1.
Frequency of events for the different experimental conditions. are control experiments to NOC condition, while are control experiments to LAT and conditions. Errors were determined following a bootstrapping procedure. Asterisks indicate statistical differences between distributions of bootstrap samples.
| Condition | (s) | Frequency () |
|---|---|---|
| 1.66 | 1.0 ± 0.1 | |
| NOC | 1.64 | 0.62 ± 0.05 * |
| 1.1 | 1.3 ± 0.1 | |
| LAT | 1.1 | 1.6 ± 0.2 * |
| 1.2 | 1.1 ± 0.1 * |
Interestingly, the three cytoskeletal networks have an impact on the number of active impulses suffered by mitochondria. For cells with partially depolymerized microtubules (NOC) or in the absence of vimentin filaments () the frequency of active events is reduced with respect to control cells. On the other hand, the absence of F-actin (LAT) resulted in an increased number of events per trajectory.
Also, we explored the stationary fluctuations of K. We computed the median of K(t) for each trajectory and analyzed their distribution under different experimental conditions (Supplementary Fig. S11). Since outliers () are rare events, the median represents a robust estimate of the stationary value of K(t). We also calculated the mean of , and the results were consistent with the ones obtained for the median. Notably, we found a shift towards larger values of K for latrunculin-B-treated cells and for the vimentin mutant.
Altogether, these results go in the same direction as those obtained with the MSD analysis and support the hypothesis that microtubules are the main source of mechanical stimulation for mitochondria, while F-actin acts as a force absorber/dampener. Additionally, the reduction of active events in the vimentin mutant condition reinforces the notion that intermediate filaments confine mitochondria to remain in close proximity to microtubules, thereby favoring their mechanical contact.
Discussion
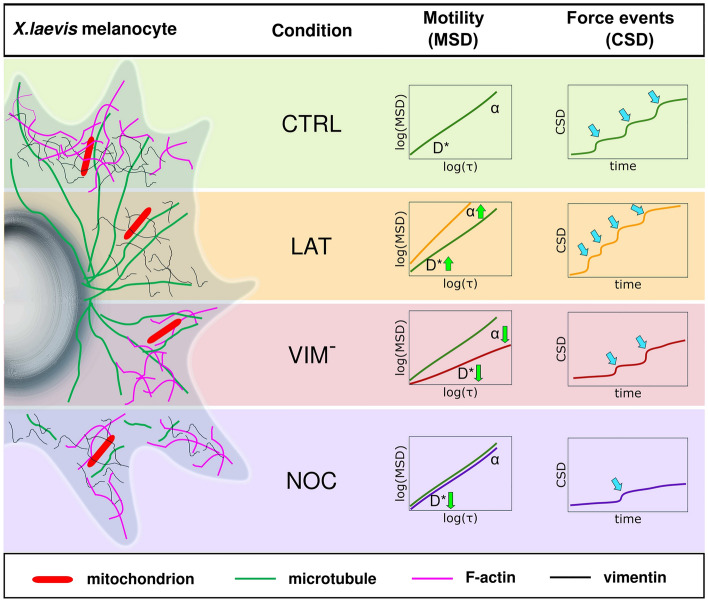
In this study, we employed two statistical tools to investigate the dynamics of filamentous mitochondria and their interactions with the cytoskeleton in living cells. Particularly, we developed a novel methodology to identify and quantify the pattern of active forces exerted on these organelles. The tools were used to analyze time-lapse confocal images of mitochondria within X. laevis melanocytes and quantify their motion regimes and the active forces acting on them. The results obtained are summarized in Fig. 4.
Fig. 4.
Schematic representation of the different experimental conditions and the corresponding MSD and CSD analyses. Mitochondria within X. laevis melanocytes were analyzed under control conditions (CTRL) and after disrupting the cytoskeletal networks with different treatments: latrunculin-B (LAT) was used to disrupt F-actin; cells were transiently transfected with a dominant-negative vimentin mutant (mCherry-vim(1-138), ); microtubules were partially depolymerized with nocodazole (NOC). Mean Square Displacement (MSD) analysis was fitted with an anomalous diffusion model that features and . On average, CTRL (green line) and NOC (violet line) conditions displayed a diffusive behavior (), while LAT (orange line) and (red line) showed superdiffusive () and subdiffusive () behaviors, respectively. Mitochondrial motility () increased in the absence of F-actin and was reduced in NOC and conditions. Green arrows indicate these tendencies. We detected the number of force events (blue arrows) acting on mitochondria through the Cumulative Square Displacement (CSD). The frequency of these events was higher in the absence of F-actin and lower when vimentin or microtubule networks were disrupted.
Firstly, the mitochondrial center of mass trajectories were recovered and the individual MSDs were computed as a function of the time lag . A generalized diffusion model was fitted to the data in order to explore the different diffusive regimes (Fig. 2). The exponents of the MSD were widely distributed around , indicating that, in general, the forces acting on the organelles are balanced46. However, sub-diffusive and super-diffusive populations were also found under some explored conditions, suggesting an imbalance between active and passive forces in those cases. This imbalance was more notable in the case of cells treated with latrunculin-B, where the super-diffusive population dominates, indicating the prevalence of directed active forces acting on the mitochondria in the absence of F-actin.
Furthermore, the effective diffusion coefficient obtained from the MSD analysis reveals that the organelle’s motility strongly depends on the integrity of the cytoskeletal networks. This parameter shows that mitochondrial motion and fluctuations are severely restricted when the microtubule network is impaired, suggesting that these filaments and their associated motors are responsible for the mechanical impulses affecting mitochondria47. In the same direction, the lower value of the effective diffusion coefficient obtained for vimentin-disrupted cells suggests that this network would reinforce the interaction between microtubules and mitochondria, maybe by confining the organelles close to them31. In contrast, the absence of F-actin significantly increases mitochondrial motility, highlighting that actin filaments may damp the mechanical fluctuations of these organelles.
Even though the center of mass is one of the most well-known descriptors of organelle dynamics, it falls short of a complete characterization when talking about filamentous organelles like mitochondria. If the organelles are being subject to active transport, they will present processive trajectories of the center mass, and then the analysis of it will reciprocate the actual motion. However, this is not the case for most of the time. Mitochondria deform and wiggle by the action of different forces, not only the molecular motors’ action. Thus, it is interesting to study the motion/dynamics of all the material points of the organelle to gain information about other sources of deformation to better understand filament deformation and causes. Nonetheless, this is a challenging task as we are considering displacements of many points in different directions.
One way to address this difficulty is considering the (average) square displacements distribution K. So, complementary to the MSD analysis, we propose another quantitative tool: the Cumulative Square Displacement (CSD), which would allow the detection of instantaneous changes in mitochondrial motion that stand out its steady-state behavior. Numerical simulations of a semiflexible filament in a thermal bath and subjected to stochastic localized forces support this hypothesis, thus providing a method for detecting the temporal pattern of these active forces in a non-invasive way.
With the aid of an automated algorithm, we identified the onset of force events from the CSD analysis of individual mitochondria and explored the probability of their occurrence under different experimental conditions (Fig. 3). We found that this frequency was around 1 for control cells and that this value decreases under nocodazole treatment. Also, the frequency was slightly reduced in vimentin-disrupted cells. In contrast, the absence of F-actin reveals a increase in the frequency of events, reinforcing our previous conclusions that these filaments would shield mitochondria from mechanical stimuli.
On the other hand, the basal values of K(t) are related to the slope of the CSD vs. time plot and reflect the stationary fluctuations acting on mitochondria in the cytoplasm. These fluctuations are originated by the presence of thermal noise, but also non-thermal forces might contribute to this jittering. In fact, any stochastic pattern of instantaneous and high frequency random forces could, in principle, result in a linear dependence of the CSD with time. Similarly to the MSD behavior in an enhanced diffusive-like regime46, where an effective diffusion coefficient is found, the stationary values of K would be a descriptor of the active microenvironment. Further studies should be conducted to explore this region of the data, which could provide information about the apparent viscosity, crowding, and rapid non-thermal fluctuations.
Our study demonstrates that both MSD and CSD serve as valuable statistical tools for obtaining quantitative information on mitochondria mechanobiology. It is noteworthy that CSD enables the detection of individual force events and, potentially, allows for the characterization of their duration and intensity in relation to the microenvironment. This requires calibration and further investigation in controlled experiments. The interaction between mitochondria and the cytoskeleton is pivotal in mechanotransduction, and our research aims to contribute to this emerging field.
Methods
Cell culture and transfection
Immortalized Xenopus laevis melanocytes stably expressing the Xenopus tau-like protein XTP fused to EGFP were cultured as previously described in Fernández Casafuz et al7. This cell line was kindly provided by Dr. Vladimir I Gelfand (Northwestern University, Chicago, IL) and has been previously described in Olesen et al45. Briefly, melanocytes were grown in 70% L-15 medium (Sigma-Aldrich) supplemented with 10% of bovine fetal serum (Internegocios S.A.) and Phenylthiourea48. Transfection of the dominant-negative construct mCherry-vim(1-138) was performed using Lipofectamine 2000 (Invitrogen).
Sample preparation for imaging
Melanocytes were cultured on 25 mm round coverslips placed into 35 mm dishes in 2.0 ml of complete medium. For microscopy measurements, the coverslips were mounted in a chamber designed for the microscope. Nocodazole (16 M) and latrunculin-B (10M) drugs (Sigma-Aldrich) were used to induce depolymerization of microtubules and F-actin, respectively7. The cells expressing mCherry-vim(1-138) were observed 24 h after transfection. Mitochondria labeling was carried out by incubating the cells with 100 nM MitoTracker Deep Red FM (Invitrogen).
Confocal microscopy
Microscopy measurements were detailed in Fernández Casafuz et al7. Briefly, images of X. laevis cells were acquired in a FV1000 Olympus confocal microscope using a Olympus UPlanSApo 60x oil immersion objective (NA=1.35). EGFP-XTP and MitoTracker Deep Red FM were excited with a multi-line Argon laser set at 488 nm and a solid diode laser of 635 nm. Fluorescence emitted from the sample was detected in the range of 505-525 nm (EGFP-XTP) and 655-755 nm (MitoTracker Deep Red FM). Time-lapse images (50–200 frames) were registered with a temporal and spatial resolution of 0.5-1.6 s and 63-110 nm, respectively.
Image analysis and mitochondria tracking
Individual mitochondria from the microscopy images were tracked using Jfilament 2D49, an ImageJ/Fiji plugin, as explained in Fernández Casafuz et al7. In summary, the shape of the organelle is manually initialized and the software uses open active contours to deform the initial segment to match the shape of the mitochondrion. Thus we obtained the curvilinear coordinates for each frame of the time-lapses. A total of 89 or 48 mitochondria were tracked for control and each of the other cellular conditions, respectively. Due to the organelles’ proximity and photobleaching, the total time of the trackings varied from 40 to 250 s (i.e. 50 to 200 frames analyzed).
Numerical simulations of a semiflexible filament
We used a Worm-Like Chain Model41 similar to that used in50. The model and the simulations are described in detail in the Supplementary Section 1. Briefly, a semiflexible filament is modeled as a one dimensional array of beads connected by springs (Supplementary Fig. S1). The mechanical parameters were taken as those reported for mitochondria in X. laevis melanophores7. The variables used in the simulations are displayed in Supplementary Tables S1 and S2. The filament is immersed in a pure viscous fluid and thermally fluctuates against a Stokes drag force. Short-duration piconewton kicks are applied stochastically on individual beads. The magnitudes of these forces are comparable to forces exerted by molecular motors on intracellular cargoes13,51.
After each simulation step, the coordinates x and y of the filament shape were calculated. The simulations had a duration of 150 s each and the data was saved using a sampling time of 1 s, comparable with the experimental sampling times. The filament shapes were analyzed following the same procedures as those used for the experimental data. Representative outcomes of the simulations are illustrated in Supplementary Figs. S2 and S3.
The simulation algorithms were written in Python.
Fitting the MSD data to an anomalous diffusion model
The MSD was computed from the x and y coordinates of the center of mass trajectories as:
| 7 |
where t and are the absolute and lag time, respectively, and the brackets represent the time average. Both t and are multiples of the sampling time .
MSD data was fitted with an anomalous diffusion model similar to that proposed in previous works23,25,
| 8 |
where is the residual MSD given by the tracking error, which was less than 60 nm.
To prevent inaccuracies caused by statistical spread when calculating the MSD, only data points where is less than of the total trajectory time were used for fitting52.
A Gaussian mixture model was used to compare the distributions of values obtained for the different treatments (see Supplementary Section S2).
Events detection algorithm
We developed an algorithm to automatically detect extreme values from the K distribution of each trajectory, and define single events based on this data. Briefly, we used a thresholding criteria: any K value larger than a threshold value was considered an outlier, with . Q3 and IQR are the third quartile of the distribution of K and the interquartile range, respectively, and q is a positive number.
To determine the best choice for q, we used numerical simulations where the force patterns were known and explored the performance of the rule for different values of q (Supplementary Fig. S7). We evaluated the performance by computing two magnitudes: Sensitivity and False Discovery Rate. The first magnitude analyzes false negatives -whether outliers were detected during periods of active forces-, while the second accounts for false positives -whether the detection corresponds to actual periods of active forces. Based on these analyses, a value of was chosen for the determination of . The details are described in the Supplementary Section 3.
Once the outliers from a given trajectory are obtained, the determination of single events is done by splitting the data into groups that are assumed to be caused by the action of the same force. Following an arbitrary criterion we defined that consecutive outliers separated by a time or are considered part of the same event. Otherwise, they belong to different events. Supplementary Fig. S9 illustrates this condition.
After that, the number of events per trajectory can be calculated straightforwardly. In order to reduce statistical errors, we computed the frequency of events of an experimental condition, e.g. control experiments, as the sum of all the events in every trajectory divided by the sum of the duration of each individual trajectory. To assess the statistical significance of the results, confidence intervals of the frequency were obtained following a bootstrapping procedure with samples with reposition53. A Kolmogorov-Smirnov Test was used to evaluate differences between bootstrap results in each treatment and control.
Statistical analysis
The results are expressed as the median plus/minus the standard error unless otherwise specified. The standard error of the estimator was calculated using a non-parametric bootstrap procedure, where new samples of the same size were obtained by randomly sampling (with replacement) from the observed data to approximate the population. We computed the median for each bootstrap sample to generate bootstrap sampling distributions and obtained the variance to assess the standard error53. The number of bootstrap repetitions is specified in the text for each case.
A custom-made hypothesis test54 was performed to determine if the medians of different data groups were significantly different. P-values were obtained as follows:
| 9 |
where F is the standard normal distribution, and g1 and g2 represent the data groups. A P-value of less than 0.05 was considered to indicate a significant difference between the data sets.
Statistical analysis, curve fitting, and plotting were performed using Python libraries.
Supplementary Information
Acknowledgements
This research was supported by Agencia Nacional de Promoción de la Investigación, el Desarrollo Tecnológico y la Innovación, Argentina (PICT 2019-2185 to LB). ABFC acknowledges the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) graduate fellowship. MCDR, AGM and LB are members of CONICET.
Author contributions
All authors conceptualized the idea for the manuscript. A.B.F.C. and M.C.D.R. conducted the experiments. A.B.F.C. and A.M.B. analyzed most of the data and performed the numerical simulations. A.G.M. and L.B. supervised the work. All authors contributed to the writing of the manuscript. All authors reviewed the manuscript.
Data availability
The data that support the findings of this study, as well as the custom-written Python routines, are available from the corresponding authors upon reasonable request. A repository containing an example of code used to calculate the Cumulative Square Displacement (CSD) and detect events for a tracked mitochondrion can be downloaded from: https://github.com/mitochondriaChannel/CSD-and-k-example
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Agustina Belén Fernández Casafuz, Email: afcasafuz@ic.fcen.uba.ar.
Luciana Bruno, Email: luciana.bruno@ic.fcen.uba.ar.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-74734-5.
References
- 1.Nunnari, J. & Suomalainen, A. Mitochondria: In sickness and in health. Cell148, 1145–1159 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Su, É., Villard, C. & Manneville, J.-B. Mitochondria: At the crossroads between mechanobiology and cell metabolism. Biol. Cell115(9), e2300010 (2023). [DOI] [PubMed] [Google Scholar]
- 3.Phuyal, S., Romani, P., Dupont, S. & Farhan, H. Mechanobiology of organelles: Illuminating their roles in mechanosensing and mechanotransduction. Trends Cell Biol.33(12), 1049–1061 (2023). [DOI] [PubMed] [Google Scholar]
- 4.Moore, A. S. & Holzbaur, E. L. Mitochondrial-cytoskeletal interactions: dynamic associations that facilitate network function and remodeling. Curr. Opin. Physio.3, 94–100 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.De Rossi, M. C., Levi, V. & Bruno, L. Retraction of rod-like mitochondria during microtubule-dependent transport. Biosci. Rep.38, BSR20180208 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shah, M., Chacko, L. A., Joseph, J. P. & Ananthanarayanan, V. Mitochondrial dynamics, positioning and function mediated by cytoskeletal interactions. Cell. Mol. Life Sci.78, 3969–3986 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fernández Casafuz, A. B., De Rossi, M. C. & Bruno, L. Mitochondrial cellular organization and shape fluctuations are differentially modulated by cytoskeletal networks. Sci. Rep.13, 4065 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huang, D. et al. Mitochondrial dynamics: Working with the cytoskeleton and intracellular organelles to mediate mechanotransduction. Aging Dis.14, 1511 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Feng, Q. & Kornmann, B. Mechanical forces on cellular organelles. J. Cell Sci.131, jcs218479 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Helle, S. C. J. et al. Mechanical force induces mitochondrial fission. Elife6, e30292 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bartolák-Suki, E., Imsirovic, J., Nishibori, Y., Krishnan, R. & Suki, B. Regulation of mitochondrial structure and dynamics by the cytoskeleton and mechanical factors. Int. J. Mol. Sci.18, 1812 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fatima, N. U. & Ananthanarayanan, V. Mitochondrial movers and shapers: recent insights into regulators of fission, fusion and transport. Curr. Opin. Cell Biol.80, 102150 (2023). [DOI] [PubMed] [Google Scholar]
- 13.Howard, J. et al. Mechanics of motor proteins and the cytoskeleton (Sinauer associates Sunderland, MA, 2001). [Google Scholar]
- 14.Boldogh, I. R. & Pon, L. A. Mitochondria on the move. Trends Cell Biol.17, 502–510 (2007). [DOI] [PubMed] [Google Scholar]
- 15.Kruppa, A. J. & Buss, F. Motor proteins at the mitochondria-cytoskeleton interface. J. cell Sci.134, jcs226084 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mahecic, D. et al. Mitochondrial membrane tension governs fission. Cell Rep.35, 108947 (2021). [DOI] [PubMed] [Google Scholar]
- 17.Liu, X. et al. Mechanical force induces drp1-dependent asymmetrical mitochondrial fission for quality control. bioRxiv 2022–10 (2022).
- 18.Song, Y. et al. Light-inducible deformation of mitochondria in live cells. Cell Chem. Biol.29, 109–119 (2022). [DOI] [PubMed] [Google Scholar]
- 19.Tharp, K. M. et al. Adhesion-mediated mechanosignaling forces mitohormesis. Cell Metab.33, 1322–1341 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zamponi, N. et al. Mitochondrial network complexity emerges from fission/fusion dynamics. Sci. Rep.8, 1–10 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wong, Y. C., Kim, S., Peng, W. & Krainc, D. Regulation and function of mitochondria-lysosome membrane contact sites in cellular homeostasis. Trends Cell Biol.29, 500–513 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Casafuz, A. B. F., De Rossi, M. C. & Bruno, L. Morphological fluctuations of individual mitochondria in living cells. J. Phys.: Condens. Matter34, 094005 (2021). [DOI] [PubMed] [Google Scholar]
- 23.Eisenstecken, T., Gompper, G. & Winkler, R. G. Internal dynamics of semiflexible polymers with active noise. J. Chem. Phys.Bold">146, 154903 (2017). [DOI] [PubMed] [Google Scholar]
- 24.Ghosh, A. & Gov, N. Dynamics of active semiflexible polymers. Biophys. J .107, 1065–1073 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vandebroek, H. & Vanderzande, C. Dynamics of a polymer in an active and viscoelastic bath. Phys. Rev. E92, 060601 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Battle, C. et al. Broken detailed balance at mesoscopic scales in active biological systems. Science352, 604–607 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gnesotto, F. S., Mura, F., Gladrow, J. & Broedersz, C. P. Broken detailed balance and non-equilibrium dynamics in living systems: a review. Rep. Prog. Phys.81, 066601 (2018). [DOI] [PubMed] [Google Scholar]
- 28.Pallavicini, C. et al. Characterization of microtubule buckling in living cells. Eur. Biophys. J.46, 581–594 (2017). [DOI] [PubMed] [Google Scholar]
- 29.Gladrow, J., Fakhri, N., MacKintosh, F. C., Schmidt, C. & Broedersz, C. Broken detailed balance of filament dynamics in active networks. Phys. Rev. Lett.116, 248301 (2016). [DOI] [PubMed] [Google Scholar]
- 30.Wenger, J., Brigante, A., Casafuz, A. B. F., Bruno, L. & Monastra, A. Inference of the force pattern acting on a semiflexible filament from shape analysis. Phys. Rev. E108, 064402 (2023). [DOI] [PubMed] [Google Scholar]
- 31.Schwarz, N. & Leube, R. E. Intermediate filaments as organizers of cellular space: How they affect mitochondrial structure and function. Cells5, 30 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Muñoz-Gil, G. et al. Objective comparison of methods to decode anomalous diffusion. Nat. Commun.12, 6253 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wohl, I. & Sherman, E. Atp-dependent diffusion entropy and homogeneity in living cells. Entropy21, 962 (2019). [Google Scholar]
- 34.Weiss, M., Elsner, M., Kartberg, F. & Nilsson, T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J .87, 3518–3524 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Banks, D. S. & Fradin, C. Anomalous diffusion of proteins due to molecular crowding. Biophys. J .89, 2960–2971 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Golding, I. & Cox, E. C. Physical nature of bacterial cytoplasm. Phys. Rev. Lett.96, 098102 (2006). [DOI] [PubMed] [Google Scholar]
- 37.Caspi, A., Granek, R. & Elbaum, M. Enhanced diffusion in active intracellular transport. Phys. Rev. Lett.85, 5655 (2000). [DOI] [PubMed] [Google Scholar]
- 38.De Rossi, M. C., Bruno, L., Wolosiuk, A., Despósito, M. A. & Levi, V. When size does matter: Organelle size influences the properties of transport mediated by molecular motors. Biochimica et Biophysica Acta (BBA)-General Subjects1830, 5095–5103 (2013). [DOI] [PubMed] [Google Scholar]
- 39.Reverey, J. F. et al. Superdiffusion dominates intracellular particle motion in the supercrowded cytoplasm of pathogenic acanthamoeba castellanii. Sci. Rep.5, 11690 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fedotov, S., Korabel, N., Waigh, T. A., Han, D. & Allan, V. J. Memory effects and lévy walk dynamics in intracellular transport of cargoes. Phys. Rev. E98, 042136 (2018). [Google Scholar]
- 41.Gauger, E. & Stark, H. Numerical study of a microscopic artificial swimmer. Phys. Rev. E74, 021907 (2006). [DOI] [PubMed] [Google Scholar]
- 42.Potokar, M. et al. Cytoskeleton and vesicle mobility in astrocytes. Traffic8, 12–20 (2007). [DOI] [PubMed] [Google Scholar]
- 43.Hendricks, A. G., Holzbaur, E. L. & Goldman, Y. E. Force measurements on cargoes in living cells reveal collective dynamics of microtubule motors. Proc. Natl. Acad. Sci.109, 18447–18452 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Levi, V., Serpinskaya, A. S., Gratton, E. & Gelfand, V. Organelle transport along microtubules in xenopus melanophores: Evidence for cooperation between multiple motors. Biophys. J .90, 318–327 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Olesen, O. F., Kawabata-Fukui, H., Yoshizato, K. & Noro, N. Molecular cloning of xtp, a tau-like microtubule-associated protein from xenopus laevis tadpoles. Gene283, 299–309 (2002). [DOI] [PubMed] [Google Scholar]
- 46.Brangwynne, C. P., Koenderink, G. H., MacKintosh, F. C. & Weitz, D. A. Intracellular transport by active diffusion. Trends Cell Biol.19, 423–427 (2009). [DOI] [PubMed] [Google Scholar]
- 47.Xie, J. & Minc, N. Cytoskeleton force exertion in bulk cytoplasm. Front. Cell Dev. Biol.8, 69 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gross, S. P. et al. Interactions and regulation of molecular motors in xenopus melanophores. J. Cell Biol.156, 855–865 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Smith, M. B. et al. Segmentation and tracking of cytoskeletal filaments using open active contours. Cytoskeleton67, 693–705 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Monastra, A. G., Carusela, M. F., van der Velde, G., D’angelo, M. V. & Bruno, L. Evolution of instabilities in filament buckling processes. Phys. Rev. E99, 033004 (2019). [DOI] [PubMed] [Google Scholar]
- 51.Gittes, F., Meyhöfer, E., Baek, S. & Howard, J. Directional loading of the kinesin motor molecule as it buckles a microtubule. Biophys. J .70, 418–429 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Saxton, M. J. & Jacobson, K. Single-particle tracking: Applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct.26, 373–399 (1997). [DOI] [PubMed] [Google Scholar]
- 53.Kulesa, A., Krzywinski, M., Blainey, P. & Altman, N. Sampling distributions and the bootstrap: The bootstrap can be used to assess uncertainty of sample estimates. Nat. Methods12, 477 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.De Rossi, M. C. et al. Asymmetries in kinesin-2 and cytoplasmic dynein contributions to melanosome transport. FEBS Lett.589, 2763–2768 (2015). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study, as well as the custom-written Python routines, are available from the corresponding authors upon reasonable request. A repository containing an example of code used to calculate the Cumulative Square Displacement (CSD) and detect events for a tracked mitochondrion can be downloaded from: https://github.com/mitochondriaChannel/CSD-and-k-example