Machine learning unravels inherent structural patterns in Escherichia coli Hi-C matrices and predicts chromosome dynamics

Abstract

High dimensional nature of the chromosomal conformation contact map (‘Hi-C Map’), even for microscopically small bacterial cell, poses challenges for extracting meaningful information related to its complex organization. Here we first demonstrate that an artificial deep neural network-based machine-learnt (ML) low-dimensional representation of a recently reported Hi-C interaction map of archetypal bacteria Escherichia coli can decode crucial underlying structural pattern. The ML-derived representation of Hi-C map can automatically detect a set of spatially distinct domains across E. coli genome, sharing reminiscences of six putative macro-domains previously posited via recombination assay. Subsequently, a ML-generated model assimilates the intricate relationship between large array of Hi-C-derived chromosomal contact probabilities and respective diffusive dynamics of each individual chromosomal gene and identifies an optimal number of functionally important chromosomal contact-pairs that are majorly responsible for heterogenous, coordinate-dependent sub-diffusive motions of chromosomal loci. Finally, the ML models, trained on wild-type E. coli show-cased its predictive capabilities on mutant bacterial strains, shedding light on the structural and dynamic nuances of ΔMatP30MM and ΔMukBEF22MM chromosomes. Overall our results illuminate the power of ML techniques in unraveling the complex relationship between structure and dynamics of bacterial chromosomal loci, promising meaningful connections between ML-derived insights and biological phenomena.

Graphical Abstract

Graphical Abstract.

Introduction

The archetypal bacterium Escherichia coli possesses a super-coiled circular DNA with a length of 1.6 mm and a size of 4.64 Mega basepair (Mb), confined within a (2–4) μm long spherocylinder (1,2). Over the years, our understanding of the E. coli chromosome has evolved significantly. Initially it was thought that chromosome is a just like a complex blob of various macromolecules such as DNA, proteins, RNA, etc. However, subsequent findings (3–6) reveal that, instead of a complex, blob-like architecture, it consists of a well-organized structure with distinct domains known as macro domains(MDs) (7–12). In this regard, various chromosome conformation capture techniques (13–15) provide us with crucial information, unraveling the spatial organization of the genome, especially in understanding higher-order structures. Recent upgrade in high throughput genome sequencing technique (Hi-C) allows to investigate the three-dimensional conformation of E. coli chromosomal DNA (16). This innovative method generates a high-resolution contact map, referred to as the Hi-C matrix which captures the proximity and frequency of contact between various regions of E. coli chromosome. Furthermore, the Hi-C matrices for different mutant provide valuable insights into the functions of nucleoid-associated proteins (NAPs) and their roles in maintaining the nucleoid’s structure (16). The resulting chromosomal organization significantly influences the dynamic behaviour of chromosomal loci. Previous fluorescence based experimental studies have revealed that these chromosomal loci move subdiffusively (17–20), with their motion strongly influenced by genomic coordinates, showcasing a remarkable level of heterogeneity in their dynamics (19). Integrating this Hi-C-derived contact information into a polymer-based model has enabled development of data-informed integrative studies to furnish a plethora of structural and dynamical details regarding the E. coli chromosome (21–24). These theoretical studies achieve a level of experimental accuracy that enhances our comprehension of the intricacies governing the organization and dynamical behavior of the E. coli chromosome.

The Hi-C-derived chromosomal contact map represents a multi-dimensional interaction matrix (25,26). Even for a prokaryotic cell such as E. coli, with singular circular DNA of 4.6 Mb sequence-length, the Hi-C matrix (16) manifests a dimension as large as (928 × 928) at a 5 Kb resolution. As a result, discerning meaningful information via its visual inspection of extremely large dimensional heterogenous interaction map can be challenging. In recent years, the state of the art machine learning (ML) techniques have emerged as powerful tools for automated extraction of valuable insights from large dimensional data. Notably, most ML-based investigations have centered around eukaryotic chromosomes, benefiting from extensive data sets spanning various replication stages and chromosomes. The inherent complexity of eukaryotic cells, which possess multiple chromosomes, affords opportunities for examining both intra and interchromosomal contacts. These studies are mainly focused on (i) subcompartment annotation of the genome (27,28) by using inter-chromosomal contacts, (ii) enhancing the resolution of Hi-C (29,30) data and (iii) prediction of contact frequency maps using DNA sequence information (31). In contrast, ML-related studies for prokaryotic chromosomes are not as well-developed, primarily due to the challenges posed by the lower resolution and smaller quantity of available data. In light of this, we pose following questions :

• What underlies a ML-derived low-dimensional representation of the Hi-C map of E. coli chromosome?

• Can we quantitatively extract a subset of minimal chromosomal contact informations that would sufficiently reconstruct the experimentally observed (19) heterogeneous sub-diffusive motion of chromosomal loci?

• To what extent would the ML-based learning of wild-type chromosomal contact information aid in the prediction of Hi-C map of NAP-devoid mutant?

To address these questions, we first employ an artificial neural network (ANN) based frame-work known as Autoencoder, in a bid to uncover crucial structural insights embedded within this large Hi-C matrix. As would be revealed in first part of Results section, a latent space representation of the Hi-C map successfully identified various MDs with a high degree of accuracy with experimentally derived MDs. In the later part of the manuscript, in a complementary approach, we integrate Hi-C contacts into a polymer-based model, predicting diffusive dynamics of a large number of chromosomal loci using a supervised machine learning technique called Random Forest (RF) regression. As would be unveiled in the manuscript, the proposed regression model successfully recover the coordinate-dependent heterogeneous subdiffusion (19) of chromosomal loci. Moreover, we extract important features from the input data that are crucial in maintaining this dynamical behavior of the loci. By incorporating only these important features related to Hi-C contacts into the polymer model, we successfully reproduce loci dynamics. Finally, we provide our insight on extent of predictive ability of both structure and dynamics of two NAP-devoid mutants of the chromosome (namely ΔMatP30MM and ΔMukBEF22MM) by ML models (Autoencoder and RF) trained on wild-type chromosome.

Results

Unsupervised ML model identifies a meaningful intrinsic structural pattern embedded within the Hi-C matrix of E. coli chromosome

Overview of ML architecture

We employed an unsupervised machine learning algorithm known as Autoencoder (32,33) to unveil the essential structural insights embedded within the Hi-C matrix. Autoencoder is a type of unsupervised deep neural network characterized by a dual structure comprising an encoder and a decoder, with a bottleneck in between (Figure 1A). In this architecture, the encoder converts the input data from a high-dimensional space to a lower-dimensional representation known as the latent space. Subsequently, the decoder reconstructs the initial input data from this latent space. This process involves the adjustment of model parameters, primarily weights and biases. Consequently, the compressed representation within the latent space reflects a non-linear transformation of the original input data, encapsulating crucial information or patterns inherent in the input datasets.

Figure 1.

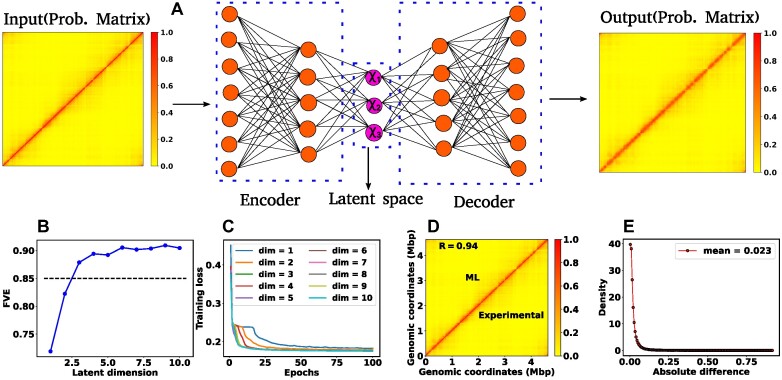
Architecture of the Autoencoder and training robustness. (A) Schematic of the Autoencoder, an unsupervised machine learning algorithm. It consists of an encoder and a decoder and in between there is a bottleneck. The encoder transforms high-dimensional input data to a lower-dimensional latent space, while the decoder reconstructs the initial input data from the latent space. This process involves adjusting model parameters, primarily weights, and biases. Each dimension in the latent space corresponds to a latent variable. Here, χ₁, χ₂ and χ₃ represent three latent variables. (B) The variation of FVE with respect to the latent dimension (L_d). A L_d = 3 was chosen, ensuring an FVE of at least 0.85, signifying that the Autoencoder’s reconstruction captures a minimum of 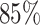of the variance in the input data. (C) Training loss as a function of epochs for different latent space dimensions (L_d). Notably, the training loss achieves saturation for all L_d > 1 beyond 25 epochs. (D) Genome-wide contact probability map between the experimental and ML-derived Hi-C matrix. (E) Histogram of the absolute difference between experimental and ML-derived contact probability matrices. The Pearson correlation coefficient(PCC) is 0.94, and the absolute difference in mean values is 0.023, indicating a substantial agreement in chromosomal interactions.

In our ML model, the input comprises a single Hi-C probability matrix with dimensions 928 × 928 (4640 kb/5 kb = 928). The Autoencoder architecture is structured with a total of nine sequential layers featuring neuron counts of 928, 500, 200, 100, L_d, 100, 200, 500 and 928, respectively, where L_d denotes the dimension of the latent space. After setting up the Autoencoder architecture, we need to choose L_d judiciously. To determine this dimension, we computed the Fraction of Variance Explained (FVE) through reconstruction, which is defined as

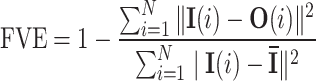(1)

Here, I(i), O(i) and 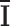represent the input, output, and mean input, respectively, and N = 928 corresponds to the number of rows in the Hi-C matrix. Figure 1(B) represents the variation of the FVE as a function of latent dimension. We opted for a latent dimension of L_d = 3, as it helps to achieve an FVE of at least 0.85, meaning that the Autoencoder’s reconstruction accounts for a minimum of 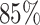of the variance in the input Hi-C data. This choice of latent space dimension not only ensures effective data representation but also affords flexibility in visualizing the compressed data.

To assess the training robustness across various latent space dimensions (L_d) concerning the number of epochs, we have plotted the training loss as a function of epochs for different L_d (Figure 1(C)). The figure clearly illustrates that beyond epochs = 25, the training loss reaches a point of saturation for all L_d > 1. This observation implies that selecting a number of epochs greater than 25 is a prudent choice. In our model, we opted for 100 epochs and in the Method section, additional specifics regarding the training of the Autoencoder are discussed. In a similar vein, we conducted a comparison between the input (experimental) and output (reconstructed) matrices. Figures 1(D) and (E) compare the genome-wide contact probability map between the experimental and ML (reconstructed by the Autoencoder with L_d = 3) contact probability matrix, along with a histogram showing the difference between the two matrices. Our findings reveal a Pearson correlation coefficient (PCC) of 0.94 between the experimental and ML contact probability matrices. Additionally, the absolute difference in the mean values is 0.023, indicating a substantively strong agreement between experimental and ML-derived chromosomal interactions.

The pattern emergent from latent space of the ML-model recovers key Macro-domains across E. coli genome

We aim to understand the biological significance of the lower-dimensional representation (L_d = 3) of the input data. To achieve this, we generated a scatter plot of the latent space data and conducted clustering using the K-means algorithm (34,35). Our hypothesis is that each cluster signifies specific domains within the bacterial chromosome, inherently encoded in the Hi-C matrix. Biologically, these large-scale structurally distinct domains are referred to as macrodomains(MDs) (7–12). It is noteworthy that the actual molecular mechanisms governing macrodomain organization remain incompletely understood, and the precise boundaries of these MDs have been found to vary across different reports (7–11). For example, in 2000, Niki et al. (7) identified mainly four macrodomains: Ori, Right, Ter and Left. Later, other experimental studies by Valens et al. (8) and Espéli et al. (10) identified two more macrodomains, NSR and NSL. The variations in macrodomain boundaries observed across different studies are primarily attributed due to the applied method itself (12). In our study, we have utilized the MDs boundary as reported by Espéli et al. (10) which is more recent.

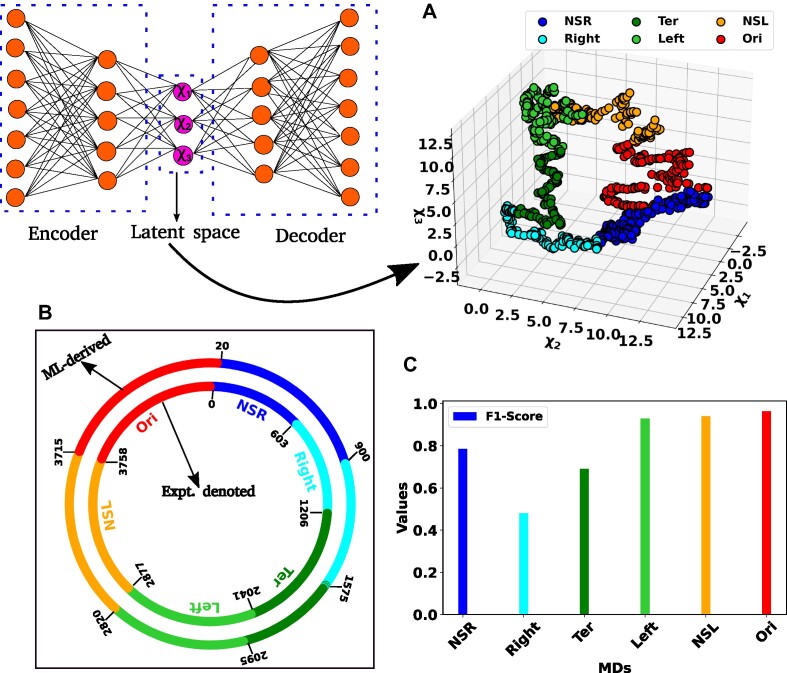
In Figure 2(A), a scatter plot illustrates the three dimensional (L_d = 3, χ₁, χ₂ and χ₃) representation of the latent space, with distinct color-coded clusters representing various MDs of the chromosome. From experimental study (10), we possess a priori knowledge regarding the base pairs of each macrodomain. Additionally, through clustering, we have obtained base pair information for each macrodomain. Subsequently, we conducted a detailed comparison between experimentally denoted and (ML)-derived MDs by schematically drawing the DNA as a circle (Figure 2B). The inner and outer circles, featuring various color-coded regions, represent the experimentally denoted and ML-derived macrodomains, respectively, with base pair information annotated in kilo bases (kb). A visual inspection indicates substantial agreement between MDs, barring discrepancies in the NSR, Right, and Ter MDs. Quantitative comparison between actual (experimentally denoted) and predicted (ML-derived) MDs is facilitated by the confusion matrix (see SI for details). Metrics such as Accuracy, Precision, Recall, and F1-Score can be computed from the confusion matrix as follows.

Figure 2.

Representation of the latent space and classification of different macrodomains. (A) Three dimensional scatter plot of the latent space variable χ₁, χ₂ and χ₃. The data has been clustered using K-means clustering. The various color-coded clusters are representing distinct macrodomains (MDs) within the bacterial chromosome. (B) The comparison between experimentally denoted and machine learning (ML)-derived MDs. The inner and outer circles, each encoded by various color-coded regions, delineate the experimentally denoted and ML-derived macrodomains, respectively, with base pair information annotated in kilo bases (kb). (C) The bar plot of the F1-score for different MDs. The higher values of the F1-Score indicated the better classification.

where TP, TN, FP and FN stand for ‘True Positive’, ‘True Negative’, ‘False Positive’ and ‘False Negative’, respectively. Figure 2(C) shows a bar plot of the F1-score for each MD. F1-scores exceeding 0.92 for the Left, NSL MDs suggest a strong match between actual and predicted classes. Conversely, lower F1-Scores for the other three MDs indicate a moderate alignment, consistent with observations in Figure 2(B). Nevertheless, the overall accuracy for all classes stands at 0.82, indicative of a robust correlation between experimentally denoted and ML-predicted MDs. In summary, our unsupervised ML model (Autoencoder) offers a potent automated approach for MDs identification, demonstrating a high degree of accuracy with experimentally derived MDs.

ML-based identification of genomic contacts crucial for E. coli heterogeneous dynamics

In the preceding section, we delved into the intrinsic structural properties of E. coli chromosome embedded within the Hi-C matrix, which led to an automated discovery of segmented macrodomains in a ML-derived low-dimensional subspace. In this section, we now pose the question: Can we identify the crucial subset of chromosomal contacts in Hi-C map, that hold key to the heterogenous, cooordinate-dependent diffusivities (19,22) of chromosomal loci? Towards this end, we employed a ML-based protocol namely Random Forest Regression to extract dynamical information by leveraging the structural properties of the chromosome, such as the pairwise distance between chromosomal beads. This supervised, trees-based algorithm, initially proposed by Breiman et al. (36,37), is a potent tool widely used for both classification and regression tasks. Random Forest Regression operates by randomly selecting input data from training datasets and creating an ensemble of trees (forests) based on these features and labels of the input data. These ensembles of trees are called ‘decision trees’. The final results are derived by averaging (for regression) or voting (for classification) from the outputs of these decision trees. Notably, the Random Forest possesses a distinctive ability to pinpoint the most crucial features within the training datasets.

Data preparation and supervised ML architecture

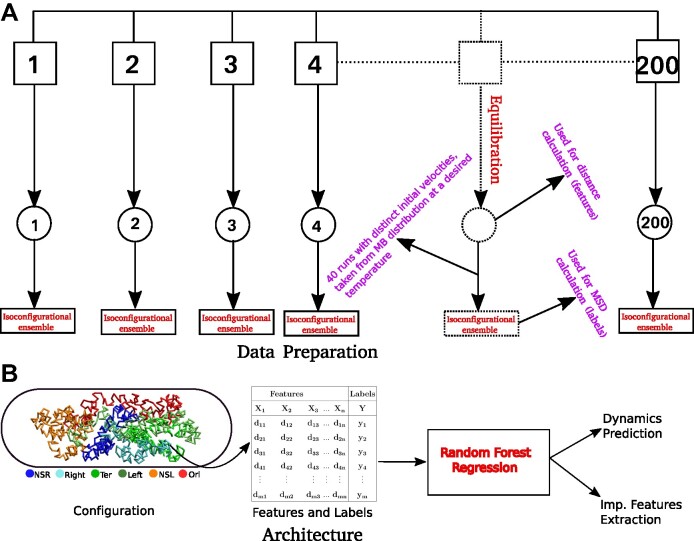
We implemented a bead-in-a-spring polymer model to simulate the bacterial chromosome and generated a set of 200 distinct initial DNA configurations. In brief, the resolution of each bead is 5 × 10³ bp (5 kb), similar to the Hi-C matrix resolution (16). Each bead has a diameter denoted by σ, and the chromosome is confined within a spherocylindrical boundary that mimics the cell wall. The bonded interactions between adjacent beads have been modeled by harmonic springs, while the non-bonded interactions are represented by the repulsive component of the Lennard-Jones potential V_nb(r) = 4ε(σ/r)¹², where ε is the potential depth, and r is the distance between two beads. The Hi-C interactions are also modeled as effective springs with a spring constant and bond lengths dependent on the strength of the contact probabilities. Following energy minimization of the initial configurations, Brownian Dynamics simulations are conducted for each configuration at a temperature of k_BT = 1.0 and friction γ = 1.0. The length and time scales are represented in the unit of σ (the diameter of each bead) and 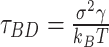(Brownian time), respectively throughout the manuscript. The simulations are run for a time duration of 10³τ_BD with a time step δt = 1 × 10⁻⁴τ_BD, ensuring proper equilibration of each configuration. After equilibration, the pairwise distances are computed using the last snapshot of each run (totaling 200), serving as features for our machine-learning model. The dynamics of each DNA bead are quantified by calculating the mean squared displacement (MSD). For this measurement, we simulate each equilibrium configuration 40 times through Brownian dynamics simulations, drawing distinct velocities from the Maxwell–Boltzmann distribution at a desired temperature of k_BT = 1.0. These trajectories, with varying initial velocities, are called isoconfigurational ensembles (38,39). Each ensemble simulation was carried out for a duration of 100τ_BD. We computed the MSD of each particle i and averaged over the different runs (isoconfigurational ensembles) i.e.

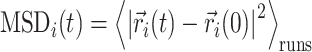(2)

where 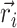represents the position of ith particle and angular bracket signifies the average over isoconfigurational ensembles. So from the equilibrium configuration, we have calculated the pair-wise distance of the chromosomal beads and the MSDs of individual beads from the isoconfigurational ensembles. These two quantities serve as features and labels, respectively, for our machine-learning algorithm, Random Forest. By using this technique we can predict the dynamics of bacterial chromosomal loci and extract the important chromosomal contact features which are necessary to maintain the dynamics. The entire process of data preparation and the machine learning architecture are schematically depicted in Figure 3A and B, respectively.

Figure 3.

Schematic representation of the Data preparation and the architecture of Random Forest (RF) regression model. (A) Data Preparation: At the very beginning we generated a set of 200 distinct initial configuration of DNA using bead-in-a-spring polymer model. We ran the Brownian dynamics simulation for each configuration for a time span of 10³τ_BD,to ensure proper equilibration. Following equilibration, pairwise distances were computed using the last snapshot of each run (totaling 200), serving as features for our machine-learning model. For the MSD measurement, we simulate each equilibrium configuration 40 times through Brownian dynamics simulations, drawing distinct velocities from the Maxwell–Boltzmann distribution at a desired temperature of k_BT = 1.0. These ensemble (40 trajectory each) are called iso-configurational ensembles. (B) Architecture: We utilized the pair wise distance between beads and MSDs of each bead. These two quantities serves as features and labels respectively, in our ML model(RF). After training of the Random Forest (RF) with this datasets, we predicted the dynamics of individual beads. For training and testing, 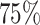and 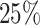of the total datasets, were used. Additionally, from the trained model, we extracted important features contributing to the maintenance of dynamical properties.

Comparison between the actual and ML-predicted MSDs of different loci and their exponents

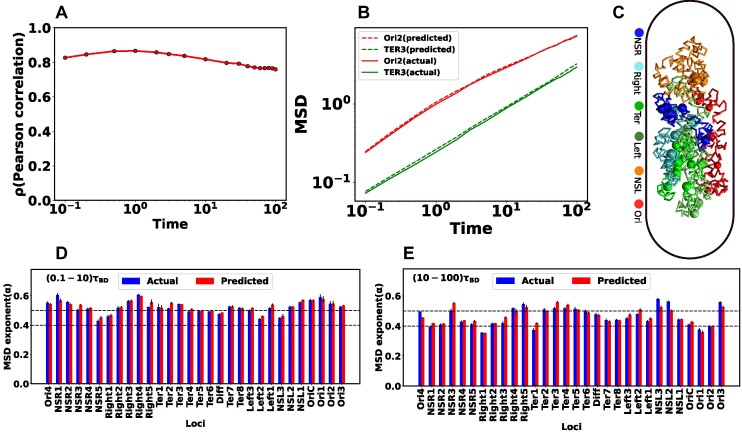
Upon training the Random Forest regression model, we proceeded to predict the dynamics of individual chromosome loci. The selection of specific loci was based on a prior experimental study conducted by Javer et al. (19), which suggested that chromosomal loci belonging to the Ter region exhibit slower motion, while those in the Ori region demonstrate faster motion. To assess the accuracy of ML predictions, we computed the PCC, denoted by ρ, between the predicted and actual MSD values. Figure 4A shows the variation of ρ as a function of time. Remarkably, the correlation ρ exhibits higher values (>0.8) for shorter time intervals. However, the correlation shows a slight decrease for longer duration. Now we will delve into the dynamic properties of distinct loci within the DNA. Each macro domain is comprised of various loci identified by Espeli et al. (10) based on their genomic coordinates. Figure 4B represents the comparison between the actual and predicted MSD as a function of time for two distinct loci, Ori2 and Ter3. This figure distinctly reveals a close alignment between the actual MSDs (solid line) and the predicted MSDs (dotted line).

Figure 4.

Comparison between the actual and predicted MSD values and their exponents. (A) Pearson Correlation Coefficient (PCC) between actual and predicted MSDs as a function of time. During shorter time intervals, PCC demonstrates higher values (>0.8). Conversely, there is a marginal decrease in the PCC for longer time intervals. (B) Comparison of actual and predicted MSDs as a function of time for two particular loci Ori2 and Ter3. The dotted line represents the predicted MSDs, while the solid line depicts the actual MSDs. These plots illustrate a notable concordance between the observed and predicted MSDs. (C) Equilibrated snapshots of the simulated chromosome. The macrodomains are highlighted by distinct color-coded chunks, and the loci associated with each macrodomain are depicted through a spherical bead representation. Comparing the MSD exponents between observed and predicted values is illustrated for two distinct time intervals: (D) (0.1−10)τ_BD (short time) and (E) (10−100)τ_BD (long time). Notably, all loci exhibit heterogeneous subdiffusive motion, irrespective of the time intervals. During the short time, the actual MSD exponents for all loci closely align with the predicted exponents. However, for the long time, a slight deviation in exponents between the actual and predicted values becomes apparent. In all the plots, both the MSD and time are expressed in terms of σ² and τ_BD respectively.

Now, we aim to characterize the type of diffusion for individual loci. In Figure 4C, we present an equilibrated snapshot of the bacterial chromosome, with each color-coded chunk depicting a distinct macrodomain(MD). Each MD is comprised of various loci represented as spherical beads. We fitted the MSD values (both actual and predicted) of each individual loci with a power law:

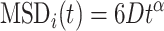(3)

where t, D and α are the time, diffusion constant, and exponent, respectively. Depending on the exponent α, one can categorize the type of diffusion; for example, α = 1 corresponds to normal diffusion, α < 1 signifies subdiffusion, and α > 1, indicates superdiffusion. Figures 4D and E depicts the comparison of MSD exponents between actual and ML-predicted values for two different time intervals, namely (0.1−10)τ_BD (short time) and (10−100)τ_BD (long time), respectively. From these figures, it is evident that for the short time, the actual MSD exponents for all loci closely match the predicted exponents. However, for the long time, there is a slight deviation in exponents between the actual and predicted values. As the PCC between the actual and predicted MSD values deviates for longer times (as seen in Figure 4A), this discrepancy is also reflected in the exponent values. However, for both timescales, the observed and predicted dynamics exhibit subdiffusion, showcasing significant variability along the genomic coordinates, thereby indicating a heterogeneous nature of the dynamics. We found the ML-model to be robust against multiple hyperparameter (see Figure S1a, b) and related supplemental results SR1).

To get a better insight into these deviations, we have calculated the Pearson correlation coefficient (PCC) between the actual and predicted MSD values over a long time range (100−500)τ_BD. Supplementary Figure S2A shows the PCC as a function of time, with the relevant time window highlighted by vertical lines. The figure indicates that PCC values decrease over time. As we use structure-based features (pairwise distance) to predict dynamics, the model starts to forget initial structural information over longer timescales, potentially causing a decrease in PCC values. This effect is also evident in the MSD exponent values (Supplementary Figure S2B). At longer times, the MSD exponents exhibit heterogeneous subdiffusion, but there is a deviation between the predicted and actual MSD exponents. However, these deviations are not substantial. Converting the reduced time unit to actual values shows that 500τ_BD = 100 min (1 τ_BD ≈ 12 s), which is longer than the cell division time of E. coli (∼75 min) (19). Therefore, one should consider the replication and segregation in our model. In our study, we used a time of 100τ_BD = 20 min, which is much shorter than the cell division time in minimal medium. This is also consistent with our previous study (22).

Identifying important chromosomal contact features crucial for loci dynamics

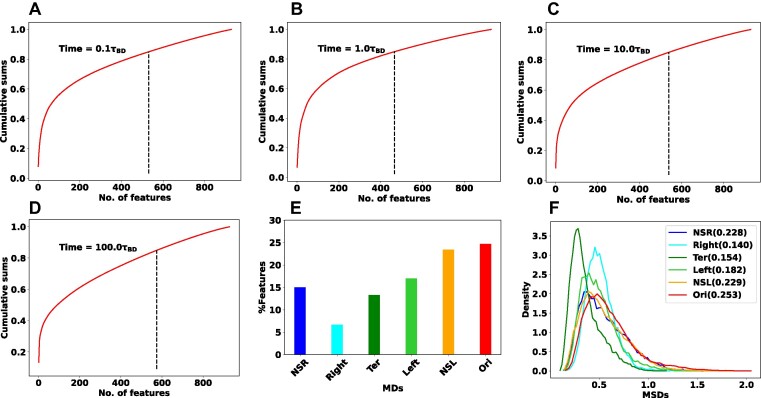
In general, the RF enlightens us about the quantitative extent of significance of each feature by evaluating its impact on impurity. In classification tasks, impurity is assessed through Gini impurity or information gain, while in regression, it involves variance reduction (36,37). During the training, within the decision trees, the greater the reduction in impurity caused by a feature, the more pivotal that feature becomes. In our RF regression model, we have a total of 928 inter-gene distance-based features. Each feature represents the distance between one particular DNA beads with all other beads. To explore the time-dependent importance of these features, we computed cumulative sums of feature importance. Figure 5A–D depicts the cumulative sums of feature importance as a function of the total number of features for different time points: 0.1τ_BD, 1.0τ_BD, 10.0τ_BD, and 100.0τ_BD, respectively. In each plot, the vertical black dotted line highlights the number of features that contribute to 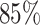of the total feature importance score. We named the particular number of features as top features. A closer examination of the black dotted lines reveals that the number of top features is dynamic i.e. varying with time.

Figure 5.

Important features specific to each macrodomain. Cumulative sums of feature importance as a function of the total number of features for different time points (A) 0.1τ_BD, (B) 1.0τ_BD, (C) 10.0τ_BD and (D) 100.0τ_BD respectively. Each plot includes a vertical black dotted line indicating the number of features responsible for 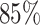of the overall feature importance score (referred to as top features). The number of top features is varying with time. (E) The bar plot of the percentage-wise contributions of top features with respect to different macrodomains. Notably, Ori MD exhibits a predominant share of top features, while Right MD showcases a comparatively smaller proportion of these top features. (F) Distribution of the MSD values for all the MDs at the specific time point. The standard deviation of each distribution is reported in the legend of the plot. Notably, Ori MD shows a wider distribution compared to Right MD.

To get deeper insights into the feature importance, we have selected the top features at a particular time 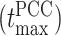when the PCC between the actual and predicted MSDs becomes maximum. In this context, we pinpointed a total of 466 top features representing the 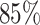of the total feature important score. Within the set of 466 top features, we computed the percentage-wise contributions from each macrodomain. Figure 5E represents the bar plot of the 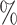of top features with respect to different macrodomains. Quite interestingly the percentage-wise contribution of top features is not uniform with respect to the various macrodomains. Specifically, Ori MD exhibits the most substantial contribution, whereas Right MD demonstrates a comparatively smaller contribution. In the same spirit, we also identified the top features that remain common across different times, totaling 207 in number. Subsequently, we have also plotted the percentage-wise contributions of common top features from each macrodomain (Supplementary Figure S3). The plot shows a very similar trend as Figure 5E.

To understand this nonuniform contributions of MDs in feature importance, we have plotted the distribution of the MSD values for different MDs at the specific time point 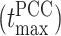. Figure 5F shows the distribution of the MSD values for all the MDs and the standard deviation of each distribution is reported in the legend of the plot. Notably, the plot reveals a significantly broader distribution of MSD values for Ori MD in comparison to Right MD. In the context of our machine learning model, where MSD values serve as labels for supervised learning, these findings imply that the RF regression model requires a greater number of features to construct accurate decision trees when faced with a broad distribution of training data, and conversely, fewer features are needed in the case of a narrower distribution

Can chromosome dynamics be reconstructed using only ML-derived important features?

For a more comprehensive grasp of functional implication of the ML-derived top features, we decided to consider only these particular distance-based chromosomal contact features from Hi-C map and incorporate them in our particle-based DNA model. Precisely, originally totaling 17 302 Hi-C contacts, we have now reduced it to 12 233, resulting in a notable reduction of approximately .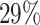

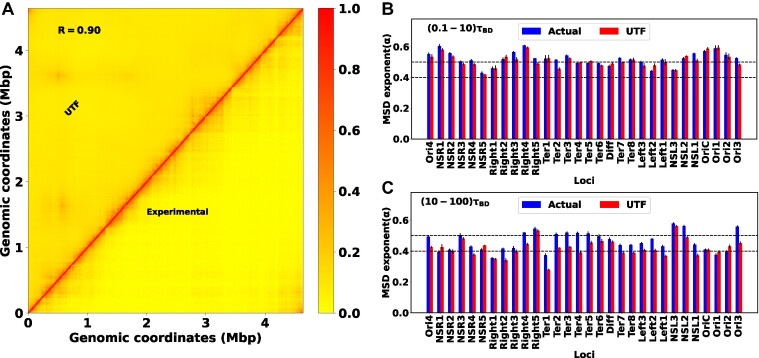
By incorporating these subset of Hi-C contacts, we conducted a new set of simulations and compared the outcomes with our initial modelling results. We named the previous set as ‘actual’ and the current one as ‘UTF’ (using top features). Figure 6A showcases a heat map of Hi-C contact probability, where the upper and lower triangular matrices represent simulated (UTF) and experimental contact probabilities, respectively. The high PCC of 0.90 between these matrices signifies robust agreement. In terms of dynamics, we have also calculated the MSD exponent of each loci. Figure 6B and C presents bar plots of the MSD exponent for all loci at two timescales: (0.1−10)τ_BD and (10−100)τ_BD, respectively. At a shorter time scale, the MSD exponent between the actual and UTF aligns well. However, deviations emerge at longer timescales. These deviations are believed to originate from the dynamic nature of top features. From Figure 5A–D, it is clear that the number of top features varies largely over time. But in our new set of simulations (UTF), we have only incorporated the top features related Hi-C contacts, at a particular time when the PCC between the actual and predicted MSDs becomes maximum. This modelling approach may overlook crucial features relevant for later times, impacting the accuracy of the exponent. Additionally, Figure 4A shows that the PCC between the actual and predicted MSDs is lower at a longer time. These effects will always provide the deviation of the exponent at a larger time scale irrespective of the time-dependent features engineering.

Figure 6.

Reproduce the structure and dynamics by using important features. (A) The heat map between the experimental and simulated (UTF) contact probability matrix for WT30MM. A PCC value of 0.90 between these matrices indicates strong agreement. The bar plot of the MSD exponent for different loci at two timescales: (B) (0.1−10)τ_BD and (C) (10−100)τ_BD, respectively. At a shorter time scale, the MSD exponent between the actual and UTF matches quite well. However, at a larger time scale, they start to deviate.

Nevertheless, the deviations of the exponent are not so huge. Based on this observation, we can assert that RF regression is a powerful technique for predicting dynamics and engaging in feature engineering. The concept of important features allows us to extract the effective Hi-C contacts that can qualitatively provide the structure and dynamics.

Probing prediction ability of ML-model on NAP-devoid Mutant

To what extent can ML recreate Hi-C matrix of Mutant chromosome?

E. coli intricately maintains a chromosome architecture characterized by distinct macrodomains. Several proteins are responsible for this structural management. These proteins, known as nucleoid-associated proteins (NAPs), contribute to the orchestration of chromosomal organization (40,41). Within this category, certain NAPs exhibit localized binding to chromosomes, while others engage in nonspecific binding. These multifaceted NAPs play discernible roles in shaping the overall organization of the chromosome. Among the NAPs, MatP stands out as a key player responsible for isolating the Ter MD from the rest of the chromosome. Specifically, MatP exhibits specific binding to 23 sites within the Ter MD, known as matS sites (11,42). Notably, in the absence of MatP, there is an enrichment in long-range contacts within the Ter MD and its adjacent domains (16). Another essential protein in the realm of chromosomal structure maintenance is MukBEF, which actively facilitates long-range contacts outside the Ter MD (43). Interestingly, when MukBEF is absent, a reduction in long-range contacts is observed across all MDs except for the Ter MD (16).

We decided to investigate the extent of feasibility of recreating Hi-C matrices for two distinct mutants, namely ΔMatP30MM and ΔMukBEF22MM, using the ML model(Autoencoder) that we had trained on wildtype (WT30MM) Hi-C map. This approach would allow us to assess the extent of intrinsic information within the WT matrix that contributes to the accuracy of reconstructing the chromosome contact map of mutants. Importantly, we do not intend to retrain the model with mutant data. Rather, the ML model (Autoencoder) aims to utilize the pre-optimized weight and bias values derived from the WT Hi-C data to generate the mutant Hi-C matrices.

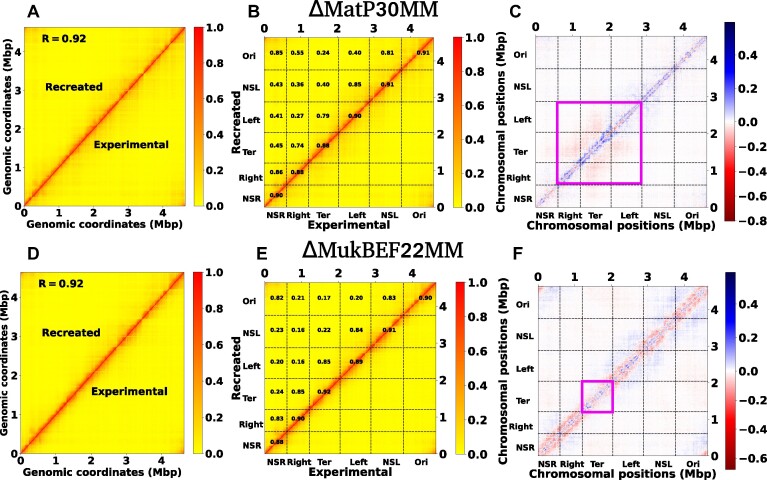
In Figure 7A and Supplementary Figure S4A, we compare the contact probability maps of the experimental and recreated Hi-C matrices for ΔMatP30MM and a histogram illustrating the matrix differences respectively. The substantial agreement between these matrices is emphasized by a PCC value of 0.92 and an absolute difference in mean values of 0.027. For a more detailed examination of the Hi-C matrices, we computed PCC within distinct macrodomains (MDs) (Figure 7B). The correlation is notably high between individual MDs and their adjacent MDs, contrasting with the lower correlation observed for MDs that are farther apart. While the experimental and recreated matrices may seem similar at first glance, a closer examination through a heat map of their differences reveals specific dissimilarities (Figure 7C). Notably, there is a butterfly-shaped region in the Ter and its adjacent domains, highlighted within the magenta box. These findings imply that the recreated Hi-C fails to accurately capture the interactions within the Ter and its flanking domains. Similarly, in Figure 7D, Supplementary Figure S4B, and Figure 7E, we depict the contact probability map, distribution of the difference in the contact matrix, and MDs-wise PCC between the experimental and recreated Hi-C matrices of ΔMukBEF22MM. The overall PCC (0.92), mean difference values (0.03), and individual PCC of each MD indicate a robust agreement between these matrices. However, a closer examination of the difference heatmap (Figure 7F) reveals long-range contacts across all MDs, except for the Ter MD (highlighted by the magenta box). This observation suggests that the recreated matrix fails to appropriately capture the long-range reduction of interactions for all domains except the Ter.

Figure 7.

Recreation of the Hi-C matrix for different mutant by using machine learning trained model on wild type Hi-C matrix. (A) Heat map between the experimental and ML recreated contact probability matrix for ΔMatP30MM. A Pearson correlation coefficient(PCC) value of 0.92 indicates a reasonably strong agreement between them. (B) Within the heat map of the contact probability matrix, individual PCC values for each MD are presented. The PCC are notably high between individual MDs and their adjacent MDs. (C) The heat map of the difference matrix (experimental and ML recreated) reveals a butterfly-shaped region inside the Ter and its flanking domains, denoted by the magenta box. This observation suggests that the ML-recreated matrix fails to accurately capture the interactions within the Ter and its nearby domains. (D–F) depict similar plots as in (A), (B) and (C), respectively. The only difference is that here we compare the experimental and ML recreated Hi-C matrix for ΔMukBEF22MM. From figure (F), it is evident that there are long-range contacts across all MDs except the Ter, suggesting that the ML-derived matrix cannot accurately capture the long-range reduction of contacts for all MDs except the Ter.

The unsupervised ML model operates within the constraints of the information it has been exposed to during training, unable to generate entirely novel insights beyond its training data. Essentially, it excels at recognizing patterns within the provided datasets. Consequently, when the model is trained solely on the WT Hi-C matrix without exposure to mutant data, it inevitably falls short in accurately capturing the modified interactions specific to mutants compared to the WT type. For instance, in the recreation of the ΔMatP30MM Hi-C matrix, the model fails to adequately capture the nuanced interactions within the Ter and its flanking MDs. Similarly, for the ΔMukBEF22MM Hi-C matrix, the model fails to accurately represent the reduction in long-range interactions for all MDs, except the Ter. Interestingly, the WT training model manages to capture various other intrinsic information crucial for recreating mutant Hi-C matrices. To support this, we have trained the same model with a random matrix whose diagonal elements are 1 and all other elements are between (0−1) (see Method section). Attempting to reconstruct the ΔMatP30MM with this trained model resulted in an extremely poor PCC of 0.03 (Supplementary Figure S5). Together these results suggest that our unsupervised ML model (Autoencoder) provides a powerful way to reconstruct the Hi-C of the mutant which is semi-quantitatively accurate.

How close does the ML-derived model replicate the dynamics of different mutants?

In our earlier discussion on the intrinsic structural patterns within the Hi-C matrix, we observed that the WT training model effectively captures the mutant Hi-C matrices in a semi-quantitative manner. Now, our focus is on predicting the dynamics of chromosomal loci for various mutants using the training model on WT data. In this scenario, the model utilizes previously trained ‘decision trees’ to predict the dynamics. Supplementary Figure S6 shows the PCC(ρ) between the actual and predicted MSDs over time for both WT and mutant (ΔMatP30MM and ΔMukBEF22MM) chromosomes. The figure indicates that the correlations for both mutants are lower compared to the WT chromosome. Additionally, the correlation for ΔMukBEF22MM deviates more from WT compared to ΔMatP30MM, suggesting that the WT training model is less accurate in capturing loci dynamics for ΔMukBEF22MM. A closer examination of the Hi-C matrices for WT and mutant cases reveals distinct patterns. For ΔMatP30MM, the contact probability in the Ter and its flanking domains deviates from the WT matrix. In contrast, for ΔMukBEF22MM, the contact probability for all macrodomains deviates from the WT matrix, except for Ter MD. This suggests that when training the model with the WT matrix, it captures information more useful for predicting the dynamics of ΔMatP30MM compared to ΔMukBEF22MM. Consequently, when predicting the chromosome dynamics for ΔMatP30MM using WT training data, the deviation in correlation is less compared to ΔMukBEF22MM.

To understand the differences in the dynamics derived from a trained model with WT, we have calculated the key features for mutant bacteria using the same protocol as for wild-type bacteria. After training a random forest regression model with distance-based features and MSD values as labels for mutant bacteria, we have identified the important features for these two mutants. Supplementary Figures S7A and S7B show the MD-wise feature importance of the top features for ΔMatP30MM and ΔMukBEF22MM, respectively. These plots suggest that the MD-wise contribution of the top features is similar to that of wild-type bacteria. However, quite interestingly, the total number of top features for mutant bacteria differs from that of wild-type bacteria. Specifically, the number of top features is 383 for ΔMatP30MM, compared to 466 for wild-type bacteria, and 323 for ΔMukBEF22MM. To better understand the contribution of top features, we have computed the MD-wise contribution of the top features with respect to the total number of features (928) instead of the total number of top features. Supplementary Figure S7C represents the percentage-wise contribution of top features for each MD for wild-type and mutant bacteria. This plot indicates that for mutant bacteria, the percentage-wise contribution for each MD is lower compared to wild-type bacteria. These observations suggest that the top features governing the dynamics in mutant bacteria are different from those in wild-type bacteria. This difference might be a crucial factor for the deviation in the dynamics predicted from wild-type training data for mutant bacteria.

Discussions and summary

The organization and dynamics of the bacterial DNA are very complex and not yet fully explored. To address this, the utilization of the Hi-C integrated (21–24,44) and cross-linked (45,46) based polymer model offers a versatile means of exploring the organization and dynamics of E. coli DNA. In this study, we present a comprehensive approach, employing a set of machine learning (ML) algorithms to gain insights into the structural and dynamical aspects of bacterial chromosome. By leveraging a combination of Autoencoder-based structural analysis, and RF regression for predicting chromosomal dynamics, our work provides valuable insights into an intricate pattern of bacterial chromosomal organization and it emergent dynamics.

In the first part of the study, we mainly focused on extracting essential structural information, that is hidden underneath the Hi-C matrix, using an unsupervised deep neural network known as Autoencoder. The low-dimensional representation of the Hi-C data interestingly identifies chromosomal macrodomains (MDs) as key structural pattern in an automated way (Figures 2). Notably, the comparison between MDs derived from our ML model (Autoencoder) and those experimentally identified reveals a high correlation, suggesting meaningful connections between the ML-derived insights and real-world biological phenomena. However, Figure 2B suggests that there are significant differences exist between the ML-derived and the experimentally denoted MDs, particularly in the Right and Ter regions. We speculated that utilizing a higher-dimensional latent space could enhance the results. To test this hypothesis, we clustered the data in a four-dimensional latent space (L_d = 4). In Supplementary Figure S8(A), a comparison between the ML-derived and experimentally identified MDs for a latent dimension of L_d = 4 is presented, revealing notable improvements in MDs classification compared to L_d = 3. Furthermore, we quantified this enhancement by computing the F1-score for each MD. Supplementary Figure S8B shows the comparison of F1-scores across different MDs for two latent dimensions (L_d = 3, 4). While there is a slight decrease in the F1-score for Left, NSL and Ori, significant improvements are observed for the other three MDs. The overall accuracy is 0.87 for L_d = 4, compared to 0.82 for L_d = 3. Although the higher dimension latent space provides the improvement in the results, the visualization of the latent space in 4d is not possible. Therefore, we kept all of the analysis in latent dimension L_d = 3. Additionally, there exist various other Autoencoder techniques like Denoising Autoencoder (47), Variational Autoencoder (48), etc. The usage of these advanced techniques could potentially improve the overall identification of the MDs. Moreover, when recreating the Hi-C matrix for various mutants using wild-type (WT) training data (Figures 7), our model demonstrates the ability to capture diverse intrinsic information crucial for reconstructing mutant Hi-C matrices. Significantly, the observed structural properties closely align with established experimental findings, underscoring the effectiveness of our approach in capturing biologically relevant phenomena.

In general, the partitioning of the eukaryotic chromosome into A and B compartments is achieved through principal component analysis (PCA) (15,26). We have also employed PCA to identify macrodomains for E. coli. Subsequently, we clustered the data for the first three principal components (PC-1, PC-2 and PC-3) using the K-means clustering algorithm. Supplementary Figure S9(A) presents a schematic representation of the macrodomains derived from machine learning (Autoencoder), PCA and experimental data. To compare how the PCA and ML-derived macrodomains match with experimentally identified macrodomains, we calculated the F1-Score for both methods (PCA, Autoencoder). Supplementary Figure S9(B) shows a comparison of the F1-Scores for macrodomains derived from these two techniques. This figure suggests that the Autoencoder outperforms PCA in identifying macrodomains, particularly for four specific regions: NSR, Left, NSl and Ori. However, for two other regions, PCA performs better than the Autoencoder. Nevertheless, the overall accuracy for identifying macrodomains using PCA is 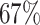, while the overall accuracy for the Autoencoder is 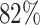. Thus, the utilization of the ML-based non-linear technique Autoencoder provides a superior method for identifying macrodomains compared to the traditional linear technique PCA. There are also other advantages of using the Autoencoder over PCA, such as the ability to recreate the mutant matrix from wild-type training data. This helps in understanding the inherent information contained in the wild-type matrix, which is important for studying mutant bacteria. While PCA allows for the projection of mutant data along the principal components of the wild-type matrix, it does not enable the recreation of the mutant matrix.

After delving into the structural insights extracted from the Hi-C data, the second part of our study focused on harnessing the power of ML to predict the crucial subsets of chromosomal contact features that can optimally explain the previously reported heterogeneous subdiffusion of chromosomal loci. We employed a Hi-C embedded polymer model for the E. coli chromosome, representing short and long-range Hi-C contacts as effective springs with spring constants dependent on contact probabilities. Subsequently, we utilized RF regression, a powerful supervised machine learning algorithm, to predict the dynamics and MSD exponent of individual chromosomal loci. Our results demonstrated a high correlation between the predicted and actual MSD values for shorter time scales (Figures 4). These observations highlight the efficacy of our machine learning model in capturing the complex relationship between structural features and dynamic behavior. However, at a large time scale, the correlation between the actual and predicted values decreases. We hypothesized that at larger time scales, the system loses its initial structural information, leading to a reduction in correlation. Despite this decrease, it remained relatively modest.

We systematically evaluated the robustness of our RF regression model by varying hyperparameters (Supplementary Figures S1). The consistent performance across different hyperparameter values affirmed the reliability of our machine-learning approach. An essential aspect of our study involved extracting top features through feature importance analysis, providing valuable insights into the critical elements influencing chromosomal dynamics. However, these top features are dynamic rather than static, exhibiting variations over time (Figure 5A–D). The distribution of top features at a particular time across different macrodomains revealed non-uniform contributions (Figure 5E). Particularly, the Ori macrodomain exhibited a more substantial contribution compared to the right macrodomain. This non-uniformity was further elucidated by examining the distribution of MSD values for different macrodomains, with Ori displaying a broader distribution (Figure 5F). These findings indicate that the model requires more features to accurately capture dynamics when faced with a broader distribution of training data. Moreover, by incorporating the top features associated with Hi-C contacts into a polymer-based model, we can effectively reconstruct both the experimental Hi-C matrix and the dynamical behavior of chromosomal loci at a short time scale (Figures 6). These findings strongly imply the utility of our RF regression model for feature engineering, specifically in extracting the important Hi-C contacts that play a crucial role in influencing chromosomal dynamics. However, our model does have limitations; for instance, it may not fully capture interactions specific to mutants as it is trained solely on wild-type data.

Our work enhances the broader understanding of bacterial chromosome via computational modeling with ML techniques. The identification of macrodomains and the prediction of chromosomal dynamics offer a comprehensive view of the intricate interplay between structure and function in bacterial genomes. However, our approach can be extended beyond the realm of bacterial chromosomes. We are optimistic about the broader applicability of our methodologies in addressing more complex systems, including proteins and glass, to extract structural insights and predict dynamics. In the realm of glassy systems, there has recently been a plethora of studies predicting dynamics using a combination of structural properties and diverse machine-learning algorithms (49–56). While many of these studies leverage a multitude of structural features for dynamic predictions, we hope that our approach may offer an effective avenue for predicting dynamics and facilitating feature engineering.

Methods

The training of the Autoencoder

The Autoencoder in our study consists of nine fully connected sequential layers. We have used a single Hi-C contact probability matrix for training the Autoencoder. We utilize the Leaky rectified linear unit (ReLU) activation function for each layer, except for the last layer. Given that our Hi-C contacts fall within the range of 0 to 1, the sigmoid activation function is applied to the final layer. To optimize the weights and biases of each node, we utilize the Adam optimizer (57) to minimize the loss function. We choose binary cross-entropy (BCE) (27,58) as a loss function which is defined as

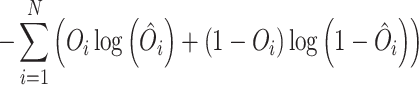(4)

where 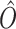, and O are the model output, target output, and N = 928 respectively. The Autoencoder is trained with a batch size of 30 for input data and a learning rate of 0.001. Notably, in training the Autoencoder on the Random matrix, we have used the same architecture, modifying only the dimension of the latent space L_d. Our observations indicate that achieving a Pearson Correlation Coefficient (PCC) value of 0.79 between the actual random matrix and the Autoencoder-derived matrix necessitates setting L_d to 40 (Supplementary Figure S10). All aspects related to the Autoencoder, including training and implementation, are conducted using the Python implementation of Tensorflow (59) and Keras (60).

Training-testing split

In our ML model (RF), we allocate 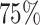of the data for training and 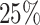for testing. This partitioning ensures that the dimensions of the training and testing data are as follows: features_training[m, n] = [runs × 928, 928] = [150 × 928, 928], labels_training[m] = [runs × 928] = [150 × 928] and features_testing[m, n] = [runs × 928, 928] = [50 × 928, 928], labels_testing[m] = [runs × 928] = [50 × 928].

Simulation model details

We have applied our previously established bead-spring model (21,22) for integrating Hi-C data in E. coli chromosome, where each bead corresponds to 5 × 10³ bp (5 kb). The harmonic interaction between adjacent beads is governed by a spring constant of k_spring = 300k_BT/σ², where σ denotes the bead diameter. The inclusion of Hi-C contacts in the polymer chain introduces an effective spring with a spring constant dependent on contact probabilities. This process involves: (i) transforming the Hi-C probability matrix into a distance matrix using the formula:

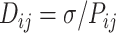(5)

where i and j are the row and column index of the matrix respectively. (ii) By using D_ij, we have calculated the effective spring constant as:

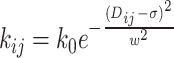(6)

Here, k₀ serves as the upper bound of the spring constant, and w² is a constant value. However, previous studies (61,62) on eukaryotes suggest that the relationship between D_ij and P_ij follows 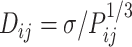or 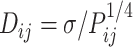. We have also verified that these types of relationships yield similar dynamic behavior of the chromosomal loci with proper optimization of w² value. In our simulation, we have maintained the values of k₀ and w² consistent with our previous study (21,22), specifically k₀ = 10k_BT/σ² and w² = 0.3. The potential related to Hi-C contacts, denoted as E_{Hi − C}(r_ij), is expressed as:

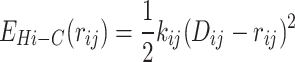(7)

In our simulation, contacts with a spring constant k_ij < 10⁻⁷ are disregarded to avoid unnecessary low-value contacts. additionally, the nonbonded interactions between beads are modeled using the repulsive part of the Lenard-Jones potential, i.e., 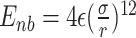. All particles are confined within a spherocylinder, mimicking the cell wall, with a length of L = 45.754σ and diameter d = 12.181σ. The confinement potential is defined as:

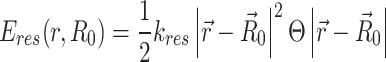(8)

Here, R₀ represents the center of the spherocylinder, and k_res is the spring constant controlling confinement softness (set to 310k_BT/σ²). The step function Θ activates if any particle surpasses the confinement boundaries. The total Hamiltonian of the system is given by:

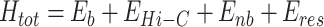(9)

Here, E_b, E_{Hi − C}, E_nb and E_res represent the potentials for bonded, Hi-C restraining, non-bonded, and confinement restraining interactions, respectively. All the simulations were conducted using an modified version of open-source software GROMACS 5.0.6 (63), while for the implementation of random forest regression, we utilized the Python library known as scikit-learn (64).

Calculation of Hi-C contacts

We have calculated the Hi-C matrix using our simulation trajectories. For each time series configuration, we have computed the pairwise distance D_ij between each bead and then converted the distance into a probability value using the formula P_ij = σ/D_ij, where σ is the diameter of each bead, and i and j are the bead indices. Finally, we have averaged these probability values over all the frames and trajectories.

Data availability

All data are present within the manuscript. The code and accompanying documentation for training the Autoencoder and Random Forest regression model can be accessed through GitHub at the following URL: https://github.com/palash892/Hi-C_ML_structure-dynamics (also archived in Zenodo at https://doi.org/10.5281/zenodo.13312410).

Supplementary data

Supplementary Data are available at NAR Online.

Funding

Tata Institute of Fundamental Research Hyderabad, India; Department of Atomic Energy, Government of India [RTI 4007]. Funding for open access charge: Intramural research.

Conflict of interest statement. None declared.