Field-tunable quantum disordered ground state in the triangular-lattice antiferromagnet NaYbO₂

Abstract

Antiferromagnetically coupled $S=1/2$ spins on an isotropic triangular lattice are the paradigm of frustrated quantum magnetism, but structurally ideal realizations are rare. Here, we investigate NaYbO₂, which hosts an ideal triangular lattice of effective $J_{\text{eff}}=1/2$ moments with no inherent site disorder. No signatures of conventional magnetic order appear down to 50 mK, strongly suggesting a quantum spin liquid ground state. We observe a two-peak specific heat and a nearly quadratic temperature dependence, in agreement with expectations for a two-dimensional Dirac spin liquid. Application of a magnetic field strongly perturbs the quantum disordered ground state and induces a clear transition into a collinear ordered state, consistent with a long-predicted up–up–down structure for a triangular-lattice XXZ Hamiltonian driven by quantum fluctuations. The observation of spin liquid signatures in zero field and quantum-induced ordering in intermediate fields in the same compound demonstrates an intrinsically quantum disordered ground state. We conclude that NaYbO₂ is a model, versatile platform for exploring spin liquid physics with full tunability of field and temperature.

Exotic ground states of quantum antiferromagnets are encouraged by the combination of low dimensionality, geometric frustration and inherent anisotropies. Planar triangular lattices are long-sought platforms for stabilizing them^1–7; however, ideal manifestations that do not break crystallographic or exchange symmetries when approaching the quantum regime are rare. The organic compounds κ-(BEDT-TTF)₂Cu₂(CN)₃ (ref. ⁸) and EtMe₃Sb[Pd(dmit)₂]₂ (ref. ⁹) are two promising examples of triangular lattices with $S=1/2$ moments and a dynamically disordered spin ground state. However, $S=1/2$ inorganic analogues such as Ba₃CoSb₂O₉ (refs. ^10,11) and NaTiO₂ (refs. ^12–14) either order magnetically or undergo a lattice deformation when cooling. A roadblock in inorganic systems is the identification of a material with a high crystallographic symmetry, rigid structure and minimal defect mechanisms that also contains magnetic ions possessing strong quantum fluctuations. Ideally, the magnetic ions should reside at high-symmetry positions that preclude antisymmetric Dzyaloshinskii–Moriya exchange from lifting geometric frustration.

As an alternative to $S=1/2$-based compounds, rare-earth ions with ground state doublets also engender enhanced quantum fluctuations. Recent studies have shown that the spin–orbit entangled $J_{\text{eff}}=1/2$ moments of Yb³⁺ ions on a triangular lattice may exhibit a variety of nearly degenerate states^15–22. Given the appropriate anisotropies and proximity to phase boundaries, spin liquid states are predicted to appear²². Recent experimental studies of one candidate material, YbMgGaO₄, report continuum spin dynamics and a spin-liquid-like ground state; however, chemical disorder endemic to the mixed occupancies of magnesium and gallium atoms on the same crystallographic site of this material has clouded interpretation^15–23. Alternative models propose that the random cation distribution incites exchange disorder, facilitating the formation of a weakly bound spin glass state that experimentally resembles a spin liquid^24–26. Fully removing this exchange disorder and accessing the physics inherent to an ideal triangular lattice of $J_{\text{eff}}=1/2$ moments remains a challenge.

The rare-earth moments in compounds of the form NaRO₂ (where R are rare-earth ions) are known to form an ideal triangular lattice in the $\text{α}$-NaFeO₂ ($R$-3m) structure. Previous studies suggest that they realize a large degree of magnetic frustration^27–29, and NaYbO₂ in particular stands out as an appealing candidate material. Specifically, the NaYbO₂ lattice promotes enhanced exchange through short nearest-neighbour bonds, and the ytterbium (Yb) moments occupy high-symmetry sites that forbid Dzyaloshinskii–Moriya interactions. This, combined with large crystal field splitting between the ground state and first excited doublet^20,21, renders this lattice an appealing framework.

Here, we present an investigation of the triangular lattice of Yb moments in NaYbO₂. Our data show that the lattice is robust and forms with fully occupied sodium and oxygen sites, minimizing potential chemical/exchange disorder. Furthermore, the structure preserves the ideal equilateral triangular lattice into the quantum regime beyond the point at which the majority of the magnetic entropy has frozen out. Zero-field susceptibility data collected down to 50 mK reveal no signatures of spin freezing or glassiness, and heat capacity data collected over the same temperature range reveal only a broad two-peak structure—a common signature of the onset of short-range correlations in materials thought to host quantum disordered ground states^30–33. This disordered state is strongly perturbed via the application of a magnetic field that induces antiferromagnetic order consistent with an up–up–down plateau state for the triangular lattice and reflects an underlying XXZ Hamiltonian with enhanced fluctuations due to interlayer frustration. Our data reveal that NaYbO₂ hosts an enticing quantum disordered ground state controllable via modest external fields and presents a cleanly tunable platform for exploring order to quantum disorder phase boundaries inherent to the XXZ triangular lattice.

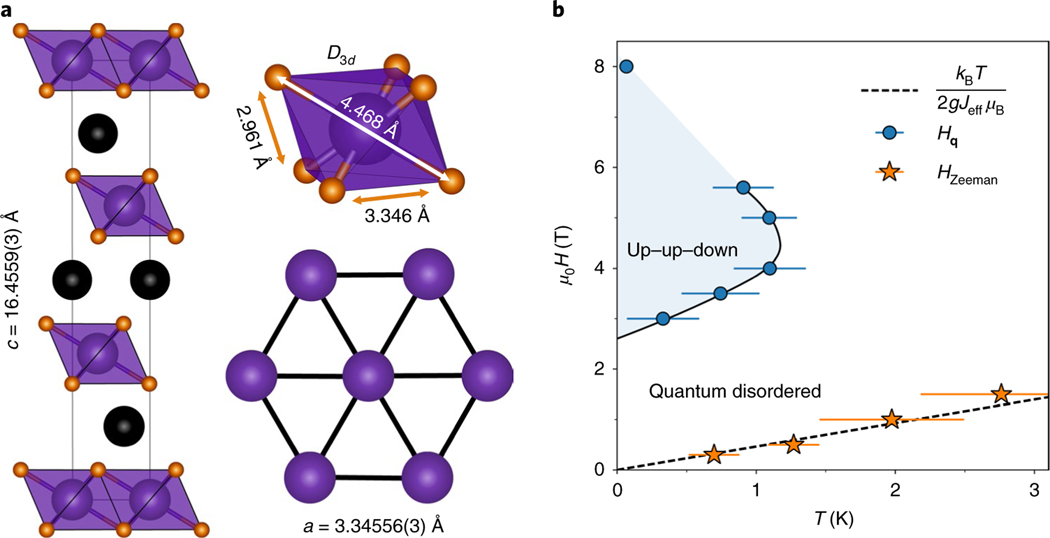
Polycrystalline NaYbO₂ was synthesized and characterized via neutron powder diffraction measurements (see Methods for further synthesis and experiment details). Figure 1a shows the structure at 1.6 K, revealing R3m symmetry with fully occupied sodium and oxygen sites. The $D_{3d}$ distorted YbO₆ octahedra and bond lengths are illustrated, and a similar YbO₆ environment in YbMgGaO₄ is known to generate a large 38 meV splitting between the first excited state and the ground state doublet^20,21. A comparison of the Yb environments of the two materials is provided in Supplementary Table 2. At low temperatures, the ground state therefore behaves as an isolated $J_{\text{eff}}=1/2$ Kramers doublet. Nearest-neighbour Yb–Yb distances were refined to 3.3507(1) Å at 300 K, consistent with previous reports^27–29, and naively support enhanced exchange relative to other frustrated Yb-based compounds.

Fig. 1 |. Crystal structure and magnetic ($H$, $T$) phase diagram of NaYbO₂.

a, Refined NaYbO₂ structure (1.6 K, R3m) contains equilateral triangular layers of $D_{3d}$ YbO₆ distorted octahedra separated by 3.346 Å. Sodium cations refine to full occupation, creating a uniform chemical environment surrounding the triangular layers. Purple spheres, Yb atoms; black spheres, Na atoms; brown spheres, O atoms. b, Low-temperature phase boundary between quantum disordered and antiferromagnetic ordered states in NaYbO₂, plotted as a function of field and temperature, extracted from a.c. susceptibility and neutron-scattering experiments. The dashed line denotes the boundary of Zeeman-driven quenching of a minority fraction of free Yb moments under field, above which free moments are quenched. These free moments coexist with a quantum disordered ground state. Values in parentheses and error bars indicate one standard deviation. $k_{\mathrm{B}}$ is the Boltzmann constant, $H_{\mathbf{q}}$ denotes the onset temperature of the up–up–down ordered state and $H_{\text{Zeeman}}$ denotes the suppression in magnetic susceptibility observed due to the quenching of a small fraction of free Yb moments.

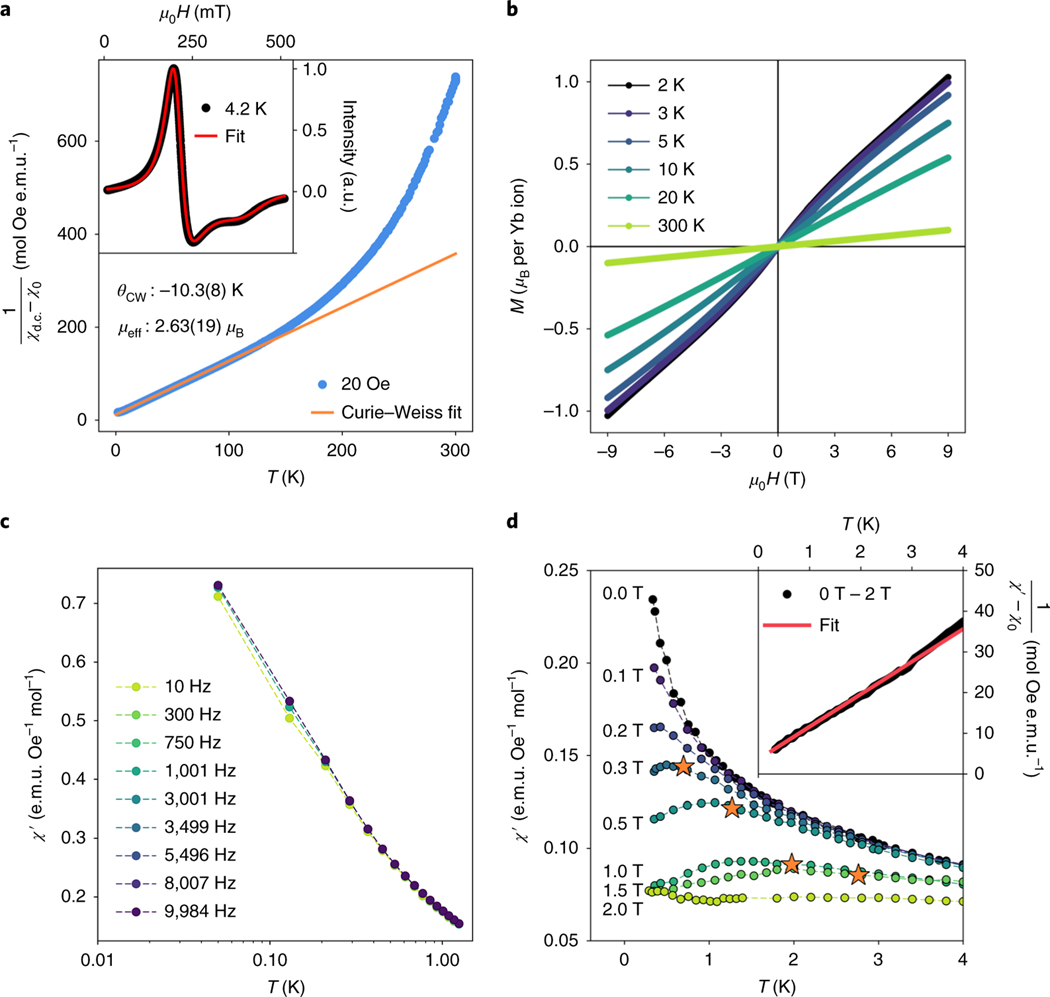
Characterizing this exchange, magnetic susceptibility ($\chi$) and magnetization data are plotted in Figs. 2 and 3. Below 50 K, the Van Vleck contribution to the susceptibility is negligible. The data from 20 K to 100 K were modelled by Curie–Weiss fits of the form $\frac{1}{\chi -{\chi }_0}={\left(\frac{C}{T-{\theta }_{\mathrm{C}\mathrm{W}}}\right)}^{-1}$ (where $C$ is specific heat, $T$ is temperature, ${\chi }_0$ the temperature-independent contribition to the susceptibility and ${\theta }_{\mathrm{C}\mathrm{W}}$ is the Curie–Weiss temperature), shown in Fig. 2a, and yield a local moment of 2.63(8) Bohr magnetons $\left({\mu }_{\mathrm{B}}\right)$ with an antiferromagnetic ${\theta }_{\mathrm{C}\mathrm{W}}=-10.3\left(8\right)$ K. Relative to YbMgGaO₄, ${\theta }_{\mathrm{C}\mathrm{W}}$ is substantially enhanced $\left({\theta }_{\mathrm{C}\mathrm{W}}=-4\mathrm{K}\right)$^15,16,18,20, consistent with enhanced exchange. The local moment suggests a heightened $g$-factor, which was validated via electron paramagnetic resonance (EPR) measurements (Fig. 2a inset). A powder-averaged $g$-factor of $g_{\text{avg}}=3.03$ is implied by the local moment extracted from susceptibility data. Fits to the EPR line shape reveal anisotropic $g$-factors of $g_{ab}=3.294\left(8\right)$ and $g_c=1.726\left(9\right)$ corresponding to the triangular a–b plane and c axis, respectively.

Fig. 2 |. Low-field magnetization and magnetic susceptibility data.

a, Low-temperature Curie–Weiss fit to the constant field magnetic susceptibility ${\chi }_{\text{d.c.}}$ in a temperature range free from Van Vleck contributions from high-energy crystal field doublets (where the majority of trivalent Yb ions are in the $J_{\text{eff}}=1/2$ ground state). A large mean-field interaction strength of −10.3(8) K with an effective local moment, ${\mu }_{\text{eff}}$, of 2.63(19) ${\mu }_{\mathrm{B}}$ is fit with a temperature-independent ${\chi }_0=0.0053\left(3\right)$ e.m.u. mol⁻¹ background term. Inset: EPR data collected at 4.2 K fit to anisotropic $g$-factors of $g_{ab}=3.294\left(8\right)$ and $g_c=1.726\left(9\right)$. b, Isothermal magnetization versus field data reaching only 67% of the expected $1.5{\mu }_{\mathrm{B}}$ per Yb ion polarized moment under ${\mu }_{0}H=9\mathrm{T}$. c, Temperature and frequency dependence of a.c. magnetic susceptibility ${\chi }^{\prime }\left(T\right)$ from 50 mK to 4 K under zero field. d, ${\chi }^{\prime }\left(T\right)$ data collected under applied magnetic fields. A minority fraction of free Yb moments are quenched at low temperatures and high fields, resulting in a peak in ${\chi }^{\prime }\left(T\right)$, and the downward inflection parameterizing this Zeeman splitting is denoted by orange stars. Inset shows field-subtracted $0\mathrm{T}-2\mathrm{T}{\chi }^{\prime }\left(T\right)$ data between 1 K and 3 K and a Curie–Weiss fit quantifying the fraction of free Yb moments in the system, as described in the text. Values in parentheses and error bars indicate one standard deviation. a.u., arbitrary units.

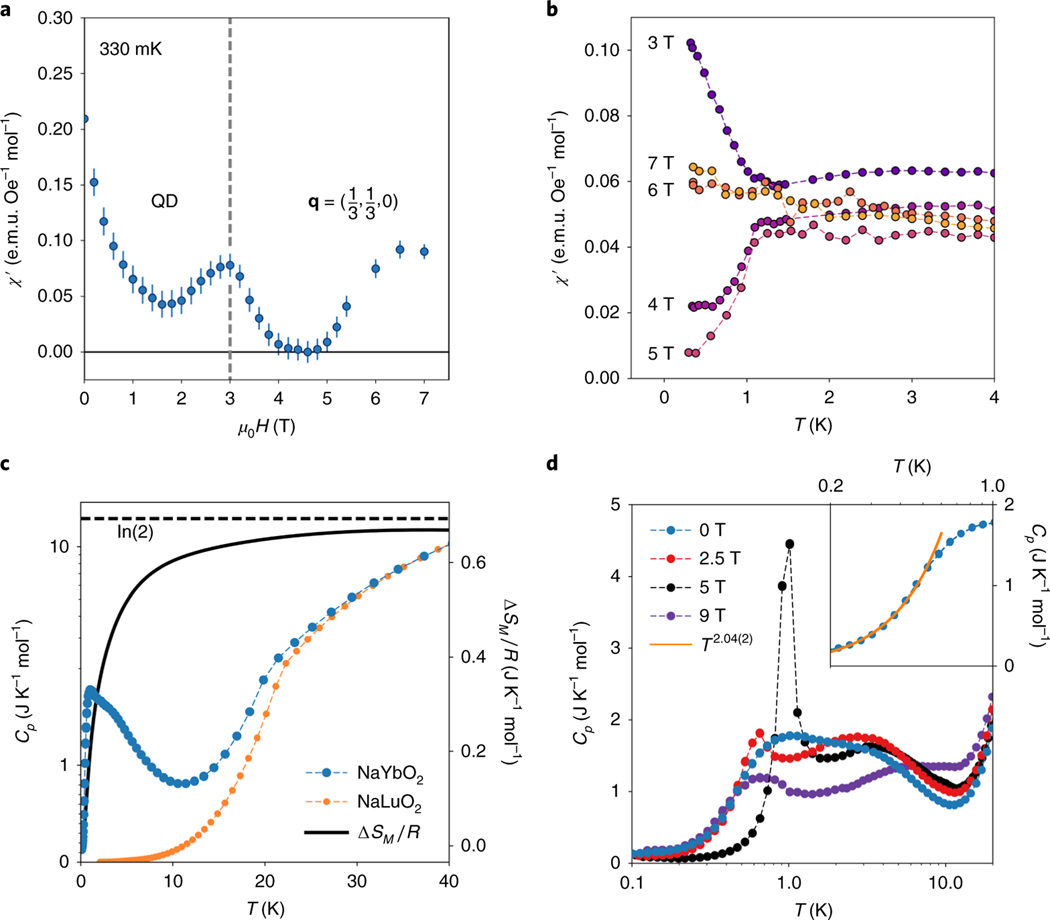
Fig. 3 |. High-field magnetic susceptibility and heat capacity data.

a, ${\chi }^{\prime }\left(H\right)$ data collected at 330 mK showing the phase boundary (dashed line) between the quantum disordered (QD) ground state and magnetically ordered $\mathbf{q}=(1/3,1/3,0)$ state near 3 T. A second transition back into the quantum disordered state or a quantum paramagnetic phase begins at higher fields. b, ${\chi }^{\prime }\left(T\right)$ data collected under a series of magnetic fields that traverse the ordered state; 4 T and 5 T ${\chi }^{\prime }\left(T\right)$ data illustrate the onset of the ordered phase below 1 K, while 6 T and 7 T data suggest partial re-entry into a disordered magnetic state. c, Specific heat of NaYbO₂ measured down to 80 mK under zero field and overplotted with the non-magnetic NaLuO₂ analogue. The resulting magnetic entropy $\mathrm{\Delta }{S}_M$ approaches 95% of $R\text{ln}\left(2\right)$. d, Values of $C_p\left(T\right)$ under varying magnetic fields. The lower peak centred around 1K develops a sharp anomaly at 5 T, indicative of the phase transition into the $\mathbf{q}=(1/3,1/3,0)$ state that is suppressed by 9 T. The inset shows the low-temperature portion of the $0\mathrm{T}{C}_p\left(T\right)$ data fit to a power law. The resulting fit to $T^{2.04}$ is shown as a solid yellow line through the data. Error bars denote one standard deviation of the data.

Although the saturated moment for this system is expected to be approximately $1.5{\mu }_{\mathrm{B}}$ per Yb ion, $M\left(H\right)$ (where $M$ is magnetization and $H$ is magnetic field strength) measurements collected at 2 K up to 9 T (Fig. 2b) were able to polarize Yb moments up to $1{\mu }_{\mathrm{B}}$ only, consistent with notable ${\theta }_{\mathrm{C}\mathrm{W}}$ exchange. Figure 2c shows zero-field a.c. susceptibility data collected down to 50 mK. No signatures of freezing, frequency dependence or long-range order are observed. Instead, ${\chi }^{\prime }\left(T\right)$ continues to diverge as the sample is cooled, generating an empirical frustration parameter of ${\theta }_{\mathrm{C}\mathrm{W}}/0.050$ $K>200$. As we will later argue, this zero-field state is an inherently quantum disordered state dressed by a small fraction of free Yb moments that are quenched in a magnetic field.

Data on ${\chi }^{\prime }\left(T\right)$ collected under a variety of $H$ fields are plotted in Fig. 2d. Under small $H$ values, the divergence in ${\chi }^{\prime }\left(T\right)$ (the real part of the a.c. susceptibility) is suppressed and a maximum appears. The temperature of this maximum increases with field until ${\mu }_{0}H=2\mathrm{T}$ (where ${\mu }_0$ is the permeability of free space) is reached, beyond which ${\chi }^{\prime }\left(T\right)$ becomes nearly temperature independent. The inflection in ${\chi }^{\prime }\left(T\right)$ increases linearly with $H$ and is plotted in Fig. 1b. This matches the expected Zeeman splitting $\left(\mathrm{\Delta }E\right)$ of isolated $J_{\text{eff}}=1/2$ moments, $\mathrm{\Delta }E=2{\mu }_{\mathrm{R}}{g}_{\text{avg}}{J}_{\text{eff}}H$, and suggests that ${\chi }^{\prime }\left(T\right)$ at ${\mu }_{0}H=2\mathrm{T}$ represents the remaining majority of the correlated/bound Yb moments. As an estimate of the fraction of free spins, ${\mu }_{0}H=0\mathrm{T}$ data were fit to a Curie–Weiss form after removing the majority response accessed at ${\mu }_{0}H=2\mathrm{T}$. Fits to a Curie–Weiss form between 1 K and 4 K (Fig. 2d) are described by a model of 14.4(6)% free spins with a full moment of $2.63{\mu }_{\mathrm{B}}$ and ${\theta }_{\mathrm{C}\mathrm{W}}=-0.45\left(4\right)\mathrm{K}$. In addition, 2 K $M\left(H\right)$ data plotted in Supplementary Fig. 2d were fit to a two-component model of Brillouin-like free spins and exchange-field-bound moments, which yielded a free spin fraction of approximately 7%. These fits roughly parametrize the limits of a free spin fraction in the material and suggest that free spins coexist within a quantum disordered ground state.

At higher fields, the nearly temperature-independent ${\chi }^{\prime }\left(T\right)$ at 2 T evolves into an ordered state. Isothermal ${\chi }^{\prime }\left(H\right)$ data at 330 mK plotted in Fig. 3a show an increase in the susceptibility as a phase boundary is traversed at 3 T, followed by nearly total suppression of ${\chi }^{\prime }\left(H\right)$ at 5 T. For ${\mu }_{0}H>5\mathrm{T}$, ${\chi }^{\prime }\left(H\right)$ begins to recover, suggesting a higher-field phase boundary—one marking the quenching of the ordered state as spins are further polarized toward a quantum paramagnetic phase. Data collected across the ordered regime are plotted in Fig. 3b and show a sharp transition below 1 K at ${\mu }_{0}H=4\mathrm{T}$. The probable origin of the enhancement in ${\chi }^{\prime }\left(T\right)$ when entering the ordered state at 3 T is the proximity of the quantum critical point associated with the nearby 0 K phase boundary. These quantum fluctuations are suppressed when crossing the finite-temperature phase boundaries away from this point.

To further characterize NaYbO₂, heat capacity measurements were performed. Figure 3c shows the zero-field $C\left(T\right)$ of both NaYbO₂ and a non-magnetic comparator, NaLuO₂, plotted from 80 mK to 40 K. Consistent with susceptibility data, no sharp anomaly indicative of the onset of long-range order is observed in NaYbO₂. Instead, a broad feature comprising two peaks is apparent—one peak centred near 1 K and the other near 2.5 K. Two peaks in $C\left(T\right)$ are predicted in a number of theoretical models for both trian gular^34,35 and kagome-based^36,37 Heisenberg lattices where a quantum spin liquid state appears. Integrating the magnetic entropy, $\mathrm{\Delta }{S}_M\left(T\right)$, with the lattice contribution subtracted yields an entropy reaching 95% of $R\text{ln}\left(2\right)$ where $R$ is the ideal gas constant and is consistent with the nominal $J_{\text{eff}}=1/2$ magnetic doublet of NaYbO₂.

When applying a magnetic field, data in Fig. 3d show that the 2.5 K peak in specific heat as a function of temperature, $C_p\left(T\right)$, where pressure ($p$) is constant, shifts upward in temperature, similar to other frustrated magnets; however, under 5 T, a sharp anomaly appears near 1 K and is coincident with the downturn in ${\chi }^{\prime }\left(T\right)$ at this field. Under 9 T, this sharp peak broadens and shifts lower in temperature as the system is driven into the disordered state. Integrated under 5 T, the magnetic entropy matches that of 0 T, and the lowest-temperature $C_p\left(T\right)$ is strongly suppressed once order is generated. This is consistent with the suppression of low-energy spin fluctuations when entering the ordered state, which return when the high-field quantum paramagnetic phase is approached. Determining the precise form of the zero-field $C_p\left(T\right)$ is complicated by a nuclear Schottky feature that dominates below 100 mK (Supplementary Fig. 2c); however, attempts to do so away from this feature yield $C\left(T\right)\propto T^2$, as shown in the inset of Fig. 3d.

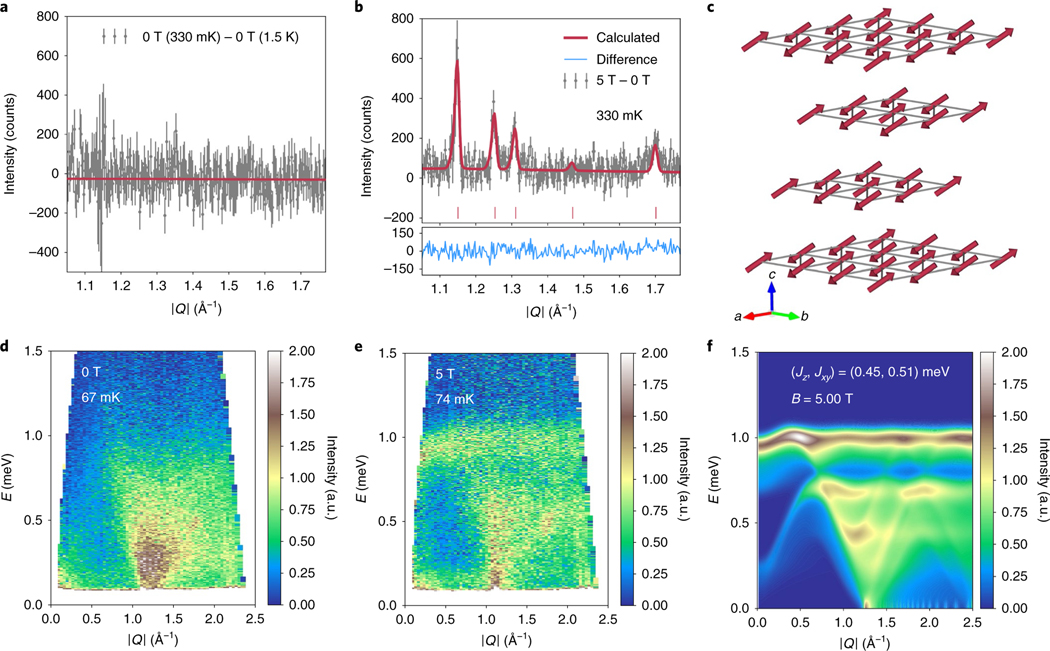
Low-temperature neutron-scattering measurements were also performed. Figure 4a shows temperature-subtracted (330 mK − 1.5 K) diffraction data and the absence of zero-field magnetic order. Field-subtracted data at 450 mK plotted in Fig. 4b reveal that under 5 T, new superlattice reflections appear at the momentum transfers $\mathbf{Q}=(1/3,1/3,0),(1/3,1/3,1)$ and (1/3, 1/3, 3). Given the symmetry constraints of the R3m structure, these either represent a 120° non-collinear spin structure or an up–up–down pattern of spin order. The absence of a reflection at $\mathbf{Q}=(1/3,1/3,2)$ suggests that the field-induced order is collinear. Additionally, magnetic intensity appears at the $\mathbf{Q}=(0,0,3)$ position, consistent with the two-q or two-propagation vector structure $(\mathbf{q}=(1/3,1/3,0)+\mathbf{q}=(0,0,0\left)\right)$ expected for the equal-moment up–up–down state³⁸. The best fit to this model is shown in Fig. 4c, where spins refine to be oriented nearly parallel to the (1, −1, −1) direction with an ordered moment of $1.36\pm 0.1{\mu }_{\mathrm{B}}$. This value is less than the $1.5{\mu }_{\mathrm{B}}$ expected, probably due to the presence of a minority fraction of free moments as well as the influence of remnant fluctuations in the ordered state. Magnetic peaks are resolution-limited with a minimum spin–spin correlation length ${\xi }_{\mathrm{m}\mathrm{i}\mathrm{n}}=450\text{Å}$. Further data collected at 67 mK determine the low-temperature, magnetic field phase boundaries (Supplementary Fig. 4b).

Fig. 4 |. Neutron diffraction and inelastic neutron-scattering data.

a, Temperature-subtracted neutron powder diffraction data (330 mK − 1.5 K) collected under 0 T, showing the absence of low-temperature magnetic order. The red line is a constant fit to the subtracted data. b, Under an applied field of 5 T at 450 mK, new magnetic peaks appear at (1/3, 1/3, $z$) positions ($z=0,1,3$), corresponding to an ordering wave vector of $\mathbf{q}=(1/3,1/3,0)$. The data were refined by analysing field-subtracted data (5 T − 0 T), which are constrained by the suppressed (1/3, 1/3, 2) reflection. c, The best fit to the 5 T induced magnetic state using the two-q structure $\mathbf{q}=(1/3,1/3,0)+\mathbf{q}=(0,0,0)$ is generated by a collinear spin structure with Yb moments of $1.36\left(10\right){\mu }_{\mathrm{B}}$. The displayed structure aligns moments approximately along the <1, −1, −1> direction and has six symmetrically equivalent structures generated by three-fold in-plane rotational and mirror symmetries. d, Inelastic neutron-scattering spectrum collected at 67 mK and 0 T. e, Inelastic neutron-scattering spectrum collected at 74 mK and ${\mu }_{0}H=5\mathrm{T}$. f, Linear spin wave calculations showing the powder-averaged $S(Q,E)$ for a two-dimensional triangular lattice of anisotropic ${\mathrm{Y}\mathrm{b}}^{3+}$ moments of NaYbO₂ in a 5 T field and three-sublattice ordering. Error bars denote one standard deviation of the data.

Inelastic scattering data plotted in Fig. 4d,e reveal a renormalization of the low-energy spin dynamics when transitioning from the quantum disordered state into the up–up–down phase. The zero-field data show a diffuse spectrum of excitations centred around the (1/3, 1/3, 0) wave vector, and when applying a 5 T field, much of this spectral weight is shifted into the elastic channel and a nearly flat band of excitations centred at 1 meV. Powder-averaged linear spin wave calculations assuming a purely two-dimensional triangular lattice in a 5 T magnetic field reproduce this flat feature, and the simulated dynamic structure factor $S(Q,E)$ is plotted in Fig. 4f. This simulation was generated using nearest-neighbour coupling with a nearly Heisenberg Hamiltonian with a slight easy-plane anisotropy, $J_z=0.45$ and $J_{xy}=0.51$ meV. The subtle downturn at low $\mathbf{\text{Q}}$ of the 1 meV band requires easy-plane anisotropy, as discussed in the Supplementary Information.

We now discuss the implications of our results. The similar YbO₆ octahedra of NaYbO₂ and YbMgGaO₄ intimate that the local crystal fields and in-plane exchange couplings between Yb ions are comparable; however, the main distinction between the two systems is the much shorter interplane distance in NaYbO₂. This suggests that the interlayer coupling is non-negligible, and therefore, a minimal Hamiltonian should include nearest-neighbour bonds within the planes and between neighbouring layers. Based on the structure, a symmetry analysis leads to the following exchange Hamiltonian:

$$\begin{gathered} H_{2d}=\sum _{ij} \left\{J_{xy}\left(S_i^x{S}_j^x+S_i^y{S}_j^y\right)+J_z{S}_i^z{S}_j^z+J_c\left({\widehat{\mathbf{e}}}_{ij}\cdot S_i\right)\right. \\ \left.\left({\widehat{\mathbf{e}}}_{ij}\cdot S_j\right)+J_{cz}\left[\left(\widehat{\mathbf{z}}\cdot {\widehat{\mathbf{e}}}_{ij}\times S_i\right)S_j^z+\left(\widehat{\mathbf{z}}\cdot {\widehat{\mathbf{e}}}_{ij}\times S_j\right)S_i^z\right]\right\} \\ {H}^{\prime }=\sum _{ij} \left\{J_{xy}^{\prime }\left(S_i^x{S}_j^x+S_i^y{S}_j^y\right)+J_z^{\prime }{S}_i^z{S}_j^z+J_c^{\prime }\left({\widehat{\mathbf{f}}}_{ij}\cdot S_i\right)\right. \\ \left.\left({\widehat{\mathbf{f}}}_{ij}\cdot S_j\right)+J_{cz}^{\prime }\left[\left({\widehat{\mathbf{f}}}_{ij}\cdot S_i\right)S_j^z+\left({\widehat{\mathbf{f}}}_{ij}\cdot S_j\right)S_i^z\right]\right\} \end{gathered}$$

The first line $H_{2d}$ contains interactions within a triangular layer, and the second between layers. The unit vectors ${\widehat{\mathbf{e}}}_{ij}$ are oriented along the $ij$ bond, and ${\widehat{\mathbf{f}}}_{ij}$ is a unit vector along the projection of the $ij$ bond into the a–b plane. The in-plane Hamiltonian is identical to that in YbMgGaO₄, but is rewritten here (following Iaconis et al.³⁹) in a more physically transparent ‘compass model’ form. The interlayer exchange $H^{\prime }$ in the second line also has a compass-like structure. We expect that this form applies to the full family of delafossite-like antiferromagnets, ARX₂ (A = alkali metal, R = rare earth and X = chalcogen ions), with dipolar Kramers doublets on the R site, sharing the space group 166.

Notably, $H_{2d}$ contains a wide range of phase space favouring three types of classical orders: (1) three-sublattice 120° structures, (2) collinear two-sublattice stripe phases and (3) out-of-plane Ising anisotropy with up–up–down structures. Because we do not observe zero-field order, and we expect that interplane exchange is substantial, we infer that the interactions in $H^{\prime }$ should be frustrated by the in-plane order or correlations. Consideration of the coupling between layers $J^{\prime }$ uniquely singles out the three-sublattice 120° structure: to leading order, only this in-plane order allows the staggered magnetization to effectively cancel the exchange field between neighbouring planes (see Supplementary Information)³⁹. This is even true to a large extent also for the anisotropic $J_c^{\prime }$ and $J_{cz}^{\prime }$ couplings.

Using this deduction that NaYbO₂ has 120° correlations, we expect fluctuations among many classically degenerate or nearly degenerate states to strongly suppress order. Furthermore, recent density matrix renormalization group studies of $H_{2d}$ find that for $S=1/2$ quantum spins, a spin liquid state indeed occurs in a corner of the classically 120° ordered phase space with moderate $J_{cz}$ coupling⁴⁰. Consequently, it is plausible that a spin liquid state occurs in NaYbO₂, and if so, it is likely to be smoothly connected to the spin liquid of the two-dimensional problem. The optimal spin liquid ground state for the 2d model based on variational parton calculations³⁹ is a U(1) Dirac state with gapless fermionic spinons described theoretically as a 2+1 -dimensional quantum electrodynamics (QED) conformal field theory: QED₃. The second implication of our Hamiltonian in this regime is that, on applying a magnetic field, the degeneracy is strongly lifted. This is because a large part of the zero-field cancellation is reliant on the specific 120° structure of the in-plane ground state, which is modified by the application of a magnetic field. Therefore, it is natural to expect ordering to become more robust in an applied magnetic field. The three-sublattice (1/3, 1/3, 0) wave vector is indeed germane to triangular antiferromagnets in a magnetic field, which stabilize a quantized magnetization plateau at 1/3 saturation in XXZ models^41,42.

With this in mind, we return to a discussion of the data. Theory predicts that for the $2d$ U(1) Dirac state, $C_p\left(T\right)$ is quadratic in temperature, consistent with measurements⁴³. An alternative explanation of $T^2$ specific heat might come from the degenerate line of spiral states found by Rastelli and Tassi for the zero-field rhombohedral XXZ model⁴⁴, which has $2d$-like spin fluctuations despite $3d$ coupling. The incommensurate long-range order of the Rastelli–Tassi spiral does not appear in our measurements; however, the field-induced Bragg peaks seen in experiment are consistent with the three-sublattice plateau states that emerge in the XXZ model in a field^41,45. Indeed, the magnetization at 5 T, where the ordered phase is maximal, is approximately 1/3 of the expected saturation moment and corresponds to a plateau where $\chi \left(T\right)=\partial M/\partial H$ reaches zero. The best fit to neutron diffraction data further corresponds to the equal-moment two-q up–up–down structure of the plateau state.

The two peaks observed in the zero-field $C_p\left(T\right)$ of NaYbO₂ evoke a number of theoretical models of Heisenberg spins on both triangular^34,35 and kagome^36,37 lattices that predict dual entropy anomalies when cooling into spin liquid ground states. Both peaks are rarely observed experimentally, and interpretations of the nature of each peak vary with the specific model. Exact diagonalization studies of the XXZ Hamiltonian on a triangular lattice predict a high-temperature peak corresponding to the formation of trimers of doublet states (that is, short-range correlations), followed by a lower-temperature peak that marks the onset of a quantum spin singlet state³⁵. Recent work exploring the $S=1/2$ triangular lattice using tensor renormalization group techniques predicts a dual $C_p\left(T\right)$ anomaly with the lower-temperature peak signifying the onset of short-range/incipient order and the upper peak reflective of the onset of gapped low-energy chiral fluctuations³¹. The ratio of low-temperature to high-temperature peak temperatures predicted in this $S=1/2$ model, $T_1/T_{\mathrm{h}}\approx 0.36$, is consistent with those observed in NaYbO₂, and the $J\approx 5$ K inferred from the model is reasonably close to the ${\theta }_{\mathrm{C}\mathrm{W}}$ determined from susceptibility data.

Our data demonstrate that the nearly ideal triangular lattice of Yb ions in NaYbO₂ realize an unconventional quantum disordered ground state. Unlike the majority of other spin liquid candidates such as herbertsmithite (ZnCu₃(OH)₆Cl₂) (ref. ⁴⁶), the ground state in NaYbO₂ can be driven into an intermediate antiferromagnetic ordered regime in relatively weak magnetic fields. The origin of the small fraction of free spins coexisting with this ground state remains an open question; however, they are not reflective of trivial disorder, which favours the least collinear state⁴⁷. Additionally, rather than hosting a purely two-dimensional network of spins where the two-dimensionality precludes long-range order such as in Ba₈CoNb₆O₂₄ (refs. ^48,49), interlayer geometric frustration is critical to the exclusion of order in NaYbO₂. This results in the strong perturbation that field provides to a complex interplay between interlayer frustration and the nearly degenerate ground states inherent to the XXZ triangular-lattice Hamiltonian. Due to this, NaYbO₂ uniquely stands able to provide considerable insight into the critical phase behaviour that manifests at the phase boundaries between the ordered and quantum disordered states in a chemically ideal frustrated triangular lattice.

Methods

Sample preparation.

Polycrystalline NaYbO₂ powder was prepared by a solidstate reaction of Yb₂O₃ (99.99%, Alfa Aesar) with Na₂CO₃ (99.997%, Alfa Aesar) in a 1/1.25 molar ratio and reacted at 1,000 °C for three days, with subsequent regrinding and reheating to 1,000 °C for another day. A slight excess of Na₂CO₃ remains in the powder and is required to prevent the formation of magnetic Yb₂O₃ impurities and stabilize the NaYbO₂ phase while reacting. In contrast to previous reports^27–29, attempts to remove this excess Na₂CO₃ via washing with common solvents (acidic/basic/neutral water, methanol, ethanol, isopropanol) induced NaYbO₂ degradation and Yb₂O₃ reformation. Therefore, the initial reaction was optimized to include minimal non-magnetic Na₂CO₃ impurities while maintaining complete reaction of Yb₂O₃ powder. All subsequent measurements accounted for the known Na₂CO₃ impurity fractions present in samples. All samples were stored in a dry, inert atmosphere and minimally exposed to atmospheric conditions before measurements. Neutron diffraction data show that the Na content of NaYbO₂ is stoichiometric within resolution (~1%). Although managing alkali content in many compounds can be challenging, the strong preference for Yb³⁺ aids in yielding fully occupied Na sites.

Neutron diffraction.

Powder neutron diffraction data were collected on a high-resolution neutron powder diffractometer (BT-1, National Institute of Standards and Technology (NIST)). For zero-field measurements, the instrument was equipped with a cryostat capable of reaching 1.6–300 K. A 7 T vertical field cryostat with a ³He insert was used to collect magnetic field data at 0 T, 5 T and 7 T between 0.33 K and 1.5 K. Samples were placed in a vanadium canister for high-temperature measurements and a copper cell for low-temperature measurements. The 300 K data were collected with neutrons of wavelengths 1.5399 Å and 2.0774 Å produced by a Cu(311) and Ge(311) monochromator, respectively. All other temperatures used neutrons of wavelength 2.0774 Å for maximum intensity. Rietveld refinement was performed with the FullProf software suite⁵⁰ and GSAS/EXPGUI programs^51,52, and fits to the data at 300 K and 1.6 K are shown in Supplementary Fig. 1. Additional inelastic neutron-scattering data were collected on a disc chopper spectrometer (NIST) in a 10 T magnetic field with a dilution insert. Incident neutrons with 5 Å wavelength were used with the medium-resolution chopper setting.

Magnetic measurements.

Magnetic properties were measured using several different instruments. Isothermal d.c. magnetization up to 9 T was collected on a physical property measurement system (PPMS, Quantum Design) with a vibrating sample magnetometer insert, and low-field d.c. magnetic susceptibility from 2 K to 300 K was obtained on a magnetic property measurement system (MPMS3, Quantum Design). Isothermal a.c. susceptibility in applied fields up to 7 T and temperature-dependent a.c. magnetic susceptibility were measured on an a.c. susceptometer at 711.4 Hz with a 0.1 Oe (7.96 A m⁻¹) drive field and a ³He insert capable of cooling to 330 mK. All fields collected are displayed in Supplementary Fig. 1. Within our a.c. susceptibility measurements at 711.4 Hz, the sample holder’s contribution is nearly linear at this range, and this frequency-dependent background was subtracted. This was confirmed via frequency sweeps of the empty holder loaded with an equivalent amount of silver paint and thermal-link wire used for the experiment. Further zero-field, frequency-dependent, a.c. susceptibility data between 10 Hz and 10 kHz and between 50 mK and 4 K were collected with the a.c. susceptibility for dilution refrigerator option on a PPMS with a 1 Oe drive field. Measurements of the empty sample holder were performed in this a.c. susceptibility for dilution refrigerator set-up at various excitation amplitudes and frequencies to quantify the total background. Trim coils were then used to cancel (null) the measured frequency-dependent background.

EPR spectra were recorded at 4.2 K with an EMXplus (Bruker) EPR spectrometer in the perpendicular operation mode. The observed resonance line shape was modelled with the EasySpin package implemented in MATLAB (ref. ⁵³). Broadening of the EPR line shape was observed and could be fit to a normal distribution of the out-of-plane $g_c$-factor (full-width at half-maximum = 0.40(7)) with no resolvable broadening in the in-plane $g_{ab}$-factor.

Heat capacity measurements.

Specific heat measurements between 80 mK and 300 K were performed for sintered pellets of NaYbO₂ under zero-field conditions on a PPMS using the dilution refrigerator insert for temperatures below 1.8 K. Data under 2.5 T, 5 T, and 9 T applied fields were also collected. The magnetic portion of specific heat was determined by subtracting the non-magnetic structural analogue NaLuO₂ measured between 2 K and 200 K (this was zero within resolution for temperatures <2 K). Calculated entropy was determined by integrating $C_{\text{mag}}/T$ (where $C_{\text{mag}}$ is the magnetic contribution to the heat capacity) between 80 mK and 40 K.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request. Neutron data were collected on the BT-1 diffractometer and the Disk Chopper Spectrometer at the NIST Center for Neutron Research.