Abstract
A novel method for creating “golden” 3D center-out radial MRI sampling trajectories was developed and analyzed. This method, called ELECTRO (ELECTRic potential energy Optimized), uses repulsive forces to minimize electric potential energy. An objective function 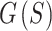 , the electric potential energies of all subsets of consecutive readouts in a 3D radial trajectory, and its reduced form were minimized using a multi-stage optimization strategy. A metric called normalized mean nearest neighbor angular distance (NMNA) was proposed for describing distributions of points on a sphere. ELECTRO and other relevant golden trajectories were compared in silico using NMNA and point spread function analysis. Consecutive readouts from an ELECTRO trajectory were well spread out, with consistent NMNA values across sphere sizes (σNMNA = 0.005) and between regions on the sphere (NMNA ≈ 1.49). Conversely, the supergolden trajectory had poor consistency in NMNA values (σNMNA = 0.090) and clustering (NMNA = 1.28 at the pole with 40,000 readouts) that lead to artifact in the point spread function. Multi-stage optimization was faster than single-stage and obtained lower values of
, the electric potential energies of all subsets of consecutive readouts in a 3D radial trajectory, and its reduced form were minimized using a multi-stage optimization strategy. A metric called normalized mean nearest neighbor angular distance (NMNA) was proposed for describing distributions of points on a sphere. ELECTRO and other relevant golden trajectories were compared in silico using NMNA and point spread function analysis. Consecutive readouts from an ELECTRO trajectory were well spread out, with consistent NMNA values across sphere sizes (σNMNA = 0.005) and between regions on the sphere (NMNA ≈ 1.49). Conversely, the supergolden trajectory had poor consistency in NMNA values (σNMNA = 0.090) and clustering (NMNA = 1.28 at the pole with 40,000 readouts) that lead to artifact in the point spread function. Multi-stage optimization was faster than single-stage and obtained lower values of 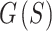 (e.g., 0.87 vs. 0.91, for a sphere size of 40). In conclusion, ELECTRO trajectories are more golden than other 3D center-out radial trajectories, making them a suitable candidate for dynamic 3D MR imaging.
(e.g., 0.87 vs. 0.91, for a sphere size of 40). In conclusion, ELECTRO trajectories are more golden than other 3D center-out radial trajectories, making them a suitable candidate for dynamic 3D MR imaging.
Keywords: Golden, K-space sampling trajectories, 3D dynamic MRI, Optimization
Subject terms: Biomedical engineering, Computational science
Introduction
In MRI, non-Cartesian sampling trajectories based on the golden ratio are a popular choice for accelerated dynamic 2D imaging applications. The golden ratio can produce a set of points that sample the unit interval such that, informally, all subsets of consecutive points are well spread out1–3. This property translates to sampling of the semi-circle and circle for golden angle radial4 and spiral trajectories respectively. As a result of this golden property and reconstruction algorithms that can tolerate undersampling5,6, golden angle k-space data are well suited for reconstruction in multiple different ways. Data can be binned according to a sliding window of arbitrary width for studies that require real-time images7. For cardiovascular imaging, data from different heart beats can be combined and reconstructed into a representative cine of the cardiac cycle. And all data can be reconstructed together for time-averaged imaging, coil sensitivity map estimation8,9, or motion estimation10. Certain motion-compensated cardiovascular MRI techniques rely on the use of all these types of reconstructions in a single reconstruction pipeline11–14. Reconstruction techniques that sort k-space data into high-dimensional spaces to simultaneously resolve multiple physiological dimensions (e.g., cardiac, respiratory, contrast) also make use of golden angle trajectories15,16.
Designing a “golden angle” radial trajectory in 3D is considerably more difficult for several reasons. Data readouts that are simply rotated in the same direction about the origin will sample a circle instead of the whole sphere. Under the spherical coordinate system, incrementing the polar angle linearly will result in a denser distribution of samples towards the poles. The concept of uniformity of points on a sphere is more difficult to define than the uniformity of points on a circle. Different optimization objectives for distributing points evenly on the sphere can lead to different global solutions17. There are challenges to visually evaluating trajectories for uniformity in 3D, and regions with poor uniformity may not be apparent or may only become apparent after a certain number of readouts. The golden 3D radial trajectory18, based on the 2D golden mean19, has been regarded as the 3D counterpart to the 2D golden angle radial trajectory. However, it may not be the only trajectory worthy of the title “golden”. To differentiate it from the others, and since it is related to the supergolden ratio20, we will refer to it as the supergolden trajectory for the remainder of this paper. Figure 1 shows the readout directions for the center-out supergolden trajectory, together with other trajectory distributions that are described in more detail below.
Fig. 1.
Points on the sphere represent the readout directions for 3D center-out radial trajectories. The blue-red-green colormap indicates the order of readouts. A narrow view of the sphere is shown since point patterns mainly vary as a function of the polar angle. The Normalized Mean Nearest neighbor Angular distance (NMNA) is used to describe points on the unit sphere (see Methods). A randomly distributed set of points will, on average, produce an NMNA value of 1. Clustered distributions of points will tend to have NMNA values below 1, while higher values indicate points are more evenly spread out. (A) Examples of five different trajectories with 40,000 readouts each. (B) Example point distributions with different values of NMNA.
The supergolden trajectory is calculated by first generating a sequence of well-distributed points in the unit square, and then mapping these points to the sphere using an inverse cylindrical equal-area projection21, thus obtaining the direction for each spoke. However, this mapping causes varying degrees of spatial distortion everywhere (except for two lines of latitude), with the distortion being most severe towards the north and south poles21 (Fig. 2A–C). The resulting point clustering on the sphere can range from none to severe, depending on the distribution in the square of points to be mapped. The degree of clustering also changes as a function of the number of readouts in the trajectory. For the center-out supergolden trajectory with 40,000 readouts (Fig. 1A), readouts near the z-axis form spiral clusters while those towards the equator form vertical lines. Such clustering reduces the sampling efficiency of the trajectory and negatively affects the image quality.
Fig. 2.
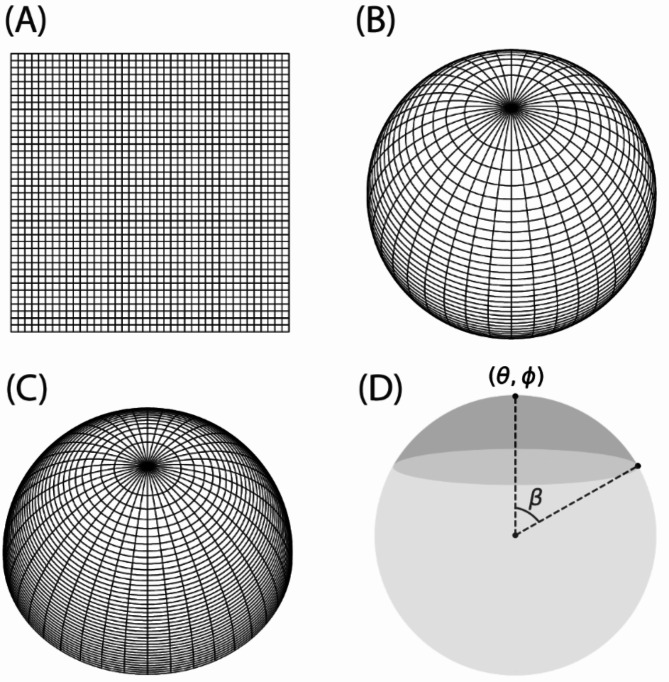
(A) A set of points forming a square grid. (B) The square grid mapped to the sphere using an inverse cylindrical equal-area projection. (C) The square grid mapped to the top hemisphere. Both cases show how space is distorted. (D) A spherical cap and its parameters.
In this work, we develop a novel method for determining readout directions and their ordering for flexible 3D center-out radial MRI. This method represents readout directions as point charges on the surface of the unit sphere. The total electric potential energy (EPE) is then minimized using repulsive/Coulomb forces, producing distributions of points that tend towards spherical uniformity. The problem of distributing points on the sphere is of interest across many disciplines22,23, and EPE and repulsive forces are intuitive ways to obtain distributions of points that are well spread out17,24–28. We use EPE to represent the desired properties of a trajectory, thereby producing ELECTRic potential energy Optimized (ELECTRO) 3D radial trajectories. To pursue the flexibility of golden trajectories in image reconstruction, ELECTRO trajectories are produced where all subsets of consecutive readouts are well spread out. An efficient GPU implementation of the optimization algorithm was developed, enabling the pre-calculation of trajectories that are large enough for many MRI applications. Also, we propose a new measure for describing distributions of points on the unit sphere, based on the angular distances between nearest neighbors. We theoretically evaluate ELECTRO and other golden trajectories using the new measure and point spread function (PSF) analysis.
Theory
Relevant sampling trajectories
This section defines four 3D center-out radial trajectories that (to varying degrees) evenly sample the sphere continuously in time: supergolden, plastic, 2D bit-reversed29, and Halton trajectories. These trajectories are shown in (Fig. 1A).
The unit square can be filled with points 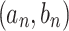 according to the sequence
according to the sequence
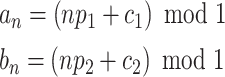 |
1 |
for 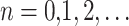 , where
, where 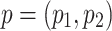 is a pair of positive real numbers and
is a pair of positive real numbers and 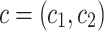 is a nonnegative initial offset. For the trajectories in this paper,
is a nonnegative initial offset. For the trajectories in this paper, 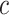 is set to zero. These points can then be mapped to the unit sphere using the inverse cylindrical equal-area projection21 (in Cartesian coordinates),
is set to zero. These points can then be mapped to the unit sphere using the inverse cylindrical equal-area projection21 (in Cartesian coordinates),
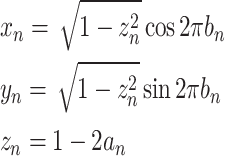 |
2 |
thus forming the unit readout direction 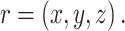 To map to the top hemisphere only, Eq. (2) can be modified so that
To map to the top hemisphere only, Eq. (2) can be modified so that 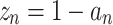 .
.
A center-out radial version of the supergolden trajectory18 can be defined by setting 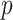 to the 2D golden mean19. Chan et al.18 derived the 2D golden mean through the eigenvectors of a matrix related to Narayana’s cows sequence. Alternatively, the 2D golden mean can be derived from the positive root of the polynomial
to the 2D golden mean19. Chan et al.18 derived the 2D golden mean through the eigenvectors of a matrix related to Narayana’s cows sequence. Alternatively, the 2D golden mean can be derived from the positive root of the polynomial 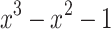 , which is also known as the supergolden ratio,
, which is also known as the supergolden ratio, 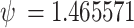 …. The 2D golden mean can be expressed as
…. The 2D golden mean can be expressed as 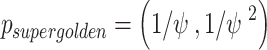 . Geometrically, the point
. Geometrically, the point 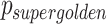 creates a supergolden rectangle in the unit square, where the width of the square is in the supergolden ratio with the longer side of the rectangle, and the longer side of the rectangle is in the supergolden ratio with the shorter side. We note that the order of assignment of
creates a supergolden rectangle in the unit square, where the width of the square is in the supergolden ratio with the longer side of the rectangle, and the longer side of the rectangle is in the supergolden ratio with the shorter side. We note that the order of assignment of 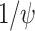 and
and 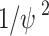 to
to 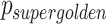 is arbitrary, with the two possibilities producing different patterns of sample clustering on the sphere. We follow the order used in Chan et al. and assign
is arbitrary, with the two possibilities producing different patterns of sample clustering on the sphere. We follow the order used in Chan et al. and assign 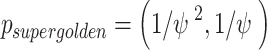 .
.
Similarly, a “golden” 3D center-out radial trajectory based on the plastic ratio30, 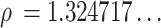 , can be generated by setting
, can be generated by setting 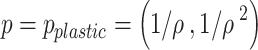 . The plastic ratio is the positive root of the polynomial
. The plastic ratio is the positive root of the polynomial 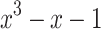 , and the point
, and the point 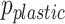 creates a plastic rectangle in the unit square. The plastic ratio is related to the Padovan sequence. Though we have not observed trajectories based on the plastic ratio in MRI, the plastic ratio has been associated with quasirandom sequences on the sphere31, and has properties similar to the supergolden 3D radial trajectory. To distinguish between these two “golden” trajectories, we call the trajectory associated with the plastic ratio the plastic trajectory.
creates a plastic rectangle in the unit square. The plastic ratio is related to the Padovan sequence. Though we have not observed trajectories based on the plastic ratio in MRI, the plastic ratio has been associated with quasirandom sequences on the sphere31, and has properties similar to the supergolden 3D radial trajectory. To distinguish between these two “golden” trajectories, we call the trajectory associated with the plastic ratio the plastic trajectory.
Another alternative to generating readout directions that are well-distributed throughout time is to use methods related to base-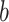 digit reversal. Trajectories based on base-2 digit reversal (i.e. bit-reversal) have been studied for 2D and 3D radial18,32. Furthermore, 3D center-out radial trajectories based on a 2D bit-reversal algorithm29 have been applied to dynamic pulmonary imaging33,34. The 2D bit-reversed 3D radial trajectory reorders the readout directions from a uniform spiral trajectory35, and depends on two positive integer parameters whose product equals the total number of readouts. Bit-reversal is closely related to the base-2 van der Corput sequence, which is a 1D sequence that quasirandomly samples the unit interval. Halton sequences generalize the van der Corput sequences to higher dimensions36. A 2D Halton sequence, that uses the base-2 and base-3 van der Corput sequences as its first and second dimensions respectively, samples the unit square in a quasirandom manner. We map these points to the sphere using Eq. (2) and call the corresponding trajectory the Halton trajectory. These four trajectories will be evaluated alongside ELECTRO trajectories.
digit reversal. Trajectories based on base-2 digit reversal (i.e. bit-reversal) have been studied for 2D and 3D radial18,32. Furthermore, 3D center-out radial trajectories based on a 2D bit-reversal algorithm29 have been applied to dynamic pulmonary imaging33,34. The 2D bit-reversed 3D radial trajectory reorders the readout directions from a uniform spiral trajectory35, and depends on two positive integer parameters whose product equals the total number of readouts. Bit-reversal is closely related to the base-2 van der Corput sequence, which is a 1D sequence that quasirandomly samples the unit interval. Halton sequences generalize the van der Corput sequences to higher dimensions36. A 2D Halton sequence, that uses the base-2 and base-3 van der Corput sequences as its first and second dimensions respectively, samples the unit square in a quasirandom manner. We map these points to the sphere using Eq. (2) and call the corresponding trajectory the Halton trajectory. These four trajectories will be evaluated alongside ELECTRO trajectories.
Electric potential energy of one sphere
A 3D center-out radial trajectory with a set of 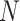 readout directions
readout directions 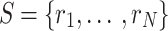 can be represented as
can be represented as 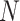 points on the unit sphere, each with unit charge. Let the total EPE of
points on the unit sphere, each with unit charge. Let the total EPE of 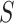 be
be
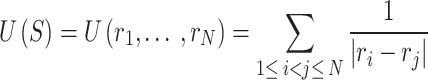 |
3 |
The objective is to find a set of points that minimizes 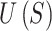 , subject to the constraints
, subject to the constraints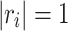 for
for 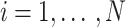 . The minimization can be carried out by performing gradient descent on every point
. The minimization can be carried out by performing gradient descent on every point 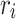 in a single iteration, and then projecting every point back onto the unit sphere. The negative gradient of
in a single iteration, and then projecting every point back onto the unit sphere. The negative gradient of 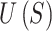 with respect to
with respect to 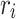 is the net force exerted on the point at
is the net force exerted on the point at 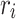 by all the other points. At the
by all the other points. At the 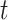 -th iteration, the net force on
-th iteration, the net force on 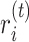 is
is
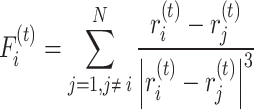 |
4 |
Thus the update to 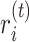 is (including the projection onto the sphere)
is (including the projection onto the sphere)
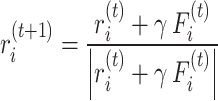 |
5 |
for some step size 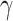 . Optimization of
. Optimization of 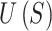 would produce a set of points that are well-distributed on the sphere, but this would not directly impose any preference on the sequential ordering of these points.
would produce a set of points that are well-distributed on the sphere, but this would not directly impose any preference on the sequential ordering of these points.
Electric potential energy of multiple spheres
The golden angle 2D radial trajectory samples the unit circle such that all subsets of consecutive readouts are well spread out. To produce a 3D center-out radial trajectory with this property on the unit sphere, we divide the trajectory into consecutive, overlapping subsets of points of size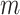 . We refer to
. We refer to 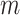 as the sphere size – the number of points on a given sphere. The goal is then to minimize the total EPE across all spheres, and the objective function is as follows. A sequence of
as the sphere size – the number of points on a given sphere. The goal is then to minimize the total EPE across all spheres, and the objective function is as follows. A sequence of 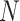 points can form
points can form 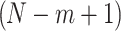 spheres, such that each sphere contains
spheres, such that each sphere contains 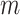 consecutive points. The EPE of each of these spheres can be summed to form the function
consecutive points. The EPE of each of these spheres can be summed to form the function
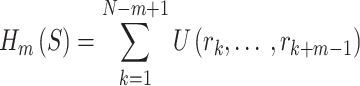 |
6 |
The formation of this function is illustrated in (Fig. 3A). Minimizing 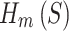 would cause the points in every sphere to be well spread out. To produce a trajectory where subsets of all sizes from
would cause the points in every sphere to be well spread out. To produce a trajectory where subsets of all sizes from 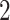 to
to 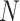 contain points that are well spread out, we propose to optimize the following function.
contain points that are well spread out, we propose to optimize the following function.
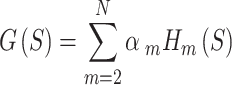 |
7 |
Fig. 3.
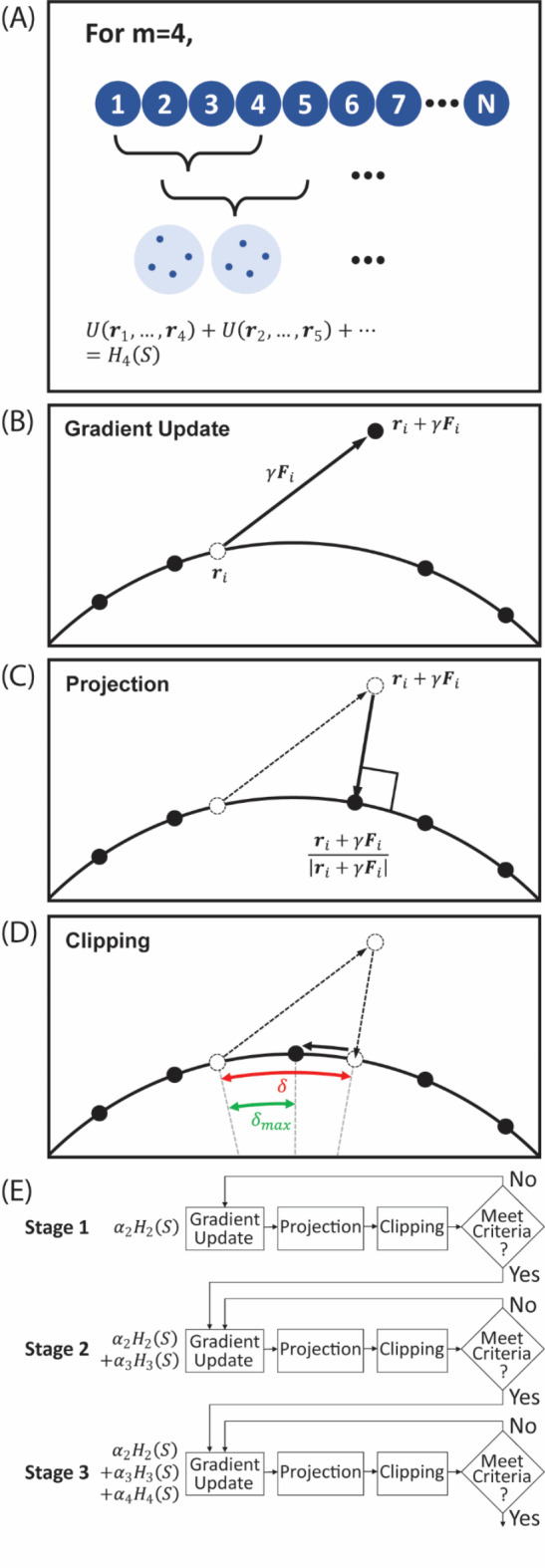
Overview of the ELECTRO optimization process. (A) Spheres with 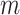 points are formed by considering all possible subsets of
points are formed by considering all possible subsets of 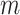 consecutive points (sphere size
consecutive points (sphere size 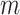 ). The total EPE of all these spheres is
). The total EPE of all these spheres is 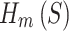 . (B) Gradient update for one of the points. (C) The point gets projected back onto the unit sphere. (D) Angular displacement gets clipped if it exceeds
. (B) Gradient update for one of the points. (C) The point gets projected back onto the unit sphere. (D) Angular displacement gets clipped if it exceeds 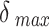 . (E) Flowchart of the multi-stage optimization process.
. (E) Flowchart of the multi-stage optimization process.
This function contains the EPE of every possible sphere of consecutive points (naturally excluding spheres with 0 or 1 point in them). 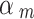 is a nonnegative scalar that gives weighting to the EPE of spheres of different sizes. For spheres with a lower number of points, the distances between points are larger, energies are lower, and forces are weaker on average. Consequently, it would be more difficult for points in smaller spheres to repel each other to their optimal positions when in the presence of stronger forces from spheres with a higher density of points. The weighting
is a nonnegative scalar that gives weighting to the EPE of spheres of different sizes. For spheres with a lower number of points, the distances between points are larger, energies are lower, and forces are weaker on average. Consequently, it would be more difficult for points in smaller spheres to repel each other to their optimal positions when in the presence of stronger forces from spheres with a higher density of points. The weighting 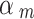 provides a means to adjust these forces so that points are appropriately distributed.
provides a means to adjust these forces so that points are appropriately distributed.
Alternatively, 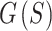 can be viewed as the EPE of one sphere (as in Eq. (3)), except now the energies between pairs of points have different weightings. By substitution of Eqs. (3) and (6) into (7), and then factoring,
can be viewed as the EPE of one sphere (as in Eq. (3)), except now the energies between pairs of points have different weightings. By substitution of Eqs. (3) and (6) into (7), and then factoring, 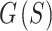 can be written as,
can be written as,
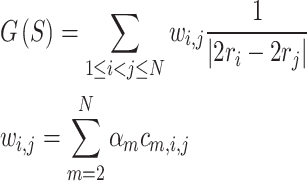 |
8 |
where 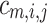 is a count of the number of spheres of size
is a count of the number of spheres of size 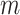 that contain the points
that contain the points 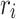 and
and 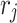 . The negative gradient of
. The negative gradient of 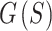 with respect to
with respect to 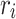 is similar to Eq. (4) except now the forces are weighted by
is similar to Eq. (4) except now the forces are weighted by 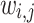 .
.
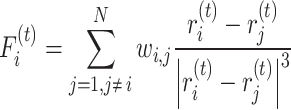 |
9 |
It follows from the definition of 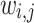 that, informally, points that are closer to each other in sequence ordering (points are closer to each other in sequence ordering when
that, informally, points that are closer to each other in sequence ordering (points are closer to each other in sequence ordering when 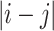 is smaller) will have greater weighting on their energies/forces. Consequently, points closer to each other in sequence ordering will tend to be farther apart on the sphere, and points far from each other in sequence ordering may be closer together on the sphere. The optimization process and its implementation, along with the definition of a metric to quantify point spacing on the unit sphere (normalized mean nearest neighbor angular distance, NMNA), are described in the following Methods section.
is smaller) will have greater weighting on their energies/forces. Consequently, points closer to each other in sequence ordering will tend to be farther apart on the sphere, and points far from each other in sequence ordering may be closer together on the sphere. The optimization process and its implementation, along with the definition of a metric to quantify point spacing on the unit sphere (normalized mean nearest neighbor angular distance, NMNA), are described in the following Methods section.
Methods
Multi-stage optimization
Finding a good configuration of points through the minimization of 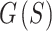 is challenging due to the large number of forces involved in the problem. We propose a strategy that first moves points to their approximate optimal positions, and then gradually adjusts these positions to obtain a more precise configuration. We do this systematically with a multi-stage optimization, where the EPE in the smaller spheres are minimized first, before adding the larger spheres into the objective function. For example, in the first stage, the EPE of all spheres of size 2 are minimized, i.e.,
is challenging due to the large number of forces involved in the problem. We propose a strategy that first moves points to their approximate optimal positions, and then gradually adjusts these positions to obtain a more precise configuration. We do this systematically with a multi-stage optimization, where the EPE in the smaller spheres are minimized first, before adding the larger spheres into the objective function. For example, in the first stage, the EPE of all spheres of size 2 are minimized, i.e., 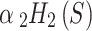 . In the next stage, continuing from the final point positions of the previous stage, the EPE of all spheres of sizes 2 and 3 are minimized, i.e.,
. In the next stage, continuing from the final point positions of the previous stage, the EPE of all spheres of sizes 2 and 3 are minimized, i.e., 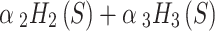 . This would continue until the final stage in which the full function
. This would continue until the final stage in which the full function 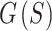 is minimized. In each stage, several iterations are performed. Each iteration consists of a gradient update, a projection onto the unit sphere, a clipping of angular displacements, and a criterion check for moving to the next stage (Fig. 3B–E). As the optimization transitions to the next stage, points that did not interact previously (their energies were not included in the objective function) may be in very close proximity to each other. Such resulting large forces would cause points to be displaced far from their previous near optimal positions. To prevent this, points with angular displacements (after gradient update and projection) that are larger than some maximum angular distance
is minimized. In each stage, several iterations are performed. Each iteration consists of a gradient update, a projection onto the unit sphere, a clipping of angular displacements, and a criterion check for moving to the next stage (Fig. 3B–E). As the optimization transitions to the next stage, points that did not interact previously (their energies were not included in the objective function) may be in very close proximity to each other. Such resulting large forces would cause points to be displaced far from their previous near optimal positions. To prevent this, points with angular displacements (after gradient update and projection) that are larger than some maximum angular distance 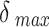 have their angular displacements clipped to
have their angular displacements clipped to 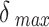 .
.
Normalized mean nearest neighbor angular distance
We propose to describe the spacing of points in a region of the unit sphere using a measure called the Normalized Mean Nearest neighbor Angular distance (NMNA). The angular distance between two points is 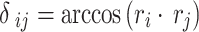 . Let the angular distance from
. Let the angular distance from 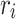 to its nearest neighbor be
to its nearest neighbor be 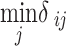 such that
such that 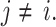 Let
Let 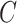 be a spherical cap on the unit sphere centered at the spherical polar and azimuthal coordinates
be a spherical cap on the unit sphere centered at the spherical polar and azimuthal coordinates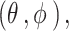 where
where 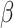 is the angle between the center and the edge of the cap (Fig. 2D). Let
is the angle between the center and the edge of the cap (Fig. 2D). Let 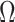 be the set of indices of the points that are on the spherical cap,
be the set of indices of the points that are on the spherical cap, 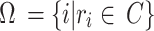 . The number of points in
. The number of points in 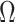 is
is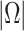 . Then the NMNA is defined as
. Then the NMNA is defined as
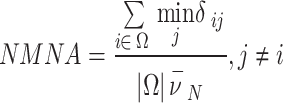 |
10 |
When 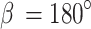 , the spherical cap is the same as the whole sphere and
, the spherical cap is the same as the whole sphere and 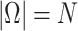 .
. 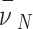 is the expected value of the nearest neighbor angular distance of
is the expected value of the nearest neighbor angular distance of 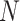 points randomly distributed on the unit sphere (its derivation is provided in the Appendix, which has similarities to others in the literature37,38). Even though the summation is performed over points on the spherical cap only, all points on the sphere are considered in the calculation of the nearest neighbor to
points randomly distributed on the unit sphere (its derivation is provided in the Appendix, which has similarities to others in the literature37,38). Even though the summation is performed over points on the spherical cap only, all points on the sphere are considered in the calculation of the nearest neighbor to 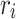 (even those outside of the spherical cap).
(even those outside of the spherical cap).
Similar to the measure of spacing for points in a flat region37,39, a randomly distributed set of points would produce an NMNA value of 1 on average. Point distributions that are more clustered than the average random distribution will produce NMNA values between 0 and 1, while increasing NMNA values indicate that points are better spread out. Figure 1 shows different distributions of points on the sphere and their corresponding global NMNA values. The NMNA of the uniform spiral of points is near 2.00. Since this measure only considers nearest neighbor angular distances, clustered distributions that appear very different may have the same NMNA. For example, the distributions labelled Clustered 1 and Clustered 2 both have NMNA values of 0.50, but there are larger unsampled spaces in Clustered 1 than Clustered 2.
Implementation
Experiments and analyses were carried out in Python on a high-performance computing node with Intel Xeon Gold 6130 and NVIDIA Tesla V100 16GB processors. Computations that involved large summations (e.g., energies, forces, nearest neighbor angular distances) were parallelized using CuPy/CUDA40.
Optimization parameters
We define a length that is characteristic of a unit sphere with 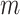 points, limiting it to a maximum of the diameter of the unit sphere.
points, limiting it to a maximum of the diameter of the unit sphere.
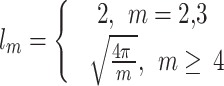 |
11 |
The corresponding characteristic angle is defined as 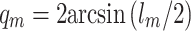 . For all experiments values of
. For all experiments values of 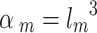 were used. Such values of
were used. Such values of 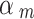 normalize the forces from different size spheres so that they are each relative to the characteristic length. This effectively scales up the forces in smaller
normalize the forces from different size spheres so that they are each relative to the characteristic length. This effectively scales up the forces in smaller 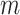 spheres and scales down the forces in larger
spheres and scales down the forces in larger 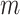 spheres.
spheres.
Still, the forces are proportional to the number of spheres that contain the corresponding pairs of points, and the points in the middle of the sequence are part of more spheres than points at the ends. This includes spheres of every size 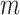 . We normalize for this by including a factor in the step size parameter
. We normalize for this by including a factor in the step size parameter 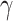 that will approximately average the forces.
that will approximately average the forces.
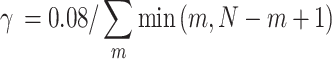 |
12 |
The summation is performed over all 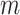 that have corresponding non-zero values for
that have corresponding non-zero values for 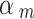 . The value in the denominator is a count of the number of spheres that contain the middle point in an
. The value in the denominator is a count of the number of spheres that contain the middle point in an 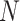 -point sequence. The value of 0.08 was determined empirically.
-point sequence. The value of 0.08 was determined empirically.
In the multi-stage optimizations, angular displacements were clipped to 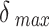 , which was set to half the characteristic angle of the largest size
, which was set to half the characteristic angle of the largest size 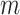 sphere in the current stage. No clipping of angular displacements was performed for the non-multi-stage optimizations. For the multi-stage optimizations, the criterion for advancing to the next stage was when no point moved more than 1% of the characteristic angle of the size
sphere in the current stage. No clipping of angular displacements was performed for the non-multi-stage optimizations. For the multi-stage optimizations, the criterion for advancing to the next stage was when no point moved more than 1% of the characteristic angle of the size 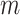 sphere to be added in the next stage. All optimizations were initialized using a random distribution of points.
sphere to be added in the next stage. All optimizations were initialized using a random distribution of points.
Reducing the number of sphere sizes
The definition of 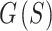 in Eqs. (7) and (8) involves the EPE of spheres of all sizes from
in Eqs. (7) and (8) involves the EPE of spheres of all sizes from 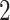 to
to 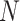 . For large
. For large 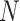 , the amount of space required to pre-compute and store
, the amount of space required to pre-compute and store 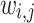 exceeds the memory of most GPUs. Consequently,
exceeds the memory of most GPUs. Consequently, 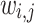 is recalculated each iteration, adding a nested loop of approximately size
is recalculated each iteration, adding a nested loop of approximately size 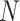 and significantly increasing computation time. As the golden angle 2D radial trajectory is more uniform when the number of readouts is a Fibonacci number, we reduce computation time by only optimizing for sphere sizes corresponding to the numbers in Narayana’s cows sequence41 greater than 1, i.e.
and significantly increasing computation time. As the golden angle 2D radial trajectory is more uniform when the number of readouts is a Fibonacci number, we reduce computation time by only optimizing for sphere sizes corresponding to the numbers in Narayana’s cows sequence41 greater than 1, i.e. 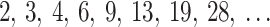 , stopping before the number
, stopping before the number 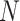 is exceeded. If the sequence does not end on
is exceeded. If the sequence does not end on 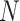 ,
, 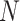 is appended. This approach reduces computation time by reducing the size of the inner loop that calculates
is appended. This approach reduces computation time by reducing the size of the inner loop that calculates 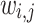 and by reducing the number of stages in the multi-stage optimization. The terms in Narayana’s cows sequence grow approximately exponentially (with the base being the supergolden ratio), meaning the larger numbers in the sequence are spaced farther apart than the smaller numbers. This suitably reduces to a greater degree the number of later stages in the optimization, which are more computationally expensive but less significant because points move very little. For example, if the points in a sphere with 10,000 points are well spread out, 9999 of those points are already well spread out, 9998 of those points are already well spread out, etc.
and by reducing the number of stages in the multi-stage optimization. The terms in Narayana’s cows sequence grow approximately exponentially (with the base being the supergolden ratio), meaning the larger numbers in the sequence are spaced farther apart than the smaller numbers. This suitably reduces to a greater degree the number of later stages in the optimization, which are more computationally expensive but less significant because points move very little. For example, if the points in a sphere with 10,000 points are well spread out, 9999 of those points are already well spread out, 9998 of those points are already well spread out, etc.
Evaluation of experimental factors on image quality
To evaluate the experimental performance of different trajectories, realistic retrospective simulations of image acquisition and reconstruction were performed. These simulations were based on an established digital phantom of the adult thorax, created using MRXCAT42. Signal reception was based on a simulated 24-elemental coil array. Image acquisition assumed a trapezoidal readout gradient (480 µs rise time, 1280 µs readout), a 64 kHz acquisition bandwidth (16 µs dwell time), and a total of 40,000 center-out radial spokes. Sphere sizes (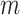 ) of 40,000, 20,000 and 10,000 were considered.
) of 40,000, 20,000 and 10,000 were considered.
Image reconstruction was performed using JSENSE to estimate coil sensitivity maps followed by iterative SENSE reconstruction9. Sampling density compensation was performed using the same approach as that described for the calculation of PSFs.
To evaluate the effect of gradient delay errors, representative values measured experimentally on a commercial scanner (1.5T Avanto, Siemens Healthineers) were applied to the three gradient axes (0, 1 and 4 µs along the x-, y- and z-axes, respectively). Image reconstructions were performed both with and without gradient delays, and with and without correcting for gradient delays. Differences between the reconstructed images and the ground truth digital phantom were then quantified based on the RMSE calculated over the entire volume of the digital thoracic phantom for each trajectory, sphere size, and gradient delay condition (none, present and uncorrected, present but retrospectively corrected). Note that retrospectively corrected gradient delays provide the actual k-space sampling pattern, but this will differ from the intended design. Hence, by evaluating each of these gradient delay conditions, one may determine if different trajectories are more sensitive to this perturbation.
Results
Comparing optimization strategies
Four ELECTRO trajectories were produced to demonstrate the effects of using the multi-stage optimization strategy and the effects of reducing the number of sphere sizes to be optimized. Computation time for the non-multi-stage optimization with all sphere sizes limited this comparison to trajectories with only 2500 readouts. Each optimization was run for 30,000 iterations. First, these four trajectories were analyzed by evaluating the full objective function 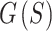 for each iteration of the optimization, even if the full
for each iteration of the optimization, even if the full 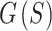 was not used for that stage or optimization strategy (Fig. 4A). The multi-stage optimization strategies initially ignore most of the terms in
was not used for that stage or optimization strategy (Fig. 4A). The multi-stage optimization strategies initially ignore most of the terms in 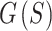 , resulting in a delayed drop in
, resulting in a delayed drop in 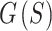 compared to the non-multi-stage optimization strategies. However, the multi-stage optimization strategies both converged to lower values of
compared to the non-multi-stage optimization strategies. However, the multi-stage optimization strategies both converged to lower values of 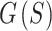 .
.
Fig. 4.
Comparison between non-multi-stage and multi-stage optimizations, and between optimizing all sphere sizes and only those corresponding to the numbers in Narayana’s cows sequence. (A) The full objective function 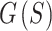 (all sphere sizes included) was evaluated for each iteration (2500 readouts). (B–C) For the final solution, a normalized
(all sphere sizes included) was evaluated for each iteration (2500 readouts). (B–C) For the final solution, a normalized 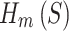 was evaluated and shown for a range of sphere sizes.
was evaluated and shown for a range of sphere sizes.
In the multi-stage optimization, each point experiences forces from at most 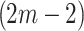 other points, where
other points, where 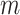 is the largest sphere size in the current stage. Without multi-stage optimization, each point experiences forces from every other point. This makes it difficult for a point to reach its optimal position because it would need to push through many other points and the forces pushing a point to its optimal position get weaker as the point gets closer. The fewer force interactions in the earlier stages of the multi-stage approach allows points to move more easily to their approximate optimal positions. As the optimization proceeds to the later stages these points stay approximately in the same position, while obtaining low energy configurations for both the small and large spheres. Figure S1 in the Supplementary Material contains videos showing the point movements for each of the four optimization strategies. The multi-stage optimization strategy is also more computationally efficient because it has fewer forces to compute in all stages except for the last, where the number of forces to be calculated is the same as a non-multi-stage optimization.
is the largest sphere size in the current stage. Without multi-stage optimization, each point experiences forces from every other point. This makes it difficult for a point to reach its optimal position because it would need to push through many other points and the forces pushing a point to its optimal position get weaker as the point gets closer. The fewer force interactions in the earlier stages of the multi-stage approach allows points to move more easily to their approximate optimal positions. As the optimization proceeds to the later stages these points stay approximately in the same position, while obtaining low energy configurations for both the small and large spheres. Figure S1 in the Supplementary Material contains videos showing the point movements for each of the four optimization strategies. The multi-stage optimization strategy is also more computationally efficient because it has fewer forces to compute in all stages except for the last, where the number of forces to be calculated is the same as a non-multi-stage optimization.
For the final solution of each type of optimization, 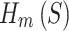 was evaluated and compared in Fig. 4B and C. Figure 4B shows the range of sphere sizes from 2 to 64, while Fig. 4C shows the range of sphere sizes from 2437 to 2500. To enable visual comparison,
was evaluated and compared in Fig. 4B and C. Figure 4B shows the range of sphere sizes from 2 to 64, while Fig. 4C shows the range of sphere sizes from 2437 to 2500. To enable visual comparison, 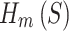 was normalized by dividing by the number of spheres
was normalized by dividing by the number of spheres 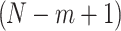 and by dividing by the number of interactions in a size
and by dividing by the number of interactions in a size 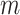 sphere,
sphere, 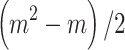 . Figure 4B shows that the energies for the smaller sphere sizes were indeed lower for the multi-stage optimizations. Figure 4B and C show that optimizing for only the sphere sizes from Narayana’s cows sequence resulted in lower energies for the smaller sphere sizes, but higher energies for the larger sphere sizes. This trade-off may be favorable for cine and real-time imaging where it is more important for smaller bundles of readouts to be well spread out. For the non-multi-stage optimizations, optimizing for only Narayana’s cows sphere sizes resulted in a lower
. Figure 4B shows that the energies for the smaller sphere sizes were indeed lower for the multi-stage optimizations. Figure 4B and C show that optimizing for only the sphere sizes from Narayana’s cows sequence resulted in lower energies for the smaller sphere sizes, but higher energies for the larger sphere sizes. This trade-off may be favorable for cine and real-time imaging where it is more important for smaller bundles of readouts to be well spread out. For the non-multi-stage optimizations, optimizing for only Narayana’s cows sphere sizes resulted in a lower 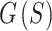 (Fig. 4A), likely from the lower energies of the smaller sphere sizes. On the other hand, for the multi-stage optimizations, optimizing for all sphere sizes resulted in convergence to the lowest value of
(Fig. 4A), likely from the lower energies of the smaller sphere sizes. On the other hand, for the multi-stage optimizations, optimizing for all sphere sizes resulted in convergence to the lowest value of 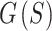 out of the four methods. However, the multi-stage optimization with Narayana’s cows sphere sizes requires much less computation than that with all sphere sizes. The former reached the final stage in 7 s, at iteration 1824, while the latter reached the final stage in 330 s, at iteration 3956. To keep computation times feasible for the larger ELECTRO trajectories, we proceed with the rest of our analysis using the multi-stage optimization with Narayana’s cows sphere sizes.
out of the four methods. However, the multi-stage optimization with Narayana’s cows sphere sizes requires much less computation than that with all sphere sizes. The former reached the final stage in 7 s, at iteration 1824, while the latter reached the final stage in 330 s, at iteration 3956. To keep computation times feasible for the larger ELECTRO trajectories, we proceed with the rest of our analysis using the multi-stage optimization with Narayana’s cows sphere sizes.
ELECTRO trajectories with increasing N
ELECTRO trajectories using the multi-stage optimization with Narayana’s cows sphere sizes were produced for 10,000, 20,000, 40,000, and 80,000 readouts. The optimizations were set to run for 10,000 iterations, except for the ELECTRO trajectory with 80,000 readouts, which was set to run for 20,000 iterations because it had more stages and it converged more slowly. The global NMNA of the first 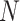 readouts and the last
readouts and the last 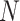 readouts were evaluated for each trajectory and the values are shown in Fig. 5. All ELECTRO trajectories appear to have a drop in NMNA towards the highest sphere sizes, suggesting that under the current scheme the weights
readouts were evaluated for each trajectory and the values are shown in Fig. 5. All ELECTRO trajectories appear to have a drop in NMNA towards the highest sphere sizes, suggesting that under the current scheme the weights 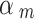 for the highest
for the highest 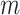 are too small or there should be more sphere sizes included in
are too small or there should be more sphere sizes included in 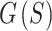 in the highest
in the highest 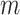 range. This drop in NMNA correlates with the higher energies for the larger sphere sizes in Fig. 4C. To avoid this potential sampling bias, these trajectories can simply be truncated given the NMNA is fairly consistent for most
range. This drop in NMNA correlates with the higher energies for the larger sphere sizes in Fig. 4C. To avoid this potential sampling bias, these trajectories can simply be truncated given the NMNA is fairly consistent for most 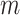 , e.g., take only the first 60,000 readouts from the ELECTRO trajectory optimized for 80,000 readouts. The 80,000 readout ELECTRO trajectory took 7.8 h to reach the final stage (at iteration 10,026) and 76.3 h to complete all 20,000 iterations.
, e.g., take only the first 60,000 readouts from the ELECTRO trajectory optimized for 80,000 readouts. The 80,000 readout ELECTRO trajectory took 7.8 h to reach the final stage (at iteration 10,026) and 76.3 h to complete all 20,000 iterations.
Fig. 5.
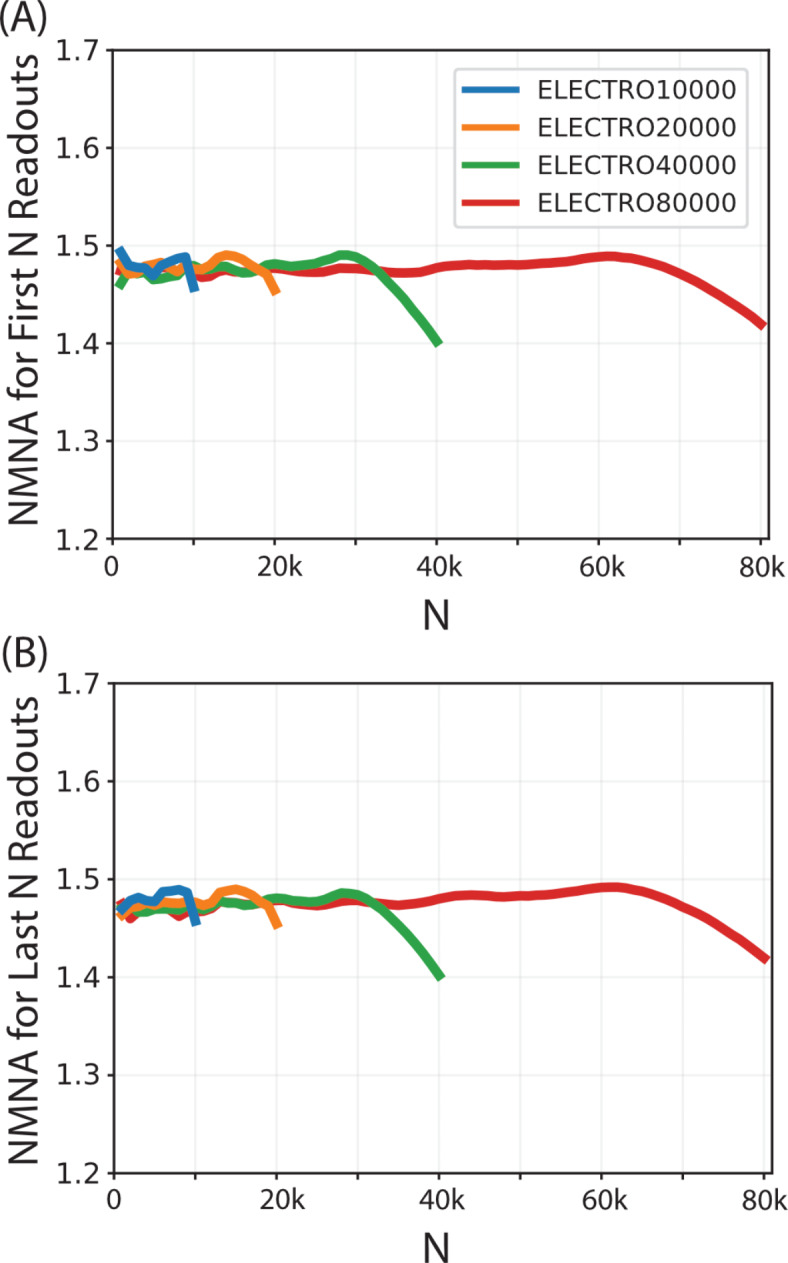
ELECTRO trajectories were produced for 10,000, 20,000, 40,000, and 80,000 readouts. The global NMNA was evaluated for the first  and last
and last  readouts.
readouts.
Regional point distribution analysis
The regional NMNA was evaluated for five spherical caps on the unit sphere. Since the spatial distortion from the inverse cylindrical equal-area projection varies as a function of the polar angle  but not the azimuthal angle
but not the azimuthal angle 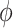 (Fig. 2A–C), four spherical caps were positioned at
(Fig. 2A–C), four spherical caps were positioned at 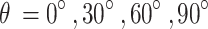 , each with
, each with 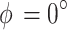 and cap angle
and cap angle 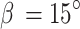 . The fifth spherical cap was the whole sphere. The NMNA was evaluated as a function of the first
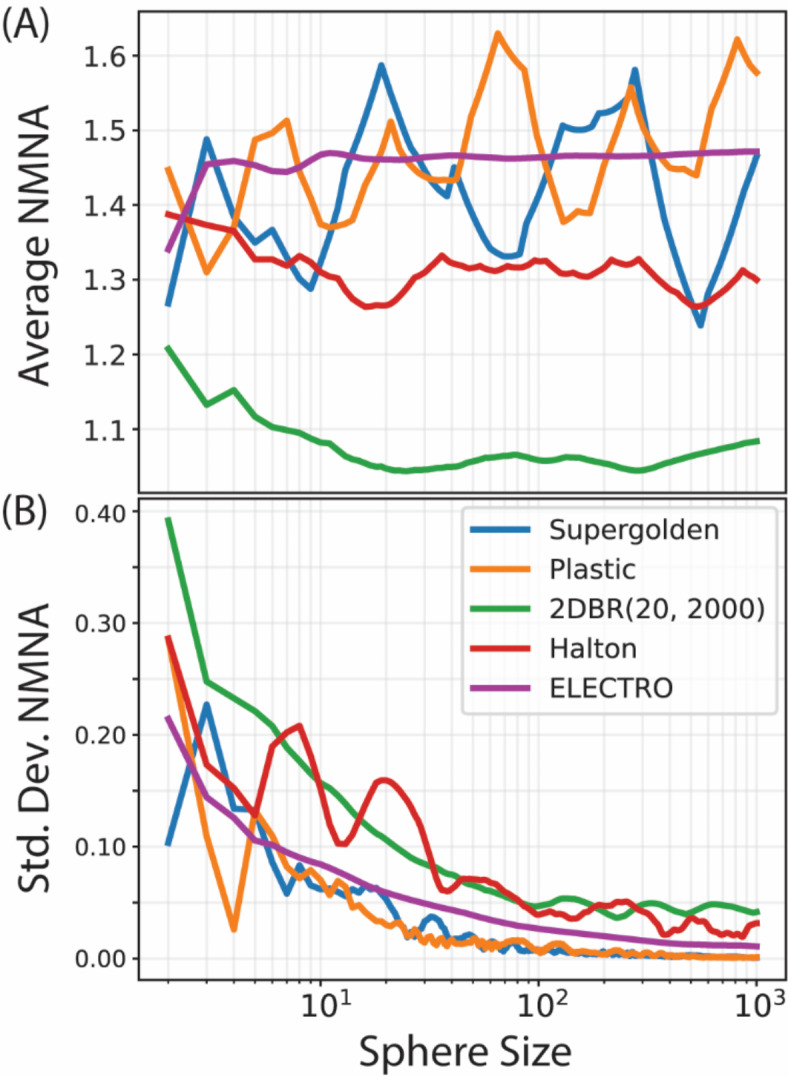
. The fifth spherical cap was the whole sphere. The NMNA was evaluated as a function of the first 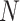 readouts of the ELECTRO, supergolden, plastic, 2D bit-reversed, and Halton trajectories. This was evaluated up to 80,000 spokes for every trajectory except for the 2D bit-reversed trajectory, which only had 40,000 spokes so that the same trajectory can be used in the next analysis (i.e., Fig. 7). The two parameters used for the 2D bit-reversed trajectory were 20 and 2000. Figure 6A– E compare the regional NMNA between the different spherical caps for each trajectory. Figure 6F compares the global NMNA between the different trajectories. The supergolden and plastic trajectories have the largest variation in regional NMNA between the four regions of the sphere, and large changes in regional NMNA as a function of
readouts of the ELECTRO, supergolden, plastic, 2D bit-reversed, and Halton trajectories. This was evaluated up to 80,000 spokes for every trajectory except for the 2D bit-reversed trajectory, which only had 40,000 spokes so that the same trajectory can be used in the next analysis (i.e., Fig. 7). The two parameters used for the 2D bit-reversed trajectory were 20 and 2000. Figure 6A– E compare the regional NMNA between the different spherical caps for each trajectory. Figure 6F compares the global NMNA between the different trajectories. The supergolden and plastic trajectories have the largest variation in regional NMNA between the four regions of the sphere, and large changes in regional NMNA as a function of 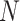 . The NMNA of the 2D bit-reversed trajectory generally increases as a function of
. The NMNA of the 2D bit-reversed trajectory generally increases as a function of 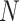 , until near uniformity when all readouts are included. The 2D bit-reversed, Halton, and ELECTRO trajectories have relatively little variation in regional NMNA between the four regions. The Halton and ELECTRO trajectories have relatively consistent values of NMNA for all
, until near uniformity when all readouts are included. The 2D bit-reversed, Halton, and ELECTRO trajectories have relatively little variation in regional NMNA between the four regions. The Halton and ELECTRO trajectories have relatively consistent values of NMNA for all 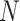 evaluated, though the values for the ELECTRO trajectory are higher. Like the global NMNA, the regional NMNA has drops at large sphere sizes for the ELECTRO trajectory. The supergolden trajectory at 40,000 readouts has greater clustering in the region at
evaluated, though the values for the ELECTRO trajectory are higher. Like the global NMNA, the regional NMNA has drops at large sphere sizes for the ELECTRO trajectory. The supergolden trajectory at 40,000 readouts has greater clustering in the region at 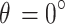 than the Halton trajectory. This can be seen both visually (Fig. 1A) and in their regional NMNA values (1.28 for supergolden and 1.33 for Halton), but the global NMNA of the supergolden trajectory remains higher than that of the Halton trajectory (1.37 for supergolden and 1.24 for Halton). This highlights the importance of regional analysis and how local information can be lost due to global averaging.
than the Halton trajectory. This can be seen both visually (Fig. 1A) and in their regional NMNA values (1.28 for supergolden and 1.33 for Halton), but the global NMNA of the supergolden trajectory remains higher than that of the Halton trajectory (1.37 for supergolden and 1.24 for Halton). This highlights the importance of regional analysis and how local information can be lost due to global averaging.
Fig. 7.
Comparison of NMNA values for the lower range of sphere sizes containing realistic temporal resolutions for cine and real-time MRI applications. Five center-out radial trajectories with 40,000 readouts are compared. (A) Average NMNA and (B) standard deviation of NMNA.
Fig. 6.
Regional point distribution analysis of the trajectories using NMNA. (A–E ) Regional NMNA of five center-out radial trajectories. Four regions at different polar angles were evaluated. (F) The NMNA averaged over the whole sphere for each of the five trajectories.
Uniformity of the smaller spheres
For each of the sphere sizes from 2 to 1000, the global NMNA was calculated for each of the 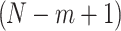 spheres. The average and standard deviation of the values were evaluated for each sphere size, and the results are shown in Fig. 7A and B respectively. Computation time limits this analysis to the lower range of sphere sizes, though this range includes realistic temporal resolutions for cine and real-time MRI applications. Trajectories with 40,000 readouts were included in this comparison. The ELECTRO trajectory with 80,000 readouts was truncated by taking the first 40,000 readouts. To measure the flatness of the curves,
spheres. The average and standard deviation of the values were evaluated for each sphere size, and the results are shown in Fig. 7A and B respectively. Computation time limits this analysis to the lower range of sphere sizes, though this range includes realistic temporal resolutions for cine and real-time MRI applications. Trajectories with 40,000 readouts were included in this comparison. The ELECTRO trajectory with 80,000 readouts was truncated by taking the first 40,000 readouts. To measure the flatness of the curves, 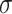 , in Fig. 7A the standard deviation of the values in each curve was calculated. In the range of sphere sizes from 2 to 1000, the ELECTRO trajectory has stable values for the average NMNA (
, in Fig. 7A the standard deviation of the values in each curve was calculated. In the range of sphere sizes from 2 to 1000, the ELECTRO trajectory has stable values for the average NMNA (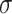 =0.005) that are consistently higher than those from the Halton and 2D bit-reversed trajectories (except for the sphere size of 2, for which the Halton trajectory has a higher average NMNA). The supergolden and plastic trajectories have average NMNA values that dramatically oscillate above and below the values of the ELECTRO trajectory (
=0.005) that are consistently higher than those from the Halton and 2D bit-reversed trajectories (except for the sphere size of 2, for which the Halton trajectory has a higher average NMNA). The supergolden and plastic trajectories have average NMNA values that dramatically oscillate above and below the values of the ELECTRO trajectory (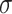 =0.090 and
=0.090 and 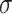 =0.070 respectively). The 2D bit-reversed and Halton curves have moderate flatness values at
=0.070 respectively). The 2D bit-reversed and Halton curves have moderate flatness values at 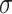 =0.014 and
=0.014 and 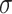 =0.019 respectively. The standard deviation of the NMNA (Fig. 7B) is generally lowest for the supergolden and plastic trajectories, followed by the ELECTRO trajectory and then the Halton and 2D bit-reversed trajectories. Compared to the supergolden trajectory, the ELECTRO trajectory had significantly higher (Welch’s t-test,
=0.019 respectively. The standard deviation of the NMNA (Fig. 7B) is generally lowest for the supergolden and plastic trajectories, followed by the ELECTRO trajectory and then the Halton and 2D bit-reversed trajectories. Compared to the supergolden trajectory, the ELECTRO trajectory had significantly higher (Welch’s t-test, 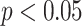 ) average NMNA values for 771 sphere sizes, while the supergolden trajectory had significantly higher values for 227 sphere sizes. Compared to the plastic trajectory, the ELECTRO trajectory had significantly higher average NMNA values for 336 sphere sizes, while the plastic trajectory had significantly higher values for 662 sphere sizes. Between the supergolden and plastic trajectories, the supergolden trajectory had significantly higher values for 222 sphere sizes while the plastic trajectory had significantly higher values for 777 sphere sizes.
) average NMNA values for 771 sphere sizes, while the supergolden trajectory had significantly higher values for 227 sphere sizes. Compared to the plastic trajectory, the ELECTRO trajectory had significantly higher average NMNA values for 336 sphere sizes, while the plastic trajectory had significantly higher values for 662 sphere sizes. Between the supergolden and plastic trajectories, the supergolden trajectory had significantly higher values for 222 sphere sizes while the plastic trajectory had significantly higher values for 777 sphere sizes.
Point spread function analysis
PSFs were calculated for the 40,000 spoke 3D center-out radial trajectories. Radial spokes with instantaneous gradient ramping were used (i.e., no uneven sampling on the spoke). The density compensation function was derived geometrically, assuming all points in a spherical shell occupied the same volume (no compensation for uneven angular spacing). The same density compensation function was used for each trajectory. The non-uniform fast Fourier transform43 from the SigPy library (https://github.com/mikgroup/sigpy) was used.
The three orthogonal center planes of the PSFs (Fig. 8) show the different aliasing artifacts from each trajectory and their directional dependence. Most noticeably, the PSF of the supergolden trajectory has disk-like artifacts in the mid z-plane, likely caused by the spiral sample clustering around the z-axis (Fig. 1A). The supergolden, plastic, 2D bit-reversed, and Halton trajectories all have one type of aliasing pattern in their mid x- and y-planes and a different type of aliasing pattern in their mid z-planes. This is likely a result of using the spherical polar and azimuthal angles in their derivation, which results in a symmetry about the z-axis. Of these four trajectories, the differences in aliasing pattern can be seen within the 1 FOV radius for the supergolden, plastic, and Halton trajectories, while the differences for the 2D bit-reversed trajectory are mainly outside of the 1 FOV radius. The ELECTRO trajectory is the only trajectory that has PSF mid planes that are indistinguishable from each other. The PSFs of the Halton and ELECTRO trajectories have mostly streak-like aliasing, correlating with the random-like pattern of their readout directions, while the PSFs of the supergolden and plastic trajectories have blade-like aliasing, which may correspond to their readouts having patterns that are regularly repeated azimuthally. Having incoherent aliasing artifact is favorable for L1-regularized image reconstructions such as compressed sensing6 and total-variation minimization44, while not having any directional dependence simplifies the assumptions to be made in these reconstructions. Any exponentially increasing sequence could be tried instead (e.g. Fibonacci or Padovan), where the base of the exponent would be chosen to control the trade-off between computation time and spacing between the numbers in the sequence. Narayana’s cows sequence was chosen because its base sits between those of the Fibonacci and Padovan sequences.
Fig. 8.
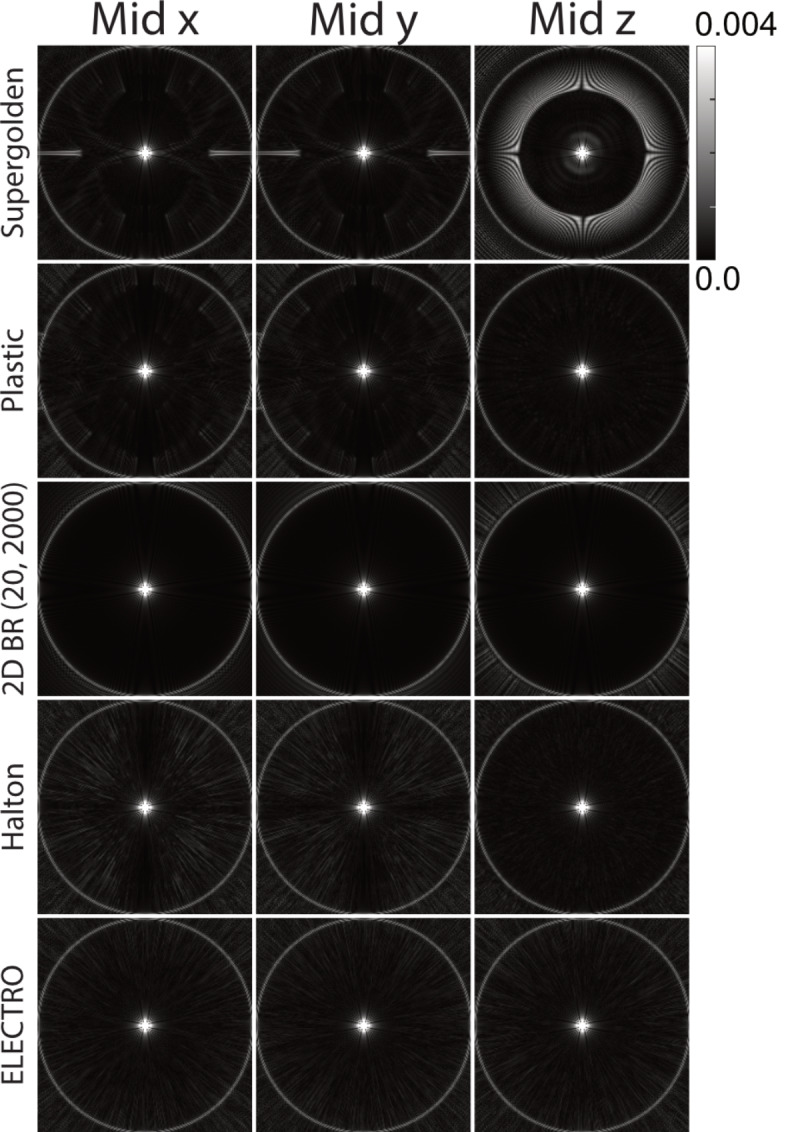
Point spread function comparison between five different 3D center-out radial trajectories. A narrow display window of [0, 0.004] was used. Images show the three orthogonal center planes at 2x FOV. The center planes of the ELECTRO PSF are indistinguishable from each other.
Evaluation of experimental factors on image quality
As described in the Methods section, numerical simulations of image acquisition and reconstruction were performed using the different trajectories to evaluate the effect of realistic experimental factors on image quality. Image quality was quantified based on the root mean squared error (RMSE) between the ground truth image (digital thoracic phantom) and the reconstructed images.
Of the factors tested, an uncorrected gradient delay produced the bigger change in RMSE across all trajectories. For example, for a sphere size of 40,000, the RMSE for all trajectories in the absence of gradient delay was less than 1% of the maximum signal of the ground truth image. Under conditions of experimentally realistic and uncorrected gradient delays, this error rose over six to eight-fold; however, following retrospective gradient delay correction, RMSE values returned to their baseline values. Similar behaviour was found for a sphere size of 20,000, with RMSE values rising from 1 to 2% to 5–6%, but again returning to baseline after correction. Finally, for a sphere size of 10,000, baseline RMSE values ranged between 5 and 8%, rising to 7.5–9.5%, and returned to baseline after correction. These findings demonstrate that, although RMSE values varied across sphere sizes and between trajectories, gradient delay errors after retrospective correction had a small influence on image quality.
Discussion
A new method has been developed for determining the readout directions for 3D center-out radial trajectories. By minimizing the energy function 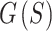 a “golden” trajectory is produced where all subsets of consecutive spokes are well spread out across the sphere. ELECTRO trajectories produced this way are arguably more golden than the supergolden and plastic trajectories. The NMNA of ELECTRO trajectories is more consistent across sphere sizes compared to the supergolden and plastic trajectories, whose NMNA values rise and drop significantly around the values of the ELECTRO trajectory (Fig. 7A). The regional NMNA varies most significantly for the supergolden and plastic trajectories (Fig. 6A–E). There is a regularity to the square of points related to the supergolden and plastic trajectories (points are modulo 1 multiples of
a “golden” trajectory is produced where all subsets of consecutive spokes are well spread out across the sphere. ELECTRO trajectories produced this way are arguably more golden than the supergolden and plastic trajectories. The NMNA of ELECTRO trajectories is more consistent across sphere sizes compared to the supergolden and plastic trajectories, whose NMNA values rise and drop significantly around the values of the ELECTRO trajectory (Fig. 7A). The regional NMNA varies most significantly for the supergolden and plastic trajectories (Fig. 6A–E). There is a regularity to the square of points related to the supergolden and plastic trajectories (points are modulo 1 multiples of 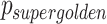 or
or 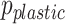 ). This regularity persists when the square of points is mapped to the sphere, giving rise to regular patterns of points that may include clustering (Fig. 1A). The square-to-sphere mapping stretches space azimuthally and polarly, but in different proportions depending on the polar angle (Fig. 2A–C). For these reasons, the regional NMNA varies as a function of the polar angle. This variation of regular patterns correlates with the directionally dependent structured aliasing patterns seen in their PSFs (Fig. 8). While the Halton trajectory also maps a square of points to the sphere, the points are not multiples of each other, and do not have the same degree of regularity. The NMNA is relatively consistent between regions of the ELECTRO trajectory (Fig. 6E) and its PSF has isotropic streak-like aliasing patterns (Fig. 8). These characteristics make ELECTRO trajectories more similar to the 2D golden angle radial trajectory, which is near uniform for all subsets of consecutive spokes and is not biased in any direction.
). This regularity persists when the square of points is mapped to the sphere, giving rise to regular patterns of points that may include clustering (Fig. 1A). The square-to-sphere mapping stretches space azimuthally and polarly, but in different proportions depending on the polar angle (Fig. 2A–C). For these reasons, the regional NMNA varies as a function of the polar angle. This variation of regular patterns correlates with the directionally dependent structured aliasing patterns seen in their PSFs (Fig. 8). While the Halton trajectory also maps a square of points to the sphere, the points are not multiples of each other, and do not have the same degree of regularity. The NMNA is relatively consistent between regions of the ELECTRO trajectory (Fig. 6E) and its PSF has isotropic streak-like aliasing patterns (Fig. 8). These characteristics make ELECTRO trajectories more similar to the 2D golden angle radial trajectory, which is near uniform for all subsets of consecutive spokes and is not biased in any direction.
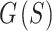 was minimized through a multi-stage process that converges faster and achieves lower energy solutions compared to minimizing all of
was minimized through a multi-stage process that converges faster and achieves lower energy solutions compared to minimizing all of 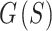 in a single stage (Fig. 4A). A reduced version of
in a single stage (Fig. 4A). A reduced version of 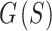 (Narayana’s cows) was minimized primarily to shorten computation times but minimizing the full
(Narayana’s cows) was minimized primarily to shorten computation times but minimizing the full 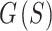 may yield even lower energy solutions. Narayana’s cows sequence improves computational performance by reducing the size of the optimization landscape and, at smaller sphere sizes, sampling of the landscape is still favorable for optimization. The number of points added to the sphere per iteration is also smaller, which can facilitate optimization at smaller sphere sizes (at large sphere sizes, cows are far apart, and convergence may be worse than by optimizing for all sphere sizes). In the current GPU implementation, each thread calculates the weighted force for a pair of points and adds the weighted force to the net forces of the corresponding two points. This summation can be divided amongst multiple GPUs, and the partial summations from each GPU can be combined afterward. Faster computation may enable the calculation of better point distributions and allow the production of trajectories with a greater number of readouts. Additionally, efficient storage and retrieval of pre-computed
may yield even lower energy solutions. Narayana’s cows sequence improves computational performance by reducing the size of the optimization landscape and, at smaller sphere sizes, sampling of the landscape is still favorable for optimization. The number of points added to the sphere per iteration is also smaller, which can facilitate optimization at smaller sphere sizes (at large sphere sizes, cows are far apart, and convergence may be worse than by optimizing for all sphere sizes). In the current GPU implementation, each thread calculates the weighted force for a pair of points and adds the weighted force to the net forces of the corresponding two points. This summation can be divided amongst multiple GPUs, and the partial summations from each GPU can be combined afterward. Faster computation may enable the calculation of better point distributions and allow the production of trajectories with a greater number of readouts. Additionally, efficient storage and retrieval of pre-computed  can further reduce computation time. Computation of an ELECTRO trajectory for each value of
can further reduce computation time. Computation of an ELECTRO trajectory for each value of 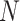 may not be necessary since the NMNA is quite consistent between ELECTRO trajectories with different
may not be necessary since the NMNA is quite consistent between ELECTRO trajectories with different 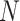 (Fig. 5). We expect that it would be practical to produce a single, high quality ELECTRO trajectory large enough for all foreseeable MRI applications, and then truncate it as needed. Such an endeavor would require, at least, the discussed improvements in hardware and software.
(Fig. 5). We expect that it would be practical to produce a single, high quality ELECTRO trajectory large enough for all foreseeable MRI applications, and then truncate it as needed. Such an endeavor would require, at least, the discussed improvements in hardware and software.
The weighting of the energies 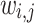 in Eq. (8) was derived from a multiple-spheres perspective of the problem, which consisted of the weighting
in Eq. (8) was derived from a multiple-spheres perspective of the problem, which consisted of the weighting 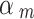 for each of the different sphere sizes.
for each of the different sphere sizes. 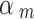 provides a handle for tuning the trajectory to specific temporal resolutions, if the desired temporal resolutions are known before data acquisition. Also, adjusting
provides a handle for tuning the trajectory to specific temporal resolutions, if the desired temporal resolutions are known before data acquisition. Also, adjusting 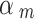 may improve the characteristic drop in NMNA for the large sphere sizes near
may improve the characteristic drop in NMNA for the large sphere sizes near 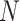 (Figs. 5 and 6E), as may changing the sphere sizes included in the optimization. For this work, the choices for these parameters were kept simple to avoid hand-tuning, but they may not be optimal. Alternatively, it may be possible to derive
(Figs. 5 and 6E), as may changing the sphere sizes included in the optimization. For this work, the choices for these parameters were kept simple to avoid hand-tuning, but they may not be optimal. Alternatively, it may be possible to derive 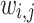 from functions that decrease as the distance between points in sequence ordering
from functions that decrease as the distance between points in sequence ordering 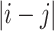 increases.
increases.
The ELECTRO readout directions were applied to 3D center-out radial trajectories, but these same directions can be used to distribute other trajectories, such as radial-cones45, Seiffert’s spirals46, and corkscrews47,48. Development and analysis were carried out for center-out radial, though extension of this method to full spoke radial is possible with minor adjustments. Each full spoke would need to have two points on the sphere symmetric through the origin, since the heads and tails together should be well spaced out. Most 3D full spoke radial trajectories have clustering near the 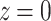 plane49,50, because the heads and tails together were not explicitly considered in their design18,51–53. Full spoke ELECTRO trajectories would not have this issue.
plane49,50, because the heads and tails together were not explicitly considered in their design18,51–53. Full spoke ELECTRO trajectories would not have this issue.
Potential extensions to this work include comparison to data-driven approaches for k-space trajectory design. For example, previous literature has demonstrated a generalized framework for the stochastic optimization of 3D non-Cartesian sampling trajectories (SNOPY)54. This approach has been applied to 3D center-out trajectories to create optimized but complex and non-linear trajectories. A computational complexity introduced by this approach would be the joint optimization of such complex trajectories across different sphere sizes, to support reconstruction at different temporal resolutions. Through our simulated experiments, we have demonstrated that ELECTRO can compensate for potential imaging errors with the application of gradient delay corrections. Hence, our approach is compatible with existing methods for coil combination and gradient delay corrections.
A new measure called the NMNA was proposed for describing a distribution of points on the sphere. The NMNA was used to analyze points in subregions of the sphere, whereas most methods in the literature have analyzed the entire sphere of points together18,35,52,53,55, which disregards anisotropy in the distribution of points. The NMNA has several differences from the mean nearest neighbor distance measure37, which was later called the clustered-random-regular (CRR) continuum38,53. This measure was derived under the assumptions of the Poisson distribution37, which are unsuitable for a finite number of points on a finite surface area. When applied to a distribution of points on the sphere, there is a bias in the CRR when the number of points is small. The 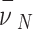 in NMNA was derived specifically for points on a sphere, which involved the use of the binomial distribution instead (see Appendix). We do not call our measure CRR because we do not believe that clustering, randomness, and regularity lie on a continuum. For example, the supergolden trajectory with 40,000 readouts has regularly repeating vertical line clusters at
in NMNA was derived specifically for points on a sphere, which involved the use of the binomial distribution instead (see Appendix). We do not call our measure CRR because we do not believe that clustering, randomness, and regularity lie on a continuum. For example, the supergolden trajectory with 40,000 readouts has regularly repeating vertical line clusters at 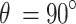 (Fig. 1A), resulting in a regional NMNA value above 1 (Fig. 6A). Though EPE was used as the objective function for ELECTRO, it was challenging to use EPE as a measure for comparing distributions of points. EPE was difficult to normalize as a function of
(Fig. 1A), resulting in a regional NMNA value above 1 (Fig. 6A). Though EPE was used as the objective function for ELECTRO, it was challenging to use EPE as a measure for comparing distributions of points. EPE was difficult to normalize as a function of 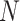 and it was relatively insensitive to different distributions of points, likely because the EPE includes the distances between all points rather than just the nearest neighbor.
and it was relatively insensitive to different distributions of points, likely because the EPE includes the distances between all points rather than just the nearest neighbor.
Conclusion
This work demonstrates the potential of obtaining a golden 3D radial trajectory from the optimization of electric potential energy. ELECTRO trajectories have more consistent NMNA values across sphere sizes and between regions of the sphere when compared to other trajectories. The readouts of the established supergolden trajectory form clusters around the z-axis that reduce the efficiency of k-space sampling and leads to structured image aliasing artifact, while ELECTRO trajectories are not biased in any direction. Further analysis focused on ELECTRO trajectories themselves and the optimization process may yield new insights and lead to better and even more efficient solutions.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Author contributions
The authors confirm contribution to the paper as follows: study conception and design: CH, DSG, CKM; technical development and analysis: CH; manuscript preparation and review: CH, DSG, CKM. All authors reviewed the results and approved the final version of the manuscript.
Data availability
Source code and simulation output are available from the lead author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-74437-x.
References
- 1.Hardy, G. H. & Wright, E. M. An Introduction to the Theory of Numbers (Oxford University Press, 1968).
- 2.Phillips, T. The most irrational number. Am. Math. Soc..
- 3.Ellenberg, J. The most irrational number. Slate (2021).
- 4.Winkelmann, S., Schaeffter, T., Koehler, T., Eggers, H. & Doessel, O. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans. Med. Imaging 26, 68–76 (2007). [DOI] [PubMed] [Google Scholar]
- 5.Pruessmann, K. P., Weiger, M., Börnert, P. & Boesiger, P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn. Reson. Med. 46, 638–651 (2001). [DOI] [PubMed] [Google Scholar]
- 6.Lustig, M., Donoho, D., Pauly, J. M. & Sparse, M. R. I. The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Hopfgartner, A. J. & others. Dynamic MRI of the TMJ under physical load. Dento Maxillo Facial Radiol. 42, 20120436 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Walsh, D. O., Gmitro, A. F. & Marcellin, M. W. Adaptive reconstruction of phased array MR imagery. Magn. Reson. Med. 43, 682–690 (2000). [DOI] [PubMed] [Google Scholar]
- 9.Ying, L. & Sheng, J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn. Reson. Med. 57, 1196–1202 (2007). [DOI] [PubMed] [Google Scholar]
- 10.Falcão, M. B. L. & others. Focused navigation for respiratory-motion-corrected free-running radial 4D flow MRI. Magn Reson Med. 90, 117–132 (2023). [DOI] [PMC free article] [PubMed]
- 11.Roy, C. W., Seed, M., Kingdom, J. C. & Macgowan, C. K. Motion compensated cine CMR of the fetal heart using radial undersampling and compressed sensing. J. Cardiovasc. Magn. Reson. 19, 29 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Goolaub, D. S. & others. Multidimensional fetal flow imaging with cardiovascular magnetic resonance: a feasibility study. J Cardiovasc Magn Reson. 20, 77 (2018). [DOI] [PMC free article] [PubMed]
- 13.Chaptinel, J. & others. Fetal cardiac cine magnetic resonance imaging in utero. Sci Rep. 7, 15540 (2017). [DOI] [PMC free article] [PubMed]
- 14.Hansen, M. S., Sørensen, T. S., Arai, A. E. & Kellman, P. Retrospective reconstruction of high temporal resolution cine images from real-time MRI using iterative motion correction. Magn. Reson. Med. 68, 741–750 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feng, L. & others. XD-GRASP: golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn. Reson. Med. 75, 775–788 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chandarana, H. Others. Respiratory motion-resolved compressed sensing reconstruction of free-breathing radial acquisition for dynamic liver magnetic resonance imaging. Invest. Radiol. 50, 749–756 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Erber, T. & Hockney, G. M. Equilibrium configurations of N equal charges on a sphere. J. Phys. Math. Gen. 24, L1369–L1377 (1991). [Google Scholar]
- 18.Chan, R. W. Others. Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magn. Reson. Med. 61, 354–363 (2009). [DOI] [PubMed] [Google Scholar]
- 19.Anderson, P. G. Multidimensional Golden means. In: (Anderson, P. G., Eds) Applications of Fibonacci Numbers (Springer, 1993). [Google Scholar]
- 20.The on-line encyclopedia of integer sequences. Entry A092526. (2023).
- 21.Snyder, J. P. Map projections: A working manual. (1987).
- 22.Thomson, J. J. On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. Lond. Edinb. Dublin Philos. Mag J. Sci. 7, 237–265 (1904). [Google Scholar]
- 23.Smale, S. Mathematical problems for the next century. Math. Intell. 20, 7–15 (1998). [Google Scholar]
- 24.Schauman, S. S., Okell, T. W. & Chiew, M. The set increment with limited views encoding ratio (SILVER) method for optimizing radial sampling of dynamic MRI. bioRxiv10.1101/2020.06.25.171017 (2021).
- 25.Jones, D. K., Horsfield, M. A. & Simmons, A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn. Reson. Med. 42, 515–525 (1999). [PubMed] [Google Scholar]
- 26.Lazarus, C. & others SPARKLING: variable-density k-space filling curves for accelerated T2*-weighted MRI. Magn. Reson. Med. 81, 3643–3661 (2019). [DOI] [PubMed] [Google Scholar]
- 27.Lazarus, C. & others. 3D variable-density SPARKLING trajectories for high-resolution T2*-weighted magnetic resonance imaging. NMR Biomed. 33, e4349 (2020). [DOI] [PubMed]
- 28.Chaithya, G. R. & others Optimizing full 3D SPARKLING trajectories for high-resolution magnetic resonance imaging. IEEE Trans. Med. Imaging 41, 2105–2117 (2022). [DOI] [PubMed] [Google Scholar]
- 29.Johnson, K. M. & Email Reproducing 3D radial bit reversed trajectory. (2022).
- 30.The on-line encyclopedia of integer sequences. Entry A060006. (2023).
- 31.Roberts, M. The unreasonable effectiveness of quasirandom sequences. (2020).
- 32.Chan, R. W., Ramsay, E. A., Cheung, E. Y. & Plewes, D. B. The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI. Magn. Reson. Med. 67, 363–377 (2012). [DOI] [PubMed] [Google Scholar]
- 33.Jiang, W. & others. Motion robust high resolution 3D free-breathing pulmonary MRI using dynamic 3D image self-navigator. Magn. Reson. Med. 79, 2954–2967 (2018). [DOI] [PMC free article] [PubMed]
- 34.Ong, F. & others Extreme MRI: large-scale volumetric dynamic imaging from continuous non-gated acquisitions. Magn. Reson. Med. 84, 1763–1780 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wong, S. T. S. & Roos, M. S. A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magn. Reson. Med. 32, 778–784 (1994). [DOI] [PubMed] [Google Scholar]
- 36.Halton, J. H. On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numer. Math. 2, 84–90 (1960). [Google Scholar]
- 37.Clark, P. J. & Evans, F. C. Distance to Nearest Neighbor as a measure of spatial relationships in populations. Ecology 35, 445–453 (1954). [Google Scholar]
- 38.Scott, D. & Tout, C. A. Nearest neighbour analysis of random distributions on a sphere. Mon. Not R Astron. Soc. 241, 109–117 (1989). [Google Scholar]
- 39.Dry, M., Preiss, K., Wagemans, J. & Clustering randomness, and regularity: spatial distributions and human performance on the traveling salesperson problem and Minimum spanning tree problem. J. Probl. Solving 4, 1–17 (2012). [Google Scholar]
- 40.Okuta, R. et al. A NumPy-Compatible Library for NVIDIA GPU Calculations. in Proceedings of Workshop on Machine Learning Systems (LearningSys) in The Thirty-first Annual Conference on Neural Information Processing Systems (NIPS) (2017).
- 41.The on-line encyclopedia of integer sequences. Entry A000930. (2023).
- 42.Wissmann, L., Santelli, C., Segars, W. P. & Kozerke, S. MRXCAT: realistic numerical phantoms for cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 16, 63 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Beatty, P. J., Nishimura, D. G. & Pauly, J. M. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans. Med. Imaging 24, 799–808 (2005). [DOI] [PubMed] [Google Scholar]
- 44.Rudin, L. I., Osher, S. & Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. Nonlinear Phenom. 60, 259–268 (1992). [Google Scholar]
- 45.Johnson, K. M. Hybrid radial-cones trajectory for accelerated MRI. Magn. Reson. Med. 77, 1068–1081 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Speidel, T., Metze, P. & Rasche, V. Efficient 3D low-discrepancy k-space sampling using highly adaptable seiffert spirals. IEEE Trans. Med. Imaging 38, 1833–1840 (2019). [DOI] [PubMed] [Google Scholar]
- 47.Bydder, M. & others. A study of 3D radial density adapted trajectories for sodium imaging. Magn. Reson. Imaging 83, 89–95 (2021). [DOI] [PubMed] [Google Scholar]
- 48.Boada, F. E., Gillen, J. S., Shen, G. X., Chang, S. Y. & Thulborn, K. R. Fast three dimensional sodium imaging. Magn. Reson. Med. 37, 706–715 (1997). [DOI] [PubMed] [Google Scholar]
- 49.Krishnamoorthy, G., Smink, J., Tourais, J., Breeuwer, M. & Kouwenhoven, M. Variable anisotropic FOV for 3D radial imaging with spiral phyllotaxis (VASP). Magn. Reson. Med. 85, 68–77 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Koay, C. G. A simple scheme for generating nearly uniform distribution of antipodally symmetric points on the unit sphere. J. Comput. Sci. 2, 377–381 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Larson, P. E. Z., Gurney, P. T. & Nishimura, D. G. Anisotropic field-of-views in radial imaging. IEEE Trans. Med. Imaging 27, 47–57 (2008). [DOI] [PubMed] [Google Scholar]
- 52.Piccini, D., Littmann, A., Nielles-Vallespin, S. & Zenge, M. O. Spiral phyllotaxis: the natural way to construct a 3D radial trajectory in MRI. Magn. Reson. Med. 66, 1049–1056 (2011). [DOI] [PubMed] [Google Scholar]
- 53.Fyrdahl, A., Holst, K., Caidahl, K., Ugander, M. & Sigfridsson, A. Generalization of three-dimensional golden-angle radial acquisition to reduce eddy current artifacts in bSSFP CMR imaging. Magn. Reson. Mater. Phys. Biol. Med. 34, 109–118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wang, G., Nielsen, J. F., Fessler, J. A. & Noll, D. C. Stochastic optimization of three-dimensional non-cartesian sampling trajectory. Magn. Reson. Med. 90, 417–431 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Fyrdahl, A. & others Three-dimensional sector-wise golden angle-improved k-space uniformity after electrocardiogram binning. Magn. Reson. Med. 90, 1041–1052 (2023). [DOI] [PubMed] [Google Scholar]
- 56.Zwillinger, D. (ed) CRC Standard Mathematical Tables and Formulas. Thirty-third edition. Boca Raton, FL CRC Press, 2018). 10.1201/9781315154978
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source code and simulation output are available from the lead author on reasonable request.