Accurate birth weight prediction from fetal biometry using the Gompertz model

Abstract

Objectives

Monitoring of fetal growth and estimation of birth weight is of clinical importance. During pregnancy, ultrasound fetal biometry values including femur length, head circumference, abdominal circumference, biparietal diameter are measured and used to place fetuses on “growth charts”. There is no simple growth-model-based, predictive formula in use for fetal biometry. Estimation of fetal weight at birth currently depends on ultrasound data taken a short time before birth.

Study design

Our cohort (“Seethapathy cohort”) consists of ultrasound biometry measurements and other data for 774 pregnant women in Chennai, India, 2015–2017. We use the Gompertz model, a standard model for constrained growth, with just three intuitive parameters, to model the growth of fetal biometry, and a machine learning (ML) model trained on these parameters to predict birth weight (BW).

Results

The Gompertz model convincingly fits the growth of fetal biometry values. Two Gompertz parameters—$t_0$ (inflection time) and $c$ (rate of decrease of growth rate)—seem universal to all fetuses, while the third, $A$, is an overall scale specific to each fetus, capturing individual variation. On the Seethapathy cohort we can infer $A$ for each fetus from ultrasound data available by the 24 or 35 weeks. Our ML model predicts birth weight with < 8 % error, outperforming published methods that have access to late-term ultrasound data. The same model gives an 8.4 % error in BW prediction on an independent validation cohort of 365 women.

Conclusions

The Gompertz model fits fetal biometry growth and enables birth weight estimation without need of late-term ultrasounds. Aside from its clinical predictive value, we suggest its use for future growth standards, with almost all variation described by a single scale parameter $A$.

1. Introduction

Assessment of fetal growth is an integral part of antenatal care. Babies that are born small or large for their gestational age are known to be at an increased risk for adverse pregnancy outcomes. Accurate prediction of fetal weight at birth is useful to clinicians.

The growth of a human embryo is monitored by ultrasound biometric measurements, most commonly of femur length (FL), abdominal circumference (AC), head circumference (HC) and biparietal diameter (BPD). The growth curve of each of these has a sigmoidal shape, with the rate of growth larger midway through gestation and smaller in early and late pregnancy. Ideal growth is described in tabular and graphical form in publications from WHO [1], [2], NICHD [3], [4] and INTERGROWTH [5].

Fetal weight cannot be directly measured during gestation. Several formulas exist in the literature, reviewed in Discussion, but all assume the availability of late-term ultrasound measurements (within a week before delivery). Prediction of birth weight using routinely taken ultrasound measurements (usually three or four sets, prior to 35 weeks) remains a challenge.

Here we use our in-house cohort of 774 women (which we call the “Seethapathy cohort”, described in Methods, Section 2.1) to model the growth of FL, AC, HC, BPD.

The Gompertz growth formula is due to Gompertz [6] and Wosilait et al. [7], [8] used it to model fetal growth volume in aggregated data. It is parametrized as $f\left(t\right)=\mathit{A}\exp \left(-\exp \left(-c\left(t-t_0\right)\right)\right)$ (see Methods, Section 2.2 for an explanation of the parametrization), with three intuitive parameters: an “inflection time” $t_0$ (when the growth shape shifts from concave-up to concave-down); a “shape parameter” $c$; and an overall scale parameter $A$.

We find that the Gompertz formula fits the growth of four ultrasound biometry measurements FL, AC, HC and BPD on individual fetuses on our in-house cohort, and also agrees with the published growth standards from INTERGROWTH and WHO. This enables its extrapolative use from existing ultrasound. We estimate the value of A for each biometry from available ultrasound data (up to 24 weeks or up to 35 weeks) and use this estimated A to predict the ultrasound parameters at birth. Finally, we incorporate these parameters A and the predicted final biometry values in a regression formula to estimate the fetal weight at birth and demonstrate performance superior to literature formulas that require late-term ultrasound measurements.

2. Materials and methods

2.1. Study design and participants

We used a dataset of 3235 pregnant women from Chennai who were registered and gave birth at Seethapathy Clinic and Hospital, Chennai, between 2015 and 2017 and for whom ultrasound biometry measurements were available. This is a general private hospital whose ob-gyn department caters to all pregnancies; about 20 % may be considered high-risk. Ultrasound is routinely done at 11–13 (first trimester screening) and again at 18–22 weeks (to rule out any structural abnormalities). All women also get a third trimester scan, whose timing varies. For low-risk women, a scan for growth would be done typically at 35–36 weeks. For high-risk women an additional scan at 28–30 weeks may be performed. Four ultrasound fetal measurements—HC, AC, BPD, and FL—were considered. Only women with singleton pregnancies who had at least three sets of ultrasound measurements, with the first scan dated 15 weeks, were included in the analysis, yielding 933 eligible subjects. We excluded cases of duplicate measurements or outliers; participants whose second ultrasound was performed after 24 weeks (at least two measurements are required for fitting parameters at 24 weeks); and subjects whose final ultrasound measurements were prior to 27 weeks. The final cohort comprised 774 women.

Table 1 shows cohort characteristics, which were optionally used in birth weight predictions (supporting Fig. S1). Traditional risk factors such as family history, PCOS, high BMI were used to label “at risk for GDM”. Anemia was diagnosed as Hb < 11 gm/dl, and hypothyroidism is overt hypothyroidism for which they were on thyroxine replacement. A histogram of birth weight distributions and delivery date distributions in supporting Fig. S6.

Table 1.

Data summary considered for the study. Parameters measured on first hospital visit except as indicated.

Cohort characteristics $\left. (n=774\right)$	Mean $\pm$ std or $\%$
Age (years)	$28.2\pm 3.8$
Height (cm)	$158.6\pm 5.9$
Weight (kg)	$64.5\pm 11.7$
Body mass index ($\frac{\mathit{kg}}{m^2}$)	$25.6\pm 4.3$
Weight gain (kg, from first to last visit)	$9.9\pm 4.2$
Fasting blood sugar (mg/dL)	$80.9\pm 5.9$
At risk for GDM (gestational diabetes mellitus)	46.45 %
Diagnosed as anemic	15.2 %
Diagnosed with hypothyroidism	$15.1\%$
Diagnosed with hypertensive disorders	$1.2\%$
Diagnosed with gestational diabetes mellitus	22.1 %

2.2. Gompertz growth model

The Gompertz equation for the growth of a parameter $X$ as a function of time $t$ is:

$$\begin{array}{c}X\left(t\right)=A{e}^{-e^{-c\left(t-t_0\right)}}\end{array}$$ (1)

Here, A is an overall scale factor, c is a shape parameter (it is the retardation rate of the growth rate), and $t_0$ is a time offset (it represents the time at the inflection point of the curve). The formula is derived and further discussed in supplementary material; see also ref [9]. While previous researchers [7], [8] applied this formula to fetal volumes or weights, we apply it to each of the individual biometry values (that is, X is HC, AC, BPD or FL).

For each ultrasound biometry measurement, we fit $t_0$ and $c$ over our population of fetuses but fit $A$ individually for each fetus. Our data, and comparisons with published growth standards and tables, suggest that $t_0$ and $c$ can be treated as universal parameters, and almost all variation in normal fetal growth is explained by the scale parameter $A$. Similar to INTERGROWTH’s formulas for the mean and standard deviation of each biometry measurement, we compute a population mean $A$ and its standard deviation.

2.3. Predicting birth weight of fetus

A predictive model was developed for the prediction of birth weight from ultrasound measurements taken at 24 weeks or earlier, or 35 weeks or earlier, using linear regression. Linear regression fits a linear model that makes a linear relationship between input features and target variables. The parameter regression coefficient and intercept are estimated by least squares (least sum of squared errors).

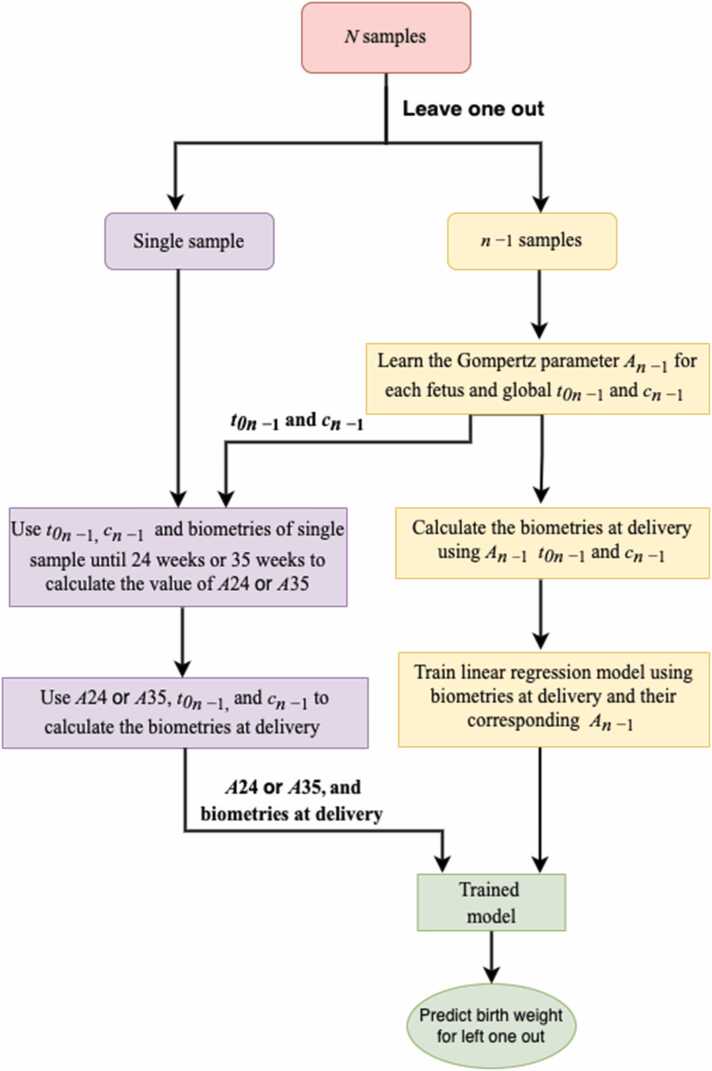
For each fetus, $A$ was computed using measurements taken up until 24 weeks or up until 35 weeks. In $X=\mathit{A}\exp \left(-\exp \left(-c\left(t-t_0\right)\right)\right)$ where $c$ and $t_0$ are universal values, $A$ was chosen to minimize the sum of squared errors between the predicted and observed biometry values $X$ at the measured times $t$. Biometry values at delivery were then predicted by substituting the GA at delivery for $t$. These values, and their corresponding $A$ were used as input parameters for birth weight prediction. Birth weight was predicted using the standard leave one out cross-validation (LOOCV) technique, where all data except the fetus under consideration are used for training the model and the left-out fetus’ weight is predicted using that model. Therefore, the predicted biometry values and $A$ for each fetus, and global $t_0$ and $c$, were re-learned at each LOOCV step. This ensures that there is no data leakage, i.e. at no point is the data on which the model is tested ever used in training the model. This is shown as a flowchart in Fig. 1. Models were implemented in python with the scikit-learn package. We compared our results with the INTERGROWTH (Eq. 2), the four Hadlock (Eq. 3) and Shepard (Eq. 4) formulas for the estimated fetal weight (EFW) [10]. Hadlock 2 (using AC, FL, BPD) is presented here, and the other three in supporting fig S3 and supporting table S1.

Fig. 1.

Flowchart for birth weight prediction using LOOCV.

INTERGROWTH (units: g, cm):

$${\log }_e\left(\mathit{EFW}\right)=5.084820-54.06633\times {\left(AC/100\right)}^3-95.80076\times {\left(AC/100\right)}^3\times \log \left(AC/100\right)+3.136370\times (\mathit{HC}\mathrm{⁄}100)$$ (2)

Hadlock 2 (units: g, cm):

$${\log }_{10}\left(\mathit{EFW}\right)=1.335-0.0034\times \mathit{AC}\times \mathit{FL}+0.0316\times \mathit{BPD}+0.0457\times \mathit{AC}+0.1623\times \mathit{FL}$$ (3)

Shepard (units: kg, cm):

$${\log }_{10}\left(\mathit{EFW}\right)=-1.7492+0.166\times \mathit{BPD}+0.046\times \mathit{AC}-0.002546\times \mathit{AC}\times \mathit{BPD}$$ (4)

The model was evaluated by computing the mean absolute percentage error (MAPE) and root mean square error (RMSE) using predicted and actual birth weights, in all cases.

2.4. Validation cohort

The validation cohort was obtained from South Indian Pregnancy Research Network (SIPNET), with data contributed from six hospitals in Chennai, Pondicherry, Hyderabad, and Kochi, in India. As with the Seethapathy cohort, the validation cohort was screened for subjects with at least three available sets of ultrasound biometry measurements, resulting in 365 subjects.

Birth weights were predicted with fetal biometry as input, using the machine learning model constructed on the Seethapathy cohort. The linear regression model was trained on the full Seethapathy cohort, and then predictions were made on the validation cohort.

3. Results

3.1. The Gompertz formula fits biometry measurements for the Seethapathy cohort

Table 2 shows the values of globally fitted $t_0$ and $c$, and the mean and standard deviation of individually fitted $A$, on the Seethapathy cohort

Table 2.

Gompertz parameters fitted to the Seethapathy cohort.

Ultrasound measurements	Range ($A$)	Mean ($A$) $\pm$ Std ($A$)	$t_0$	$c$
Head circumference	$\left[\mathrm{352,424}\right]$	$382.63\pm 10.41$	$17.65$	$0.088$
Abdominal circumference	$\left[\mathrm{340,456}\right]$	$392.26\pm 15.36$	$20.03$	$0.081$
Biparietal diameter	$\left[\mathrm{100,123}\right]$	$110.99\pm 3.49$	$18.21$	$0.084$
Femur length	$\left[\mathrm{65,83}\right]$	$74.93\pm 2.55$	$18.92$	$0.122$

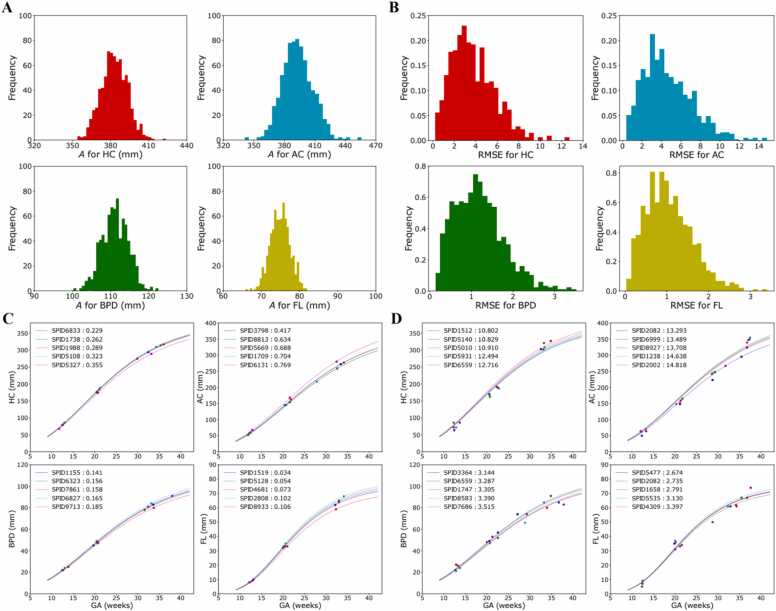
The distribution of $A$ over the individual fetuses is shown in Fig. 2A. Each fetus’ root mean squared error (RMSE) was determined by comparing the fitted function (with optimized $A$) with the original measurement. Fig. 2B shows the distribution of the RMSE. Fig. 2C and D show, respectively, the five best and worst-fitting fetuses to the Gompertz curve.

Fig. 2.

Distribution of $A$, root mean square error and quality of fit to Gompertz equation, A: Distribution of $A$ for the four biometry parameters we study. B: Distribution of the root mean squared error for the fit to the Gompertz function. C: Five best-fitting fetuses to the Gompertz curve, for each biometry parameter. D: Five worst-fitting fetuses to the Gompertz curve, for each parameter.

3.2. We can accurately predict final biometry and individual birth weights from available ultrasound

We predict birth weight using, as input, our predicted ultrasound measurements at delivery and individual $A$ values for each fetus (using the Gompertz formula) as described in Methods, Section 2.3. Supporting Fig. S2 shows that our estimates of biometry at delivery are correlated with the actual birth weights.

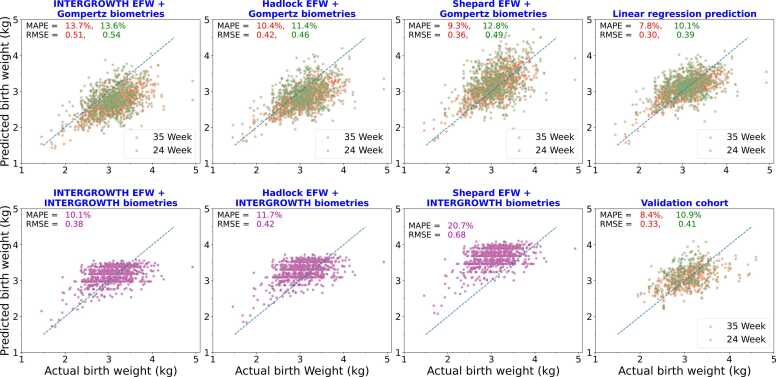
Fig. 3 shows birth weight predictions when we use available ultrasound data up until 24 weeks (green) and 35 weeks (blue), using linear regression, compared with the predictions of the INTERGROWTH, Shepard, and Hadlock 2 formulas. As detailed in Methods, t₀ and c are global parameters, while A is calculated for each individual fetus by a best fit of the Gompertz formula to all available ultrasound data, up until 24 weeks or up until 35 weeks. For fetuses that perfectly fit the Gompertz curve, thus, there will be no change in the estimate of A, but in general the 35 weeks data will provide better estimates. The four Hadlock formulas are shown in supporting table S1 and their performance shown in supporting fig S3. Hadlock 2 performs best. In all these formulas we used our predicted fetal biometry values at term using the Gompertz equation and INTERGROWTH mean formula. Our individualized prediction, from early ultrasound parameters, clearly outperforms population-average formulas in predicting birth weight for individual fetuses. The MAPE for predictions made using all ultrasounds up to 35 weeks is about $7.8\%$. This information can be useful to clinicians making decisions on intervention. Fig. 3 shows the biometry values obtained from INTERGROWTH mean formula saturates after some time hence not able to predict the larger birth weight’s fetuses whereas Gompertz predicted biometry values show a linear correlation with birth weight (supporting Fig. S2).

Fig. 3.

Birth weight prediction at delivery, using formulas from INTERGROWTH, Shepard, Hadlock, and linear regression. In these scatterplots, each dot represents an individual fetus, its x-coordinate gives the actual birth weight, and the y-coordinate the predicted birth weight; dots closer to the dotted diagonal are better predictions. The MAPE,“mean absolute percentage error” is the average of absolute values of all percentage errors, over all points, and the RMSE,“root mean squared error”, is the square root of the average of the squared errors over all points. A–C: The final fetal biometry predicted by Gompertz formula, with $A$ inferred from ultrasound scans up until 24 weeks (green) or 35 weeks (red), were plugged in to the literature formulas to predict birth weight. D: Birth weight predicted by simple linear regression using Gompertz-predicted biometry values. This was done in a leave-one-out manner to avoid data-leakage (Methods). E–G: Birth weight predicted using literature formulas with the INTERGROWTH mean biometry values for the gestational age at delivery. H: Birth weight prediction of the model trained on the full Seethapathy cohort, on an independent validation cohort, again with $A$ calculated from 24 weeks (green) or 35 weeks (red) scans.

Eq. 5, obtained using linear regression, can be used to estimate birth weight for fetuses, given estimates of final biometry and of the Gompertz scale parameters obtained from available ultrasound measurements. (Units: EFW in kg, biometry in mm)

$$\begin{array}{c}\mathit{EFW}=0.0461\times \mathit{BPD}-0.0358\times A_{\mathit{BPD}}+0.0242\times \mathit{FL}+0.0195\times \mathit{HC}+0.0155\times A_{\mathit{AC}}\\ -0.0133\times A_{\mathit{HC}}-0.00778\times A_{\mathit{FL}}-0.00462\times \mathit{AC}-4.28\end{array}$$ (5)

Marginal improvement was obtained using maternal parameters and LASSO regression (supporting Fig. S1).

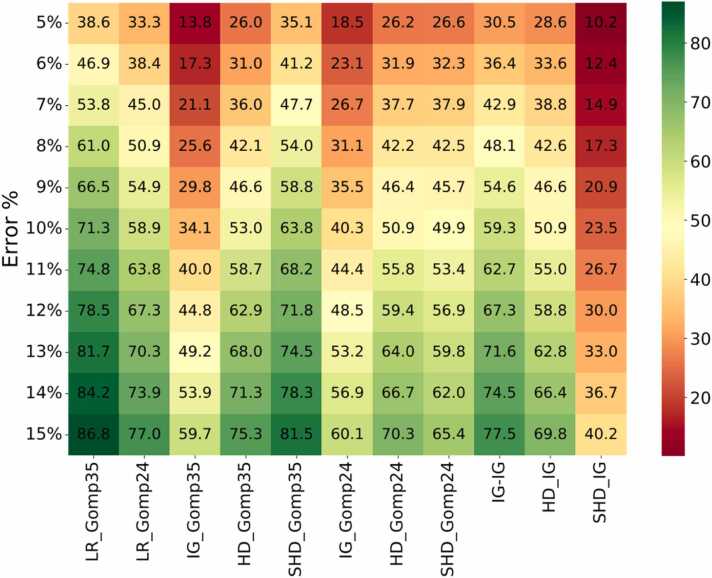
Fig. 4 shows, as a heatmap, the percentage of fetuses that fall within various prediction accuracies. In particular, with ultrasound data up until 35 weeks, our linear regression formula predicts 71.3 % of birth weights within 10 % accuracy. Shepard with Gompertz parameters (35 weeks) is next best at 63.8 % cases predicted within 10 % accuracy. Supporting Figs. S4 and S5 show the percentages under- and over-predicted by each method; it appears that our LR method is balanced, while INTERGROWTH and HADLOCK underpredict when using Gompertz biometry predictions, and Shepard overpredicts when using INTERGROWTH biometry estimates.

Fig. 4.

The percentage of fetuses whose birthweight is predicted within a given error rate, according to 11 methods. Here, LR=our linear regression formula, IG=INTERGROWTH, HD=Hadlock, SHD=Shepard, Gomp24 =Gompertz prediction of final biometry using ultrasound data up until 24 weeks, Gomp35 =Gompertz prediction of final biometry using ultrasound data up until 35 weeks. So, for LR_Gomp35 and IG_Gomp35, the Gompertz-predicted final biometry were used in our linear regression model and in the INTERGROWTH formula respectively. For IG_IG, HD_IG, SHD_IG, the INTERGROWTH optimal fetal biometry at birth were used for prediction.

3.3. A model trained on the Seethapathy cohort performs well in birth weight prediction on validation cohort

As described in Methods, Section 2.3, we trained a model on the Seethapathy cohort and then predicted individual birth weights on the validation cohort. Using ultrasound data up until 24 weeks and up until 35 weeks, MAPE and RMSE on the validation cohort (Fig. 4H) are comparable with our predictions on the Seethapathy cohort, lending confidence in our prediction model.

3.4. The Gompertz model improves SGA prediction across all models

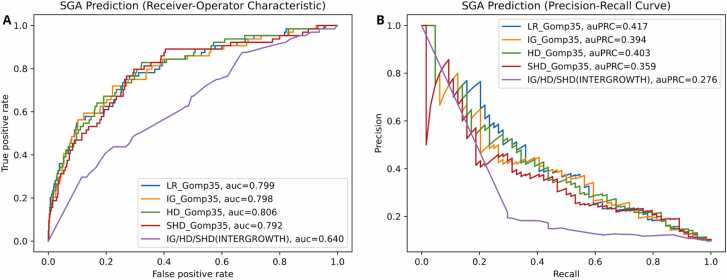
We asked whether the predicted birth weights are indicators of “small for gestational age” (SGA), defined here as the bottom 10 % of all full-term births (≥ 38 weeks) in our cohort. There were 659 fetuses in this cohort of which 64 were SGA by this definition. We used two metrics: the area under the “receiver operator characteristic” curve (auc or auROC), and the area under the “precision-recall curve” (auc or auPRC). The ROC curve compares sensitivity (true positive rate, that is, the fraction of truly positive cases that are called positive) with the false positive rate (1 −specificity), while the PRC compares sensitivity (also called precision) with recall (the fraction of positive predictions that are truly positive). These are shown in Fig. 5. For unbalanced datasets such as this, the auPRC is preferred as a metric, and our method performs best on this.

Fig. 5.

The performance of the various algorithms in Fig. 3 for SGA prediction, where we took the bottom 10 % of full-term fetuses by birth weight as SGA. On the left, the “receiver operator characteristic” that plots true positive rate (also called sensitivity) versus false positive rate (which is 1 −specificity). On the right, a plot of precision (fraction of predicted positive values that are truly positive) against recall (another name of sensitivity). This dataset is unbalanced (only 10 % of cases are truly positive for SGA by our definition), and the auPRC is regarded as a better metric in such cases. We find that while our algorithm for predicting the fetal weight best predicts SGA, the use of predicted Gompertz biometry values at birth improves the performance of all algorithms (also suggested in Fig. 3), obviating the need for a late-term ultrasound.

However, the main conclusion here is that our prediction of biometry values at birth improves the performance of all methods. This is also the case in Fig. 3 where the other birth weight formulas (INTERGROWTH, Hadlock, Shepard) perform much better if we use full-term biometry values predicted by the Gompertz formula.

4. Discussion

In this work, we have demonstrated that the Gompertz growth formula is an excellent fit to ultrasound biometry (HC, AC, FL, BPD) during gestation, both on the Seethapathy cohort and on published growth standards; that in each biometry individual variation among fetuses is described by a single scale parameter; that we can estimate final biometry values with high accuracy using routinely-taken ultrasound data (prior to 35 weeks), enabling the use of birth weight formulas that otherwise require an ultrasound scan shortly before delivery. Finally, we supply our own formula for the birth weight, whose accuracy (MAPE 7.8 %) is superior to the reported errors of previously published formulas (Hadlock [17], Shepard [16], INTERGROWTH [18]; see also [10]) that depend on late-term ultrasound data (within 7 days before delivery). If we lack such late-term ultrasound data and use estimates of final biometry values from the INTERGROWTH formula instead of the Gompertz model, weight predictions of the literature formulas are significantly poorer. In real life it is logistically difficult to obtain a scan within 7 days before birth. Thus, our prediction of biometry values at birth has real-world value.

Originally introduced by Gompertz [6] in the context of modeling population size as a function of age, this formula has since been used in many biological systems including tumor growth [11] and cell population growth [12]. (see Tjørve and Tjørve [9] for a detailed review). Wosilait et al. [7], [8] previously used the Gompertz model to describe the growth of fetal volume, modelled as an ellipsoid, using pooled fetal data (single data point per aborted or stillborn fetus) from sources dating back to 1909. We use it for linear fetal biometries: we note that if each of length, breadth, height, of an ellipsoid, satisfies the Gompertz formula, then so does the volume of the ellipsoid.

Other sigmoidal functions have been proposed for fetal growth. Todros et al. [13] evaluated three sigmoidal formulas: a cubic polynomial function $a+\mathit{bt}+c{t}^3$, a logistic-logarithmic function $a/\left(1+\mathit{bt}-c\right)$, and an exponential-power function $a{t}^2{e}^{-\mathit{bt}}$ (where $t$ is the menstrual or the corrected age, and $a$, $b$, $c$ are parameters). Rossavik and Deter [14] proposed the formula $c{t}^{k+\mathit{st}}$ to describe the growth of a parameter. We note that with 3 or 4 routinely taken sets of ultrasound measurements, fitting a 2- or 3-parameter formula is prone to overfitting. Deter et al. [15] apply the Rossavik formula to a cohort of 18 patients, taking ultrasound data at 2–3-week intervals, which enables fitting all coefficients. They can then predict fetal growth after 24 weeks based on data before 24 weeks. In contrast, we find we can treat two Gompertz parameters (shape $c$ and inflection time $t_0$) as universal and we fit only $A$, the scale, to individual fetuses, but predict future growth with good success based on this limited data.

Several formulas exist to predict fetal weight at term, and estimate fetal weight during gestation, based on ultrasound measurements: for example, Shepard et al. [16], Hadlock et al. [17] (who supplied four formulas using different combinations of biometry measurements), INTERGROWTH [18]. Kong et al. [10] compared the INTERGROWTH formula, fourth Hadlock formula (using HC, AC, FL, and BPD) and Shepard formula on a cohort of 423 singleton pregnancies where ultrasound measurements were taken within a week before delivery (in 63% of cases, within 3 days before delivery). They report mean absolute percentage errors (MAPE) of 7.34 (Hadlock), 9.00 (Shepard) and 9.07 (INTERGROWTH). Milner and Arezina (2018) [19], in a systematic review, assessed 11 different EFW formulas and find the third Hadlock formula (using HC, AC and FL) most accurate. They again consider only studies where women had their last scans within seven days before delivery. They report a mean percentage error (MPE) of $-1.5\%$but a random error (standard deviation of MPE) of 9.2%. MPE can be misleadingly small, because large positive and negative errors cancel; therefore we (like Kong et al.) have used mean absolute percentage error (MAPE) in this work.

Using the Gompertz formula predictively with routinely taken ultrasound measurements up until 24 or 35 weeks, we thus outperform Shepard and INTERGROWTH formulas as reported by Kong et al. and come close to Hadlock, even though we lack the final-week ultrasound data that they require. Our MAPE is also less than the SD of best MPE reported in Milner et al. Using our estimated final biometry values, we outperform Hadlock, Shepard and INTERGROWTH on our own cohorts. In case a late-term ultrasound is in fact available, those measurements can be directly plugged into our formula.

As discussed in supporting text, we also find that the Gompertz formula is a very good fit for the INTERGROWTH and WHO standards, with relative errors of less than 2% and 1%, respectively, except for FL, which has a relative error of less than 3% for both. Moreover, the values of $t_0$ and $c$ are close to the values obtained on the Seethapathy cohort, suggesting that these can indeed be treated as almost universal parameters and most fetal growth variability can be explained by the single parameter $A$.

Growth standards from WHO [1] and INTERGROWTH [5] are not specific to race or country and assume healthy, well-nourished, middle-to-high-income populations. However, WHO [2] and NICHD [4] find significant variation by race and country despite no known environmental or socioeconomic factors. The Seethapathy cohort too was largely of middle-to-high-income healthy urban women. It would be of future interest to apply the Gompertz formula to study variations among populations and ethnicities, as well as in populations with non-ideal nutritional or health status, and particularly to see if $c$ (the rate of retardation of fetal growth) and $t_0$ (the inflection time of growth) varies in such populations.

Ethical approval and informed consent

The study was approved by the Independent Ethics Committee, Fetal Care Research Foundation Chennai, India (ref FCRF/IRB-P6/2022). Informed written consent was obtained from all patients.

Funding

We acknowledge funding from BIRAC grant bt/ki-data0404/06/18 (LN, GM, UR, RS), and the IMSc Centre for Disease Modelling (ICDM) funded via an apex project at IMSc by the Department of Atomic Energy, Government of India (CK, RS). The funders had no role in the data collection, research, analysis, writing or submission of the manuscript.

CRediT authorship contribution statement

Uma Ram: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing – review & editing. Leelavati Narlikar: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. Rahul Siddharthan: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. Gautam Menon: Conceptualization, Funding acquisition, Methodology, Supervision, Writing – review & editing. Chandrani Kumari: Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors (Chandrani Kumari, Gautam Menon, Leelavati Narlikar, Uma Ram, Rahul Siddharthan) declare that they have no financial and personal relationships with other people or organizations that could inappropriately influence (bias) their work.

Appendix A. Supplementary material

Supplementary material

.

Supplementary material

.