Emergence of cyclic hypoxia and the impact of PARP inhibitors on tumor progression

Abstract

Tumor hypoxia is a dynamic phenomenon marked by fluctuations in oxygen levels across both rapid (seconds to minutes) and slow (hours to days) time scales. While short hypoxia cycles are relatively well understood, the mechanisms behind longer cycles remain largely unclear. In this paper, we present a novel mechanistic mathematical model that explains slow hypoxia cycles through feedback loops involving vascular expansion and regression, oxygen-regulated tumor growth, and toxic cytokine production. Our study reveals that, for the emergence of slow hypoxia cycles, endothelial cells must adapt by decreasing receptor activation as ligand concentration increases. Additionally, the interaction between tumor cells and toxic cytokines influences frequency and intensity of these cycles. By examining the effects of pharmacological interventions, specifically poly (ADP-ribose) polymerase inhibitors, we also demonstrate how targeting cell proliferation can help regulate oxygen levels. Our findings enhance the understanding of hypoxia regulation and suggest PARP proteins as promising therapeutic targets.

Introduction

Hypoxia, defined as an insufficient supply of oxygen, has long been recognized as a contributing factor to the tumor microenvironment (TME)¹. Elevated levels of hypoxia are a poor prognostic factor for solid tumors. Within the hypoxic TME, cancer cells undergo various adaptations, including alterations in signaling pathways, the activation of hypoxia-induced immune tolerance, and the development of resistance to chemotherapy and radiation therapy². Hypoxic regions manifest within the TME due to the excessive proliferation of cancer cells in poorly vascularized areas, resulting in an inadequate supply of nutrients and oxygen. Among the various adaptive responses to hypoxia, a notable mechanism involves the secretion of hypoxia-inducible angiogenic factors, such as vascular endothelial growth factor (VEGF). The upregulation of VEGF secretion promotes the re-vascularization of hypoxic regions within the tumor through tumor-induced angiogenesis. However, the resultant vasculature is often immature and lacks the structure observed in normal vasculature. Consequently, solid tumors consistently harbor hypoxic regions throughout their evolution, favoring the survival of aggressive cell types capable of thriving in this challenging and oxygen-deprived environment.

The Tie-Angiopoietin signaling pathway is a fundamental player in vascular remodeling and angiogenesis. It plays a crucial role in regulating vascular states. The activation of this pathway, facilitated by the receptor tyrosine kinase Tie2, depends on two angiopoietin ligands, Ang1 and Ang2, exhibiting partial competitive behavior³. Ang1 is essential for vascular homeostasis⁴, while Ang2, whose expression is modulated by various factors including hypoxia and VEGF, drives vascular remodeling by destabilizing the endothelium^5,6. The behavior of hypoxic cancer cells emerges from the intricate interplay among local oxygenation, hypoxia-induced signaling, such as stabilization of hypoxia-inducible factors (HIFs), and consequent regulation of angiopoietin production (Ang1 and Ang2), genetic defects, and damage caused by reactive oxygen species (ROS)². In solid tumors, this intricate interplay is responsible for dynamic fluctuations in oxygen levels, leading cells to encompass diverse degrees of hypoxia and necrosis, as well as regions (and periods) characterized by acute hypoxia and subsequent reoxygenation.

Hypoxia within the TME is a dynamic phenomenon. Oxygen levels in solid tumors exhibit fluctuations both spatially and temporally, giving rise to what is known as cyclic hypoxia. This phenomenon has been quantified in tumors and has been correlated with poor prognosis and resistance to treatment^7,8. While chronic hypoxia, characterized by sustained and relatively constant low levels of oxygen, typically affects poorly vascularized tumor regions, cyclic hypoxia occurs independently of the proximity to blood vessels. The characteristic time scales of these cyclic fluctuations vary from seconds to hours or days^9–11. The mechanisms governing rapid, high-frequency oxygen fluctuations are reasonably well-understood and are often linked to vasomotor activity. However, slower cycles of hypoxia, occurring over longer time scales, are less well-understood and are typically attributed to processes like vascular remodeling^12,13. These fluctuations within the TME contribute to the emergence and survival of more aggressive cells that display resistance to standard treatments^10,14. Understanding the underlying mechanisms of slow-cyclic hypoxia is crucial for developing targeted therapeutic approaches to counter its impact on cancer progression and treatment resistance.

The hypoxic TME poses a therapeutic challenge, often resulting in a poor prognosis. This is attributed to several factors, including the clonal selection of hypoxia-resistant cancer cells, DNA damage, resistance to chemotherapy and radiotherapy, and an elevated rate of metastasis. The complex and dynamic nature of the hypoxic TME underscores the need for targeted therapeutic strategies to address its multifaceted impact on cancer progression and treatment outcomes.

In this study, our primary objective is to address the challenge of constructing a mechanistic and innovative model capable of accurately capturing the emergence of slow-cycling hypoxia. To accomplish this goal, we adopt an integrative methodology that merges mathematical modeling with experimental data. We introduce a comprehensive model that effectively accounts for the slowest cycles of hypoxia, i.e., those occurring over time scales ranging from hours to days. Moreover, building upon this model, we propose a therapeutic strategy targeting cyclic hypoxia, leveraging the impact of poly (ADP-ribose) polymerases (PARPs) on both tumor and endothelial cells (EC). This mechanism is grounded in the intricate feedback loop involving vascular expansion/regression, oxygen-regulated tumor growth, and the production of toxic cytokines by the tumor in the absence of sufficient oxygen supply^15,16. Specifically, we propose two hypotheses regarding the emergence and regulation of slow-cyclic hypoxia. First, the emergence of these cycles depends upon adaptations in endothelial cells, which are essential for generating slow cycles of hypoxia. The VEGF receptor, belonging to the family of receptor tyrosine kinases (RTKs), undergoes activation dependent on both VEGF binding and receptor dimerization. Various models of VEGF receptor dimerization and their implications for signal transduction have been formulated¹⁷. Some of these models predict a bell-shaped response curve concerning receptor activation, measured in terms of the relation between phosphorylation levels of the SH2 domains and VEGF concentration^17,18. This implies that VEGFR activation increases as VEGF concentration rises until a threshold concentration is reached, maximizing the VEGFR response. Beyond this concentration, the response diminishes as VEGF concentration continues to increase. Regarding the regulation of slow-cyclic hypoxia, the feedback loop between tumor growth, oxygen levels, and cytokine expression plays a crucial role. Cytokines, produced by tumor cells in the absence of sufficient oxygen, are toxic to the tumor cells themselves, leading to cell death¹⁶. Cytokine-dependent upregulation of cell death alleviates oxygen pressure, resulting in an increased oxygen supply for the remaining tumor cells to proliferate, thus sustaining the cycle. Our in-silico findings indicate that the generation of slow-cyclic hypoxia hinges on the adaptation of endothelial cells. This adaptation leads to a regime where receptor response decreases as VEGF concentration increases. Furthermore, the feedback system involving cells, oxygen, and cytokines dictates the characteristics of these cycles, including their frequency and persistence over time. Precisely, the mechanism of cytokines production and its rate are crucial for obtaining sustained (in time) hypoxia cycles. This insight provides a valuable perspective for understanding the intricate dynamics of the proposed feedback system and its role in fostering prolonged hypoxic conditions within the tumor microenvironment. Moreover, it paves the way for designing new experiments focused on studying and controlling slow hypoxia cycles.

Our model’s predictive capabilities allowed us to evaluate the potential impact of PARP inhibitors on mitigating slow-cycling hypoxia, a critical step toward identifying effective therapeutic strategies for cancer treatment. PARP proteins are a component of the DNA damage response machinery of the cell. Several pharmacological inhibitors have been developed that block the DNA repair activity of PARP1. In cancer therapy, PARP inhibitors are used in BRCA1/2-deficient tumors to exploit a specific DNA repair pathway (deficiency in homologous recombination), leading to synthetic lethality and tumor cell death¹⁹. In this paper, we report a series of experiments examining the effects of PARP inhibitors on both cancer cells and endothelial cells. These experiments have been instrumental in quantitatively characterizing the drug’s influence on the growth of both cell types. Our model demonstrates significant potential in quantitatively replicating experimental findings. This quantitative understanding predicts that PARP inhibitors can impede the occurrence of slow-cyclic hypoxia and stabilize vascular supply. These findings not only advance our understanding of tumor biology but also offer promising avenues for developing targeted therapies based on PARP inhibitors. Such therapies could disrupt hypoxia-mediated tumor progression by directly impairing the proliferation of tumor or endothelial cells.

The insight into the role of VEGF and cytokine signaling in controlling hypoxia cycles, as well as the predictive assessment of the therapeutic effects of PARP inhibitors, represents a significant contribution to the field. The former provides valuable insights into the mechanisms underlying the slower kinetics of cyclic hypoxia, which are still not well-defined. The latter sheds light on the potential application of PARP inhibitors in mitigating the development of these prolonged hypoxic conditions within the tumor microenvironment. The integration of experimental data with our mechanistic model significantly enhances our capacity to make informed predictions regarding the efficacy of PARP inhibitors as a targeted therapeutic intervention for managing slow-cyclic hypoxia. By coupling empirical observations with our mathematical framework, we gain a more comprehensive understanding of the underlying biological mechanisms and their responses to pharmacological interventions. As such, our study provides important findings that may guide the development and optimization of therapeutic strategies aimed at ameliorating the effects of slow-cyclic hypoxia in various clinical contexts.

Results

Ang2 antagonizes Ang1 activity

We initially analyze and validate the dynamical evolution of the angiopoietin module, which accounts for interactions among Ang1 and Ang2 ligands, the Tie2 receptor, the corresponding ligand-receptor complexes, and pTie2, i.e., the phosphorylated form of the receptor (see Fig. 1 for a schematic description of their interactions). In this context, we present a novel mathematical model to investigate and simulate the behavior of the angiopoietin system, aiming to enhance our understanding of the complex regulatory processes within the angiopoietin signaling pathway. Its evolution is given by system (1). A detailed description of this mathematical model and its derivation is provided in Supplementary Note 1. To validate the proposed model, we utilize experimental results from³, specifically focusing on the partial agonist/antagonist activity of Ang2 against Ang1 in Tie2 signaling. The experiments measured levels of Tie2 phosphorylation when ramping up the concentration of Ang2 under constant Ang1 stimulation. The result demonstrated an Ang2 dose-dependent reduction in Tie2 phosphorylation (see Figure 6B of ref. ³). To replicate these experimental outcomes, we isolate the angiopoietin module and simulate it by assuming no Ang2 production. Figure 2 compares experimental (black) and in-silico (red) results, illustrating that the model can accurately replicate the experimental dose-dependent attenuation of Ang1-induced Tie2 signaling by Ang2. Thus, this outcome provides initial validation for the proposed angiopoietin model.

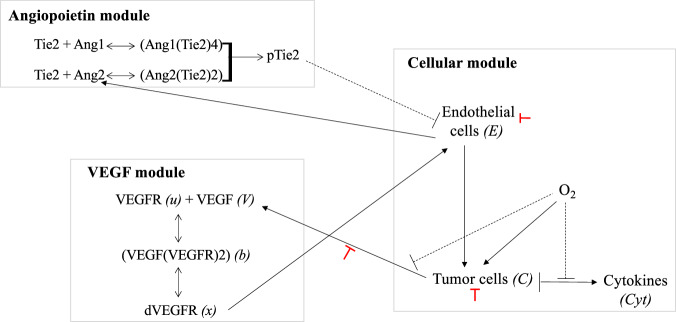
Fig. 1. Overview of the model.

This figure schematically shows the three modules involved in the model and the interactions between them. The angiopoietin module accounts for the dynamics of Ang1, Ang2, Tie2, their corresponding complexes, and the phosphorylated form of the Tie2 receptor. The VEGF module accounts for the activation of VEGFR: upon binding of VEGF to its receptor, the VEGF/VEGFR complex forms a dimer. The VEGFRs within the dimer cross-phosphorylate their SH2 domains, thus acquiring tyrosine kinase activity. The cellular module accounts for the coupling between oxygen, cancer cells, endothelial cells, and cytokines dynamics. Continuous black lines with arrows refer to a positive feedback/influence of one agent on another, while dashed black lines with vertical bars refer to a negative feedback/influence. Red lines with vertical bars refer to the negative effects of PARP inhibitors on the indicated interaction. In the bracket, we indicate the variables used in the model to refer to the different agents (when it is different from the name of the population).

Fig. 2. Ang2 antagonizes the activity of Ang1.

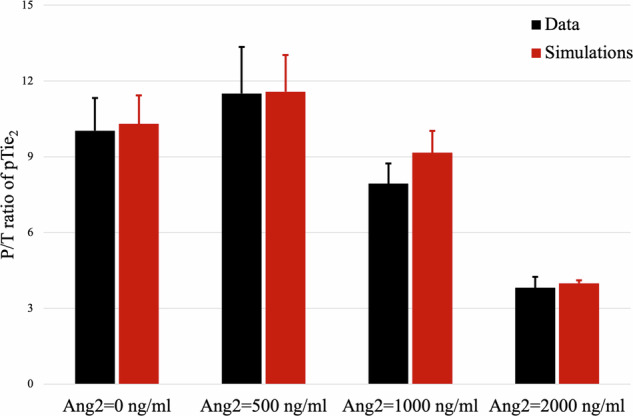
Comparison between in-vitro (black) and in-silico (red) values of the P/T ratio (phosphorylated/total Tie2). In-vitro data are taken from Figure 6B in ref. ³. In-silico results are obtained by simulating for 30 min the angiopoietin module given by Eq. (1) with h_Ang2 = 0. Each pair of columns refers to the results obtained for the value of the initial Ang2 concentration indicated below the columns. Means ± std in the simulations are obtained by varying the initial concentration of Tie2, which was not indicated in the experimental data. The concentration of Ang1 is held fixed at 100 ng/ml.

The accuracy of the angiopoietin model in capturing the agonist/antagonist impact of Ang2 on Ang1-induced Tie2 phosphorylation is visually demonstrated in Fig. 2 and quantified in Table 1. The strong agreement between in-silico results and experimental observations highlights the capability of our mathematical model to faithfully reproduce the dynamics of the angiopoietin system. It effectively captures both qualitative and quantitative aspects of Ang2’s impact on Ang1-induced Tie2 phosphorylation.

Table 1.

Comparison between in-vitro and in-silico results concerning the variation of the P/T ratio for a constant concentration of Ang1 = 100 ng/ml and different Ang2 concentrations

Ang2	Exp. mean	Exp. std	Num. mean	Num. std
0 ng/ml	10.0308	1.2923	10.3	1.1246
500 ng/ml	11.5077	1.8462	11.5734	1.4547
1000 ng/ml	7.9385	0.8	9.1570	0.8647
2000 ng/ml	3.8154	0.4308	3.9891	0.116

Mean and standard deviation are provided for both experimental and numerical values. The former is taken from ref. ³.

Bimodality in the VEGFR response to VEGF levels and interplay of dVEGF, pTie2-driven EC proliferation, and cytokines are key to the emergence of slow-cyclic hypoxia

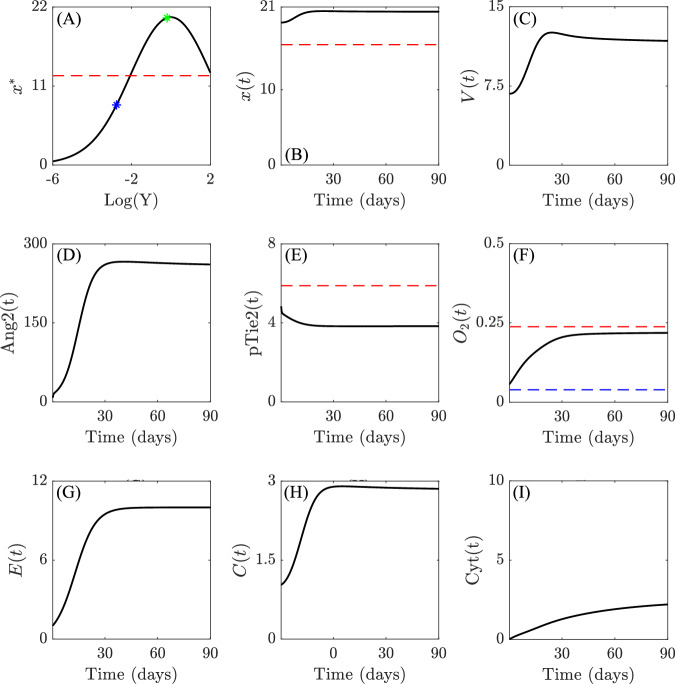
We use our mechanistic model to investigate the potential induction of slow-cyclic hypoxia through the interplay between various signaling pathways influencing the dynamics of the endothelial and tumor cell compartment. Specifically, we examine the impact of the bimodal response curve, describing how VEGFR activation levels change with varying concentrations of VEGF^17,18. Given this property, we model two scenarios regarding the production and release of VEGF by the tumor. First, we examine our mathematical model under conditions of low VEGF secretion. These are typical, for instance, of early-stage neoplasias. In these conditions, a direct relationship exists between VEGF and VEGFR dimerization (dVEGFR), where an increase in the concentration of VEGF correlates with an increase in the concentrations of dVEGFR. Next, we consider a scenario where a massive release of VEGF into the environment results in the saturation of the VEGFR system^18,20,21. This leads to a reduction in receptor dimerization and downstream pathway activation, characterized by an inverse relationship between VEGF and dVEGFR. This scenario may more typically manifest in (but is not limited to) advanced-stage neoplasias, where prolonged hypoxic conditions can lead to massive VEGF release. We consider the behavior of the system under these two markedly different regimes of ECs response to VEGF stimulation. Simulations of the model under VEGF levels producing a direct relationship between VEGF and dVEGFR (Fig. 3A) show that the system tends to its equilibrium configuration, with the expected transient phase depicted in Fig. 3. During this phase, the cell population grows until the system reaches a balance between population size and oxygen availability.

Fig. 3. Early-stage tumor evolution.

Qualitative results of the evolution of the systems (1)-(2)-(3) for parameter values listed in Supplementary Table 2 (provided in Supplementary Note 2) in the early-stage tumor scenario. A shows the qualitative relationship between between VEGF (V(t)) and the equilibrium state of the dimerized form of VEGFR (x^*), i.e., x^* as a function of $Y:=\frac{k_{\mathrm{on}}}{k_{\mathrm{off}}}V$, where k_on and k_off are the binding and unbinding rates between V and u, respectively¹⁸. The blue marker indicates the value of x^* for V(0), while the green marker indicates the value of x^* at $V_{\max }$, which represents a numerically observed upper bound for the ligand concentration. Red dashed lines in (A) and (B) refer to the threshold th_x, above which EC proliferation is stimulated, the one in (E) plot to the threshold th_pTie2, below which vessel destabilization might happen, while the red and blue in (F) refers to normoxia-hypoxia (5% O₂) and hypoxia-severe hypoxia (1% O₂) thresholds, respectively. The remaining subplots (B–I) show the evolution of the variables of interest of systems (1)-(2)-(3) over time, providing insights into the dynamics of the system in response to the specified relationships between VEGF and dVEGFR. Simulations are run for 90 days. The numerical results are shown from the starting time T₀ = 0.27 days, while the initial transient dynamics of self-adaptation of the populations are collected in Supplementary Fig. 6 in Supplementary Note 4. All y-axes refer to the non-dimensionalized density or concentrations of the indicated agents.

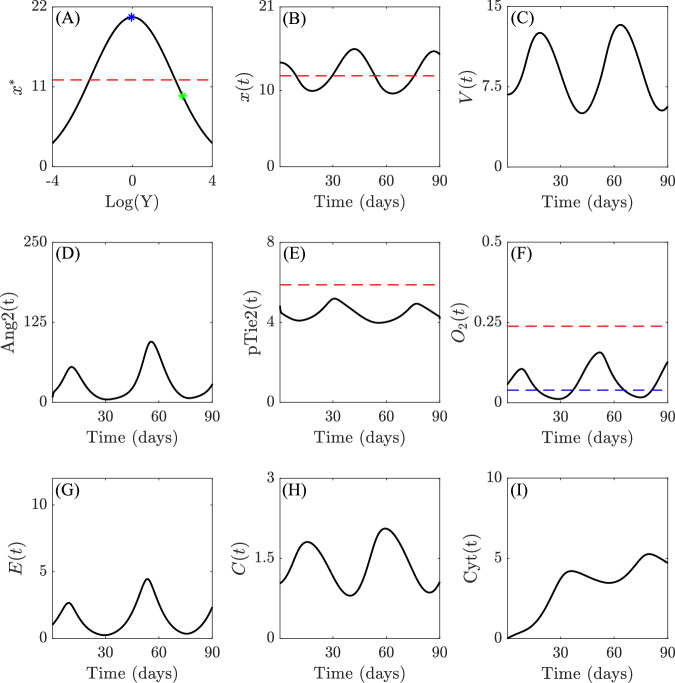
A different scenario emerges when higher rates of VEGF secretion are considered. Specifically, assuming an indirect relationship between VEGF and dVEGFR, we observe an inverse correlation between VEGF concentration and dimerized (active) VEGFR (Fig. 4A–C). Thus, increasing VEGF secretion leads to the downregulation of EC activation (Fig. 4C and G). This behavior induces the emergence of slow-cyclic hypoxia in the dynamical evolution of oxygen concentration (Fig. 4F). Throughout the entire duration of the simulation, we observe oscillations in oxygen concentration that correlate with similar oscillations in all other populations, notably VEGF and dVEGFR, which are inversely correlated, endothelial and tumor cells, as well as cytokines. These oscillations are sustained (over time), as can be better observed in Supplementary Fig. 5 in Supplementary Note 4, which shows the model evolution over a period of 180 days. This provides a mechanistic explanation for slow-cyclic hypoxia, which emerges from the interplay between the VEGF-dVEGF relation, dVEGF and pTie2-driven EC proliferation, and O₂-driven tumor cell proliferation. In particular, we suggest that the first two elements are at the core of the underlying mechanism allowing for the onset of slow-cyclic hypoxia.

Fig. 4. Slow-cyclic hypoxia in advanced-stage tumor.

Qualitative results of the evolution of systems (1)-(2)-(3) for parameter values listed in Supplementary Table 2 (provided in Supplementary Note 2) are shown for the advanced-stage tumor case. A shows the qualitative relationship between VEGF (V(t)) and the equilibrium states of the dimerized form of VEGFR (x^*), i.e., x^* as a function of $Y:=\frac{k_{\mathrm{on}}}{k_{\mathrm{off}}}V$. The blue marker indicates the value of x^* for V(0), while the green marker indicates the value of x^* at $V_{\max }$, which represents a numerically observed upper bound for the ligand concentration. Red dashed lines in (A) and (B) refer to the threshold th_x, above which EC proliferation is stimulated, the one in (E) to the threshold th_pTie2, below which vessel destabilization might happen, while the red and blue in (F) refers to normoxia-hypoxia (5% O₂) and hypoxia-severe hypoxia (1% O₂) thresholds, respectively. The remaining subplots (B–I) show the evolution of the variables of interest of systems (1)-(2)-(3) over time, providing insights into the dynamics of the system in response to the specified relationships between VEGF and dVEGFR. Simulations are run for 90 days. The numerical results are shown from the starting time T₀ = 0.27 days, while the initial transient dynamics of self-adaptation of the populations are collected in Supplementary Fig. 7 in Supplementary Note 4. All the y-axis refer to non-dimensionalized density or concentrations of the indicated agent.

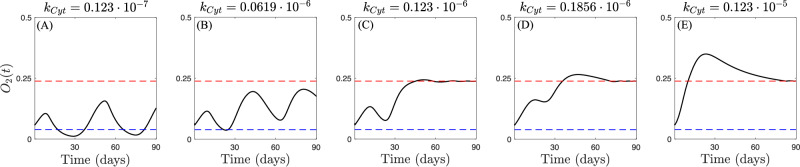
If the VEGF-dVEGF relationship is suggested as a necessary mechanism for the emergence of slow-cyclic hypoxia, its characteristics are controlled by the environmental conditions in which the system is embedded. We use our model to investigate the potential impact of the tumor-cytokines-oxygen feedback loop on the fluctuations characterizing slow-cyclic hypoxia. Specifically, we hypothesize that lower cytokine production (or equivalently, weaker effects on tumor cell death) results in more sustained and stable oxygen fluctuations. We examine the behavior of the system under the same conditions as those in Fig. 4, and we simulate the model for different cytokine production levels. The results are shown in Fig. 5. While the negative feedback of tumor-produced cytokines on tumor cells is inevitable in the absence of sufficient oxygen supply, the strength of this mechanism controls the frequency and perpetuation of cyclic hypoxia. Stronger cytokine impacts on tumor cells lead to greater impairment of the cancer population. Consequently, under these conditions, oxygen fluctuations are either inhibited (Fig. 5E) or limited to transient stages (Fig. 5C, D). Conversely, weaker cytokine effects on tumor cells result in more frequent (Fig. 5B) and potentially stable over time (Fig. 5A) oxygen fluctuations.

Fig. 5. Impact of cytokines-oxygen-tumor feedback on slow-cyclic hypoxia.

Qualitative results of the evolution of systems (1)-(2)-(3) in the advanced-stage tumor scenario for increasing values of cytokine production rate k_Cyt. Red and blue dashed lines in panels (A–E) represent the normoxia-hypoxia (5% O₂) and hypoxia-severe hypoxia (1% O₂) thresholds, respectively.

PARP inhibitors suppress slow cycles of hypoxia

We now explore the effects of two different types of PARP inhibitors, PJ-34²² and olaparib (OLAP)²³, on slow-cyclic hypoxia. First, we examine how PJ-34 affects VEGF production by tumor cells, as well as VEGF-induced proliferation of endothelial cells. Subsequently, we analyze the specific effects of olaparib on tumor cell proliferation. Finally, we qualitatively study their impact on the emergence and the evolution of slow cyclic hypoxia.

PARP inhibitor PJ-34 reduces VEGF production by cancer cells and represses VEGF-induced EC proliferation

Experiments detailed in²⁴ suggest that the administration of PARP inhibitors under 1% hypoxic conditions does not appear to alter the propensity of tumor cells to produce VEGF. However, it does result in a significant reduction in the amount of VEGFs that are produced by the cells. To replicate this experimental data, we employ a simplified version of our mathematical model to simulate the ratio between VEGF produced under therapy administration (T) and in the control case (C), namely VEGF produced when no therapy is administered. The effects of PARP inhibitors on VEGF are incorporated in our mathematical model through the functions h_2,V(PI), which appears in the equations for VEGF in (2). Further details are provided in Section S.2 of the Supplementary Note 1. The results of this analysis are shown in Fig. 6A, where we present a comparison between experimental data (black) and in-silico results (red). This analysis demonstrates that our model accurately captures the behavior observed in the experiments in²⁴.

Fig. 6. PJ-34 effects on VEGF production and EC proliferation.

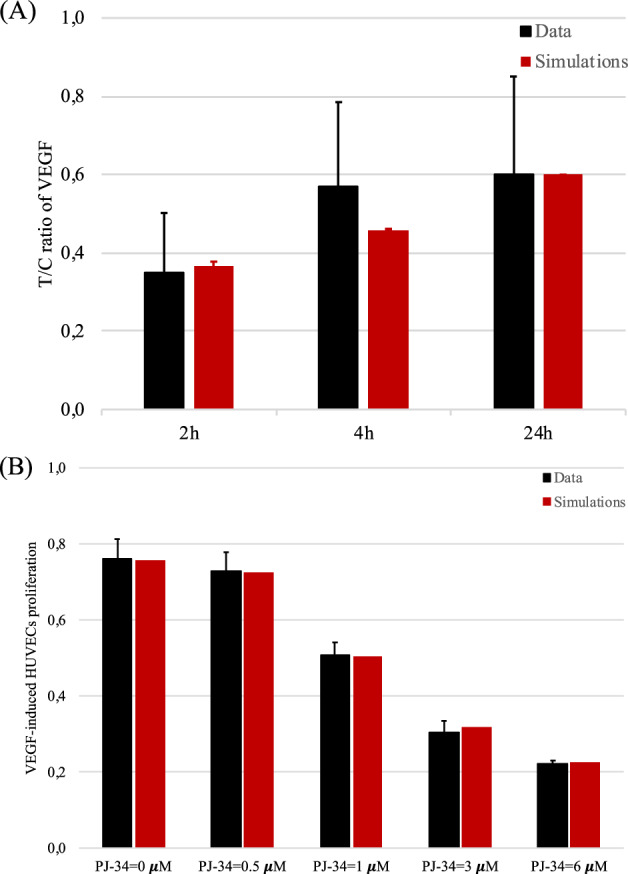
A Comparison between in-vitro (black) and in-silico (red) levels of the T/C ratio of VEGF produced by tumor cells under the effect of the PJ-34 treatment (T) and in normal conditions (C). In-vitro data were obtained from Figure 2H in ref. ²⁴. In-silico results were obtained by simulating the VEGF and cell modules given by Eqs. (2) and (3) under fixed oxygen conditions (O₂ = 1%). Each pair of columns refers to the results obtained at different time instants, i.e., 2 h, 4 h, and 24 h, respectively. Means ± std in the simulations are obtained by varying the initial concentration of VEGF, which was not indicated in the experimental data. B Comparison between in-vitro (black) and in-silico (red) levels of EC populations under the effect of the PJ-34 treatment for 24 h at different concentrations, which are indicated below each pair of columns. In-vitro data were obtained from Figure 2 in ref. ²⁵. In-silico results were obtained by simulating the VEGF and cell modules given by Eqs. (2) and (3). Cell density was quantified after 24 h of simulations.

We proceed analyzing the effect of PJ-34 on the VEGF-mediated proliferation of endothelial cells. Our analysis is based on the data presented in Figure 2 of ref. ²⁵, where the authors report the dose-dependent impact of PJ-34 in reducing VEGF-mediated EC proliferation. The study reveals that in the absence of VEGFs, no effects on EC proliferation are observed when PJ-34 is administered. However, a significant reduction is detected upon stimulation with VEGF. We simulate the cellular module of our model under normoxic conditions, assuming that the concentration of the dimerized receptor x is sufficiently high to enable EC proliferation (x(t) > x_th) and, thus, mimicking in this way the effect of a VEGF stimulus. We incorporate the function h_2,E(PI) to account for the effects of PARP inhibitors on ECs. The exponent n_E was calibrated using the data from²⁵. Further details are provided in Section S.3 of the Supplementary Note 1. The results of this analysis are presented in Fig. 6B, where we compare experimental data (black) with in-silico results (red). These results demonstrate the effectiveness of our model in capturing the qualitative decreasing trend in EC proliferation with increasing doses of PJ-34. Moreover, with a proper choice of the exponent n_E, it quantitatively reproduces its evolution. To better evaluate the relative decrement of the EC density for the different concentrations of PJ-34 and test the model accuracy, we define the index

$$\text{Dec}:=\frac{E\left(\text{PJ}\text{-}34=0\right)-E\left(\text{PJ}\text{-}34=\text{PJ}\text{-}34^{*}\right)}{E\left(\text{PJ}\text{-}34=0\right)}$$

with PJ-34^* ∈ {0.5, 1, 3, 6} μM. We evaluate Dec values for both the experimental data and the in-silico simulations, collecting the results in Table 2.

Table 2.

Comparison between experimental and numerical results concerning the relative decrement of the EC density under the effects of PARP inhibitors

PJ-34*	Exp. EC density	Exp. Dec	Num. EC density	Num. Dec
0 μM	0.7609		0.7568
0.5 μM	0.7283	4.3%	0.7246	4.3%
1 μM	0.5087	33.1%	0.5055	33.2%
3 μM	0.3043	60%	0.3175	58%
6 μM	0.2217	70.9%	0.2263	70.1%

The first row (PJ-34 = 0 μM) is reported as a matter of comparison for the other cases.

PARP inhibitor OLAP reduces tumor cell proliferation

We present novel experimental findings along with corresponding in-silico results related to the effects of OLAP on the proliferation of uveal melanoma (MUM2B) cells. Conducted under normoxic conditions with a saturated concentration of VEGF to allow unrestricted cell proliferation, our experiments involved initial cell density assessments and measurements at 24 h, 48 h, and 72 h across four different OLAP doses: 0 μM, 1 μM, 3 μM, and 5 μM. The top row of Fig. 7 illustrates the experimental results, showing that OLAP induces a dose-dependent reduction in tumor proliferation. The highest OLAP dose (black line) nearly halves the tumor density compared to the control case (lightest blue line).

Fig. 7. OLAP effects on tumor proliferation.

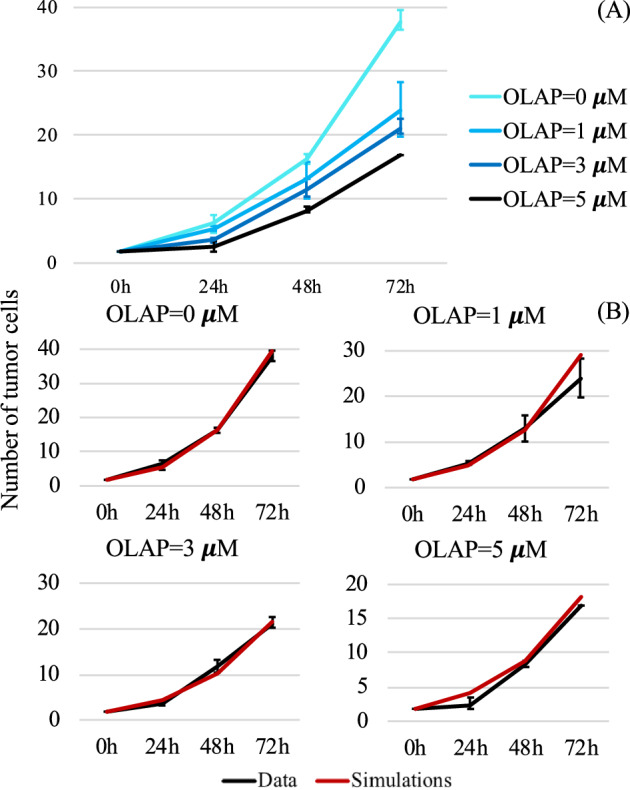
A In-vitro data concerning tumor proliferation under the effects of OLAP at different concentrations (mean ± std; n = 3). The number of tumor cells is given in thousands. B Comparison between in-vitro (black) and in-silico (red) levels of the tumor population at 0, 24 h, 48 h, and 72 h for the 4 different concentrations of OLAP. In-silico results were obtained by simulating the tumor cell equation (first equation in (3)) under fixed normoxic conditions. The number of tumor cells on the y-axis is given in thousands.

To assess the predictive capability of our model regarding the effect of OLAP on tumor cell proliferation, we simulate the cellular module under normoxic conditions. The constant tumor production rate ${\overline{k}}_C$ has been calibrated using the data obtained for OLAP = 0 μM. The simulated model incorporates the function h_2,C(PI) to account for the effects of OLAP on tumor cells. Further details are provided in Section S.3 of the Supplementary Note 1. The middle and bottom rows of Fig. 7 provide a comparison between experimental data (black) and in-silico results (red). Our model accurately captures the effect of OLAP on tumor proliferation, as depicted in Fig. 7. After calibrating the tumor proliferation rate to match the experimental growth rate observed for OLAP = 0 μM, we use the calibrated model to in-silico replicate the finding concerning the effect of increasing OLAP doses. Our model is able to consistently reproduce the dose-dependent reduction in tumor proliferation across all four cases. In particular, in all the scenarios the values obtained numerically for the number of tumor cells at 24, 48, and 72 h replicate the experimental trends both qualitatively and quantitatively, matching the experimental ranges identified by the black error bars. This underscores the model’s capability to capture OLAP’s ability to halve the total number of tumor cells when administered at the highest dose of 5 μM.

PARP inhibitors hinder slow-cyclic hypoxia

Finally, we integrate the acquired information regarding the effects of PARP inhibitors on EC and tumor cell proliferation to analyze how PARP inhibitors may influence the emergence of slow-cyclic hypoxia. We consider systems (1)-(2)-(3) with the same choice of parameters used in Fig. 4. We concentrate on O₂ dynamics, specifically examining how the dynamics of hypoxia cycles change with increasing doses of PARP inhibitors. We explore two distinct scenarios: the first accounts for the effects of OLAP on tumor cell proliferation, while the second delves into the impact of PJ-34 on EC proliferation. The results are shown in Fig. 8.

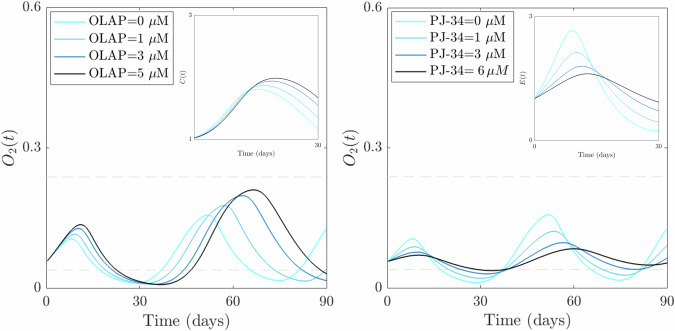
Fig. 8. PARP inhibitor effects on the emergence of slow-cyclic hypoxia.

Qualitative results of the evolution of systems (1)-(2)-(3) in the advanced-stage tumor case for increasing doses of PARP inhibitors. The left plot shows the qualitative evolution of O₂ when OLAP impact on tumor proliferation is considered in the control case (the lightest blue line) and for increasing doses of the drug. The inset shows a zoom-in of tumor evolution in the time interval [0,30] days, where the first cycle of hypoxia emerges. The right plot shows the qualitative evolution of O₂ when PJ-34 impact on EC proliferation is considered in the control case (lightest blue line) and for increasing doses of the drug. The inset plot shows the corresponding EC evolution in the time interval [0,30] days, where the first cycle of hypoxia emerges.

Our results demonstrate that both approaches, namely targeting EC or tumor cell proliferation, lead to the attenuation and eventual disappearance of the slow-cyclic hypoxia phenomenon (see Fig. 8). In particular, the impact of PARP inhibitors on the oxygen dynamics appears stronger when endothelial cell proliferation is impaired, rather than when tumor proliferation is reduced. The O₂ dynamics become regularized in the presence of the two drugs, with more enhanced effects on cycle disappearance for PJ-34 administration. This aligns with experimental findings that emphasize the ability of PARP inhibitors to normalize abnormal vasculature, with a consequent attenuation of hyperpermeability, increased vascular pericyte coverage, a more normal basement membrane^26,27. We also include in both scenarios the evolution of the population impacted by the drug (tumor in the left plot, EC in the right plot) during the time window characterized by the first slow-cyclic hypoxia phenomenon, i.e., [0,30] days. Consistently with the previously obtained results (Figs. 6B and 7), the insets show a qualitative reduction in both cell population densities, with a strong and more evident effect on EC dynamics.

Discussion

This work introduces a comprehensive model that integrates cellular and molecular mechanisms to explore the interplay between the Tie-Ang and the VEGF-VEGFR signaling pathways, oxygen and endothelial cell dynamics, and tumor and cytokine interactions. The study aims to elucidate the mechanisms behind the emergence of the phenomenon of slow-cyclic hypoxia in the tumor microenvironment, its characteristic time scales, and possible control strategies. Our in-silico results firstly suggest the significance of endothelial cell adaptation to VEGF and angiopoietin signals for generating prolonged hypoxic cycles. According to our model, the bimodal response of the dimerized form of the VEGF receptor in the feedback system is a necessary factor for the emergence of slow-cyclic hypoxia under appropriate angiopoietin stimulation. Furthermore, our computational experiments underscore the pivotal role of the feedback loop among tumors, oxygen levels, and cytokine production in regulating hypoxia cycles. We identify a crucial balance between oxygen deficiency and cytokine production necessary for sustaining prolonged hypoxia cycles. These findings suggest potential targets for reducing hypoxia cycles by directly controlling and enhancing cytokine activity within the tumor microenvironment.

We investigate the effect of PARP inhibitors in the system as a therapeutic approach targeting hypoxic conditions. In particular, we use both already published data concerning the effects of such therapies on endothelial cell proliferation (Fig. 6B) and VEGF production (Fig. 6A) and novel data regarding their effects on tumor growth (Fig. 7). Both the experimental and the in-silico results demonstrate a clear impairment of tumor and endothelial cell proliferative capabilities, along with a decrease in VEGF production under the effect of inhibitors of the PARP proteins. Notably, exploiting our model’s potential, we establish a connection between PARP inhibitors, which modulate HIF transcription pathways under hypoxic conditions, and the emergence or inhibition of slow-cyclic hypoxia. Specifically, PARP inhibitors exhibit a positive impact on oxygen dynamics, showing evident effects of regularization on the underlying vasculature responsible for oxygen supply.

To assess the model’s reliability, the novel angiopoietin module introduced in this study and the investigation of PARP inhibitors’ effects have been contrasted against different experimental data (Figs. 2, 6, and 7). The model successfully replicates the experimental trends, demonstrating its reliability and potential predictive capabilities. This makes it suitable for exploring the effects of novel therapeutic interventions targeting hypoxia cycles through in-silico experiments.

The model offers insights and proposes mechanisms that potentially drive the emergence of slow-cycle hypoxia and control its evolution through in-silico experiments. While these predictions have not yet been experimentally validated, they suggest avenues for designing new experiments. Specifically, leveraging novel in-vitro experimental platforms currently under investigation could allow for the induction and control of dVEGFR/VEGF dynamics. This would enable the observation of their impact on the co-evolution of endothelial and cancer cells under both constant and varying oxygen conditions.

In summary, this paper introduces a novel mathematical model that integrates various in-vitro and in-silico findings to elucidate the role of specific mechanisms in driving slow-cyclic hypoxia and evaluate potential therapeutic strategies based on PARP inhibitors. For the former, we propose the dVEGFR/VEGF relationship as a key trigger for the emergence of cycles, while the cytokine response acts as a controlling mechanism for their evolution. For the latter, PARP inhibitors have experimentally demonstrated their potential in impairing tumor response to hypoxia, and our in-silico results suggest their possible role in regularizing vasculature and reducing oxygen fluctuations. Therefore, the results underscore the model’s ability to capture experimental outcomes, highlighting its predictive capacity and significance in understanding the complex interactions within the proposed biological systems.

Methods

Cell culture

Human uveal melanoma cells MUM2B were cultured in RPMI 1640 medium (Gibco, Waltham, MA, USA) supplemented with 2 mM l-glutamine, 10% fetal bovine serum, and 1% penicillin/streptomycin (PAA Laboratories, Austria). Human umbilical vein endothelial cells (HUVEC) were grown in endothelial cell growth medium (Cell Applications, Germany). Both cell lines were cultured in a cell incubator at 37^∘C and 5% CO2.

Cell proliferation and viability

MUM2B (3 × 10⁴ cells per well) and HUVEC (6 × 10⁴ cells per well) were cultured in 12 well plates and treated with Olaparib at 1 μM, 3 μM, and 5 μM for 24 h, 48 h and 72 h. Images were taken on an Olympus CKX41 light microscope coupled to an Olympus E-330 camera (Olympus, Hamburg, Germany). Cell proliferation and viability were determined by Trypan Blue exclusion assay. 10 μl of Trypan Blue (Sigma) / cell mixture was loaded in a Neubauer chamber and viable (unstained) and nonviable (stained) cells were counted separately.

Data analysis

Results are shown as the mean of the independent replicates. To detect outliers a Grubbs’ Test was carried out with a significant level of 0.05.

Mathematical model

A mechanistic model based on a system of ordinary differential equations (ODEs) was developed to describe the population dynamics outlined in Fig. 1. The model operates at two main levels of description: molecular and cellular level. At the molecular level, it captures dynamic interactions within the Tie-Ang (angiopoietin module) and the VEGF-VEGFR (VEGF module) signaling pathways. Ligand-receptor binding dynamics are described by reaction rates accounting for binding-unbinding processes, receptor dimerization, and subsequent pathway activation in both cases. Precisely, the Tie-Ang signaling system is governed by the following ODE system:

$$\left\{\begin{array}{c}\frac{d\text{Ang1}}{dt}=-F_1\hfill \\ \frac{d\left(\text{Ang}1\left(\text{Tie}2\right)4\right)}{dt}=F_1\hfill \\ \frac{d\text{Ang2}}{dt}=-F_2+h_{\mathrm{Ang2}}\left(V\right)E-d_{\mathrm{Ang2}}\text{Ang2}\hfill \\ \frac{d\text{(Ang2(Tie2)2)}}{dt}=F_2\hfill \\ \frac{d\text{Tie2}}{dt}=-4F_1-2F_2\hfill \\ \frac{d\text{pTie2}}{dt}=\frac{d\text{Tie2}}{dt}P\left(R\right)\hfill \end{array}\right)$$ 1

It describes the evolution of the angiopoietin ligands, Ang1 and Ang2, their oligomeric forms, (Ang1(Tie2)4) and (Ang2(Tie2)2), the Tie2 receptor, and its phosphorylated form, namely pTie2. The dynamics are driven by the binding/unbinding rates F₁ and F₂ and the reaction term P(R) that governs Tie2 phosphorylation. In particular, the variable R represents the ratio between the phosphorylated Tie2 and the free Tie2 receptor. Moreover, this module is coupled with the other two through the production term in the Ang2 equation, which describes the VEGF-induced production of this ligand by endothelial cells. The VEGF-VEGFR signaling cascade is described with the following ODE system:

$$\left\{\begin{array}{c}\frac{dV}{dt}=k_V{h}_{1,V}\left(O_2\right)h_{2,V}\left(\text{PI}\right)C-k_{\mathrm{on}}Vu-d_{V}V\hfill \\ \frac{du}{dt}=k_{\mathrm{off}}b-k_{\mathrm{on}}Vu+k_{\mathrm{off}}^{x}x-k_{\mathrm{on}}^x\pi {\mathrm{\Delta }}^2\rho ub\hfill \\ \frac{db}{dt}=-k_{\mathrm{off}}b+k_{\mathrm{on}}Vu+k_{\mathrm{off}}^{x}x-k_{\mathrm{on}}^x\pi {\mathrm{\Delta }}^2\rho ub\hfill \\ \frac{dx}{dt}=-k_{\mathrm{off}}^{x}x+k_{\mathrm{on}}^x\pi {\mathrm{\Delta }}^2\rho ub.\hfill \end{array}\right)$$ 2

It accounts for the dynamics of VEGF (V), VEGFR (u), the (VEGF(VEGFR)2) dimer (b), and the dimerized form of the receptor (x). It follows the framework proposed in¹⁸, adding the evolution for the ligand V. Its evolution accounts for VEGF production by tumor cells under oxygen-deprived conditions (modeled through the function h_1,V(O₂) ), a natural decay term, and the binding with VEGF receptors. Moreover, the VEGF equation mediates the coupling between the VEGF and the cellular modules. Transitioning to the cellular level, the model aims to predict how these molecular mechanisms collectively shape the behavior of tumor (C) and endothelial cells (E), as well as the evolution of oxygen (O₂) and cytokines (Cyt). The evolution of their dynamics is described by the following ODE system:

$$\left\{\begin{array}{c}\frac{dC}{dt}=h_{1,C}\left(O_2\right)h_{2,C}\left(\text{PI}\right)C\left(1-\frac{C}{K_C}\right)-d_{C}CCyt\hfill \\ \frac{dE}{dt}=h_{1,E}\left(\text{pTie2},x\right)h_{2,E}\left(\text{PI}\right)E\left(1-\frac{E}{K_E}\right)\hfill \\ \frac{d{O}_2}{dt}=k_{O_2,p}E-k_{O_2,c}C{O}_2-d_{O_2}{O}_2\hfill \\ \frac{dCyt}{dt}=k_{Cyt}\frac{C}{O_2}-d_{Cyt}Cyt.\hfill \end{array}\right)$$ 3

The proliferation processes of the tumor and endothelial cells are controlled by nutrient availability and molecular signaling, while the evolution of the oxygen and cytokines is driven by production and consumption/decay mechanisms. Both in the VEGF and in the cellular module, the effects of PARP inhibitors on VEGF, tumor, and endothelial cells are modeled with the functions h_2,i(PI) for i = V, C, E. For a detailed description of the model construction, we refer to Supplementary Note 1.

Numerical method

The non-dimensionalized version (described in Supplementary Note 3) of the systems of ordinary differential equations (1)-(2)-(3), coupled with proper initial conditions, detailed described in Supplementary Table 3 of Supplementary Note 3, was numerically solved with a self-developed code in Matlab (MathWorks Inc., Natick, MA). For the time discretization, we implemented a fourth-order Runge-Kutta method over a total of 5.184 ⋅ 10⁵ time points.

Author contributions

Conceptualization: M.C., T.A., J.S. Data curation: M.C., V.C.F., F.J.O., T.A., J.S. Methodology: M.C., T.A., J.S. Formal analysis: M.C. Investigation: M.C., V.C.F., F.J.O., T.A., J.S. Software: M.C. Visualization: M.C., T.A., J.S. Validation: M.C., V.C.F., F.J.O., T.A., J.S. Resources: M.C., F.J.O., T.A., JS. Writing—original draft preparation: M.C., T.A., J.S. Writing—review and editing: M.C., F.J.O., T.A., J.S. Supervision: F.J.O., T.A., J.S. Funding acquisition: M.C., F.J.O., T.A., J.S. All authors contributed to the article and approved the submitted version.

Data availability

All relevant data are within the manuscript and its Supporting Information file.

Code availability

The Matlab codes are available in the GitHub repository https://github.com/mconte93/Cyclic_Hypoxia_Study.git.

Competing interests

The authors declare no competing interest.

Supplementary information

The online version contains supplementary material available at 10.1038/s41540-024-00453-2.