Abstract
Energy and its dissipation are fundamental to all living systems, including cells. Insufficient abundance of energy carriers—as caused by the additional burden of artificial genetic circuits—shifts a cell’s priority to survival, also impairing the functionality of the genetic circuit. Moreover, recent works have shown the importance of energy expenditure in information transmission. Despite living organisms being non-equilibrium systems, non-equilibrium models capable of accounting for energy dissipation and non-equilibrium response curves are not yet employed in genetic design automation (GDA) software. To this end, we introduce Energy Aware Technology Mapping, the automated design of genetic logic circuits with respect to energy efficiency and functionality. The basis for this is an energy aware non-equilibrium steady state model of gene expression, capturing characteristics like energy dissipation—which we link to the entropy production rate—and transcriptional bursting, relevant to eukaryotes as well as prokaryotes. Our evaluation shows that a genetic logic circuit’s functional performance and energy efficiency are disjoint optimization goals. For our benchmark, energy efficiency improves by 37.2% on average when comparing to functionally optimized variants. We discover a linear increase in energy expenditure and overall protein expression with the circuit size, where Energy Aware Technology Mapping allows for designing genetic logic circuits with the energetic costs of circuits that are one to two gates smaller. Structural variants improve this further, while results show the Pareto dominance among structures of a single Boolean function. By incorporating energy demand into the design, Energy Aware Technology Mapping enables energy efficiency by design. This extends current GDA tools and complements approaches coping with burden in vivo.
Keywords: genetic design automation, energy, non-equilibrium, thermodynamics, synthetic biology, gene-expression, technology mapping, metabolic burden, computer aided design, entropy production rate
1. Introduction
Life is non-equilibrium,1 and so energy and its dissipation is essential for life and the function of biological organisms and systems.2,3 While the absence of energy is incompatible with life,1,2 a decrease in its availability has detrimental effects on a cell’s metabolism, and consequently, on its growth, fitness, and gene expression.4−10 Such a decrease can be caused by insufficient nutrition4 of cells, but also by the burden imposed by the insertion of engineered genetic circuits8,10 and the expression of heterologous proteins.5 Metabolic burden, also observed in Saccharomyces cerevisiae and Escherichia coli, refers to the diversion of resources from the host to synthetic constructs, affecting the availability of energy, nutrients, ribosomes, and RNA polymerase, as well as reducing cellular fitness.5,6 This allocation away from maintenance and growth compromises the host organism’s physiological functions. As the functionality of synthetic constructs such as engineered genetic circuits depends on sufficient dynamics of proteins and other molecules,11 reliable and well-functioning host organisms are essential.7,10 Consequently, a trade-off between function and energy efficiency emerges, affecting reaction levels even at the promoter scale.12−14
The described importance of energy did not hinder the wide application of equilibrium gene expression models.15−18 Developed in the context of bacterial transcription, these models assume that regulatory mechanisms, such as transcription factor binding to DNA, operate at thermodynamic equilibrium.15−17,19 While this is reasonable from a modeling perspective for prokaryotes, non-equilibrium processes and the inherent energy dissipation are essential for gene regulation.1,3,19−23 In particular, the sharpness and sensitivity of non-equilibrium gene expression models surpasses the so-called Hopfield barriers,3,12,21 which set an upper limit in the equilibrium case and were first described by J. Hopfield in the context of kinetic proofreading.24 This indicates, that energy expenditure can be key to the sharpness and sensitivity of the eukaryotic gene response.12,100 Besides, transcriptional bursting is characteristic of eukaryotic gene expression,12,25−28 but also occurs in prokaryotes.23,29 These bursts are characterized by durations of transcriptional activity significantly longer than the binding of single transcription factors, which lasts a few seconds.21,26,28 Mechanisms for this may include multistep activation, where transcription factor abundance modulates transcriptional activity, or cooperative exchange, where the burst period is determined by transcription factors rapidly swapping positions due to cooperative binding.25,26,28
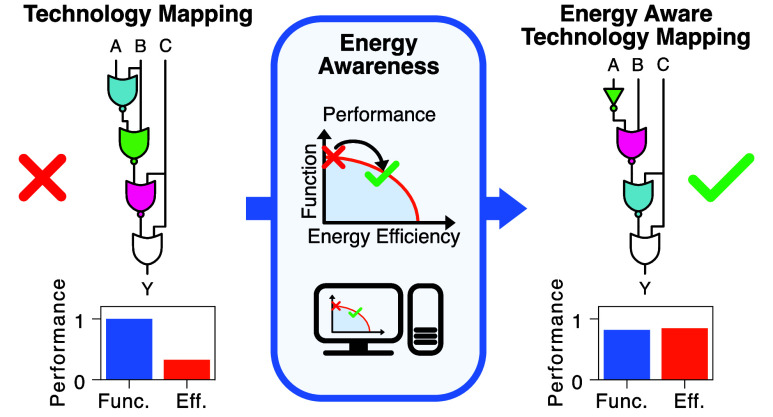
Despite these challenges, the targeted engineering of biological systems advances rapidly, with standards and tools aiding in or automating their design being created,11,31−101 while the awareness with respect to resources such as energy increases.8−10,37−39 One branch of tools is Genetic Design Automation (GDA) software.11,18,30,36,40,41 These tools solve the task of creating genetic logic circuits realizing Boolean functions with modules characterized in a gate library,11,18,30,40,41 the so-called technology mapping. The term originates from the synthesis of electronic circuits, with Figure 1 presenting an exemplary pipeline for GDA. Compared to electronics, technology mapping in GDA needs to solve additional, more complex tasks for typically smaller circuits. Particularly, it may not draw gates from the library multiple times, since it needs to consider crosstalk among genetic components. GDA tools optimize the characteristics of genetic logic circuits by evaluating them with the use of models on the basis of in silico experiments. The primary objective is functionality, which expresses the circuit’s ability to implement the Boolean function in terms of a distance related to the minimum fold change between the two Boolean states.11,30 To be meaningful, the employed models have to capture the characteristics inherent to the cells and constructs under consideration, such as the input-output characteristics of gene expression cascades, non-equilibrium attributes like energy dissipation, and transcriptional bursting.
Figure 1.
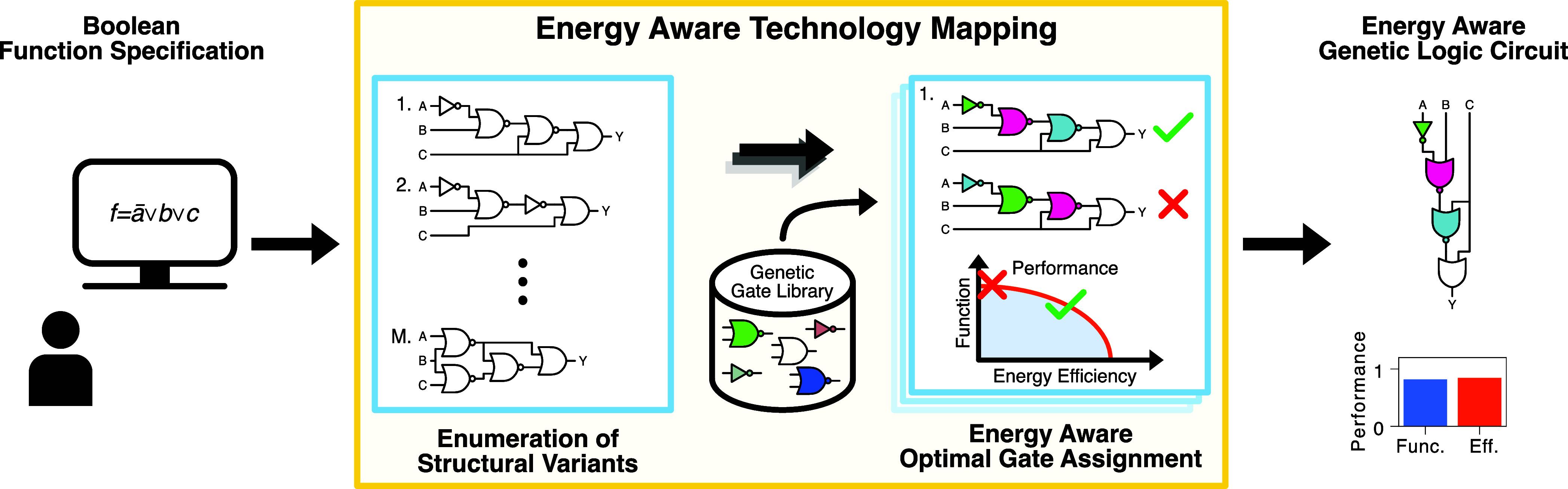
Energy Aware Technology Mapping. We here present the technology mapping pipeline at the example of the proposed Energy Aware Technology Mapping. With the specification of the Boolean function to realize as input, the technology mapping first enumerates structural variants.30 For each circuit structure obtained, we perform in silico an energy aware gate assignment. This takes into account the genetic logic circuit’s performance with respect to both, energy efficiency and functionality. After successful completion of the process, the user receives the automatically designed genetic logic circuit.
Otero-Muras and Banga42 present a tool for automating the engineering of synthetic metabolic pathways on the basis of Pareto optimal designs. These metabolic pathways are defined by the user, with genetic logic circuits being a possible branch. iBioSim36,43 is a tool for the automatized construction of genetic circuits, their simulation and model representation. The absence of an automatized flow from Boolean specifications to a DNA sequence highlights that this tool does not primarily target the automated design of genetic logic circuits. Cello11,40,41 implements a complete user interface for engineering genetic logic circuits. The user can specify the desired Boolean function using a traditional hardware design language. The given function is then transformed to a functionally equivalent circuit which only uses elements of the provided libraries for S. cerevisiae and E. coli. The gate assignment is optimized to maximize the smallest fold change between circuit output values corresponding to the distinct Boolean states ON and OFF, the Cello-score. ARCTIC18,30 extends the focus on the robustness of the resulting genetic logic circuits. By introducing particle based simulation, the E-score, and structural variants, this tool accounts for the stochastic nature of genetic gates and extends GDA’s design space by circuit topologies. The 2023 version of this tool introduced context-awareness and accounts for effects such as crosstalk between transcription factors and noncognate promoters, or titration of transcription factors to noncognate binding sites.
While the awareness of energy, in particular, and resources, in general, increases,8−10,37−39 it is not yet part of GDA. The same holds for non-equilibrium models of gene expression, accounting for energy expenditure and sharpness beyond the Hopfield barriers.12 To this end, we introduce Energy Aware Technology Mapping, the design of genetic logic circuits with respect to functionality and energy efficiency (see Figure 1). Our method is based on a probabilistic non-equilibrium steady state (NESS) model of gene expression, accounting for non-equilibrium characteristics like energy dissipation2,3 and promoter architectures varying in the number of binding sites, activation steps, and cognate transcription factors. To characterize gene expression, we derive the functional and energetic response curve as a function of transcription factor abundance. In particular, we relate the entropy production rate of our model to its thermodynamic energy dissipation rate.
Energy Aware Technology Mapping uses this model for the in silico simulation of genetic logic circuits. This allows us to explore the trade-off between functionality and energy efficiency for genetic logic circuits, where we introduce energy efficiency as the reciprocal of a circuit’s energy demand. To this end, we first consider the Boolean circuits presented by Nielsen et al.11 and continue with the evaluation of the impact of structural variants and the associated Pareto fronts. The Pareto fronts give rise to the performance of the structure independent of the optimization objective considered. By discussing means for multi-objective optimization, we allow to trade-off the objectives function and energy efficiency in a joint optimization.
The results and methods we present here are implemented in the technology mapping framework ARCTIC. ARCTIC is available at https://www.rs.tu-darmstadt.de/ARCTIC.
2. Results and Discussion
2.1. Energy Aware Gene Expression Model
Gene expression is an inherently non-equilibrium process,1,44 depending on the presence of energy carriers and building blocks like ATP and charged tRNA. While gene expression is subject to regulation at various levels,3,45,46 we focus on transcriptional regulation through the binding of activating or inhibiting transcription factors. In this section, we present the response characteristics of a single protein-coding gene whose promoter has one or more binding sites for cognate transcription factors. To this end, we describe the dynamics of the promoter and of the abundances of its associated mRNA and protein via a stochastic chemical reaction network (CRN). In contrast to combinatorial (equilibrium) promoter models, the use of a kinetic model enables the description of energy-dissipating (non-equilibrium) promoters. In particular, we obtain the mean energy dissipation rate and the non-equilibrium steady state (NESS) mean and variance of protein abundance as a function of the transcription factor concentration. These non-equilibrium response curves are used to characterize the genes realizing the gates for the technology mapping and possess attributes like increased sharpness in comparison to their equilibrium counterparts.12 We will first elucidate the kinetic model and then introduce the thermodynamic concepts necessary to relate the kinetic model to its energy dissipation rate.
2.1.1. Model Description as a CRN
A CRN
is composed of the chemical species X1,...,XN, and elementary reactions  with stoichiometric balance equations
with stoichiometric balance equations
| 1 |
where the backward reaction
microscopically reverses the forward reaction. Here, ui and wi are the substrate and product coefficients respectively,
which define the stoichiometric change vector νXm = [wi(m) – ui(m)]i for species X. Assuming the stochastic law of mass
action,47 we assign state-dependent reaction
rates (propensity functions) 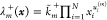 ,
, 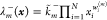 to each reaction
to each reaction 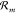 , where
, where 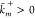 and
and 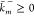 are the rate constants. A reaction is called
microscopically reversible if
are the rate constants. A reaction is called
microscopically reversible if 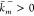 . The concept of microscopic reversibility
is important for the later thermodynamic treatment. For brevity, we
simply write reversible instead of microscopically reversible in the
following.
. The concept of microscopic reversibility
is important for the later thermodynamic treatment. For brevity, we
simply write reversible instead of microscopically reversible in the
following.
We partition the vector X of random variables into the promoter state Z, and the RNA and protein abundances R and P. The promoter can switch reversibly between a finite number
of states zi, and in
each state RNA synthesis events occur according to the state’s
transcriptional activity ai ≥ 0. In this work, we define the transcriptional activity ai in terms of relative promoter
units (RPU), a unitless quantity characterizing the promoter activity
in relation to a reference promoter.11,40 For the promoter
state representation, we make use of a one-hot encoding by different
species, so that at any time Z(t) is a standard unit vector (ei) with a single one at position i. One can extend this naturally to represent multiple promoters
in different states. RNA synthesis, protein synthesis, and degradation
are modeled as single reactions, neglecting their multistep construction.2 Although each of the elementary steps of these
synthesis and degradation reactions is reversible, we assume that
the rate constants of the microscopically reversed composite reactions
are negligibly small, leading to microscopic irreversibility. In Figure 2A and B, we represent
an exemplary instantiation of the gene expression model, where the
promoter (A) has three binding sites for a single cognate transcription
factor and two distinct levels of transcriptional activity. Since
our model allows for multiple distinct transcription factors, their
concentrations are given by the vector c. Depending on this vector, the transition rates of the promoter
(as in Figure 2A) relate
to eq 1 as 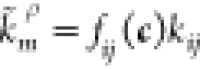 , where ρ = + for j > i and ρ = – otherwise. The functions fij describe the dependence
of the transition rate from promoter state zi to zj on the transcription factor concentrations with associated
stoichiometric change vector νZm = ej–ei.
, where ρ = + for j > i and ρ = – otherwise. The functions fij describe the dependence
of the transition rate from promoter state zi to zj on the transcription factor concentrations with associated
stoichiometric change vector νZm = ej–ei.
Figure 2.
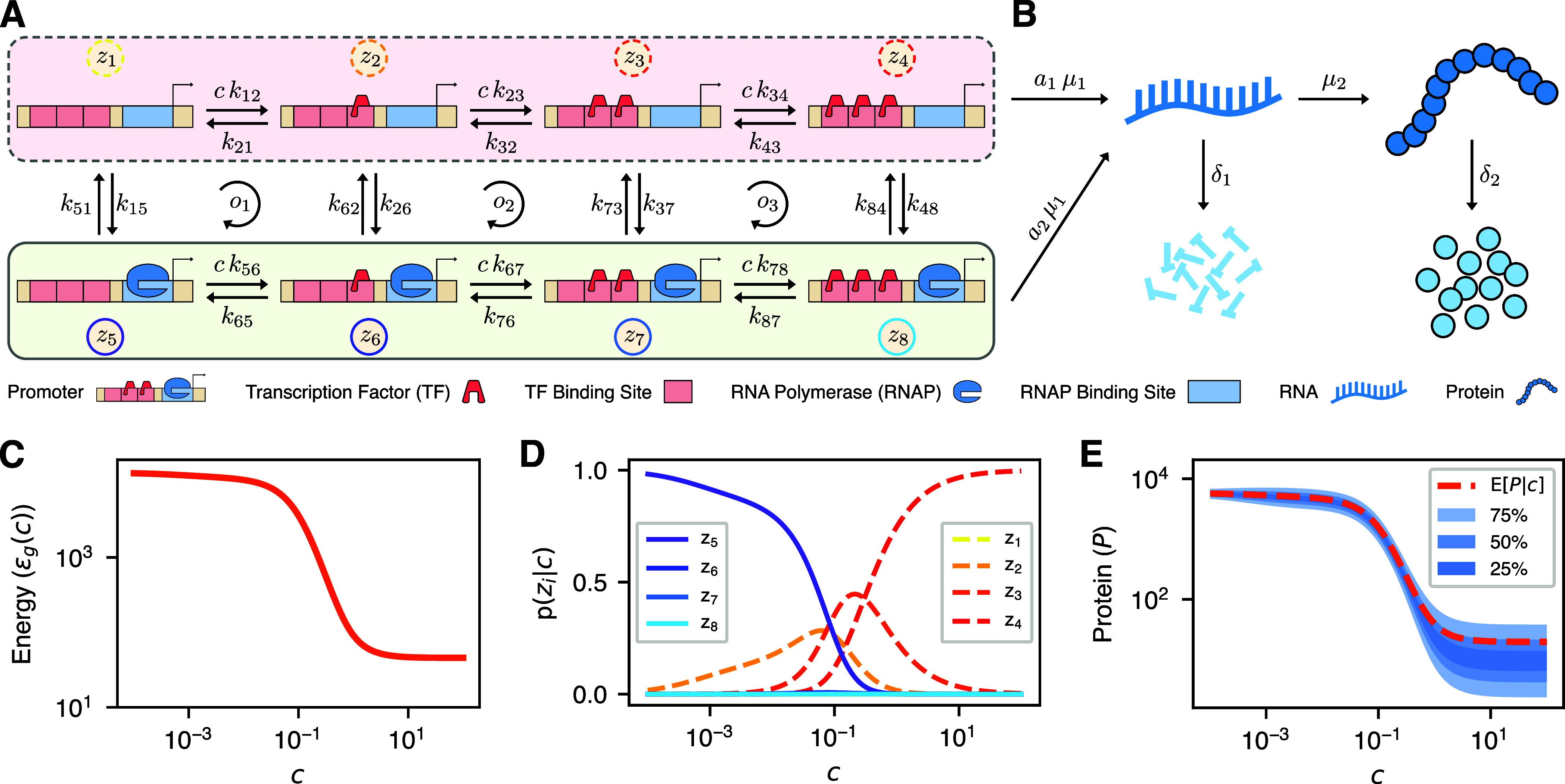
Energy aware gene expression model. (A,B) Schematic description of the proposed model consisting of the promoter model (A) and the reactions describing the RNA and protein dynamics (B). (A) The promoter model is instantiated with two levels of transcriptional activity and allows for binding up to three transcription factors. The transcription factor concentration enters via the variable c, with the transcriptional active states (zi with i = 5, 6, 7, 8) featuring transcription rate a2μ1 and the inactive states (zi with i = 1, 2, 3, 4) the basal rate a1 μ1 (a2 > a1). (B) Besides transcription, the dynamics include translation (μ2) and the respective degradation reactions (δ1 and δ2). (C–E) Exemplary response characteristic of the model as a function of the transcription factor abundance c. We here showcase inhibitory behavior of the transcription factor, while the model can also capture activatory behavior. (D) Visualization of the steady state probabilities of each state. As c increases, the probability mass shifts from state z5 to z2 and z3 before concentrating in z4. The corresponding protein distribution is shown in (E) by its mean and three quantile intervals. (C) Presents the expected energy dissipation rate of the overall model. Comparing (C) and (E), one notices the proportionality between energy dissipation rate and protein abundance.
The CRN representation of a promoter model generally is more versatile, as it may describe not only the number of bound transcription factors but also different DNA conformations in a possible multistep transcriptional activation.12 Such conformations can be, for example, open and closed loop complexes or different chromatin states.12,20,48 Since transcriptional activity in our model is independent of the binding states of the transcription factors, this model can represent transcriptional bursts in both the multistep activation model and the exchange model.12,25−29 By turning the reaction rate constants themselves into random variables, one can extend our model to include extrinsic noise caused by external context factors as described by refs (49−51). It should be noted that reversible ATP-dependent reactions ATP ⇌ ADP + Pi always produce ATP in the reverse direction. Consequently, if any promoter state change is predominantly ATP-consuming in one direction, but not ATP-producing in the reverse direction, then there are at least two distinct reactions involved.
2.1.2. Kinetic Response Curve of a Single Gene
The evolution of the distribution of the state of the gene expression system p(X(t) = x) is described by the chemical master equation given in Supporting Information Section S1.3. Using the Chapman-Kolmogorov backward equation, we derive the mean and variance of the non-equilibrium steady state RNA and protein distributions in Supporting Information Section S2, and derive the promoter’s steady state distribution πi(c) = limt→∞p(Z(t) = ei) by applying the methods in Section 4.2 to the propensity matrix Λ = Λ(c) of the promoter, with Λij(c) = fij(c)kij. Together with the transcriptional activity ai associated with each promoter state zi, the average transcriptional activity of the promoter is
| 2 |
The protein’s mean and variance and the RNA’s mean are given by
| 3 |
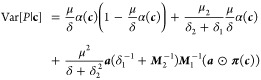 |
4 |
where μ = μ1μ2, δ = δ1δ2, a = [a1,...,an], ⊙ is the Hadamard product, and Mi = (δiIn – ΛT) with In the n times n identity matrix. The quantities in eqs 3 and 4 are the characteristic response curves of a gene depending on the transcription factor concentrations c. By decomposing the transcription rate into μ1 and the state dependent factors ai, the ai are relative quantities that can be interpreted and estimated in the context of RPU, while the quantities μ1, μ2, δ1, δ2 have to be identified only once and can be reused for other models in the same organism. Later on, we use the response curves for the NESS simulation of the in silico gene circuit realizing the genetic logic circuit within the technology mapping. To allow for energy awareness in the technology mapping, we proceed by establishing a link between the kinetic model and its energy dissipation rate in order to derive an energetic response curve as a function of transcription factor abundance c.
2.1.3. Stochastic Thermodynamics of Open CRNs
In stochastic thermodynamics, each state x of the system is associated with its Gibbs free energy g(x). Upon reaction 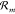 in the forward direction, the Gibbs free
energy change is Δg(m)(x) = g(x + νXm) – g(x), where
in the forward direction, the Gibbs free
energy change is Δg(m)(x) = g(x + νXm) – g(x), where 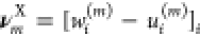 . Further, the system is assumed to be in
contact with a heat bath of temperature T. A system
consisting of a CRN and a heat bath is called a closed CRN, which—following
the zeroth law of thermodynamics—relaxes to equilibrium.52 In equilibrium, the mean energy dissipation
rate is zero.47 A system that exhibits
a zero net change in Gibbs free energy along any closed cycle in its
state space can be considered a closed system. For instance, this
is the case in the promoter in Figure 2A, if none of the transitions require additional energy
carriers. Otherwise these energy carrying species need to be accounted
for in the stoichiometric equations. Furthermore, for the dynamics
of RNA and protein, it is necessary to take into account the building
blocks whose recycling after degradation requires the expenditure
of energy.
. Further, the system is assumed to be in
contact with a heat bath of temperature T. A system
consisting of a CRN and a heat bath is called a closed CRN, which—following
the zeroth law of thermodynamics—relaxes to equilibrium.52 In equilibrium, the mean energy dissipation
rate is zero.47 A system that exhibits
a zero net change in Gibbs free energy along any closed cycle in its
state space can be considered a closed system. For instance, this
is the case in the promoter in Figure 2A, if none of the transitions require additional energy
carriers. Otherwise these energy carrying species need to be accounted
for in the stoichiometric equations. Furthermore, for the dynamics
of RNA and protein, it is necessary to take into account the building
blocks whose recycling after degradation requires the expenditure
of energy.
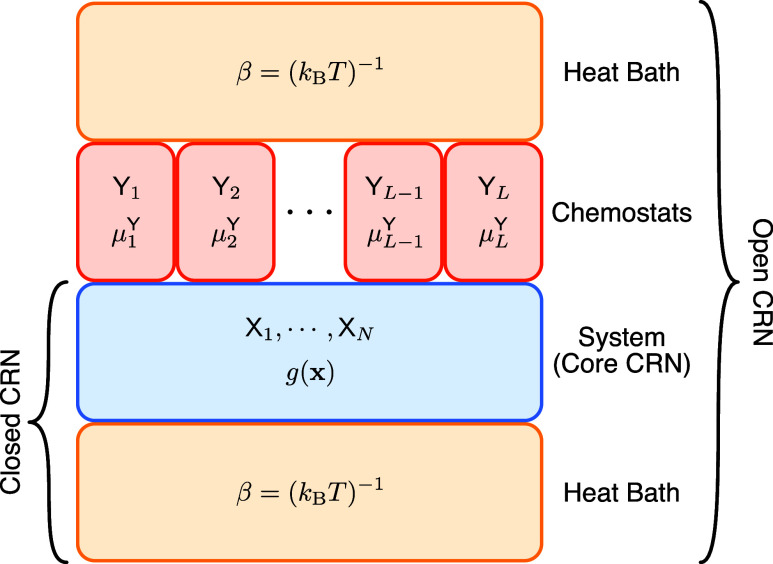
We thus assume that the reactions 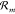 actually include species Y1,...,YL, which are controlled by the cell to always
have constant concentrations. Usually, these are energy carriers like
ATP and its hydrolysis products like ADP and phosphate (Pi). By coupling our CRN to these species, we obtain an open CRN described
by the stoichiometric balance equations
actually include species Y1,...,YL, which are controlled by the cell to always
have constant concentrations. Usually, these are energy carriers like
ATP and its hydrolysis products like ADP and phosphate (Pi). By coupling our CRN to these species, we obtain an open CRN described
by the stoichiometric balance equations
| 5 |
where the species Y1,...,YL act as chemostats and υj and ωj are the respective
substrate and product coefficients. Figure 3 illustrates the composition of closed and
open CRNs. The Gibbs free energy change of the chemostat species associated
with reaction 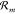 is Δμ(m) = ∑Lj=1 μYj(ω(m)l – υ(m)j), where μYj is the chemical potential of species
Yj. Identifying W(±m)chem =
∓Δμ(m) as the chemical
work done on the core system by the chemostat upon reaction
is Δμ(m) = ∑Lj=1 μYj(ω(m)l – υ(m)j), where μYj is the chemical potential of species
Yj. Identifying W(±m)chem =
∓Δμ(m) as the chemical
work done on the core system by the chemostat upon reaction 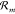 in the forward and backward direction,
respectively, we introduce the energy dissipated into the environment
per reaction as the difference of chemical work and Gibbs free energy
change
in the forward and backward direction,
respectively, we introduce the energy dissipated into the environment
per reaction as the difference of chemical work and Gibbs free energy
change
| 6 |
Figure 3.
Schematic description of an open CRN. Contrasting open and closed chemical reaction networks, the difference originating in adding chemostat species Yi with associated chemical potential μjY can be easily observed. The core CRN itself is characterized by the Gibbs free energy g(x), while both, the closed and open CRN, are in contact to the heat bath with parameter β. The abundance of the chemostat species is kept constant, in our case by the cellular environment, and results in a chemical potential that drives the core CRN. In this work, the chemostat species refer to cellular energy carriers like ATP and the products of corresponding hydrolysis reactions.
The expected energy dissipation rate Q̇ is then given by
| 7 |
as we show in Supporting Information Section S3.2. For open CRNs the propensity functions
of any reversible reaction 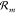 (i.e., k+m > 0 implies k–m > 0) are related to the energy changes by the thermodynamic
consistency relation52
(i.e., k+m > 0 implies k–m > 0) are related to the energy changes by the thermodynamic
consistency relation52
| 8 |
which associates the rates of the reactions
with the corresponding energy dissipation and 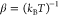 parametrizing the heat bath with temperature T and Boltzmann constant kB.
If all reactions of an open CRN
parametrizing the heat bath with temperature T and Boltzmann constant kB.
If all reactions of an open CRN 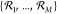 are reversible, then we may use eq 8 to identify the energy
dissipation rate with the entropy flow into the environment
are reversible, then we may use eq 8 to identify the energy
dissipation rate with the entropy flow into the environment
| 9 |
where J+m(x,t) = p(X(t) = x)λ+m(x) and J–m(x,t) = p(X(t) = x + νXm)λ–m(x + νXm) represent the forward and backward probability
fluxes of reaction 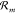 with net flux Jm(x,t) = J+m(x,t) – J–m(x,t).
with net flux Jm(x,t) = J+m(x,t) – J–m(x,t).
2.1.4. Relation between Energy Dissipation and Entropy Production Rate of the NESS
The entropy production
rate47,53,54 is the sum
of the entropy change rate of the system and the entropy flow into
the environment, that is, 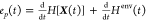 , where H[X(t)] is the Shannon entropy (H[X(t)] =
−∑x p(X(t) = x) ln(p(X(t)
= x))). At steady state (or in the limit t → ∞) we have
, where H[X(t)] is the Shannon entropy (H[X(t)] =
−∑x p(X(t) = x) ln(p(X(t)
= x))). At steady state (or in the limit t → ∞) we have 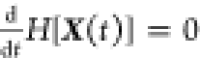 and hence the mean energy dissipation rate
(in units of kBT) of
the NESS is given by the entropy production rate, i.e.,
and hence the mean energy dissipation rate
(in units of kBT) of
the NESS is given by the entropy production rate, i.e.,
| 10 |
Due to the central relevance of this relationship, we recommend Supporting Information Section S3 and in particular Section S3.3 to the reader, where we derive and discuss the relationship between entropy production rate and energy dissipation rate in depth.
2.1.5. Energetic Response Curve of a Single Gene
Following the above, we express the energetic response curve to the transcription factor concentrations c in terms of ϵg(c), the overall mean energy dissipation rate of the NESS. This rate is given as the sum
| 11 |
of the contributions of the promoter ϵp(c), the RNA dynamics ϵtx(c), and the protein dynamics ϵtl(c).
In particular, we use the relationship between energy dissipation and entropy production to quantify the energy dissipation rate of the promoter as ϵp(c) = kBTep, since it is assumed to satisfy the microscopic reversibility requirement. Note that since the entropy production rate is calculated without the knowledge of chemical potentials μYj or the Gibbs free energy changes Δg(m), the expression is valid for a variety of different promoter topologies, provided the promoter topology is accurate. To derive the NESS entropy production rate of the finite state promoter, we make use of Schnakenberg’s method,53 which we outline in Supporting Information Section S4. Using this method gives
| 12 |
as derived in Supporting
Information Section S4.1 and consequently
the promoter’s energy dissipation rate is ϵp(c) = ep/β. Here, Joi denotes the probability flux
along the cycle oi as
presented in Figure 2A and 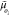 is the change in chemical potential—also
known as thermodynamic force—associated with a single run through
cycle oi. The products
of each flux (Joi) and force
is the change in chemical potential—also
known as thermodynamic force—associated with a single run through
cycle oi. The products
of each flux (Joi) and force 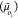 pair resemble the well-known expression
for electrical power, i.e., the product of a voltage (force) and the
induced electrical current (flux). We remark that in the steady state
the entropy production rate and hence the energy dissipation rate
do not depend on the Gibbs free energy of the states (see Supporting
Information Section S4.1). As a consequence,
the rate of energy dissipation (e.g. heat dissipation) and the rate
of energy expenditure (e.g. energy intake) are equivalent.
pair resemble the well-known expression
for electrical power, i.e., the product of a voltage (force) and the
induced electrical current (flux). We remark that in the steady state
the entropy production rate and hence the energy dissipation rate
do not depend on the Gibbs free energy of the states (see Supporting
Information Section S4.1). As a consequence,
the rate of energy dissipation (e.g. heat dissipation) and the rate
of energy expenditure (e.g. energy intake) are equivalent.
Since our transcription and translation model lacks microscopic reversibility, the thermodynamic consistency relation (eq 8) is not well-defined. However, under the assumptions given in Supporting Information Section S3.4, we only need to provide the chemical work per reaction in addition to the rate constants to obtain the energy dissipation of these reactions via eq 7. Here we derive these quantities from an intuitive heuristic perspective, while the corresponding considerations involving eq 7 are presented in Supporting Information Section S3.4.
Considering the energy required per RNA molecule first, we subsume
all length dependent energy requirements for RNA synthesis and degradation
in er and the length
independent ones in 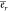 . Taking the RNA length lr in nucleotides into account, the energy
per RNA molecule is
. Taking the RNA length lr in nucleotides into account, the energy
per RNA molecule is 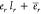 . For the protein synthesis and degradation,
we define the energies ep and
. For the protein synthesis and degradation,
we define the energies ep and 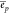 analogously and define lp as the protein length in amino acids.
To obtain the actual energy expenditure, we have to account for the
synthesis and degradation rates. In particular, these rates are given
by δ1E[R|c] and δ2E[P|c] for RNA and
protein, respectively. Multiplying the rate of molecule synthesis
and degradation with the associated energy yields
analogously and define lp as the protein length in amino acids.
To obtain the actual energy expenditure, we have to account for the
synthesis and degradation rates. In particular, these rates are given
by δ1E[R|c] and δ2E[P|c] for RNA and
protein, respectively. Multiplying the rate of molecule synthesis
and degradation with the associated energy yields
| 13 |
as the expected energy expenditure rates of the RNA and protein dynamics.
2.2. Energy Aware Technology Mapping
With the energy aware NESS model of gene expression at hand, we now present the steps for incorporating it into the technology mapping process. This gives rise to Energy Aware Technology Mapping.
2.2.1. From Genetic Logic Circuits to Genes and Back
The efficient technology mapping of genetic logic circuits gets enabled by large scale in silico experiments. Depending on the focus, in silico evaluations can target different levels of abstraction as exemplified in Figure 4A. These abstractions not only differ with respect to the modules they are composed of, but also in the signals considered. While Boolean logic circuits make use of Boolean signals, the genetic logic circuits we consider here use the promoter activity in relative promoter units (RPU), with protein abundance serving as signal carrier in the underlying gene circuits. With the model we present in this work, we target the gene expression level, where genes express proteins that act as transcription factors and repress the expression level of the genes associated with their cognate promoter. As such, this approach can resemble in silico the in vivo implementation of a genetic logic circuit inside cells as described by Chen et al.40.
Figure 4.
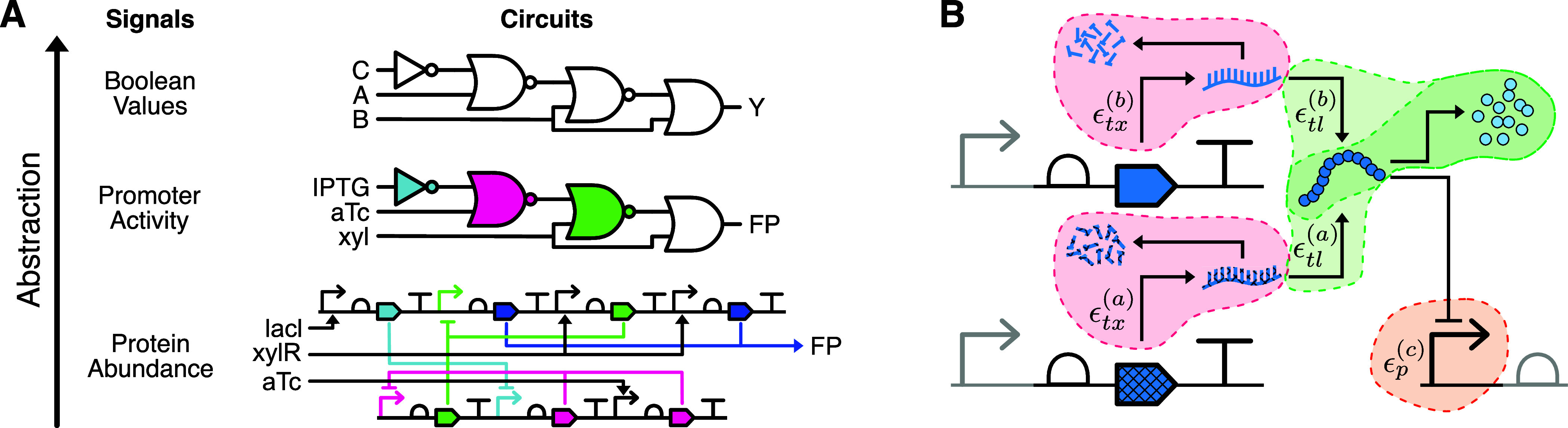
From genes to logic circuits. (A) Visualization of the abstraction levels encountered in GDA. The gene circuit at the bottom realizes the behavior within the cell and is the circuit our model is applied to. It relies on protein concentrations as signal carriers. Defined on top, the genetic logic circuit provides a convenient interpretation in terms of gates, familiar to engineering disciplines and the basis for GDA. The Boolean logic circuit shadows all implementational details and presents the function to realize. (B) Overview on the energy demands of a genetic NOR gate following the implementation of ref (40). The gate consists of the genes a, b, and c, with the preceding and succeeding gates greyed out. ϵtx denotes the energy dissipation rate of the RNA dynamics, ϵtl of the protein dynamics, and ϵp is the energy dissipation rate of the promoter.
To make use of our NESS gene expression model within the genetic logic circuit centered technology mapping, we first obtain the corresponding gene circuit. In the next step, the Boolean input values are translated to the respective promoter activities, from which we then derive the corresponding inducer concentrations. The gene circuit is evaluated by applying our model in topological order to the genes. By deriving the promoter activity associated with the abundance of the reporter protein, we finally obtain the output representation at the genetic logic circuit level.
2.2.2. Functional Performance of Genetic Logic Circuits
In order to complete the loop, we could apply a
thresholding to the promoter activity values and obtain the associated
Boolean value. Within the technology mapping, the performance of this
thresholding approach is subsumed in the score S,
effectively measuring the distance between activity levels representing
ON and OFF states. Formally, we define the genetic logic circuit as
the tuple (γ, q), where γ is the circuit’s
structure and q the corresponding assignment of genetic
gates. We derive the score S = S(γ, q) by evaluating the genetic logic circuit in silico for all Boolean input conditions 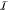 (with
(with 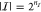 for
for 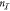 inputs). The obtained circuit output values
in terms of promoter activities are subsumed in
inputs). The obtained circuit output values
in terms of promoter activities are subsumed in 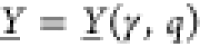 in case they shall represent an OFF state
and
in case they shall represent an OFF state
and 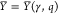 otherwise. Identifying the elementary scoring
function with s, the score S(γ, q) is given by
otherwise. Identifying the elementary scoring
function with s, the score S(γ, q) is given by
where 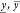 can be scalar values, as in the case of
the Cello-score11, or empirical distributions,
as for the E-score.30 Within Section 4.4.1, we extend
on the definition of the E-score and its application
to empirical distributions.
can be scalar values, as in the case of
the Cello-score11, or empirical distributions,
as for the E-score.30 Within Section 4.4.1, we extend
on the definition of the E-score and its application
to empirical distributions.
2.2.3. Energy Expenditure of Genetic Logic Circuits
Besides the functional characterization, our gene expression model
allows for insights into the energetics of the genetic logic circuit.
For this, we define 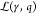 as the set of genetic logic gates included
in the circuit (γ, q). Furthermore, we identify
the genes expressing the transcription factor associated with gate
as the set of genetic logic gates included
in the circuit (γ, q). Furthermore, we identify
the genes expressing the transcription factor associated with gate 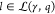 with the index set
with the index set 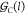 and the genes with cognate promoters with
the index set
and the genes with cognate promoters with
the index set 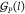 . The energy expenditure rate of gate
. The energy expenditure rate of gate 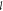 is the aggregation of the single parts
contributions, given by
is the aggregation of the single parts
contributions, given by
| 14 |
where 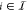 identifies the Boolean input condition
and
identifies the Boolean input condition
and 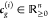 denotes the concentrations of the cognate
transcription factors of gene g for the respective
input condition. Within Figure 4B, we present this using the example of a genetic NOR gate
following the implementation of Chen et al.40. Taking all gates
denotes the concentrations of the cognate
transcription factors of gene g for the respective
input condition. Within Figure 4B, we present this using the example of a genetic NOR gate
following the implementation of Chen et al.40. Taking all gates 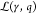 of the genetic logic circuit into account,
the energy dissipation rate of the whole circuit for the ith input assignment is
of the genetic logic circuit into account,
the energy dissipation rate of the whole circuit for the ith input assignment is
| 15 |
We define the average and maximum expected energy expenditure rates E(γ, q) and Emax(γ, q) of the genetic logic circuit (γ, q) as
| 16 |
Depending on the type of application and the constraints enforced, both, E and Emax, are valid objective functions for the energetic optimization. In the case of stochastic evaluation, the aggregation functions in eq 16 extend naturally.
2.2.4. Technology Mapping of Genetic Logic Circuits
The previous two sections have introduced different metrics for the evaluation of genetic logic circuits. It is the task of the technology mapping to design a topology from the available gate types that realizes the desired Boolean function. To this end, our tool systematically enumerates all possible variants of logic gate types and topologies. Each of these possible solutions requires the assignment of genetic gates, which is determined by heuristic optimization. To incorporate the functionality and energy efficiency into the scoring of the resulting circuits, either multiobjective or constrained optimization can be applied.
2.3. The Energy and Function Trade-Off of Genetic Logic Circuits
With the energy aware gene expression model included into the technology mapping framework ARCTIC,18,30 we can explore the design space of genetic logic circuits with respect to both, functionality and energy efficiency. For this purpose, we consider the genetic logic gates introduced with Chen et al.40. In particular, we calibrate the parameters of our model to capture the response characteristics encoded in the cytometry data provided by ref (40) as described in Methods Section 4.3. We then use the obtained parametrizations to derive a genetic gate library for S. cerevisiae, consisting of 12 genetic logic gates utilizing nine independent transcription factors.
We start our evaluation by investigating
the energy expenditure rates encountered in mapping genetic logic
circuits and consider their relation to circuit functionality. Based
on the insights gained, a systematic evaluation of the circuit structure’s
effect on the energy efficiency of genetic logic circuits follows
up. In this context, we also consider the Pareto fronts and the application
of multiobjective optimization. To emphasize comparability among genetic
logic circuits as well as function and energy, we introduce the notion
of energy efficiency, or briefly efficiency, E̅ as the inverse of the energy measure (i.e., 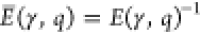 or
or 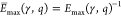 ) and apply normalization to the best scores
encountered in the considered benchmark set.
) and apply normalization to the best scores
encountered in the considered benchmark set.
2.3.1. Function and Energy Optima are Disjoint
To assess the energy landscape of genetic logic circuits, we evaluate the technology mapping results of 33 logic circuits, each realizing a different Boolean function. The choice of circuits follows Nielsen et al.11 and encompasses circuits ranging from two to seven gates. For the purpose of this evaluation, we optimize each circuit for the two objectives function and energy and constrain the other in the respective case. While the minimum functional score to achieve is identical for all circuits, the upper limit on the energy dissipation rate during functional optimization is chosen in dependence to the gate count (see Methods Section 4.4).
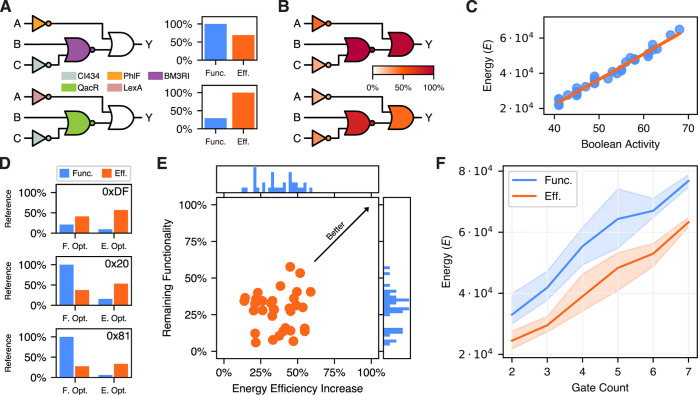
Starting with a small circuit first, Figure 5A presents the function and energy optimized genetic logic circuits for 0x2F (3 gates). Despite the same structure, the different gate assignments feature significant differences in function and energy. In particular, the energy optimized version decreases the functionality by 70.7% to improve energy efficiency by 44.4% in comparison to the version optimized for function. This is a decrease in fold change by a factor of 3.4 and a decrease in energy resource consumption by 30.8%. In addition, the disjoint optimality of function and energy indicates a trade-off between the two optimization goals considered. Increasing the number of gates does not change this, as we observe by considering the results for circuits 0xDF (4 gates), 0x20 (5 gates), and 0x81 (7 gates) in Figure 5D. However, the absolute level of energy expenditure changes in both, the functionally and efficiency optimized circuits. While we estimate an energy expenditure rate of 29,401kBT s–1 for circuit 0x2F, this increases to 38,251kBT s–1 for circuit 0xDF, 40,901kBT s–1 for circuit 0x20, and 64,865kBT s–1 for 0x81 in the energy optimized case. With an average contribution of 98.8%, our model predicts protein synthesis and degradation to account for the largest portion of energy expenditure.
Figure 5.
Function and energy as disjoint optimization targets. (A) Circuit 0x2F (3 gates) is optimized for function (top) and energy efficiency (bottom). The bar plots on the right present the performance of the genetic logic circuits depicted on the left for both evaluation criteria. Clearly, the optima are disjoint. (B) Visualization of the mean energy expenditure rate per gate (lower is better) for 0x2F over all Boolean input conditions, optimized for functionality (top) and energy efficiency (bottom) and normalized to the largest value. The energy expenditure of the NOR and OR gate differ significantly between the two implementations, impacting the overall energy efficiency significantly [see (A)]. (C) Boolean activity as an heuristic for the energy expenditure of a genetic logic circuit. Here compared to the energy of circuits with the objective energy efficiency. (D) The optimization results of circuits 0xDF (4 gates), 0x20 (5 gates), and 0x81 (7 gates), normalized to the maximum functional score and energy efficiency observed in the benchmark. Again, optimizing for either of the two objectives decreases the performance of the genetic logic circuits with respect to the other. (E) Analysis of the cost of energy efficiency increase on the benchmark. While the optimization for energy improves energy efficiency up to 58.9%, the functionality score is often decreased significantly. (F) Relationship between expected energy dissipation rate of the circuit and its gate count. The bold line is the mean and the shaded areas present the minimum and maximum intervals, with the colors indicating the optimization objective. This figure reveals a near linear relationship between energy dissipation rate and gate count. However, the optimization objective sets the offset. Comparing the objectives, optimization for energy efficiency allows to implement genetic logic circuits of six gates with the energetic requirements of functionally optimized four gate circuits.
Figure 5B provides information on the differences of energy dissipation for the respective optimization goals. Presenting the energy per gate averaged over all input assignments, we observe that the two NOT gates differ only slightly between the functionally (top) and energetically (bottom) optimized variants. With 61.8%, the OR gate conduces the majority of energy saving. However, this is a direct result from the change in gate assignment of the respective preceding gates, as in comparison to the functionally optimized version their maximum expression levels are roughly halved. In consequence, the circuit’s score—which assesses the fold change—drops proportionally. For functions 0xDF, 0x20, and 0x81, we observe the same behavior, with most energy savings resulting from gates closer to the output and only minor improvements and sometimes even worsening from gates close to the input of the circuit. Thereby, the largest energy savings are achieved by significantly reducing the expression levels of Boolean ON states.
Shifting the perspective to the set of all circuits, the optimization for energy increases energy efficiency up to 58.9% and on average by 37.2% (see Figure 5E). However, this comes at a cost, as there is often only a small gap between the functionality constraint and the actual functionality score, as observable in the average remaining score of 28.5%. Figure 5E highlights this by visualizing the relationship between function and energy efficiency for the two cases of optimization. Reconsidering the relation between circuit size and energy, Figure 5F indicates the linear relationship between these quantities for the circuits taken into account for both optimization objectives. Comparing the results for efficiency and functionally optimized circuits among different circuit sizes, we see that a fixed energy budget allows for larger circuits when optimized for energy efficiency. On the other side, circuits designed by Energy Aware Technology Mapping feature an energetic advantage of at least one gate.
These results indicate an inherent trade-off between the two objectives energy efficiency and functionality for genetic logic circuits. Considering the in vivo realization of circuits, the expression level based signaling requires sufficient fold change to differentiate between distinct logic levels. In the presence of basal expression, fold change is achieved by sufficiently high levels of protein abundance, with the energy expenditure increasing proportionally. As part of the optimization for energy efficiency, the expression levels are reduced to a minimum viable level. However, the lower limit on the score ensures that despite the drop in functionality, the circuit’s function is preserved (see Methods Section 4.4). The observation of highest energy savings at the circuit outputs can result from level separation as a requirement for the function of gate cascades11,18 and minor optimization potential at the circuit inputs. However, Engelmann et al.18 point out that these last gates are critical for the functional performance of a circuit. Again, this indicates the exclusiveness of the objectives considered.
An aspect not explicitly targeted yet but relevant for the overall energy expenditure is the gate technology. The gate library40 used provides transcription factor based gates, requiring the expression of heterologous proteins. Since our model and other studies5,9,55−57 consider heterologous protein expression rate to be proportional to energy expenditure and protein dynamics to dominate the energy consumed by gene expression, RNA-based gates could significantly reduce the overall energy consumed.
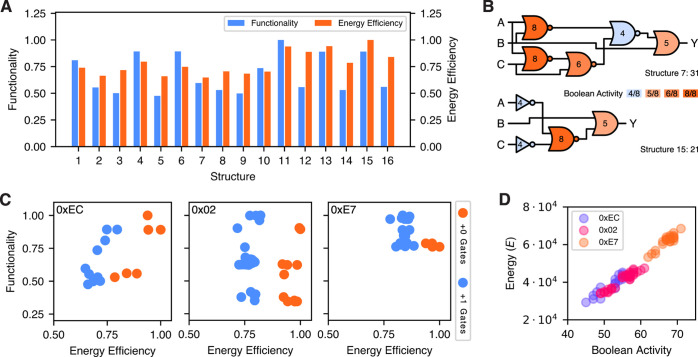
Driven by the relation between circuit size and energy dissipation, we present a precise heuristic for the energy expenditure rate of a genetic logic circuit. This heuristic is given by the Boolean activity of a structure, which reduces the estimation to counting the states which require protein expression. More formally, we consider the truth tables of the gates constituting the circuit structure. For each NOT and NOR gate, the number of Boolean ON states the respective input gates feature is counted. To the circuit’s inputs and outputs, special treatment applies. The inputs are counted as if they were always ON, as their in vivo implementation makes use of constitutive promoters. For the outputs (simple buffer or implicit OR), the number of ON states is counted, as this refers to the protein level ideally representing this state. The overall Boolean activity is then obtained by summing up all the individual contributions for all possible Boolean input conditions. Figure 5C presents the relationship between the Boolean activity and the energy dissipation rate of genetic logic circuits optimized with respect to energy efficiency. With a Pearson correlation coefficient of 0.989 (0.940 for functional optimization), this easy-to-use heuristic is highly predictive.
2.3.2. Promoter’s Energy Expenditure Peaks in Transition Region
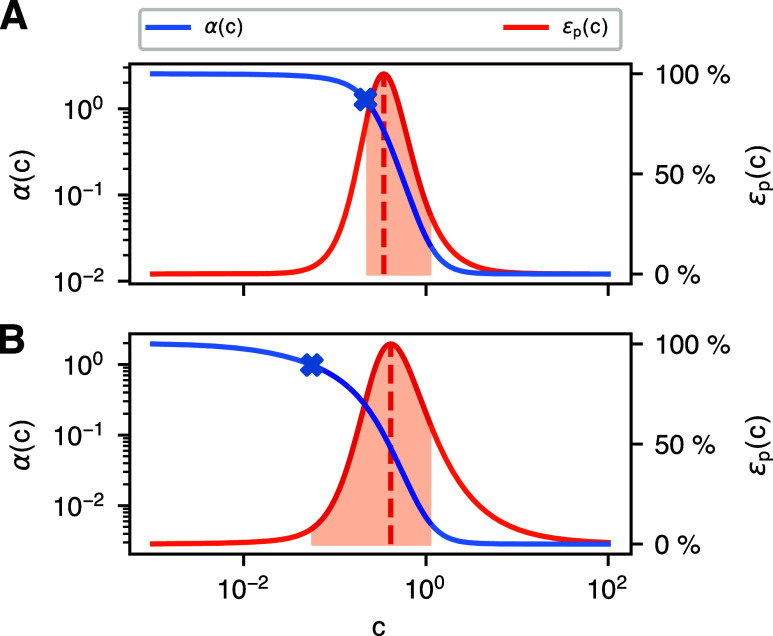
The circuit level trade-off is dominated by the protein expression level. In order to gain insight into the gate and promoter level, we focus here on the promoter energy, the entropy production rate. Figure 6 presents the entropy production rate and average promoter activity as a function of transcription factor abundance for two exemplary genetic gates. All gates (see Supporting Information Figure S7) feature a peaked entropy production rate, with the energy dissipation mostly concentrated in the transition region of the gate’s response curve, and becoming more peaked as the transition becomes sharper. In addition, the entropy production rate is often highest (dashed line) close to the steepest descend (marker) of promoter activity (see Figure 6A) in the linear domain, with Figure 6B presenting a counterexample to this.
Figure 6.
Peaked entropy production rate in transition region. The average promoter activity and the corresponding entropy production rates of two exemplary promoter models as a function of transcription factor abundance c. These promoter models vary in the instantiation of the promoter architecture in Figure 2A. We highlight the transition region, which connects the two saturated regions of promoter activity. In most cases, entropy (ϵp(c) = ep(c) β–1) is highest (dashed line) within this transition region. Besides, this entropy production peak is often close to the steepest descend (marker) of promoter activity [see (A)] in the linear domain, but not in all cases [see (B)].
Considering the saturated regions for low and high input transcription factor levels, promoter energy dissipation rates decrease significantly. In the context of genetic logic circuits, these regions represent the Boolean states one wants the gates to attain, giving rise to only minor contributions of the promoters to the overall energy dissipation of well functioning genetic logic circuits. Despite this, 21 of 33 efficiency optimized circuits feature a lower promoter energy dissipation rate in comparison to their functionally optimized pendants.
2.3.3. Circuit Structure Shapes Energy Expenditure
The previous results indicate a strong connection between the size of a circuit and its energy expenditure rate. However, not all circuits of a certain size perform equally well, which brings the structure of a genetic logic circuit into focus. The structural variants approach implemented in ARCTIC18,30 allows for optimizing the structure in addition to the gate assignment. In doing so, Schladt et al.30 demonstrate the benefits of including the structure of the circuit into the optimization process for functionality. Guided by these insights, we employ the structural variants approach to evaluate the structure’s impact on circuit performance with respect to functionality and energy efficiency.
For the evaluation of the structural variants, we consider exemplary the three Boolean functions 0xEC (3 gates), 0x02 (4 gates), and 0xE7 (5 gates), and allow for a single excess gate compared to the minimal structure. We apply the same constrained optimization as in the previous section, but optimize only for energy efficiency. Figure 7A provides a first intuition of the effect of structural variants by presenting the results of function 0xEC. The 16 different structures differ significantly in their functional but also energetic characteristics. The worst structure has a 54.3% higher energy expenditure rate than the best, and on average, the structural variants improve energy efficiency by 30.7%. Among the presented variants also the functionality varies, with an observed maximum improvement of 52.4%. Even more important is, that some structures (i.e., 11, 13, and 15) are significantly better than others in terms of both, energy efficiency and functionality.
Figure 7.
Impact of the logic circuit structure on energy efficiency. (A) We here present the functionality and energy efficiency of the structural variants of function 0xEC optimized with respect to energy efficiency. The structures feature different characteristics in both, the energy efficiency and functionality, with an average improvement of energy efficiency by 30.7% when considering the best structure. Normalization refers in both cases to the best value encountered. (B) The Boolean activity per gate for structures 7 and 15 of function 0xEC, which exhibit the worst and best energy efficiency. In comparison to structure 7, structure 15 features 10 active states less. This manifests in a significantly higher energy efficiency of structure 15 [see (A)]. (C) Overview on the distribution of energy optimized variants for the three functions 0xEC (3 gates), 0x02 (4 gates), and 0xE7 (5 gates), where the gate counts refer to the smallest structure obtained. Within the figures, the colors code for the number of excess gates, showing that smaller structures are beneficial for energy efficiency. However, for larger circuits the consideration of excess gates proves beneficial for functionality. The values are normalized with respect to the best values obtained for each function, while the clustering results from the discrete nature of gate assignment. (D) Also for the structural variants, the correlation between Boolean activity and the energy dissipation is significant albeit varies among the different functions (0.927 for 0xEC, 0.960 for 0x02, and 0.934 for 0xE7).
Figure 7B provides a detailed insight into the Boolean activity of the least (structure 7) and most (structure 15) energy efficient structures. For each gate, its accumulated Boolean activity over all Boolean circuit input assignments is depicted. The difference of 10 active states between the two circuits manifests itself in a significantly differing energy efficiency. Examining the structures in detail, there are two causes for this difference. First, structure 15 features one gate less compared to structure 7. Second, the way in which the Boolean function is computed leads to a lower average activity of the gates in structure 15 (6.2 for structure 7 vs 5.25 for structure 15). This is partly caused by the usage of NOT gates over NOR gates in structure 15. In the given gate architecture, NOR gates feature an independently expressed transcription factor for each input, leading to a potential doubling of energy expenditure in one of four output states.
To emphasize our understanding of the relationship between energy efficiency, functionality and structure, Figure 7C showcases for each of the considered functions the performance of the structures in terms of energy efficiency and functionality. Structures with less gates are more energy efficient than their larger counterparts. However, with the exception of 0xEC, the larger circuits have better functional performance, although the smaller ones are quite close. Considering the energy efficiency improvements possible, these decrease with increasing circuit size as the average improvement of 0x02 is 21.4% and of 0xE7 16.1%. Besides, some structures lead to superior designs with respect to both objectives.
Reconsidering the Boolean activity, we here investigate whether this heuristic is expressive for structures with the same Boolean function. Presented in Figure 7D, Boolean activity and energy expenditure again correlate significantly, with a correlation coefficient of 0.982. However, when considering single functions, the correlation reduces to 0.927 in the worst case.
The predictive power of Boolean activity and the dependence on the Boolean function indicate the relevance of the circuit structure to energy efficiency. We confirm this here by pointing out the improvements that can be made by considering structural variants in the context of energy efficiency. As the structures differ in the number of states requiring protein expression, they allow for increasing energy efficiency and can also be beneficial for functional performance.
2.3.4. Pareto Dominance Among Structures
Until now, we only considered the extremes of being either energetically or functional optimal. In a design approach, one would trade-off these objectives to achieve the best performance in relation to the energy spent. To this end, we analyze the Pareto front of 10 structures for Boolean function 0xF7. In particular, we perform a parameter sweep over the energy constraint for each of the 10 structures. This gives rise to the functional best genetic circuit adhering to the energy constraint. The constraint is chosen so that the range of energy levels identified by an initial sampling is equally divided into 20 intervals.
The Pareto fronts obtained show the exclusivity of energetic and functional optimality by giving rise to an anti-proportional characteristic. Considering exemplary the Pareto front of structure 4 (Figure 8A), which we present in Figure 8C, we observe that an increase in efficiency leads to a decrease of functionality and vice versa. In addition, we observe characteristic clustering at different levels of functional performance, likely being caused by different genetic gates at the later positions of the circuit.18 Despite this, the Pareto area presents a near convex shape and allows for a smooth trade-off between function and energy. Our evaluations of exemplary structures for the Boolean function 0x26 featuring six genetic gates each also presents the antiproportionality but does not exhibit the observed smoothness.
Figure 8.
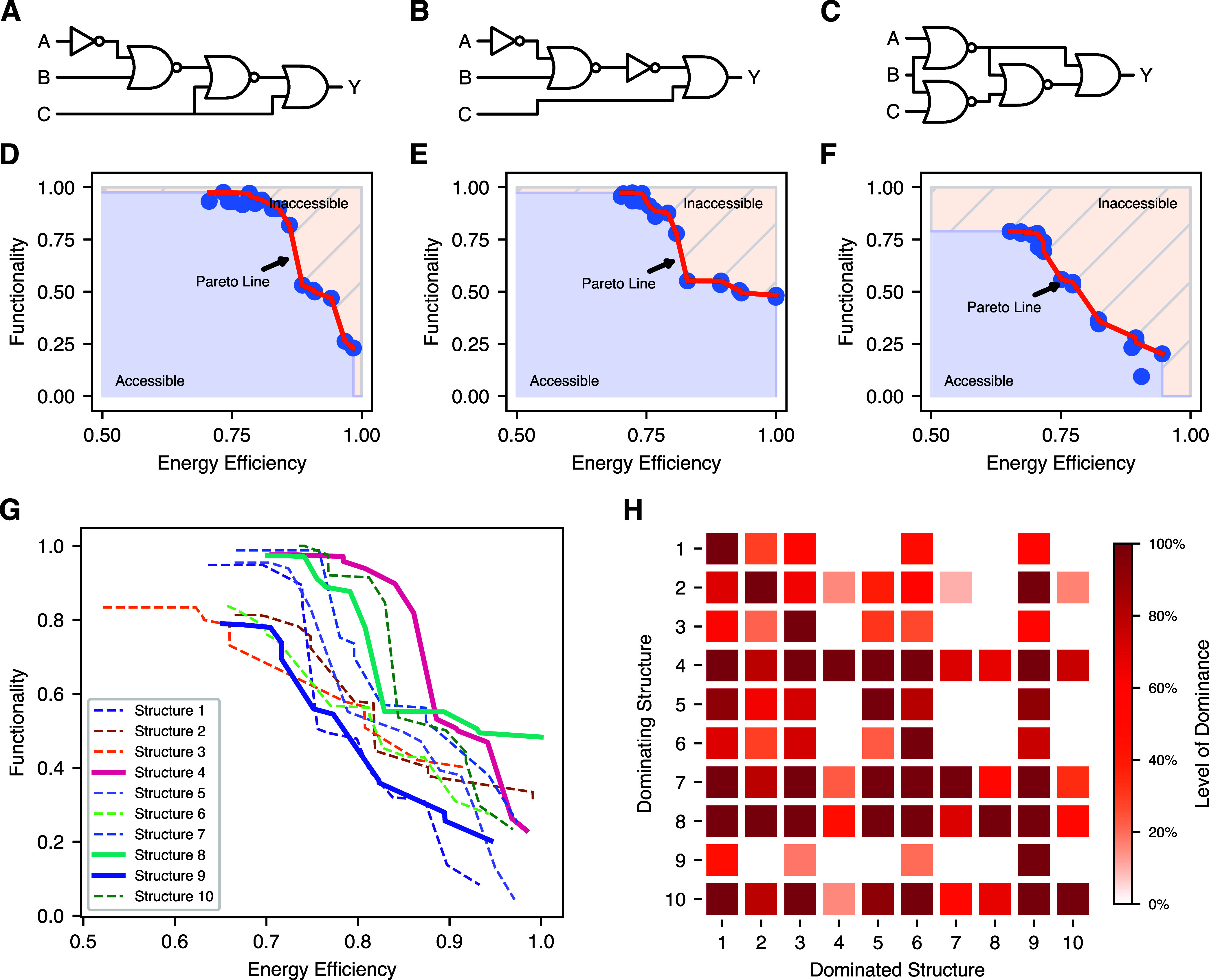
Pareto front of the boolean function 0xF7. (A–C) Three exemplary structures of the Boolean function 0xF7. In particular, structure 4 in (A), structure 8 in (B) and structure 9 in (C). (D–F) The Pareto fronts of the structures presented in (A–C), where (D) presents the one of structure 4, (E) the one of structure 8, and (F) corresponds to structure 9, respectively. Normalized with respect to the optimum in each dimension, the Pareto fronts (D–F) exhibit different characteristics with the discontinuities and nonmonotonicity resulting from discrete gate assignment and stochastic optimization. (D) Combines high functional performance with moderate energy requirements while (E) allows the highest energy efficiency still preserving a moderate functional performance. The Pareto front of structure 9 [see Figure (F)] exhibits a near linear relationship between functionality and energy efficiency, with an inferior overall performance. (G) We here illustrate the Pareto fronts of all the structures of 0xF7 jointly to emphasize comparability among them. Highlighting the Pareto fronts presented in (D–F) by bold lines, their relationship to one another gets obvious. In addition, one observes that the Pareto front of structure 9 is inferior to others for any configuration. Figure (H) visualizes this quantitatively by presenting the dominance among Pareto fronts. In detail, the rows indicate the structure corresponding to the Pareto front dominating the respective Pareto front denoted in the column. This comparison emphasizes the dominating behavior of structures 4, 8, and 10 over the others with respect to both optimization goals.
Continuing with the Pareto fronts of structures 8 and 9 as visualized in Figure 8E and F, we observe that the general relationship persists while the exact form changes. Specifically, the front in Figure (E) appears to be inferior to that in (D), as the circuits based on structure 4 in most cases have a higher functional performance than those of structure 8 when a fixed constraint is imposed. The reason for this is structure 4 requiring less energy to achieve high functional performance. However, when approaching the limits of energy efficiency, structure 8 (Figure 8E) is more robust in terms of the functional score achieved. Structure 9 (Figure 8F) has an almost linear transition region, but is inferior to both of the previous with respect to any optimization objective as well as the joint optimization.
Inspired by the inferior performance of structure 9 along the whole Pareto front, we compare the Pareto fronts of all structural variants of Boolean function 0xF7 in Figure 8G. The Pareto fronts are even more diverse than the ones already considered (highlighted by bold lines). Structures 4 and 8 dominate almost all trade-offs of energy efficiency and functionality. In contrast, seven out of ten structures do not allow the optimization to reach the best solution for any considered trade-off. Figure 8H visualizes this quantitatively by presenting the level of dominance between the structures. We refer to the level of dominance as the portion of configurations in which a structure outperforms another in terms of efficiency and functionality. Most prominent are the four rows featuring a large number of dark squares. These are the rows of structures 4, 7, 8, and 10, which dominate the Pareto fronts of the inferior structures either completely or almost completely.
Constrained optimization allows the exploration of the Pareto front of genetic logic circuits in terms of energy efficiency and functionality on the basis of multiple optimizations. However, if a desired trade-off is defined in advance, multiobjective optimization is an alternative that allows circuits to be designed with respect to both objectives in a single joint optimization.58 Dealing with the two objectives functionality and energy efficiency as represented by the quantities S and E̅, one approach to realize multiobjective optimization is scalarization. In the case of scalarization, the objective functions are aggregated into a single objective, to which one can apply conventional optimization methods as the simulated annealing presented by Schladt et al.30.
Due to the well behaving shape of the
Pareto fronts examined, we
here suggest a linear scalarization, which is also known as the weighting
method.58,59 For its efficient application ahead of identifying
the whole Pareto front, the scores need to be normalized.58 To this end, we introduce Sr and 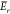 as reference maxima of the respective scores,
which one obtains by an initial evaluation. In dependence to the weight
parameter ϕ ∈ [0, 1], we express the scalarized performance
of the genetic logic circuit (γ, q) by V(γ, q), which we define as
as reference maxima of the respective scores,
which one obtains by an initial evaluation. In dependence to the weight
parameter ϕ ∈ [0, 1], we express the scalarized performance
of the genetic logic circuit (γ, q) by V(γ, q), which we define as
By the choice of the parameter ϕ, one implements the trade-off between the two objectives energy efficiency and functionality.
3. Conclusion and Outlook
In this work, we present an energy aware gene expression model characterizing the non-equilibrium steady state (NESS) in terms of the first and second order moments and the associated energy requirements, which we relate to the model’s entropy production rate. This model can account for promoter architectures varying in the number of binding sites, activation steps, and cognate transcription factors. In contrast to the widely employed equilibrium models, the presented model captures non-equilibrium characteristics like increased sensitivity and sharpness, which are especially relevant in the context of eukaryotes. This includes the dissipation of energy, which is essential to life. In combination with the probabilistic NESS description and the presented relation between energy and entropy production rate, this allows for further evaluation of the trade-off between function and energy, beyond the scope of genetic logic circuits.
With this model at hand, we establish Energy Aware Technology Mapping, the design of genetic logic circuits with respect to function and energy efficiency. The in silico evaluation based on 33 Boolean circuits improves energy efficiency by 37.2% on average, but reduces the functionality to 28.5% compared to the functionally optimized variants. These improvements result from decreases in expression levels representing Boolean ON states, simultaneously decreasing the circuit’s functional performance. With respect to structural variants, we show that different structures of a single Boolean function vary in their energetic characteristic and can be beneficial for energy efficiency (up to 22.7% on average) and functionality. This also extends to the case of multiobjective optimization, as shown in the Pareto evaluation.
Based on the findings in this study, one can further improve the design of genetic logic circuits with respect to energy by creating energy aware genetic gate libraries. This can include protein based gates focusing on robust functioning despite lower expression levels, the use of shorter transcription factors as signaling molecules, gates omitting translation by employing RNA based signals or any combination thereof. Due to its parameterized design, it is possible to adapt our approach directly to these cases.
To validate the theoretical framework of our proposed Energy Aware Technology Mapping for genetic logic circuits, we outline potential experimental evaluations. The simplest method to evaluate energy efficiency involves observing cell growth and viability by measuring optical density at 600 nm (OD600) and cell count.60 An alternative is the direct measurement of metabolites related to the energetic state of the cell in vivo, for which ATP sensors could be employed.61,62 A more complex, yet powerful, method is RNA sequencing (RNA-seq). Sequencing the transcriptome of cells harboring synthetic circuits would not only reveal the transcripts associated with the circuits but also allows to check for upregulation and downregulation of genes linked to overall cell fitness.63 As our approach addresses the increased metabolic burden that larger circuits impose, incorporating energy expenditure while maintaining circuit functionality could enable the development of larger circuits that operate effectively in vivo.
In conclusion, our results provide strong evidence for a tug of war between functionality and energy efficiency in the context of genetic logic circuits. This matches previous results on the relation between energy expenditure and precision and sharpness. Additionally, the consideration of structural variants proves relevant also in the case of energy efficiency. Since it is beneficial to consider structural variants regardless of the optimization goal, disregarding them is likely to lead to suboptimal solutions in terms of both, energy efficiency and functionality. Given the proportionality between energy consumption and the rate of heterologous protein expression, optimization of energy can effectively reduce the expression of heterologous proteins, thereby allowing for energy efficiency by design. This is particularly relevant in the context of metabolic burden, as it allows cellular fitness to be maintained by reducing the amount of resources diverted from the host by synthetic constructs. In that sense, the well being of the host organism ensures the desired functionality of the genetic logic circuit. The energetic advantage of one to two gates provided by Energy Aware Technology Mapping can be crucial for implementing the circuit in vivo in a resource constrained host organism.
4. Methods
We here present the methods most relevant to our work. This is complemented by the Supporting Information.
4.1. Gene Circuit Simulation
The input to the gene circuit are the concentrations of the inducer molecules. While in vivo the inducer binds to constitutively expressed repressive transcription factors, we realize the dependency on the inducer levels by a lookup table based approach, matching a degenerate promoter model with the desired promoter activity to the provided inducer concentration. For the simulation of the gene circuit, we apply our energy aware gene expression model one after another to the genes within the circuit. Thereby, one has to preserve topological order, meaning that a gene can only be evaluated when all genes expressing the cognate transcription factor have already been evaluated. To obtain the concentration of the protein encoded by a gene, we apply a log–normal closure to the moments provided by eqs 3 and 4 and draw a sample. In case multiple genes express the same protein, the protein’s final concentration is the superposition of the single genes’ contributions. By performing this approach many times in parallel, one obtains an empirical distribution predicting the population dynamics of cells implementing the particular genetic logic circuit. While this is a sampling based approach, one can instead propagate the mean or the median as the protein abundance to yield a point estimate. For a more formal treatment of probabilistic genetic logic circuit simulation, we refer the interested reader to the work of Schladt et al.30.
4.2. Steady State Distribution of CTMCs and Kirchhoff’s Theorem
The unique steady state distribution of an ergodic CTMC with n states can be derived by using its propensity matrix Λ, defined in row sum zero form. The first step is to identify the null-space, respectively solving for the left eigenvector v = [v1,...,vn] corresponding to the eigenvalue 0 of Λ.
The steady state distribution π is then defined as
Schnakenberg53 and later Andrieux and Gaspard64 describe an alternative approach, called Kirchhoff’s theorem, which was originally described by G. Kirchhoff and is based on the enumeration of spanning trees. The subsequent contains a rather informal description, wherefore we refer the interested reader to refs (53) and (64).
Before we start with the method itself, let us first recall the definition of a spanning tree. A spanning tree of an undirected graph is a tree and a subgraph containing all the vertices of the graph. We derive the undirected graph by identifying the vertices of the graph with the states in the state space of our CTMC. Next, the forward and backward reactions between two states are aggregated into a single undirected edge, connecting the vertices associated with the states.
We continue with enumerating all possible spanning trees of the graph. In total, there are nt trees and we refer to the jth with Tj. Next, we introduce the function Πi(Tj), which maps the spanning tree Tj to the subgraph of the CTMC’s state space that includes the reactions being part of the spanning tree and directed to state zi. In particular, this is done by setting zi as the root node and successively traversing the edges in the spanning tree Tj. Each edge corresponds to two reactions, where the one pointing in the direction of the root node is preserved and the other is dropped. The result is a directed tree, consisting of the reactions that lead from any initial state to the root state zi. With the previous, we assign the value
to each state zi, where the product runs over the propensities of the reactions in Πi(Tj). As before the steady state distribution is given by
While in theory this method is not limited by the size of the CTMC’s state space, the practical applicability depends on the complexity of the obtained graph’s topology.53 However, this approach provides an appealing way to derive the steady state distribution analytically. As such, our implementation makes use of the steady state distribution derived from Kirchhoff’s theorem for the promoter architectures considered, while it also provides the simpler eigenvector approach for other architectures.
4.3. Parameter Estimation
The estimation of a parameter set matching the characteristics of the part to capture is essential for the expressiveness of the model within a technology mapping application. As our model captures mean and variance of the response characteristic, data sources giving rise to both are ideal. One possible source is cytometry data obtained for different inducer concentrations. As the histograms provide rich information on the distribution, the mean and variance can be derived by evaluating
where (b1,...,bM) are the bin centers and (ω1,...,ωM) are the frequencies in a histogram with M bins.
As model instantiation, we use a promoter architecture featuring three binding sites for a single cognate transcription factor and having only two activation steps with respect to transcriptional activity as depicted in Figure 2AB. Since we collapse states with equal number of transcription factors bound into a single state, we obtain a CTMC of eight states and 20 reactions transitioning between these states. In addition, we constrain all the states corresponding to the same transcriptional activation level to have the same promoter activity ai. Since the reaction rate constants for RNA and protein dynamics are fixed in dependence to the organism (see Supporting Information Section S7), our model instantiation features 22 parameters. 20 for the reaction rate constants of the promoter CTMC and two for the two levels of promoter activity. From an intuitive perspective, the rate constants between two states of differing promoter activity levels balance the output dynamic maximally achievable. The reactions depending on the transcription factor abundance and their reverse reactions then determine the location of the transition. In foregoing evaluations, the chosen instantiation features well balance between the complexity of the model and the capabilities of modeling response characteristics of interest, especially the sharpness encountered. However, the variance in the data is not completely explained by this, likely caused by extrinsic noise49−51 not accounted for in this model.
For parameter estimation, we apply gradient based optimization and minimize the logarithmic difference between the prediction of the model and the reference data from Chen et al.40. We constrain the reaction rate constants to the range [10–5, 105], penalize non monotonic response characteristics, and by weighting the error we prioritize model quality in the saturated regions. In this context, it is important to note that the parameter estimation considers mean and variance. The mean dynamics itself are insufficient to uniquely identify a set of reaction rate constants as outlined at the end of Supporting Information Section S2.2. Please refer to Supporting Information Section S5.2 for a detailed description of the parameter estimation process.
4.4. ARCTIC
ARCTIC18,30 is the technology mapping framework for genetic logic circuits used in this work. It takes a combinational Boolean specification as input and constructs all possible structural variants for this specification based on a given library of gates. It then uses different scoring methods to optimize the assignment of library gates to the elements of the topologies. In this way, it can search for the best performing genetic circuit for a given Boolean specification.
ARCTIC offers different circuit models and scores that focus on robust genetic circuits. It implements different optimization methods to leverage these models and to explore the design space. In this work, the Simulated Annealing heuristic has been used. It applies a neighborhood structure leveraging functional proximity of gates and is flexible in terms of the used design objective.30
We employed deterministic and sampling based simulations. The evaluation on the benchmark set as well as the structural variants made use of the deterministic approach taking the average into account. The constraint optimization used a Cello-score11 or E-score30 of 200 as lower bound on the functionality, which corresponds to a 200 fold change of the median values. This bound is sufficient for circuit functionality and, in combination with a sampling based approach and the E-score, still allows for robust circuit designs. During optimization for circuit function, the upper bound on the energy expenditure was set in dependence to the circuits size, allowing for 20,000kBT s–1 per gate. In the Pareto evaluation, we employ the sampling based approach with the E-score and consider 1000 samples for each output distribution.
4.4.1. E-Score
The E-score30 is a generalization
of Cello’s circuit score11 to the
case where circuit outputs are random variables. This takes stochastic
effects in populations of cellular hosts into account. Intuitively,
the more “distance” lies between distributions that
represent ON states and those that represent OFF states, the higher
a circuit is scored. The E-score is calculated as
the exponential of a modified 1-Wasserstein distance between empirical
distributions of the logarithms of the concentrations or copy-numbers
of the output chemical species. Consider first two sets of N samples 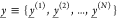 and
and 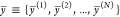 that represent two empirical circuit output
distributions. The set y̲ consists of those
samples corresponding to an anticipated circuit output of Boolean
OFF and y̅ consists of those samples corresponding
to an anticipated circuit output of Boolean ON. We then calculate
the modified 1-Wasserstein distance
that represent two empirical circuit output
distributions. The set y̲ consists of those
samples corresponding to an anticipated circuit output of Boolean
OFF and y̅ consists of those samples corresponding
to an anticipated circuit output of Boolean ON. We then calculate
the modified 1-Wasserstein distance 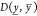 on the samples’ logarithms by
on the samples’ logarithms by
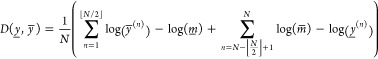 |
where m̲ and m̅ are the medians of y̲ and y̅ respectively. Consider now having several sample
sets 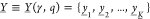 representing logical OFF states and
representing logical OFF states and 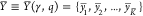 logical ON states, where each individual
sample set corresponds to one of
logical ON states, where each individual
sample set corresponds to one of 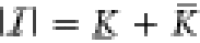 different Boolean input conditions of a
circuit with structure γ and assignment q.
The circuit’s E-score is then obtained by
different Boolean input conditions of a
circuit with structure γ and assignment q.
The circuit’s E-score is then obtained by
| 17 |
It is shown in ref (30) that S(γ,q) simplifies to Cello’s circuit score for γ and q if N = 1 and the single samples correspond to Cello’s approximations for the median. Note that the exponentiation in eq 17 can be applied after taking the minimum to obtain the score S.
Acknowledgments
The authors acknowledge all people in the Self-Organizing Systems and Computer Systems labs for the valuable discussions. We especially thank the anonymous reviewers for their valuable comments and suggestions, and Eike Mentzendorff for advice on multiobjective optimization. For the use of SBOLCanvas, we acknowledge Terry et al.,65 Quinn et al.,32 and the SBOL community.31 Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. E.K. was supported by ERC-PoC grant PLATE (101082333). J.M. was supported by the MSCA-DN SYNSENSO (GA 101072980). N.E. acknowledges funding by the German Research Foundation (DFG) as part of the project B4 within the Collaborative Research Center (CRC) 1053-MAKI. H.G.G. was supported by NIH R01 Awards R01GM139913 and 1R01GM152815, by the Koret-UC Berkeley-Tel Aviv University Initiative in Computational Biology and Bioinformatics, and by a Winkler Scholar Faculty Award. H.G.G. is also a Chan Zuckerberg Biohub Investigator (Biohub – San Francisco).
Data Availability Statement
The model is implemented as part of the technology mapping framework ARCTIC, which is available at https://www.rs.tu-darmstadt.de/ARCTIC.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssynbio.4c00395.
Derivations of moment equations, the CRN of the model presented, background on chemical reaction networks, further methods and extended figures and tables (PDF)
Author Contributions
H.K., C.H., and H.G. provided the research idea and contributed methodology. E.K. derived the model, implemented the model and the Energy Aware Technology Mapping in ARCTIC, and designed and did evaluation of Energy Aware Technology Mapping. M.G. and E.K. performed mathematical analysis of stochastic thermodynamics. T.S. provided the interface for ARCTIC and executed evaluation. J.M. and M.M. contributed to the biological background. N.E. contributed to ARCTIC and the E-score. All authors contributed to the writing of the paper.
The authors declare no competing financial interest.
Special Issue
Published as part of ACS Synthetic Biology special issue “IWBDA 2023”.
Supplementary Material
References
- Zoller B.; Gregor T.; Tkačik G. Eukaryotic gene regulation at equilibrium, or non?. Curr. Opin. Syst. Biol. 2022, 31, 100435. 10.1016/j.coisb.2022.100435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberts B.; Johnson A.; Lewis J.; Raff M.; Roberts K.; Walter P.. Molecular Biology of the Cell, 6th ed.; Garland Science: New York, NY, 2017. [Google Scholar]
- Ahsendorf T.; Wong F.; Eils R.; Gunawardena J. A framework for modelling gene regulation which accommodates non-equilibrium mechanisms. BMC Biol. 2014, 12, 102–123. 10.1186/s12915-014-0102-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broach J. R. Nutritional Control of Growth and Development in Yeast. Genetics 2012, 192, 73–105. 10.1534/genetics.111.135731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastberg L. L. B.; Ard R.; Jensen M. K.; Workman C. T. Burden Imposed by Heterologous Protein Production in Two Major Industrial Yeast Cell Factories: Identifying Sources and Mitigation Strategies. Front. Fungal Biol. 2022, 3, 827704. 10.3389/ffunb.2022.827704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G.; Yan Q.; Jones J. A.; Tang Y. J.; Fong S. S.; Koffas M. A. Metabolic Burden: Cornerstones in Synthetic Biology and Metabolic Engineering Applications. Trends Biotechnol. 2016, 34, 652–664. 10.1016/j.tibtech.2016.02.010. [DOI] [PubMed] [Google Scholar]
- Nikolados E.-M.; Weiße A. Y.; Ceroni F.; Oyarzún D. A. Growth Defects and Loss-of-Function in Synthetic Gene Circuits. ACS Synth. Biol. 2019, 8, 1231–1240. 10.1021/acssynbio.8b00531. [DOI] [PubMed] [Google Scholar]
- Ceroni F.; Algar R.; Stan G.-B.; Ellis T. Quantifying cellular capacity identifies gene expression designs with reduced burden. Nat. Methods 2015, 12, 415–418. 10.1038/nmeth.3339. [DOI] [PubMed] [Google Scholar]
- Weiße A. Y.; Oyarzún D. A.; Danos V.; Swain P. S. Mechanistic links between cellular trade-offs, gene expression, and growth. Proc. Natl. Acad. Sci. U.S.A. 2015, 112, E1038–E1047. 10.1073/pnas.1416533112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radde N.; Mortensen G. A.; Bhat D.; Shah S.; Clements J. J.; Leonard S. P.; McGuffie M. J.; Mishler D. M.; Barrick J. E. Measuring the Burden of Hundreds of BioBricks Defines an Evolutionary Limit on Constructability in Synthetic Biology. Nat. Commun. 2024, 15, 6242. 10.1038/s41467-024-50639-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen A. A. K.; Der B. S.; Shin J.; Vaidyanathan P.; Paralanov V.; Strychalski E. A.; Ross D.; Densmore D.; Voigt C. A. Genetic circuit design automation. Science 2016, 352, aac7341. 10.1126/science.aac7341. [DOI] [PubMed] [Google Scholar]
- Lammers N. C.; Flamholz A. I.; Garcia H. G. Competing constraints shape the nonequilibrium limits of cellular decision-making. Proc. Natl. Acad. Sci. U.S.A. 2023, 120, e2211203120 10.1073/pnas.2211203120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barato A. C.; Seifert U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 114, 158101. 10.1103/physrevlett.114.158101. [DOI] [PubMed] [Google Scholar]
- Seifert U. Stochastic thermodynamics: From principles to the cost of precision. Phys. A 2018, 504, 176–191. 10.1016/j.physa.2017.10.024. [DOI] [Google Scholar]
- Bintu L.; Buchler N. E.; Garcia H. G.; Gerland U.; Hwa T.; Kondev J.; Phillips R. Transcriptional regulation by the numbers: models. Curr. Opin. Genet. Dev. 2005, 15, 116–124. 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bintu L.; Buchler N. E.; Garcia H. G.; Gerland U.; Hwa T.; Kondev J.; Kuhlman T.; Phillips R. Transcriptional regulation by the numbers: applications. Curr. Opin. Genet. Dev. 2005, 15, 125–135. 10.1016/j.gde.2005.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison M.; Razo-Mejia M.; Phillips R. Reconciling kinetic and thermodynamic models of bacterial transcription. PLoS Comput. Biol. 2021, 17, e1008572 10.1371/journal.pcbi.1008572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelmann N.; Schwarz T.; Kubaczka E.; Hochberger C.; Koeppl H. Context-Aware Technology Mapping in Genetic Design Automation. ACS Synth. Biol. 2023, 12, 446–459. 10.1021/acssynbio.2c00361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estrada J.; Wong F.; DePace A.; Gunawardena J. Information Integration and Energy Expenditure in Gene Regulation. Cell 2016, 166, 234–244. 10.1016/j.cell.2016.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eck E.; Liu J.; Kazemzadeh-Atoufi M.; Ghoreishi S.; Blythe S. A.; Garcia H. G. Quantitative dissection of transcription in development yields evidence for transcription-factor-driven chromatin accessibility. Elife 2020, 9, e56429 10.7554/elife.56429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grah R.; Zoller B.; Tkačik G. Nonequilibrium models of optimal enhancer function. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 31614–31622. 10.1073/pnas.2006731117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zong Y.; Zhang H. M.; Lyu C.; Ji X.; Hou J.; Guo X.; Ouyang Q.; Lou C. Insulated Transcriptional Elements Enable Precise Design of Genetic Circuits. Nat. Commun. 2017, 8, 52. 10.1038/s41467-017-00063-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galbusera L.Non Equilibrium Dynamics in Escherichia Coli’s Gene Regulatory Network. Doctoral Thesis; University of Basel, 2020. [Google Scholar]
- Hopfield J. J. Kinetic Proofreading: A New Mechanism for Reducing Errors in Biosynthetic Processes Requiring High Specificity. Proc. Natl. Acad. Sci. U.S.A. 1974, 71, 4135–4139. 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J.; Estrada J.; Johnson G.; Vincent B. J.; Ricci-Tam C.; Bragdon M. D. J.; Shulgina Y.; Cha A.; Wunderlich Z.; Gunawardena J.; DePace A. H. Dissecting the sharp response of a canonical developmental enhancer reveals multiple sources of cooperativity. eLife 2019, 8, 41266. 10.7554/eLife.41266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meeussen J. V.; Lenstra T. L. Time will tell: comparing timescales to gain insight into transcriptional bursting. Trends Genet. 2024, 40, 160–174. 10.1016/j.tig.2023.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomp W.; Meeussen J. V.; Lenstra T. L. Transcription factor exchange enables prolonged transcriptional bursts. Mol. Cell 2024, 84, 1036–1048.e9. 10.1016/j.molcel.2024.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolas D.; Phillips N. E.; Naef F. What shapes eukaryotic transcriptional bursting?. Mol. BioSyst. 2017, 13, 1280–1290. 10.1039/c7mb00154a. [DOI] [PubMed] [Google Scholar]
- Lammers N. C.; Kim Y. J.; Zhao J.; Garcia H. G. A matter of time: Using dynamics and theory to uncover mechanisms of transcriptional bursting. Curr. Opin. Cell Biol. 2020, 67, 147–157. 10.1016/j.ceb.2020.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding I.; Paulsson J.; Zawilski S. M.; Cox E. C. Real-Time Kinetics of Gene Activity in Individual Bacteria. Cell 2005, 123, 1025–1036. 10.1016/j.cell.2005.09.031. [DOI] [PubMed] [Google Scholar]
- Schladt T.; Engelmann N.; Kubaczka E.; Hochberger C.; Koeppl H. Automated Design of Robust Genetic Circuits: Structural Variants and Parameter Uncertainty. ACS Synth. Biol. 2021, 10, 3316–3329. 10.1021/acssynbio.1c00193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galdzicki M.; Clancy K. P.; Oberortner E.; Pocock M.; Quinn J. Y.; Rodriguez C. A.; Roehner N.; Wilson M. L.; Adam L.; Anderson J. C.; Bartley B. A.; et al. The Synthetic Biology Open Language (SBOL) provides a community standard for communicating designs in synthetic biology. Nat. Biotechnol. 2014, 32, 545–550. 10.1038/nbt.2891. [DOI] [PubMed] [Google Scholar]
- Quinn J. Y.; Cox R. S.; Adler A.; Beal J.; Bhatia S.; Cai Y.; Chen J.; Clancy K.; Galdzicki M.; Hillson N. J.; Le Novère N.; et al. SBOL Visual: A Graphical Language for Genetic Designs. PLoS Biol. 2015, 13, e1002310 10.1371/journal.pbio.1002310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linshiz G.; Stawski N.; Poust S.; Bi C.; Keasling J. D.; Hillson N. J. PaR-PaR Laboratory Automation Platform. ACS Synth. Biol. 2013, 2, 216–222. 10.1021/sb300075t. [DOI] [PubMed] [Google Scholar]
- Salis H. M.The Ribosome Binding Site Calculator; Elsevier, 2011; Vol. 498, pp 19–42. [DOI] [PubMed] [Google Scholar]
- LaFleur T. L.; Hossain A.; Salis H. M. Automated model-predictive design of synthetic promoters to control transcriptional profiles in bacteria. Nat. Commun. 2022, 13, 5159. 10.1038/s41467-022-32829-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers C. J.; Barker N.; Jones K.; Kuwahara H.; Madsen C.; Nguyen N.-P. D. iBioSim: a tool for the analysis and design of genetic circuits. Bioinformatics 2009, 25, 2848–2849. 10.1093/bioinformatics/btp457. [DOI] [PubMed] [Google Scholar]
- Buecherl L.; Myers C. J. Engineering genetic circuits: advancements in genetic design automation tools and standards for synthetic biology. Current Opinion in Microbiology 2022, 68, 102155. 10.1016/j.mib.2022.102155. [DOI] [PubMed] [Google Scholar]
- Ceroni F.; Boo A.; Furini S.; Gorochowski T. E.; Borkowski O.; Ladak Y. N.; Awan A. R.; Gilbert C.; Stan G.-B.; Ellis T. Burden-driven feedback control of gene expression. Nat. Methods 2018, 15, 387–393. 10.1038/nmeth.4635. [DOI] [PubMed] [Google Scholar]
- McBride C. D.; Grunberg T. W.; Del Vecchio D. Design of genetic circuits that are robust to resource competition. Curr. Opin. Syst. Biol. 2021, 28, 100357. 10.1016/j.coisb.2021.100357. [DOI] [Google Scholar]
- Sechkar K.; Steel H.; Perrino G.; Stan G.-B. A coarse-grained bacterial cell model for resource-aware analysis and design of synthetic gene circuits. Nat. Commun. 2024, 15, 1981. 10.1038/s41467-024-46410-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y.; Zhang S.; Young E. M.; Jones T. S.; Densmore D.; Voigt C. A. Genetic circuit design automation for yeast. Nat. Microbiol. 2020, 5, 1349–1360. 10.1038/s41564-020-0757-2. [DOI] [PubMed] [Google Scholar]
- Jones T. S.; Oliveira S. M. D.; Myers C. J.; Voigt C. A.; Densmore D. Genetic circuit design automation with Cello 2.0. Nat. Protoc. 2022, 17, 1097–1113. 10.1038/s41596-021-00675-2. [DOI] [PubMed] [Google Scholar]
- Otero-Muras I.; Banga R. Automated Design Framework for Synthetic Biology Exploiting Pareto Optimality. ACS Synth. Biol. 2017, 6, 1180–1193. 10.1021/acssynbio.6b00306. [DOI] [PubMed] [Google Scholar]
- Watanabe L.; Nguyen T.; Zhang M.; Zundel Z.; Zhang Z.; Madsen C.; Roehner N.; Myers C. iBioSim 3: A Tool for Model-Based Genetic Circuit Design. ACS Synth. Biol. 2018, 8, 1560–1563. 10.1021/acssynbio.8b00078. [DOI] [PubMed] [Google Scholar]
- Schmiedl T.; Seifert U. Stochastic thermodynamics of chemical reaction networks. J. Chem. Phys. 2007, 126, 044101. 10.1063/1.2428297. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Zhou T. Promoter-mediated Transcriptional Dynamics. Biophys. J. 2014, 106, 479–488. 10.1016/j.bpj.2013.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leppek K.; Das R.; Barna M. Functional 5′ UTR mRNA structures in eukaryotic translation regulation and how to find them. Nat. Rev. Mol. Cell Biol. 2018, 19, 158–174. 10.1038/nrm.2017.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian H., Ge H.. Stochastic Chemical Reaction Systems in Biology; Springer International Publishing, 2021. [Google Scholar]
- Hasenauer J.; Wolf V.; Kazeroonian A.; Theis F. J. Method of conditional moments (MCM) for the Chemical Master Equation. J. Math. Biol. 2014, 69, 687–735. 10.1007/s00285-013-0711-5. [DOI] [PubMed] [Google Scholar]
- Zechner C.; Ruess J.; Krenn P.; Pelet S.; Peter M.; Lygeros J.; Koeppl H. Moment-based inference predicts bimodality in transient gene expression. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 8340–8345. 10.1073/pnas.1200161109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zechner C.; Unger M.; Pelet S.; Peter M.; Koeppl H. Scalable inference of heterogeneous reaction kinetics from pooled single-cell recordings. Nat. Methods 2014, 11, 197–202. 10.1038/nmeth.2794. [DOI] [PubMed] [Google Scholar]
- Albayrak C.; Jordi C. A.; Zechner C.; Lin J.; Bichsel C. A.; Khammash M.; Tay S. Digital Quantification of Proteins and mRNA in Single Mammalian Cells. Mol. Cell 2016, 61, 914–924. 10.1016/j.molcel.2016.02.030. [DOI] [PubMed] [Google Scholar]
- Rao R.; Esposito M. Conservation laws and work fluctuation relations in chemical reaction networks. J. Chem. Phys. 2018, 149, 245101. 10.1063/1.5042253. [DOI] [PubMed] [Google Scholar]
- Schnakenberg J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys. 1976, 48, 571–585. 10.1103/revmodphys.48.571. [DOI] [Google Scholar]
- Lebowitz J. L.; Spohn H. A Gallavotti–Cohen-Type Symmetry in the Large Deviation Functional for Stochastic Dynamics. J. Stat. Phys. 1999, 95, 333–365. 10.1023/a:1004589714161. [DOI] [Google Scholar]
- Glick B. R. Metabolic load and heterologous gene expression. Biotechnol. Adv. 1995, 13, 247–261. 10.1016/0734-9750(95)00004-a. [DOI] [PubMed] [Google Scholar]
- Wagner A. Energy Constraints on the Evolution of Gene Expression. Mol. Biol. Evol. 2005, 22, 1365–1374. 10.1093/molbev/msi126. [DOI] [PubMed] [Google Scholar]
- Lynch M.; Marinov G. K. The Bioenergetic Costs of a Gene. Proc. Natl. Acad. Sci. U.S.A. 2015, 112, 15690–15695. 10.1073/pnas.1514974112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miettinen K.Nonlinear Multiobjective Optimization. Springer Science & Business Media, 1999; Vol. 12. [Google Scholar]
- Gass S.; Saaty T. The computational algorithm for the parametric objective function. Nav. Res. Logist. Q. 1955, 2, 39–45. 10.1002/nav.3800020106. [DOI] [Google Scholar]
- Klumpp S.; Zhang Z.; Hwa T. Growth-rate dependent global effects on gene expression in bacteria. Cell 2009, 139, 1366–1375. 10.1016/j.cell.2009.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng Y.; Beahm D. R.; Ionov S.; Sarpeshkar R. Measuring and modeling energy and power consumption in living microbial cells with a synthetic ATP reporter. BMC Biol. 2021, 19, 101. 10.1186/s12915-021-01023-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botman D.; Van Heerden J. H.; Teusink B. An Improved ATP FRET Sensor For Yeast Shows Heterogeneity During Nutrient Transitions. ACS Sens. 2020, 5, 814–822. 10.1021/acssensors.9b02475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorochowski T. E.; Espah Borujeni A.; Park Y.; Nielsen A. A.; Zhang J.; Der B. S.; Gordon D. B.; Voigt C. A. Genetic circuit characterization and debugging using RNA-seq. Mol. Syst. Biol. 2017, 13, 952. 10.15252/msb.20167461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrieux D.; Gaspard P. Fluctuation Theorem for Currents and Schnakenberg Network Theory. J. Stat. Phys. 2007, 127, 107–131. 10.1007/s10955-006-9233-5. [DOI] [Google Scholar]
- Terry L.; Earl J.; Thayer S.; Bridge S.; Myers C. J. SBOLCanvas: A Visual Editor for Genetic Designs. ACS Synth. Biol. 2021, 10, 1792–1796. 10.1021/acssynbio.1c00096. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The model is implemented as part of the technology mapping framework ARCTIC, which is available at https://www.rs.tu-darmstadt.de/ARCTIC.