Abstract
Chiral active materials display odd dynamical effects in both their elastic and viscous responses. We show that the most symmetric mesophase with 2D odd elasticity in three dimensions is chiral, polar, and columnar, with 2D translational order in the plane perpendicular to the columns and no elastic restoring force for their relative sliding. We derive its hydrodynamic equations from those of a chiral active variant of model H. The most striking prediction of the odd dynamics is two distinct types of column oscillation whose frequencies do not vanish at zero wavenumber. In addition, activity leads to a buckling instability coming from the generic force-dipole active stress analogous to the mechanical Helfrich–Hurault instability in passive materials, while the chiral torque-dipole active stress fundamentally modifies the instability by the selection of helical column undulations.
Keywords: chiral liquid crystal, active matter, columnar liquid crystals
Significance Statement.
We establish minimal ingredients for the emergence of odd elasticity and odd viscosity—certain asymmetries in the relation of stress to strain and strain-rate—in a 3D fluid. The resulting structure is that of a columnar liquid crystal with polar and chiral active stresses. Predicted outcomes include oscillatory dynamics without mechanical inertia, with viscous hydrodynamics leading to a frequency that remains nonzero in the limit of infinite wavelength, in marked contrast to 2D odd elasticity. These oscillations should be seen in vitro in biofilament-motor complexes and are likely to arise in living columnar structures such as axons and muscle.
Introduction
Living matter continually converts chemical energy into work. A description of mechanics and statistics of such microscopically driven materials must either explicitly account for this chemistry (1, 2) or introduce a parameter that breaks time-reversal symmetry at the microscopic level (3–8). This latter description, termed active matter, has been used to describe the novel dynamics, mechanics, and statistics of a plethora of broken-symmetry phases (9–16). In chiral (17, 18) 2D solids, an active mechanical effect that is the subject of much current attention is “odd elasticity” (13, 15, 19), a generalized relation between stress and strain, breaking a fundamental symmetry or reciprocity that holds in thermal equilibrium. This phenomenon was recently highlighted in a setting related to developmental biology (20) though anticipated in part in early studies on rotating Rayleigh–Bénard convection (21, 22). A key feature is the existence of elastic oscillations in a regime in which mechanical inertia is manifestly negligible. This odd dynamics results from a ratio of elastic and viscous coefficients and, in fact, can arise in two distinct ways: as a ratio of odd elasticity to even viscosity or of even elasticity to odd viscosity. In this article, we show how odd coefficients emerge naturally through spontaneous translation symmetry-breaking in an active system, in concert with two discrete asymmetries: chirality, i.e. the impossibility of superimposing individual units or structures on their mirror images (18), and polarity, a vector orientation or lack of inversion symmetry. We will do this in the spirit of the classical treatments (23–26) that yield the elastic properties of a solid as a density wave in a fluid. This requires augmenting model H (27) to include active processes (28, 29), chirality (12), and polar symmetry breaking. The 3D odd viscosity—a contribution to the tensor connecting stress and strain rate antisymmetric under an exchange of the first and second pair of indices (30, 31)—that then naturally arises also plays an important role in our treatment.
The long-range effects of active stresses emerge through fluid flow, whereas odd elasticity is a property of solids in two or more dimensions. Odd dynamics also arises in 3D chiral active mesophases with spatially modulated order (12, 21), where the elasticity of the spatial modulation couples to Stokesian hydrodynamics along any fluid directions. We present a study of the most symmetric system—a polar and chiral active columnar phase (32–35) with 2D translational order and one fluid direction—possessing odd elasticity in three dimensions. Our article is the first exploration of columnar materials in active systems, despite the abundance of filamentous assemblies in soft matter and biology (36–39). Not only is chirality the rule in biological matter, the monomeric units of most biopolymers are noncentrosymmetric. In particular, the microtubule bundles comprising the axon in nerve cell are a realization of active, columnar, chiral, macroscopically polar matter (40, 41). Columnar packings of DNA (37, 42, 43), if rendered active by transcription, are another candidate.
Our main result is the prediction of elastic oscillations in chiral and polar active columnar phases in an inertialess regime. Despite columnar materials breaking 3D rotation symmetry and 2D translation symmetry, the slow dynamics of the structure is governed by the elastic displacement of the columns. This comes from a combination of elastic forces and Stokesian friction coming from the conserved momentum density. In all systems with translational order, the low Reynolds number dynamics of the displacement field reads .a For modes with wavenumber q, the mobility scales as , due to the long-range nature of the Stokes flow while the elastic force density scales as , yielding a characteristic relaxation rate independent of the magnitude of the wavevector for most directions. However, in equilibrium lamellar or columnar systems, there is no elastic response for material deformations with wavevector in liquid directions. In analogy with the lamellar case (10, 12, 16, 44), activity creates a column tension, and hence a nonvanishing response, even for purely along the columns. In contrast to the lamellar case, active columnar materials display an emergent nonreciprocal dynamics of , a consequence of the odd elastic and viscous response of chiral polar systems. Each embodies nonreciprocity individually, through and , respectively; the effective nonreciprocal dynamics, in the form of oscillatory modes due to the two components of the displacement field behaving like a position–momentum pair, emerges by combining the nonreciprocal part of one with the reciprocal part of the other. The two ways of doing this— and —have physically distinct dynamical signatures. Not only the “even–even” but also the “odd–odd” combinations contribute to the reciprocal response. Importantly, because of the long-range nature of the Stokesian dynamics, the oscillation frequency of this mode does not vanish in the limit of zero wavenumber. The frequency and the very existence of this odd collective oscillation, however, does depend on the angle between and the column axis. Indeed, the 3D character of the columnar material is essential: incompressibility forbids this mode for in-plane perturbations.
Our additional predictions include a fundamental buckling instability driven by an apolar (force dipole) active stress in common with the lamellar case (12); in sharp contrast, the effect of chiral (torque dipole) active stresses is to remodel the structure. We now present in detail the theory from which these results follow.
A polarizable chiral active suspension
We consider a bulk, 3D, two-component system with 3D scalar number density ψ of active polar and chiral units and momentum density , as functions of position and time t, with overall incompressibility: a constant total mass density ρ and for the joint velocity field . The degree of vectorial alignment of the particles is accounted for by the polar order parameter field . ψ obeys the conserving dynamics:
| (1) |
where F is the free energy that would control the dynamics in the absence of activity; we discuss its form after constructing the dynamical equations for the velocity and the polarization fields.
We consider systems in which the Reynolds number is small at the scales of interest, as is the case for typical microbial and soft matter systems. In this limit, the velocity field is governed by the Stokes equation, with viscous forces balancing active and passive forces in the suspension:
| (2) |
where is the viscosity tensor whose general form we will discuss in later sections, Π is the pressure that enforces the incompressibility constraint , and is the active stress. We ignore additional passive force densities involving and (45) whose effects in the polar columnar phase are subdominant to the active terms that we consider.
The expression of active stress in terms of ψ and has three parts, all leading to terms at the same order in gradients in the polar columnar phase:
| (3) |
where the superscript S denotes symmetrization on the free indices, and is the Levi–Civita tensor. The first term is familiar from active model H (12, 28, 29, 46). The second is the standard active stress for liquid crystals (5, 47–49). The third, with coefficient , requires both chirality and polarity and is fundamentally biaxial. A force density with the symmetry of has not hitherto been examined in active systems. Because it is chiral, changes sign, i.e. , when the handedness of the particles composing the system is changed. In a system that is not homochiral, its value would depend on local chiral density. Similar comments apply to all chiral terms to be discussed in this article.
The polarization equation, ignoring advection by hydrodynamic flow and motility, is (45):
| (4) |
where and are respectively the antisymmetric and symmetric parts of the velocity gradient tensor with components .
To complete the description of the polarizable and chiral active fluid, we need to specify the free energy F. To do this, we first separate (50) ψ into the small-wavenumber part of the active-particle concentration, and which is modulated on average in the columnar phase. The former plays no role in the hydrodynamics of column displacements and will not be discussed further. We then work with a free energy where and
| (5) |
This concludes our construction of the model of a fluid containing chiral and polar active elements. We use this dynamical description in the next sections to obtain a theory of polar, chiral, active columnar materials in which odd elasticity emerges spontaneously.
Breaking polar and translation symmetry: generation of odd elastic force density
While the active fluid described above contains motile units, it cannot form a polar nematic phase (51). This is because a uniaxial orientational order is necessarily unstable in bulk Stokesian active fluids (5, 47, 52). Instead, when and α are both negative, the fluid spontaneously breaks both translation and rotation symmetries to form a polar and chiral columnar phase, at least in the absence of activity. The steady-state value of is and that of is:
| (6) |
where are the vectors of the reciprocal lattice formed by the columnar phase in the plane transverse to . In the analysis below, we take the fundamental star of a triangular structure with the scale favored by the free energy and . Importantly, polar order evades instability (5, 47) here only because it is accompanied by translational order. Ignoring singularities such as dislocations (11), we now ascertain the effect of activity on the dynamics of the equilibrium columnar state.b Considering broken-symmetry fluctuations about the state , writing the phase of as and , the free energy becomes:
| (7) |
where are functions of and . The nonlinear elastic strain tensor has components , with ranging over ; we retain only its linearized form in this article. We will assume, as in equilibrium systems, that relaxes to in a microscopic time. This assumption holds in the system under consideration provided (14, 47).
Expanding ψ and in terms of in (2) and (3), we obtain the displacement field-dependent part of the force density whose linearized form is (Supplementary material):
| (8) |
where is the 2D Levi–Civita tensor and we have defined the modified Lamé coefficients and , which are renormalized by the active terms in (3) with the ζs being functions of , , , , and . The active force density has a piece (Fig. 1B) analogous to column tension, that would have been forbidden in equilibrium materials due to a combination of rotation invariance and time-reversal symmetry. This is akin to the activity-induced emergence of a layer tension in lamellar materials (10, 16, 44) or an effective elasticity modulus in active nematic elastomers (14) or a line tension or surface tension in polymers (53) or membranes (54, 55) in active fluids. The chiral force density emerging from the term in (3)—exactly the odd elasticity discussed in 2D active solids (13, 15)—arises naturally in this 3D system through polarity and the spontaneous breaking of translation symmetry, (see Fig. 1A). The nondimensional ratio of odd and even shear moduli was measured in a 2D active solid composed of starfish embryos (20) to be . We expect the bulk and shear moduli, and to have similar magnitude; in epithelial monolayers, these are of the order of (56). ζ is related to the standard active stress which is estimated to be between 5–1,000 Pa for cytoskeletal gels (57, 58) and can be higher for epithelial systems.
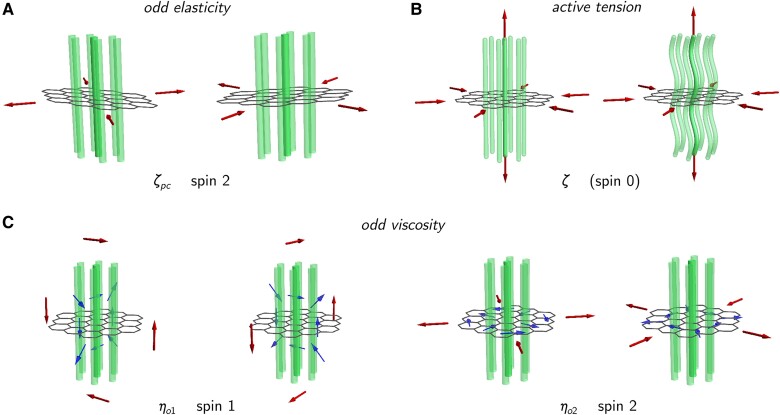
Fig. 1.
Schematic illustration of stresses (indicated by red arrows) in an active columnar phase; columns are shown as green tubes and the hexagonal arrangement by a centre-plane mesh. A) There is a single odd elastic modulus in polar chiral materials () coupling deviatoric elastic strains to in-plane deviatoric stresses, with a twist between polarizations; these stresses and strains carry spin 2. The elastic strains are visualized by the deformation to the regular hexagonal lattice. B) The regular dipolar activity (ζ) contributes an active tension and precipitates a Helfrich–Hurault-like undulational instability that is isotropic (spin 0) with respect to the elastic, in-plane directions. C) There are two odd viscous coefficients ( and ) associated to twisted couplings between deviatoric shear flows in the spin 1 and spin 2 irreps and corresponding stresses. The structure of the fluid velocity in these couplings is indicated by blue arrows.
While the primary effect of achiral active force densities in the columnar materials is analogous to those in active lamellar phases—in the sense that they both endow the system with rigidities that would vanish in equilibrium—the effect of chirality in these two systems is truly distinct. In particular, the 2D odd elastic force density has no analog in lamellar materials.
Odd viscosity and odd elasticity
We now discuss the general form of the viscosity in a polar chiral columnar material, including its odd contributions. For a uniaxial system with at least sixfold symmetry perpendicular to the preferred axis, the deviatoric part of the velocity gradient tensor is decomposed into irreducible representations (irreps) as ; the 1D irrep has spin 0, while the 2D irreps have spin 1 and spin 2, respectively. The viscosity tensor maps these irreps of the velocity gradients to a corresponding decomposition of the stress. The normal viscous response is an identity between corresponding irreps, implying three coefficients of viscosityc in the even viscous stress: .
Rotations within the two 2D irreps yields “odd” linear mechanical responses. Of course, a rotation requires uniquely defining a vector perpendicular to a given displacement or velocity . In three dimensions, this requires chirality in the form of the Levi–Civita tensor , a preferred axis, say the normal to the xy plane, and a polarity along that axis, hence a unique . We can then unambiguously write . Applying this construction to the linear relation between stress and velocity gradient for any 3D chiral system with a polarity along yieldsd (Supplementary material):
| (9) |
where are the odd viscosities (59) of the spin 1 and spin 2 irreps, respectively, and we have set , as these anisotropic contributions to the even viscous response do not qualitatively modify the linearized dynamics of the state of interest. We show a schematic of the two odd viscosities in Fig. 1C. The nondimensional ratios and are expected to increase with activity and chirality. The ratio reaches as high as in 2D chiral colloidal fluids on substrates (60, 61), which is very different from the material we consider. We see no reason why it cannot be substantially higher in 3D systems. Though we call viscosities, they are not dissipative coefficients in the momentum equation: they break Onsager symmetry and have no relation to noises. Unlike the stress that ultimately resulted in 2D odd elasticity, the odd viscous stress we describe is allowed in any chiral material with broken time-reversal and polar anisotropy. Equation (9) implies the odd viscous force density:
| (10) |
where the contribution appears in 2D, chiral active fluids (19, 30, 31) where it can be absorbed into a redefinition of the pressure in an incompressible system. In contrast, the 3D incompressibility constraint for our system permits to affect bulk flows and column oscillations. The odd viscous force density , with no analog in 2D fluids, has an important consequence for the mode structure we discuss in the next section.
We now rationalize the odd elasticity constructed in section Breaking polar and translation symmetry: generation of odd elastic force density in a manner analogous to the foregoing treatment of odd viscosities. In a columnar material, the component of strain is absorbed by the polarization fluctuations (33) and incurs a cost only at next order in gradients in the form of column-bending elasticity. Leading-order elasticity survives only for the orthogonal strains which under the local symmetry decompose as . The antisymmetric part represents a rigid rotation and does not generate a stress; there are therefore three moduli, two even, a bulk and shear modulus, and one odd. We show a schematic of the odd elasticity in Fig. 1A. However, our approach that naturally yields odd elasticity as a consequence of translation symmetry breaking in active model H establishes it as a new generalized rigidity arising in active, chiral materials.
Less formally, there are two odd viscosities and one odd elastic modulus because the velocity field is 3D whereas the displacement field in a columnar phase has only two components. In phases with a three-component displacement field, there would be two odd elastic moduli.
Putting everything together: wavenumber-independent odd oscillations in liquid crystals
The linearized Stokes equation containing both the odd elastic force density discussed in Sec. 2 and the odd viscous force density discussed in Sec. 3 is
| (11) |
where Π is the pressure enforcing the 3D incompressibility constraint . To leading order in gradients, the dynamics of the displacement field reads . Fourier transforming and solving for the velocity field yields a dynamical equation for the displacement field in the form (Supplementary material), where arises from and from the viscous force densities with an odd part due to .
For much of the rest of the article, we will assume that the magnitudes and signs of these active terms lie in the range in which the columnar phase is linearly stable. Instabilities, when they arise, can do so through both even–even and odd–odd combinations of mobility and force density; a comment about the even–even case is in order here. The achiral active force density in an incompressible columnar system is exactly the same as that of an external stress, uniaxial along the columns or, equivalently, isotropic in the plane normal to them even considering the full nonlinear dynamics. This is analogous to active smectics (12). This implies that as in cholesterics and smectics (12), leads to a spontaneous Helfrich–Hurault instability (62) with, however, a degeneracy in the polarization of the 2D column-undulation field. In a finite system of lateral size L, this instability happens beyond a critical active stress (Supplementary material). As in lamellar phases (12), the nonlinear mapping implies that beyond this instability an active achiral columnar material assumes the same state as an equilibrium columnar subject to an external stress.
We now turn to an examination of the effect of odd elasticity and viscosity on the dynamics of active, polar, and chiral columnar phases when they are linearly stable. We begin with odd elasticity alone, setting . The resulting response of the columnar material to a perturbation with wavevector has the form . Defining its components and along and transverse to we find that , couples the and dynamics at zeroth order in wavenumber (Supplementary material):
| (12) |
| (13) |
This Poisson-bracket-like coupling is truly 3D, vanishing for or .e As discussed in the Introduction section, (12) and (13) lead to an oscillatory response for large-enough , vanishing only for perturbations purely in the plane or purely along . Figure 2A shows a representative time series of the column distortions associated to this odd oscillation; the dynamics is right-handed for positive . The general expression for the eigenfrequency displayed in Supplementary material is complicated, but its essential features can be seen in its form for ,
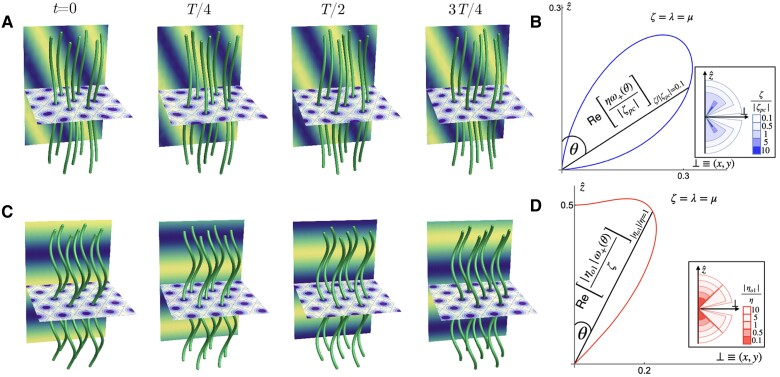
Fig. 2.
Odd dynamical oscillations in active polar chiral columnar phases. A) Odd elastic plane wave solution of (12) and (13) due to ; here, and . The horizontal plane shows a density plot of ψ and the background plane indicates the phase and direction of the plane wave. Columns are shown as green tubes and images are given for every quarter of an oscillation period (T). B) Polar plot of —the oscillation frequency, nondimensionalized by the active timescale —of the odd elastic oscillations due to the combination of even mobility and odd force density for . corresponds to a perturbation purely along the (polarity) direction while corresponds to a perturbation purely along the in-plane, crystalline directions. Inset: Colour-coded sectors (with different radii to ensure visibility) showing the range of θ—the angle between the wavevector of perturbation and —that elicits an oscillatory response for various values of . This demonstrates that the angular range increases with decreasing . While the angular range for extends almost to , there is no oscillatory response for a perturbation with wavevector along . Instead, at small θ. C) Odd oscillations from the interplay of odd mobility and even force density, : plane wave solution of (15) and (16) with wavevector purely along the column axis direction. Here, . D) Polar plot of —the oscillation frequency, nondimensionalized by the timescale —of odd oscillations due to the combination of odd mobility and even force density for . Here, . Inset: Colour-coded sectors (with different radii to ensure visibility) showing the range of θ—the angle between the wavevector of perturbation and —that elicits an oscillatory response for various values of . Note that the oscillation vanishes for because the mobility due to vanishes at this value in incompressible materials as can be seen from the expression of below (16).
| (14) |
Equation (14) describes an oscillatory mode when . For a general angle between and , the response is oscillatory when . This implies that when is larger than the other active and elastic terms, a perturbation with a wavevector almost fully along also leads to an oscillatory response with at small θ. We display the angular ranges in which we predict an oscillatory response in Fig. 2B for various values of .
It is instructive to compare with the dispersive wave induced by nonreciprocity in 2D compressible solids on frictional substrates (15), where odd elasticity leads to the dynamics and . In active polar and chiral columnar phases, the presence of momentum conservation and 3D incompressibility leads to a radically different mode structure. Momentum conservation induces a long-range interaction, replacing the dispersive wave with an oscillatory mode whose frequency is nonvanishing but nonanalytic for . In the presence of a momentum sink, the damping in the momentum equation would ultimately imply a dispersive wave at small wavenumbers. Indeed, if the columnar material is confined in a geometry which has a finite extent ℓ in the z direction, with porous walls such that the fluid can flow out of the system, then one can replace with to obtain the displacement dynamics in Ref. (15) quoted above. Note that the 3D character of the active liquid crystal remains crucial, as the mode involves a z-variation of the z-component of the velocity field at the scale of the system.
If instead the confinement is on a scale ℓ in the ⊥ plane, the odd elastic coupling for takes the form and . The possibility of active nondispersive waves à la (54, 55) is, however, ruled out by the effective damping rates and of and , respectively. The resulting eigenfrequencies and have no real part.
We now turn to the dynamics with nonzero odd viscosities and examine their effect on the displacement dynamics focusing on the character of the oscillatory response due to the combination of and . The equations of motion for and are (Supplementary material):
| (15) |
| (16) |
with and . We highlight a few important features of (16) and (15). As discussed in the Introduction section, odd–odd and even–even couplings of mobility and force density lead to dissipative terms, and odd–even or even–odd to reactive couplings between and , as is generically the case in chiral active systems (13).
Importantly, while the odd force vanishes for perturbations purely along the z-direction, the apolar and achiral active force density does not. Of the two odd contributions to the mobility, one vanishes for perturbations purely along , but the other does not. In fact, for a perturbation with the coupled dynamics (15) and (16) has eigenfrequencies implying an oscillatory response even for perturbations purely along , Fig. 2C. That is, unlike in Fig. 2B, the eigenfrequency no longer vanishes in the limit. We emphasize that this is purely due to odd viscosity of 3D polar, chiral materials—and its interplay with achiral active line tension—and not odd elasticity. Significantly, a perturbation with wavevector purely in the xy-plane still does not elicit an oscillatory response since, due to incompressibility, vanishes at this order in wavenumber. In Fig. 2D, we show a polar plot for the eigenfrequency of oscillations for arbitrary and display the angular range that elicits an oscillatory response for different values of in the inset. This oscillation is left-handed for positive .
The handedness of the oscillation for a general wavevector depends on both odd viscosities, and , and on the direction of the mode, through the combination . This changes sign for wavevectors making an angle , when such a θ exists.
Thus, odd viscosity and odd elasticity both lead to oscillatory responses—with distinct characteristics—with wavenumber-independent frequencies thanks to the long-ranged character of Stokesian hydrodynamics. The ratio of viscosity to elasticity is a timescale, which oddness converts from the relaxation or growth time of a perturbation to the time-period of an oscillation.
Achiral, apolar, or both
We now examine the response of higher-symmetry columnar material to perturbations, starting with systems which are neither polar nor chiral, ruling out terms that break symmetry or contain an odd number of Levi–Civita tensors. In this limit in (3), in (8) and odd viscosities vanish, and
| (17) |
| (18) |
are linearly decoupled. Activity, entering solely through ζ, still ensures that the static structure factor of displacement fluctuations, calculated by augmenting (17) and (18) with appropriate white, Gaussian noises (Supplementary material), scales as (for ) along all spatial directions (thereby cutting off the viscosity divergences that arise (35) in the equilibrium columnar phasef).
We now discuss an apolar but chiral material. All the chiral effects discussed till this point also require breaking inversion symmetry. However, chiral but apolar fluids have extra active stresses which were not included in (3) because they are subdominant to the stress in polar materials. In a gradient expansion, the leading-order active chiral stress in apolar materials is , introduced in Ref. (12). The resulting force density (Supplementary material) couples and fluctuations,
| (19) |
| (20) |
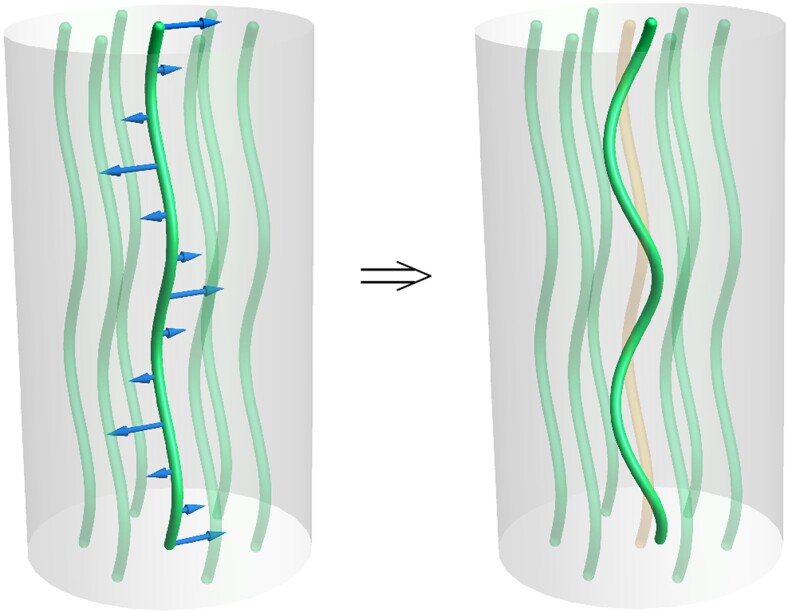
albeit at higher gradient order than elasticity, yielding, for wavevectors purely along , mode frequencies . That is, chiral activity reduces the relaxation rate of one of the modes while enhancing that of the other. Another example of such a macroscopic manifestation of chirality in an active hydrodynamic instability is the preferential direction of self-shearing in epithelia (63). For the favored mode is a left-handed helical distortion, Fig. 3. Interestingly, unlike odd elasticity in 2D chiral solids (15) and polar columnar materials discussed above, here resembles a dissipative (though of course potentially destabilizing) Onsager coupling between and . Note that this coupling originates from the same stress in active model H* that led to an odd elastic force density in active layered materials directed primarily along contours of constant mean curvature of the layers (12). For the columnar phase, in contrast, these transverse chiral flows generate a deformation of the columns into helices even at linear order (see Fig. 3).
Fig. 3.
The chiral activity creates transverse flows (blue arrows) to a planar column undulation (green cylinders) and resulting a helical twisting of the columns. For clarity, this is shown only for the highlighted central column, whose initial planar undulation is displayed in orange. The helices are left-handed when is positive and give a macroscopic signature of the microscopic chiral activity.
Finally, activity fails to create a difference between apolar materials and achiral but polar columnar materials in the hydrodynamic limit. The lowest-order additional polar active force density is subleading in gradients, doesn’t couple and , and simply modifies in (17), (18).
Discussion
We have described the Stokesian hydrodynamics of active columnar phases, including both chiral and polar materials. The polar chiral activity realizes an oscillatory response of the columns with a frequency that scales with wavenumber q as and is a ratio of either odd elasticity to even viscosity, or even elasticity to odd viscosity. Estimates for biological tissues using measurements on MDCK epithelial monolayers (56) suggest a frequency in the Hz range, consistent with the timescale of odd dynamics in Ref. (20). Three-dimensionality and the viscous hydrodynamic interaction are essential to the mechanism. Active columnar phases offer an idealized representation of the odd mechanics of many living and synthetic active chiral materials. Axons and epithelia, for example, have a columnar structure and a natural polarity, so chiral activity in these tissues should generate odd dynamical effects. Columnar liquid crystals with macroscopic polarity (64), if suffused with chiral microswimmers, could realize a material in which to test our predictions. The odd dynamics of muscle tissue (65) should display distinctive contributions due to chirality.
The achiral active stress is analogous to an applied mechanical stress and produces a Helfrich–Hurault instability of the columns with degeneracy in the polarization of the undulations. In chiral active columnar materials, explicitly breaks parity, lifting the degeneracy and favoring one sign of helical column undulation. This highlights the emergence of qualitatively different effects from the same chiral stress in distinct broken-symmetry phases of active model H*.
An interesting extension of our results would be to determine the effects of confinement and boundary conditions on the column undulations and their associated odd mechanics. Similarly, it will be important to determine the effect of activity on the behavior of defects (66) in columnar phases as biological tissues and filament assemblies are often highly disordered and more complex. However, the basic oscillatory dynamics we have described will still be present. Finally, our predictions are based largely on linear stability analysis. An understanding of the evolution beyond the linear regime and the final state of the system requires a direct numerical solution of the nonlinear equations of motion.
Supplementary Material
Acknowledgments
We thank Jacques Prost for valuable discussions. S.J.K., A.M., and S.R. would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programmes “New Statistical Physics in Living Matter: non-equilibrium states under Adaptive Control” and “Anti-diffusive dynamics: from sub-cellular to astrophysical scales” where a part of the work on this paper was undertaken. We also thank NORDITA (The Nordic Institute for Theoretical Physics), Sweden for support and hospitality during the programmes “Hydrodynamics at all scales” (A.M. and S.R.) and “Current and Future Themes in Soft & Biological Active Matter” (G.P.A. and S.R.) where a part of the work on this article was carried out. A.M., G.P.A., and S.R. thank ICTS-TIFR for support and hospitality during the programme “Active Matter and Beyond” during which a part of this work was undertaken. SR acknowledges a Rothschild Distinguished Visiting Fellowship awarded by Isaac Newton Institute.
Notes
The treatment applies generically to any such state, with our ignorance of the details of the base state buried in the phenomenological coefficients (67). Departures from the generic case would require special tuning of coefficients (14, 68, 69).
A uniaxial system has five viscosities of which the two bulk viscosities play no role in the incompressible limit.
Its equivalent is ruled out in an incompressible, 2D odd gel where, to , and the longitudinal velocity vanish. In the present work, however, incompressibility constrains the 3D velocity field and, therefore, at for a perturbation with nonzero z component.
Contributor Information
S J Kole, Centre for Condensed Matter Theory, Department of Physics, Indian Institute of Science, Bangalore, Karnataka 560 012, India; INI, University of Cambridge, Cambridge CB3 0EH, United Kingdom; DAMTP, Centre for Mathematical Sciences, University of Cambridge, Cambridge CB3 0EH, United Kingdom.
Gareth P Alexander, Department of Physics, University of Warwick, Coventry CV4 7AL, United Kingdom.
Ananyo Maitra, Laboratoire de Physique Théorique et Modélisation, CNRS UMR 8089, CY Cergy Paris Université, Cergy-Pontoise Cedex F-95032, France; Laboratoire Jean Perrin, Sorbonne Université and CNRS, Paris F-75005, France.
Sriram Ramaswamy, Centre for Condensed Matter Theory, Department of Physics, Indian Institute of Science, Bangalore, Karnataka 560 012, India; International Centre for Theoretical Sciences, Tata Institute of Fundamental Research, Bangalore, Karnataka 560 089, India.
Supplementary Material
Supplementary material is available at PNAS Nexus online.
Funding
S.J.K. acknowledges support through a Raman-Charpak Fellowship of CEFIPRA, hosted by Cesare Nardini, SPEC, CEA-Saclay. A.M. was supported in part by a TALENT fellowship awarded by CY Cergy Paris Université and an ANR grant, PSAM. S.R. was supported in part by a J C Bose Fellowship of the SERB, India and a Simons Visiting Professorship of ICTS. This work was supported by EPSRC grant no. EP/R014604/1.
Author Contributions
S.J.K., G.P.A., A.M., and S.R. conceived the project, performed the theoretical analyses, and wrote and reviewed the manuscript.
Preprints
A preprint of this article is published at arXiv: https://arxiv.org/abs/2404.19514.
Data Availability
This article does not contain any data.
References
- 1. Markovich T, Fodor É, Tjhung E, Cates ME. 2021. Thermodynamics of active field theories: energetic cost of coupling to reservoirs. Phys Rev X. 11(2):021057. [Google Scholar]
- 2. Weber CA, Zwicker D, Jülicher F, Lee CF. 2019. Physics of active emulsions. Rep Prog Phys. 82(6):064601. [DOI] [PubMed] [Google Scholar]
- 3. Dadhichi LP, Maitra A, Ramaswamy S. 2018. Origins and diagnostics of the nonequilibrium character of active systems. J Stat Mech: Theory Exp. 2018(12):123201. [Google Scholar]
- 4. Jülicher F, Grill SW, Salbreux G. 2018. Hydrodynamic theory of active matter. Rep Prog Phys. 81(7):076601. [DOI] [PubMed] [Google Scholar]
- 5. Marchetti MC, et al. 2013. Hydrodynamics of soft active matter. Rev Mod Phys. 85:1143–1189. [Google Scholar]
- 6. Prost J, Jülicher F, Joanny J-F. 2015. Active gel physics. Nat Phys. 11:111–117. [Google Scholar]
- 7. Ramaswamy S. 2010. The mechanics and statistics of active matter. Annu Rev Condens Matter Phys. 1(1):323–345. [Google Scholar]
- 8. Ramaswamy S. 2017. Active matter. J Stat Mech: Theory Exp. 2017(5):054002. [Google Scholar]
- 9. Adar RM, Joanny J-F. 2021. Permeation instabilities in active polar gels. Phys Rev Lett. 127:188001. [DOI] [PubMed] [Google Scholar]
- 10. Adhyapak TC, Ramaswamy S, Toner J. 2013. Live soap: stability, order, and fluctuations in apolar active smectics. Phys Rev Lett. 110:118102. [DOI] [PubMed] [Google Scholar]
- 11. Jülicher F, Prost J, Toner J. 2022. Broken living layers: dislocations in active smectic liquid crystals. Phys Rev E. 106(5):054607. [DOI] [PubMed] [Google Scholar]
- 12. Kole SJ, Alexander GP, Ramaswamy S, Maitra A. 2021. Layered chiral active matter: beyond odd elasticity. Phys Rev Lett. 126:248001. [DOI] [PubMed] [Google Scholar]
- 13. Maitra A, Lenz M, Voituriez R. 2020. Chiral active hexatics: giant number fluctuations, waves, and destruction of order. Phys Rev Lett. 125:238005. [DOI] [PubMed] [Google Scholar]
- 14. Maitra A, Ramaswamy S. 2019. Oriented active solids. Phys Rev Lett. 123:238001. [DOI] [PubMed] [Google Scholar]
- 15. Scheibner C, et al. 2020. Odd elasticity. Nat Phys. 16:475–480. [Google Scholar]
- 16. Whitfield CA, et al. 2017. Hydrodynamic instabilities in active cholesteric liquid crystals. Eur Phys J E. 40:50. [DOI] [PubMed] [Google Scholar]
- 17. Harris AB, Kamien RD, Lubensky TC. 1999. Molecular chirality and chiral parameters. Rev Mod Phys. 71:1745–1757. [Google Scholar]
- 18. Kelvin WTB. 1894. The molecular tactics of a crystal. Oxford: Clarendon Press. [Google Scholar]
- 19. Fruchart M, Scheibner C, Vitelli V. 2023. Odd viscosity and odd elasticity. Ann Rev Condens Matter Phys. 14:471–510. [Google Scholar]
- 20. Tan TH, et al. 2022. Odd dynamics of living chiral crystals. Nature. 607(7918):287–293. [DOI] [PubMed] [Google Scholar]
- 21. Echebarria B, Riecke H. 2000. Instabilities of hexagonal patterns with broken chiral symmetry. Phys D: Nonlinear Phenom. 139(1–2):97–108. [Google Scholar]
- 22. Echebarria B, Riecke H. 2000. Stability of oscillating hexagons in rotating convection. Phys D: Nonlinear Phenom. 143(1-4):187–204. [DOI] [PubMed] [Google Scholar]
- 23. Archer AJ. 2005. Density functional theory for the freezing of soft-core fluids. Phys Rev E. 72(5):051501. [DOI] [PubMed] [Google Scholar]
- 24. Ebner C, Krishnamurthy HR, Pandit R. 1991. Density-functional theory for classical fluids and solids. Phys Rev A. 43(8):4355. [DOI] [PubMed] [Google Scholar]
- 25. Emmerich H, et al. 2012. Phase-field-crystal models for condensed matter dynamics on atomic length and diffusive time scales: an overview. Adv Phys. 61(6):665–743. [Google Scholar]
- 26. Ramakrishnan TV, Yussouff M. 1979. First-principles order-parameter theory of freezing. Phys Rev B. 19(5):2775. [Google Scholar]
- 27. Hohenberg PC, Halperin BI. 1977. Theory of dynamic critical phenomena. Rev Mod Phys. 49:435–479. [Google Scholar]
- 28. Singh R, Cates ME. 2019. Hydrodynamically interrupted droplet growth in scalar active matter. Phys Rev Lett. 123:148005. [DOI] [PubMed] [Google Scholar]
- 29. Tiribocchi A, Wittkowski R, Marenduzzo D, Cates ME. 2015. Active model H: scalar active matter in a momentum-conserving fluid. Phys Rev Lett. 115:188302. [DOI] [PubMed] [Google Scholar]
- 30. Avron JE. 1998. Odd viscosity. J Stat Phys. 92:543–557. [Google Scholar]
- 31. Banerjee D, Souslov A, Abanov AG, Vitelli V. 2017. Odd viscosity in chiral active fluids. Nat Commun. 8(1):1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Chandrasekhar S, Sadashiva BK, Suresh KA. 1977. Liquid crystals of disc-like molecules. Pramana. 9:471–480. [Google Scholar]
- 33. de Gennes PG, Prost J. 1993. The physics of liquid crystals. Oxford: Clarendon. [Google Scholar]
- 34. Prost J, Clark NA. 1980. Hydrodynamic properties of two dimensionally ordered liquid crystals. In: Chandrasekhar S, editor. Proceedings of the international conference on liquid crystals, Bangalore, 1979. Philadelphia: Heyden. [Google Scholar]
- 35. Ramaswamy S, Toner J. 1983. Breakdown of conventional hydrodynamics in three-dimensional systems with long-ranged two-dimensional translational order. Phys Rev A. 28(5):3159. [Google Scholar]
- 36. Atkinson DW, Santangelo CD, Grason GM. 2021. Mechanics of metric frustration in contorted filament bundles: from local symmetry to columnar elasticity. Phys Rev Lett. 127(21):218002. [DOI] [PubMed] [Google Scholar]
- 37. Barberi L, Livolant F, Leforestier A, Lenz M. 2021. Local structure of DNA toroids reveals curvature-dependent intermolecular forces. Nucleic Acids Res. 49(7):3709–3718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Grason GM. 2015. Colloquium: geometry and optimal packing of twisted columns and filaments. Rev Mod Phys. 87(2):401. [Google Scholar]
- 39. Lübke J, Egger V, Sakmann B, Feldmeyer D. 2000. Columnar organization of dendrites and axons of single and synaptically coupled excitatory spiny neurons in layer 4 of the rat barrel cortex. J Neurosci. 20(14):5300–5311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Ahmadi A, Marchetti MC, Liverpool TB. 2006. Hydrodynamics of isotropic and liquid crystalline active polymer solutions. Phys Rev E. 74(6):061913. [DOI] [PubMed] [Google Scholar]
- 41. Rao AN, Baas PW. 2018. Polarity sorting of microtubules in the axon. Trends Neurosci. 41(2):77–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Leforestier A, et al. 2008. Expression of chirality in columnar hexagonal phases or DNA and nucleosomes. Comptes Rendus Chimie. 11(3):229–244. [Google Scholar]
- 43. Livolant F, Levelut AM, Doucet J, Benoit JP. 1989. The highly concentrated liquid-crystalline phase of DNA is columnar hexagonal. Nature. 339(6227):724–726. [DOI] [PubMed] [Google Scholar]
- 44. Chen L, Toner J. 2013. Universality for moving stripes: a hydrodynamic theory of polar active smectics. Phys Rev Lett. 111:088701. [DOI] [PubMed] [Google Scholar]
- 45. Stark H, Lubensky TC. 2005. Poisson bracket approach to the dynamics of nematic liquid crystals: the role of spin angular momentum. Phys Rev E. 72:051714. [DOI] [PubMed] [Google Scholar]
- 46. Finlayson BA, Scriven LE. 1969. Convective instability by active stress. Proc R Soc Lond A. 310:183–219. [Google Scholar]
- 47. Simha RA, Ramaswamy S. 2002. Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys Rev Lett. 89:058101. [DOI] [PubMed] [Google Scholar]
- 48. Hatwalne Y, Ramaswamy S, Rao M, Simha RA. 2004. Rheology of active-particle suspensions. Phys Rev Lett. 92(11):118101. [DOI] [PubMed] [Google Scholar]
- 49. Toner J, Tu Y, Ramaswamy S. 2005. Hydrodynamics and phases of flocks. Ann Phys (N Y). 318(1):170–244. [Google Scholar]
- 50. Heinonen V, et al. 2016. Consistent hydrodynamics for phase field crystals. Phys Rev Lett. 116(2):024303. [DOI] [PubMed] [Google Scholar]
- 51. Chen X, et al. 2020. First-principles experimental demonstration of ferroelectricity in a thermotropic nematic liquid crystal: polar domains and striking electro-optics. Proc Natl Acad Sci U S A. 117(25):14021–14031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Maitra A. 2023. Two-dimensional long-range uniaxial order in three-dimensional active fluids. Nat Phys. 19(5):733–740. [Google Scholar]
- 53. Kikuchi N, et al. 2009. Buckling, stiffening, and negative dissipation in the dynamics of a biopolymer in an active medium. Proc Natl Acad Sci U S A. 106(47):19776–19779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Maitra A, Srivastava P, Rao M, Ramaswamy S. 2014. Activating membranes. Phys Rev Lett. 112(25):258101. [DOI] [PubMed] [Google Scholar]
- 55. Ramaswamy S, Toner J, Prost J. 2000. Nonequilibrium fluctuations, traveling waves, and instabilities in active membranes. Phys Rev Lett. 84(15):3494. [DOI] [PubMed] [Google Scholar]
- 56. Harris AR, et al. 2012. Characterizing the mechanics of cultured cell monolayers. Proc Natl Acad Sci U S A. 109(41):16449–16454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Joanny J-F, Prost J. 2009. Active gels as a description of the actin-myosin cytoskeleton. HFSP J. 3(2):94–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Kumar A, Maitra A, Sumit M, Ramaswamy S, Shivashankar GV. 2014. Actomyosin contractility rotates the cell nucleus. Sci Rep. 4(1):3781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Khain T, Scheibner C, Fruchart M, Vitelli V. 2022. Stokes flows in three-dimensional fluids with odd and parity-violating viscosities. J Fluid Mech. 934:A23. [Google Scholar]
- 60. de Wit XM, Fruchart M, Khain T, Toschi F, Vitelli V. 2024. Pattern formation by turbulent cascades. Nature. 627(8004):515–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Soni V, et al. 2019. The odd free surface flows of a colloidal chiral fluid. Nat Phys. 15(11):1188–1194. [Google Scholar]
- 62. Blanc C, et al. 2023. Helfrich-Hurault elastic instabilities driven by geometrical frustration. Rev Mod Phys. 95(1):015004. [Google Scholar]
- 63. Duclos G, et al. 2018. Spontaneous shear flow in confined cellular nematics. Nat Phys. 14(7):728–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Guilleme J, et al. 2015. A columnar liquid crystal with permanent polar order. J Mater Chem C. 3(5):985–989. [Google Scholar]
- 65. Shankar S, Mahadevan L. 2024. Active hydraulics and odd elasticity of muscle fibres. Nat Phys. 20:1501–1508. [Google Scholar]
- 66. Prost J. 1990. Point defects and lock-in faults in columnar phases. Liq Cryst. 8(1):123–130. [Google Scholar]
- 67. Forster D. 2018. Hydrodynamic fluctuations, broken symmetry, and correlation functions. CRC Press. [Google Scholar]
- 68. Pomeau Y, Zaleski S, Manneville P. 1983. Dislocation motion in cellular structures. Phys Rev A. 27(5):2710. [Google Scholar]
- 69. Tesauro G, Cross MC. 1986. Climbing of dislocations in nonequilibrium patterns. Phys Rev A. 34(2):1363. [DOI] [PubMed] [Google Scholar]
- 70. Andreev AV, Son DT, Spivak B. 2010. Hydrodynamics of liquids of chiral molecules and suspensions containing chiral particles. Phys Rev Lett. 104(19):198301. [DOI] [PubMed] [Google Scholar]
- 71. Mazenko GF, Ramaswamy S, Toner J. 1983. Breakdown of conventional hydrodynamics for smectic-a, hexatic-b, and cholesteric liquid crystals. Phys Rev A. 28(3):1618. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This article does not contain any data.