Phase transitions of associative biomacromolecules

Abstract

Multivalent proteins and nucleic acids, collectively referred to as multivalent associative biomacromolecules, provide the driving forces for the formation and compositional regulation of biomolecular condensates. Here, we review the key concepts of phase transitions of aqueous solutions of associative biomacromolecules, specifically proteins that include folded domains and intrinsically disordered regions. The phase transitions of these systems come under the rubric of coupled associative and segregative transitions. The concepts underlying these processes are presented and their relevance to biomolecular condensates is discussed.

1.0. INTRODUCTION

There is growing recognition that cellular matter and physiologically relevant biochemical reactions are organized in space and time via the formation, regulation, and dissolution of mesoscale bodies known as biomolecular condensates ¹. These mesoscale membraneless assemblies, comprising hundreds of distinct macromolecules, are concentrated into small volumes, and delineated by internal and external interfaces ^{1, 2}. Here, mesoscale refers to the scale that straddles the molecular (nanometer) and cellular (micron) scales. Biomolecular condensates – or just condensates from now on – have distinct molecular compositions that are organized inhomogeneously ³, and into a range of stoichiometries ⁴. Measurements to date suggest that the material properties of condensates are akin to those of viscoelastic materials ⁵ with either terminally viscous or terminally elastic properties ⁶. Here, terminal refer to the long-time behaviors of condensates.

Importantly, the emerging consensus is that spontaneous phase transitions contribute either directly, or in concert with active processes, to the formation and dissolution of condensates ^{2, 7}. This has prompted a growing interest in the physical chemistry of phase transitions; specifically the topics of phase separation ⁸ and gelation ⁹. Key results, through the period of 2006-2012, helped catalyze the surge of interest in spontaneous and driven phase transitions in cell biology and biophysical chemistry. In this review, we describe the conceptual underpinnings that pertain to the equilibrium phase transitions of macromolecules that drive the formation and dissolution of condensates in cells ¹⁰, and of simple facsimiles of condensates in vitro ^{11, 12}.

1.1. Physical gelation of biomacromolecules

The importance of phase transitions such as physical gelation ¹³, generalized in the mathematical literature as bond percolation ¹⁴, was recognized by Görlich and coworkers in their efforts to reconstitute and describe the sieve-like selective permeability of nuclear pore complexes ¹⁵. For molecules that are capable of reversible associations, physical gelation is a continuous, reversible networking transition ¹⁶ driven by the physical, non-covalent crosslinking of specific motifs ¹⁷. Key nuclear pore proteins ¹⁸, specifically intrinsically disordered regions (IDRs) within these proteins, feature cohesive motifs known as stickers that enable gelation ^{15, 18, 19}. The relevant stickers are Phe-Gly motifs or Gly-Leu-Phe-Gly motifs. Accordingly, above protein-specific threshold concentrations, known as percolation thresholds, the IDRs in question form system-spanning networks known as physical gels, which are also known as hydrogels because more than 95% of their volume is water. In reconstituted systems, the hydrogels consist of macromolecules forming reversible physical (non-covalent) crosslinks with one another. Growing evidence points to the selectivity of partitioning into nuclear pore facsimiles being determined by the specific chemistries within the IDRs of nuclear pore proteins ²⁰.

Proteins and peptides can undergo sequence- and structure-specific physical gelation, providing they feature the requisite valence (number) of cohesive motifs or stickers that enable networking through reversible physical crosslinks. Thermoreversible gelation was demonstrated by Schneider and coworkers in the context of various peptide-based hydrogels ²¹. Likewise, several researchers in the biomaterials community have demonstrated that reversible hydrogels can form through the incorporation of multiple alpha helical elements ²² and other types of structures ²³. Reversible gelation driven by IDRs from RNA binding proteins was demonstrated by McKnight and colleagues ²⁴.

1.2. Seeking precision in defining physical gels

Physical gels are defined by physical crosslinks, whereas chemical gels are defined by chemical (covalent) crosslinks ¹⁶. Physical gels can be strong or weak, and this depends on the strengths of the physical crosslinks vis-à-vis thermal energy (k_BT) ¹⁶. From a formal standpoint a gel should never be automatically conflated with a solid ²⁵ or a glass ²⁶. Further, the process of physical gelation, which is a manifestation of bond percolation in the systems of interest for this review ²⁷, is not something that only happens when a material hardens or vitrifies. Of course, the ability of a material to form system-spanning networks of physical crosslinks creates the possibility of vitrification ²⁸. This would be true if the timescales of molecular transport are intrinsically faster than the timescales associated with the making and breaking of physical crosslinks. This scenario can also arise as a function of age of the material, leading to the phenomenon of aging^{26, 29}.

A clear case for not automatically conflating a physical gel with a hardened or vitrified state of matter comes from what we know about liquid water. In its liquid form, water forms a system-spanning network defined by networks of intermolecular hydrogen bonds, with each water molecule being able to physically crosslink with at least four other molecules on average ³⁰. And yet, except for aficionados of hydration phenomena, no one speaks of the gel-like structure of water. This error of omission is not a major concern, since in most cases the timescales for making and breaking hydrogen bonds are faster than the timescales for the self-diffusion of water.

To summarize, a physical gel is a percolated, system-spanning network defined by a network of physical crosslinks. The rheological properties of gels will be determined by the interplay between at least two competing timescales, viz., the timescales for molecular transport and the timescales associated with the making and breaking of physical crosslinks. Therefore, our use of the term gel, which adheres to Flory’s original usage ¹³ and refers to the system forming a percolated network, focuses purely on connectivity and makes no mention of density or composition.

1.3. Intrinsically disordered proteins and solvent quality

The relevance of the physics of associations among polymers in aqueous solvents and the interplay between chain-chain and chain-solvent interactions was further appreciated with the realization that many proteomes encompass conformationally heterogeneous regions that are intrinsically disordered ³¹. This realization highlighted the importance of solvent quality and the sequence-specific modulation of solvent quality for describing conformational and phase equilibria of intrinsically disordered proteins / regions (IDPs / IDRs) ³². A major surprise was the discovery that water is a poor solvent for homopolypeptides such as polyglutamine ³³ and polyglycine ³⁴. The latter is a perfect mimic of the polypeptide backbone without any sidechains ³⁵. The observations for polyglutamine were also found to be true of prion-like low complexity domains that are enriched in glutamine, asparagine, and glycine ³⁶. These findings indicated that IDRs bereft of both charged residues and canonical hydrophobic residues adopt conformations that minimize interactions with aqueous solvents ³⁷. Accordingly, such domains are prime candidates to study drivers of phase separation ^{37, 38}, which is a segregative phase transition. Strikingly, three synergistic studies namely those of Mao et al., ³⁹, Marsh and Forman-Kay⁴⁰, and Müller-Späth et al.,⁴¹ showed that charged sidechains can modulate the intrinsic preferences of polypeptide backbones, thus contributing to conformational expansion and increased solubility of IDRs with requisite sequence features. These findings collectively demonstrated that the composition-specific balance of chain-solvent, solvent-solvent, and chain-chain interactions can generate distinct flavors of IDRs in terms of their conformational equilibria ^{42, 43}.

1.4. The importance of phase separation in live cells

In cells, interest in specific segregative transitions such as liquid-liquid phase separation ⁴⁴ grew out of work by Brangwynne, Hyman and coworkers ⁴⁵. They showed that the formation of ribonucleoprotein bodies known as P granules in the germline of C. elegans could be explained using the physics of phase separation. Specifically, P granules were shown to form and dissolve as protein and RNA concentrations rose above or fell below distinct thresholds. Further, the P granules were relatively round, flowed in response to external forces, and fused with one another as a function of time. These observations were used to propose that P granules behave like viscous Newtonian fluids wherein the stresses arising from flow are directly proportional to the flow velocity. Recent measurements, in live cells, have provided convincing evidence for the thermodynamics of phase separation being directly relevant for how specific P granule proteins set up facsimiles of these bodies ¹⁰.

1.5. Phase separation and physical gelation

In 2012, Rosen and coworkers demonstrated the importance of the coupling between physical gelation i.e., percolation and phase separation for describing assemblies formed by multivalent proteins comprising folded domains connected by disordered linkers ⁴⁶. The physical properties of disordered linkers that connect folded domains contribute to controlling the extent of coupling between percolation and phase separation ⁴⁷. Linkers between stickers – intrinsically foldable domains in the cases they studied ⁴⁸ – encode a preference for being well solvated or agnostic about solvation. While well-solvated linkers act to suppress phase separation and weaken percolation, the linkers that are agnostic with respect to solvation status enhance percolation by coupling this process to phase separation ⁴⁷.

1.6. Multivalent associative macromolecules and their phase transitions

Macromolecular solutions are mixtures of different types of macromolecules dissolved in a complex solvent ⁴⁹. The overall free energy of the macromolecular solution can be parsed as a sum of two terms viz., (i) the free energy of mixing ^{50, 51} and (ii) the free energies of reversible associations among macromolecules ⁵². Phase separation is defined by segregation of macromolecules from an incompatible solvent or from other incompatible macromolecules ^{50, 51}. Therefore, we refer to phase separation as a segregative transition that gives rise to two or more compositionally distinct phases that coexist with one another.

Macromolecules can undergo reversible associations mediated by physical, non-covalent interactions among specific types of cohesive motifs. These motifs enable intra- and intermolecular hydrogen bonds, a hierarchy of electrostatic interactions, and interactions among aromatic and / or hydrophobic groups ⁵³. Above a system-specific threshold concentration, known as the percolation threshold, multivalent associative macromolecules can form system-spanning networks ^{13, 52–54}. This process is a continuous, purely geometric transition known as percolation ¹⁴. On its own, percolation does not give rise to distinct coexisting phases, but instead it generates a single, highly connected network known as a gel ⁵⁵. In fact, even simple hard sphere fluids can undergo a percolation transition, depending on the density of the fluid. Here, the system-spanning network is formed by two types of species viz., the hard spheres and the voids that are created by the packing of hard spheres ⁵⁶. We refer to percolation, which is a purely geometric transition, as an associative or networking transition because the associating species are included into a system spanning network.

The cellular milieu comprises different types of macromolecules in a complex solvent. In such systems, associative and segregative transitions will be coupled to one another. Accordingly, a solution of multivalent associative macromolecules can undergo coupled associative and segregative phase transitions. We abbreviate these coupled transitions as COAST. Phase separation is a segregative transition because it leads to the segregation of the system into two or more separate, albeit coexisting phases. Phase transitions that are associative are continuous transitions and they do not create distinct coexisting segregated phases. Instead, they are defined either by purely geometric or topological considerations. They can also be driven by conformational changes or self-assembly, which we will lumped under the general category of symmetry breaking ⁵⁷. For systems of multivalent associative macromolecules, the relevant associative transitions are percolation or symmetry breaking causing by collective and continuous changes, with concentration, to extent of physical crosslinking ⁵⁸. These can be further coupled to continuous symmetry breaking operations such as conformational changes or changes to oligomerization states.

At this juncture, it is worth emphasizing that the distinction between segregative and associative phase transitions that we introduce here is adapted from theories of associative macromolecules ⁵²– the topic of this review. It is different from a recent definition introduced by Minton ⁵⁹. Their focus was on phase separation as the only form of phase transition. In the Minton picture, phase separation driven by attractive interactions versus repulsive interactions are distinguished as being associative versus segregative, respectively. This, as we will discuss at length, is a simplifying definition that becomes imprecise because it excludes any considerations of solvent-mediated effects and reduces interactions among macromolecules as being effectively attractive or repulsive. Such simplifications are only possible if the interactions are reduced to a single energy scale that is captured by a Flory χ parameter ⁵⁰ or the equivalent second virial coefficient ¹⁶. In complex mixtures such as ternary or n-nary mixture of macromolecules in a solvent, we must consider the interplay between solvent-mediated homotypic and heterotypic interactions between macromolecules, and the mutual (in)compatibility of macromolecules with the solvent and with one another. As noted by Tanaka ⁶⁰, the effective two-body interactions, viz., χ which capture the two types of free energies that prevail in macromolecular solutions, can be parsed into a solvation term that drives segregative transitions and an associative term that drives networking. Therefore, COAST-like processes in solutions of multivalent associative macromolecules are driven by a combination of macromolecular and solvent (in)compatibility, which contributes to the free energy of mixing, and reversible associations, which drive percolation.

In multivalent associative macromolecules ^{9, 61} the term associativity refers to the presence of stickers that enable either isotropic or anisotropic site- or chemistry-specific interactions that are more favorable and larger in magnitude than the isotropic solvent-mediated interactions ^{60, 61}. In soft matter systems, multivalent associative macromolecules can be modeled as patchy colloids featuring patches or stickers of defined sizes and orientations that enable site-specific interactions among the colloidal particles ⁶². Intrinsically foldable domains of proteins ⁶³ that feature hotspots for specificity of binding are exemplars of patchy particles ⁹. Flexible linear polymers can feature stickers that enable specific intra- or interpolymer crosslinks. Such systems are known as linear associative polymers. It is worth emphasizing that while biologists tend to conflate the term sticky or stickers to imply non-specific interactions, the term stickers, which was introduced almost four decades ago in the polymer literature, refers to motifs that enable site- or sequence-specific interactions. The strengths of specific interactions involving reversible sticker-sticker crosslinks can span at least an order of magnitude (or more) vis-à-vis thermal energy ^{3, 64–67}. The surfaces of folded domains and regions that are interspersed between stickers in IDRs act as spacers. While stickers enable site-specific interactions, spacers influence the overall solubility while also influencing the cooperativity of networks of sticker-sticker interactions ⁹.

The partitioning of the sequence of a linear associative polymer or the surface of a patchy colloid into stickers versus spacers often becomes a matter of operational convenience, especially for associative biomacromolecules. The reality is that the interactions energies in such systems feature hierarchical continuum that are also context dependent. The polypeptide backbone and the phosphodiester linkages along nucleic acid backbones are ubiquitous in protein versus nucleic acid systems, respectively. These provide the background against which amnio acid sidechain or nucleobase interactions are to be referenced. The direct interactions of backbones will be influenced by sidechain or nucleobase chemistries. Therefore, the stickers-and-spacers formalism is not exact or complete in that the identities of stickers and spacers are neither immutable nor is the binary classification truly rigorous. Instead, the formalism provides a useful, zeroth order abstraction to compare sequence-specific driving forces for phase transitions. Further, the parsing of amino acid sidechains and nucleobases into stickers versus spacers for a given context allows one to perform separation of function mutagenesis analysis, querying the contributions of distinct chemistries to the segregative versus associative phase transitions.

Site- and sequence-specific interactions of stickers give rise to reversible crosslinks ⁶⁵. Different types of stickers will encode a hierarchy of specific interactions depending on the types of stickers that are incorporated into the sequence of an IDR ^{65, 66} and where they land on the surfaces or interiors of folded domains ⁴⁸. Among the relevant, specific sticker-sticker interactions are hydrogen bonds, salt bridges, solvent-mediated ionic interactions, the hierarchies of interactions among groups with multipole moments, associations among hydrophobic residues ⁶⁸, and the range of interactions that involve pi systems, which include stacking, cation-pi interactions, and orienting pi systems by combining these systems with hydrogen bonds ^{49, 65}.

Most condensates also include a range of nucleic acid molecules ⁶⁹. The delineation of stickers versus spacers can be applied to nucleic acids as well, ^{70, 71}. Here, the specificity of base pairing and base stacking drive secondary structure formation within the nucleic acid polymers, and the specificity of intermolecular crosslinking ⁷². Sequence regions that disrupt the specificity of inter-base interactions will act as spacers.

1.7. Associative macromolecules drive the formation of condensates

Facsimiles of condensates and bona fide condensates in live cells appear to form and dissolve through phase transitions described by order parameters ⁷³. The order parameter for purely segregative transitions is the density for a one-component system or the compositional vector for complex mixtures of macromolecules, solutes, and a solvent. For purely associative transitions such as percolation, the order parameter describes the connectedness of molecules, the topology of the network that forms, the extent of crosslinking, and the number densities of connected clusters ^{16, 17, 52, 55}. Changes in conformation across the phase boundary or the onset of crystalline or semi-crystalline order are defined by distinct order parameters ⁵⁸. For processes that combine segregative, associative, and transitions that involve the breaking of symmetry, the order parameter will be a vector or a tensor. Components of order parameters change abruptly at the onset of a phase transition ⁷⁴. However, the different components of order parameter vectors or tensors might be differently responsive to changes in stimuli that drive phase transitions.

Processes such as phase separation coupled to percolation (PSCP) ⁷⁵ and complex coacervation ⁷⁶ are exemplars of processes that come under the rubric of COAST. As such, there is no formal distinction between PCSP and complex coacervation. However, we make the distinction for two reasons: First, complex coacervation is an established term and second, it requires the consideration of electrostatic interactions and their attendant complexities such as the range of the interactions and the competing effects of macroions and solutions ions. In many systems, one can get away without worrying about these complexities. Therefore, we reserve PSCP for systems where charge effects are likely to play either a minor role or can be treated without consideration of the spatial range or correlation effects of electrostatic interactions. Other COAST-like processes include polymerization induced phase separation ^{4, 77}, micellization (also referred to as pseudo phase separation or microphase separation) ^{78, 79}, surfactant influenced ⁸⁰ and thermodynamically controlled microphase separation ⁸¹, which can also be realized when stickers are clustered into linear blocks along the sequence of interest ^{61, 82}.

Other processes that can give rise to condensates include active processes that are coupled to COAST-like spontaneous processes or purely active processes such as reaction- or motility-controlled phase separation ⁸³ and active emulsification ⁸⁴. Spontaneous cooperative processes that are likely contributors are clustering via short-range attractions and long-range repulsions (so-called SALR-controlled processes) ⁸⁵. Additionally, condensate formation can also be under dynamical control, and these processes include homogeneous or multistep ⁸⁶ nucleation-mediated growth ⁸⁷, or spinodal decomposition ^{73, 87, 88}, a variant of which is viscoelastic phase separation ⁸⁹.

1.8. Scope of the review

This review focuses on spontaneous phase transitions that come under the rubric of COAST. The primary focus is on PSCP ⁷⁵. Any model for the spontaneous process of condensate formation and dissolution must integrate the contributions of associative effects originating from site- or sequence-specific interactions and segregative effects originating from the interplay of configurational and solvation effects that have both entropic and enthalpic components. Biomacromolecules, specifically the protein and nucleic acid components of nuclear and cytosolic condensates, are complex mixtures defined by finite sizes, heterogeneity and hierarchies of sequence-encoded interactions, conformational heterogeneity, and thermodynamic consequences of post-transcriptional and post-translational modifications. While simple concepts provide a useful starting point for describing how condensates form and dissolve, the complexity of these systems also necessitates the development of new physics, even for describing spontaneous phase transitions. This is especially true for multicomponent systems.

Our focus on spontaneous phase transitions comes from the fact that it highlights the intrinsic, evolutionarily selected, sequence-encoded, and solution-condition-mediated processes that are likely to be coopted and modulated by active processes and the diverse components within cellular milieus ⁹⁰. COAST-like processes are intrinsic consequences of the information written into protein and nucleic acid sequences. These are likely to be leveraged by a blend of equilibrium and non-equilibrium processes that are operative in live cells ^{7, 90, 91}. Our objective is to provide clarity regarding phase transitions that come under the rubric of COAST. To start, we will introduce the foundations of purely segregative and purely associative phase transitions. We will then segue to descriptions of how these processes are coupled, and why this coupling appears to be important for describing the how condensates form and dissolve through reversible phase transitions.

2.0. PHASE SEPARATION – ONE-COMPONENT SYSTEMS

Phase separation is a segregative transition whereby the system of interest separates (segregates) into two or more coexisting phases. Note that segregative transitions can also be referred to as demixing transitions. The nomenclature of X-Y phase separation is reserved for the formation of two coexisting phases X and Y. Here, X-Y specifies the types of coexisting phases that can form. Phase separation that gives rise to two coexisting phases can come in different flavors, such as liquid-liquid phase separation, liquid-solid phase separation, liquid-liquid-crystalline phase separation, etc. In binary mixtures, such as a single type of macromolecule in a solvent, segregative transitions arise due to macromolecule-solvent interactions that, on average, are unfavorable compared to the arithmetic mean of macromolecule-macromolecule and solvent-solvent interactions ⁵⁰. In multicomponent systems, segregative transitions are governed by a blend of pairwise favorable versus unfavorable interactions among the different components ⁹². In systems with only one type of molecule, segregative transitions are density transitions, and we discuss these first.

2.1. Systems of hard molecules

One-component fluids comprising spherical particles are the simplest systems that one can use to develop an atomistic description of phase separation. Consider the case of a system of hard spheres, each of diameter σ that cannot interpenetrate. These particles interact via purely elastic collisions (Figure 1A). For a pair of particles with position vectors r_i and r_j, the interaction potential (Figure 1B) can be written as:

$$U\left(r_i,r_j\right)=\{\begin{array}{c}0\text{if}\left|r_i-r_j\right|\ge \sigma \\ \infty \text{if}\left|r_i-r_j\right|<\sigma \end{array};$$ (1)

Figure 1: Hard sphere fluids can undergo density transitions viz., phase separation.

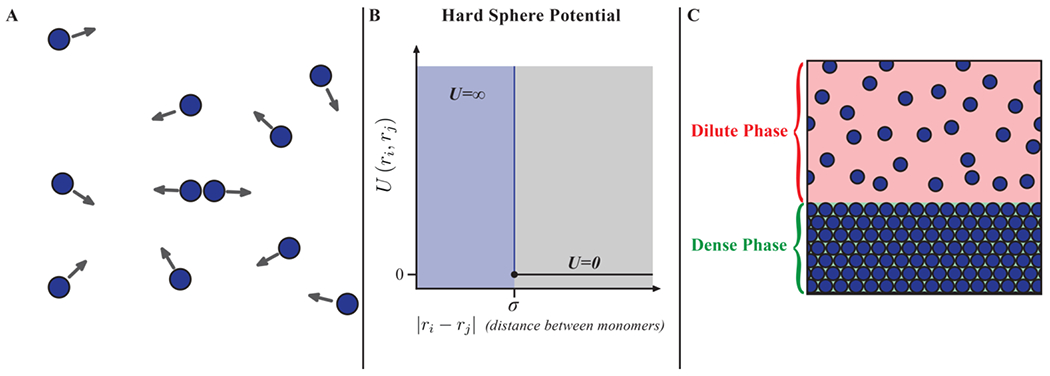
(A) System of hard spheres. The arrows indicate that the collisions among the molecules are purely elastic. (B) Potential for a pair of hard spheres. (C) A segregative density transition gives rise to two coexisting phases of different densities separated by an interface, as depicted here.

Note that systems of purely repulsive hard molecules, irrespective of their shape, will lack attractive interactions. Molecular dynamics simulations by Alder and Wainwright ⁹³ and Monte Carlo simulations by Wood and Jacobson ⁹⁴ showed that a fluid of hard spheres undergoes a freezing transition that can be described as liquid-solid phase separation. This is because, above a critical density, the hard sphere fluid minimizes its free energy, purely entropic in this case, by separating into two coexisting phases. The coexisting phases are a low-density liquid and a high-density solid.

The onset of the equilibrium freezing transition can be anticipated by the density dependence of the radial distribution function $g\left(r\right)$ ⁹⁵. This function quantifies the relative probability of realizing a specific inter-particle distance r referenced to the relevant probability in a non-interacting, and hence ideal, gas. A typical profile for $g\left(r\right)$ shows the characteristic short-range order and long-range disorder that one expects for a liquid. However, above a critical density, the face-centered cubic packing of spheres ⁹⁶ is manifest on all length scales, leading to an equilibrium freezing transition. The separation of a hard sphere fluid into species of two distinct coexisting densities (Figure 1C) is described using a coexistence curve.

The density dependence of the phase transition of a fluid of N hard spheres can be rationalized using the configuration integral, which is written as:

$$Z_N=\frac{1}{V^N}\int \exp \left[\frac{\sum _{i,j<i}U\left(r_i,r_j\right)}{k_{B}T}\right]d^{3N}r;$$ (2)

Here, V is the system volume, k_B is the Boltzmann constant, and T is the temperature of the system. For a hard sphere fluid, where the pair potential is described by Equation (1), the configuration integral in Equation (2) is independent of temperature. Thus, the thermodynamic properties, correlation functions, and structural properties depend only on the number density given by the pre-factor in Equation (2). At high densities, a hard sphere fluid undergoes an equilibrium freezing transition to increase its accessible volume. This is an example of an entropically-driven segregative transition, which for a one-component system is a density transition.

Density transitions can also be realized for fluids of hard rods ⁹⁷, hard ellipsoids, or hard discs ⁹⁸ (Figure 2). In such systems, which have served as touchstones for the description of phase behaviors of lipids ⁹⁹, the spherical symmetry in hard sphere fluids is broken by the aspherical geometries of the molecules ¹⁰⁰. Accordingly, the density transition gives rise to various liquid crystalline phases that depend on the shapes of the underlying molecules. The segregative transitions one observes in systems of hard molecules are entropically driven and are a consequence of the bulk densities of molecules crossing specific, shape-dependent thresholds.

Figure 2:

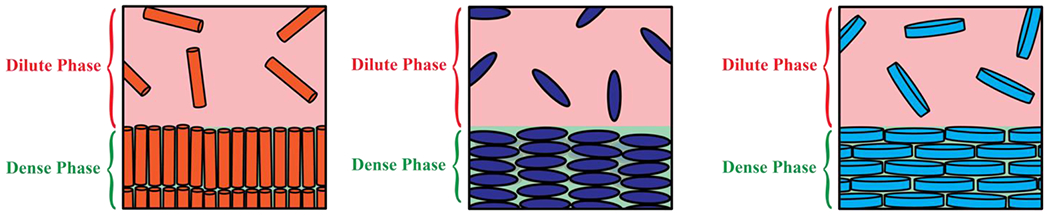
Systems of hard aspherical molecules including rods, ellipsoids, and discoids can also undergo segregative transitions.

2.2. Phase separation in one-component systems with repulsive and attractive interactions

The simplest generalization of a fluid of hard spheres is that of a van der Waals fluid. The hard-core repulsions are softened via a short-range repulsive potential, and a cohesive, longer-range term is included to capture dispersive interactions, which are attractive in nature. A typical pair potential for a van der Waals fluid is the 12-6 Lennard-Jones potential written as:

$$U_{\mathrm{LJ}}\left(r_i,r_j\right)=4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{\left|r_i-r_j\right|}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{\left|r_i-r_j\right|}\right)}^6\right];$$ (3)

Here, ${\epsilon }_{ij}$ is the well depth of the minimum in the Lennard-Jones potential and σ_ij is the effective hard-core diameter for a pair of particles.

As shown by Weeks, Chandler, and Andersen ¹⁰¹, the short-range repulsive forces completely determine the equilibrium structure of the van der Waals fluid ¹⁰². The interaction potential for a pair of particles effectively consists of hard spheres in an attractive, uniform background that mimics the longer-range attractive interactions known as van der Waals forces. Inclusion of the attractive interactions allows for temperature-dependent responses of the fluid. As a result, there exists a combination of pressures and temperatures for which the system of Lennard-Jones particles can separate into coexisting liquid and vapor phases. Additionally, the separation into distinct coexisting solid phases can be observed by modulating the exponent of the repulsive arm of the Lennard-Jones potential ¹⁰³.

The main point is that simple models describe how segregative density transitions arise and give rise to distinct pairs of coexisting phases. Further, there are singular combinations of pressure and temperature, known as triple points, where three distinct phases can coexist. Therefore, even a one-component system can be spatially organized to achieve phases of distinct densities coexisting with one another. The interactions in these simple models are isotropic, and changes to pressure and temperature engender density transitions. Alternatively, changes to the bulk density for fixed pressure and temperature also engender segregative transitions, giving rise to different types of coexisting phases.

2.3. Purely entropically-driven phase separation can drive spatial organization in cells

The universal requirement of steric exclusion can give rise to entropically-driven phase separation and the formation of distinct coexisting phases. The repulsive forces at short range are orders of magnitude larger than the intermediate or long-range attractions ^{102, 104}. Accordingly, if one were to be naïve and view a cell as a bag of hard molecules and self-avoiding polymers of different shapes and sizes, then distinct segregative transitions are likely to be realized as the densities of different molecules cross threshold values ⁸. Biochemical activity would control the production and degradation of the molecules of interest, and changes to cellular volumes that accompany the production or degradation of molecules would enable spatial organization via purely segregative transitions.

Indeed, the physics of entropically-driven segregative transitions of self-avoiding polymers has proven to be effective at explaining chromosomal segregation in rod-shaped bacteria under the right conditions ¹⁰⁵. In this model, circular DNA molecules are treated as self-avoiding, ring-like polymers. The well-mixed state limits the configurational degrees of freedom of the self-avoiding ring-like polymers, thus extracting an entropic penalty ¹⁰⁵. This penalty is alleviated by separation into two distinct chromosome-rich territories that coexist with one another (Figure 3). The role of specific protein co-factors and specific geometries observed as part of bacterial chromosomal segregation can be explained using models whereby protein binding enables physical crosslinking, thereby generating topological constraints that are layered upon the entropically-driven segregative transitions ¹⁰⁶. In a similar vein, segregative transitions of rod-like molecules, captured by Onsager’s model for liquid-liquid-crystalline phase separation ⁹⁷, has had a profound impact on our understanding of membrane phase behavior ¹⁰⁷.

Figure 3:

Entropically-driven phase separation helps explain bacterial chromosomal segregation.

The preceding discussion makes the point that the physics of entropically-driven phase separation, which only considers the density transitions of hard molecules, can explain many of the basic foundations of spatial organization in cells. Here, hard molecules refer to generalizations of hard spheres that include complex shapes and sizes. Such systems do not have any attractive interactions. And yet, phase separation can be realized based purely on the absolute densities of hard particles in a single-component fluid or the relative densities of different types of hard particles in multicomponent mixtures. This point was made in the 1960s by A.G. Ogston ¹⁰⁸ who noted that “any system of two solutes which interact only entropically will satisfy the conditions for “incompatible” phase separation providing only that the molecules are of different size”. There will be the inevitable criticism of the logic in this paragraph because biological organization must be about relative affinities and the specificities they engender. This is undeniable. However, the point of the current paragraph is that spatial sorting and compartmentalization are emergent properties in even the simplest systems viz., collections of hard molecules. In such systems, the steep energetic penalties for steric overlap, and the maximation of entropy through shape complementarity are sufficient to enable phase separation above a density threshold. These discussions highlight why phase separation is logical rather than “implausible”¹⁰⁹ as a route for compartmentalization or spatial organization in cells.

In the soft matter literature, the segregative transitions of hard spheres have been studied in the presence of active processes that either steer particles in specific directions ⁸³(Figure 4) or account for the presence of chemical reactions ¹¹⁰. In the simplest instantiations of active segregation, an external force augments the intermolecular interactions, and generates local density fluctuations to enable local density transitions. Active processes can be drivers of segregative transitions, and this topic has received considerable attention in the physical ^{83, 110, 111} and chemical literatures ¹¹².

Figure 4: Example of movement-induced (motility-induced) phase separation ⁸³.

The figure shows active Brownian particles that are self-propelled in an external field. Propulsion creates flows and local inhomogeneities that can drive segregative transitions.

3.0. PHASE SEPARATION IN COMPLEX MIXTURES

3.1. Mean-field theories for free energies of mixing and the interaction parameter χ

From a physical chemistry standpoint, cells may be viewed as complex mixtures of an assortment of macromolecules, solutes, and metabolites, all dissolved in a non-ideal aqueous milieu. Here, complexity refers to the different molarities, stoichiometries, and volume fractions of the different molecules. How does one describe the thermodynamics of mixing and segregation in complex mixtures? The mean field theories of Hildebrand ¹¹³, generalized by Flory ⁵⁰ and Huggins ⁵¹ for polymer solutions and blends, provide a useful starting point.

For mixtures of molecules, the fundamental quantity of interest is $\Delta {\text{µ}}_{\text{mix}}$, which is the free energy density of mixing. This quantifies the change in free energy per molecule of the system that is associated with transferring molecules that make up the mixture from their pure, single-component, homogeneous phases to a mixture defined by the volume fractions of ${\text{ϕ}}_{\text{i}}$ for each of the species i. We consider a binary mixture of molecules of type A and B dispersed randomly on a cubic lattice. For simplicity, one ignores three-body and higher-order interactions. Further, we shall assume that there are no volume changes upon mixing ¹⁶. In this scenario, the free energy of mixing is written as:

$$\text{Δ}{\text{μ}}_{\text{mix}}=k_{B}T\left[\frac{{\text{ϕ}}_{\text{A}}}{N_{\text{A}}}\text{In}{\text{ϕ}}_{\text{A}}+\frac{{\text{ϕ}}_{\text{B}}}{N_B}\text{In}{\text{ϕ}}_B+\chi {\text{ϕ}}_{\text{A}}{\text{ϕ}}_B\right];$$ (4)

Here, ${\text{ϕ}}_{\text{A}}$ and ${\text{ϕ}}_{\text{B}}$ are the volume fractions of molecules of type A and B. N_A and N_B are ≈ 1 if A and B are rigid, roughly spherical macromolecules such as stable globular proteins, colloidal particles, or small molecules such as solutes, metabolites, or drugs. If A and B are flexible, linear macromolecules, then N_A and N_B refer to the degree of polymerization quantified as the number of chemical or Kuhn monomers within the molecules. The interaction parameter $\chi$ is a dimensionless parameter that quantifies the differences among the magnitudes of the pairwise interactions in the mixture. It is defined as:

$$\chi =\frac{z}{2}\frac{\left(2u_{\text{AB}}-u_{\text{AA}}-u_{\text{BB}}\right)}{k_{B}T};$$ (5)

Here, z is the coordination number of the lattice used to model macromolecules as gases of monomers. The free energy of mixing is a sum of entropic and energetic contributions. In an ideal mixture, $\chi =0$, and this can arise from a counterbalancing of the pairwise interactions energies, namely, 2u_AB and the sum $u_{\mathrm{AA}}+u_{\mathrm{BB}}$ . The free energy of mixing is purely entropic when $\chi =0$, and this entropy always favors mixing. In an ideal mixture, the composition in any volume element within the system will match the overall composition. Therefore, such a system will be homogeneous and is described as a random mixture. Unlike a one-component system, where density alone can generate a segregative transition, in a mixture, there is the added consideration of mixing of the degrees of freedom. In this case, entropy always favors mixing.

The mixing of A and B molecules can be enhanced beyond the ideal case if χ is negative. In this scenario, the one-phase system is always preferred. Even so, there will be compositional inhomogeneities with respect to volume elements that correspond to the molecular scale. This is because the system will strive to enhance favorable, pairwise A-B interactions over the less favorable or even unfavorable A-A or B-B interactions. An ionic liquid ¹¹⁴, comprising a mixture of oppositely charged ions sans a solvent, would be an exemplar of such a mixture.

3.2. Phase separation becomes a formal possibility when χ is positive

In a binary mixture of A and B molecules, we can set ${\text{ϕ}}_{\text{A}}=\text{ϕ}$, and ${\text{ϕ}}_{\text{B}}=\left(1-\text{ϕ}\right)$ because of conservation of mass, i.e., ${\text{ϕ}}_{\text{A}}+{\text{ϕ}}_{\text{B}}=1$. The system is closed, and hence the overall composition of the mixture is a conserved order parameter. If $\chi$ is positive, then there exists some threshold volume fraction $\text{ϕ}={\text{ϕ}}_{\text{sat}}$ above which the one-phase, homogeneous mixture is no longer thermodynamically stable ⁴⁹. The one-phase mixture becomes saturated, and to minimize the overall free energy of mixing, the system separates into coexisting dilute and dense phases ⁴⁹. For a fixed temperature, the value of ${\text{ϕ}}_{\text{sat}}$ depends on the magnitude of $\chi$ and the relative molecular weights of the A and B molecules. The compositions of the coexisting phases, denoted as ${\text{ϕ}}_{\text{sat}}$ and ${\text{ϕ}}_{\text{dense}}$, will be temperature dependent. Phase separation leads to an interface between the two coexisting phases. If A is a macromolecule, such as a linear polymer, with each molecule being defined by N chemical monomers, and B is a low-molecular weight solvent, then there will be transport of solvent across the interface to help equalize the chemical potentials. This scenario describes an osmotic solution, whereby the exchange of solvent across the phase boundary will be opposed by the increased pressure within the dense phase. This pressure, known as the osmotic pressure, is a colligative property that quantifies the free energy difference between a polymer solution and a pure solvent, and at equilibrium it must be equalized between the two coexisting phases ^{115, 116}. Therefore, the compositions ${\text{ϕ}}_{\text{sat}}$ and ${\text{ϕ}}_{\text{dense}}$ are set by equalizing chemical potentials and the osmotic pressures across the two phases ¹¹⁵. If we denote the chemical potential of the macromolecule at temperature T as ${\mu }_{m,T}$ and the osmotic pressure as Π_T then the requirements for chemical and osmotic equilibrium are:

$$\begin{gathered} {\text{μ}}_{\text{m},T}\left({\text{ϕ}}_{\text{sat}}\right)={\text{μ}}_{\text{m},T}\left({\text{ϕ}}_{\text{dense}}\right) \\ \text{and} \\ {\prod }_{\text{m},T}\left({\text{ϕ}}_{\text{sat}}\right)={\prod }_{\text{m},T}\left({\text{ϕ}}_{\text{dense}}\right); \end{gathered}$$ (6)

In theoretical work, the preferred units for concentration are volume fractions, $\text{ϕ}$, which quantify the amount of the system volume that is taken up by the polymers. However, experimentalists prefer molar units or mg / ml denoted as c. And so, analysis of experimental data is usually performed in molar units. For an A-B mixture that is a polymer solution, A is a linear polymer and B is the solvent.

The determinants of ${\text{ϕ}}_{\text{sat}}$ or $c_{\text{sat}}$ are the solution temperature, the degree of polymerization N_A, and the value of $\chi$. Following Flory^{16, 64}, one can write $\chi \approx u+u\prime /T$. Here, u is an athermal entropic term, and u′ is an effective pairwise energy determined by the interplay of polymer-solvent, polymer-polymer, and solvent-solvent interactions. Therefore, the value of χ is determined by the solution temperature, and the relevant parameters are T and N_A. Above c_sat, the overall free energy of the system is minimized by separation of the system into a dense, polymer-rich phase that coexists with a dilute, polymer-deficient phase. The compositions of the dense and dilute phases quantified by c_dense and c_dilute, respectively refer to the temperature-dependent concentration of polymers in the dense versus dilute phases. The precise values of c_dense and c_dilute are governed by the equalization of chemical potentials and osmotic pressures across the phase boundary. Since the dilute phase is saturated at c_sat, the value of c_dilute is the same as c_sat. The value of c_dense will depend on the amount of solvent that is present in the dense phase. If the dense phase is akin to a polymer melt, then the volume fraction of the dense phase will approach unity, i.e., ${\text{ϕ}}_{\text{dense}}\approx 1$. This is clearly not the case for biomolecular condensates as shown first by Gall and coworkers in their measurements of mass densities in nucleoli, Cajal bodies, and nuclear speckles ¹¹⁷. Their estimates suggest that ${\text{ϕ}}_{\text{dense}}$ is less than 0.1. Clearly, condensates encompass considerable amounts of solvent, and this has become clear from several in vitro and in vivo measurements ^{11, 64, 66, 118, 119}. and these estimates have been

Given the mean-field, lattice gas nature of the Flory-Huggins theory, the simplest description of the coexisting phases is that of a dilute gas of chemical or Kuhn monomers derived from each polymer that coexists with a dense melt of polymers. This is rather like liquid-vapor phase separation. However, this description ignores the abundance of the solvent in the polymer-deficient dilute phase. As a result, the coexisting phases are better described as a dilute polymer solution, rich in a low-molecular weight solvent, that coexists with a polymer-rich phase. This has given rise to the term liquid-liquid phase separation for the phase behaviors of biopolymer solutions that are described using the Flory-Huggins theory ^{44, 49}.

3.3. χ, osmotic second virial coefficients, and excluded volumes

We shall consider an A-B mixture, which comprises a macromolecule A in a solvent B. If the macromolecule is a linear polymer with n_p chemical monomers or n_k Kuhn monomers, then the volume occupied by the chemical or Kuhn monomers (i.e., residues in a protein sequence) is proportional to b³, where b is the size of each monomer. The effective work done to bring a pair of monomers to within a distance r of one another is the potential of mean force W(r). The excluded volume per monomer (v_ex), which has also been referred to as the effective solvation volume (v_es)⁴⁷, is the effective volume that is set aside for interactions of each monomer with the surrounding solvent. It is quantified by averaging over all inter-monomer distances in the entire solution volume. Accordingly, v_ex is computed as:

$${\text{v}}_{\text{ex}}=-{\int }_0^{\infty }\left[\exp \left(-\frac{W\left(r\right)}{k_{\text{B}}T}\right)-1\right]r^{2}dr;$$ (7)

The excluded volume can be positive, zero, or negative ¹⁶. Therefore, a positive excluded volume implies that the polymer is in a good solvent, and the effective pairwise interactions among the monomers are, on average, repulsive. If, on average, the effective monomer-solvent interactions are counterbalanced by the monomer-monomer and solvent-solvent interactions, then the excluded volume is zero. This situation corresponds to a theta or inert solvent for the polymer. Finally, the excluded volume is negative if the monomer-monomer interactions are, on average, attractive. In this scenario, the polymer is in a poor solvent. The conformations of polymers in dilute solutions ⁴³, and the overall phase behavior in polymer solutions are determined by the sign and magnitude of v_ex ³⁷.

The osmotic second virial coefficient B₂ is a well-known, and well-established measure of the effective strengths of pairwise macromolecular interactions in a solvent ¹²⁰. It can be defined using ¹²¹ $B_2^{\prime }=B_2{M}_w^2$ as:

$${\text{B}}_2^{\prime }=-2\pi {\int }_0^{\infty }\left[\exp \left(-\frac{W\left(r\right)}{k_{B}T}\right)-1\right]r^{2}dr;$$ (8)

As in Equation (7), the term $W\left(r\right)$ captures the distance-dependent solvent-averaged potential of mean force between a pair of macromolecules that are a distance r apart from one another in the solvent, and M_w is the molecular weight of the macromolecule ¹²¹. The value and sign of B₂ will vary with solution conditions such as the temperature, pH, or concentration of solution ions. Negative values of B₂ imply net attractions among the macromolecules. Conversely, positive values of B₂ imply net repulsions among the macromolecules. In an ideal mixture, B₂ is zero, and the attractions and repulsions are counterbalanced, on average. The integrands of Equations (7) and (8) that lead to v_ex and B₂, respectively are identical to one another implying that ${\text{v}}_{\text{ex}}=2\pi {\text{B}}_2^{\prime }$.

In an A-B mixture, the osmotic pressure can be computed as the partial derivative of the free energy of mixing as:

$$\prod =\frac{{\text{ϕ}}_{\text{A}}^2}{{\text{B}}^3}{\frac{\partial \Delta {\text{μ}}_{\text{mix}}}{\partial \text{ϕ}}|}_{n_{\text{A}}};$$ (9)

Here, n_A is the number of macromolecules of type A in a solvent of type B. Note that n_A is kept constant. In a dilute mixture of A and B molecules, where N_A and N_B are the number of chemical or Kuhn monomers per A and B molecules, respectively, the osmotic pressure can be written in terms of the virial expansions as:

$$\begin{gathered} \text{Π}=\frac{k_{B}T}{b^3}\left[\frac{{\text{ϕ}}_{\text{A}}}{N_{\text{A}}}+\frac{{\text{ϕ}}_{\text{A}}^2}{2}\left(\frac{1}{N_{\text{B}}}-2\chi \right)+\frac{{\text{ϕ}}_{\text{A}}^3}{3N_{\text{B}}}+\dots \right] \\ \text{Setting}{c}_n=\frac{{\text{ϕ}}_{\text{A}}}{b^3} \\ \text{Π}=k_{B}T\left[\frac{c_{\text{A}}}{N_{\text{A}}}+\left(\frac{1}{N_B}-2\chi \right)+\frac{b^3{c}_n^2}{2}+\frac{b^6{c}_n^3}{3N_B}+\dots \right]; \\ \text{Because,}{\text{v}}_{\text{ex}}=\left(\frac{1}{N_B}-2\chi \right)b^3,\text{it}\text{follows}\text{that}: \\ \text{Π}=k_{B}T\left[\frac{c_n}{N_{\text{A}}}+\frac{{\text{v}}_{\text{ex}}{c}_n^2}{2}+w{c}_n^3+\dots \right] \end{gathered}$$ (10)

If A is a linear polymer with N_A monomers, and B is a low molecular weight solvent with $N_{\text{B}}\approx 1$ , then ${\text{v}}_{\text{ex}}=(1–2\chi )b^3$ . In Equation (10), c_n is the number density of macromolecular monomers in molar units. The pre-factors of each of the higher-order terms are known as virial coefficients. In dilute solutions, terms beyond the ${\text{v}}_{\text{ex}}$ term become negligibly small. Accordingly, using what is known as a Zimm plot ¹²², which is a plot of: $\frac{\text{Π}}{c{k}_{\text{B}}T}$ versus c, one can estimate the magnitude and sign of the osmotic second virial coefficient denoted as B₂.

There are a few ways to generate a Zimm plot. The traditional approach uses static light scattering ¹²³, which was recently used by Safari et al., to study the effective interactions between TPX2 molecules ¹²⁴. To access a broader range of B₂ values, one can use static laser light scattering ¹¹⁸. These measurements are performed as a function of polymer concentration. Other approaches include direct measurements of osmotic pressure, which is a readily accessible colligative property of polymer solutions. Given the challenge of expressing and purifying large amounts of biomacromolecules, one can also use fluorescence correlation spectroscopy, and the concentration-dependent deviation in diffusion coefficients to back-calculate the second virial coefficient. This approach was demonstrated by Wei et al., ¹¹⁸, and it requires that certain hydrodynamic criteria be satisfied. In the next section, we describe the inferences one can glean from knowledge of second virial coefficients.

3.4. Interactions that drive phase separation in n-nary mixtures in a complex solvent

Cells are complex mixtures comprising an assortment of macromolecules in a solvent that is itself rather complex ¹²⁵. The Flory-Huggins theory can be generalized for a mixture of more than two molecules. There are now multiple χ parameters, one for each pair of molecules in the mixture. Accordingly, in compact notation, for a system with n macromolecules in a complex solvent, one can write the free energy of mixing in terms of a compositional vector $\Phi$ and an interaction matrix $\Gamma$. The free energy of mixing is written as: $\Delta {\text{µ}}_{\text{mix}}=k_{\text{B}}T({\Phi }_N\prime ln\Phi +\Phi \prime \text{X}\Phi )$. Here, $\Phi \prime =({\text{ϕ}}_1,\dots ,{\text{ϕ}}_n)$ is the compositional row vector, $\Phi$ is the transpose of this vector, and ${{\text{Φ}}_{\text{N}}}^{\prime }$ is the vector $({\text{ϕ}}_1/N_1\dots ,{\text{ϕ}}_n/N_n)$ where each $N_i$ is the number of chemical or Kuhn monomers in species i. Finally, the X matrix is written as:

$$\text{X}\equiv \left(\begin{array}{ccccc}{\chi }_{11}& {\chi }_{12}& {\chi }_{13}& \cdots & {\chi }_{1n}\\ {\chi }_{21}& {\chi }_{22}& {\chi }_{23}& \cdots & {\chi }_{2n}\\ {\chi }_{31}& {\chi }_{32}& {\chi }_{33}& \cdots & {\chi }_{3n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\chi }_{n1}& {\chi }_{n2}& {\chi }_{n3}& \cdots & {\chi }_{nn}\end{array}\right)$$ (11)

In the notation used here, each ${\chi }_{ii}$ term quantifies the effective strengths of solvent-mediated homotypic interactions. Each of the ${\chi }_{ii}$ terms will be as defined in Equation (5) where we shall now set A to be the solvent, and B to be macromolecule i. Knowing the elements of the Γ matrix will help in identifying the macromolecular drivers – or scaffolds – of phase separation in complex mixtures. As we will discuss below, each element of the Γ-matrix is directly related to a measurable parameter viz., the appropriate osmotic second virial coefficient. Therefore, the combination of measurements and computations that allow one to populate the elements of the Γ-matrix will provide a direct route to identifying macromolecular scaffolds ^{1, 126} that are the main drivers of phase separation.

Notice that each element of the Γ-matrix is a pairwise interaction parameter and is therefore proportional to the corresponding second virial coefficient such that ${\chi }_{ij}\propto {\text{B}}_{ij}$. Therefore the Γ-matrix and the matrix of second virial coefficients, denoted as B are equivalent. Since the phase behavior of the mixture, including the numbers of coexistence phases are, to first order, determined by the signs and magnitudes of the elements of the B matrix, it helps to be able to measure or estimate each of these elements. One approach would be to measure the diagonal elements B_ii using the Zimm plot and estimate ¹²⁷ ${\text{B}}_{ij}$ as ${\text{B}}_{ij}={\left({\text{B}}_{ii}{\text{B}}_{jj}\right)}^{\frac{1}{2}}$. Note that this only works if the net charge for each of the macromolecules is close to zero because excess charge creates imbalances requiring an accounting for the preferential effects of counter- and co-ions drawn from the solution. For macromolecules with a net charge, it becomes imperative to measure ${\text{B}}_{ii}$ , ${\text{B}}_{jj}$ , and ${\text{B}}_{ij}$ separately. These measurements will need to be performed as a function of pH and salt concentration.

When B_ij needs to be measured, one can do so by fixing the concentrations of solvent components, and one of species i or j, and measure either scattering or osmotic pressure as a function of the concentration of species j or species i. The relevant B_ij can then be extracted from application of the Zimm analysis to the data. These measurements will need to be performed in the presence of the solvent of interest, which makes it imperative that the contribution of the solvent to each B_ij term be dereferenced through separate measurements of B_ii and B_jj in the solvent of interest. Computations can help with the generation of estimates of each of the elements of the B-matrix ¹²¹, although the effects of components of the complex solvent, which is never just deionized water, can contribute in non-trivial ways. Therefore, computations must account for the complex solvent in computationally tractable ways, and this remains a persistent challenge.

Why and how does a B-matrix help with describing the overall phase behavior of a complex mixture? Given a B-matrix, an empirical route to identifying scaffolds and co-scaffolds is to compute the norm using all elements that are negative and identifying the fraction of the elements that contribute to at least 90% of this norm. This is an ad hoc maximum-likelihood threshold that is based on the consideration that the relative contributions of scaffolds or co-scaffolds with respect to non-scaffolds must exceed thermal energy k_BT. Given its central importance, a defining challenge for physical chemists in the condensate field is to compute the B-matrix elements from sequence and structure information of macromolecules that make up the complex mixture of interest.

3.5. Gibbs phase rule and mean field models for phase separation in n-nary mixtures

For mixtures, with n distinct types of macromolecules in a solvent, there are n(n–1)/2 distinct χ parameters that contribute to the overall phase behavior. Note that the elements of the B-matrix will change with temperature, pressure, and changes to solution conditions. By the Gibbs phase rule, if there are n components in the system, and p coexisting phases, then the number of thermodynamic degrees of freedom is defined as: F = n – p + 2. The maximal number of phases that can coexist with one another is computed by setting F to be zero and solving for p. Therefore, the maximum number of phases that can coexist with one another will be n + 2. Accordingly, for a one-component system, such as a fluid of van der Waals spheres, n = 1 and the maximum number of coexisting phases is three where a vapor, liquid, and solid coexist at a triple point defined by a specific value of the temperature and pressure. For a system where we fix the temperature and pressure, and n ≥ 2, a maximum of n phases can coexist with one another. Accordingly, at a fixed temperature and pressure, a mixture with n-distinct types of macromolecules in a solvent will have n+1 distinct components, and in theory, such a system can feature a maximum of n+1 coexisting phases. The most trivial scenario pertains to a macromolecule-rich phase and a solvent-rich phase coexisting with one another ¹²⁸ (Figure 5A).

Figure 5: Scenarios for phase separation.

(A) The coexistence of two phases, one that is polymer-rich and another that is solvent-rich. (B) A scenario that is reminiscent of the ternary PEG, dextran, water system whereby two phases, rich in different types of polymers, coexist with one another. (C) The formation of distinct phases, each enriched in a specific type of polymer.

Jacobs and Frenkel¹²⁸ developed a mean field model that rests on the variance of the distribution of pairwise interaction energies, which we shall denote as σ₂. This quantity is used to predict the expected phase behaviors of a mixture of n-macromolecules. Note that the distribution of pairwise interactions is the same as the distribution of elements that make up the B-matrix. In the formalism of Jacobs and Frenkel, if σ₂ is small, essentially less than k_BT, and n, the number of distinct types of macromolecules is large (n being larger than the limit below which the central limit theorem does not apply), then the prediction is of the scenario depicted in Figure 5A.

If σ₂ is large (greater than 2k_BT) and n is finite, being ~10, then Jacobs and Frenkel predict that one or a small set of mutually compatible macromolecules will form a phase that coexists with a second dense phase enriched in a distinct set of mutually compatible macromolecules ^{128, 129}. Examples such as these are “water-in-water” systems ¹³⁰, where the solvent composition will be roughly the same across the two coexisting phases. This scenario is readily illustrated in synthetic systems comprising the polymers polyethylene glycol (PEG) and dextran ¹³⁰. Here, one observes the separation into coexisting PEG-rich and dextran-rich phases (Figure 5B). PEG and dextran are water-soluble polymers that are incompatible with one another. Accordingly, χ_PD is positive, whereas χ_PW and χ_DW are negative. Note that ${\chi }_{PD},{\chi }_{PW}$ and ${\chi }_{DW}$ are measures of the effective two-body interactions in the ternary mixture for PEG and dextran, PEG and water, and dextran and water, respectively. In the ternary mixture of PEG, dextran and water, the molecular components can separate into a PEG-rich and dextran-rich phase coexisting with one another. The solvent content in these phases will be determined by the favorable solvation of both polymeric systems.

If the set of n(n – 1)/2 values for the different χ parameters in the Γ matrix are dominated by the diagonal elements both in terms of magnitude and their sign, then, from a formal standpoint, n distinct phases, each enriched in one type of macromolecule, can coexist with one another and a dilute phase that is enriched in the solvent (Figure 5C). In cells ¹³¹ and even in vitro ¹³², one observes multilayered condensates ¹³³ with significant spatial inhomogeneities ¹³⁴. Such spatially organized structures, which are also observed in synthetic polymer mixtures ¹³⁵ and designed systems ¹³⁶, cannot be described by mean-field models because the order parameter Φ as used in such models only quantifies the compositions of coexisting phases, not their spatial inhomogeneities.

Overall, an assessment of the ability of a mixture of n macromolecules to undergo segregative transitions that give rise to two or more coexisting phases will be determined by the elements in the B- or Γ-matrix. The preceding discussions highlight the importance of measuring second virial coefficients in binary (macromolecule plus solvent) and ternary mixtures (pairs of macromolecules in the solvent of interest). Being able to compute the elements of the relevant B- or Γ-matrix would represent a major advance in the field. There are serious efforts underway to make this happen and building on these efforts for the assortment of associative macromolecules of different chemistries and architectures is imperative. Of course, a key challenge is that cellular milieus are complex solvents comprising an assortment of mono- and multivalent ions, region-specific concentrations of protons, osmolytes, metabolites, and small molecule solutes, and finite concentrations of seemingly inert entities that can act as macromolecular crowders. These complexities of the solvent require the accounting of coefficients that quantify preferential interaction or preferential exclusion effects. Further, crowders that are inert will take up volume and this will deplete the macromolecules of free volume, thereby inducing what is known as depletion-mediated attraction. The effects of confinement into tight spaces will also have a direct impact on the apparent solvent quality. And finally, the presence of surfaces of membranes, cytoskeletal networks, and other scaffolds of cellular structures can impact the overall solubility profiles in ways require descriptions in terms of the Gibbs adsorption isotherm ¹³⁷. Perturbations or large-scale changes to cellular volumes or components of the cellular milieu, either through active regulation or spontaneous changes in response to stimuli, will have a direct bearing on solvent quality and the driving forces for phase separation. One such physiologically relevant parameter, especially in single cell organisms or in plant systems, is temperature. Changes to temperature will drive thermoresponsive phase transitions, as we describe next.

3.6. Thermoresponsive phase behavior

Phase separation in macromolecular solutions will be responsive to changes in solution conditions ¹³⁸. In aqueous solutions, one of the parameters of interest is temperature, and the phase behavior of interest is referred to as thermoresponsive phase behavior. A polymer solution can have an upper critical solution temperature (UCST) (Figure 6A) or a lower critical solution temperature (LCST) (Figure 6B) ¹³⁸.

Figure 6: Coexistence curves for different types of thermoresponsive phase transitions.

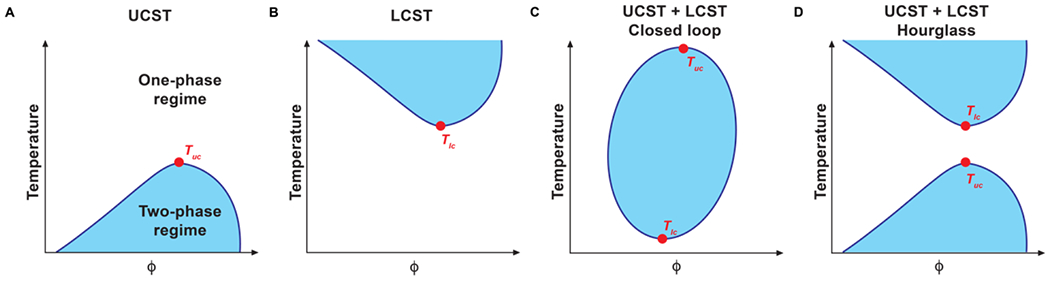
The systems depicted in (A) and (B) have an upper critical solution temperature (UCST) and a lower critical solution temperature (LCST), respectively. (C) shows a system with both a UCST and an LCST, where the two-phase regime exists between these critical temperatures, resulting in a closed loop. (D) shows a system with both a UCST and an LCST, with a two-phase regime above the UCST and below the LCST, resulting in an hourglass shape.

For systems featuring a UCST, the macromolecular solution separates into two coexisting phases below a critical solution temperature denoted as T_uc. For systems exhibiting lower critical solution temperature, the polymer solution separates into two phases above a critical solution temperature denoted as T_lc. The two segregative transitions are driven by different considerations. UCST phase behavior is primarily an enthalpically driven process. As T_uc is approached, χ approaches zero because the effective polymer-polymer interactions become less attractive, implying that χ becomes less positive.

LCST phase behavior is entropically driven and enthalpically stabilized ^{138, 139}. The entropic penalty associated with organizing solvent molecules around functional groups along the chain will increase with increasing temperature. This penalty is reduced by the release of solvent, and the segregation of polymers into a solvent-deficient phase. The interactions within the solvent-deficient, polymer-rich phase will be a combination of direct inter-polymer contacts and bridging contacts wherein components of the single or multicomponent solvent act as bridges between functional groups of the polymers ¹³⁹. Since the two types of transitions have different driving forces, it follows that a polymer solution can have access to both USCT and LCST types of segregative transitions. For homopolymers, this can be achieved by changing the composition of the solvent ¹⁴⁰. For heteropolymers, this can be achieved by the inclusion of sequence features that encode both types of transitions.

We propose, based on a growing corpus of data ^{71, 139}, that binary solutions comprising biopolymers and / or synthetic polymers in an aqueous solvent will likely have access to both UCST and LCST phase behavior ¹⁴¹ (Figure 6C). Whether the upper and lower critical solution temperatures viz., T_uc and T_lc, are in the accessible range between 0˚C and 100˚C will depend on a combination of the solution conditions, specifically the prospect of “co-(non)solvency” ¹⁴², salt concentration, pH, and hydrostatic pressure, and the types of chemistries that are dominant within the macromolecule ^{140, 142}. Some systems may even feature two closed loops, and this will give rise to apparent hourglass shapes for the coexistence curves in the accessible temperature range ^{138, 140} (Figure 6D).

4.0. ASSOCIATIVE MACROMOLECULES

The preceding discussions focused mainly on segregative transitions i.e., phase separation of macromolecules. However, biomacromolecules engage in site- and sequence-specific interactions. These interactions enable reversible associations known as binding ¹⁴³ that give rise to complexes of defined structures and numbers / stoichiometries of components ¹⁴⁴. Accordingly, we describe the networking transitions, which are purely associative in nature, that arise from accounting of site-specific or chemistry-specific interactions alone. This leads us to the concept of percolation. Once we have introduced the concepts of percolation and demonstrated how percolation thresholds are computed for systems with different numbers and types of cohesive motifs i.e., stickers, we will segue to considering the coupling between phase separation and percolation or more generally, the coupling of associative and segregative transitions.

4.1. Percolation transitions in solutions of associative macromolecules

The simplest instantiation of an associative molecule is a hard sphere with an attractive patch (Figure 7A). The patch contributes three features, namely its size vis-à-vis the size of the spherical particle, the interaction strength and range of interaction between pairs of patches ¹⁴⁵. Attractive interactions between pairs of patches enable site-specific reversible crosslinks that form between particles. In a gas of patchy particles, the strengths of attractive interactions with respect to k_BT will be the main determinant of the lifetimes of inter-particle crosslinks. In a fluid of patchy particles, the density of particles will make an additional contribution to the lifetimes of crosslinks.

Figure 7: Patchy particles and the structures they form through site-specific interactions.

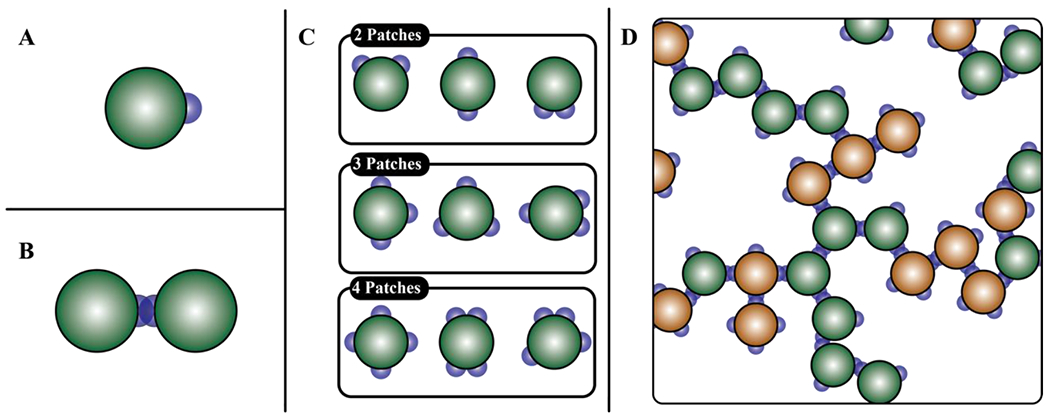
(A) Particle with a single patch. (B) Dimer formed by the interaction of particles, each with a single patch. (C) Particles with two, three, and four patches. (D) System spanning network formed by particles with three and four patches.

Janus particles have single attractive patches located at precise locations on the surfaces that are otherwise repulsive. Such systems can make dimers through the site-specific crosslinks (Figure 7B). However, these systems can also form an assortment of spatial or linear clusters that depend on the size of the attractive patch with respect to the surface area of the particle ^{62, 146}. For example, cooperative linear polymerization can be realized through clusters of intermediate size if the patch covers more than 30% of the surface of the particle ¹⁴⁷. Janus particles that are generators of various spatial or linear aggregates can now be synthesized to generate precise self-assembled geometries ¹⁴⁸. If we presume that the patches are an order of magnitude smaller than the size of the particle, then a system of particles, each with two patches, can make linear polymers.

What if each of the particles has three or more patches, where each patch is an order of magnitude smaller than the size of the particle (Figure 7C)? Clusters of various sizes will form as each particle can make reversible crosslinks with up to three different particles ⁶². New particles can be added to grow the network, thereby increasing the average size of clusters. For a given concentration of particles with three or more patches or stickers, there will be a characteristic distribution of cluster sizes defined by the range of attractions between the patches and the locations of patches on the surface of each particle. The average cluster size will grow continuously with concentration, such that above a threshold concentration known as a percolation threshold (c_perc), the particles form a system-spanning network ¹⁴⁹ (Figure 7D). As the bulk concentration of particles grows above c_perc, the network grows until all particles are incorporated into a single large cluster.

Below c_perc, the concentration of macromolecules within each of the clusters that forms can be higher than the bulk concentration c_bulk. This difference in local concentration of macromolecules within a cluster and the bulk will likely increase with cluster size, where the cluster size is defined by the number of molecules within the cluster ¹⁶. Above c_perc, the incorporation of clusters into the system-spanning network helps reset the concentration within the network to be akin to that of the bulk. The uptake of solvent by the network can cause swelling of the network. The structures of macromolecules, which determine the types and strengths of crosslinks that can form, will determine the network architecture and all the relevant material properties of the network, which is a physical gel.

Unlike phase separation, percolation is a continuous and inclusive transition rather than a first-order segregative one ¹⁶. Specifically, percolation is a geometric transition that quantifies the changes to connectivity of molecules. Therefore, the extent of connectivity for a fixed concentration or the concentration for a fixed extent of connectivity are the relevant order parameters ¹⁶. These change continuously and the transition cannot be described in terms of the coexistence of distinct pre-percolation sol and post-percolation gel phases. Therefore, the sol and gel fractions cannot and should not be estimated by equalizing chemical potentials of the sol and gel fraction. Instead, above the percolation threshold, the sol fraction is incorporated into the gel fraction. As a result, a chemically crosslinked gel can swell to include the solvent or shrink to exclude solvent. In contrast, a physically crosslinked gel can form or break apart in response to changes in solvent. The extent of crosslinking, and the topologies this generates, will set up shear stresses within the crosslinked network ⁵³. These stresses will contribute to elastic or storage moduli, and enable the generation of non-random networking of molecules that can lead to spatially inhomogeneous organizations or sponge-like architectures that have been reported for biomolecular condensates ¹¹⁷.

Percolation can happen independently of phase separation. For spherical, patchy particles, the percolation threshold can be estimated by knowing the number of patches per particle, which we refer to as the valence. The percolation threshold is also determined by the strength of each crosslink that forms when patches form reversible crosslinks with one another. The topologies of networks that emerge from percolation are determined by the sequence-specific interactions and conformations adopted by the underlying macromolecules ¹⁵⁰. The physics of patchy spherical particles can be transferred, at least via mean-field models, to describe percolation transitions of linear associative polymers ^{55, 61, 151}. In such models, a solution of associative polymers can be modeled, to zeroth order, as a gas with a finite concentration of stickers ²⁷. This is made feasible by modeling polymers above their overlap concentrations ¹⁶.

4.2. Mean-field models for percolation

In biochemical reactions, the totality of reversible associations can give rise to two types of species viz., a homogeneous distribution of clusters with a precise numbers of molecules per cluster or a heterogeneous distribution of clusters, featuring clusters of different numbers of molecules per clusters. Both types of end products can be described using the formalism of binding polynomials. The number of molecules within a cluster is referred to as the molecularity of the cluster. A microscopic binding reaction consists of clusters that form through reversible associations whereby x number of molecules come together to form a cluster via homotypic associations or x numbers of molecules of type A come together with y numbers of molecules of type B to generate a cluster with x molecules of type A and y molecules of type B. Both scenarios refer to reactions of precise stoichiometries. In the opposite limit, one can also have what are known as isodesmic associations ¹⁵². In such processes, there is an elementary association constant, and the average molecularity of a species in solution increases monotonically with concentration ¹⁵³. Macroscopically, such processes are not the same as binding, because the numbers of molecules per cluster do not have a precise upper bound, even though each microscopic step can be modeled as a binding reaction ¹⁵⁴.

We now consider a system of associative macromolecules such as patchy particles in a solvent or linear polymers with n_s stickers interspersed by spacers. The macromolecules can associate via sticker-sticker interactions. The mean-field model considers a gas of stickers. This is applicable for describing spherical particles with stickers as patches. It is also applicable for describing the sticker-sticker interactions between linear associative polymers for concentrations that lie above the overlap regime. In this regime, there is no formal distinction between intra- and intermolecular interactions ¹⁶. To keep matters simple, we shall assume that all sticker-sticker interactions are intermolecular in nature.

In the system of associative macromolecules, where each molecule features three or more stickers, each molecule can make different types of physical crosslinks pictured in Figure 8. Formally, all three crosslinks can be between the same pair of molecules, giving rise to a dimer that cannot grow (Figure 8A). This network-terminating scenario will minimize the entropy of crosslinking. However, there are other options to consider. Every option that is not a closed dimer can seed a network that can grow to a certain size (Figure 8B–C). Accordingly, for a fixed concentration of polymers, there is a threshold extent of association denoted as p_perc above which the polymers form a system-spanning network due to the network of specific physical crosslinks. If each molecule has n_s stickers and each sticker can make up to k bonds or crosslinks, then the Flory-Stockmayer criterion ^{13, 54} for p_perc is written as: $p_{\text{perc}}={\left(n_{\text{f}}–1\right)}^{-1}$ . Here, $n_{\text{f}}=k{n}_s$ is the functionality of each sticker. If k =1, then n_s = 3 is the minimum number of stickers per molecule that is required to realize a percolation transition.

Figure 8: Clusters versus percolation.

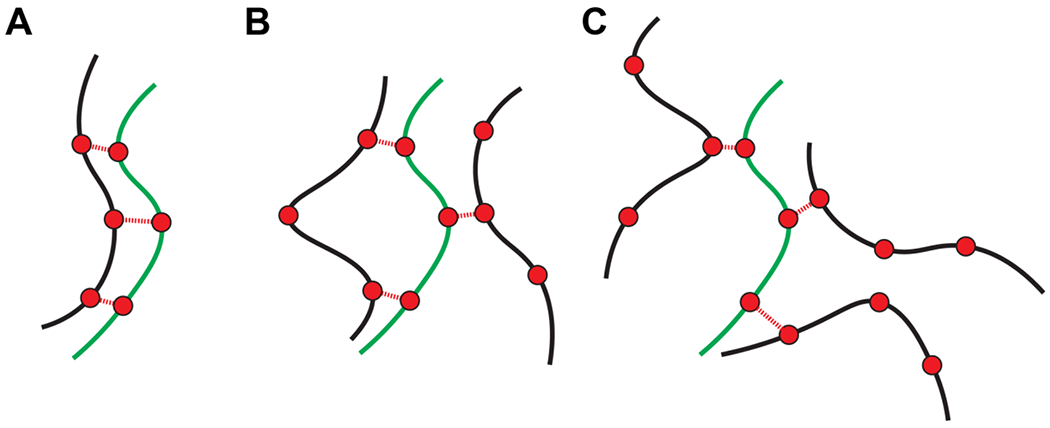
(A) A dimer forms that cannot grow into a network. (B) and (C) Trimers of different topologies featuring unsatisfied stickers that poise the system to grow and become a percolated network.

For a fixed set of sticker types, there is a threshold concentration denoted as c_perc above which the polymer solution forms a percolated, system-spanning network. The network size grows continuously above c_perc until all molecules are incorporated into the network. The topology of the network will be governed by the structures or architectures of the underlying molecules that make up the network. The value of c_perc will be determined by the numbers of stickers and the interaction strengths of stickers. The estimation of c_perc can be generalized to consider multiple sticker types such that the hierarchy of interaction strengths and valences of different sticker types will contribute directly to c_perc.

Binding reactions can drive percolation transitions, which is a geometric transition characterized by a networking of multivalent macromolecules. However, percolation cannot be described using binding isotherms. Instead, percolation requires the formal description of a networking transition – a problem that has been solved for various topologies and dimensions in mathematical theories of percolation ¹⁴. Below, we summarize models that are in the spirit of the original Flory-Stockmayer formalism for percolation ^{13, 54}. Our summary is of the model developed by Choi et al.,²⁷ as detailed in the Appendix of their work.

We consider a set of N associative macromolecules, each with n_i stickers of type i. For simplicity, we shall assume that each sticker can engage in a single physical crosslink. We consider a pair of stickers i and j that form a physical crosslink denoted as $i\leftrightarrow j$ . This leads to a gain in energy of ε_ij. The formation of a $i\leftrightarrow j$ crosslink will constrain the sticker pairs i and j to a “bond volume” v_ij. We introduce a parameter ${\lambda }_{ij}=v_{ij}\text{exp}(–{\epsilon }_{ij}/k_{\text{B}}T)$ . In the Flory-Stockmayer framework ^{13, 54}, a macromolecule that is part of a network can only make a crosslink to a free macromolecule. We shall write the free energy of the system as $F=–k_{\text{B}}T$ lnZ. Here, Z is the partition function that is computed by assuming a mean field model for a gas of stickers. It is written as:

$$Z=\text{Ω}\prod _{i,j}\exp \left(-\frac{N_{ij}{\epsilon }_{ij}}{k_{B}T}\right){\left(\frac{v_{ij}}{V}\right)}^{N_{ij}};$$ (12)

In Equation (12), i and j are the indices of the sticker types, N_ij is the total number of paired stickers of type i and j, V is the volume of the system, and Ω is a factor that quantifies the number of unique combinations of stickers that yield N_ij sticker pairs of type i-j. Minimization of F, the mean field free energy, with respect to N_ii, the number of homotypic pairs of stickers, and N_ij the number of heterotypic pairs of stickers, subject to the assumption of weak interactions, i.e., ${\lambda }_{ij}\left(N{n}_i–N_{ij}\right)/V<<1$ and ${\lambda }_{ij}\left(N{n}_j–N_{ij}\right)/V<<1$ leads to an estimate for the average number of interacting stickers per macromolecule p, which becomes:

$$p\approx c\frac{\sum _i{\lambda }_{ii}{n}_i^2+2\sum _{i\ne j}{\lambda }_{ij}{n}_i{n}_j}{\sum _i{n}_i-1};$$ (13)

Here, c is the concentration of macromolecules. According to the Flory-Stockmayer criterion ^{13, 54} , the average number of interacting stickers per macromolecule at the percolation threshold p_perc is estimated using:

$$p_{\text{perc}}=\frac{1}{\sum _i{n}_i-1};$$ (14)

Inserting the expression for p_perc shown in Equation (14) into the left-hand side of Equation (13), we obtain the following expression for c_perc:

$$c_{\text{perc}}\approx \frac{1}{\sum _i{\lambda }_{ii}{n}_i^2+2\sum _{i\ne j}{\lambda }_{ij}{n}_i{n}_j};$$ (15)

Knowledge of the number of stickers of type i, the bond volumes v_ij, and the interaction strength ε_ij is sufficient for a mean field estimate of the percolation threshold c_perc.

5.0. COUPLING OF ASSOCIATIVE AND SEGREGATIVE TRANSITIONS

In multivalent systems, there is always the formal possibility of percolation above a threshold concentration c_perc. Conversely, in a poor solvent, where v_ex is negative and χ is positive, the one-phase, well-mixed solution can become saturated, and the free energy of mixing is minimized by phase separation of the macromolecular solution that is realized beyond a χ-dependent threshold concentration designated as c_sat. The key questions are two-fold: Can phase separation (the segregative process) and percolation (the associative process) be coupled to another? And what is the nature of this coupling i.e., how do the segregative and associative transitions influence one another?

A fluid of patchy particles can undergo segregative transitions if the density crosses a threshold value. The strengths of site-specific, inter-patch interactions, and the sizes of the patches will rescale the density threshold for segregative transitions when compared to the hard sphere fluid. Accordingly, the phase transitions of a square-well fluid consisting of hard sphere molecules with a single patch are the simplest examples of systems featuring site-specific interactions that also undergo phase separation.

Phase transitions of spherical patchy particles will come under the rubric of COAST if at least a fraction of the particles have at least three patches. The system will undergo phase separation and this will depend on the sizes of particles, the densities of particles, the sizes of the patches vis-à-vis the particles, and the ranges as well as strengths of interactions between patches ¹⁵⁵. This is also true for solutions of linear or branched associative polymers where each polymer has at least three stickers that can engage in intermolecular interactions. Indeed, as shown in the literature on associative polymers, there is always the formal possibility that phase separation can be coupled to percolation ^{47, 52, 55, 156}. In a binary mixture, if we denote the threshold concentration for phase separation as c_sat, then the system will separate into two coexisting phases of concentrations c_sat and c_dense if the bulk concentration c_bulk is greater than c_sat. There are two realistic possibilities for the interplay between phase separation and percolation ^{47, 156}. If c_bulk is greater than c_sat and $c_{\text{sat}}<c_{\text{perc}}<c_{\text{dense}}$, then phase separation and percolation are coupled. Conversely, if c_perc < c_sat, then percolation is realized without phase separation.

Dense phases or condensates that form via PSCP are gel-like because percolated networks form within the dense phases. Whether the condensates have the rheological properties of solids, glasses, or liquids will depend on the interplay between the timescales for the making and breaking of crosslinks and the timescales for translational motions of molecules within the dense phase and across the phase boundary ¹⁵⁷.

5.1. The stickers-and-spacers framework

The amplitudes of the conformational fluctuations of flexible macromolecules, a feature we do not consider when discussing rigid patchy particles, will contribute directly to the behaviors of flexible polymers in different concentration regimes ¹⁶. A key parameter is the overlap volume fraction ¹⁵⁸, which is the concentration above which the likelihood of realizing intermolecular interactions is higher than the likelihood of realizing intramolecular interactions ¹⁶. The overlap concentration changes with solvent quality, decreasing significantly in a good solvent where $\chi$ is negative, and increasing to a plateau value in a poor solvent where $\chi$ is positive ¹⁵⁸. Despite the decreased overlap concentration for a homopolymer in a good solvent, the increased likelihood of intermolecular associations is offset by the relatively repulsive intermolecular interactions ¹⁵⁹. Conversely, homopolymers in poor solvents typically undergo associative transitions and phase separation at concentrations that are well below the overlap concentration. Accordingly, the overall phase behavior is determined mainly by the magnitude of $\chi$.

For associative polymers, there is an intricate interplay between the effects of $\chi$ and the contributions of sticker-sticker interactions. As a result, segregative transitions can be realized even for slightly negative, zero, or slightly positive values of χ ¹⁵¹. Here, slightly negative values refer to slightly positive values of v_ex, where v_ex is less than 10% the volume of the chemical or Kuhn monomer. The realization of segregative transitions for zero, or slightly positive values of v_ex is a consequence of three contributions viz., (i) the multivalence of associative interactions involving stickers, (ii) the cooperativity of sticker-sticker interactions in dense phases, and (iii) the fact that configurational entropy of spacers can still be maximized through a mixing of chain degrees of freedom (a consequence of overlap) within dense phases. As a result, segregative transitions are feasible for weak sticker-sticker interactions (vis-à-vis k_BT) if the sticker valence is high when compared to the minimal value of three. Conversely, for strong sticker-sticker interactions (again with respect to k_BT), lower sticker valencies will be sufficient to enable segregative transitions. Additionally, for zero, slightly positive or even slightly negative values of v_ex, the overlap concentration will be low, and it can be lowered further by increasing the degree of polymerization. This provides a boost to the associative interactions driven by inter-sticker crosslinks. What emerges is not only percolation through the network of sticker-sticker interactions, but phase separation through the effects of non-sticker regions, known formally as spacers, and synergy between associative and segregative transitions. The resultant phase transition is referred to as phase separation coupled to percolation (PSCP).

At this juncture, it would be useful to provide a brief non-chronological overview of the stickers-and-spacers framework for molecular liquids, patchy colloids, and linear associative polymers. The theory of molecular association in liquids dates to the 1950s at least. These theories were developed to explain deviations of colligative properties such as freezing point depression from expectations based on the assumption of ideal mixtures ¹⁶⁰. This led to the development of models that accounted for strong, anisotropic effects in hydrogen-bonding liquids ¹⁶¹. These were added to augment the regular solution theories of Hildebrand ¹¹³, on which the Flory-Huggins model is based. In the 1970s, considerable attention was focused on the development of polymeric materials that showed shear-thickening behaviors for application as adhesives and coatings ¹⁶². In such systems, the intrinsic viscosity of polymers increases with time and concentration ¹⁶³. These rheological properties were traced to specific features of polymers namely, the presence of multiple strong, self-associating functional groups known as stickers ^163–165. Ionomers, i.e., polymers featuring a small number of uniformly spaced ionic groups along otherwise neutral scaffolds, were among the first systems studied that came under the rubric of associating or associative polymers ¹⁶². These systems were shown to form strong physical gels. They also exhibited a range of microphases such as spherical or cylindrical micelles, the ability to form aggregates of specific size ¹⁶⁶, and the ability of micelles or aggregates to crosslink into higher order macrophases or gels ¹⁶⁷. In the 1990s the theories of associative polymers focused intensely on the roles of spacers, the regions interspersed between stickers, as modulators of percolation thresholds, and the determinants of the extent of coupling between phase separation and percolation. The key finding was that polymers with an overall χ ≈ 0 or even slightly positive could undergo phase separation due to the influence of the strong associative nature of stickers. This picture deviated from expectations based on homopolymers in a solvent. There were animated discussions regarding the merits of certain assumption, the most important being the treatment of the sol and gel as coexisting phases and the equalization of chemical potentials across the sol-gel “boundary”. These issues were satisfactorily resolved, and by 2010 a mature framework emerged ^{53, 168}, based on mean field models, for describing associations among polymers in the overlap regime, and the coupling of these associations to phase separation, which continues to be described by a Flory-Huggins formalism. Generalizations were made to describe polyelectrolytes crosslinked by multivalent counterions ¹⁶⁹. The contributions of Cates ¹⁷⁰, Freed ¹⁷¹, Halperin ¹⁷², Joanny ¹⁷³, Khokhlov ¹⁷⁴, Rubinstein ^{55, 61}, Semenov ⁵⁵, Tanaka ^{52, 60, 175}, Wertheim ^{165, 167, 176}, Witten ¹⁷⁷, and many others have inspired computational and theoretical approaches ^{29, 178} aimed at explaining a growing corpus of experimental data in the condensate field and regarding observations made for soft materials ¹⁷⁹.

5.2. Mapping stickers and spacers onto architectures of associative macromolecules

Colloidal particles range in size from nanometers to microns, and they are collections of atoms held together by strong cohesive interactions rather than by covalent bonds. In the early literature, proteins were viewed as being akin to colloidal particles. Advances in structural biology rendered such coarse-grained descriptions as being moot. However, the colloidal picture is still useful for structure-based coarse graining ¹⁸⁰ that enables analytical or semi-analytical descriptions of segregative transitions. The addition of attractive patches onto colloidal particles generates a mapping from high-resolution structural descriptions to a coarse-grained model that preserves the feature of proteins engaging in site-specific interactions. In this mapping, the patches that enable site-specific interactions are known as stickers because they enable highly specific, reversible crosslinks. The remaining surface features are collectively known as spacers. The hard versus soft interactions of spacers (which refers to the steepness of the repulsive potentials used to model steric exclusion) and the possible presence of uniform attractions mediated by spacers will be the main contributors to segregative transitions. Rigid or semi-rigid folded domains of proteins can be mapped onto patchy colloids (Figure 9A).

Figure 9: Mapping of proteins onto different physical instantiations of associative macromolecules.

(A) shows how intrinsically foldable domains (IFDs) may be mapped onto patchy colloids. (B) shows how intrinsically disordered regions (IDRs) may be mapped onto flexible, linear associative polymers. (C) shows how full-length proteins with IFDs and IDRs may be mapped onto specific combinations of patchy colloids and linear polymers. In all cases, black regions indicate spacers, and red and green regions indicate different types of stickers. Blue regions in (C) indicate oligomerization domains that behave as strong stickers.

IDRs modeled as autonomous units can be mapped onto flexible, linear associative polymers as shown in Figure 9B. Here, the stickers enable specific intra- and intermolecular crosslinks. These stickers can be short linear motifs, specific types of molecular recognition features ¹⁸¹, or individual residues. An IDR can feature many different sticker types. These include different chemistries, different sizes of stickers, and differences in the structures of the motifs that make up stickers.

In IDRs, the stickers can be uniformly distributed along the sequence, randomly distributed along the sequence, or arranged into distinct blocks ¹⁸². Depending on the number of distinct types of stickers, the segregation of stickers into distinct blocks gives rise to polymers with block copolymeric architectures ⁶¹. Such systems typically form microphases, such as spherical or cylindrical micelles or lamellae that have fixed sizes and molecularities ^{78, 79, 183}.

Associative macromolecules, specifically proteins, often feature a combination of folded domains and IDRs ⁹. Depending on whether there is oligomerization through the folded domains, the architectures can be linear, branched, or a combination thereof (Figure 9C). Further, reversible associations that give rise to oligomers of precise or variable molecularities can also enable many combinatorial options for generating associative macromolecules.

5.3. Separable contributions to segregative and associative transitions

Both patchy particles and associative polymers can undergo phase transitions that come under the rubric of COAST. The concentration regimes where these transitions become accessible can be fundamentally different for the two types of architectures. This is tied to the fact that flexible systems enable overlaps of molecules at macromolecular concentrations that are orders of magnitude lower than for rigid molecules. As a result, hybrid molecular architectures, featuring patchy colloids interspersed by flexible polymers, will provide tunability of the overall phase behavior ¹⁸⁴. The underlying architectures of associative macromolecules also affect the network topologies of dense phases formed by phase separation.

Processes that come under the rubric of COAST are driven by a combination of solubility-determining interactions, encapsulated in the osmotic second virial coefficient, and specific interactions between stickers. Formally, it is easy to prescribe a clear separation between the two types of interactions, but in practice this is difficult. To clarify this point, we first ask if there is a connection between the dissociation constant for dimer formation and the second virial coefficient. As a thought experiment or in a computer simulation, one can perform the following assessments: First, we quantify the free energy of association by an alchemical replacement of the stickers, where, for simplicity, all units along the chain are identical to one another. This free energy of association, which we refer to as ∆µ_a, is attributable solely to the contribution from the second virial coefficient. Next, we consider dimerization by adding one sticker at a time. The free energy of association that results from addition of each of the stickers is referred to as ∆µ_s, where s refers to the number of stickers that have been incorporated into the calculation. The difference denoted as $\Delta \Delta {\text{µ}}_{\text{excess}}=\left(\Delta {\text{µ}}_{\text{s}}–\Delta {\text{µ}}_{\text{a}}\right)$ quantifies the difference between the contributions of specific associations from s stickers versus solvent-mediated associations of the sticker-free system.

Solvent-mediated interactions, which drive segregative transitions, have been referred to as “non-specific” interactions ^{59, 60, 109, 185}. We do not subscribe to this type of simplification because solvent effects can be rather complex and highly specific to the macromolecules being studied ¹⁸⁶. Instead, the contributions of different interactions that we attempt to capture in our prescription of ∆∆µ_excess can be cast as a rescaling of χ, whereby the rescaled version is written as: $(\chi \prime =\chi +{\chi }_{\text{assoc.}})$ ^{52, 53}. Here, χ is the polymer-specific, sticker-free contribution of pairwise interactions to the free-energy density of a polymer solution, and ${\chi }_{\text{assoc}}$ quantifies how χ is augmented by the contributions of specific sticker-sticker interactions.

Although the contributions to χ and ${\chi }_{\text{assoc.}}$ are formally separable, this can be non-trivial from an experimental standpoint. One way of approaching this is to use two distinct assays. A scattering-based assay or measurements of colligative properties, which averages over all configurations of the polymer and solvent, yields an estimate of B₂ and hence χ. This can be complemented by a site-specific assay for binding, such as one that quantifies the change in quantum yield of the intrinsic fluorescence or changes in fluorescence lifetimes of locations proximal to the site of interest, coupled to mutagenesis, which can be used to infer ${\chi }_{\text{assoc.}}$ by referencing it to the measurement of B₂ for the mutant that lacks the sticker(s). In this approach, the contribution of specificity is the contribution to the pairwise dissociation constant that cannot be explained by the contribution from B₂ alone. Alternatively, one can compare calorimetric enthalpies to enthalpies derived from the measured osmotic second virial coefficients. The difference between these enthalpies represents the contribution from specific interactions.

Importantly, for a fixed set of solution conditions, the osmotic second virial coefficient is a quantification of the effective strength and nature of pairwise associations of macromolecules in solution. It quantifies an effective free energy of dimerization in solution and can only describe the formation of higher-order assemblies based on pairwise interactions among the molecules. However, higher-order associations whereby the assembly cannot be thought of as a sum of dimers, will require the consideration of higher-order terms in the virial expansion. Accordingly, in the rescaling of χ, the ${\chi }_{\text{assoc.}}$ term often features a concentration dependence to account for higher-order species that can be generated by site- or residue-specific inter-sticker interactions ^{52, 53}.

Overall, the addition of stickers, i.e., associative groups to a macromolecule, will rescale the effective two-body interactions and require that we consider more than just the second virial coefficient, which, as we have discussed, is the primary determinant of polymer solubility ^{52, 53}. These considerations are incorporated into ${\chi }_{\text{assoc.}}$, which will also be concentration-dependent to allow for the prospect of pre-percolation clusters forming and growing continuously with concentration ^{52, 53}.

The most tractable and well-studied system for understanding PSCP transitions are linear multivalent proteins (Figure 9C). Here, pairs of multivalent proteins make complementary, site-specific interactions through their folded domains. Well-established examples include the poly-SH3 and poly-PRM as well as the poly-SUMO and poly-SIM systems in aqueous solvents ^{1, 46–48, 126, 187}. Here, the folded domains encompass stickers at specific sites. These sites make complementary heterotypic interactions viz., SH3 with the PRM and SUMO with the SIM. The linkers are the primary spacers that contribute to the excluded volume and hence to the coupling between segregative and associative transitions ¹⁸⁸. The surfaces of folded domains, specifically their electrostatic features governed by both homotypic and heterotypic interactions, can also contribute to the osmotic second virial coefficient ^{46, 48, 187, 188}. Therefore, the surfaces of folded domains may be viewed as auxiliary spacers. These surfaces can also contribute as auxiliary stickers based on the presence of complementary motifs within the linkers and the surface of the folded domain.

Harmon et al., studied the simple example of a patchy-colloid-like folded domain and a disordered linker that lacks any auxiliary motifs ⁴⁷. Further, the excluded volume, which they referred to as the effective solvation volume (v_es), of the linkers was set to be zero or greater than zero. Harmon et al., showed that linkers for which v_es = 0 will undergo PSCP-like transitions. They discerned this using two distinct order parameters, one for detecting segregative transitions and the other for associative transitions. For the former, the relevant order parameter is the concentration of macromolecules. For the latter, the relevant order parameter is the connectivity of molecules and hence the number of molecules within the single largest cluster. Choi et al., later formalized the distinction of the two order parameters, using radial distribution functions to detect the onset of spatial inhomogeneities and the presence of two phases of two different macromolecular densities, namely, a dense and a dilute phase ¹⁸⁹.

The coupling of segregative and associative transitions can be quantified by computing c_perc using generalizations of Flory-Stockmayer theory^{13, 54}. The mean field theories for gelation put forth by Flory ¹³ and Stockmayer ⁵⁴ allow one to estimate c_perc just by knowing the valence and intrinsic affinity of the stickers. In particular, the Flory-Stockmayer theory allows one to estimate the threshold concentration above which a system-spanning network is formed by a gas of stickers as described above in Section 4.

Harmon et al., computed a ratio they referred to as c′, which they defined as the ratio of the percolation threshold estimated from their simulations to the percolation threshold estimated based on the mean-field Flory-Stockmayer theory ^{13, 54}. If c′ < 1, then tethering the stickers to linkers enables a positive cooperativity of the percolation transition. This positive cooperativity implies that the percolated network is realized at concentrations that are lower than would be feasible for a gas of stickers. This comes about due to a coupling of associative and segregative transitions and the formation of a dense phase that is in essence gel-like. Further, the probability of forming a new inter-sticker crosslink is enhanced in the presence of an extant crosslink, and this positive cooperativity is enabled in the dense phase and is facilitated by the linkers of zero effective solvation volume.

Essentially, the segregation into dense and dilute coexisting phases is an emergent property of the coupling between the flexible nature of the spacers, their solvation preferences, and the associative, specific interactions of the stickers. Although Harmon et al., did not study what transpires when v_es is negative (i.e., χ > 0), the expectation for this scenario is intuitive in that segregative transitions can be enhanced by the properties of the spacers. Such a scenario can lead to precipitation if the spacers become strongly segregative, which would happen if the positivity of χ increases substantially vis-à-vis the dissociation constant of sticker-sticker interactions.

For linkers of zero or slightly negative v_es, the segregative and associative transitions can be fully decoupled if the linkers are long, or if the intrinsic sticker-sticker interactions are not much stronger than k_BT. In this scenario, percolation, in accord with Flory-Stockmayer theory, will occur without phase separation ⁴⁷.

Interestingly, up to a point, the PSCP behavior is preserved even for positive values of v_es (i.e., negative values of χ) ⁴⁷. However, depending on the interplay between the affinity of sticker-sticker interactions and the magnitude of the positive v_es (negative χ), the segregative transition can become significantly destabilized. Large positive values of v_es, specifically those that approach the upper limit of v_es, will suppress phase separation. Further, the high effective solvation volumes of the spacers will also hinder the networking transitions, thus causing an upshift of c_perc when compared to the Flory-Stockmayer limit.

Taken together, the domain-linker plus motif-linker systems allow for a clear delineation of stickers versus spacers. This has allowed for the extraction of rules that enable the design of systems where the associative percolation transition and segregative phase separation can be strongly coupled or fully decoupled. The relevant parameters are the sticker valence, the sticker-sticker interaction strengths, the effective solvation volumes of spacers, and the flexibility and length of spacers / linkers.

Recent work has shown that the findings can be transferred onto IDRs studied as autonomous units. This requires more elaborate efforts to delineate stickers and spacers, bringing to bear the combination of experimental and computational methods that are also deployed for the study of sequence-ensemble relationships of IDPs ^{64, 66}. The overall approach to identifying stickers versus spacers leverages the one-to-one correspondence between the interactions that contribute to collapse transitions of individual polymers in ultra-dilute solutions and the multichain interactions that contribute to phase separation ^{3, 63, 64, 66}.

5.4. Associative macromolecules form pre-percolation clusters in subsaturated solutions

In their work on the phase transitions of linear multivalent proteins, Li et al., described their observations as being “macroscopic liquid-liquid phase separation that is thermodynamically coupled to sol-gel transitions in the droplet phase” ⁴⁶. This phrasing describes PSCP, which is a process that comes under the rubric of COAST.

Depending on the strengths and valence (number) of stickers, associative macromolecules can form clusters at very low concentrations. Clusters that form below c_sat are referred to as pre-percolation clusters that form in the sol or pre-gel when describing gelation or percolation decoupled from phase separation. For a given bulk concentration c_bulk that is below the saturation concentration $\left(c_{\text{bulk}}<c_{\text{sat}}\right)$, the distribution of cluster sizes, $p\left(n_{\text{cluster}}|c_{\text{bulk}}\right)$ will be determined by the sticker valence, the sticker-sticker interaction strengths, and the macromolecular concentration c_bulk or, more precisely, the degree of sub-saturation defined as $s_{\text{sub}}=\text{ln}\left(c_{\text{bulk}}/c_{\text{sat}}\right)$. The reversible associations will be describable by a series of microscopic reversible steps ⁵².

The expectation of polydisperse clusters in a sol provides a definitive test for whether the process of condensate formation is purely segregative or if it comes under the rubric of COAST ⁵². For purely segregative transitions, the subsaturated solutions defined by the bulk concentration being below c_sat are best described as a disperse gas of unassociated macromolecules ¹⁹⁰. The key point is that for purely segregative transitions, the only relevant energy scale in a binary mixture will be prescribed by χ. Clustering in sub-saturated solutions will be bounded, because the likelihood of cluster formation, which will change with s_sub, will become zero for clusters comprising small numbers of molecules ¹⁹⁰. However, if associative and segregative transitions are coupled, then the subsaturated solution is a sol, defined by an assortment of clusters characterized by reversible crosslinks. The size distribution of pre-percolation clusters is typically heavy tailed (Figure 10), implying that, while most of the species in solution are likely to be dispersed monomers and oligomers, there is a finite likelihood of observing mesoscale clusters ¹⁹⁰.

Figure 10:

Schematic of an exponentially bounded (black dashed curve) versus heavy-tailed (red solid curve) version of p(n_cluster|c_bulk).

In a sol-like description for the coexisting dilute phase, the likelihood of forming polydisperse clusters will increase with increasing concentration. Recent in vitro studies provide definitive evidence for the presence of heterogeneous distributions of pre-percolation clusters in subsaturated solutions ¹⁹⁰. Detecting these species requires the use of a combination of methods in vitro that allows one to access the totality of species that form in subsaturated solutions ¹⁹⁰. Each of the methods used by Kar et al.,¹⁹⁰ has distinct advantages and limitations. Dynamic light scattering (DLS) is sensitive to the most abundant species and the largest, least abundant species. However, the abundance of distinct species cannot be quantified using DLS. Instead, nanoparticle tracking analysis (NTA) was needed to quantify abundance ¹⁹⁰. However, this too is a scattering-based method, and hence only the abundance of the largest species, which is in the 1% range or lower depending on bulk concentration could be quantified. Methods based on measurements of fluorescence anisotropy or fluorescence correlation spectroscopy (FCS) were also used, and these relied on the use of mixtures of unlabeled and fluorescently tagged proteins ¹⁹⁰. However, anisotropies plateau past a certain size, as explained by Kar et al., ¹⁹⁰ and the ability to detect species that grow becomes increasingly challenging using FCS because of the low mobilities and low abundance of such species. These limitations were overcome using methods based on ultrafast mixing and confocal detection in microfluidic channels ¹⁹¹. In these methods, one separates mixing of species from transport, and hence one can get a full readout of the entire size distribution. Fluorescence anisotropy measurements using free-to-move molecular rotors ¹⁹² coupled to fluorescence intensity distribution analysis provided the most definitive assessments of the continuous evolution of size distributions and the heavy-tailed nature of these distributions as a function of protein concentration. Kar et al., ¹⁹⁰ brought all these methods to bear on the quantification of species distributions in sub-saturated solutions of the protein FUS and other FET family proteins. These measurements, performed at a series of sub-saturations, provided definitive evidence of the presence of monomers, oligomers, and mesoscale clusters ¹⁹⁰.

A recent complementary study focused on the distribution of species formed in sub-saturated solutions of the proteins Rubisco and EPYC1 ¹⁹³. These studies largely corroborated the findings of Kar et al., with one discrepancy. The authors noted the absence of a heavy tailed distribution and an absence of mesoscale species. They proposed that this might be due to differences in the cluster landscape organized by heterotypic interactions versus purely homotypic interactions. This may well be true, and ongoing studies will help clarify the role of the interplay between homotypic and heterotypic interactions as determinants of cluster distributions. However, it is worth emphasizing that the work of He et al., ¹⁹³ used only FCS, and this has intrinsic limitations as explained in detail by Kar et al., ¹⁹⁰.

In vivo, the most striking example of pre-percolation clusters comes from work on the nuclear protein negative elongation factor (NELF) that forms condensates in response to stress, thereby arresting transcription thus functioning as intranuclear stress granules ¹⁹⁴. Using confocal microscopy, Lan et al., noted a uniform distribution of NELFs in the nucleoplasm when stress is absent ¹⁹⁵. However, using highly inclined and laminated optical sheet microscopy, Lan et al., discovered that NELF proteins form a polydisperse distribution of clusters in the nucleus ¹⁹⁵. The size distribution of clusters has a heavy-tailed shape. Interestingly, at the onset of stress, the clusters condense to form condensates that sequester essential transcription factors. The sol that coexists with condensates features distributions that are reminiscent of what they observe at ultra-low expressions. When the MAP kinase P38 is inhibited, condensates do not form, but the clusters persist. Lan et al., postulate that the multisite phosphorylation of the NELFs enables a change in stickers that drives condensate formation. Their work demonstrates a clear separation of interactions that drives clusters versus condensates. The IDRs in the NELFs are essential for cluster and condensate formation as well. One of the key takeaways is that the free-energy profiles for condensate formation, which they extract from their data, are rather flat ¹⁹⁵. This supports the proposal we make below for homogeneous nucleation not being the mechanism by which condensates form. Further, the in vitro and in vivo studies that use multipronged approaches highlight the weaknesses of drawing definitive conclusions based on one set of methods, especially when the methods in question have diffraction limited spatial resolutions. There is clearly much to learn by integrating measurements that probe the nano-, meso-, and micron-scales. And the integrated contributions of segregative and associative effects are likely to become clear only through interrogations that span the multitude of length scales. A recent study highlights the importance of multiscale, multi-resolution studies of condensate structures and the fact that networks of interactions undergird condensate structures ¹⁹⁶. The sponge-like structures observed by Gall and colleagues for nucleoli and Cajal bodies ¹¹⁷ are evident even for the simplest of condensates, both computationally ³, and experimentally ¹⁹⁶.

5.5. Implications of pre-percolation clusters for dynamics of phase transitions

The local concentration of macromolecules within clusters will be higher than c_bulk. Notice that such concentration inhomogeneities are also present in atomic and molecular liquids as is evident in the peaks and troughs of radial distribution functions ^{30, 102}. The concentration inhomogeneity within a cluster comprising n_cluster molecules can be defined as $\psi =\left(c_{\text{B}ulk}/c_{cluster}\right)$. Here, c_bulk and c_cluster are the concentrations of macromolecules within the bulk and cluster, respectively. An inhomogeneity refers to values of ψ being less than or greater than one. Values of ψ < 1 are realizable through intermolecular associations. The expectation is that the inhomogeneity ψ becomes more pronounced, decreasing to be below one, as cluster sizes increase. While this is not what we expect for a distinct phase of uniform density, the finite sizes of clusters allow for this scenario as a formal possibility. Further, the overall solubility sets up c_sat, the threshold concentration above which the one-phase regime is saturated. Accordingly, the buildup of local concentration inhomogeneities through cluster formation will be governed by the structure (functional form) of the cluster distribution $p\left(n_{\text{cluster}}|s_{\text{sub}}\right)$, which quantifies the probability of realizing a cluster with n_cluster molecules for a given subsaturation s_sub.

The combination of the system becoming supersaturated for $c_{\text{bulk}}>c_{\text{sat}}$ and the concentration inhomogeneities engendered by pre-percolation clusters of size n_cluster will drive a combination of segregative and associative (networking) transitions. The dynamics of the coupling between clustering and macroscopic phase separation were recently measured by Kar et al., using dynamic light scattering and time-resolved microscopy ¹⁹⁰. These data provide a qualitative picture of the transition from pre-percolation clusters in the sub-saturated sol to a coexistence of the sol with dense condensates featuring percolated networks of macromolecules.

The presence of pre-percolation clusters appears to rule out homogeneous nucleation and growth as the operative mechanism for a COAST-like process. Homogeneous nucleation rests on the notion of a single energy scale defined by χ ^{87, 197}. This can only be operative for a purely segregative transition that lacks any surface defects or seeds. Instead, describing the dynamics of a COAST-like process such as PSCP requires that one accounts for the presence of pre-percolation species that form and dissolve on timescales that are considerably more rapid than the time it takes for condensate formation via homogeneous nucleation, coarsening, or some variation thereof.

A reasonable postulate is that pre-percolation clusters enhance the rates for phase separation in supersaturated solutions because the clusters poise the system for segregative transitions. It is also conceivable that pre-percolation clusters erect a sort of kinetic proof-reading barrier if the clusters are to undergo significant rearrangement within the condensate, or new interactions must be added to drive condensate formation. The latter has been reported recently to explain the transition of NELF clusters to NELF condensates in the context of forming condensates that sequester essential transcription factors in response to nuclear stresses ¹⁹⁵.

5.6. Examples of systems that undergo phase separation coupled to percolation

There are several examples of multivalent proteins that drive PSCP. The importance of multivalence was established in the domain-linker-domain systems interacting with motif-linker-motif systems that Li et al., studied ⁴⁶. This work showed how valence matters for associative transitions. It also showed that the result of phase transitions are spherical droplets that are now referred to as condensates. These dense phases cannot come from percolation alone. However, the formation of dense phases can be explained by understanding the roles of linkers, which were resolved by Harmon et al., ⁴⁷.

A clear prediction for PSCP would be the observation of pre-percolation clusters conforming to a heavy-tailed distribution that should form in sub-saturated solutions. Li et al.,⁴⁶ reported what they termed as oligomers. Kar et al., showed that polydisperse clusters form in sub-saturated solutions ¹⁹⁰. Their observations were concordant with a heavy-tailed distribution. Support for these observations in vivo comes from the work of Lan et al.,¹⁹⁵ which we have already summarized.

In their recent molecular cartography inside cells, Cho et al.,¹⁹⁸ made an interesting observation. They found that components of stress granules, specifically ATXN2L, NUFIP2, and FXR1, which are all RNA binding proteins, have “texture” in terms of their cytoplasmic colocalization even in the absence of stress. In their parlance, texture refers to detectable preferential localization. Given the resolution of their approach, colocalization refers to the types of pre-percolation clusters observed by Kar et al., in vitro, and Lan et al., in the nucleus. RNA binding proteins with multiple RNA recognition motifs tethered by a combination of prion-like low complexity domains and Arg-rich IDRs seem to be prominent drivers of pre-percolation clusters via homotypic interactions. Heterotypic interactions with RNA transcripts likely modulate the cluster distributions and / or coopt pre-percolation clusters to form condensates.

Work on the UBQLN2 system has identified stickers that contribute to modulating the phase boundary, whereas spacers alter the material properties ¹⁹⁹. These results build on the findings of Wang et al., ⁶⁵ for the FET family proteins. They observed a clear correlation between joint valence of Arg and Tyr stickers and the percolation threshold, which also tracks with the saturation concentration (a measure of phase separation). However, changes to spacers largely left c_sat and the percolation thresholds unchanged. They did, however, have a direct impact on the material properties of condensates, including their aging dynamics. This work led to the development of a generalized theory to account for the presence of multiple sticker types within associative macromolecules ²⁷.

Direct experimental evidence for PSCP and the fact that PSCP leads to network structures within condensates comes from work of Bremer et al., ⁶⁶ and Farag et al, ³. A recent computational study leverages the findings of Bremer et al., ⁶⁶ to show that the internal structures of macromolecules within condensates follows graph theoretical expectations of small-world percolated networks ³. These features result directly from the hierarchy of interactions that are encoded by the stickers and the very different interactions, namely solubility-determining ones, that are controlled by the spacers ³. The predictions of spatial inhomogeneities within condensates formed by PLCDs and other low complexity domains was borne out in recent single molecule imaging studies reported by Wu et al., ¹⁹⁶.

A common method by which spacer properties are leveraged to modulate PSCP in biology appears to be post-translational modifications. These modifications can change the driving forces for segregative transitions by enabling significant changes to v_es, especially if the modifications add or delete charged residues that increase the overall net charge per residue ⁴⁷. Post translational modifications can also impact associative transitions and the overall coupling inherent to processes defined by COAST by modulating sticker valences or sticker diversity, and hence impacting the hierarchy of sticker-sticker interactions. For example, phosphorylation of spacer residues, namely serine and threonine residues, has been observed to impact phase behavior, activity, and function for RNA Polymerase II (Pol II) ²⁰⁰. These multisite phosphorylation reactions place negative charges on the corresponding spacer residues, thereby increasing their contributions to v_es and adding de novo electrostatic interactions.

In the context of Pol II, Guo et al., ²⁰⁰ found that the conversion from hypo-phosphorylated Pol II to hyper-phosphorylated Pol II is associated with a shift from Pol II integrating into transcriptional condensates, which contain high concentrations of mediator complex proteins, to Pol II integrating into splicing condensates, which contain high concentrations of serine-arginine dipeptide rich (SR-rich) proteins ²⁰¹. The implication is that hypo-phosphorylated Pol II interacts with mediator complex proteins, such as MED1, via specific IDR-IDR interactions, whereas hyper-phosphorylated Pol II interacts with SR-rich proteins, such as SRSF2, via electrostatic interactions. Importantly, hypo-phosphorylated Pol II is not recruited to splicing condensates and hyper-phosphorylated Pol II is not recruited to transcriptional condensates, suggesting that these changes to spacer residues, and hence the driving forces for segregative transitions, as well the coupling between associative and segregative transitions, change the interactions that dominate Pol II PSCP and the specificity of recruitment into condensates.

Other post translational modifications that modulate the effects of spacer residues include acetylation, which, unlike phosphorylation, neutralizes charged residues. For example, Bock et al., discovered that N-terminal acetylation of the FUS protein had a negligible effect on monomeric conformations but they still promoted phase separation ²⁰². It is worth noting that these and other studies focus mainly on quantitative assessments of the order parameter for phase separation. The consequences of the coupling to associative transitions, namely percolation, are seldom if ever investigated in vitro or in live cells. This requires an investigation of the spatial organization of molecules within condensates ^{131, 196}. In this context, the findings of Qamar et al., ²⁰³ highlighted the polydispersity of FUS sequences that are generated by mono-methylation, symmetric di-methylation, and asymmetric di-methylation of Arg residues in FUS. Even though these modifications do not alter the charge of Arg, they likely influence the hierarchy of sticker-sticker interactions involving Arg residues from disordered Arg-rich regions within FUS and other FET family proteins.

5.7. Complex coacervation

Aqueous solutions of oppositely charged macromolecules can undergo spontaneous phase transitions that are known as complex coacervation ^{76, 204}. Although the formation of a dense coacervate phase is usually associated with phase separation alone, a percolation transition will also occur, due to the macromolecules interacting via reversible physical crosslinks. Here, the crosslinks are primarily ionic interactions. We distinguish complex coacervation from PSCP that is based on short-range interactions, because of the focus in the former is on long-range electrostatic interactions that drive the intermolecular associations among oppositely charged macromolecules and the contributions of counterion release to the driving forces for phase transitions.

Complex coacervation involves different types of linear, flexible oppositely charged polymers ²⁰⁵. It can also be realized by interactions involving low-molecular weight surfactants and / or nanoparticles. Studies of synthetic polymeric complex coacervates have been useful for mapping out the phase behavior as a function of salt, pH, and temperature ^{205, 206}. For example, in recent work Neitzel et al., ²⁰⁵ studied the coacervation of co-polyelectrolytes with equivalent fractions of charged and neutral ethylene oxide monomers incorporated into the sequences of the polymers. This provides a titration of the charge content and its effect on the properties of coacervates and the salt dependence of complex coacervation.

We are starting to learn more about the complex interplay of complementary charge-charge interactions, the release of counterions (Figure 11A), the preferential accumulation or depletion of solution ions (Figure 11B), the impact of linear patterning of ionic groups (Figure 11C), and the effects of charge regulation whereby proton uptake and release can modulate the charge densities of associating macromolecules (Figure 11D). In their thermodynamic characterization of complex coacervation of poly(ethylene-imine) with either poly-aspartic acid and / or poly-glutamic acid, Priftis et al., ²⁰⁷ discovered that complex coacervation is driven by the release of counterions and enthalpically disfavored. Further, the water content of coacervates was found to be dependent on the salt concentration, highlighting the modulation of water activity as an important feature of coacervation.

Figure 11: Schematics summarizing the physical principles of complex coacervation.

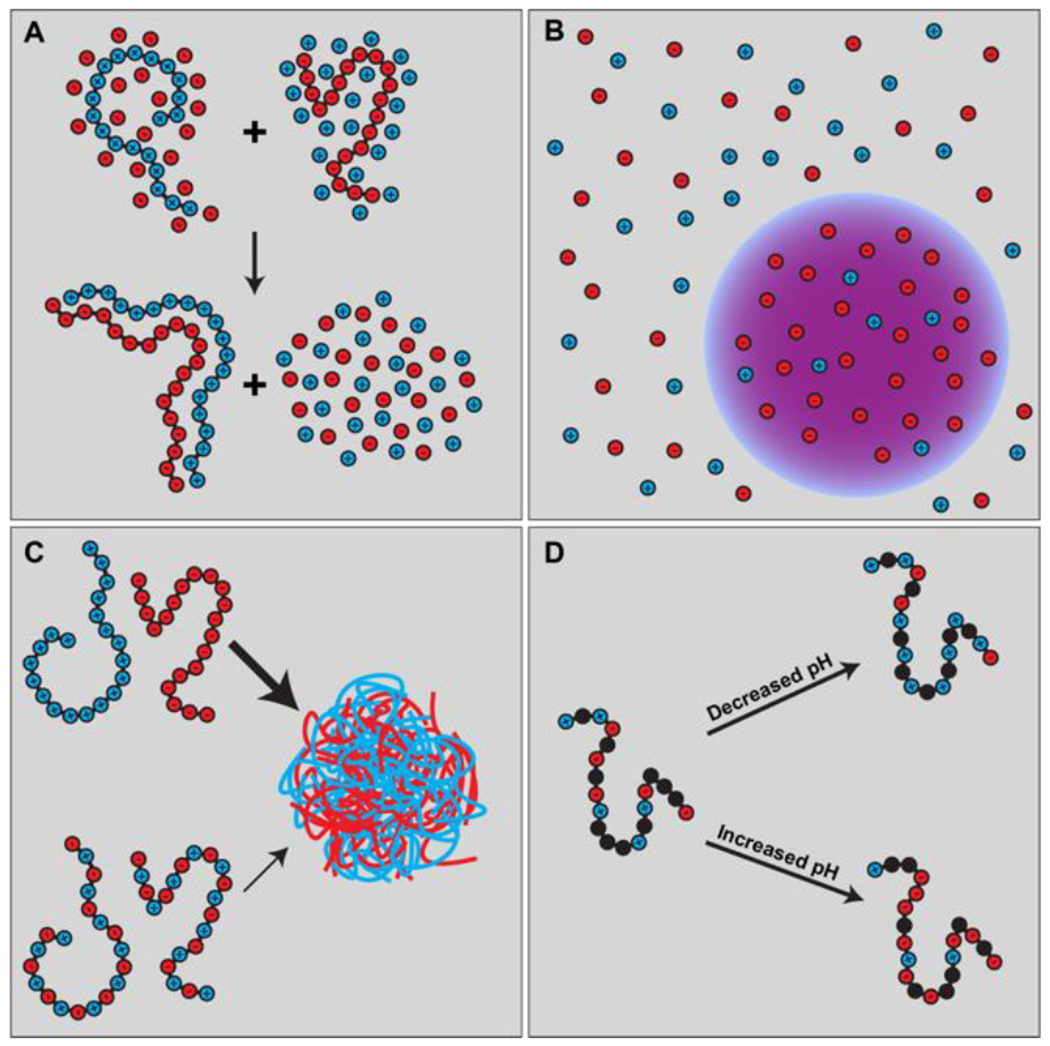
(A) Two polyelectrolytes, a polycation (left) and polyanion (right) can form a complex driven by a combination of complementary electrostatic interactions and the release of counterions. (B) and (C) show the formation of coexisting dilute and dense phase (coacervate) from the vantage point of the salt (B) and the polyelectrolytes (C). (D) The charge states of ionizable residues will be sensitive to pH and this can affect the complexation and coacervation of polyelectrolytes and polyampholytes (schematic shows the latter).

Complex coacervation is a phenomenon wherein association via complexation drives segregative behavior. Simple theories such as the mean-field theory of Voorn and Overbeek ²⁰⁸ have provided a useful starting point, even if the tenets of this theory have not held up to close scrutiny. The Voorn-Overbeek theory provides a prescription for the free-energy of mixing. It simply adds to the Flory-Huggins formalism by including a Debye-Hückel term for the electrostatic interactions. The overall expression for the free energy ∆F_VO has the form:

$$\frac{l^3\Delta F_{\text{VO}}}{V{k}_{B}T}=\sum _i\frac{{\text{ϕ}}_i}{N_i}\text{In}{\text{ϕ}}_i+\frac{1}{2}\sum _{i,j}{\chi }_{ij}{\text{ϕ}}_i{\text{ϕ}}_j-\alpha {\left(\sum _i{\sigma }_i{\text{ϕ}}_i\right)}^{\frac{3}{2}};$$ (16)

In a system of volume V, the first two terms on the right-hand side of the equation correspond to the entropy of mixing and the energy of mixing. The third term incorporates the contributions from electrostatic interactions for Kuhn monomers of length l. The summand in the third term involves σ_i, which is a ratio of the number density to the volume fraction of the charges for the i^th type of macromolecule. The proportionality constant α modulates the strength of the electrostatic interactions as a function of the thermal energy ⁴⁹.

For a three-component system consisting of two oppositely charged polyelectrolytes and a complex solvent comprising water and solution ions, the theory predicts demixing, as given by the negative curvature of the free energy as a function of the volume fraction $\text{ϕ}$. Including the effects of salt requires a description of the phase behavior now in terms of three order parameters, namely the volume fractions of the two polymers ${\text{ϕ}}_{P1},{\text{ϕ}}_{P2}$, and the volume fraction of the salt in question, ϕ_S ⁷⁶. Assuming a 1:1 ratio of the complexing polyelectrolytes, it follows that ${\text{ϕ}}_{P1}={\text{ϕ}}_{P2}={\text{ϕ}}_P$, and the phase diagram of interest becomes a projection onto the plane $\left({\text{ϕ}}_P,{\text{ϕ}}_S\right)$.

Progress is being made to incorporate the effects of correlations, which are expected to be significant, given that ionic groups are tethered to make polymers. Perry and Sing adapted liquid-state integral equation theories, specifically the polymer reference interaction site model to account for excluded volume and chain connectivity in their descriptions of complex coacervation ²⁰⁹. The transfer matrix model of Sing and coworkers ²¹⁰ incorporates the effects of proton binding and release ²⁰⁶ as well as the release or preferential uptake for solution ions as drivers of coacervation. By enumerating all possible adjacent pairwise interactions, they calculate the grand canonical partition function for a polymer chain in an ionic solution, thereby accounting for pH effects. Their model can also be applied to study the effects of charge patterning on the phase behavior ²¹¹. Separate studies by de Pablo, Tirrell, and coworkers have analyzed the importance of charge blockiness for cooperativity in polyelectrolytic coacervates ²¹¹. The more biologically relevant cases involving polyampholyte mixtures are not well understood, even though polyampholytes are useful models for many IDRs ²¹².

The importance of complex coacervation, especially for understanding the formation and regulated dissolution of various nuclear bodies cannot be understated ²¹³. In fact, one can think of the nucleus as a set of coexisting phases, each forming under the regulation of a network of complex coacervation processes. Therefore, each nuclear body may be viewed as a distinct complex coacervatome – a term that emphasizes the fact that these bodies form via the collective phase behaviors of networks of polyelectrolytes and polyampholytes that are further regulated by solution ions (charge renormalization), proton uptake and release (charge regulation) ²¹³, and active processes such as enzyme catalyzed post-translational and post-transcriptional modifications. Never has it been more imperative that we go beyond simple synthetic systems – even though they are already quite challenging ²¹⁴ – and study complex mixtures of multivalent associative macromolecules that undergo networked complex-coacervation-type phase transitions.

Pak et al., interrogated the complexities of complex coacervation in live cells ²¹⁵. Their findings uncovered numerous surprises, including the discovery of stickers, which they referred to as charge interacting elements. The recent works of Greig et al., ²⁰¹ and King et al., ²¹⁶ point to some of the advances that are underway to interrogate complex coacervatomes in live cells and as reconstitutions.

5.8. The Sweatman model of short-range attractions and long-range repulsions

Sweatman has proposed an alternative to macrophase separation that is based on a model that invokes the interplay of short-range attractions and long-range repulsions (SALR). This SALR model is intended to describe how in vivo facsimiles of condensates might come about ⁸⁵. Inspiration for the SALR model comes from the behaviors of charged colloidal particles in aqueous solutions. As noted by Sweatman, SALR allows for the formation of size-limited, liquid-like, or solid-like clusters within a gas or liquid.

For systems characterized by short-range attractions and long-range repulsions, the free energy of the system is minimized for finite cluster sizes ⁸⁵. The merits of this proposal were tested using Monte Carlo simulations based on local and cluster moves. The simulations were performed with single-component systems in an implicit solvent. The main tenets of SALR can be mapped onto models introduced decades ago to distinguish diffusion-limited colloidal aggregation ²¹⁷ versus reaction-limited colloidal aggregation ²¹⁸. In diffusion-limited colloidal aggregation, uniformly sticky particles form open, fractal-like structures because the rate of influx in the non-equilibrium system is considerably faster than the reconfiguration times of clusters and the particles therein. Conversely, in reaction-limited colloidal aggregation, the cluster growth and hence the resultant morphologies are tied to whether the colloidal particles are in the right orientation to associate or react.

Sweatman’s model introduces the competing effect of long-range repulsions. The presence of the latter engenders an instability for clusters beyond clusters that go beyond a certain size. Accordingly, associative particles with a net charge can grow to a certain size via short-range attractions. Beyond a certain size threshold, which depends on the valence of patches that drive attractive interactions and the magnitude and range of the repulsions among collections of particles, an instability sets in, and this leads to clusters or mesophases of fixed size. It appears that the recent observations of Petry and coworkers ²¹⁹ might well fit into the SALR framework.

Sweatman has argued that the SALR-like behavior of colloidal systems is likely to be a plausible explanation, as compared to macrophase separation, for the observation that condensates within cells do not grow beyond a certain size. The suppressor of coarsening behavior in cells that comes from SALR-like behavior is proposed to involve crowding-induced depletion-mediated attractions at short range ²²⁰. However, the source of the emergence of long-range repulsions is unclear, although the assumption is that this comes from the buildup of clusters of molecules that have a net charge. Early work by Potemkin et al.,²²¹ showed that in solutions of associating polyelectrolytes, an interplay between the energetics of sticker-sticker interactions and the translational entropy of counterions can create regimes in the space of temperature and salt concentration where macrophase separation is suppressed and clusters of optimum sizes are formed. This suggests that the balancing of forces is always a possibility and it does not require the invoking of active processes to achieve clusters of optimal sizes ⁸⁴.

6.0. FULL PHASE DIAGRAMS FOR ASSOCIATIVE MACROMOLECULES

6.1. Single type of macromolecule in a solvent

We now turn to the topic of constructing phase diagrams and interpreting relevant features. To start, we shall consider the example of an associative macromolecule in an aqueous solvent. Of course, the solvent is never just deionized water. Instead, it comprises a complex mixture of solutes, ions, and buffering agents, in addition to water. All components will have an influence on the overall phase behavior, especially the segregative transition, via the Flory χ parameter. For a fixed set of solution conditions, one can assess how the phase behavior changes with temperature. This is readily achieved in vitro ^{66, 118, 136, 222}, and recently, Fritsch et al., measured a full phase boundary in the (ϕ, T) plane in live cells ¹⁰. For each of the temperatures one can access, measurements have been reported that quantify c_sat and c_dense for a variety of systems. The locus of these points constitutes the coexistence curve. For a given temperature, a tie line connects the concentrations of the coexisting phases. Since the temperature is uniform across the system, the tie line is horizontal for a coexistence curve that is plotted on the (c, T) plane, where c = c_bulk is the bulk macromolecular concentration. Note that c_sat and c_dense will vary with temperature. Measurements for various systems with UCST behavior show that c_sat increases by orders of magnitude as temperature increases ⁶⁶. In contrast, c_dense changes minimally with temperature.

Impressively, coexistence curves have been reconstructed from measurements in live cells as well ^{10, 73, 223}. Some of these measurements have been aided by the development and deployment of optogenetic methods ^{47, 159}. In this case, the ordinate is no longer the temperature. Instead, it is either the strength of the light activation or the effective valence enabled by a high local concentration through light activation. In a fascinating recent study, a bona fide phase boundary was generated for the P-granule protein PGL3 by manipulating the local temperature. This work demonstrated that P-granule assembly was tied to the generation of a temperature gradient, and that its formation and dissolution, in a live cell, could be explained by thermoresponsive phase separation of PGL3 ³³.

One can also fix temperature and measure the local concentrations of coexisting phases at different salt concentrations ²²², different pH values, or even different concentrations of other small molecule solutes. Across the phase boundary the concentrations of macromolecules and the concentrations of analytes (salt, protons, metabolite, or solute) will be determined by the equalization of macromolecular chemical potentials and osmotic pressure, as well as the equalization of chemical potentials of the analyte in question. The coexistence curves are now mapped on a $\left(c_{\text{am}},c_{\text{an}}\right)$ plane, where c_am and c_an refer, respectively, to the bulk concentration of the associative macromolecule and c_an is the bulk concentration of the analyte. Tie lines on the $\left(c_{\text{am}},c_{\text{an}}\right)$ plane are not constrained to be horizontal, although this is possible under special circumstances. Differences in solvent-mediated interactions across the phase boundary will lead to ties lines that have nonzero slopes (Figure 12). A positive slope would imply an increased concentration of the analyte in the dense phase, whereas a negative slope implies the opposite.

Figure 12: Coexistence curve or phase boundary in the (c_am, c_an)-plane.

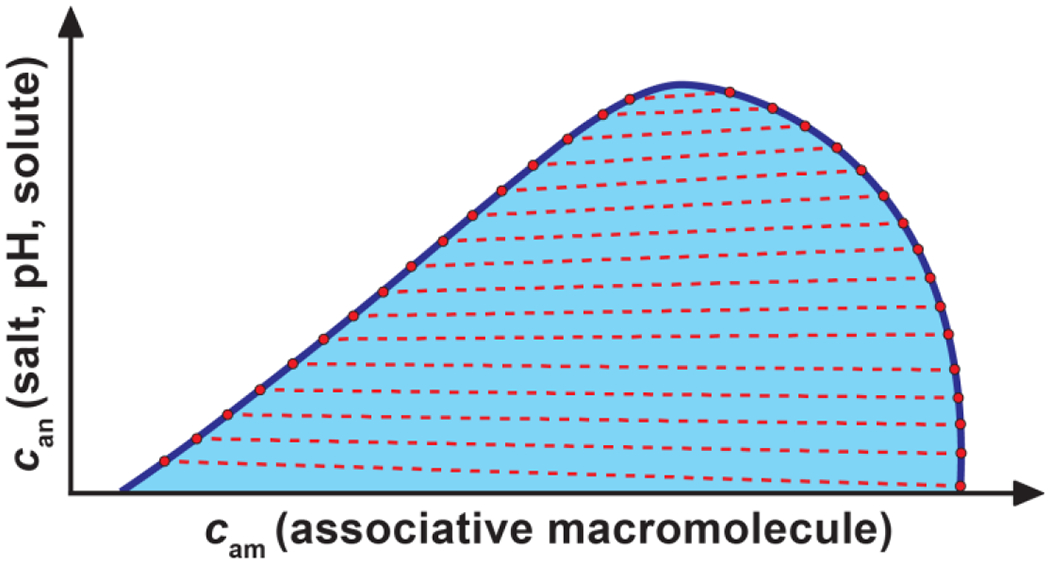
The phase boundary is in blue, the two-phase region is in pale blue, and the coexisting phases are joined by dashed red lines, which are tie lines. Tie lines may have positive slopes, implying an accumulation of the analyte in the dense phase, negative slopes, implying a depletion of the analyte from the dense phase, or horizontal slopes, implying equal preference of the analyte for the dense and dilute phases. Note that the slopes of tie lines can change sign as the critical point is approached, which is what we depict in this schematic.

Recent advances have allowed for the direct and high-throughput measurements of the slopes of tie lines ²²⁴, and this will open the door to measuring concentrations of analytes within dense and dilute phases of associative macromolecules. As noted above, solvents in vitro are complex mixtures of small molecules and ions. In cells, the complexity of the solvent increases due to the presence of other macromolecules that act as crowders that are preferentially excluded from condensates. Crowders could also be co-drivers of condensates through preferential interactions with the associative macromolecule of interest ^{224, 225}. Being able to measure tie lines provides direct inferences regarding the preferential interactions or preferential exclusion of macromolecular components of complex mixtures. In vitro, such measurements of dilute and dense phase concentrations and of the slopes of tie lines are likely to be aided by recent advances in HPLC-based methods ²²⁶.

6.2. Annotating measured coexistence curves with percolation lines

Measuring the percolation threshold invariably involves a combination of extrapolation and computations. As shown in Figure 13, one can map the coexistence curve and perform measurements outside the two-phase regime at macromolecular concentrations above the overlap concentration. The results of these measurements, which query the onset of turbidity without the formation of coexisting phases, can be performed for a series of macromolecular concentrations above the overlap regime and extrapolated into the two-phase regime using a suitable theory. Bracha et al., have used the onset of hysteretic behavior as a proxy for mapping the percolation line in live cells ⁷³. This arises from the realization that because c_dense is greater than c_perc, percolation can dynamically arrest phase separation. Therefore, cycles of light activation and deactivation, performed in a pulsatile manner, afford a dynamical route to map the percolation line.

Figure 13: Coexistence curve (blue) and percolation line (dashed and solid green) for a solution of associative polymers undergoing UCST-style phase separation coupled to percolation.

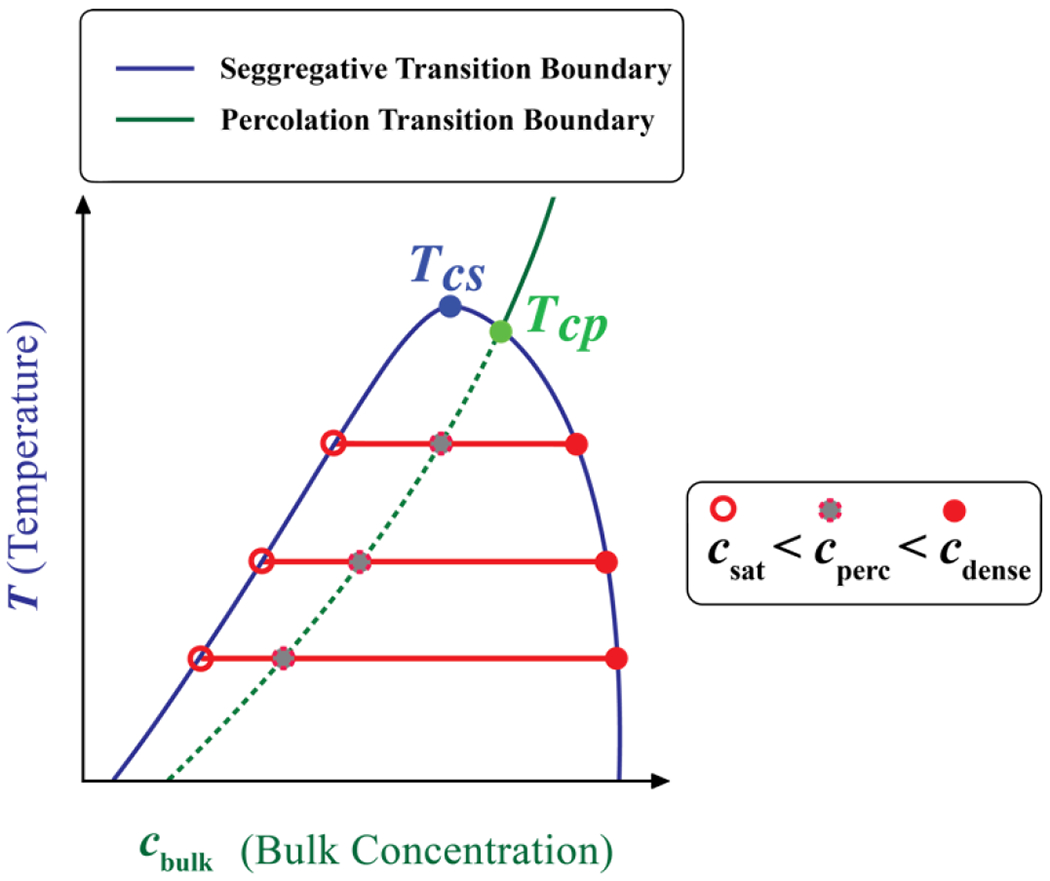
The red lines are tie lines (see section 6.1) that connect coexisting dilute and dense phases. There are two critical temperatures, T_cs for the segregative transition and T_cp for the percolation transition. For temperatures below T_cs and above T_cp there is the formal possibility of phase separation without percolation. Whether this regime is accessible or not will depend on the gap between the two critical temperatures T_cs and T_cp.

The generalized percolation model developed by Choi et al.,²⁷ provides a joint theoretical and experimental route for quantifying percolation lines. If one measures the apparent dissociation constant of site- or sequence-specific binding for the macromolecules to themselves in a concentration regime that is outside the two-phase regime, then this information, combined with knowledge of the sticker valence can be used to compute the percolation line. Alternatively, one can map how phase boundaries shift with titrations of sticker valence or sticker strengths, while keeping the identities and positions of spacers fixed. This provides a handle on the effective strengths of sticker-sticker interactions. Zeng et al.,²²⁷ used this information, combined with the theory of Choi et al., ²⁷ to compute percolation lines for a series of variants of the prion-like low complexity domain of the hnRNP-A1 protein.

In computations that rely on coarse-grained and architecture- or sequence-specific models of associative macromolecules, one can deploy two sets of order parameters that, when quantified independently, provide a direct readout of the coexistence curves and percolation lines. Choi et al., have introduced these order parameters as part of their LaSSI model, a lattice-based engine for computing architecture- and / or sequence-specific coexistence curves and percolation lines ¹⁸⁹. The order parameter for computing coexistence curves is based on analyses that detect the onset of spatial inhomogeneities in pair distribution functions. The order parameter for computing the onset of percolation is based on quantification of the number of molecules that make up the single largest cluster in the system.

6.3. Spinodals and critical points

Below the coexistence curve, referred to as a binodal for a system of two coexisting phases, lies the spinodal or instability line. Between the binodal and spinodal, the one-phase system is metastable. In contrast, below the spinodal, the one-phase system is unstable. Accordingly, below the spinodal, the dynamics of phase separation and / or PSCP are governed purely by the dynamics of macromolecular transport and the dynamics of making and breaking physical crosslinks. The spinodal line is typically well above the overlap regime. As a result, below the spinodal, the system makes bicontinuous structures, whereby spines of macromolecular regions are connected to one another, leaving small, solvent-rich regions embedded within them. Interestingly, evidence for spinodal decomposition has been observed in live cells, both for artificial systems ⁷³ and for a system that forms foci at membranes in response to hypertonic stress ⁸⁸.

The binodal and spinodal coincide at the critical point. At this point, one expects so-called ultraviolet divergence, featuring large-scale density fluctuations in the system. An intriguing suggestion is that some systems, in live cells, might be close to the critical point ²²⁸. In vitro, near-critical behavior has been observed for systems such as the Laf-1 protein in the presence of RNA molecules ¹¹⁸. The challenge at this juncture is measuring the onset of criticality both in vitro and in live cells. Most biophysical measurements are confounded by the large fluctuations encountered in the vicinity of critical points. However, the universality of critical exponents ⁷⁴, and the applicability of theories of critical phenomena pave the way for joint experimental, computational, and theoretical studies that quantify the phase behaviors near critical points.

6.4. Phase behavior near critical points

Prior to discussing phase behavior at the critical point, we clarify the distinctions between discontinuous and continuous transitions. This is relevant because the concept of a critical point is only applicable for a continuous transition. First, we shall consider a one-component system that can be in a liquid, solid, or vapor phase (Figure 14). As noted by Widom ¹⁰⁴, there are two distinct equilibrium regimes to consider. At the triple point, which is defined by a specific temperature and pressure, the liquid coexists with the vapor and solid phases. The densities of the one-component system in the liquid, solid, and vapor phase are set by equalization of the chemical potentials, such that ${\text{µ}}_{\text{liquid}}={\text{µ}}_{\text{solid}}={\text{µ}}_{\text{vapor}}$. However, there is a second equilibrium regime of the liquid, defined by the existence of a critical point. This is the singularity where the vapor-liquid coexistence curve terminates. Past the critical point, the system forms a single fluid phase, and one cannot speak of coexisting liquid and vapor phases. The key point is that the equilibrium states of the liquid in the vicinity of the triple point are very different from the equilibrium state of the liquid at the critical point. In the vicinity of the triple point, the liquid is “ordinary” in the parlance of Widom ¹⁰⁴, because the equilibrium state of the simplest liquids (see Section 2.2) is defined mainly by short-range repulsions. In contrast, at the critical point, long-range attractions make substantive contributions, and this engenders fluctuations whose wavelengths are considerably larger than the dimensions of the constituent molecules. The upshot is that at there are two distinct types of interactions that contribute to the liquid state at the triple point versus the critical point. Near the triple point, the equilibrium phase transitions, be they solid-to-liquid (melting), vapor-to-liquid (condensation) or vapor-to-solid (sublimation), or their converse, are first-order transitions, accompanied by a latent heat and discontinuous changes in the specific heat capacity. However, at the critical point, the phase transition is continuous and does not involve a latent heat. Instead, it involves some sort of symmetry breaking operation with respect to the underlying physical laws.

Figure 14: Pressure-temperature phase diagram of a substance that can be in a liquid, solid, or vapor phase.

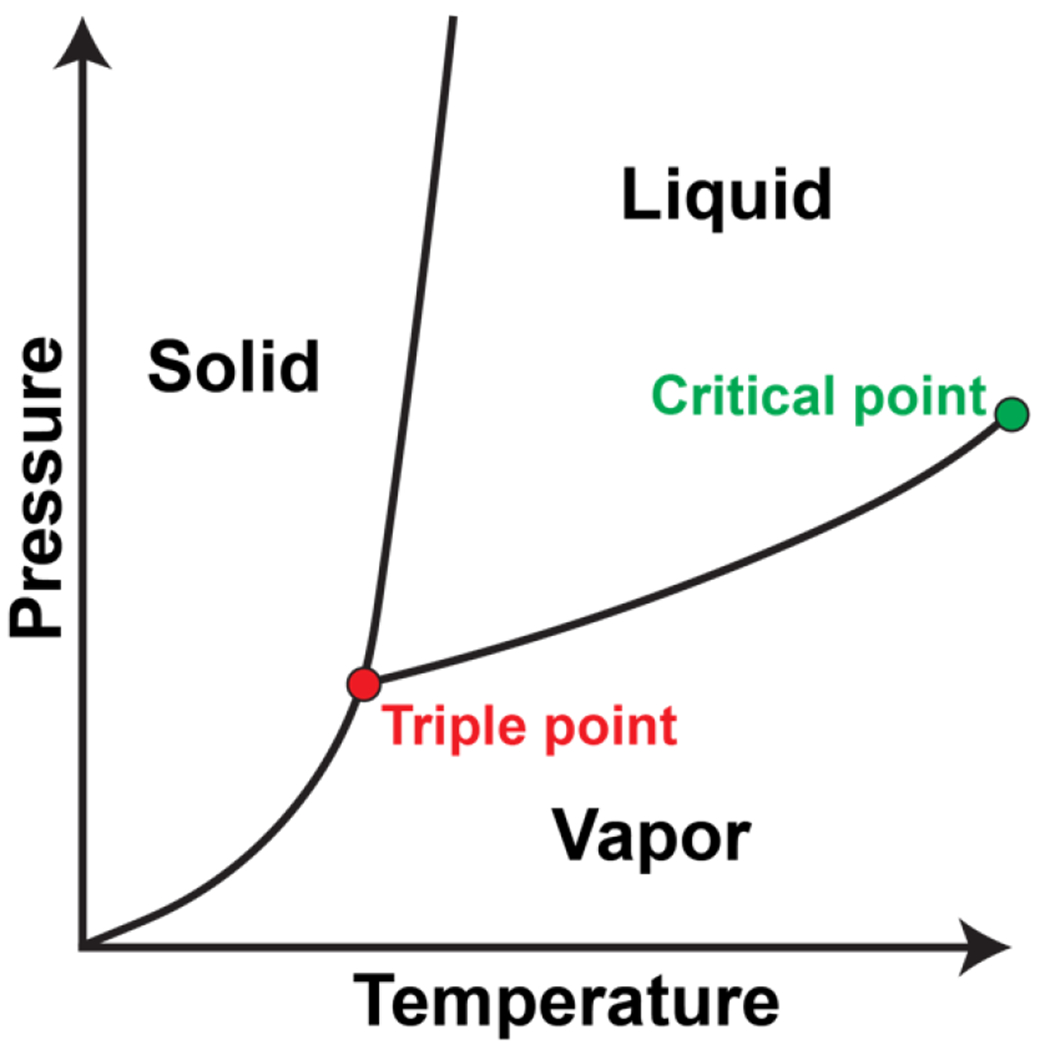
The red circle indicates the triple point where all three phases coexist. The green circle indicates the critical point where the vapor-liquid coexistence curve terminates. Beyond this critical point, the system forms a single fluid phase.

If we extend the framework laid out above to the problem of phase separation in binary mixtures, it follows that away from the critical point, phase separation is a first-order, compositional and / or density transition. Therefore, whether condensation via processes that come under the rubric of COAST, specifically the segregative transition, is being measured in the vicinity of or away from the critical point will dictate how the phase behavior is to be conceived and analyzed. This brings us to analyses that have guided recent efforts on the computational ^{229, 230} and experimental side of the condensate literature ⁸⁷. These analyses gloss over the physical considerations outlined by Widom ¹⁰⁴.

In the (ϕ,T) or (c,T) plane, the critical point is defined in terms of a critical volume fraction ϕ_c and the critical temperature T_c. In a system that undergoes a UCST-type phase transition, the width of the two-phase regime for a given temperature T can be written as: $({\text{ϕ}}_{\text{dense}}–{\text{ϕ}}_{\text{sat}})\propto {\left(T_c–T\right)}^{\text{β}}$. Here, β is the relevant critical exponent that describes how the order parameter vanishes as T_c is approached. For phase separation, the order parameter is the $({\text{ϕ}}_{\text{dense}}–{\text{ϕ}}_{\text{sat}})$, which is the width of the two-phase regime. The critical exponent is thought to be universal in its applicability to any system undergoing phase separation.

The classical mean-field theory of Landau ²³¹ predicts a value of β = 0.5. In accord with its mean-field nature, the Flory-Huggins theory also yields a value of β = 0.5 ¹⁶. Simulations of the Ising model show that β ≈ 0.3264 for d = 3 ⁷⁴. Many computational studies have assumed that phase separation belongs to the same universality class as an Ising model in d = 3 ^{229, 232}. Accordingly, one often sees an imposition of the expectation that the order parameter will scale as (T_c – T)^0.33. This is then used to extract T_c through numerical fitting ²³³ of the computed binodals ^{229, 230, 232}. Are these expectations valid? Data for polystyrene in methylcyclohexane ²³⁴ show the presence of two regimes, a mean-field regime below T_c, where the order parameter scales as (T_c – T)^0.5, and a critical regime, where the order parameter scales as (T_c – T)^0.33. These data also show a clear crossover between the two regimes. The implication is that there are two different regimes for the density fluctuations, one where short-range, Flory-style interactions dominate, and another regime near the critical point, where the density fluctuations are likely to be large enough to be divergent.

Unlike the data for polystyrene in methylcyclohexane ²³⁴, none of the measurements reported in the literature for finite-sized, multivalent associative biomacromolecules show this crossover behavior. Instead, the data appear to be well described by the mean-field exponent of 0.5 ⁶⁴. Therefore, the data to date suggest that the width of the two-phase regime scales as (T_c – T)^0.5 and not with an Ising-like exponent of 0.33. This would be in accord with the expectation of phase separation being a first-order transition, dominated by short-range interactions that are the defining hallmark of descriptions of phase behaviors in Flory-style theories. Alternatively, if phase separation involves dominant contributions from long-range interactions and large-scale fluctuations, which would be the hallmark of a continuous transition, then the observed exponent should be 0.33. However, this does not appear to be the case. Note that the discussion here applies only to the critical regime for phase separation. As shown in Figure 13, there will be two critical points in a PSCP-type process, namely one corresponding to the terminus of the liquid-liquid phase transition and one corresponding to the terminus of the percolation line. What is currently missing is a rigorous description of how these critical temperatures are determined and how the gap between these values changes based on polymer architectures and interaction strengths.

6.5. Mixtures of two types of macromolecules in complex solvents

The simplest extension that goes beyond an associative macromolecule in a complex solvent is that of two types of associative macromolecules in a complex solvent. Examples of such ternary systems are two different multivalent proteins in a solvent ^{126, 187, 235} or a protein and RNA molecule in a solvent ²³⁶. We shall consider a mixture of associative macromolecules, labeled A and B, in a solvent. For fixed solution conditions, the ternary system can be treated as a pseudo binary system. The phase behavior, which refers to the coupling of phase separation and percolation, will be governed by the relative strengths of homotypic (A-A versus B-B) and heterotypic (A-B) interactions. As is always the case for associative macromolecules, the homotypic and heterotypic interactions will be influenced by solubility-determining contributions, i.e., χ_AA, χ_BB, and χ_AB, and the effects of site- or sequence-specific binding, which contribute to χ_assoc.. Note that χ_assoc. will also be a matrix of coefficients, except the elements of the matrix will be dependent on concentration.

We shall consider the shapes of phase boundaries drawn in the (c_A, c_B) plane. Here, c_A and c_B are the concentrations of macromolecules A and B, respectively. The shapes of coexistence curves will depend on the blend of homotypic versus heterotypic interactions (Figure 15). Likewise, the slopes of tie lines will depend on the interplay between homotypic versus heterotypic interactions and the stoichiometric ratios of A to B. Perfectly horizontal or perfectly vertical tie lines imply the dominance of A-A or B-B homotypic interactions, respectively. If and only if the tie lines are horizontal or vertical can we expect there to be a single macromolecular c_sat that contributes to the segregative phase transition. For systems with sloped tie lines, both the slopes of the tie lines and the intercepts at the coexistence curve will determine the concentrations of the coexisting phases ^{92, 189, 224}. These concentrations will change as the stoichiometry of A and B change. Therefore, it is incorrect to expect fixed c_sat values for the A and B molecules ^{109, 237}.

Figure 15: Shapes of phase boundaries for systems with A and B macromolecules.

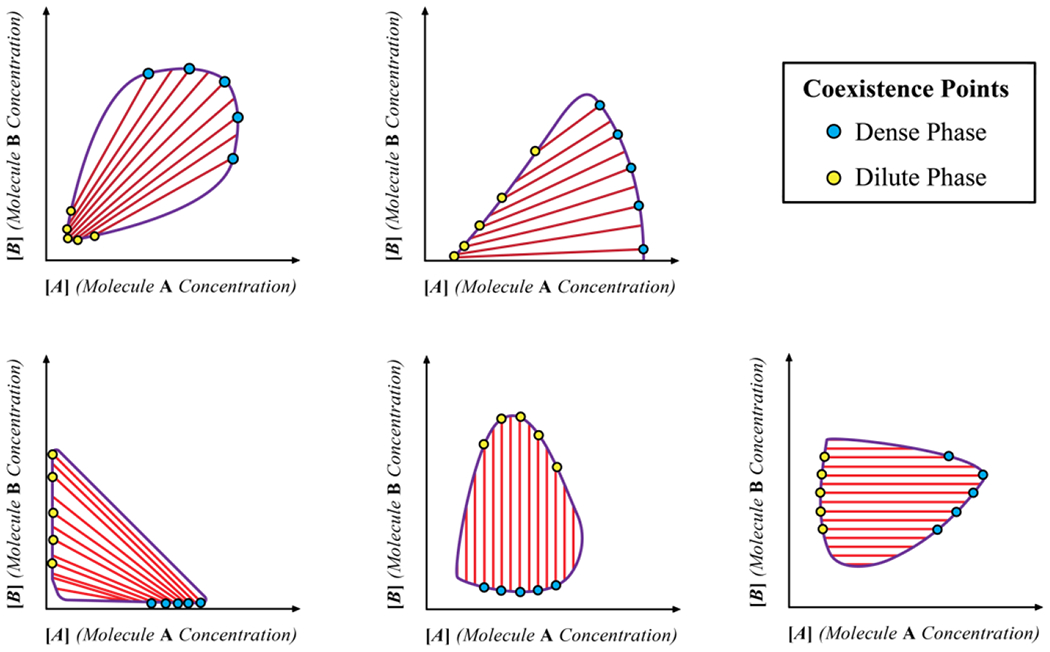
The solution conditions are fixed. The top left panel shows the case of a system where the phase behavior is driven purely by heterotypic interactions. The top middle panel shows the case where homotypic interactions among A molecules are equivalent to or outcompeting the heterotypic interactions. The bottom left panel shows the converse scenario. The bottom middle and bottom right panels show phase boundaries for the mixture where the drivers of phase transitions are purely A-A or B-B homotypic interactions. In all cases, the yellow circles designate coexisting dilute phases, and the blue circles are coexisting dense phases. Intercepts drawn from the yellow and blue circles to the abscissa and ordinate will quantify the concentrations of the coexisting dilute and dense phases, respectively. In each panel, the red lines are the tie lines.

Can the concentrations of A and B molecules in dilute and dense coexisting phases be measured? The answer is yes and doing so requires the quantification of concentrations of A and B molecules in the coexisting dilute and dense phases, or measurement of one of these concentrations, and the simultaneous measurement of the slopes of tie lines. Recent methods have shown precisely how these can be extracted ^{224, 226}. Importantly, these measurements must be performed for different ratios of A and B molecules. The simplest way to approach this would be to fix the concentration of one of the macromolecules and map the onset of phase separation as a function of the concentration of the second macromolecule. The geometry of elliptical versus parabolic phase boundaries provides readymade constraints for the spectrum of measurements that are to be performed. These measurements are neither challenging nor impossible ¹⁰⁹. They are, however, imperative ⁷⁵.

6.6. Extending to complex mixtures of macromolecules

At first glance, the complexities of multidimensional phase diagrams, which are highly informative regarding the driving forces for the phase transitions of associative macromolecules, might seem too daunting to navigate, let alone measure ¹⁰⁹. However, it is entirely tractable via advances in experiments, theory, and computations. The recent works of Yang et al., ¹² Sanders et al.,²³⁸ and Guillén-Boixet et al.,¹¹ directed at cytosolic stress granules provide a telling illustration of how one can proceed.

Using a combination of selective knockdown and knockout experiments, Yang et al., identified 34 essential proteins that constitute the core network of stress granules ¹². Of these, a pair of proteins, G3BP1/2, proved to be necessary and sufficient for assembling bona fide stress granules in live cells. Sanders et al., ²³⁸ were able to uncover the roles of other members of the G3BP1/2 network, showing that their stoichiometric ratios contribute directly to the modulation of G3BP1/2 phase behavior. Guillén-Boixet et al., ¹¹ showed that stress granules form mainly through heterotypic interactions among G3BP1/2 and naked, unfolded RNA molecules that are released via stress-induced polysomal runoffs. The blend of heterotypic and homotypic interactions determines the overall shapes of phase boundaries and the responsiveness of stress granules to other macromolecular components. These components are not passive clients that partition into stress granules. Instead, they act as ligands that modulate phase boundaries, and as co-drivers of phase behavior that impart spatial organization onto stress granules through their homotypic interactions.

Similar successes have been reported for in vitro reconstitutions of facsimiles of P-bodies comprising at least seven different macromolecular components ²³⁹. Recently, King et al., demonstrated the reconstitution of facsimiles of fibrillar centers and dense fibrillar components of nucleoli using a systematic approach that involves a collection of different macromolecular components ²¹⁶. Importantly, their work demonstrates that the blend of interactions and interactors, discerned using unbiased approaches, ensures that facsimiles of nucleolar layers can form at concentrations of associative macromolecules that are below the endogenous levels. This requires the reconstitution of synergistic networks of homotypic and heterotypic interactions.

There is no doubt that a lot needs to be done in terms of interrogating multicomponent condensates to uncover the drivers of these condensates. Recent studies show how the interplay of substrate-binding folded domains, the network of condensate-specific IDRs, and the distinctive features of constituent nucleic acids contribute thermodynamically to the formation of selective, coexisting phases within nuclei ^{194, 201, 216}. Therefore, the physical principles underlying the phase behaviors of networks of associative macromolecules are clearly operative in describing how different condensates form, coexist with one another, and mutually regulate one another. The physical principles of complex mixtures are not discussed anywhere near as often as those of simple systems. It is also important to appreciate that naïve extrapolations of the physics of simple systems cannot explain the complexities of multicomponent mixtures. A few of the considerations that need attention are listed below.

The Gibbs phase rule sets the upper bound on the number of coexisting phases. We consider a system with n_am associative macromolecules. Let there be n_con constraints on the system. The constraints refer to concentrations that cannot change due to the nature of the system. If there are n_ph possible coexisting phases ²⁴⁰, then for fixed temperature and pressure, there are n_df thermodynamic degrees of freedom in the system. This is estimated as: $n_{\text{df}}=n_{\text{am}}–n_{\text{con}}–n{­}_{\text{ph}}$. The degrees of freedom refer to the number of macromolecular concentrations that we can choose freely or that cells can freely titrate. If we have two coexisting phases, $n{­}_{\text{ph}}=2$, then the number of concentrations that can be titrated experimentally or within a cell will be $n_{\text{am}}–n_{con}–2$. Considerations such as copy numbers and expression levels go into determining n_con.

For a system with n_am associative macromolecules featuring three or more stickers that can engage in intermolecular interactions, the question is how many phases can coexist with one another for a given set of conditions. The upper limit on the number of coexisting phases will be $\left(n_{\text{am}}–n_{\text{con}}\right)$. Nuclear speckles, nucleoli, stress granules, P-bodies, the mitochondrial nucleoid, and other multilayered structures can be described as structures defined by more than two coexisting phases. For n_ph coexisting phases, the tie object is an (n_ph-1)-simplex, where a simplex is the mathematical generalization of a tetrahedron to arbitrary dimension (Figure 16). If n_ph = 2, then the tie object is a 1-simplex or a tie line. However, if we have three coexisting phases, as with a spatially organized condensates that coexists with a dilute phase, then the tie object is a 2-simplex, which is a triangle. Based on the number of layers one observes in a cellular condensate, one can work out the number of coexisting phases. The concept of a tie simplex, combined with efforts such as those of Yang et al., ¹² to identify the core scaffolds, will allow one to map diagrams that combine coexistence curves and percolation lines, in the appropriate n_ph+1-dimensional space.

Figure 16: Ellipsoidal phase boundary for a system with three associative macromolecules in a solvent.

If three phases can coexist, as would be the case for the nucleolus ¹³² or nuclear speckle ¹³¹, then the tie simplex is a 2-simplex, which is a triangle. The concentrations of the macromolecules in the three coexisting phases will be determined by the direction cosines that define each side of the triangle.

As for the slopes of tie simplexes, this too will depend on the number of coexisting phases. If we are referring to two coexisting phases, then we will have a tie line with a certain slope. If there are more than two coexisting phases, the line is generalized to n_ph dimensions, i.e., a plane if n_ph is three, and instead of a slope we have direction cosines describing a simplex gradient. The simplex gradient tells us about the relative interplay of homotypic versus heterotypic interactions. These considerations regarding the complexities of multidimensional phase diagrams are coming into sharp focus in the condensate field. Uncovering these complexities and developing new physical concepts will be essential to understand the how condensates form and dissolve.

7.0. DISTINGUISHING BINDING FROM PHASE TRANSITIONS

It has been argued that the phase behavior in multicomponent systems is highly complex and imparts fragility unto a system that organizes via phase transitions¹⁰⁹. It has also been argued that in contrast to phase transitions, the collective properties of complex networks of macromolecules can be reduced to binding isotherms governed by networks of site-specific interactions defined by precise stoichiometries and structures ¹⁰⁹. As noted at the outset, direct measurements of stoichiometries directly contradict this line of thinking ^{4, 241}. There are two additional challenges with the arguments being made in the literature ¹⁰⁹. First, site-specific binding in complex systems cannot be described by simple binding constants. Instead, it requires the description of linkage effects, the construction, through measurement, of terms that make up all the coefficients of binding polynomials and uncovering nested hierarchies of interactions that contribute to allosteric regulation ^{143, 144, 242}. This is just as difficult ²⁴³, if not more so, than studying phase behaviors in complex mixtures. Importantly, the presence of molecules exhibiting high degrees of conformational heterogeneity and measurements demonstrating the presence of distributions of stoichiometries in condensates combined with polydisperse distributions of pre-percolation clusters, essentially rule out a simple, binding-isotherm-based description for condensate formation and dissolution. It is worth noting that one seldom sees binding isotherms for complex mixtures and if they are presented, all site-specific interactions are lumped into a single, apparent dissociation constant.

Are processes that come under the rubric of COAST even necessary, or can all the processes we have described to this point be lumped under the rubric of binding ¹⁰⁹? Binding defines the formation of assemblies of precise molecularities ¹⁴³. This would be true at all concentrations, with the populations of the specific species being modulated by the overall concentration ²⁴⁴. However, phase transitions are infinitely cooperative transitions ²⁴⁵ and give rise to emergent properties whereby specific equilibria are only accessible beyond specific concentration thresholds.

7.1. Binding without phase transitions gives rise to complexes of fixed stoichiometries

We reiterate the results of Harmon et al., who showed that the properties of spacers help delineate the distinctions among reversible binding reactions on the one hand versus coupled / decoupled associative and segregative transitions on the other ⁴⁷. The properties of spacers that tether domains together determine whether phase separation and percolation are coupled, or if phase separation is suppressed and percolation is fundamentally altered by the effective solvation volumes of spacers.

For spacers of zero effective solvation volume, there is an optimal regime for spacer lengths where the coupling of phase separation and percolation is most pronounced. Above this window of optimal spacer lengths, percolation is realized without phase separation. What happens below this window? If the spacers are too stiff or too short, then percolation is suppressed, and phase separation will not be realized at most physiologically relevant concentrations, no matter the value of the excluded volume. Instead, complexes of precise molecularities will form, and describing their formation will not require the consideration of either phase separation or percolation. Instead, the thermodynamic equilibria of the system can be described fully using binding isotherms, binding polynomials, and analysis of these to extract linkage effects, if any.

In addition to spacer effects, Wingreen and colleagues have generalized the observations of percolation-suppressing interactions by studying the assemblies formed by rigid multivalent particles featuring precise, site-specific interaction modes ²⁴⁶. They arrived at a prediction they refer to as the magic number effect, highlighting how specific sticker valences can lead to a saturation of all binding sites. This suppresses the possibility of percolation. The requirements articulated are two-fold: The inter-sticker interactions must be in the realm of 7 – 10 k_BT and the associating particles must be rigid. However, even for systems that satisfy these requirements, the deviations of valence from the so-called magic number will lead to percolation because the binding sites are not saturable through assemblies of precise molecularities despite the clear presence of site-specific interactions.

7.2. Rigidity is not sufficient to suppress phase separation

The fact that rigidity alone is insufficient for suppressing COAST-like processes is manifest in observations that glycolytic enzymes can form condensates in the synapse ²⁴⁷. The enzymes in question are multivalent proteins that lack any IDRs. However, the binding sites cannot be saturated through the formation of complexes of precise molecularities. Instead, these systems, which fit the description of being patchy colloids, form from an assortment of complexes that drive PSCP transitions above threshold concentrations that can be influenced by solution conditions. This is an example of a rigid multivalent system that makes networks and condensates through processes based on COAST. Similar effects have been observed for the Speckle type BTB / POZ protein ²⁴⁸, and for the auxin responsive factors where polymerization of plant homeodomains ⁴ drives multivalence of IDRs that in turn drives PSCP-like transitions. Similar examples of polymerization induced phase separation, which is a distinct exemplar of a COAST-like process ⁷⁷, have been documented for condensate forming systems in plants ²⁴⁹.

7.3. High affinity disordered complexes can suppress phase separation

Counterexamples, where systems feature intrinsic disorder and high multivalence, and do not undergo PSCP transitions include the high-affinity complex formed by prothymosin Alpha and the histone protein H1 ²⁵⁰. Both molecules are intrinsically disordered polyelectrolytes ^{41, 250, 251}. Despite being intrinsically disordered and ionomer-like in terms of their high multivalence of associative groups, prothymosin Alpha and H1 form highly stable 1:1 complexes via charge complexation ^{250, 251}. The measured affinities of these complexes are in the picomolar range. However, the complexes that form are disordered, and this is manifest in the observation that no single binding mode is preferred ^{250, 251}. Disordered complexes are sometimes referred to as being fuzzy complexes ²⁵². Such complexes need not be weak, as is often asserted in the literature ¹⁰⁹. Instead, as shown by Schuler and coworkers, complementary electrostatic interactions between two oppositely charged polyelectrolytes, combined with the release of large numbers of counterions, provide the driving forces for the formation of highly stable, albeit disordered, 1:1 complexes that fit the definition of being fuzzy ^{250, 251}.

It is now clear that the overall phase diagram of the prothymosin Alpha and H1 system and related ones are highly sensitive to salt concentrations, salt types, and the strengths of the 1:1 interactions ²⁵³. They can even enable realization of the magic number effect. The latter has been shown to be true for the interactions of H1 with DNA ²⁵⁴. Depending on the valence, i.e., number of complementary nucleotides, H1 and cognate DNA molecules can either form complexes of precise molecularities or undergo phase separation via complex coacervation. So, the magic number effect can be operative even in semi-flexible and disordered systems ²⁵⁴.

Overall, sections 7.1 – 7.3 highlight how phase transitions can be suppressed in favor of binding that gives rise to stoichiometric complexes. These sections also discuss how the rules of suppression of phase transitions can be overcome with subtle changes to enable phase transitions that give rise to diverse stoichiometries. The upshot is that the molecular architectures, the interplay of rigidity and flexibility, the overlap concentrations, the valence as well as chemistries of stickers, and the nature of spacers will determine whether a complex has defined stoichiometry that forms via reversible binding or features a multitude of stoichiometries that form via reversible phase transitions. This brings us to the topic of how site-specific binding of ligands can influence phase equilibria.

7.4. Impact of site-specific ligand binding on phase equilibria

Condensates typically contain hundreds of distinct types of macromolecules ²⁵⁵. However, the current working hypothesis is that only a small number of homotypic and heterotypic interactions, defined by macromolecules that contribute large negative values in the Γ-matrix will be the likely drivers of condensate formation. The non-driver or non-scaffold molecules can be ligands, solutes, or metabolites. Direct support for this hypothesis comes from the works of Yang et al.,¹², Sanders et al.,²³⁸ and Xing et al.,²³⁹.

Solutes and metabolites can be preferentially excluded from, or they can preferentially interact with, the scaffold macromolecules in either dilute or dense phases ²⁵⁶. These preferential exclusion or preferential interaction effects, which explain the effects of protective and destabilizing osmolytes on protein stability in dilute solutions ²⁵⁷, are likely to be important modulators of macromolecular solubility ²⁵⁸.

Additionally, there are molecules, referred to as ligands, that bind site-specifically and preferentially to scaffold molecules across the phase boundary ²⁵⁹. Preferential binding through site-specific interactions refers to the relative affinity of ligands to sticker versus spacer sites on scaffold molecules within the dense versus dilute phase ^259–261. Specifically, phase separation is weakened if the ligand prefers to bind to sites on the scaffold in the dilute phase versus the dense phase ^260–262. Conversely, phase separation is strengthened if the ligand preferentially binds to scaffold sites in the dense phase as compared to scaffold sites in the dilute phase. The extent to which phase separation is weakened or enhanced by specific types of ligands can be put on a quantitative footing using the framework of polyphasic linkage.

Recent work has uncovered a set of rules for ligands as drivers or enhancers of PSCP of associative macromolecules that drive phase transitions via homotypic interactions ^{53, 186}. These rules are valid if we assume an absence of ligand-induced conformational changes or changes to assembly states that alter the intrinsic valence of stickers. The rules that have emerged are as follows: Monovalent ligands weaken the PSCP of scaffolds. This is true regardless of whether the ligands bind site-specifically to scaffold stickers or spacers. If the monovalent ligands bind to scaffold stickers, then suppression of phase separation occurs through direct binding and thus competition with scaffold-scaffold interactions. Conversely, for monovalent ligands that bind to scaffold spacers, the weakening of phase separation is realized by enhancing the excluded volumes of spacers.

A ligand, by definition, has a lower valence of stickers when compared to scaffolds. However, ligands can be multivalent. The site-specific binding of multivalent ligands to scaffold stickers generally weakens scaffold phase separation by replacing some of the inter-scaffold crosslinks with ligand-scaffold crosslinks. The effects of multivalent ligands are also determined by the relative strengths of the scaffold-ligand and scaffold-scaffold inter-sticker interactions. If the scaffold-ligand interaction affinity is greater than that of the scaffold-scaffold interaction, the PSCP-weakening effect of multivalent ligands that bind stickers is lowered, and these ligands can promote scaffold phase separation. Multivalent ligands that bind site-specifically to scaffold spacers will promote scaffold phase separation by contributing additional crosslinks among scaffold molecules. However, the magnitude of these effects will depend on ligand concentrations, and whether ligands bind to single or multiple sites on scaffolds. It is also worth noting that the number of binding sites need not be the same across the phase boundary.

The recent work of Dao et al., ²⁶³ has demonstrated the veracity of the rules developed by Ruff et al., ^{53, 186}. We propose that the regulatory effects of ligands will likely enable the tuning of driving forces for PSCP in cells. The scenario we envisage is the expression of ligands of various types that contributes to the modulation of the driving forces for phase separation. The effects of networks of ligands, and the effects of ligands on the driving forces for phase transitions in multicomponent systems are areas of active interest ²⁶¹.

8.0. INTERFACES AND MATERIAL PROPERTIES

8.1. Interfaces between phases and interfacial free energies

Coexisting phases are delineated by phase boundaries. For a one-component fluid, the densities of coexisting phases are governed by establishing chemical, mechanical, and thermal equilibrium across the phase boundary. Chemical equilibrium is achieved by equalizing chemical potentials across the phase boundary. Likewise, thermal, and mechanical equilibria are established by equalizing the temperature and pressure, respectively, across the phase boundary. An interface of finite thickness and interfacial free energy will delineate the boundary between coexisting phases. A finite, positive interfacial free energy arises from the drive to minimize the numbers of molecules that lie at the interface between the coexisting phases.

For spherical particles featuring isotropic interactions, a simple molecular model can be deployed to estimate the interfacial free energy density, defined as the free energy cost to increase the interfacial area by one square meter (using MKSA units). For water at 20˚C, the interfacial free energy density at the vapor-liquid interface is 7.28 × 10⁻² Nm^-1. This interfacial free energy density, denoted as µ_int, can be written as ${\mu }_{\text{int}}=\frac{w}{2\text{A}}$. Here, w is proportional to the heat of vaporization, and a is the area per molecule. For a water molecule, the radius r = 1.4 × 10⁻¹⁰ m, a = 2.46 × 10⁻¹⁹ m², and w = 3.59 × 10⁻²⁰ J. If we assume spherical geometries for the molecules, it follows that µ_int decreases as r^–2 as the radius r of the spherical molecule increases. Accordingly, for macromolecules, substitution of a with the surface areas of macromolecules suggests a substantial lowering of the interfacial free energy density. This simple calculation assumes of an interface with a featureless medium taken to be an ideal gas. Such a model is useful for setting up expectations regarding contributions of molecular length scales to interfacial free energy densities. For condensates, the relevant length scales are those of macromolecules versus those of components of the solvent, including water and solution ions. In this context, it is worth noting that interfacial tensions, a measure of interfacial free energy density that is associated with changes to the shape of the interface, have been measured to be ultra-low for synthetic and naturally occurring coacervates as well as condensates ^{132, 264, 265}. A simple explanation for the low values of interfacial tensions, vis-à-vis the air-water interface, is the differences in sizes of macromolecules versus those of solvent components. However, there are numerous considerations that are glossed over in these simple, size-based rationalization, one of which we discuss below.

The interfacial free energy density is minimized by reducing the area of the interface. This can happen by shape changes, whereby the interface becomes more spherical. Contributions to changes in interfacial free energy densities that arise purely from changes in the shapes of interfaces are referred to as interfacial tension ²⁶⁶. This, we denote as γ. For water at the vapor-liquid interface or for the interface between purely viscous liquids, µ_int is dominated by the interfacial tension ²⁶⁷. However, changes to the interfacial free energy density can also come about without a macroscopic change in shape ^{79, 268}, as happens at the liquid-ice interface, when compared to the liquid-solid interface in argon ²⁶⁹. Here, minimization of the interfacial free energy density comes from a compression of the interface ²⁷⁰, which involves rotational degrees of freedom in the case of water ²⁶⁹. Compression derives from an increase in pressure that is caused by stress in the interface of the coexisting dense phase. If the two coexisting phases are Newtonian liquids, or a liquid and a vapor, then the interfacial stress f will be the same as the interfacial tension γ. However, if the coexisting phases are complex fluids with an elastic component, or one of the phases is some form of solid, then the interfacial stress f will be smaller than the interfacial tension γ. In this scenario, the interfacial area can be minimized through compressive forces that minimize the anisotropic stresses, and the resultant interface need not be spherical. Aspherical interfaces have been reported in several contexts ^{4, 241}. These can result from dynamical arrest ^{62, 72, 133, 271}, especially when RNA is involved ²⁷², or equilibrium considerations that define the interfaces of complex materials. Comparative analyses of these interfaces on distinct length scales are imperative to understand the complexities that contribute to the characteristics of interfaces and reactions at interfaces ²⁷³.

Recent work has highlighted a feature referred to as interfacial resistance ²⁷⁴. This has emerged from careful analysis of molecular flux across interfaces. Specifically, Taylor et al., ²⁷⁴ leveraged Fluorescence Recovery After Photobleaching (FRAP) measurements by complete or partial bleaching of condensate regions. They noted that one often assumes that local equilibrium is established at the interface. This implies the absence of resistance across the interface. Taylor et al., estimated interfacial resistance using a series of systematic FRAP measurements. They recast the equations for flux across interfaces to account for the presence of interfacial resistance. A key question pertains to the relative contributions of interfacial tension versus interfacial stress to the interfacial resistance. How changes in shape versus changes in size of the interface and the distinctive conformational characteristics of interfaces ^{3, 275} contribute to interfacial resistance remain unresolved.

Overall, the interfacial free energy density is governed by joint contributions from interfacial tension, which is the drive to minimize the interfacial free energy by changing the shape of the interface, and from interfacial stresses, which refer to the drive to minimize the interfacial free energy through compressive forces that do not involve changes in overall shape. Whether we should focus exclusively on interfacial tension or a combination that includes both stresses and interfacial tension will depend on whether the interface is uniform on all length scales beyond the molecular scale ²⁷⁶. This is also tied to whether the system is purely viscous or viscoelastic. In general, non-uniformities due to compressive forces will require that we account for both interfacial tension and stresses.

Condensates are likely to be complex, viscoelastic materials featuring elastic components or even solid-like attributes. Further, because condensate interfaces involve macromolecules, the interfacial tensions are likely to be orders of magnitude smaller than that of the vapor-liquid interface for systems consisting only of small molecules. Accordingly, the contributions from anisotropic interfacial stresses are likely to play a large role in determining the interfacial free energy.

Recent investigations have started to probe the molecular aspects of condensate interfaces ²⁷⁷. A key finding is that the thickness of the interface is larger than the average size of a macromolecule within the condensate. Farag et al.,³ have predicted, using a computational model of prion-like low complexity domains, that molecules at the interface are likely to be highly expanded and oriented perpendicular to the interface. Their definition of the interface was inspired by the work of Fisk and Widom ²⁷⁸. The rationale for the observation of Farag et al.,³ is that the interfacial free energy is minimized by having small sections of many chains exposed at the interface, as opposed to large sections of a few chains. This finding also points to the presence of unsatisfied, non-crosslinked stickers being present at interfaces. Accordingly, it is plausible that expanded conformations with unsatisfied stickers are the prime sites for enhancing biochemical reaction efficiencies. Indeed, fibril formation appears to be significantly enhanced by the presence of cohesive, fibril-forming stickers at interfaces of condensates formed by prion-like low complexity domains ²⁷⁹.

Drawing on observations from the microdroplet literature, Stroberg and Schnell have proposed that the interfaces of condensates might be where reaction efficiencies are enhanced by several orders of magnitude ²⁸⁰. This has to do with the unique properties of interfaces, including interfacial electrostatic potentials, reduced dimensionality, the creation of electric double layers, and the recently uncovered conformational features of interfaces mentioned above. Substrate channeling and product inhibition are likely to be made more efficient at interfaces than in bulk solutions or within condensates. Accordingly, an important area of investigation in condensate research is the nature of internal interfaces within condensates and the properties of interfaces between coexisting dense and dilute phases. Of particular interest is the nature of interfaces formed when the mechanism involves complex coacervation ²⁶⁴ because nuclear bodies, specifically those implicated in transcriptional and post-transcriptional regulation, are likely to be driven by some form of complex coacervation.

8.2. Adsorption to solid substrates and wetting

An interface is a generic term used to describe a region that separates two distinguishable bulk phases. The interface is either a physical slab or a mathematical plane as defined by Gibbs ²⁸¹. The key point is that properties that distinguish the bulk phases from one another, such as the density, composition, or conformation, are different in the interface from those of the two bulk phases. The term surface is only applicable if the interface involves a vapor on one side.

Wetting, or more precisely, the extent of wetting, is a measure of the interfacial free energy between coexisting bulk phases. It is quantified in terms of a contact angle. Importantly, wetting always involves interactions among three separated volumes that meet at a triple line. For example, in the work of Feric et al., ¹³² they measured contact angles by forming a droplet of the protein of interest, nucleophosmin 1 or fibrillarin, at the interface of air and a solid surface that was coated with a hydrophobic or hydrophilic material. So, the contact angle in this case was the contact angle of Young ²⁸², denoted as θ_Y and measured as $\text{cos}({\theta }_Y)=({\gamma }_{\text{SV}}–{\gamma }_{\text{SL}})/{\gamma }_{\text{LV}}$ Here, the interfacial free energy densities γ_SV, γ_SL, and γ_LV are the free energy penalties associated with increasing the interfacial areas at the solid-vapor (SV), solid-liquid (SL), and liquid-vapor (LV) interfaces. The droplet formed by the protein is the wetting phase, and the solid substrate with different coatings is the wetted phase. Young’s equation applies if and only if the interfacial energy densities are isotropic ²⁸².

Partial wetting is the term used to describe any contact angle between 0˚ and 180˚. Complete wetting refers to the case of the contact angle being zero, whereas non-wetting refers to the case of the contact angle being 180˚. Partial wetting interpolates between these limits. Wetting or partial wetting may be enabled by adsorption, which is defined as the adhesion of atoms, small molecules, polymers, colloids, or ions from a gas, liquid, or dissolved solid onto an interface (Figure 17). In the parlance of adsorption, the interface is the adsorbate and the entities that adsorb are the adsorbents. Here, the adsorbate is analogous to the wetted phase in our descriptions of wetting. Unlike wetting, adsorption may occur across only two separated volumes. Hence, if a phase-separable system is in contact with a distinct interface, wetting can only occur above the saturation concentration, in the two-phase regime, whereas adsorption may also occur below the saturation concentration, in the one-phase regime. So, one can speak of adsorption in the one-phase system, which becomes relevant in the context of prewetting (see below). Adsorption is central to any analysis of wetting and wetting transitions. Importantly, adsorption at interfaces can modify the interfacial free energy density.

Figure 17: Adsorption and wetting of a polymer onto a solid surface.

The solvent is shown in blue and the solid surface is shown in gray. The red chains indicate a polymeric species able to undergo phase separation at the proper conditions. The yellow dashed curves outline the adsorbing or wetting polymers. In (A), the polymer is in the one-phase regime and adsorbs onto the substrate. In (B) and (C), the polymer has undergone phase separation and the nascent dense phase partially wets the surface. The contact angle, θ_Y, may be above 90°, indicating poor wetting (B), or below 90°, indicating good wetting (C). In (D), the polymer-rich dense phase completely wets the surface.

Adsorption and its impact on the interfacial free energy density γ is described by the Gibbs adsorption equation or adsorption isotherm. It relies on invoking a Gibbs dividing surface ²⁸¹, which refers to the fact that the interface between coexisting phases has a finite thickness ³. There is a transition region that separates the two phases. In the transition region, the density is between that of the dense and dilute coexisting phases. The Gibbs dividing surface is a mathematical plane onto which all thermodynamic variables pertaining to the extensive quantities of the interface are projected ^{281, 282}. The value of the variable of interest is computed by subtracting out the value obtained from a reference that consists of the contributions from the two bulk phases. This becomes an interfacial excess quantity ²⁸². We shall denote Γ_i, as the specific interfacial excess number of moles of component i or more simply as the adsorption coefficient of component i.

The Gibbs adsorption equation, written as: $d\gamma =s^{I}dT–\sum {\Gamma }_{i}d{\mu }_i$ quantifies the variation of the interfacial free energy density γ with changes in T and the chemical potentials of species i, denoted as µ_i. Here, s^I is the specific interfacial excess entropy. At constant temperature, this becomes the equation for the Gibbs adsorption isotherm, which for a system with two components A and B is: $d\gamma =–{\Gamma }_{\text{A}}d{\mu }_{\text{A}}–{\Gamma }_{\text{B}}d{\mu }_{\text{B}}$. Here, the two components A and B could be the polymer and the solvent, respectively. Using the Gibbs-Duhem equation, we can eliminate one of the chemical potentials. If A is the solvent, and we eliminate the chemical potential of the solvent, the Gibbs adsorption isotherm is written in terms of the solute B. If the coexisting phases are denoted as ´ and ´´, then from the vantage point of the ´ phase, the Gibbs adsorption isotherm is rewritten in terms of the numbers of moles of A and B molecules in the ´ phase as: $(d\gamma /d{\mu }_{\text{B}})={\Gamma }_{\text{A}}\left(n_{\text{B}}´/n_{\text{A}}´\right)–{\Gamma }_{\text{B}}$. The interfacial free energy density γ is not proportional to adsorption. Instead, it is the slope dγ/dµ_B i.e., the change in the interfacial free energy density with the chemical potential of the solute, that is proportional to adsorption ²⁸².

8.3. Wetting transitions and phase separation

Adsorption can give rise to wetting transitions. If we consider two condensed phases α′ and α″ in contact and in equilibrium with a solid substrate s, as would be the case for phase separation occurring on the surface of a cover slip of a microscope, then the equation of Young gives us the following:${\text{γ}}_{\text{α}´\text{α}´´}cos\text{θ}={\text{γ}}_{s\text{α}´´}–{\text{γ}}_{s\text{α}´}$ . The α′ and α″ phases are in equilibrium below their critical point T_c. Assuming this is a system with an upper critical solution temperature, then as T_c is approached from below, the interfacial free energy density ${\mathrm{\gamma }}_{\mathrm{\alpha }´\mathrm{\alpha }´´}$ will scale as ${\left(T_c–T\right)}^{\beta }$. Here, β is expected to be between 0.3 and 0.4. Further, as T approaches T_c, the difference $({\mathrm{\gamma }}_{s\mathrm{\alpha }´´}–{\mathrm{\gamma }}_{s\mathrm{\alpha }´})$ will approach zero and will scale as (T_c – T)^{1.3 282}. The implication is that θ will tend to zero as T approaches T_c. The value of T at which θ = 0 is the wetting temperature T_W. Wetting transitions can either be first-order or critical. While cosθ approaches unity continuously in both cases, in a first-order wetting transition, the derivative of cosθ with respect to T will be discontinuous at T_W. In a critical wetting transition, the derivative of cosθ with respect to T will be continuous at T_W ²⁸².

8.4. Adsorption transitions, prewetting, and the connection to pre-percolation clusters

The linkage of adsorption coupled to phase equilibria has been used to describe the condensation of a pioneer transcription factor on the surface of DNA ²⁸³. Morin et al., also invoked what they referred to as prewetting transitions. The review of Kaplan et al., ²⁸² is very useful for understanding the underlying concepts and terminology. Here, we consider a wetting transition from the perspective of a two-component system, such as a macromolecule in a solvent, in contact with a vapor phase. This is readily realized for a one- or two-phase system in a cuvette that has an interface with air. Using the terminology of Kaplan et al., the α-phase for this system is the one-phase regime ²⁸². Conversely, the α′ and α″ phases represent the two coexisting phases in the two-phase regime. If the α-phase is a polymer-solvent binary mixture, then α′ and α″ are the polymer-rich and solvent-rich phases, respectively. If the α-phase is a mixture of two distinct liquids, then α′ and α″ are each rich in one of the liquids. We now consider adsorption from the vapor of one of the components, say the polymer in a binary mixture of polymer plus solvent, onto the α-phase. Note that all it takes is for either the polymer or solvent to be the volatile component for there to be a finite concentration of species in the vapor. The concentrations will be infinitesimally small away from the boiling point. Increasing the chemical potential of the polymer in the vapor phase will result in increased adsorption of the polymer onto the α phase. This increase will terminate at a finite value, which coincides with the separation of the α phase into α′ and α″. If the system happens to be above T_W, the separation of the α-phase into two coexisting phases α′ and α″ will result in α′ completely wetting α′′. If the system is below T_W, the separation of the α-phase into two coexisting phases α′ and α″ will result in α′ partially wetting α′′.

Above a threshold chemical potential of a macromolecule, the slope of the interfacial free energy density due to adsorption may change. This refers to an adsorption transition or the crossing of a prewetting line. This can happen either continuously or discontinuously. For the former, the adsorption transition is a first-order process, whereas for the latter it is a higher-order process. When the coexistence line is approached from the one-phase regime, divergence of adsorption indicates the onset of phase separation and complete wetting. In contrast to divergent adsorption, conventional adsorption can prevail in the absence of phase separation or complete wetting ²⁸².

In the preceding two paragraphs, adsorption of polymers from a vapor onto the interface of the one-phase system – the α-phase – leads to either a partial wetting transition below T_W or a complete wetting transition above T_W. If the one-phase system is not in contact with a vapor, then, at first glance, there is no adsorption possible. However, given the concept of prewetting, we see a direct connection between monotonic adsorptive transitions and the formation of pre-percolation clusters given that both occur in sub-saturated solutions ¹⁹⁰. If we replace molecules adsorbing from a vapor onto the interface between the vapor and the one-phase regime with molecules sticking to one another to give rise to clusters of different size, then we are describing physisorption via cohesion rather than adhesion. Clusters enable a partitioning of molecules from the bulk, and instead of adsorption or the extent of adsorption, we speak of clustering or the mean cluster size. When the cluster size diverges, we have phase separation that gives rise to two coexisting phases. As a result, there is a formal connection between prewetting and the formation of pre-percolation clusters since both are realized in subsaturated solutions.

Within cells, there can be well defined interfaces or surfaces that mimic solids. Prewetting can lower the threshold concentration for phase separation. This is what Morin et al., observed for the pioneer transcription factor in the presence of a DNA surface, leading to their invocation of the physics of prewetting ²⁸³. However, since they did not measure the change in the interfacial free energy density as a function of the chemical potential of the pioneer transcription factor, we regard their work as being suggestive of prewetting without formal proof of prewetting. Overall, the effects of adsorption, site-specific binding via ligands, pre-percolation clusters, and the interplay between homotypic and heterotypic interactions among scaffolds must be accounted for in their entirety to understand the full complexities of spontaneous COAST-like processes.

8.5. Summary of key concepts pertaining to interfaces

We conclude this section by summarizing the concepts from the physics of adsorption at interfaces. We consider a system comprising macromolecules A and B that associate with one another and separate from the solvent. This gives rise to a dense phase, which is the condensate, that is enriched in macromolecules A and B. The condensate coexists with a solvent-rich phase that is dilute in terms of the concentrations of macromolecules A and B. Next, we add a third macromolecule, designated as C, that can associate with macromolecule A, and will have interactions with the solvent that are akin to those of macromolecule B. At low concentrations of macromolecule C, associations between macromolecules A and C drive adsorption of macromolecule C onto the interface between the condensate and the solvent-rich phase. If the concentration is increased, this adsorption may enable the creation of a nascent dense-phase, rich in macromolecule C, that partially wets the interface. One can measure a contact angle of the adsorbent phase rich in macromolecule C at the triple line defined by the three-way interface of the original condensate, the dilute phase, and the nascent phase. A contact angle that is less than 90˚ characterizes a nascent phase that is a good wetter of the condensate. As the concentration of macromolecule C increases further, the nascent phase can grow via adsorption to lower the contact angle. When the contact angle becomes zero, the system has undergone a complete wetting transition, and the system is now characterized by three coexisting phases viz., the original condensate, a dilute phase that is deficient in macromolecules and rich in solvent, and a new dense phase rich in macromolecule C that completely wets the condensate. At the interface of the original condensate and the new dense phase enriched in macromolecule C, there can be further adsorption leading to an equilibrium two-dimensional skin referred to as a complexion or grain boundary ²⁸². The role of complexions namely, bona fide equilibrium 2-dimensional regions that are not coexisting bulk phases, needs special attention and consideration in the context of multilayered condensates such as nucleoli ²⁸⁴ and nuclear speckles ¹³¹.

The expectations summarized here, which are based on the physics of adsorption, and the cascade of wetting transitions it induces, are directly relevant to the spontaneous driving forces that determine the organization of several nuclear bodies, including the nucleolus ²⁸⁴. The rules that govern the intrinsic driving forces for generating complex architectures of condensates, driven in part by interface-mediated interactions, are starting to come into focus ²⁷⁵.

8.6. Condensates are viscoelastic materials

Within a condensate, the concentration of associative macromolecules that are scaffolds will be well above the percolation threshold. As a result, condensates are percolated networks of associative macromolecules. The structures of condensates are best described as gel-like with a network structure These can be weak or strong gels. Further, condensates are expected to feature significant spatial inhomogeneities due to physical crosslinking, as has been shown by Farag et al., ³ and Wu et al., ¹⁹⁶. This gives rise to a distribution of mesh sizes, inhomogeneous molecular transport ²⁸⁵, and dynamic moduli characteristic of viscoelastic materials, such as Maxwell fluids or generalized Maxwell fluids with multiple relaxation times ²⁶. It is worth emphasizing that probing mesh sizes by querying the uptake or mobility of spherical particles in a complex matrix is fraught with numerous assumptions, as articulated in cautionary notes by Rubinstein and coworkers. There will likely be a coupling of hopping and diffusion ²⁸⁶, and regimes where the motions of even non-sticky molecules will either be diffusive or be confined within tubes ²⁸⁷. Overall, the framework of the sticky Rouse model ²⁸⁸ seems relevant for describing dynamics of condensates and the motions of probes within condensates.

On the topic of viscoelasticity, it is worth noting that a recent study, aided by a combination of atomic force microscopy and interferometry, has shown that intrinsically foldable domains are viscoelastic materials with intrinsic stiffness constants and internal friction ²⁸⁹. This has direct implications for modeling viscoelastic materials, where a network of molecules is organized in topologically distinct ways around the connections of underlying Maxwell (or other) elements that are viscoelastic in nature.

The material properties of viscoelastic materials, their aging, the internal stresses versus dissipation, the interplay between shear thinning versus shear thickening, and the possibility of a transition from a viscoelastic material to a viscoplastic material is only now coming into focus in the condensate field. These studies will require a treatise unto their own, and the rheological characterization of condensates will require measurements that go well beyond what is currently in vogue. This much is clear: measurements based exclusively on fluorescence recovery after photobleaching are uninformative regarding the complex material properties of condensates ²⁴¹. It is also increasingly clear that macromolecules are inhomogeneously organized within condensates ^{3, 285}. A uniform blob, which is what diffraction-limited microscopy suggests, is almost certainly not true of the organization of macromolecules within condensates. The spatial inhomogeneities will be direct determinants of the interplay between viscous versus elastic moduli. Since inhomogeneities arise from the extent and nature of crosslinking, it follows that aging properties of condensates, including changes to their terminal behaviors, will be tied to time-dependent evolutions of collective material properties ²⁹⁰. These emergent, dynamical properties of condensates are likely to be regulated by active processes.

In recent work, Zhou and colleagues have studied the fusion dynamics of different types of condensates and proposed an interesting distinction that arises from analysis of the data using a “viscocapillary model” ²⁹¹. They proposed the existence of a single stress relaxation rate and suggest that condensates organized around folded domains i.e., patchy colloid-like domains show shear-thickening behavior. In contrast, Zhou and colleagues propose that condensates organized around IDRs show shear thinning behavior ^{291, 292}. Here, shear thinning, and shear thickening refer, respectively, to the decrease versus increase of viscosity with time. The shear thinning behavior is what one conventionally expects for Maxwell fluids and related viscoelastic materials that feature terminal viscous behaviors. Zhou and coworkers have proposed that the shear thickening behavior they observe arises from the stronger, site-specific interactions involving folded domains, which are apparently weakened and more distributed for IDRs. This is an intriguing proposal that calls for closer scrutiny. The key is to measure three distinct quantities viz., the timescales for making and breaking crosslinks, the individual and correlated motions of molecules within condensates, and the speeds of fusion, paying attention to the possibility of metastable states defined by a balancing of viscous and elastic forces ²⁹³. Recent work from Banerjee and coworkers has demonstrated the types of measurements that will be needed for proper adjudication of material properties of condensates ^{6, 294}. Being able to adapt these measurements to complex condensates in vitro and in vivo remains a key challenge for the condensate field. However, such measurements are essential if we are to understand whether material properties are germane to biochemical functions of condensates in cells and in vitro.

8.7. Internal environments of condensates

Finally, and importantly, the current working assumption is that the internal environments within condensates, specifically the properties of solvents, are the same as those of the coexisting dilute phases in vitro or the coexisting cellular milieus in vivo. This implies that the strengths of interactions, the conformations of macromolecules, the valence of stickers, and the excluded volumes of spacers are the same across phase boundaries. There are a few studies ²⁹⁵ that challenge this simplifying view. What is needed are measurements of the internal solvent properties of condensates. This will require a combination of time-resolved spectroscopies and / or chemical-biology-based approaches that can probe the internal solution environment of condensates as well as condensate interfaces. Of course, none of this will be trivial, but it is clearly essential. This provides an opportunity for innovation at the intersection of multiple disciplines, including soft matter physics and physical as well as analytical chemistry. A useful starting point is the copious literature on partitioning of solutes and the considerations of solvent non-idealities in aqueous two-phase systems ²⁹⁶. The recent work of Wu et al., ¹⁹⁶ shows that the interiors of condensates formed by intrinsically disordered low complexity domains are more hydrophobic than the coexisting dilute phases. Further, there are hotspots within interiors that are more hydrophobic than the background of condensates, suggesting that one cannot assume that molecules partitioning into condensates are crossing a boundary into materials of uniform hydrophobicity ¹⁹⁶. These considerations and others need scrutiny, higher resolution investigations ¹⁹⁶, and models for partitioning that rely on the tenets of inhomogeneous fluid solvation ²⁹⁷.

9.0. OVERALL SUMMARY AND CONCLUSIONS

9.1. Addressing critiques of phase transitions in cell biology

Advances in structural biology and the ongoing technological revolution of cryo-electron tomography are yielding important insights regarding the arrangements of molecules in large complexes, wherein the molecules are flash-frozen in specific snapshots ²⁹⁸. By averaging over information collected for many particles, one can obtain a detailed picture of site-specific contacts forming in large complexes. The fact that such contacts exist in all manner of complexes cannot be denied. However, does what we see in a specific structural instantiation tell us what we need to know about the driving forces for forming assemblies that are often rather dynamic with components exchanging on a range of timescales? Indeed, the fastest timescales being commensurate with the rates of diffusion of macromolecules. If the condensates are precise organizations of essentially rigid macromolecules, each networked to generate a perfectly elastic material, then a model based purely on site-specific interactions seems reasonable ¹⁰⁹. Even in this scenario, the cooperativity that gives rise to emergent properties of the assembly cannot be described purely as a sum of all site-specific contacts. These problems have been addressed over decades of work on the many complexities of binding polynomials, linkage effects, and cooperativity of binding ²⁴⁴.

Cooperativity of conformational transitions or reversible associations is a defining hallmark of biomolecular systems that feature robustness and the ability to adapt. This is true even if the energetics of interest can be described using purely site-specific interactions ²⁹⁹. Unlike conformational transitions such as a protein folding / unfolding or binding, where cooperativity is tuned by considerations of site size, phase transitions are defined by unlimited or infinite cooperativity ²⁴⁵. This comes from the spectrum of interactions that go well beyond just site-specific contributions. IDRs, especially those that belong to specific regions on so-called diagrams-of-states ⁴², are likely to afford access to multiple energy and length scales, both in terms of interactions as well as fluctuations ³⁰⁰.

It is worth noting, as detailed below, that site-specific interactions enabled by the surfaces of folded domains, and IDR-mediated interactions are describable by the same physico-chemical principles. Salt bridges, pi-pi interactions, associations of hydrophobic groups, and weakly polar interactions (first described for folded proteins ³⁰¹), are shared by folded domains and IDRs. It is not as though folded domains, and their site-specific interactions engage in mysterious forces that do not have a basis in physical chemistry. What is worth noting is that while the interactions among IDRs may not be site-specific in the spirit of certain definitions ¹⁰⁹, they are exemplars of specificity in terms of the chemistries of species that contribute to the interactions ³⁰². Further, the binding sites are distributed across IDRs, and the fluctuations engendered by conformational heterogeneity leads to changes in binding specificity, which one would quantify in terms of binding capacity ³⁰³ – a direct analog of heat capacity that quantifies enthalpy fluctuations. Accordingly, one suggestion is to refer to interactions among IDRs as being manifestations of chemical specificity ³⁰⁴. This specificity will vary with context and can be modulated by post translational modifications as well as charge regulation effects ²¹³. Importantly, there appear to be condensate-specific molecular grammars, and these are being uncovered using novel methods ³⁰⁵ to identify distinguishing sequence features of IDRs ^{182, 201, 216, 305, 306}.

Most critiques of phase separation as a route for condensate formation and dissolution are centered on the premise that current descriptions for the driving forces for phase transitions apparently invoke only weak, non-specific, and highly dynamic interactions driven solely by IDRs ¹⁰⁹. As highlighted throughout this review, a comprehensive accounting of the driving forces for segregative and associative transitions, and the coupling of these transitions, does not make any assertions about purely IDR-driven processes. However, it is also important to be clear in defining IDRs. Too often one reads about IDRs being “unstructured regions” that engage in weak, transient, and non-specific interactions ³⁰⁷. This is incorrect, because the specificity, although distributed across sites and sequence regions, is clearly present ^{42, 212, 304, 308}. The interactions may be on the order of k_BT, but these are interactions described by physical chemistry principles, as are interactions that are apparently specific and stoichiometric. Therefore, it does not follow that interactions mediated by IDRs are weak and non-specific, and hence promiscuous. In fact, the purported promiscuity has never been rigorously demonstrated, although this is often the claim. Studies that strive to make the point about IDR interactions being “non-specific” ¹⁸⁵, often miss the essential definition of specificity ^{309, 310} or how it must be quantified ^{310, 311}. A single assay intended to query interoperability of IDRs is inadequate because the information written into the IDR sequences often controls more than one phenotype ^{312, 313}, thus requiring the interrogation of the totality of functions and phenotypes that are influenced by the IDR of interest.

In much the same way that the structures of folded domains are determined by the precise linear sequence of amino acids, it follows that the conformational ensembles of IDRs are highly sequence specific. This sequence or chemical specificity can be challenging to uncover and often requires a combination of analytical, spectroscopic, and computational methods. The combinations of these methods have yielded a series of rules and heuristics that organize the sequence space of IDRs into distinct categories, each defined by distinct sequence-ensemble relationships ^{32, 42, 314}. Indeed, differences in sequence-specific IDR ensembles can be traced down to the atomic resolution ³¹⁵.

The functions of IDRs are driven by specific patterns of sequence-encoded interactions that enable specificity of molecular recognition ^{308, 316}. Even fluctuations are sequence-specific ³¹⁷, and so is the recognition of fluctuations ^{250, 308, 316, 318, 319}. It used to be argued that complexes formed by IDRs are weak when compared to complexes formed by folded domains. However, the distribution of affinities, quantified by Shammas et al., ³²⁰ in terms of the distributions of apparent dissociation constants, show that complexes formed by folded domains, and IDRs span similar ranges of values. There, however, are clear differences in terms of the dissociation and association rates, and unlike folded domains, it appears that specificity in recognition, at least in some cases, is exerted through kinetic rather than thermodynamic considerations ^{321, 322}.

In biology and biochemistry, complexes characterized by apparent dissociation constants that are in the nanomolar range are thought of as being strong complexes. By this criterion, recent studies have shown that the formation of conformationally heterogeneous complexes involves sequence-specific interactions that can be regarded as ultra-strong ³¹⁸, giving rise to complexes whose dissociation constants are in the picomolar range ^{250, 254, 318, 319}. Likewise, the barriers to interconversions between distinct conformations can also be heterogeneous. This gives rise to broad distributions of timescales for conformational interconversions ³²³ that are mediated by local conformational preferences, long-range correlations ³²⁴, and solvation ³²⁵.

Taken together, what has emerged is a description of distinct sequence families of IDRs, each defined by distinct sequence-ensemble relationships. While conformational heterogeneity is a defining hallmark of IDRs both as autonomous units and in complexes ³²⁶, the extent of heterogeneity and the type of heterogeneity is highly sequence- and context-specific ³²⁷. Indeed, all aspects of the charge states and conformational ensembles are governed by the combination of amino acid composition and the patterns of specific chemistries along the linear sequence.

Studies have shown that small differences in amino acid chemistries are of immense significance ³²⁸. As a result, Ser and Thr are not always interoperable ⁶⁶, nor are Arg and Lys ^{201, 302, 329}, Glu and Asp ^{302, 329, 330}, Gln and Asn, or Phe and Tyr ⁶⁶. Any interoperability is highly sequence- or context-specific ⁶³. This is relevant because alignments of sequences of intrinsically foldable domains often consider the substitutions listed above as exemplars of sequence similarity. Further, until recently, the hypervariability of IDRs within functional families was seen as a challenge for describing the evolution of specificity in IDRs. The thinking continues to be that because IDRs cannot be aligned without the introduction and extensions of gaps using traditional multiple sequence alignment approaches, it must follow that IDRs are interoperable with random regions derived from orthogonal systems. This has been contradicted through studies that have introduced the concept of conformational buffering ³¹³. Further, new methods that are being brought to bear for alignments of IDRs have helped uncover functionally relevant sequence features within orthologs and paralogs ^{305, 306}. New alignment-free methods have also been introduced to uncover non-random patterns in IDRs ^{182, 316}. The totality of these efforts has demonstrated that while IDRs may be evolving under different rates when compared to intrinsically foldable domains ³¹⁶, their sequence features are also under evolutionary selection.

Overall, what has emerged is that one can reliably define IDRs as belonging to specific sequence families. There is specificity of “IDR structure” ³²¹, and the “structure” we speak of lies within the entirety of how we describe sequence-specific ensembles of conformational states and charge states that can be highly responsive to solution conditions and complementary interactions with other macromolecules.

Systems exhibiting conformational heterogeneity are defined by distribution functions. This description allows one to incorporate the full range of complex hierarchies of time-, length-, and energy-scales ³³¹. These realizations pave the way for describing the phase behaviors of IDRs as autonomous units and of IDRs tethered to folded domains, both of which involve a blend of specific and solubility-mediating interactions. The emergent consequences of such interactions are encapsulated in processes that come under the rubric of COAST.

9.2. Concluding remarks

The features that drive PSCP and related processes that come under the rubric of COAST include: (i) a combination of multivalence of stickers; (ii) a diversity of sticker types and a hierarchy of sticker-sticker interactions; (iii) the effective solvation volumes of spacers, be they linear or surface spacers; (iv) any effective attractions among stickers and spacers; (v) the stabilities of domains that encompass stickers; (vi) the conformational properties of the disordered regions; and (vii) the likelihood of emergent changes to each of these properties either through post-translational modifications or through coupled homotypic and heterotypic associations. While it is tempting to fixate on the specificity of sticker-sticker interactions, it is worth appreciating that stickers constitute less than 20% of the linear sequence– at least in IDRs studied to date. The important effects of spacers as drivers of phase separation, and their coevolution with stickers cannot be understated, and is beginning to be appreciated ^{3, 47, 66, 156, 260, 261, 332}.

There undoubtedly are scenarios where large assemblies of precise molecularities can form via cooperative binding transitions that operate via a collective network of site-specific interactions. The emerging rules summarized to this point suggest that competing factors contribute to network-terminating binding reactions versus network-generating processes based on COAST. It does appear that, while binding via site-specific interactions of rigid or semi-rigid multivalent entities can explain the formation of assemblies with precise molecularities, such observations are special cases of general processes that come under the rubric of COAST.

In essence, the phase behaviors of interest are of associative macromolecules in a solvent itself comprising an assortment of associative small molecules. In addition to water, a typical aqueous buffer comprises an assortment of solution ions, including monovalent and multivalent inorganic ions, osmolytes, cosolutes or cosolvents, buffering agents, and a finite concentration of differently solvated hydronium and hydroxide ions. All these components can be regarded as associative small molecules. Further, as emphasized throughout this review, cellular milieus comprise finite concentrations of macromolecules beyond the ones of direct interest to this investigation. Therefore, if we disregard the possibility of associative transitions and focus purely on phase separation, then we neglect to capture much of the physics. The converse is also true because purely associative transitions will turn the entire system of interest into a single, system-spanning network. Such a scenario affords zero advantages from a functional or compartmentalization perspective. Associative and segregative phase transitions are of equal importance and ignoring either will provide only a limited understanding of how evolution has enabled the practical realization of the full spectrum of COAST-like processes.

The current review has strived to put considerations of associative and segregative transitions on an equal footing. There is a lot of turf that we have not covered. Among the glaring omissions are discussions of complexities and advances in complex coacervation, the impressive body of work that accounts for the role of active processes, the numerous complexities that contribute to the material properties or internal environments of condensates, and the crucial roles of RNA molecules ³³³. There clearly is a lot more to come. The hope is that the current review provides a useful starting point for understanding and appreciating the numerous complexities of associative macromolecules and their spontaneous phase transitions.

Biographies

Biographies

Samuel Cohen is a postdoc in the lab of Rohit Pappu at Washington University in St. Louis. Cohen is working to understand the physical determinants of rheological properties of biomolecular condensates using theories of polymer dynamics and computational rheometry. He is also interested in the theory of liquids, the physics of phase transitions specifically complex coacervation, and biologically relevant spectroscopic and imaging techniques. Cohen did his Ph.D. work at the University of Maryland, training with John Fourkas and John Weeks. During his Ph.D., Cohen focused on the role of electrostatic forces in liquid structure and on modeling transport and spectroscopic phenomena in liquids at interfaces. He did some of his Ph.D. work as a Chateaubriand Fellow at the Laboratoire Interdisciplinaire de Physique in Grenoble, France.

Furqan Dar received his B.A. in Physics from Kenyon College in 2016. He then went on to receive his Ph.D. in Physics from Washington University in St. Louis in 2022 under the supervision of Rohit Pappu. Dar is currently a postdoctoral scientist in the Pappu Lab where his research focuses on understanding the multi-faceted mechanisms driving the formation and modulation of biomolecular condensates. His specific focus is on the phase behaviors of multicomponent systems and the formation of heterogeneous distributions of clusters in sub-saturated solutions. Dar is the lead developer of LaSSI, which is a lattice-based engine for simulations of architecture- and sequence-specific phase behaviors of associative biomacromolecules.

Mina Farag graduated from Johns Hopkins University with a B.A. in Biophysics and Mathematics. He is currently pursuing an M.D. / Ph.D. dual degree from Washington University in St. Louis. His Ph.D. work is being performed under the supervision of Rohit Pappu with an expected graduation in 2023 and final graduation date with the M.D. and Ph.D. slated for May 2025. Farag’s research focuses on the sequence-specific driving forces for, and the organizations of, biomolecular condensates that form via interactions involving intrinsically disordered proteins. Farag recently discovered that interfaces of condensates are defined by unique conformational properties when compared to the coexisting dilute and dense phases.

Mrityunjoy Kar received his BSc. Honors and MSc. degrees in Chemistry at Vidyasagar University, Midnapore, India. As a Ph.D. student, Kar studied Polymer chemistry and nanomaterial science under the supervision of Sayam Sengupta at the CSIR-National Chemical Laboratory, Pune, India. He did postdoctoral research at the University of California San Diego, USA, for two years in the group of Shyni Varghese. Kar then moved to the Max Planck Institute of Molecular Cell Biology (MPI-CBG) in Dresden, Germany where is currently a postdoc in the lab of Anthony A. Hyman. Kar also works in close collaboration with Rohit Pappu. Kar has focused on the physico-chemical mechanisms underlying the driving forces for phase transitions of RNA-binding proteins. He made the key discovery of heterogeneous distributions of clusters forming in sub-saturated solutions of these proteins.

Rohit Pappu received his BSc. in Physics, Mathematics and Electronics from St. Joseph’s College, Bangalore University, India. In 1996, Pappu received this Ph.D. in Biological Physics from Tufts University. His thesis work with the late David L. Weaver focused on novel algorithms for Brownian dynamics simulations of polypeptides based on systematically coarse-grained and reversible coarse-graining models based on the use of electrostatic multipoles, and chemical kinetics approximations of the diffusion-collision model for protein folding. Pappu completed two postdoctoral stints, one in the lab of Jay W. Ponder at Washington University School of Medicine, working on potential smoothing algorithms for enhanced conformational sampling, and the second with George D. Rose at Johns Hopkins University working on polymer physics descriptions of unfolded states of proteins. In 2001, Pappu joined the faculty of the Biomedical Engineering department at Washington University in St. Louis, where he continues as a faculty member. He is currently the Gene K. Beare Distinguished Professor of Engineering and Director of the Center for Biomolecular Condensates. Pappu’s research program focuses on the biophysical principles underlying the form, function, and evolution of intrinsically disordered proteins. Pappu is also deeply interested in the physics of phase transitions of biopolymers and in the physio-chemical principles underlying the assembly and functions of biomolecular condensates.