Abstract
Plants with constitutive defense chemicals exist widely in nature. The phenomenon is backed by abundant data from plant chemical ecology. Sufficient data are also available to conclude that plant defenses act as deterrent and repellent to attacking herbivores, particularly deleterious generalist insects. In the wild, generalist species are usually not endemic, meaning they are not restricted to certain plant species in a region. Therefore, our objective is to inspect theoretically whether evolution of chemical defenses in all plant species eradicate an endemic by any generalist species. The objective is addressed by developing deterministic ordinary differential equations under the following conditions: Plants without constitutive defenses are susceptible to oviposition by generalist insects, while they become defended against generalists by storing chemical defenses. From the models, we explicitly obtain that a generalist-free stable state is only possible if the vast majority of all plant individuals have chemical defenses. The model also allows one to predict the highest possible percentage of undefended plant individuals, which may be considered as free-riders.
Keywords: Susceptible plants, Constitutive defense, Mathematical modeling, Generalist insects, Endemic, Non-endemic, Stability analysis, Plant-herbivore interactions
Subject terms: Ecological modelling, Evolutionary ecology, Applied mathematics, Ecology, Evolution, Plant sciences
Introduction
Plants store chemical defenses constitutively during their normal course of development1–3. Ample evidences of such defenses are available in nature2,3, as reviewed in the subsection ‘Examples of plant defenses’ below. Crucial roles of these constitutive defense compounds are to deter and repel deleterious generalist insects4–8. Several experimental studies tested the effects of plant defense. There is a slight difference in the meaning of plant deterrent and repellent chemicals. A plant deterrent is a chemical that prevents feeding and oviposition by insects, while a plant repellent is a chemical that causes insects to move away from its source5,9,10. If plants do not evolve constitutive defenses, then they are susceptible to generalist insects for oviposition. The phenomenon is expressed by Fig. 1.
Fig. 1.
Plant defense vs generalist insects. Pictures drawn in “AutoDraw” (Google Creative Lab).
According to some estimations, more than 100,000 different secondary compounds are found in plants11–13. In chemical ecology, a plausible theory could be that all individuals of every plant species have constitutive chemical defenses, even plants edible by humans3,5,11,14. Edible plants do involve some defense chemicals, which can, however, be tolerated due to their low concentrations and are often appreciated as flavors, like in black and white mustard or the numerous varieties of cabbage.
Although the theory that all plants have chemical defenses is confirmed by plentiful experimental evidence3, it has not been mathematically assessed yet. So, in this study, a proof of this theory is sought by building deterministic models, based on autonomous ordinary differential equations (ODEs). Specifically, the research question is whether any generalist insect species can become endemic if nearly all plant individuals (of all species) store chemical defenses. To be noted, generalist insects have a high diet breadth, but they do not feed permanently on specific plant species of a particular region15–18, which makes them non-endemic in the wild. This ability of being non-endemic or using multiple resources could have ecological and evolutionary advantage to generalists. Previous studies explained that generalists increase their fitness through access to various host plant species18–21. Although models have been proposed to understand the role of volatile and non-volatile organic compounds in plant-herbivore interactions22–25, it is not exactly clear how the non-endemic behavior of generalists is correlated to the multifaceted (ecological) roles of plant toxins.
The main contributions of this study are two models and conclusions derived from them:
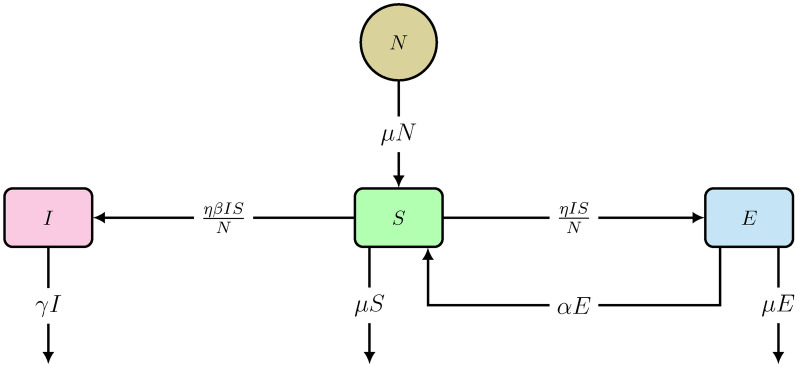
In the first model, a hypothetical situation is considered, where plants do not have constitutive defense compounds. This is done to investigate whether plants can avoid a generalist endemic without evolving chemical defenses. As depicted in Fig. 1, generalists oviposit on plants if defense compounds are absent. The undefended plants (of any species) are distinguished into two sections: Susceptible plants and exploited plants. Susceptible plants are likely to be exploited through oviposition by generalist insects, whereas exploited plants already have insect eggs (singly or in clutches) laid on them. The growth of the insect population is directly determined by the mean number of laid eggs. The flux across the compartments is expressed by the flowchart shown in Fig. 2. This model is influenced by the classic SIR model in epidemiology26–29.
The second model is based on the first one and includes, in addition, the phenomenon that new plants can germinate with chemical defenses and, thus, become defended against generalists. Defended plants are not susceptible to generalists, as expressed in Fig. 1. To formulate this model, the technique used for SIR models with vaccination (SIRV) or immunization27–30 is applied, where the total plant population includes the susceptible, exploited and defended plants. In case of plants, immunization could be the process of evolving chemical defenses to become defended against generalist herbivores13,31. From this model, one can investigate what percentage of plants have to germinate with chemical defenses to avoid a generalist endemic. That would theoretically explain the widespread occurrence of constitutive defense in plants32–36.
Fig. 2.
Basic scheme of the susceptible-exploited-insects model.
The paper structure is as follows: Models are built in two subsections of the “Models” section. Next, simulated figures are provided in the Illustration of results section. Thereafter, the results of the models and future perspectives are expressed in the Discussion. Finally, the Conclusion is devoted to the main message of this study, model limitations and possible application domains. The required calculations for the stability analysis of the models are given separately in the Supplementary Information.
Examples of plant defenses
Some examples of plants with defenses are provided by proanthocyanidins (PAs) in bilberry, peanuts, plums, cranberries, curry, and cinnamon plants37; flavonoids in fruits, vegetables, tea, cocoa and wine38; glucosinolates in the Brassicaceae plant family (including cabbage, rape and black mustard)39,40; caffeine in coffee, tea, cacao and kola plants41,42; nicotine in tobacco43; cannabinoids in cannabis44; terpenes and formylated phloroglucinol compounds (FPCs) in rose gum (Eucalyptus grandis)45; morphine in opium poppy46; cardenolides in milkweed47; atropine in deadly nightsade3; mimosine in Persian silk (Mimosa) and river tamarind (Leucaena) trees48,49; coniine in hemlock50; hydrogen cyanide (HCN) in cyanogenic plants, such as almonds, cassava, bamboo etc.51; colchicine in naked ladies (Colchicum autumnale) plant52 and so on.
Some examples regarding the effects of plant defenses on insects are given in the following. Proanthocyanidins act as feeding deterrents to the gypsy moth (Lymantria dispar), brown-tail moth (Euproctis chrysorrhoea) and winter moth (Operophtera brumata)53–55; flavonoids deter African armyworm (Spodoptera exempta), fall armyworm (Spodoptera frugiperda) and African cotton leafworm Spodoptera littoralis56,57; isoflavonoids are deterrents to cotton bollworm (Helicoverpa armigera), African cotton leafworm and fall armyworm (S. frugiperda)58; glucosinolates are deterrent and repellent to cabbage moth (Mamestra brassicae), southern armyworm (Spodoptera eridania), cabbage looper (Trichoplusia ni) and green peach aphid (Myzus persicae)40; caffeine deters beet armyworms and cotton aphids59,60; nicotine, cannabinoids and morphine can be deterrents to many insect herbivores43,61,62, and terpenes in lavender are repellent to the clothes moth63. Lavender oil is commercially used by humans to protect clothes from this insect63. Furthermore, cardenolides deter Nephila spiders64; atropine is a feeding deterrent to gypsy moth larvae, Lymantria dispar65; mimosine can suppress insect growth66,67; coniine and hydrogen cyanide (HCN) are poisonous to several groups of insects68,69; colchicine sterilizes Bactrocera tau (walker) fly and kills Melanoplus differentialis and Gryllus assimilis70,71 etc.
Models
The deterministic dynamical system is based on three variables, and I. S is the number of susceptible plants, E is the number of exploited plants and I is the insect population at time t. The sum of susceptible and exploited plants is equal to the total plant population in the first model:
| 1 |
where N denotes the total number of plants in a region. Moreover, initially, all plants are susceptible to generalist insects, so that the initial value of S reads:
| 2 |
Therefore, from Eq. (1). Insects can emerge (e.g. by invasion) in a group or singly initially, i.e. .
Model excluding plant defense
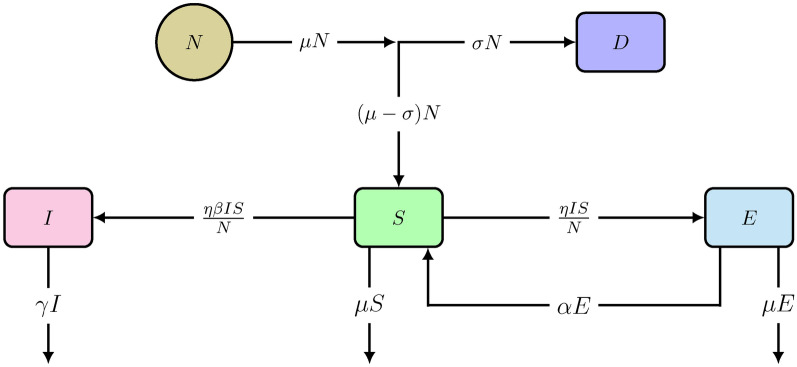
The first model is developed from the fluxes between the S, E and I compartments, including demography and re-susceptibility in plants, shown by the scheme in Fig. 3. So, it is named as SEI model. In that Figure, is the oviposition number (constant), i.e. the number of plants exploited by an insect per day, is the deposition number (constant), i.e. the mean number of eggs deposited by an insect per exploited plant per day and is the natural death rate (constant) for an insect, which is the reciprocal of the average lifespan () of an insect.
Fig. 3.
Scheme of the SEI model (3) with demographic effect and re-susceptibility in plants. Variables and parameters are explained in the text.
In order to keep constant, we assume that the germination (reproductive growth) and death rate constants (per capita) are the same in plants, denoted by . Although somewhat artificial, this assumption is also made in many SIR type models to keep the total population constant29,30. Exploited plants can be re-susceptible to insects attack, because a plant can be exploited (by insects) multiple times in its lifetime. Let be the per capita rate at which exploited plants become re-susceptible. The rate equations are:
| 3a |
| 3b |
| 3c |
where the germination rate constant of plants is proportional to the total plant population (N) and all new germinated plants are susceptible as well. Since (Eq. (1)), the sum of the above Eqs. (3a) and (3b) gives:
| 4 |
Equation (4) confirms that the total plant population is a constant if the rate constants of plant germination and death are equal. The normalized term S/N in Eqs. (3a), (3b) and (3c) represents the prevalence of susceptibility. From the commencement of the attack, the insect population increases in Eq. (3c) if:
which is, under the condition , equivalent to:
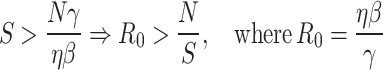 |
5 |
Since from Eqs. (1) and (2), Eq. (5) leads to:
| 6 |
where is the reproduction number of an insect, i.e. the number of viable eggs laid by an insect in its lifetime. Since an insect can lay between 100 and 2000 eggs (mean values) in its lifetime72–75, we obtain . So, the insect population (I) grows initially from the commencement of attack.
The model (3) has a non-endemic equilibrium (oviposition and generalist free):
| 7 |
is asymptotically stable for , shown in the Supplementary Information S1 and illustrated in Figs. 5 and 6A. However, since all insects lay an exceptionally high number of eggs74, is practically impossible when host plants (N) are abundant in a region. In contrast, becomes an unstable equilibrium (a saddle point) for , as illustrated in Fig. 6B and the Supplementary Information S1. The instability of for explains that plants cannot eradicate the generalists. Moreover, the model (3) has an endemic equilibrium (including oviposition and generalist insects) for :
| 8 |
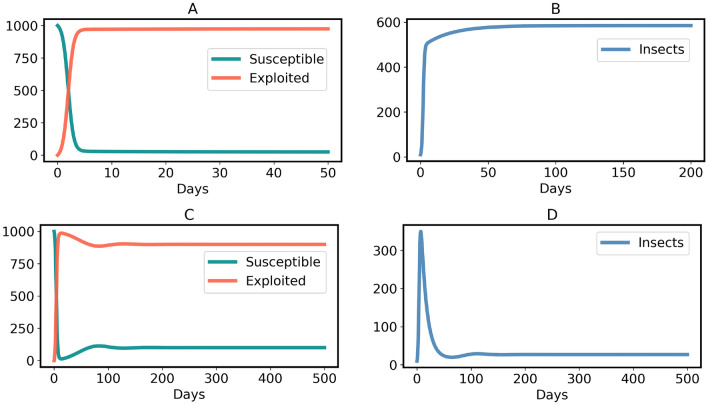
is an asymptotically stable equilibrium, which is either a stable node or a stable focus, the proof is given in the Supplementary Information S2. It is important to note that all three variables are positive in the endemic state. This implies, in particular, that even in the long run, a certain percentage of plants is susceptible. The reason is that permanently, some plants are germinating (with birth rate constant ) and some are returning to the susceptible state (with rate constant ). Persistence of the insect population creates a problem for plants, because then the insects continue damaging plants in the stable endemic state, shown by the time-courses in Fig. 7. Therefore, the conditions of model 3 are not sufficient to stop an endemic by generalists. However, generalists are usually non-endemic in the wild19,76–79, including generalist insect species15–18. So, an advancement is made in model (3) to verify whether evolution of constitutive defenses in plants can end the generalist endemic.
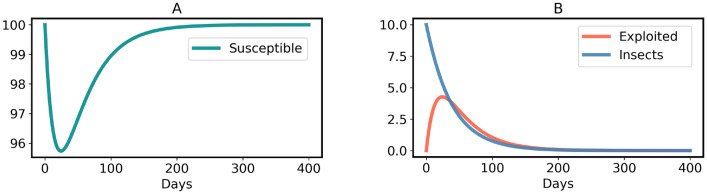
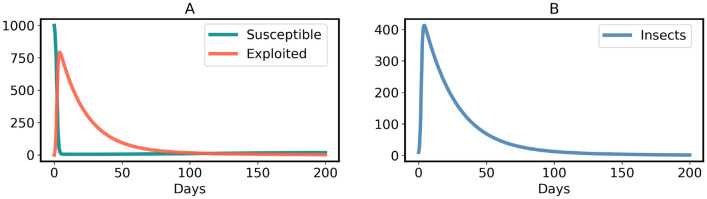
Fig. 5.
Time-courses (A, B) of model (3) converge to when . Parameters: and .
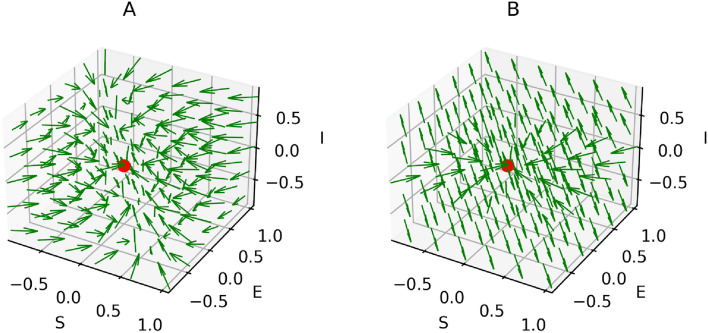
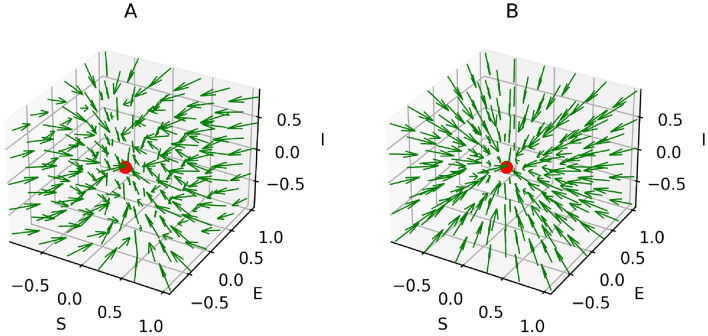
Fig. 6.
Phase portraits of , obtained from model (3). (A) Stable for . Parameters are the same as in Fig. 5. (B) Unstable for . Parameters: and .
Fig. 7.
Time-course of model (3) when . (A, B) Case where is a stable node. Parameters: and . (C, D) Case where is a stable focus. Parameters: and .
Model including plant defense
A new parameter is introduced, representing the per capita rate at which new plants germinate with chemical defenses. These defended plants, denoted by the compartment D, are not hosts to generalists. Obviously, (with being the per capita reproduction or germination rate constant). The fluxes between the compartments are as shown in Fig. 3 with an additional flux to the compartment of defended plants (D) and a modification in the flux entering the susceptible compartment, expressed by the scheme in Fig. 4.
Fig. 4.
Scheme of the SEDI model (9) with demographic effect, re-susceptibility and germinated plants defended against generalists. Variables and parameters are explained in the text.
The rate equations are:
| 9a |
| 9b |
| 9c |
| 9d |
where the germinating plants enter the susceptible compartment at a per capita rate , shown in Fig. 4. The model (9) has an additional ODE representing the growth rate in defended plants (D), Eq. (9c). This main structural difference between models (3) and (9) allows us to assess the benefit of chemical defense evolved in plants. This new model (9) is called SEDI model, where the total plant population (N) is equal to the sum of susceptible, exploited and defended plants (). Thus, the sum of Eqs. (9a), (9b) and (9c) gives:
| 10 |
Eq. (10) proves that the total plant population is a constant in model (9) if the germination and death rate constants (per capita) are assumed to be equal.
The four-dimensional model (9) can be reduced to three dimensions, because D is the only variable occurring in the ODE (9c). The solution of that equation is not needed (although it can easily be found analytically) since the implicit functions of and I in the right-hand sides of the ODEs (9a), (9b) and (9d) are sufficient to analyze the behavior of model (9) in view of equilibria in and their stability. The model (9) has two possible equilibrium points. The non-endemic (oviposition and insect free) equilibrium is:
| 11 |
where is the fraction of germinated plants (per capita) that evolved constitutive defense. To be noted , because . Interestingly, some susceptible plants () are not oviposited by generalist insects for . is asymptotically stable for , proved in the Supplementary Information S3 and illustrated by Figs. 9 and 10B. For , is asymptotically stable if and only if:
| 12 |
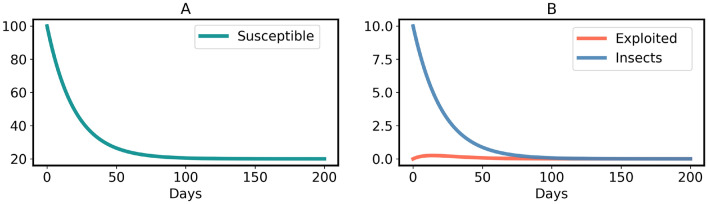
In the extreme case , this is equivalent to the condition mentioned above. Calculations of deriving and the proof of its asymptotic stability for are given in the Supplementary Information S3. The time-course and phase-portrait of stable at are illustrated by Figs. 8 and 10A, respectively.
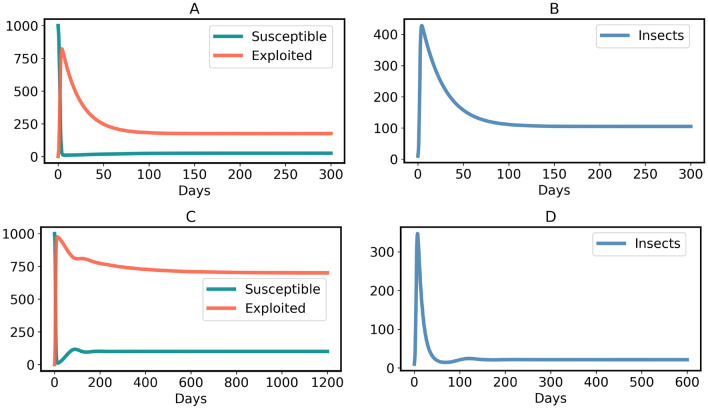
Fig. 9.
Time-courses (A, B) of model (9) converge to when . Parameters are the same as in Fig. 8 except for .
Fig. 10.
Phase portraits of , obtained from model (9). (A) Stable for and . Parameters: and . (B) Stable for . Parameters are the same as in Fig. 9.
Fig. 8.
Time-courses of model (9) converge to when . Parameters: and .
The endemic equilibrium of the model (9) is:
| 13 |
Generalists are non-endemic in the wild if the endemic equilibrium (13) does not exist at all, i.e. the insect and oviposition free equilibrium () is the only possible stable equilibrium. This is achieved if and only if the inequality (12) holds true, because exploited plants and generalists would be negative in the equilibrium (13) for . In contrast, the endemic equilibrium of generalists exists and is stable (either a stable node or a stable focus) if , shown by the time-courses in Fig. 11. The derivation and stability analysis of are given in the Supplementary information S4. Although is stable for shown by Figs. 9 and 10B, the case is only feasible if the host plants of generalist insects are quite low in a region.
Fig. 11.
Time-course of model (9) for . (A, B) Case where is a stable node. Parameters: and . (C, D) Case where is a stable focus. and .
It is interesting to obtain that evolution of constitutive defense in plants depends on the reproduction number () of insects. Condition (12) can be interpreted as follows. In order to stop an endemic by generalist insects, not all plant individuals need to store chemical defenses. For example, if a generalist insect species has , then . Therefore, that particular generalist species cannot be endemic if more than of all plants germinate with deterrent chemicals. Since for all insect species74, condition (12) also proves that if nearly all plants are germinated with chemical defenses, generalist insects become non-endemic in the wild. This phenomenon is shown by Figs. 8 and 10A. In other words, a few plants can remain undefended because if insects appeared (as a fluctuation of the free equilibrium), then these few plants would be insufficient to enable sufficient reproduction of insects.
Illustration of results
Discussion
The main results of this study are as follows:
If plants do not evolve chemical defenses, an endemic by generalist insects happens for , Fig. 7. That result means generalists become native herbivores of plants in a certain region. However, as stated before, such phenomenon is not evident in the wild15–18.
If a fraction of all plants are germinated with chemical defenses, but condition (12) is not fulfilled, the generalist endemic persists, Fig. 11. However, this result is not consistent with the observations mentioned in the previous point15–18.
Plants display a generalist-free (non-endemic) stable equilibrium for if and only if nearly all plants are germinated with chemical defenses (i.e. constitutive plant defense), expressed by condition (12) and shown in Figs. 8 and 10A. That practically (though not literally) justifies the theory that all plants have chemical defenses3,5,11,14 due to the nonexistence of generalist endemic species in the wild15–18.
If the reproduction number () of generalist insects in a region is below one, they cannot be endemic, Figs. 9 and 10B. This case is feasible when sufficient host plants are unavailable.
Condition (12) is necessary and sufficient for the generalist insect species to be non-endemic. That means is the only stable steady state if and occurs if is the only stable steady state, where . Since we obtained that nearly all plants should germinate with chemical defenses, some exceptions could be possible in plant chemical ecology. These exceptions could be considered as free-riders. The concept of free-riders is often used in game theory80,81. However, the costs of producing defense chemicals are neglected for the sake of simplicity. Therefore, the free-riders do not have any physiological advantages in comparison to defended plants. If costs were included, as is done in many game-theoretical models80,81, a dilemma occurs. The free-riders then have a higher growth rate and could outcompete defended plants, so that the population becomes susceptible to herbivores. Various ways of resolving the dilemma have been proposed in biological contexts other than plant-herbivore interactions, such as spatial structure82.
Interestingly, a few plants can be found that may not invest sufficiently in constitutive defense35,83,84. For example, blue lupin (Lupinus angustiflius) may not produce any alkaloids even after suffering from herbivory85 and the invasive plant Lespedeza cuneata is inadequately defended constitutively against herbivory86. However, such examples are rare in plant chemical ecology. The basic model (3) without plant defense could be written as a model without vital dynamics, that is, without germination and death rates, and still having the conservation relation . However, for the model (9) with plant defense, considering the plant germination rate is important to describe constitutive defense, which is present in plants during the normal course of development from germination on1,2.
The method is developed under the framework of stability theory. Stability theory is widely used in epidemiology28–30,87, eco-epidemiology88–91, population dynamics27,92 and other fields of mathematical biology or ecology28,29 to determine the asymptotic properties of solutions or equilibrium points in a long interval of time. In this field of study, the biological or ecological phenomena are expressed by a system of differential equations27,92. Stable equilibria of that system refer to the fixed points, where the entire system converge27,29,92. For example, vaccinating a certain percentage of a population eradicates an epidemic, because vaccination above the threshold makes the endemic-free equilibrium of the SIRV model (SIR model with vaccination) asymptotically stable28,29. Similarly, from model (9), it can be claimed that nearly all plants have evolved chemical defenses, because only then the generalist endemic free equilibrium is asymptotically stable.
Generalist insects are polyphagous by nature93,94, thus, select a wide range of host plants16. Nevertheless, plant defense negatively affects them due to their lack of specialism95–98. For example, glucosinolates and their hydrolyzed toxic isothiocyanate products of the Brassicaceae plant family reduce the development rate and cause high mortality of lepidopteran generalists98,99, such as Spodoptera exigua, Spodoptera littoralis, Mamestra brassicae, Trichoplusia ni, and Helicoverpa armigera96. Specialist insects, on the other hand, have evolved efficient counter-defense or resistance against host plant toxins95,97,99. Moreover, specialist insects use plant defense chemicals as a cue to identify host plants for oviposition33,36,100–102. Thus, plant defense could increase the pressure of specialist insect herbivores33,36. That is a direct contrast between the selection behavior of specialist vs generalist insects. It is not exactly clear how plants are benefiting against specialists by evolving defenses. However, plant defenses can attract the natural enemies of insect herbivores36,103, which leads to the tritrophic interaction104. That can be a possible explanation.
The indirect role of plant defense compounds and their subsequent products is attracting predators and parasitoids of deleterious insects33,36,103–105. For example, in Pieris rapae infested Arabidopsis plants, nitriles (a less toxic hydrolyzed products of glucosinolates) can recruit the parasitoid wasp Cotesia rubecula106; isothiocyanates in the Brassica plants can recruit Trichogramma chilonis wasps during infestation by Plutella xylostella107; entomopathogenic nematodes are recruited by insect-damaged maize roots108. Tritrophic interaction by herbivore-induced plant volatiles (HIPVs) has been modelled before109,110, where the emergence of natural enemies reduce the deleterious insect population. Although in this study, the indirect role of plant defenses is not considered, it could be an interesting refinement of the model (9).
A study conducted on microorganisms showed that the generalist genera are older than specialist genera in an evolutionary timescale111. Therefore, it is possible that the fundamental cause for plant species evolving chemical defenses was to eradicate the deleterious generalists4–8. However, for a holistic understanding, it is important to investigate the plants’ benefit of evolving chemical defenses against different group of deleterious insects (generalists and specialists) together33,36. Especially, it is known that specialists cause damage by being locally endemic to specific niches111,112. This leaves us with multiple questions: Whether tritrophic interaction is capable of ending a specialist-driven endemic, whether the chemical defense of plants is responsible for the endemics by specialists etc. It is worthwhile tackling these questions by mathematical modeling in the future.
Conclusion
From the main results of this study, it can be concluded that generalist insects are non-endemic in the wild, because nearly all plants are germinated with secondary metabolites. However, that does not mean generalists become extinct. They can survive with a low reproduction number () on host plants. Although clear results are obtained, the main limitation of these models is the assumption of a constant total population of plants, i.e. in model (3) and in model (9), where N is constant. It would be intriguing to verify the results by advancing these models to describe overall growing plant populations109,110, in analogy to vital dynamics in SIR models29,30.
The study fits within the context of plant protection, insect behavior and pest control issues, which could be interesting not only for wildlife practitioners, but also for crop protection. Since generalists are only temporary visitors, crop protection measures should be more relevant against endemic specialist insect pests36. Several pest control methods, such as application of insecticides113, intercropping or mixed cropping114, sterile insect technique (SIT)115 etc. are practiced to save crop plants from deleterious insects. Including these control measures will be promising extensions to the model (9), which could expedite the eradication process of insect pests. Moreover, since plants are susceptible to both specialists and generalists, it would be significant to expand the model for both groups of insect (pest) species.
Supplementary Information
Acknowledgements
Stimulating discussions with Abdel H. Halloway and Jonathan Gershenzon are gratefully acknowledged. Financial support by the German Research Foundation (DFG) in the SFB 1127 ChemBioSys project no. 239748522 to S.S. and the Jena School of Microbial Communication (JSMC) to S.D. is gratefully acknowledged. S. C. thanks the IMPRS “Chemical Communication in Ecological Systems” for training and support.
Author contributions
S.C. conceptualized the study and developed the models. S.C. and S.D. wrote the original draft, analyzed the models, did the simulations and provided the calculations. S.S. supervised the study and refined the model and manuscript draft. All authors verified the results and reviewed the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Data availability
All data generated or analyzed during this study are included in this published article [and its supplementary information file].
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-74771-0.
References
- 1.Dicke, M. Induced responses to herbivory by r. karban and i.t. baldwin. Trends Ecol. Evol.13(2), 83 (1998). [DOI] [PubMed] [Google Scholar]
- 2.Textor, S. & Gershenzon, J. Herbivore induction of the glucosinolate-myrosinase defense system: Major trends, biochemical bases and ecological significance. Phytochem. Rev.8(1), 149–170 (2009). [Google Scholar]
- 3.Vickery, M. Plant poisons: their occurrence, biochemistry and physiological properties. Sci. Prog. 93, 181–221 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fraenkel, G. S. Raison d’etre of secondary plant substances. Science129(3361), 1466–1470 (1959). [DOI] [PubMed] [Google Scholar]
- 5.Bernays, E. & Chapman, R. The evolution of deterrent responses in plant-feeding insects. In Perspectives in Chemoreception and Behavior. Proceedings in Life Sciences (eds. Chapman, R. F. et al.) (Springer, 1987).
- 6.Wittstock, U. & Gershenzon, J. Constitutive plant toxins and their role in defense against herbivores and pathogens. Curr. Opin. Plant Biol.5, 300–307 (2002). [DOI] [PubMed] [Google Scholar]
- 7.Hartmann, T. From waste products to ecochemicals: Fifty years research of plant secondary metabolism. Phytochemistry68(22), 2831–2846 (2007). [DOI] [PubMed] [Google Scholar]
- 8.War, A. R. et al. Mechanisms of plant defense against insect herbivores. Plant Signal. Behav. 7(10), 1306–1320 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dethier, V. G., Browne, B. L. & Smith, C. N. The designation of chemicals in terms of the responses they elicit from insects. J. Econ. Entomol.53(1), 134–136 (1960). [DOI] [PubMed]
- 10.Klun, J. A., Khrimian, A. & Debboun, M. Repellent and deterrent effects of SS220, picaridin, and deet suppress human blood feeding by Aedes aegypti, Anopheles stephensi, and Phlebotomus papatasi. J. Med. Entomol. 43(1), 34–39 (2006). [DOI] [PubMed]
- 11.Swain, T. Secondary compounds as protective agents. Annu. Rev. Plant Physiol.28(1), 479–501 (1977). [Google Scholar]
- 12.Singer, A. C., Crowley, D. E. & Thompson, I. P. Secondary plant metabolites in phytoremediation and biotransformation. Trends Biotechnol. 21(3), 123–130 (2003). [DOI] [PubMed]
- 13.Divekar, P. A. et al. Plant secondary metabolites as defense tools against herbivores for sustainable crop protection. Int. J. Mol. Sci. 23(5), 2690 (2022). [DOI] [PMC free article] [PubMed]
- 14.Gershenzon, J. & Ullah, C. Plants protect themselves from herbivores by optimizing the distribution of chemical defenses. Proc. Natl. Acad. Sci.119(4), 2120277119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Walter, G. H. & Benfield, M. D. Temporal host plant use in three polyphagous heliothinae, with special reference to Helicoverpa punctigera (wallengren) (noctuidae: Lepidoptera). Austral Ecol.19, 458–465 (1994).
- 16.Ali, J. G. & Agrawal, A. A. Specialist versus generalist insect herbivores and plant defense. Trends Plant Sci.17(5), 293–302 (2012). [DOI] [PubMed] [Google Scholar]
- 17.Wang, Y. et al. Higher plasticity in feeding preference of a generalist than a specialist: Experiments with two closely related helicoverpa species. Sci. Rep.7, 17876 (2017). [DOI] [PMC free article] [PubMed]
- 18.Rafter, M. A. & Walter, G. H. Generalising about generalists? a perspective on the role of pattern and process in investigating herbivorous insects that use multiple host species. Arthropod-Plant Interact14, 1–20 (2020). [Google Scholar]
- 19.Futuyma, D. J. & Moreno, G. The evolution of ecological specialization. Annu. Rev. Ecol. Syst. 19, 207–233 (1988). [Google Scholar]
- 20.Mason, P. A., Wilkes, S. R., Lill, J. T. & Singer, M. S. Abundance trumps quality: Bi-trophic performance and parasitism risk fail to explain host use in the fall webworm. Oikos120, 1509–1518 (2011).
- 21.Murphy, S. M. & Loewy, K. J. Trade-offs in host choice of an herbivorous insect based on parasitism and larval performance. Oecologia179, 741–751 (2015). [DOI] [PubMed] [Google Scholar]
- 22.Buonomo, B., Giannino, F. , Saussure, S. & Venturino, E. Effects of limited volatiles release by plants in tritrophic interactions. Math. Biosci. Eng.16(5), 3331–3344 (2019). [DOI] [PubMed]
- 23.Mondal, R., Kesh, D & Mukherjee, D. Role of induced volatile emission modelling tritrophic interaction. Differ. Equ. Dyn. Syst. 30, 749–765 (2022).
- 24.Yuan, H. et al. Development of a widely targeted volatilomics method for profiling volatilomes in plants. Mol. Plant 15(1), 189–202 (2022). [DOI] [PubMed]
- 25.Mezzomo, P. et al. Variation in induced responses in volatile and non-volatile metabolites among sixwillow species: Do willow species share responses to herbivory?. Phytochem.226, 114222 (2024). [DOI] [PubMed]
- 26.Kermack, W. O. & McKendrick, A. G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 115(772), 700–721 (1927). [Google Scholar]
- 27.Murray, J. D. Mathematical Biology. I An Introduction 3rd edn. (Springer, 2002). [Google Scholar]
- 28.Brauer, F. & Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology 2nd edn. (Springer, 2001). [Google Scholar]
- 29.Martcheva, M. An Introduction to Mathematical Epidemiology 1st edn. (Springer, 2015). [Google Scholar]
- 30.Makinde, O. D. Adomian decomposition approach to a SIR epidemic model with constant vaccinationstrategy. Appl. Math. Comput.184(2), 842–848 (2007). [Google Scholar]
- 31.Kothari, I. L. & Patel, M. Plant immunization. Indian J. Exp. Biol.42(3), 244–252 (2004). [PubMed] [Google Scholar]
- 32.Jong, T. J. Why fast-growing plants do not bother about defence. Oikos74(3), 545–548 (1995). [Google Scholar]
- 33.Van der Meijden, E. Plant defence, an evolutionary dilemma: Contrasting effects of (specialist andgeneralist) herbivores and natural enemies. Entomol. Exp. Appl.80(1), 307–310 (1996).
- 34.Åström, M. & Lundberg, P. Plant defence and stochastic risk of herbivory. Evol. Ecol.8(3), 288–298 (1994). [Google Scholar]
- 35.Ito, K. & Sakai, S. Optimal defense strategy against herbivory in plants: Conditions selecting for induced defense, constitutive defense, and no-defense. J. Theor. Biol.260(3), 453–459 (2009). [DOI] [PubMed] [Google Scholar]
- 36.Chakraborty, S., Gershenzon, J. & Schuster, S. Selection pressure by specialist and generalist insectherbivores leads to optimal constitutive plant defense, a mathematical model. Ecol. Evol. 13, 10763 (2023). [DOI] [PMC free article] [PubMed]
- 37.Yu, D., Huang, T., Tian, B. & Zhan, J. Advances in biosynthesis and biological functions ofproanthocyanidins in horticultural plants. Foods 9(12), 1774 (2020). [DOI] [PMC free article] [PubMed]
- 38.Panche, A. N., Diwan, A. D., Chandra, S. R. Flavonoids: An overview. J. Nutr. Sci.29(5), 47 (2016). [DOI] [PMC free article] [PubMed]
- 39.Halkier, B. A. & Gershenzon, J. Biology and biochemistry of glucosinolates. Annu. Rev. Plant Biol.57, 303–333 (2006). [DOI] [PubMed] [Google Scholar]
- 40.Hopkins, R. J., van Dam, N. M. & van Loon, J. J. A. Role of glucosinolates in insect plant relationshipsand multitrophic interactions. Annu. Rev. Entomol. 54, 57–83 (2009). [DOI] [PubMed]
- 41.Ashihara, H. & Crozier, A. Biosynthesis and metabolism of caffeine and related purine alkaloids in plants. Adv. Bot. Res.30, 117–205 (1999). [Google Scholar]
- 42.Kim, Y. S. & Sano, H. Pathogen resistance of transgenic tobacco plants producing caffeine. Phytochemistry69(4), 882–888 (2008). [DOI] [PubMed] [Google Scholar]
- 43.Steppuhn, A., Gase, K., Krock. B., Halitschke, R., Baldwin. I. T. Nicotine’s defensive function in nature. PLoS Biol. 2(8), 217 (2004). [DOI] [PMC free article] [PubMed]
- 44.Lambert, D. M. & Fowler, C. J. The endocannabinoid system: Drug targets, lead compounds, and potential therapeutic applications. J. Med. Chem.48(16), 5059–5087 (2005). [DOI] [PubMed] [Google Scholar]
- 45.Henery, M. L., Wallis, I. R., Stone, C. & Foley, W. J. Methyl jasmonate does not induce changes inEucalyptus grandis leaves that alter the effect of constitutive defences on larvae of a specialistherbivore. Oecologia156(4), 847–859 (2008). [DOI] [PubMed]
- 46.Zulak, K. G., Khan, M. F., Alcantara, J., Schriemer, D. C. & Facchini, P. J. Plant defense responses inopium poppy cell cultures revealed by liquid chromatography-tandem mass spectrometry proteomics. Mol. Cell. Proteom. 8(1), 86–98 (2009). [DOI] [PubMed]
- 47.Agrawal, A. A., Petschenka, G., Bingham, R.A., Weber, M.G., & Rasmann, S. Toxic cardenolides:Chemical ecology and coevolution of specialized plant-herbivore interactions. New Phytol. 194(1), 28–45 (2012). [DOI] [PubMed]
- 48.Adams, R. & Jones, V. V. The structure of leucenol. J. Am. Chem. Soc.69(7), 1803–1805 (1947). [DOI] [PubMed] [Google Scholar]
- 49.Honda, M. D. H. & Borthakur, D. Mimosine facilitates metallic cation uptake by plants through formation of mimosine-cation complexes. Plant Mol. Biol.102, 431–445 (2020). [DOI] [PubMed] [Google Scholar]
- 50.Barceloux, D. G. Poison hemlock (Conium maculatum L.). Medical Toxicology of Natural Substances: Foods, Fungi, Medicinal Herbs, Plants, and Venomous Animals 796–799 (Wiley, 2008). [Google Scholar]
- 51.Moller, B. L. Functional diversifications of cyanogenic glucosides. Curr. Opin. Plant Biol.13, 338–347 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Rousseau, G., Clément, J. Fezard, J. B. & Laribi, S. Intoxication au colchique par confusion avec l’ail desours (Colchicum poisoning by confusion with wild garlic (Allium ursinum)). Rev. Med. Interne 43(9), 559–561 (2022). [DOI] [PubMed]
- 53.Feeny, P. P. Effect of oak leaf tannins on larval growth of the winter moth Operophtera brumata . J. Insect Physiol. 14, 805–817 (1968).
- 54.Bernays, E. A. Plant tannins and insect herbivores: An appraisal. Ecol. Entomol.6, 353–360 (1981). [Google Scholar]
- 55.Pradit, N., Mescher, M. C., Wang, Y., Vorsa, N. & Rodriguez-Saona, C. Phytoplasma infection ofcranberries benefits non-vector phytophagous insects. Front. Ecol. Evol. 7, 181 (2019).
- 56.Simmonds, M. S. J., Blaney, W. M. & Fellows, L. E. Behavioural and electrophysiological study ofantifeedant mechanisms associated with polyhydroxy alkaloids. J. Chem. Ecol.16, 3167–3196 (1990). [DOI] [PubMed]
- 57.Wahba, T. F., El-Bassyouni, G. T., El-Shamy, A. M. & Wahba, M. N., Nanoinert diatomaceous andemamectin benzoate: Enhancing wheat protection against fall armyworms for sustainablemanagement. S. Afr. J. Bot.169, 413–425 (2024).
- 58.Simmonds, M. S. J. & Stevenson, P. C. Effects of isoflavonoids from cicer on larvae of Heliocoverpaarmigera. J. Chem. Ecol.27, 965–977 (2001). [DOI] [PubMed]
- 59.Nathanson, J. A. Caffeine and related methylxanthines: Possible naturally occurring pesticides. Science226(4671), 184–187 (1984). [DOI] [PubMed] [Google Scholar]
- 60.Kim, Y.-S., Lim, S., Kang, K.-K. & Jung, Y.-J, Resistance against beet armyworms and cotton aphids incaffeine-producing transgenic chrysanthemum. Plant Biotechnol.28(4), 393–395 (2011).
- 61.Park, S. H. et al. Contrasting roles of cannabidiol as an insecticide and rescuing agent for ethanolinduceddeath in the tobacco hornworm Manduca sexta. Sci. Rep.9, 10481 (2019). [DOI] [PMC free article] [PubMed]
- 62.Howe, G. A. & Jander, G. Plant immunity to insect herbivores. Annu. Rev. Plant Biol.59, 41–66 (2008). [DOI] [PubMed] [Google Scholar]
- 63.Plarre, R., et al. Effects of oil of cloves and citronellol, two commercially available repellents, againstthe webbing clothes moth Tineola bisselliella. Hum (lepidoptera: Tineidae). Anzeiger Schsadlingskunde Pflanzenschutz Umweltschutz70, 45–50 (1997).
- 64.Petschenka, G., Bramer, C., Pankoke, H. & Dobler, S. Evidence for a deterrent effect of cardenolides onNephila spiders. Basic Appl. Ecol.12(3), 260–267 (2011).
- 65.Shields, V. D. C. et al. The effect of varying alkaloid concentrations on the feeding behavior of gypsymoth larvae, Lymantria dispar (L.) (lepidoptera: Lymantriidae). Arthropod Plant Interact.2(2), 101–107 (2008). [DOI] [PMC free article] [PubMed]
- 66.Ishaaya, I., Hirashima, A., Yablonski, S., Tawata, S. & Morifusa, E. Mimosine, a nonprotein amino acid, inhibits growth and enzyme systems in Tribolium castaneum. Pestic. Biochem. Physiol.39, 35–42 (1991).
- 67.Nguyen, B. C. Q., Chompoo, J. & Tawata, S. Insecticidal and nematicidal activities of novel mimosine derivatives. Molecules20, 16741–16756 (2015). [DOI] [PMC free article] [PubMed]
- 68.Robin, M. Yellow pitcher plant or trumpets (Sarracenia flava). United States Department of Agriculture. United States Department of Agriculture Forest Service (Retrieved 3 May 2015).
- 69.Polunin, N. High-concentration hydrogen cyanide fumigation of fungi and bacteria. Nature150, 682–684 (1942). [Google Scholar]
- 70.Dooley, T. P. The influence of colchicine on the germ cells of insects, Melanoplus differentialis and Gryllus assimilis, with special reference to the cytoplasmic inclusions. Proc. Iowa Acad. Sci.46(1), 445–446 (1939).
- 71.Li, X. et al. Effects of four chemosterilants on Bactrocera tau. Ecotoxicol. Environ. Saf.243, 114028 (2022). [DOI] [PubMed]
- 72.Clausen, C. P. Entomophagous Insects (McGraw-Hill, 1940). [Google Scholar]
- 73.Wilson, E. O. The Insect Societies (Harvard University Press, 1971). [Google Scholar]
- 74.Hinton, H. E. Biology of Insect Eggs (Pergamon Press, 1981). [Google Scholar]
- 75.Holldöbler, B. & Wilson, E. O. The Ants (Harvard University Press, 1990). [Google Scholar]
- 76.Devictor, V. et al. Defining and measuring ecological specialization. J. Appl. Ecol.47, 15–25 (2010).
- 77.Poisot, T., Bever, J. D., Nemri, A., Thrall, P. H. & Hochberg, M. E. A conceptual framework for the evolution of ecological specialisation. Ecol. Lett.14, 841–851 (2011). [DOI] [PMC free article] [PubMed]
- 78.Büchi, L. & Vuilleumier, S. Coexistence of specialist and generalist species is shaped by dispersal and environmental factors. Am. Nat.183(5), 612–624 (2014). [DOI] [PubMed] [Google Scholar]
- 79.Kneitel, J. M. Occupancy and environmental responses of habitat specialists and generalists depend on dispersal traits. Ecosphere9(3), 02143 (2018). [Google Scholar]
- 80.Denison, R. F. et al. Cooperation in the rhizosphere and the “free rider’’ problem. Ecology84, 838–845 (2003).
- 81.Delton, A. W., Cosmides, L., Guemo, M., Robertson T. E. & Tooby, J. The psychosemantics of free riding: Dissecting the architecture of a moral concept. J. Pers. Soc. Psychol.102(6), 1252–1270 (2012). [DOI] [PMC free article] [PubMed]
- 82.Schuster, S. et al. Cooperation and cheating in microbial exoenzyme production—theoretical analysis for biotechnological applications. Biotechnol. J.5, 751–758 (2010). [DOI] [PubMed]
- 83.Strauss, S. Y. & Agrawal, A. A. The ecology and evolution of plant tolerance to herbivory. Trends Ecol. Evol.14, 179–185 (1999). [DOI] [PubMed] [Google Scholar]
- 84.Maron, J. L. & Crone, E. Herbivory: Effects on plant abundance, distribution and population growth. Proc. R. Soc. B: Biol. Sci.273(1601), 2575–2584 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.del Pilar Vilariño, M., Mareggiani, G., Grass, M. Y., Leicach, S. R. & Ravetta, D. A. Post damage alkaloid concentration in sweet and bitter lupin varieties and its effect on subsequent herbivory. J. Appl. Entomol.129, 233–238 (2005).
- 86.Beaton, L. L., Van Zandt, P. A., Esselman, E. J. & Knight, T. M. Comparison of the herbivore defense and competitive ability of ancestral and modern genotypes of an invasive plant, Lespedeza cuneata. Oikos120, 1413–1419 (2011).
- 87.Adak, D., Majumder, A. & Bairagi, N. Mathematical perspective of covid-19 pandemic: Disease extinction criteria in deterministic and stochastic models. Chaos Soliton. Fract.42, 110381 (2021). [DOI] [PMC free article] [PubMed]
- 88.Chattopadhyay, J. & Bairagi, N. Pelicans at risk in salton sea—an eco-epidemiological model. Ecol. Model.136(2–3), 103–112 (2001). [Google Scholar]
- 89.Chattopadhyay, J. & Pal, S. Viral infection on phytoplankton-zooplankton system-a mathematical model. Ecol. Model.151(1), 15–28 (2002). [Google Scholar]
- 90.Chattopadhyay, J., Srinivasu, P. D. N. & Bairagi, N. Pelicans at risk in salton sea-an eco-epidemiological model-ii. Ecol. Model.167(1–2), 199–211 (2003).
- 91.Pal, S., Chatterjee, S. & Chattopadhyay, J. Role of toxin and nutrient for the occurrence and termination of plankton bloom-results drawn from field observations and a mathematical model. Biosystems90(1), 87–100 (2007). [DOI] [PubMed]
- 92.Kot, M. Elements of Mathematical Ecology (Cambridge University Press, 2001). [Google Scholar]
- 93.Schoonhoven, L. M., van Loon, J. J. A. & Dicke, M. Insect-Plant Biology (Oxford University Press, 2005).
- 94.Mello, M. O. & Silva-Filho, M. C. Plant-insect interactions: An evolutionary arms race between two distinct defense mechanisms. Braz. J. Plant. Physiol.14, 71–81 (2002). [Google Scholar]
- 95.Jeschke, V. et al. How glucosinolates affect generalist lepidopteran larvae: Growth, development and glucosinolate metabolism. Front. Plant Sci.8, 1995 (2017). [DOI] [PMC free article] [PubMed]
- 96.Jeschke, V. et al. So much for glucosinolates: A generalist does survive and develop on brassicas, but at what cost?. Plants10(5), 962 (2021). [DOI] [PMC free article] [PubMed]
- 97.Chakraborty, S., Gershenzon, J. & Schuster, S. Comparing two strategies of counter-defense against plant toxins: A modeling study on plant-herbivore interactions. Front. Ecol. Evol.11, 1197757 (2023).
- 98.Chakraborty, S. & Schuster, S. How plant toxins cause early larval mortality in herbivorous insects: An explanation by modeling the net energy curve. Toxins16(2), 72 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Sun, R. et al. Tritrophic metabolism of plant chemical defenses and its effects on herbivore and predator performance. ELife8, 51029 (2019). [DOI] [PMC free article] [PubMed]
- 100.Mewis, I. Z., Ulrich, C. H. & Schnitzler, W. H. The role of glucosinolates and their hydrolysis products in oviposition and host-plant finding by cabbage webworm, Hellula undalis. Entomol. Exp. Appl.105, 129–139 (2002).
- 101.Renwick, J. A, Haribal, M., Gouinguené, S. & Städler, E. Isothiocyanates stimulating oviposition by the diamondback moth, Plutella xylostella. J. Chem. Ecol.32(4), 755–766 (2006). [DOI] [PubMed] [Google Scholar]
- 102.Kos, M. et al. Relative importance of plant-mediated bottom-up and top-down forces on herbivore abundance on Brassica oleracea. Funct. Ecol.25(5), 1113–1124 (2011).
- 103.Dicke, M. & Baldwin, I. T. The evolutionary context for herbivore-induced plant volatiles: Beyond the ‘cry for help’. Trends Plant Sci.15(3), 167–175 (2010). [DOI] [PubMed] [Google Scholar]
- 104.Turlings, T. C. J. & Erb, M. Tritrophic interactions mediated by herbivore-induced plant volatiles: Mechanisms, ecological relevance, and application potential. Annu. Rev. Entomol.63(1), 433–452 (2018). [DOI] [PubMed] [Google Scholar]
- 105.Thaler, J. S. Jasmonate-inducible plant defences cause increased parasitism of herbivores. Nature399, 686–688 (1999). [Google Scholar]
- 106.Van Poecke, R. M. P., Posthumus, M. A. & Dicke, M. Herbivore-induced volatile production by arabidopsis thaliana leads to attraction of the parasitoid cotesia rubecula: Chemical, behavioral, and gene-expression analysis. J. Chem. Ecol.27(10), 1911–1928 (2001). [DOI] [PubMed]
- 107.Reddy, G. V., Holopainen, J. K. & Guerrero, A. Olfactory responses of plutella xylostella natural enemies to host pheromone, larval frass, and green leaf cabbage volatiles. J. Chem. Ecol.28(1), 131–143 (2002). [DOI] [PubMed]
- 108.Rasmann, S. et al. Recruitment of entomopathogenic nematodes by insect-damaged maize roots. Nature434, 732–737 (2005). [DOI] [PubMed]
- 109.Liu, Y. et al. Modelling tritrophic interactions mediated by induced defence volatiles. Ecol. Model.220(23), 3241–3247 (2009).
- 110.Fergola, P. & Wang, W. On the influences of defensive volatiles of plants in tritrophic interactions. J. Biol. Syst.19(2), 345–363 (2011). [Google Scholar]
- 111.von Meijenfeldt, F. A. B., Hogeweg, P. & Dutilh, B. E. A social niche breadth score reveals niche range strategies of generalists and specialists. Nat. Ecol. Evol.7, 768–781 (2023). [DOI] [PMC free article] [PubMed]
- 112.Behroozian, M., Ejtehadi, H., Memariani, F., Pierce, S. & Mesdaghi, M. Are endemic species necessarily ecological specialists? functional variability and niche differentiation of two threatened dianthus species in the montane steppes of northeastern iran. Sci. Rep.10, 11774 (2020). [DOI] [PMC free article] [PubMed]
- 113.Zhang, Z. et al. Design, synthesis and biological activity of diamide compounds based on 3-substituent of the pyrazole ring†. Pest Manag. Sci.78(5), 2022–2033 (2022). [DOI] [PubMed]
- 114.Letourneau, D. K. et al. Does plant diversity benefit agroecosystems? A synthetic review. Ecol. Appl.21(1), 9–21 (2011). [DOI] [PubMed]
- 115.Bourtzis, K. & Vreysen, M. J. B. Sterile insect technique (sit) and its applications. Insects12(7), 638 (2021). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated or analyzed during this study are included in this published article [and its supplementary information file].