Molecular dynamics studies of the HIV-1 TAR and its complex with argininamide

Abstract

The dynamic behavior of HIV-1 TAR and its complex with argininamide is investigated by means of molecular dynamics simulations starting from NMR structures, with explicit inclusion of water and periodic boundary conditions particle mesh Ewald representation of the electrostatic energy. During simulations of free and argininamide-bound TAR, local structural patterns, as determined by NMR experiments, were reproduced. An interdomain motion was observed in the simulations of free TAR, which is absent in the case of bound TAR, leading to the conclusion that the free conformation of TAR is intrinsically more flexible than the bound conformation. In particular, in the bound conformation the TAR–argininamide interface is very well ordered, as a result of the formation of a U·A·U base triple, which imposes structural constraints on the global conformation of the molecule. Free energy analysis, which includes solvation contributions, was used to evaluate the influence of van der Waals and electrostatic terms on formation of the complex and on the conformational rearrangement from free to bound TAR.

INTRODUCTION

The regulation of viral gene expression in human immunodeficiency virus (HIV) requires highly specific RNA–protein interactions, which have been widely studied as a possible target for anti-HIV intervention. In particular, HIV Tat protein is known to activate viral gene transcription by interacting with the transactivation-responsive region (TAR), a stem–loop portion of the nascent RNA transcript. Upon binding to TAR, Tat recruits a cyclin-dependent kinase called CDK9 to the viral promoter, which relieves the transcriptional block by phosphorylating the C-terminal domain (CTD) of RNA polymerase II (1).

TAR is the first 59 nt of the nascent pre-mRNA transcript and its apical portion (nt G17–G45) directly binds to peptides that span the arginine-rich region of Tat (1). Extensive mutagenesis studies have shown that the binding site for Tat involves the trinucleotide bulge and adjacent base pairs. In particular, U23, the first nucleotide in the bulge, and two base pairs above the bulge (G26-C39 and A27-U38) are required for sequence-specific interaction (2–4). Other important contacts involve the phosphates P22, P23 and P40, located in the lower stem, and two base pairs below the bulge, A22-U40 and G21-C41 (2,5,6).

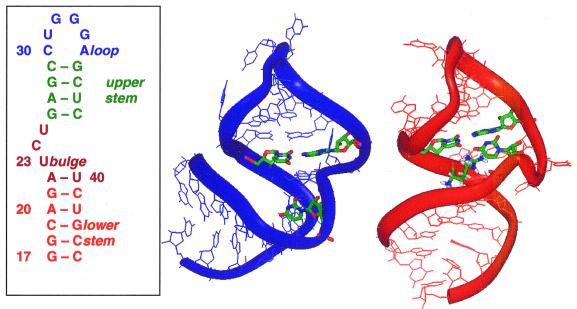
The binding of Tat to TAR is mediated by a single arginine present in the basic region of Tat protein (5). Furthermore, it has been shown that free arginine is able to specifically bind to TAR in a manner similar to that of the arginine within Tat (7). NMR studies have been performed on HIV-1 TAR bound to arginine-rich peptides and to a single argininamide (8–10). Argininamide is the amide derivative of arginine, which binds to TAR with slightly higher affinity due to the absence of a negative charge on the carboxyl group (7). These studies have revealed that the binding interaction results in a conformational rearrangement primarily involving the nucleotides in the RNA bulge. The two conformations as determined by NMR experiments (9) are shown in Figure 1, together with the secondary structure of TAR.

Figure 1.

Secondary structure of HIV-1 TAR and NMR structures of bound and free TAR.

NMR studies by Puglisi et al. identified a specific binding site for arginine (or argininamide), which involves hydrogen bonding of nucleotide G26 and phosphates P22 and P23 to the guanidinium group in the side chain of arginine (8). In their proposed model this interaction is stabilized by the formation of a base triple between U23 and the base pair A27-U38 (8), which are essential nucleotides for binding (2,3). However, no direct NMR evidence for the base triple was obtained. Further evidence for the existence of a base triple comes from NMR studies with mutated TAR RNA sequences that either disrupted or favored the formation of the base triple, including an isomorphic C23⁺-G27-C38 triple mutant (11). Moreover, the triple was consistent with NMR data from the HIV-2 TAR–argininamide complex (12) and, subsequently, direct NOE evidence was obtained for formation of the C23⁺-G27-C38 triple mutant of HIV-2 TAR (13).

In a subsequent NMR study Aboul-ela et al. (9) obtained a much larger set of NOE data and were able to fully determine the structure of HIV-1 TAR bound to argininamide or to a Tat-derived peptide, called ADP-1 (residues 37–72). The peptide contains the core and the basic region of Tat that closely resembles the binding specificity of full-length Tat. The derived TAR RNA structures are virtually identical in the two cases, suggesting that a single arginine within the basic region of Tat drives the conformational rearrangement from free to bound TAR. The ADP-1 peptide was not included in the structure due to lack of spectral assignments, but the bound arginine was determined. Upon the conformational rearrangement critical functional groups are repositioned, allowing the formation of additional contacts between Tat and the base pairs adjacent to the bulge in TAR. Within the 20 NMR derived structures different regions of TAR RNA have different patterns of structural definition. The helical stems are defined with a higher degree of precision than the apical loop and the bulge. Within the bulge C24 and U25 are flexible and exposed to the solvent while the position of U23 is more defined and at a pronounced angle relative to A27 and G26. Even if positioned adjacent to the major groove, U23 is too distant to interact with A27 and the presence of a U23-A27-U38 triple is not consistent with their NOE data (9).

In contrast, a more recent NMR investigation by Long and Crothers (10) of TAR bound to a 24 residue Tat peptide maintains that the base triple is present, based on the observation of NOEs between the U23 and the A27 imino protons. The discrepancy may be attributed to the nature of the peptide preparations utilized in the two NMR studies (14).

The unbound conformation of TAR has also been the object of study by both NMR and X-ray experiments (10,15,16). Aboul-ela et al. found that the first two residues in the bulge, U23 and C24, are stacked over A22 (15); this stacking results in a distortion of the backbone and in bending of the helix direction from the lower to the upper stem. Discontinuity in the helix axis is also observed in hydrodynamic and optical experiments on free TAR (17,18). A high resolution crystal structure determined by Ippolito and Steitz shows remarkably different features (16), particularly in the looped out bulged residues, which are stacked continuously between the lower and the upper stems. The conformation of the bulged backbone is stabilized by the presence of metal ions, which reduces the electrostatic repulsion between near backbone phosphates. However, the concentration of metal ions in their sample greatly exceeds intracellular concentrations, challenging any definite biological implications.

Long and Crothers partially reconciled these two structures of unbound TAR by suggesting that free TAR exists in two conformations, one highly populated (major conformer) and the other with a lower population (minor conformer) (10). The major conformer is similar to the structure found by Aboul-ela et al. U23 is stacked upon the lower stem, while C24 and U25 adopt flexible conformations. The angle between the axes of the two helical stems is estimated to be 45°, in agreement with transient electric birefringence studies (17). The two stems in the minor conformer, in contrast, seem to be coaxially stacked on each other, resembling the crystal structure (16).

In the present work we address some dynamic and structural questions on free and bound HIV-1 TAR using molecular dynamics simulations starting from NMR solution structures. A general question is whether the less defined region in the NMR structure of free TAR is due to the lack of long-range NOE signals or to the intrinsic flexibility of the configuration. Moreover, it is expected that the regions with base pairing will be well conserved during the simulations, while the non-canonical elements or single-stranded regions will be more flexible. However, some non-paired bases (for example U23) are involved in functionally important contacts and their behavior may be less flexible. In particular, it is interesting to examine how ordered the argininamide-binding site is in the complex and which interactions dominate. This latter question is addressed with free energy analyses, in which solvation terms were included through a continuum solvent model.

Recent simulations of RNA and RNA–protein systems show good agreement with experimental structural data (19–24). Free energy analyses, using a combination of molecular mechanics and continuum solvation studies, are of more recent development and have been applied to nucleic acids (25–28) and protein–nucleic acid complexes (21,29).

MATERIALS AND METHODS

The coordinates of the free TAR molecule (code 1ANR) and of the TAR–arginine complex (code 1ARJ) were obtained from the Brookhaven Protein Data Bank (PDB) (30). In both cases 20 NMR structures are present. The choice of the starting structures was done on the basis of local structural differences in root mean square distances (RMSDs) and on how representative a given structure was relative to the NMR family. For the bound TAR complex an arginine was present in the PDB file instead of the argininamide: in order to model the argininamide, which is the ligand actually used in the NMR study (9), the hydroxyl group of the arginine was substituted with an amide group. The force field parameters for the amide atoms were taken from the amide group of asparagine and the charges were slightly modified in order to neutralize the group.

All molecular dynamics simulations were performed using the Cornell et al. force field (31) and the AMBER 5.0 suite of programs. The program EDIT was used to add 27 Na⁺ ions to the TAR–argininamide complex (29 in the case of free TAR) in order to neutralize the system. A rectangular box of TIP3P water molecules (32) was added to solvate the complex, keeping a 10 Å minimum distance between each face of the box and the solute (15 Å in the case of structure 8 of bound TAR). To give some examples, the final system contained 18 664 (28 810) atoms within a box dimension of 61 × 70 × 58 ų (61 × 70 × 58 ų) in the case of structure 2 of free TAR (structure 8 of bound TAR).

Both systems were minimized and equilibrated with the same protocol, using the program SANDER. Initially the water molecules were relaxed around the fixed solute with 40 ps of dynamics. The whole system was minimized for 3000 steps and then heated up to 300 K in stages of 10 ps at 50 K, 20 ps at 150 K and 30 ps at 300 K, using the Berendsen temperature algorithm (33) with separate solute–solvent and solvent–solvent coupling. This gradual heating is necessary to equally distribute the kinetic energy to the many degrees of freedom. After this equilibration phase the production phase followed at 300 K for up to ∼1 ns.

All bonds involving hydrogen atoms were constrained using the SHAKE algorithm (34), so that a 2 fs time step could be used. Periodic boundary conditions were applied and the particle mesh Ewald (PME) approach (35) was used to accurately treat electrostatic interactions. All simulations were performed on 16 processors on a Cray T3E at the San Diego Supercomputer Center for a total CPU time of ∼3600 h for the 1 ns simulation of the TAR–argininamide complex and 3100 h for the 1 ns simulation of free TAR.

The trajectory analysis of RMSDs, atomic fluctuations and hydrogen bonding occupancies were performed using CARNAL. A hydrogen bond was considered occupied when the acceptor–donor distance was <4 Å and acceptor–hydrogen–donor angle was ±60° reletive to the ideal. The TAR–RNA interhelical angle was obtained by defining the upper stem and lower stem helix axis vectors, based on the center of geometry of the base pairing residues in the upper stem (residues 26–29 and 36–39) and the lower stem (residues 17–22 and 40–45), and then computing the angle between the two vectors.

The energy analyses involved the calculation of energies for ‘snapshot’ configurations taken at 10 ps interval from the molecular dynamics trajectories, followed by averaging of the values (27). The free energy is estimated as the sum of the molecular mechanical energy and the solvation free energy: G = E_MM + G_PB + G_np. The molecular mechanical energy (E_MM = E_BADH + E_{van der Waals} + E_{electrosatics}) of the solute was computed with the same force field used in the molecular dynamics simulations, with no cut-off for the evaluation of non-bonded interactions. No solute entropy contribution was evaluated.

The Poisson–Boltzmann approximation (36) was used to compute the electrostatic part of the solvation free energy (G_PB) at each snapshot. In this approach the solvent is treated as a continuum of high dielectric (ɛ = 80) and the solute as a low dielectric medium (ɛ = 1) with embedded charges taken from the Cornell et al. force field (31). The linearized version of the Poisson–Boltzmann equation was solved numerically using the DELPHI 2.0 program, which uses iterative finite difference methods on a cubic lattice (36). One thousand iterations were performed for each calculation. The cubic lattice, which had a grid spacing of 0.5 Å, was 80% filled with the solute. The solute atomic radii were taken from the PARSE set (25,37).

The non-polar contribution to the solvation free energy (G_np) was estimated from the solvent-accessible surface area (SASA) using the algorithm of Sanner (38), i.e. G_np = γ (SASA) + β, where γ = 0.00542 kcal/mol and β = 0.92 kcal/mol. When making the final averages of the snapshot values we skipped the first 200 ps of equilibration (20 snapshots), during which the energy is decreasing. In the last 800 ps the energy is more stable and consequently the standard deviations get smaller.

The representative structures for the conformation of the triple in bound TAR were selected using the program NMRCLUST (39), which automatically clusters a family of structures based on their pairwise RMSDs fitted to the whole molecule or to a particular region.

RESULTS AND DISCUSSION

Choice of the starting structures

The average pairwise RMSD within the 20 NMR structures of free TAR determined by Aboul-ela et al. (15) was 6.8 Å (see column 3 of Table 1). As the authors point out, due to the lack of long-range NOE signals the conformation of RNA molecules as determined by NMR may have a poor overall definition even if the structure is locally well resolved. In the case of free TAR the large RMSD is caused partially by the presence of flexible solvent-exposed nucleotides in the loop and bulge and by an interhelical domain motion. This is described by the large variation in the angle between the lower and upper stems (35.8–137.4°). The local RMSDs are lower: the average RMSD within the lower stem (nt G17-G21 and C41-C45) is 1.4 Å and within the upper stem (G26-C29 and G36-C39) 1.5 Å. The bulge (A22-U25 and U40) and loop (C30-A35) contain solvent-exposed nucleotides which are poorly positioned and increase their RMSD (3.4 Å for the bulge and 4.3 Å for the loop; see column 3 of Table 1). A particular structural feature in the bulge is stacking of the two first unpaired bases of the bulge (U23 and C24) over A22; this stacking is responsible for the deviation in the direction of the upper stem with respect to the lower stem.

Table 1. Average (Ave) RMSDs of the 1 ns molecular dynamics (MD) trajectory for free TAR (structure 2) relative to the initial structure, other NMR structures and pairwise within the 20 NMR family of structures.

RMSD	MD to starting NMR structure (Å)			MD to NMR structures (Å)			Within NMR structures (Å)
	Ave	Max	Min	Ave	Max	Min	Ave	Max	Min
All atom	4.0	5.5	0.9	6.6	10.8	4.1	6.8	12.0	2.9
Lower stem	1.2	2.1	0.6	1.6	1.9	1.1	1.4	1.9	0.8
Bulge	2.1	2.9	0.7	3.0	5.7	2.0	3.4	6.3	1.4
Upper stem	1.6	2.1	0.7	2.0	3.0	1.5	1.5	2.6	1.0
Loop	3.4	4.2	0.7	4.7	5.8	3.6	4.3	6.4	1.4

The minimum (Min) and maximum (Max) values are also measured for the corresponding RNA region.

The NMR structure of argininamide-bound TAR is somewhat better defined, with an average pairwise RMSD of 4.6 Å between the 20 structures (see column 3 of Table 2). In this case flexible nucleotides are also present in the bulge and in the loop and the interhelical angle varies between 66.4° and 127.7°. The local RMSD for the upper stem is the same as in free TAR (1.5 Å), while the lower stem is less precisely defined (2.7 Å), due to a distortion of the base pairing in the two first base pairs (G17-C45 and G18-C44) present in some of the NMR structures. The RMSDs fitted to the bulge and loop are similar to those of free TAR (2.7 and 4.3 Å, respectively).

Table 2. Average (Ave) RMSDs of the 1 ns molecular dynamics (MD) trajectory for bound TAR (structure 8) relative to the initial structure, relative to other NMR structures and pairwise within the 20 NMR structures.

RMSD	MD to starting NMR structure (Å)			MD to NMR structures (Å)			Within NMR structures (Å)
	Ave	Max	Min	Ave	Max	Min	Ave	Max	Min
All atom	2.7	3.8	1.2	4.7	6.5	3.2	4.6	7.4	2.1
Lower stem	1.6	2.8	0.7	2.6	4.1	1.6	2.7	4.7	0.7
Bulge	2.2	2.8	0.9	2.4	3.2	1.9	1.9	3.2	0.8
Upper stem	1.2	1.5	0.7	1.6	2.4	1.1	1.5	2.8	0.8
Loop	2.4	3.3	1.1	4.9	6.2	3.2	4.3	6.8	1.4

The minimum (Min) and maximum (Max) values for each fitted RNA region are also reported.

Given the structural variability present in the NMR families of free and bound TAR, we repeated the MD simulations for different structures within the same family. We performed two ‘long’ (1 ns) simulations, one on free TAR and one on bound TAR, and a few ‘shorter’ ones to assess the validity of our observations. For the ‘long’ simulation of free TAR we chose model 2 as the starting structure, which has low local RMSDs compared to the other NMR models. The other models simulated are 16 and 3, having, respectively, the largest and an intermediate interhelical angle (137.4° and 88.6°, respectively). In this way the high variability of interstem stacking present in the NMR family is well represented.

In the case of bound TAR only a few models possess a regular base pairing in the lower stem. Model 8, which was chosen for the ‘long’ simulation, has such characteristics, together with an average RMSD of 4.2 Å, matching the average pairwise RMSD within NMR structures (4.6 Å). We simulated two additional models (1 and 15) in order to validate our observations on the base triple (see below).

Analysis of the trajectories

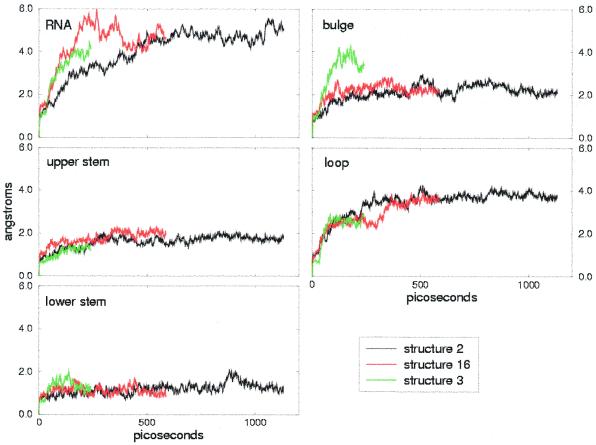
The RMSDs from the initial structures are reported in Figures 2 and 3 for the simulations of free and bound TAR, respectively. The overall RMSDs are shown, together with the RMSD of each domain: lower stem, bulge, upper stem and loop. Free TAR has larger overall RMSDs compared to bound TAR, which averages 4.0 Å during the 1 ns trajectory versus 2.7 Å for bound TAR (Tables 1 and 2, first column). This discrepancy reflects the different degree of precision in the global definition of the NMR families and supports the conclusion that TAR is more flexible in its free conformation than when bound to argininamide.

Figure 2.

Free TAR trajectory RMSDs, calculated on all atoms, and local RNA regions (lower stem, bulge, upper stem and loop) relative to the starting structures. Each color refers to one of the three simulations performed.

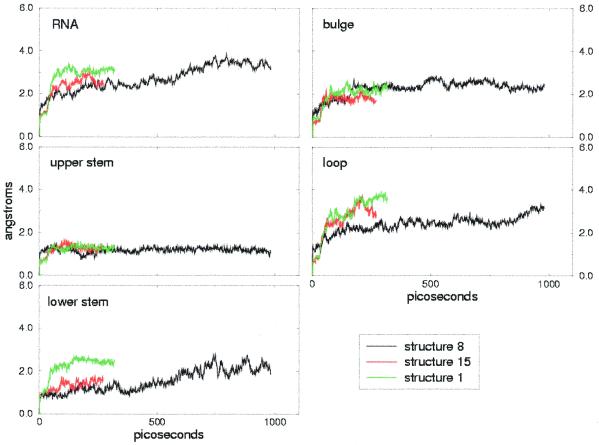
Figure 3.

Bound TAR RMSDs calculated on all heavy atoms and RNA regions (lower stem, bulge, upper stem and loop) relative to the starting structure. Each color refers to one of the three simulations performed.

With few exceptions (see below) the local RMSDs show good agreement within different structures of the same NMR families, which is particularly interesting in the case of free TAR, where the structures differ significantly due to the variation in inter-helical angle. In both cases (i.e. free and bound TAR) the most stable regions are the lower and upper stems. The average RMSDs for the stems lie in the range 1.2–1.6 Å, except for structures 1 and 8 of bound TAR (Fig. 3, bottom left). This increased RMSD for the lower stem of the bound TAR RNA structure 1 is due to a distorted base pairing of the two first base pairs in the lower stem, which is also present in other structures of the NMR family. In contrast, the increase in RMSD for the lower stem of structure 8 during the last 400 ps is due to a local rearrangement from a bent structure to one with parallel base pairs, rather than to a distortion of the base pairing.

Compared to the upper and lower stems, the loop is more flexible, with an average local RMSD of 2.4 Å in bound TAR and 3.4 Å in free TAR, during the 1 ns simulations. In the case of bound TAR the RMSDs for the loop differ slightly within the models (Fig. 3). Indeed, in model 8 the higher stability is due to the presence of hydrogen bonding interactions between C30 and G39, which stabilize the conformation of the loop. Some of these hydrogen bonds are also present in models 15 and 1, but are not maintained during the simulations.

Apart from structure 3 of free TAR, the RMSDs fitted to the bulge are in the range 2.0–2.2 Å for both the bound and free conformations. Even if the conformation of the bulge is totally different, the structural flexibility is the same: U23 is well positioned both in free TAR, where it is stacked over A22, and in bound TAR, where it participates in binding of argininamide. Moreover, in both cases U25 is solvent exposed, while C24 is stacked over U23 in free TAR and pointing to the solvent in bound TAR. In the case of structure 3 of free TAR the larger RMSD of the bulge is due to disruption of the A22-U40 base pairing, which additionally widens the major groove. The A22-U40 base pair is expected to be unstable, since no NOE cross-peaks are found corresponding to this pair (8).

The overall and local RMSD values are summarized in Tables 1 and 2 for the 1 ns simulations and in both cases compare reasonably with the pairwise RMSDs within the 20 NMR structures.

Interhelical motion

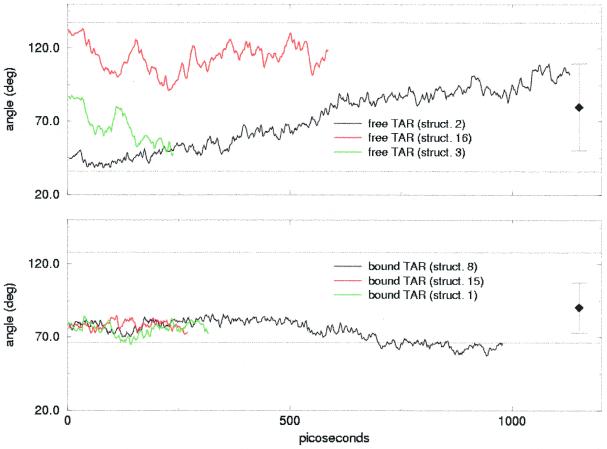
The larger overall RMSDs of free TAR compared to those of bound TAR can be explained in terms of an interdomain motion, which occurs in all the simulations of free TAR. As shown in Figure 4, the angle between the direction of the lower and the upper stem undergoes large variations: a generally constant increase is observed in the case of structure 2, while large fluctuations are present in the cases of models 3 and 16. This different behavior is reflected in the overall RMSD (Fig. 2), which directly jumps to values >4 Å for structures 16 and 3 while it increases more smoothly for structure 2.

Figure 4.

Interhelical angle traced over the simulations of free TAR (top) and bound TAR (bottom). The horizontal dotted lines indicate the maximum and minimum interhelical angles in the NMR family, while the single squares with error bars are the average angles with standard deviations within the NMR family.

In contrast, the interhelical motion for bound TAR is much less wide in all the simulations performed. Though we cannot exclude the possibility that the large variation in the interstem angle is caused by the poor definition of the starting structures, our results support the conclusion that TAR in its free conformation is globally flexible and that this flexibility is manifested through an interdomain motion. Indeed, if the overall conformation of free TAR may not be well defined due to the absence of long-range NOE constraints, the larger spread of the interhelical angle in the NMR family with respect to bound TAR may be caused by an intrinsic flexibility of the conformation.

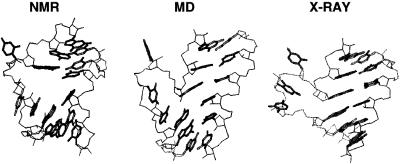
As already observed, the structures with an initial interhelical angle >80° undergo large fluctuations in interhelical angle with a 50° range and on the 100 ps scale. Structure 2 has instead a lower (<50°) initial interhelical angle, which increases to a value >100° during the simulation, with small fluctuations. Though it reaches values >80°, it does not show the fluctuations present in the other two models and is by contrast more stable in the 600–1000 ps time interval. Correspondently, the overall RMSD (Fig. 2) reaches a stable plateau after 600 ps. Indeed, after 600 ps the two stems in the molecular dynamics structure partially stack on each other, resulting in a globally more stable conformation which shares some common characteristics with the crystal structure found by Ippolito and Steitz (16). Figure 5 compares the conformation of the bulge in the starting NMR structure to the molecular dynamics final structure and to the X-ray structure. In the molecular dynamics structure the separation between the two stems is reduced and the interhelical angle increases with respect to the NMR structure. In both the molecular dynamics and the X-ray structures the two stems stack on each other. However, the conformation of the nucleotides in the bulge is different: though distorted, the stacking of bases U23 and C24 over A22 is still present and prevents complete exposure to the solvent. As found by the recent NMR study by Long and Crothers, free TAR can exist in two conformations (10). One conformation is similar to the NMR starting structure, with an open major groove and a large distortion in the direction of the stems, while the other conformation is more similar to the X-ray structure of Ippolito and Steitz (16). Our final molecular dynamics structure could be an intermediate state between the two conformers.

Figure 5.

Conformation of the nucleotides in the bulge and surrounding region. On the left is the initial NMR structure by Aboul-ela et al., in the center is the final MD structure and on the right is the X-ray structure of Ippolito and Steitz.

The TAR–argininamide interface and U23-A27-U38 base triple formation

The binding site for argininamide is placed within the bulge and involves nucleotide U23, base pair A22-U40 and two base pairs above the bulge (G26-C39 and A27-U38). Three nitrogen atoms in the guanidinium group of argininamide can participate in hydrogen bonds, namely Nη1, Nη2 and Nɛ. In almost all NMR structures two of these nitrogen atoms are at hydrogen bonding distance from G26. In structure 8, Nη1 and Nɛ are hydrogen bonded to N7 and O6 in G26, while in structures 1 and 15 the nitrogen atoms at hydrogen bonding distance to G26 are Nη1 and Nη2. During the molecular dynamics simulation these hydrogen bonds are maintained with a very high occupancy (>90% in most cases), as shown in Table 3. The stability of the hydrogen bonds between G26 and argininamide is consistent with the essential role played by the G26-C39 base pair in recognition of Tat (2–4).

Table 3. Occupation of hydrogen bonds between argininamide (ARM) and G26 and between ARM and the phosphate oxygens of U23 and A22 during the simulations.

	Structure 8	Structure 1	Structure 15	Present in structure
ARM NH2–G26 N7	94.1%	100.0%	92.6%	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20
ARM NH2–G26 O6	92.1%	51.8%	73.0%	1, 3, 4, 7, 9, 10, 12, 13, 14, 15, 19, 20
ARM NH1–G26 N7	–	72.5%	40.0%	6, 18
ARM NH1–G26 O6	–	100.0%	99.3%	1, 4, 6, 7, 9, 10, 14, 15, 17, 18, 20
ARM NE–G26 N7	15.4%	–	–	2, 9, 10
ARM NE–G26 O6	99.8%	–	–	2, 8, 9, 10, 19
ARM NH2–U23 O2P	–	99.4%	–	–
ARM NE–U23 O2P	–	99.7%	–	–
ARM NH1–U23 O1P	2.6%	–	–	8
ARM NE–A22 O1P	–	–	–	16
ARM NH1–A22 O1P	–	–	–	2
ARM NH2–A22 O1P	–	–	–	16

The last column on the right reports the NMR structures in which the indicated atoms are within hydrogen bond distance. In the structures indicated in bold the donor–hydrogen–acceptor angle is within 60°.

In the so-called arginine fork model (7,8) the phosphate oxygen atoms of U23 and A22 are hydrogen bonded to a guanidinium nitrogen. Our simulations do not give general support to this feature, which is also lacking in NMR structures. However, the formation of stable hydrogen bonds between the phosphate oxygen of U23 and the two Nη is observed in the case of structure 1 (Table 3).

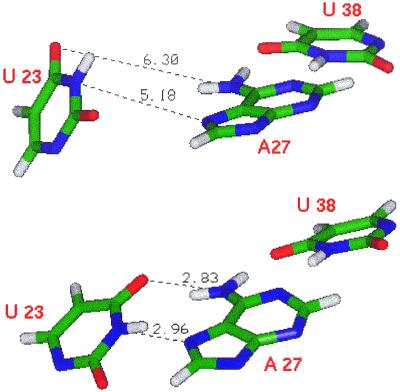
In contrast, our simulations support another feature which was present in the original model of the arginine-binding interface by Puglisi et al. (7,8), namely the U23-A27-U38 base triple. In the starting NMR structures of Aboul-ela et al. the base U23 is too far away to form a hydrogen bond with A27. As shown in Figure 5, we found that this base triple is in fact formed during the simulations, i.e. U23 and A27 become closer and more co-planar, allowing the formation of stable hydrogen bonds (Table 4). The formation of hydrogen bonds between U23 and A27 is mainly accomplished by a rotation that positions base U23 in the same plane as A27 and U38. The simulated models (1, 8 and 15) are representative of the structures in the NMR family: a clustering of the NMR structures based on the RMSD fitted to nucleotides 23, 27 and 38 and argininamide results in three families of structures, each containing one of the models used (Table 5). We can conclude that, on average, the triple forms, since every cluster is represented in the molecular dynamics simulations.

Table 4. Percent occupation of hydrogen bonding pairs between U23 and A27 during the MD simulation and within the NMR structures.

	U23 N3–A27 N7				U23 O4–A27 N6
	Occupied (%)	Ave	Max	Min	Occupied (%)	Ave	Max	Min
Structure 8	92.1				96.4
Distance (Å)		3.2	5.9	2.7		3.1	6.9	2.6
Angle (°)		18.8	90.7	0.4		14.9	74.6	0.6
Structure 1	86.7				84.5
Distance (Å)		3.1	5.7	2.6		3.5	6.2	2.6
Angle (°)		22.3	63.2	0.9		21.0	64.9	1.4
Structure 15	75.2				57.4
Distance (Å)		3.5	5.5	2.7		4.1	6.4	2.7
Angle (°)		29.6	91.9	1.2		17.6	57.6	0.9
NMR structures	0				0
Distance (Å)		5.1	7.2	4.2		6.0	8.5	4.0
Angle (°)		72.6	109.4	57.0		32.5	65.1	10.9

Average (Ave), maximum (Max) and minimum (Min) acceptor–donor distances and acceptor–hydrogen–donor angles are also reported. The occupancies of the hydrogen bonds in the simulations of structures 1 and 15 are lower than those for structure 8, due to the shorter simulation time. Indeed, it takes ∼200 ps for the triple to form (see Fig. 6), while the short simulations last for ∼300 ps.

Table 5. Results of a clustering analysis performed on the PDB structure for bound TAR based on the RMSD fit of the U23-A27-U38 triple and arginine.

	Cluster 1	Cluster 2	Cluster 3
Spread	1.2 Å	1.2 Å	1.1 Å
Representative model	12	15	1
Structures	4, 7, 8, 9, 10, 12, 13, 20	6, 11, 14, 15, 17, 18	1, 2, 3

The spread is the average pairwise RMSD within the same cluster, while the representative model is the one with the lowest RMSD with respect to the other structures in the cluster. Models 5, 16 and 19 are considered outliers since their RMSDs to each cluster are significantly greater than the spread.

Other NMR studies have given evidence of the formation of the base triple. Earlier NMR studies by Puglisi et al. (8) and Long an Crothers (14) predicted its existence and structural studies on HIV-2 TAR by Brodsky and Williamson (12) also indicated formation of the base triple. Moreover, in two independent NMR structures of the BIV tat peptide–TAR RNA complex a U·A·U base triple is present (40,41).

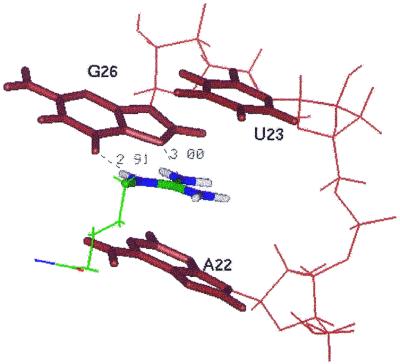
The presence of the U23-A27-U38 base triple is crucial to the binding of argininamide to TAR since it stabilizes the position of U23 over the guanidinium group of the arginine side chain. Due to the rotation of base U23, the guanidinium group of argininamide is stacked below U23. The binding pocket that develops upon base triple formation is thus constituted by the guanidinium group hydrogen bonded to G26 and sandwiched between A22 and U23 (Fig. 6). The network of hydrogen bonding and stacking interactions makes this group structurally rigid, although it is located within the flexible bulge. Indeed, during the last 600 ps of the 1 ns trajectory the average RMSD of the average structure fitted to the binding pocket (i.e. bases G26 and A22 and base triple U23-A27-U38) is only 0.46 Å. This number is less than the RMSD fitted to the same bases within NMR structures (0.65 Å) and is comparable with the average RMSD of three adjacent base pairs in the upper stem (0.39 Å), i.e. the most conserved region in the RNA molecule.

Figure 6.

Base triple in bound TAR. (Top) Positions of U23-A27-U38 in the starting structure. (Bottom) The same triple after 270 ps of molecular dynamics simulation. U38-A27 forms a Watson–Crick base pair; U23 is initially far from the pair, but gets closer and co-planar with U38-A27 during the simulation. Hydrogen bonding acceptor–donor distances are reported.

A very similar conformation of the binding site was found in the HIV-2 TAR–argininamide complex by Brodsky and Williamson (12). Apart from the absence of the unimportant bulge residue C24, the sequence of HIV-2 TAR is the same as HIV-1 TAR. The presence of a shorter bulge improves the dynamic properties and allowed the detection of a large number of NOE signals, which in turn led to the derivation of structures with high resolution. In their structures the position of the guanidinium group is well defined within the ‘arginine sandwich’, involving the same residues as in our molecular dynamics structure, while the amide side of the argininamide is poorly positioned. Moreover, they also give no evidence for the existence of the arginine fork, suggesting that the phosphates of A22 and U23 may, however, help argininamide bind to TAR through favorable electrostatic interactions. In the following section we will evaluate this possibility and give an estimate of the strengths of these interactions.

Free energy analysis

We performed a free energy analysis on free TAR and the TAR–argininamide complex: the results are reported in Table 6. Only the ‘long’ trajectories were analyzed since they span a phase space large enough for evaluation of the free energy. The molecular mechanical energy was computed from the molecular mechanics force field as the sum of bonded (internal energy) and non-bonded (van der Waals plus electrostatic) interactions. The solvation energy is the sum of an electrostatic term, calculated by the Poisson–Boltzmann equation (36), and a non-polar term estimated from the solvent-accessible surface area of the molecule (25).

Table 6. Molecular mechanics and solvation free energy analysis for the TAR–argininamide complex and free TAR.

Contribution	Complex (AB)	Bound TAR (A)	Free TAR (fA)	ARM (B)	Binding energies
	mean (± SD)	mean (± SD)	mean (± SD)	mean (± SD)	[AB – (B + A)] mean (± SD)	[AB – (fB + fA)] mean (± SD)
EBADH	1400 (20.0)	1371 (19.0)	1365 (19.0)	30 (4.7)	0 (0.0)	7 (28.0)
Evan der Waals	–267 (15.0)	–245 (15.0)	–231 (16.0)	1 (0.9)	–23 (2.5)	–37 (21.0)
Eelectrostatics	793 (67.0)	2471 (85.0)	2001 (180.0)	–146 (3.6)	–1532 (26.0)	–1057 (192.0)
EMM total	1926 (68.0)	3597 (87.0)	3134 (177.0)	–116 (3.5)	–1555 (27.0)	–1087 (190.0)
GPB	–8925 (62.0)	–10244 (84.0)	–9792 (175.0)	–229 (2.6)	1547 (29.0)	1091 (185.0)
Gnp	31 (0.3)	31 (0.4)	32 (0.9)	3.1 (0.2)	–3.7 (0.2)	–5 (0.9)
G(PB+electrostatics)	–8132 (16.0)	–7772 (16.0)	–7791 (16.0)	–375 (2.4)	15 (5.1)	34 (23.0)
Gsolvation	–8894 (62.0)	–10212 (84.0)	–9759 (175.0)	–226 (2.6)	1543 (29.0)	1086 (185.0)
G(MM+solv)	–6968 (19.0)	–6615 (19.0)	–6625 (18.0)	–341 (3.2)	–11.7 (4.0)	–1 (26.0)

Average values (means ± SD) of the different components are reported. The results for the free ligand (fB) are not reported since they only differ slightly from the bound ligand energies.

Although no internal entropy (TΔS) term has been included, the analysis results in a reasonable value of –11 kcal/mol for the free energy difference between the TAR–argininamide complex (AB in Table 6) and the separate components, TAR (A) and argininamide (B), in their bound conformation. In agreement with numerous studies (42–46), docking of the ligand (argininamide) to the receptor (TAR RNA) is driven by non-electrostatic contributions, i.e. van der Waals and non-polar solvation energies, while it is disfavored by the total electrostatic (solvation plus Coulombic) term. In fact, the internal electrostatic energy of the complex is lower, but does not fully compensate for the unfavorable change in electrostatics of solvation. These results support a model of the argininamide-binding site in which Van der Waals stacking interactions between the guanidinium group and the surrounding residues play an important role in binding.

A comparison between the energies of the two conformations of TAR results in a higher free energy for the bound receptor alone, consistent with that observed in other protein–RNA complexes (47). Just as found for the RNA interaction with U1A protein, the unbound conformation of the RNA compared to the bound form of the RNA is indeed more stable by a physically reasonable value of ∼10 kcal/mol in the absence of the ligand. The bound conformation of TAR is largely disfavored by the electrostatic term in vacuo, which has a value 470 kcal/mol higher than free TAR. The Poisson–Boltzmann solvation term moderates this difference but does not change the trend, bringing ΔG_{(PB+electrostatics)} to 19 kcal/mol. Docking of the charged ligand evidently allows a conformation which would be electrostatically unfavorable. The lower van der Waals term for the bound conformation is somewhat unexpected, since the transition from free to bound TAR involves disruption of the stacking between A22, U23 and C24 in the bulge. Indeed, evaluation of the van der Waals energy for these residues alone during the simulation gives a value 6 kcal/mol lower for the stacked conformation than the unstacked one. Probably the higher flexibility of the molecule does not allow a proper optimization of the van der Waals energy in other parts of the molecule.

Nonetheless, in contrast to cases of protein–protein and protein–ligand complexes, the absolute free energy of association of –1 kcal/mol is more unfavorable. If one considers the –TΔS term, typical values for small protein ligands (46; Donini and Kollman, submitted for publication; Kuhn and Kollman, submitted for publication) are ∼10–20 kcal/mol, which would make ΔG ∼ 20 kcal/mol more positive in absolute value than found experimentally. This error could arise from the tendency of continuum models to overestimate ΔG desolvation in binding of charged groups to macromolecules or to non-optimum continuum solvation parameters. We are currently investigating the latter possibility (J.Wang, W.Wang and P.A.Kollman, manuscript in preparation).

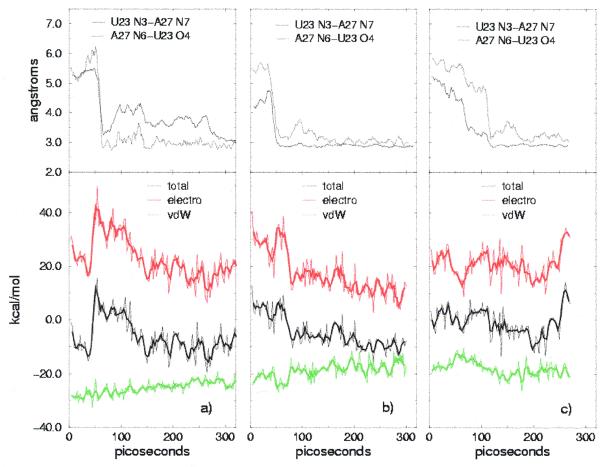
To evaluate the influence of base triple formation on the energy balance, we monitored the time evolution of the interaction free energy [i.e. AB – (A + B)]. No relevant change can be seen in the free energy of the complex due to large fluctuations, while there is a clear correlation between the interaction energy term and formation of the base triple. In Figure 6 the interaction energy is shown together with the van der Waals and total electrostatic terms for the three simulations and compared with the donor–acceptor distances in the U23-A38 hydrogen bonds, which are a measure of formation of the triple. Structures 1 and 8 share similar features: the van der Waals term increases constantly while the total electrostatic term shows crossing of an energy barrier, which corresponds to the abrupt change in the donor–acceptor distances. This latter feature is more evident in structure 8, where it is also present in the total interaction energy, while it is washed out in structure 1. A possible explanation for this barrier crossing is that formation of the base triple is initially favored in the receptor alone, since new hydrogen bonding interactions lower its energy without affecting the interaction energy. Equilibration following crossing of the barrier may be due to a more convenient positioning of the argininamide in the new conformation of the binding interface. Remarkably, the value of the interaction energy after the initial equilibration is similar for the two structures, despite the differences in the argininamide–TAR interface, i.e. different hydrogen bonding of the guanidinium group to G26 and presence of a hydrogen bond with the oxygen phosphate of U23 for structure 1. Structure 15 shows a different behavior, both for the interaction energy terms and the base triple distances. This difference, together with the higher interaction energy, may be due to a non-optimized geometry of the interface. Indeed, the free energy of the complex calculated in the 180–270 ps time interval is –6894 kcal/mol, ∼30 kcal/mol higher than that for structures 8 and 1 in the same time interval (–6932 and –6929 kcal/mol, respectively). 7 8

Figure 7.

Conformation of the binding pocket for argininamide averaged during the last 600 ps of molecular dynamics simulation. The guanidinium group is stacked between A22 and U23 and hydrogen bonded to G26.

Figure 8.

(a) (Top) Tracking the distances between donor and acceptor in U23 and A27 during the simulation of structure 8. (Bottom) Time evolution of the interaction free energy [AB – (A+B)] for structure 8. Electrostatic (electro) and van der Waals terms (vdW) are shown in different colors, the thicker lines representing 3-point running averages. (b) As (a) for structure 1. (c) As (a) for structure 15.

As already stated in the previous section, only in the case of structure 1 could we detect stable formation of hydrogen bonds between the guanidinium group of argininamide and the phosphate of U23 (Table 3). These findings do not support the arginine fork model, which was initially proposed in order to explain the interference of ethylation of phosphates P22 and P23 on arginine–TAR binding (7,8). Nonetheless, the phosphates of A22 and U23 may contribute to binding of argininamide by favorable electrostatic interactions. In order to test this hypothesis, we repeated the energy calculations with reduced charges on phosphates P22 and P23. A (negative) unit charge was subtracted from each phosphate, reducing by 0.25 a.u. the partial charge on the oxygens. As a result, the interaction energy for structure 8 changes from –11.7 to –8.0 kcal/mol, i.e. the complex became less stable by 3.7 kcal/mol. Similarly, in the case of structure 15 the interaction energy increases by 4.7 kcal/mol. There is no remarkable difference when P22 and P23 are reduced separately in the case of structure 8, the change in energy being 2.0 and 2.2 kcal/mol, respectively. Different results are obtained in the case of structure 1, where the charge reduction on P23 brings the energy from –6.1 up to 6.1 kcal/mol, in agreement with the detection of stable hydrogen bonds between this phosphate and the guanidinium group of arginamide. In contrast, the same changes on P22 causes only a small (0.3 kcal/mol) increase in the interaction term. These results agree with the previously cited ethylation interference data, since they show how the anionic phosphates P22 and P23 contribute to binding of argininamide to TAR. In the cases of structures 8 and 15 both phosphates contribute; in the case of structure 1 P22 interactions predominate.

CONCLUSIONS

We have presented a molecular dynamics study of HIV TAR RNA and of its complex with argininamide. In both cases, the patterns of local flexibility are in agreement with experimental observations and the larger global conformational flexibility of free TAR with respect to the complex has been reproduced. Indeed, an interdomain motion was observed in all the simulations of free TAR, although with different features. While large fluctuations are present for structures with a large initial interhelical angle, structure 2 reaches a more compact configuration of the bulge, which resembles the X-ray structure of Ippolito and Steitz (16). In a recent NMR study (10) two free TAR conformers were detected, one with the stems unstacked and a widened major groove in the bulge region, as in the NMR structures, and the other with continuous stacking and the bulge nucleotides extruding from the helix, as in the X-ray structure. We suggest that a transition between the two conformers may be taking place during the simulation.

During the simulations of the TAR–argininamide complex we observed formation of a base triple involving bases U23, A27 and U38. The presence of a U23-A27-U38 base triple in the bound form of TAR is a debated subject: while the NMR studies of Puglisi et al. (8) and Long and Crothers (10) found this feature, the detailed NMR study of Aboul-ela et al. (9) maintains that it is not present, even if U23 is positioned in the vicinity of A27 and U38. Starting from three representative structures within their 20 NMR models, we were able to detect stable formation of this base triple, giving additional evidence for its presence in the complex and emphasizing its importance in the docking of argininamide to TAR. The U·A·U triple imposes a clear-cut constraint in the overall conformation of TAR, since a nucleotide in the bulge is forced to interact with a base pair in the upper stem. No such feature is present in the free conformation, explaining why free TAR is globally more flexible than bound TAR.

By means of free energy analysis with solvation terms we could estimate that van der Waals interactions mainly favor docking of argininamide to TAR, emphasizing the importance of the stacking interactions between the guanidinium group and the interface. During the molecular dynamics trajectories, however, a lower interaction energy is reached upon optimization of the total electrostatic term, rather than the van der Waals contribution: while the first shows a clear correlation with formation of the base triple, the second is quite insensitive to the structural rearrangement. Finally, although our simulations do not support the so-called arginine fork model of the TAR–arginine interface, we showed the importance of electrostatic interactions of the guanidinium group with phosphates at positions 22 and 23.