Unsupervised representation learning of Kohn–Sham states and consequences for downstream predictions of many-body effects

Abstract

Representation learning for the electronic structure problem is a major challenge of machine learning in computational condensed matter and materials physics. Within quantum mechanical first principles approaches, density functional theory (DFT) is the preeminent tool for understanding electronic structure, and the high-dimensional DFT wavefunctions serve as building blocks for downstream calculations of correlated many-body excitations and related physical observables. Here, we use variational autoencoders (VAE) for the unsupervised learning of DFT wavefunctions and show that these wavefunctions lie in a low-dimensional manifold within latent space. Our model autonomously determines the optimal representation of the electronic structure, avoiding limitations due to manual feature engineering. To demonstrate the utility of the latent space representation of the DFT wavefunction, we use it for the supervised training of neural networks (NN) for downstream prediction of quasiparticle bandstructures within the GW formalism. The GW prediction achieves a low error of 0.11 eV for a combined test set of two-dimensional metals and semiconductors, suggesting that the latent space representation captures key physical information from the original data. Finally, we explore the generative ability and interpretability of the VAE representation.

Representation learning for the electronic structure problem is a major challenge in computational physics. Here, authors learn a low-dimensional representation of the wave function and apply it for downstream prediction of many-body effects.

Introduction

Recently, machine learning (ML) has emerged as a powerful tool in condensed matter and materials physics, achieving substantial progress across areas including the identification of phase transitions^1–7, quantum state reconstruction^8–10, prediction of topological order^11,12, symmetry^13–19 and the study of electronic structure^20–23. Among these ML applications, exploring the electronic structure of real materials is of particular interest, since it allows for the extension of computationally intensive predictive quantum theories to understand the physics of larger and more complex systems, such as moiré systems^13,24–32 and defect states^33–39. Within atomistic first principles theories, density functional theory (DFT)⁴⁰ is the most commonly used approach for studying the electronic structure of materials. In principle, DFT gives accurate descriptions of the ground state charge density, but quantitative prediction of excited-state properties (including bandstructure) requires the introduction of excitations from the many-body ground state^41,42. However, DFT can be used as a starting point for many-body calculations, where the wavefunctions within Kohn–Sham DFT are used to construct correlation functions for the excited states^43,44. Therefore, harnessing the information embedded in the Kohn–Sham (KS) wavefunction⁴⁰ becomes crucial for downstream applications. Here, a key challenge lies in distilling a succinct representation of the electronic structure while preserving the essential information⁴⁵.

In contrast to the notable achievements of ML descriptors for crystal geometry and chemical composition^46–50, the electronic structure of materials remains extremely challenging to learn. The high dimensionality of the KS wavefunction of real materials creates a complex data structure, making direct pattern detection challenging. Secondly, electronic structure is highly nonlinear and sensitive to both crystal configuration and intricate non-local correlations, making it difficult to develop a general ML model applicable across a broad spectrum of materials. ML models for electronic structure have been mostly confined to the study of specific subsets of materials, such as molecules⁵¹, perovskites^52–54, or layered transition metal dichalcogenides (TMDs)⁵⁵. In most of these approaches, the ML has focused on the prediction of single-valued properties, such as band gaps, largely due to the challenges of identifying well-defined, interpretable, and efficient representations of the electronic structure^56–59. Recently, the development of operator representations, which capture more nuanced data about the underlying quantum states, has provided new opportunities for the prediction of full band structures. These techniques involve the physically informed selection of specific operators as fingerprints. Examples include the early successful use of energy decomposed operator matrix elements (ENDOME), combined with radially decomposed projected density of states (RAE-PDOS), to predict quasiparticle (QP) band structures⁶⁰, and the use of spectral operator representations to predict material transparency⁶¹. However, the choice of descriptors in such approaches is informed by human physical intuition on the domain science side. This raises the question of whether more fundamental or generalizable descriptors can be learned, independent of human selection.

Variational autoencoders (VAEs)^62,63, a class of probabilistic models that combine variational inference with autoencoders used to compress and decompress high dimensional data, stand out as a promising tool for learning electronic structure in a way that allows for unsupervised training and thus avoids feature engineering. The effectiveness of VAE compression has been demonstrated for various applications across condensed matter physics, including quantum state compression⁶⁴, detection of critical features in phase transitions⁶⁵ and decoupled subspaces^66,67.

Here, we show that a well-crafted VAE is capable of representing KS-DFT wavefunctions on a manifold within a significantly compressed latent space, which is ${10}^3-{10}^4$ times smaller than the original input. Importantly, these succinct representations retain the physical information inherent in the initial data. To validate the efficacy of the VAE latent space in practical applications, we then build a supervised deep learning model for downstream prediction of k-resolved quasiparticle energies within the many-body GW approximation^68,69, whose input includes VAE representations of KS states. This model yields a mean absolute error (MAE) of 0.11 eV, when applied to a test set of two-dimensional (2D) metals and insulators, which is comparable to the intrinsic numerical error of the GW approach^32,44,70. Moreover, the VAE inherently predicts a smooth, physically realistic band structure, in contrast with previous models, which required an additional manually-imposed smoothing function to remove unphysical variations⁶⁰. Lastly, we address the interpretability of the VAE representation and show that the success of electronic structure representation learning and downstream GW prediction is derived from the smoothness of the VAE latent space, which corresponds to the smoothness of the wavefunction in k-space. Because of this property, the VAE can serve as a promising wavefunction generator capable of predicting realistic wavefunctions at arbitrary points in latent space, which has the potential to be used for both wavefunction interpolation in k-space and materials design and discovery across the compositional phase space.

Results and discussion

VAE for electronic structure representation

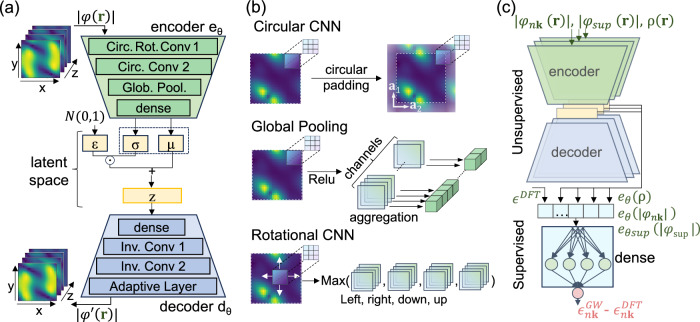
As Fig. 1a shows, the architecture of our VAE consists of two complementary sets of NN: the encoder ($e_{\theta }$) and the decoder ($d_{\theta }$). The encoder maps the input of high-dimensional KS wavefunction moduli $\mid {\varphi }_{n\mathbf{k}}\left(\mathbf{r}\right)\mid \in {\mathbb{R}}^{R_x\times R_y\times R_z}$ to a low-dimensional vector ($\mathbf{\mu }\in {\mathbb{R}}^p,\mathbf{\sigma }\in {\mathbb{R}}^p$) of variational mean and deviation in the latent space. Here, $p\ll R_x\times R_y\times R_z$, where $p$ represents the dimension of the latent space, and $R_{x,y,z}$ is the dimension of the real-space wavefunction ϕ_nk(r) in the unit cell, where the wavefunction is indexed by the band n and the crystal momentum (k-point) $\mathbf{k}$. Conversely, the decoder, mirroring the structure of the encoder, has an opposite function, which is to reconstruct the input wavefunction from its low-dimensional latent vector ($\mathbf{\mu },\mathbf{\sigma }$). In essence, the VAE can be conceptualized as an information bottleneck for electronic structure, where the encoder acts as a data refinement process, discarding redundant information and noise from the input wavefunction. Meanwhile, the decoder ensures that vital physical information is preserved for wavefunction recovery. Since the KS state is essentially a spatial distribution with local patterns, convolutional neural networks (CNN)^71–74 provide a practical framework for the first two layers of the encoder and decoder.

Fig. 1. Neural network architecture of variational autoencoders (VAE) for crystal systems.

a Schematic of the VAE. The encoder (green trapezoid) consists of a rotational convolutional neural network (CNN), a circular CNN, a global pooling layer and one flattened dense layer, which are explicitly presented in (b). The encoder maps a real space wavefunction to a latent space vector of variational mean $\mathbf{\mu }$ and variance $\mathit{\sigma }$. Z is the sampled latent vector, drawn from a variational Gaussian distribution using a reparameterization trick⁶³. The decoder (blue trapezoid) has symmetric neural networks (NN) structures. The latent space serves as an information bottleneck for the VAE as its dimensions are ${10}^3-{10}^4$ smaller than the input and output (represented by the colormaps of the wavefunction in real space). b The circular CNN layer includes circular padding techniques based on the periodic boundary conditions. The width of the circular padding equals the size of the CNN kernel so that the output of the CNN has the same periodicity as the input. Global pooling layers output the average value of each channel from the CNN feature map. Rotational CNN layers scan the input along four directions and outputs the max of (left, right, up, down) feature maps to the next layer. The detail of model parameters and additional benchmarks are listed in Supplementary Note 1. c Schematic of the overall semi-supervised learning model, including both the unsupervised VAE and supervised dense NN. The VAE inputs are the Kohn–Sham (KS) wavefunction modulus ${\mid \phi }_{n\mathbf{k}}\left(\mathbf{r}\right)\mid$, all super states ${\mid \phi }_{\sup }\left(\mathbf{r}\right)\mid$ and charge density $\rho \left(\mathbf{r}\right)$ in real space. The input layer of the supervised dense NN is comprised of density functional theory (DFT) energies, denoted as ${\epsilon }^{DFT}$, along with low dimensional effective representations of ${\phi }_{n\mathbf{k}}\left(\mathbf{r}\right)$, ${\phi }_{\sup }\left(\mathbf{r}\right)$ and $\rho \left(\mathbf{r}\right)$ denoted as $e_{\theta }\left({\phi }_{n\mathbf{k}}\left(\mathbf{r}\right)\right)$, $e_{\theta \sup }\left({\phi }_{\sup }\left(\mathbf{r}\right)\right)$ and $e_{\theta \rho }\left(\rho \left(\mathbf{r}\right)\right)$ respectively. These representations are encoded within the VAE latent space (yellow square) through an encoder with parameters $\theta ,\theta$_sup and ${\theta }_{\rho }$, which are unsupervisedly trained for all KS wavefunctions, super states and charge density.

By imposing a distribution of latent variables close to a standard normal distribution $N\left(0,\mathrm{I}\right)$ during training, the VAE is capable of a smooth mapping from the connected KS states $\mid n,\mathbf{k}⟩$ and $\mid n,\mathbf{k}+\mathrm{\Delta }\mathbf{k}⟩$ to nearby points in the latent space, enabling generative power after training. We define the total VAE loss function as:

$$\mathcal{L}=\frac{1}{T}{\sum }_{n\mathbf{k}}^T\mid \mid \mid {\varphi }_{n\mathbf{k}}\mid -d_{\theta }\left(e_{\theta }\left(\mid {\varphi }_{n\mathbf{k}}\mid \right)\right)\mid {\mid }^2+\beta \cdot \frac{1}{T}{\sum }_{n\mathbf{k}}^T{\sum }_{j=1}^p\frac{1}{2}\left(-1+{\sigma }_{n\mathbf{k}}^{{\left(j\right)}^2}+{\mu }_{n\mathbf{k}}^{{\left(j\right)}^2}-\log {\sigma }_{n\mathbf{k}}^{{\left(j\right)}^2}\right)$$ 1

where the first term is the mean squared error (MSE) of the reconstructed wavefunctions, and the second term is the Kullback-Leibler (KL) divergence, which forces the latent space to approach a normal $N\left(0,\mathrm{I}\right)$ distribution. The parameter $\beta$ is the weight of KL divergence, tuning the degree of regularization of the latent space. $T$ is the total number of KS states in the training set and, and $j$ is an index in the latent space.

Additionally, we design our VAE to respect rotational and translational symmetries of the crystal so that downstream prediction of physical observables will not vary with the choice of unit cell. As shown in Fig. 1a, b, we insert a global average pooling (GAP)⁷⁵ layer between the CNN and the dense layer in the encoder. The GAP layer allows CNNs to accept inputs of varying sizes and produce a fixed-length output, which is crucial for the subsequent fully connected layers in the encoder. By aggregating the spatial information of the feature maps, the GAP layer also enforces translational invariance with respect to the unphysical degree of freedom that arises from the choice of the origin of the unit cell. Then, we include a circular padding technique in the CNNs⁷⁶ to account for the periodic boundary conditions of the crystal system. The first layer of the encoder features a discrete rotational CNN⁷⁷ along the lattice constant directions, which select out the combined feature maps with maximum summation value to preserve invariance to the choice of lattice vectors and direction. With such a CNN, given the same material, data from any continuously complete periodicity of a specific KS state will generate the same latent space. This allows us to capture properties associated with physical symmetries of the crystal without explicitly including symmetry labels. Finally, to ensure that the VAE-generated wavefunction’s size aligns with the input, allowing us to define a proper loss function, we include an adaptive layer as the final layer in our decoder.

By feeding DFT wavefunctions to our VAE model, we can interpret the vector ($\mathbf{\mu },\mathbf{\sigma }$) in latent space as a low-dimensional effective representation associated with the individual KS state. This representation has several advantages: (i) it is smooth due to the smooth nature of the neural network; (ii) it can handle translational invariance and periodic boundary conditions, (iii) it can handle any symmetry and cell size; (iv) even when trained with unit cell data, it can be extended to supercells beyond a single unit cell. More details and benchmarks regarding the VAE model are given in Supplementary Notes 1–3.

Neural network for downstream prediction of GW band structures

Due to its ground-state nature, DFT calculations can yield inaccurate single-particle band structures and tend to underestimate the band gap of semiconductors compared to experiment^78–80. To incorporate the many-electron correlation effects that are missing in DFT and obtain accurate quasiparticle (QP) bandstructures, one can replace the effective single-particle exchange correlation potential in DFT with non-local and energy-dependent self energy calculated within the GW approximation in many-body perturbation theory^43,68,81,82. This approach proves highly effective for computing QP bandstructures in a wide range of materials⁴³. However, in practice, constructing a GW self-energy, even for small systems^{70,81,83–86}, is much more computationally expensive than DFT, and this remains a bottleneck to the broader adoption of the GW approach for high throughput studies. Therefore, in the context of understanding materials’ excited-state properties, a natural approach is to use low-fidelity techniques like density functional theory (DFT) to try and predict the results of high-fidelity, computationally intensive many-body calculations. Currently, most ML work in this field focuses on the use of indirect predictors for model training, using, for instance, crystal geometry, chemical composition, and the DFT bandgap as input^{46–49,56,57}. These methods, however, are generally limited to single value prediction of the band gap, and only effective within specific subsets of materials, such as inorganic solids⁵⁹. Operator fingerprint methods like ENDOME and RAD-PDOS extend predictive capability to k-resolved band structures, but the selection of features in these models heavily relies on human intuition and can introduce unphysical fluctuations in band structures, which are then smoothed in post-processing⁶⁰. There have also been ML models dedicated to predicting the screened dielectric function^87–89, which can speed up GW calculations but don’t provide information that is generalizable to different systems.

Due to the challenging nature of capturing non-local frequency-dependent correlations in the electronic structure, we select the downstream prediction of GW bandstructures as proof of principle of the effectiveness of our VAE latent vector representation of the KS wavefunctions. We develop a supervised deep NN on top of the VAE latent space to predict many-body GW corrections. The goal of this NN is to successfully learn the diagonal part of GW self-energy ${\mathrm{\Sigma }}_{n\mathbf{k}}^{GW}$^68,69:

$${\mathrm{\Sigma }}_{n\mathbf{k}}^{GW}=\frac{i}{2\pi \mathrm{V}}{\sum }_{{\mathbf{GG}}^{\prime }}{\sum }_{\overrightarrow{q}}^{BZ}{\sum }_m^{all}{\int }_{-\infty }^{\infty }d{\omega }^{\prime }{W}_{{\mathbf{GG}}^{\prime }}\left(\overrightarrow{q},{\omega }^{\prime }\right)\times \frac{{\rho }_{n\mathbf{k},m\mathbf{k}-\mathit{q}}\left(\mathbf{G}\right){\rho }_{n\mathbf{k},m\mathbf{k}-\mathbf{q}}^{*}\left({\mathbf{G}}^{\prime }\right)}{{\epsilon }_{n,\mathbf{k}}+{\omega }^{\prime }-{\epsilon }_{m,\mathbf{k}-\mathbf{q}}+i\eta \cdot \mathrm{sgn}\left({\epsilon }_{m,\mathbf{k}-\mathbf{q}}-\mu \right)}$$ 2

where $\mathbf{G}$ is a reciprocal lattice vector; $\mathbf{q}$ is the difference between any two k-vectors $\mathbf{k}-{\mathbf{k}}^{\prime }$ and is integrated over the Brillouin zone (BZ); $\epsilon$ is KS-DFT energy; and ${\rho }_{n\mathbf{k},m\mathbf{k}-\mathbf{q}}\left(\mathbf{G}\right)=⟨n\mathbf{k}∣e^{i\left(\mathbf{q}+\mathbf{G}\right)\mathbf{r}}∣m\mathbf{k}-\mathbf{q}⟩$. $W_{{\mathbf{GG}}^{\prime }}$ is the screened Colomb interaction calculated within the random phase approximation, and $\omega$ is the frequency dependence of the self energy. Notably, the calculation of the GW self energy includes a sum over infinite bands, m. In practice, the sum over states is treated as a convergence parameter, and the number of bands included in the summation is of the same order as the number of reciprocal lattice vectors $\overrightarrow{G}$ included in $W$.

The diagonal self-energy matrix element for a specific state $\mid n,\mathbf{k}⟩$ shown in Eq.(2) can be expressed as: ${\mathrm{\Sigma }}_{n\mathbf{k}}^{GW}=f\left({\varphi }_{n\mathbf{k}},{\epsilon }_{n\mathbf{k}},\mathbf{\varphi },\mathit{\epsilon },\rho \right)$, where ${\varphi }_{n\mathbf{k}}\in {\mathbb{C}}^{R_x\times R_y\times R_z}$ and $\mathbf{\varphi }\in {\mathbb{C}}^{N\times R_x\times R_y\times R_z}$ are the KS state vectors; $\rho \in {\mathbb{R}}^{R_x\times R_y\times R_z}$ is the charge density; $N$ is the total number of occupied and unoccupied states ${\mid n}^{\prime },{\mathbf{k}}^{\prime }⟩$ used in GW calculations. ${\epsilon }_{n\mathbf{k}}\in {\mathbb{R}}^1$ and $\mathit{\epsilon }\in {\mathbb{R}}^N$ are the corresponding DFT eigenvalues. Here, we note that $\mathbf{\varphi }$ includes ${\varphi }_{n\mathbf{k}}$ and $\mathit{\epsilon }$ includes ${\epsilon }_{n\mathbf{k}}$, but we include both terms explicitly in the function f to make later steps more transparent. The output ${\mathrm{\Sigma }}_{n\mathbf{k}}^{GW}\in {\mathbb{R}}^1$ is the GW self energy. Due to the closed-form expression of the self-energy, mathematically, we expect that a simple dense NN can acquire an understanding of the non-linear mapping from the KS wavefunction and energies to ${\mathrm{\Sigma }}_{n\mathbf{k}}^{GW}$, which consists of the mapping of (${\mathbb{C}}^{\left(N+1\right)\times \left(R_x\times R_y\times R_z\right)},{\mathbb{R}}^{R_x\times R_y\times R_z},{\mathbb{R}}^{\left(N+1\right)}\to {\mathbb{R}}^1$)^90,91.

However, two significant challenges prevent the application of a simple NN model such as ${\widehat{\mathrm{\Sigma }}}_{n\mathbf{k}}^{GW}={\widehat{f}}_{NN}\left({\varphi }_{n\mathbf{k}},{\epsilon }_{n\mathbf{k}},\mathbf{\varphi },\mathit{\epsilon },\rho ,\mathbf{\eta }\right)$, where ${\widehat{\mathrm{\Sigma }}}_{n\mathbf{k}}^{GW}\in {\mathbb{R}}^1$ is the NN predicted self-energy, and $\overrightarrow{\eta }$ are the parameters of the model. (i) Due to the high computational cost of the GW algorithm, only a limited subset of GW energies near the Fermi level can be exactly calculated and used for the supervised learning training set, denoted as ${\mathit{\Sigma }}_{n\mathbf{k}}^{train}\in {\mathbb{R}}^{N_{train}}$. As a result, $N_{train}\ll \left(N+1\right)\times \left(R_x\times R_y\times R_z\right)$, and overfitting is inevitable (see Supplementary Fig. 8). (ii) The curse of dimensionality makes it formidable to learn the nonlinear mapping from a high-dimensional sparse $\mathbf{\varphi }$ wavefunction space to the self-energy ${\mathit{\Sigma }}_{n\mathbf{k}}^{train}$ space. To address these challenges, we adopt the manifold assumption^92–95 that the DFT electronic wavefunction in real space can be modeled as lying on a low-dimensional manifold. Additionally, we assume that two DFT wavefunctions mapped to nearby points on the manifold should have comparable contributions to the final GW energy corrections. If these two assumptions hold true, then the VAE is ideal for downstream prediction of GW self energies.

Here, to capture the non-local correlation, the pseudobands approximation^96–98 is further employed for all states. That is, DFT wave functions with close energies are summed into effective super states (see Supplementary Note 6). We assume that the manifold assumption also applies to the super states and charge density, and the VAE is used to further remove redundant information in them. Eventually, our semi-supervised, physics-informed model reads:

$${\widehat{\mathrm{\Sigma }}}_{n\mathbf{k}}^{GW}={\widehat{f}}_{NN}\left(e_{\theta }\left({\varphi }_{n\mathbf{k}}\left(\mathbf{r}\right)\right),{\epsilon }_{n\mathbf{k}},e_{\theta \sup }\left({\mathbf{\varphi }}_{\sup }\left(\mathbf{r}\right)\right),{\mathit{\epsilon }}_{\sup },e_{\theta \rho }\left(\rho \right),𝛈\right)$$ 3

where $e_{\theta }$, $e_{\theta \sup }$ and $e_{\theta \rho }$ are encoders exclusively trained for KS states, super states and charge density respectively. The schematic workflow of our model is shown in Fig. 1b. The output of the NN is the predicted GW diagonal self-energies ${\widehat{\mathrm{\Sigma }}}_{n\mathbf{k}}^{GW}={\widehat{\epsilon }}_{n\mathbf{k}}^{GW}-{\epsilon }_{n\mathbf{k}}^{DFT}$, and the inputs are the wavefunction of $\mid n,\mathbf{k}⟩$, super bands corresponding to occupied and unoccupied states on a uniform k-grid, and the ground state energies. These inputs are identical to the input of an explicit GW calculation to eliminate bias due to feature selection.

Application to dataset of 2D materials

To benchmark the predictive power of our model, we select 302 materials with unit cells of 3 to 4 atoms, including both metals and insulators, from the Computational 2D Materials Database (C2DB)^99–101, for training and validation. For the unsupervised VAE training, our dataset is comprised of 68,384 DFT electronic states sampled on a 6 × 6 × 1 uniform k-grid, which are randomly split into 90% training set and 10% test set. For supervised training of GW corrections, the entire GW energy dataset is randomly partitioned into two subsets: 10% (2201 electronic states) is allocated as the test set, while the remaining 90% (19801 electronic states) is designated as the training set. We further completely exclude a small subset of 30 materials from the training set for the VAE and three monolayer TMD materials—MoS₂, WS₂, and CrS₂—from both the VAE and GW training datasets. Comprehensive details regarding dataset, training dynamics and additional benchmarks are listed in Supplementary Note 5.

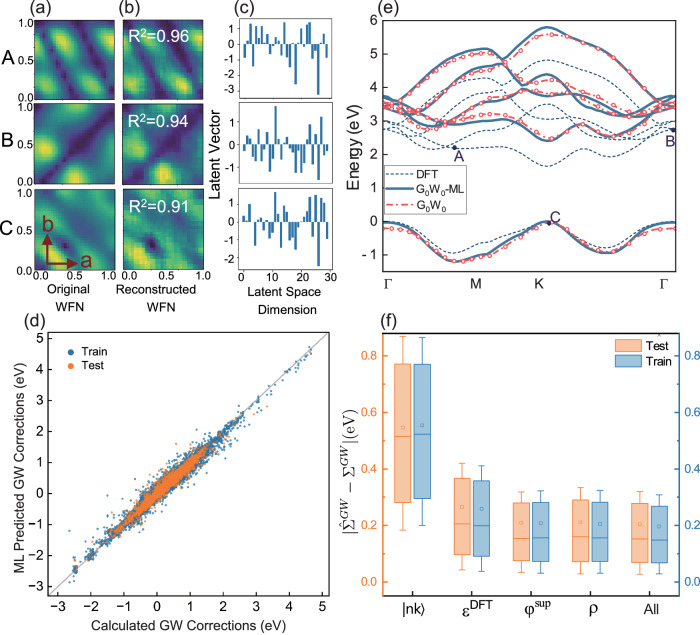
Figure 2a shows three DFT electronic wavefunctions, A, B, and C, for monolayer MoS₂, which is completely excluded from the training data, within the x-y plane of the unit cell, which correspond to the dark blue circles shown in Fig. 2e. Figure 2b shows the VAE-reconstructed wavefunction of states A, B and C, which are nearly identical to the original wavefunction after recovery from the low-dimensional latent space with high coefficients of determination, $R^2$, of 0.96, 0.94 and 0.91 respectively. Figure 2c shows the VAE variational mean vector $\overrightarrow{\mu }$ for states A, B and C respectively. Overall, the $R^2$ of the VAE-reconstructed wavefunction is 0.92 across the test set when compared with the amplitude of the original DFT wavefunction, and the normalization of the wavefunction is preserved within 1% (see Supplementary Fig. 10). Remarkably, the VAE-reconstructed wavefunctions reproduce the ground state charge density, the physically relevant quantity in DFT, with a high $R^2=0.99$ even though the total charge density is never used in the VAE training. The results demonstrate that the original electronic wavefunction in the high-dimensional real space can be effectively compressed by ${10}^3-{10}^4$ times into a representative vector in ${\mathbb{R}}^{p=30}$ in a way that still preserves the vital information needed for reconstruction. Our autonomously determined representation is over 100 times more compact than previous electronic fingerprint approaches⁶⁰.

Fig. 2. Application of crystal variational autoencoders (VAE) and downstream GW predictions.

a Density functional theory (DFT) calculated wavefunction of states A, B and C in MoS₂ (see (e)) used as input to VAE encoder, in crystal coordinates in units of the lattice vector. WFN denotes wavefunction. b VAE reconstructed wavefunctions of states A, B and C through latent space decoding. c Low-dimensional variational mean latent space for states A, B and C. (d) parity plot comparing the exact calculated values (x-axis) to the Machine learning (ML) predicted values (y-axis) of the GW correction for individual states. Blue (orange) dots represent training (test) sets. The mean absolute error (MAE) for the training set and test set are 0.06 and 0.11 eV respectively. The total number of data points in training (test) set are 19801(2201). e ML predicted GW band structures (blue solid curve) and calculated PBE band structures (blue dashed line) for monolayer MoS₂. The red circles are the exactly calculated quasiparticle (QP) energies from GW self-energy. The red dashed lines are the interpolated GW band structures. f Whisker plot of ML predicted GW error without utilizing representations of KS states $\mid n\mathbf{k}⟩$, DFT energies ${\mathit{\epsilon }}^{DFT}$, superstates ${\mathbf{\phi }}^{super}$ or charge density $\mathit{\rho }$. "All" denotes using all information. The orange (blue) boxes represent the test (training) set. The total number of data points under each box are 19801(2201) for training(test) sets. Each box plot displays the absolute error distribution of the self energies $∣{\widehat{\Sigma }}_{n\mathbf{k}}^{GW}-{\Sigma }_{n\mathbf{k}}^{GW}∣$, highlighting the median (box center line, i.e. Q2), 25th – 75th percentiles of dataset (lower and upper boundary of box, i.e. Q1 and Q3), mean (small square within box) and outlier cutoff (lower and upper whisker mark are defined as Q1-(Q3-Q1)$\times$0.2 and Q1 + (Q3-Q1)$\times$0.2, so all datapoints beyond the range are considered outliers). The training process spans 1,000 epochs. Source data are provided as a Source Data file.

Figure 2d shows the comparison between the GW corrections calculated explicitly and predicted by the downstream ML model, where orange (blue) dots represent the test (training) sets. The model yields an MAE of 0.06 eV ($R^2=0.96$) and 0.11 eV ($R^2=0.94$) for the training and test sets respectively, confirming that the VAE-learned representations of the DFT wavefunctions contain sufficient information to describe the non-local GW self-energy. We emphasize that the GW correction is more than a simple scissor shift. The average standard deviation of GW corrections across all bands and k-points in each material is 0.54 eV, which is much larger than the prediction accuracy of 0.11 eV (see Supplementary Fig. 4). Figure 2e shows the ML predicted GW band structure of monolayer MoS₂, which agrees remarkably with results obtained by explicit GW calculation (red circles in the bandstructure). Due to the generative power of the VAE latent space⁶³, even in the absence of electronic states along the high-symmetry path and the material MoS₂ in the training set, our model can accurately predict a smooth GW bandstructure along $\mathrm{\Gamma }-\mathrm{M}-\mathrm{K}-\mathrm{\Gamma }$ for MoS₂. Figure 2f shows how each individual input affects the accuracy of the GW NN model. We find that excluding the latent space representation of the wavefunction $\mid n,\mathbf{k}⟩$ in training significantly reduces the $R^2$ value by 0.5, directly showing the importance of VAE representation of individual KS states in GW prediction. GW calculations can also be accomplished through the self-consistent Sternheimer equation, utilizing solely the occupied electronic states^102–104, so in principle, inclusion of empty state information through the use of super states is not strictly necessary. Here, excluding the super states encoding the empty states reduces the $R^2$ value by 0.05. More details regarding training dynamics are presented in Supplementary Figs. 5–7.

Interpretability and generative power of the latent space

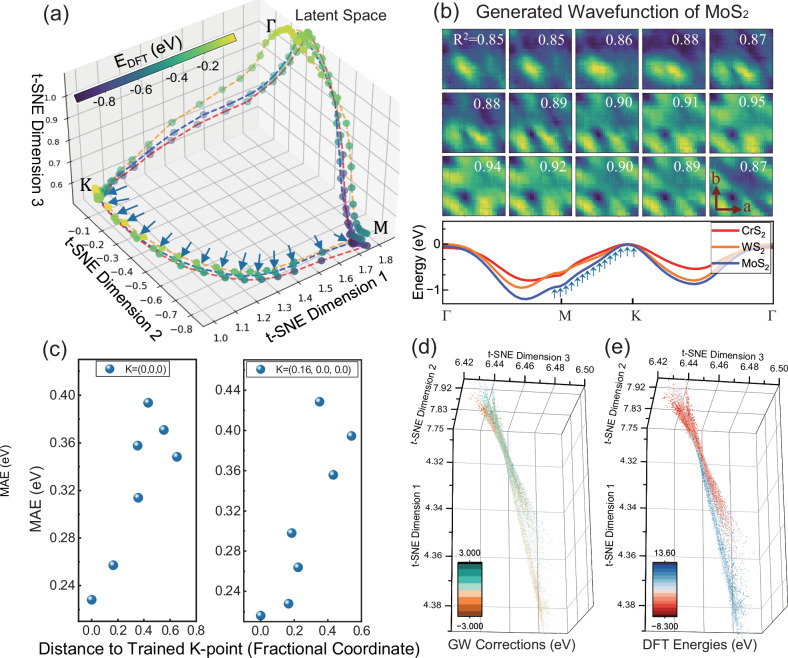
Next, to understand the generative power of our model, we open up the black box of the VAE and explore the meaning of the latent space obtained from unsupervised learning. We utilize a 3D t-distributed stochastic neighbor embedding (t-SNE) to visualize the VAE latent space for the electronic structure. As depicted in Fig. 3a, the circles linked by blue dashed lines represent the latent points of the first valence band states along the Γ-K-M-Γ high symmetry path of monolayer MoS₂. These points form a continuous and enclosed trajectory in the latent space, corresponding to the smooth closed path in the k-space shown in the lower bandstructure of Fig. 3b. For comparison, the latent trajectories from two other TMD monolayers WS₂ (blue) and CrS₂ (red), are also shown in Fig. 3a. The similarity in the electronic structures of these three TMDs (see Fig. 3b) is encoded in the similarities of the paths in latent space. To further demonstrate the generative power of the VAE, Fig. 3b shows the continuous evolution of 15 VAE generated real-space KS wavefunction moduli from M-K in the first valence band of monolayer MoS₂. The generated wavefunctions are constructed using the VAE decoder, which processes sampled points along a smooth curve from K to M in the latent space, denoted by the blue arrows in Fig. 3a. Notably, even though the VAE training set is only comprised of states sampled on a uniform k-point grid, and these three TMDs are entirely excluded from the training set, the generated wavefunction in Fig. 3b can still have a high R² around 0.9, showing the VAE accurately generates wavefunctions that the training has never seen. The underlying reason is that the three trajectories in Fig. 3a lie on the smooth latent surface learned by the well-trained VAE, where similar states are mapped to neighboring points in the latent space. Therefore, the smoothness and regularity of the VAE latent space can be used to quantify the extrapolative and generative power of our model and suggest that any sampled points from the learned latent surface are physically meaningful and can be reconstructed back to a wavefunction.

Fig. 3. Interpretation and generative ability of low dimensional representation of Kohn–Sham (KS) states learnt by variational autoencoder (VAE).

a 3D t-distributed stochastic neighbor embedding (t-SNE) visualization of the $\mathbf{\mu }$ latent space for KS wavefunctions in the first valence band along $\mathrm{\Gamma }-\mathrm{M}-\mathrm{K}-\mathrm{\Gamma }$ for the transition metal dichalcogenide (TMD) monolayers MoS₂, WS₂ and CrS₂, as shown in the lower band structures in (b). The dots (latent points) are mapped from the high-dimensional electronic wavefunction with color coded by Density Functional Theory (DFT) energies. The blue, orange and red dashed lines connect latent points corresponding to the KS states from the first valence band of MoS₂, WS₂ and CrS₂ respectively. Blue arrows denote latent points of 15 states along $\mathrm{M}-\mathrm{K}$ from MoS₂, as shown in (b). b Generated real-space wavefunction moduli decoded from latent points, which are sampled from the smooth latent curve of monolayer MoS₂, for each KS state from $\mathrm{M}-\mathrm{K}$ in the first valence band. The inset white number represents the R² value, showing the correlation with the explicitly calculated wavefunction. The order of states are in row-major order and from left to right. The lower figure represents the DFT bandstructures of monolayer MoS₂ (Blue), WS₂ (Orange) and CrS₂ (Red)_. The blue arrows indicate the KS states shown in the upper figures. The leftmost arrow indicates the first (top left) state shown in the upper part. c Mean absolute error (MAE) of GW prediction for different k-points and generative power for k-point interpolation. Here, the model is trained exclusively using GW energies at the $\mathrm{\Gamma }$ (left panel) point or $\mathbf{k}=\left(\mathrm{0.1667,\; 0,\; 0}\right)$ (right panel). The x-axis is the distance from the trained k-point to the untrained k-points in reciprocal space. d-e 3D t-SNE components of VAE latent $\mathbf{\mu }$ vector of 22002 KS wavefunction with GW labels, whose color are mapped to the GW correction ${ϵ}^{GW}-{ϵ}^{DFT}$ corrections (d) and DFT energies ${ϵ}^{DFT}$ (e) respectively. Source data are provided as a Source Data file.

Additionally, to explain the success of our model in predicting GW corrections at arbitrary k-points, we investigate how the supervised training at certain k-points affects the GW prediction at untrained k-points in the BZ. Figure 3c illustrates the average GW MAE for different k-points, as predicted by a dense NN that is only trained with GW energies at the $\mathrm{\Gamma }$ point (left panel) or a single finite momentum k-point (right panel). Notably, the prediction error tends to be lower for k-points in proximity to the trained k-point, contrasting with higher errors for those farther away from the trained k-point. This trend originates from the smoothness of the VAE latent space, indicating that two states that are close in the latent space should contribute comparably to the GW corrections, as they are also expected to be close in k-space as shown in Fig. 3b. This explains the capability of our model to accurately predict k-resolved GW band structures when trained with limited and uniform k-grid data.

Finally, to further verify the manifold assumption for electronic structure in real materials and explore how GW energies correlate to the VAE-coded representation, we apply the 3D t-SNE on top of the latent mean $\mathbf{\mu }$ space for all 22002 states with GW labels, whose colors are coded to their calculated GW-correction (Fig. 3d) and DFT energies (Fig. 3e). The t-SNE analysis provides direct evidence for the manifold assumption that the VAE effectively maps the latent $\overrightarrow{\mu }$ space of the electronic wavefunction to a smooth manifold even for different materials. More intriguingly, even though the unsupervised VAE learning procedure is entirely independent of GW labels, the magnitude of both the GW corrections and DFT energies exhibit a distinct pattern with different branches in the manifold corresponding to the magnitude of different GW corrections or DFT energies, as opposed to a random distribution. As a result, the t-SNE analysis serves as a crucial validation, demonstrating that unsupervised representation learning can effectively capture the inherent statistical correlation between GW energies and the electronic wavefunction. Thus, the unsupervised VAE acts as a form of pre-learning, which can significantly lower the barrier for the subsequent supervised learning of GW self energies.

In summary, we demonstrate that a properly designed VAE model can unsupervisedly learn KS DFT wavefunctions, compressing them as a low-dimensional latent space, in a way that preserves physical observables like total charge density and fundamental information needed for downstream prediction of excited-state properties. Since our model autonomously determines the crucial information for preservation through the unsupervised reconstruction of wavefunction data, it can establish a low-dimensional representation that avoids limitations due to feature engineering and selection. The representations preserve the translational invariance, discrete rotational invariance, and periodic boundary conditions of crystals with different cell sizes and symmetry. Our VAE model achieves a $R^2$ of 0.92 when reconstructing the wavefunctions in the test set. To further test the effectiveness of the VAE representation of KS states, we train a supervised dense NN for downstream prediction of GW self-energies on top of the latent space of KS states. The resulting model demonstrates a remarkably low MAE of 0.11 eV on a test set and can be used to predict both arbitrary k-points and materials held back from the training set. While other ML models have been used to predict GW bandstructure, the main advantage of our approach lies in our ability to interpret the smoothness of the latent space in relation to the completeness of our training set across both k-space and the space of material chemical and structural composition. This eliminates unphysical oscillations seen in previous models and allows us to confidently evaluate the generalizability of our model to states outside the training set improving its generative power. The smooth evolution of KS states in k-space can be mapped to a smooth trajectory in the latent space, and the sampled points from this continuous trajectory are physically meaningful and can also be reconstructed, enabling the generation of wavefunctions (and related physical observables) at uncalculated points at no additional cost. Here, in this first demonstration, we focus on predicting GW bandstructures of 2D materials, but we expect this framework to be generalizable to other crystalline systems and downstream applications, given expanded training sets. Notably, VAE wavefunction generation suggests a general route to building ML models for many post-Hartree-Fock (HF) corrections, including quantum Monte Carlo (QMC)¹⁰⁵, Density Matrix Downfolding¹⁰⁶, coupled cluster singles and doubles (CCSD)^107,108, and complete active space configuration interaction (CASCI)^109,110, all of which rely on the construction of higher-order wavefunctions, Green’s functions, and density matrices from DFT wavefunctions.

Methods

This section describes the details of construction of the translationally invariant variational autoencoder (VAE) model, downstream neural networks, and first principles density functional theory (DFT) and GW dataset. The mathematical proof of invariance, training dynamics, ground state applications of the latent space, additional benchmarks, and analysis of the pseudobands approximation are given in the Supplementary Notes. The atomic structure of materials used in this study are from the open database: Computational 2D Materials Database (C2DB)^99–101.

Translationally invariant VAE

Our model is developed utilizing the Pytorch package with parameters shown in Table 1¹¹¹. The first column categorizes each layer by its functionality, alongside the respective layer indices. Specifically, ‘Conv2d’ denotes a two-dimensional CNN layer, ‘RotationalConv2d’ denotes the two-dimensional rotational CNN layer. A kernel size of $3\times 3$ and 320 channels per CNN layer are sufficient to recover KS states with an overall R² score exceeding 0.87. ‘ReLU’ stands for the rectified linear unit, an activation function renowned for its widespread application in neural networks¹¹². ‘MaxPool2d’ indicates the max pooling layer, while the ‘Flatten’ layer plays a pivotal role by transforming the multi-dimensional outputs from preceding layers into a format suitable for the subsequent fully connected layers. ‘AdaptiveAvgPool2d’ indicates the GAP layer by specifying output as $1\times 1$. The ‘Linear’ layer refers to the fully connected layer. ‘Sigmoid’ is mentioned as a nonlinear activation function that generates an output ranging from 0 to 1¹¹³, which is ideal for modeling the reconstruction of wavefunction moduli. The architecture’s layout is further detailed by listing the number of parameters contained within each model layer in the second column.

Table 1.

VAE Parameters

Layer (type)	Parameter number
RotationalConv2d-1	115,520
MaxPool2d-3	0
Conv2d-4	921,920
ReLU-5	0
AdaptiveAvgPool2d-6	0
Flatten-7	0
Linear-8	19,260
Linear-9	48,608
ReLU-10	0
Unflatten-11	0
ConvTranspose2d-12	17,340
ReLU-13	0
ConvTranspose2d-14	9,640
Sigmoid-15	0
Total Trainable Parameters	1,132,288

The table shows the detail of each layer of variational autoencoder (VAE).

The input grid size (resolution) of wavefunctions in real space within a primitive unit cell depends on both the crystal lattice and the kinetic energy cutoff of the plane wave basis in the density functional theory (DFT) calculations. However, even if the number of trainable parameters in the convolutional neural network (CNN) layers remains constant regardless of the size of the input grid, the fully connected dense layer always requires the same input size from the output of the CNN layer. To address this, a commonly used preprocessing technique is cropping/resizing before passing input to CNN. However, this straightforward method does not adequately account for the freedom to choose the origin of the unit cell and the invariance of physical properties under discrete translational and rotational symmetries.

The main bottlenecks faced by using a simply rigid and uniform grid are (i) lack of preservation of translational invariance, (ii) lack of preservation of discrete rotational symmetry, (iii) improper handling of periodic boundary conditions (PBC), and (iv) lost information about unit cell size and symmetry. To address these issues and improve the generalizability of the VAE, we integrate a circular CNN layer, global average pooling layer, and rotational CNN technique in the encoder as shown in Fig. 1a, b As a result, the latent vector ${\mathbf{z}}_{\mathit{i}}\mathit{\in }{\mathbb{R}}^{\mathit{p}}$ of KS state $\mid i⟩$ are invariant to the unphysical degree of freedom of arbitrary translation and lattice constant selection. In addition, given the same crystal structure, ${\mathbf{z}}_{\mathit{i}}$ are a representation of $∣i⟩$ in the whole real space, so it is identical for different supercells constructed from the same unit cell. i.e.,

$${\mathbf{z}}_{\mathit{i}}=f_{NN}\left({\mathbf{z}}_{\mathbf{1},\mathbf{1},\mathit{i}}\right)=f_{NN}\left({\mathbf{z}}_{\mathit{m},\mathit{n},\mathit{i}}\right)$$

where ${\mathbf{z}}_{\mathit{m},\mathit{n},\mathit{i}}\mathit{\in }{\mathbb{R}}^C$ are the output of the last CNN layer, $\mathrm{C}$ is the number of channels, and $m,n$ are arbitrary positive integers defining the number of primitive cells in a supercell. $f_{NN}$ is the fully connected neural network following the CNN. The mathematical demonstration, model parameters, and corresponding benchmark are detailed in Supplementary Note 1.

For the downstream prediction of GW bandstructures, we employ a vanilla neural network including three fully connected layers with 13,801 trainable parameters. To reduce the risk of training set dependence, we also adapt k-fold cross validation for our evaluating model, where the data set is evenly split into 10 subsets (see Supplementary Fig. 6c). To visualize the latent space learnt by the VAE, we employed 3D t-distributed stochastic neighbor embedding (t-SNE). The perplexity in t-SNE calculations is set as 10,000 (22,002 datapoints in dataset) to balance the preservation of the global and local structure of the high dimensional data.

DFT and GW dataset

To benchmark the predictive power of our model, we select 302 materials from the Computational 2D Materials Database (C2DB)^99–101, which was also used in the work of Knøsgaard et al.⁶⁰, for training and validation. The dataset includes both metals and semiconductors across all crystal systems (we note that previous ML for GW prediction in this database was restricted to the subset of semiconducting materials) with the number of atoms ranging from 3 to 4. For the unsupervised VAE training, our dataset is comprised of 68,384 DFT electronic states sampled on a 6 × 6 × 1 uniform k-grid for 302 2D materials, which are randomly split into 90% training set and 10% test set. We include the same number of conduction states as valence states for each material in the VAE training, ensuring a comprehensive understanding of the electronic structure of both occupied and unoccupied states. For supervised training of GW corrections, the entire GW energy dataset is randomly partitioned into two subsets: 10% (2201 electronic states) is allocated as the test set, while the remaining 90% (19801 electronic states) is designated as the training set. We further completely exclude a small subset of 30 materials from the training set for the VAE and three monolayer TMD materials—MoS₂, WS₂, and CrS₂—from both the VAE and GW training datasets. The DFT and GW datasets are generated using GPAW^114,115. Comprehensive details regarding dataset, training dynamics and additional benchmarks are listed in Supplementary Note 5.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

B.H. and D.Y.Q. conceived and designed the workflow of the project. B.H. and J.W. developed the Python code for VAE model and downstream prediction NNs. All authors analyzed the data and wrote the manuscript. D.Y.Q. supervised the work and helped interpret the results.

Peer review

Peer review information

Nature Communications thanks Shivesh Pathak and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data (KS wavefunction and GW energies of 302 materials) generated in this study have been deposited in the Materials Data Facility repository under 10.18126/rpa1-yp91. Source data are provided with this paper.

Code availability

Code associated with this work is available from the public github repository https://github.com/bwhou1997/VAE-DFT with 10.5281/zenodo.13617033¹¹⁶ and from Code Ocean¹¹⁷.

Competing interests

The authors declare no competing interests

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53748-7.