A single-photon emitter coupled to a phononic-crystal resonator in the resolved-sideband regime

Abstract

A promising route towards the deterministic creation and annihilation of single-phonons is to couple a single-photon emitter to a mechanical resonator. The challenge lies in reaching the resolved-sideband regime with a large coupling rate and a high mechanical quality factor. We achieve this by coupling self-assembled InAs quantum dots to a small mode-volume phononic-crystal resonator with mechanical frequency Ω_m/2π = 1.466 GHz and quality factor Q_m = 2.1 × 10³. Thanks to the high coupling rate of g_ep/2π = 2.9 MHz, and by exploiting a matching condition between the effective Rabi and mechanical frequencies, we observe the interaction between the two systems via correlations in the emitted photons. Our results represent a major step towards quantum control of the mechanical resonator via a single-photon emitter.

Coupling a single-photon emitter to a mechanical resonator enables the generation of single phonons. Here, the authors study the interaction of a single-photon emitter and a phononic-crystal resonator in the sideband-resolved regime.

Introduction

Coupling a quantum system to a mechanical resonator is of both fundamental and technological interest. A highly studied area is the use of photons to control the state of a mechanical system¹. To enhance the interaction, cavities have been introduced in the form of two mirrors facing each other², ring resonators³, photonic crystals⁴, and microwave resonators⁵. Additionally, various quantum systems have been coupled to mechanical resonators, for instance superconducting qubits⁶, atomic ensembles⁷, and solid-state emitters⁸.

For phononic quantum technologies⁹, it becomes necessary to create one phonon at a time¹⁰. Using optical cavities, this is achieved with a highly attenuated laser pulse; the phonon creation is probabilistic with a probability much below one¹⁰. An alternative approach is to use a single-photon emitter in the resolved sideband regime. With π-pulse excitation on the blue sideband, phonons can be created on demand. The advantage of the single-emitter is that it breaks the harmonicity of the cavity’s photon ladder. Furthermore, the theory has shown that the single emitter itself can be used to laser-cool the mechanical system to its ground state¹¹.

To date, different kinds of single-photon emitters have been coupled to mechanical resonators: colour centres^12,13, rare-earth ions¹⁴, 2D-materials¹⁵, and quantum dots^8,16–29. So far, the sensitivity to mechanical motion is low and the interaction between the two systems was probed by driving the mechanical resonator, i.e., by adding phonons. However, to explore single-phonon applications, it is crucial to operate in the few-phonon regime, ultimately in the quantum ground state³⁰.

Semiconductor quantum dots (QDs) are excellent emitters of high-quality single-photons^31–34. The upper level, the exciton, couples to lattice vibrations via a strain-induced deformation potential^11,22,35. In the resolved-sideband regime, the angular frequency of the mechanical resonance, Ω_m, must be larger than the radiative decay rate of the QD exciton, Γ_R. In addition, for optical driving of the phonon sidebands, it is important that Ω_m is also larger than the inhomogeneously-broadened linewidth, Γ_inh³⁶. Satisfying these two conditions is challenging for many reasons. First, the mechanical frequencies need to be in the gigahertz regime, where mechanical loss rates tend to be high³⁷. Second, obtaining narrow optical linewidths (i.e., small inhomogeneous broadening) on QDs embedded in mechanical resonators can be difficult³⁵. Third, for high exciton-phonon coupling rates, the mechanical resonator size needs to be small such that the implementation of a phononic shield becomes necessary³⁸.

In this work, we face the aforementioned challenges by coupling self-assembled InAs QDs³⁹ to a phononic-crystal resonator (PnCR) with Ω_m/2π = 1.466 GHz and Q_m = 2.1 × 10³. We achieve narrow optical linewidths and hence a high sensitivity of the QD’s optical response to the mechanics. We drive the QD’s optical transition resonantly and analyse the emitted photons using quantum optics techniques. Specifically, a measurement of the auto-correlation function reveals the mechanical motion when the effective Rabi frequency matches the mechanical resonance frequency. We detect the interaction of a quantum emitter and a mechanical resonator in the few-phonon regime with 〈n_m〉 = 58 (thermal motion at 4.2 K) and extract a state-of-the-art exciton-phonon coupling rate of g_ep/2π = 2.9 MHz.

Results

Sample design and characterisation

The mechanical resonator is etched into a 180 nm GaAs membrane. The membrane hosts InAs QDs; the QDs are embedded in a p-i-n diode, see inset to Fig. 1a^40–42. Figure 1a, b shows finite-element simulations of the PnCR. The mechanical in-plane breathing mode is tightly confined by the phononic bandgap structure³⁸ and shows a highly homogeneous strain profile in the centre of the resonator (see Supplementary Note 1). The PnCR consists of seven holes (phononic-shield unit cells) etched into the membrane⁴⁰, see Fig. 2a. Due to the small beam cross-section (960 × 180 nm²), the breathing mode has a mode volume as small as 4 × 10⁻³λ³ (with λ = 3.25 μm). As a result, our simulations predict a low effective mass m_eff = 7.4 × 10⁻¹⁶kg, a large zero-point motion x_zpf = 2.7 × 10⁻¹⁵m, and a high exciton-phonon coupling rate $g_{\mathrm{ep}}^{\mathrm{sim}}/2\pi =$3.2 MHz (see Supplementary Note 1). The thermal phonon occupation of the breathing mode is 〈n_m〉 = 58 at 4.2 K. The PnCR does not support an optical cavity but this could be included in subsequent designs.

Fig. 1. Finite-element simulations of a quantum dot coupled to a mechanical resonator.

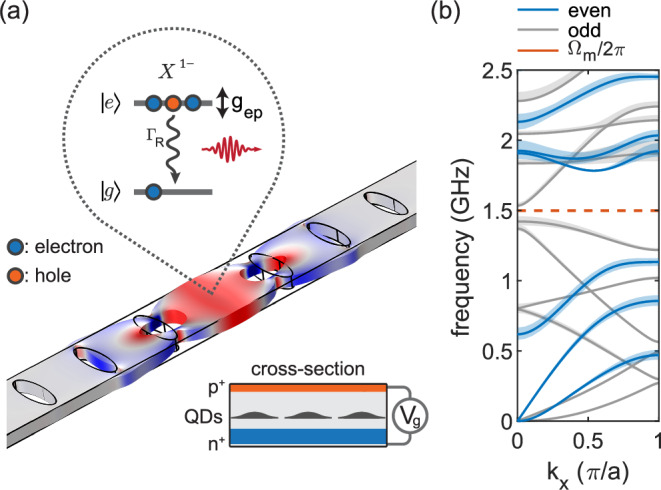
a Phononic-crystal resonator hosting a semiconductor diode-structure for quantum dot (QD) charge control (see cross-section). The QD emits single photons and its excited state is dispersively coupled to the mechanical motion via a deformation potential (example given for the negative trion X¹⁻). The resonator consists of a well-isolated mechanical mode at Ω_m/2π ≈ 1.5 GHz tightly confined by the surrounding phononic shield. b Band diagram of the phononic shield. The width of the bandgap is 0.65 GHz and 0.11 GHz for even and odd modes in terms of the z-symmetry, respectively. Shaded areas represent band broadening upon varying the air-hole parameters by  ±20 nm.

Fig. 2. Quantum dot characterisation.

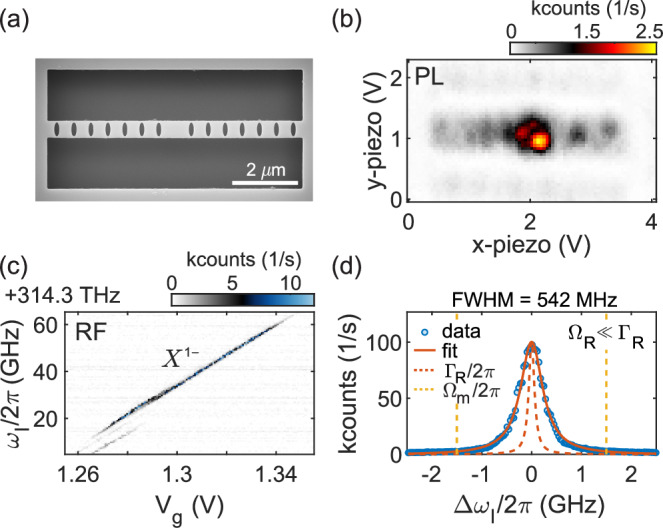
a Scanning electron-microscope image of the fabricated device with seven shield elements on each side. b Photoluminescence (PL) map showing several QDs in the centre of the phononic-crystal beam. c Resonance fluorescence (RF) charge-plateau scan of the negative trion (X¹⁻) of a QD close to the resonator’s centre. d Low-power frequency scan to determine the inhomogeneously-broadened linewidth, Γ_inh/2π = 550 MHz. The data are fitted to a Lorentzian. The transform limit (Γ_R/2π) and the sideband position (Δω_l = ± Ω_m) are shown.

We select a QD with a potentially large exciton-phonon coupling rate from a photoluminescence map^37,43. Figure 2b shows several bright QDs located around the centre of the beam. Switching to resonant excitation of a single QD, a plateau map of the negative trion X¹⁻ is recorded, see Fig. 2c. Upon changing the applied gate voltage, V_g, the emission frequency is tuned (via the dc Stark effect) over a frequency range of more than 50 times the QD’s linewidth. The lifetime of the excited state is extracted from a pulsed measurement τ_R = 1.18 ns, which corresponds to a radiative decay rate of Γ_R = 2π × 135 MHz (see Supplementary Note 3). On account of the diode structure and optimised nano-fabrication, we obtain narrow optical linewidths, here, a factor of four above the transform limit Γ_inh = 4Γ_R, see Fig. 2d.

Exciton-phonon interaction

In the absence of an optical cavity, the only way to detect the mechanical motion is via the QD. It is crucial to consider how the exciton-phonon coupling can be measured, in particular, the coupling to mechanical oscillations driven only by thermal noise (i.e., the Brownian motion).

In the unresolved-sideband regime, mechanical noise results in fluctuations in the intensity of the resonance fluorescence³⁵. The relative sensitivity is proportional to the square of the normalised derivative of the resonance fluorescence counts (with respect to laser detuning), see Fig. 3b. The highest sensitivity is obtained at low excitation power and laser detunings corresponding to half the optical linewidth³⁵. In the resolved sideband regime, this technique fails. The mechanical resonator oscillates back and forth several times during the exciton lifetime, resulting in acoustic sidebands at Δω_l = ± Ω_m³⁷, such that the resonance fluorescence intensity becomes insensitive to the mechanical motion.

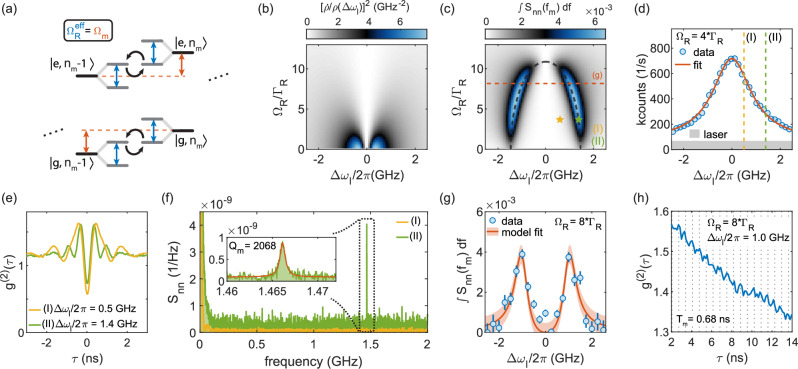
Fig. 3. Exciton-phonon coupling strength.

a Phonon-energy-ladder diagram for a driven two-level system. The excitation laser dresses the two-level system. The interaction between the two systems is strongest when the dressed-state splitting (effective Rabi frequency, ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}/2\pi$) is equal to the sideband separation (mechanical frequency, Ω_m/2π). b Simulated mechanical-noise sensitivity in the unresolved-sideband regime, given by the derivative of the QD counts. c Simulated mechanical-noise sensitivity of the current device. ∫S_nn(f_m)df is the integrated noise power of the mechanical resonace. The condition of ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$ is highlighted by the dashed black line. d QD linewidth at elevated excitation power (Ω_R = 4Γ_R) as used in the thermal-motion measurement. e Auto-correlation measurements at two different detunings (i) and (ii) (see dashed lines in (d) and stars in (c)). The larger detuning corresponds to ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$. f Noise-power spectra obtained from (e) reveal the mechanical peak only for optimal effective Rabi frequency (detuning (ii), green line). g Integrated mechanical noise in dependence on the laser detuning. An exciton-phonon coupling rate of g_ep/2π = 2.9 MHz is extracted from a model-fit to the data. Data and fit errors are given by one standard deviation. h Zoom-in of a 14-h auto-correlation measurement, showing mechanical oscillations. Dashed lines show the expected noise peaks, spaced by T_m = 2π/Ω_m = 0.68ns.

An alternative scheme relies on driving the system at a resonance condition close to the mechanical sidebands. The quantum dot is driven with frequency detuning Δω_l/2π and Rabi coupling Ω_R. The field created by the QD oscillates at the effective Rabi frequency, ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}/2\pi$, where ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}=\sqrt{{\mathrm{\Omega }}_{\mathrm{R}}^2+\mathrm{\Delta }{\omega }_{\mathrm{l}}^2}$. The resonance condition is that the effective Rabi frequency should match the mechanical resonance frequency, Ω_m/2π, i.e., ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$⁴⁴. Fulfilling this condition, the mechanical motion becomes visible in the auto-correlation function of the emitted photons.

To analyse this resonance precisely, we simulate a driven two-level system with parameters appropriate to our system. The mechanical coupling is introduced via a frequency shift of the upper level, here the trion. The model is semi-classical: the two-level system is treated quantum mechanically; both the laser drive and the mechanics are treated classically. We assume that the mechanical phase is static with respect to the time dynamics of the quantum emitter^45,46. To obtain the time-dependent mechanical backaction on the excited-state population, we solve the master equations numerically. Specifically, we simulate the sensitivity of the resonance fluorescence to the mechanical motion, ∫S_nn(f_m)df (where S_nn is the noise-power spectrum), as a function of laser detuning and Rabi coupling, Fig. 3c. As expected, the sensitivity is zero at small detunings and at small Rabi couplings yet large at the resonance condition.

A qualitative understanding of the resonance condition, i.e., the sensitivity resonances in Fig. 3c, can be found in the dressed-state picture. Figure 3a shows the phonon-ladder diagram where neighbouring ground and excited states are separated by the phonon energy ℏΩ_m (orange arrows). Vertical transitions correspond to transitions which conserve the phonon number of the resonator (elastic scattering), and diagonal transitions change the phonon population by  ± 1 (Stokes/anti-Stokes scattering). The optical excitation dresses the energy levels of the quantum emitter and splits them by an energy $\hslash {\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}=\hslash \sqrt{{\mathrm{\Omega }}_{\mathrm{R}}^2+\mathrm{\Delta }{\omega }_{\mathrm{l}}^2}$ (blue arrows). The sensitivity of the QD to the mechanical resonator is strongest whenever a combination of Ω_R and Δω_l is chosen such that ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$⁴⁴. In the dressed-state picture, the condition ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$ means that states involving different phonon numbers are degenerate and mechanical quanta can be exchanged without the cost of energy (black arrows).This picture applies specifically to a two-level system and not to a harmonic system such as a cavity for which there is a ladder of excited states. In cavity opto-mechanics, the resonance condition is simply Δω_l = Ω_m and is independent of the laser power.

At low excitation powers (Ω_R ≪ Γ_m) the resonance condition implies detuning the laser to the blue or red sideband. At high excitation powers (Ω_R > Γ_m), the laser detuning needs to be smaller than the mechanical frequency. Above Ω_R > Ω_m (Ω_m = 10.8Γ_R here), the resonance condition can no longer be met and the sensitivity is therefore small. The signal-to-noise ratio increases with higher QD counts, and the simulation shows that there is a maximum around Ω_R ≈ 8Γ_R (see Supplementary Note 5).

Detection of thermal motion

The simulations motivate the choice of ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}$ in the experiment. We perform two individual measurements with parameter sets (Rabi frequency and laser detuning) (I) ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}<{\mathrm{\Omega }}_{\mathrm{m}}$ and (II) ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$. Here, Ω_m is the mechanical frequency expected from the simulations. The measurements are performed at Ω_R = 4Γ_R, where the linewidth is just slightly power broadened. Ω_R is calibrated with a power series measurement (see Supplementary Note 3). Figure 3d shows the associated linewidth scan. Due to the high optical power, the background level (unsuppressed laser) increases. For (I) the laser detuning corresponds to Δω_l/2π = 0.5 GHz (yellow line) and for (II) Δω_l/2π = 1.4 GHz (green line).

To probe the QD-mechanical interaction we record 8 h of auto-correlation data while repeatedly suppressing the laser and correcting for a small spectral drift (see Supplementary Note 3). Figure 3e shows the auto-correlation measurements for (I) and (II). Close to zero delays, Rabi oscillations of ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}/2\pi$ are visible, with frequencies matching those expected from the calibration. The dip at τ = 0 (a measure of the single-photon purity) reaches values far from zero on account of the increased laser background (see Fig. 3d and Supplementary Note 3). The noise-power spectrum, S_nn, is obtained from the auto-correlation measurement via Fourier transform (see Supplementary Note 4)³⁵. Figure 3f shows S_nn for configurations (I) and (II) obtained from an auto-correlation with a maximum time delay of ${\tau }_{\max }=$ 500 ns and time binning of τ_bin = 50 ps. In case (II) (green spectra), a prominent peak is visible at a frequency of 1.466 GHz. In case (I) (yellow spectra), no peaks are visible, although the click rate on the detectors is much higher and the noise floor is much lower than for (II).

We identify the peak at 1.466 GHz as the mechanical resonance on two grounds. First, S_nn follows the dependence on ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}$ as predicted by the simulations. Second, the frequency at the peak, 1.466 GHz, lies very close to the mechanical resonance frequency obtained from finite-element simulations, 1.496 GHz. Thus, the coupled hybrid system is in the resolved-sideband regime with Ω_m ≈ 11Γ_R but more importantly Ω_m ≈ 2.7Γ_inh.

The inset to Fig. 3f displays the mechanical noise-peak with high resolution (FFT of auto-correlation with ${\tau }_{\max }=$ 8 μs and τ_bin = 50ps). A mechanical quality factor as high as Q_m = 2.1 × 10³ is extracted via a Lorentzian fit. This justifies the assumption in the simulations that the mechanical damping rate is much less than than the QD’s radiative decay rate.

Exciton-phonon coupling rate

To estimate the exciton-phonon coupling rate, $g_{\mathrm{ep}}=\left(\delta {\omega }_{\mathrm{QD}}/\delta x\right)\cdot x_{\mathrm{zpf}}$, we perform the noise-power measurement upon sweeping the laser detuning (at fixed laser power). We chose Ω_R = 8Γ_R, for which the highest interaction between the two systems is expected at Δω_l/2π = 1.0 GHz. Figure 3g shows the integrated noise power versus laser detuning. For each data point, 1 h of auto-correlation data are recorded. Via a model fit to the data, an exciton-phonon coupling strength of g_ep/2π = 2.9 MHz is extracted. This agrees very well with the simulated value, 3.2 MHz. Finally, we repeat the auto-correlation measurement with optimised parameters for the highest signal-to-noise ratio, see Fig. 3h. The oscillations due to the interaction with the mechanical resonator now become visible, even without a Fourier transform.

A prominent feature of the noise spectra, Fig. 3f, is that only one peak is observed. Furthermore, both the mechanical frequency and the coupling g_ep/2π are very close to the simulated values. These observations show that the phononic resonator operates as per design: modes in the gap are both decoupled from the environment via the phononic shield and highly confined to the central island. The many mechanical modes lying outside the bandgap are highly damped and are therefore not observed. Considering that the phononic shield works well, it is likely that the mechanism limiting the mechanical quality factor is related to damping mechanisms within the material. Notably, GaAs gigahertz-frequency mechanical resonators with mechanical quality factors exceeding 10⁴ have been achieved^8,47. This suggests that the present mechanical quality factor is limited by surface losses and/or losses within the doped regions. One approach to reduce these losses could be surface passivation^48–50. Moreover, the quality factor could also be enhanced via soft clamping and further strain engineering^51,52.

Discussion

The figure of merit for the mechanical signal strength is the thermal coupling rate normalised to the mechanical angular frequency, $g_{\mathrm{ep}}^{\mathrm{th}}/{\mathrm{\Omega }}_{\mathrm{m}}$ with $g_{\mathrm{ep}}^{\mathrm{th}}=g_{\mathrm{ep}}\sqrt{2⟨n_{\mathrm{m}}⟩}$. To enhance the signal strength, it is important to improve g_ep further without increasing the mechanical frequency. This can be achieved by either reducing the width of the beam and thus the effective mass ($g_{\mathrm{ep}}\propto m_{\mathrm{eff}}^{-1/2}$), or by choosing a two-dimensional resonator design hosting a degenerate breathing mode.

For single-phonon experiments, it is crucial to reach below 〈n_m〉 = 1. To estimate the backaction on the mechanical resonator, we perform additional simulations in which the mechanical resonator is described in a fully quantum way with decay to a thermal bath (see Supplementary Note 5). Also here, the strongest interaction is found when ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$. Currently, the change in phonon number that we achieve with red-detuned driving is too small (below two, see Supplementary Note 5) to be detectable in the auto-correlation measurement. The cooling performance can be improved by increasing the mechanical quality factor, reducing the inhomogeneous broadening, and by increasing the coupling rate. At 4.2 K, a measurable change in phonon population could be achieved with the present system via a five-fold increase in the mechanical quality factor (Q_m = 10⁴). However, the lowest phonon number would still be much above one (see Supplementary Note 5). An alternative approach is to start at a bath temperature of 100mK where 〈n_m〉 = 0.98. With a five-fold enhanced Q_m, a two-fold increased g_ep, and a transform-limited linewidth⁵³, the lowest phonon occupation that can be reached is 〈n_m〉 = 0.56, a suitable starting point for single-phonon experiments.

In summary, we present a QD coupled to a phononic-crystal resonator in the resolved-sideband regime. Upon resonant excitation, the QD has a narrow optical linewidth and a high mechanical sensitivity. We demonstrate that the interaction between the two systems is strongest when matching the eigenfrequency of the dressed QD with the mechanical frequency: ${\mathrm{\Omega }}_{\mathrm{R}}^{\mathrm{eff}}={\mathrm{\Omega }}_{\mathrm{m}}$. Satisfying this condition allows us to observe even the thermally-driven mechanical oscillations (at 4.2 K) and to determine precisely the mechanical resonator’s frequency. Via the noise power spectrum, we determine the exciton-phonon coupling, g_ep/2π = 2.9 MHz (an unprecedentedly high value), and the mechanical quality factor, 2.1 × 10³. The low mechanical damping rate results in a high Q_m ⋅ f_m product of 3.0 × 10¹² Hz, which allows for 34 mechanical oscillations before coherence is lost.

As an outlook, we mention that cooling the present device to millikelvin temperatures is sufficient to reach 〈n_m〉 < 1. Cooling (and heating) of the mechanical resonator via optical driving of the QD should become possible with slightly improved device parameters. Furthermore, several QDs can be included in the same mechanical resonator facilitating a coherent exciton-exciton coupling. There are prospects of coupling the spin to the mechanical motion in a similar phononic resonator: this also allows deterministic single-phonon creation, in this case via spin relaxation⁵⁴, and potentially facilitates a coherent coupling between spins in separate QDs.

Author contributions

S.S., A.D.W. and A.L. designed and grew the QD sample. C.S., L.Z., G.N.N., A.J. and R.J.W. designed the mechanical structures following the scheme developed by P.L. and L.M.; Y.W., L.M., and P.L. fabricated the mechanical structures. C.S. and L.Z. performed the simulations. C.S., G.N.N., L.Z., A.J., M.E. and R.J.W. carried out the experiments and analysed the data. C.S., G.N.N. and R.J.W. wrote the manuscript with input from all the authors.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that supports this work is available from the corresponding author upon request.

Code availability

The code used for this work is available from the corresponding author upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53882-2.