Submesoscales are a significant turbulence source in global ocean surface boundary layer

Abstract

The turbulent ocean surface boundary layer is a key part of the climate system affecting both the energy and carbon cycles. Accurately simulating the boundary layer is critical in improving climate model performance, which deeply relies on our understanding of the turbulence in the boundary layer. Turbulent energy sources in the boundary layer are traditionally believed to be dominated by waves, winds and convection. Recently, submesoscale phenomena with spatial scales of 0.1~10 km at ocean fronts have been shown to also make a contribution. Here, by applying a non-dimensional turbulent kinetic energy budget equation, we show that the submesoscale geostrophic shear production at fronts is a significant turbulent energy source within the ocean boundary layer away from the sea surface. The contribution reaches 34% of the total dissipation in winter and 17% in summer at the mid-depth of the boundary layer, despite its intermittency in space and time. This work indicates fundamental deficiencies in previous conceptions of ocean boundary layer turbulence, and invites a reappraisal of the sampling scale in observations, model resolution and parameterizations, and other consequences of the global energy budget.

This study shows that submesoscale processes at ocean fronts are a significant source of turbulent energy within the ocean boundary layer away from the sea surface, with a contribution reaching 34% of the total energy dissipation in winter.

Introduction

The ocean surface boundary layer (OSBL), a turbulent upper layer in the ocean, provides the channel for the atmosphere to communicate with the ocean interior. Intense air-sea exchanges of momentum and heat energize small-scale (<100 m) turbulence and make the OSBL the most turbulent layer in the ocean¹. OSBL turbulence modulates the transfer of momentum, heat and dissolved gases between the sea surface and ocean interior. These exchanges affect the water properties of the ocean, thereby influencing climate variability on timescales from days to centuries^2–6. Turbulence also enhances the upward flow of nutrients to the light-filled biologically-productive layers, a control on primary ocean productivity^7,8. OSBL turbulence is not resolved in most ocean and climate models and is usually represented by parameterizations.

Studies in the last decades have been conducted to quantify the contributions from OSBL processes including winds, waves, and convection^9–11 to OSBL turbulence. These prior assessments focused only on the sources of turbulent kinetic energy (TKE) that are effectively one-dimensional—consistent with classical conceptions of boundary layer turbulence and easily determined by the available data and models. Extensive work has now documented that OSBL turbulence can be significantly altered in frontal regions with strong vertical shears providing a significant source of TKE via submesoscale phenomena with spatial scales of 0.1~10 km¹². Observations also show that classical scalings of OBSL turbulence are deficient^13,14, while a significant contribution of fronts to OSBL turbulence has been reported^15–17. This geostrophic shear production turbulence (GSP) source due to submesoscales relies on horizontal buoyancy gradients and is therefore fundamentally informed by two-dimensional flow parameters. This mixing is important for both vertical and horizontal exchange of properties at ocean fronts, but is not included in prior global assessments of OSBL turbulence, nor currently widely-used parameterizations^18,19.

In this work, GSP is found to be a significant, yet highly intermittent, contributor to global OSBL turbulence away from the sea surface. To show this we extend the Belcher. ¹⁰ approach to determining sources of TKE production by surface forcing to include GSP contributions, and we compare the relative significance of four kinds of turbulence: geostrophic shear production turbulence at fronts (GSP), Langmuir shear production turbulence due to waves (LSP), ageostrophic shear production turbulence due to surface wind stress (AGSP) and vertical buoyancy production turbulence due to surface buoyancy loss (VBP) in the global OSBL. GSP is found to be a leading contributor to turbulence at the mid-depth of the OSBL in winter. The result is robust to the analysis choices, and provides a clue to reasons for the OSBL bias in ocean and climate model simulations and a direction to improve model capability for climate change projections.

Results

Distributions of the turbulence sources

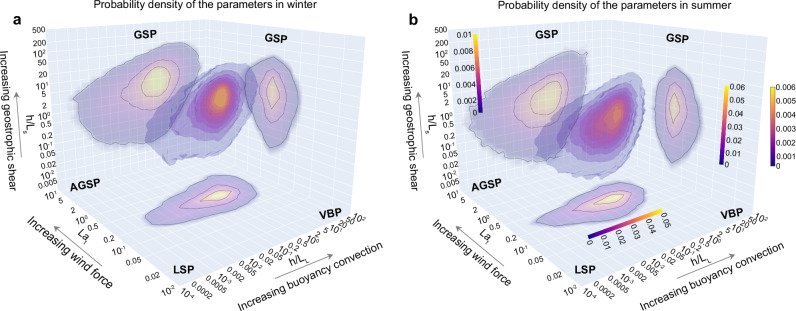
The relative contributions of four sources of turbulence, waves (LSP), fronts (GSP), surface buoyancy loss (VBP) and wind (AGSP) to OSBL turbulence are determined by three non-dimensional parameters, the turbulent Langmuir number La_t, the ratio of the boundary layer depth to the Langmuir stability length h/L_L, and the ratio of the boundary layer depth to the geostrophic shear stability length h/L_s (Methods). The relative importance of wind forcing, waves, buoyancy convection and geostrophic shear are reflected by location along the three axes of the plots in Fig. 1.

Fig. 1. Three-dimensional global probability density of the three parameters.

a The probability density in winter. b The probability density in summer. The three parameters are turbulent Langmuir number La_t of the x-axis, the ratio of the boundary layer depth to the Langmuir stability length h/L_L of the y-axis, and the ratio of the boundary layer depth to the geostrophic shear stability length h/L_s of the z-axis. Two-dimensional projections of the distributions are also shown. The black contours enclose 30%, 60%, and 90% of the global values. Each source of turbulence is labeled (GSP: geostrophic shear production turbulence; LSP Langmuir shear production turbulence, VBP vertical buoyancy production turbulence, AGSP ageostrophic shear production turbulence) and the contribution of fronts (i.e., GSP) is highlighted as the geostrophic shear along the z-axis is increased.

La_t of the x-axis governs the wind-forced turbulence source (AGSP) against the wave-forced turbulence source (LSP), and LSP dominates over AGSP when La_t < 0.3¹⁰. The global distribution of La_t shows seasonality of LSP and AGSP consistent with that found in Belcher et al. ¹⁰. The parameter h/L_L of the y-axis measures the source of convective turbulence (VBP) against LSP. Large h/L_L values (h/L_L > 1) indicate a dominant role of VBP over LSP. This ratio is much larger in winter (generally >1), implying a generally more dominant role of LSP over VBP.

To measure the relative GSP magnitude, the ratio h/L_s is used²⁰. The geostrophic shear stability length L_s depends on the strength of horizontal buoyancy gradients associated with fronts. Estimation of this quantity requires a rescaling of the resolved model buoyancy gradients, which is done assuming frontal arrest under the Turbulent Thermal Wind balance (TTW; Methods)²¹, although we emphasize that major results are qualitatively robust to this choice as assessed below. Much of the estimated global distribution is characterized by h/L_s > 1 in the z-axis, indicating the frontal contribution to TKE production (GSP) dominates over wind-forced turbulence (AGSP). Seasonal variation of h/L_s is also significant, with larger h/L_s values in winter resulting from more active submesoscale fronts with intense horizontal density gradients²² that outpace the enhanced AGSP associated with winter storms.

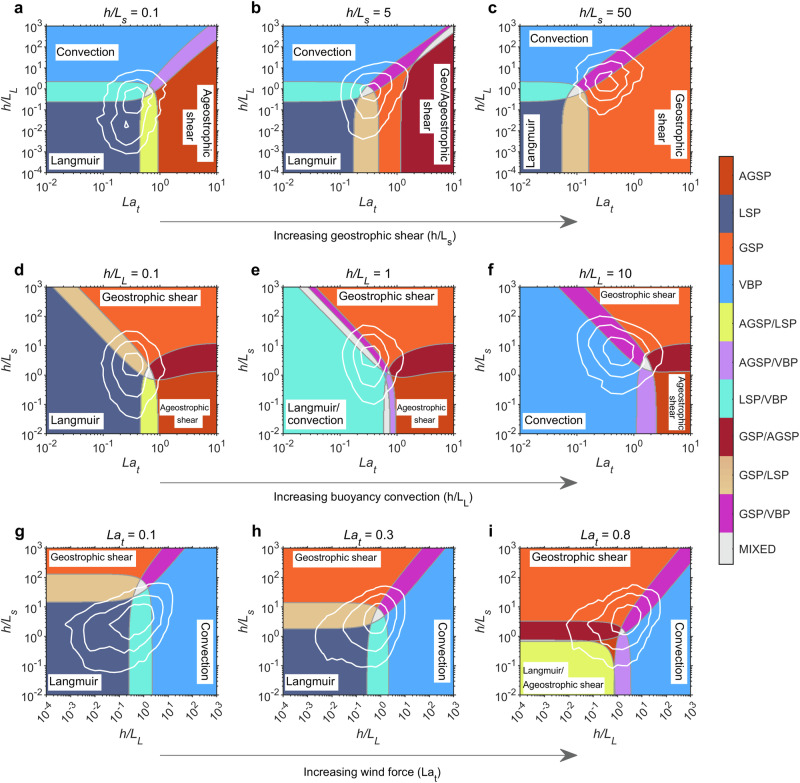
Dissipation regimes in parameter space

Two-dimensional probability distribution slices overlapped on regime maps derived from Fig. 1 are shown (Fig. 2). The La_t-h/L_L projection, neglecting the geostrophic shear, has been discussed by Belcher et al. and Li et al. ^10,11 who argued for a significant role of LSP in generating OSBL turbulence. As the parameter h/L_s is introduced, the regimes are changed. The percentiles indicate that the global OSBL is generally under LSP and LSP/VBP regimes for locations with weak geostrophic shears (Fig. 2a). GSP begins to play a role while LSP and AGSP are weakened as the geostrophic shear increases (Fig. 2d, g).

Fig. 2. Turbulence regimes in parameter slices in winter.

a h/L_s = 0.1. b h/L_s = 5. c h/L_s = 50. d h/L_L = 0.1. e h/L_L = 1. f h/L_L = 10. g La_t = 0.1. h La_t = 0.3. i, La_t = 0.8. The regimes (GSP: geostrophic shear production turbulence; LSP: Langmuir shear production turbulence; VBP: vertical buoyancy production turbulence; AGSP: ageostrophic shear production turbulence) denoted by different color patches are defined by the dominant production terms in the turbulent kinetic energy (TKE) budget. The white contours enclose 30%, 60%, and 90% of the locations with the corresponding values. A regime is considered dominant when its contribution exceeds 75% of the total dissipation, otherwise, it is a two-turbulence-mixed regime when two TKE sources both contribute more than 25% while all others contribute less than 25%, and lastly, it is a mixed regime if more than three sources of turbulence contribute more than 25%¹¹. The distributions indicate that GSP is an important regime for ocean surface boundary layer turbulence over the globe, especially at locations with strong frontal geostrophic shears.

The La_t-h/L_s space shows the dependence of the regimes on buoyancy convection. When the surface buoyancy convection is weak, the enclosed contours show that most of the locations are dominated by LSP, GSP and their mixed regime, indicating an important role of GSP globally in these conditions (Fig. 2b). The contribution of LSP turbulence is finally eliminated as the surface buoyancy loss continues to increase, and GSP and VBP dominate OSBL turbulence (Fig. 2e, h).

In the h/L_L-h/L_s space, LSP and VBP dominate OSBL turbulence when La_t is small (Fig. 2c). The percentile distributions show that almost 90% of the locations with small La_t are dominated by LSP, VBP and their mixed regimes. As the wind forcing becomes stronger, the contribution from LSP is decreased but GSP and AGSP become more important. When the wind forcing is sufficiently strong, more than 90% of the corresponding locations are under a mix of AGSP, GSP, VBP (Fig. 2i).

In summer, as the wind force, buoyancy loss and geostrophic shear are all weakened, the distributions of these parameters are shifted to small values (Supplementary Fig. 1). The role of LSP is generally strengthened, while other turbulence sources are weakened. In particular, the relative importance of GSP is weakened from winter to summer, which is the opposite behavior of LSP.

Dissipation magnitudes globally

According to both mean and median absolute dissipation rates, LSP has the largest magnitude in both seasons (Fig. 3; Supplementary Fig. 2). The dominant role of LSP has been reported by previous studies^10,11. Without considering GSP, Li et al. ¹¹ found the OSBL is dominated by LSP (e.g., the Southern Ocean), or VBP (e.g., tropical regions), and mixed LSP and VBP (i.e., mid-latitude regions). By contrast, GSP is here shown to often be larger than the VBP and AGSP contributions, and to rival LSP in winter. GSP is stronger in winter, especially so in the western boundary currents and the Southern Ocean. Overall, the relative contributions of GSP to the total dissipation averaged over the globe are 34% in winter and 17% in summer.

Fig. 3. Probability density functions (PDFs) of the turbulence sources.

a PDFs of the four sources, geostrophic shear production turbulence, (GSP; orange), Langmuir shear production turbulence (LSP; dark blue), vertical buoyancy production turbulence (VBP; light blue), ageostrophic shear production turbulence (AGSP; dark red). in winter. b PDFs of the four sources in summer. The dots indicate the corresponding global mean value of each distribution. The log-normal distribution of the PDFs suggests that the mean and integral of ocean surface boundary layer dissipation are determined by intermittent high dissipation rates. The highest intermittency of GSP can also be derived from the distributions.

Probability density functions (PDFs) of all turbulence sources show nearly log-skew-normal distributions (Fig. 3), consistent with both intermittent alternating energy sources²³ and the forward cascade of oceanic turbulence²⁴. In such distributions, the large mean rates are determined by intermittent extreme events, rather than the accumulation. Compared with the other sources, GSP has the widest distribution, implying it has the highest intermittency and the greatest difference between its average and median values. This highlights a challenge in observational estimates of integrated contributions of frontal turbulence. Extremely sharp fronts, while covering very limited spatial extent and oftentimes being transient, can be associated with sufficiently large GSP so as to significantly influence the mean values.

Turbulent energy sources globally

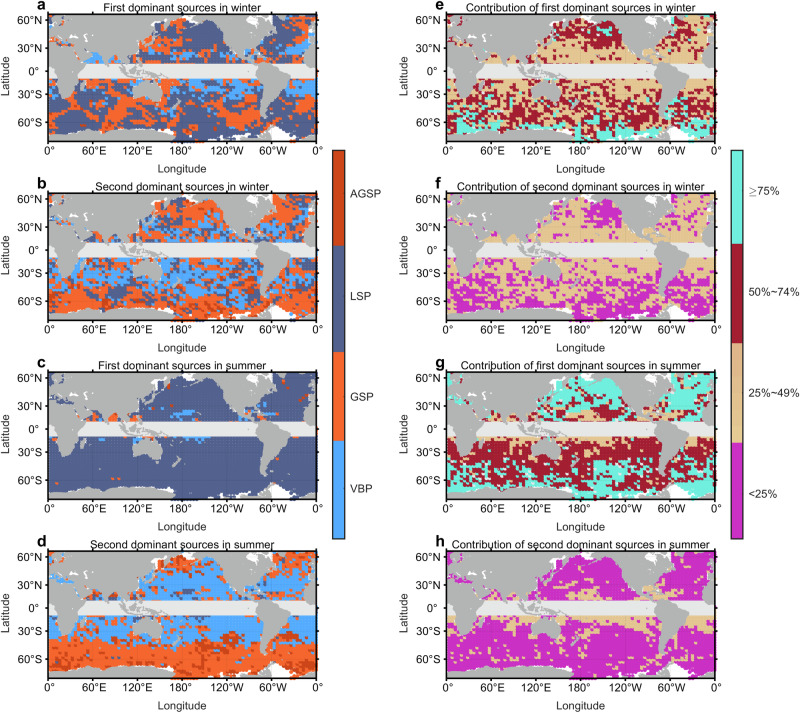
The spatial distribution of the global turbulence sources can be determined by ranking the relative contributions of the four sources by location. Figure 4 maps the top two turbulence sources over the globe and the associated contributions relative to the total dissipation in different seasons. In winter, LSP is the most spatially prevalent source, accounting for 44% of the global locations, especially at mid and high latitudes (Fig. 4a). The spatial prevalence of GSP is 37% and is most common at low and mid latitudes, while some locations at low latitudes are controlled by VBP (16% of all locations). A latitudinal dependence in the percentage contribution of the principal source is evident, with the largest source generally contributing less than 50% of the total dissipation at low latitudes, growing to larger than 75% at high latitudes. The contribution of VBP (35%) and GSP (34%) become the most dominant regimes in the map of the secondary sources (Fig. 4b).

Fig. 4. Global distributions of the two most likely dominant sources at each location.

a The first most likely dominant sources (GSP: geostrophic shear production turbulence; LSP: Langmuir shear production turbulence; VBP: vertical buoyancy production turbulence; AGSP: ageostrophic shear production turbulence) in winter. b The second most likely dominant sources in winter. c The first most likely dominant sources in summer. d The second most likely dominant sources in summer. Their relative contribution percentages to the total mean dissipation (%) are shown in (e–h). The relative contributions shown in e–h indicate that the summation of the top two sources can explain most (Pct_1st +Pct_2nd > 55%) of the total dissipation. GSP turbulence is the first largest contributor at low and mid latitudes in winter, and still the second largest contributor at high latitudes in both seasons.

Overall, considering the top two sources, GSP is the most spatially extensive primary source, providing a leading contribution to turbulence in 71% of the locations considered. By contrast, it is 70% for LSP and 51% for VBP. Moreover, the relative contribution of GSP explicitly shows where GSP dominates OBSL turbulence, such as the western North Pacific Ocean, the Eastern North Atlantic Ocean in winter, and the Southern Ocean in both seasons (Supplementary Fig. 3). Thus, while individual sharp fronts cover very limited spatial area, their contribution to OSBL turbulence may have broad impact.

In summer the distribution of energy sources changes, consistent with changes in surface forcing and the known seasonality of submesoscale turbulence^22,25,26. LSP is the most spatially-prevalent source over the globe, except for a few tropical regions with significant GSP and VBP contributions. LSP accounts for 84% of all summer locations, much larger than other sources (11% for GSP and 4% for VBP). This dominance is highlighted by the relative contribution shown in Fig. 4g, which indicates that the LSP may be responsible for more than 50% of global OSBL turbulence production outside of the tropics. For the second dominant sources, it is GSP at high latitudes while VBP at low latitudes (Fig. 4d).

Discussion

The results here suggest that ocean fronts make a leading-order contribution to OSBL turbulence in many parts of the global ocean. This result differs fundamentally from classic conceptual models assuming horizontally uniform flows, and it implies parameterizations of OSBL turbulence that account only for wind, wave, and convective sources of turbulence are deficient. A schematic diagram of the four kinds of turbulence sources and their relative contributions is shown in Fig. 5. Nevertheless, its quantitative estimation heavily relies on the robustness of the calculation of the horizontal buoyancy gradient. Here the robustness of these results is also tested by using other two alternative methods.

Fig. 5. A schematic diagram of the four turbulence sources.

Geostrophic shear production turbulence (GSP), Langmuir shear production turbulence (LSP), vertical buoyancy production turbulence (VBP), and ageostrophic shear production turbulence (AGSP) represent the turbulence sources from Langmuir circulation, geostrophic current shear, vertical convection, and ageostrophic current shear. LSP is the shear to turbulence from Stokes drifts due to winds and waves. GSP is the shear to turbulence from geostrophic currents at fronts with down-front winds. VBP is the convection to turbulence by gravitational instability due to surface buoyancy loss. AGSP is the shear to turbulence from ageostrophic currents induced by winds. The left two pie charts show the spatial prevalence of each turbulence source in winter and summer, while the right two show the relative contribution of each source to the total dissipation magnitude averaged over the globe (LSP: dark blue; GSP: orange; VBP: light blue; AGSP: dark red). These percentages indicate that GSP is a prevalent and significant source of OSBL turbulence over the globe.

First, GSP is calculated based directly on the raw resolved buoyancy gradients of the numerical model (“uncorrected” method). These estimates can therefore be thought of as a conservative lower bound^21,27. Second, we rescale the buoyancy gradients by assuming a horizontal buoyancy density gradient spectrum consistent with white noise from the effective resolution down to the frontal arrest scale (“no-slope” method)²⁸. This approach leads to a larger estimate of the horizontal buoyancy gradient (or smaller L_s), and thus provides an upper bound of GSP dissipation.

Unsurprisingly, the role of GSP is weakened for the uncorrected case, while it is strengthened for the no-slope case (Supplementary Figs. 4 and 5). Taking the uncorrected and no-slope estimates as effective upper and lower uncertainty bounds, the mean relative contributions of GSP are 34% with the uncertainty of [27%, 37%] in winter and 17% [16%, 18%] in summer. The dominant locations for each energy source and their averages and percentiles (Supplementary Table 1) indicate that GSP still emerges as a major global source of TKE in the boundary layer even when using the most conservative approach of estimating the horizontal buoyancy gradient directly from the marginally submesoscale-permitting 1/48° model run solution, suggesting the robust role of fronts in energizing global boundary layer turbulence.

The turbulence sources discovered here are only applicable under down-front wind component and destabilizing conditions. According to our evaluation, the conditions are met about 31% and 21% of the time in winter and summer (the globally-averaged percentages of times with down-front wind component and destabilizing conditions over the whole months), respectively. It means GSP contributes 34% in a third of the winter. This is the most conservative estimation since even in up-front wind conditions GSP is expected to have a vertical structure similar to AGSP^20,29 and a comparable magnitude of the GSP contribution to the down-front case will be derived. If we assume the parameter A_G = 0.5 in the TKE equation (see Methods) is still applicable in up-front conditions, the GSP contribution will become 35% [28%, 38%] in 65% of winter and 18% [17%, 19%] in 40% of summer. Meanwhile, the TKE model is a linear superposition of different kinds of turbulence and their interactions are not considered. For strong baroclinic fronts, VBP turbulence is inhibited and the surface buoyancy flux tends to characterize GSP turbulence¹⁸. Likewise, frontal processes, such as mixed layer instability, tend to restratify the OSBL and generate positive VBP, also reducing the VBP dominance^30,31. The full range of these types of interactions between turbulence energy sources is not yet known, however additional work on this topic will help further refine future estimates of the global sources of OSBL turbulence.

It is noteworthy that the relative contributions of the turbulence sources vary with depth within the OSBL, as the vertical decreasing rates of their intensities are different. The relative contribution at the OSBL mid-depth revealed in this work suggests a significant role of GSP turbulence to the exchanges between the OSBL and the ocean interior. However, its contribution is not represented in most regional and climate ocean models, which may be hypothesized to be one of the key reasons leading to simulated biases of the OSBL. Due to the small frontal arrest scale, parameterizing GSP turbulence, as would be natural in a model with strict kinetic energy conservation³², offers an alternative future approach to include its contribution in ocean models. Despite that a scheme parameterizing GSP has been proposed¹⁸, limitations should be noted (such as the rescaling of the frontal buoyancy gradient is not considered) and further research is needed.

Methods

Model data

Oceanic data including velocity, temperature, and salinity are from a submesoscale-permitting global model, LLC4320. LLC4320 was simulated by the Massachusetts Institute of Technology general circulation model (MITgcm) on a Latitude-Longitude polar Cap (LLC) grid^33,34. The model has a spatial resolution of 1/48^o and 90 vertical layers. The model was initialized successively from a set of simulations with resolutions of 1/6^o, 1/12^o, and 1/24^o. The K-Profile Parameterization scheme (KPP) was applied in the simulation. The atmospheric forcing to drive the simulation was from the European Centre for Medium Range Weather Forecasting (ECMWF) with resolutions of 6 hours in time and 0.14^o in space. Tidal forcing was also included in the simulation. LLC4320 was run for 14 months of simulation time, from September 2011 to November 2012, and essential state variables were stored at hourly snapshots. The model result has been validated against in situ observations^34,35 and has been widely used for the analysis of submesoscale seasonality, energy cascade and air-sea flux^22,25,36. The ECMWF surface fluxes are applied to evaluate OSBL turbulence. For consistency, we directly use the outputted sea surface fluxes from the simulation, except for the Stokes drift—from ECMWF ERA5 which has a spatial resolution of 0.5^°. In this work, data in February and August are chosen for analysis. All results shown in this work are subsampled with a grid spacing of 4^°.

Before the LLC4320 data are used for further analysis, the performance of LLC4320 in reproducing OSBL fronts needs to be assessed. However, a direct assessment of the buoyancy gradients is impossible since high resolution global observations are not available. Considering satellite-derived sea surface temperature (SST) usually have high spatial resolution around 1 km, a quantitative comparison of SST between LLC4320 and Visible Infrared Imaging Radiometer Suite (VIIRS) L2 products (with spatial resolutions from 0.75 km at nadir to 1.5 km at the swath edge) is conducted. Here, SST from LLC4320 is the uppermost 0.5-m layer of the simulation. Recently, LLC4320 is demonstrated to reproduce the observed distribution of SST patterns well both globally and regionally³⁷. Nevertheless, as OSBL fronts are focused in this work, the spatial SST variance is assessed using the first-order structure function³⁸. As the VIIRS L2 data have missing values due to clouds, the structure function can avoid the effect of these missing values and statistically demonstrates the capability of the LLC4320 model in reproducing SST variances.

The first-order structure function here is defined as the difference of SST between the pair of points, x, and x + r, namely,

$$\delta =SST\left(\mathbf{x}+\mathbf{r}\right)-SST\left(\mathbf{x}\right)$$ 1

Then the probability density functions (PDFs) of SST structure function δ at different scales (r = 100 km, 80 km, 60 km, 50 km, 40 km, 30 km, 20 km, 10 km and 5 km) are calculated based on VIIRS and LLC4320 data in the same period (February and August of 2012). To avoid the effect of the missing values in VIIRS, we interpolate the LLC4320 data onto the VIIRS grids at the corresponding dates, and then avoid the corresponding missing-value regions. Due to the spatial resolution limitation, the structure function probabilities of large separations r from LLC4320 are expected to be consistent with VIIRS. But as r decreases below the effective resolution, the PDFs from LLC4320 are speculated to underestimate the SST frontal magnitude from VIIRS. The calculated PDF differences between these two datasets in different regions confirm the speculation (Supplementary Fig. 6). The negligible differences between LLC4320 and VIIRS on separation scales larger than the effective resolution indicate that LLC4320 reproduces observed SST jumps well. However, as the scale decreases below the effective resolution, the underprediction of SST jumps begins to become more and more consequential. The positive bias in probability at small SST jump magnitude and negative bias in probability at large SST jump magnitude imply that at small spatial scale LLC4320 overpredicts small SST jumps and underpredicts large SST jumps compared to the real ocean. So, this misestimation is corrected on the buoyancy gradients (refer to section Buoyancy gradient rescaling).

In addition to SST, we further evaluate the capability of the LLC4320 simulation to reproduce the OSBL thickness which is a crucial factor in determining the dissipation magnitudes. However, a direct comparison of the OSBL thickness to observation is currently impossible. Here, we compare it to the surface mixed layer from LLC4320 and Argo observations (Supplementary Fig. 7), since they should be dynamically close after temporally averaging. The temporally averaged OSBL thickness is close to the mixed layer thickness in LLC4320 (the root mean squares of the bias are less than 5 m over the globe) which tends to simulate relatively deeper mixed layer depths compared to the observations, especially in the winter month (the root mean square of the global mixed layer thickness bias is 13.5 m in February but 24.4 m in August). This may be attributed to the unresolved restratifying processes such as small-scale mixed layer instability and symmetric instability^27,39. Nevertheless, compared to the observations, despite the quantitative bias, the global pattern of the layer thicknesses from LLC4320 generally resembles the observed one in different seasons.

Non-dimensional turbulent kinetic energy budget

The TKE budget in the OSBL can be expressed as follows:

$$\frac{\partial ē}{\partial t}=-\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\frac{\partial \overline{{\mathbf{u}}_s}}{\partial z}-\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\frac{\partial \overline{{\mathbf{u}}_g}}{\partial z}-\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\frac{\partial \overline{{\mathbf{u}}_a}}{\partial z}+\overline{w^{\prime }{b}^{\prime }}-ϵ+F_e.$$ 2

Here, the overbars and primes denote time averages and perturbations. $e=\frac{1}{2}\left({{\mathbf{u}}^{\prime }}^2+{w^{\prime }}^2\right)$ is the TKE. The horizontal velocity is decomposed into three components, the Stokes drift component, ${\mathbf{u}}_s$, the geostrophic component, ${\mathbf{u}}_g$, and the ageostrophic component, ${\mathbf{u}}_a$, each of which has an associated vertical shear production term. These production terms are denoted LSP, GSP, and AGSP, respectively. The fourth term on the right-hand side of Equation (2) is the vertical buoyancy production (VBP) which generates TKE when the ocean surface loses buoyancy through surface cooling or salt fluxes. The fifth term is the molecular dissipation of TKE. The last term is the vertical TKE transport. Assuming a steady state and a negligible F_e, an equilibrium is reached between the TKE dissipation and the TKE sources,

$$ϵ=-\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\frac{\partial \overline{{\mathit{u}}_s}}{\partial z}-\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\frac{\partial \overline{{\mathit{u}}_g}}{\partial z}-\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\frac{\partial \overline{{\mathit{u}}_a}}{\partial z}+\overline{w^{\prime }{b}^{\prime }}$$ 3

This equation can be simplified into a non-dimensional expression for the TKE budget under destabilizing surface buoyancy forcing at the mid-depth of the OSBL,

$$\frac{ϵ\left(z=0.5h\right)}{{u_{*}}^3/h}=A_L{{La}_t}^{-2}+A_G\frac{h}{L_S}+A_S+A_C{{La}_t}^{-2}\frac{h}{L_L}$$ 4

where h is the OSBL thickness as determined by using an offline KPP scheme, $u_{*}=\sqrt{\frac{∣{\mathit{\tau }}_w∣}{\rho }}$ is the friction velocity (τ_w is the sea surface wind stress, ρ is the seawater density), ${La}_t=\sqrt{\frac{u_{*}}{u_s}}$ is the turbulent Langmuir number⁴⁰. The effect of misalignments between Stokes drift, wind direction and Langmuir cells is considered in the calculation⁴¹. $L_S=\frac{u_{*}f}{M^2\cos \theta }$ is the geostrophic shear stability length (f is the Coriolis parameter, $M^2=∣{\nabla }_{h}b∣$ is the horizontal buoyancy gradient magnitude, θ is the angle between the wind and the frontal geostrophic shear vectors)²⁰, $L_L=\frac{{u_{*}}^2{u}_s}{B_0}$ is the Langmuir stability length (B₀ is the sea surface buoyancy flux)¹⁰. Other parameters are taken as the following values: $A_L=0.22,A_G=0.5,A_S=2\left[1-\exp \left(-0.5{La}_t\right)\right],A_C=0.3$. The equation extends the TKE budget equation of Belcher et al. ¹⁰ by including the GSP term. According to Thomas and Taylor⁴², the GSP production with down-front winds peaks at a value approaching the Ekman buoyancy flux near the surface and follows a near-linear profile with depth in the OSBL. So, the parameter A_G = 0.5 in the GSP term is determined by the vertical structure of GSP under forced symmetric instability at fronts⁴². In the budget equation, the contribution of horizontal shear production is not considered, which may become non-negligible at OSBL frontal regions where the OSBL frontal scale is comparable to the OSBL thickness¹².

Here, dynamic processes that lead to dissipation and OBSL deepening are the focus, so destabilizing sea surface buoyancy flux is considered. Moreover, a steady state of the TKE budget equation requires an external force for sustained GSP¹⁸, and so only the down-front wind condition is analyzed⁴². It is noteworthy that this amounts to a conservative estimate of GSP, as it has been reported elsewhere¹⁶ that VBP tends to interact with GSP and strengthen GSP under destabilizing conditions. However,  this interaction and other transient GSP events are neglected. Nevertheless, further comparison with the OSMOSIS observations demonstrates the robustness of the TKE model under surface buoyancy loss which can statistically reproduce OSBL dissipation (see section below).

For each LLC4320 grid point with a wind vector component of down-front winds and destabilizing sea surface buoyancy flux, the horizontal buoyancy gradient M² is calculated and the TKE model is applied. However, the directly calculated M² heavily depends on the spatial resolution. To eliminate this dependence, the calculated M² is rescaled according to its spectral characteristic by assuming OSBL fronts are arrested under TTW balance (see sections below). Because OSBL fronts are not always arrested (such as during frontogenesis and frontolysis), the estimation of the submesoscale turbulence here is a maximum magnitude that OSBL fronts can reach, not an average over their whole life. This does not qualitatively alter our results is confirmed above by analysis of the raw model buoyancy gradients, which likewise indicate a leading role for GSP in OSBL turbulence.

Validation of the TKE model

To further validate the TKE production model the analysis is applied to in situ observations from the OSMOSIS project^17,43 $\left(\mathrm{estimating}\frac{{u_{*}}^3}{h},{La}_t,\frac{h}{L_L},\mathrm{and}\frac{h}{L_s}\right)$ and the results are compared to the directly observed dissipation rate. As a part of the OSMOSIS project, nine moorings were deployed in the northeast Atlantic Ocean for the period September 2012–September 2013. With a centrally located mooring, the remaining moorings consisted of two quadrilaterals. It is a 13 km × 13 km outer box consisting of four moorings, while it is a 2.5 km × 2.5 km inner one consisting of the remaining four. The resolution of the inner mooring is tended to resolve submesoscale fronts^17,43. The moorings were equipped with Conductivity–Temperature–Depth (CTD) instruments spanning a depth range of 30–530 m with a sampling rate of 5 min. In this work, temperature and salinity observed at the central and inner moorings are used for analysis. Temperature and salinity are interpolated vertically into 10-m bins in the range of 50–300 m. In addition to the mooring array, seagliders were also deployed during the OSMOSIS project, and dissipation rates in the upper ocean were derived from the glider observations⁴⁴.

In the TKE model, the quantities to be determined are calculated as follows. The OSBL thickness h is determined as the depth where the observed dissipation rate decreases to a threshold value of 1 × 10^-8 W kg⁻¹. It should be noted that, from a dynamical perspective, determining the OSBL thickness based on the turbulent dissipation threshold is the most direct and reasonable method. However, since the LLC4320 model uses the KPP turbulence closure scheme, which does not output turbulent dissipation rates but instead determines the OSBL thickness based on the Richardson number—a parameter related to the generation of turbulence due to flow instability—we employed an offline KPP method to determine the OSBL thickness to maintain dynamical consistency with the model results. Then, the dissipation rate at the OSBL mid depth is obtained. The frictional and the convective velocities, u_* and w_* are calculated based on the atmospheric momentum and buoyancy fluxes provided by the ECMWF ERA5 with a spatial resolution of 0.25^o. The Stokes drift u_s, and other wave parameters, are provided from the ECMWF ERA5 with a spatial resolution of 0.5^o. The buoyancy gradient M² is calculated using the observations of the central and inner moorings. As the inner moorings can only partially resolve submesoscale fronts, we also correct the buoyancy gradient using the rescaling method with the amplification factor derived from the LLC4320.

The mooring observations are confined below 50 m, hence the validation is conducted in winter (January 2013–April 2013) during which the ocean has a deep OSBL thickness in excess of 100 m. All data are interpolated to the times of the glider observations. Furthermore, compared to C_L = 0.25, (derived from turbulence resolving numerical simulations), we decide to use C_L = 1 in the frontal arrest scale equation (Equation (10)) which is found to reproduce a better result (Supplementary Fig. 8). As discussed in Bonder et al. ²¹, the parameter C_L is on the same order of magnitude as the Richardson number Ri, i.e., C_L ~ Ri. In Bodner et al. ²¹, shear turbulence is believed to shift Ri to ~0.25 based on Large Eddy Simulations (LES). But in the real ocean, the OSBL, especially at frontal regions, tends to stay near a neutral state with Ri ~ 1 due to restratification processes¹⁸ and geostrophic adjustment^45,46 that were not consistently within the scope of the LES setups examined in Bodner et al. ²¹, which may explain why using C_L ~ Ri ~ 1 tends to reproduce dissipate rates closer to the observations at OSMOSIS. Ri is expected to be regionally dependent over the globe, so using C_L = 1 gives a conservative lower bound estimate of the GSP magnitude in this work.

The expectation is that the produced energy will balance the dissipation of energy, although the transport of energy by the oceanic flow can locally violate this balance. The time series of the dissipation rate at the OSBL mid-depth exhibits dramatic intermittency with variation across several orders of magnitude (Supplementary Fig. 8a). When observed dissipation is compared with the summed combination of LSP, VBP and AGSP, the sum is typically too small, especially around the moderate dissipation intensity ~1.0 × 10⁻⁷W kg⁻¹. Including the dissipation from a four-source sum, with GSP, better reproduces the moderate-dissipation events (although it also predicts too few weak dissipation events). PDFs of the dissipation demonstrate the capability of the TKE production model more explicitly (Supplementary Fig. 8b). The production without GSP tends to underestimate the observed dissipation—that is a sink stronger than the sources. By contrast, GSP events shift the PDF towards larger values, correcting the underestimation. Notably, the corrected PDF peak is more consistent with observations. With the introduction of GSP the PDF shape has significantly improved, with the results for skewness and kurtosis both indicating a closer match with observations (skewness: from 1.07 to 0.89 compared with 0.9; kurtosis: from 2.75 to 2.19 compared with 2.25).

A further comparison between the dissipation rates estimated using glider observations and estimates from the LLC4320 simulation is conducted to assess if the buoyancy gradient correction is justified (Supplementary Fig. 8c). As there is no overlap between the OSMOSIS winter observation period (January 2013–April 2013) and the winter simulated with LLC4320 (here January 2012–April 2012), the non-dimensional values scaled by the simultaneously observed/modeled ${u_{*}}^3/h$ are compared. The production from LLC4320 shows a general similarity to the OSMOSIS production, both when GSP is included and excluded—so long as the LLC4320 GSP is corrected for limited model resolution (Supplementary Fig. 8c). Using only the uncorrected GSP for LLC4320 (i.e., calculated based on the original buoyancy gradients from the LLC4320 without rescaling) underestimates the observed dissipation.

In addition to the single-point comparison, a comparison over the North Atlantic is also conducted between LLC4320 and eNATL60 to figure out if the result is sensitive to the choice of ocean models. eNATL60 was simulated based on Nucleus for European Modelling of the Ocean (NEMO) covering the North Atlantic with a spatial resolution of 1/60^o. Considering the significant role of GSP turbulence in winter, hourly outputs in Feb 2010 were retrieved. Due to the different simulation periods, the PDFs of the non-dimensional dissipation rates from the four sources are compared (Supplementary Fig. 9). The PDF distributions of the four turbulence sources are similar between the two simulations, demonstrating the consistency of the analysis method and results here which are mostly insensitive to the choice among submesoscale-permitting ocean models.

The result here is quite different from Buckingham et al. ⁴³, who reported a less important contribution of GSP to OSBL dissipation. In addition to the buoyancy gradient correction—which adjusts for limitations in the horizontal resolution of the mooring array (Supplementary Fig. 10)—another key difference that should be noted is the depth investigated. A fixed depth of 45 m is used in Buckingham et al. ⁴³, which is much shallower in winter compared to the mid-depth of the mixed layer used here. LSP turbulence tends to concentrate near the surface and decreases more sharply with depth compared to GSP turbulence. Our work suggests an increasing relative significance of GSP turbulence away from the surface.

Buoyancy gradient rescaling

The buoyancy gradient from the LLC4320 is rescaled to account for the effect of horizontal resolution in the numerical model following the method in Fox-Kemper et al. ²⁸. The power spectrum of the buoyancy averaged over the OSBL tends to decay with a constant slope (usually around k⁻²). Thus, the spectrum of the horizontal buoyancy gradient averaged in the OSBL tends to be flat or white, i.e., ~k⁰. Assuming an isotropic, power-law behavior with a spectral slope of k^a for the buoyancy gradient, the integral of the buoyancy gradient over an integrated domain L_b range down to the effective model resolution L_eff can be related to the wavenumber spectrum ${\mathcal{B}}_0{k}^a$

$${\int }_{L_{eff}}^{L_b}{\int }_0^{2\pi }{∣⟨{\nabla }_{H}b⟩∣}^{2}rd\theta dr={\int }_{\frac{2\pi }{L_b}}^{\frac{2\pi }{L_{eff}}}{\mathcal{B}}_0{k}^{a}dk$$ 5

Similarly, the integral from the basin scale down to the frontal scale L_f is

$${\int }_{L_f}^{L_b}{\int }_0^{2\pi }{∣⟨{\nabla }_{H}b⟩∣}^{2}rd\theta dr={\int }_{\frac{2\pi }{L_b}}^{\frac{2\pi }{L_f}}{\mathcal{B}}_0{k}^{a}dk$$ 6

Combing these two equations yields an estimate for the degree of underestimation of the modeled buoyancy gradient magnitude relative to that at the frontal scale,

$$\frac{{\int }_{L_{eff}}^{L_b}{\int }_0^{2\pi }{∣{\nabla }_{H}b∣}^{2}rd\theta dr}{{\int }_{L_f}^{L_b}{\int }_0^{2\pi }{∣{\nabla }_{H}b∣}^{2}rd\theta dr}=\frac{{\int }_{\frac{2\pi }{L_b}}^{\frac{2\pi }{L_{eff}}}{\mathcal{B}}_0{k}^{a}dk}{{\int }_{\frac{2\pi }{L_b}}^{\frac{2\pi }{L_f}}{\mathcal{B}}_0{k}^{a}dk}={\left(\frac{L_f}{L_{eff}}\right)}^{1+a}\frac{1^{1+a}-{\frac{L_{eff}}{L_b}}^{1+a}}{1^{1+a}-{\frac{L_f}{L_b}}^{1+a}}\approx {\left(\frac{L_f}{L_{eff}}\right)}^{1+a}$$ 7

If a = 0, the equation scales as estimated in Fox-Kemper et al. ²⁸ (“no-slope corrected”). However, according to our evaluation based on the LLC4320 result, the spectra in zonal and meridional at different regions generally have slightly negative slopes, rather than zero slopes (Supplementary Fig. 11). Estimates of the slope are therefore derived by linearly fitting over the range determined by the domain size and the effective resolution L_eff = 7∆s (this resolution corresponds roughly to the maximum resolved wavenumber before the spectra roll off sharply due to numerical dissipation)³⁴. Based on the slopes over the globe, the original buoyancy gradient magnitude derived directly from LLC4320 (“uncorrected”) is rescaled based on the estimated true frontal width (“corrected”) by,

$${\nabla }_H{b}_f={\left(\frac{L_{eff}}{L_f}\right)}^{\frac{1+a}{2}}{\nabla }_H{b}_{\mathit{△}\mathrm{s}}$$ 8

It should be noted that the amplification factor ${\left(\frac{L_{eff}}{L_f}\right)}^{\frac{1+a}{2}}$ is directly taken as 1 at low latitudes when L_eff < L_f, i.e., where fronts are resolved. As shown in Supplementary Fig. 12, the amplification factor ${\left(\frac{L_{eff}}{L_f}\right)}^{\frac{1+a}{2}}$ exceeds 6 at mid-latitudes. The correction dynamically reproduces the buoyancy gradient associated with small-scale submesoscale fronts that are not resolved by the LLC4320 simulation.

Calculation of frontal arrest scale

Geostrophic adjustment theory predicts that the width of a front tends to follow the local deformation radius⁴⁶. But in the OSBL, strong turbulence breaks the geostrophic balance, and near-surface fronts are sharpened by strain-induced and surface-induced frontogenesis until they are arrested at a smaller scale by surface-forced turbulence, typically on a scale where TTW balance holds^12,47–49. Thus, the front width under TTW is believed to be the scale where the fronts in the OSBL are arrested and persistent. For the TTW balance,

$${\nabla }_{H}b=-f\mathbf{k}\times \frac{\partial \overline{\mathit{u}}}{\partial z}+\frac{{\partial }^2}{\partial z^2}\left(\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}\right)$$ 9

the Reynolds stress term can be parameterized as $\overline{{\mathbf{u}}^{\prime }{w}^{\prime }}={\left(m_{*}{u_{*}}^3+n_{*}{w_{*}}^3\right)}^{2/3}$ from the planetary boundary layer scheme (ePBL; Reichl and Hallberg⁵⁰). Thus, a scaling method for the arrested frontal width is proposed by Bodner et al. ²¹

$$L_f=C_L\frac{{\left(m_{*}{u_{*}}^3+n_{*}{w_{*}}^3\right)}^{2/3}}{f^{2}h}$$ 10

Here, only destabilizing surface buoyancy forcing that produces TKE is considered. Under the destabilizing condition, the mechanical coefficient m_* measures the efficiency of the mechanical forcing in changing OSBL TKE and is scaled by combining Equations (29) and (36) of Reichl and Hallberg⁵⁰ rather than a constant as in Bodner et al. ²¹, while the convection coefficient n_* = 0.066 measures the efficiency of the buoyancy forcing in changing OSBL TKE and is taken as a constant. $w_{*}={\left(B_{0}h\right)}^{1/3}$ is the convective velocity. f is the Coriolis parameter, h is the OSBL thickness, and C_L is a constant parameter. In this work, we decide to use a more conservative value of C_L = 1 based on a comparison with observations (refer to section Validation of the TKE model) instead of C_L = 0.25 suggested by Bodner et al. ²¹ based on a limited number of LES. Details are referred to Bodner et al. ²¹. Till now, no direct observations of arrested OSBL fronts have been reported globally. However, as discussed in Bodner et al. ²¹ and also compared with indirect observations⁵¹ and other LES results¹², the theory reproduces dynamically consistent frontal scale. The arrest scale here provides a dynamically lower bound of the frontal width for the buoyancy gradient rescaling, since not every OSBL front reaches its arrest scale in the real ocean.

The frontal width is calculated based on the LLC4320 outputs. We evaluate the robustness of that dataset using a simulation of upper ocean mixing without feedback using the General Ocean Turbulence Model (GOTM). GOTM is a one-dimensional water column model that is focused on ocean turbulence⁵². The version of GOTM used here is compiled with the ePBL closure^11,50. On each grid point of the subsampled 4^o LLC4320 grids, GOTM simulation is conducted for two months, February and August. The initial and boundary conditions are provided by LLC4320. For consistency, we also directly use the outputted sea surface fluxes from the simulation, which are provided by the ECMWF dataset. The vertical spacings of the simulations are as fine as centimeters, which ensures the capability of the GOTM in reproducing the OSBL. As Bodner et al. ²¹ proposed the frontal arrest scale based on the ePBL, we apply the ePBL scheme in the GOTM simulations. Hence, the frontal scale calculated from the GOTM outputs tends to be more dynamically consistent.

By comparing the frontal scales between the GOTM and LLC4320, we can estimate the sensitivity of the frontal width to the sub-grid turbulence closures (Supplementary Fig. 13). The frontal width over the globe varies across several orders of magnitude with latitude, from hundreds of meters to tens of kilometers. The frontal width is larger in summer than in winter. Despite using different sub-grid turbulence schemes (KPP in LLC4320 and ePBL in GOTM), the calculated frontal widths resemble each other which demonstrates that the frontal scale calculated here is insensitive to the turbulence closures. Finally, while the GSP and horizontal shear production of the fronts themselves should contribute somewhat to the turbulence causing the arrest, the robustness of the frontal width estimates to various TKE energy sources indicates these effects are unlikely to change the result significantly. These results indicates that the calculated frontal width is not sensitive to the details of the model and its chosen sub-grid turbulence closure.

Author contributions

J.D., B.F. and J.W. conceived the experiments, analyzed the results and wrote the manuscript. A.B. helped with the analysis of the numerical simulations. Y.X. helped with the analysis of the observations. J.D., B.F., J.W., A.B., S.B. and C.D. reviewed the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The LLC4320 data can be directly accessed from the ECCO Data Portal (https://data.nas.nasa.gov/ecco/data.php), or conveniently downloaded using the xmitgcm package (https://xmitgcm.readthedocs.io/en/latest/index.html). The Stokes drift of the ECMWF ERA5 is accessible at the Copernicus Climate Change Service (C3S) Climate Date Store (10.24381/cds.adbb2d47). The OSMOSIS data is available at the British Oceanographic Data Centre after registration (https://www.bodc.ac.uk/data/bodc_database/nodb/search/). The VIIRS L2 SST product is available at the JPL Physical Oceanography Distributed Active Archive Center (10.5067/GHVRS-2PO28). The data for reproducing the figures in the paper are available at 10.5281/zenodo.13954663⁵³.

Code availability

The codes used for generating the figures in the paper can be accessed at 10.5281/zenodo.13954663⁵³.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53959-y.