Abstract
The fabrication of fuel cells relies on a rapid laser welding process. However, challenges arise with the occurrence of humping when the welding speed surpasses a critical threshold, which poses difficulties in achieving a smooth surface finish and a consistent weld strength. This study aims to elucidate the humping mechanisms by analyzing the morphology of molten pool and the characteristics of melt flow at varying welding speeds via in situ synchrotron high-speed X-ray imaging and computational fluid dynamics simulations. Our findings indicate that the short keyhole rear wall, the high backward melt velocity, and the prolonged tail of molten pool are the primary factors contributing to the onset of humping. Furthermore, a dimensionless humping index () was introduced, which successfully captured the onset threshold of humping across different literatures. This index not only provides a quantitative description of the humping formation tendency but also serves as a valuable tool for optimizing the laser welding process.
Subject terms: Mechanical engineering, Materials for devices, Fluid dynamics, Metals and alloys
Humping defects in high-speed laser welding of stainless steel are investigated here using in situ synchrotron X-ray imaging and fluid dynamics simulations. High welding speeds cause a short keyhole rear wall, high backward melt velocity, and long molten pool tail, leading to humping.
Introduction
The laser welding process offers several advantages, including a small heat-affected zone, fast welding speed, and high flexibility in welding path design1. These benefits make it well-suited for fuel cell fabrication, which requires long and narrow welding paths between bipolar plates2,3. Thin foils are preferred for these plates as they can reduce weight4 and enable more complex channel designs5. Welding metal foils is also applied in other applications such as motor rotors and electronic device connectors6. While increasing the laser welding speed enhances productivity, the formation of humps is particularly a major issue that limits the maximum welding speed7–9. Humps manifest as severe periodic undulations along the top surface of the weld seam. They not only pose difficulties in achieving a smooth surface finish but also significantly deteriorate the weld strength by reducing the effective bonded region. In laser welding, the occurrence of humping is influenced by laser parameters such as laser welding speed, power, and spot diameter10. Interestingly, the issue of humping is not unique to laser welding. It is also encountered in other arc-based and laser-based processes, such as arc welding11–14, wire arc additive manufacturing15–17, and powder bed fusion18,19, as the moving speed of the heat source increases. It indicates that the mechanisms governing humping are associated with the heat and mass transfer in the molten pool (MP), regardless of its origin.
The current understanding of humping can be summarized as follows. First, it always occurs at the end of MP once a critical welding speed is exceeded. Second, the formation of humps is primarily linked to the high backward melt velocity created at a high welding speed, so lowering the heat input proves effective in eliminating humping17. The shallower inclination angle of the MP boundary also reduces the deceleration rate of the backward melt velocity7,9. Third, a high welding speed results in a long and narrow MP, which is more susceptible to Rayleigh instability20,21, where a cylinder liquid phase tends to fragment into multiple droplets as the length-to-width ratio increases. However, the above understandings primarily relied on simulations and assumptions, lacking real-time experimental validation. In addition, the existing understanding is predominantly qualitative rather than quantitative, posing challenges in predicting humping under diverse process conditions.
The analyses of keyhole and fluid dynamics during the laser welding process require in situ characterization techniques7,22–25 or numerical simulations9,13,20,26. Previous studies implemented a high-speed optical camera positioned from the top to capture optical images7,22 or vapor plume23 for studying keyhole dynamics. However, this method is limited in providing information solely on the tilting angle of the keyhole front wall and cannot capture the shape of the keyhole rear wall or trailing MP. Another approach involved using transparent glass on one side of the weld to observe the keyhole from a side view24, which, however, does not fully replicate real welding conditions. In this research, in situ high-speed synchrotron X-ray imaging was adopted to resolve the limitations mentioned above. This technique has been successfully employed to analyze keyhole instability27, morphology28, and pore formation mechanisms29,30 in additive manufacturing.
In this study, in situ high-speed synchrotron X-ray imaging was employed to investigate the humping phenomenon in high-speed laser welding. The geometries of the keyhole and MP offered a crucial understanding into the mechanisms of humping formation. Then, computational fluid dynamics (CFD) simulations were conducted to analyze the characteristics of melt flow within MP, where the streamlines and volumetric flow rates provide further insights into the effects of the MP tail on humping. Lastly, a dimensionless humping index for the laser welding process was developed. This index not only identified the onset threshold of humping across different references but also described the humping tendency. It can serve as a valuable tool to predict humping in laser welding and to optimize the laser welding process.
Results
In situ characterization of humping during high-speed laser welding
The in situ high-speed synchrotron X-ray observation of laser welding was carried out at beamline 32-ID-B at Argonne National Laboratory (ANL), using a ytterbium single-mode continuous wave fiber laser (YLR-500-AC) with a spot diameter of 43 µm. The tested material was an 85 µm-thick 439 stainless steel foil. Two foils were overlap-welded from the top while in situ X-ray images were acquired from the side. More details on the experimental setup can be found in the “Methods” section and Supplementary Fig. 1a. The corresponding power for each condition was determined beforehand at Edison Welding Institute (EWI) using a single-mode continuous wave laser (nLIGHT AFX-1000) with the same spot diameter (43 µm). The laser power was iteratively increased until full penetration was achieved, as shown in Fig. 1a. Full penetration is crucial in the fabrication of fuel cells to prevent leakage between channels. It is worth noting that due to the equipment setup at ANL, the fastest laser welding speed adopted was 1.42 m/s, slightly lower than the fastest speed used at EWI (1.50 m/s). The process parameters and the corresponding heat input were summarized in Supplementary Table 1. The appearances of the weld seams are presented in Fig. 1b, showing that the critical welding speed for the onset of humping is 1.00 m/s. While the number of humps slightly decreased as the welding speed increased beyond this threshold, the surface topography of the weld seams (Fig. 1c) revealed that the average height of humps increased from 40.73 ± 8.63 µm at 1.00 m/s to 58.70 ± 14.82 µm at 1.42 m/s. This observation suggests that the momentum of the backward melt flow continued to intensify with the welding speed, exacerbating the humping phenomenon. On the other hand, the T-peel strengths of the welds (defined as the load per unit length of weld) were tested following the configuration in refs. 31,32. Laser welds made at EWI were used because the sample size for in situ X-ray imaging was too small for mechanical testing. The results, presented in Supplementary Fig. 2, indicate that the T-peel strength decreased when the welding speed exceeded 1.00 m/s due to the occurrence of humping.
Fig. 1. Laser power determination and weld characterization.
a Corresponding laser powers at each welding speed determined at Edison Welding Institute (EWI) by incrementally increasing the laser power until full penetration was achieved. b Top surfaces of weld seams at the welding speeds of 0.33, 1.00, and 1.42 m/s obtained by optical microscopy. Note that the fastest speed was adopted as 1.42 m/s instead of 1.50 m/s due to the equipment setup at Argonne National Lab (ANL). c Surface topography of weld seams at 1.00 and 1.42 m/s obtained by optical profilometry, and the average hump height relative to the weld top surface.
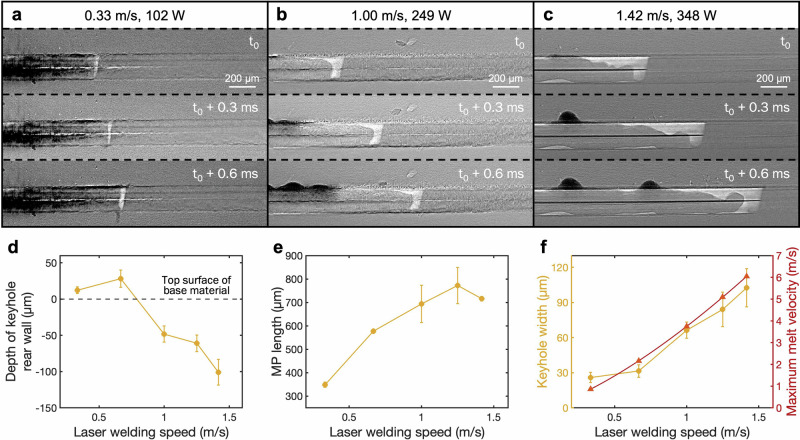
The results of in situ high-speed synchrotron X-ray observations are presented in Fig. 2a–c, where the keyhole and humping phenomena during laser welding were successfully captured. For a comprehensive view of all in situ observations for five different welding speeds, refer to Supplementary Movies 1–5. The moving speed of the keyhole recorded during the in situ observations was consistent with the set welding speed. A keyhole is a less dense space filled with dilute metal vapor compared to liquid MP, therefore providing sufficient contrast for X-ray observation. However, because of the small difference in the attenuation rates between the liquid and solid phases of stainless steel, the MP dimensions can only be measured from the fluctuating wavy patterns on the top surface. It is worth noting that the use of thin foils in this study prevented the formation of deep keyholes and deep-keyhole-induced porosity observed in other literatures29,30,33.
Fig. 2. In situ synchrotron X-ray observations and keyhole/molten pool measurements during laser welding.
a–c In situ high-speed synchrotron X-ray observations of laser welding at the welding speeds of 0.33, 1.00, and 1.42 m/s at times , , and ms, where was arbitrarily selected. See Supplementary Movies 1–5 for in situ observations at five different welding speeds. d Depth of keyhole rear wall. e Molten pool (MP) length. f Keyhole width (measured) and maximum melt velocity (, calculated by Eq. 1). The error bars in (d–f) represent the standard deviation, calculated from at least 3 measurements for each sample from the in situ observations.
Several key characteristics of the keyhole and MP geometries were quantified from the in situ X-ray observations to comprehend the humping mechanisms. First, the depth of the keyhole rear wall indicates the extent of the geometrical barrier to the backward melt flow, whereas a shorter keyhole rear wall suggests a reduced barrier to the backward melt flow. As the laser welding speed increased from 0.33 to 1.42 m/s (Fig. 2d), the depth of the keyhole rear wall gradually declined from 12.25 ± 4.50 µm to −100.82 ± 17.72 µm, which was significantly beneath the top surface.
Second, a longer MP length reduces the effectiveness of the MP tail to decelerate the melt flow. The MP length was determined as the average of the minimum instantaneous MP length observed in each humping cycle under conditions where humping occurred, which will be discussed in the following section and Fig. 3a. It increased from approximately 350 µm at laser welding speed of 0.33 m/s to the highest value of 770 µm when the laser welding speed reached 1.25 m/s, as shown in Fig. 2e. A prolonged MP not only suggests an increased propensity for humping based on the Rayleigh instability criterion20,21 but also indicates that it is ineffective in decelerating the backward volumetric flow. This phenomenon will be discussed in the section on CFD simulations.
Fig. 3. Analysis of humping cycle behavior.
a Instantaneous molten pool (MP) length on top surface and waviness of the front part of MP, with the starting periods of humping marked in gray. b Examples of MP waviness changes during humping. At the start of humping ( ms), the average MP waviness was lower. Near an end ( ms), the MP surface showed higher waviness because of the steeper gradient of the backward melt flow’s volumetric rate.
Third, a greater melt velocity increases the volumetric flow rate of the backward melt flow. In terms of melt flow velocity measurement, literatures reported adding W or Ta tracer particles during in situ X-ray experiments34–36. However, this approach is limited by the particle size relative to the MP dimensions and the feasibility of materials premixing. This approach has been applied in arc welding34 for its larger MP size and powder bed fusion35,36 where tracer particles were premixed with the powder bed. These experiments provided direct melt flow observations, and it should be noted that quantitative velocity measurements using a single X-ray source from a side view, producing 2D images, may be inaccurate as they may not fully capture the complexities of 3D flow dynamics.
Because of the limitation of using tracer particles in this research, the maximum melt velocity () was calculated by an analytical approach proposed by Beck et al.37 based on the continuity equation as follow:
| 1 |
where is the laser welding speed, is the specific heat, is the density, is the spot radius, is the thermal conductivity, and is the latent heat of fusion. , , are the boiling, melting, and room temperatures, respectively. Because occurs on the keyhole side wall, as described by Beck et al.37, the values of , , and are obtained at from the thermophysical databases11,38,39, which is listed in Supplementary Table 2. The was consistently simulated using CFD models, which will be discussed in Fig. 4a, b in the CFD simulation section. It is noted that among laser welding parameters, is related to the spot diameter and welding speed, however, not affected by the laser power based on this equation. The calculated result is shown in Fig. 2f, where significantly increases with the welding speed. Besides, the width of the keyhole, measured at the depth between two welded materials, was found to be correlated with the maximum melt velocity (Fig. 2f). This correlation is consistent with the assumption of this model, where occurs on the keyhole side wall and is predominantly horizontal. Therefore, a greater melt velocity leads to a more elongated keyhole.
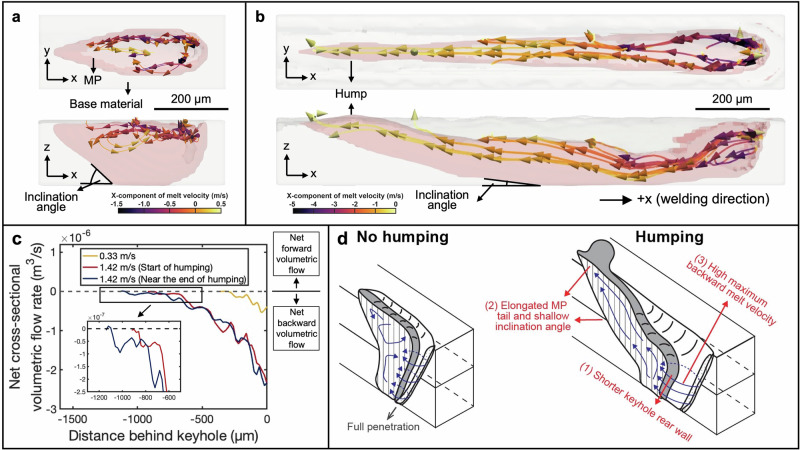
Fig. 4. CFD simulation and flow rate analysis on humping.
a, b Top and side views of streamlines extracted from CFD simulation results at the welding speeds of 0.33 and 1.42 m/s, respectively. c Net cross-sectional volumetric flow rate extracted from different distances of y-z cross-sections behind the keyhole at the welding speeds of 0.33 m/s, 1.42 m/s (start of humping), and 1.42 m/s (near the end of humping), respectively. An enlarged view highlights the curves around the molten pool (MP) tail at 1.42 m/s. d Schematic diagram showing the formation mechanisms of humping.
Periodic formation of humping
The occurrence of humps is periodic. Berger et al. first introduced the concept of conservation of volume flow to explain this phenomenon8, where the melt is incompressible, and the excessive melt is deflected upward at the end of MP to form a hump. Xue et al. conducted simulation9, proving that the melt accumulation and the Rayleigh instability collectively triggered the onset of humping. However, the above analyses were based on a high-speed optical camera from the top view8 or simulation9. Therefore, the in situ X-ray observation in this study provided clearer real-time observation of these phenomena.
The humping cycle was analyzed at the welding speed of 1.42 m/s with the instantaneous MP length on the top surface and the waviness of the front part of MP, as illustrated in Fig. 3a. The waviness is an indication of the gradient of volumetric flow rate, as a steeper gradient leads to a more excessive volume of backward melt and therefore a higher waviness. More details of their measurements can be found in the “Methods” section. Once the instantaneous MP length reached a minimum, a new hump was initiated because the MP tail cannot accommodate all backward melt flow at this moment. The humping served as an approach to release the excessive melt, slightly extending the instantaneous MP length on the surface. This period was defined as the start of humping, marked in gray in Fig. 3a. During this period, the front part of the MP showed minimal waviness as the release of melt reduced the gradient of volumetric melt flow. After humping started, the growth of the hump gradually slowed down. As a result, the release of melt became less effective despite the increasing MP length, leading to a higher MP waviness near the end of humping. Finally, when the instantaneous MP length reached another minimum, a new humping cycle was triggered, repeating the process and forming periodic humps. The current observation offers direct evidence supporting the humping theory based on the conservation of volume8.
Computational fluid dynamics (CFD) simulation
In situ high-speed synchrotron X-ray imaging provided crucial insights into the morphologies of keyhole and MP and their effects on humping formation in the laser welding process. Then, CFD simulation was conducted to quantitatively analyze the melt flow within MP. The 3D CFD model accounted for flow dynamics, eliminating the challenges of using 2D projected synchrotron X-ray images for velocity measurements. The details on the setup of CFD simulation can be found in the “Methods” section and Supplementary Fig. 3, and the material’s thermophysical properties can be found in Supplementary Fig. 4. The simulation was validated with the MP dimensions (length, width, depth) and the humping characteristics (linear number density and average height of humps), as summarized in Supplementary Table 3. The simulation successfully captured the shorter keyhole rear wall, shallower inclination angle of the MP boundary, and the more elongated keyhole along the welding direction at the higher welding speed, aligning well with the experimental findings from in situ high-speed synchrotron X-ray imaging.
Streamlines were then extracted from the simulation models using the Runge–Kutta integration method40 to visualize melt flow (Fig. 4, b). occurred on the keyhole side wall and gradually decelerated as the melt entered the trailing MP. At the welding speed of 0.33 m/s (Fig. 4a), the melt flow gradually diminished to zero at roughly the midpoint of MP and then re-entered the MP before the solidification front reached it. In contrast, at the welding speed of 1.42 m/s (Fig. 4b), the melt flow remained directed backward and could not return to the MP, so it eventually traversed the entire MP length and be deflected upward to form a hump (as highlighted in the blue streamlines).
The net cross-sectional volumetric flow rate (Fig. 4c), defined as the flow rates across the y-z cross-sections ( +x is the welding direction), accounts for the effects of melt velocity and melt volume. It provides a quantitative assessment of backward melt accumulation toward the MP tail. A negative value indicates that the net volumetric flow rate is in the -x direction (backward). At the welding speed of 0.33 m/s, the flow rate was relatively low (~) at the front of the MP and nearly zero at the MP tail. At the welding speed of 1.42 m/s, the flow rate became more negative (~) at the front of the MP and remained negative across the entire MP, indicating greater melt accumulation toward the MP tail and leading to humping. In addition, the gradient of the volumetric flow rate decreased from the front to the rear of the MP, suggesting that the elongated MP tail could not effectively slow down the backward melt flow due to the shallow inclination angle of the MP boundary (Fig. 4b). The flow rates were then extracted at the start and near the end of humping to understand its periodic nature. At the start (blue curve in Fig. 4c), the entire MP exhibited a significant net backward volumetric all the way to the MP tail, leading to humping. Conversely, near the end of humping (orange curve in Fig. 4c), the MP length extended by approximately 200 µm and possessed a near-zero net volumetric flow rate (enlarged view in Fig. 4c). It created additional volume in the MP tail to accommodate the melt, resulting in a gradual stop of humping. This periodic humping, characterized by alternating melt accumulation and MP length extension, is consistent with the conservation of volume8 and the experimental observations in this study.
Based on the analyses of in situ high-speed synchrotron X-ray imaging and CFD simulation, the formation mechanisms of humping are illustrated in Fig. 4d. First, as the laser welding speed increases, the depth of the keyhole rear wall becomes deeper beneath the surface of the base material, reducing the barrier to backward melt flow. Second, the MP length extends with the laser welding speed, failing to decelerate the melt flow effectively because of the shallower inclination angle and becoming more prone to Rayleigh instability. Third, the maximum backward melt velocity also rises significantly, increasing the volumetric flow toward the MP tail. These factors enhance backward melt velocity and reduce the flow barrier, leading to greater melt accumulation at the MP tail and triggering humping. When humping occurs, excess melt is released by slightly extending the MP length, which causes the humping to cease temporarily. Therefore, the phenomenon occurs periodically rather than continuously.
Development of index for humping tendency
The prediction of humping in laser welding usually relies on simulation. Alternatively, a dimensionless index can be developed to calculate the humping tendency based solely on process parameters and material properties. This approach is simpler and more efficient since it eliminates the need for complex fluid dynamics calculations. Meng et al.41 have introduced the dimensionless humping index for the arc welding process, but its application to laser welding is limited due to inherent disparities between the two processes. In addition, laser welding lacks certain MP characteristics present in arc welding, such as temperature increase and gouging length.
The Buckingham theorem was first employed to determine the number of dimensionless groups, where a system with variables and fundamental units can be described by dimensionless groups. In this study, there are 6 variables, i.e., maximum melt velocity (), MP length (), density (), specific heat (), thermal conductivity (), and surface tension coefficient (). It is noted that the depth of the keyhole rear wall was not included as a variable, because it is correlated with the MP length (Fig. 2d, e). The above 6 variables involve 4 fundamental units, which are mass (), length (), time (), and temperature (). Therefore, the theorem suggests two dimensionless groups representing the system as follows.
| 2 |
| 3 |
is the Peclet number (Pe)42, which indicates the relative importance of convection and conduction in heat transfer within the melt pool. is the Weber number, representing the free surface deformation tendency41. Note that all materials properties were extracted at the melting (liquidus) temperature from the thermophysical databases11,38,39 and were listed in Supplementary Table 2, given that the temperature at the end of MP is close to the liquidus temperature.
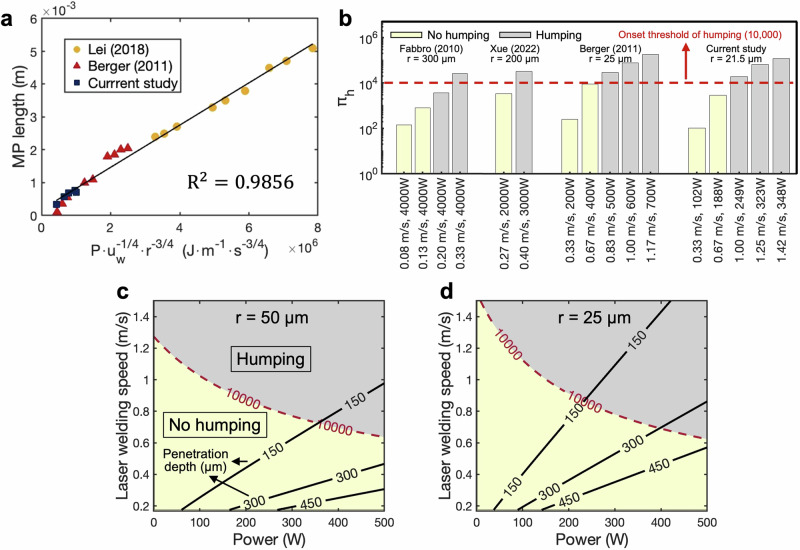
and can be calculated with only the process parameters (: spot radius, : laser welding speed, : power) and material properties (, , , and ). was calculated by Eq. 1, with the calculation results shown in Fig. 2f. For the MP dimensions (depth and length), the scaling law was adopted. Studies have reported that the MP depth can be scaled with 22,43 for the same material. The scaling of MP length () has not been previously reported due to its requirement of in situ observation. In this work, linear fitting was performed with experimental data and literature data8,44, as shown in Fig. 5a, following the equation:
| 4 |
Fig. 5. Humping threshold analysis using dimensionless humping index (πh).
a Scaling law between the MP length and ( = 0.9856) performed using the experimental results from the current study and other literatures8,44. b Calculated dimensionless humping index . The onset threshold occurs at approximately 10,000 across different published data8,9,22. c, d Process windows with (light yellow) and without humping (light gray) separated by the 10,000-isoline of and penetration depth calculated by scaling law22,43 at the spot radii () of 50 and 25 µm, respectively.
This relationship has the highest value (0.9856) among all exponent combinations for each process parameter. The MP length was determined as the average minimum instantaneous MP length in each humping cycle (Fig. 3a). It is noted that the scaling law for the MP length is slightly different from the case for the MP depth (scaled with ).
Multiple combinations of and can be formed; however, a simple product of them can form the dimensionless humping index ().
| 5 |
The values of , , , and were obtained at from the thermophysical databases11,38,39, as listed in Supplementary Table 2. Both and were obtained from Eqs. 1 and 4, respectively, rather than from the simulation results. The calculated results using the data from the current study and other references8,9,22 are shown in Fig. 5b. This dimensionless humping index captures the onset threshold at approximately 10,000 of and describes the humping tendency. It is also in good agreement with the study from Kawahito et al.10, where among the process parameters (,, and ), the humping tendency increases with a higher , a greater , and a finer when the other two parameters are fixed. It also aligns well with the conclusions from the in situ high-speed synchrotron X-ray imaging and CFD simulation, where a longer or a greater increases the humping tendency.
In addition, the model allows for the prediction of the critical laser welding speed and the corresponding power where humping begins to occur. Figure 5c, d shows the isolines of several penetration depths and the 10,000-isoline of calculated at = 50 and 25 µm, respectively. The intersection points between each penetration depth and the 10,000-isoline of represent the critical laser welding speeds and power. The model suggests several methods to enhance the critical laser welding speed for the same material system by reducing . The first approach is to employ a finer , which requires a lower for the same penetration depth. As a result, both and decrease, as indicated by Eqs. 1 and 4, leading to a reduced and an increased critical laser welding speed. By comparing Fig. 5c with Fig. 5d, it is evident that the critical welding speed increases from 0.72 to 0.87 m/s at a penetration depth of 150 µm when is reduced from 50 to 25 µm. In this study, the experimental results for spot radii of 21.5 and 13 µm are presented in Supplementary Fig. 5. The second approach is to reduce the thickness of the base material, which lowers the required for full penetration and consequently decreases because of the reduced and (Eqs. 1 and 4). As shown in Fig. 5d, the critical welding speed increases from 0.68 to 0.87 m/s at =25 µm when the thickness is reduced from 300 to 150 µm. The third approach is to employ an adjustable ring mode laser45,46, where a portion of the power is distributed to the outer ring. It allows the power of the central beam to be decreased while maintaining the same penetration depth, leading to a shorter (Eq. 4), a reduced , and therefore a greater critical laser welding speed.
Humping is an issue that occurs not only in laser welding but also in arc welding and additive manufacturing at a high-moving speed of heat source. This study identified the formation mechanisms of humping by analyzing keyhole and MP morphologies and melt flow characteristics at various welding speeds via in situ high-speed synchrotron X-ray imaging and CFD simulation. The mechanisms are concluded as follows. First, a high welding speed leads to a shorter keyhole rear wall, therefore reducing the barrier to the backward melt flow. Second, a prolonged MP tail at a high welding speed is not only ineffective in decelerating the backward melt flow owing to the shallower inclination angle but also susceptible to Rayleigh’s instability. Third, the maximum backward melt velocity increases substantially with the welding speed, leading to a significant increase in the backward volumetric flow rate of melt. These factors collectively enhance the melt accumulation towards the MP tail, ultimately causing humping. In addition, humping occurs periodically rather than continuously because of the alternating accumulation of excessive melt at the start of humping and the extension of the MP length when humping is near its end.
Lastly, a dimensionless humping index () was developed for the laser welding process using Buckingham’s π theorem. This index, based solely on process parameters and material properties, quantitatively depicts humping formation tendency and serves as a crucial tool for optimizing laser welding by predicting critical laser welding speed and power. It also suggests several approaches to enhance the critical welding speed through reducing , including reducing the spot radius, decreasing the thickness of base material, and utilizing an adjustable ring mode laser.
Methods
In situ high-speed synchrotron X-ray imaging and laser welding
In situ high-speed synchrotron X-ray imaging of laser welding was conducted at beamline 32-ID-B at ANL using a ytterbium single-mode continuous wave fiber laser source (YLR-500-AC) with a spot size of 43 µm, a wavelength of 1070 ± 10 nm, a maximum power of 520 W, and an X–Y galvo-scanner (intelliSCANde 30). The experimental setup is presented in Supplementary Fig. 1a, b. The laser welding configuration involved overlapping two vertically stacked stainless steel foils welded from the top. An Al alloy fixture was designed to clamp the foils and prevent movement, featuring a 300 µm-wide opening for the laser (Supplementary Fig. 1b). The Al alloy was chosen for its lower X-ray attenuation compared to steel47. A pseudo pink X-ray beam, with the 1st harmonic energy at 24.7 keV, was generated using an 18 mm undulator and directed through the sample from the side during the laser welding process. The propagated X-ray signal was recorded with a high-speed camera (Photron FastCam SA–Z) at a frame rate of 50,000 (temporal resolution = 20 µs). The tested material was an 85 µm-thick 439 stainless steel (Cleveland Steel, USA). The specimens were cut by electrical discharge machining into the dimension in Supplementary Fig. 1c, with a gauge width of only 500 µm due to the high extent of attenuation of X-ray on stainless steels.
Laser welding at EWI was performed using a single-mode continuous wave fiber laser (nLIGHT AFX-1000) with the same spot diameter (43 µm) and wavelength (1070 ± 10 nm) as that used at ANL. The laser has a maximum power of 550 W and is equipped with an X–Y galvo-scanner (Scanlab HurryScan20).
Image processing and quantification
The in situ X-ray images were processed by using ImageJ. Two different approaches to image processing were employed for the following purposes. In the first approach, each image was subtracted by the average of the initial 50 images to reveal the change of contrast during the welding process compared to the initial condition. For the second approach, each image was successively subtracted by the preceding time frame, revealing the contrast variations between two consecutive time frames, and providing a clearer visualization of the MP lengths on the top surfaces. Following both methods, the brightness and contrast of images were modified manually to enhance the image contrast.
The boundaries of the keyhole and MP were first manually delineated, followed by interpolation using MATLAB to achieve smooth boundaries. The dividing point between the keyhole and MP was defined as the initial point on the keyhole rear wall with a slope of −1. The z coordinate at this point was defined as the depth of the keyhole rear wall. Then, the region between this point and the one 350 µm behind the keyhole front wall was defined as the front part of MP. This curve was then linearly fitted, with its root mean square error defined as the MP waviness.
Optical micrograph and surface topography
The top surfaces of laser weld seams were characterized by optical micrography and profilometry using Keyence VX–X3100. The laser confocal method was employed to measure the surface topography of the weld seams. To calibrate the weld seam into a horizontal surface, the measurements were adjusted using quadratic correction based on the positional data from the base materials adjacent to the weld seam.
CFD simulation modeling
The simulation of the laser welding process was performed using CFD modeling with Flow-3D under the following assumptions: (1) The melt flow was laminar, incompressible, and Newtonian. (2) The plasma inside the keyhole and the spattering were not considered. (3) No heat or mass transfer occurred at any faces of the simulation domain. The dimensions of the simulation domain are depicted in Supplementary Fig. 3a, consisting of uniformly divided cubic grids with an edge length of 10 µm. The domain lengths were set to 3 and 8 mm for welding speeds of 0.33 and 1.42 m/s, resulting in a total number of 384,000 and 1,536,000 cells, respectively. Laser welding was conducted in the +x direction, with lengths of 2 and 7 mm corresponding to the respective welding speeds. The laser beam, with a spot diameter of 43 µm, was considered a surface heat source, which is a method commonly used in other studies9,18,38,48–50 to simulate laser-material interaction. In this heat source, the heat flux was divided into each mesh, following the Gaussian distribution shown in Supplementary Fig. 3b. The laser beam was reflected and absorbed based on the material absorptivity48.
The coupled governing equations in the CFD modeling included conservation of momentum, energy, and continuity48. Laser absorption, thermal conduction, surface radiation, and convection were incorporated for energy calculation. The temperature-dependent laser absorptivity data were acquired from the reference51, and the temperature-dependent physical properties were obtained from references11,38,39, as shown in Supplementary Fig. 4. The recoil pressure was temperature-dependent, following with a = 6000 Pa and b = 652. The primary forces considered in the model included recoil pressure, surface tension, viscosity, buoyancy, and gravity. Additional details regarding the force setup can be found in ref. 52.
The validation of the CFD simulation models was performed based on the MP dimensions (length, width, depth) and the humping characteristics (linear number density and average height of humps), as listed in Supplementary Table 3. The differences of each key metric between experiments and simulations were all below 10%. Additionally, the showed a good agreement between the analytical calculation (Eq. 1) and the CFD simulations, as listed in Supplementary Table 4.
Supplementary information
Description of Additional Supplementary Files
Source data
Acknowledgements
This material is based upon work supported by the U.S. Department of Energy’s Office of Energy Efficiency and Renewable Energy (EERE) under the Hydrogen and Fuel Cell Technologies Office Award Number DE-EE0009616. This research used resources of the Advanced Photon Source, a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The authors would like to thank the experimental support from Alex Deriy at the 32-ID beamline. We also acknowledge Zixuan Wan’s support for the discussions on CFD simulation. The views expressed herein do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Author contributions
S.X. and J.L. conceived and supervised the project. S.J.C., K.F., and Z.L. led and conducted the experiments. Z.L. performed image analyses (with the help from S.J.C., K.F., J.L., and S.X.) and CFD simulation. Z.L. and J.L. wrote the manuscript.
Peer review
Peer review information
Nature Communications thanks Van Anh Nguyen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files. Source data are provided with this paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-53888-w.
References
- 1.Katayama, S. Handbook of Laser Welding Technologies (Elsevier, 2013).
- 2.Haddad, E. et al. Laser micro welding with fiber lasers for battery and fuel cell based electromobility. J. Adv. Join. Processes5, 100085 (2022). [Google Scholar]
- 3.Yi, P., Du, X., Kan, Y., Peng, L. & Lai, X. Modeling and experimental study of laser welding distortion of thin metallic bipolar plates for PEM fuel cells. Int. J. Hydrog. Energy40, 4850–4860 (2015). [Google Scholar]
- 4.Tawfik, H., Hung, Y. & Mahajan, D. Metal bipolar plates for PEM fuel cell—a review. J. Power Sources163, 755–767 (2007). [Google Scholar]
- 5.Barzegari, M. M. & Khatir, F. A. Study of thickness distribution and dimensional accuracy of stamped metallic bipolar plates. Int. J. Hydrog. Energy44, 31360–31371 (2019). [Google Scholar]
- 6.Manh, N. H. et al. Development of a novel GTAW process for joining ultra-thin metal sheets. J. Manuf. Processes80, 683–691 (2022). [Google Scholar]
- 7.Ai, Y. et al. Investigation of the humping formation in the high power and high speed laser welding. Opt. Lasers Eng.107, 102–111 (2018). [Google Scholar]
- 8.Berger, P., Hügel, H., Hess, A., Weber, R. & Graf, T. Understanding of humping based on conservation of volume flow. Phys. Procedia12, 232–240 (2011). [Google Scholar]
- 9.Xue, B. et al. Humping formation and suppression in high-speed laser welding. Materials15, 2420 (2022). [DOI] [PMC free article] [PubMed]
- 10.Kawahito, Y., Mizutani, M. & Katayama, S. High quality welding of stainless steel with 10 kW high power fibre laser. Sci. Technol. Weld. Join.14, 288–294 (2009). [Google Scholar]
- 11.Meng, X., Qin, G. & Zou, Z. Investigation of humping defect in high speed gas tungsten arc welding by numerical modelling. Mater. Des.94, 69–78 (2016). [Google Scholar]
- 12.Nguyen, T. C., Weckman, D. C., Johnson, D. A. & Kerr, H. W. The humping phenomenon during high speed gas metal arc welding. Sci. Technol. Weld. Join.10, 447–459 (2005). [Google Scholar]
- 13.Wu, D., Hua, X., Ye, D. & Li, F. Understanding of humping formation and suppression mechanisms using the numerical simulation. Int. J. Heat Mass Transf.104, 634–643 (2017). [Google Scholar]
- 14.Soderstrom, E. & Mendez, P. Humping mechanisms present in high speed welding. Sci. Technol. Weld. Join.11, 572–579 (2006). [Google Scholar]
- 15.Yuan, L. et al. Investigation of humping phenomenon for the multi-directional robotic wire and arc additive manufacturing. Robot Comput. Integr. Manuf.63, 101916 (2020). [Google Scholar]
- 16.Yuan, L. et al. Fabrication of metallic parts with overhanging structures using the robotic wire arc additive manufacturing. J. Manuf. Processes63, 24–34 (2021). [Google Scholar]
- 17.Koli, Y., Yuvaraj, N., Sivanandam, A. & Vipin Control of humping phenomenon and analyzing mechanical properties of Al–Si wire-arc additive manufacturing fabricated samples using cold metal transfer process. Proc. Inst. Mech. Eng. C. J. Mech. Eng. Sci.236, 984–996 (2021). [Google Scholar]
- 18.Tang, C., Le, K. Q. & Wong, C. H. Physics of humping formation in laser powder bed fusion. Int. J. Heat Mass Transf.149, 119172 (2020). [Google Scholar]
- 19.Bhatt, A. et al. In situ characterisation of surface roughness and its amplification during multilayer single-track laser powder bed fusion additive manufacturing. Addit. Manuf.77, 103809 (2023). [Google Scholar]
- 20.Gratzke, U., Kapadia, P. D., Dowden, J., Kroos, J. & Simon, G. Theoretical approach to the humping phenomenon in welding processes. J. Phys. D Appl. Phys.25, 1640 (1992). [Google Scholar]
- 21.Ai, Y., Liu, X., Huang, Y. & Yu, L. Numerical analysis of the influence of molten pool instability on the weld formation during the high speed fiber laser welding. Int. J. Heat Mass Transf.160, 120103 (2020). [Google Scholar]
- 22.Fabbro, R. Melt pool and keyhole behaviour analysis for deep penetration laser welding. J. Phys. D Appl. Phys.43, 445501 (2010). [Google Scholar]
- 23.Xue, B., Chang, B. & Du, D. Monitoring of high-speed laser welding process based on vapor plume. Opt. Laser Technol.147, 107649 (2022). [Google Scholar]
- 24.Zhang, D. et al. Dynamic keyhole behavior and keyhole instability in high power fiber laser welding of stainless steel. Opt. Laser Technol.114, 1–9 (2019). [Google Scholar]
- 25.Van Nguyen, A., Tashiro, S., Ngo, M. H., Van Bui, H. & Tanaka, M. Effect of the eddies formed inside a weld pool on welding defects during plasma keyhole arc welding. J. Manuf. Processes59, 649–657 (2020). [Google Scholar]
- 26.Wang, L., Wu, C., Chen, J. & Gao, J. Influence of the external magnetic field on fluid flow, temperature profile and humping bead in high speed gas metal arc welding. Int. J. Heat Mass Transf.116, 1282–1291 (2018). [Google Scholar]
- 27.Gan, Z. et al. Universal scaling laws of keyhole stability and porosity in 3D printing of metals. Nat. Commun.12, 2379 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cunningham, R. et al. Keyhole threshold and morphology in laser melting revealed by ultrahigh-speed x-ray imaging. Science363, 849–852 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Huang, Y. et al. Keyhole fluctuation and pore formation mechanisms during laser powder bed fusion additive manufacturing. Nat. Commun.13, 1170 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhao, C. et al. Critical instability at moving keyhole tip generates porosity in laser melting. Science370, 1080–1086 (2020). [DOI] [PubMed] [Google Scholar]
- 31.Standard Test Method for Peel Resistance of Adhesives (T-Peel Test). ASTM D1876, American Society for Testing and Materials. (2015).
- 32.Das, A., Fritz, R., Finuf, M. & Masters, I. Blue laser welding of multi-layered AISI 316L stainless steel micro-foils. Opt. Laser Technol.132, 106498 (2020). [Google Scholar]
- 33.Bayat, M. et al. Keyhole-induced porosities in laser-based powder bed fusion (L-PBF) of Ti6Al4V: high-fidelity modelling and experimental validation. Addit. Manuf.30, 100835 (2019). [Google Scholar]
- 34.Aucott, L. et al. Revealing internal flow behaviour in arc welding and additive manufacturing of metals. Nat. Commun.9, 5414 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Guo, Q. et al. Revealing melt flow instabilities in laser powder bed fusion additive manufacturing of aluminum alloy via in-situ high-speed X-ray imaging. Int. J. Mach. Tools Manuf.175, 103861 (2022). [Google Scholar]
- 36.Hojjatzadeh, S. M. H. et al. Pore elimination mechanisms during 3D printing of metals. Nat. Commun.10, 3088 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Beck, M., Berger, P., Dausinger, F. & Huegel, H. Aspects of keyhole/melt interaction in high-speed laser welding. Proc. SPIE1397, 769–774 (1991). [Google Scholar]
- 38.Chen, N. et al. Microstructural characteristics and crack formation in additively manufactured bimetal material of 316L stainless steel and Inconel 625. Addit. Manuf.32, 101037 (2020). [Google Scholar]
- 39.Kim, C. S. Thermophysical Properties of Stainless Steels (Argonne National Lab., Ill, USA, 1975).
- 40.Wischgoll, T. & Scheuermann, G. Detection and visualization of closed streamlines in planar flows. IEEE Trans. Vis. Comput. Graph.7, 165–172 (2001). [Google Scholar]
- 41.Meng, X., Qin, G. & Zou, Z. Characterization of molten pool behavior and humping formation tendency in high-speed gas tungsten arc welding. Int. J. Heat Mass Transf.117, 508–516 (2018). [Google Scholar]
- 42.van Elsen, M., Al‐Bender, F. & Kruth, J. Application of dimensional analysis to selective laser melting. Rapid Prototyp. J.14, 15–22 (2008). [Google Scholar]
- 43.Rubenchik, A. M., King, W. E. & Wu, S. S. Scaling laws for the additive manufacturing. J. Mater. Process. Technol.257, 234–243 (2018). [Google Scholar]
- 44.Lei, T., Rong, Y., Xu, J. & Huang, Y. Experiment study and regression analysis of molten pool in laser welding. Opt. Laser Technol.108, 534–541 (2018). [Google Scholar]
- 45.Wang, L., Gao, X. & Kong, F. Keyhole dynamic status and spatter behavior during welding of stainless steel with adjustable-ring mode laser beam. J. Manuf. Processes74, 201–219 (2022). [Google Scholar]
- 46.Li, J., Jiang, P., Geng, S. & Xiong, J. Numerical and experimental study on keyhole dynamics and pore formation mechanisms during adjustable-ring-mode laser welding of medium-thick aluminum alloy. Int. J. Heat Mass Transf.214, 124443 (2023). [Google Scholar]
- 47.Jackson, D. F. & Hawkes, D. J. X-ray attenuation coefficients of elements and mixtures. Phys. Rep.70, 169–233 (1981). [Google Scholar]
- 48.Dal, M. & Fabbro, R. [INVITED] An overview of the state of art in laser welding simulation. Opt. Laser Technol.78, 2–14 (2016). [Google Scholar]
- 49.Cho, W.-I., Na, S.-J., Thomy, C. & Vollertsen, F. Numerical simulation of molten pool dynamics in high power disk laser welding. J. Mater. Process. Technol.212, 262–275 (2012). [Google Scholar]
- 50.Lee, Y. & Farson, D. F. Simulation of transport phenomena and melt pool shape for multiple layer additive manufacturing. J. Laser Appl.28, 012006 (2015). [Google Scholar]
- 51.Kwon, H., Baek, W.-K., Kim, M.-S., Shin, W.-S. & Yoh, J. J. Temperature-dependent absorptance of painted aluminum, stainless steel 304, and titanium for 1.07μm and 10.6μm laser beams. Opt. Lasers Eng.50, 114–121 (2012). [Google Scholar]
- 52.Wan, Z. et al. Novel measures for spatter prediction in laser welding of thin-gage zinc-coated steel. Int. J. Heat Mass Transf.167, 120830 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Files
Data Availability Statement
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files. Source data are provided with this paper.