Luck, skill, and depth of competition in games and social hierarchies

Abstract

Patterns of wins and lo sses in pairwise contests, such as occur in sports and games, consumer research and paired comparison studies, and human and animal social hierarchies, are commonly analyzed using probabilistic models that allow one to quantify the strength of competitors or predict the outcome of future contests. Here, we generalize this approach to incorporate two additional features: an element of randomness or luck that leads to upset wins, and a “depth of competition” variable that measures the complexity of a game or hierarchy. Fitting the resulting model, we estimate depth and luck in a range of games, sports, and social situations. In general, we find that social competition tends to be “deep,” meaning it has a pronounced hierarchy with many distinct levels, but also that there is often a nonzero chance of an upset victory. Competition in sports and games, by contrast, tends to be shallow, and in most cases, there is little evidence of upset wins.

Competition is more intense in human social hierarchies than in sports leagues, but less than in animal hierarchies.

INTRODUCTION

One of the oldest and best-studied problems in data science is the ranking of a set of items, individuals, or teams based on the results of pairwise comparisons between them. Such problems arise in sports, games, and other competitive human interactions; in paired comparison surveys in market research and consumer choice; in revealed-preference studies of human behavior; and in studies of social hierarchies in both humans and animals. In each of these settings, one has a set of comparisons between pairs of items or competitors, with outcomes of the form “A beats B” or “A is preferred to B,” and the goal is to determine a ranking of competitors from best to worst, allowing for the fact that the data may be sparse (there may be no data for many pairs) or contradictory (e.g., A beats B beats C beats A). A group of chess players might play in a tournament, for example, and record wins and losses against each other. Consumers might express preferences between pairs of competing products, either directly in a survey or implicitly through their purchases or other actions. A flock of chickens might peck each other as a researcher records who pecked whom to establish the classic “pecking order.”

A large number of methods have been proposed for solving ranking problems of this kind—see (1–3) for reviews. Here, we consider one of the most common, which uses a statistical model for wins and losses and then fits that model to observed win/loss data. In the most widely adopted version, one considers a population of n competitors labeled by i = 1…n and assigns to each a real score parameter s_i ∈ [−∞, ∞]. Then the probability that i beats j in a single pairwise match or contest is assumed to be some function of the difference of their scores: p_ij = f(s_i−s_j). The score function f(s) satisfies the following axioms:

1) It is increasing in s, because, by definition, a better competitor has a higher probability of winning than a worse one.

2) It tends to 1 as s → ∞ and to 0 as s →−∞, meaning that an infinitely good player always wins and an infinitely poor one always loses.

3) It is antisymmetric about its midpoint at s = 0, with the form

$$f(-s)=1-f(s)$$ (1)

because the probability of losing is one minus the probability of winning. As a corollary, this also implies that the probability f(0) of beating an evenly matched opponent is always $\frac{1}{2}$.

Subject to these constraints, the function can still take a wide variety of forms, but the most popular choice by far is the logistic function f(s) = 1/(1 + e^−s)—shown as the bold curve in Fig. 1A—which gives

$$f(s_i-s_j)=\frac{e^{s_i}}{e^{s_i}+e^{s_j}}$$ (2)

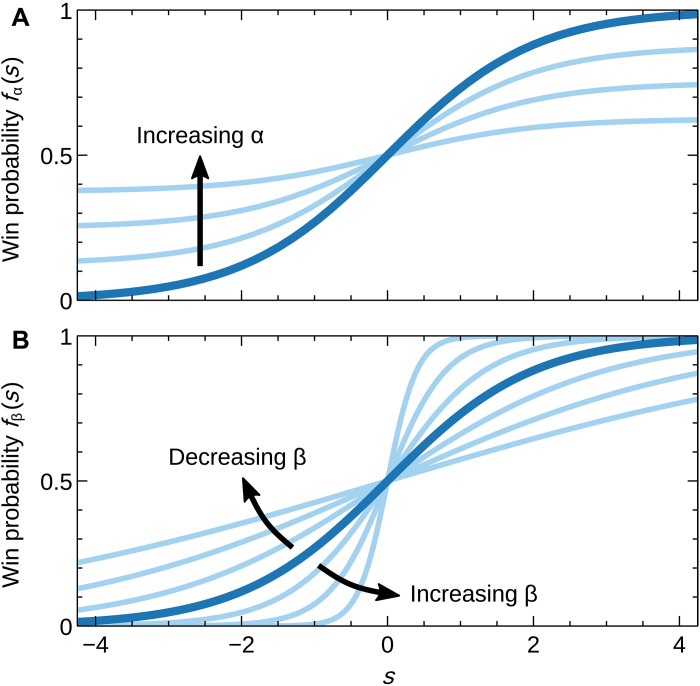
Fig. 1. Score functions.

(A) The bold curve represents the standard logistic function f(s) = 1/(1 + e^−s) used in the Bradley-Terry model. The remaining curves show the function f_α of Eq. 8 for increasing values of the luck parameter α. (B) The score function f_β of Eq. 9 for different values of the depth of competition β, both greater than 1 (steeper) and less than 1 (shallower).

The resulting model is known as the Bradley-Terry model, after R. Bradley and M. Terry who described it in 1952 (4), although it was (unknown to them) first introduced much earlier, by Zermelo in 1929 (5).

Given the model, one can estimate the values of the score parameters s_i by a number of standard methods, including maximum likelihood estimation (4–8), maximum a posteriori estimation (9), or Bayesian methods (10, 11), then rank competitors from best to worst in order of their scores. The fitted model can also be used to predict the outcome of future contests between any pair of competitors, even if they have never directly competed in the past.

This approach is effective and widely used, but the standard Bradley-Terry model is a simplistic representation of the patterns of actual competition and omits many important elements found in real-world interactions. Generalizations of the model have been proposed that incorporate some of these elements, such as the possibility of ties or draws between competitors (12, 13), multiway competition as in a horse race (14, 15), the “home-field advantage” of playing on your own turf (16), or multidimensional score parameters that allow for intransitive win probabilities between competitors (17, 18). Here, we consider a further extension of the model that incorporates two additional features of particular interest, which have received comparatively little previous attention: the element of luck inherent for instance in games of chance, and the notion of “depth of competition,” which captures the complexity of games or the number of distinct levels in a social hierarchy. In the remainder of the paper, we define and motivate this model and then describe a Bayesian approach for fitting it to data, which we use to infer the values of the luck and depth variables for a variety of real-world datasets drawn from different arenas of human and animal competition. Our results suggest that social hierarchies are in general deeper and may have a larger element of luck to their dynamics than recreational games and sports, which tend to be shallower and show little evidence of a luck component.

Software implementations of the various methods described in this paper are available at https://github.com/maxjerdee/pairwise-ranking and https://doi.org/10.5061/dryad.kh18932fc.

THE MODEL

Suppose we observe m matches between n players. The outcomes of the matches can be represented by an n × n matrix A with element A_ij equal to the number of times player i beats player j. Within the standard Bradley-Terry model, the probability of a win is given by Eq. 2 and, assuming the matches to be statistically independent, the probability or likelihood of the complete set of observed outcomes is

$$P(\mathit{A}\mid \mathit{s})={\displaystyle \prod _{\mathit{ij}}}f{(s_i-s_j)}^{A_{\mathit{ij}}}={\displaystyle \prod _{\mathit{ij}}}{\left(\frac{e^{s_i}}{e^{s_i}+e^{s_j}}\right)}^{A_{\mathit{ij}}}$$ (3)

where s is the vector with elements s_i and terms that only depend on the data A have been dropped. (We assume that the structure of the tournament—who plays whom—is determined separately, so that Eq. 3 is a distribution over the directions of the wins and losses only and not over which pairs of players competed.)

The scores are traditionally estimated by the method of maximum likelihood, maximizing Eq. 3 with respect to all s_i simultaneously to give estimates

$$\widehat{\mathit{s}}={\text{argmax}}_{\mathit{s}}P(\mathit{A}\mid \mathit{s})$$ (4)

These maximum likelihood estimates (MLEs) can then be sorted to give a ranking of the competitors, or simply reported as measures of strength in their own right. The widely used Elo ranking system for chess players, for example, is essentially a version of this approach, but extended to allow for dynamic updates as new matches are added to the dataset.

The maximum likelihood approach unfortunately has some drawbacks. For one, the likelihood is invariant under a uniform additive shift of all scores s_i and hence the scores are not strictly identifiable, though this issue can easily be fixed by normalization. A more serious problem is that the likelihood maximum does not exist at all unless the network of interactions—the directed network with adjacency matrix A—is strongly connected (meaning there is a directed chain of victories from any player to any other), and the maximum likelihood estimation procedure fails, with the divergence of some or all of the scores, unless this relatively stringent condition is met.

This issue can be addressed by introducing a prior on the scores and adopting a Bayesian perspective. A variety of potential priors for this purpose have been systematically examined by Whelan (9), who, after careful consideration, recommends a Gaussian prior with mean zero. The variance is arbitrary—it merely sets the scale on which the score s is measured—but for subsequent convenience, we here choose a variance of $\frac{1}{2}$ so that the prior on s takes the form

$$P(\mathit{s})={\displaystyle \prod _{i=1}^n}\frac{1}{\sqrt{\mathrm{\pi }}} e^{-s_i^2}$$ (5)

An alternative prior, also recommended by Whelan, is the logistic distribution

$$P_L(\mathit{s})={\displaystyle \prod _{i=1}^n}\frac{1}{(1+e^{s_i})(1+e^{-s_i})}$$ (6)

In practice, the Gaussian and logistic distributions are similar in shape and the choice of one or the other does not make a great deal of difference. The logistic distribution is perhaps the less natural of the two and we primarily use the Gaussian distribution here, but the logistic distribution does have the advantage of leading to faster numerical algorithms and we have used it in previous work for this reason (8, 19). We also include it in the basket of models that we compare the section on predicting wins and losses.

Once we have defined a prior on the scores, we can calculate a maximum a posteriori (MAP) estimate of their values as

$$\widehat{\mathit{s}}={\text{argmax}}_{\mathit{s}}P(\mathit{s}\mid \mathit{A})={\text{argmax}}_{\mathit{s}}P(\mathit{A}\mid \mathit{s})P(\mathit{s})$$ (7)

The MAP estimate always exists regardless of whether the interaction network is strongly connected, and using a prior also eliminates the invariance of the probability under an additive shift and hence the need for normalization. As an alternative to computing a MAP estimate, we can also simply return the full posterior distribution P(s ∣ A), which gives us complete information on the expected values and uncertainty of the scores given the observed data.

EXTENSIONS OF THE MODEL

In this section, we define generalizations of the Bradley-Terry model that extend the score function f in two useful ways, while keeping other aspects of the model fixed, including the normal prior. The specific generalizations we consider involve dilation or contraction of the score function in the vertical and horizontal directions. Vertical variation controls the element of luck that allows a weak player to sometimes beat a strong one; horizontal variation controls the depth of competition, a measure of the complexity of a game or contest.

Upset wins and luck

The first generalization of the Bradley-Terry model that we consider is one where the function f is contracted in the vertical direction, as shown in Fig. 1A. We parameterize this function in the form

$$f_{\mathrm{\alpha }}(s)=\frac{1}{2}\mathrm{\alpha }+(1-\mathrm{\alpha })\frac{1}{1+e^{-s}}$$ (8)

with α ∈ [0,1]. In the traditional Bradley-Terry model, f(s) tends to 0 and 1 as s → ±∞, as discussed in Introduction, but in the modified model with α > 0, this is no longer the case. One can think of the parameter α as controlling the probability of an “upset win” in which an infinitely good player loses or an infinitely bad player wins. (The probabilities of these two events must be the same because of the antisymmetry condition, Eq. 1.)

For some games or competitions it is reasonable that f(s) tends to zero and one at the limits. In a game like chess that has no element of randomness, an infinitely good player may indeed win every time. In a game of pure luck like roulette, on the other hand, both players have equal probability $\frac{1}{2}$ of winning, regardless of skill. These two cases correspond to the extreme values α = 0 and α = 1, respectively, in Eq. 8. Values in between represent games that combine both luck and skill, like poker or backgammon, with the precise value of α representing the proportion of luck. For this reason, we refer to α as the luck parameter, or simply the “luck.”

One could also consider the chance of the weaker player winning in the standard Bradley-Terry model to be an example of luck or an upset win, but that is not how we use these words here. In the present context, the luck α describes the probability of winning the game even if one’s opponent is infinitely good, which is zero in the standard model but nonzero in the model of Eq. 8 with α > 0.

Another way to think about α is to imagine a game as a mixture of a luck portion and a skill portion. With probability α, the players play a game of pure chance in which the winner is chosen at random, for instance, by the toss of a coin. Alternatively, with probability 1−α, they play a game of skill, such as chess, and the winner is chosen with the standard Bradley-Terry probability. The overall probability of winning is then given by Eq. 8 and the parameter α represents the fraction of time the game is decided by pure luck. By fitting Eq. 8 to observed win-loss data, we can learn the luck inherent in a competition or hierarchy. We do this for a variety of datasets in the Results section.

Depth of competition

The second generalization we consider is one where the function f is dilated or contracted in the horizontal direction, as shown in Fig. 1B, by a uniform factor β > 0; thus

$$f_{\mathrm{\beta }}(s)=\frac{1}{1+e^{-\mathrm{\beta s}}}$$ (9)

The slope of this function at s = 0 is given by

$$f{\prime }_{\mathrm{\beta }}(0)={\left[\frac{\mathrm{\beta }{e}^{-\mathrm{\beta s}}}{{(1+e^{-\mathrm{\beta s}})}^2}\right]}_{s=0}=\frac{1}{4}\mathrm{\beta }$$ (10)

so β is simply proportional to the slope. A more functional way of thinking about β is in terms of the probability that the stronger of a typical pair of competitors will win. With a normal prior on s of variance $\frac{1}{2}$ as in Eq. 5, the difference s_i − s_j between the scores of a randomly chosen pair of competitors will be a priori normally distributed with variance 1, meaning the scores will be separated by an average (root mean square) distance of 1. Consider two players separated by this average distance. If β is small, making f_β a relatively flat function (the shallowest curve in Fig. 1B), the probability p_ij of the stronger player winning will be close to $\frac{1}{2}$ and there is a substantial chance that the weaker player will win. Conversely, if β is large, then p_ij will be close to 1 (the steepest curve in Fig. 1B) and the stronger player is very likely to prevail.

Thus, one way to understand the parameter β is as a measure of the imbalance in strength or skill between the average pair of players. When β is large, the contestants in the average game are very unevenly matched. As we will shortly see, this is a common situation in social hierarchies, but not in sports and games, perhaps because contests between unevenly matched opponents are less rewarding both for spectators and for the competitors themselves.

Another way to think about β is in terms of the number of levels of skill or strength in a competition. Suppose we define one “level” as the distance Δs = s_i − s_j between scores such that i beats j with a certain probability q. For a win probability of the form of Eq. 9, we have q = 1/(1 + e^−βΔs), and hence

$$\mathrm{\Delta }s=\frac{1}{\mathrm{\beta }}\text{log}\frac{q}{1-q}$$ (11)

Considering again the typical pair of players a distance 1 apart, the number of levels between them is

$$\frac{1}{\mathrm{\Delta }s}=\frac{\mathrm{\beta }}{\text{log}[q/(1-q)]}$$ (12)

Thus, the number of levels is simply proportional to β. Let us choose the probability q such that the constant of proportionality is 1, meaning log[q/(1 − q)] = 1 or

$$q=\frac{1}{1+e^{-1}}=0.731$$ (13)

With this definition, a level is the skill difference Δs between two players such that the better one wins 73% of the time and our parameter β is simply equal to the number of such levels between the average pair of players.

In this interpretation, β can be thought of as a measure of the complexity or depth of a game or competition. A “deep” game, in this sense, is one that can be played at many levels, with players at each level markedly better than those at the level below. Chess, which is played at a wide range of skill levels from beginner to grandmaster, might be an example.

This concept of depth has a long history. For example, in an article in the trade publication Inside Backgammon in 1992 (20), world backgammon champion W. Robertie defined a “skill differential” as the strength difference between two players that results in the better one winning 70 to 75% of the time—precisely our definition of a level—and the “complexity number” of a sport or game as the number of such skill differentials that separate the best player from the worst. Cauwet et al. (21) have defined a similar but more formal measure of game depth that they call “playing-level complexity.” There has also been discussion in the animal behavior literature of the “steepness” of animal dominance hierarchies (22), which appears to correspond to roughly the same idea.

One should be careful about the details. Robertie and Cauwet et al. both define their measures in terms of the skill range between the best and worst players, but this could be problematic in that the range will depend on the particular sample of players one has and will tend to increase as the sample size gets larger, which seems undesirable. Our definition avoids this by considering not the best and worst players in a competition but the average pair of players, which gives a depth measure that is asymptotically independent of sample size.

Even when defined in this way, however, the number of levels is not solely about the intrinsic complexity of the game, but does also depend on who is competing. For example, if a certain competition is restricted to contestants who all fall in a narrow skill range, then β will be small even for a complex game. In a world-class chess tournament, for instance, where every player is an international master or better, the number of levels of play will be relatively small although chess as a whole has many levels. Thus, empirical values of β combine aspects of the complexity of the game with aspects of the competing population.

For this reason, we avoid terms such as complexity number and “depth of game” that imply a focus on the game alone and refer to β instead as the depth of competition, which we feel better reflects its meaning. (A variety of alternative notions of depth are discussed in section S5.)

Combined model

Combining both the luck and depth of competition variables into a single model gives us the score function

$$f_{\mathrm{\alpha \beta }}(s)=\frac{1}{2}\mathrm{\alpha }+(1-\mathrm{\alpha })\frac{1}{1+e^{-\mathrm{\beta s}}}$$ (14)

In the Results, we fit this form to observed data from a range of different areas of study to infer the values of α and β. In the process, one can also infer the scores s_i, which can be used to rank the participants or predict the outcome of unobserved contests, and we explore this angle later in the paper. In this section, however, our primary focus is on α and β and on understanding the varying levels of luck and depth in different kinds of competition.

To perform the fit, we consider again a dataset represented by its adjacency matrix A and write the data likelihood in the form of Eq. 3

$$P(\mathit{A}\mid \mathit{s},\mathrm{\alpha },\mathrm{\beta })={\displaystyle \prod _{\mathit{ij}}}{f}_{\mathrm{\alpha \beta }}{(s_i-s_j)}^{A_{\mathit{ij}}}$$ (15)

The scores s are assumed to have the Gaussian prior of Eq. 5, and we assume a uniform (least informative) prior on α, which means P(α) = 1. We cannot use a uniform prior on β, because it has infinite support, so instead we use a prior that is approximately uniform over “reasonable” values of β and decays in some slow but integrable manner outside this range. A suitable choice in the present case is (the positive half of) a Cauchy distribution centered at zero

$$P(\mathrm{\beta })=\frac{2w/\mathrm{\pi }}{{\mathrm{\beta }}^2+w^2}$$ (16)

where w controls the scale on which the function decays. Here we use w = 4, which roughly corresponds to the range of variation in β that we see in real-world datasets, and has the convenient property of giving a uniform prior on the angle of f_β(s) at the origin.

It is worth mentioning that the choice of prior on β does have an effect on the results in some cases. When datasets are large and dense, priors tend to have relatively little impact because the posterior distribution is narrowly peaked around the same set of values no matter what choice we make. However, some of the datasets we study here are quite sparse, and for these, the results can vary with the choice of prior. Our qualitative conclusions remain the same in all cases, but it is worth bearing in mind that the quantitative details can change.

Combining the likelihood and priors, we now have

$$P(\mathit{s},\mathrm{\alpha },\mathrm{\beta }\mid \mathit{A})=P(\mathit{A}\mid \mathit{s},\mathrm{\alpha },\mathrm{\beta })\frac{P(\mathrm{\alpha })P(\mathrm{\beta })P(\mathit{s})}{P(\mathit{A})}$$ (17)

The prior on A is unknown but constant, so it can be ignored. We now draw from the distribution P(s, α, β ∣ A) to obtain a representative sample of values s, α, β. In our calculations, we generate the samples using the Hamiltonian Monte Carlo method (23) as implemented in the probabilistic programming language Stan (24), which is ideal for sampling from continuous parameter spaces such as this. The running time to obtain the samples depends on the computational cost per iteration, which is proportional to the number of matches m, and on the Monte Carlo mixing time, which is roughly proportional to the number of competitors n. The total running time thus scales roughly as O(mn). In practice, a few thousand samples are sufficient to get a good picture of the distribution of α and β, which, in our implementation, takes anywhere from a few seconds to an hour or so for our largest datasets.

Minimum violations ranking

One special case of our model worth mentioning is the limit β → ∞ for fixed α > 0. In this limit, the function f_αβ(s) becomes a step function with value

$$f_{\mathrm{\alpha },\infty }(s)=\left\{\begin{array}{cc}\frac{1}{2}\mathrm{\alpha }\hfill & \text{if} s<0,\hfill \\ \frac{1}{2}\hfill & \text{if} s=0,\hfill \\ 1-\frac{1}{2}\mathrm{\alpha }\hfill & \text{if} s>0.\hfill \end{array}\right.$$ (18)

For this choice, the data likelihood becomes

$$P(\mathit{A}\mid \mathit{s},\mathrm{\alpha },\mathrm{\beta })={\left(\frac{1}{2}\mathrm{\alpha }\right)}^v{(1-\frac{1}{2}\mathrm{\alpha })}^{m-v}$$ (19)

where m is the total number of games/interactions/comparisons and v is the number of “violations,” meaning games where the weaker player won. Then, the log-likelihood is

$$\begin{array}{c}\text{log} P(\mathit{A}\mid \mathit{s},\mathrm{\alpha },\mathrm{\beta })=-v \text{log}\frac{1-\frac{1}{2}\mathrm{\alpha }}{\frac{1}{2}\mathrm{\alpha }}+m \text{log}(1-\frac{1}{2}\mathrm{\alpha })\\ =-\mathit{Av}-B\end{array}$$ (20)

where A and B are positive constants. This log-likelihood is maximized when the number of violations v is minimized, which leads to the so-called minimum violations ranking, the ranking such that the minimum number of games are won by the weaker player. Thus, the minimum violations ranking can be thought of as the limit of our model in the special case where β → ∞.

RESULTS

We have applied these methods to a range of datasets representing competition in sports and games as well as social hierarchies in both humans and animals. The datasets we study are listed in Table 1.

Table 1. Datasets in order of increasing depth of competition $\widehat{\mathrm{\beta }}$.

Here, n is the number of participants and m is the number of matches/interactions. Further information on the datasets is given in the section S1.

	Dataset	$\widehat{\mathrm{\beta }}$	n	m	Description	Ref.
Sports/games	Scrabble	0.68	587	23,477	Scrabble tournament matches 2004–2008	(26)
	Basketball	1.01	240	10,002	National Basketball Association games 2015–2022	(27)
	Chess	1.17	917	7,007	Online chess games on lichess.com in 2016	(28)
	Tennis	1.44	1,272	29,397	Association of Tennis Professionals men’s matches 2010–2019	(29)
	Soccer	1.73	1,976	7,208	Men’s international association football matches 2010–2019	(30)
	Video games	1.77	125	1,951	Super Smash Bros Melee tournament matches in 2022	(31)
Human	Friends	3.54	774	2,799	High-school friend nominations	(32)
	CS departments	4.25	205	4,388	Doctoral graduates of one department hired as faculty in another	(33)
	Business schools	4.36	112	7,856	Doctoral graduates of one department hired as faculty in another	(33)
Animal	Vervet monkeys	6.01	41	2,930	Dominance interactions among a group of wild vervet monkeys	(34)
	Dogs	8.74	27	1,143	Aggressive behaviors in a group of domestic dogs	(35)
	Baboons	13.19	53	4,464	Dominance interactions among a group of captive baboons	(36)
	Sparrows	22.92	26	1,238	Attacks and avoidances among sparrows in captivity	(37)
	Mice	26.48	30	1,230	Dominance interactions among mice in captivity	(38)
	Hyenas	100.58	29	1,913	Dominance interactions among hyenas in captivity	(39)

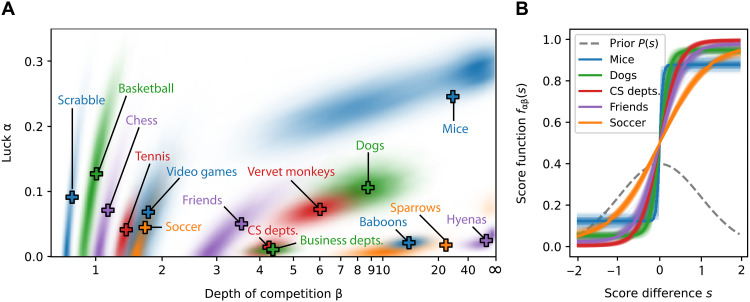
Figure 2A summarizes our results for the posterior probability density of the luck and depth parameters. The axes of the figure indicate the values of α and β and each cloud is an estimate of P(α, β ∣ A), computed as a kernel density estimate from Monte Carlo sampled values of α and β. The + signs in the figure represent the mean values of α and β for each dataset computed directly by averaging the samples.

Fig. 2. Posterior distributions of luck and depth, and fitted score functions.

(A) Each cloud represents the posterior distribution P(α, β ∣ A) of the luck and depth parameters for a single dataset, calculated from the Monte Carlo sampled values of α and β using a Gaussian kernel density estimate. The + signs indicate the expected values $\widehat{\mathrm{\alpha }},\widehat{\mathrm{\beta }}$ of the parameters for each dataset. (B) The bold curve in each case corresponds to the expected values $\widehat{\mathrm{\alpha }},\widehat{\mathrm{\beta }}$, while the other surrounding curves are for a selection of values sampled from the posterior distribution, to give an idea of the variation around the average.

The figure reveals some interesting trends. Note first that all of the sports and games—chess, basketball, video games, etc.—appear on the left-hand side of the plot in the region of low depth of competition, while all the social hierarchies are on the right with higher depth. We conjecture that the low depth of the sports and games is a result of a preference for matches to be between roughly evenly matched opponents, as discussed in the “Depth of competition” section. For a game to be entertaining to play or watch, the outcome of matches should not be too predictable, but in a sport or league with high depth, the average pairing is very uneven, with the stronger player very likely to win. Low depth of competition ensures that matches are unpredictable and hence entertaining. In games such as chess, which have high intrinsic depth, the depth can be reduced by restricting tournaments to players in a narrow skill range, such as world-class players, and this is commonly done in many sports and games. We explore this interpretation further in section S5.

There are no such considerations at play in social hierarchies. Such hierarchies are not, by and large, spectator sports, and there is nothing to stop them having high depth of competition. The results in Fig. 2A indicate that in general they do, though the animal hierarchies are deeper than the human ones. A high depth in this context indicates a hierarchy in which the order of dominance between the typical pair of competitors is clear. This accords with the conventional wisdom concerning hierarchies of both humans and animals, where it appears that participants are in general clear about the rank ordering.

Another distinction that emerges from Fig. 2A is that the results for sports and games generally do not give strong support to a nonzero luck parameter. The expected values, indicated by the + signs, are nonzero in most cases, but the clouds representing the posterior distributions give significant weight to points close to the α = 0 line, indicating that we cannot rule out the possibility that α = 0 in these competitions. For many of the social hierarchies, on the other hand, there is strong evidence for a nonzero amount of luck, with the posterior distribution having most of its weight well away from α = 0, a finding that accords with our intuition about social hierarchies. There would be little point in having any competition at all within a social hierarchy if the outcomes of all contests were foregone. If participants knew that every competitive interaction was going to end with the higher-ranked individual winning and the lower-ranked one backing down, then there would be no reason to compete. It is only because there is a significant chance of a win that competition occurs at all.

An interesting counter-example to this observation comes from the two faculty hierarchies, which represent hiring practices at US universities and colleges. The interactions in this dataset indicate when one university hires a faculty candidate who received their doctoral training at another university, which is considered a win for the university where the candidate trained. The high depth of competition and low luck parameter for these datasets indicates that there is a pronounced hierarchy of hiring with a clear pecking order and that the pecking order is rarely violated. Lower-ranked universities hire the graduates of higher-ranked ones, but the reverse rarely happens.

Figure 2B shows a selection of the fitted functions f_αβ(s) for five of the datasets. For each dataset, we show in bold the curve for the expected values $\widehat{\mathrm{\alpha }},\widehat{\mathrm{\beta }}$ along with 10 other curves for values of α, β sampled from the posterior distribution, to give an indication of the amount of variation around the average. We see, for example, that the curve for the soccer dataset has a shallow slope (low depth of competition) but is close to zero and one at the limits (low luck). The curve for the mice dataset, by contrast, is steep (high depth) but clearly has limits well away from zero and one (nonzero luck).

Luck and parameter identifiability

Inherent in the view of competition that underlies our model are two different types of randomness. There is the randomness inherent in the probabilistic nature of the model: Even when one player is better than the other, there is always a chance they may lose, so long as the players’ levels of skill are not too severely imbalanced. However, there is also the randomness introduced by the luck parameter, which applies no matter how imbalanced the players are, even if one is infinitely better than the other.

In a low-depth situation, it can be difficult to distinguish between these two types of randomness. When depth is low, there are few (or no) players who are very good or very bad, so there are few matches where a good player is unequivocally observed to lose because of the element of luck. In mathematical terms, the score function f(s) in a low-depth competition is shallow in its central portion, close to the origin, and moreover, it is only this portion that gets probed by the matches, because there are few contests between badly mismatched players. However, a score function with a shallow center can be generated either by a large value of α or a small value of β—the functional forms are very similar either way.

In practice, this means that the values of α and β suffer from poor identifiability in this low-depth regime. This is visible in Fig. 2A as the long, thin probability clouds of the sports and games on the left-hand side of the plot. For these, there is a set of parameter value pairs α, β that fall roughly along a curve in the plot and that all have similar posterior probability, and hence, it becomes difficult to pin down the true parameter values. This phenomenon particularly affects the luck parameter α, whose spread is so broad in this regime that we cannot reliably determine whether it is nonzero.

As depth increases, on the other hand, we expect that there will be a larger number of competitors who are either very strong or very weak, and from the outcomes of their matches, we can determine the level of luck with more certainty. This is reflected in the distributions on the right of Fig. 2A, for many of which it is possible to say clearly that α is nonzero.

An alternative view of the same behavior is that the long thin probability clouds in the figure imply the existence of a particular combination of luck and depth that is narrowly constrained for each dataset, and an orthogonal combination that is highly uncertain. In section S6, we define a measure of “predictability” of competition in terms of the amount of information needed to communicate the outcomes of all matches in a dataset and show that this predictability corresponds precisely to the narrowly defined direction in the figure, so that predictability can be estimated accurately in all cases, even when there is considerable uncertainty about the raw parameters α and β.

Predicting wins and losses

In addition to allowing us to infer the luck and depth parameters and rank competitors, our model can also be used to predict the outcomes of unobserved matches. If we fit the model to data from a group of competitors, we can use the fitted model to predict the winner of a new contest between two of those same competitors. The ability to accurately perform such predictions can form the basis for consumer product recommendations and marketing, algorithms for guiding competitive strategies in sports and games, and the setting of odds for betting, among other things.

We can test the performance of our model in this prediction task using a cross-validation approach. For any dataset A, we randomly remove or “hold out” a small portion of the matches or interactions and then fit the model to the remaining “training” dataset. Then, we use the fitted model to predict the outcome of the held-out matches and compare the results with the actual outcomes of those same matches.

The simplest version of this calculation involves fitting our model to the training data by making point estimates of the parameters and scores. We first estimate the expected posterior values $\widehat{\mathrm{\alpha }},\widehat{\mathrm{\beta }}$ of the parameters given the training data. Then, given these parameter values, we maximize the posterior probability as a function of s to obtain MAP estimates $\widehat{\mathit{s}}$ of the scores. Last, we use the combined parameter values and scores to calculate the probability ${\widehat{p}}_{\mathit{ij}}=f_{\widehat{\mathrm{\alpha }}\widehat{\mathrm{\beta }}}({\widehat{s}}_i-{\widehat{s}}_j)$ that a held-out match between i and j was won by i, with f_αβ(s) as in Eq. 14. Further discussion of the procedure is given in section S3.

We can quantify the performance of our predictions by computing the log-likelihood of the actual outcomes of the held-out matches under the predicted probabilities ${\widehat{p}}_{\mathit{ij}}$. If W_ij is the number of times that i actually won against j, then the log-likelihood per game is

$$Q=\frac{{\sum }_{\mathit{ij}}{W}_{\mathit{ij}} \text{log} {\widehat{p}}_{\mathit{ij}}}{{\sum }_{\mathit{ij}}{W}_{\mathit{ij}}}$$ (21)

This measure naturally rewards cases where the model is confident in the correct answer (${\widehat{p}}_{\mathit{ij}}$ close to 1) and heavily penalizes cases where the model is confident in the wrong answer (${\widehat{p}}_{\mathit{ij}}$ close to 0). Note that the log-likelihood is equal to minus the description length of the data—the amount of information needed to describe the true sequence of wins and losses in the held-out data given the estimated probabilities ${\widehat{p}}_{\mathit{ij}}$—so models with high log-likelihood are more parsimonious in describing the true pattern of wins and losses. (An alternative way to quantify performance would be simply to compute the fraction of correct predictions made by each model. Some results from this approach are given in section S2, and are largely in agreement with the results for log-likelihood.)

To place the performance of our proposed model in context, we compare it against a basket of other ranking models and methods, including widely used standards, some recently proposed approaches, and some variants of the approach proposed in this paper. As a baseline, we compare performance against the standard Bradley-Terry model with a logistic prior, which is commonly used in many ranking tasks, particularly in sports, and which we have ourselves used and recommended in the past (8). We measure the performance of all other models against this one by calculating the difference in the log-likelihood per match (Eq. 21). The other models we test are as follows:

1) The luck-plus-depth model of this paper.

2) A depth-only variant in which the parameter α is set to zero.

3) A luck-only variant in which the parameter β is set to ∞, which is equivalent to minimum violations ranking.

4) The Bradley-Terry model under maximum likelihood estimation, which is equivalent to imposing an improper uniform prior. Note that maximum likelihood estimates diverge if a player wins (or loses) all of their matches, and to avoid this, in keeping with previous work (25), we impose a very weak L2 regularization of the scores, which is equivalent to a MAP estimate with Gaussian prior of width σ = 100.

5) The “SpringRank” model of De Bacco et al. (25), which ranks competitors using a physically motivated mass-and-spring model.

This is a representative selection of ranking models but not comprehensive, excluding for instance models that incorporate information beyond wins and losses, and multidimensional models (17, 18). The proportion of data held out in the cross-validation was 20% in all cases, chosen uniformly at random, and at least 50 random repetitions of the complete process were performed for each model for each of the datasets listed in Table 1.

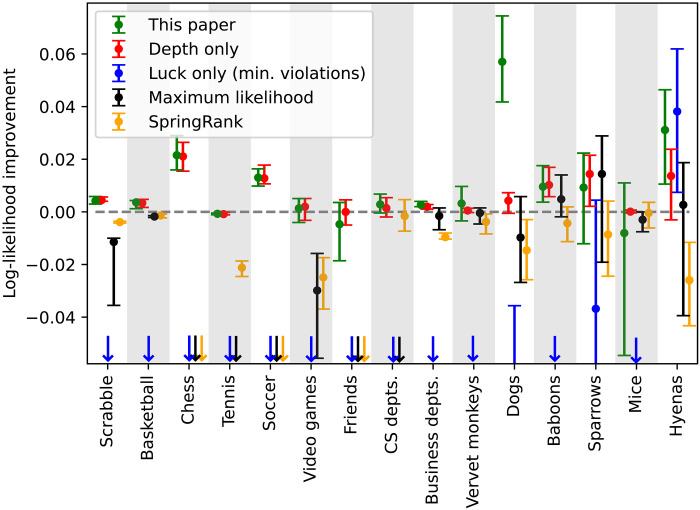
The results are summarized in Fig. 3. The horizontal dashed line in the figure represents the baseline set by the Bradley-Terry model and the points with error bars represent the increase (or decrease) in log-likelihood relative to this level for each model and dataset. The error bars represent the upper and lower quartiles of variation of the results over the random repetitions. (We use quartiles rather than standard deviations because the distributions are highly nonnormal in some cases.)

Fig. 3. Comparative performance of the method of this paper and a selection of competing methods.

Performance is measured in terms of the log-likelihood (base 2) of the actual outcomes of matches within the fitted model, which is also equal to minus the description length in bits required to transmit the win/loss data given the fitted model. Log-likelihoods are plotted relative to that of the standard Bradley-Terry model with a logistic prior (the horizontal dashed line). Error bars represent upper and lower quartiles over at least 50 random repetitions of the cross-validation procedure in each case. The arrows along the bottom of the plot indicate cases where the log-likelihood is outside the range of the plot.

We note a number of things about these results. First, the model of this paper performs best on our tests for every dataset without exception, within the statistical uncertainty, although the depth-only version of the model is also competitive in many cases, particularly for the sports and games. The latter observation is unsurprising, because, as we have said, there is little evidence for α > 0 in the games. For the particular case of the dominance hierarchy of hyenas, the minimum violations ranking is competitive, which is also unsurprising: As shown in Fig. 2, this hierarchy is very deep—the value of β is over 100—and hence there is little difference between our model and the minimum violations ranking. For all the other datasets, the minimum violations ranking performs worse—usually much worse—than our model. (Arrows at the bottom of the figure indicate results so poor they fall off the bottom of the scale.) The maximum likelihood fit to the Bradley-Terry model also performs quite poorly, a notable observation given that this is one of the most popular ranking algorithms in many settings. It even performs markedly worse than the same Bradley-Terry model with a logistic prior. Last, we note that the SpringRank algorithm of (25) is relatively competitive in these tests, though it still falls short of the model of this paper and the standard Bradley-Terry model with logistic prior.

As mentioned above, our selection of models excludes multidimensional models, which have substantially larger parameter spaces and allow for a wider range of behaviors, such as intransitive competition, and which could, in principle, provide better fits to the data. In other tests (not shown here), we found one such model, the blade-chest model of Chen and Joachims (17), that outperforms our model on four of the animal datasets (dogs, baboons, sparrows, and hyenas), although it performs poorly in most other cases. This could suggest the presence of intransitivity in these datasets.

DISCUSSION

Here, we have studied the ranking of competitors based on pairwise comparisons between them, as happens for instance in sports, games, and social hierarchies. Building on the standard Bradley-Terry ranking model, we have extended the model to include two additional features: an element of luck that allows weak competitors to occasionally beat strong ones, and a depth of competition parameter that captures the number of distinguishable levels of play in a hierarchy. Deep hierarchies with many levels correspond to complex games or social structures. We have fitted the proposed model to datasets representing social hierarchies among both humans and animals and a range of sports and games, including chess, basketball, soccer, and video games. The fits give us estimates of the luck and depth of competition in each of these examples and we find a clear pattern in the results: sports and games tend to have shallow depth and little evidence of a luck component, while social hierarchies are significantly deeper and more often have an element of luck, with the animal hierarchies being deeper than the human ones.

We also test our model’s ability to predict the outcome of contests. Using a cross-validation approach, we find that the model performs as well as or better than every other model tested in predictive tasks and very significantly better than the most common previous methods such as maximum likelihood fits to the Bradley-Terry model or minimum violations rankings.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S4

Table S1

References