Electronic and magnetic excitations in La₃Ni₂O₇

Abstract

High-temperature superconductivity was discovered in the pressurized nickelate La₃Ni₂O₇ which has a unique bilayer structure and mixed valence state of nickel. The properties at ambient pressure contain crucial information of the fundamental interactions and bosons mediating superconducting pairing. Here, using X-ray absorption spectroscopy and resonant inelastic X-ray scattering, we identified that Ni 3$d_{x^2-y^2}$, Ni 3$d_{z^2}$, and ligand oxygen 2p orbitals dominate the low-energy physics with a small charge-transfer energy. Well-defined optical-like magnetic excitations soften into quasi-static spin-density-wave ordering, evidencing the strong electronic correlation and rich magnetic properties. Based on an effective Heisenberg spin model, we extract a much stronger inter-layer effective magnetic superexchange than the intra-layer ones and propose two viable magnetic structures. Our findings emphasize that the Ni 3$d_{z^2}$ orbital bonding within the bilayer induces novel electronic and magnetic excitations, setting the stage for further exploration of La₃Ni₂O₇ superconductor.

It was recently found that a certain nickelate compound, La₃Ni₂O₇, at moderately high pressures has a superconducting phase that persists to above liquid nitrogen temperatures. Here, by studying the parent phase at ambient pressure, Chen et al uncover rich magnetic properties and show the vital role of the strong bonding of the inter-layer Ni orbitals in the magnetic and electronic excitations.

Introduction

The striking discovery of high-temperature superconductivity (HTSC) at 80 K in a bilayer nickelate La₃Ni₂O₇ under a pressure of about 14 GPa ignited a new wave of studying HTSC in nickelates^1–7. Unlike cuprate superconductors with a Cu²⁺ 3d⁹ electron configuration, La₃Ni₂O₇ hosts Ni ions with mixed 2 + (3d⁸) and 3 + (3d⁷) valences with unpaired electrons in both 3$d_{x^2-y^2}$ and 3$d_{z^2}$ orbitals from a Ni-O bilayer structure^1,2,8–13. In particular, the molecular bonding between the two inter-layer Ni 3$d_{z^2}$ orbitals through the apical O p_z orbital, together with Ni 3$d_{x^2-y^2}$ orbitals, are proposed by theory as a critical ingredient for the low-energy electronic structure of La₃Ni₂O₇^2,8–22. The orbital character governing the electronic properties of the unconventional superconductors is essential for understanding the underlying pairing mechanism. In cuprates, the small charge-transfer energy and strong hybridisation between Cu 3$d_{x^2-y^2}$ and O 2p orbitals lead to the formation of the strongly correlated Zhang-Rice singlet band, which serves as the foundation for describing the electronic properties including the superconducting pairing interaction with $d_{x^2-y^2}$ symmetry²³. On the other hand, the iron-based superconductors feature relatively weaker correlation and multiple 3d bands near the Fermi surface²⁴. The orbital-dependent correlation and the strong anisotropy in the electronic hopping result in a distinct s pairing symmetry. At first sight, La₃Ni₂O₇ appears to be a sibling of iron-based superconductors owing to the multi-orbital nature and the bad metallicity in the undoped parental phase. However, perovskite nickelates are also known to exhibit strong electronic correlation and small charge-transfer energy^25,26, resembling cuprates. Theories to date vary in their opinions on which orbitals are most relevant for the electronic properties, especially the superconductivity, in La₃Ni₂O₇^8,9,15–22.

The antiferromagnetic (AFM) superexchange interaction is accepted as another important ingredient of unconventional superconductors. Upon the doping of charge carriers, the long-range AFM-ordered parental phase evolves into one with short-range AFM spin fluctuations, which may mediate the superconducting pairing. In a sizable part of the phase diagram, the interplay among spin, charge, and lattice degrees of freedom often leads to exotic ordering phases such as the periodic density modulation of charge or spin. In cuprates and iron-based superconductors, charge (CDW) and spin density waves (SDW) intertwine with superconducting phase which is regarded as being closely relevant to HTSC^23,24. The bilayer structure and the multi-orbital nature of La₃Ni₂O₇ have profound impact on its magnetism as well, which plays a pivotal role in theories on this novel superconductor^1,8,27,28. Some theory suggest the importance of the interlayer antiferromagnetic coupling J_z between $d_{z^2}$ orbitals^1,8; some others advocate that the strong interlayer coupling would cause the bilayer splitting of band structure, while in-plane magnetic exchange interactions play a dominant role in superconductivity^12,15. In the as-grown La₃Ni₂O₇ crystal at ambient pressure, resistivity measurements found a kink-like transition at around 153 K implying a possible CDW or SDW state²⁹. NMR studies found CDW order possibly mixed with SDW order in polycrystalline La₃Ni₂O₇³⁰, and most recently SDW order was revealed in single crystal La₃Ni₂O₇³¹. In addition, μSR experiments suggested that a static long-range magnetic order emerges in polycrystalline La₃Ni₂O₇  ~ 150 K^32,33. Despite the proposals of potential density waves, NMR and μSR experiments reported that the magnetic moment per Ni site is  ~ 0.08 μ_B and 0.3–0.7 μ_B, respectively^31,33.

Given the currently limited knowledge on the essential electronic and magnetic properties, such as the charge-transfer energy and the magnetic exchange interactions, experimental verification is indispensable. In this work, we employ X-ray absorption spectroscopy (XAS) and resonant inelastic X-ray scattering (RIXS) at both Ni L₃-edge and O K-edge of La₃Ni₂O₇ single crystal at ambient pressure. These spectroscopic and scattering techniques are sensitive to low-energy electronic and magnetic structures together with elementary excitations, and thus are ideally suited for tackling the core issues in La₃Ni₂O₇.

Results

Electronic structure of La₃Ni₂O₇

As-grown La₃Ni₂O₇ crystallises in an orthorhombic structure with the space group of Amam¹. We define the reciprocal space index (H, K, L) based on the pseudo-tetragonal unit cell (Fig. 1a, b, “Method” section). Figure 1c shows the experimental geometry, in which the incident X-ray is linearly polarised, while the scattered X-ray is typically non-polarised but otherwise polarised if stated explicitly (see “Method” section).

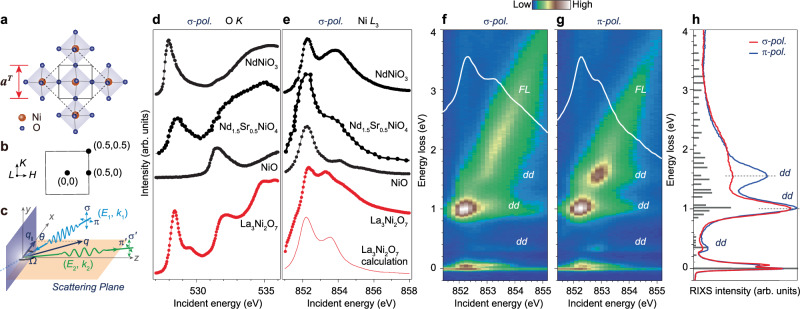
Fig. 1. XAS spectra and the incident energy-dependent RIXS maps in La₃Ni₂O₇.

a Schematic top view of the NiO₂ plane in La₃Ni₂O₇. The solid black square represents the pseudo-tetragonal unit cell with a lattice constant a^T  ~ 3.833 Å, while the dashed black square represents the real orthorhombic in-plane unit cell when considering the tilting of Ni-O octahedra. b In-plane Brillouin zone (BZ) for the pseudo-tetragonal unit cell. c Sketch of the RIXS experimental geometry. Details of the setup are described in Method. d, e σ polarised XAS spectra of La₃Ni₂O₇ (red filled circles) taken at the O K-edge (d) and Ni L₃-edge (e), respectively. The latter is displayed after subtracting the background of La M₄-edge. The calculated Ni L₃-XAS (red curve) is also shown. XAS spectra measured on NiO (Ni²⁺) and NdNiO₃ (Ni³⁺) (black-filled circles) are presented as references. The XAS data of Nd_1.5Sr_0.5NiO₄ extracted from ref. ⁴² are also displayed. f, g RIXS intensity maps measured as a function of incident photon energy with σ- (f) and π- (g) polarised photons, respectively. The corresponding XAS spectrum is superimposed as a solid white curve on each map. Both XAS and RIXS spectra were collected at 20 K at a grazing-in incident angle of 20°. h Integral RIXS spectra in (f) and (g) over the incident energy range [851.8 eV, 853.4 eV]. The grey solid bars display the multiplet calculations for the Ni L₃-RIXS.

Figure 1d, e illustrate XAS spectra of La₃Ni₂O₇ taken near the O K-edge and Ni L₃-edge, respectively. A sizable O K- pre-edge peak at  ~ 528.5 eV originates from oxygen 1s electron excitations into the unoccupied oxygen 2p ligand hole state near the Fermi level, as observed for the Zhang-Rice singlet state in cuprate superconductors³⁴. The Ni L₃-XAS data show a sharp resonant peak around 852.4 eV, followed by a broad satellite peak at a higher energy. As the Ni valence 2.5+ of La₃Ni₂O₇ falls in between the archetypal nickelates NiO and NdNiO₃, the XAS spectra of La₃Ni₂O₇ can be qualitatively understood in relation to these two. NiO is a canonical charge-transfer insulator in the Zaanen-Sawatzky-Allen classification, whose large charge-transfer energy Δ (≈5 eV) suppresses the charge fluctuations between the Ni 3d and ligand oxygen 2p orbitals despite their large orbital hopping integral³⁵. Consequently, its ground state is well described by $\alpha ∣3d^8⟩+\beta ∣3d^9\underset{\_}{L}⟩$ (α² + β² ≲ 1 and $\underset{\_}{L}$ denotes a ligand hole) with a dominant 3d⁸ character (α² ≈ 0.8)^35,36. On the other hand, the perovskite NdNiO₃ with a nominal 3d⁷ configuration is widely acknowledged as a negative charge-transfer system, where electrons from ligand oxygen spontaneously transfer onto Ni cations, resulting in a ground state with a leading 3$d^8\underset{\_}{L}$ contribution^{25,26,37–39}. Such a substantial ligand hole concentration is underscored by the pronounced pre-edge hole peak in the O K-edge XAS of NdNiO₃, similar to that of La₃Ni₂O₇ (Fig. 1d). This is distinct from NiO, where the pre-peak is absent, and the unoccupied ligand states are at an elevated energy across the charge-transfer gap. For the Ni L₃-XAS, the prominent resonant peak of La₃Ni₂O₇ is also observed for NiO and NdNiO₃ at a similar energy (Fig. 1e), which was previously identified as the Ni 2p  → 3d⁸ or 3d⁸ + 3$d^8\underset{\_}{L}$ transitions into the half-filled e_g states, respectively^36,39. A broad satellite peak at a higher energy is likewise seen for NdNiO₃, originating mainly from a part of its ground state wavefunction that contains additional ligand holes^39–41. Similar spectral profiles are present at nominally half-doped nickelate Nd_1.5Sr_0.5NiO₄ at both the O K- and Ni L₃- edges⁴². The above suggests a predominant 3d⁸ occupancy on the Ni cation in La₃Ni₂O₇, accompanied by a significant amount of ligand holes.

Figure 1f, g shows the incident-energy-dependent RIXS measurements of La₃Ni₂O₇ across the Ni L₃-edge. A clear low-energy excitation (~70 meV) is observed near the elastic peak which will be discussed in the next section. The sharp XAS resonance at  ~852.4 eV decays mainly to a final state of a localised excitation at ~1 eV, known as the t_2g → e_g dd orbital excitation similar to NiO and NdNiO₃^40,43,44. The band-like fluorescence excitation, resonating across the broad satellite XAS peak, stems from the delocalised Ni-O hybridised continuum states^40,41. The intensity distribution of the fluorescence contracts under π polarisation that couples stronger to the 3$d_{z^2}$ orbital, indicative of a smaller out-of-plane bandwidth arising from the quasi-two-dimensional structure. In addition, distinct from NdNiO₃, two extra dd excitations show up in La₃Ni₂O₇ (at around 0.4 eV and 1.6 eV). They exhibit stronger intensities under π polarisation, suggesting a more prominent involvement of the 3$d_{z^2}$ orbital in them.

To gain a quantitative understanding of XAS and RIXS measurements, we built a double-cluster model capturing the bilayer structure of La₃Ni₂O₇ and then carried out multiplet calculations for Ni L₃- XAS and RIXS spectra (see details in Supplementary Note 2). Systematic optimisations of the calculated spectra suggest that the charge-transfer energy Δ falls between 0 and 2 eV, pointing out the rather small-charge-transfer nature of La₃Ni₂O₇⁴⁵. This result is reasonable since Δ is  ~ 5 eV and  ~ 0 for NiO and NdNiO₃, respectively^41,46. With the estimated range of Δ, the ground state wavefunction of La₃Ni₂O₇ can be deduced to approximately $\alpha ∣3d^8⟩+\beta ∣3d^8\underset{\_}{L}⟩+\gamma ∣3d^7⟩$ with leading α² and β². The calculated XAS for Δ = 0.5 eV is shown in Fig. 1e, which corresponds to a ground state with (α², β², γ²)  ≈ (0.4, 0.3, 0.2).

The two sets of RIXS excitations centred around 0.4 eV and 1.0 eV in Fig. 1h are well captured in the calculated RIXS spectra. The higher-energy excitation around 1.6 eV is less prominent in calculation partly due to the limited degrees of freedom in the model. To further understand the nature of these excitations, we characterise these excited states in the double-cluster model by evaluating their corresponding orbital occupations and wave function configurations. The excitations at 0.4 eV involve charge transfers between the orbitals of z² and x² − y² symmetry and are of mixed charge and spin type. The peak centred around 1 eV involves the transition between the $d_{z^2}$ and d_xz/yz orbitals, which characterise the crystal-field splitting between the 3d e_g and t_2g orbitals. They involve relatively small movements of the ligand states, signifying almost pure dd-type excitations. Higher-energy excitations between 1.3 ~ 1.5 eV correspond to more complex dd-type excitations, involving transitions between all 3d orbitals. The excitation energy is somewhat lower than that observed in experiment, potentially owing to the limited in-plane size of the cluster model, which may underrepresent the bandwidth of the planar orbitals. Note that there is evident fluctuation of wave function configuration weights between the local d⁷ and $d^8\underset{\_}{L}$ as well as the global d⁷d⁸ and $d^8{d}^8\underset{\_}{L}$ over almost the entire energy range owing to the small charge-transfer energy (Supplementary Note 2). Remarkably, we found that both the XAS line shape and the lower dd excitation ( ~ 0.4 eV) in RIXS show marked difference upon tuning the inter-layer hopping strength mediated by the 3$d_{z^2}$ -O_AP 2p_z - 3$d_{z^2}$ orbital overlap in the calculation (O_AP stands for the apical oxygen), underlining the importance of the inter-layer coupling for the electronic structure (Supplementary Note 2). This result is consistent with previous experimental report¹, and lends support to several recent theoretical works emphasising on the importance of the bilayer structure^2,8,13–20.

Magnetic excitations

Figure 2 summarises the detailed energy-momentum dependence of low-energy excitations in La₃Ni₂O₇ taken at the incident energy of 852.4 eV corresponding to the sharp resonance peak of Ni L₃-XAS. Figure 2a, b show strongly dispersive excitations along directions illustrated in insets. The excitations reach maximal energy of about 70 meV at (0, 0) and (0.5, 0) while softening to zero energy (within the experimental energy resolution) at (0.25, 0.25) where a quasi-elastic scattering peak is formed. The latter signals the formation of translational symmetry breaking, i. e, a superstructure along (π, π) direction with a size four times of the crystal lattice structure. Similar dispersive low-energy excitations also appear when excited by π incident X-rays polarisation (Fig. S6). Along the out-of-plane direction, this mode does not exhibit sizable dispersion as a function of L, indicating its quasi-two-dimensional nature (Fig. 2c).

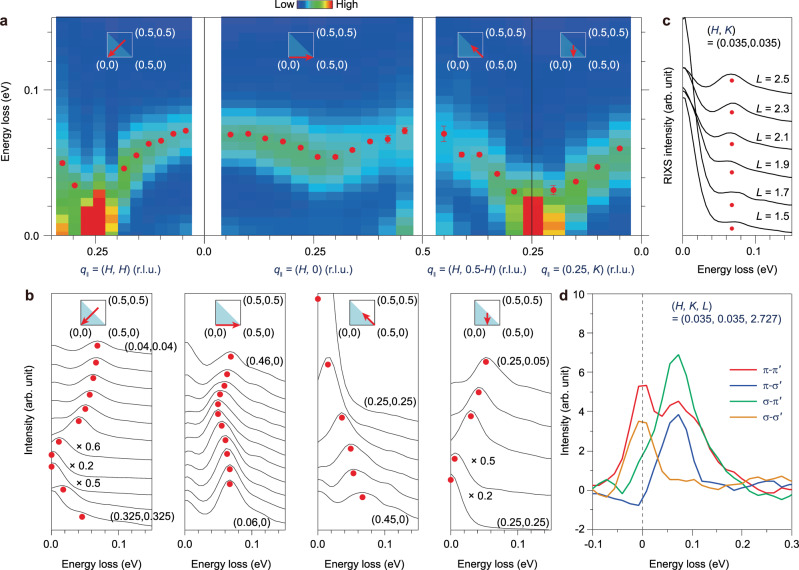
Fig. 2. Energy-momentum dependent magnon in La₃Ni₂O₇.

a RIXS intensity maps along high-symmetry directions as indicated in the insets. Data were collected at 20 K using σ-polarised X-ray at the Ni L₃-edge of 852.4 eV. The red filled circles depict the peak positions of magnetic excitations here and throughout all panels of this figure. b RIXS spectra at representative projected in-plane momentum transfers. The weaker excitations at  ~ 120 meV may result from the multi-magnons. c L scan of RIXS spectra at the fixed q_∥ = (0.035, 0.035). d Polarimetric RIXS data at q = (0.035, 0.035, 2.727). The spectra are decomposed into $\pi -{\pi }^{\prime }$, $\pi -{\sigma }^{\prime }$, $\sigma -{\sigma }^{\prime }$ and $\sigma -{\pi }^{\prime }$ components.

As both magnon and phonon could contribute to the low-energy excitations, the polarimetric RIXS was employed to analyse the outgoing X-rays linear polarisation for unravelling the origin of these excitations (see Methods). Clearly, as shown in Fig. 2d, the inelastic excitation is present under the $\pi -{\pi }^{\prime }$, $\pi -{\sigma }^{\prime }$, and $\sigma -{\pi }^{\prime }$ channels, while gets much reduced under the $\sigma -{\sigma }^{\prime }$ channel. Such behaviour is in agreement with the assumption of a magnetic origin of the scattering and a recent polarimetric RIXS study on magnons in cuprates^47,48. Our multiplet RIXS calculation of magnetic excitations in the double-cluster model confirmed the outgoing polarisation dependence (Fig. S5). Concerning phonons, in principle, their spectra weight should be present in the $\sigma -{\sigma }^{\prime }$ channel. However, the corresponding polarimetric RIXS spectrum shows negligible spectral weight hence a minute contribution to the Ni L₃-RIXS (Fig. 2d). We therefore conclude that the low-energy excitations observed at the Ni L₃-edge are dominated by magnons. Interestingly, in the half-doped nickelate La_3/2Sr_1/2NiO₄, which has the same nominal Ni^2.5+ valence state as La₃Ni₂O₇, an SDW order is formed near the wavevector (0.25, 0.25) from which a low-energy magnon emerges⁴⁹. The similar superstructure and the magnon softening near the order wavevector suggest an SDW order exists in La₃Ni₂O₇. The only difference is the dispersion near Γ point: the magnon in La_3/2Sr_1/2NiO₄ is acoustic-like, whereas in La₃Ni₂O₇ they are dominantly optical-like (Fig. 2a).

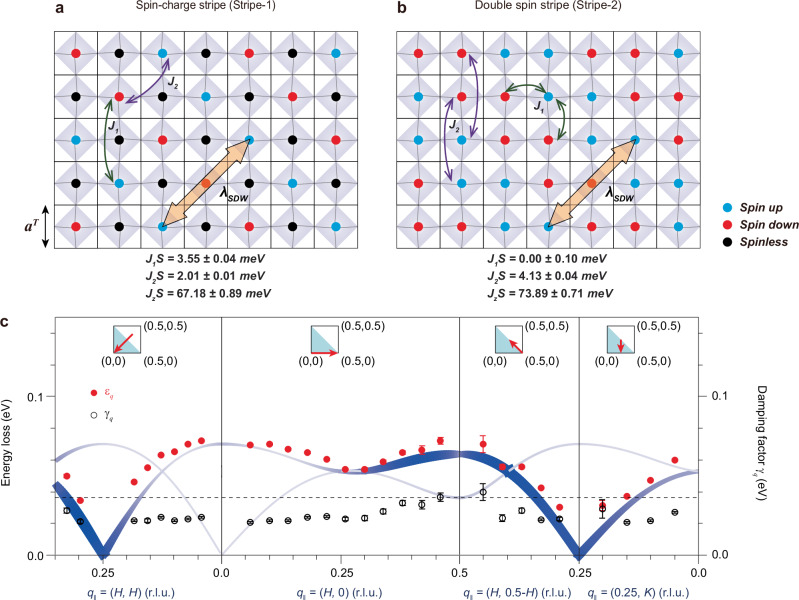
By fitting the magnon spectra to a damped harmonic oscillator (DHO) function χ^″(q, ω), we extracted the peak energy and width of the magnon (Supplementary Note 4)⁵⁰. Three possible spin configurations consistent with the spin order at Q = (0.25, 0.25) can be constructed: the diagonal spin-charge stripe order as in half-doped La_3/2Sr_1/2NiO₄ where Ni²⁺ spin and nominal Ni³⁺ charge stripes intertwined (Stripe-1, Fig. 3a)⁴⁹; the SDW order could also be realised with homogeneous valence state Ni^2.5+, i. e. , a double-spin stripe order (Stripe-2, Fig. 3b) that is similar to the bi-collinear spin order in FeTe⁵¹; by exchanging the Stripe-1 charge stripe positions with those of a spin stripe, a third spin configuration could be achieved as a double spin-charge stripe order (Stripe-3 in Fig. S11c). For all these SDW orders, owing to the strong bilayer bonding, spins are antiferromagnetically aligned in the top and bottom NiO₂ layers. To obtain the magnetic interaction parameters, we constructed an effective J₁-J₂-J_z Heisenberg model: $H={\sum }_i{J}_z{\overrightarrow{S}}_i^t\cdot {\overrightarrow{S}}_i^b+{\sum }_{⟨ij⟩\alpha }{J}_1{\overrightarrow{S}}_i^{\alpha }\cdot {\overrightarrow{S}}_j^{\alpha }+{\sum }_{⟨⟨ij⟩⟩\alpha }{J}_2{\overrightarrow{S}}_i^{\alpha }\cdot {\overrightarrow{S}}_j^{\alpha }$, where α is the layer index for the bottom (b) or top (t) layer, J₁ and J₂ are the nearest-neighbour and next-nearest-neighbour exchange couplings, respectively, in a single NiO₂ layer, and J_z is the inter-layer exchange coupling along the c-axis. Owing to the metallic background, the exchange couplings JS should be considered as the Weiss molecular field governing the spin dynamics for a spin density wave order. All JS values are fitted to the experimental magnon dispersion by solving the semiclassic torque equations⁵² (Supplementary Note 6). We found that the magnon dispersions based on both Stripe-1 and Stripe-2 spin configurations agree with our RIXS result (Fig. 3c and Supplementary Note 6). Owing to the scattering matrix effect, the simulated acoustic magnon spectra are significantly weaker than the optical magnon, consistent with the experimental findings. In general, the inter-layer effective superexchange interaction is an order of magnitude larger than that of the intra-layer. The finding of a dominant magnetic interaction along the molecular bonding direction is in good accordance with previous theoretical calculation². Interestingly, J₂S here shows comparable strength to that in the half-doped La_3/2Sr_1/2NiO₄⁴⁹. For the Stripe-2, the fitted J₁S is negligibly weak comparing to the dominant inter-layer exchange interaction leading to a similar spin dynamics and magnon dispersion as in Stripe-1. Based on the above results and the currently limited information, we can conjecture the true spin configuration of La₃Ni₂O₇ is either Stripe-1 or Stripe-2 or their mixture (see details in Supplementary Note 5).

Fig. 3. The spin configuration and the magnon dispersion of La₃Ni₂O₇.

a The spin configurations for the spin-charge stripe order (Stripe-1). To simplify the sketch only nickel cations are shown. The blue, red and black circles represent spin up Ni²⁺, spin down Ni²⁺, and the spinless Ni³⁺ sites, respectively. The solid lines illustrate the in-plane pseudo-tetragonal unit cells and the grey cubics represent the Ni-O octahedra. The fitted values of J₁S, J₂S, and J_zS based on this spin configuration are noted (see details in Supplementary Note 6). b The spin configuration for the double spin stripe (Stripe-2), and the fitted value of J₁S, J₂S, and J_zS. c The experimental magnon dispersion ϵ_q (red filled circles) and damping factor γ_q (black open circles) versus projected in-plane momentum transfer q_∥ along high-symmetry directions at 20 K. See fitting details in Supplementary Note 4. Error bars of ϵ_q were estimated by combining the uncertainty of the elastic peak position, linear background, and the standard deviation of the fits. Error bars of γ_q were estimated by combining the standard deviation of the fits. The horizontal dashed line marks the total energy resolution (36 meV). The results of an effective J₁-J₂-J_z Heisenberg model based on Stripe-1 order are overlaid. The results from the model based on Stripe-2 are also consistent with the experimental data. All calculations are performed based on single-domain configurations, without considering the effects of twinning. The blue curves represent the dispersion of two magnon modes, where the thickness of the lines and the depth of their colour represent the mode intensity. The detailed parameters are listed in Supplementary Note 6.

Spin-density-wave order

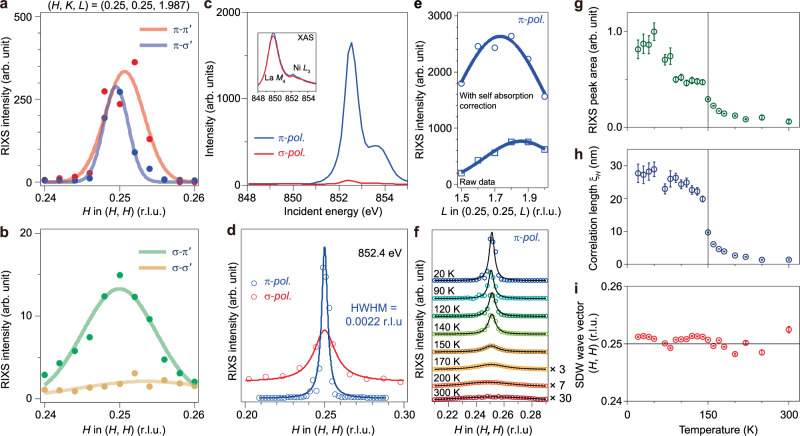
We now took an explicit examination on the SDW order. Polarimetric RIXS was used to confirm the magnetic origin of low-energy excitations, likewise, it was applied to characterise the SDW order in La₃Ni₂O₇. The momentum-dependent quasi-elastic SDW scattering peak shows the same trend as magnon, i. e. , sizable scattering intensities under $\pi -{\pi }^{\prime }$, $\pi -{\sigma }^{\prime }$, and $\sigma -{\pi }^{\prime }$ except for $\sigma -{\sigma }^{\prime }$ (Fig. 4a, b), confirming the magnetic origin of such SDW order. The same polarisation dependence was found in the polarimetric resonant X-ray scattering study of the magnetic order in NdNiO₃⁵³. Further insight into the nature of the SDW was gained through the energy dependence of the SDW scattering at its order wavevector across the Ni L₃-edge (Fig. 4c). Unlike the XAS spectra where La M₄ shows a greater absorption intensity than that of Ni L₃, the SDW scattering predominantly results from the Ni 3d - O 2p hybridised states. Furthermore, the SDW scattering peak exhibits a colossal polarisation dependence, namely, its intensity probed under π polarisation is ~30 times higher than that with σ polarisation. Figure 4d gives an example taken with 852.4 eV photons, which may indicate its strong association with Ni 3$d_{z^2}$ orbital. For that under π polarisation, the fitted peak centre value is  ~0.25 r.l.u. The half-width at half-maximum Γ = 0.0022 ± 0.0002 r.l.u. of the scattering peak corresponds to the in-plane correlation length (ξ_H = 1/Γ) of  ~ 27.7 nm. This is comparable to that of the long-range CDW order in La_1.875Ba_0.125CuO₄ (~20 nm)⁵⁴. A much broader peak with HWHM of about 0.3 r.l.u. is observed as a function of L along the direction of (0.25, 0.25, L), which corresponds to a short out-of-plane correlation length ξ_L of  ~ 0.2 nm, establishing the quasi-two-dimensional nature of the SDW order in La₃Ni₂O₇ (Fig. 4e).

Fig. 4. SDW order at (0.25, 0.25) of La₃Ni₂O₇.

a, b Polarimetric SDW data. The spectra are decomposed into $\pi {\pi }^{\prime }$, $\pi {\sigma }^{\prime }$, $\sigma {\sigma }^{\prime }$ and $\sigma {\pi }^{\prime }$ components. c SDW peaks intensities as a function of incident photon energy and polarisation. The inset shows the XAS spectra at the La M₄-edge and the Ni L₃-edge. d SDW integrated intensity as a function of projected momentum transfer (q_∥) along the (H, H) direction. e SDW intensity as a function of L at the fixed q_∥ = (0.25,0.25). f SDW peaks and their Lorentzian fits along the (H, H) direction at various temperatures. g–i Temperature dependence of the SDW peak area (g), the correlation length (h) and the SDW wave vector position (i). Normal and polarimetric SDW intensity was integrated over an energy window equivalent to the FWHM energy resolution of 36 meV and 55 meV, respectively. The error bars represent the standard deviation derived from the Lorentzian fitting of the SDW peak.

The temperature dependence of the SDW order illustrates a substantial reduction in both the intensity and the correlation length when the temperature is raised above  ~ 150 K (Fig. 4f-h), while the SDW wavevector does not exhibit a discernible temperature dependence (Fig. 4i). The discovery of the SDW with a characteristic temperature of around 150 K is in line with the transport, NMR and μSR studies on La₃Ni₂O₇^29–32.

Discussion

Our RIXS and XAS measurements revealed the dispersive magnon and SDW order below 150 K in La₃Ni₂O₇. Detailed analysis suggests that Ni 3$d_{x^2-y^2}$, Ni 3$d_{z^2}$, and O 2p orbitals dominate the low-energy physics with charge-transfer energy less than 2 eV, and the inter-layer effective magnetic superexchange interaction is much larger than the intra-layer ones. These give critical information for constructing the minimal orbital model for La₃Ni₂O₇ superconductor. It is worth noting that the predominant inter-layer superexchange in La₃Ni₂O₇ is rather unique owing to the strong molecular bonding of partially unoccupied inter-layer Ni 3$d_{z^2}$ orbitals. The situation can neither be realised in multilayer cuprates nor in multilayer nickelates with reduced valence states^55–57. In the latter two cases, the almost fully occupied Cu or Ni 3$d_{z^2}$ orbitals reduce substantially the inter-layer electronic hopping or the molecular bonding strength.

Apart from the extraordinary bilayer structure and the associated predominant magnetic exchange interaction, the electronic structure of La₃Ni₂O₇ fits in general into the family of Ruddlesden-Popper (RP) nickelates. The formation of the Zhang-Rice-like hole band, the small charge-transfer energy, and the well-defined dispersive magnon allude to its nature of the strong electronic correlations⁵⁸. The above are typical characteristics of the strongly correlated cuprates where charge- and spin-density modulation can take place. Moreover, the occurrence of SDW order at (0.25, 0.25) is reminiscent of that in the half-doped single-layer La_3/2Sr_1/2NiO₄, where a spin-charge stripe order exists, and implies the same picture in La₃Ni₂O₇ as illustrated in the scenario of Stripe-1 (Fig. 3a)^45,49,59. Indeed in layered half-doped RP nickelates, manganites, and cobaltates, the spin-charge intertwined order is prevailing^59–61. On the other hand, the double spin stripe order accommodating homogeneous charge density (Stripe-2, Fig. 3b) may be possible too as the 3$d_{x^2-y^2}$ orbitals are more itinerant in-plane than the 3$d_{z^2}$ orbitals. Verifying the magnetic structure of transition metal oxides is possible via resonant soft X-ray scattering^53,62. The final choice of the ground state magnetic structure depends on multiple competing interactions which may also impact on the superconductivity. Some theoretical studies taking the viewpoint of the strong inter-layer hybridisation suggest either d-wave or (d + is)-wave pairing symmetry with a dominant d-wave component^19–22. While in the weaker interaction regime, studies predict that La₃Ni₂O₇ host s_±-wave pairing symmetry^8,9,15–18.

Finally, we would like to extrapolate our findings to superconducting La₃Ni₂O₇, here, a moderately high pressure induces a structural phase transition accompanied by a few percent shrinkage of the lattice constants, and the Ni-O-Ni bonding angles between adjacent NiO₆ octahedra straighten to 180°¹. Consequently, the electronic hopping is likely to increase, potentially suppressing density waves that compete with the superconductivity^63,64. Furthermore, the magnetic superexchange J_z may get significantly enlarged due to the increased hopping along Ni-O_AP-Ni. Despite the presence of Zhang-Rice singlet physics and competing orders as in cuprates, the reinforced molecular orbital bonding and the dominating inter-layer AFM interaction may be novel additions to the HTSC of such a bilayer nickelate superconductor.

Methods

Sample fabrication

La₃Ni₂O₇ sample was fabricated by the high oxygen pressure floating zone technique and the details are described in²⁹. The sample quality was checked by X-ray diffraction (XRD) and Laue diffraction (see details in Supplementary Note 1). Samples were cleaved to get a flat, clean surface before RIXS measurements.

XAS and RIXS measurements

XAS and RIXS measurements were performed at Beamline I21 at Diamond Light Source⁶⁵. In this work, we describe the structural properties of La₃Ni₂O₇ referencing to a pseudo-tetragonal unit cell with cell parameters a^T = b^T  ~ 3.833 Å and c = 20.45 Å. Reciprocal lattice units (r.l.u.) are defined (where 2π/a^T = 2π/b^T = 2π/c = 1) with Q = Ha^T * + Kb^T * + Lc^*. The crystallographic a^T-c (b^T-c) plane of La₃Ni₂O₇ single crystal was aligned within the horizontal scattering plane (Fig. 1c). The polar angular offsets (θ and χ) of the crystal were aligned by the (002) diffraction peak, and the azimuthal offset (ϕ) by SDW order peak, such that the c^* axis lays in the scattering plane. The spectrometer arm was at a fixed position of Ω = 154° except for L scans where variable Ω was employed.

XAS spectra were collected with a grazing incidence angle of θ₀ = 20° to probe both in-plane and out-of-plane unoccupied states. All XAS measurements were done at a temperature of 20 K with the exit slit opening to 30 μm. Total electron yield XAS spectra were collected using the draincurrent and normalised to the incoming beam intensity. Both linear vertical (σ) and horizontal (π) polarisations were used.

Energy-dependent RIXS measurements were performed at the grazing incidence angle of θ₀ = 20° and the temperature of 20 K. The exit slit was open to 30 μm corresponding to an average energy resolution of 40 meV (FWHM). The incident energy range went from 851 to 855 eV in steps of 0.2 eV to fully capture the resonance behaviour across the Ni-L₃ absorption peaks.

Momentum-dependent RIXS measurements were performed at the resonant energy of 852.4 eV at a temperature of 20 K with the exit slit opening to 20 μm corresponding to an average energy resolution of 36 meV (FWHM). The momentum resolution is 0.002 r.l.u. near the SDW wavevector at the Ni L₃-edge. RIXS spectra were collected using both σ and π polarisations. The grazing out geometry (θ > Ω/2) was applied for the acquisition of RIXS spectra shown in the main text.

Polarimetric RIXS apparatus employs a graded multilayer designed for the Ni L₃-edge with a grazing incidence angle of 20° lying perpendicular to the scattering plane. Measurements were performed at Q = (0.035, 0.035, L) and around (0.25, 0.25, L) to analyse the outgoing X-rays linear polarisation of the magnon and SDW ordering, respectively. The total energy resolution of the polarimetric RIXS is  ~ 55 meV (FWHM). Since the multilayer does not work at the exact Brewster’s angle, the outgoing polarised RIXS (the indirect RIXS) from the reflection of the multilayer will be a mixture of linearly polarised spectra. The direct and indirect RIXS spectral intensities are then given by the following formula:

$$I_{direct}=I_{{\sigma }^{\prime }}+I_{{\pi }^{\prime }}$$ 1

$$I_{indirect}=R_{{\sigma }^{\prime }}{I}_{{\sigma }^{\prime }}+R_{{\pi }^{\prime }}{I}_{{\pi }^{\prime }}$$ 2

where I_direct and I_indirect stands for the outgoing nonpolarised and mixed polarised RIXS spectral intensity, respectively. From the above formula, the outgoing ${\sigma }^{\prime }$ and ${\pi }^{\prime }$ polarised RIXS spectra can be deduced:

$$I_{{\pi }^{\prime }}=\frac{I_{indirect}-R_{{\sigma }^{\prime }}{I}_{direct}}{R_{{\pi }^{\prime }}-R_{{\sigma }^{\prime }}}$$ 3

$$I_{{\sigma }^{\prime }}=\frac{I_{indirect}-R_{{\pi }^{\prime }}{I}_{direct}}{R_{{\sigma }^{\prime }}-R_{{\pi }^{\prime }}}$$ 4

In the above, $R_{{\sigma }^{\prime }}$ ($R_{{\pi }^{\prime }}$) refers to the multilayer reflectivity of the outgoing ${\sigma }^{\prime }$ (${\pi }^{\prime }$) polarised X-ray photon. At the Ni L₃-edge, $R_{{\sigma }^{\prime }}$ and $R_{{\pi }^{\prime }}$ is 14.1% and 9.1%, respectively, based on the calibration of the multilayer.

Theoretical calculations

The Ni L₃-edge XAS and RIXS calculations shown in Fig. 1 were performed employing a fully correlated Ni₂O₁₁ cluster model, accounting for the two corner-sharing NiO₆ octahedra within the pseudo-tetragonal unit cell. The noninteracting part of the Hamiltonian integrates material-specific on-site energies and hybridisations involving Ni 3d and O 2p orbitals, along with spin-orbit coupling within the Ni core 2p and 3d shells. Full Coulomb interactions within the Ni 3d shell and between the Ni 2p and 3d shells are included, with parametrization by Slater integrals scaled at 0.8 based on atomic Hartree-Fock values⁶⁶. Comprehensive details regarding model construction and relevant parameters are described in Supplementary Note 2. The model was solved using the exact diagonalization method as implemented in QUANTY⁶⁷.

The DFT calculations employ the Vienna ab-initio simulation package (VASP) code⁶⁸ with the projector augmented wave (PAW) method⁶⁹. The Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional⁷⁰ is used. The energy cutoff energy for expanding the wave functions into a plane-wave basis is set to be 500 eV. The Γ-centred k-mesh is used in KPOINTS files which are generated by VASPKIT⁷¹ with the KPT-resolved value equal to 0.02 for different unit cells. The SDW orders are calculated using the simplified rotation invariant approach based on the DFT+U method introduced by Dudarev et al. ⁷². Then, the effective Heisenberg interactions for the SDW orders are constructed. The magnon dispersions within the linear spin wave theory are calculated using the torque equation formalism^52,57. The RIXS intensity for the magnon mode in the σ-π polarisation channel is calculated following the reference⁷³. More details can be found in Supplementary Note 5 and 6.

Author contributions

J.C., X.Y.C., D.W.S., S.A., M.G.-F., D.L.F. and K.-J.Z. conducted XAS and RIXS experiments at Diamond Light Source. X.Y.C., S.A., J.C. and K.-J.Z. analysed the data. J.M., K.J. and J.P.H. performed DFT and stripe states calculations. J.L. and Y.L. performed multiplet calculations. H.L.S., X.H., and M.W. fabricated samples. X.Y.C. and Z.C.J. performed XRD and Laue measurements. K.-J.Z., K.J., Y.L., D.W.S., D.L.F. and X.Y.C. wrote the manuscript, with input from all authors. D.L.F. and K.-J.Z. are responsible for project direction and planning.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data shown in the main text are available via Zenodo data repository (10.5281/zenodo.13955595).

Code availability

All code used to perform the XAS and RIXS calculation is available from the corresponding authors upon reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53863-5.