Microcavity-assisted multi-resonant metasurfaces enabling versatile wavefront engineering

Abstract

Metasurfaces have exhibited exceptional proficiency in precisely modulating light properties within narrow wavelength spectra. However, there is a growing demand for multi-resonant metasurfaces capable of wavefront engineering across broad spectral ranges. In this study, we introduce a microcavity-assisted multi-resonant metasurface platform that integrates subwavelength meta-atoms with a specially designed distributed Bragg reflector (DBR) substrate. This platform enables the simultaneous excitation of various resonant modes within the metasurface, resulting in multiple high-Q resonances spanning from the visible to the near-infrared (NIR) regions. The developed metasurface generates up to 15 high-Q resonant peaks across the visible-NIR spectrum, achieving a maximum efficiency of 81% (70.7%) in simulation (experiment) with an average efficiency of 76.6% (54.5%) and a standard deviation of 4.1% (11.1%). Additionally, we demonstrate the versatility of the multi-resonant metasurface in amplitude, phase, and wavefront modulations at peak wavelengths. By integrating structural color printing and vectorial holographic imaging, our proposed metasurface platform shows potential for applications in optical displays and encryption. This work paves the way for the development of next-generation multi-resonant metasurfaces with broad-ranging applications in photonics and beyond.

Previous multi-wavelength metasurfaces are restricted to a few wavelengths or lack wavefront control ability. Here, the authors introduce a microcavity-assisted metasurface that achieves multi-resonant wavefront engineering at 15 high-Q peak wavelengths from 480 nm to 1000 nm.

Introduction

Recent advancements in nanofabrication techniques have facilitated the miniaturization of nanophotonic elements to dimensions comparable to, or even smaller than, the wavelength of light. This miniaturization has given rise to a unique category of low-profile optical devices that can control light properties at a subwavelength scale. Among these innovations, metasurfaces prevail as subwavelength scatterer arrays, offering compact and planar alternatives to conventional bulk optics^1–3. Metasurfaces have already found applications in variety of devices, such as focusing mirrors and lenses^4,5 and quantum light source generators^6–8. These devices play a pivotal role in advancing next-generation optical systems, including chip-based light detection and ranging devices⁹, compact augmented reality/virtual reality (AR/VR) glasses^10,11, and quantum techniques^6,7.

Delving into the realm of metasurface optics reveals a captivating array of possibilities. In certain cases, such as depth sensing¹², quantum entangled photon manipulation⁷, and nonlinear light generation¹³, enhancing light-matter interactions for wavefront engineering and field enhancement within a narrow wavelength spectrum proves effective. Nevertheless, there are scenarios that demand a more expansive strategy. This involves creating numerous resonances and utilizing these multi-resonant properties over a broad spectral range. Such applications include enhancing both excitation and emission rates concurrently in photoluminescence processes, capturing signals from multiple analytes simultaneously, and enabling intricate nanoscale functionalities with wavelength-multiplexed capabilities like hyperspectral imaging and color routing¹⁴. To cater to the diverse requirements of multi-wavelength nanophotonics, conventional single-resonant nanostructures must transition into sophisticated multi-resonant metasurface systems.

In the past, the introduction of multi-resonant features in a metasurface typically relied on mode hybridization, which was accomplished by disrupting the symmetry of the system. This disruption encompassed variations in the geometric dimensions of nanostructures¹⁵, alterations in the material composition within the unit^16,17, and employing asymmetric excitation methods¹⁸. Moreover, the coupling between super-radiative and sub-radiative modes can give rise to Fano resonance^19,20, resulting in a few resonant peaks around the central wavelength of the super-radiative mode. Additionally, employing multiple nanoparticles arranged into different periodicities could lead to the hybridization of lattice resonance²¹, generating multiple resonant peaks across the spectral range of interest. The incorporation of lattice resonance and microcavity modes also contributes to the generation of multiple resonances²². Indeed, these approaches are specifically designed not only to increase the number of resonance but also to enhance the Q-factor of resonant peaks, thereby enhancing near-field intensity for diverse applications including optical detection²³, active nanophotonics²⁴, and imaging systems^25,26. However, their potential for either realizing numerous resonances or achieving wavefront engineering at specific resonant wavelengths is limited by the constrained degree of freedom in structural design. This limitation emerges from the necessity to optimize meta-atoms within metasurfaces to display sharp resonance features at the desired operating wavelength. Consequently, the requirement for specific mode coupling to generate multiple high-Q resonances imposes restrictions on the structural dimensions and shapes of meta-atoms, thereby significantly curtailing the achievable amplitude modulation and range of phase shifts essential for effective wavefront control in metasurfaces. As a result, these metasurfaces often face severe constraints, as individual meta-atoms typically exhibit only a few resonant peaks without the ability to control phase within the desired wavelength range. This constraint poses a barrier to the broader utilization of metasurfaces with multi-resonance capabilities in various optical functionalities.

Recently, various approaches have emerged to realize multi-resonant metasurfaces for wavefront engineering. One straightforward method involves spatially multiplexing the constituent building blocks, where individual meta-atoms are designed to operate at specific wavelengths²⁷. This approach facilitates the creation of wavelength-engineered metasurfaces through in-plane segmenting/interleaving or vertically stacking the optimized meta-atoms^28–30. However, this approach comes with challenges because near-field interactions between neighboring meta-atoms and metasurface chips can lead to crosstalk, potentially causing a significant degradation in the performance of metasurfaces. Furthermore, it is important to note that the highest working efficiency is constrained by 1/N, where N represents the number of wavelength channels. This limitation renders the metasurface impractical as the number of wavelength channels (that is, resonant peaks) increases. Additionally, the complexity associated with fabricating multilayer stacking metasurfaces places restrictions on their real-world applications. Another example of a multi-resonant metasurface involves using dispersion engineering meta-atoms^31–34. However, to support a broadband response, all meta-atoms must exhibit a smooth dispersive behavior. This requirement poses significant challenges in realizing multiple responses with numerous resonant features and in achieving wavelength-controlled optical functionalities using dispersion engineering meta-atoms. In short, the advancement of a multi-resonant metasurface platform continues to be a formidable research challenge. This platform should ideally entail a straightforward design process that eliminates the need for interleaving meta-atoms, possesses a flexible ability for controlling both amplitude and phase shift, and provides multiple narrow resonant responses simultaneously within the optical spectrum.

Here, we introduce and validate a microcavity-assisted multi-resonant high-Q plasmonic metasurface platform by integrating subwavelength meta-atoms with a specially designed μm-scale distributed Bragg reflector (DBR) mirror. It has been demonstrated that combining a Fabry–Pérot (FP) cavity, formed by two DBR mirrors, with a metasurface can achieve a single high-Q resonance for narrowband color filtering³⁵. In this work, the DBR substrate represents a class of patterned interface featuring spatially varying meta-atoms that couple with specific optical modes, including plasmonic modes in meta-atoms and FP cavity modes within the alternating layers of the DBR mirror. As a result of the simultaneous excitation of various resonant modes within the metasurface and their interactions, we can achieve multiple high-Q resonances spanning a broad spectrum, ranging from the visible to the near-infrared (NIR) regions. In contrast to previously reported multi-resonant metasurfaces, which were always limited to presenting fewer than 3 resonant peaks or dips, whereas the metasurface proposed here can produce 15 resonant peaks across the visible-NIR spectrum from 480 nm to 1000 nm. Moreover, it is noteworthy that the operating efficiency at individual wavelengths remains unaffected by the number of resonances, a challenge that was previously encountered in interleaved metasurfaces. To showcase the versatility of the developed multi-resonant metasurface, we demonstrate its ability to modulate amplitude, phase, and wavefront across all high-Q resonant peaks. Finally, as a proof-of-concept, we illustrate one potential application of the platform in optical information encryption by integrating structural color printing and vectorial holographic imaging.

Results

Design principle of multi-resonant metasurface

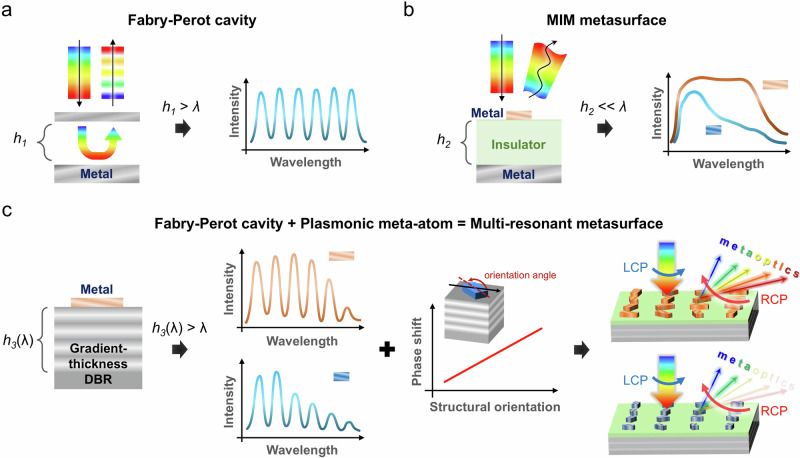
The design principle begins with an optical FP cavity that includes a partially reflecting mirror, a metallic mirror with full reflection, and a dielectric layer sandwiched between them. As illustrated in Fig. 1a, multiple resonances become apparent in the reflection spectrum when the round-trip optical phase aligns with the resonant condition of the cavity. This phenomenon arises from the ability of FP cavity to confine and store light energy for an extended period, resulting in more pronounced and narrow resonant peaks in the optical spectrum. To ensure the resonance condition (h₁ = mλ/n, where m = 1, 2, … is the order of cavity resonance, λ is the wavelength in free space, and n is the refractive index of the dielectric layer) is met, it is necessary for the thickness of the dielectric layer to exceed the effective wavelength of light³⁶. Although it is feasible to modulate the reflection intensity through various methods, such as adjusting the incident angle or manipulating the optical properties of the cavity materials, achieving precise control over the phase shift of individual high-Q peaks within a FP cavity typically necessitates more intricate techniques. In contrast, an metal-insulator-metal (MIM) metasurface (refer to Fig. 1b) can effectively modulate not only the reflection amplitude but also the operating spectral bandwidth and phase shift by tuning the geometric properties (size, shape, structural orientation, etc.) of the topmost nanostructures^37–39. In this configuration, the insulator layer is optically thin, enabling strong near-field coupling between the metallic nanostructures and the back reflector. To achieve multiple high-Q resonances and enable flexible control of individual reflection peaks, our approach entails replacing i. the metallic mirror with a gradient-thickness DBR mirror and ii. partially reflecting mirror within the FP cavity with plasmonic meta-atoms. The introduced meta-atoms provide an additional approach for modulating both the amplitude and phase shift of resonant peaks. To preserve the FP cavity characteristics, the dielectric spacer between the meta-atom and the alternating layers that completely reflected the light must have a thickness exceeding the working wavelengths, as illustrated in Fig. 1c. In principle, the main difference between the proposed multi-resonant metasurface and previously reported MIM metasurfaces lies in the nature of the cavity dielectric. For the proposed multi-resonant metasurface, the interface that completely reflects incident light varies with wavelength, causing the effective cavity dielectric h₃(λ) to be dispersive (more details and discussions can be found in the following sections). In contrast, the cavity dielectric thickness in MIM metasurfaces remains constant for all wavelengths within the operating spectrum. Since the optical response of the gradient-thickness DBR-based multi-resonant metasurface arises from a combination of the optical behaviors of MIM metasurfaces and FP cavities, the reflection intensity of individual resonant peaks can be finely adjusted by tuning the physical dimensions of the meta-atom (refer to the left panel of Fig. 1c). Moreover, the operational range, including high-Q resonant peaks, can be delineated by the broad reflection bandwidth of the DBR mirror. This bandwidth is modifiable by changing the constituent materials in a DBR mirror. Finally, by integrating the geometric phase method, precise control over the phase shift at each resonant peak becomes feasible, thereby enabling wavefront control for all resonant peaks (see right panel of Fig. 1c).

Fig. 1. Conceptual illustration of multi-resonant metasurfaces.

Schematic illustration for (a) an FP cavity, (b) an MIM metasurface, and (c) the proposed multi-resonant metasurface. To induce cavity modes in an FP cavity, the dielectric layer thickness (h₁) must exceed the wavelength of the incident light. The wavelength of the reflected beam is discrete because only those that satisfy the FP condition can be highly reflected. However, controlling the wavefront of the reflected beam using an FP cavity is challenging. For MIM metasurfaces, wavefront engineering can be achieved by optimizing the physical properties of the metallic meta-atom and adjusting the thickness of the dielectric spacer (h₂), leading to the attainment of either a relatively broad or narrow reflection band. It is crucial to maintain h₂ at an optically smaller scale than the wavelength for MIM metasurfaces. By replacing the metallic mirror with a gradient-thickness DBR, a multi-resonant high-Q feature is introduced, offering greater flexibility in modulating the spectral profile and enabling wavefront engineering at individual resonant wavelengths. In this case, the incident light is highly reflected at different interfaces within the DBR mirror, making the dielectric spacer thickness h₃(λ) dependent on the wavelength of incidence. Additionally, introducing a geometric phase through the rotation of the topmost nanostructures allows precise wavefront control at each resonant wavelength. The blue and brown blocks in (b) and (c) represent meta-atoms viewed from the top, each with varying sizes.

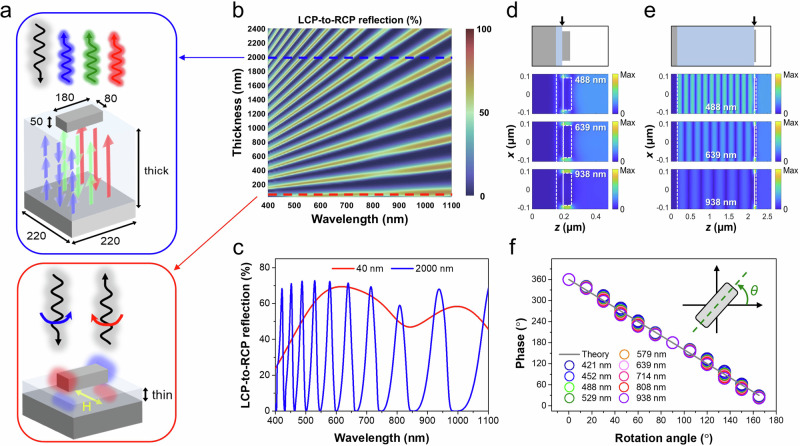
To validate the concept, we first investigate the reflection spectrum concerning the conversion of left-handed circular polarization (LCP) to right-handed circular polarization (RCP) for an MIM metasurface. As shown in Fig. 2b, multiple high-Q peaks become apparent when the dielectric spacer exceeds a critical value in thickness. Moreover, the number of resonances escalates with an increase in the spacer thickness. This behavior is reminiscent of what is typically observed in a standard FP cavity (refer to Supplementary Fig. 1). To delve deeper into the physics underlying the proposed multi-resonant high-Q metasurface, we compare the spectrum for the LCP-to-RCP conversion efficiency using two different dielectric spacer thicknesses, as shown in Fig. 2c. As can be seen in the red curve of Fig. 2c, the circular polarization conversion spectrum exhibits a relatively broadband characteristic when the spacer thickness is at a subwavelength scale. This is due to the fact that the FP cavity effect is not applicable for thin dielectric spacers, and instead, the system is dominated by gap plasmons⁴⁰ (refer to the bottom panel of Fig. 2a for visualization and Fig. 2d for the numerically simulated field distribution). When the thickness of SiO₂ increased from 40 nm to 2000 nm, the initially broad working bands transformed into discrete high-Q peaks, as shown in the blue curve of Fig. 2c. Notably, the peaks at shorter wavelengths exhibit a higher Q-factor compared to those at longer wavelengths (see Supplementary Fig. 2 for the numerical results). This phenomenon primarily arises from the excitation of higher FP cavity modes at shorter wavelengths, as illustrated in the top panel of Fig. 2a and numerically supported in Fig. 2e. Furthermore, it is essential to emphasize that the reflection intensity remains consistently high for all high-Q resonances. The efficiency experiences a slight decrease at ~840 nm, primarily attributed to the interband transition absorption of Al. As discussed, the changes in reflection at individual peaks within the working bandwidth can be explained as the result of combining the reflection intensity from an MIM metasurface and an FP cavity. Consequently, the LCP-to-RCP conversion efficiency decreases as the wavelength shifts from 500 nm to 800 nm, and it increases as the wavelength further redshifts. More details and discussions can be found in Supplementary Note 1. Since all incident light is completely reflected at the metallic mirror-dielectric interface, the cavity dielectric thickness can be precisely determined when the SiO₂ thickness is defined. As a result, the spectral features and peak wavelengths of an MIM metasurface can be analytically predicted⁴¹ (see Supplementary Note 2).

Fig. 2. Nanophotonic resonance transition in MIM metasurfaces.

a A schematic illustration representing the operational mechanism of an MIM metasurface with varying spacer thicknesses. The values in the top panel represent the geometric dimensions of the MIM metasurface (unit: nm). b Mapping of LCP-to-RCP polarization conversion for an MIM metasurface (Al-SiO₂-Al) in relation to dielectric spacer thickness and wavelength. c Simulated spectra of LCP-to-RCP polarization conversion for MIM metasurfaces with 40-nm-thick and 2000-nm-thick SiO₂ layers, extracted from the region along the red and blue dashed lines in (b). d, e Cross-sectional electric field distributions for MIM metasurfaces with a 40-nm-thick and a 2000-nm-thick SiO₂ spacer layer. The upper image presents a schematic cross-sectional view, with a black arrow indicating the position of the interface between the nanostructure and the SiO₂ spacer. The wavelengths are randomly selected to clarify the resonant modes. f Numerical phase shift in LCP-to-RCP polarization as a function of structural orientation angle for resonant peaks. The spacer thickness is 2000 nm.

To achieve a 2π phase shift for all high-Q resonance peaks, we introduced the geometric phase method, which can effectively modulate the phase shift regardless of wavelength. Figure 2f presents the phase shift as a function of the structural orientation angle of the topmost meta-atom. The continued applicability of the geometric phase across all peak wavelengths is evident. A noteworthy departure from previous studies lies in our methodology, contrasting with approaches that primarily utilized gap plasmon-based MIM metasurfaces^30,42 or all-dielectric metasurfaces^43,44. In our study, we demonstrate that the geometric phase method retains its effectiveness even when the meta-atom is positioned at an optical distance from the back reflector. This is attributed to the ability of meta-atoms to function as a partially reflecting mirror, relying on their eigen-resonances. Consequently, the geometric phase effect continues to operate when the coupling between the meta-atom and the reflector is supported by the FP cavity modes.

Multi-resonant high-Q metasurface using a gradient-thickness DBR mirror

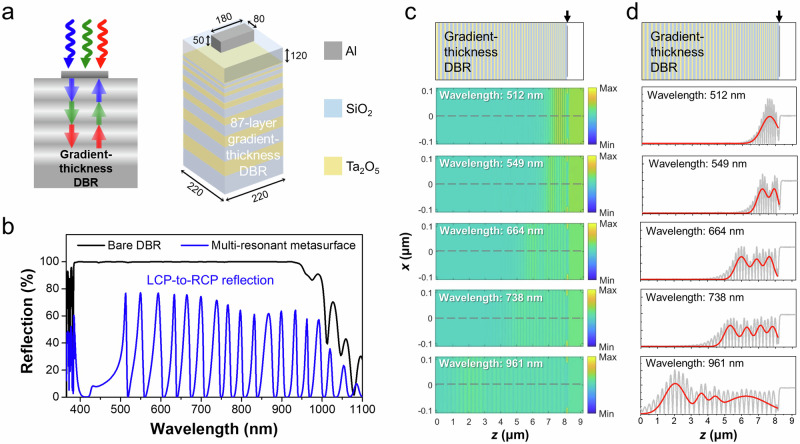
Next, we verify that the multi-resonant high-Q response can be achieved by substituting the metallic mirror with a DBR reflector. To generate multiple high-Q resonances across a broad range of wavelengths, deliberate design features have been incorporated into the SiO₂ and Ta₂O₅ layers to introduce gradient thickness variations within the DBR reflector (see Supplementary Fig. 5 for more details). The left image in Fig. 3a schematically illustrates the FP cavity modes in the gradient-thickness DBR mirror. As high reflection in a DBR substrate is achieved through multiple reflection and transmission processes at interfaces, the travel of light within the dielectric layers must satisfy conditions for both high reflection intensity and FP cavity responses. The right image in Fig. 3a shows the schematic of the multi-resonant high-Q metasurface, while the corresponding reflection spectrum is displayed in Fig. 3b. As expected, multiple resonant responses are observed within the high reflection window of the gradient-thickness DBR. It is worth mentioning that the Q-factor of all resonant peaks (additional results can be found in Supplementary Fig. 6) is relatively higher compared to previous reports on plasmonic metasurfaces. In typical plasmonic metasurfaces, the Q-factor of resonant peaks is usually lower than 10 due to the inherently high optical loss of surface plasmons²². Another distinct feature is that the peaks at shorter wavelengths (higher frequencies) are more widely separated than those at longer wavelengths, as shown in Supplementary Fig. 7. This occurs because the dielectric layers within the DBR also serve as the cavity dielectric, and the designed gradient-thickness DBR reflects shorter wavelengths at the top regions of the DBR. Consequently, visible wavelengths have less space to excite additional cavity modes within the DBR substrate. In contrast, for the MIM metasurface, where a metallic layer is used as the back reflector, the cavity dielectric is well-defined, and all peak wavelengths share the same effective thickness of the cavity dielectric. As a result, the peak separation at shorter wavelengths is much smaller than at longer wavelengths and gradually increases as it transitions to the NIR region, as illustrated in Supplementary Fig. 8. For a more in-depth exploration of the FP cavity response in this multi-resonant high-Q metasurface, we have randomly selected 5 peak wavelengths from Fig. 3b and presented the corresponding electric field distributions. The field distribution for other peak wavelengths is available in Supplementary Fig. 9. As shown in Figs. 3c and 3d, the field distribution within the gradient-thickness DBR exhibits characteristics akin to an FP cavity with standing wave-like patterns. A noteworthy observation is the initiation of the standing wave feature near the SiO₂ dielectric layer, which gradually extends to encompass more regions within the DBR layers as the incident wavelength shifts towards longer values. This behavior is primarily attributed to the varying thicknesses of the constituent layers within the DBR mirror. The layer closest to the glass substrate is the thickest, while the layer adjacent to the SiO₂ dielectric spacer is the thinnest. Consequently, incident light with short wavelengths is fully reflected at a specific interface close to the dielectric spacer, and FP-like field profiles occur above this particular interface for shorter wavelengths. Indeed, there is a noticeable trend where a relatively broad peak emerges initially near the interface of the DBR mirror and SiO₂ spacer. As the wavelength increases, this peak shifts towards regions farther from the interface of the DBR mirror and SiO₂ spacer. This observation suggests that the fundamental FP mode is genuinely activated and is linked to the thickness of the dielectric layers within the DBR mirror (similar results can be observed when the dielectric spacer is optically thick, see discussions in Supplementary Note 3). Furthermore, as the incident wavelength shifts towards longer values, the standing wave-like field profile exhibits an increased number of “nodes” with varying widths. This behavior stands in stark contrast to the commonly observed FP cavities, where a single dielectric spacer layer is typically employed as the cavity material. Consequently, the Q-factor of resonant peaks at shorter wavelengths possesses a relatively lower value compared to those at longer wavelengths, which is contrary to observations in a normal FP cavity (refer to Supplementary Fig. 2 and Supplementary Fig. 6 for comparison). Essentially, the observed standing wave feature is intricately tied to the varying layer thicknesses within the DBR mirror, influencing the reflection behavior and field profiles at different interfaces depending on the incident wavelength. Consequently, it becomes significantly more challenging to analytically predict the spectral features of the gradient-thickness DBR-based multi-resonant metasurface using the multilayer model (see Supplementary Note 2). These features closely resemble the distinctive characteristics of an FP cavity, providing confirmation that the FP cavity effect persists when the dielectric spacer is composed of either a single layer with a considerable thickness or multiple layers with gradient thicknesses. Additionally, it is important to notice that a multi-resonant high-Q response can be achieved by combining both scenarios (further details and discussions are available in Supplementary Note 3). Importantly, these multiple high-Q peaks manifest exclusively within the high reflection window of the DBR substrate.

Fig. 3. Multi-resonant high-Q metasurface with a gradient-thickness DBR.

a The left panel illustrates the working principle for FP cavity modes within a gradient-thickness DBR. The dimensions of the meta-atom are depicted in the right panel. Unit: nm. A 120-nm-thick SiO₂ layer is sandwiched between the nanostructure and the DBR substrate. b Simulated LCP-to-LCP reflection spectrum (black curve) and LCP-to-RCP reflection spectrum (blue curve) for a bare gradient-thickness DBR substrate and a multi-resonant metasurface, respectively. c Electric field distribution of the RCP component for the multi-resonant metasurface at 5 wavelengths under LCP illumination. d Cross-sectional electric field distribution for the multi-resonant metasurface, which are extracted from the region along the red dashed lines in (c). In the upper image, a schematic of the cross-sectional view is presented, with a black arrow indicating the position of the interface between the meta-atom and the SiO₂ spacer. The red curves result from multi-peak fitting for visual guidance.

Optical modulations with multi-resonant high-Q metasurfaces

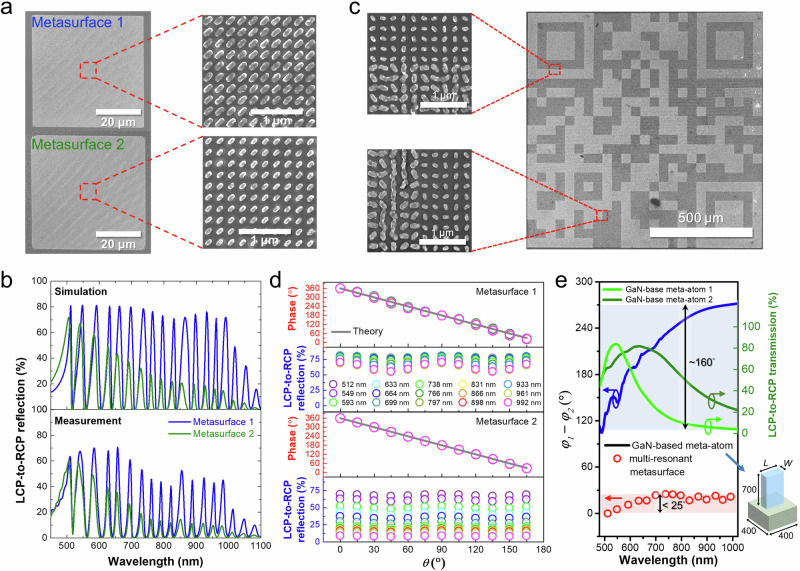
After delving into the physics behind the observed multiple high-Q responses, we subsequently show that both the amplitude and phase at resonant peaks can be flexibly adjusted for multi-wavelength wavefront engineering. Given that the topmost plasmonic meta-atoms effectively act as the partially reflecting mirror in the FP cavity and the effective refractive index of the meta-atoms is dictated by their physical dimensions, the amplitude modulation at individual peaks can be achieved by tuning the geometric size of the topmost plasmonic meta-atom, as discussed in Supplementary Note 1. To experimentally validate this concept, we designed and fabricated two multi-resonant high-Q metasurfaces. Both metasurfaces feature the same DBR mirror and dielectric spacer but differ in the physical dimensions of the plasmonic meta-atoms. Figure 4a shows the SEM images of these multi-resonant metasurfaces. Upon closer inspection of the enlarged images, the high uniformity of the fabricated meta-atoms is evident in both metasurfaces, despite their substantial differences in size. As theoretically expected, both metasurfaces generate multiple resonant peaks in the circular polarization spectrum, spanning a broad spectral range encompassing the visible and NIR regions, as shown in Fig. 4b. The experimentally measured spectra closely aligned with the numerical simulations, demonstrating a high degree of consistency in terms of conversion efficiency, individual peak position, and the number of peaks. This agreement confirms the validity of the proposed metasurface configuration for achieving multi-resonant properties and amplitude modulation across all resonant wavelengths. Supplementary Fig. 12a represents the Q-factor of resonant peaks. Once more, both the numerically and experimentally observed Q-factors of all resonant peaks in the two metasurfaces are notably higher than previous studies. A decrease in the Q-factor is noticeable at a wavelength of ~850 nm in both metasurfaces, attributable to the interband transition loss of Al. The numerically simulated resonant wavelength offset between the two metasurfaces is slightly smaller than the experimental data (see Supplementary Fig. 12b). This discrepancy can be attributed to variations in the thickness and refractive index of the real samples. Indeed, the variation in reflection intensity can be leveraged to create a binary image by designing multiple multi-resonant metasurfaces, each with distinct conversion efficiencies in reflection. In a demonstration of the concept, we presented a bicolor QR code utilizing the designed multi-resonant high-Q metasurfaces. Figure 4c shows the SEM image of the constructed QR code, providing a distinct and recognizable pattern that reinforces the points discussed earlier.

Fig. 4. Optical modulations of multi-resonant high-Q metasurfaces.

a SEM images of two multi-resonant high-Q metasurfaces. The topmost meta-atoms of metasurface 1 measure 180 nm in length, 80 nm in width, with a thickness of 50 nm. For metasurface 2, the corresponding dimensions are 130 nm in length, 70 nm in width, and a thickness of 50 nm. The SiO₂ spacer is 120 nm. The right panels show enlarged images corresponding to the aforementioned details. b Simulated and measured LCP-to-RCP reflection spectra for multi-resonant metasurface 1 and metasurface 2. c The SEM images depict the QR code composed of two multi-resonant metasurfaces. d The top panels plot LCP-to-RCP phase shift as a function of structural orientation angle at resonant peaks ranging from 500 nm to 1000 nm. The cross-polarized conversion efficiency with various structural angles θ is shown in the bottom panels. e The blue curve and red circles show the phase difference between conventional dielectric meta-atoms (GaN on Al₂O₃) and multi-resonant metasurfaces, respectively. The bottom-right shows the schematic of the GaN-based meta-atom. GaN-based meta-atom 1: L = 350 nm, W = 120 nm; GaN-based meta-atom 2: L = 260 nm, W = 70 nm.

Figure 4d clearly verifies the capability of the developed multi-resonant high-Q metasurfaces for phase modulation. In illustrating the versatility of the generated multi-wavelength response for wavefront engineering, we incorporate the multi-resonant metasurface design into a metasurface hologram. A metasurface hologram, also refer to meta-hologram, utilizes subwavelength structures to intricately manipulate both amplitude and phase information at a local level for precise wavefront control. The integration of a meta-hologram with additional degrees of freedom, particularly polarization and wavelength, known as a multi-color vectorial meta-hologram, holds great promise in various applications, including vectorial beam generation, AR/VR imaging, full-color displays, and optical encryption. However, the challenge in achieving a multi-color meta-hologram in previous studies lies in the integration of different meta-atoms within a single pixel, each functioning at distinct wavelengths^45,46. This integration presents a difficulty as the efficiency of the metasurface tends to diminish with an increasing number of meta-structures within a pixel. In contrast, the introduction of the multi-resonant high-Q metasurface enables the creation of full-color holographic images by aligning the peak wavelengths. Moreover, the metasurface can be multiplexed with polarization to generate a multi-color vectorial meta-hologram, offering applications in dynamic optical encryption.

In contrast to conventional geometric phase metasurfaces, which typically exhibit broadband amplitude responses, our proposed meta-atoms feature multiple high-Q resonances. This design choice allows for the selection of desired wavelengths while minimizing crosstalk from unwanted wavelengths. Additionally, given that two different sizes of meta-atoms are employed for QR code encoding, it is crucial to minimize the propagation phase difference at the desired wavelength between these meta-atoms to prevent dispersion-induced effects on the holographic phase profile. Simulation results depicted by the red circles in Fig. 4e demonstrate that the phase difference between the two proposed multi-resonant metasurfaces is less than 25°. In contrast, conventional all-dielectric metasurfaces exhibit a dispersive propagation phase resulting in a phase difference of ~160°, as indicated by the blue line in Fig. 4e. Therefore, our proposed multi-resonant metasurface effectively suppresses dispersive phase responses, facilitating the realization of a multi-color vectorial meta-hologram with QR code color printing. This innovation holds great promise for optical display and encryption applications.

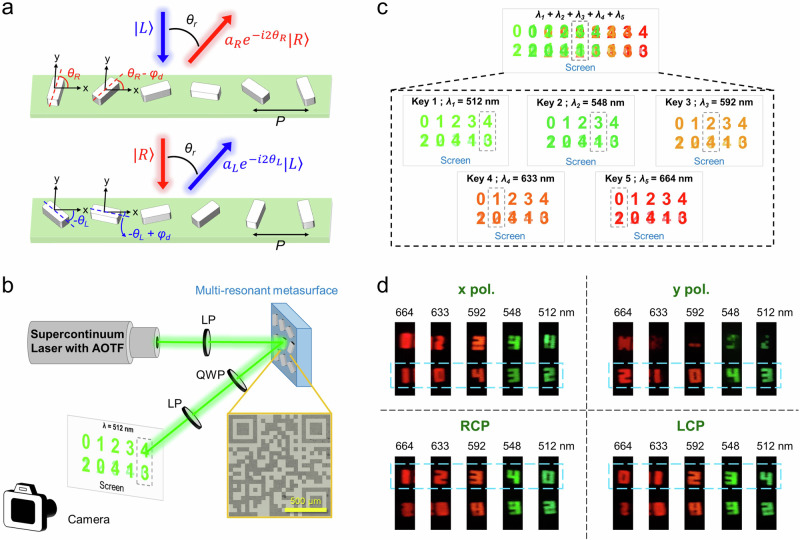
To establish a vectorial meta-hologram, we employ two series of phase gradient metasurfaces, as shown in Fig. 5a. The top-line meta-atoms rotate with an initial orientation angle θ_R, converting incoming LCP light into RCP light with amplitude modulation (a_R). Simultaneously, it introduces a geometric phase of −2θ_R, expressed as $\mid L⟩\to a_R{e}^{-i2{\theta }_R}\mid R⟩$. In contrast, the bottom-line meta-atoms rotates with an initial orientation angle –θ_L, transforming RCP into LCP with amplitude (a_L). This imparts an opposing geometric phase of −2θ_L, represented as $\mid R⟩\to a_L{e}^{-i2{\theta }_L}\mid L⟩$. Therefore, the phase difference φ between RCP and LCP light can be described as 2(θ_R–θ_L). Additionally, both lines undergo an opposite orientation angle increment of φ_d, aligning the top RCP and bottom LCP light to a shared angle ${\theta }_r=\arcsin \left(\frac{2_{{\phi }_d}}{k_{0}P}\right)$, where k₀ denotes the wavenumber of light in free space, and P is the period of the meta-atom⁴⁷. By manipulating both θ_R and θ_L at each pixel, the RCP and LCP images can be independently designed. This allows for the creation of diverse polarization profiles by overlaying the RCP and LCP images within the deflection angle θ_r (see more discussions in Supplementary Note 4).

Fig. 5. Vectorial holographic imaging with multi-resonant metasurfaces.

a Two sets of PB phase gradient metasurfaces with opposing orientation angle increments. This design is intended to deflect both LCP and RCP images at the same angle, enabling controllable amplitude and phase distributions. The goal is to create a vectorial holographic image. b Schematic illustration of the optical setup used to experimentally characterize the holographic imaging of multi-resonant metasurfaces. The inset shows an optical microscope image of the fabricated sample. The images displayed on the screen schematically illustrate the expected results when the metasurface is illuminated by a 512 nm laser and characterized under circular polarization states. The gray dashed region indicates the designed observation position for information decryption. LP linear polarizer, QWP quarter-wave plate, AOFT acousto-optic tunable filter. c Schematic for the comprehensive vectorial holographic imaging at five peak wavelengths. All images spatially overlap when illuminated with five laser wavelengths simultaneously (top panel). When images are captured at the same spatial position (highlighted by the gray dashed rectangles in the bottom panel), distinct images emerge upon switching the laser wavelength. In each image, the numbers in the first row correspond to circular polarizations, while those in the second row correspond to linear polarizations. As an example, only the images in the first row, representing LCP states, are clearly observed in the bottom panel. d Experimental results of the vectorial holographic imaging at the designed observation angle. The bottom regions of each image correspond to the linear polarization channel, while the top regions are designated for circular polarization states. The dashed rectangles highlight the locations where the target numbers are expected to appear when all conditions (incident wavelength, polarization states, and observation angle) are met. More results can be found in Supplementary Fig. 18.

Figure 5b displays the optical setup used to evaluate the imaging performance of the multi-wavelength meta-hologram. A supercontinuum laser, in conjunction with an acousto-optic tunable filter, is used to select the incident wavelength. A linear polarizer (LP) is employed to define the incident polarization. The generated holographic images are projected onto a screen and recorded using a visible camera. These images are specifically designed to reveal the intended optical information only when the incident wavelength (Key N; λ_N), polarization state, and the spatial observation position are precisely aligned (refer to Supplementary Fig. 13). A quarter-wave plate (QWP) and an LP are placed in front of the camera to filter the polarization of the holographic images. Figure 5c schematically represents the designed multi-color holographic imaging concept. In the top panel of Fig. 5c, all color images overlap spatially when the metasurface is illuminated with a broadband light source, resulting in no discernible information on the screen. However, if images are captured at a fixed position (as indicated by the gray dashed rectangle in the top panel, which corresponds to the individual gray dashed rectangles in the bottom panel), distinct numbers in different colors become visible as the incident wavelength varies. To encrypt and decrypt the signal, two orthogonally polarized lights are superimposed at specific angles. For instance, LCP and RCP holographic images are placed in one region, while x-polarization (LP-0°) and y-polarization (LP-90°) images are placed in another. Each holographic image of these polarization states contains five digits ranging from 0 to 4. According to Eq. S5, the deflection angle of the images is dependent on the wavelength. By predefining the positions of the five holographic images, we can ensure they deflect at the same angle when illuminated by incident light of five different wavelengths. Therefore, by selecting a specific observation angle and changing the incident light wavelength, the observed numbers will correspondingly vary from 0 to 4 (refer to the bottom panel in Fig. 5c for the case of LCP). In fact, ensuring uniform holographic image sizes at different wavelengths requires the rescaling of each image during the encoding process into the metasurfaces. Further details and discussions can be found in Supplementary Note 5. Figure 5d presents experimentally captured holographic images at five wavelengths for four specifically designed polarization states. By varying the incident wavelength, the predesigned numbers become observable. The correct numbers are identified by pairing the QWP and LP. When the CCD’s position is fixed (i.e., images are captured at the same observation angle), all numbers are located nearly in the center of each image and exhibit nearly identical imaging sizes. This consistency validates the design and discussions outlined above.

Multi-resonant metasurfaces for optical encryption involves the integration of vectorial holographic images with structural colors

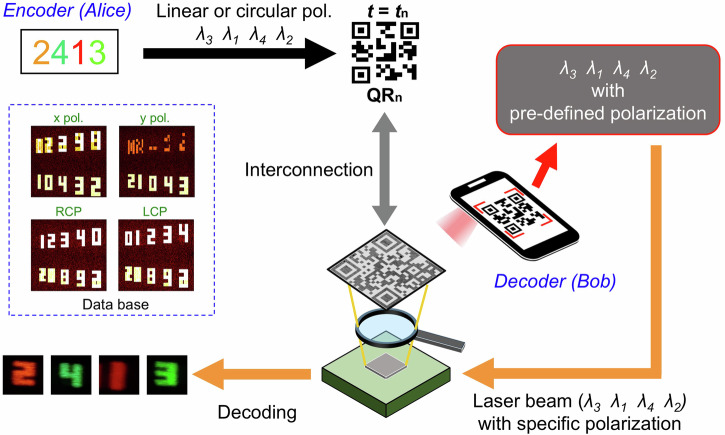
Finally, we propose a potential application in high-security optical encryption by integrating vectorial holographic images with structural colors, enabled by the development of multi-resonant high-Q metasurfaces. As a proof-of-concept demonstration, Fig. 6 schematically illustrates the processes involved in information decryption. The proposed metasurface exhibits multi-resonances at five wavelengths within the visible region (512 nm, 548 nm, 592 nm, 633 nm, 664 nm), enabling the design of a quinary encoding system. We would like to emphasize that the quinary encoding system is presented as an example. In reality, many other methods can be explored and further developed to create a more comprehensive optical information encryption system with metasurfaces^48–51. We employ the vectorial Fourier metasurface technique to generate vectorial holographic images in the far field. As a proof of concept, the polarization of the holographic images includes x-polarization, y-polarization, RCP, and LCP, each featuring five digital numbers from 0-4 (as demonstrated in Fig. 5d). Consequently, a total of 4 × 5 = 20 digits can be utilized for information encryption. It is worth noting that the information of the QR code can be dynamically altered in real-time using a dynamic QR code generator, facilitating real-time communication between the encrypter (e.g., Bob) and decrypter (e.g., Alice). The input wavelength ${\lambda }_m^i$ (i = 1, 2, 3, 4 indicating x-polarization, y-polarization, LCP and RCP, respectively; m = 1, 2, 3, 4, 5 denoting the wavelength channel) is encrypted in the QR code by Bob and can be scanned from the color print of the meta-hologram by Alice. For instance, if ${\lambda }_4^1$ = 633 nm, Alice can illuminate the meta-hologram with a laser of wavelength 633 nm. Subsequently, she can use a linear polarizer to identify the polarization of the images and categorize the x-polarized digits. The final digit can be ascertained by reading the number at the angle θ_r, allowing for the retrieval of the encoded information. In this manner, four digits in the quinary encoding system can be decrypted. As an example, if Bob wishes to transfer a code of 195 to Alice, he can encode the following information in the QR code: ${\lambda }_5^1$ = 664 nm, ${\lambda }_1^1$ = 512 nm, ${\lambda }_3^1$ = 592 nm, and ${\lambda }_4^1$ = 633 nm. By employing the decryption method described previously, Alice can decrypt the encoding information and obtain a code of 1240. However, since the information is based on the quinary encoding system, it needs to be converted as 0 × 5⁰ + 4 × 5¹ + 2 × 5² + 1 × 5³, thus allowing Alice to ultimately decrypt the code of 195.

Fig. 6. Schematic illustration of the real-time multi-channel optical encryption process.

The proposed potential optical encryption method combines vectorial holographic images with structural colors using multi-resonant high-Q metasurfaces, offering a possibility for secure quinary encoding system.

Discussion

In summary, we illustrated the development and validation of a microcavity-assisted multi-resonant metasurface platform capable of manipulating wavefronts across a broad spectral range. This platform achieves multiple resonant peaks by integrating subwavelength meta-atoms with a gradient-thickness DBR substrate. A gradient-thickness DBR mirror is chosen over a conventional λ/4 DBR mirror due to its ability to produce multiple high-Q resonances across a wider wavelength range, whereas the λ/4 DBR is limited to a narrower reflection bandwidth centered around its design wavelength. Although stacking two λ/4 DBR mirrors can extend the reflection range, it only supports high-Q resonances in specific wavelength regions (see Supplementary Fig. 22). This integration enables the coupling of plasmonic modes in the meta-atoms with FP modes within the alternating layers of the DBR mirror, which is crucial for achieving the multi-resonance feature. In contrast to previous multi-wavelength metasurfaces that are limited to presenting a few resonant peaks, our platform can generate up to 15 resonant peaks across the visible-NIR spectrum from 480 nm to 1000 nm while maintaining high operating efficiency, regardless of the number of peaks. As demonstrated in this work, the multi-resonant metasurface achieves a maximum efficiency of 81% (70.7%) in simulation (experiment) across 15 high-Q resonant peaks, with an average efficiency of 76.6% (54.5%) and a standard deviation of 4.1% (11.1%), respectively. The FP cavity characteristics ensure that each resonant peak exhibits a higher Q-factor than those typically seen in highly lossy plasmonic nanostructures. Furthermore, we demonstrated the versatility of our multi-resonant metasurface in modulating amplitude, phase, and wavefront at the peak wavelengths—a feat that was previously challenging (see Supplementary Table S1 for a comparison with previously reported high-Q metasurfaces). This versatility underscores its potential for advanced optical and nanophotonics applications. Moreover, the integration of vectorial holographic imaging and structural color printing vividly showcases the versatility of the developed multi-resonant high-Q metasurface, with broad applications in optical communication, bio-photonics, and information encryption. It is important to note that our proposal for optical information encryption serves as just one potential application of the wavefront control capabilities enabled by the multi-resonant high-Q metasurface developed in this work. The primary focus remains on demonstrating the versatility and potential of this metasurface platform for various applications, with encryption being one of many possibilities.

Indeed, the vectorial holographic imaging demonstrated in this study was restricted to the visible range due to the wavelength limitations of the camera (canon EOS 6D) used to capture the images. To verify wavefront control across all peak wavelengths from the visible to the NIR regions, we designed, fabricated, and optically characterized a gradient-phase metasurface featuring the developed multi-resonant capability. As illustrated in Supplementary Figs. 15 and 16, anomalous beam deflections were observed not only in the visible range but also in the NIR wavelengths, confirming the broadband response of the multi-resonant metasurface for wavefront engineering. Although imperfections in the sizes of fabricated meta-atoms may affect the circular conversion efficiency at specific wavelengths (see Supplementary Fig. 17), these variations do not significantly degrade the vectorial holographic imaging or information encryption performance, as long as the images remain detectable.

This study introduces a fundamentally different approach and optical behavior compared to conventional MIM-based metasurfaces, particularly in how multi-resonance spectral profiles can be tuned. In MIM metasurfaces, cavity resonance is governed by a fixed dielectric layer, simplifying the modeling of their spectral response. However, this fixed dielectric also results in higher Q-factors at shorter wavelengths (see Supplementary Fig. 2), as the cavity dielectric remains constant across all wavelengths. As a result, MIM metasurfaces have limited flexibility in controlling high-Q resonances, which always originate at shorter wavelengths, making it challenging to achieve resonances solely at longer wavelengths without also encountering peaks at shorter ones. In contrast, the gradient-thickness DBR-based metasurfaces presented here operate via a distinct mechanism, where interference within the dielectric layers creates tunable cavity effects. Light reflects and penetrates at various depths within the DBR structure depending on the wavelength and the thickness of the alternating dielectric layers. This tunability in resonance locations offers a significant advantage over the fixed nature of MIM metasurfaces, allowing for high-Q resonances to exhibit an opposite trend (see Supplementary Figs. 6, 9, 23, and 24) or to be specifically tailored for certain wavelength ranges, such as focusing exclusively on longer wavelengths (refer to Supplementary Fig. 25).

Another significant benefit of the proposed DBR-based metasurface is its practical ease of fabrication. While MIM metasurfaces require thick, micrometer-scale dielectric layers to generate multi-resonant high-Q responses, these layers can be challenging to fabricate due to cracking issues with standard deposition techniques. In contrast, the alternating dielectric layers in the DBR-based metasurface are on the nanometer scale, making them much easier to deposit experimentally. Furthermore, the gradient-thickness DBR-based metasurface allows greater control over the density and spacing of high-Q resonances, whereas the density in MIM metasurfaces is typically fixed.

It is worth noting that while the operating spectral window is within the visible-NIR spectrum, the proposed metasurface can, in principle, be adjusted to any desired wavelength band. The bandwidth of all multi-resonant peaks covered can also be flexibly modified by adjusting the high reflection window of the DBR substrate. Finally, we would like to highlight that both the peak efficiency and the number of high-Q peaks can be further enhanced. The peak efficiency can be improved by replacing the Al meta-atoms with metals that possess a higher plasmonic Q-factor, such as Ag. The number of high-Q peaks can be increased by adjusting the dielectric spacer thickness between the meta-atom and the DBR mirror (see Supplementary Fig. 26). This research breakthrough not only overcomes existing constraints in metasurface optics but also sets the stage for the creation of ultra-compact electro-optical devices with significant implications for sensing, imaging, and quantum communication. Looking ahead, the development of multi-resonant metasurfaces offers exciting prospects for various applications in photonics and beyond. The envisioned metasurface platform holds transformative potential for optical systems, marking the dawn of a new era for chip-based technologies and driving the field of nanophotonics into uncharted territories.

Methods

Sample fabrication

Firstly, a 120-nm-thick Al film is deposited onto a pre-prepared DBR substrate using thermal evaporation. Subsequently, a layer of SiO₂ with the designed thickness is deposited using a magnetron sputtering machine. Next, a layer of PMMA A4 photoresist is spin-coated onto the substrate at 600 rpm for 10 s, followed by 6000 rpm for 1 min. The sample is then baked on a hot plate at 180 °C for 3 min to dry the photoresist. Before e-beam exposure, a conductive polymer (Espacer) is spin-coated onto the sample to reduce the charging effect during the exposure process. The nanostructures are defined via e-beam exposure using an ELS-BODEN system. After exposure, the conductive polymer is removed with DI water, followed by the development process using a developer (MIBK: IPA = 1:3) for 2 min. The sample is then rinsed in IPA for 30 s to stop the development reaction (fixation). Following the development and fixation steps, a 50-nm-thick Al layer is deposited by thermal evaporation at a rate of 1 Å/s. Finally, the Al nanostructures are defined through a lift-off process by immersing the sample in acetone, which removes the remaining photoresist and leaves behind the desired Al meta-atoms. The gradient-thickness DBR mirror was procured directly from LiveStrong Optoelectronics Co., Ltd. To ensure precise control over the material quality and thickness during the deposition process, an e-gun system combined with ion-assisted deposition technique (OPFC-1300CBI/DBI from Optorun) was employed.

Numerical simulation

All numerical simulations were performed using the Frequency Domain Solver, which employs the Finite Element Method within the CST Studio Suite software. To predict the optical response of the DBR substrate, we modeled a 200 nm × 200 nm area with unit cell boundary conditions, effectively simulating the reflection spectrum of a substrate with an infinite area. For the parameter sweep and calculation of the plasmonic meta-atom, unit cell boundary conditions were used in both the x and y directions to simulate reflection and phase shift in an array configuration.

Design flow for the multi-resonant metasurface

To design a multi-resonant metasurface, the first step is to establish the working bandwidth, which is dictated by the high reflection window of the gradient-thickness DBR mirror. Next, we refine the plasmonic meta-atom positioned on the DBR mirror by adjusting its geometric parameters, such as the thickness, linewidth, and length of the Al nanostructure used in this study. For the PB phase effect to be validated, the nanostructure must be anisotropic in shape. The optimization process continues until we achieve the maximum circular polarization conversion at all peak wavelengths. Finally, the spectral positions of resonant peaks can be shifted by tuning the thin dielectric spacer between the topmost meta-atom and the DBR substrate. In practice, the shape of nanostructure can vary based on the desired spectral response, and the optimization concludes when the target spectral profile is attained.

Author contributions

P.C.W. and S.-H.H. conceived the original idea and designed the research; S.-H.H. designed and optimized the multi-wavelength meta-atoms, built up the optical setup, performed the numerical simulations, prepared the metasurface sample, and performed the optical measurement; H.-P.S. fabricated the large-scale meta-hologram, assisted in numerical simulations, and analyzed the data; C.Y.C. and Y.C.L. assisted in conducting the numerical simulations, sample fabrication, and optical measurements; Y.S. discussed and analyzed the results; Z.Y. and Q.S. developed the Matlab code for holographic imaging and analyzed the results; P.C.W. organized the project, designed experiments, analyzed the results, and prepared the manuscript; Y.S., Q.S., and P.C.W. supervised and coordinated the project; All authors discussed the results and commented on the manuscript.

Peer review

Peer review information

Nature Communications thanks Ho Wai Howard Lee, David Dang and the other, anonymous, reviewer for their contribution to the peer review of this work. A peer review file is available.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54057-9.