Abstract
Film-thermoelectric cooling devices are expected to provide a promising active thermal management solution with the continues increase of the power density of integrated circuit chips and other electronic devices. However, because the microstructure-related performance of thermoelectric films has not been perfectly matched with the device configuration, the potential of planar devices on chip heat dissipation has still not been fully exploited. Here, by liquid Te assistant growth method, highly (00 l) orientated Bi2Te3-based films which is comparable to single crystals are obtained in polycrystal films in this work. The high mobility stem from high orientation and low lattice thermal conductivity resulting from excess Te induced staggered stacking faults leads to high in-plane zT values ~1.53 and ~1.10 for P-type Bi0.4Sb1.6Te3 and N-type Bi2Te3 films, respectively. The planar devices basing on the geometrically designed high orientation films produce a remarkable temperature reduction of ~8.2 K in the hot spot elimination experiment, demonstrating the great benefit of Te assistant growth method for oriented planar Bi2Te3 films and planar devices devices design, and also bring great enlightenment to the next generation active thermal management for integrated circuits.
Subject terms: Electronic properties and materials, Electronic devices
The authors fabricate highly (00l) orientated Bi2Te3-based films by liquid Te assistant growth method, showing high mobility stemming from high orientation and low lattice thermal conductivity, resulting from excess Te induced staggered stacking faults.
Introduction
The heat dissipation problem of the chip package has become a key bottleneck limiting the performance of electronics products. In some mobile electronics application, the heat flux could increase over 100 W/cm2, and induces dynamic hot spots with temperature over 100 degree C, which greatly deteriorates the performance and service lifetime of customer electronics. Film thermoelectric cooling devices(f-TEC), which based on the Peltier effect1, have great advantages such as miniature2, high reliability, and especially, high response speed3 that is compatible with the dynamic operation of circuit chips and is highly expected as one of the solutions for the dynamic hot spots dissipation of chips.
In past decades, two typical configurations of f-TECs have been developed4. One is the vertical f-TEC which can pump the heat from the hot spot directly to the packaging heat sink in the cross-plane direction. This type f-TEC could reach a high cooling density up to 200 (W/cm2)5, but it also increases local heat dissipation load for the back end heat sink due to the large power consumption of f-TEC itself. Therefore, the benefit of the high cooling density of vertical f-TEC is often offset by the backward heat flow, and can hardly contributes to the hot spot dissipation6. The other configuration is the planar f-TEC which could spread the heat from the local hot spot to a broader plane (Fig. 1a). Despite the cooling density of the planar configuration is not so high as the vertical types, it could also clip the transient peak temperature of the hot spot and increase the transfer area to the heat sink7, thus providing more flexibility for integrational thermal management solution.
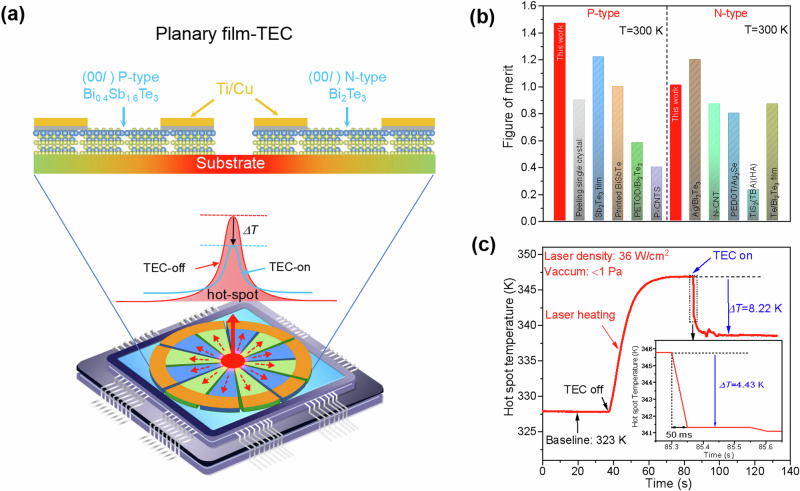
Fig. 1. Planar f-TEC for hot spot cooling.
a Schematic illustration of planar f-TEC working process for hot spot cooling and the f-TEC structure; (b) zT value @300 K obtained in this work together with reported values of P-type13,35–38 and N-type10,24,39–41 films for comparison; (c)The cooling ability for laser heated hot spot with f-TEC prepared in this work.
The cooling ability of both types of f-TECs largely depend on the figure of merit of constituted thermoelectric materials, which is qualified by zT = S2T/ρ(κE+κL), where S, T, ρ,κE and κL are Seebeck coefficient, absolute temperature, electrical resistivity, electronic and lattice component of the thermal conductivity, respectively. Bi2Te3 is the state-of-art mostly adopted material8 to construct various vertical3/planar f-TECs7. Nevertheless, since Bi2Te3 has a typical layered crystal structure and shows superior thermoelectric power factor parallel to the (00 l) planes, thus, in order to realize the maximum cooling ability, the film orientation needs to be consistent with the direction of heat flow in specific device configuration (Fig. 1a). However, since the (00 l) orientation would greatly decrease when the thickness is above several micrometers, the in-plane power factor (PF, defined as S2/ρ) and zTs of widely electrodeposited9, magnetron sputtered10 or thermally deposited inorganic Bi2Te3 films11 are still far from that of bulk Bi2Te3 alloys12 or Bi2Te3 single crystal nanosheets13 (PF ~ 42 μWcm−1K−2 and zT ~ 1.1). As a result, the planar thin film devices consistently fail to achieve large cooling ability, and the feasibility of planar f-TEC for removing hot spot is still underestimated.
In this work, a simple Te-rich gradient deposition method was developed for achieving highly orientated Bi2Te3-based thick films. The gradiently increased extra Te accelerated small grains grow planarly when annealing near Te melting point temperature, and also facilitated the Bi-Te antisite defect blossom into staggered stacking faults in the lattice. The films are highly (00 l) orientated which is comparable to single crystals or single crystal nanosheets. Benefiting from the high in-plane carrier mobility stemming from high (00 l) orientation, and the low lattice thermal conductivity resulting from in-plane staggered stacking faults, the films show rather high power factor (~45 μWcm−1K−2 for P-type and ~30 μWcm−1K−2 for N-type (Fig. S1) which is comparable to reported single crystal sheets13, and superior in-plane zT values of 1.53 for P-type Bi0.4Sb1.6Te3 and 1.10 for N-type Bi2Te3, respectively (Fig. 1b). Based on the high in-plane TE performance, the planar f-TEC generates a high-record (Fig. 1c) temperature reduction (ΔT ~ 8.2 K) for the hot spot simulated by laser heating. In detail, the initial temperature reduction reaches 4.43 K within 50 ms, exhibiting an excellent response speed and demonstrating great potential for active hot spot elimination.
Results and discussion
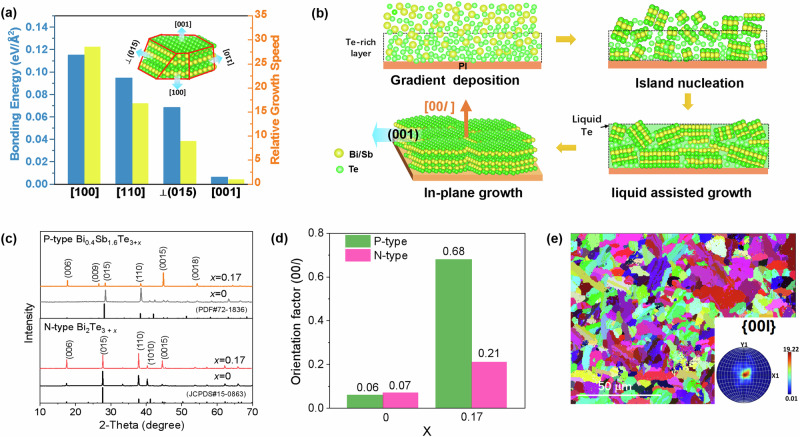
The P-type Bi0.4Sb1.6Te3 and N-type Bi2Te3 films were deposited by a two-step magnetron co-sputtering process in this work. Firstly, the Bi0.4Sb1.6Te3 or Bi2Te3 targets are sputtered together with an additional Te target for a given time, and then Te target is powered off, only the compound target is sputtered to reach the desired thickness of ~4 μm. Thus, the as-deposited film is rich of Te atoms at the bottom with a certain thickness (Fig. S2). In principle, the amorphous atoms nucleate in random orientations initially, and then the crystal nuclears grow up gradually during the post-annealing. According to the chemical bonding theory of single crystal growth14, the anisotropic growth rate can be expressed by , where Euvw and Auvw is the chemical bonding energy and the projection area of growth unit along the [uvw] direction at the growth plane, duvw is the net space of (hkl) planes along the [uvw] direction, and K is the growth constant. For Bi2Te3 compound, the calculated chemical bonding energy and the anisotropic growth rate of different crystal orientations clearly show that the growth rate along (00 l) planes is almost ten times higher than that of vertical (015) planes, and also about 3 times higher than that along (015) planes, as shown in Fig. 2a. When the annealing temperature is up to 673 K, which is close to the melting point of Te, the extra Te atoms at the bottom tend to form a liquid amorphous phase, as proved by XRD patterns (Fig. S3) and the differential scanning calorimeter (DSC) curve near 675 K (Fig. S4). The liquid Te at the bottom would rapidly diffuse to the whole films, which could further accelerate the anisotropy growth rate. Meanwhile, since the vertical space is limited by the total thickness of the as-deposited film, the grains which is parallel to the substrate would grow much larger than those vertical to the substrate, then they could dissolve the small grains that are not parallel to the substrate (the process sketch is illustrated in Fig. 2b). This phenomenon is highly consistent with the liquid-phase sintering process of bulk ceramics and powder metallurgy materials15,16. Therefore, the films exhibit an extremely high (00 l) orientation, which is desired for the planer f-TEC. As shown in Fig. 2c, after annealing at 673 K for 1 hour, the intensity of (00 l) peaks gradually increase and the intensity of (015) peaks decrease simultaneously with the increase of Te content at room temperature (Fig. 2c and Fig. S5) for both P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x films. Especially, for P-type Bi0.4Sb1.6Te3+x films, the orientation factor F jumps from 0.08 for x = 0 to 0.68 fo x = 0.17, and then to 0.84 for x = 0.24, which is comparable to the zone-melting crystals (Fig. 2d and Fig. S6). Moreover, the sharply enhanced (00 l) orientation is also consistent with the large planar grain size of SEM and EBSD result as presented in Fig. 2e and Figs. S7–S10. For P-type Bi0.4Sb1.6Te3+x films with x = 0.17, the mean grain size obviously enlarged from 0.21μm to 5.41μm, and the orientation becomes more intense and concentrated in (00 l) crystal direction, indicating the gradient deposition of extra Te greatly enhance the (00 l) orientation. Meanwhile, the EDS images in Fig. S8 showed that trace of residual Te precipitate at the grain boundaries, but the final components inside of Bi0.4Sb1.6Te3 and Bi2Te3 grains are close to the stoichiometric ratio (Table S1).
Fig. 2. Orientation enhancement by Te-assistant growth for Bi2Te3-based films.
a The bonding energy and relative growth speed for different crystal directions of Bi2Te3; (b) and the sketch map of in-plane growth of Bi2Te3 film with additional Te; The room temperature XRD patterns (c) and corresponding orientation factor F (d) for P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x films (x = 0 and 0.17); (e)The EBSD images and the polar diagram inset of P-type x = 0.17 sample.
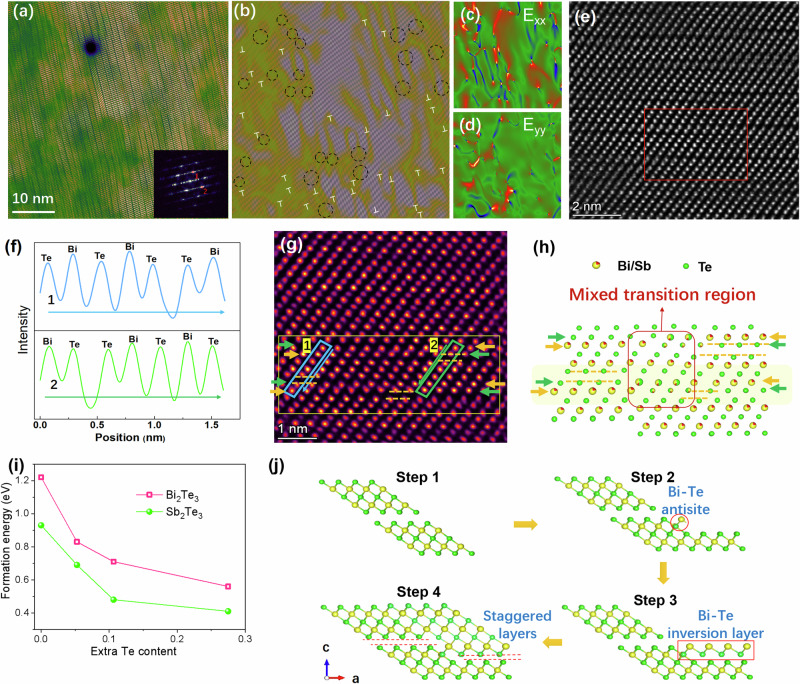
The liquid-Te assisted growth based on gradient deposition not only elevate the (00 l) orientation, but also bring abundant hierarchical microstructure for the films. The microstructure of grains for P-type x = 0.17 sample is characterized by high-resolution transmission electron microscopy (HRTEM) in Fig. 3. Normally, repetitive quintuple layers with a sequence of Te–(BiSb)–Te–(BiSb)–Te were stacked to form the regular Van der Waals layered structure of Bi2Te3. However, in current study, tremendous of staggered stacking faults can be found through out the whole film as shown in Fig. 3a, b. These staggered structure can be clearly identified as that a bilayer in one quintuple-layer unit splits out and combines with the adjacent quintuple layers unit forming a new seven-layer unit. The atomic configuration is carefully examined by Aberration-corrected high-angle annular dark-field (HAADF) in Fig. 3e, where the intensity of atomic columns is roughly proportional to atomic number (Fig. 3f). The bilayer of Te–(BiSb) in Zone 1 gradually split out from the original quintuple layers unit and changed into inverse (BiSb)-Te bilayer, thus combines with upper quintuple layers unit and forms new Van der Waals gap (Fig. 3g). The original two folds of Te–(BiSb)–Te–(BiSb)–Te unit was reformed by the group of triple Te–(BiSb)–Te layers and Te–(BiSb)–Te–(BiSb)–Te–(BiSb)–Te sevenlayers. This split-recombination behavior could occur in every few dozens of lattice distance in both direction of along and vertical the Van der Waals layers, thus induce tense of lattice strain comparing with the regular Van der Waals lattice, as shown in Fig. 3c, d and Figs. S11, S12. This phenomenon is very similar with the defects evolution of (Bi/Sb)2(Te/Se)3 single crystal under in-situ stress, which was reported by Lu13. Differently, the staggered stacking faults in current study is formed during the annealing process and can be stably maintained, other than formed under external mechanical stress. The formation of this staggered stacking faults structure can be assumed caused by that in Te rich circumstance the (Bi/Sb)-Te antisite defect is more easily to generate compared with normal stoichiometry, and the continuous arrangement of antisite defects leads to the exposed Bi/Sb chemical bonds connect with the Te atoms in the next lattice unit and leaving Te to Te vader Wal gap with the original lattice unit. This hypothesis is verified by the calculated formation energy of antisite defects in Bi2Te3 and Sb2Te3 under different Te chemical potential. As shown in Fig. 3i, with Te content increasing, the formation energies of both Bi-Te or Sb-Te antisites are apparently reduced. Each Bi-Te antisite defect can be served as a nucleation and induce an inverse (Bi/Sb)-Te bilayer, thus eventually forming the dispersed staggered layers structure in the whole films, as exhibited in Fig. 3j.
Fig. 3. Microscopic staggered defects in liquid-Te assisted growth.
a HAADF-STEM image, (b) the corresponding inverse Fourier transform image and (c, d) GPA results along xx and yy direction of the P-type Bi0.4Sb1.6Te3+x (x = 0.17) sample. a shows tense of staggerd layers structure among the lattice, and the symbol ⊥ in (b) indicates dislocations and the black circle represents the termination point of the staggered stacking faults, showing tense of staggered layers structure among the lattice; (e) high-magnification image of the staggerd layers structure; (f) the image intensity along the arrow 1 and 2 in the enlarged high-magnification TEM image (g) of the single typical staggered layers; (h) the atomic configuration map of the single typical staggered layers in (g); (i) the formation energy of typical defects in Bi2Te3 and Sb2Te3 compounds under different Te chemical potential; (j) the sketch map of staggered layers generation mechanism.
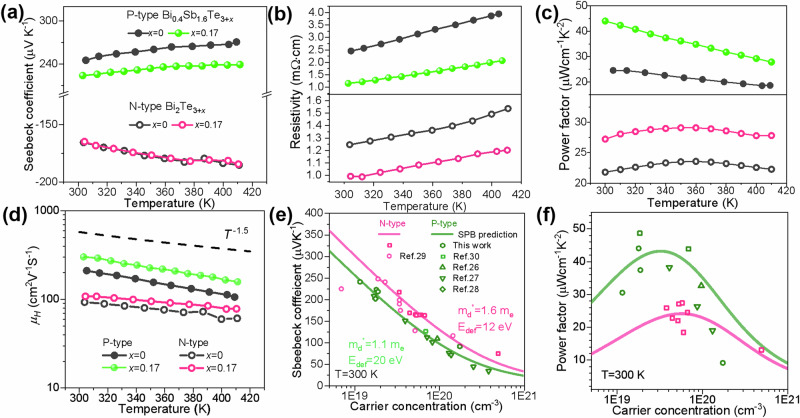
The hierarchical microstructure leads to a significant improvement of thermoelectrical performance of Bi2Te3-based films. Firstly, the enlarged grain size and high orientation are beneficial for the in-plane electrical properties. The temperature-dependent Seebeck coefficient, resistivity, and power factor for P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x films are displayed in Fig. 4a–c and Fig. S13, individually. All the samples studied here show a typical degenerate semiconductor behavior, meaning an increase of Seebeck and resistivity with increasing temperature. Since most extra Te has been evaporated after annealing, the carrier concentration tends to reach stabilization when x is above 0.17 both for P-type and N-type films, as shown in Fig. S14. For P-type films in this work, the hall carrier concentration-dependent hall mobility is greatly enhanced to about ~300 cm2V−1s−1 for x = 0.17 sample at room temperature because of the high orientation, which is comparable to bulk zone-melting crystal13, while the carrier mobility of N-type x = 0.17 is also up to 120 cm2V−1s−1 (Fig. S14). The hall carrier concentration dependent Seebeck coefficient, hall mobility, and power factor for both P-type and N-type are displayed in Fig. 4d–f, together with those of bulk Bi0.4Sb1.6Te3 and Bi2Te3 data for comparison17–21. For both N-type and P-type films the hall carrier concentration dependent Seebeck coefficient in this work are consistent with those of reported bulk materials and the predicted solid line, which is based on the single parabolic band model22,23. The density of state effective mass and deformation potential about md*~1.1 me, Edef ~ 20 eV for P-type and md*~1.6 me, Edef ~ 12 eV for N-type films are taken individually for the solid Pisarenko lines. The models adopted above took the acoustic phonon scattering as the dominated scattering mechanism, which can be demonstrated by the T−1.5 temperature dependent hall mobility in Fig. 4d. Benefiting from the high mobility induced by high (00l) orientation and large grain size, the final power factor of P-type films reaches ~45 μWcm−1K−2 at room temperature (Fig. 4c), which is comparable to zone-melting Bi0.4Sb1.6Te3 crystals17–21, and outbalancing most of the reported thermoelectric films. Besides, the power factor of ~30 μWcm−1K−2 for N-type films at room temperature also ranks ahead among the reported high values10,24,25. These results further indicate that a high orientation is beneficial for the electrical properties of Bi2Te3-based thermoelectric films.
Fig. 4. The electrical properties of P- and N-type Bi2Te3-based films.
The temperature-dependent electrical properities including Seebeck coefficient (a), resitivity (b), power factor (c) and mobility (d) for P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x (x = 0 and 0.17) films; The room temperature hall carrier concentration-dependent Seebeck coefficient (e), power factor (f) for P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x (0 ≤ x ≤ 0.24) films in this work, with a comparison to those of reported bulk materials17–20,42.
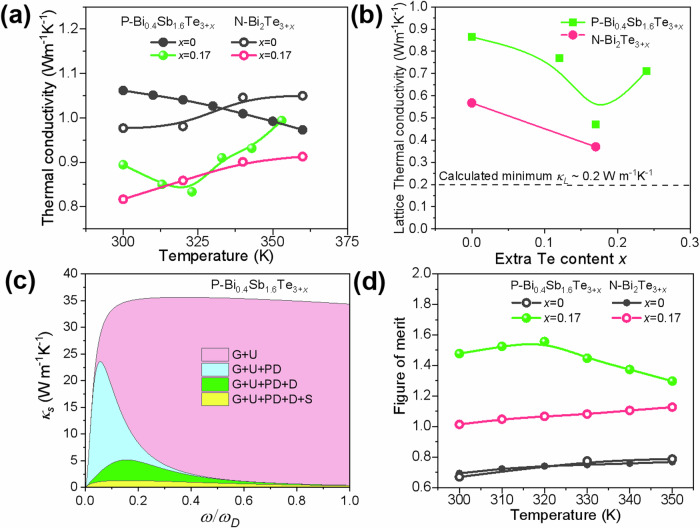
On the other hand, the dispersed staggered layers structure induced by the liquid Te assisted growth could greatly enhance the phonon scattering, thus depress the thermal conductivity. As discussed above, the staggered layers structure is more likely a mixture of dislocations and stacking faults. The beginning of the splitting gap of layers can be regarded as the dislocation core formed by the absent layers thus exhibits one dimensional character, meanwhile the inverse (Bi/Sb)-Te bilayers can be regarded as two-dimensional stacking faults. Both of these defects and the induced concentrated stress could greatly scatter phonons. The thermal conductivity of the films were measured by TPET method26 (details can be found in supporting information) and the corresponding raw data used to fit the thermal diffusion coefficient are illustrated in Tables S2, S3. The thermal conductivity of gradiently deposited samples is obviously lower for both P-type and N-type films, although they have larger grain size after liquid Te assisted growth. The lattice thermal conductivity is estimated by subtracting the electronic component (κE = LT/ρ) from total thermal conductivity, where the Lorenz factor (L) is determined based on a single parabolic band model approximation. The lattice thermal conductivity is as low as 0.45 Wm−1K−1 at room temperature for P-type x = 0.17 sample and ~0.3 Wm−1K−1 for N-type x = 0.17 sample (Fig. 5b), which approaches the minimum value according to Cahill model10. We further carefully fit the lattice thermal conductivity of P-type Bi0.4Sb1.6Te3+x films according to Debye–Callaway model and exhibit the results in Fig. 5c, Fig. S15 and Tables S4, S5. The dispersed staggered structure greatly enhanced the scattering effect from dislocations and stacking faults, especially for the low-frequency range in the phonon spectrum. Benefiting from the high power factor and the low lattice thermal conductivity, the final figure of merit value ~ 1.47 for P-type Bi0.4Sb1.6Te3+x and ~ 1.02 for N-type Bi2Te3+x film are achieved at room temperature when x = 0.17, as shown in Fig. 5d, and with the increase of temperature, the maximum zTs could achieve 1.53 and 1.10, respectively.
Fig. 5. Thermal transport properties, and zT of P- and N-type films.
a Temperature dependent total thermal conductivity and (b) lattice thermal conductivity versus Te content for P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x films; (c) Room-temperature spectral lattice thermal conductivity (κs) calculated using the Debye–Callaway model. G represents grain boundary scattering, U refers to the Umklapp process, PD refers to the point defect scattering, and D refers to the dislocation scattering, and S refers to the stacking faults scattering. d thermoelectric figure of merit for P-type Bi0.4Sb1.6Te3+x and N-type Bi2Te3+x films in this work.
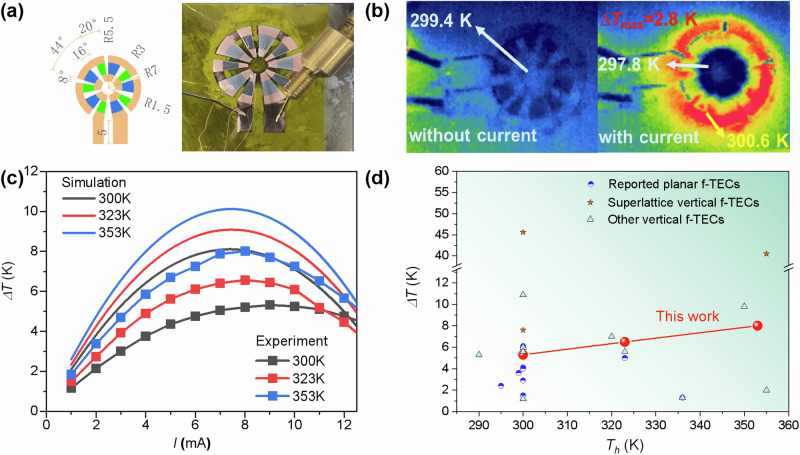
To further demonstrate the cooling ability of the obtained thermoelectric films, a five pairs planar f-TEC was designed by finite-element simulations as shown in Fig. S16. As shown in Fig. 6a with geometric drawing, the final film thermoelectric cooler had a lateral dimension of 7 mm with outer radius, and in vertiacal dimension, thermoelectric P/N films ~4 μm, Ti diffusion barrier ~500 nm and Cu electrode ~2 μm in thicknesses are deposited on PI substrate in order with designed patterns by masks. As captured by an inferred camera, the film thermoelectric cooler (f-TEC) shows 2.8 K temperature difference in air between the center and outside of the device when the working current is 8 mA (Fig. 6b). Furthermore, a high maximum ΔT (ΔTmax) ~ 5.3 K for Th = 300 K can be obtained in the vacuum, and it increases to 8.01 K when Th = 353 K (Fig. 6c, d), which is superior to the reported planar f-TEC modules as shown in Fig. 6d. This steady ΔTmax value is also consistent with the result in the transient laser hot spot elimination test as shown in Fig. 1d and repeated test in Fig. S17, which demonstrated the high reliability of the f-TEC prepared in this work and highlights the high superiority of gradient sputter process for the TE performance improvement of Bi2Te3-based films. Considering the total thickness of the Bi2Te3-based TE film is about 4 μm, the additional out-plane interfacial thermal resistance is only equivalent to about 0.04 cm2K/W. This value is about one level lower than current typical thermal interface materials27, which would not significantly worsen the out-plane heat transfer to the heat sink in the chip package. Meanwhile, this planar device can also serve as flexible TEG device, and provides a highest power density of 298.2 W/m2 among the published works at the temperature difference ~50 K, as shown in Fig. S18, which shows great potential on wearable electronics.
Fig. 6. Cooling Performance of obtained planar film thermoelectric devices.
The optimized geometric dimensions and f-TEC prepared in this work (a); the cooling ability in air captured by inferred camera at 300 K (b); the current dependent cooling temperature of simulation and experiment result at different hot end temperatures (c); the maximum cooling temperature at different hot end temperatures, together with the reported planar7,10,43–49, superlattice vertical5,50 and other vertical f-TECs for comparison2,3,5,50–53 (d).
This work systemically developed a gradient co-sputter method to obtain high thermoelectric performances of Bi2Te3-based films. The promotion of the extra Te phase and post-annealing near the Te melting point can effectively facilitate the growth of grains and enhance the orientation of (00 l) plane comparable to single crystals. Meanwhile, the rapid growth of the grains in the Te-rich circumstance could promote the formation of Bi/Sb-Te antisite and induce tremendous of staggered stacking faults defects. On account of the high orientation and large grain size induced high power factor and stacking defects induced low lattice thermal conductivity, high zT values of ~1.5 for P-type Bi0.4Sb1.6Te3 and ~1.1 for N-type Bi2Te3 films have been achieved near room temperature in this work. Based on the high performance TE films, a planar f-TEC was designed and fabricated on PI substrate. The transient hot spot eliminating experiment simulated by laser heating showed that such planar f-TEC could realize a remarkable temperature reduction ΔT ~ 8.2 K in few milliseconds, which verified the feasibility of planar f-TEC for chip cooling. It is worth noting that, the sputtering process is highly compatible with the CMOS process, and also costs much less than MBE and MOCVD technologies for superlattice films, therefore, giving it a great potential to embed in chips integration process or packaging process and enlightening the future development of thermal management design for the electronics industry.
Methods
Magnetron sputtering for n- and P-type thermoelectric materials
Polycrystalline P-type Bi0.4Sb1.6Te3 and N-type Bi2Te3 films with thickness of 4 μm are deposited on flexible clean PI substrates by a two-step magnetron sputtering process, and the as-deposited films are composed of Te-rich bottom layer and the nominal composition up layer. The magnetron sputtering equipment for deposition of BST/BT films is PVD75 PRO (Kurt J. Lesker Company). The samples in this work are named after Bi0.4Sb1.6Te3+x (x = 0, 0.12, 0.17, 0.24) (P-type) and Bi2Te3+x (x = 0, 0.08, 0.12 and 0.17) (N-type) where x is the calculated extra Te content. The obtained as-deposited films were then annealed at 673 K (N-type) and 723 K (P-type) for 1 h for the uniform distribution of Te. The raw commercial Bi2Te3, Bi0.4Sb1.6Te3 and Te targets are 76.2 mm in diameter (99.99% purity) from Zhongnuo Advanced Material (Beijing) Technology Co., Ltd. The targets are 15 cm below the substrates. To supplement different content of Te, the Te target adopts different co-sputtering ratio of the whole process time (0, 50%,70% and 100%) to provide different proportion of excess Te for Bi0.4Sb1.6Te3+x (x = 0, 0.12, 0.17, 0.24) and Bi2Te3+x (x = 0, 0.08, 0.12 and 0.17) for BST/BT film. The proportion of time is consistent with the change trend of Te supplement. The BST/BT target is sputtered and deposited using a DC power supply (90 W), but the Te target is powered by the RF supply (30 W). The total deposition time is 135 mins for the 4 μm film when fabricating the devices.
Film thermoelectric device design and integration
A five pairs of planar film device is designed and the geometric size is optimized by COMSOL simulation based on the thermoelectric property of obtained N-type and P-type films. In simulation, the whole system is placed in a vacuum insulated environment, the boundary temperature of the hot end of the device is set to be 300 K, and contact resistance of 5 µΩ cm2 is adopted. The structure size with inner radius ~1.5 mm, outer radius ~7 mm, electrode width ~1.5 mm are used for the planar film device. And the total angle of each pair is 56°, the spacing of adjacent pairs is 16°, the spacing with n/p-legs is 8°. The specific angles of p/n-legs were optimized within the range of 24° ± 8°. The device with optimized geometry is fabricated with designed masks and the layers are stacked with thermoelectric films (4 μm), Cu electrode (2 μm) and barrier layer Ti (500 nm) individually on 50 μm PI substrate.
Transient photo-electro-thermal (TPET) technique for thermal conductivity measurement
In the TPET method26, TE films were cut into thin strips and suspended between two aluminum electrodes to record the temperature rise induced voltage increase by an oscilloscope when vertical laser was applied. The characteristic time ∆tc is identified from the θnorm (normalized temperature elevation) ~t curve when θnorm reaches 0.8665. And the measured thermal diffusivity can be determined as αmea = 0.2026L2/∆tc. The measurement was carried on with different length samples, and the total thermal diffusivity (αcon) of the samples and support film could be obtained from the intercept of the fitted line which is determined by thermal diffusion (αmea) and the square of sample length (L2).
| 1 |
ρ is the density, Cp is the specific heat, εr is the emissivity of sample, σ is the Stephen–Boltzmann constant, d is the thickness of the sample respectively.
The thermal diffusivity coefficient of the film (αTE) was obtained by deducting the thermal diffusivity of the PI film (αsub) apart from the total thermal diffusivity (αcon) of the film and substrate according to the following equations.
| 2 |
| 3 |
| 4 |
In this work, the thickness of PI substrate is 6 µm, and the measured αsub is measured by the same method. The uncertainty of the result is about 5% considering the heat loss due to heat radiation and heat in the direction perpendicular to the sample and substrate.
Device cooling and generation performance measurement
The thermoelectric cooling temperature was evaluated by a homemade thermoelectric cooling test system under the vacuum of 0.5 ~ 1.0 Pa. Thermocouples were pressed on the center and outer circle of the f-TEC to collect the temperature, and a direct current (Keithley, 6221) with scan step of 1 mA in the range of 0 ~ 15 mA was supplied. An infrared camera was taken to capture the actual temperature difference between the center cold side and the outer circle hot side at room temperature in air when the device was working. The laser heat dissipation experiment to simulate the chip’s hot spot heat dissipation was also completed on this platform, and the device was placed at an ambient temperature of 327 K to simulate the chip’s working temperature. The input power of the laser with a wave of 808 nm (MDL-H-808-6W) is from 1.0 W to 6.0 W, and the spot diameter is 3.0 mm. All the heating is by irradiating the center of the device vertically at 300 K. The thermocouple was used to measure the temperature at hot and cold ends when scanning the current to the device. The power generation test of the device was conducted on same platform. The temperature rise of the hot end (Th) of device was provided by an external copper-based heating block, and the temperature control of the cold end (Tc = 300 K) was provided by the heat sink. During the test, a nanovoltmeter was used (Keithley, 2181 A) to obtain the voltage under different conditions of ∆T.
Debye–Callaway model for fitting lattice thermal conductivity
According to the Debye–Callaway model, the lattice thermal conductivity with doping or alloying can be calculated with the following equation28:
| 5 |
The integrand item in conjunction with the coefficient of above equation is the spectral lattice thermal conductivity (κs), namely:
| 6 |
where kB is the Boltzmann constant, νs is average sound speed, ℏ is the reduced Plank constant, θD is Debye temperature, τtot is total relaxation time and x = ℏω/kBT (ω denoting the phonon frequency) is the reduced phonon frequency. Due to the particularity of staggered stacking faults in this work, we considered five phonon scattering mechanisms here, including Umklappp phonon-phonon scattering, grain boundary scattering, point defect scattering, dislocation scattering, and stacking faults scattering, which are given by:
| 7 |
Umklappp phonon-phonon scattering29:
| 8 |
Grain boundary scattering:
| 9 |
| 10 |
For dislocation scattering, there are two parts of scattering sources, dislocation cores and dislocation strain, which can respectively be given by refs. 10,32
| 11 |
Stacking faults scattering33,34:
| 12 |
where γ is the Gruneisen parameter, θD is the Debye temperature, νs is average sound speed, is the average atomic mass, is the average atomic volume, Γ is the disorder scattering parameter, L is the average grain size, Bd is the Burgers vector and b is the 2D dimension of staggered stacking faults, which were both considered as the van der waals gap, Nd is the dislocation density, r is the Poisson’s ratio, and Ns is the number of staggered layers in a line of unit length, respectively, which can be obtained.
Then, the overall phonon scattering relaxation time is expressed as:
| 13 |
where A, B, C, D and E are the fitting parameters for point defect scattering, phonon–phonon Umklapp scattering, dislocations core and strain scattering, stacking faults scattering, respectively.
Supplementary information
Acknowledgements
This work was funded by Key-Area Research and Development Program of Guangdong Province (No. 2024B0101040002), the Shenzhen Science and Technology Research Funding (NO. JCYJ20210324115611030 and RCBS20221008093339097), Guang Dong Basic and Applied Basic Research Foundation (No. 2022B1515020066), the National Natural Science foundation of China (52472268 and 22309120), the National Key R&D Program of China (2021YFB3201100). We would also acknowledge Prof. Lidong Chen from Shanghai Institute of ceramics, Chinese academy of Science for the discussion about research proposal, Dr. Jinni Shen from Fuzhou University for the discussion about anisotropic growth calculation, Mrs. Yang Zhang and Mr. Chuansheng Ma from Instrument Analysis Center of Xi’an Jiaotong University for the support of advanced electron microscopies.
Author contributions
G.D., J.F., and G.Q. contributed equally to this work. G.D. performed the P-type films synthesis, T.E. performance test and the devices simulation; G.Q. carried out the N-type films synthesis, T.E. performance test and the devices fabrication; J.F., G.Li, Y.X., Y.Y.and H.W. carried out the microstructure characterization; Q.C., L.X., C.L., J.Y. and J.L. performed the ab calculation. Y.L., Y.Q. carried out the steady and transient test of the TEC device and thermal conductivity characterization. J.L. performed the TE property modeling and wrote the manuscript. R.L. designed and supervised the experiments, performed manuscript revision. R.S. gave the supervision for the research project. All authors contributed to the data analysis, discussed the results and commented on the manuscript.
Peer review
Peer review information
Nature Communications thanks Gao Qing (Max) Lu, Dongwang Yang, and Peng-an Zong reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
Most of the original data are found in the supplementary Information. All data generated are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Guoying Dong, Jianghe Feng, Guojuan Qiu.
Contributor Information
Haijun Wu, Email: wuhaijunnavy@xjtu.edu.cn.
Juan Li, Email: j.li1@siat.ac.cn.
Ruiheng Liu, Email: rh.liu@siat.ac.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-54017-3.
References
- 1.Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science321, 1457–1461 (2008). [DOI] [PubMed] [Google Scholar]
- 2.Snyder, G. J., Lim, J. R., Huang, C. K. & Fleurial, J. P. Thermoelectric microdevice fabricated by a MEMS-like electrochemical process. Nat. Mater.2, 528–531 (2003). [DOI] [PubMed] [Google Scholar]
- 3.Li, G. et al. Integrated microthermoelectric coolers with rapid response time and high device reliability. Nat. Electron.1, 555–561 (2018). [Google Scholar]
- 4.Zhang, Q. H., Deng, K. F., Wilkens, L., Reith, H. & Nielsch, K. Micro-thermoelectric devices. Nat. Electron.5, 333–347 (2022). [Google Scholar]
- 5.Bulman, G. et al. Superlattice-based thin-film thermoelectric modules with high cooling fluxes. Nat. Commun.7, 10302 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kim, C. et al. Effect of thermoelectric leg thickness in a planar thin film TEC device on different substrates. Electron Mater. Lett.15, 686–692 (2019). [Google Scholar]
- 7.Cheol Kim, M.-W. J. et al. Planar-radial structured thermoelectric cooler for local hot spot cooling in mobile electronics. 2020 IEEE 70th Electronic Components and Technology Conference (2020).
- 8.Venkatasubramanian, R., Siivola, E. & Colpitts, T. O’Quinn B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature413, 597–602 (2001). [DOI] [PubMed] [Google Scholar]
- 9.Manzano, C. V. et al. Anisotropic effects on the thermoelectric properties of highly oriented electrodeposited Bi2Te3 films. Sci. Rep.6, 19129 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zheng, Z.-H. et al. Harvesting waste heat with flexible Bi2Te3 thermoelectric thin film. Nat. Sustain.6, 180–191 (2022). [Google Scholar]
- 11.Tan, M., Hao, Y., Deng, Y., Yan, D. & Wu, Z. Tilt-structure and high-performance of hierarchical Bi1.5Sb0.5Te3 nanopillar arrays. Sci. Rep.8, 6384 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Poudel, B. et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science320, 634–638 (2008). [DOI] [PubMed] [Google Scholar]
- 13.Lu, Y. et al. Staggered-layer-boosted flexible Bi2Te3 films with high thermoelectric performance. Nat. Nanotechnol.18, 1281–1288 (2023). [DOI] [PubMed] [Google Scholar]
- 14.Sun, C. & Xue, D. Chemical bonding theory of single crystal growth and its application to ϕ 3′′ YAG bulk crystal. Crystengcomm16, 2129–2135 (2014). [Google Scholar]
- 15.Pan, Y. et al. Synergistic modulation of mobility and thermal conductivity in (Bi,Sb)2Te3 towards high thermoelectric performance. Energ. Environ. Sci.12, 624–630 (2019). [Google Scholar]
- 16.Melnikov, A. Powder metallurgy for thermoelectrics. Met. Powder Rep.71, 279–284 (2016). [Google Scholar]
- 17.Testardi, L. R., Bierly, J. N. & Donahoe, F. J. Transport properties of p-type Bi2Te3-Sb2Te3 alloys in the temperature range 80–370 °K. J. Phys. Chem. Solids23, 1209–1217 (1962). [Google Scholar]
- 18.Gaidukova, V.S., Erofeev, R. S., Ovechkina, V. N. Characteristics of the energy spectrum of solid solutions in the SbTe-BiTe system, 17. Neorg. Mater. Izv. Akad. Nauk SSSR, 1981.
- 19.Jiang, J., Chen, L., Bai, S., Yao, Q. & Wang, Q. Thermoelectric properties of p-type (Bi2Te3)x(Sb2Te3)1−x crystals prepared via zone melting. J. Cryst. Growth277, 258–263 (2005). [Google Scholar]
- 20.Scherrer, S. S. Bismuth Telluride, Antimony Telluride and their Solid Solutions (CRC Press, 1995).
- 21.Rowe, D. M. CRC Handbook of thermoelectric (CRC Press, 1995).
- 22.May, A. F. Materials, Preparation, and Characterization in Thermoelectrics (CRC Press, 2017).
- 23.Kane, E. O. Band structure of indium antimonide. J. Phys. Chem. Solids1, 249–261 (1957). [Google Scholar]
- 24.Jin, Q. et al. Flexible layer-structured Bi2Te3 thermoelectric on a carbon nanotube scaffold. Nat. Mater.18, 62–68 (2019). [DOI] [PubMed] [Google Scholar]
- 25.Zhao, W. et al. Flexible carbon nanotube papers with improved thermoelectric properties. Energy Environ. Sci.5, 5364–5369 (2012). [Google Scholar]
- 26.Wang, T., Wang, X., Guo, J., Luo, Z. & Cen, K. Characterization of thermal diffusivity of micro/nanoscale wires by transient photo-electro-thermal technique. Appl. Phys. A87, 599–605 (2007). [Google Scholar]
- 27.Wang, Z. et al. A roadmap review of thermally conductive polymer composites: critical factors, progress, and prospects. Adv. Funct. Mater.33, 23011549 (2023). [Google Scholar]
- 28.Cahill, D. G., Watson, S. K. & Pohl, R. O. lower limit to the hermal-conductivity of disordered crystals. Phys. Rev. B46, 6131–6140.49 (1992). [DOI] [PubMed] [Google Scholar]
- 29.Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev.113, 1046–1051 (1959). [Google Scholar]
- 30.CALLAWAY, J. & VONBAEYER, H. C. Effect of point imperfections on lattice thermal conductivity. Phys. Rev.120, 1149 (1960). [Google Scholar]
- 31.Yang, J., Meisner, G. P. & Chen, L. Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds. Appl. Phys. Lett.85, 1140–1142 (2004). [Google Scholar]
- 32.Chen, Z. W. & Pei, Y. Z. Lattice dislocations enhancing thermoelectric PbTe in addition to band convergence. Adv. Mater.29, 1606768 (2017). [DOI] [PubMed] [Google Scholar]
- 33.Singh, B. K., Menon, V. J. & Sood, K. C. Phonon conductivity of plastically deformed crystals: Role of stacking faults and dislocations. Phys. Rev. B74, 184302 (2006). [Google Scholar]
- 34.Klemens, P. G. Solid State Physics Vol. 7, 1–98 (Academic Press, 1958).
- 35.Tan, M., Deng, Y. & Hao, Y. Enhanced thermoelectric properties and layered structure of Sb2Te3 films induced by special (0 0l) crystal plane. Chem. Phys. Lett.584, 159–164 (2013). [Google Scholar]
- 36.Varghese, T. et al. Flexible thermoelectric devices of ultrahigh power factor by scalable printing and interface engineering. Adv. Funct. Mater.30, 1905796 (2019). [Google Scholar]
- 37.Wang, L. et al. Exceptional thermoelectric properties of flexible organic-inorganic hybrids with monodispersed and periodic nanophase. Nat. Commun.9, 3817 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.An, C. J., Kang, Y. H., Song, H., Jeong, Y. & Cho, S. Y. High-performance flexible thermoelectric generator by control of electronic structure of directly spun carbon nanotube webs with various molecular dopants. J. Mater. Chem. A5, 15631–15639 (2017). [Google Scholar]
- 39.Lu, Y. et al. Ultrahigh performance PEDOT/Ag2Se/CuAgSe composite film for wearable thermoelectric power generators. Mater. Today Phys.14, 100223 (2020). [Google Scholar]
- 40.Wan, C. et al. Ultrahigh thermoelectric power factor in flexible hybrid inorganic-organic superlattice. Nat. Commun.8, 1024 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shang, H. J. et al. Highly (00l)-oriented Bi2Te3/Te heterostructure thin films with enhanced power factor. Nanoscale10, 20189–20195 (2018). [DOI] [PubMed] [Google Scholar]
- 42.Stordeur, M., Stölzer, M., Sobotta, H. & Riede, V. Investigation of the valence band structure of thermoelectric (Bi1−xSbx)2Te3 single crystals. Phys. Status Solidi (B)150, 165–176 (1998). [Google Scholar]
- 43.Goncalves, L. M. et al. Fabrication of flexible thermoelectric microcoolers using planar thin-film technologies. J. Micromech. Microeng.17, S168–S173 (2007). [Google Scholar]
- 44.Xiao, Z. & Zhu, X. On-chip sensing of thermoelectric thin film’s merit. Sensors (Basel)15, 17232–17240 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tan, M. et al. Oriented growth of A2Te3 (A = Sb, Bi) films and their devices with enhanced thermoelectric performance. Sens. Actuators A Phys.171, 252–259 (2011). [Google Scholar]
- 46.Tan, M. et al. Fabrication of highly (0 0 l)-textured Sb2Te3 film and corresponding thermoelectric device with enhanced performance. J. Electron Mater.41, 3031–3038 (2012). [Google Scholar]
- 47.Hines, M., Lenhardt, J., Lu, M., Jiang, L. & Xiao, Z. Cooling effect of nanoscale Bi2Te3/Sb2Te3 multilayered thermoelectric thin films. J. Vac. Sci. Technol. A Vac. Surf. Films30, 041509 (2012). [Google Scholar]
- 48.Corbett, S. et al. Electrodeposited thin-film micro-thermoelectric coolers with extreme heat flux handling and microsecond time response. ACS Appl. Mater. Interfaces13, 1773–1782 (2021). [DOI] [PubMed] [Google Scholar]
- 49.Zhao, Y. et al. Excellent thermoelectric performance from in situ reaction between Co nanoparticles and BiSbTe flexible films. ACS Appl. Mater. Interfaces13, 58746–58753 (2021). [DOI] [PubMed] [Google Scholar]
- 50.Chowdhury, I. et al. On-chip cooling by superlattice-based thin-film thermoelectrics. Nat. Nanotechnol.4, 235–238 (2009). [DOI] [PubMed] [Google Scholar]
- 51.da Silva, L. W. & Kaviany, M. Fabrication and measured performance of a first-generation microthermoelectric cooler. J. Microelectromech. Syst.14, 1110–1117 (2005). [Google Scholar]
- 52.Bottner, H. et al. New thermoelectric components using microsystem technologies. J. Microelectromech. Syst.13, 414–420 (2004). [Google Scholar]
- 53.Huang, I. Y. et al. Development of low-cost micro-thermoelectric coolers utilizing MEMS technology. Sens. Actuators A Phys.148, 176–185 (2008). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Most of the original data are found in the supplementary Information. All data generated are available from the corresponding author on reasonable request.