Unidirectional Chiral Emission via Twisted Bi-layer Metasurfaces

Abstract

Controlling and channeling light emissions from unpolarized quantum dots into specific directions with chiral polarization remains a key challenge in modern photonics. Stacked metasurface designs offer a potential compact solution for chirality and directionality engineering. However, experimental observations of directional chiral radiation from resonant metasurfaces with quantum emitters remain obscure. In this paper, we present experimental observations of unidirectional chiral emission from a twisted bi-layer metasurface via multi-dimensional control, including twist angle, interlayer distance, and lateral displacement between the top and bottom layers, as enabled by doublet alignment lithography (DAL). First, maintaining alignment, the metasurface demonstrates a resonant intrinsic optical chirality with near-unity circular dichroism of 0.94 and reflectance difference of 74%, where a high circular dichroism greater than 0.9 persists across a wide range of angles from −11 to 11 degrees. Second, engineered lateral displacement induces a unidirectional chiral resonance, resulting in unidirectional chiral emission from the quantum dots deposited onto the metasurface. Our bi-layer metasurfaces offer a universal compact platform for efficient radiation manipulation over a wide angular range, promising potential applications in miniaturized lasers, grating couplers, and chiral nanoantennas.

Simultaneous control of the direction and polarization of quantum emission using photonic nanostructures is a long-standing challenge in photonics. Here, the authors experimentally demonstrate unidirectional chiral emission from a twisted bilayer metasurface with multi-dimensional control.

Introduction

Collimation and directional radiation from quantum emitters pose challenges across various optical applications, including sensing, optical communication¹, and quantum optics^2–4. Traditional solutions involve bulky optical components like lenses, beam splitters, and mirrors, while compact lasers^5,6 and integrated photonic technologies⁷ demand efficient miniaturized optical devices capable of emission amplification and radiation channeling. Various methods have been explored for directional emission control, including nano-antennas^8–11, phase-gradient metasurfaces¹², hybrid plasmon-emitter coupled metasurfaces^13,14, chiral photonic-crystal waveguides¹⁵, and photonic lattices under vortex excitation¹⁶. Unfortunately, these approaches often require precise emitter positioning, emitter chirality, or complex excitation techniques.

Dielectric metasurfaces with unidirectional resonant modes^17–20, which emit solely to one side, offer a promising solution for controlling radiation direction. Randomly polarized emitters distributed across the metasurface can couple to these resonant modes through near-field interactions, radiating according to the resonance’s far-field properties. Unidirectional resonances can be derived from symmetry-protected bound-in-continuum (BIC) resonances²¹ by breaking up-down symmetry^17,18. This symmetry breaking splits the BIC resonance into two points of opposite chirality in momentum space. Further increasing the asymmetry merges these chirality points, thereby restricting resonant radiation to one side. However, the impact of unidirectional resonance polarization properties on the opposite side of the metasurface remains an unexplored area. Meanwhile, various resonant nanostructures with strong chiral effects at normal light incidence (i.e., intrinsic chirality) have been explored, including multi-height metasurfaces^22–25, flat metasurfaces^26–32, slant-geometry metasurfaces^33,34, stacked and twisted bi-layer nanostructures^35–39, and chiral nanocavities^40,41. Efforts have also been made to achieve absolute chirality at oblique light incidence (i.e., extrinsic chirality) in flat metasurfaces with broken symmetry^42–44 or precise engineering of synthetic valleys in the folded Brillouin zone⁴⁵. Nonetheless, these designs often retain certain mirror symmetries, resulting in symmetric polarization and intensity patterns of emission. In general, the transition from extrinsic to intrinsic chirality is achievable by tilting the walls of the structure which results in a continuous migration of the chirality points in the momentum space^33,34, similar to the recipe of unidirectionality. In most of these cases, chiral resonances in metasurfaces evolve from the achiral modes found in flat metasurfaces and, thus, are considered indivisible entities, missing one or several degrees of design freedom. On the contrary, stacked designs with vertical and lateral offsets naturally introduce a phase shift into the electromagnetic wave scattering problem, allowing for chirality²⁴ and directionality engineering⁴⁶. Ultimately, while both unidirectional and chiral resonances were demonstrated, observations of unidirectional chiral remain obscure, likely due to the challenge of achieving multidimensional precise control.

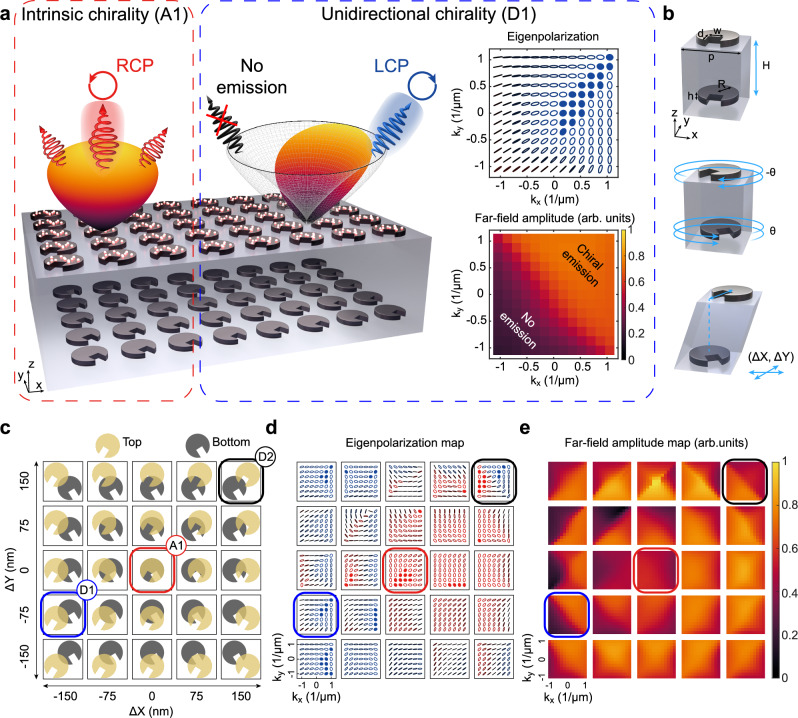
In this paper, we design and fabricate twisted bi-layer metasurfaces and demonstrate the chirality and radiation directionality of resonant modes. As illustrated in Fig. 1a, the design comprises two layers of metasurfaces, each represented by a square array (pitch p) of silicon (Si) discs (radius R and thickness h) with rectangular notches (depth d and width w). The bottom discs are fully embedded in fused silica, whereas the top discs are positioned in the air on a fused silica separation layer. This design has three degrees of freedom for full control of the optical response, as depicted in Fig. 1b: (i) the top and bottom metasurfaces are separated by distance $H$; (ii) the notches are cut at angles $\mp \theta$ with respect to the y-axis in the top and bottom discs; (iii) the centers of the top and bottom discs are shifted in lateral directions by $\Delta X$ and $\Delta Y$.

Fig. 1. Multi-dimensional control of radiation directionality and polarization patterns from twisted bi-layer metasurface.

a Twisted bi-layer metasurface and a schematic illustration of the two designs A1 (aligned discs) and D1 (displaced discs) exhibiting, respectively, intrinsically chiral and unidirectional chiral emission pattern in the top half-space as per experimentally measured emission in Fig. 4. Inset: Detailed maps of eigenpolarization and far-field amplitude in the top half-space for the design D1 exhibiting unidirectional chiral resonance. b Three designing parameters applied to the structure unit cell: twist angle $\theta$ between the y-axis and notches of the top and bottom discs, interlayer distance $H$, and lateral displacement ($\Delta X,\Delta Y$). The unit cell is characterized by pitch p, disc radius R, and thickness h, depth $d$ and width $w$ of rectangular notches. c Unit cell (top view) of bi-layer metasurfaces with possible lateral shifts ranging from −150 nm to 150 nm in both directions. d, e Corresponding maps of eigenpolarization and far-field amplitude for the anti-symmetric (lowest) resonant mode. Red and blue colors indicate elliptical polarizations with dominating RCP and LCP components, and black color indicates linear polarization. Filled circles indicate chiral resonances.

We showcase multiple configurations of bi-layer metasurfaces with broad potential for light manipulation: the red, blue, and black squares in Fig. 1c−e indicate configurations A1/A2 (aligned, no lateral shift), D1, and D2 (displaced), respectively. In the near-field coupling regime with small interlayer separation (A1), the bi-layer twisted metasurface exhibits a single resonance of wide-angle intrinsic chirality (illustrated in Fig. 1a, left panel). At the intermediate coupling regime with enlarged interlayer separation (A2), two closely spaced intrinsically chiral resonances suitable for chirality switching emerge. The introduction of lateral displacement between the constituent layers (D1 and D2) dramatically modifies the radiation properties of the resonant mode in reciprocal space, revealing a unidirectional chiral resonance of the metasurface D1 (Fig. 1a, right panel). Integrating this metasurface with perovskite quantum dots (QDs) produces a distinctive emission pattern in the upper half-space. Circularly polarized (CP) light is resonantly emitted along the positive x-axis, while emission is strongly suppressed in the opposite direction.

We term this effect unidirectional chiral emission. The radiation pattern is influenced by a strong asymmetry in the up-down direction, which is inverted along the lateral directions. This results in off-normal chiral emission, distinct from the highly collimated chiral emission reported previously³³. In that study, the emission is confined to the normal direction due to the rapid increase in the quasi-BIC Q-factor near the Γ-point. In contrast, our metasurfaces exhibit superior performance compared to other designs, which typically feature symmetrically positioned points of opposite chirality in momentum space and radiate over a broad solid angle^42–44. This work suggests the potential for full multi-dimensional control of polarization response, enabling reconfigurable metasurface design via its integration with nano-electro-mechanical systems⁴⁷ or via scaling to the terahertz frequencies⁴⁸.

Results

Designing twisted bi-layer metasurfaces

We commence the analysis by considering two stacked metasurfaces comprising discs without notches, both metasurfaces are fully embedded in fused silica. Each constituent single-layer metasurface has a four-fold in-plane rotational symmetry ($D_{4h}$), and all non-degenerate resonances below the diffraction opening are BIC at Γ-point (normal light incidence). The introduction of notches breaks the rotational symmetry and allows polarization-selective coupling to the radiation continuum (i.e., the notch size serves as the asymmetry parameter⁴⁹), which can be conveniently described using an effective dipole model (Supplementary Note 1). Owing to the high symmetry of the original near-field distribution (Supplementary Note 2), the lowest transverse electric (TE) resonance of a single-layer metasurface with a notch angle θ selectively interacts with waves polarized as $\mathbf{e}=\left(\cos \theta ,\sin \theta \right)$.

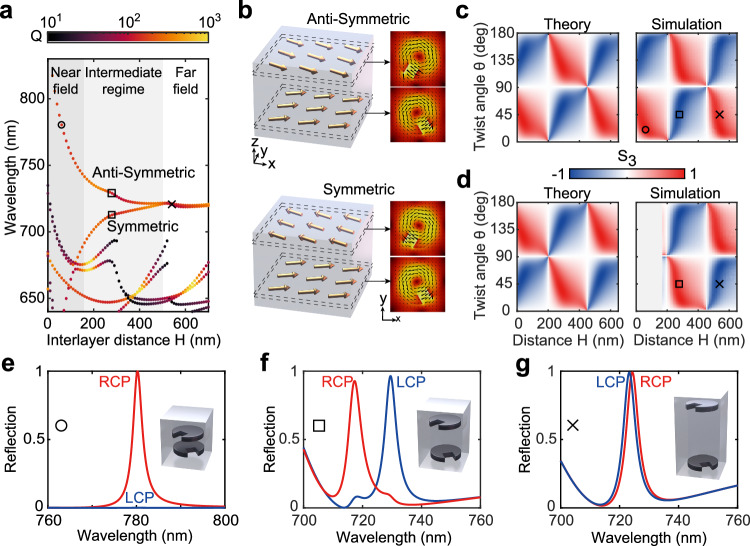
Due to interlayer coupling, the resonances of the bi-layer metasurface are hybrids of the modes from the two constituent metasurfaces. The dependence of the resonant frequencies on the interlayer distance $H$ is shown in Fig. 2a. When the constituent metasurfaces are well-aligned ($\Delta X=\Delta Y=0$), the bi-layer metasurface exhibits a two-fold symmetry of rotation around the y-axis; hence, all the hybrid modes transform like irreducible representations of the $C_2$ group. As shown in Fig. 2b, the two lowest-energy modes are hybrids of the TE modes in the constituent metasurfaces, categorized as symmetric and anti-symmetric with respect to $C_2$ flipping symmetry.

Fig. 2. Design principles for the twisted bi-layer metasurfaces.

a Resonant energies of the coupled modes in the bi-layer metasurface in dependence on the interlayer distance. b Dipole representation of the anti-symmetric and symmetric coupled modes of the bi-layer metasurface. c, d Resonance chirality maps of the anti-symmetric and symmetric hybrid modes in twisted bi-layer metasurfaces with varied twist angle θ and interlayer distance H. Gray area in (d) indicates the range of interlayer distances at which the symmetric mode strongly hybridizes with the higher-order modes. e−g Reflection spectra of the bi-layer metasurfaces that operate in the near-field, intermediate, and far-field coupling regimes, respectively. The circle, square, and cross signs correspond to structure parameters (H = 50 nm, θ = 20^o), (H = 280 nm, θ = 45^o), and (H = 530 nm, θ = 45^o) shown in (a−d).

Tuning $\theta$ and $H$ is crucial for achieving absolute intrinsic chirality in these modes. While each isolated metasurface exhibits linear polarization determined by the notch angle, interlayer coupling induces elliptical polarization in each layer. Consequently, the far-field polarization of the bi-layer metasurface is shaped by two arrays of elliptically polarized dipoles that conform to $C_2$ symmetry. The vertical offset of these dipoles introduces an additional propagation phase, which, under certain conditions, can result in purely circular polarization of the hybrid resonant mode.

To evaluate the far-field response of the bi-layer metasurface, we approximate the electric fields of the resonant modes in constituent metasurfaces with dipoles, ${\mathbf{D}}_1^{\mathrm{self}}=\left(\cos \theta ,-\sin \theta \right)$, ${\mathbf{D}}_2^{\mathrm{self}}=\pm \left(\cos \theta ,\sin \theta \right)$, where $\pm$ sign stands for the anti-symmetric and symmetric with mode, respectively. During coupling, the excited modes emit far-field radiation that propagates through the intermediate layer and induces nonresonant electric fields in the counterpart metasurfaces with coupling coefficient $r$ being the background reflection coefficient of a single-layer metasurface (details of the coupling model are provided in Supplementary Notes 3 and 4). These induced fields are approximated by the dipoles ${\mathbf{D}}_{1,2}^{\mathrm{ind}}$. The coupled dipoles appear as a sum of the resonant and nonresonant terms:

$$\begin{array}{cc}\hfill {\mathbf{D}}_1^{\mathrm{ind}}={re}^{-i{k}_{0}nH}{\mathbf{D}}_2^{\mathrm{self}},\hfill & \hfill {\mathbf{D}}_2^{\mathrm{ind}}={re}^{-i{k}_{0}nH}{\mathbf{D}}_1^{\mathrm{self}},\hfill \\ \hfill {\mathbf{D}}_n={\mathbf{D}}_n^{\mathrm{self}}+{\mathbf{D}}_n^{\mathrm{ind}},\hfill & \hfill n=1,2.\hfill \end{array}$$ 1

Due to the nonzero imaginary part of the coupling-induced fields ${\mathbf{D}}_n^{\mathrm{ind}}$, light scattered by the top and bottom metasurfaces generally has an elliptical rather than linear polarization.

Under RCP and LCP waves with electric fields ${\mathbf{e}}^{\mathrm{R},\mathrm{L}}=\left(1,\pm i\right)/\surd 2$ normally incident on the bi-layer metasurface from the top, a hybrid mode is excited with amplitudes:

$${\mathrm{\alpha }}^{\mathrm{R},\mathrm{L}}={\mathbf{e}}^{\mathrm{R},\mathrm{L}}{\mathbf{D}}_1+{e^{-i{k}_{0}n\left(H+h\right)}\mathbf{e}}^{\mathrm{R},\mathrm{L}}{\mathbf{D}}_2.$$ 2

The normalized third Stokes parameter or the resonance far-field polarization, which we call the resonance chirality (RC), can be evaluated as:

$${\mathrm{S}}_3=\frac{{∣{\mathrm{\alpha }}^{\mathrm{R}}∣}^2-{∣{\mathrm{\alpha }}^{\mathrm{L}}∣}^2}{{∣{\mathrm{\alpha }}^{\mathrm{R}}∣}^2+{∣{\mathrm{\alpha }}^{\mathrm{L}}∣}^2}.$$ 3

Using our coupled dipole model, we calculate RC for the bi-layer metasurfaces with varied θ and $H$ (Fig. 2c, d, left panels), demonstrating complete agreement with the full-wave simulations (Fig. 2c, d, right panels).

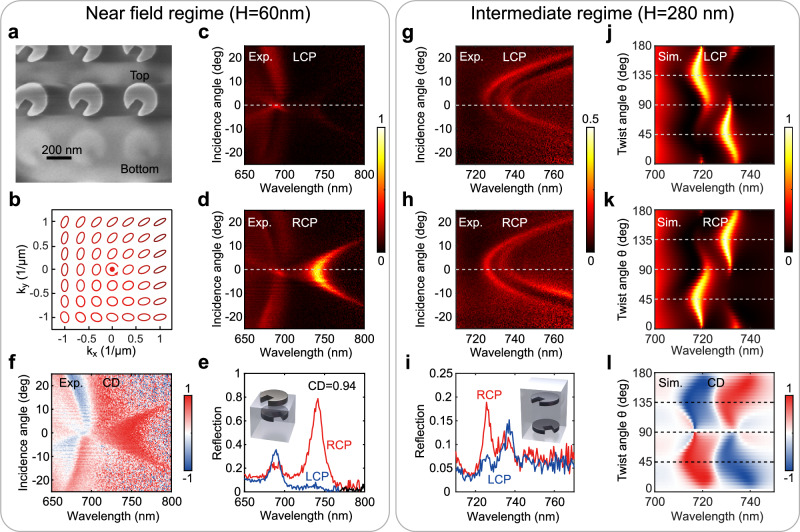
As indicated in Fig. 2a, the mode coupling can be divided into three regimes: near-field, intermediate, and far-field. In the near-field regime (H is comparable to the notch size), the symmetric and anti-symmetric modes are well separated spectrally, where only the anti-symmetric mode with the lowest energy is available, and the symmetric mode couples to higher order resonances and even radiates into the first diffraction order. According to the chirality map (see Fig. 2c), the optimized near-field design ($H=50$ nm, $\theta ={20}^0$) exhibits absolute intrinsic chirality in Fig. 2e. Meanwhile, strong near-field coupling ensures that even the modes of moderately dissimilar metasurfaces (e.g., metasurfaces having different dielectric environments) can hybridize into chiral modes (Supplementary Note 5). Thus, in the near-field regime, we can design an open structure with only the bottom discs fully embedded in silica and the top discs in the air. This enables a versatile chiral metasurface platform to be integrated with quantum emitters. In the intermediate regime (H is comparable to the disc size), the energy splitting, albeit weaker, is still governed by the near fields that resemble those of the unperturbed BIC mode. However, in this regime, e.g., ($H=280$ nm, $\theta ={45}^{\mathrm{o}}$), both symmetric and anti-symmetric quasi-BIC modes are accessible and exhibit high chirality while coupling to waves with opposite circular polarizations (Fig. 2f). When H exceeds the metasurface period, purely far-field coupling determines the properties of the coupled resonances. The energy splitting becomes insufficient, and two chiral resonances spectrally overlap (see Fig. 2a, g), no matter how $\theta$ changes (Supplementary Note 6).

Intrinsic wide-angle chirality

The designed metasurface of configuration A1 (open structure, $\theta ={32}^{\mathrm{o}},H=60\mathrm{nm},\mathrm{\Delta }X=\mathrm{\Delta }Y=0$ nm, other parameters listed in Methods) operated in the near-field regime is fabricated by a DAL technique (see details in the Methods). The scanning electron microscope (SEM) image shown in Fig. 3a confirms the perfect alignment of the top and bottom layers of metasurfaces. The corresponding map of the calculated anti-symmetric resonance eigenpolarization in the reciprocal space is shown in Fig. 3b, indicating maximum intrinsic chirality. Moreobver, the resonance is primarily RCP-polarized at all oblique incidence angles. Figure 3c, d demonstrate the measured angle-resolved reflection spectra for the structure under LCP and RCP illumination, which we denote $R^{\mathrm{LCP}}$ and $R^{\mathrm{RCP}}$. Examining the spectra under normal incidence (Fig. 3e), we calculate the maximum circular dichroism (CD), which is defined as $\mathrm{CD}=\left(R^{\mathrm{RCP}}-R^{\mathrm{LCP}}\right)/\left(R^{\mathrm{RCP}}+R^{\mathrm{LCP}}\right)$ to be 0.94 at resonance and the maximum reflectance difference $\mathrm{\Delta }R$ of 74% (experiment). Due to the relatively large notch size, wide-angle intrinsic chirality with a high CD larger than 0.9 is observed at angles ranging from −11^o to 11^o, as shown in Fig. 3f.

Fig. 3. Twisted bi-layer metasurfaces operating in near-field and intermediate coupling regimes.

a SEM image of the bi-layer twisted metasurface with the near-field coupling. The total area of the top metasurface is slightly smaller than the area of the bottom metasurface, thus allowing us to visualize both layers near the edge of the top metasurface. b Calculated eigenpolarization map of the anti-symmetric resonance of the near-field coupling design. c, d Measured angle-resolved reflection spectra under LCP and RCP illumination. e Measured reflection spectra at normal incidence corresponding to the dashed lines in (c, d). f Angle-resolved circular dichroism (CD) heatmap. g, h Measured LCP and RCP angle-resolved-reflection spectra of bi-layer twisted metasurface in the intermediate coupling regime. i Corresponding reflection spectra at normal incidence. j, k Simulated LCP and RCP reflection spectra at normal incidence of the bi-layer metasurface with variable twist angle operating in the intermediate coupling regime. l CD spectra calculated based on (j, k).

To observe chiral modes in the intermediate regime, we investigate the metasurface of configuration A2 ($\theta ={18}^{\mathrm{o}},H=280\mathrm{nm},\mathrm{\Delta }X=\mathrm{\Delta }Y=0$ nm, other parameters listed in Methods) with maximized chirality of the symmetric mode. Configuration A2 is fully embedded into fused silica, with a 500-nm-thick fused silica layer above the top metasurface. By designing a smaller notch size, the resonant modes have a greater radiative Q-factor than the modes of configuration A1. This allows one to spectrally separate the two resonant features associated with the symmetric and anti-symmetric modes. Figure 3g, h illustrate the measured LCP and RCP reflection spectra, respectively. Two sharp resonant modes are observed; however, the magnitude of resonant reflection is not as high as that for configuration A1. This should be attributed to small radiative losses of the resonance and the presence of nonradiative losses, which are inevitable even in all-dielectric structures due to the finite size of the sample and scattering on fabrication irregularities. In the bi-layer structure, these irregularities are caused by the surface roughness of the silicon discs in each layer and variations in the thickness of the SiO₂ separation layer. Nevertheless, configuration A2 demonstrates a chiral response at a normal incidence of illumination associated with the symmetric mode (Fig. 3i), which accords well with the predictions of the dipole model.

The two sharp resonant modes in the intermediate regime can be potentially exploited for chirality switching. We show simulated reflection coefficients with variable θ under LCP and RCP illumination in Fig. 3j, k. Considering a bi-layer metasurface with twist angle θ = 45^o, symmetric and anti-symmetric resonances predominantly couple to RCP and LCP incoming waves, respectively. At θ = 90^o (notches at opposite sides), the chirality vanishes as the effective dipoles of such modes are either co-directional or counter-directional. At θ = 135^o, the modes become chiral again, albeit the chirality of the modes switches (Fig. 3l). Such changes in the angle θ can be achieved through rotation of the top and bottom metasurfaces with respect to each other. Although, in general, the unit cell size of two stacked and twisted metasurfaces forming a Moiré pattern⁵⁰ differs from the original unit cell size of a single metasurface, relative rotations by 2Δθ = 90° preserve the unit cell size, thus avoiding the undesired diffraction effects. In this sense, a square or hexagonal unit cell with a notched disc is preferable for bi-layer chiral structures. We envision this kind of system with an ability for relative Moiré-like rotation of stacked quasi-BIC layers as a prospective candidate for an active chirality switching device.

Unidirectional chirality engineering by lateral displacement

One common feature of all stacked structures, namely, layer lateral alignment, is another important parameter that allows the engineering of both the polarization and directionality characteristics of the bi-layer metasurface. The proposed coupling model assumes precise alignment of the top and bottom discs. Under this condition, the unperturbed bi-layer metasurface without notches exhibits 4-fold rotational symmetry with respect to the vertical z-axis, ensuring that both symmetric and anti-symmetric modes are BIC. However, the introduction of lateral displacement breaks the symmetry, rendering the modes radiative even without notches. Thus, two types of symmetry breaking, e.g., etched notches and lateral displacement, determine the polarization selection rules, providing additional design flexibility (Fig. 1c). To systematically investigate the effect of lateral displacement, we calculate maps of far-field polarization and amplitude in the top half-space for the anti-symmetric mode of bi-layer metasurfaces with varied displacement in Fig. 1d, e (an extended map with finer resolution if presented in Supplementary Note 7). All other structure parameters remain consistent with A1.

Metasurfaces featuring selected displacements can exhibit significant asymmetry in far-field amplitude in reciprocal space. For example, configuration D1, highlighted in the blue square in Fig. 1c−e, with a displacement of $\Delta X=-150$ nm, $\Delta Y=-75$ nm is expected to resonantly radiate LCP waves along the positive x and x = y directions, as well as elliptically polarized waves along the positive y direction (refer to Fig. 1a, right panel). Conversely, resonance radiation along the negative x, y, and x = y directions is notably suppressed. Similar maps illustrating resonance radiation properties in the bottom half-space are provided in Supplementary Note 7, showing that total radiative losses do not completely vanish but are redistributed between upward and downward propagating radiation, resulting in unidirectionality across a broad area of reciprocal space.

In contrast, configuration D2 with a different displacement of $\Delta X=+150$ nm, $\Delta Y=+150$ nm (indicated by the black square in Fig. 1c−e) does not demonstrate significant radiation asymmetry in the top half-space but exhibits pronounced extrinsic chirality. To underscore the various possibilities of resonance polarization control, we analyze experimental angle-resolved resonant reflection spectra for configuration D2 in Supplementary Note 8, registering CD values up to 0.85.

Unidirectional chiral emission

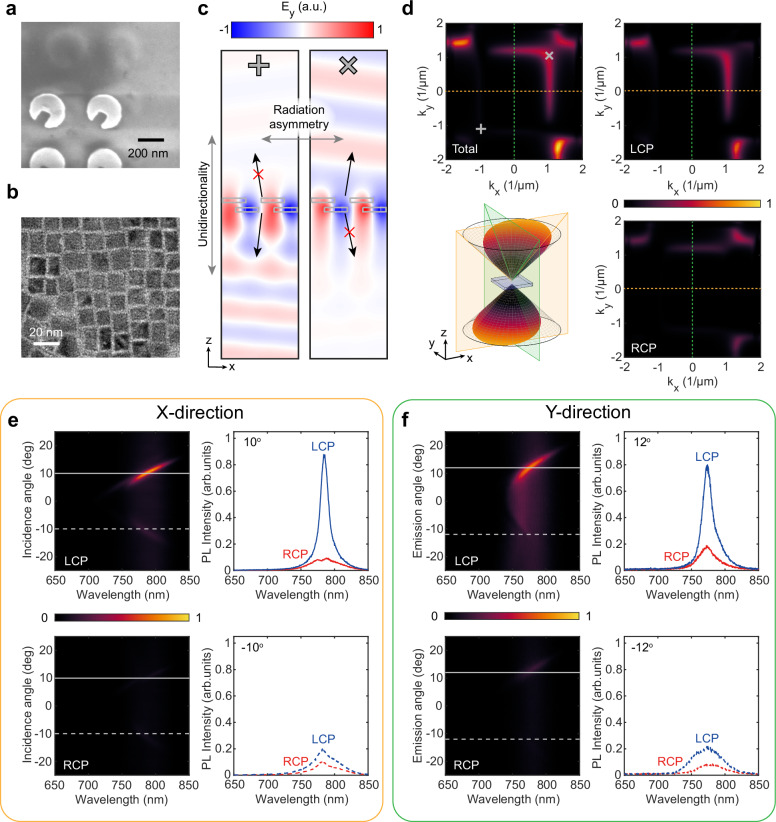
The designed twisted bi-layer metasurface D1 can be exploited as a highly asymmetric router of light to achieve unidirectional chiral emission when it is integrated with active materials, such as perovskite QD, as illustrated in Fig. 1a. A thin layer of FAPbI₃ QDs is deposited on top of DAL-fabricated metasurface D1 (Fig. 4a) using the drop-cast technique⁵¹. The QDs (Fig. 4b) are excited using a 532 nm continuous wave (CW) pump laser, and the photoluminescence signal is harvested in the top half-space in the 650−850 nm wavelength range. Figure 4c shows the cross-section of the bi-layer metasurface in the x-z plane and the resonant electric field profile for the anti-symmetric mode at $\left(k_x,k_y\right)=\pm \left(1.05,1.05\right)$ μm^-1. The patent unidirectionality at these opposite points of the reciprocal space also leads to pronounced emission asymmetry at opposite incidence angles. To visualize the radiation intensity and polarization patterns, we simulate emission at 770 nm wavelength from a point dipole source located at the center of the top disc notch (see Fig. 4d). As expected from the far-field amplitude and polarization maps in Fig. 1, emission in the top half-space is suppressed along the negative x and y directions because of full redirection into the bottom half-space (see Supplementary Note 9), while along the positive x direction, the emission is LCP. The additional emission intensity peaks along the diagonal directions are associated with the higher-frequency symmetric resonant mode.

Fig. 4. Unidirectional chiral emission.

a SEM image of the laterally displaced bi-layer twisted metasurface. b Transmission electron microscope (TEM) image of the perovskite QDs. c Resonant electric field profiles at two opposite points of reciprocal space $\left(k_x,k_y\right)=\pm \left(1.05,1.05\right)1/$μm. d Calculated emission intensity at wavelength 770 nm. e Left column: Measured angle-resolved photoluminescence spectra in the x-z plane (LCP and RCP components). Right column: Emission intensities at $\pm {10}^{\mathrm{o}}$. f Left column: Measured angle-resolved photoluminescence spectra in the y-z plane (LCP and RCP components). Right column: Emission intensities at $\pm {12}^{\mathrm{o}}$.

We measure the emission of QDs along the x and y directions, represented by the orange and green planes in Fig. 4d, respectively. Experimentally measured angle-resolved and polarization-resolved emission intensities along the x direction are depicted in Fig. 4e. Positive emission angles ($k_x>0$) exhibit a strong resonant LCP signal, while negative angles show suppressed resonance radiation, resulting in a nearly background emission profile. These results align with numerical emission simulations (Supplementary Note 9). Emission spectra measured along the y direction, shown in Fig. 4f, also demonstrate similar radiation asymmetry: the intensity of elliptically polarized resonant emission, with a dominant LCP component at positive emission angles, significantly exceeds that at negative angles. Both experimental and simulated angle-resolved emission spectra showcase asymmetric chiral emission patterns due to the property of unidirectionality, a feature not achieved in any previous designs for extrinsic chirality^42–45. These observations corroborate that the radiation unidirectionality in the bi-layer metasurface is not a special resonance feature at a single point in the reciprocal space but rather a broad-angle effect.

Additionally, we measure the emission spectra from D2 integrated with the QDs (see Supplementary Note 8). While the emission intensity is symmetric with respect to the emission angle, the polarization of the emission associated with the resonant mode changes drastically from RCP at $k_y=0,k_x<0$ to LCP-dominated elliptical at $k_y=0,k_x>0$.

Discussion

In summary, we have designed and demonstrated twisted bi-layer metasurfaces made of notched dielectric discs, showcasing their potential as a promising platform for simultaneous control over light polarization and propagation direction. First, precise tailoring of interlayer distance and the angle between the notches of the top and bottom discs introduces structure asymmetry that enables tunable resonant modes selective to specific wave polarizations. For structures with subwavelength interlayer distances and optimized chirality, measured CD values at normal incidence reach 0.94, with reflection differences of up to 74%. Second, by increasing the interlayer distance, we experimentally demonstrate the emergence of two hybrid quasi-BIC modes and propose a mechanism of active chirality switching for these modes. Third, the introduction of lateral displacement between the top and bottom layers allows manipulation of resonance directionality and eigenpolarization patterns in reciprocal space, revealing a metasurface with unidirectional resonance and strong radiation asymmetry. Finally, we demonstrate unidirectional circularly polarized emission from the bilayer twisted metasurface integrated with perovskite quantum dots. We anticipate that our design can be brought to lower operational frequencies and then readily integrated with nano-electro-mechanical systems to achieve reconfigurable chiral metasurface systems capable of actively manipulating emission angle, wavelength, and polarization.

Doublet alignment lithography (DAL) is a precise and powerful technique for rapid prototyping in proof-of-concept experiments. However, it is time-consuming and typically limited to patterning areas of a few mm². For scaling up to mass production and commercial applications, it is crucial to develop higher throughput lithography techniques, such as photolithography with DUV/EUV⁵² or nanoimprint⁵³ lithography with accurate alignment capabilities. Additionally, achieving uniform deposition of perovskite quantum dots over large areas remains challenging. Advancing the directed self-assembly method, which has been optimized for uniform deposition of Au⁵⁴ and up-conversion nanoparticles⁵⁵, may provide a viable solution.

Methods

Simulation

All calculations were conducted using COMSOL Multiphysics implementation of the finite element method. Periodic boundary conditions with Floquet periodicity in x and y directors were used with two ports on the top and bottom of the structure (z-direction). Eight additional diffraction channels (diffraction orders (±1,0) and (0, ± 1) with in-plane and out-of-plane polarization) were turned on in the bottom port to simulate diffraction into the substrate. Optical spectra of the structures were calculated using the wavelength domain study with excitation from the top port, while the resonant properties of the structure were calculated using eigenfrequency study. Simulations of the resonant modes of the metasurfaces were conducted using the COMSOL eigenfrequency solver. COMSOL build-in integration functions were applied to the simulated resonant fields to calculate the effective dipoles. Additional calculations based on the analytical coupling model and resonant dipoles post-processing were done in MATLAB.

To simulate the resonance-assisted photoluminescence emission, the top and bottom ports were replaced with scattering boundary conditions. A point emitter is characterized by a dipole moment $d=\left(\cos \theta ,-\sin \theta \right)/\left(\omega -{\omega }_r-i\gamma \right)$ was put in the center of the top disc notch to model a perovskite QD. The emitter was characterized by resonant frequency ${\omega }_r=384.6$ THz (which corresponds to a wavelength $\lambda =780$ nm) and damping factor $\gamma$ = 13 THz, which ensured a relatively broad range of emission wavelengths and a good approximation of the background emission dependence on the wavelength observed in the experiment.

All simulations related to the theory of intrinsically chiral resonances in bi-layer metasurfaces with alignment (Fig. 2) were conducted using the following parameters: pitch $p=400$ nm, disc radius $R=145$ nm, thickness $h=50$ nm, depth $d=100$ nm and width $w=80$ nm of rectangular notches. The complex refractive index of silicon was obtained from ellipsometry measurements, the refractive index of the embedding silicon dioxide is 1.45. For better simulation-to-experiment comparison, supporting simulations for experimentally fabricated samples were conducted with a silicon dioxide refractive index of 1.52. Configuration A1 had parameters $p=450$ nm, $R=135$ nm, $h=50$ nm, $d=115$ nm, $w=80$ nm, $\theta ={32}^{\mathrm{o}},H=60$ nm,$\mathrm{\Delta }X=\mathrm{\Delta }Y=0$ nm, top discs were in the air (open structure). Configuration A2 had parameters $p=400$ nm, $R=145$ nm, $h=50$ nm, $d=100$ nm, $w=80$ nm, $\theta ={18}^{\mathrm{o}},H=280$ nm,$\mathrm{\Delta }X=\mathrm{\Delta }Y=0$ nm, the structure was fully embedded in silicon dioxide. Configurations D1 and D2 had the same structural parameters as structure A1 but with $\Delta X=-150$ nm, $\Delta Y=-75$ nm, and $\Delta X=180$ nm, $\Delta Y=120$ nm, respectively.

Fabrication

The fabrication was done using the doublet alignment lithography (DAL) technique (see Supplementary Methods 1). The bi-layer metasurfaces were fabricated layer by layer with a nanofabrication process based on electron beam lithography (EBL), lift-off, etching, and alignment. First, an amorphous Si (a-Si) layer with a thickness of 50 nm was grown on a thoroughly cleaning glass substrate (length and width of 26 mm and 20 mm) using inductively coupled plasma-enhanced chemical vapor deposition (ICP CVD, Oxford Instrument Plasmalab System. 100) (Supplementary Fig. 18a, b). To prepare for the well-aligned bi-layer metasurface, a pair of gold (Au) alignment markers with a distance of 16 mm was patterned by EBL, followed by Au evaporation and lift-off process (Supplementary Fig. 18c). After that, the bottom Si disks with notches were patterned based on the 1^st aligned EBL process (Supplementary Fig. 18d). The patterned a-Si sample was then etched using a chlorine (Cl₂)-based inductively-coupled-plasma reactive-ion etching (ICP RIE, Oxford Instruments Plasmalab System 100) with an ICP power of 300 watts, an RF power of 100 watts under a pressure of 5 mTor and a temperature of 0 °C. Then, the middle SiO₂ was uniformly distributed by spin coating of commercially available Fox 16 resist at a speed of 5000 rpm without ramping up the process (Supplementary Fig. 18e). As a result, the notches of the bottom disks could be filled while the top surface of SiO₂ is flat, which promises a fully embedded environment. After that, CF₄ gas-based RIE was performed to thin the middle SiO₂ layer to 60 (280) nm for the configurations in near-field (intermediate) regimes. The thickness of the final SiO₂ layer was confirmed by a thin film analyzer (FILMETRICS, F50). Subsequently, another 50 nm a-Si layer was deposited using ICP CVD to prepare for the top disk (Supplementary Fig. 18f). In the next step, we carried out the 2nd aligned EBL process to pattern the top silicon notch nanostructures and the Cl₂-based etching (Supplementary Fig. 18g). To fabricate the embedded structure, another SiO₂ layer was covered on top of the open structure by spin-coating (Supplementary Fig. 18i). Similarly, the bi-layer metasurface with displacement can be realized through the intentional shift of exposure position (Supplementary Fig. 18h). The FaPbI₃ QDs were deposited onto the top silicon disc array via the drop-casting method to realize unidirectional spin emission (Supplementary Fig. 18j). An SEM image of the metasurface with deposited QDs is shown in Supplementary Fig. 19.

Quantum emitter synthesis

The FAPbI₃ QD synthesis has been elaborated in detail in ref. ⁵⁶. The supernatant of the synthesized FAPbI₃ solution was separated after centrifugation for 10 min. The supernatant was then filtered using a microfilter with a 0.2 μm pore size and diluted 1:1 with toluene for the final solution. The bi-layer metasurface was treated with oxygen plasma at room temperature for 10 min to make the surface more adhesive. Immediately after, FAPbI₃ QD solution was drop-cast onto the sample in a nitrogen-filled glove box at room temperature. The samples were stored in the dark in a nitrogen atmosphere at room temperature until further use.

Back-focal-plane reflectance measurement

The photonic bands’ mode dispersions were measured in a homebuilt Fourier plane setup (Supplementary Fig. 20 in Supplementary Methods 2). A white-light beam generated by a halogen lamp was right (left) circularly polarized using a linear polarizer (Thorlabs LPVISE100-A) and a quarter-wave plate (Thorlabs AQWP10M-580) where the axis of the linear polarizer at 45° (or-45°) to the fast axis of the quarter-wave plate. Circularly polarized light was focused on the sample surface with an area of 50 × 50 µm² using a 50 × objective lens with a numerical aperture (NA) of 0.6. The reflected light was collected and imaged by two lenses and measured by the spectrometer. The angle-resolved spectrum was measured using a monochromator slit as the line aperture in the Fourier plane. The measured raw reflectance spectrum was normalized to the background reflectance of a flat silver film.

Photoluminescence (PL) spectra measurement

The optical setup for the characterization of light emission is depicted in Supplementary Fig. 21 in Supplementary Methods 2. A continuous-wave (CW) laser at 532 nm was used as the excitation light source (laser power of 125 mW). It first went through a dichroic mirror (FF552-Di02-25x36) to be reflected on the sample surface. After that, the emitted light from perovskite passes a longpass filter (Thorlabs FELH0650) to cut the effect of the laser source. The circular polarization of light was characterized by a quarter waveplate and a linear polarizer. All measurements were conducted at room temperature.

Author contributions

D.G., S.A., C.W.Q., Z.D., and L.W. conceived the project idea. C.W.Q., Z.D., and L.W. supervised the project. D.G., C.W.Q., and L.W. developed the theoretical background. D.G. performed numerical simulations. S.A. and Z.D. fabricated the samples. H.Y.L.L. provided support on the SEM image, and F.T. prepared the substrates. L.J.L. and Z.K.T. synthesized the quantum dots. S.A. performed the optical measurements. S.G., J.X., and Z.D. assisted with the optical measurement setup. D.G., S.A., C.W.Q., Z.D., and L.W. wrote the manuscript. All authors contributed to the data analysis and proofread the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The authors declare that the data supporting the findings of this study are available within the paper, its supplementary information files, or from the corresponding authors upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54262-6.