Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Oct 29;12(45):16692–16699. doi: 10.1021/acssuschemeng.4c06166

Advancing Rare-Earth (4f) and Actinide (5f) Separation through Machine Learning and Automated High-Throughput Experiments

Logan J Augustine †, Yufei Wang ‡, Sara L Adelman ‡,*, Enrique R Batista †, Stosh A Kozimor ‡,*, Danny Perez †,*, Joshua Schrier §, Ping Yang †,*
PMCID: PMC11558677  PMID: 39545104

Abstract

graphic file with name sc4c06166_0005.jpg

Identifying improved and sustainable alternatives to “classic” separation techniques is an active research field due to its potential widespread impact in fundamental and applied chemistry. As basic purification methodologies, like liquid–liquid extraction, undergo continuous refinement by chemists and engineers, identifying new conditions that outperform existing techniques can be difficult. A major contributor to this challenging problem is the need to explore a vast experimental space to identify the precise conditions that optimize the separation procedure. The advent of artificial intelligence and the advancement of robotic technologies offer the potential to shift the traditional design paradigm. Toward that end, we applied a combination of Bayesian Optimization and high-throughput robotic experiments on the liquid–liquid extraction of thorium (Th4+) and demonstrated that this approach speeds up discovery and significantly accelerates the optimization process. By using Bayesian Optimization as a guide, our automated instrument carried out a total of 339 distribution ratio measurements, corresponding to 113 unique conditions, identifying the optimal experimental conditions with reduced experimental efforts by an estimated 74% compared to a traditional full screening approach. This time and cost saving is particularly significant for radioactive materials, as it not only is more economical and sustainable but also minimizes human exposure to radioactivity.

Keywords: high-throughput experimentation, Bayesian Optimization, separations, liquid−liquid extraction, robotics, actinides

Short abstract

High-throughput experimentation with Bayesian Optimization accelerates the development of sustainable separation methods for liquid−liquid extraction in the reprocessing of rare-earth and actinide elements.

Introduction

Chemical separations, e.g., chromatography, crystallization, (co)precipitation, and liquid–liquid extraction, represent some of most fundamental operations performed by chemists and engineers.1,2 Among these methods, liquid–liquid extraction is the core technique for the separation and purification of metals and has been refined by chemists and engineers for centuries. This method finds widespread application in supporting the growing need to separate rare-earth (4f) and actinide (5f) elements for emerging technologies and clean energy. The difficulty lies in the highly similar physical and chemical properties of these f-elements.3−5 While liquid–liquid extraction methods for these elements have been studied for decades, developing new economic and environmentally sustainable conditions that outperform existing methods remains a significant challenge.1,6

A major barrier in developing new separation methodologies is the need to identify the experimental conditions that optimize key partitioning values such as distribution ratios, separation factors, and separation kinetics. In liquid–liquid extraction, variables like analyte, extractant, holdback agent identities, and concentrations, along with the organic diluent, temperature, mixing rates, and contact times all need to be optimized.7−10 However, systematically determining how each variable impacts partitioning parameters is a daunting task due to the vast experimental space that must be explored; a space often too large to be adequately covered in a reasonable amount of time. Typically, experimental campaigns significantly reduce the exploration space by systematically varying a single variable or very few at a time, potentially missing multifactor interactions needed to find the true optimum. Overcoming this issue could substantially advance the development of new methodologies in liquid–liquid extraction.

Advances in robotic laboratories using high-throughput experimentation allows for expanded, multidimensional experimental spaces to be thoroughly explored in less time than traditional screening or Edisonian approaches.11−16 However, as the total number of experiments needed to fully explore an experimental space grows exponentially with the number of variables, evaluation of the entire space can quickly become inefficient. Statistical analysis and strategic machine learning decision-making techniques, such as Design of Experiments (DoE)17−20 or genetic algorithms21−24 can be used to select more informative experiments and guide robotic experimental campaigns. Bayesian Optimization25−27 represents a nonparametric, response surface modeling technique that has been gaining traction in fields such as material science,28−32 drug and molecular design,33−37 reaction optimization,38−40 and experimental imaging.41−44 The method employs a surrogate model to establish a probabilistic model of the expensive-to-query experimental response function. Gaussian Processes are frequently chosen surrogate models because they provide both predictions and uncertainties for the unobserved regions of the response surface. An acquisition function is then used to determine the next sampling points on the response surface, strategically selecting regions based on their potential for high performance (exploitation) and significant uncertainties (exploration). As new experimental data is acquired, the probability distribution of the prior Gaussian Process model is updated, enhancing the efficiency of the exploration on the experimental space. Unlike many conventional DoE methods, where the sampling pattern is predetermined, Bayesian Optimization dynamically adapts the experimental design in response to new data and learns the true response surface in real-time.45,46

Herein, a custom-designed, experimental robotics platform was developed to support challenging actinide chemical reprocessing campaigns. The high-throughput instrument, affectionately named the LANL Super Separator, automates almost every step in liquid–liquid extraction, chromatography, crystallization, and (co)precipitation processes. It provides rigorous control over variables such as analyte, extractant, and holdback concentrations, pH, temperatures, contact times, and mixing rates. This methodology significantly enhances the robustness of data acquisition and increases experimental throughput to an estimated 200 measurements per day. Additionally, the instrument was specifically designed to be compatible with radiological samples, thereby increasing worker safety when handling these hazardous chemicals.

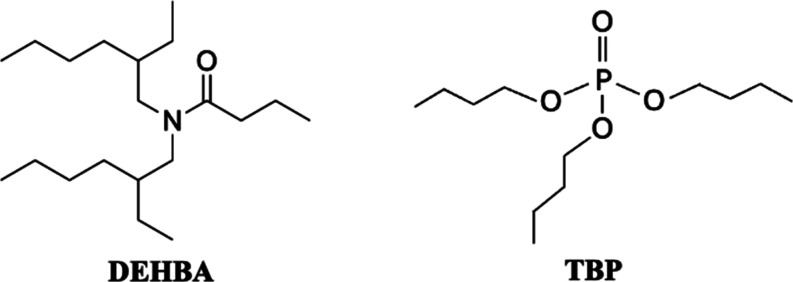
In this study, we integrated Bayesian Optimization with the LANL Super Separator to guide experiments and optimize the liquid–liquid extraction of Th4+ contacted with an organic phase containing N,N-di-2-ethylhexylbutyramide (DEHBA) and tributyl phosphate (TBP) (Figure 1). The extraction process was simultaneously characterized against four experimental variables, specifically, Th4+(aq) concentration, HNO3(aq) concentration, DEHBA(org) concentration, and temperature. By using this automated high-throughput platform, the Th4+ distribution ratio was successfully optimized after conducting a total of 339 liquid–liquid extraction measurements. Considering that a complete characterization of the experimental space would require performing an estimated 1296 total measurements using a typical high-throughput screening method, our approach achieved optimization while saving 74% of the experimental time and effort. This underscores the efficacy and necessity of combining high-throughput experimentation with machine learning for efficiently identifying the optimal separation conditions for a liquid–liquid extraction system.

Figure 1.

Figure 1

Open in a new tab

Chemical structure of N,N-di-2-ethylhexylbutyramide (DEHBA) and n-tributyl phosphate (TBP).

Experimental Section

General Considerations

CAUTION! Thorium-232 (232Th, t1/2 = 1.4 × 1010 y)47 and progeny products constitute health threats because of radioactive decay. Hence, all experiments that involved manipulation of these radionuclides were conducted in a radiological buffer area that contained HEPA filtered hoods, continuous air monitors, negative pressure gloveboxes, and monitoring equipment appropriate for α-, β-, and γ-particle detection. Entrance to the laboratory space was controlled with a hand and foot monitoring instrument for α-, β-, and γ- emitting isotopes and a full body personal contamination monitoring station.

All chemical manipulations were carried out within a chemical fume hood with no attempt to exclude air and moisture. All reagents were obtained commercially and used as received: hydrated thorium nitrate (Th(NO3)4·5H2O, 99%, guaranteed reagent grade, EM Science), aqueous solutions of nitric acid (HNO3(aq), 70 w%, Optima grade, Thermo Fisher Scientific), n-dodecane (anhydrous, ≥99%, Sigma-Aldrich), n-tributyl phosphate (TBP, 96.5%, Spectrum Chemical MFG Corporation), and N,N-di-2-ethylhexylbutyramide (DEHBA, ≥95%, Aurum Pharmatech LLC). Water (H2O) was deionized, passed through a Barnstead water purification system to achieve resistivity of >18.2 MΩ·cm, and purified further via distillation within a Teflon apparatus (Savillex).

Preparation of Stock Solutions

Ten different HNO3(aq) stock solutions (0.1, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 8.0, 10.0, and 15.5 M) were prepared by volumetrically diluting nitric acid (70 w%) with water. A 0.01 M Th4+(aq) in 0.1 M HNO3(aq) stock solution was generated by charging a 20 mL volumetric flask with solid Th(NO3)4·5H2O (114.0 mg, 200 μmol). The powder was then dissolved in 1 mL of 0.1 M HNO3(aq), and the resulting colorless solution was further diluted with 0.1 M HNO3(aq) until the final volume was 20 mL. The DEHBA stock solution was prepared by charging a 50 mL volumetric flask with DEHBA (779 mg, 2.50 mmol) and diluting to 50 mL with n-dodecane. Each stock solution was then loaded into 20 mL scintillation vials used by the LANL Super Separator for automated dispensing.

Automated Liquid–Liquid Extraction Procedure

All liquid–liquid extraction experiments were performed using the LANL Super Separator (Figures S1 and S2), a custom-designed Big Kahuna automated instrument from Unchained Laboratories Inc. Its two robotic arms are equipped with instrumentation for automated liquid dispensing that can deliver solutions up to 10 mL in volume with an accuracy and precision of ±10 μL and ±5%, respectively. Additionally, the platform is equipped with two temperature-controlled vortexers and four ambient temperature vortexers, all of which mix the contacted organic and aqueous phases at controlled speeds and times. Two software packages, Library Studio and Automation Studio, were used to design and execute the liquid–liquid extraction workflows described below, both of which were provided by Unchained Laboratories Inc. to interface with the LANL Super Separator.

Each extraction experiment followed previously reported procedures48−50 and consisted of the following three steps:

  • (1)

    Conditioning: Initial organic phases were generated manually by volumetrically diluting the DEHBA stock solution with 20 v% TBP in n-dodecane until the desired DEHBA concentration was achieved. The volume concentration of TBP was constant for all the experiments. These were then loaded onto the experimental deck of the LANL Super Separator and contacted with equal volumes (200–400 μL depending on conditions) of HNO3(aq) in 4 mL Wheaton glass vials and vortexed at 1000 rpm for 30 min. The concentrations of both HNO3(aq) and DEHBA(org) during this step matched their respective values used in the liquid–liquid extraction experiments. The pre-equilibrated organic phases were then manually separated from the Th-free HNO3(aq) solutions using an Eco-mini centrifuge (United Scientific) and used for the following liquid–liquid extraction experiments.

  • (2)

    Extraction: The initial aqueous feed concentrations of Th4+(aq) and HNO3(aq) were generated by mixing varied volumes of the Th4+(aq) stock solution, the appropriate HNO3(aq) stock solution, and H2O into 2 mL Eppendorf microtubes inside the LANL Super Separator. From there, equal volumes of the Th4+(aq)/HNO3(aq) aqueous phase and preconditioned DEHBA/TBP/n-dodecane organic phase were contacted and vortexed at 1000 rpm for 30 min. The total volume of the biphasic mixture varied from 0.2–2 mL depending on the extraction conditions. Extraction experiments were then manually transferred from the LANL Super Separator and centrifuged at 3000 rpm for 30 s. Following transfer back to the LANL Super Separator, aliquots of the aqueous raffinate phases were transferred via automated pipet into 4 mL Wheaton glass vials for further analysis.

  • (3)

    Characterization: The extraction performance at each experimental condition was characterized through the thorium distribution ratio (DTh), as shown in eq 1.

graphic file with name sc4c06166_m001.jpg 1

Here, [Th]org and [Th]aq represent the final Th4+ concentrations in the organic and aqueous phase postextraction, respectively. [Th]org was calculated by subtracting the thorium concentration in the aqueous raffinate, [Th]aq = [Th]raf, from that in the initial aqueous feed, [Th]feed, based on the conservation of mass. All liquid–liquid extraction experiments at a given condition were performed in triplicate, therefore, reported DTh values represent the average of the triplicated measurements with error bars determined as a single standard deviation of the measurements.

Quantification of Th4+ via ICP-AES

[Th]feed and [Th]raf were determined by inductively coupled plasma-atomic emission spectroscopy (ICP-AES) using a PerkinElmer Avio 500 instrument. Here, 4–200 μL aliquots of the aqueous feed and raffinate phases were transferred into 4 mL Wheaton glass vials and diluted 10–1000× with 0.1 M HNO3(aq). Due to the tendency of Th to adhere to surfaces of the ICP sample introduction hardware, we incorporated an extended wash time of 50 s with a solution of 0.1 M HNO3(aq) doped with 0.01 w% HF(aq) between samples. This wash prevented buildup of thorium and allowed for its robust quantification. Additionally, we used a delay time of 65 s and a solution flow rate of 1.00 mL/min.

Seven calibration standards (0–10 ppm) were prepared using a Th4+(aq) standard (1000 ppm, Inorganic Ventures in 7% HNO3(aq)) to construct a calibration line for Th4+(aq) in 0.1 M HNO3(aq). The lower limit of detection (LLOD) and lower limit of quantification (LLOQ) for Th4+ concentrations were determined by measuring the signal from seven 0.1 M HNO3(aq) blanks and using eqs 2 and 3, respectively.

graphic file with name sc4c06166_m002.jpg 2
graphic file with name sc4c06166_m003.jpg 3

Here, sbl was the standard deviation in the y-intercept of the ICP-AES signal intensity from the calibration curve and m was the slope of the calibration curve (obtained by the least-squares method). For LLOD, the factor of 3 represents a confidence level of 95%. For the LLOQ, the factor of 10 represents the signal intensity threshold for ten times greater than the observed noise from the measurement.51,52

Bayesian Optimization

All Gaussian Process modeling and Bayesian Optimization were conducted through an in-house Python code using the sci-kit learn53 and scipy54 libraries. Initial length-scale hyperparameters for the Gaussian Process kernel function (eq S6) were set to the mean value of each dimension and bound by a factor of 10 above and below the minimum and maximum values of that dimension, respectively. The measured DTh standard deviation values were used as input noise. Final kernel hyperparameters were found within their bounds by maximizing the log-marginal likelihood of data during the fitting process. Upon training the Gaussian Process model to observed measurements, new experimental sampling points were determined through maximum locations using the Kriging Believer acquisition function. The acquisition function was generated within the in-house Python code based on refs (55−57) with a pseudocode provided in Section S3.

Results and Discussion

Monoamide Extraction Dataset

Given the high cost associated with conducting extensive experimental measurements for actinide systems, we compiled a comprehensive dataset from literature to test the concept of Bayesian Optimization and benchmark the algorithms. Here, we selected the N,N-dialkyl monoamide class as extractants because they have been studied since 196058 for their enhanced environment sustainability for liquid–liquid extraction compared to the conventional tributyl phosphate, offering improved selectivity and reduced secondary waste.59−64 Thus, the extraction of f-elements with these molecules represents an ideal case to test our integrated Bayesian Optimization and high-throughput experimentation workflow as it allows us to directly compare our results with a significant amount of data accumulated within the same chemical space to validate our optimization process.

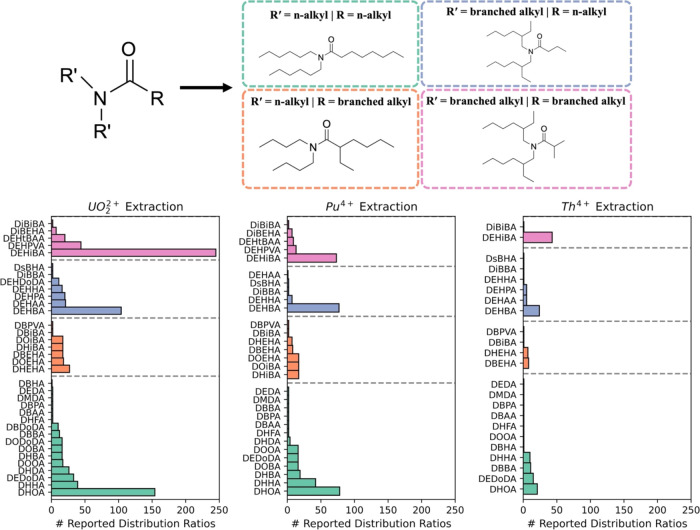
Figure 2 illustrates a breakdown of the extractants used with UO22+, Pu4+, and Th4+—the most reported actinides, while Figure S3 provides a complete summary of the whole dataset, which contains a total of 2132 distribution ratios from previously reported experiments involving 35 unique monoamides and 11 different actinides (note that these refer to unique experimental conditions, not accounting for possible duplicated or triplicated experiments performed by a group in each condition). The most extensively studied system is the extraction of UO2+2 with the N,N-di-2-ethylhexylisobutyramide (DEHiBA) extractant, which has 245 reported UO2+2 distribution ratio values (DU). Most other systems within the dataset were only characterized with a number of experiments in the low tens. Therefore, we chose to use the UO2+2 with DEHiBA dataset to develop the Bayesian Optimization methodology (Section S2) before applying the technique to support experiments on the LANL Super Separator. Here, the performance of the anisotropic Radial Basis Function (RBF) and Matérn kernels were compared for predicting DU, while the sampling strategies of the Kriging Believer, Thompson Sampling, Distance Exploration, and Random acquisition functions were examined in their efficiency for finding the maximum DU value. Virtual Bayesian Optimization campaigns showed that a combination of the RBF kernel and the Kriging Believer acquisition function was able to identify the maximum DU value within the dataset by only needing to perform (at most) 90 total experiments inside an experimental space of 244 experiments (Section S2c). This represents a significant acceleration in the identification of the optimal separation conditions by saving 63% of time and effort compared to a complete sampling of the experimental space traditionally done in high-throughput experimentation.

Figure 2.

Figure 2

Open in a new tab

Dataset composed for the theoretical test. (Top) General structure of symmetric N,N-dialkyl monoamides and the four unique categories they are classified into based on n-alkyl or branched alkyl groups. (Bottom) A breakdown of the total number of reported distribution ratios for the UO2+2, Pu4+, and Th4+ cations with various N,N-dialkyl monoamide extractants. A complete list of the acronyms used for the monoamide names can be found in Table S1.

High-Throughput Measurement and Optimization of Liquid–Liquid Extraction of Th4+

Due to the encouraging results from the virtual optimization campaigns of UO2+2 extraction with DEHiBA, high-throughput experimentation coupled with Bayesian Optimization was deployed using the LANL Super Separator to screen extraction conditions and optimize the extraction of Th4+ by DEHBA into a 20 v% TBP/n-dodecane organic phase. Figure 3 provides our initial four-dimensional experimental input space where Th4+ distribution ratios (DTh) were measured as a function of (1) initial [Th4+(aq)] ([Th]feed), (2) initial [HNO3(aq)], (3) initial [DEHBA(org)], and (4) temperature. Here, the use of low [Th]feed, low [DEHBA(org)], and a 20 v% TBP(constant)/n-dodecane organic phase to act as phase modifier and a coextractant was chosen to help prevent the third-phase formation. This choice kept us in a more idealized scenario to show a proof-of-principle to the Bayesian Optimization methodology.

Figure 3.

Figure 3

Open in a new tab

(Top) Sampling locations and measured DTh values across the four-dimensional experimental input space after four Bayesian Optimization cycles on the extraction of Th4+(aq) by DEHBA in 20 v% TBP/n-dodecane. (Bottom) Measured vs predicted DTh values of the first four cycles. Error bars represent a single standard deviation from the predicted and measured values, while the legend reports the mean absolute error (MAE) between the values.

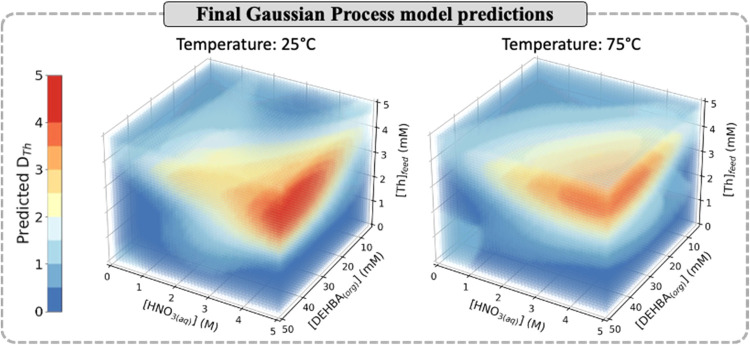
In total, this experimental space can be discretized into 432 unique conditions within a typical experimental grid, resulting in 1296 measurements needing to be performed to completely characterize the region (accounting for experiments performed in triplicate). The experimental sampling locations and liquid–liquid extraction optimization performance is also displayed in Figure 3, where convergence of the DTh values was observed after four complete experimental cycles (113 unique conditions and 339 total measurements performed). Overall, a maximum DTh value of 4.85 ± 0.8 was measured (Cycle 2) using the experimental conditions of [Th]feed = 3.0 mM, [HNO3(aq)] = 4.0 M, [DEHBA(org)] = 40 mM, and temperature = 25 °C. A fifth batch of predicted experimental conditions was generated from the measurements and resulted in a single DTh prediction of 4.58 ± 0.12, while all other values were <3.19 ± 0.23. Since none of these conditions were expected to improve upon our current maximum DTh value, and the Gaussian Process model showed accurate prediction inside the experimental space (Cycle 4, Figure 3), this marked the end of our experimental optimization campaign. Figure 4 displays the final Gaussian Process model predictions over the experimental input space based on the measured DTh values. The trends qualitatively follow previous reports for Th4+ extraction with N,N-dialkyl monoamides,59−62 such as increases in [HNO3(aq)], [DEHBA(org)], and [Th]feed leading to higher DTh values, while increasing the temperature decreases the overall Th4+ extraction. Overall, examination of the model’s predictions at 25 °C identifies a region of higher DTh values (>3.0) corresponding to the experimental ranges of: [Th]feed = 3.0–5.0 mM, [HNO3(aq)] = 4.0–5.0 M, and [DEHBA] = 20–50 mM.

Figure 4.

Figure 4

Open in a new tab

Heat map showing the predicted DTh values from the final GP model.

Previous literature has discussed the limitations of Bayesian Optimization where the method can perform poorly and potentially get trapped in local optima when optimizing over large dimensional spaces (≥20 dimensions).26,65,66 As this study was of relatively low dimension (four-dimensional), we expect the identified optimal region to be the global maximum of our initial experimental space. This can be supported by our virtual Bayesian Optimization experimentation on the UO2+2 with DEHiBA dataset where we were able to always find the global maximum for the DU value over a similar experimental input space (Section S3c). Additionally, the overall experimental trends identified in Figure 4 follow previous literature observations for actinide separation by monoamides, further supporting we have identified the global maximum DTh value.

Comparison to Other Optimization Approaches

As robotic automation and high-throughput experimentation have seen major growth in both the pharmaceutical and material communities, only recently have these approaches been applied to optimize reactions involving radioactive elements67 and the separation of f-elements.68 In the work, both studies used high-throughput experimentation to fully screen the experimental space before determining the optimal conditions. By combining our automated experiments with Bayesian Optimization, we were able to significantly reduce the experimental time and effort needed to optimize the separation conditions by 74% compared to a full screening approach. To further explore the performance of Bayesian Optimization, the final Gaussian Process model predictions (Figure 4) were used as a surrogate response surface to compare the method to different optimization approaches (Section S5). Here, scanning the experimental space by varying one-factor-at-a-time (OFAT) identified the maximum DTh after a total of ∼120 experiments, while random sampling needed ∼220 experiments to identify the optimal conditions (Figure S12). Additionally, response surface modeling using DoE full-factorial sampling showed that even fitting a cubic polynomial function to four-level factorial sampling (256 experiments), could not predict the location of highest DTh value within the experimental space (Figure S13). As we were able to identify the maximum DTh value in Cycle 2 (52 total experiments), this shows the advantage of using Bayesian Optimization for liquid–liquid extraction over other experimental optimization techniques.

Importance of Keeping a “Human-in-the-Loop”

During our experimental optimization campaign, a DTh value of 6.58 ± 0.05 was measured at Cycle 2 (Section S4). Upon reaching convergence of the DTh values inside our initial experimental space after four experimental cycles, this measurement led us to explore conditions beyond our initial bounds in an effort to improve upon our currently highest measured DTh value. Here, the Gaussian Process model predicted that nitric acid concentrations beyond 5.0 M could yield even higher DTh values, therefore, a new experimental batch using a tighter grid centered around the 6.58 ± 0.05 value and expanding out 6.0 M [HNO3(aq)] was generated. Upon measurement of this new batch, no DTh values were observed >4.03, and a drastic decrease in the model performance was observed (Cycle 5, Figure S11a). As many of these measurements were performed at experimental conditions similar to those that achieved the 6.58 ± 0.05 value, it was suspected that this may have resulted from an anomalous experiment and was contaminating the Gaussian Process model. To investigate this further, the 6.58 experiment was removed from the dataset and Gaussian Process model retraining was performed at each cycle again. This resulted in improved predictions in Cycles 4 and 5 (Figure S11b), strongly suggesting an experimental anomaly. Overall, this demonstrates the significant benefits of keeping a “human-in-the-loop” when performing automated experiments.69 Here, examination of our results after four experimental cycles caused us to adapt our initial experimental space in an effort to improve the DTh values. However, this shift in the campaign was unnecessary as it was caused by an anomalous experiment contaminating the Gaussian Process model. By keeping a human-in-the-loop and consistently monitoring the performance of the Gaussian Process model after each cycle, we were able to detect this anomaly, remove it from the dataset, and finalize the campaign.

Conclusions

In this study, Bayesian Optimization was coupled with automation-enabled high-throughput experimentation to optimize experimental conditions for actinide extraction. Overall, this work describes an alternative approach toward conducting fundamental studies in separation science. By using the liquid–liquid extraction of Th4+(aq) with DEHBA in 20 v% TBP/n-dodecane as a “proof-of principle” system, we estimate the Bayesian Optimization method was able to save ∼74% of experimental time and effort in optimizing the conditions within the bounds of our initial experimental space. The approach can be readily expanded to other experimental variables such as ionic strength and scaled up to higher concentrations to simulate industry conditions. Future work will examine applying the method to other challenging separation methods, such as chromatography, crystallization, and (co)precipitation, to effectively optimize the procedures currently operating within restrictive existing safety envelopes, leading to new methods centered around economic and environmental sustainability.

Acknowledgments

We greatly appreciate Gabriel Hall from Pacific Northwest National Laboratory and Peter Zalupski from Idaho National Laboratory for sharing their invaluable UO22+ and DEHiBA experimental datasets. We gratefully acknowledge the support of the U.S. Department of Energy, Office of Nuclear Energy, through the NE-43 Office of Materials and Chemical Technologies under the Material Recovery and Waste Form Development Campaign Program (L.J.A., Y.W., S.A.K., P.Y.). We acknowledge the support by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Element Chemistry Program under contract KC0302031 E3M2 at Los Alamos National Laboratory (LANL) (S.L.A., E.R.B., J.S., D.P.). Funding for the design, procurement, and installation of the LANL Super Separator was provided by the DOE Office of Science, Office of Basic Energy Sciences, Separation Program and by the US Department of Energy, National Nuclear Security Association (NNSA), Plutonium Modernization Program (NA-191). This research used resources of National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award BES-ERCAP0023367. This work was conducted at Los Alamos National Laboratory, which is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (contract no. 89233218CNA000001).

Data Availability Statement

The N,N-dialkyl monoamide dataset and final results from the high-throughput experimentation on the extraction of Th4+(aq) by DEHBA in 20 v% TBP/n-dodecane can be made available as excel files to readers upon request. Additionally, both data sets have been uploaded to the Separation Archive for f-elements (SAFE) at https://safe.lanl.gov.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssuschemeng.4c06166.

  • Additional details, figures, and tables involving the LANL Super Separator, N,N-dialkyl monoamide dataset, Bayesian Optimization methodology, anomalous experiment results, comparison to various optimization methods, and full data of the extraction of Th4+(aq) by DEHBA in 20 v% TBP/n-dodecane (PDF)

Author Contributions

∥ L.J.A. and Y.W. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

sc4c06166_si_001.pdf (6.3MB, pdf)

References

  1. A Research Agenda for Transforming Separation Science; The National Academies Press, 2019 10.17226/25421. [DOI] [Google Scholar]
  2. Sholl D. S.; Lively R. P. Seven chemical separations to change the world. Nature 2016, 532 (7600), 435–437. 10.1038/532435a. [DOI] [PubMed] [Google Scholar]
  3. Nash K. L. A Review of the Basic Chemistry and Recent Developments in Trivalent F-elements Separations. Solvent Extr. Ion Exch. 1993, 11 (4), 729–768. 10.1080/07366299308918184. [DOI] [Google Scholar]
  4. Leoncini A.; Huskens J.; Verboom W. Ligands for f-element extraction used in the nuclear fuel cycle. Chem. Soc. Rev. 2017, 46 (23), 7229–7273. 10.1039/C7CS00574A. [DOI] [PubMed] [Google Scholar]
  5. Neidig M. L.; Clark D. L.; Martin R. L. Covalency in f-element complexes. Coord. Chem. Rev. 2013, 257 (2), 394–406. 10.1016/j.ccr.2012.04.029. [DOI] [Google Scholar]
  6. Moyer B. A.; Lumetta G. J.; Bruffey S. H.; Finkeldei S.; Marsden K. C.; Simpson M. F.; Jensen M. P.; Zalupski P. R.; Clark A. E.; Yang P.. Innovative Separations Research and Development Needs for Advanced Fuel Cycles; Oak Ridge National Lab.(ORNL): Oak Ridge, TN (United States), 2022 10.2172/1844866. [DOI] [Google Scholar]
  7. Choppin G. R.; Nash K. L. Actinide Separation Science. Radiochimca Acta 1995, 70–71, 225–236. 10.1524/ract.1995.7071.s1.225. [DOI] [Google Scholar]
  8. Nash K. L.; Choppin G. R. Separations Chemistry for Actinide Elements: Recent Developments and Historical Perspective. Sep. Sci. Technol. 1997, 32 (1–4), 255–274. 10.1080/01496399708003198. [DOI] [Google Scholar]
  9. Nash K. L.; Madic C.; Mathur J. N.; Lacquement J.. Actinide Separation Science and Technology. In The Chemistry of the Actinide and Transactinide Elements; Morss L. R.; Edelstein N. M.; Fuger J., Eds.; Springer: Netherlands, 2006; pp 2622–2798. [Google Scholar]
  10. Mathur J. N.; Murali M. S.; Nash K. L. Actinide Partitioning—A Review. Solvent Extr. Ion Exch. 2001, 19 (3), 357–390. 10.1081/SEI-100103276. [DOI] [Google Scholar]
  11. Burger B.; Maffettone P. M.; Gusev V. V.; Aitchison C. M.; Bai Y.; Wang X.; Li X.; Alston B. M.; Li B.; Clowes R.; Rankin N.; Harris B.; Sprick R. S.; Cooper A. I. A mobile robotic chemist. Nature 2020, 583 (7815), 237–241. 10.1038/s41586-020-2442-2. [DOI] [PubMed] [Google Scholar]
  12. Langner S.; Häse F.; Perea J. D.; Stubhan T.; Hauch J.; Roch L. M.; Heumueller T.; Aspuru-Guzik A.; Brabec C. J. Beyond Ternary OPV: High-Throughput Experimentation and Self-Driving Laboratories Optimize Multicomponent Systems. Adv. Mater. 2020, 32 (14), 1907801 10.1002/adma.201907801. [DOI] [PubMed] [Google Scholar]
  13. Coley C. W.; Eyke N. S.; Jensen K. F. Autonomous Discovery in the Chemical Sciences Part I: Progress. Angew. Chem., Int. Ed. 2020, 59 (51), 22858–22893. 10.1002/anie.201909987. [DOI] [PubMed] [Google Scholar]
  14. Coley C. W.; Eyke N. S.; Jensen K. F. Autonomous Discovery in the Chemical Sciences Part II: Outlook. Angew. Chem., Int. Ed. 2020, 59 (52), 23414–23436. 10.1002/anie.201909989. [DOI] [PubMed] [Google Scholar]
  15. Häse F.; Roch L. M.; Aspuru-Guzik A. Next-Generation Experimentation with Self-Driving Laboratories. Trends Chem. 2019, 1 (3), 282–291. 10.1016/j.trechm.2019.02.007. [DOI] [Google Scholar]
  16. Li Z.; Najeeb M. A.; Alves L.; Sherman A. Z.; Shekar V.; Cruz Parrilla P.; Pendleton I. M.; Wang W.; Nega P. W.; Zeller M.; Schrier J.; Norquist A. J.; Chan E. M. Robot-Accelerated Perovskite Investigation and Discovery. Chem. Mater. 2020, 32 (13), 5650–5663. 10.1021/acs.chemmater.0c01153. [DOI] [Google Scholar]
  17. Montgomery D. C.Design and Analysis of Experiments; Wiley, 2019. [Google Scholar]
  18. Myers R. H.; Montgomery D. C.; Anderson-Cook C. M.. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons, 2016. [Google Scholar]
  19. Murray P. M.; Bellany F.; Benhamou L.; Bučar D.-K.; Tabor A. B.; Sheppard T. D. The application of design of experiments (DoE) reaction optimization and solvent selection in the development of new synthetic chemistry. Org. Biomol. Chem. 2016, 14 (8), 2373–2384. 10.1039/C5OB01892G. [DOI] [PubMed] [Google Scholar]
  20. Weissman S. A.; Anderson N. G. Design of Experiments (DoE) and Process Optimization. A Review of Recent Publications. Org. Process Res. Dev. 2015, 19 (11), 1605–1633. 10.1021/op500169m. [DOI] [Google Scholar]
  21. Yang L.; Liu S.; Chang C.; Yang S.; Shen W. An efficient and invertible machine learning-driven multi-objective optimization architecture for light olefins separation system. Chem. Eng. Sci. 2024, 285, 119553 10.1016/j.ces.2023.119553. [DOI] [Google Scholar]
  22. Yang A.; Kong Z. Y.; Sun S.; Sunarso J.; Ren J.; Shen W. Design and Multiobjective Optimization of a Novel Double Extractive Dividing Wall Column with a Side Reboiler Scheme for the Recovery of Ethyl Acetate and Methanol from Wastewater. Ind. Eng. Chem. Res. 2023, 62 (44), 18591–18602. 10.1021/acs.iecr.3c02191. [DOI] [Google Scholar]
  23. Qi L.; Yang A.; Kong Z. Y.; Sun S.; Shen W. Insight on the sustainable design and multi-objective optimization for separating the ternary azeotropic mixture of toluene/n-butanol/water by natural decanting coupled with pressure swing distillation. Sep. Purif. Technol. 2023, 313, 123434 10.1016/j.seppur.2023.123434. [DOI] [Google Scholar]
  24. Shen T.; Teng L.; Hu Y.; Shen W. Systematic screening procedure and innovative energy-saving design for ionic liquid-based extractive distillation process. Front. Chem. Sci. Eng. 2023, 17 (1), 34–45. 10.1007/s11705-022-2234-3. [DOI] [Google Scholar]
  25. Shahriari B.; Swersky K.; Wang Z.; Adams R. P.; Freitas N. d. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104 (1), 148–175. 10.1109/JPROC.2015.2494218. [DOI] [Google Scholar]
  26. Frazier P. I.A tutorial on Bayesian optimization, arXiv:1807.02811. arXiv.org e-Print archive. https://doi.org/10.48550/arXiv.1807.02811 (accessed 2018). [Google Scholar]
  27. Snoek J.; Larochelle H.; Adams R. P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951–2959. [Google Scholar]
  28. Frazier P. I.; Wang J.. Bayesian Optimization for Materials Design. In Information Science for Materials Discovery and Design; Lookman T.; Alexander F. J.; Rajan K., Eds.; Springer International Publishing, 2016; pp 45–75. [Google Scholar]
  29. Liang Q.; Gongora A. E.; Ren Z.; Tiihonen A.; Liu Z.; Sun S.; Deneault J. R.; Bash D.; Mekki-Berrada F.; Khan S. A.; Hippalgaonkar K.; Maruyama B.; Brown K. A.; Fisher Iii J.; Buonassisi T. Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains. npj Comput. Mater. 2021, 7 (1), 188. 10.1038/s41524-021-00656-9. [DOI] [Google Scholar]
  30. Zhang Y.; Apley D. W.; Chen W. Bayesian Optimization for Materials Design with Mixed Quantitative and Qualitative Variables. Sci. Rep. 2020, 10 (1), 4924 10.1038/s41598-020-60652-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Vahid A.; Rana S.; Gupta S.; Vellanki P.; Venkatesh S.; Dorin T. New Bayesian-Optimization-Based Design of High-Strength 7xxx-Series Alloys from Recycled Aluminum. JOM 2018, 70 (11), 2704–2709. 10.1007/s11837-018-2984-z. [DOI] [Google Scholar]
  32. Li C.; Rubín de Celis Leal D.; Rana S.; Gupta S.; Sutti A.; Greenhill S.; Slezak T.; Height M.; Venkatesh S. Rapid Bayesian optimization for synthesis of short polymer fiber materials. Sci. Rep. 2017, 7 (1), 5683 10.1038/s41598-017-05723-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rapp J. T.; Bremer B. J.; Romero P. A. Self-driving laboratories to autonomously navigate the protein fitness landscape. Nat. Chem. Eng. 2024, 1 (1), 97–107. 10.1038/s44286-023-00002-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Nambiar A. M. K.; Breen C. P.; Hart T.; Kulesza T.; Jamison T. F.; Jensen K. F. Bayesian Optimization of Computer-Proposed Multistep Synthetic Routes on an Automated Robotic Flow Platform. ACS Cent. Sci 2022, 8 (6), 825–836. 10.1021/acscentsci.2c00207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Graff D. E.; Shakhnovich E. I.; Coley C. W. Accelerating high-throughput virtual screening through molecular pool-based active learning. Chem. Sci. 2021, 12 (22), 7866–7881. 10.1039/D0SC06805E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pyzer-Knapp E. O. Bayesian optimization for accelerated drug discovery. IBM J. Res. Dev. 2018, 62 (6), 2:1–2:7. 10.1147/JRD.2018.2881731. [DOI] [Google Scholar]
  37. Bellamy H.; Rehim A. A.; Orhobor O. I.; King R. Batched Bayesian Optimization for Drug Design in Noisy Environments. J. Chem. Inf. Model. 2022, 62 (17), 3970–3981. 10.1021/acs.jcim.2c00602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Shields B. J.; Stevens J.; Li J.; Parasram M.; Damani F.; Alvarado J. I. M.; Janey J. M.; Adams R. P.; Doyle A. G. Bayesian reaction optimization as a tool for chemical synthesis. Nature 2021, 590 (7844), 89–96. 10.1038/s41586-021-03213-y. [DOI] [PubMed] [Google Scholar]
  39. Torres J. A. G.; Lau S. H.; Anchuri P.; Stevens J. M.; Tabora J. E.; Li J.; Borovika A.; Adams R. P.; Doyle A. G. A Multi-Objective Active Learning Platform and Web App for Reaction Optimization. J. Am. Chem. Soc. 2022, 144 (43), 19999–20007. 10.1021/jacs.2c08592. [DOI] [PubMed] [Google Scholar]
  40. Christensen M.; Yunker L. P. E.; Adedeji F.; Häse F.; Roch L. M.; Gensch T.; dos Passos Gomes G.; Zepel T.; Sigman M. S.; Aspuru-Guzik A.; Hein J. E. Data-science driven autonomous process optimization. Commun. Chem. 2021, 4 (1), 112 10.1038/s42004-021-00550-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Noack M. M.; Doerk G. S.; Li R.; Fukuto M.; Yager K. G. Advances in Kriging-Based Autonomous X-Ray Scattering Experiments. Sci. Rep. 2020, 10 (1), 1325 10.1038/s41598-020-57887-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Noack M. M.; Doerk G. S.; Li R.; Streit J. K.; Vaia R. A.; Yager K. G.; Fukuto M. Autonomous materials discovery driven by Gaussian process regression with inhomogeneous measurement noise and anisotropic kernels. Sci. Rep. 2020, 10 (1), 17663 10.1038/s41598-020-74394-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Noack M. M.; Yager K. G.; Fukuto M.; Doerk G. S.; Li R.; Sethian J. A. A Kriging-Based Approach to Autonomous Experimentation with Applications to X-Ray Scattering. Sci. Rep. 2019, 9 (1), 11809 10.1038/s41598-019-48114-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Noack M. M.; Zwart P. H.; Ushizima D. M.; Fukuto M.; Yager K. G.; Elbert K. C.; Murray C. B.; Stein A.; Doerk G. S.; Tsai E. H. R.; Li R.; Freychet G.; Zhernenkov M.; Holman H.-Y. N.; Lee S.; Chen L.; Rotenberg E.; Weber T.; Goc Y. L.; Boehm M.; Steffens P.; Mutti P.; Sethian J. A. Gaussian processes for autonomous data acquisition at large-scale synchrotron and neutron facilities. Nat. Rev. Phys. 2021, 3 (10), 685–697. 10.1038/s42254-021-00345-y. [DOI] [Google Scholar]
  45. Greenhill S.; Rana S.; Gupta S.; Vellanki P.; Venkatesh S. Bayesian Optimization for Adaptive Experimental Design: A Review. IEEE Access 2020, 8, 13937–13948. 10.1109/ACCESS.2020.2966228. [DOI] [Google Scholar]
  46. Garud S. S.; Karimi I. A.; Kraft M. Design of computer experiments: A review. Comput. Chem. Eng. 2017, 106, 71–95. 10.1016/j.compchemeng.2017.05.010. [DOI] [Google Scholar]
  47. Ricard-McCutchan E.Evaluated Nuclear Structure Data File (ENSDF), 2022/02/14 ed.; National Nuclear Data Center at Brookhaven National Laboratory: Nuclear Data Sheets, 2022. [Google Scholar]
  48. Wang Y.; Abergel R. J. Radiochemical Separation Techniques in Classroom Settings. J. Chem. Educ. 2023, 100 (4), 1603–1612. 10.1021/acs.jchemed.2c01193. [DOI] [Google Scholar]
  49. Wang Y.; Deblonde G. J. P.; Abergel R. J. Hydroxypyridinone Derivatives: A Low-pH Alternative to Polyaminocarboxylates for TALSPEAK-like Separation of Trivalent Actinides from Lanthanides. ACS Omega 2020, 5 (22), 12996–13005. 10.1021/acsomega.0c00873. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wang Y.; Zhang Z.; Abergel R. J. Hydroxypyridinone-based stabilization of Np(IV) enabling efficient U/Np/Pu separations in the Adapted PUREX process. Sep. Purif. Technol. 2021, 259, 118178 10.1016/j.seppur.2020.118178. [DOI] [Google Scholar]
  51. Skoog D. A.; Holler F. J.; Crouch S. R.. Principles of Instrumental Analysis; Thomson Brooks/Cole, 2007. [Google Scholar]
  52. Harris D. C.Quantitative Chemical Analysis; Macmillan, 2010. [Google Scholar]
  53. Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Prettenhofer P.; Weiss R.; Dubourg V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  54. Virtanen P.; Gommers R.; Oliphant T. E.; Haberland M.; Reddy T.; Cournapeau D.; Burovski E.; Peterson P.; Weckesser W.; Bright J.; et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17 (3), 261–272. 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Ginsbourger D.; Le Riche R.; Carraro L.. Kriging Is Well-Suited to Parallelize Optimization. In Computational Intelligence in Expensive Optimization Problems; Tenne Y.; Goh C.-K., Eds.; Springer Berlin Heidelberg, 2010; pp 131–162. [Google Scholar]
  56. Ginsbourger D.; Le Riche R.; Carraro L. A.. Multi-points Criterion for Deterministic Parallel Global Optimization based on Gaussian Processes. 2008.
  57. Schonlau M.Computer Experiments and Global Optimization; University of Waterloo, 1997. [Google Scholar]
  58. Siddall T. H. III. Effects of structure of N,N-DIsubstituted Amides on Their Extraction of Actinide and Zirconium Nitrates and of Nitric Acid1. J. Phys. Chem. A 1960, 64 (12), 1863–1866. 10.1021/j100841a014. [DOI] [Google Scholar]
  59. Pathak P. N. N,N-Dialkyl amides as extractants for spent fuel reprocessing: an overview. J. Radioanal. Nucl. Chem. 2014, 300 (1), 7–15. 10.1007/s10967-014-2961-0. [DOI] [Google Scholar]
  60. McCann K.; Drader J. A.; Braley J. C. Comparing Branched versus Straight-chained Monoamide Extractants for Actinide Recovery. Sep. Purif. Rev. 2018, 47 (1), 49–65. 10.1080/15422119.2017.1321018. [DOI] [Google Scholar]
  61. Manchanda V. K.; Pathak P. N. Amides and diamides as promising extractants in the back end of the nuclear fuel cycle: an overview. Sep. Purif. Technol. 2004, 35 (2), 85–103. 10.1016/j.seppur.2003.09.005. [DOI] [Google Scholar]
  62. Gasparini G. M.; Grossi G. Review Article Long Chain Disubstituted Aliphatic Amides as Extracting Agents in Industrial Applications of Solvent Extraction. Solvent Extr. Ion Exch. 1986, 4 (6), 1233–1271. 10.1080/07366298608917921. [DOI] [Google Scholar]
  63. Hall G. B.; Bessen N. P.; Zalupski P. R.; Campbell E. L.; Grimes T. S.; Peterman D. R.; Lumetta G. J. Extraction of Neptunium, Plutonium, Americium, Zirconium, and Technetium by Di-(2-Ethylhexyl)-Iso-Butyramide (DEHiBA) at High Metal Loadings. Solvent Extr. Ion Exch. 2023, 41 (5), 545–563. 10.1080/07366299.2023.2215833. [DOI] [Google Scholar]
  64. Hall G. B.; Campbell E. L.; Bessen N. P.; Graham T. R.; Cho H.; RisenHuber M.; Heller F. D.; Lumetta G. J. Extraction of Nitric Acid and Uranium with DEHiBA under High Loading Conditions. Inorg. Chem. 2023, 62 (17), 6711–6721. 10.1021/acs.inorgchem.3c00288. [DOI] [PubMed] [Google Scholar]
  65. Eriksson D.; Jankowiak M.. High-dimensional Bayesian optimization with sparse axis-aligned subspaces. In Uncertainty in Artificial Intelligence; PMLR, 2021; pp 493–503. [Google Scholar]
  66. Moriconi R.; Deisenroth M. P.; Sesh Kumar K. S. High-dimensional Bayesian optimization using low-dimensional feature spaces. Mach. Learn. 2020, 109 (9), 1925–1943. 10.1007/s10994-020-05899-z. [DOI] [Google Scholar]
  67. Webb E. W.; Cheng K.; Winton W. P.; Klein B. J. C.; Bowden G. D.; Horikawa M.; Liu S. W.; Wright J. S.; Verhoog S.; Kalyani D.; Wismer M.; Krska S. W.; Sanford M. S.; Scott P. J. H. Development of High-Throughput Experimentation Approaches for Rapid Radiochemical Exploration. J. Am. Chem. Soc. 2024, 146 (15), 10581–10590. 10.1021/jacs.3c14822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. An L.; Yao Y.; Hall T. B.; Zhao F.; Qi L. Agile synthesis and automated, high-throughput evaluation of diglycolamides for liquid–liquid extraction of rare-earth elements. Green Chem. 2024, 26 (12), 7188–7197. 10.1039/D4GC01146E. [DOI] [Google Scholar]
  69. Hysmith H.; Foadian E.; Padhy S. P.; Kalinin S. V.; Moore R. G.; Ovchinnikova O.; Ahmadi M. The future of self-driving laboratories: From Human in the Loop Interactive AI to Gamification. Digital Discovery 2024, 3, 621. 10.1039/D4DD00040D. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

sc4c06166_si_001.pdf (6.3MB, pdf)

Data Availability Statement

The N,N-dialkyl monoamide dataset and final results from the high-throughput experimentation on the extraction of Th4+(aq) by DEHBA in 20 v% TBP/n-dodecane can be made available as excel files to readers upon request. Additionally, both data sets have been uploaded to the Separation Archive for f-elements (SAFE) at https://safe.lanl.gov.

Articles from ACS Sustainable Chemistry & Engineering are provided here courtesy of American Chemical Society

RESOURCES