Transport phase diagram and anomalous metallicity in superconducting infinite-layer nickelates

Abstract

Despite obvious similarities in their electronic and crystallographic structures, it remains unclear whether the interactions that shape the normal and superconducting (SC) state properties of high-T_c cuprates and infinite-layer nickelates (ILNs) have the same origin. This question has been brought into sharper focus with recent studies on ILNs of improved crystallinity that reveal a SC dome of comparable extent and similar transport properties above T_c as the hole-doped cuprates. The evolution of these properties in the magnetic-field-induced normal state, however, has yet to be determined. Here, we examine the magnetotransport properties of new-generation Nd_1−xSr_xNiO₂ films in the T → 0 limit across the phase diagram in fields up to 54 T. This extensive study reveals that the limiting low-T form of the normal-state resistivity in ILNs exhibits non-Fermi-liquid behaviour over an extended doping range inside the SC dome, rather than at a singular quantum critical point. While there are clear differences in the charge dynamics of ILNs and cuprates, most notably in the magnetoresistance, our findings reveal that both systems exhibit anomalous metallicity characteristic of a quantum critical phase.

Recent advancements in the sample quality of infinite-layer nickelates have made systematic comparisons with cuprates increasingly relevant. Hsu et al. report anomalous electronic transport in high-crystallinity (Nd,Sr)NiO₂ at large magnetic fields, map out the transport phase diagram, and discuss similarities and differences with cuprates.

Introduction

In most metals, the resistivity (ρ) follows a power-law temperature (T) or magnetic field (H) dependence in the limiting low-T and low- to intermediate-H regimes. The exponent of this power law is a useful indicator of the nature of the electronic ground state and the dominant interactions that scatter the itinerant electrons. In conventional correlated metals, the low-energy excitations are coherent Landau quasiparticles described within a Fermi-liquid (FL) framework. Accordingly, the change in electrical resistivity Δρ due to varying T and H is both quadratic albeit for different reasons; Δρ(T) and Δρ(H) being proportional to the scattering rate (in this case, inter-electron scattering) and scattering time (and its k-space anisotropy), respectively.

In ‘strange’ metals – epitomised by the high-T_c cuprates – Δρ scales linearly with both T and H over an anomalously broad parameter space, suggesting a breakdown of the quasiparticle description¹. An alternative form of anomalous metallicity, often found in correlated metals proximate to a quantum critical point (QCP) of magnetic² origin, is characterised by a resistivity with an unconventional power-law exponent i.e. Δρ(T) ∝ T ⁿ with 1 < n < 2 and, in some cases, a H-linear magnetoresistance (MR)^3,4. While the microscopic mechanism responsible for this unconventional behaviour is actively debated, it is an empirical fact that a dome of superconductivity often lies in close proximity to such anomalous metallicity. Examples include the iron-based superconductors⁵, multilayer graphene superlattices⁶, and heavy-fermion metals⁷. It is therefore widely believed that unconventional SC and non-FL behaviours are intrinsically linked. Indeed, the strength of superconductivity is often found to peak near the QCP, motivating the conjecture that critical fluctuations of the electronic order parameter are responsible for both the pairing interaction and the anomalous metallicity^7,8.

A SC dome is also realised in the ILNs^9–11. Moreover, there are observations of short-ranged spin fluctuations^12–15 as well as signatures of charge order^16–18 in this system, while interlocking stripe order – known to exist in single-^19,20 and tri-layer^21,22 rare-earth nickelates – has also been conjectured²³, providing an appropriate backdrop for strong correlation physics and anomalous or strange metallicity to emerge. While rapid progress has been made in the improvement of sample quality^24,25 and new families have been synthesised^10,26–29, information on the limiting form of the normal-state transport properties of ILNs remains sparse, particularly within the temperature and doping range in which superconductivity is observed. This is in large part due to the challenging synthesis conditions required to produce high-quality ILN films, the field strengths required to suppress the superconductivity^30,31, and the ubiquitous persistence of an anomalous low-T resistivity upturn³² that complicates the analysis. Very recently, by adopting (LaAlO₃)_0.3(Sr₂TaAlO₆)_0.7 (LSAT) as the substrate of choice and alleviating the epitaxial strain in the intermediate perovskite phase, a series of highly crystalline Nd_1−xSr_xNiO₂ (NSNO) films largely devoid of extended defects have been prepared over a wide range of Sr doping x²⁴.

This material advancement has motivated a critical examination of the transport properties across the NSNO phase diagram, which now hosts an expanded SC dome (in both T and x) comparable to that found in La_2−xSr_xCuO₄ (LSCO)²⁴. A T-linear in-plane resistivity ρ_ab is also found to persist over an extended T range near the optimal doping level (x_opt), with a slope dρ_ab/dT similar to that found near x_opt in LSCO²⁴. However, the precise form of ρ_ab(T) beyond x_opt and its doping dependence have not yet been ascertained, raising several key questions: does NSNO also exhibit strange metallic behaviour like LSCO (with an extended doping range of non-FL transport properties³³) or is the T-linearity seen at higher temperature confined to a singular putative QCP underneath its SC dome? Furthermore, are the low-energy excitations in SC nickelates Landau quasiparticles?

In order to shed more light on these outstanding issues, we have carried out a detailed magnetotransport study on a series of NSNO/LSAT thin films, spanning a broad doping range from slightly underdoped (UD) to highly overdoped (OD), in temperatures down to 0.3 K and magnetic fields up to 54 T. By systematically analysing the high-field magnetotransport data, in combination with previously reported lower-field data²⁴, we uncover the following characteristics of normal-state charge transport in NSNO: 1) the resistivity upturn, while still present, undergoes a qualitative change across x_opt, suggesting that the driving force behind the weakly insulating behaviour in UD-NSNO is quenched beyond x_opt; 2) the in-plane MR exhibits neither Kohler nor quadrature scaling; rather, the strong T-dependence of the MR appears to reflect the presence of strong k-space anisotropy predominantly in the elastic scattering channel; and 3) the low-T resistivity in the (field-induced) normal state of OD-NSNO (0.175 ≤ x ≤ 0.325) is best described by a non-integer power law Δρ(T) ∝ T ⁿ with n ≈ 1.5, consistent with a scenario of dominant magnetic scattering. The T − x phase diagram thus revealed bears signatures found in other unconventional superconductors near a putative QCP^34,35, though the persistence of the non-FL form of Δρ(T) over an extended doping range beyond x_opt is more reminiscent of the quantum critical phase observed in hole-doped cuprates. The distinct form of Δρ(T) and the MR, however, suggests that the physical processes that drive the anomalous metallicity (and by inference, the superconductivity) in ILNs may be different from those that prevail in their cuprate counterparts.

Results

Transport phase diagram

Figure 1 summarises the evolution of the in-plane resistivity across the NSNO phase diagram. By examining the form of ρ_ab(T) up to 300 K, we deduce a number of key features. Firstly, we find that the narrow window of T-linear resistivity centred around x_opt evolves into a broad asymmetric fan of T-linearity bounded from below by an onset temperature T₁(x) that tends towards zero as x → x_opt. Secondly, the prominent resistive upturn (dρ_ab/dT < 0) found in UD films below a second characteristic temperature T₀ is strongly suppressed beyond x_opt (Fig. 2). Between T₀ and T₂ in the UD region, and below T₂ in the heavily OD films, Δρ_ab(T) ∝ T ². In the intermediate regime between x_opt and the end of the SC dome, ρ_ab(T) exhibits an anomalous T-dependence that can best be described by a single non-integer power-law with an exponent n = 1.45 ± 0.05 across the entire OD regime. The upper bound of this anomalous form of ρ_ab(T) is also relatively insensitive to x with T_n ~ 50 K. Collectively, these findings reveal that the SC dome of NSNO hosts a state that exhibits anomalous metallicity. Below we examine in detail the evolution of this anomalous metallicity with x, T and H.

Fig. 1. Temperature–doping (T–x) phase diagram of Nd_1−xSr_xNiO₂ inferred from electrical transport.

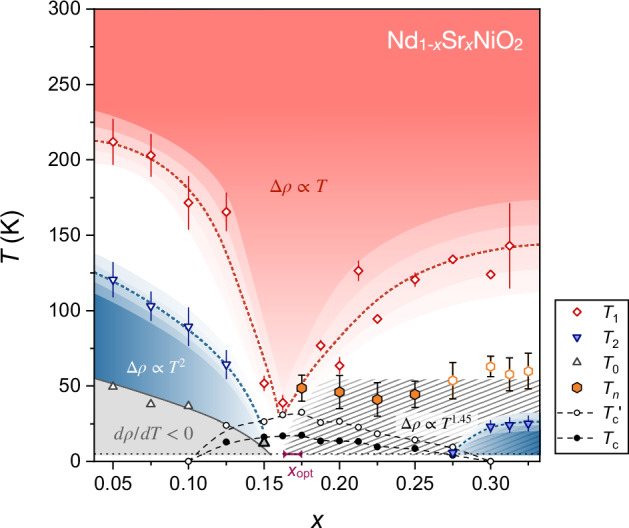
T₁ is the temperature below which ρ_ab(T) deviates from the T-linear behaviour found at T≥ 250 K; T₂ and T_n are the temperatures above which ρ_ab(T) deviates from a T² and Tⁿ(n = 1.45 ± 0.05) dependence, respectively; T₀ is the temperature at which ρ_ab(T) shows a minimum (above 5 K); T_c is the critical temperature defined using the 50% ρ_n criterion and $T_{\mathrm{c}}^{\prime }$ is the onset temperature of superconducting fluctuations as signalled by a steep upturn in dρ_ab/dT. Error bars reflect the uncertainties derived from two independent extraction methods (see Supplementary Figs. 1 and 2 for details). Open and filled symbols correspond to measurements taken in zero and large (>10 T) magnetic fields, respectively, except for T_c and $T_{\mathrm{c}}^{\prime }$ that are extracted from zero-field resistivity data. The T–x phase diagram is dissected at optimal doping x_opt ≈ 0.17 into an underdoped region (UD; x ≤ 0.16) within which the correlation-driven insulating state dρ/dT < 0; grey shading) is found and an overdoped region (OD; x ≥ 0.175) in which a non-Fermi liquid resistivity (Δρ(T) ∝ T^1.45±0.05) is found below T_n ~ 50 K. A small region of T² resistivity, marked by blue shadings, emerges beyond x ≥ 0.275. Finally, an asymmetric fan-shaped region of T-linear resistivity, marked by red shading, is found above the apex of the SC dome. A similar fan of high-T T-linear resistivity is also seen in LSCO (ref. ⁶¹) albeit emerging at a higher temperature.

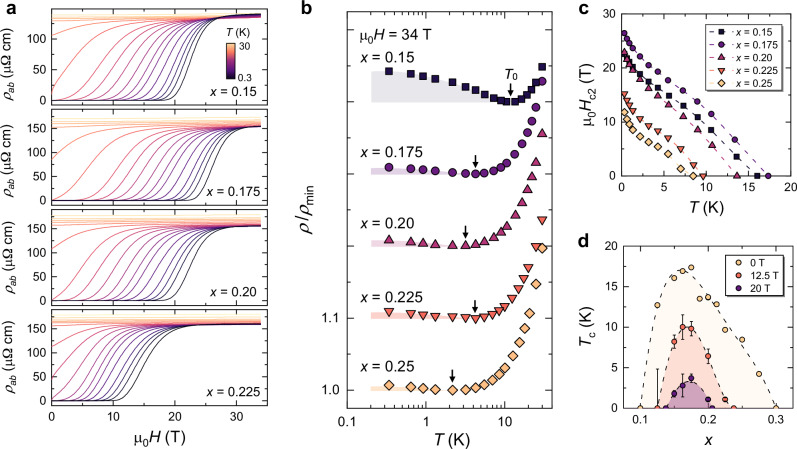
Fig. 2. Resistivity upturn across optimal doping in Nd_1−xSr_xNiO₂.

a Magnetoresistivity isotherms ρ_ab(H) for 0.3 K ≤T≤ 30 K with H ∣∣ c, for the specified x values. b Resistivity in the field-induced normal state (μ₀H = 34 T), normalised by the minimal values $\rho /{\rho }_{\min }$. Data for each x is vertically shifted by 0.1 for clarity. Above x = 0.17, the magnitude of each resistivity upturn is small ($\rho /{\rho }_{\min }\lesssim$ 1%; illustrated by the coloured shadings) and neither the magnitude of the upturn nor the corresponding T₀ shows any strong dependence on x. c Upper critical field μ₀H_c2 extracted using the 50% ρ_n criterion (${\rho }_{\mathrm{n}}\equiv {\rho }_{ab}\left(T_{\mathrm{c}}^{\prime }\right)$). A small but pronounced upturn in H_c2 below 2 K is observed for all x. d Evolution of the SC dome under varying magnetic field strengths. T_c values in finite fields are inferred from isothermal field sweeps shown in a using the 50% ρ_n criterion (Supplementary Fig. 1). Error bars in T_c reflect the difference between the two neighbouring temperatures with ρ_ab(μ₀H) closest to 50% of ρ_n. At μ₀H = 12.5 and 20 T, the maximal T_c remains centred around x_opt ≈ 0.17.

Doping endpoint of the correlation-driven resistivity upturn

Previous magnetotransport measurements²⁴ in magnetic fields up to 14 T revealed that the resistive upturn in UD-NSNO is essentially field-insensitive and accompanied by a reduction in the Hall carrier density with decreasing T, suggesting that these upturns are caused by a competing electronic order, such as the charge order recently found in underdoped ILNs^16–18. Figure 2a shows the in-plane magnetoresistivity ρ_ab(H) measured between 0.3 and 30 K for samples in the slightly UD to OD regime (0.15 ≤ x ≤ 0.225). The upper critical fields μ₀H_c2 inferred using the 50% ρ_n criterion show a characteristic upturn below 2 K (Fig. 2c), consistent with previous reports^31,36. Despite the relatively low T_c, a large magnetic field (>30 T) is required to access the normal state below 1 K (Fig. 2d). By plotting ρ_ab(T) in the field-induced normal state (Fig. 2b) we find a marked reduction in the low-T upturn with no clear doping dependence in its onset temperature T₀ or normalised magnitude (<1%). This contrasts with what is observed below x_opt^24,32 and suggests that the resistivity upturns above and below x_opt have different origins. Previous measurements at x ≥ 0.275 found that the resistivity upturn in the highly OD region can be effectively suppressed by magnetic fields and is likely caused, at least in large part, by disorder-induced localisation²⁴. Here, we conclude that the correlation-driven resistivity upturn found in UD-NSNO and the responsible interaction are quenched at x_opt.

Magnetoresistance near optimal doping

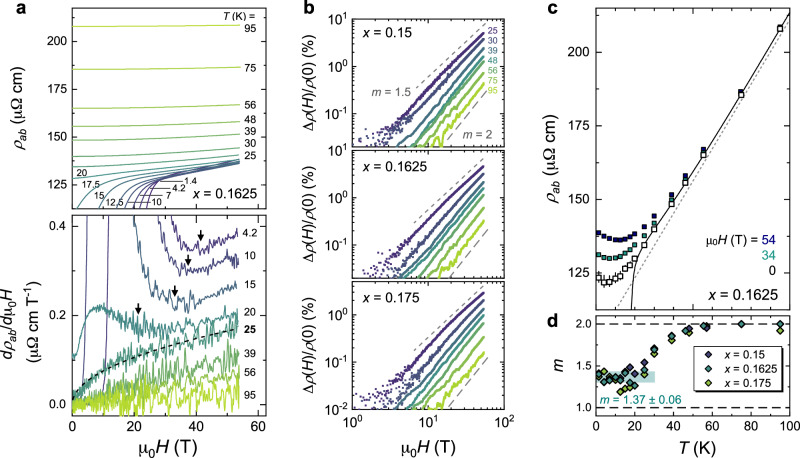
The large H_c2 values found near x_opt require field strengths in excess of 34 T in order to track the normal-state MR far below T_c. Figure 3 shows MR data for three films (x = 0.15, 0.1625, 0.175) obtained in pulsed magnetic fields up to 54 T. An insightful way to distinguish between different forms of MR is to examine the field derivative dρ_ab/dH and its T dependence, as illustrated in the lower panel of Fig. 3a. At T > 35 K, dρ_ab/dH  ∝ H, confirming that the MR follows a conventional H² behaviour. Below 35 K, however, dρ_ab/dH develops a marked curvature, most clearly revealed in the trace at T = 25 K. Despite the apparent downturn in dρ_ab/dH with increasing H, at no point does dρ_ab/dH become constant, indicating that the strictly H-linear MR ubiquitously found across the strange metal regime in hole-doped cuprates³⁷ is not realised in ILNs, at least in the field range studied.

Fig. 3. High-field magnetoresistivity near optimal doping.

a Magnetoresistivity isotherms (top panel) and corresponding field-derivatives (bottom panel) for x = 0.1625. Arrows mark the field strengths above which dρ_ab/dH increases with H, signalling the recovery of normal-state behaviour. Note that the dρ_ab/dH traces plotted here are not vertically shifted. Dashed line overlaying the 25-K derivative is a fit using Δρ(H) = βH^m with m = 1.48 ± 0.01. b Fractional MR  = [ρ(H) − ρ(0)]/ρ(0) versus H on a log-log scale for specified x. The lower and upper dashed lines denote a H² and H^1.5 dependence, respectively. c ρ_ab(T) for x = 0.1625. Open symbols are the extrapolated zero-field resistivity from the high-field data (see extrapolation details in Supplementary Fig. 7). A superlinear-in-T behaviour is found below  ≲ 50 K down to T₀(H), as seen from a deviation from the high-T T-linear behaviour illustrated by the grey dashed line. d Power-law exponent m of the MR H-dependence versus T. m values are extracted by fitting the MR curves within the field range in which normal-state behaviour is recovered (Fig. Supplementary Fig. 7). m evolves from 2 at T≥50 K to a low-T plateau at 1.37 ± 0.06 (green shading) for all x ≈ x_opt.

Another notable feature of Fig. 3a is the marked increase in dρ_ab/dH with decreasing T. Indeed, the slope of the MR (i.e. magnitude of dρ_ab/dH) increases by more than one order of magnitude between 95 and 4.2 K, despite the fact that the zero-field resistivity ρ(0) changes by only a factor of 2, leading to a strong violation of the Kohler scaling observed in conventional metals (Supplementary Fig. 4). Within a Boltzmann theoretical framework, the rapid increase in MR magnitude with decreasing T can only be reconciled by invoking a corresponding and marked increase in the k-space anisotropy of the mean-free-path ℓ, predominantly in the elastic scattering channel (see further details in Supplementary Note C). Alternative functional forms to describe the normal-state MR behaviour, including a standard two-carrier model (Δρ(H) = AH ²/(1 + BH ²)) or a dual-component model (Δρ(H) = β₁H + β₂H ²), fail to capture the MR data over an appreciable T and H window (Supplementary Fig. 5). The absence of a convergence of dρ_ab/dH curves at the high-field limit (Fig. 3a and Supplementary Fig. 10) also indicates that the limiting low-T MR fails to follow the quadrature form $\mathrm{\Delta }\rho \left(H\right)=\sqrt{{\left(\alpha k_{\mathrm{B}}T\right)}^2+{\left(\gamma {\mu }_{\mathrm{B}}{\mu }_{0}H\right)}^2}$ observed in hole-doped cuprates³⁷ and quantum critical metals^3,4 (Supplementary Fig. 4).

Empirically, we find the MR data (at least above 10 T) can be best described by a single power law Δρ(H) = β_mH ^m for all three x ≈ x_opt. As demonstrated in Fig. 3b via log-log plots of the fractional MR Δρ(H)/ρ(0), m evolves smoothly from 2 at T≥ 50 K to  ≈ 1.5 at 25 K, above which ρ(0) is experimentally known. Applying the power-law MR analysis to the field-induced normal state below T_c (as inferred from the field scale above which ρ(H) shows a positive curvature; Supplementary Figs. 6–9), we find that m converges to an anomalous value 1.37 ± 0.06 for all three dopings near x_opt (Fig. 3d), suggesting an anomalous nature of the metallic ground state at x ≈ x_opt that is distinct from that of the cuprates or other quantum critical metals.

Non-Fermi liquid zero-field resistivity

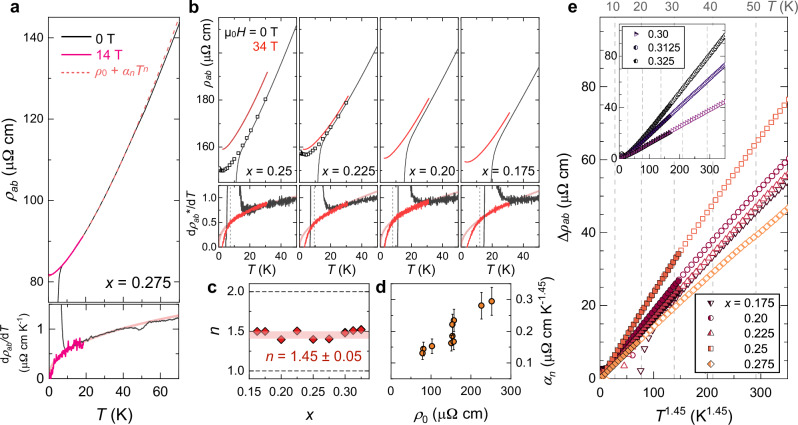
The diminished magnitude (≲1%) and temperature scale (≲4 K) of the resistive upturn for x ≥ x_opt provides an opportunity to investigate the evolution of ρ_ab(T) in NSNO over a more extended temperature and doping range than previous studies²⁴. Figure 4 shows ρ_ab(T) measured at zero and fixed field strengths (μ₀H = 34 T for 0.175 ≤ x ≤ 0.25; 14 T for x = 0.275 (from previous work²⁴); 12 T for x ≥ 0.30). The x = 0.275 film has the lowest T₀ = 0.96 K with a vanishingly small upturn and a negligible MR at 14 T, providing the best opportunity to examine the functional form of normal-state ρ(T) as T → 0. Note that the 0-T and 14-T data are in good agreement within the common temperature range, indicating that the application of magnetic field reveals the normal-state behaviour of ρ_ab(T) below T_c without affecting its functional form.

Fig. 4. Non-Fermi-liquid resistivity power law in overdoped Nd_1−xSr_xNiO₂.

a ρ_ab(T) and corresponding derivative dρ_ab/dT of a highly overdoped Nd_1−xSr_xNiO₂ (x = 0.275). A moderate magnetic field of 14 T can suppress SC completely without inducing a noticeable MR. The prominent curvature in dρ_ab/dT suggests that the normal-state ρ_ab(T) can be described by a power-law behaviour Δρ(T) ∝ Tⁿ with 1 < n < 2, for which n = 1.41 ± 0.02 is found. b ρ_ab(T) and d${\rho }_{ab}^{*}$/dT (normalised by their respective 50-K values) for 0.25 ≥ x ≥ 0.175. For x = 0.25 and 0.225, extrapolated normal-state zero-field resistivity is shown in open squares (see Supplementary Fig. 12). Faint coloured lines in dρ_ab/dT panels are fits made to the 34-T data between 3T₀ (vertical dashed lines) and 30 K, assuming a power-law resistivity ρ(T) = ρ₀ + α_nTⁿ. c Extracted low-T resistivity power-law exponent n. A constant value of n = 1.45 ± 0.05 (red shading) is found over a wide doping range. d Prefactor of the power-law resistivity α_n versus residual resistivity ρ₀, assuming n = 1.45 for all OD films. The error bars in α_n correspond to the geometric uncertainties of measured samples, typical of 15%. e Main panel: Residual-free resistivity Δρ_ab = ρ_ab(T) − ρ₀ versus T^1.45 for 0.175 ≤ x ≤ 0.275. Inset: Corresponding plot for 0.3 ≤x≤ 0.325. Open and filled symbols are data measured under zero and large applied magnetic fields (34 T for 0.175 ≤ x ≤ 0.25; 14 T for x = 0.275; 12 T for x≥0.30), respectively.

Inspection of dρ_ab/dT (Fig. 4a) reveals a small kink at 3 K, below which dρ_ab/dT is T-linear (within noise level) with a near zero 0-K intercept. This is consistent with Δρ(T) ∝ T ² albeit over a narrow T-window. An alternative functional form incorporating both T-linear and T ² components: ρ(T) = ρ₀ + α₁T + α₂T ², used previously to describe the limiting low-T resistivity of hole-doped cuprates³³, is found to hold over the T-window 3 K ≤T≤ 18 K with a corresponding T-linear behaviour in dρ_ab/dT and a finite 0-K intercept. Indeed, the ratio of the low- and high-T T-linear coefficients in NSNO and LSCO are found to show a very similar evolution with x within experimental uncertainty (Supplementary Note A.2 and Supplementary Fig. 3). For the T-linear term to be intrinsic, the kink in dρ_ab/dT below 3 K would have to reflect the beginning of influence of the resistive upturn. On the other hand, if the pronounced downward curvature in dρ_ab/dT is intrinsic, then ρ_ab(T) can be better described by a power-law function: ρ(T) = ρ₀ + α_nT ⁿ with 1 < n < 2 over a wider T-window. To extract the power-law exponent n with any possible impact of the residual upturn minimised, we fit dρ_ab/dT(μ₀H = 14 T) using dρ_ab/dT = nα_nT ⁿ⁻¹ within a T-window between 3T₀ and 18 K (the highest temperature measured). The extracted n = 1.41 ± 0.02 from the 14-T data is found to describe dρ_ab/dT(μ₀H = 0) up to 60 K. We note that varying the lower T-limit for the power-law fitting between 2T₀ and 5T₀ does not affect the extracted n, as nα_nT ⁿ⁻¹ is constrained to go through the origin, demonstrating that the extraction of the resistivity power-law parameters is robust despite the presence of these small resistive upturns in OD-NSNO.

By examining ρ_ab(T) of OD films with 0.25 ≥ x ≥ 0.175, we again find for all x that the dρ_ab/dT curves measured at 34 T exhibit a pronounced downward curvature and connect smoothly to the 0-T data in the normal state (Fig. 4b). Overall, the power-law function can describe the experimental data over the widest temperature range among the three functional forms considered (Supplementary Figs. 13 and 14) and, remarkably, the extracted n for 0.175 ≤ x ≤ 0.325 converges within a narrow range n = 1.45 ± 0.05 (Fig. 4c). The approximate linear-in-T ^1.45 behaviour of the normal-state ρ_ab(T) can also be seen in Fig. 4e, where the residual-free resistivity Δρ_ab(T) is plotted against T ^1.45 for all OD films. Interestingly, the power-law resistivity prefactor α_n is found to correlate to the residual resistivity ρ₀ more strongly than to x (Supplementary Fig. 14). Thus, we conclude that the low-T ρ_ab(T) in OD-NSNO is best described by a power-law behaviour ρ(T) = ρ₀ + α_nT ⁿ, with an unconventional n ≈ 1.5, though the alternative T + T ² form reminiscent of the hole-doped cuprates cannot be definitely ruled out. Irrespective of this, the extended doping range over which the low-T ρ_ab(T) exhibits non-FL behaviour is inconsistent with scenarios based on a standard QCP and is more reflective of the quantum critical phase and strange metal physics manifest in the cuprates.

Discussion

Through a systematic investigation over a wide parameter space, we have uncovered the anomalous resistivity and MR behaviour of NSNO and mapped out its evolution across the phase diagram. While we are not aware of existing theoretical models that could produce the anomalous MR power law found in optimally doped NSNO at T ≲ T_c, similar behaviour has previously been observed in other superconductors^38,39. To investigate whether such a MR behaviour can be explained within a conventional theoretical (Boltzmann) framework, we performed a series of numerical simulations using calculated Fermi surface parameterisation for the superconducting nickelates⁴⁰ and various models to describe the k-space scattering rate anisotropy:

$$1/\tau \left(\varphi ,T\right)=1/{\tau }_0\left(T\right)+1/{\tau }_k\left(\varphi ,T\right),$$ 1

where 1/τ is the inverse of the carrier lifetime (i.e. scattering rate), ϕ is the angle around the Fermi surface, 1/τ₀ is the isotropic (k-independent, inelastic) scattering rate, and 1/τ_k is the anisotropic (k-dependent, elastic) scattering rate. We find that the normal-state MR with an apparent power-law behaviour can be qualitatively reproduced using 1/τ(ϕ) models with a large scattering rate anisotropy $\left({\tau }_{k,\max }^{-1}/{\tau }_0^{-1}\ge 5\right)$ (Supplementary Fig. 11 and Supplementary Table 1). The significant increase in the MR magnitude with decreasing T (Fig. 3) thus reflects a rapid increase in the scattering rate anisotropy and, given the modest change in zero-field resistivity (ρ(95 K)/ρ(4.2 K) ≲ 2), a dramatic increase in ${\tau }_{k,\max }^{-1}\left(4.2\mathrm{K}\right)$/${\tau }_{k,\max }^{-1}\left(95\mathrm{K}\right)$ exceeding one order of magnitude. Moreover, we find that the best quantitative agreement is achieved by excluding the contribution from the putative rare-earth (RE) Fermi pocket, implying that the RE band contributes minimally to the charge transport, at least for x ≈ x_opt. While the power-law MR can be (at least) qualitatively captured using the Boltzmann framework, we note that these simulations only serve to illustrate one possible scenario for the observed MR in NSNO, and the precise Fermi surface geometry and scattering rate anisotropy remain to be established.

A T ^1.5 resistivity power law has been observed in a variety of correlated electron systems with magnetic order, including heavy-fermion superconductors^41–43, d-electron itinerant ferromagnets (IFMs)^44–46, and metallic spin glasses (SGs)^47,48. In heavy-fermion systems, a T ^1.5 resistivity is typically found within a fan-like region centred around a putative antiferromagnetic QCP, sandwiched by regions of T ² resistivity. In contrast, in IFM and SG, T ^1.5 resistivity is found as T → 0 over an extended region of pressure^44,45 or magnetic dopant⁴⁷. While at present we cannot rule out the presence of an antiferromagnetic QCP at x ≈ 0.275, we find no enhancement in the prefactor of T ² resistivity as x → 0.275 (assuming ρ(T) = ρ₀ + A₂T ² for the limiting low-T behaviour; Supplementary Fig. 14) which would signify a divergence of the quasiparticle effective mass upon approach to a putative QCP^2,34. (We note here that the low-T resistivity plateau found in the T ² resistivity regime in x≥0.30, with a small negative MR, is unlikely to be associated with short-lived superconducting puddles as found in other superconductors in the 2D limit^49,50, for which a large positive MR is expected.) The IFMs known to exhibit a T ^1.5 resistivity (beyond the pressure-tuned ferromagnetic QCP), namely MnSi and ZrZn₂, lie well within the clean limit with a residual resistivity ρ₀ ≲ 0.5 μΩ cm (refs. ^44,45), two orders of magnitude lower than that of the current NSNO series. Moreover, the power-law exponent of IFMs is highly sensitive to applied magnetic field and approaches 2 at μ₀H > 1 T (refs. ^51,52). These distinct differences suggest that the interactions responsible for the T ^1.5 resistivity in IFMs are unlikely to be manifest in NSNO. Metallic SGs, on the other hand, are disordered systems (ρ₀ ≫ 10 μΩ cm) without long-range magnetic order. Notably, in some SGs, a T ² resistivity is recovered at high doping levels as T → 0 (ref. ⁴⁷), as found here in heavily OD-NSNO. We also find approximate T ^1.5 resistivity in overdoped Pr_1−xSr_xNiO₂ (x = 0.24) and La_1−xSr_xNiO₂ (x = 0.28; Supplementary Fig. 16), implying that the unconventional resistivity power law is intrinsic to the Ni-O lattice and not influenced by the respective lanthanide ion. Given that signatures of short-range spin order have been observed in ILNs^13–15, we postulate that the observation of an extended non-FL power-law resistivity in superconducting nickelates could be a consequence of their metallic SG state.

Typically, a low-T resistivity power law with an unconventional exponent (n < 2) is considered to be manifestation of a FL instability and the associated low-energy excitations are no longer coherent quasiparticles; the electrical current in these unconventional metals originates from diffusive motion of the interacting electrons^2,53. In the case of a metallic SG, however, it has been theoretically shown that there the quasiparticles remain intact despite the appearance of non-FL behaviour in the electrical transport^54,55. The specific heat coefficient and T ² resistivity in the disordered state in turn are not critically enhanced. Nonetheless, the unconventional power law supports the strongly correlated nature of the itinerant electrons and hints at the coexistence of SG and SC in the ILNs¹⁵. Importantly, the manifestation of approximate T ^1.5 resistivity power law provides evidence for dominant magnetic scatterings in the normal ground state, and supports the existence of a fluctuating magnetic order intrinsic to the Ni-O lattice^12,15 under hole doping.

It has been suggested that the presence of RE Fermi pockets leads to an effective hole doping into the Ni-O lattice⁵⁶ that is responsible for the absence of static antiferromagnetic order in the nominally undoped ILNs. If true, the similar dρ_ab/dT observed in NSNO and LSCO near their respective x_opt are then coincidental, and the comparison of the doping effect should be made between LSCO at x ≈ 0.15 and NSNO x ≳ 0.20. (The fact that the present NSNO thin films exhibit nearly identical dρ_ab/dT values as found in high-quality LSCO single crystals strongly suggests that neither extended defects – known to affect the transport properties of earlier NSNO films – and/or dominant electron-phonon scattering are playing a major role in quantifying the in-plane resistivity values of these next-generation films; see Supplementary Notes A and F for further discussions.) Nevertheless, in all OD-NSNO investigated in this work, we do not observe a predominantly T-linear resistivity (over an extended T-window at low T; Supplementary Fig. 14), suggesting the potential presence of an additional band is not the leading cause for the absent strange metallicity. Secondly, if the low-energy excitations in the low-T normal state of superconducting ILNs are indeed quasiparticles, as is the case in SGs, it may explain certain aspects of the transport characteristics of OD-NSNO. In this scenario, x_opt would not correspond to a conventional QCP at which a T-linear resistivity as T → 0 is found and the quasiparticles are destroyed. Nonetheless, experimental signatures of a low-T SG state have also been detected in LSCO near optimal doping⁵⁷, hinting that a SG state and strange metallicity are not mutually exclusive. Finally, a series of recent experiments^15–18,58 has found that the landscape of competing orders in the ILNs is considerably different than that in the cuprates⁵⁹. It is therefore likely that an intricate interplay between the various electronic orders (further discussions in Supplementary Note F) play a dominant role in determining the transport characteristics (and mediating superconductivity) in the ILNs.

While the exact mechanism responsible for the anomalous metallicity remains to be identified, our results highlight the impact of magnetic interactions in governing the charge transport of normal-state electrons. We thus expect our present study lays important groundwork for understanding of quantum phenomena in the ILNs and provides useful constraints for a viable theoretical model for the anomalous metallicity (and superconductivity) emerging upon doping the NiO₂ planar square lattice.

Methods

Thin film growth

NSNO thin films of approximately 15 unit cells were grown on LSAT (001) substrates with a SrTiO₃ capping layer of approximately 4 unit cells using pulsed laser deposition technique²⁴. We confirm that, other than the additionally synthesised x = 0.1625 sample, the thin film samples presented here are the exact same samples that were studied in Lee et al.²⁴.

Magnetotransport measurements

Gold wires of 25-μm diameter were attached to ultrasonically bonded Al leads using DuPont 4929N silver paint. An AC current of 5 or 10 μA with a frequency of 13–30 Hz was used in DC field measurements and 5–10 kHz for pulsed field measurements. Magnetic fields, applied parallel to the crystalline c-axis, were generated up to 14 T using a Physical Properties Measurement System by Quantum Design Inc., up to 34 T using a Florida-Bitter magnet coupled to a ³He refrigerator at the High Field Magnet Laboratory in Radboud University, the Netherlands, and up to 54 T using a pulsed-field magnet at the Laboratoire National des Champs Magnétiques Intenses in Toulouse, France.

Tight-binding model

We adopt the tight-binding model developed in a recent study on the electronic structure of superconducting five-layer nickelate Nd₆Ni₅O₁₂⁴⁰. The Fermi surface of Nd₆Ni₅O₁₂ contains five sheets derived from the Ni $d_{x^2-y^2}$ band and one sheet from the Nd d band. The Ni-3 and Ni-1 bands (following the notation of Table I in ref. ⁴⁰) are chosen to simulate the Fermi surface of Nd_1−xSr_xNiO₂ near optimal doping, given the current lack of experimentally established doping evolution of Fermi surface in this system, based on their close similarity to the DFT-derived Fermi surface of LaNiO₂ at k_z = 0 and k_z = π/c, respectively⁶⁰.

Magnetoresistivity simulations

We calculate the magnetoresistivity using the Chambers solution to the Boltzmann transport equation with generalised to quasi-2D systems with anisotropic scatterings:

$${\sigma }_{ij}=\frac{e^2}{4{\pi }^3}\int d^3\mathbf{k}D\left(\mathbf{k}\right)v_i\left[\mathbf{k}\left(t=0\right)\right]{\int }_{-\infty }^{0}dt{v}_j\left[\mathbf{k}\left(t\right)\right]e^{t/\tau },$$ 2

where ∫ d ³k is an integral over the first Brillouin zone, D(k) is the density of states at point k, v_i is the ith component of the quasiparticle velocity, and ${\int }_{-\infty }^{0}dt$ is an integral over the quasiparticle lifetime τ. The scattering rate anisotropy enters through 1/τ(ϕ) parametrised by:

$$\frac{1}{\tau \left(\varphi \right)}=\frac{1}{{\tau }_0}+\frac{1}{{\tau }_k}\mid f\left(2\varphi \right){\mid }^{\nu },$$ 3

where ϕ is the azimuthal angle around the Fermi surface, 1/τ₀ is the ϕ-independent isotropic scattering rate, 1/τ_k is the maximum anisotropic scattering rate found in the Brillouin zone (i.e. ’hot spots’), f is the function that characterises the scattering rate anisotropy (i.e. sine/cosine function for the nodal/antinodal hotspot model, respectively), and ν is a variable exponent (ν = 4, 8, 10, or 12). Note that no scattering rate anisotropy is applied to the Nd pocket. For the MR simulations including both the k_z = 0 and k_z = π/c Ni sheets, the contribution to the total conductivity is halved to maintain the total carrier number close to half-filling; for MR simulations including the Nd pocket, the entire contribution from the Nd pocket is added into the total conductivity.

Author contributions

Y.-T.H., K.L., H.Y.H. and N.E.H. initiated the project. K.L. and B.Y.W. synthesised and characterised the nickelate thin films. Y.-T.H., S.B., C.D., A.C., A.K., and I.H-D. performed the high-field magnetotransport measurements. Y.-T.H., C.D., A.C., and N.E.H. analysed the data. Y.-T.H. and N.E.H. wrote the manuscript with input from all authors.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that support the findings of this study are available from the Dryad data repository (10.5061/dryad.8sf7m0czw). Any additional data are available from the corresponding authors upon request.

Code availability

The codes associated with the band structure and transport coefficient calculations that support this study are available from the corresponding authors upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54135-y.