Thermal imaging through hot emissive windows

Abstract

It is not currently possible for an infrared camera to see through a hot window. The window’s own blinding thermal emission prevents objects on the other side from being imaged. Here, we demonstrate a path to overcoming this challenge by coating a hot window with an asymmetrically emitting infrared metasurface whose specially engineered imaginary index of refraction produces an asymmetric spatial distribution of absorption losses in its constituent nanoscale resonators. Operating at 873 K, this metasurface-coated window suppresses thermal emission towards the camera while being sufficiently transparent for thermal imaging, doubling the thermal imaging contrast when compared to a control window at the same temperature

It is not currently possible for an infrared camera to see through a hot window. Now Ciril Samuel Prasad and colleagues report a metasurface-coated window which suppresses thermal emission towards an IR camera while being sufficiently transparent for thermal imaging.

Introduction

The challenging problem of enhancing thermal emission in some directions while suppressing it in others is exacerbated for hot windows because they must remain transparent over the same spectral region. Since the reflectance, emissivity/absorbance, and transmittance add up to unity in each direction, an asymmetry in emissivity is equivalent to an asymmetry in reflectance for a given transmittance. Moreover, emissivity close to unity in any direction must reduce transmittance toward zero. Thus, reduced transmittance is often the price paid for achieving asymmetric emissivity (and reflectivity) in passive devices.

The difficulty of viewing a hot object through a hot emissive window is illustrated in Fig. 1^1–3. When imaging an object through a window, the thermal radiation emitted by the object passes through the window before reaching the camera’s sensor. This is a case of information transfer over a noisy channel: the thermal radiation carries information (e.g. temperature) about the object being imaged, while emission from the window adds to the background noise received by the camera. Considering the window as a channel for electromagnetic information transfer and its own self-emission as a major source of noise, the signal-to-noise ratio (SNR) at the detector is determined by the ratio $\chi =\mathcal{T}/ϵ$, where $\mathcal{T}$ is the transmission of the window, and ϵ represents the emissivity of the window in the direction facing the camera. Thus, suppressing thermal emission toward the camera while preserving transmission is essential for improving SNR through the window.

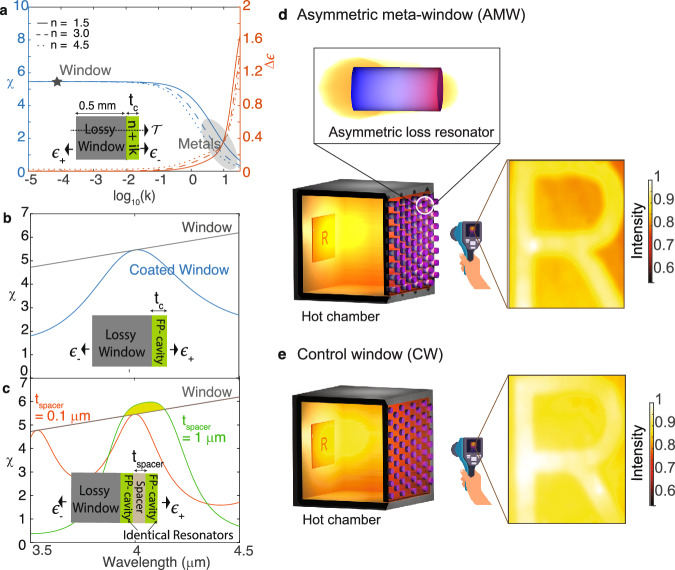
Fig. 1. Breaking loss symmetry in coupled resonant emitters to enhance thermal imaging contrast.

a The calculated SNR χ (blue) with ϵ₋ facing the camera, and the asymmetric emissivity Δϵ (red) as a function of the imaginary index of the coating layer (t_c = 10 nm) on a bare absorbing window, for λ = 4 μm. The solid, dashed, and dotted curves represent n = 1.5, 3.0, and 4.5 respectively. The window (gray star) has index n = 1.5 and k = 10⁻⁴, while metals (shaded in gray) have varied n but large k. The inset illustrates the geometry in which the coating breaks the parity symmetry of the window. The enhanced and suppressed surface emissivities on either sides are represented by ϵ₊ and ϵ₋, respectively, while $\mathcal{T}$ represents the transmission through the structure. b χ as function of wavelength λ for a bare window (black) and with a low loss dielectric coating (n = 3, k = 10⁻⁶, t_c = 2 μm) that supports a Fabry Perot resonance at λ = 4 μm (blue). c Calculated χ when identical cavities (n = 3, k = 10⁻⁶, t_c = 2 μm) are separated by a spacer layer (n = 1.2, k = 0, t_spacer = 0.1 μm (red) and 1 μm (green)). The loss symmetry of the coupled cavity system is broken when the spacer thickness is large, enhancing χ over the bare window (shaded in green). The windows of our thermal imaging setup, illustrated in (d), are created by arraying the coupled resonators with broken loss symmetry (shown in inset) to make up the AMW. In the CW (e), the imaginary index is not a design parameter, and absorption loss is distributed uniformly in the resonant cavity, resulting in nearly symmetric emission. Our approach makes the absorption loss asymmetric along the cavity (d), leading to asymmetric thermal emission but maintaining transmission. The normalized thermal images of an object inside a hot chamber, measured using a mid-IR camera (FLIR A6701), are captured through the AMW and CW, respectively. The whole chamber, including the window, was held at 873 K.

One solution is to use a lower-loss dielectric window in the conventional design, producing nearly identical emissions from both sides. Unfortunately, this is usually impractical due to the unavailability, fragility, or incompatibility of transparent refractory dielectric materials. An ideal solution would be a coating that suppresses thermal emission selectively toward the camera while maintaining window transparency. If ϵ₊ and ϵ₋ respectively represent the higher and lower emissivity values for an asymmetrically emitting structure, emission asymmetry

$$\mathrm{\Delta }ϵ=2\left(\frac{{ϵ}_{+}-{ϵ}_{-}}{{ϵ}_{+}+{ϵ}_{-}}\right)$$ 1

can be achieved over broadband by breaking the parity symmetry of the window (Fig. 1a inset), such as by coating the window with a thin layer of metal (t_c = 10 nm) or a high-index dielectric. However, such coatings cannot improve the ratio χ beyond that of the bare window due to its reduced transmission (Fig. 1a). Enhancing SNR across the entire bandwidth would increase the channel capacity⁴, but since a passive electromagnetic channel at thermal equilibrium has limited capacity⁵, enhancing χ at all wavelengths would violate the laws of thermodynamics.

However, enhancing SNR in a finite bandwidth does not violate thermodynamic laws. For example, resonant systems render thermal radiation more coherent, which allows better control^6–19. Tailoring resonant coatings, such as dielectric Fabry-Perot cavities, enables optimization of χ within targeted spectral ranges while compromising performance elsewhere, thus navigating within thermodynamic constraints. Conventional resonators, usually composed of plasmonic, photonic, photonic crystal, or metamaterial components, rely on engineering the spatial distribution of the real refractive index to tame thermal radiation^20–24. Resonators with high spatial and spectral coherence have been demonstrated^20,25,26, as small form factor metasurfaces designed for thermal imaging with performance optimized by computational imaging and machine learning techniques^27–30. But in these examples, the imaginary refractive index responsible for absorption loss and thermal radiation was not a design parameter, so losses were tolerated to the extent needed to achieve the desired thermal emission brightness. Consequently, the trade-off between transmission and emission suppression still exists in such passive resonators, and χ never surpasses the limit set by the window (Fig. 1b).

This limitation with the conventional resonator design may be overcome by engineering loss through the distribution of the imaginary refractive indices of a metamaterial. The imaginary index is a powerful design tool for light sources, and optimizing its spatial distribution can lead to new paradigms of thermal emitter design³¹. Drawing inspiration from non-Hermitian optics³², a coupled Fabry-Perot resonator system—two identical lossless resonators coupled via a spacer layer—may be designed such that χ can surpass that of the bare window near resonance (Fig. 1c). Here, one resonator supports a lossy Fabry-Perot mode while the other resonator supports a low-loss mode resonant at the same frequency. When these two modes are weakly coupled by a thick spacer layer, the resultant modes of the system resonate at the same frequency but with different damping. This loss asymmetry is the key to asymmetric emission without compromising transmission.

Here we report the design and fabrication of coupled resonators engineered with asymmetric loss to demonstrate an asymmetrically-emitting metasurface window (AMW) (Fig. 1d).

To contrast the operation of our AMW, we fabricated a control window (CW) comprised of an array of single dielectric cavities resonant at the same frequency as those in the AMW.

Figure 1d and e show that the quality of infrared (IR) imaging through the hot window is perceptibly lower in the lower χ CW case than for the “one-way” semi-transparent AMW with higher χ. Spatially engineered metasurfaces like those presented here could also address the outstanding challenge of camera narcissism³³ and will find applications in the areas of energy conservation, energy harvesting, and radiative cooling as well.

Results and discussion

Asymmetric meta-window design and characterization

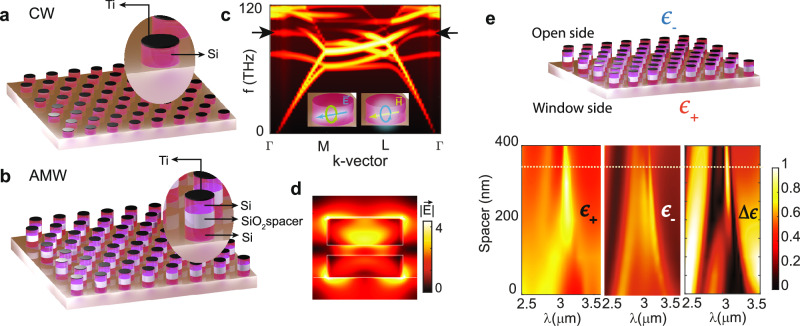
Our CW employs a two dimensional hexagonal array of single silicon disk resonators, while our AMW similarly arrays stacked pairs of identical silicon resonators separated by a silica spacer (Fig. 2b). The silicon nanodisk resonators making up our CW and AMW (Fig. 2a and b) support a quasi-bound state in the continuum (QBIC) mode for achieving high-quality resonances with negligible scattering. We used nano-resonators instead of planar Fabry-Perot resonators because the latter are known to delaminate when heated to high temperatures³⁴, while nano-structures better relax thermal stress and remain intact at higher temperatures³⁵. The QBIC mode originates from the destructive interference of electric and magnetic dipolar modes of the silicon disk resonator³⁶, facilitating tight confinement of the resonant mode. The QBIC mode may be seen as the flat band in the TM bandstructure of the hexagonal array of silicon resonators in Fig. 2c.

Fig. 2. Design for the control window (CW) and the asymmetric meta-window (AMW).

Schematic of (a) CW and (b) AMW with insets showing the individual resonator structure. c Calculated TM band structure of a hexagonal array of cylindrical silicon resonators with a period of 2 μm, height of 600 nm, and radius of 700 nm, showing a QBIC mode as a flat band (marked with black arrows) near the Γ point. The insets describe the magnetic and electric dipolar modes excited in each resonator that interfere to create the QBIC mode. d The calculated cross-sectional electric field profile at the resonance (λ = 3.06 μm) of the AMW resonators with a spacer thickness of 350 nm (weak coupling), showing very different field strengths in the two resonators. e Normal direction emissivity (ϵ) from the AMW toward the window side (higher emissivity, ϵ₊), open side (lower emissivity, ϵ₋) and Δϵ as a function of spacer thickness. The horizontal white line marks the spacer thickness (350 nm) considered in (d).

For the convenience of this proof-of-concept demonstration, we introduced loss by placing a 10-nm layer of titanium on one of the resonators, instead of using the losses from the fused silica window substrate itself, as in Fig. 1b and c. The metal layer simulates the effect of naturally occurring dielectric losses at elevated temperatures that increase in one resonator more than the other, thereby creating an imaginary index gradient that can suppress emission and enhance transmission (Supplementary Note 3 and Fig. S3). This thin titanium layer adds high loss over the entire spectrum of interest, making the condition for weak coupling of resonators easily accessible in experiments. A sub-micron thick spacer layer is sufficient for weakly coupling the resonators when the resonator loss is high. Of course, such a metal layer would not be used for the case of an actual lossy window substrate. In that case, a much thicker spacer layer is required, which was beyond our ability to fabricate.

Thus, both the CW silicon disk resonator and the top resonator in the AMW are damped by the 10 nm thick titanium layer on top, whose effect on resonator absorption loss or thermal emission may be observed in the divergence of the Poynting vector (Supplementary Note 2 and Fig. S2). The modes in the two silicon disk resonators of the AMW, one damped and one undamped, create an asymmetric absorption loss whose asymmetry is controlled by spacer thickness. For small spacer thicknesses, the resonators are tightly coupled, and no loss asymmetry is created. For larger spacer thicknesses, the modes in the disk pair become weakly coupled to each other, so the modes are nearly all confined to their respective resonators, and the desired loss asymmetry is achieved. Supplementary Note 1 and Fig. S1 provide more information.

The asymmetric absorption/thermal emission from the AMW may be seen in the calculated emissivity of the window plotted in Fig. 2e. The emissivity (ϵ), calculated in the normal direction to the window at the resonant wavelength, is plotted as a function of spacer thickness to elicit the underlying physics. When the spacer thickness is small, the resonant modes in the individual disks couple strongly and spread across both resonators. In this case, the disk pair acts like a single large cavity that resonates at a lower frequency than the individual disk. The fundamental and the higher-order resonant modes of this large cavity show up in the emissivity plot for 0–150 nm spacer thicknesses. In this tightly coupled regime, the absorption loss asymmetry in the cavity is negligible. Although the emissivity is weaker toward the open “camera” side (ϵ₋) than toward the window “object” side (ϵ₊), this small emission asymmetry is caused by the symmetry-breaking placement of the coating on only one side of the window, not the resonators themselves.

In contrast, when the spacer thickness is greater than 150 nm, a single resonant mode in this weak coupling regime may be observed with a near unity ϵ₊ away from the camera, while ϵ₋ is only 50% toward the camera at the same resonance wavelength. This emissivity contrast is the result of the asymmetry in absorption loss, as can be observed in Fig. 2d, which plots the calculated cross-sectional electric field distribution in a weakly coupled AMW disk pair with a 350 nm thick spacer. At its 3.06 μm resonant wavelength, the fields are well confined within the disks, as expected for a QBIC mode, and the field is stronger in the top disk where additional damping from the thin titanium layer occurs. This asymmetric distribution of the field in the weakly coupled regime of the resonator pair is the key to achieving asymmetric absorption or thermal emission from this window.

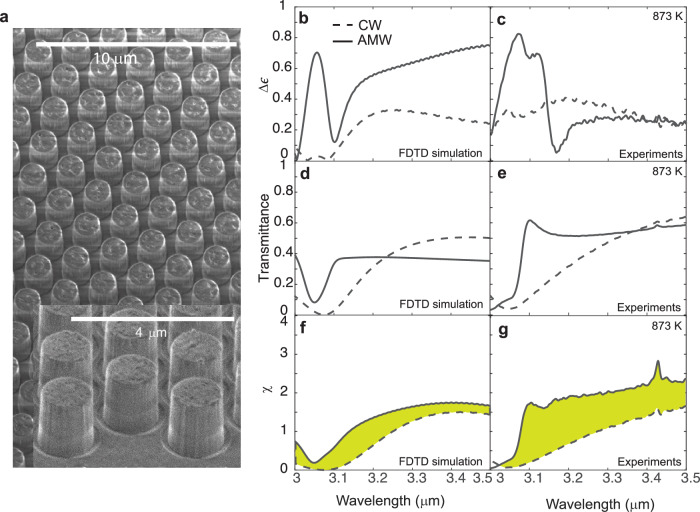
To create our AMW sample, we fabricated an array of amorphous silicon nanodisk pairs, each separated by a 350 nm thick silicon oxide spacer, all on a fused silica window. The top silicon disk was covered by a 10 nm thick layer of titanium, as described in the schematic of Fig. 2b. Figure 3a shows a scanning electron microscope (SEM) image of our fabricated AMW sample, composed of a hexagonal array of disk stacks with near-vertical side walls. To create the CW sample, we used the same planar nanofabrication processes to make a hexagonal array of single silicon nanodisks topped with a 10 nm titanium layer on a separate fused silica window.

Fig. 3. Emission asymmetry, transmittance, and χ of control window (CW) and asymmetric meta-window (AMW) at 873 K.

a Scanning electron micrograph of the fabricated AMW, with 350 nm thick spacers, on a fused silica window. b, c show the calculated and measured Δϵ spectra, respectively. The dashed and solid lines plot these quantities for the CW and AMW, respectively. Likewise, (d) and (e) show the calculated and measured transmission spectra, and (f) and (g) show the calculated and measured χ, all with ϵ₋ facing the camera. The spectral range with enhanced χ for AMW is shaded in green.

We measured the transmission ($\mathcal{T}$) and emissivity (ϵ₊ and ϵ₋) on both sides of the windows at 873 K for near normal angles (0–4°) (see “Methods” section). We used a low NA objective that narrowly measured the emission response from the coupled single-mode system in the normal direction, which also simulates the common case of thermal cameras situated at a considerable distance with a large depth of focus. Both CW and AMW samples show resonantly enhanced ϵ₊ near reonance (Supplementary Note 4 and Fig. S4). The calculated and experimentally measured Δϵ spectra are shown in Fig. 3b and c, respectively. Δϵ at resonance is nearly three times larger at 3.06 μm for the AMW than for the CW. Thus, the AMW effectively suppresses emission toward the open (camera) side near resonance. Indeed, over a finite 3.0–3.5 μm bandwidth surrounding the resonance, the integrated emitted power in ϵ₋ is 34% less for the AMW than for the CW. For more, see SI section on Transmitted and emitted power from AMW and CW.

Of course, asymmetric emission is only one of the two requirements for enhancing χ. The other requirement is to maintain adequate transmissivity through the window. Figure 3d and e plot the calculated and measured transmittance spectra of the CW and AMW samples. The transmittance through the windows is the same in both directions because of reciprocity. The plots show that the transmittance dips considerably at resonance due to the enhanced absorption caused by the asymmetry.

Our AMW design, inspired by non-Hermitian optics, balances the needs for good transmittance and emissivity asymmetry required to achieve thermal imaging through an emissive hot window. Specifically, notice the resonant transmittance dips for the CW case (dotted curves) in Fig. 3e have very different linewidths or roll-off rates than for the AMW case (solid curves). Though both the CW and AMW have the same total absorption loss, the spatial distribution of the loss in the AMW makes its resonance narrower than that in the CW. In the language of coupled mode theory, the disk pair in the AMW supports two modes with the same resonant frequency, but with different damping or quality factors.

This trade off in bandwidth and imaging performance enhancement is fundamental, a consequence of the thermodynamic constraints mentioned earlier. The quality factor of the resonance transmittance dip observed for our AMW and CW samples is directly related to the thermal imaging problem at hand. Thermal cameras operate over a rather broad bandwidth, and all thermal photons in this bandwidth are collected by the camera. If the resonant transmittance dip is sharp, then the average transmittance of the AMW in the camera’s bandwidth does not suffer much. Here, the transmitted power for the AMW is 44% more than the CW in the 3.0–3.5 μm band (Supplementary Note 5 and Supplementary Table 1).

In summary, the mode with higher damping, confined mostly to the top disk, controls emissivity, while the high-quality mode, confined mostly to the bottom disk, controls transmittance. The AMW transmittance spectrum shows a narrower, higher-quality resonance than the CW, and the AMW top disk mode with higher damping enables a large asymmetric emissivity. Such a combination of properties is not possible for a conventional (e.g. CW) design, where only the real index is considered as a design parameter. Our AMW relaxes the trade-off between emission asymmetry and average transmittance, producing higher values for χ than from the CW (Fig. 3f and g). Thus, spatially engineering the imaginary index provides a powerful design tool for nanophotonic devices and a means for thermal imaging through a hot emissive window.

Thermal imaging and contrast enhancement

To illustrate the role of a window’s optical properties on thermal imaging further, we apply the Weber contrast definition³⁷ to the case of thermal imaging through a hot emissive window. We assume that the object to be imaged, its background, and the window are all at temperature T and are all closer to each other than to the camera. If the imaging bandwidth is infinitesimally small at a central wavelength λ, the contrast ratio CR is given by

$$CR\left(\lambda \right)=\frac{{ϵ}_{BG}-{ϵ}_{obj}}{{ϵ}_{BG}+\frac{1}{\chi }}$$ 2

where $\chi =\mathcal{T}/ϵ$, and ϵ_Obj, ϵ_BG, and ϵ = ϵ₋, are the emissivities of the object, background, and window surface facing the camera, respectively (see Supplementary Note 6, Eqs. S2–S5). Notice that in Eq. (2) for a fixed object and background emissivity, χ controls CR. This emphasizes the direct link between the optical properties of the window and the contrast observed in thermal imaging.

Equation (2) indicates that contrast at λ will be low if the emissivity of the hot window $ϵ\ge {ϵ}_{BG}\mathcal{T}$. It is in this regime of high window emissivity and/or low window transmissivity that CR may be enhanced by window engineering. This condition may be written as $ϵ\ge \frac{{ϵ}_{BG}}{1+{ϵ}_{BG}}\left(1-\mathcal{R}\right)$, which simplifies to $ϵ\ge \frac{{ϵ}_{BG}}{1+{ϵ}_{BG}}$ for the case of negligible reflection from the window $\mathcal{R}$. Clearly, the need for window engineering depends sensitively on the background emissivity ϵ_BG. If the value for ϵ_BG is taken to be 0.2 (emissivity of tungsten at 873 K), window engineering will appreciably improve thermal imaging contrast when window emissivity is 0.12 or higher, assuming a window reflection of 30%. Most high-temperature mid-IR transparent materials qualify for this condition at temperatures above 873 K^3,38. See Fig. S5 for emissivity spectra of fused silica and sapphire windows at high temperatures.

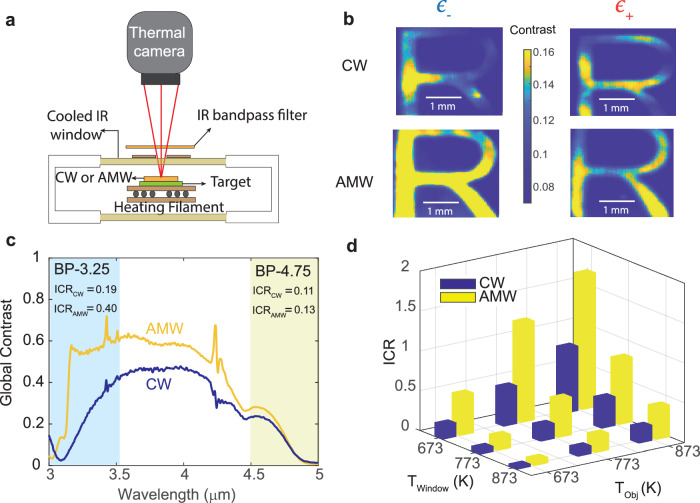
To demonstrate the effect of an engineered window on thermal imaging contrast, we prepared an emissive object, overlaid it with the sample window (either a control or asymmetric meta-window), heated everything to 873 K in a vacuum chamber equipped with a water-cooled IR window for optical access, and used a mid-wave IR camera (FLIR A6701) to image the scene (Fig. 4a). The emissive object was prepared by depositing carbon in the shape of the letter “R” on a tungsten substrate (Supplementary Note 7, Fig. S6a). Carbon has an emissivity close to 0.6 while tungsten has an emissivity of about 0.2 at 873 K (Supplementary Note 8 and Fig. S7a and b). We employed a commercially available IR filter (Supplementary Note 9 and Fig. S8) with a passband of 3.0–3.5 μm (labeled BP-3.25) in front of the camera to limit the imaging spectral bandwidth.

Fig. 4. Contrast in thermal imaging through the hot emissive control window (CW) and asymmetric meta-window (AMW).

a Schematic of the thermal imaging set-up employed to capture thermal images of the object through sample windows. b Weber contrast map of thermal images of the object (carbon film on tungsten patterned in the shape of the letter R), captured using a mid-IR camera (FLIR A6701) through the CW and AMW with the low or high emissivity surface (ϵ₋ or ϵ₊) facing the camera. The object, chamber, and windows are held at 873 K. The images were acquired with a BP-3.25 (3.0–3.5 μm) bandpass filter in front of the camera. c The global contrast ratio (CR) corresponding to the CW and AMW is calculated using Eq. (2) for each wavelength. The calculations use measured emissivity spectra of the carbon film, tungsten, CW (ϵ₋), and AMW (ϵ₋) at 873 K. The shaded regions correspond to the bandwidths of filters BP-3.25 and BP-4.75, and the inset tables show the integrated contrast (ICR) values in the respective spectral bands. d ICR is calculated using measured emissivity and transmission spectra of the CW and AMW when the object and window are at different temperatures (T_Obj and T_Window, respectively).

The image of the object through the AMW and CW using the BP-3.25 filter is shown in Fig. 1d and e, respectively. The object is more clearly discerned through the AMW than the CW. Moreover, a contrast map may be generated using the Weber contrast formula applied at each image pixel (Eq. S7). Figure 4b displays this contrast map for the AMW and CW in the 3.0–3.5 μm spectral band, with the object, background, and windows again held at 873 K. The AMW outperforms the CW with the camera facing ϵ₋, while there is little contrast enhancement when the windows are flipped over and the camera faces ϵ₊. When imaging far from the resonance using a filter with a 4.5–5.0 μm passband (labeled BP-4.75), the contrast maps of the thermal images also show poor contrast for all configurations and indicate no advantage of the AMW over CW (Fig. S9).

The advantage of the AMW over CW would have been even more obvious if the contrast maps had been spectrally resolved more narrowly. This can be illustrated by calculating global contrast CR from Eq. (2) at each wavelength, using the measured χ of our windows, the measured emissivity of the object (carbon black), and the estimated background emissivity for the tungsten substrate (Fig. 4c). Because the transmission dips at resonance cause a contrast dip for both the CW and the AMW, the best AMW performance over CW occurs not at the 3.06 μm resonant wavelength but just to the red side of it. Due to the low-loss mode in the weakly coupled disk resonators of the AMW, the transmission dip from the AMW is spectrally sharper than that for the CW. Thus, the global contrast for the AMW recovers sharply from its resonance dip at 3.06 μm to deliver advantageous asymmetric emission (and good transmission) in the near resonance 3.0–3.5 μm wavelength range.

However, because thermal imaging usually occurs over a broad spectral region, a more practical assessment of the AMW contrast enhancement within the camera bandwidth is accomplished by calculating the integrated contrast (ICR), using integrals of emissivities weighted by the appropriate blackbody emission curves (Eq. S6). The ICR values for the AMW and CW for the two spectral passband ranges are shown in the numerical insets of Fig. 4c, again assuming the window, object, and background are at 873 K. In the 3.0–3.5 μm wavelength range, the AMW outperforms the CW by two times. This difference in contrast explains easily observable improvement in image quality from the CW to the AMW in Fig. 1. In the 4.5–5.0 μm wavelength range far from resonance, the ICR values are lower and similar for the AMW and CW as the emission from the fused silica window substrate exceeds emission from resonators.

Note that throughout the measurements, both the object and window were kept at the same temperature. However, in practical applications, the window and object can be at different temperatures. To explore how differing object (T_Obj) and window (T_Window) temperatures affect thermal imaging contrast, we measure the emissivity and transmission of the CW and AMW at different temperatures (Fig. S5a and S7a) and use those values to calculate ICR for the 3.0–3.5 μm imaging bandwidth. Figure 4d shows the ICR for the CW and AMW for nine combinations of object and window temperatures. Here, the background and object are assumed to be at the same temperature. When the window is cooler than the object, ICR increases for both the AMW and CW. This is not surprising as the window emission decreases and transmission increases with cooling. On the other hand, when the window is hotter than the object, the ICR drops for both the AMW and the CW, but even then the AMW outperforms the CW for all combinations of window and object temperatures considered here.

In conclusion, we demonstrated thermal imaging through a hot window using a specially engineered asymmetric meta-window that suppressed emission towards the camera while maintaining fairly good transmission in the imaging bandwidth. The asymmetrically emitting meta-window demonstrates a path for overcoming this long-standing thermal imaging problem by engineering the spatial distribution of absorptive loss. Drawing inspiration from non-Hermitian optics, the loss distribution in the coupled resonator window coating was arranged to support two degenerate modes, one with enhanced damping and the other with reduced damping. The reduced damping mode maintained fairly good transmission in the imaging bandwidth, while the enhanced damping mode was responsible for suppressing emission toward the camera. Thus, imaging with our meta-window demonstrated more than twice the contrast of the control window at 873 K over the chosen passband. This demonstration illustrates the power of using the imaginary index as a design parameter for nanophotonic thermal devices, thereby enabling transformative functionalities for energy, imaging, and sensing applications.

Methods

Fabrication of metasurface

The CW and AMW samples were fabricated on a 0.5 mm thick fused silica window. A layer of amorphous Si (600 nm) was deposited on the window for the CW, and layers of amorphous Si (500 nm), SiO₂ (350 nm), and amorphous Si (600 nm) were deposited for the AMW using plasma enhanced chemical vapor deposition (PlasmaTherm Versaline). A layer of e-beam resist (PMMA A4) and E-spacer was coated on the surface, and patterning was performed using standard e-beam lithography (Elionix ELS-G100). To introduce optical losses, a thin layer of Ti (10 nm) was deposited on the top Si layer using an e-beam evaporator (Sharon). Next, an etch mask was deposited with 40 nm and 28 nm of Al₂O₃ and Cr, respectively, using an e-beam evaporator. Following a liftoff in acetone, the nanocylinders are formed using a reactive ion etch (Oxford, Plasmalab System 100/ICP 180) with a mixture of C₄F₈, SF₆, CF₄, and O₂ at flow rates of 50, 5, 25, and 2 sccm, respectively. The capacitively- and inductively-coupled RF powers were maintained at 75 and 200 W, respectively.

Emissivity measurements

Reflectance (see Supplementary Note 10 and Fig. S10) and transmission spectra of the metasurface were measured at elevated temperatures using a vacuum chamber with a heated stage (MicroOptik-MHCS1200) coupled to a FTIR microscope (ThermoFischer). A thermocouple (type S) was placed close to the metasurface (1 mm away) and object (0.5 mm away) to measure the temperature. A refractive objective (Edmund Optics) with low numerical aperture (0.08) was used for the measurements. A polished tungsten chip was used as the reference for reflectance measurements to obtain absolute values. Emissivity (equal to absorption) was calculated as $1-\mathcal{R}-\mathcal{T}$. The sharp peaks in Fig. 4c are FTIR system artifacts: the peak near 4.3 μm originates from slight variations in atmospheric CO₂ levels between sample and reference measurements, while the narrow peaks near 3.4 μm are due to C-H vibrations from residual organic contaminants on the chamber windows.

Thermal imaging

The imaging object was fabricated using standard e-beam lithography followed by carbon coating on a polished tungsten chip (MTI-corp) 0.5 mm thick (Fig. S6a). The object chip was placed inside a vacuum chamber (MicroOptik-MHCS1200) on a heating stage. The metasurface (Fig. S6b) was placed directly on top of this object chip, and the stage was heated to 873 K. The vacuum chamber is equipped with a water-cooled IR transparent window for optically accessing the inside of the chamber. A thermal camera (FLIR A6701) that operates in the 3–5 μm wavelength range was used to capture the thermal images of the object chip through the metasurface. An IR bandpass filter (BP-3.25/BP-4.75) was placed between the chamber and the camera (Fig. 4a). The camera exposure time was fixed at 0.1 ms for all measurements.

Simulation methods

Full-wave electromagnetic simulations were performed using a finite-difference-time-domain solver (Lumerical). Si and SiO₂ optical constants were obtained by fitting measured reflectance and transmission of thin films with Drude-Lorentz model for permittivity. Simulations performed with normally incident input light used a plane-wave source.

Author contributions

H.O.E. posed the problem. G.V.N., C.S.P., and H.O.E. conceived of the approach. G.V.N. supervised the work. C.S.P. designed the asymmetric thermal emitters and conducted the experiments. All authors wrote the manuscript.

Peer review

Peer review information

Communications Engineering thanks Wei Li and Koray Aydin for their contribution to the peer review of this work. Primary Handling Editor: [Rosamund Daw].

Data availability

The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s44172-024-00316-y.