Distinguishable topology of the task-evoked functional genome networks in HIV-1 reservoirs

Summary

HIV-1 reservoirs display a heterogeneous nature, lodging both intact and defective proviruses. To deepen our understanding of such heterogeneous HIV-1 reservoirs and their functional implications, we integrated basic concepts of graph theory to characterize the composition of HIV-1 reservoirs. Our analysis revealed noticeable topological properties in networks, featuring immunologic signatures enriched by genes harboring intact and defective proviruses, when comparing antiretroviral therapy (ART)-treated HIV-1-infected individuals and elite controllers. The key variable, the rich factor, played a pivotal role in classifying distinct topological properties in networks. The host gene expression strengthened the accuracy of classification between elite controllers and ART-treated patients. Markov chain modeling for the simulation of different graph networks demonstrated the presence of an intrinsic barrier between elite controllers and non-elite controllers. Overall, our work provides a prime example of leveraging genomic approaches alongside mathematical tools to unravel the complexities of HIV-1 reservoirs.

Graphical abstract

Highlights

• •Enriched signatures are coupled with distinct surface markers and immunity
• •Network topology is more structural in ART-treated patients than elite controllers
• •Rich factor is pivotal to determining and classifying the topology of a network
• •Graph networks evolve distinctly between elite controllers and non-elite controllers

Health sciences; Immunology; Medical specialty; Medicine; Virology

Introduction

The establishment of latent HIV-1 reservoirs is a complex disease progression mechanism. It involves various types of immune cells and responses converging at the site of HIV-1 infection, aiming at restricting viral propagation. The presence of latent proviruses, causing viral rebound upon the interruption of ART, impedes treatment efficacy. A more comprehensive understanding of the establishment of latent HIV-1 reservoirs is essential for designing a potential functional cure against HIV-1 infections.

Notably, HIV-1 reservoirs possess a heterogeneous nature: only 2%–10% of the proviruses are genetically intact^1,2,3; others that are genetically defective harbor large deletions, sequence inversions, hypermutations, and defective splice donor and acceptor sites that prevent viral replication.^2,3 Reservoir cells harboring intact proviruses are believed to serve as the main funder of viral rebound. Although the role of defective proviruses remains elusive, the study has shown the involvement of defective proviruses in HIV-specific immunity and innate sensing, rather than simply viral genome “junk.”⁴

It is important to note that a recent study detected spontaneously active HIV-1 reservoirs, which are dominated by defective proviruses anticipated in HIV-specific immunity.⁵ In addition, another more recent study identified a subset of latent cells associated with distinct features from a pool of infected cells with latent infections.⁶ Remarkably, integration sites of proviruses in this subset of latent cells were prone to be in non-genic regions and in proximity to zinc finger (ZNF) genes and heterochromatin regions.⁶ Such biases of integration resemble the features used for the characterization of the reservoir harboring intact proviruses in the status of deep latency in elite controllers⁷ or individuals with HIV-1 under prolonged ART, resulting from host immune selection⁸ (see the following paragraph). Altogether, a better understanding of the heterogeneous composition of HIV-1 reservoirs is beneficial to deepen our knowledge of HIV-1 pathogenesis.

The concept of latent HIV-1 reservoirs has been recently refreshed and now the emphasis is placed on the diverse strengths of immune-mediated selection forces acting on reservoir cells harboring intact and defective proviruses. This diversity results in distinct configurations of reservoirs between each other.^{8,9,10,11,12,13,14,15,16,17,18} The impact of immune selection pressure in elite controllers appears more pronounced than in post-treatment controllers.^7,19 Furthermore, unique phenotypic signatures associated with reservoir cells harboring intact proviruses^17,18 and distinct transcriptomic signatures in HIV-1-infected memory CD4 T cells under ART²⁰ have been reported. These findings underscore the specific microenvironment of HIV-1 reservoirs, providing a fertile ground for further investigations into their configurations.

As mentioned above, HIV-1 reservoirs are heterogeneous in terms of the reservoir site, the integrity of the proviral genome, and viral replication fitness. Furthermore, the establishment of HIV-1 reservoirs is temporally dynamic. All these attributes complicate the means to precisely tag the microenvironment of HIV-1 reservoirs. On the one hand, longitudinal biomarkers have been recently proposed to track the evolution of HIV-1 reservoirs across different stages of HIV-1 infection and disease progression associated with ART.^21,22 On the other hand, to gain a better explanation of such a variety observed in HIV-1 infection and treatment, researchers have turned to mathematical models.²³ Graph networks are widely used for representing types of relational data in many aspects, including biological data. The information encoded in the wiring patterns, i.e., topology and structures, of biological networks thus complements and somehow translates the information received from biological data. It is not surprising that graph theoretical-based tools have also been implemented for different topics in virus studies, e.g., severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) transmission network²⁴ and influenza and hepatitis diseases.²⁵ Notably, such graph network-based analysis associated with various types of omics datasets has been applied to dissect the interplay between HIV-1 and the host.²⁶

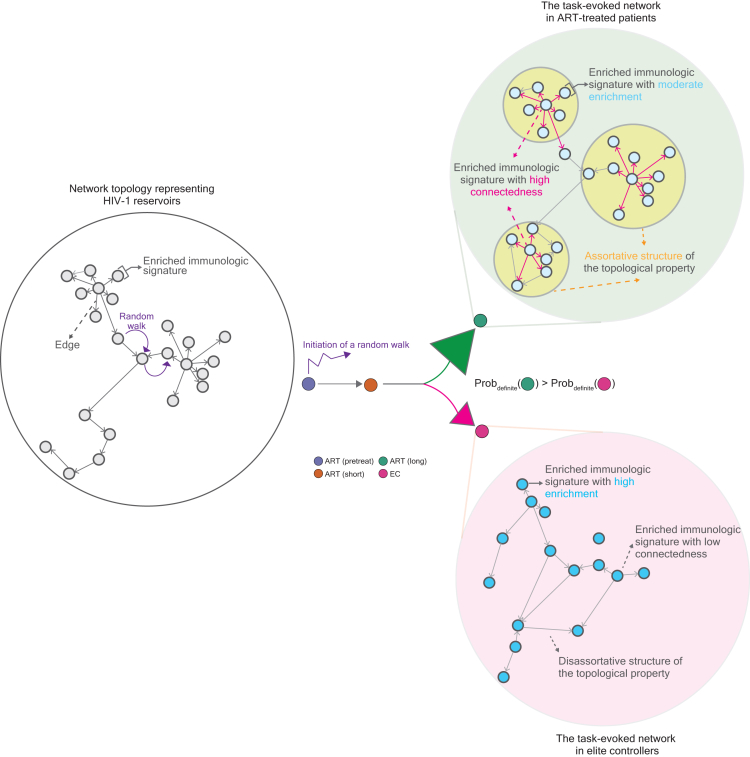
We previously observed that HIV-1-targeted genes with similar functions in immunity can form various gene sets, so-called “immunologic signatures” present at different stages of HIV-1 infections associated with ART, implying that they may be dedicated to different tasks to satisfy the need for immunity alongside HIV-1 infections.²⁷ Based on this finding, we have hypothesized that the frequency of HIV-1 integration on host genes could serve as a proxy for enriched immunologic signatures, defining specific immune cells and proinflammatory soluble factors alongside HIV-1 infection associated with ART.^27,28 Building on this hypothesis, in this current work, we further propose that HIV-1 reservoirs may be represented by a network consisting of task-evoked communities and attempt to characterize the network property structured by enriched signatures in ART-treated patients and elite controllers, distinguished by reservoirs harboring intact and defective proviruses, respectively, at a global level of network organization. Importantly, apart from the visualization of the network topology of reservoirs, we also performed the comparison of graph isomorphism based on the Pearson distance between graph networks. Finally, we applied the Markov chain Monte Carlo (MCMC) method and used it for the simulation of the evolution of the graph network. Altogether, this work introduced a fresh perspective on latent HIV-1 reservoirs through topological graphs, providing a method to characterize the network topology associated with its function.

Results

Different immunologic signatures enriched in antiretroviral therapy-treated patients and elite controllers

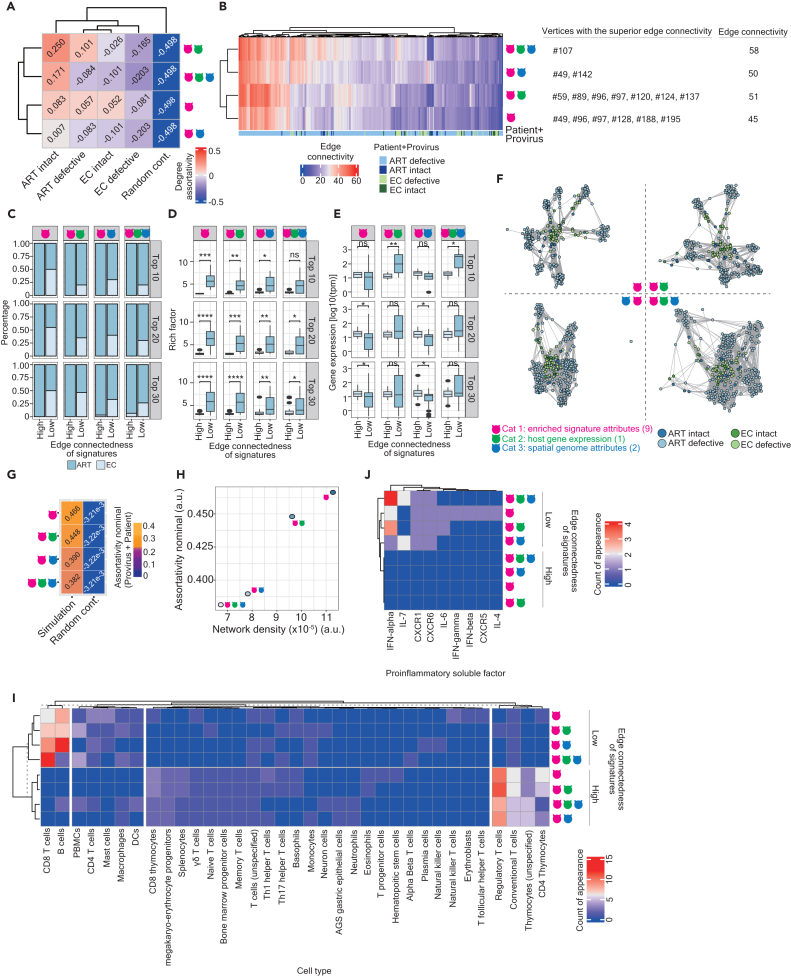
A total of 958 and 275 provirus-targeted host genes were collected respectively from HIV-1-infected individuals subjected to ART^{8,13,16,29,30,31,32,33} and elite controllers^7,19 in this study (Figure S1A). After removing duplications, unique genes were assigned to four groups (ART-intact, n = 184; ART-defective, n = 678; EC-intact, n = 90; EC-defective, n = 101). We first performed the over-representation analysis using MSigDb C7 immunologic signature gene sets on these unique genes and revealed that the majority of enriched immunologic signatures differed between reservoirs harboring intact and defective proviruses in ART-treated patients and elite controllers (Figure 1A; Tables S1, S2, S3, and S4). Given that the sample size of the input genes varies among each study, we bootstrapped 50, 60, and 70 unique genes from each of these four groups and repeated the over-representation analysis (Figure 1B). Rich factors^27,34 were further calculated to represent the fold enrichment of enriched signatures (Figure 1B). The definition and calculation of rich factors are described in STAR Methods. Significantly, relative to signatures harboring defective proviruses, signatures harboring intact proviruses displayed a higher magnitude of enrichment, and the overall enrichment was more intense in elite controllers than in ART-treated patients irrespective of the chosen sample size (Figure 1B). The same pattern was observed as the analysis was performed using all input genes without bootstrapping (Figure S1B). It is important to note that even though 4872 immunologic signatures were enriched using the whole genome (rich factor: median, 1.162; mean, 1.154), rich factors measured in these four groups showed significance compared to the control, hg38, human genome assembly GRCh38, in Figure S1B, indicating that the immunologic signatures detected in this study were significantly enriched. The overlaps of enriched signatures between different comparisons were demonstrated in Figure S1C. While an abundant number (n = 773) of signatures were enriched by genes harboring defective proviruses in ART-treated patients, less than half (n = 239) exceeded the mean of the rich factor calculated using all enriched signatures in ART-treated patients (mean: 2.799). Altogether, these findings indicate that enriched signatures were influenced by different HIV-1 reservoirs (intact versus defective) in ART-treated patients and elite controllers.

Figure 1.

Distinct enriched signatures between HIV-1-infected individuals and elite controllers

(A) A clustering heatmap illustrating immunologic signatures enriched by genes harboring intact and defective proviruses in HIV-1-infected patients and elite controllers. Parentheses beneath the column denote the integrity of the provirus genome (intact versus defective) along with the number of enriched signatures. The color scale depicts the magnitude of enrichment as represented by rich factors (S: signatures).

(B) A boxplot displaying the enrichment of signatures represented by rich factors in four groups. 50, 60, and 70 unique genes present in enriched signatures were bootstrapped and repeated in the over-representation analysis 500 times.

(C) A clustering heatmap showcasing host gene expression (tpm) of genes retrieved from enriched signatures. Parentheses beneath the column indicate the integrity of the provirus genome (intact versus defective) and the total number of retrieved genes.

(D) A boxplot, represented on a logarithmic scale, representing host gene expression (tpm) of the genes retrieved from enriched signatures. 20, 30, and 40 unique genes were bootstrapped.

(E) A bubble plot offering insights into selected enriched signatures in HIV-1-infected patients and the complete list in elite controllers. The color scale represents the enrichment magnitude as indicated by rich factors. Weight, calculated based on transcribed genes, highlights the difference between genes harboring intact versus defective proviruses in ART-treated patients and elite controllers. Signature descriptions in different colors signify unique enrichments in reservoirs: Blue (n = 5): ART-intact; Dark green (n = 7): EC-intact; Light green (n = 34): EC-defective. A Red (n = 1): Shared in reservoirs with intact and defective proviruses in elite controllers.

(F) Grouped bar chart representing the percentage of the unique genes (light blue) and those associated with cell markers (dark blue) in enriched signatures.

(G) A clustering heatmap illustrating unique genes associated with cell markers. The color scale depicts the magnitude of enrichment as represented by rich factors calculated from respective enriched signatures where the unique genes are present. The genes that are exclusively present in each of the four groups were highlighted beneath the heatmap with different color codes: Red, ART-intact; Orange, ART-defective; Blue, EC-intact; Green, EC-defective.

(H) A boxplot displaying the enrichment of signatures where the unique genes are present in enriched signatures. Statistical significance in panels (B), (D), and (H) was determined using the Wilcoxon test in R with default options; calculations were represented using boxplots, in which the median (the vertical line in the box) of data distribution and the two whiskers were marked. Significance levels are denoted as follows: ∗p 0.05, ∗∗p 0.01, ∗∗∗p 0.001, ∗∗∗∗p 0.0001.

See also Figure S1 and Tables S1, S2, S3, and S4.

Distinct transcriptome patterns of enriched signatures between antiretroviral therapy-treated patients and elite controllers

The involvement of a gene’s transcriptional status in the interaction between HIV-1 integration and enriched signatures remains unclear. To tackle this question, we collected transcriptome data from three studies, separated for ART-treated patients^13,20 and elite controllers⁷ and calculated the mean of Transcript Per Million (tpm) to overlay it with genes retrieved from signatures enriched in four groups, respectively. We observed inconsistencies in the genes targeted by intact or defective proviruses in ART-treated patients with a wide range of gene expression profiles (Figure 1C). However, in a few cases, gene expression was detectable regardless of the integrity of a provirus genome (Figure 1C). The same pattern was observed in elite controllers (Figure 1C). It is noteworthy that our observation aligns with the previous finding that host gene expression patterns are distinct among populations of HIV-1 reservoir cells (CD4⁺ T cells).²⁰ We, once again, bootstrapped 20, 30, and 40 genes retrieved from signatures enriched in four groups, respectively, and observed that relative to genes targeted by defective proviruses, genes harboring intact proviruses demonstrated a higher level of gene expression in both ART-treated patients and elite controllers (Figure 1D). Compared to ART-treated patients, the overall host gene expression of genes targeted by proviruses was moderate in elite controllers (Figures 1C and 1D) although a wide variety of gene expression in genes targeted by intact proviruses in elite controllers was observed (Figure 1D). The same pattern was observed as the analysis was performed using all input genes without bootstrapping (Figure S1D).

We further conducted a cross-comparison based on the 20 enriched signatures harboring intact proviruses against the entire list of enriched signatures harboring defective proviruses in ART-treated patients (Figure 1E) and all enriched signatures in elite controllers (Figure 1E). Subsequently, we retrieved 43 genes present in nine enriched signatures found only in reservoirs harboring intact proviruses in ART-treated patients (Figure S1C) and performed a KEGG pathway over-representation analysis (Figure S1E). Nine enriched pathways covering the immune system, infectious disease: viral, and cancer: overview were revealed (Figure S1E). No pathways were enriched when conducting the same analysis with 53 genes present in the enriched signatures harboring both intact and defective proviruses. At the signature level, we observed a moderately positive correlation (R² = 0.134) between the mean of tpm from the genes appearing in enriched signatures harboring both intact and defective proviruses in ART-treated patients (Figure S1F). In the case of elite controllers, only one enriched signature (signature description highlighted in red) was shared between the genes targeted by intact and defective proviruses (Figure 1E). We repeated the KEGG pathway over-representation analysis on genes retrieved from unique signatures enriched in reservoirs harboring either intact (n = 40) or defective (n = 67) proviruses in elite controllers. We observed that only one pathway, Lysine degradation (hsa00310), was enriched in the former case and none of the pathways was enriched in the latter case. These findings suggest that host gene expression may play a role in the identification of enriched signatures in reservoirs harboring intact versus defective proviruses in both ART-treated patients and elite controllers.

Distinct surface markers were associated with enriched signatures in antiretroviral therapy-treated patients and elite controllers

To further strengthen the concept that enriched signatures are assigned various tasks in the course of HIV-1 infection, we dissected the functionality of the genes in enriched signatures based on the CellMarker 2.0 database.³⁵ A total of 96 (52% of the total input genes in ART-intact), 602 (88.8% of the total input genes in ART-defective), 48 (53.3% of the total input genes in EC-intact), and 73 (72.3% of the total input genes in EC-defective) unique genes were identified in signatures enriched in the ART-intact, ART-defective, EC-intact, and EC-defective groups, respectively (Figure 1F). Additionally, 85 (46.2% of the total input genes in ART-intact), 499 (73.6% of the total input genes in ART-defective), 39 (43.3% of the total input genes in EC-intact), 62 (61.4% of the total input genes in EC-defective) unique genes were associated with phenotypic cell markers (Figure 1F). We coupled these unique genes with rich factors measured from corresponding enriched signatures and observed two major clusters separated by the reservoir cells harboring intact versus defective proviruses (Figure 1G). This observation may imply a distinct preference for cell markers expressed on the reservoir cells harboring either intact or defective proviruses. The cell marker profiles of reservoir cells between ART-treated patients and elite controllers were less distinguishable regardless of whether the proviruses were intact or defective proviruses (Figure 1G). We further highlighted cell marker-associated genes unique to each group: ART-intact, 33 genes; ART-defective: 431 genes; EC-intact, 6 genes; EC-defective: 20 genes (Figure 1G). Intriguingly, several genes from the zinc finger (ZNF) family, as well as those related to immunity, were highlighted (Figure 1G). While plotting the enrichment of rich factors of cell marker-associated genes unique to each group (Figure 1H), we observed the same pattern shown in Figures 1B and S1B, describing that genes targeted by intact proviruses displayed a higher magnitude of enrichment, with the overall enrichment being more intense in elite controllers than in ART-treated patients.

Distinct assortativity of network properties between antiretroviral therapy-treated patients and elite controllers

To explore how host gene expression and whether the spatial genome also influences the topological property comprising enriched signatures in different groups, we characterized the network topology (Figure S2A), representing HIV-1 reservoirs using various combinations of category attributes related to enriched signatures (Cat 1), host gene expression (Cat 2) and the spatial genome (Cat 3). Of note, for the ART-defective group, we selected the signatures with the enrichment of rich factor exceeding the mean of the enrichment scale (n = 239). With the exception of networks constructed using two and three categories of attributes in elite controllers associated with defective proviruses (Figure S2A), the majority of the network architectures were represented as disconnected graphs. This indicates that, depending on the utilization of attributes, some networks can consist of two or more subsets of enriched signatures with either low or non-correlation (Figure S2A). Relative to elite controllers, the network architecture was more assortative in ART-treated patients, especially with reservoirs harboring intact proviruses (Figure 2A). Given such a wide range of the sample size in each group, we bootstrapped 10 enriched signatures from each group followed by the calculation of the degree of assortativity based on a subnetwork-based graph structured by 10 enriched signatures (Figure S2B) and observed the same pattern shown in Figure 2A. Intriguingly, the Cat 2 attribute strengthened the topology of the network, while Cat 3 attributes failed to reinforce the network structure (Figure 2A). This suggests that Cat 1 and 2 attributes were pivotal in determining the functional property of the network. Consistent with this finding, we observed a higher level of edge connectivity between two adjacent enriched signatures in ART-treated patients compared to elite controllers (Figures 2B and 2C). A clear separation of two clusters based on edge connectivity of individual enriched signatures present in the network constructed by Cat 1 and Cat 1 and 2 attributes versus Cat 1 and 3 and all attributes implied that the presence of the spatial gnome attributes may govern the network topology in a way different from which governed by the attribute of host gene expression (Figure 2B). We listed the vertices possessing the superior edge connectivity on the right-hand side of Figure 2B.

Figure 2.

Characteristics of the network topology

(A) A clustering heatmap representing degree assortativity coefficients calculated based on individual networks, using Cat 1, Cat 1 and 2, Cat1 and 3, and all attributes. The color scale illustrates the degree of assortativity.

(B) A clustering heatmap displaying the edge connectivity of all enriched signatures across four groups. The color scale denotes the magnitude of degree connectivity. The color code annotation beneath the heatmap denotes the networks with an enriched signature.

(C) Stacked bar charts represents the proportion of the top 10, 20, and 30 ranked enriched signatures possessing either the highest or lowest edge connectivity in ART-treated patients (dark blue) versus elite controllers (light blue).

(D and E) Boxplots displaying the enrichment of signatures represented by rich factors (D) and host gene expression (tpm on a logarithmic scale) of the genes (E) between the top 10, 20, and 30 ranked enriched signatures possessing either the highest or lowest edge connectivity. Facets at the x-axis separate the networks constructed by Cat 1, Cat 1 and 2, Cat 1 and 3, and all attributes (from left to right); facets at the y axis separate the top 10, 20, and 30 ranked enriched signatures (from top to bottom).

(F) Tripartite graphs illustrating interactions among enriched signatures across four networks, using Cat 1, Cat 1 and 2, Cat1 and 3, and all attributes. Signatures marked in dark blue, light blue, dark green, and light green were enriched in reservoirs harboring intact and defective proviruses in ART-treated patients and elite controllers, respectively. Enriched signatures (vertices in tetrapartite graphs) were linked by edges representing their correlation coefficients.

(G) A heatmap representing nominal assortativity coefficients is calculated based on the tetrapartite graphs shown in panel (F).

(H) A scatterplot representing a correlation between the network density (x-axis) and nominal assortativity coefficients (y axis) based on the tetrapartite graphs shown in panel (F).

(I and J) A clustering heatmap displaying the appearance of cell types (column) (I) and proinflammatory soluble factors (column) (J) in the top 30 ranked enriched signatures possessing either the highest or lowest edge connectivity (row). The color scale represents the times of occurrence of cell types (I) or proinflammatory soluble factors (J) in the description of the top 30 ranked enriched signatures. Statistical significance in panels (D) and (E) was determined using the Wilcoxon test in R with default options; calculations were represented using boxplots, in which the median (the vertical line in the box) of data distribution and the two whiskers were marked. Significance levels are denoted as follows: ∗p 0.05, ∗∗p 0.01, ∗∗∗p 0.001, ∗∗∗∗p 0.0001.

See also Figures S2 and S3; Table S5.

While comparing the top 10, 20, and 30 ranked signatures possessing either the highest or the lowest connectedness in each network, we observed that signatures with a lower degree of connectivity were more frequently enriched in the network identified in elite controllers (Figure 2C), whereas enriched signatures with the highest degree of connectivity happened in the network mainly identified in ART-treated patients (Figure 2C). While comparing rich factors (Figure 2D) and the mean of gene expression (Figure 2E), we observed that relative to enriched signatures possessing low connectedness, those with high connectedness demonstrated a lower magnitude of enrichment (Figure 2D). This finding aligns with the previous observations that signatures enriched in ART-treated patients tend to display a lower degree of enrichment (Figures 1B and S1D). However, no clear propensity of the mean of gene expression between signatures possessing the highest and lowest connectedness was observed (Figure 2E). Overall, these findings suggest that the network architecture could be more connective in ART-treated patients than in elite controllers.

We further examined the topological interaction between two adjacent signatures located in different networks based on bipartite graphs. Initially, we observed a significant number of enriched signatures with a lack of correlation, particularly in the cases involving signatures harboring intact versus defective proviruses in ART-treated patients (Figure S3A) and signatures harboring defective proviruses in ART-treated patients versus elite controllers (Figure S3A). This observation is reflected in the larger interquartile range shown in Figure S3B and is supported by the larger average Euclidean distance (Figure S3C). Finally, we represented tetrapartite graphs illustrating the interaction of four network architectures (Figure 2F) and, once again, observed that all four networks were more structured and distinguishable, particularly when Cat 1 as well as Cat 1 and 2 attributes were applied, reflected by the assortativity calculated for each network (Figure 2G).

Additionally, we computed the network density and observed a positive correlation between assortativity and the network density (Figure 2H), confirming that the topology of the networks computed by Cat 1 attributes and Cat 1 and 2 attributes are more structural than others. In summary, these findings suggest that the structural composition of the networks differs from one another and can be influenced by attributes associated with enriched signatures and host gene expression, with the impact of the spatial genome being less influential.

Distinct cell types were associated with enriched signatures possessing the highest and the lowest edge connectedness

To elucidate whether enriched signatures that possess different degrees of connectedness were designated distinct functionalities, we sought the appearance of immune cell types (Figure 2I) and proinflammatory soluble factors (Figure 2J) in the description of ranked top 30 enriched signatures. A clear separation of two major clusters based on the appearance of cell types in signatures with the highest edge connectivity versus those with the lowest edge connectivity was observed (Figure 2I). In each major cluster, a subcluster was formed between the networks structured by Cat 1 attributes and Cat 1 and 2 attributes, implying that perhaps the usage of cell types may correlate with the network topology and a similarity was shared between the networks constructed by Cat 1 and Cat 1 and 2 attributes. In addition, we observed the prevalence of regulatory and conventional T cells and CD4 thymocytes coupled with the signatures with the highest edge connectivity, whereas the prevalence of CD8 T cells, and B cells coupled with the signatures with the lowest edge connectivity (Figure 2I). The appearance of peripheral blood mononuclear cells (PBMCs), CD4 T cells, mast cells, macrophages, and dendritic cells (DCs) demonstrated a minor increase in signatures with the lowest edge connectivity compared to those with the highest edge connectivity (Figure 2I). Notably, programmed cell death protein 1 (PD-1) was observed in one enriched signature, GSE24026_PD1_LIGATION_VS_CTRL_IN_ACT_T cell_LINE_DN, with the highest edge connectivity that is present in all networks.

No proinflammatory soluble factors were detected in signatures with the top 30 enriched signatures with the highest edge connectivity (Figure 2J). Among those with the lowest edge connectivity, we observed that CXCR1, CXCR6, and interferon (IFN)-alpha appear in all network properties, whereas interleukin (IL)-6 appear in the networks structured by Cat 1 attributes and Cat 1 and 2 attributes and IL-7 appear in the networks structured by Cat 1 and 3 attributes and all attributes (Figure 2J). CXCR5, IL-4, IFN-beta, and IFN-gamma were only observed in the network structured by Cat 1 attributes (Figure 2J). Altogether, these findings indicate that the pattern of cell types and proinflammatory soluble factors in enriched signatures with the highest edge connectivity differ from those with the lowest edge connectivity.

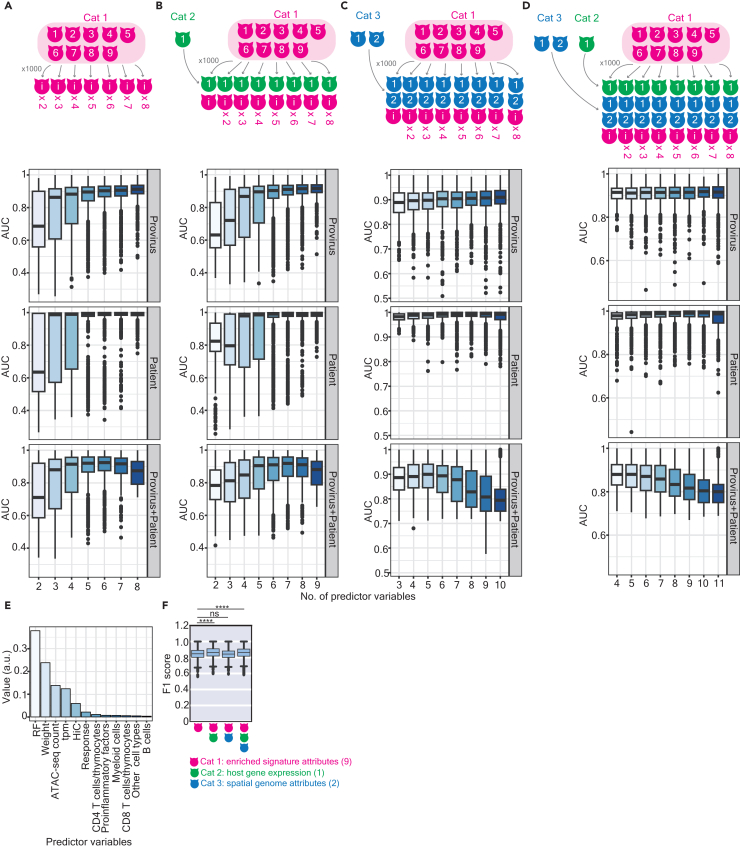
Rich factor held paramount significance for classifying network properties

To identify which attributes among the three categories could better classify different properties, we assessed the area under the curve (AUC) of receiver operating characteristic (ROC) curves using logistic regression classifiers constructed with randomly selected predictor variables (Figures 3A–3D). All classifiers effectively distinguished intact versus defective proviruses (Figures 3A–3D, top panels namely “Provirus”) and properties of enriched signatures between ART-treated patients versus elite controllers (Figures 3A–3D middle panels namely “Patient”). AUC values increased as the number of attributes in Cat 1 was added (Figures 3A–3D). However, classifiers were less effective in discriminating when considering the combined scenario of “Provirus” plus “Patient” (Figures 3A–3D, bottom panels namely “Provirus+Patient”), especially when Cat 3 attributes were included. It is important to stress that although all classifiers displayed acceptable prediction power, AUC values occasionally varied, indicating that each predictor variable possessed different propensities that could influence the network topology. We also constructed random-forest classifiers and used them to rank the importance of predictor variables (Figure 3E). The rich factor variable among all Cat 1 attributes, was of paramount importance in underpinning the prediction power of the models (Figure 3E), and using Cat 1 attributes alone was sufficient for accurate models (Figure 3F). Although the prediction power of the classifier was more adequate to predict the network in ART-treated patients than elite controllers (Figure S4A), the F1 scores demonstrated the feasibility of our models applied to both types of patients (Figures S4A and S4B). In addition, we observed that cooperation with host gene expression enhanced the robustness of classifiers (Figure 3F). Overall, these findings suggest that Cat 1 attributes, especially the rich factor, were crucial for classifying networks harboring intact versus defective proviruses in ART-treated patients and elite controllers.

Figure 3.

Classification of networks between ART-treated patients and elite controllers

(A, B, C, and D) The area under the curve (AUC) of logistic regression models, constructed by bootstrapping selected numbers of predictor variables using Cat 1 (A), Cat 1 and 2 (B), Cat 1 and 3 (C), and all attributes (D), calculated to classify the networks associated with intact versus defective proviruses (top panel), networks in ART-treated patients versus elite controllers (middle panel), and networks associated with intact versus defective proviruses, separated by ART-treated patients versus elite controllers (bottom panel). The x-axis labels represent the number of bootstrapped predictor variables used to construct models. Each classification iteration was repeated 1,000 times for statistical significance.

(E) A bar plot represents the ranking of predictor variables' importance using a random forest classifier.

(F) A boxplot illustrats the prediction power for classifying networks harboring intact versus defective proviruses, separated by ART-treated patients versus elite controllers. The F1 score was calculated based on 1,000 times of individual train-test splits in models. Asterisks indicate the significance determined by two-sided Wilcoxon rank-sum tests. Calculations from panels (A), (B), (C), (D), and (F) were represented using boxplots, in which the median (the vertical line in the box) of data distribution and the two whiskers were marked. Significance levels are denoted as follows: ∗p 0.05, ∗∗p 0.01, ∗∗∗p 0.001, ∗∗∗∗p 0.0001.

See also Figure S4 and Table S5.

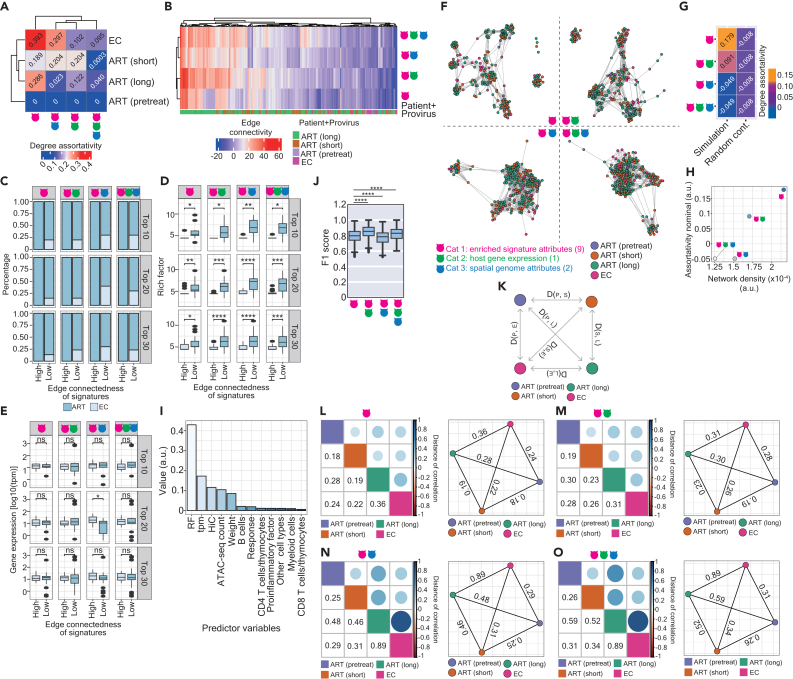
Distinct network topology in antiretroviral therapy-treated patients in a longitudinal order versus elite controllers

Given that HIV-1 integration at a genic level is not uniform, whether the genes in functional communities are selectively targeted by HIV-1 and respond to viral infections over time is also a question of interest. To tackle this question, we applied the same rationale, as described above, to investigate whether the network topology of enriched signatures changes alongside HIV-1 infections associated with ART, and compare them to that depicted in elite controllers (Figure S5A). Similar to the topology characterized in Figure S2A, the network architecture in a longitudinal order was represented as disconnected graphs (Figure S5A). The network in pretreatment HIV-1-infected individuals strongly resembled a null graph with zero degrees of assortativity (Figures 4A and S5A). We assume that this observation is likely due to the low number of enriched signatures (n = 8). Although the degree of assortativity varied among HIV-1-infected individuals subjected to short and long periods of ART and elite controllers when different category attributes were applied, it appeared that Cat 1 attributes were pivotal in offering a better network topology (Figure 4A). A higher level of degree connectivity was observed in signatures enriched in ART-treated patients than in elite controllers (Figure 4B) although the connectedness was indistinguishable among ART-treated patients at different stages of ART (Figure 4B). The coordinates of the enriched signatures and respective statuses of HIV-1 infections are listed in Table S6. We, once again, compared the top 10, 20, and 30 ranked signatures possessing either the highest or lowest connectedness in each network. The same as the finding presented in Figure 2C, signatures enriched in elite controllers can only be found in those with the lowest edge connectivity (Figure 4C). The patterns of rich factor and the mean of gene expression were also consistent with the previous observations (Figures 2D and 2E): the signatures with a lower degree of connectivity demonstrated a higher magnitude of enrichment (Figure 4D); however, no clear propensity of the mean of gene expression between signatures possessing highest and lowest connectedness was observed (Figure 4E).

Figure 4.

Characteristics of the network topology between ART-treated patients in a longitudinal order and elite controllers

(A) A clustering heatmap representing degree assortativity coefficients based on individual networks, considering various attributes for pretreatment HIV-1-infected individuals, patients subjected to a short and a long period of ART, and elite controllers.

(B) A clustering heatmap illustrating the edge connectivity of all enriched signatures in networks from HIV-1-infected individuals in a longitudinal order and elite controllers. The color scale denotes the magnitude of degree connectivity. The color code annotation beneath the heatmap denotes the networks with an enriched signature.

(C) Stacked bar charts represent the proportion of the top 10, 20, and 30 ranked enriched signatures possessing either the highest or lowest edge connectivity in ART-treated patients (dark blue) versus elite controllers (light blue).

(D and E) Boxplots displaying the enrichment of signatures represented by rich factors (D) or host gene expression (tpm on a logarithmic scale) of the genes (E) between the top 10, 20, and 30 ranked enriched signatures possessing either the highest or lowest edge connectivity. Facets at the x-axis separate the networks constructed by Cat 1, Cat 1 and 2, Cat 1 and 3, and all attributes (from left to right); facets at the y axis separate the top 10, 20, and 30 ranked enriched signatures (from top to bottom).

(F) The tetrapartite graphs illustrate the interactions among enriched signatures across four networks using different attribute combinations. Signatures marked in violet, maroon, green, and deep pink were enriched in reservoirs from pretreatment HIV-1-infected individuals, patients subjected to a short and a long period of ART, and elite controllers, respectively.

(G) A heatmap representing the degree assortativity coefficient based on tripartite graphs is shown in panel (F).

(H) A scatterplot representing a correlation between the network density (x-axis) and nominal assortativity coefficients (y axis) based on the tetrapartite graph shown in panel (F).

(I) A bar plot ranking the importance of predictor variables using a random forest classifier.

(J) A boxplot representing the prediction power for classifying networks in HIV-1-infected individuals in a longitudinal order and in elite controllers. The F1 score was calculated based on 1,000 times of individual train-test splits in models.

(K) Schematic illustration of the Pearson distance of correlation between graph networks depicted in two distinct graph networks. Colors marked in circles represent the status of HIV-1 infections and elite controllers: violet, pretreatment HIV-1-infected individuals; marron, patients subjected to a short of ART; green, patients subjected to a long of ART; deep pink, elite controllers.

(L, M, N, and O) Correlograms (left panel) represent the correlation between graph networks depicted in two graph networks. Squares alongside the diagonal in the correlogram represent the status of HIV-1 infections and elite controllers, as the same color code indicated in panel (K). The color scale represents the distance of correlation, which was also indicated below the diagonal in each correlogram. Network plots (right panel) summarizing the correlation between two graph networks. Networks constructed by different attribute combinations were shown in the panels (L), (M), (N), and (O), respectively. Statistical significance in panels (D), (E), and (J) was determined using the Wilcoxon test in R with default options; calculations were represented using boxplots, in which the median (the vertical line in the box) of data distribution and the two whiskers were marked. Significance levels are denoted as follows: ∗p 0.05, ∗∗p 0.01, ∗∗∗p 0.001, ∗∗∗∗p 0.0001.

See also Figure S5 and Table S6.

We further illustrated tetrapartite graphs depicting the interaction among three networks in a longitudinal order and the network in elite controllers (Figure 4F). Once again, we observed that Cat 1 attributes were sufficient to sustain its topology (Figures 4F and 4G). A positive correlation was observed between assortativity and the network density in networks structured by Cat 1 attributes and Cat 1 and 2 attributes; however, the correlation between these two measures in networks structured by Cat 1 and 3 attributes and all attributes faltered (Figure 4H). Subsequently, we computed the importance of each variable and found, once again, that the rich factor variable was of paramount importance for ensuring robust prediction power, followed by the host gene expression variable (Figure 4I). Of note, the host gene expression variable played an important role in distinguishing the networks between ART-treated patients and elite controllers (Figures 4J and S5B) and exhibited moderate effectiveness in classifying dynamic networks between ART-treated patients at different stages of treatment and elite controllers (Figures 4J and S5C). Overall, these findings suggest that the network architecture could be more connective in ART-treated patients than in elite controllers.

An intrinsic barrier lay between the networks of antiretroviral therapy-treated patients in a longitudinal order versus elite controllers

Our current observations that the enriched signatures in elite controllers possess distinguishable connectedness from those in ART-treated patients led us to hypothesize that the evolution of the graph network between elite controllers and non-elite controllers differs. To test this hypothesis, we further computed the Pearson distance between the graph networks from reservoirs in pretreatment HIV-1-infected individuals, patients subjected to short and long periods of ART and elite controllers (Figure 4K) and observed that the graph network between patients subjected to a long period of ART and elite controllers demonstrated the farthest graph distance, whereas the shortest graph distance was measured between pretreatment HIV-1-infected individuals and patients subjected to a short period of ART irrespective to category attributes used to construct the networks (Figures 4L–4O). This finding suggests that a lack in the graph isomorphism of the networks between ART-treated patients in a longitudinal order and elite controllers.

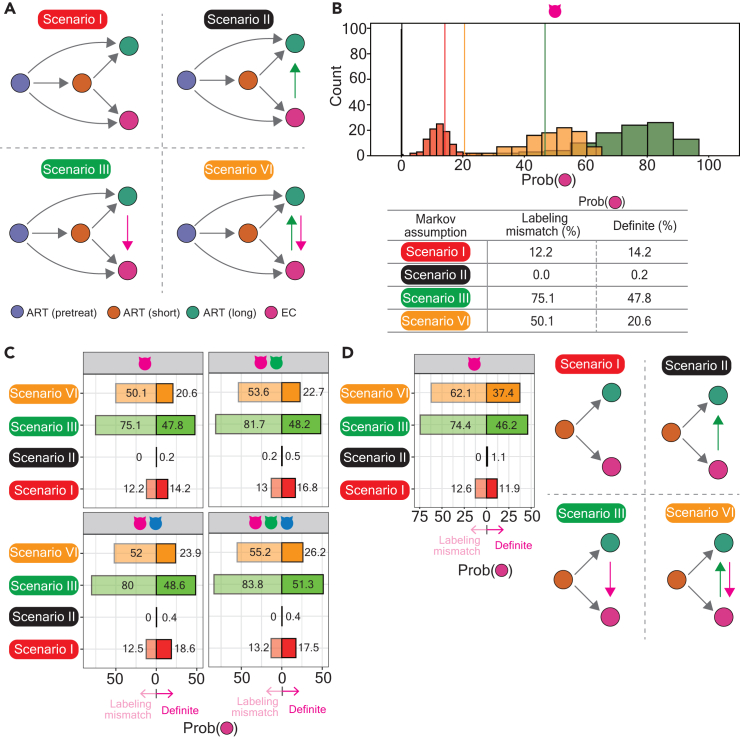
Previous studies have reported that the host genetic background of elite controllers possesses unique polymorphism and plays a pivotal role in determining the mechanism of elite control.^36,37,38 Based on this concept, we assume that the network topology in non-elite controllers should resemble that in themselves rather than that in elite controllers due to the intrinsic difference in their genetic background. To test this assumption, we tested four scenarios under Markov assumption, representing the evolution of the networks in HIV-1 reservoirs at different statuses of HIV-1 infections (Figure 5A). The difference across each scenario is highlighted in the status between patients subjected to a long period of ART and elite controllers (Figure 5A): (1) scenario I: no transition in the graph networks between these two statuses, (2) scenario II: a unidirectional trajectory is manifested from the status of elite controllers to the status of patients subjected to a long period of ART, (3) scenario III: a unidirectional trajectory is manifested from the status of patients subjected to a long period of ART to the status of elite controllers and (4) scenario IV: transition in the graph networks between these two statuses exist.

Figure 5.

MCMC modeling the dynamics of the networks alongside HIV-1 infections in ART-treated patients and in elite controllers

(A) Schematic representation of Markov assumption that consists of four scenarios. Details were described in the main text. Colors marked in circles represent the status of HIV-1 infections and elite controllers: violet, pretreatment HIV-1-infected individuals; marron, patients subjected to a short of ART; green, patients subjected to a long of ART; deep pink, elite controllers.

(B) Histogram (upper panel) representing the probability (x-axis) that random walks simulated in definite networks (solid lines) versus mislabeling networks (symmetric distributions). The probability was recorded from random walks that cease at any signature in the network of elite controllers. The color code represents four scenarios: Red, scenario I; Black, scenario II; Green, scenario III; Yellow, scenario IV. The probability recorded from random walks simulated in networks constructed by Cat 1 attributes was demonstrated in the table beneath the histogram.

(C) Bar charts summarizing the probability (x-axis) recorded in definite (the bars on the right) and mislabeling networks (the bars on the left). The y axis demonstrates four scenarios. Facets separate the networks constructed by different attribute combinations.

(D) Bar charts demonstrating the probability (x-axis) recorded in definite (the bars on the right) or mislabeling networks (the bars on the left) constructed by Cat 1 attributes. The simulation of random walks was forced to initiate from the status of patients subjected to a short period of ART, as illustrated on the right-hand side of the bar chart.

We applied MCMC modeling³⁹ and stimulated 10,000 random walks up to 10 steps in definite networks based on the Pearson correlation between two adjacent signatures illustrated in Figure 4F, as the example result shown in Figure 5B. The probability recorded by random walks simulated in definite networks was compared with those measured by random walks simulated in 100 networks constructed using labeling mismatches between vertices and statuses of HIV-1-infected individuals (here referred to as mislabeling networks). We forced random walks that initiate from a signature in the graph network from pretreatment HIV-1-infected individuals and recorded the probability that a path of random walks ends at any signature in the graph network from elite controllers. Based on our simulation results we only observed the destination of random walks that ceased in the status of either elite controllers or patients subjected to a long period of ART. The probability recorded between definite and mislabeling networks was summarized in Figure 5C, separated by different scenarios coupled with the networks constructed by different category attributes. We observed a decrease in the probability in definite networks compared with mislabeling networks in scenarios III and IV, whereas a slight increase in the probability in scenarios I and II (Figures 5B–5D). We assumed that an extremely low probability measured in scenario II was due to our observation that the majority of random walks cease at the status of patients subjected to a long period of ART. A similar pattern was observed as we forced random walks to be initiated from patients subjected to a short period of ART, except the undistinguishable probabilities were observed in scenario I (Figure 5D). These findings suggest that the transition in the graph network between elite controllers and non-elite controllers should be rare in the real world (scenario I). In addition, a low likelihood in scenarios III and IV occurs in the real world; the probability that the graph network evolves from elite controllers into the status of patients subjected to a long period of ART is however feasible (scenario II).

Discussion

While HIV-1 latency has been the subject of extensive research for many years, our current understanding remains limited in visualizing the precise location of HIV-1 reservoirs. In this work, we proactively employed graph-theoretical tools to define the topological network formed by immunologic signatures enriched in ART-treated patients and elite controllers, separated by intact and defective proviruses. Intriguingly, despite observing a substantial number of enriched signatures in reservoirs harboring defective proviruses in ART-treated patients (n = 773), 30.9% (n = 239) and 0.91% (n = 7) of the signatures with the enrichment of rich factor exceeded the mean (2.799) and the median (2.621) of the enrichment scale. Although it is at present not clear whether these signatures possessing minor enrichment either confer biological importance or represent temporary background noise, this observation may suggest that reservoir cells harboring defective proviruses should not be excluded while attempting to gain better insight into a comprehensive understanding of the HIV-1 reservoirs.

Indeed, the majority of proviral sequences detected, greater than 90%, are defective^1,2,3 and their roles remain elusive. Longitudinal studies have demonstrated that defective proviruses are subjected to different levels of immunological targeting and immune-mediated selection depending on their transcriptional and translation competence,^9,40,41 whereas proviruses that retain the ability to transcribe HIV-1 RNAs and translate viral proteins are considered to be preferentially cleared during sustained immunological pressure.¹³ Notably, recent studies have identified a subset of spontaneously active reservoirs dominated by defective proviruses.⁵ Such spontaneously active reservoirs that differ from those harboring intact proviruses could maintain and shape anti-HIV CD4⁺ and CD8⁺ T cell response during ART,⁵ underlying the biological importance of defective proviruses in HIV-specific immunity manifested by CD4⁺ and CD8⁺ T cells in the control of HIV-1 infections.^{4,5,32,40,42,43} Given that persistent defective proviruses can be detected within the first few weeks following infection,^2,41 questions, such as how ART may influence the repertoire of defective HIV proviruses and the central mechanisms used by defective proviruses against anti-HIV immune response will urgently need to be addressed.

In this study, we observed a distinct pattern of immune cell types between enriched immunologic signatures with the highest and the lowest edge connectivity (Figure 2I). A higher frequency of regulatory T cells (Tregs), conventional T cells, CD4⁺ thymocytes is associated with enriched signatures with the highest edge connectivity, whereas CD8⁺ T cells and B cells are coupled with those with the lowest edge connectivity. Although the relationship between the connectedness of enriched signatures and their functions remains unclear, the immune cells that appear here have been known to play key roles in response to HIV-1 infection and could thus be targeted for therapeutic strategies. HIV-1 infection is associated with progressive CD4⁺ lymphopenia and defective HIV-1-specific CD8⁺ responses that fail to eliminate HIV-1-infected cells. Enhancing the function or frequency of CD8⁺ T cells could improve the body’s ability to eliminate HIV-infected cells. Conversely, targeting Tregs, a subset of CD4⁺ T cells, to prevent their expansion could be beneficial, as their expansion results in immune dysfunction, tissue fibrosis, and disease progression.^44,45 CD8⁺ T cell responses are also crucial for controlling viral replication, as seen in elite controllers, who mount a higher frequency CD8⁺ T cell responses.^46,47,48,49 Additionally, broadly neutralizing monoclonal antibodies (bnAbs) are one of the antiretroviral strategies for HIV-1 prevention and were previously cloned from HIV-1-specific memory B cells isolated from HIV-1-infected individuals. Targeting these cells to enhance their function in patients could be a promising strategy for long-term defense. Intriguingly, Pensieroso et al. demonstrated that elite controllers have significantly lower percentages of naive and higher percentages of activated memory B cells, respectively, compared with non-HIV-1-infected individuals and a significantly higher frequency of resting memory B cells compared with patients subjected to ART.⁵⁰

We also observed several critical surface markers, including the checkpoint marker programmed death-1, which has been previously shown to be involved in persistent HIV-1 transcription in reservoir cells.^17,51,52,53 Additionally, interleukin and receptor proteins, along with ZNF genes, which are associated with repressive chromatin marks in CD4⁺ memory T cells and support long-term persistence of HIV-1 integrated proviruses^6,7,31 were also present in enriched immunologic signatures. Altogether, these findings suggest a linkage between the task-evoked functional genome network and HIV-1 reservoirs. Here whether such markers are expressed on the surface or inside of cells was not specified; a further understanding of the profound mechanisms designating functions to these immunologic signatures could pave the way for a comprehensive understanding of the interplay between the host functional genome and HIV-1 reservoirs.

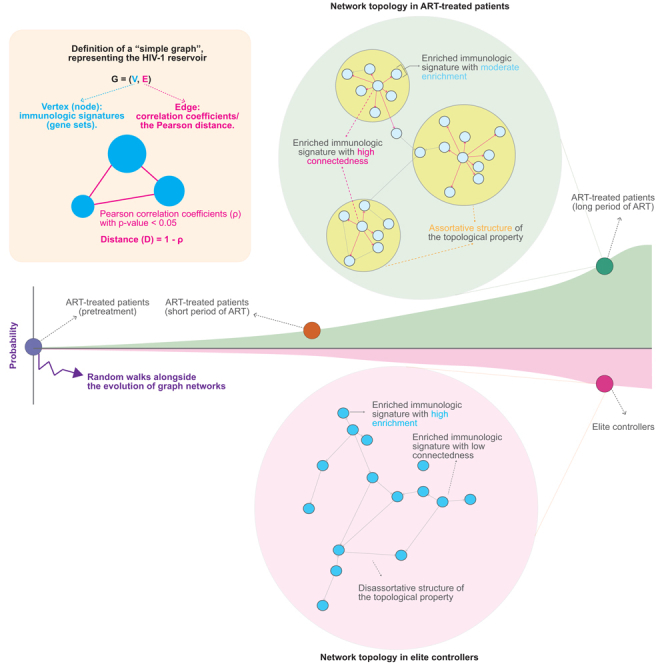
Graph-theoretical and network-based analyses, such as protein-protein,^54,55 genetic,⁵⁶ and gene regulatory^57,58 interactions have been widely applied to mine biological functions behind data. In HIV-1 research, such analyses have also been subjected to characterize the pattern of HIV-1 transmission.⁵⁹ In this study, we implemented the basic concept of graph theory and used graph-theoretical tools to depict the network topology of HIV-1 reservoirs based on correlation coefficients between two adjacent enriched immunologic signatures coupled with other attributes, including the transcriptome, and the spatial genome. We observed that Cat 1 attributes could be deemed as pillars supporting the property’s topology. The rich factor variable within Cat 1 alone already demonstrated sustained predictive strength. However, we also observed that relative to ART-treated patients, models applied to elite controllers faltered (Figure S4A), suggesting that, in elite controllers, either the sample size was small or additional factors governing such HIV-1 reservoirs have not yet been identified. Although the contribution of Cat 3 attributes was not emphasized in this work, a more detailed examination of the influence of different hierarchical 3D genome organizations on the property’s topology will be required. It is important to stress that, depending on the utilization of attributes, some networks are either disconnected graphs or subsets of enriched signatures with either low or non-correlation (Figures S2A and S5A). A further investigation into understanding what is the central mechanism that different category attributes govern the network topology and whether such isolated enriched signatures possess additional biological functions will broaden our lens to view their core-periphery structure coupled with their biological tasks. Nevertheless, in contrast to elite controllers, the characteristics of the network architecture in ART-treated patients include (1) a less intense magnitude of enrichment of signatures, (2) a high degree of assortativity, and (3) high connectedness between two adjacent vertices (Figure 6). This signifies that the network topology was more connective and structural in ART-treated patients (Figure 6).

Figure 6.

Proposed model of distinct network topologies between ART-treated patients and elite controllers

We hypothesize that an intrinsic barrier of the network topology that represents HIV-1 reservoirs lies between non-elite controllers (represented by ART-treated patients in this study) and elite controllers (details in the main text). In comparison to elite controllers, the network structured by enriched immunologic signatures in ART-treated patients is moderately enriched and exhibits a higher level of connectedness, resulting in a more assortative topology. This assortative structure is particularly in reservoirs harboring intact proviruses in ART-treated patients.

The limit of graph spectra is that they fail to provide a direct read-world interpretation of network architecture,⁶⁰ as one of the critical tasks is how to define a measure of the distance between graphs.⁶¹ To compensate for such restraint, in this work, we further calculated the Pearson distance to signify the difference between two graph networks (Figures 4K–4O). The measures demonstrated that graph networks between elite controllers and ART-treated patients were less isomorphic. This observation was further verified using the MCMC modeling³⁹ analysis in order to simulate the evolution of the graph network (Figure 5). Markov chain modeling analysis has been previously applied to studying HIV, including HIV/acquired immunodeficiency syndrome (HIV/AIDS) disease progression,^62,63 immunological and virological states in HIV-1 infected patients,⁶⁴ tracking the movement of the virus from one generation to another in a period of 20 years,⁶⁵ and the heritability of the HIV-1 reservoir size and decay under long-term suppressive ART.⁶⁶ Either discrete-time⁶² or continuous-time^63,64,65,66 Markov models embedded with multiple stages defined by virological, immunological, and clinical parameters were applied to these studies. The major difference between our study and others is that, in this work, the Markov chain model was constructed based on graph networks structured by immunologic signatures enriched in ART-treated patients in a longitudinal order and elite controllers; the edge represents the Pearson correlation coefficient between two adjacent enriched signatures (vertices). Random walks were then manifested on this directed weighted graph with assigned directions across graph networks. Despite grappling with the challenges of a limited number of integration sites retrieved from longitudinal clinical samples and elite controllers, we extrapolated our findings by simulating random walks in graph networks (Figure 5).

Simulation results in scenario I suggest that in the real world, the transition in HIV-1 reservoirs between elite controllers and non-elite controllers should be rare and perhaps the destination of network evolution has to be determined either at the early stage of HIV-1 infections or even earlier than individuals are infected. This proposition also resonates with the current understanding that the most possible mechanisms of elite control should be governed by the host genetic background.^36,37,38 Simulation results in scenario II somehow reflect the clinical observation that elite controllers may experience occasional viral load “blips” above the level of detectability by conventional assays.^67,68,69 This observation highlights one arising question in elite controllers: is there any viral replication of the proviruses that are considered to be in the state of deep latency occurring in elite controllers? Studies indicate that an inherent difference is present between viruses in the plasma and viruses in resting CD4⁺ T cells in this subject.^{36,47,68,69,70,71} At least one escape mutation is unveiled in the HIV-1 Gag in viruses detected in the plasma in elite controllers possessing HLA-B∗57⁷² rather than the proviruses in CD4⁺ T cells.⁷³ Although the mechanism that governs such a discordance remains unclear, these results show that the probability of possible viral replication in elite controllers should not be completely negligible. Simulation results in scenarios III and IV imply that the transition in graph networks from non-elite controllers to elite controllers is less feasible in the real world. This led us to postulate the existence of an intrinsic property barrier between these two groups of HIV-1-infected individuals and the ramifications of such an intrinsic influence are profound and lasting. The subsequent step involves verifying the simulation results using in vitro experiments and additional clinical datasets of HIV-1 integration as well as discerning the biological functions of individual enriched signatures in a network, with the emphasis placed on subsets of graphlets and isolated vertices. Overall, this work represents an inaugural step in utilizing genomic approaches with graph-theoretical tools to enhance our understanding of the composition of HIV-1 reservoirs.

Limitation of the study

The major limit in this work is due to the scarcity of HIV-1 integration sites retrieved from longitudinal clinical samples of HIV-1-infected individuals and elite controllers and the imbalance numbers of integration sites between intact and defective proviruses, perhaps encountering an issue of a statistical flaw. It is however a part of the nature of HIV-1: a number of defective proviruses dominate intact ones.^1,2,3 The aftermath of a discrepancy in the sample size was rescued using the bootstrapping method while presenting the magnitude of enrichment as represented by rich factors in enriched signatures (Figure 1B) and the expression of the genes in enriched signatures (Figure 1D). Such imbalance was noticed in graph networks that possess disproportionate vertices. In the follow-up investigation, graphlet (small induced subgraphs of a large network)-based methods^61,74,75 should be implemented for further characterization of the network topology.

Finally, given that a scarcity of the data that consist of HIV-1 integration and corresponding host transcriptomics in parallel is presently available, in this study, we utilized RNA-seq data that was performed using cells isolated from ART-treated patients^13,20 and elite controllers,⁷ respectively, to overlay genes that appear in enriched signatures. At this stage, we cannot verify whether these chosen RNA-seq datasets can fairly represent gene expression of HIV-1-targeted genes retrieved in all selected studies. In addition, a variety of individual gene expression of the genes present in the same enriched signatures was not taken into account in this work.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Heng-Chang Chen (heng-chang.chen@port.lukasiewicz.gov.pl).

Materials availability

This study did not generate new unique reagents.

Data and code availability

Data availability:

• •Publicly available datasets were analyzed in this study and their origins are detailed in the acquisition and proceeding with public datasets section (see later in discussion) and the key resources table.
• •The analyzed data, comprising lists of enriched immunologic signatures, coordinates between ID numbers, and incident enriched signatures associated with predictor variables are provided in Supplementary Tables.
• •A collection of experimentally supported cell makers in humans is available at the CellMarker 2.0 database (http://bio-bigdata.hrbmu.edu.cn/CellMarker or http://117.50.127.228/CellMarker/).³⁵

Code availability:

• •All code and scripts provided in this work are available on GitHub (https://github.com/HCAngelC/Network_structure_of_HIV_IS) (Please refer to the section “Software and algorithms” in the key resources table).
• •The open-source packages used in this study, which have not been assigned DOIs, are listed as follows: The R package “Hmisc” was used to calculate correlation coefficients (Harrell Jr., F., & Dupont, Ch. (2019). Hmisc: Harrell Miscellaneous. R Package Version 4.2–0. https://CRAN.R-project.org/package=Hmisc).
• •Python 3.11.6 with pandas 2.3.1 was used to construct random forest-based classifiers (https://pandas.pydata.org/docs/).
• •Python scikit-learn 1.3.2 package was used to construct random forest-based classifiers (Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825–2830, 201).
• •Any additional information required to reanalyze the data reported in this article is available from the lead contact upon request. This article reports the original code.

Acknowledgments

HCC acknowledges funding from the National Science Centre, Poland (Sonata Bis Grant UMO-2022/46/E/NZ6/00022). AKP acknowledges funding from the National Science Centre, Poland (OPUS Grant UMO-2022/45/B/NZ3/03890). MW acknowledges funding from the National Science Centre, Poland (Sonata Bis Grant UMO-2022/46/E/NZ6/00131).

Author contributions

Conceptualization, H.-C.C.; methodology, H.-C.C., and J.W.; software, H.-C.C., and J.W.; formal analysis, H.-C.C., and J.W.; investigation, H.-C.C., J.W., A.K.-P., K.W., and H.A.; resources, H.-C.C.; data curation, H.-C.C., and J.W.; writing of original draft article, H.-C.C., M.W., J.W., and K.W.; writing, article review and editing, H.-C.C., M.W., A.K.-P., and J.W.; visualization, H.-C.C., and J.W.; supervision, H.-C.C.; project administration, H.-C.C.; funding acquisition, H.-C.C.

Declaration of interests

The authors declare no conflict of interest.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
HIV-1 integration sites identified in ART-treated patients	Einkauf et al. (2019)8	Tables S3A–S3C
HIV-1 integration sites identified in ART-treated patients	Einkauf et al. (2022)13	Table S1
HIV-1 integration sites identified in ART-treated patients	Lian et al. (2023)16	Table S1
HIV-1 integration sites identified in ART-treated patients	Patro et al. (2019)29	Main text and Table S1
HIV-1 integration sites identified in ART-treated patients	Brandt et al. (2021)30	Table S1
HIV-1 integration sites identified in ART-treated patients	Huang et al. (2021)31	Table S2
HIV-1 integration sites identified in ART-treated patients	Simonetti et al. (2021)32	Figure 3; Table S3
HIV-1 integration sites identified in ART-treated patients	Joseph et al. (2022)33	Figure 2; Table S1
HIV-1 integration sites identified in elite controllers	Jiang et al. (2020)7	Tables S1 and S2
HIV-1 integration sites identified in elite controllers	Lian et al. (2021)19	Table S1
RNA-seq data from ART-treated patients	Einkauf et al. (2022)13	GEO: GSE144334
RNA-seq data from ART-treated patients	Clark et al. (2023)20	Table S3
RNA-seq data from elite controllers	Jiang et al. (2020)7	GEO: GSE144332
ATAC-seq data for ART-treated patients and elite controllers	Jiang et al. (2020)7	GEO: GSE144329
HiC data performed in ART-treated patients	Einkauf et al. (2022)13	GEO: GSE168337
List of enriched immunologic signatures harboring intact proviruses in ART-treated patients	This study	Table S1
List of enriched immunologic signatures harboring defective proviruses in ART-treated patients	This study	Table S2
List of enriched immunologic signatures harboring intact proviruses in elite controllers	This study	Table S3
List of enriched immunologic signatures harboring defective proviruses in elite controllers	This study	Table S4
A complete attribute list of enriched immunologic signatures harboring intact and defective proviruses in ART-treated patients and elite controllers	This study	Table S5
A complete attribute list of enriched immunologic signatures in pretreatment HIV-1-infected individuals, patients subjected to short and long period of ART, and elite controllers	This study	Table S6
Software and algorithms
R package “clusterProfiler” (Version 4.4.1)	Yu et al. (2012)76; Wu et al. (2021)34	https://git.bioconductor.org/packages/clusterProfiler
R package “Hmisc”	Harrell Jr., F., & Dupont, Ch. (2019). Hmisc: Harrell Miscellaneous	https://CRAN.R-project.org/package=Hmisc
R package “igraph”	Csárdi et al. (2024)77	https://igraph.org
R package “ComplexHeatmap”	Gu et al. (2016)78; Gu et al. (2022)79	https://git.bioconductor.org/packages/ComplexHeatmap
R package “stats”	N/A	https://www.r-project.org/
R package “pROC”	Robin et al. (2011)80	https://cran.r-project.org/web/packages/pROC/index.html
Python pandas 2.1.3	N/A	https://pandas.pydata.org/docs/index.html
Python scikit-learn 1.3.2 packages	Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825–2830, 201	https://scikit-learn.org/stable/whats_new/v1.3.html
Python seaborn 0.13.0 package	Waskom, M. (2021)81	https://pypi.org/project/seaborn/
Python scikit-learn package	Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825–2830, 201	https://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html
Python SciPy 1.11.3 package	Virtanen et al. (2020)82
Code and scripts	This study	https://github.com/HCAngelC/Network_structure_of_HIV_IS
Other
Molecular Signatures Database (MSigDb)	Subramanian et al. (2005)83; Liberzon et al. (2011)84; Liberzon et al. (2015)85	https://git.bioconductor.org/packages/msigdb
CellMarker 2.0 database	Hu et al. (2023)35	http://bio-bigdata.hrbmu.edu.cn/CellMarker or http://117.50.127.228/CellMarker/

Method details

Concept of the task-evoked functional genome property of HIV-1 reservoirs and its dynamic evolution

Our working hypothesis has been based on our previous findings that the HIV-1-targeted genes that share similar biological functions form different communities, so-called “immunologic signatures”^27,28; HIV-1 integration frequency within different signatures might be used as a proxy to define specific immune cell types and proinflammatory soluble factors alongside HIV-1 infections associated with ART.^27,28 To this extent, in this study, we hypothesize that different immunologic signatures may possess various ranges of connectedness, thereby structuring a task-evoked property of a network, representing HIV-1 reservoirs (Figure 6).

We plot the “simple graph” to represent each network of HIV-1 reservoirs. Based on the definition of graph theory, a simple graph $G$ is defined by $G=\left(V,E\right)$, where $V$ is a finite set of vertices, representing enriched signatures, and $E$ is a finite set of edges, representing correlation coefficients between two adjacent vertices. A detailed definition that we refer to Grinberg (2023)⁸⁶ with modifications is described as follows:

Let $G=\left(V,E\right)$ be a simple graph.

• (a)The set $V$ is called the vertex set of $G$; it is denoted by $V\left(G\right)$. One element of $V$ represents one enriched immunologic signature; the set $V$ represents all enriched immunologic signatures identified within a simple graph $G$, representing a network of HIV-1 reservoirs. Enriched immunologic signatures result from the MSigDb over-representation analysis^83,84,85 detailed in the following section using HIV-1-targeted genes.
• (b)The set $E$ is called the edge set of $G$; it is denoted by $E\left(G\right)$. One element of $E$ stands for the correlation coefficient between two adjacent vertices, referred to the definition (c), within a simple graph $G$. Each simple graph $G$ satisfies $G=\left(V\left(G\right),E\left(G\right)\right)$. Correlation coefficients are computed using the R package “Hmisc” (https://CRAN.R-project.org/package=Hmisc) detailed in the following section based on the Pearson correlation.

In the case of bipartite and tetrapartite graphs, the set $E$ covers correlation coefficients between all possible pairs of two adjacent vertices irrespective of the four groups, ART-intact, ART-defective, EC-intact, EC-defective, assigned in this study.

• (c)When $i$ and $j$ are two elements of $V$, we mark $ij$ for $\left\{i,j\right\}$; each edge of $G$ thus has the form $ij$ for two distinct elements $i$ and $j$ of $V$. Two vertices $i$ and $j$ of $G$ are said to be adjacent if $ij\in E$. In this case, the edge $ij$ is said to bridge $i$ with $j$, and the vertices $i$ and $j$ are so-called the endpoints of this edge. In this study, only edges calculated between two adjacent vertices are taken into account to compare the structure of networks.
• (d)Let $j$ be a vertex of $G$ (that is, $j\in V$). The neighbors of $j$ are the vertex $i$ of $G$ that satisfy $ij\in E$. In other words, the neighbors of $j$ are the vertices of $G$ that are adjacent to $j$.

Acquisition and proceeding with public datasets

A thorough literature search was conducted on PubMed, using the keywords (((intact) OR (intact provirus) OR (intact proviruses)) AND ((HIV) OR (HIV-1))), accessed on March 27, 2023, as previously described in Więcek and Chen (2023).²⁸ Research articles were selected from the first 1,000 cited papers in PubMed between 2005 to March 2023. For this study, we analyzed eight^{8,13,16,29,30,31,32,33} studies related to HIV-1 integration in ART-treated patients and two^7,19 studies related to elite controllers (Figure S1A). Host genes targeted by HIV-1 integration, as reported by Jiang et al. (2020),⁷ were previously analyzed and documented in Chen (2023).²⁷ Transcriptome sequencing data for ART-treated patients were retrieved from Einkauf et al. (2022)¹³ (GEO: GSE144334, RNA-seq performed with ART-treated patients’ samples) and Clark et al. (2023).²⁰ Transcriptome sequencing data for elite controllers were retrieved from Jiang et al. (2020)⁷ (GEO: GSE144332, RNA-seq performed with elite controllers’ samples). ATAC-seq (GEO: GSE144329) and HiC datasets (GEO: GSE168337) were retrieved from Jiang et al. (2020)⁷ and Einkauf et al. (2022),¹³ respectively. The total number of provirus-targeted genes retrieved from selected studies is presented in Figure S1A and the precise source location where data have been downloaded is provided in Deposited data in the key resources table.

MSigDb over-representation analysis

A total of 958 provirus-targeted host genes (200 genes harboring intact versus 758 genes harboring defective proviruses) and 275 provirus-targeted host genes (111 genes harboring intact versus 164 genes harboring defective proviruses) were collected respectively from HIV-1-infected individuals subjected to ART (eight studies)^{8,13,16,29,30,31,32,33} and elite controllers.^7,19 After removing the duplicate genes, the R package clusterProfiler (Version 4.4.1)^34,76 was used to compute enriched immunologic signatures with the function enricher() and default options. Over-representation analysis⁸⁷ was performed using C7 immunologic signature gene sets from the Molecular Signatures Database (MSigDb)^83,84,85 as the background. Enriched signatures with p-values (adjusted by the Benjamini-Hochberg method) below 0.05 were selected. Rich factors of immunologic signatures enriched in each group and in a random control labeled “hg38” (Figure S1B) were calculated by dividing GeneRatio by BgRatio with the command lines described below.^27,34

>MsigDb_output_file$GeneRatio <- as.numeric(gsub(“(\\d+)/(\\d+)”, “\\1”, MsigDb_output_file$GeneRatio, perl = T))/as.numeric(gsub(“(\\d+)/(\\d+)”, “\\2”, MsigDb_output_file$GeneRatio, perl = T))

# Convert GeneRatio to numerical variables.

>MsigDb_output_file$BgRatio <- as.numeric(gsub(“(\\d+)/(\\d+)”, “\\1”, MsigDb_output_file$BgRatio, perl = T))/as.numeric(gsub(“(\\d+)/(\\d+)”, “\\2”, MsigDb_output_file$BgRatio, perl = T))

# Convert BgRatio to numerical variables.

>MsigDb_output_file <- MsigDb_output_file %>% dplyrmutate(rich_factor = GeneRatio/BgRatio)

# Calculate rich factors.

In Figure S1B, “hg38” denotes the rich factor calculated using all protein-coding genes (rich factor: median, 1.162; mean, 1.154).

Weight was demonstrated by dividing the number of the transcribed genes per enriched signature by the total number of the transcribed genes retrieved from enriched signatures but not present in counterparts, such as genes targeted by intact proviruses rather than defective ones in either ART-treated patients or elite controllers. The outputs of over-representation analysis for genes harboring intact and defective proviruses in ART-treated patients and elite controllers are presented in this study and can be found in Tables S1, S2, S3, and S4. Outputs related to longitudinal HIV-1 integration were downloaded from Chen (2023).²⁷

Assignment of predictor variables in category 1 (Cat 1), category 2 (Cat 2), and category 3 (Cat 3) attributes

We utilized all enriched immunologic signatures from ART-intact (n = 20), EC-intact (n = 14), EC-defective (n = 36), and selected the enriched signatures in ART-defective with rich factors over the mean (2.799) of the enrichment scale (n = 239) as the input signatures (n = 309) to illustrate topological properties of the network. Nine attributes: (1) rich factor, (2) weight, (3) involvement of CD4 T cells, (4) involvement of CD8 T cells, (5) involvement of B cells, (6) involvement of myeloid cells, (7) involvement of other cell types, (8) involvement of proinflammatory factors and (9) immune response labeled in immunologic signatures were used in Cat 1 attributes. Attributes (3) to (7) were constructed based on the presence of the indicated cell type in the signature description, with a character “1” denoting its presence, and a character “0” indicating its absence. A character “1” was denoted if the proinflammatory factor was present in the signature description; otherwise, a character “0” was given. For immune response, a character “0” indicated no description in the signature description, a character “1” indicated down-regulation, and a character “2” indicated up-regulation. Attributes (1) and (2) were numeric attributes. Cat 2 attribute referred to as Transcript Per Million (tpm), calculated by dividing RNA sequencing raw reads^7,13,20 by the length of a gene in kilobases (reads per kilobase, RPK), followed by dividing by the sum of all RPK values divided by 1,000,000. Cat 3 attributes included data from ATAC-seq and intrachromosome HiC followed by high-throughput sequencing. The HiC outputs (GSM5136368, GSM5136369, and HiC_GSM5136370)¹³ with 10-kilobase resolution were combined and overlaid on genes retrieved from enriched signatures in order to determine their topological distribution using the command intersect with default options in bedtools.⁸⁸ The same pool of the gene was also overlaid on the ATAC-seq readout analyzed by Einkauf et al. (2022)¹³ to identify genes within ATAC-seq coverage regions. A comprehensive list of all attributes associated with enriched signatures harboring intact and defective proviruses in ART-treated patients and elite controllers, as well as enriched signatures obtained from longitudinal HIV-1 integrations, is provided in Tables S5 and S6, respectively.

Measurement of correlation coefficients of enriched immunologic signatures

The R package “Hmisc” (https://CRAN.R-project.org/package=Hmisc) was employed to calculate correlation coefficients between enriched signatures using the function rocrr(). Subsequently, correlation matrices were transformed into data frames containing four columns. The first two columns served as ID columns, designating two adjacent enriched signatures irrespective of the direction. The remaining columns included the correlation coefficient and the associated p-value. To filter out weak or spurious connections, correlation coefficients with a p-value >0.05 are excluded. Tables S5 and S6 provide the correspondence between ID numbers and the associated enriched signatures.

Visualization of the network architecture

Simple graph for individual network

We utilized the previously mentioned correlation matrix as the edge list to depict simple graphs. In this list, the correlation coefficients representing the edge were calculated between two adjacent vertices that represent enriched signatures. The node list consisted of a series ID for all enriched signatures, information about the integrity of a proviral genome, and the classification of HIV-1-infected individuals (ART-treated patients versus elite controllers). It is important to note that we generated separate node lists for each property. The network structure was then established using the function graph_from_data_frame() from the R package “igraph” (https://igraph.org)⁷⁷ with the following arguments: d for the edge list, vertices for the node list, and directed = FALSE to account for undirected edges in the network.

Bipartite graph for two-networks interaction

We selected two adjacent signatures enriched in distinct topological properties to illustrate their topological interactions to depict bipartite graphs. It is important to note that a direction between two adjacent enriched signatures was not considered for plotting bipartite graphs. The same function and arguments from the R package “igraph” (https://igraph.org)⁷⁷ were employed for visualizing these networks.

Tetrapartite graph for four-networks interaction

The complete edge and the node list, which includes all pairs of two adjacent enriched signatures and the corresponding correlation coefficients, were used as arguments, d and vertices, respectively, in the function graph_from_data_frame() to depict these tetrapartite graphs. Edge connectivity (Figures 2B and 4B) was calculated based on the correlation matrix resulting from the tetrapartite graph.

Measurement of edge connectivity of enriched immunologic signatures

The measure of edge connectivity is calculated based on the definition of the function degree() implemented in the R package “igraph”⁷⁷ with modification. From each enriched signature across four networks (ART-intact, ART-defective, EC-intact, and EC-defective), edge connectivity (Figures 2B and 4B) was calculated using the sum of the total number of edges per vertex based on the tetrapartite graph, representing four-networks interaction (Figures 2F and 4F). The edge connectivity is defined by the Equation below.

$$EdgeConnectivity=\sum _{i\ne j}{\sigma }_{ij}$$ (Equation 1)

where ${\sigma }_{ij}$ is the total number of edges from the vertex $i$ to the next adjacent vertex $j$. It is important to note that correlation coefficients were not taken into account in the calculation of edge connectivity. Edge connectivity was visualized using a cluster heatmap described in the following section.

Measurement of degree and nominal assortativity coefficient and euclidean distance of the network architecture

Degree and nominal assortativity coefficients were computed using the function sassortativity_degree() and assortativity_nominal() in the R package “igraph”.⁷⁷ For Figure S2B, 10 enriched signatures in each scenario were randomly sampled with replacement to obtain degree assortativity coefficients using the mentioned function, and this process was repeated 1,000 times. Statistical tests were performed with R with default options. Additionally, Euclidean distance (Figure S3C) was calculated using the function dist() with the argument method for “euclidean” in the R package “stats”, which is a part of R (https://www.r-project.org/).

Measurement of the network density

The network density is computed based on the tetrapartite graph using the mean of correlation coefficients divided by the sum of edges retrieved from all vertices in a network.

Clustering heatmap

The cluster heatmaps representing the magnitude of the enrichment of immunologic signatures (Figure 1A), host gene expression of the genes retrieved from enriched signatures (Figure 1C), assortativity analysis (Figures 2A and 4A), and edge connectivity of enriched immunologic signatures (Figures 2B and 4B), HIV-1-targeted genes associated with cell markers (Figure 1G), and the appearance of cell types (Figure 2I) and proinflammatory soluble factors (Figure 2J) in the top 30 ranked enriched signature were created using the R package ComplexHeatmap^78,79 with default options.

Classification of the networks

Logistic regression-based classification: we divided the complete dataset, containing 309 enriched signatures associated with attributes into a training set (80% of the dataset) and a testing set (20% of the dataset) for logistic regression running on R. The logistic regression model was fitted using the function glm() with the argument family specified as “binomial” in the R package “stats” (https://www.r-project.org/). Three types of responses were considered: provirus (intact versus defective provirus), patient (ART-treated patients versus elite controllers), and provirus + patient. These responses were included in an object of class “formula”. Different numbers and combinations of the “term” referred to category attributes in an object of class “formula” were bootstrapped with replacement and this process was repeated 1,000 times. Receiver operating characteristic (ROC) and the area under the curve (AUC) were calculated using the functions multiclass.roc() and auc() in the R package “pROC”,⁸⁰ respectively. The whole procedure was repeated 1,000 times for statistical robustness.

Random forest classification: Separate models were made for six classification tasks, all following the same pipeline: M1 – multiclass classification of enriched signatures harboring intact versus defective proviruses in ART-treated patients and elite controllers, M2 – binary classification of enriched signatures harboring intact versus defective proviruses in ART-treated patients, M3 – binary classification of enriched signatures harboring intact versus defective proviruses in elite controllers, M4 – multiclass classification of immunologic signatures enriched in pretreatment HIV-1-infected individuals, patients subjected to a short and long period of ART and elite controllers, M5 – as in M4, but excluding elite controllers, M6 – as in M4, but excluding pretreatment HIV-1-infected individuals. The pipeline was implemented in Python 3.11.6 using pandas 2.1.3 (https://pandas.pydata.org/docs/index.html) and scikit-learn 1.3.2 packages (https://scikit-learn.org/stable/whats_new/v1.3.html). Plots were generated using seaborn 0.13.0 package.⁸¹

First, 30% of the data was reserved for testing, ensuring class balance. Subsequently, random forest classifiers from the Python scikit-learn package (https://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html) were trained on the training set with default parameters to extract impurity-based feature importance. In all cases, all Cat 1 attributes except rich factor and weight exhibited much lower importance than other attributes and were thus removed from further classification.

Next, grid search cross-validation was conducted to select hyperparameters for the final random forest classifiers in each task. The tested hyperparameter values were included: n_estimators (20, 100), criterion (gini, log_loss), max_features (sqrt, log2), min_samples_split (3, 5, 10), min_samples_leaf (1, 4), and class_weight (None, balanced). The remaining parameters were set to default values. Given such a small size of the datasets, especially minority classes, repeated stratified k-fold validation was performed with 10 iterations of 5 randomly selected validation splits. The macro-averaged F1 score guided model selection in multiclass tasks (M1, M4-M6), while the positive class F1 score was used in binary classification tasks (M2 and M3).

Finally, a model evaluation was carried out. Due to the limited size of the datasets and the presence of minority classes, which could lead to a strong dependence of model performance on a specific selection of samples for the test set in a single train-test split, each model was independently re-trained and evaluated on 1000 randomly generated stratified 70%: 30% splits to mitigate this bias and generate robust statistics.

To compare the impact of Cat 1, 2, and 3 attributes on classification, the following approaches were employed for each task: classification using Cat 1 attributes, Cat 1 and 2 attributes, Cat 1 and 3 attributes, and all category attributes. Resulting distributions of F1 scores, macro-averaged for multiclass tasks and positive class for binary tasks, were presented using kernel density estimation (KDE) and boxplots. Median F1 scores were compared, and statistical significance was assessed using the Wilcoxon test from the Python SciPy 1.11.3 package.⁸² In some cases, KDE plots displayed multiple maxima, particularly in tasks M2 and M3 (Figures S4C and S4D), indicating binary classification tasks with small positive classes. This phenomenon is attributed to the discrete difference in F1 score resulting from even a single positive class sample having a different prediction. This underscores the importance of evaluating models across multiple independent data splits. Additionally, it is noteworthy that the accuracy of classifying the networks in longitudinal ART-treated patients versus elite controllers improved when a small sample size from pretreatment HIV-1-infected individuals was removed (Figure S5C).

Measurement of the distance between networks

To measure the distance (D) of correlation between two distinct graph networks (Figures 4L–4O), we computed Pearson correlation coefficients (ρ) between two adjacent vertices and retrieved only the edges with significant p-values. The pairwise distances of signatures are defined by the Equation below.

$$Distance\left(D\right)=1-{\rho }_P$$ (Equation 2)

where ${\rho }_P$ represents Pearson correlation coefficients with significant p-values between two adjacent vertices.

To measure weighted (directed) networks the edge weight is defined by the Equation below.

$$Weight\left(W\right)=2-D$$ (Equation 3)

where $D$ represents Pearson distance with significant p-values between two adjacent vertices, as defined in the previous Equation. The edge weight was calculated between two adjacent vertices across independent graph networks, enabling the comparison of the graph isomorphism of each tetrapartite graph.

Markov chain Monte Carlo modeling analysis

The probability of progressive evolution from source to target signatures across graph networks was measured by Markov chain Monte Carlo method³⁹ sampling random walks on directed weighted graphs with assigned directions, where nodes represent enriched signatures. Only the edges with statistically significant Pearson correlation between two adjacent signatures were restrained in graph networks. The edge weights were calculated based on Pearson correlation coefficients, as described above. Four different scenarios in Markov assumption (Figure 5A) were designed in this study. The start of a random walk was forced to be initiated from signatures in the network from either pretreatment HIV-1-infected individuals (Figure 5C) or patients subjected to a short period of ART (Figure 5D).

Briefly, for each walk a starting node with uniform probability from source signatures in a graph network was randomly chosen for simulation and designated as the current node $i$. The probability of the movement alongside the out edges was calculated as follows:

$$P\left(i,j\right)=w_{i,j}/{\mathit{deg}.out}_i$$ (Equation 4)

Where: $i,j$ – out edge between current node $i$ and node $j$; $P\left(i,j\right)$ – probability of taking edge $i,j$ in the next step of the walk; $w_{i,j}$ – weight of the edge $i,j$; ${\mathit{deg}.out}_i$ – weighted out degree of node $i$, i.e., the sum of weights of all out edges of node $i$.

An out edge was then randomly chosen according to the calculated probability, and the target signature bridged by the corresponding edge was designated the current node $k$. The process was repeated either a maximum of 10 steps or ceased at a signature where no edges were encompassed. For each scenario in Markov assumption, we sampled 10,000 random walks and tracked the termination of each path of random walks. The probability shown as percentages was calculated as follows:

$$P\left(k\right)=\left(n_k/10,000\right)\ast 100$$ (Equation 5)

Where: $P\left(k\right)$ – the probability of graph network evolution that terminates at the state, where a graph network consists of a target node $k$; $n_k$ – a total number of random walks that terminate at the state, where a graph network consists of a target node $k$.

Quantification and statistical analysis

Statistics

All statistical tests were performed using R with default options and specific details are provided in the main text and figure legends where applicable.

Published: October 21, 2024