Aladyn Individual: Bayesian Hierarchical Dynamic Genetic Modeling of Comorbidity Progression

Abstract

Early identification of high-risk individuals through the analysis of their unique disease trajectories has a strong potential to support efficient prevention and clinical management across a range of chronic conditions. In this paper we present a novel approach for dynamic modeling of the evolution of chronic disease risks over time, incorporating individual genetic predispositions. Our approach uses a hierarchical Bayesian topic model including Gaussian Processes to capture age effects. It accounts for genetic predisposition through a time-warping function and topic-dependent genetic scores, enabling both simultaneous learning and updated predictions of complex comorbidity patterns, inclusive of genomic and non-genomic effects. We systematically compare to previous approaches and provide detailed simulations at https://bookdown.org/sarahmurbut/dynamic_ehr/ and https://surbut.shinyapps.io/dynamic_ehr.

1. Introduction

Understanding the evolution of an individual’s disease risk across their lifespan is crucial to advancing personalized medicine. This insight is essential for developing therapeutics tailored to individual patients rather than their diagnosed conditions. Current predictive models, which depend on static health states, often fail to capture the complexities of individual disease progression, particularly among aging populations, intricate disease interactions, and genetic influences. Recent methodologies ([1], [2]) have sought to analyze more sophisticated data types to identify unique disease patterns within extensive healthcare systems. These methodologies use data from large populations to discern diverse patterns of comorbidity, providing insight into the unique trajectories of complex diseases. Nevertheless, these approaches are not without limitations: firstly, temporal analysis of disease patterns typically captures population-level trajectories, overlooking individuals who progress through diseases at varying rates due to underlying genetic factors. Secondly, these methods often aim to classify patterns at the population level rather than provide predictive insights. Lastly, even the most advanced approaches tend to aggregate an individual’s health conditions across all accumulated diagnoses, failing to offer a time-dependent, individual-level profile that may evolve with new diagnoses and treatments. For example, prior research [3] has demonstrated that patients within the top 5% of genetic risk for myocardial infarction experience events nearly a decade earlier than the general population and follow an accelerated pathway through associated comorbidities, for which existing population-based methods offer minimal predictive capability. Our findings reveal significant disparities in disease progression; individuals in the top 5% of genetic risk for myocardial infarction encounter events nearly a decade earlier than those at lower risk (median age of onset 53.7 [53.1–53.9] vs 62.6 years [61.4–63.1]). Our model dynamically updates and predicts accurate diagnoses 79.5% more frequently than existing topic-modeling approaches [1]. The dynamic approach adjusts disease profiles by at least 11.7% annually for 50% of the individuals in the UK Biobank and All of Us cohorts, and 65.4% experience a change greater than 10% in comorbidity profiles. Simulation results corroborate the model’s superior accuracy [51.4–41%], precision [50.9 vs 39.9%], and recall [48.4 vs 39.2%] compared to fixed-weight approaches.

This study introduces the Aladyn model, highlighting its potential for incorporating genetic factors into the analysis of disease progression. We present evidence for the model’s functionalities, utilizing estimated loadings derived from extant dynamic topic models as a foundational basis. Our primary emphasis is on the innovative method of dynamically updating individual weights, which sets our approach apart from existing methodologies.

2. Methodological Motivation

2.1. Overview

The principal aim of this study is to model temporal variations in disease probabilities across various comorbidity profiles, incorporating underlying genetic factors while considering several essential attributes. Although there are numerous clustering frameworks for electronic healthcare data ([1], [4], [2]), they face challenges in deriving shared biological interpretations, inadequately capture individual-level deviations from population trends, and fail to address temporal variations. Certain frameworks within topic modeling can approximately address this challenge, as documents typically contain multiple topics characterized by specific distributions over words [5]. In this study, these genetically informed signatures of shared disease are termed topics. Our research builds upon the foundational principles of dynamic topic models ([6]) and hierarchical Dirichlet processes [7]. However, we introduce a fundamental paradigm shift by a) extending the dimensionality of both topic weights and disease loadings to the individual level, and b) dynamically updating both topics and loadings with accumulated information. Our methodological innovation is motivated mainly by three empirical trends described next.

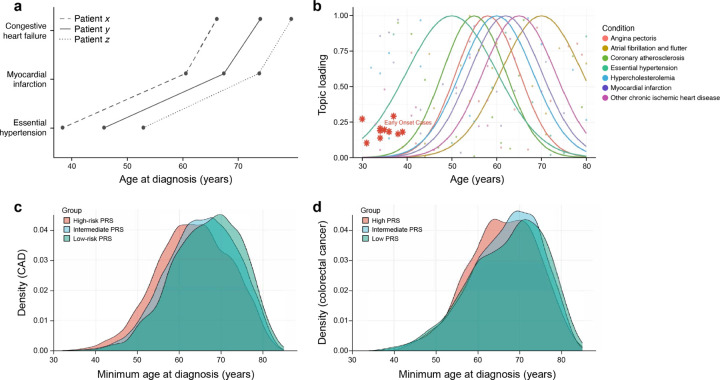
1. The likelihood of disease manifestation within a defined comorbidity profile, referred to here as a topic, demonstrates temporal variability. Different diseases under the same comorbidity topic or underlying pathological process may have varying ages of onset. For example, coronary artery disease may appear at an intermediate age, whereas heart failure may manifest at more advanced ages, indicating the progression of the underlying disease process. Each disease within a given topic has a specific distribution that indicates its occurrence propensity, and a temporal parameter that denotes its rate of change over time (Figure 1).

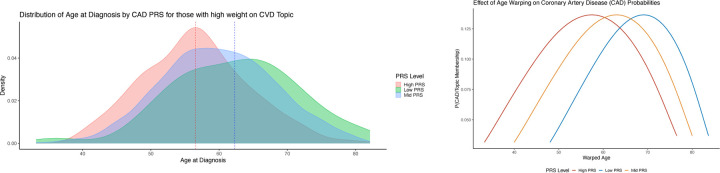
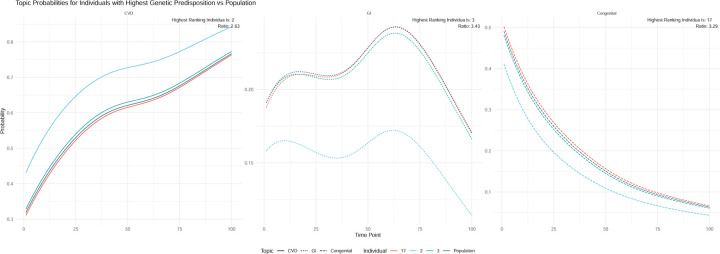
2. The variability in disease onset is substantial and is not adequately represented by traditional modeling methodologies. We observe that, even within a certain topic or profile, both the age of onset and the progression rate of diseases differ based on an individual’s genetic composition and other contributory factors (Figure 2). Instead of associating these factors post hoc, we incorporate them concurrently.

3. The heterogeneity of profiles contributing to an individual’s disease etiology exhibits temporal variability across the lifespan. These fluctuations are observed in alignment with both population-wide and individual-specific trends. Individual-specific trends are influenced by a complex interplay of genetic and non-genetic factors.

Figure 1: Differences in age of onset for prevalent conditions.

As a motivating example, we demonstrate the variation in the age of onset for a variety of common conditions within classically defined categories: this figure illustrates the range of onset ages for common conditions in the UK Biobank, N=421,707, age range 28–81.

Figure 2: Individualized timing within population-dictated disease chronology.

We demonstrate individuals heavily weighted on the cardiovascular topic with similarly ordered but chronologically distinct ages of onset for common cardiovascular conditions. We demonstrate the distribution in age of onset for common conditions, and how early onset individuals are poorly captured. We demonstrate justification for the use of genetics in estimating the warped times.

Jointly modeling both observed diagnoses and underlying genetics according to these unique time-dependent processes constitutes a novel approach. The integration of innovative diagnostic data to refine the prevalence of underlying genetic themes shows significant potential to improve predictive accuracy and enable novel discoveries. In this article, we first outline a novel framework for describing the evolution of genetically informed disease topics. We discuss the modeling of these comorbidity profiles over time, the incorporation of individual- and population-level trends, the dynamic adjustment of individual time scales within a given topic, and the updating of an individual’s profile over time. We introduce a paradigm shift in disease modeling in the following ways:

1. Individual-Level Time Warping: Accounting for differences in disease onset and progression speeds via a genetics-driven time warping function.

2. Genetic Integration: Polygenic risk scores (PRS) directly influence initial disease risk and a genetic predilection parameter that determines an individual’s trajectory adaptability, reflecting underlying genetic influence.

3. Dynamic Topic Weights: Bayesian updating of topic weights with each new diagnosis ensures our predictions always reflect the latest health information.

2.2. Connections With Topic Modeling in Natural Language Processing

Within the field of natural language processing, a ‘topic’ [8] is defined as a pattern of semantically related terms that frequently co-occur within a corpus of documents. For instance, a ‘sports’ topic may include terms such as ‘football,’ ‘basketball,’ and ‘soccer,’ whereas an ‘education’ topic might be characterized by terms such as ‘class,’ ‘campus,’ ‘teacher,’ and ‘student.’ In a similar vein, this study conceptualizes an individual’s diagnostic history as document text, where a ‘topic’ signifies a cluster of interrelated diseases that commonly co-occur within patient histories. For example, a cardiovascular topic is exemplified by a high prevalence of Myocardial Infarction and hypertension diagnoses, supplemented by additional associations with hypertension. Conversely, an endocrine topic may be primarily typified by Diabetes Mellitus and Thyroid disorders. Despite these distinctions, both topics exhibit shared associations with hypertension and hyperlipidemia, potentially due to differing etiological factors. The evolution and composition of each topic are not always evident and can be enhanced through unsupervised learning. However, traditional topic-modeling methodologies fail to adequately address the dynamic progression of diseases within a patient’s medical history. For instance, coronary artery disease may manifest at an intermediate age, while heart failure occurs predominantly at more advanced ages, reflecting the progression of the underlying pathological processes. This progression can vary in speed due to both genomic and non-genomic factors. This study introduces an age-dependent topic modeling framework to capture the varying onset of diseases throughout life. While traditional topic modeling delineates the population-level comorbidity profile, the likelihood of developing specific diseases and their onset can exhibit substantial variability among individuals. This study incorporates both genetic and non-genetic determinants to tailor the disease risk trajectory for individual prediction and pattern discovery, both within and among topics. Genetic factors enter the model in two primary ways: First, an individual with a high genetic predisposition for a particular topic is more likely to demonstrate that topic, although their age-dependent incidence function follows population-level patterns. That is, if cardiovascular disease is uncommon in the population at a young age, an individual with a high predisposition to cardiovascular disease may have a higher than average weighting on this topic, even though their weight of the overarching topic is allocated to alternative topics. Second, the rate of progression of a disease conditional on the membership of a topic can vary by genetic class within a topic.

3. Generative Model

3.1. Population-Level Topic Vocabularies Over Diseases

We first define a model for all diseases invariant to chronic or acute conditions in which a diagnosis may reoccur. In our model, each topic $k$ has an associated vocabulary distribution over diseases. This vocabulary distribution evolves over time and is modeled using a Gaussian Process $\left(\text{GP}\right)$.

Specifically, for each topic $k$ and each disease $d$, we define the parameters ${\eta }_{kdt}$ that describe the log-odds of disease $d$ occurring within topic $k$ at time $t$.

The evolution of ${\eta }_{kdt}$ over time $t$ is given by the Gaussian Process:

$${\eta }_{kdt}\sim 𝒢𝒫\left({\mu }_{kd}\left(t\right),{\text{Σ}}_{\eta }\right)$$ (1)

where ${\mu }_{kd}\left(t\right)$ is the mean function (Figure S6), and ${\sum }_{\eta }$ is the covariance matrix that captures the correlation over time. The mean function ${\mu }_{kd}\left(t\right)$ can take various forms, such as linear trends, logistic growth, exponential decay, Gaussian peaks, polynomial trends, or sinusoidal patterns, depending on the expected behavior of the disease $d$ within the topic $k$.

Given that most diseases exhibit peak activity within a limited number of topics (sparse data rows), we enforce the restriction that diseases remain active only in a small number of topics (Figure S2). This constraint ensures identifiability [8].

The covariance matrix ${\sum }_{\eta }$ is constructed using a covariance function, typically a squared exponential kernel, which ensures that the probability of the disease changes smoothly over time so that the topic-specific probability of a disease is more closely correlated with nearby times.

To map from the log-odds scale to the probability scale, we apply the softmax function to ${\eta }_{kdt}$:

$${\beta }_{kdt}=\frac{\exp \left({\eta }_{kdt}\right)}{{\sum }_{d^{\prime }=1}^D\exp \left({\eta }_{k{d}^{\prime }t}\right)},$$

where ${\beta }_{kdt}$ represents the probability of disease $d$ within the topic $k$ at time $t$.

3.2. Population-Level Topic Weights

The population-level topic weights describe how the prevalence of each topic $k$ changes over time at the population level. These weights are represented by the parameters ${\alpha }_{kt}$ for each topic $k$ at time $t$. Similarly to the disease vocabularies, the topic weights are also modeled using a Gaussian process:

$${\alpha }_{kt}\sim 𝒢𝒫\left({\mu }_k\left(t\right),{\text{Σ}}_{\alpha }\right),$$ (2)

where ${\mu }_k\left(t\right)$ is the mean function that describes the expected prevalence of topic $k$ over time, and ${\sum }_{\alpha }$ is the covariance matrix for topic weights.

3.3. Genetic Novelty: Warping for Topic-specific Disease Probabilities

A critical feature of our model is that genetics influences disease progression in two ways because we observe variation in age of disease onset for a disease even within a given topic. Secondly, we wish to improve our estimation of individual topic predilection by considering genomic predilection to disease topics. There are two critical parameters allowing for the joint incorporation of genetics into our model:

$$•\text{Time}\text{warping}\text{parameters}\rho ’\text{s}$$

$$•\text{Genetic}\text{predilection}\text{parameters}\gamma ’\text{s}.$$

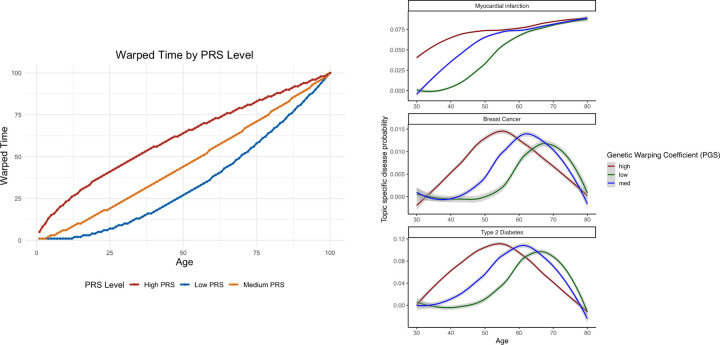
Individual genetic factors influence how each person’s disease probabilities within topics evolve over time. This is modeled through the genetic warping parameter ${\rho }_{i,k}$ for each individual $i$ and topic $k$. The warping function $t^{\prime }=W\left(t,{\rho }_{i,k}\right)$ transforms the original time index $t$ into a new time index $t^{\prime }$, effectively modulating the speed at which individual $i$ progresses through the disease probabilities of topic $k$. For instance, for an individual with a genetic warping index of 2 for topic $k$, the disease probabilities which are supposed to occur at age 60 occur at age 36, and those at age 50 occur at age 25. Critically, this is still taken from the population-level topic probabilities, so there is learning across the population.

3.4. Disease Probability within Topics: Genetics-dependent Warping of Time

For each individual, as above, the warping coefficient ${\rho }_{ik}$ governs the time scale at which the disease activity operates. Recall that we wish to map the chronologic age for every individual to the warped time, such that the appropriate population level probability values at the relevant warped time are applied to every individual’s chronologic time, so that at age 25, we would retrieve the population from age 50 for example.

For each individual $i$, topic $k$, and time $t$:

$$t_{ik}^{\prime }=\max \left(1,\tau \left(t,{\rho }_{ik},T\right)\right)$$

where:

$$\tau \left(t,{\rho }_{ik},T\right)={\left(\frac{t}{T}\right)}^{\frac{1}{{\rho }_{ik}}}\times T$$

• $T$ is the maximum time (e.g., age 100).

• ${\rho }_{ik}$ is the warping coefficient for individual $i$ and topic $k$, influenced by the genetic scores:

$${\rho }_{ik}={\mathbf{\text{w}}}^T{\mathbf{\text{g}}}_i.$$

This is a positive number.

• $\mathbf{\text{w}}$ is a vector of weights to be learned for each genetic score.

Calendar time $t$ will translate into warped time $t^{\prime }$ thus retrieving the appropriate population-level value. We use this to determine the index of the probability which is drawn for a given individual.

$${\beta }_{kdt}^{\prime }\left(i\right)={\beta }_{kd{t}_{ik}^{\prime }}$$

This allows for individual-specific variations in the progression of disease probabilities within each topic by pulling the probability from the population-level at the warped time index.

3.5. Genetic Predilection for Topic Weights

Genetics also influences an individual’s predilection for certain topics, which is represented by an adjustment to the population-level mean function of the topic weights. Each individual $i$ has a genetic predilection score ${\gamma }_{ik}$ for topic $k$. This score adjusts the population-level mean function ${\mu }_k\left(t\right)$ to create an individual-specific mean function:

$${\mu }_{ik}\left(t\right)={\mu }_k\left(t\right)+{\gamma }_{ik}$$ (3)

Individual-specific topic weights ${\alpha }_{ikt}$ are then sampled from a Gaussian process with this adjusted mean function:

$${\alpha }_{ikt}\sim 𝒢𝒫\left({\mu }_{ik}\left(t\right),{\text{Σ}}_{\alpha }\right).$$ (4)

To obtain valid probability distributions for topic proportions at each time point, we apply the softmax function to individual-specific topic weights ${\alpha }_{ikt}$. This ensures that the topic proportions sum to one at each time point:

$${\theta }_{ikt}=\frac{\exp \left({\alpha }_{ikt}\right)}{{\sum }_{k^{\prime }=1}^K\exp \left({\alpha }_{ikt}\right)}$$

3.6. Summary of Generating Model

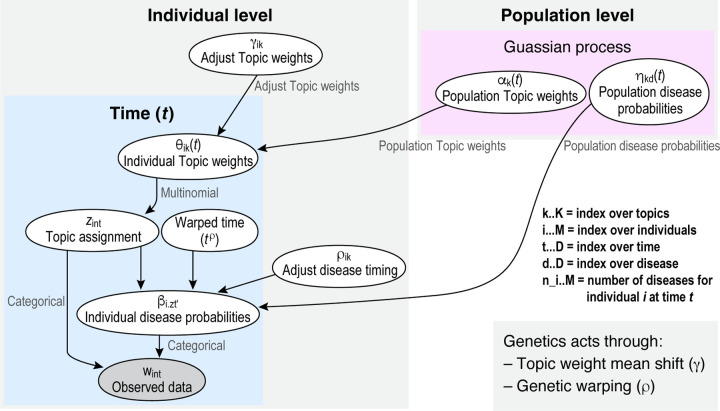
In summary, the hierarchical structure for the generative process for each individual $i$ over time $t$ can be summarized as follows. We also offer a modified plate diagram describing the evolution (Figure 5).

Figure 5: Plate Diagram Modifying Flow.

Here we illustrate the flow of our generating model. In brief, our process is governed by two population level parameters, the evolution of topic weights $\left(\alpha \right)$ and disease loadings $\left(\eta \right)$. Both arise from topic or disease specific Gaussian process with topic or disease level mean and covariance parameters. The covariance pattern arises from a Gaussian kernel in which adjacent times share probability more closely. Genetics acts in two fundamental ways to influence individual changes: The topic weights for every individual are driven by both the population mean and the individual predilection for a given topic, ${\gamma }_{ik}$. The scale at which an individual progresses through a topic specific disease is governed by a ‘warping coefficient’, ${\rho }_{ik}$. Both topic weights and disease loadings are softmax normalized at each stage to generate a proper probability distribution. Then, at each time point, a latent indicator is chosen according to an individual’s time-specific probability over topics, ${\theta }_{ik}$. This latent indicator then designates the vector of time specific disease probabilities ${\beta }_{ik{t}^{\prime }}$, which will govern the choice of observed diagnosis. The ${\beta }_{ikt}$ is generated according to the topic’s population-specific vector of disease probabilities for the time governed by the individual’s warping parameter.

1. For each topic $k$ and each disease $d$, the disease vocabulary evolves over time according to a Gaussian Process $\left(\text{GP}\right)$:

   $${\eta }_{kd}\sim \text{GP}\left({\mu }_{kd},{\text{Σ}}_{\eta }^2\right)$$
2. The topic proportions also evolve over time via a $\text{GP}$:

   $${\alpha }_k\sim \text{GP}\left({\mu }_k,{\text{Σ}}_{\alpha }^2\right)$$
3. For each individual $i$, the $\text{GP}$ from which the topic proportions ${\alpha }_{ik}$ are drawn varies depending on the genetic ‘predilection’ ${\gamma }_{ik}$:

   $${\mu }_{ik}={\mu }_k+{\gamma }_{ik}$$

   $${\alpha }_{ik}\sim \text{GP}\left({\mu }_{ik},{\text{Σ}}_{{\alpha }_k}^2\right)$$
4. The disease vocabulary is adjusted for each individual’s ‘warped’ time scale ${\rho }_{ik}$:

   $${\eta }_{kdt}^{\prime }\left(t\right)\left({\rho }_{ik}\right)={\eta }_{kd{t}_{ik}^{\prime }}$$
5. The probability of disease $d$ within topic $k$ at individual-specific ‘warped’ time ${t^{\prime }}^{{\rho }_i}$ is given by the softmax function over the natural parameter $\eta$

   $${\beta }_{kdt}^{\prime }\left(i\right)=\frac{\exp \left({\eta }_{kd{t}_{ik}^{\prime }}\right)}{{\sum }_{d^{\prime }}\exp \left({\eta }_{kd{t}_{ik}^{\prime }}\right)}$$
6. Similarly, the topic proportions for individual $i$ at time $t$ are given by the softmax function over $\alpha$:

   $${\theta }_{ikt}=\frac{\exp \left({\alpha }_{ikt}\right)}{{\sum }_{k^{\prime }}\exp \left({\alpha }_{i{k}^{\prime }t}\right)}$$
7. For each diagnosis $n$ for individual $i$ at time $t$, the topic is chosen according to the multinomial distribution based on $\theta$:

   $$z_{int}\sim \text{Mult}\left({\theta }_{i,\cdot ,t}\right)$$
8. The observed disease $w$ for each diagnosis $n$ is given by:

   $$w_{int}|z_{int},{\beta }_{\cdot ,t}\sim \text{Categorical}\left({\beta }_{kd{t}_{ik}^{\prime }}\right)$$

3.7. Simulating Diagnoses

The process of simulating diagnoses for each individual $i$ at each time point $t$ involves several steps:

1. Simulate Diagnoses Based on Time: For each time point $t$ from 1 to $T$, we calculate the expected number of diagnoses ${\lambda }_{it}$ using a Poisson distribution scaled by time in which we expect a greater number of diagnoses at later time points:

   $${\lambda }_{it}=\frac{𝒳\cdot t}{T}$$

   We then sample the number of diagnoses $N_i$ from a Poisson distribution with mean ${\lambda }_{it}$.

2. Sample Diagnoses and Topics: For each diagnosis $n$ from 1 to $N_i$:

   • Sample a topic $k$ from the individual-specific topic proportions ${\theta }_{ikt}$.
   • Use the time-warping function to adjust the time index for the sampled topic.
   • Sample a disease $d$ from the topic-specific disease probabilities ${\beta }_{kd{t}^{\prime }}$ at the warped time index.

4. Likelihood

4.1. Overview

Our model is trained on data consisting of observed diagnoses by individual and time. The likelihood of the observed data can be derived by considering the probability of observing the diagnoses given the latent variables, which include the topic weights $\left(\theta \right)$, topic loadings $\left(\beta \right)$, genetic warping parameters $\left(\rho \right)$, and genetic predilection parameters $\left(\gamma \right)$. The likelihood is the joint probability of the observed diagnoses given the latent variables. For each individual $i$, time $t$, and diagnosis $n$ for $M$ individuals:

$$ℒ=\prod _{i=1}^M\prod _{t=1}^T\prod _{n=1}^{N_i\left(t\right)}P\left(w_{int}|{\theta }_{ikt},{\beta }_{kdt},{\rho }_{i,k},{\gamma }_{ik}\right).$$

4.2. Likelihood Function

Breaking it down further, we can express the likelihood as follows.

4.2.1. Topic Assignment

The probability of assigning a topic $z_{int}$ given the topic proportions ${\theta }_{ikt}$:

$$P\left(z_{int}=k|{\theta }_{ikt},{\gamma }_{ik}\right)={\theta }_{ikt}$$

4.2.2. Genetic Warping $\left(\rho \right)$

The warping parameter ${\rho }_{i,k}$ affects the time index used in the disease probabilities $\beta$. We can express this as:

$$P\left(w_{int}|z_{int}=k,{\beta }_{kdt},{\rho }_{i,k}\right)={\beta }_{kd\left(W\left(t,{\rho }_{i,k}\right)\right)}$$ (5)

Where $W\left(t,{\rho }_{i,k}\right)$ is the warping function that transforms the original time $t$ based on the individual’s genetic warping parameter.

4.2.3. Genetic Predilection $\left(\gamma \right)$

The genetic predilection parameter ${\gamma }_{ik}$ influences the individual-specific topic proportions ${\theta }_{ikt}$. We can incorporate this into the likelihood as:

$$P\left(z_{int}=k|{\theta }_{ikt},{\gamma }_{ik}\right)={\theta }_{ikt}=\text{softmax}\left({\alpha }_{ikt}+{\gamma }_{ik}\right)$$ (6)

Where ${\alpha }_{ikt}$ is the population-level topic weight and ${\gamma }_{ik}$ is the individual’s genetic predilection for topic $k$.

4.2.4. Diagnosis Probability

Incorporating both genetic parameters, we can express the full likelihood for an individual $i$ as:

$${ℒ}_i=\prod _t\prod _n\left(\sum _k\text{softmax}\left({\alpha }_{ikt}+{\gamma }_{ik}\right)\cdot {\beta }_{kd\left(W\left(t,{\rho }_{i,k}\right)\right)}\right)$$ (7)

This formulation shows how both the topic selection and disease probabilities are influenced by the individual’s genetic parameters.

The probability of observing a diagnosis $w_{int}$ given the topic assignment $z_{int}$ and the topicspecific disease probabilities ${\beta }_{kdt}$. This involves the genetic warping function to obtain the appropriate $\beta$ at the warped time index:

$$P\left(w_{int}|z_{int}=k,{\beta }_{kdt},{\rho }_{i,k}\right)={\beta }_{k{d}_{W\left(t,{\rho }_{i,k}\right)}}.$$

Putting it all together, the joint likelihood for an individual $i$ can be written as:

$${ℒ}_i=\prod _{t=1}^T\prod _{n=1}^{N_i(t)}\left(\sum _{k=1}^K{\theta }_{ikt}{\beta }_{k{d}_{W\left(t,{\rho }_{i,k}\right)}}\right),$$

and the overall likelihood for the entire dataset is then the product over all individuals:

$ℒ=\prod _{i=1}^M{ℒ}_i=\prod _{i=1}^M\prod _{t=1}^T\prod _{n=1}^{N_i\left(t\right)}\left(\sum _{k=1}^K{\theta }_{ikt}{\beta }_{k{d}_{W\left(t,{\rho }_{i,k}\right)}}\right).$

5. Posterior Updates for Bayesian Inference

The model specification just described can be used to implement Bayesian inference and evaluate posterior distributions of all the latent variables and unknown parameters. As this is computationally very challenging for high-dimensional real-life EHR data, we implement here a practical approximation that leverages estimates developed in previous work to estimate population parameters, and allows us to focus on novel aspect of time dependencies and warping.

5.1. Updating individual topic probabilities

Considering individual patients, an important step clinically is the evaluation of the posterior probability that patient $i$‘s diagnosis $w_{int}$ at time $t$ is manifesting as a result of the action of topic $k$, based on their previous history of diagnoses. Using Bayes’ rule, this posterior probability is updated as follows:

$$P\left(z_{int}=k|w_{int},{\theta }_{\text{previous}},{\gamma }_d,{\beta }_d\right)\sim {\beta }_{kdt}\cdot P\left(z_{int}=k{\theta }_{previous},{\gamma }_d\right).$$

where ${\theta }_{previous}=\left({\theta }_{i\cdot 1},\dots ,{\theta }_{i\cdot t-1}\right)$. Also we assume that $w_{int}$ is the sole diagnosis at time $t$ for patient $i$. Multiple diagnosis updates follow the same logic, not spelled out here for brevity. This allows us to use the new diagnoses at any point in time to compute dynamic updates of an individuals’ disease probability.

5.2. Parameter Estimation

In practice, we apply a novel algorithm to update the posterior distribution over topic weights for a given set of diagnoses:

1. Initialization of ${\theta }_{ik}\left(t\right)$:

   We first initialize the estimated ${\theta }_{ik}\left(t\right)$ at time $t=1:3$ by drawing from a Dirichlet distribution:

   $${\theta }_{ik}(1:3)\sim \text{Dirichlet}\left(\alpha ,K\right)$$

   where $\alpha$ is chosen to be greater than 1 to ensure relatively uniform values across the $K$ topics.

2. Predicted $\text{GP}$ Mean:

   The predicted $\text{GP}$ mean, ${\mu }_{ki}$, is initialized using the estimated ${\theta }_{ik}\left(t\right)$ values at time $t=1:3$. The population predicted mean is also set to this value.

3. Gaussian Process Fit from time point 4 to T:

   A Gaussian Process $\left(\text{GP}\right)$ is fit using the estimated ${\theta }_{ik}\left(t\right)$ at time points $t=1:3$ to predict ${\theta }_{ik}\left(t\right)$ at time $t=4$, for both the individual and the population.

4. Subsequent Time Points:

   For each subsequent time point $t$, a Gaussian Process is fit to the estimated ${\theta }_{ik}\left(t\right)$ at time points $t=1:\left(t-1\right)$. This fit is treated as the prior prediction for ${\theta }_{ik}\left(t\right)$. The $\text{GP}$ is fit for both the population (i.e., $\text{GP}$ on $E\left({\theta }_{ik}\left(1:T-1\right)\right)$) and the individual (i.e., $\text{GP}$ on ${\theta }_{ik}\left(1:T-1\right)$).

5. Adjusted $\mathbf{\text{G}}P$ Mean:

   The adjusted $\text{GP}$ mean at time $t$ is obtained by a weighted average of the population $\text{GP}$ mean and the individual $\text{GP}$ mean.

6. Likelihood of New Diagnoses:

   For patients with new diagnoses at time $t$, the likelihood of the diagnoses is calculated as:

   $$P\left(z_t|w\right)=\prod _{d}P\left({\beta }_{kd}|Z=k\right)$$

   where ${\beta }_{kd}$ represents the disease-specific parameters given the topic $k$.

7. Combination of Prior Prediction and Likelihood:

   The prior prediction is combined with the likelihood by adding the log of the adjusted $\text{GP}$ mean and log-likelihood, then exponentiating the result to obtain the final estimate for ${\theta }_{ik}\left(t\right)$:

   $${\text{estimate}}_{{\theta }_{ik}\left(t\right)}=\exp .$$

Additional Parameters in detailed methods:

5.3. Algorithm for Posterior Updates for $\theta$

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm}}1\text{Posterior}\text{Updates}\text{for}\theta \text{Given}\beta \text{and}\text{Observed}\text{Diagnoses}}\\ \text{1:}\mathbf{\text{Input}}:\text{Previous}\text{GP}\text{predictions}\text{of}\theta \text{,}\text{genetic}\text{warping}\text{parameters}{\rho }_{i,k}\text{,}\text{genetic}\text{predilection}\\ \text{parameters}{\gamma }_{ik}\text{,}\text{observed}\text{diagnoses}D\text{,}\text{disease}\text{probabilities}\beta \\ \text{2:}\mathbf{\text{Output}}:\text{Updated}\theta \\ \text{3:}\mathbf{\text{for}}\text{each}\text{time}\text{point}t\mathbf{\text{do}}\\ \text{4:}\text{Update}\text{population}\text{GP}\text{means}{\mu }_{kt}\\ \text{5:}{\mu }_{kt}\leftarrow \text{fit\_gp}\left(1:\left((t-1\right),\text{mean}\left(estimated\_Theta\left[:,:,1:\left(t-1\right)\right]\right),\sigma \right)\\ \text{6:}\mathbf{\text{for}}\text{each}\text{individual}i\mathbf{\text{do}}\\ \text{7:}\text{Update}\text{individual}\text{GP}\text{means}{\mu }_{ikt}\\ \text{8:}{\mu }_{ikt}\leftarrow \text{fit\_gp}\left(1:\left(t-1\right),estimated\_Theta\left[i,:,1:\left(t-1\right)\right],\sigma \right)\\ \text{9:}\text{Compute}\text{individual}\text{weight}{w}_i\\ \text{10:}adjusted\_gp\_mean\left[i,:,t\right]\leftarrow w_i\cdot {\mu }_{ikt}+\left(1-w_i\right)\cdot {\mu }_{kt}\\ \text{11:}\text{Retrieve}\text{current}\text{diagnoses}\text{data}\text{for}\text{individual}i\\ \text{12:}diagnosis\text{\_}indices\leftarrow \text{map\_diagnoses}\left(diagnoses\text{\_}codes,list\text{\_}of\text{\_}diseases\right)\\ \text{13:}\text{Compute}\text{likelihood}\\ \text{14:}likelihood\leftarrow \prod \left(\beta \left[W\left(t,{\rho }_{i,k}\right)\text{,}diagnosis\text{\_}indices\right]\right)\\ \text{15:}\text{Update}\text{log}\text{proportions}\\ \text{16:}updated\text{\_}log\text{\_}proportions\leftarrow \log \left(\text{likelihood}\right)+\log \left(adjusted\text{\_}gp\text{\_}mean\left[i,:,t\right]\right)\\ \text{17:}\text{Normalize}\\ \text{18:}updated\_proportions\leftarrow \exp \left(updated\text{\_}log\text{\_}proportions\right)\text{/}\sum \left(\exp \left(updated\text{\_}log\text{\_}proportions\right)\right)\\ \text{19:}estimated\_Theta\left[i,:,t\right]\leftarrow updated\_proportions\\ \text{20:}\mathbf{\text{end}}\mathbf{\text{for}}\\ \text{21:}\mathbf{\text{end}}\mathbf{\text{for}}\end{array}}}$$

5.4. Algorithm for Posterior Updates for $\beta$ Given $\theta$

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm}}\text{2}\text{Posterior}\text{Updates}\text{for}\beta \text{Given}\theta }\\ \text{1:}\mathbf{\text{Input:}}\text{Fixed}\theta \text{,}\text{genetic}\text{warping}\text{parameters}{\rho }_{i,k}\text{,}\text{observed}\text{diagnoses}D\\ \text{2:}\mathbf{\text{Output:}}\text{Updated}\beta \\ \text{3:}\text{Initialize}\text{diagnosis\_counts}\text{and}\text{count\_array}\text{with}\text{zeros}\\ \text{4:}\mathbf{\text{for}}\text{each}\text{individual}i\mathbf{\text{do}}\\ \text{5:}\mathbf{\text{for}}\text{each}\text{topic}k\mathbf{\text{do}}\\ \text{6:}\mathbf{\text{for}}\text{each}\text{time}\text{point}t\mathbf{\text{do}}\\ \text{7:}\text{Compute}\text{original}\text{time}\text{index}\text{og\_time}=W\left(t,{\rho }_{i,k}\right)\\ \text{8:}\text{Retrieve}\text{diagnoses}\text{at}\text{time}t\text{for}\text{individual}i\\ \text{9:}\text{Update}\text{diagnosis\_counts}\text{and}\text{count\_array}\text{for}\text{each}\text{diagnosis}\\ \text{10:}\mathbf{\text{end}}\mathbf{\text{for}}\\ \text{11:}\mathbf{\text{end}}\mathbf{\text{for}}\\ \text{12:}\mathbf{\text{end}}\mathbf{\text{for}}\\ \text{13:}\text{Compute}\beta \text{as}\text{the}\text{normalized}\text{counts}\\ \text{14:}\mathbf{\text{for}}\text{each}\text{topic}k\mathbf{\text{do}}\\ \text{15:}\mathbf{\text{for}}\text{each}\text{time}\text{point}t\mathbf{\text{do}}\\ \text{16:}\text{Normalize}{\beta }_{kdt}\text{using}\text{the}\text{softmax}\text{function}\\ \text{17:}\mathbf{\text{end}}\mathbf{\text{for}}\\ \text{18:}\mathbf{\text{end}}\mathbf{\text{for}}\end{array}}}$$

5.4.1. Data

Our primary analyses are in the UK Biobank and AllofUs data sets.

UK Biobank

The UK Biobank has collected detailed health and genetic data from approximately 500,000 participants aged 40 to 69 years, recruited between 2006 and 2010. Here, we assemble EHR data for 421,707 participants with at least one EHR diagnosis recorded between the ages of 28 and 81 from 1981 forward [9], [10]. The HESIN EHR data includes coded clinical events, consultations, diagnoses, procedures, and laboratory tests, using coding systems such as READ2, CTV-3, BNF and DM + D. Furthermore, hospital inpatient data, which covers admissions, diagnoses, procedures, and discharge information, is available for the entire cohort and is coded using ICD-9, ICD-10, OPCS-3, and OPCS-4. The UK Biobank also links to national death and cancer registries to provide comprehensive health outcomes data.

All of Us

The All of Us Research Program is a diverse biomedical dataset from the United States. Currently, more than 460,000 participants have consented to share their electronic health records (EHR), with approximately 55% of these records already integrated into the program data set [11]. We used data from 239,200 people who contributed both EHR and genomic information [12]. The EHR data in All of Us include information from various health domains such as conditions, procedures, drugs, and measurements, which are standardized using vocabularies such as SNOMED, LOINC, and ICD codes. Here we use ICD10 codes harmonized to the 349 codes used in the UK Biobank.

6. Results

6.1. Model Assessment: Updated Patient Weights

In this section, we evaluate our model fit in comparison to a time-fixed weight approach, which estimates weights only once based on available information. We first demonstrate the comparison between the true weights of the topic and the estimated weights at the population level.

We demonstrate the improvement in predicted theta using our approach to a fixed weight $\left(\theta \right)$ approach.

6.2. Performance Metrics

To evaluate the performance of our predictive model, we calculate the following metrics: accuracy, precision, recall, and F1-score. These metrics are defined as follows:

Accuracy

Accuracy is the ratio of correctly predicted diagnoses to the total number of true diagnoses. It is given by:

$$\text{Accuracy}=\frac{\text{True}\text{Positives}}{\text{Total}\text{True}\text{Diagnoses}}$$

Precision

Precision is the ratio of correctly predicted diagnoses to the total number of predicted diagnoses. It is given by:

$$\text{Precision}=\frac{\text{True}\text{Positives}}{\text{True}\text{Positives}+\text{False}\text{Positives}}$$

Recall

Recall, also known as sensitivity or true positive rate, is the ratio of correctly predicted diagnoses to the total number of actual true diagnoses. It is given by:

$$\text{Recall}=\frac{\text{True}\text{Positives}}{\text{True}\text{Positives}+\text{False}\text{Negatives}}$$

F1-Score

The F1-Score is the harmonic mean of precision and recall. It provides a balance between precision and recall and is given by:

$$\text{F1-Score}=2\cdot \frac{\text{Precision}\cdot \text{Recall}}{\text{Precision}+\text{Recall}}$$

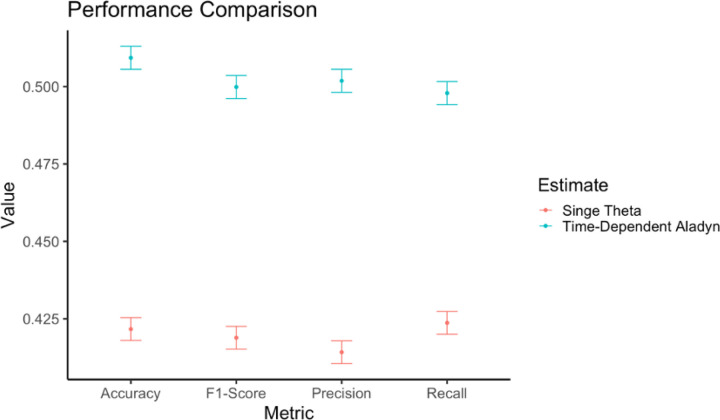
In simulations, we find that the accuracy, precision, and recall are superior with Aladyn as opposed to a fixed weight approach when comparing to true topic identifiers and using simulated diagnoses:

6.3. Disease Loadings and Time Varying Weights

We demonstrate the clarity of estimated $\beta$ for known topics ??. In brief, as in the algorithm above, we map all simulated disease counts to the unwarped time for an individual, and weight by the expected topic time varying contribution of each individual. We note that this differs fundamentally from existing approaches which only estimate weight once.

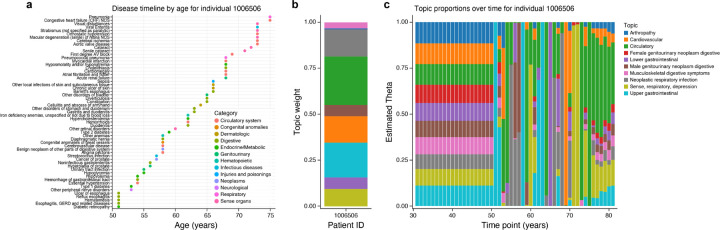
Subsequently, we evaluated the results derived from the application of time-varying weights to actual diagnoses (Figure 8). Several key distinctions are observed from existing methodologies. In particular, Aladyn exhibits the proficiency to identify population-level trajectories even amidst sparse population-level data. With the advent of new diagnoses, Aladyn refines the previously estimated weights by incorporating these new diagnoses with the topics that most effectively enhance the likelihood of the specific diagnoses. The ‘memory’ of prior diagnoses is sustained through the Gaussian process.

Figure 8: Time Varying Weights.

Here we demonstrate the actual age of diagnoses for a sample patient in the UK Biobank. We demonstrate the fit using Aladyn, and using a traditional fixed weight approach according to ATM ([1]).

Furthermore, we can see that 65.4% of the population has a shift of more than 10% and 50% of the time, the shift is greater than 11.5% (Figure S7).

6.4. Biological Meaning of Topic Weights

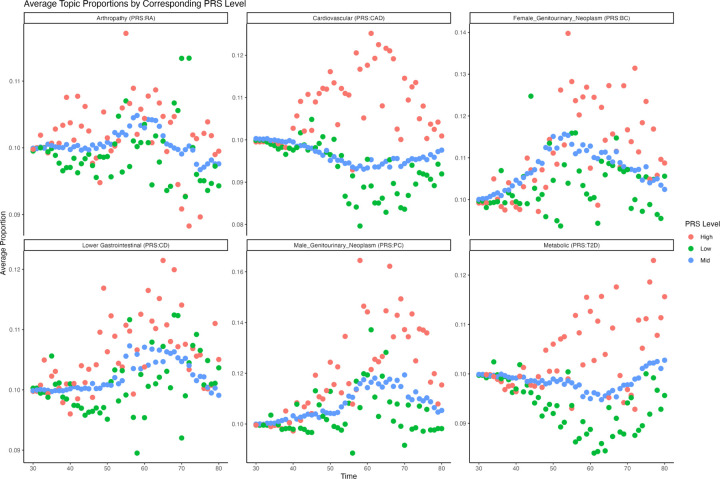
Our findings substantiate the identified warping, as temporal variations in weight reveal that individuals within the top and bottom 20% of the polygenic risk exhibit earlier (later) predictions of disease onset under our model. Furthermore, we show that individuals with true high genetic risk are highly enriched in topic weights for the expected topics when we use a cardinal polygenic risk score (PRS) as the target PRS from which to assess enrichment.

6.5. Improved Accuracy and Flexibility

Here we show the variation in topic weights when compared with a model that uses time-fixed weights. We first ask, for each condition diagnosed in real data, what proportion of the time did our model Aladyn assign to the diagnosis a time-weighted marginal probability greater than 10%, how often did the competing ATM (age dependent topic model, [1]) do so. Furthermore, we compare the nominal percentage assigned for real diagnoses.

To facilitate exploration of a dynamic time-varying model’s, we have developed and interactive web application available at https://surbut.shinyapps.io/forapp/. This tool allows users to visualize the important diseases for each topic in the UK Biobank, All of US https://surbut.shinyapps.io/aouapp/ and Mass General Brigham Biobank https://surbut.shinyapps.io/mgb_topic/.

Furthermore, we have created an app at https://surbut.shinyapps.io/dynamic_ehr/ that allows users to simulate warping, time-varying weights, and unique trajectories in real-time, providing an intuitive understanding of the Aladyn model’s functionality.

7. Limitations and Future Work

While the Aladyn model demonstrates promising outcomes, it is crucial to recognize its current limitations and potential areas for future enhancement. Model Implementation: The present iteration of Aladyn utilizes estimated loadings derived from extant dynamic topic models (i.e., [1, 6]). Individualized risk assessment is feasible by using externally estimated parameters and functions pertinent to the general population, with a focus on modeling individual variation. Nevertheless, further research would be beneficial to fully implement the model’s proprietary Bayesian learning of these loadings. The incorporation of multiple Gaussian processes and Bayesian updates within the model necessitates significant computational resources. Optimizing these algorithms for large-scale datasets remains an ongoing challenge. Although the data demonstrate superior performance relative to an existing age-dependent topic model, additional validation is recommended against a broader spectrum of state-of-the-art methodologies. Despite utilizing data from both the UK Biobank and All of Us, further evaluation on diverse populations is required to ensure the model’s wide-ranging applicability. First, there is a need to develop more efficient computational methods to handle larger datasets. This reflects on the computational challenges associated with the model and aims at improving its performance and scalability. Second, the plan includes conducting comprehensive comparisons with other leading disease progression models. This involves evaluating the performance of the Aladyn model against other models to identify strengths and weaknesses. In addition, there will be investigations into how well the model performs across a broader range of populations and disease types, ensuring its applicability and robustness in various scenarios. These efforts are aimed at addressing current limitations and expanding the model’s usability and accuracy.

8. Discussion

This modeling paradigm integrates population trends with individual genetic variations, elucidating commonalities and divergences in disease progression. The described generative model is governed by two population-level parameters: the evolution of topic weights $\left(\alpha \right)$ and disease loadings $\left(\eta \right)$. These parameters are inferred from topic- or disease-specific Gaussian processes characterized by their respective mean and covariance structures. The covariance pattern is modulated by a Gaussian kernel, ensuring that temporally adjacent points exhibit higher correlation. Crucially, genetic factors modulate individual variations through topic weights, influenced by both the population mean and individual predisposition $\left({\gamma }_{ik}\right)$, and the progression scale of a topic-specific disease, regulated by a ‘warping coefficient’ $\left({\rho }_{ik}\right)$. Topic weights and disease loadings undergo softmax normalization to ensure they form a valid probability distribution. At each time point, a latent indicator is selected based on an individual’s time-specific topic probabilities $\left({\theta }_{ik}\right)$, which subsequently determines the vector of time-specific disease probabilities $\left({\beta }_{ik{t}^{\prime }}\right)$ that dictates the observed diagnostic outcome. The diagnostic outcome is generated in accordance with the topic’s population-specific vector of disease probabilities, modulated by the individual’s warping parameter. By leveraging Gaussian processes and Bayesian updates, the model provides dynamic, personalized disease predictions. We demonstrate that the integration of genetic data with hierarchical models facilitates the amalgamation of population-level learning with individual-level prediction, thereby enhancing predictive accuracy and enabling the discovery of novel topics. We provide the results of the implementation on the dynamic topic model loadings ([6] in the UKB in supplementary figures 17–26).

The ethical implications of using genetic data for disease prediction are significant and warrant careful consideration. While Aladyn offers powerful predictive capabilities, it’s crucial to ensure that its implementation respects patient privacy, avoids genetic discrimination, and considers the psychological impact of early disease predictions. Future work should include collaborations with bioethicists to develop guidelines for the responsible use of such models in clinical settings. To promote transparency and facilitate further research, we have made the simulation code for Aladyn available on GitHub https://surbut.github.io/dynamic_ehr. We encourage the scientific community to explore, validate, and build upon our work.

Data Availability Statement

All simulations and a didactic tutorial on our model can be found at: https://bookdown.org/sarahmurbut/dynamic_ehr/. An interactive application to simulate warping, time varying weights and unique trajectories in real time can be found at: https://surbut.shinyapps.io/dynamic_ehr/.

Figure 3: Warping.

Here we demonstrate how an individual of low genetic risk will have disease probabilities ascertained from younger ages at present time, and those of high genetic risk will have probabilities of later times pushed forward. We demonstrate this behavior from our model fit on three chosen diseases.

Figure 4: Gaussian Process for Topic Weights influenced by population and individual level trajectory.

Here we demonstrate the population level trajectory and the individual predilection for a given topic.

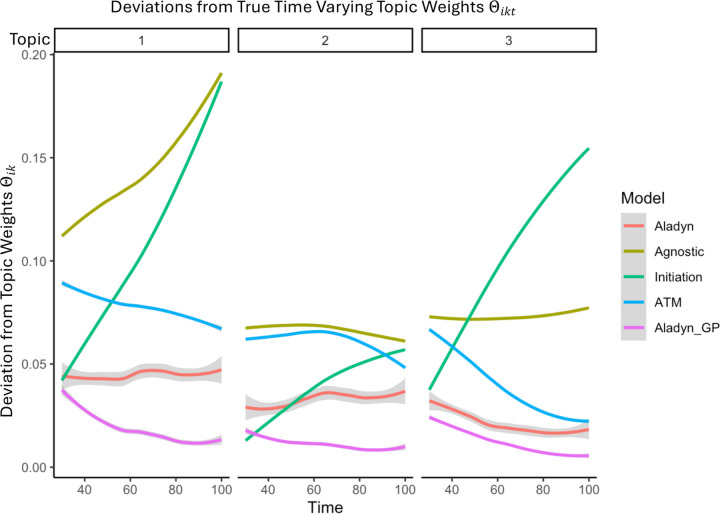
Figure 6: Delta.

Over 100 time points, we demonstrate the deviations between an approach that uses a flat estimate of ${\theta }_{ik}$ as 1/K (agnostic), an approach that uses the initiation value of ${\theta }_{ik}$ (initiation), an approach ‘ATM’ that uses the average ${\theta }_{ik}$ over all time points ([1]) and two versions of Aladyn.

Figure 7: Performance Assessment.

We demonstrate the Accuracy, Precision, Recall and F1 score of simulations using Aladyn and a fixed weight approach. Terms defined in text.

Figure 9: Marginal Probability.

Here we show that the marginal probability of disease is shifted for those with varying levels of genetic risk.

Table 1:

Notation for observed data and latent disease topics.

$D$	Number of possible diagnoses, indexed by $d$
$M$	Number of individual patients, indexed by $i$
$N_i$	Total number of diagnoses per patient
$T$	Number of possible time points, indexed by $t$
$w_{idt}$	Observed diagnosis indicator for disease $d$ patient $i$
$K$	Number of postulated topics (comorbidity profiles) indexed by $k$
$z_{idt}$	Latent (i.e. unobserved) index of the topic for diagnosis $d$ in patient $i$ at time $t$

Table 2:

Observed and Latent Variables

Observed Variables
$w_{int}$	Observed diagnosis for individual $i$ at diagnosis $n$ and time $t$
Latent Variables
${\theta }_{ikt}$	Individual-specific topic proportions at time $t$
${\beta }_{kdt}$	Topic-specific disease probabilities at time $t$
${\rho }_{i,k}$	Genetic warping parameters for individual $i$ and topic $k$
${\gamma }_{ik}$	Genetic predilection parameters for individual $i$ and topic $k$
$z_{int}$	Latent topic assignment for each diagnosis $w_{int}$

Table 3: Comparison of Model Accuracy and Probability of True Disease.

Proportion Correct is the proportion of Time Model Assigns True Disease Higher Probability. Delta is the difference in probability assigned by Aladyn vs ATM

Model	Accuracy	Proportion Correct	Delta
ATM	0.01	0.21	2.60
Aladyn	0.15	0.79	NA

Impact Statement.

Our model significantly advances healthcare for aging populations by facilitating the early identification of high-risk individuals through the analysis of their unique disease trajectories within complex comorbidity patterns. Existing models are limited in their capacity to manage diverse comorbidity patterns, particularly those that are time-dependent. We introduce an approach leveraging Bayesian hierarchical modeling to concurrently learn population-level patterns and provide updated real-time predictions across 350 diseases, thereby uncovering and forecasting intricate comorbidity patterns. This methodology paves the way for preventive measures and targeted interventions that enhance health outcomes, mitigate late-stage disease burdens, and foster healthier aging. Furthermore, our model incorporates genetic influences via a genetic predisposition parameter to estimate the lifetime risk of specific diseases and disorders, alongside a time-warping function to facilitate personalized predictions of disease trajectories.

Funding Statement

S.M.U. is supported by T32HG010464 from the National Human Genome Research Institute. A.G. is supported by National Institutes of Health (NIH) grant nos R01CA227237, R01CA244569 and R21HG010748, and awards from the Claudia Adams Barr Foundation, Louis B. Mayer Foundation, Doris Duke Charitable Foundation, Emerson Collective and Phi Beta Psi Sorority. P.N. is supported by grants R01HL1427, R01HL148565, and R01HL148050 from the National Heart, Lung, and Blood Institute, and grant 1U01HG011719 from the National Human Genome Research Institute.