Skip to main content
PMC home page
Biochemical Journal logoLink to Biochemical Journal
. 1982 May 1;203(2):351–360. doi: 10.1042/bj2030351

Half-time analysis of the integrated Michaelis equation. Simulation and use of the half-time plot and its direct linear variant in the analysis of some α-chymotrypsin-, papain- and fumarase-catalysed reactions

Christopher W Wharton 1, Ronald J Szawelski 1
PMCID: PMC1158237  PMID: 7115291

Abstract

Substitution of half-time parameters in the integrated form of the Michaelis–Menten equation for any enzyme-catalysed reaction yields an equation that gives a linear relationship between the half-time of the reaction and the substrate concentration at that point of the reaction. The logarithmic term of the integrated equation becomes a constant as a result of the substitution, which means that the use of the half-time plot of the equation requires calculation only of half-time and substrate-concentration values at various stages of the reaction. The half-time method is both simple and exact, being analogous to an [S0]/vi against [S0] plot. A direct linear form of the half-time plot has been devised that allows very simple estimation of Michaelis parameters and/or initial velocities from progress-curve data. This method involves no approximation and is statistically valid. Simulation studies have shown that linear-regression analysis of half-time plots provides unbiased estimates of the Michaelis parameters. Simulation of the effect of error in estimation of the product concentration at infinite time [P∞] reveals that this is always a cause for concern, such errors being magnified approximately an order of magnitude in the estimate of the Michaelis constant. Both the half-time plot and the direct linear form have been applied to the analysis of a variety of experimental data. The method has been shown to produce excellent results provided certain simple rules are followed regarding criteria of experimental design. A set of rules has been formulated that, if followed, allows progress-curve data to be acquired and analysed in a reliable fashion. It is apparent that the use of modern spectrophotometers in carefully designed experiments allows the collection of data characterized by low noise and accurate [P∞] estimates. [P∞] values have been found, in the present work, to be precise to within ±0.2% and noise levels have always been below 0.1% (signal-to-noise ratio≃1000). As a result of the considerations above, it is concluded that there is little to be feared with regard to the analysis of enzyme kinetics using complete progress curves, despite the generally lukewarm recommendations to be found in the literature. The saving in time, materials and experimental effort amply justify analysis of enzyme kinetics by progress-curve methods. Half-time plots linear to ≥90% of reaction have been obtained for some α-chymotrypsin-, papain- and fumarase-catalysed reactions.

Full text

PDF
354

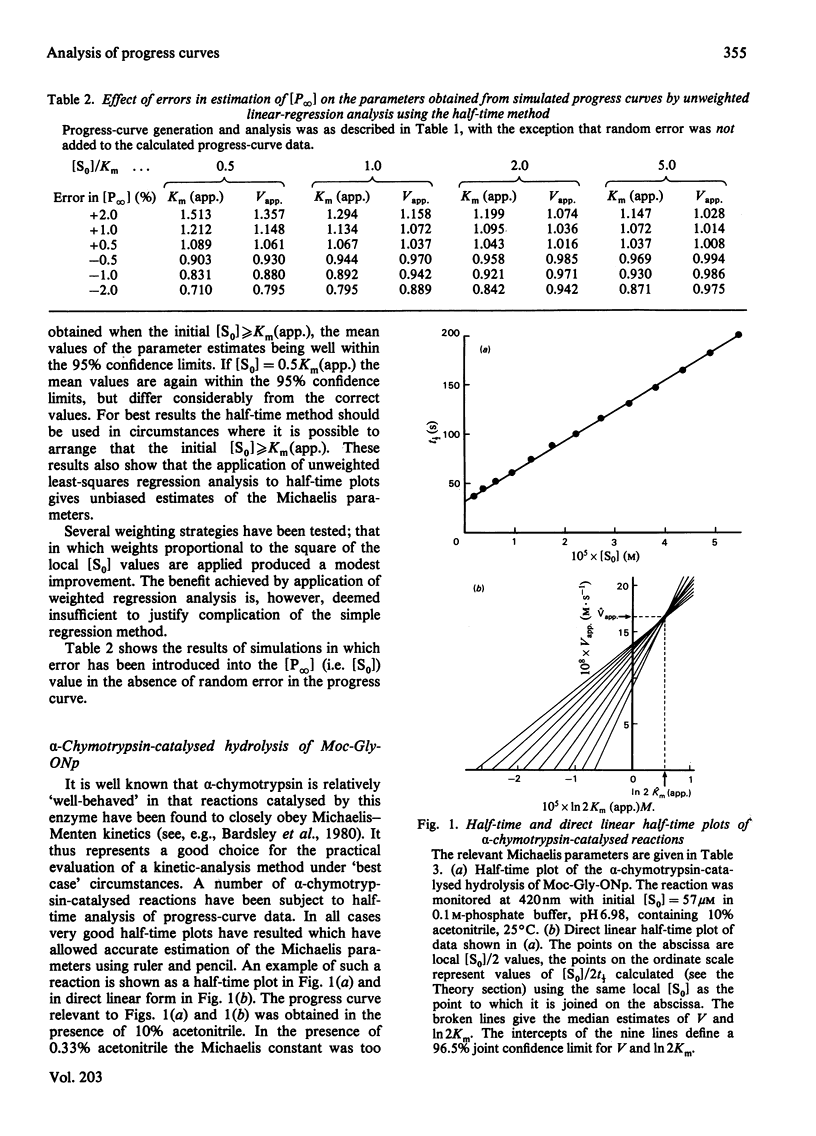
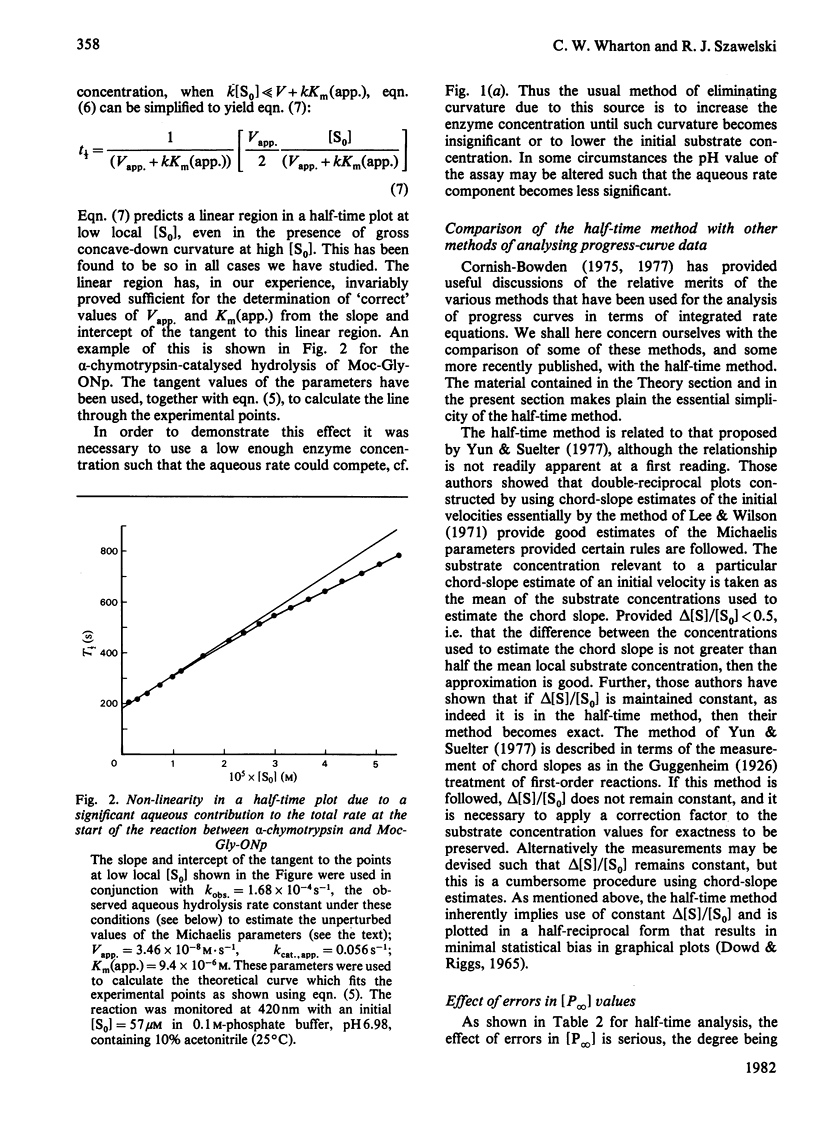
Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Alberty R. A., Bock R. M. Alteration of the Kinetic Properties of an Enzyme by the Binding of Buffer, Inhibitor, or Substrate. Proc Natl Acad Sci U S A. 1953 Sep;39(9):895–900. doi: 10.1073/pnas.39.9.895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Andersen B. Lack of deviation from Michaelis--Menten kinetics for pig heart fumarase. Biochem J. 1980 Sep 1;189(3):653–654. doi: 10.1042/bj1890653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Atkins G. L., Nimmo I. A. The reliability of Michaelis constants and maximum velocities estimated by using the integrated Michaelis-Menten equation. Biochem J. 1973 Dec;135(4):779–784. doi: 10.1042/bj1350779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Baines B. S., Brocklehurst K. A necessary modification to the preparation of papain from any high-quality latex of Carica papaya and evidence for the structural integrity of the enzyme produced by traditional methods. Biochem J. 1979 Feb 1;177(2):541–548. doi: 10.1042/bj1770541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bardsley W. G., Leff P., Kavanagh J., Waight R. D. Deviations from Michaelis-Menten kinetics. The possibility of complicated curves for simple kinetic schemes and the computer fitting of experimental data for acetylcholinesterase, acid phosphatase, adenosine deaminase, arylsulphatase, benzylamine oxidase, chymotrypsin, fumarase, galactose dehydrogenase, beta-galactosidase, lactate dehydrogenase, peroxidase and xanthine oxidase. Biochem J. 1980 Jun 1;187(3):739–765. doi: 10.1042/bj1870739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bartha F. Effect of error of the quasi-steady-state approximation on the estimation of KM and Vm from a single time curve. J Theor Biol. 1980 Sep 7;86(1):105–115. doi: 10.1016/0022-5193(80)90068-5. [DOI] [PubMed] [Google Scholar]
  7. Bates D. J., Frieden C. Full time course studies on the oxidation of reduced coenzyme by bovine liver glutamate dehydrogenase. Use of computer simulation to obtain rate and dissociation constants. J Biol Chem. 1973 Nov 25;248(22):7885–7890. [PubMed] [Google Scholar]
  8. Bates D. J., Frieden C. Treatment of enzyme kinetic data. 3. The use of the full time course of a reaction, as examined by computer simulation, in defining enzyme mechanisms. J Biol Chem. 1973 Nov 25;248(22):7878–7884. [PubMed] [Google Scholar]
  9. Cornish-Bowden A., Eisenthal R. Statistical considerations in the estimation of enzyme kinetic parameters by the direct linear plot andother methods. Biochem J. 1974 Jun;139(3):721–730. doi: 10.1042/bj1390721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cornish-Bowden A. The use of the direct linear plot for determining initial velocities. Biochem J. 1975 Aug;149(2):305–312. doi: 10.1042/bj1490305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. DOWD J. E., RIGGS D. S. A COMPARISON OF ESTIMATES OF MICHAELIS-MENTEN KINETIC CONSTANTS FROM VARIOUS LINEAR TRANSFORMATIONS. J Biol Chem. 1965 Feb;240:863–869. [PubMed] [Google Scholar]
  12. Darvey I. G., Shrager R., Kohn L. D. Integrated steady state rate equations and the determination of individual rate constants. J Biol Chem. 1975 Jun 25;250(12):4696–4701. [PubMed] [Google Scholar]
  13. Duggleby R. G., Morrison J. F. Progress curve analysis in enzyme kinetics: model discrimination and parameter estimation. Biochim Biophys Acta. 1978 Oct 12;526(2):398–409. doi: 10.1016/0005-2744(78)90131-6. [DOI] [PubMed] [Google Scholar]
  14. Duggleby R. G., Morrison J. F. The analysis of progress curves for enzyme-catalysed reactions by non-linear regression. Biochim Biophys Acta. 1977 Apr 12;481(2):297–312. doi: 10.1016/0005-2744(77)90264-9. [DOI] [PubMed] [Google Scholar]
  15. ELLMAN G. L. Tissue sulfhydryl groups. Arch Biochem Biophys. 1959 May;82(1):70–77. doi: 10.1016/0003-9861(59)90090-6. [DOI] [PubMed] [Google Scholar]
  16. Eisenthal R., Cornish-Bowden A. The direct linear plot. A new graphical procedure for estimating enzyme kinetic parameters. Biochem J. 1974 Jun;139(3):715–720. doi: 10.1042/bj1390715. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Klesov A. A., Berezin I. V. Primenie integral'noi formy uravneniia skorosti dlia opredeleniia kineticheskikh konstant fermentativnykh reaktsii. Biokhimiia. 1972 Jan-Feb;37(1):170–183. [PubMed] [Google Scholar]
  18. Lee H. J., Wilson I. B. Enzymic parameters: measurement of V and Km. Biochim Biophys Acta. 1971 Sep 22;242(3):519–522. doi: 10.1016/0005-2744(71)90144-6. [DOI] [PubMed] [Google Scholar]
  19. Newman P. F., Atkins G. L., Nimmo I. A. The effect of systematic error on the accuracy of Michaelis constants and maximum velocities estimated by using the integrated Michaelis-Menten equation. Biochem J. 1974 Dec;143(3):779–781. doi: 10.1042/bj1430779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. SCHONBAUM G. R., ZERNER B., BENDER M. L. The spectrophotometric determination of the operational normality of an alpha-chymotrypsin solution. J Biol Chem. 1961 Nov;236:2930–2935. [PubMed] [Google Scholar]
  21. Schwert G. W. Use of integrated rate equations in estimating the kinetic constants of enzyme-catalyzed reactions. J Biol Chem. 1969 Mar 10;244(5):1278–1284. [PubMed] [Google Scholar]
  22. Selwyn M. J. A simple test for inactivation of an enzyme during assay. Biochim Biophys Acta. 1965 Jul 29;105(1):193–195. doi: 10.1016/s0926-6593(65)80190-4. [DOI] [PubMed] [Google Scholar]
  23. Stayton M. M., Fromm H. J. A computer analysis of the validity of the integrated Michaelis-Menten equation. J Theor Biol. 1979 Jun 7;78(3):309–323. doi: 10.1016/0022-5193(79)90333-3. [DOI] [PubMed] [Google Scholar]
  24. Yun S. L., Suelter C. H. A simple method for calculating Km and V from a single enzyme reaction progress curve. Biochim Biophys Acta. 1977 Jan 11;480(1):1–13. doi: 10.1016/0005-2744(77)90315-1. [DOI] [PubMed] [Google Scholar]

Articles from Biochemical Journal are provided here courtesy of The Biochemical Society

RESOURCES