Kinefold web server for RNA/DNA folding path and structure prediction including pseudoknots and knots

Abstract

The Kinefold web server provides a web interface for stochastic folding simulations of nucleic acids on second to minute molecular time scales. Renaturation or co-transcriptional folding paths are simulated at the level of helix formation and dissociation in agreement with the seminal experimental results. Pseudoknots and topologically ‘entangled’ helices (i.e. knots) are efficiently predicted taking into account simple geometrical and topological constraints. To encourage interactivity, simulations launched as immediate jobs are automatically stopped after a few seconds and return adapted recommendations. Users can then choose to continue incomplete simulations using the batch queuing system or go back and modify suggested options in their initial query. Detailed output provide (i) a series of low free energy structures, (ii) an online animated folding path and (iii) a programmable trajectory plot focusing on a few helices of interest to each user. The service can be accessed at http://kinefold.curie.fr/.

INTRODUCTION

The prediction of RNA secondary structures with no known homologous sequences has been traditionally performed through free energy minimization using efficient ‘dynamic programming’ algorithms (1–6). These approaches and recent developments combining thermodynamic and homology information have now been interfaced by a number of web servers for RNA/DNA structure prediction (7–11).

Simulations of nucleic acid folding paths (12–19) can complement these primary thermodynamic approaches and provide interesting insights into DNA/RNA folding dynamics. Applications include, in particular, anomalous hybridization kinetics on DNA chips and structural rearrangements of non-coding RNA regions involved in (post)-transcriptional regulation of genetic expression.

The Kinefold web server performs online stochastic folding simulations of nucleic acids using the folding dynamics algorithm introduced by Isambert and Siggia (17) and further enhanced by the ‘exactly clustered stochastic simulation’ algorithm detailed by Xayaphoummine et al. (19). The web server was launched at Institut de Physique (Strasbourg, France) in August 2002 and operated there until August 2004, when it was relocated at Institut Curie (Section de Recherche, Paris, France).

Early features of Kinefold included the prediction of pseudoknots based on a ‘physical’ constraint model using polymer theory (17). Pseudoknot predictions were successfully tested on a variety of small pseudoknots (17), as well as on longer sequences such as 394 nt Tetrahymena group I intron (19). Predictions on folding dynamics and pathways have also been compared with folding experiments, probing natural (17) and designed DNA or RNA sequences (Viasnoff,V., Meller,A. and Isambert,H., submitted for publication and Xayaphoummine,A., Viasnoff,V., Harlepp,S. and Isambert,H., submitted for publication). In addition, the molecular basis of these stochastic folding simulations has been directly tested with detailed analysis of single-molecule micromechanical unfolding/refolding experiments performed on small RNA motifs and on 1524 nt 16S ribosomal RNA of Escherichia coli (20).

New features of Kinefold include DNA sequence folding, forced helices and topologically ‘entangled’ helices (i.e. knots), which have been recently added as simulation parameters.

OVERVIEW OF KINEFOLD FEATURES

Stochastic folding simulation of nucleic acids

Kinefold simulates nucleic acid folding paths at the level of nucleation and dissociation of RNA/DNA helix regions (12,17) (minimum 3 bp, maximum 60 bp), including pseudoknots and topologically ‘entangled’ helices. These stochastic formation and the removal of individual helices are known to be the time-limiting steps of RNA/DNA folding kinetics from the seminal experimental results (21,22). Single-strand diffusion and individual base-pair stacking/unstacking processes, which have much faster intrinsic dynamics (0.1 μs) than the relevant time scale for nucleic acid folding and unfolding (>10 μs), are assumed to be in a state of quasistatic equilibrium with the rare stochastic transitions between visited secondary structures. The folding path then consists of a discrete series of secondary structures related through successive additions or removals of single helices. Yet, it happens frequently that the trajectory will oscillate repeatedly between a few structures, and only much more slowly transit to visit new configurations. To circumvent these local kinetic traps that can severely impact the efficiency of the code, folding paths are in fact continuously averaged at the level of rapidly exchanging structures using the ‘exactly clustered stochastic simulation’ approach detailed previously (19).

Overall, Kinefold can simulate physical folding paths over second to minute molecular time scales for nucleic acid sequences up to ∼300–400 bases.

Unlike traditional RNA/DNA folding algorithms (1–6), stochastic simulations do not aim, a priori, at finding lowest free energy structures. In practice, however, they usually find those minima rather quickly, provided that the simulated molecular time is long enough. However, this relaxation time may vary significantly from sequence to sequence, even for similar sequence length and G+C-content, and users are advised to run a few independent folding simulations for each sequence submitted to the web server (see Simulated molecular time and Random seed subsections).

Ultimately, long sequences may not have enough time to reach their lowest free energy structures on physiological time scales (typically minutes) (23) and co-transcriptional folding pathways (24) likely to control proper folding into native structures in this case (Xayaphoummine,A., Viasnoff,V., Harlepp,S. and Isambert,H., submitted for publication). Besides, there are indications that co-transcriptional folding pathways of functional RNAs might be encoded into transient non-native helices (17,25). Kinefold stochastic simulations provide an effective approach to predict co-transcriptional folding paths of functional RNAs either into their lowest energy structures or into functional or misfolded kinetic traps.

Pseudoknots and topologically entangled helices

Besides addressing specific issues about folding kinetics, simulating RNA/DNA folding pathways also allows for the formation of helices interior to loops, the so-called ‘pseudoknots’ (13,17,19). We found that neglecting pseudoknots typically induces extended structural changes in secondary structure predictions (far beyond the missing pseudoknots themselves) owing to the strong cooperativity of RNA structure rearrangements (see discussion below and Supplementary Material 1).

Owing to their non-nested nature, pseudoknots are ‘intrinsically non-local in sequence space’ (i.e. crossing arcs) and difficult to include in secondary structure predictions (13,17,19,26–31). Yet, the 3D ‘physical’ constraints they cause to nucleic acid structures can be ‘locally modeled in structure space’ within substructures called ‘nets’ (17). The entropic stretching of single strands and the correlation of helix orientation within each elementary net are analytically calculated by modeling RNA/DNA helices as stiff rods and single-stranded regions as polymer springs. This is also complemented with a more global conformational entropy contribution at larger length scale (no entropic stretching of single strands at this scale) (17).

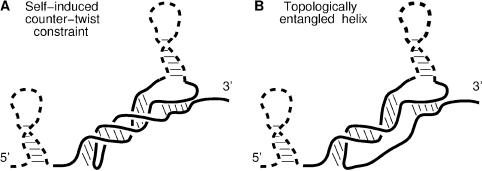
Beyond these geometric constraints, the formation of a pseudoknot may also induce helical topological constraints both on itself (Figure 1A) and on the ‘entanglement state’ of other non-nested helices in the surrounding (Figure 1B).

1. The first topological constraint (Figure 1A) arises because a pseudoknot of n helical turns requires a compensating twist of −n turns on the coil sections. While most helices are shorter than a full turn (10–11 bp), longer pseudoknots are ‘topologically destabilized’ by this self-induced entropic constraint. Hence, counter-twisting topological constraints associated with long pseudoknots do not create new or enhanced transition barriers for the nucleic acid folding/unfolding dynamics. In practice, the local contribution of self-induced topological constraints to global Boltzman weight are estimated at the level of ‘nets’ (17) with a longer apparent stretching distance on the single-strand twisting around the pseudoknot (see below).

2. Conversely, the effect of pseudoknots on the ‘entanglement state’ of other non-nested helices in their surrounding can be much more dramatic and lead to new kinetic traps for topologically ‘entangled’ helices (Figure 1B). Entangled helices are defined as helices longer than half a helix turn (>6 bp) whose unpairing transition is topologically impeded by the presence of at least one pseudoknot; when an entangled helix unpairs from an RNA/DNA structure, the newly unpaired bases cannot freely separate due to the residual ‘tangle’ [after Conway's classification of knots (32)] left behind by the unpaired helix. Such helical entanglement cannot be generally resolved until all the pseudoknots blocking its release through free rotation are simultaneously removed, hence effectively leaving entangled helices kinetically trapped. Entanglements can prevent, in particular, pseudoknots and long adjacent helices from rearranging during co-transcriptional folding owing to topologically blocked transition intermediates. This may cause long-lived metastable structures of untranslated region (UTR) RNA switches regulating the expression of downstream genes at the level of either transcription (e.g. control of early termination/antitermination) or translation (e.g. control of Shine–Dalgarno motif sequestration). Kinefold represents base pairs of entangled helices with the same color as the phosphate-ribose backbone to emphasize the apparent strength of these bonds.

Figure 1.

Helical topological constraints caused by pseudoknots. (A) Self-induced counter-twist constraints restrict the entropy of stretched single strands, hence resulting in an effective destabilization of long pseudoknots. (B) Long, topologically entangled helices leave a residual ‘tangle’ (32) behind when unpairing from the structure. This results in their effective stabilization until all pseudoknots blocking the helical entanglement are simultaneously removed.

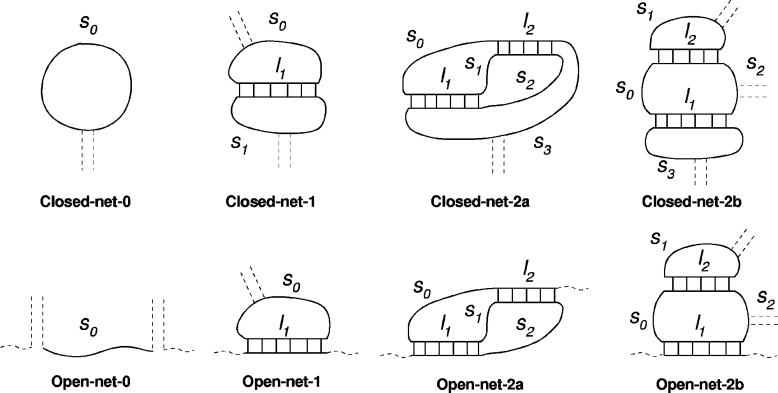
The effective helix length l for the calculation of the conformational entropy of ‘nets’ (Figure 2) depends on individual ‘entanglement states’,

$$l={\left[d^2{sin}^2(\pi n_{\text{s}}/n_{\text{p}})+h^2{(n_{\text{s}}/n_{\text{p}})}^2\right]}^{1/2},$$

for short (n_s ≤ 6 bp) or ‘entangled’ helices, and

$$l=n_{\text{s}}/6{\left[d^2{sin}^2(\pi 6/n_{\text{p}})+h^2{(6/n_{\text{p}})}^2\right]}^{1/2},$$

for long (n_s > 6 bp) pseudoknots, where n_s is the number of RNA (resp. DNA) base pairs, d = 3.3a (resp. 2.7a) is the apparent helix diameter (in base unit a = 6 Å), n_p = 11 (resp. 10) is the number of base pairs per complete turn, and h = 5a (resp. 5.6a) is the stem length for one turn (33).

Figure 2.

The eight allowed ‘nets’ enclosing up to two internal helices [see (17) for a detailed description of nets]. Single strands s₀, s₁, etc. are stretched by internal helices whose apparent lengths l₁ and l₂ depend on the ‘entanglement state’ of each helix, see main text. Conformational entropy parameters for all allowed nets and an example of transition barrier (see Supplementary Material 2) are given in Table 1.

Stochastic folding simulations are restricted to all the RNA/DNA structures that can be locally decomposed into nets with no more than two internal helices of respective length l₁ and l₂. Their conformational entropy and all entropic transition barriers to nucleate a new helix within such net are found to follow a single general form,

$${\text{e}}^{S/k}=\frac{{\text{e}}^{-A_1{l}_1^2-A_2{l}_2^2}}{D^{3/2}}\times \frac{{\text{e}}^{2A_3{l}_1{l}_2}-{\text{e}}^{-2A_3{l}_1{l}_2}}{4A_3{l}_1{l}_2}.$$

A multiplicative factor α, corresponding to the ‘confinement’ cost each time a loop is formed, is added for each helix on the structure [α = 0.0068 has been tuned to best fit the tabulated thermodynamic parameters for short loops (34,35)]. The parameters A₁, A₂, A₃ and D depend on the single-strand lengths (s₁, s₂, …, s_k), the net class and for transition barriers, on the actual transition within the net class. The expressions of A₁, A₂, A₃ and D are given in Table 1 for all the included nets, together with the most complex transition barrier for which we also provide a scanned analytic calculus in Supplementary Material 2. Conformational entropies and other transition barriers can be deduced from the later result taking simple limits.

Table 1.

Conformational entropy parameters of allowed nets and transition barriers. β = 3/2ab, with Kuhn length b = 2.5a and a = 6 Å

Class of net	D	A1	A2	A3
Open-net-0	1	0	0	0
Open-net-1	s0	β/D	0	0
Open-net-2a	s0s1 + s0s2 + s1s2	β(s1 + s2)/D	β(s0 + s1)/D	βs1/D
Open-net-2b	s1(s0 + s2)	βs1/D	β(s0 + s1 + s2)/D	βs1/D
Closed-net-0	s0	0	0	0
Closed-net-1	s0s1	β(s0 + s1)/D	0	0
Closed-net-2a	s0s3(s1 + s2) + s1s2(s0 + s3)	β(s0 + s3)(s1 + s2)/D	β(s2 + s3)(s0 + s1)/D	β(s0s2 − s1s3)/D
Closed-net-2b	s1s3(s0 + s2)	β(s0 + s2 + s3)s1/D	β(s0 + s1 + s2)s3/D	βs1s3/D
A transition barrier in closed-net-2ab (see Supplementary Material 2)	s0s3(s1 + s4)(s2 + s5) + s1s4(s0 + s3)(s2 + s5) + s2s5(s0 + s3)(s1 + s4)	β[(s1 + s4)(s0s3 + s2s5) + (s1 + s4)(s3s5 + s0s2) + s1s4 (s3 + s0 + s2 + s5)]/D	β[(s0 + s3)(s1s4 + s2s5) + (s0 + s3)(s1s5 + s2s4) + s0s3 (s1 + s4 + s2 + s5)]/D	β[s1s4(s0 + s3) + s0s3(s1 + s4) + (s2s0s4 + s5s3s1]/D

INPUT AND OPTIONS

Input, options and output for the web server are documented online by a help page with a direct link for each of the following items.

Sequence

The sequence should be a string of unmodified RNA/DNA bases (A, U/T, G, C) and may also include additional (X) bases which do not pair. X can be used to model modified bases or to investigate hybridization dynamics between two sequences by artificially connecting them with a long linker of Xs. The current length limitation is set to 400 bases for both ‘renaturation fold’ and ‘co-transcriptional fold’ simulations but, depending on their G+C-content, long sequences might not have relaxed by the maximum duration of the stochastic simulation (∼1 day). Hence, new users are strongly advised to start their query with shorter subsequences (e.g. up to 200 nt) to obtain a first understanding of the potentials and the limitations of Kinefold and its various available options described below.

RNA versus DNA

Stochastic folding simulations are performed either on RNA (default) or on DNA sequences using stacking free energy parameters from the Turner laboratory (34,35) and the SantaLucia laboratory (36), respectively. Unpublished terminal mismatches for DNA are estimated by adding 5′ and 3′ dandling end stackings, while helix–helix stacking is estimated by double counting terminal mismatches. These approximations generate smaller errors on global molecular free energy (a few percents) than the intrinsic error bars on Watson–Crick base pair stacking energies (10–15%).

Type of stochastic simulation

RNA/DNA folding pathways largely depend on folding conditions. Two types of folding scenarios are currently available (both at 37°C with 1 M NaCl and no divalent ions) and are as follows.

Renaturation fold

Folding starts from a completely denatured configuration (high temperature, no helix formed) which is then instantaneously cooled to 37°C. Alternatively, users have the possibility to force some initial helices on the structure (see Forcing helices).

Co-transcriptional fold

Folding proceeds while the sequence is being ‘synthetized’ (from its 5′ to 3′ ends). The transcription rate can be tuned to fit average transcription speeds of different RNA polymerases: a new base is typically added every 3, 20 or 200 ms with T7 phage, prokaryote or eukaryote RNA polymerase, respectively. The nascent transcript starts to fold before the whole sequence is fully available. Depending on actual sequence, co-transcriptional folding may guide folding or mislead RNA molecules into long-lived metastable configurations. An example of animated co-transcriptional folding path visualized with the Kineviewer Java applet can be found at http://kinefold.curie.fr/cgi-bin/viewer1.pl?file=HDVribozyme.coord.

Simulated molecular time

The simulated molecular time corresponds to the actual time experienced by the RNA/DNA molecule, not the time needed for the simulation to run (which can be much longer).

The web server automatically estimates a statistical folding time for each submitted sequence. However, users can also predefine the total simulated molecular time, which should be between 1 and 10 000 000 ms (i.e. ∼3 h). The ‘Enforced time’ option is very convenient to restrict the simulation time for long sequences; Above 300 bases, a good starting point is to first simulate a few independent folding paths (see Random seed) of 10 000 ms to check for early reproducibility of folding paths before requesting longer runs such as 30 000 or 100 000 ms.

Pseudoknots

They are visualized for convenience as colored single-stranded regions connected by two straight lines corresponding to the first and last base pairs of the pseudoknot. In the actual simulation, however, pseudoknots are locally treated as any regular helices and the 3D conformational entropic constraints they cause are evaluated using a coarse-grained geometric approach based on modeling RNA/DNA helices as stiff rods and single-stranded regions as polymer springs (17) (Figure 2 and Table 1). Pseudoknots are included by default in stochastic folding paths but they can also be excluded altogether by users.

We have performed extensive statistics on pseudoknot prevalence in random and natural RNA sequences [see Supplementary Material 1 and (19)]. While the proportion of pseudoknots among base pairs is typically 10–15% on average, the actual variation between different sequences is quite broad (from 0 up to 30% for G+C-rich molecules). Moreover, we found that excluding the formation of pseudoknots on an RNA structure, where they correspond to ∼10% of base pairs, typically induces much more dramatic base pair changes (>30%) owing to the strong cooperativity of secondary structure rearrangements. This has also been independently observed [Table 4 in (37)] by comparing the accuracy of secondary structure predictions without pseudoknots to known secondary structures including a small number of pseudoknots (up to 10%). In fact, we have found that the distribution of base pair identity between low energy structures with and without pseudoknots is essentially ‘flat’ (see Supplementary Material 1); there is virtually no correlation between predictions including and excluding pseudoknots. This suggests some intrinsic limitations for predicting pseudoknots through iterative approaches starting from non-pseudoknotted structures, unless they are also combined to comparative methods using homologous sequences (10,11).

Entanglements

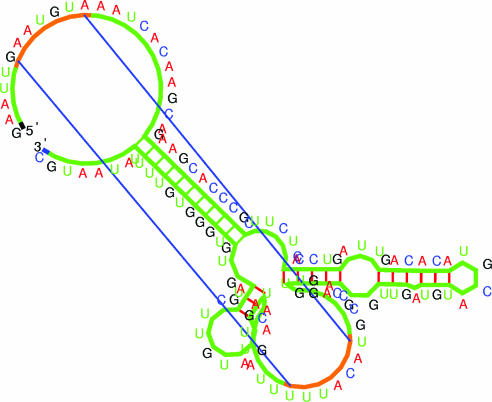
Kinefold freezes the unpairing transitions of ‘entangled’ helices (Figure 1) while they remain entangled. Meanwhile terminal zipping/unzipping adjustments still occur and ‘detailed balance’ is perfectly maintained throughout the simulation (as it should be). This new option is particularly recommended when users suspect ‘kinetically trapped alternative structures’ with their sequence. For clarity, the base pair connections of entangled helices are colored in green (Figure 3).

Figure 3.

Illustration of predicted structure including a ‘pseudoknot’ (the helix is visualized by two straight lines corresponding to the first and last base pairs) and an ‘entangled helix’ (base pairs are drawn with the same color as the phosphate-ribose backbone, see main text). The image is generated by the RNAMovies software upgraded to display pseudoknots and entangled helices (38). The structure shown is a co-transcriptional folding intermediate of the 5′-UTR of the infC gene from Bacillus subtilis. The RNA Pol at the nascent 3′ end prevents disentanglement of the entangled helix.

Tracing and forcing helices

There can be maximum of five helices (minimum 3 bp, maximum 60 bp).

Tracing helices

Users can follow whether certain helices of special interest to them are formed or not on the structure as the sequence folds. This can be helpful, in particular, to identify transient helices (minimum of three stacking base pairs) that are eventually removed in the native structure. Helix traces are graphically displayed on the trajectory plot.

Enter T i j k, with k > 2 on one line to trace when any of the consecutive base pairs i,·j, i + 1,·j − 1,…, i + k − 1·j − k + 1 is formed.

Forcing helices

In ‘renaturation fold’ mode, users may also force k > 2 consecutive base pairs on the RNA structure (minimum of three stacking base pairs). During folding, the corresponding helices will not be removed, shrunk nor extended by additional matching base pairs, while the rest of the molecule will fold normally. Forced helices, which should be non-overlapping and compatible with the pseudoknot requirements, are also graphically displayed on the trajectory plot. Improper specifications are automatically dismissed.

Enter F i j k, with k > 2 on one line to force the consecutive base pairs i·j, i + 1·j − 1, …, i + k − 1·j − k + 1 (and prevent additional extension).

Random seed

Each folding request simulates one single folding pathway. As RNA folding kinetics is a stochastic process during which certain helices are successively formed and removed somewhat randomly (see Type of stochastic simulation subsection), folding pathways may vary significantly from run to run. Hence, before drawing any positive or negative conclusions for a specific sequence, users are advised to try a few runs to look for possible variations. Independent runs are generated with different random seeds, which are integers between 1 and 10 000. One is automatically generated each time the request page is refreshed. Alternatively, it is also possible to choose a particular random seed in order to redo the very same simulation provided that all other parameters remain unchanged too with the exception of the ‘simulated molecular time’ and ‘Traced heliced’.

• In ‘renaturation fold’ mode, three independent folding pathways leading to the same structure(s) is a good indication (although not a proof) that the lowest free energy structures have been reached. Alternative scenarios may suggest long-lived metastable configurations of potential interest.

• In ‘co-transcriptional fold’ mode, robust features over a few independent runs (like for instance similar ‘trajectory plots’ for strong specific helices) are also good indications of well-defined folding pathways either toward a native structure or toward a long-lived kinetically trapped configuration.

OUTPUT

The output page provides (i) a series of low free energy structures, (ii) an online animated folding path and (iii) a programmable trajectory plot focusing on a few helices of interest to each user. Owing to space limitation, these are presented and discussed in Supplementary Material 3.