Abstract
Owing to the presence of exceptional points (EPs), non-Hermitian (NH) systems can display intriguing topological phenomena without Hermitian analogs. However, experimental characterizations of exceptional topological invariants have been restricted to second-order EPs (EP2s) in classical or semiclassical systems. We here propose an NH multi-mode system with higher-order EPs, each of which is underlain by a multifold-degenerate multipartite entangled eigenstate. We implement the NH model by controllably coupling a Josephson-junction-based electronic mode to two microwave resonators. We experimentally quantify the topological invariant for an EP3, by mapping out the complex eigenspectra of the tripartite system along a loop surrounding this EP3 in the parameter space. The nonclassicality of the realized topology is manifested by the observed quantum correlations in the corresponding eigenstates. Our results extend research of exceptional topology to fully quantum-mechanical models with multipartite entangled eigenstates.
Subject terms: Single photons and quantum effects, Quantum simulation
Exceptional topology associated with higher-order exceptional points has not been completely characterised in quantum systems. Here, the authors fill this gap performing full quantum state tomography in a system composed of a superconducting qubit coupled to two cavities, one lossless and one lossy, featuring third-order exceptional points.
Introduction
As one of the most well-tested physical theories, quantum mechanics has successfully passed numerous experimental tests. In most quantum-mechanical experiments, the system of interest is well isolated from its surrounding environment1,2, so that its dynamics is governed by the Schrödinger equation with an energy operator often called Hamiltonian. The Hermiticity of the Hamiltonian ensures that the system evolves unitarily. However, any real quantum system is inevitably coupled to the environment3, which functions by entangling its degrees of freedom with the system state4. Through this entanglement, the environment continuously monitors the system state, which inevitably produces a measurement backaction5. Under this disturbance, the system dynamics could significantly deviate from the unitary evolution even when it does not make any quantum jump. Mathematically, the state trajectory, associated with this conditional evolution, is also governed by a Schrödinger equation but with a non-Hermitian (NH) Hamiltonian6.
Due to the non-Hermiticity, two or more eigenvectors of the NH Hamiltonian can coalesce into a single one with the same eigenenergy at exceptional points (EPs)7,8. These singularities can bring about many unique phenomena, exemplified by exotic topological phenomena that are absent in Hermitian systems8–12. The past two decades have witnessed a number of experimental explorations on the NH singular features, including spectral parity-time phase transitions13–21, dynamical chiral behaviors22–28, exceptional entanglement transitions29, and NH topology30–44. The topological invariant of an NH system can be quantified in terms of the eigenvectors or the complex eigenenergies8–12. This is in distinct contrast with the Hermitian case, where the topology cannot be defined by the eigenenergies which are always real. So far, NH topology has been observed in several experiments, all of which were restricted to second-order EPs (EP2s) realized in classical systems35–39 or with a classically-driven qubit40–42. Compared to EP2s, higher-order EPs can exhibit much richer topological properties11,12,43–45, and the associated spectral topological invariants are defined in a fundamentally different manner12. Despite the fundamental interest, such invariants have not been unambiguously characterized in experiment.
We here investigate both theoretically and experimentally the quantum-mechanical exceptional topology associated with higher-order EPs in an NH composite system consisting of multiple interacting modes. These EPs result from continuous and nonunitary evolutions in the single-excitation subspace without quantum jumps46. The topological property associated to each higher-order EP can be quantified by the homotopy invariant, recently proposed by Delplace et al.12. We experimentally engineer the NH three-mode system in a superconducting circuit, where a nonlinear Xmon mode is controllably coupled to two photonic modes stored in two separated microwave resonators. The non-Hermiticity of the system is manifested by the non-negligible dissipation of one photonic mode. We find that the resulting NH Hamiltonian possesses four EP3s in the real parameter space. We quantify the homotopy invariant associated to the EP3 in the first quadrant of the parameter space, by mapping out the eigenenergies of the NH Hamiltonian along a loop surrounding this EP3. The system eigenenergies are extracted from the output states of the three-mode system in the single-excitation subspace, measured for different evolution times. As far as we know, this is the first experimental characterization of the topological invariant associated with a higher-order EP. We further note that the winding number defined by Eq. (3) is zero for the degenerate points in both the two-dimensional (2D) and 3D Hermitian systems, referred to as diabolical points (DPs), as well as for EP2s in a 2D NH system, as detailed in the Supplementary Material. Therefore, such a winding number serves as a homotopy invariant that uniquely characterizes the topology of EP3s.
Results
NH multi-mode system
The system under consideration corresponds to a multi-mode system with competing coherent nearest-neighboring interactions and incoherent dissipation, as shown in Fig. 1a. Under the competition, the system evolution is a weighted mixture of infinitely many trajectories, among which of special interest is the one without quantum jump. This trajectory is governed by the NH Hamiltonian (setting ℏ = 1)
| 1 |
where and aj denote the creation and annihilation operators of the jth mode with a decaying rate κj, λj represents the coupling coefficient between the jth and (j + 1)th modes, and H.c. is the Hermitian conjugate. The excitation number of the total system is conserved along the no-jump trajectory, as the excitation number operator, , commutes with HNH. Hereafter, we will consider the system behaviors restricted in the single-excitation subspace , where and respectively denote the ground and first excited states for the jth mode with j ranging from 1 to N.
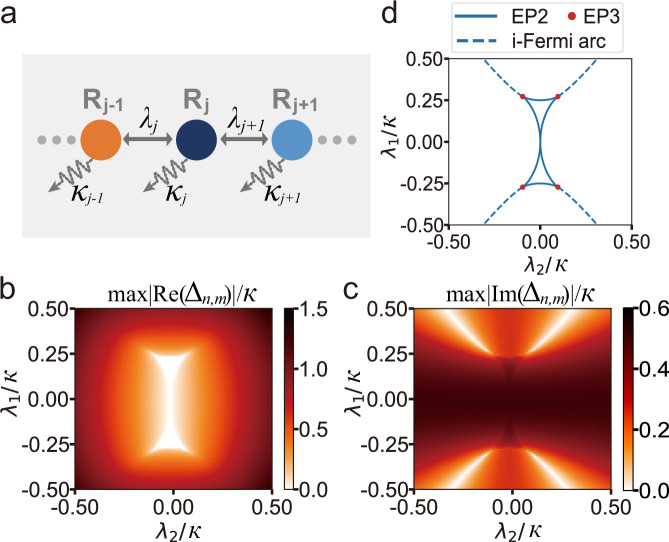
Fig. 1. Sketch of the NH multi-mode system and the spectral structure.
a Theoretical model. The system involves N modes (Rj), arranged in a linear array. The NH Hamiltonian dynamics features the competition between the nearest-neighbor swapping couplings (λj) and the energy dissipations (κj). b, c Maxima for the real (b) and imaginary (c) gaps versus λ1 and λ2 in the three-mode system. For simplicity, we set κ2 = κ3 = 0, and assume κ1 has a fixed nonzero value κ. At the three-fold degeneracy points , the maximum gap among the three complex eigenenergies vanishes. Here the parameters λ1 and λ2 are scaled in units of κ. Δn,m denotes the difference between two eigenenergies, i.e., En − Em (n ≠ m, n, m = 1, 2, 3). d The solid lines denote EP2s where a pair of eigenstates coalesce. Along the dashed lines, all three eigenenergies have the same imaginary part. Their intersection points (red dots) are EP3s connecting Fermi arcs and i-Fermi arcs.
For κj = 0 (j = 1, …, N), the Hamiltonian (1) has N real eigenenergies, which display an N-fold degeneracy for λj = 0. When one or more modes are subjected to dissipations, the eigenenergies become complex. The resulting spectral structure can display exotic topological features without Hermitian analogs. To clearly illustrate the underlying NH quantum topological physics, we consider a three-mode system. For simplicity, we assume κ2 = κ3 = 0 and drop off the subscript of κ1. Figure 1b, c shows the maximal real (imaginary) part of the gaps among the three complex eigenenergies versus λ1 and λ2. The results clearly show that the non-Hermiticity splits the real degeneracy into four EP3s at with and . At each EP3, the three eigenenergies have a vanishing real part and the same nonzero imaginary part.
The spectrum of the NH Hamiltonian exhibits a rich structure, where each of the four EP3s is connected to two curves of EP2s (solid lines in Fig. 1d), at which a pair of eigenstates and eigenenergies coalesce. The details of these eigenenergies are shown in Section S5 of the Supplementary Material. Enclosed in the EP2 contour is an isofrequency region, where all three eigenenergies have the same real part. This is a 2D generalization of the linear-like two-fold degenerate Fermi arc, which connects 2 EP2s existing in a 2D system30. In the isofrequency region, the real parts of the three complex eigenenergies vanish, so that the state evolution of the system is determined by the imaginary parts of these eigenenergies, each of which corresponds to a gaining or losing rate depending upon its sign. After a long-time evolution, only the eigenvector with the largest imaginary part can survive for the no-jump case. Since such an eigenvector is essentially a tripartite entangled state, the dynamics in the isofrequency region provides a way for robust generation and conditional stabilization of tripartite entanglement47. Such an entanglement generation and stabilization process is illustrated by the simulations presented in Section S2 of the Supplementary Material.
In addition to the real Fermi arc, each of the four EP3s emanates an i-Fermi arc (dashed lines in Fig. 1d)11, along which the imaginary parts are three-fold degenerate. With a global shift of the spectrum by a suitable imaginary value, the four i-Fermi arcs correspond to the regions where the eigenenergies are all real. In view of spectral phase transitions, each of the four EP3s corresponds to a tripoint, where three distinct phases (featuring imaginary, real, and complex energy gaps) meet together.
Experimental implementation
We perform the experiment using a circuit quantum electrodynamics device with five nonlinear Xmon modes (qubits), each controllably coupled to the common bus resonator (Rb) of a fixed frequency ωb/2π = 5.58 GHz. The NH quantum multipartite system is realized with one of these qubits (labeled as Q), the bus resonator Rb, and the readout resonator of Q, (Rr), which has a frequency ωr/2π = 6.66 GHz. The on-resonance coupling strength between Q and Rb (Rr) is gb = 2π × 20 MHz (gr = 2π × 41 MHz). The decaying rate of Q (Rb) is 0.06 (0.08) MHz, which is two orders smaller than that of Rr (κ = 5 MHz). Thus, the dissipations of Q and Rb are negligible. To realize the NH tripartite Hamiltonian in a controllable manner, two parametric modulations are simultaneously applied to Q to modulate its transition frequency as , where ω0 is the mean frequency of Q, and εj and νj respectively denote the amplitude and frequency of the jth modulation, as depicted in Fig. 2a. Under the condition ω0 + ν1 = ωr, the qubit Q interacts with the readout resonator Rr at the first upper sideband for the first modulation, with the strength λ1 = gr J1(ε1/ν1). Here, J1(μ) is the first-order Bessel function of the first kind. The second modulation is used to induce the sideband interaction between Q and Rb, with the effective photonic swapping rate λ2 controlled by ε2. The sideband interactions and the system parameters are detailed in Section S3 of the Supplementary Material. When the Rr-Q-Rb system initially has one excitation, its dynamics, associated with no-jump trajectory, is described by the NH Hamiltonian (1) with N = 3, where Rr, Q, and Rb correspond to three modes sharing a single excitation.
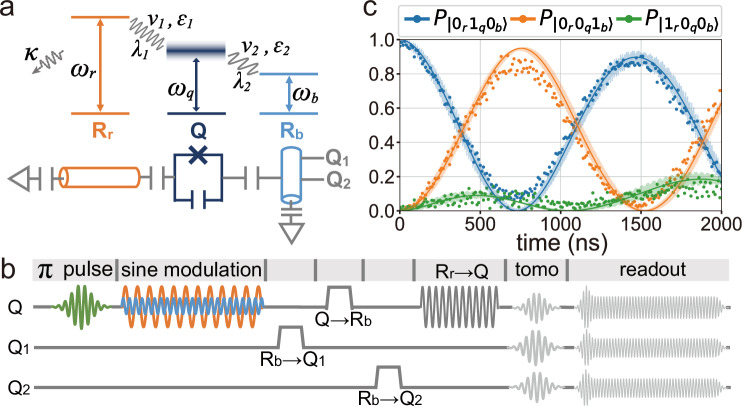
Fig. 2. Experimental implementation.
a Synthesis of the NH three-mode system. The NH Hamiltonian is realized in a circuit, where a Josephson-junction-based qubit (Q), together with a bus resonator (Rb) and a readout resonator (Rr), comprises an effective three-mode system in the single-excitation subspace. The decaying rates of Q and Rb are respectively 0.06 MHz and 0.08 MHz, both of which can be neglected compared to that of Rr, κ = 5 MHz. Q is coupled to Rr (Rb) at the first upper (lower) sideband with respect to the first (second) parametric modulation. b Pulse sequence. The qubit Q is first prepared in the excited state at its idle frequency, followed by the application of two sine modulations. The modulation frequencies (ν1, ν2) and amplitudes are tunable for controlling λ1 and λ2. After the modulating pulse, the evolved Rr-Q-Rb output state is mapped to the Q-Q2-Q1 system for readout, where Q1 and Q2 are two ancilla qubits, each of which can be controllably coupled to the bus resonator. c Observed evolutions of the populations. All data are measured for the initial state at the point λ1 = 2π × 0.21 MHz and λ2 = 2π × 0.31 MHz. The results are obtained by discarding the measurement outcome and renormalizing the remaining populations of , and in the single-excitation subspace. The solid curves are theoretical predictions using the NH Hamiltonian (1), while the fast oscillating curves are numerical simulation results using the original Hamiltonian (given in Section S3 of the Supplementary material) with frequency modulations included.
The experiment starts with the preparation of an initial single-excitation state, following which the parametric modulations are applied to Q, with the experimental pulse sequence depicted in Fig. 2b. After a preset interaction time t, the parametric modulations are switched off to have Q decoupled from both Rb and Rr. The output state of the system, associated with the no-jump trajectory, is given by
| 2 |
Here the subscripts r, q, and b label Rr, Q, and Rb, respectively. As the excitation is conserved by the NH Hamiltonian while the quantum jump breaks down this conservation, the no-jump state trajectory can be postselected by discarding the outcome with null excitation. The joint tripartite output state is read out with the assistance of two ancilla qubits, denoted as Q1 and Q2. The Rr-Q-Rb output state is mapped to the Q-Q2-Q1 system, which is realized by swapping gates (see Section S4 in the Supplementary Material). Bloch vectors of the three qubits along different axes are then measured. By correlating the outcomes of these measurements, the three-qubit density matrix is reconstructed. Removing the ground state element and renormalizing the remaining ones, we obtain the final state of the system evolving under the NH Hamiltonian. With a correction for the infidelity of the state mapping, the resulting Q-Q2-Q1 output state corresponds to the Rr-Q-Rb output state right before the state mapping. Figure 2c shows the evolution of the populations , , and for the initial state , measured at the point λ1 = 2π × 0.21 MHz and λ2 = 2π × 0.31 MHz. These populations are obtained by discarding the measurement outcome and then renormalizing the probabilities for occurrences of the three single-excitation outcomes.
Measurement of the winding number
The topological invariant associated with each EP3 can be quantified by the winding number, calculated in terms of the resultant vector 12
| 3 |
where the integral loop Cλ encloses the EP3 in the 2D parameter space. and depend upon the eigenenergies (for details, see Section S7 in the Supplementary Material), which can in principle be extracted from the output states measured for different interaction times. To simplify the measurement, we choose a square-shaped loop on the λ1–λ2 plane. The loop has four vertices (0, 0), (λm, 0), (0, λm), and (λm, λm), as shown in Fig. 3a. With this choice, the eigenspectrum can be extracted in a relatively easy manner (see Section S5 in the Supplementary Material). In our experiment, λm is set to be 2π × 1 MHz.
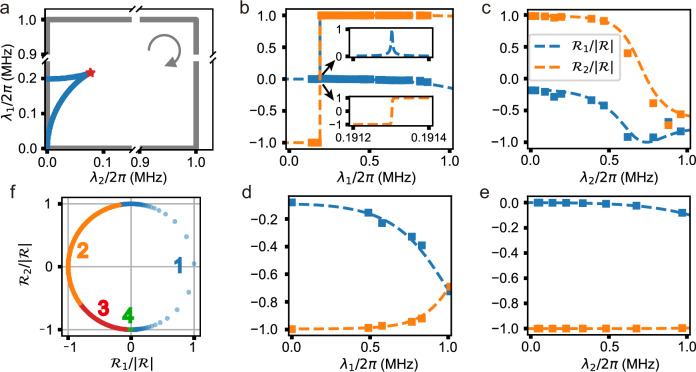
Fig. 3. Characterization of the NH topology.
a Loop traversed for extracting the winding number. The loop (gray solid line) is square-shaped with four vertices (0, 0), (λm, 0), (0, λm), and (λm, λm), where λm = 2π × 1 MHz. This loop surrounds an EP3 (red star), which connects two Fermi arcs consisting of EP2s (blue solid line). The arrow denotes the direction of the integral along the loop. b, e Normalized resultant vectors measured against λ1 with λ2 = 0 (b) and λm (d), and against λ2 with λ1 = λm (c) and 0 (e). The squares represent the components (blue) and (orange), respectively. The dotted lines denote the fitted and as functions of λ1 or λ2. The winding number, calculated with these fitted functions, is 1. f Trajectory of the rescaled unit resultant vector . The symbols “1'', “2'', “3'', and “4'', label the sections associated with the four edges of the parameter-space loop, shown in (b–e), respectively.
The eigenenergies, measured along the four edges of the square-shaped loop, are detailed in Section S8 of the Supplementary Material. For different values of λ1 or , and are calculated from the corresponding measured eigenenergies, as shown in Fig. 3b–e. The dashed lines denote the functions fitted with the measured data. We note that the rescaled unit resultant vector, defined as , is changed along a circle when the control parameter (λ1, λ2) is varied along a loop enclosing the EP3, as illustrated in Fig. 3f. On the edge with λ2 = 0, there is an EP2, within the vicinity of which the resultant vector undergoes a π rotation, as detailed in the insets of Fig. 3b. This rotation occurs in a very narrow region of the control parameter (λ1, λ2), but contributes half of the circular trajectory of . The winding number based on thus-obtained and is , which confirms that the loop encircles an EP3. In addition to the EP3, the loop surrounds infinitely multiple EP2s, which form two exceptional arcs that cross at the EP3, as illustrated in Fig. 3a. These EP2s have no contribution to the characterized topological invariant, which corresponds to the winding number of the relative angle between and 12. This implies that the spectral topological features of higher EPs are fundamentally distinct from those of EP2s. As detailed in ref. 12, the winding number defined in Eq. (3) is the simplest example of the homotopy invariants, which can quantify topological properties of multifold symmetry-protected EPs but have not been experimentally characterized so far.
In a recent acoustic experiment43, the measured local phase rigidities of the eigenvectors near an EP3 have a critical exponent coinciding with the winding number quantifying the calculated global Berry phase. However, the Berry phase itself, which characterizes the topological charge associated to the eigenvectors, has not been experimentally extracted, and neither has the eigenspectral topological invariant. In a recent experiment48, a third-order exceptional line was observed with a nitrogen-vacancy system, where the NH Hamiltonian for a single electron with three levels was constructed by the dilation method. However, the topological properties of the realized EP3 have not been experimentally characterized. As far as we know, our work represents the first measurement of homotopy invariants, of which the winding number for EP3s is the simplest example12.
To reveal the quantum correlations among the three modes, we perform quantum state tomography on the output state of the system. For different values of the control parameters, the evolutions of the measured pairwise concurrences are detailed in Section S5 of the Supplementary Material. For the edges λ1 = 0 and λ2 = 0, the system reduces to a two-mode system, so that the eigenstates can be extracted from the state evolution in a relatively easy way. At point (0, λm), the measured concurrences of the two eigenstates () for the Rb-Q subsystem, which is decoupled from Rr, are 0.997 and 0.997, respectively. At point (λm, 0), the concurrences for two measured Q-Rr eigenstates () are respectively 0.971 and 0.971. When λ1 ≠ 0 and λ2 ≠ 0, each of the three eigenstates corresponds to a tripartite entangled eigenstate, for which each mode is quantum-mechanically correlated to either of the other two modes. Experimental extraction of these eigenstates is a challenging task because each eigenstate involves four parameters to be determined. However, the observation of tripartite entangled states evolved from the initial product state , indicates that there exists tripartite entanglement in the underlying eigenstates. These observed nonclassical correlations represent another unique feature that fundamentally distinguishes the presently observed topology from those previously demonstrated in classical or semiclassical systems30–45.
Discussion
In conclusion, we have investigated the exceptional topology in interacting many-body quantum systems, with a competition between coherent couplings and incoherent dissipation. The quantum topology is manifested by the presence of multiple higher-order EPs, each of which carries a quantized topological charge and is associated with a multifold degenerate eigenstate displaying highly nonclassical correlations. The NH model is experimentally realized with a superconducting qubit, which is correlated to a lossless bus resonator and a decaying readout resonator by swapping a single photon. The topological charge at each EP3 is quantified by the winding number, extracted from the eigenspectra measured with the assistance of two ancilla qubits. Each of the corresponding eigenstates exhibits quantum entanglement, confirming the nonclassical origin of the topology. Besides fundamental interest, the demonstrated NH dynamics associated with higher-order EPs may have applications in quantum technologies, such as sensitivity enhancement in quantum metrology49 as well as fast and robust generation of quantum entanglement50.
Supplementary information
Acknowledgements
S.-B.Z. was supported by the National Natural Science Foundation of China (Grant Nos. 12274080, 12474356), and the Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0300200); Z.-B.Y. was supported by the National Natural Science Foundation of China (Grant No. 12475015) and the Innovation Program for Quantum Science and Technology (Grant Nos. 2021ZD0300200); C.-P.Y. was supported by the National Natural Science Foundation of China (Grant No. U21A20436) and the Innovation Program for Quantum Science and Technology (Grant Nos. 2021ZD0301705).
Author contributions
S.-B.Z. proposed the theoretical model and conceived the experiment. P.-R.H., W.N., X.-J.H. supervised by Z.-B.Y. and S.-B.Z., carried out the experiment. P.-R.H., R.-H.Z., S.-B.Y., F.W., Q.-P.S., C.-P.Y., and S.-B.Z. analyzed the data. S.-B.Z., Z.-B.Y., and C.-P.Y. co-wrote the paper. All authors contributed to the interpretation of observed phenomena and helped to write the paper.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Zhen-Biao Yang, Email: zbyang@fzu.edu.cn.
Chui-Ping Yang, Email: yangcp@hznu.edu.cn.
Shi-Biao Zheng, Email: t96034@fzu.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-54662-8.
References
- 1.Wineland, D. J. Nobel Lecture: superposition, entanglement, and raising Schröinger’s cat. Rev. Mod. Phys.85, 1103–1114 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Haroche, S. Nobel Lecture: controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys.85, 1083–1102 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Scully, M. O. & Zubairy, M. S. Quantum Optics (Cambridge, 2000).
- 4.Zurek, W. H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys.75, 715–775 (2003). [Google Scholar]
- 5.Ashida, Y., Gong, Z. & Ueda, M. Non-Hermitian physics. Adv. Phys.69, 249–435 (2020). [Google Scholar]
-
6.Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having
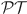 symmetry. Phys. Rev. Lett.80, 5243–5246 (1998). [Google Scholar]
symmetry. Phys. Rev. Lett.80, 5243–5246 (1998). [Google Scholar] - 7.Özdemir, Ş. K., Rotter, S., Nori, F. & Yang, L. Parity-time symmetry and exceptional points in photonics. Nat. Mater.18, 783–798 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Ding, K., Fang, C. & Ma, G. Non-Hermitian topology and exceptional-point geometries. Nat. Rev. Phys.4, 745–760 (2022). [Google Scholar]
- 9.Bergholtz, E. J., Budich, J. C. & Kunst, F. K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys.93, 015005 (2021). [Google Scholar]
- 10.Gong, Z. et al. Topological phases of non-Hermitian systems. Phys. Rev. X8, 031079 (2018). [Google Scholar]
- 11.Mandal, I. & Bergholtz, E. J. Symmetry and higher-order exceptional points. Phys. Rev. Lett.127, 186601 (2021). [DOI] [PubMed] [Google Scholar]
- 12.Delplace, P., Yoshida, T. & Hatsugai, Y. Symmetry-protected multifold exceptional points and their topological characterization. Phys. Rev. Lett.127, 186602 (2021). [DOI] [PubMed] [Google Scholar]
- 13.Choi, Y. et al. Quasieigenstate coalescence in an atom-cavity quantum composite. Phys. Rev. Lett.104, 153601 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Xiao, L. et al. Observation of critical phenomena in parity-time-symmetric quantum dynamics. Phys. Rev. Lett.123, 230401 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Öztürk, F. E. et al. Observation of a non-Hermitian phase transition in an optical quantum gas. Science372, 88–91 (2021). [DOI] [PubMed] [Google Scholar]
- 16.Peng, P. et al. Anti-parity-time symmetry with flying atoms. Nat. Phys.12, 1139–1145 (2016). [Google Scholar]
- 17.Li, J. et al. Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Commun.10, 855 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu, Y. et al. Observation of parity-time symmetry breaking in a single-spin system. Science364, 878–880 (2019). [DOI] [PubMed] [Google Scholar]
- 19.Naghiloo, M., Abbasi, M., Joglekar, Y. N. & Murch, K. W. Quantum state tomography across the exceptional point in a single dissipative qubit. Nat. Phys.15, 1232–1236 (2019). [Google Scholar]
- 20.Wang, Z. et al. Observation of the exceptional point in superconducting qubit with dissipation controlled by parametric modulation. Chin. Phys. B30, 100309 (2021). [Google Scholar]
- 21.Gao, T. et al. Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard. Natrue526, 554–558 (2015). [DOI] [PubMed] [Google Scholar]
- 22.Zhang, X.-L., Wang, S., Hou, B. & Chan, C. T. Dynamically encircling exceptional points: in situ control of encircling loops and the role of the starting point. Phys. Rev. X8, 021066 (2018). [Google Scholar]
- 23.Doppler, J. et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature537, 76–79 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Xu, H., Mason, D., Jiang, L. & Harris, J. G. E. Topological energy transfer in an optomechanical system with exceptional points. Nature537, 80–83 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Yoon, J. W. et al. Time-asymmetric loop around an exceptional point over the full optical communication band. Nature562, 86–90 (2018). [DOI] [PubMed] [Google Scholar]
- 26.Liu, W., Wu, Y., Duan, C.-K., Rong, X. & Du, J. Dynamically encircling an exceptional point in a real quantum system. Phys. Rev. Lett.126, 170506 (2021). [DOI] [PubMed] [Google Scholar]
- 27.Gou, W. et al. Tunable nonreciprocal quantum transport through a dissipative Aharonov-Bohm ring in ultracold atoms. Phys. Rev. Lett.124, 070402 (2020). [DOI] [PubMed] [Google Scholar]
- 28.Ren, Z. et al. Chiral control of quantum states in non-Hermitian spin-orbit-coupled fermions. Nat. Phys.18, 385–389 (2022). [Google Scholar]
- 29.Han, P. R. et al. Exceptional entanglement phenomena: non-Hermiticity meeting non-classicality. Phys. Rev. Lett.131, 260201 (2023). [DOI] [PubMed] [Google Scholar]
- 30.Dembowski, C. et al. Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett.86, 787–790 (2001). [DOI] [PubMed] [Google Scholar]
- 31.Zhou, H. et al. Observation of bulk Fermi arc and polarization half charge from paired exceptional points. Science359, 1009–1012 (2018). [DOI] [PubMed] [Google Scholar]
- 32.Cerjan, A. et al. Experimental realization of a Weyl exceptional ring. Nat. Photon.13, 623–628 (2019). [Google Scholar]
- 33.Liu, J. J. et al. Experimental realization of Weyl exceptional rings in a synthetic three-dimensional non-Hermitian phononic crystal. Phys. Rev. Lett.129, 084301 (2022). [DOI] [PubMed] [Google Scholar]
- 34.Zhen, B. et al. Spawning rings of exceptional points out of Dirac cones. Nature525, 354–358 (2015). [DOI] [PubMed] [Google Scholar]
- 35.Wang, K. et al. Generating arbitrary topological windings of a non-Hermitian band. Science371, 1240–1245 (2021). [DOI] [PubMed] [Google Scholar]
- 36.Wang, K., Dutt, A., Wojcik, C. C. & Fan, S. Topological complex-energy braiding of non-Hermitian bands. Nature598, 59–64 (2021). [DOI] [PubMed] [Google Scholar]
- 37.Zhang, Q. et al. Observation of acoustic non-Hermitian Bloch braids and associated topological phase transitions. Phys. Rev. Lett.130, 017201 (2023). [DOI] [PubMed] [Google Scholar]
- 38.Tang, W., Ding, K. & Ma, G. Direct measurement of topological properties of an exceptional parabola. Phys. Rev. Lett.127, 034301 (2021). [DOI] [PubMed] [Google Scholar]
- 39.Su, R. et al. Direct measurement of a non-Hermitian topological invariant in a hybrid light-matter system. Sci. Adv.7, eabj8905 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang, W. et al. Observation of non-Hermitian topology with nonunitary dynamics of solid-state spins. Phys. Rev. Lett.127, 090501 (2021). [DOI] [PubMed] [Google Scholar]
- 41.Cao, M.-M. et al. Probing complex-energy topology via non-Hermitian absorption spectroscopy in a trapped ion simulator. Phys. Rev. Lett.130, 163001 (2023). [DOI] [PubMed] [Google Scholar]
- 42.Wu, Y. et al. Observation of the knot topology of non-Hermitian systems in a single spin. Phys. Rev. A108, 052409 (2023). [Google Scholar]
- 43.Tang, W. et al. Exceptional nexus with a hybrid topological invariant. Science370, 1077–1080 (2020). [DOI] [PubMed] [Google Scholar]
- 44.Tang, W., Ding, K. & Ma, G. Realization and topological properties of third-order exceptional lines embedded in exceptional surfaces. Nat. Commun.14, 6660 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Patil, Y. S. S. et al. Measuring the knot of non-Hermitian degeneracies and non-commuting braids. Nature607, 271–275 (2022). [DOI] [PubMed] [Google Scholar]
- 46.Minganti, F., Miranowicz, A., Chhajlany, R. W. & Nori, F. Quantum exceptional points of non-Hermitian Hamiltonians and Liouvillians: the effects of quantum jumps. Phys. Rev. A100, 062131 (2019). [Google Scholar]
- 47.Teixeira, W. S., Vadimov, V., Mörstedt, T., Kund, S. & Möttönen, M. Exceptional-point-assisted entanglement, squeezing, and reset in a chain of three superconducting resonators. Phys. Rev. Res.5, 033119 (2023). [Google Scholar]
- 48.Wu, Y. et al. Third-order exceptional line in a nitrogen-vacancy spin system. Nat. Nanotechnol.19, 160–165 (2024). [DOI] [PubMed] [Google Scholar]
- 49.Chen, W., Özdemir, Ş. K., Zhao, G., Wiersig, J. & Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature548, 192–196 (2017). [DOI] [PubMed] [Google Scholar]
- 50.Li, Z.-Z., Chen, W., Abbasi, M., Murch, K. W. & Whaley, K. B. Speeding up entanglement generation by proximity to higher-order exceptional points. Phys. Rev. Lett.131, 100202 (2023). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.