Sampling motifs on phylogenetic trees

Abstract

We present a method to find motifs by simultaneously using the overrepresentation property and the evolutionary conservation property of motifs. This method is applicable to divergent species where alignment is unreliable, which overcomes a major limitation of the current methods. The method has been applied to search regulatory motifs in four yeast species based on ChIP-chip data in Saccharomyces cerevisiae and obtained 20% higher accuracy than the best current methods. We also discovered cis-regulatory elements that govern the tight regulation of ribosomal protein genes in two distantly related insects by using this method. These results demonstrate that our method will be useful for the extraction of regulatory signals in multiple genomes.

A transcription factor can bind to short DNA segments in the regulatory regions (upstream, downstream, or intronic regions) of many different genes to control their expression. The common pattern of those short DNA segments bound by one transcription factor is called a motif, often represented as a weight matrix (Fig. 1). To find motifs by experimentation is time consuming. Therefore, many computational methods, including the expectation maximization (1–4), the Gibbs sampler (5–7), the progressive alignment (8), the word enumeration (9), and others (10), have been developed to find overrepresented segments (called putative motifs) from the regulatory sequences of a set of candidate genes, which can be obtained from prior biological knowledge, microarray experiments, or ChIP-chip experiments. In general, these computational methods can be divided into two types, those using sequences from a single species (1, 5, 6, 9) and those using sequences from multiple species (2–4, 7, 8, 10). We will briefly review the methods based on multiple species below.

Fig. 1.

Transcription factor binding sites and motif weight matrix. (a) A specific transcription factor can bind to 5- to 20-bp-long specific DNA segments in the regulatory region of different genes. Each line here represents one regulatory sequence of one gene, and the small rectangles on each line represent the transcription factor binding sites, called motif instances. Note those motif instances can be anywhere in the sequences. (b) The alignment of some motif instances from a, in which the ith position of one motif instance is aligned with the ith position of other motif instances. (c) From b, by assuming a flat prior distribution for the nucleotide composition at each position in the motif, we can obtain the weight matrix of the motif by using Bayes' theorem. Each column of the weight matrix corresponds to one position in the motif, in the order of the first position to the last position in the motif. Each row tells the probabilities that the corresponding nucleotide will occur at each position of the motif, in the order of the nucleotides A, C, G, and T. If all of the numbers in one column of the weight matrix are close to 0.25, the position corresponding to this column is degenerate and not so informative. If many positions are degenerate in the motif, this motif is a weak motif.

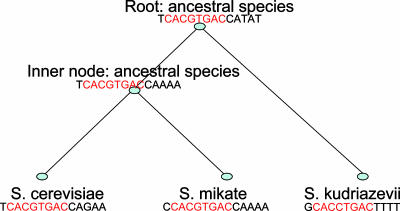
The intuition behind multiple species-based methods is that motif instances are more conserved than background sites in evolution. That is, the similarities among motif instances are higher than those among background sites in the orthologous gene sequences, which evolved from the same ancestral sequence and are in different current species. This conservation property of motifs can be illustrated more clearly by using phylogenetic trees. In Fig. 2, the motif instances show more conservation than the background sites in the gene met10 regulatory sequence in three current yeast species, Saccharomyces cerevisiae, Saccharomyces mikatae, and Saccharomyces kudriazevii. Moreover, the motif instance in S. cerevisiae is more similar to that in S. mikatae than to that in S. kudriazevii because the former two have shorter branch lengths (short divergence time) between them.

Fig. 2.

A cartoon of the evolution of the met10 gene on the phylogenetic tree. The tree tells the evolutionary history of the met10 regulatory sequence around the motif instances. That is, the ancient met10 regulatory sequence TCACGTGACCATAT at the root evolved into the regulatory sequence TCACGTGACCAAAA at the inner node and the met10 regulatory sequence GCACCTGACTTTT in yeast species S. kudriazevii; the sequence TCACGTGACCAAAA at the inner node evolved into the sequences TCACGTGACCAGAA and CCACGTGACCAAAA in the yeasts S. cerevisiae and S. mikatae, respectively. The three sequences at the bottom are orthologous sequences because they evolved from the same ancestral sequence at the root and they are in different species now. We have only the sequences at the bottom. The sequences of the ancestral species are unknown and are used here to describe the evolution model. The red nucleotides in each sequence represent the sites in the motif. Otherwise, the sites are from the background. The sites in the motif evolved according to a continuous Markov chain model, whereas the sites from the background evolved according to a different Markov chain model. Two substitution matrices are deduced from the two different Markov chain models to describe the evolution of the motif instances and the background sites, respectively. Note the length of a branch in the tree represents the time after the speciation from the corresponding ancestor. In the paper, we explicitly construct ancestral motif instances first and then find motif instances in the current species. Therefore, we do not need to worry about the correspondence of background sites in different species. That is, we do not need to know the sequences of the ancestral species (Appendix 2, which is published as supporting information on the PNAS web site).

Current methods (2–4, 7, 8, 10) using multiple species data, although already providing useful results, still suffer from one or more of the following limitations. Some of these methods can be applied only on two species (2), some treat orthologous sequences as statistically independent (8), some neglect the difference in the divergence time among species (7, 8, 10), and some try to find motifs in the aligned orthologous sequences and therefore require motif instances to be aligned correctly with the orthologous counterparts in the alignments (3, 4, 7, 8) (Data Set 1, which is published as supporting information on the PNAS web site, gives an example showing that motif instances are not always aligned correctly). To our knowledge, existing methods often perform poorly when the species are distant (say, 250 million years apart), or when the transcription factor binding sites are weak.

Here we present a method to take the evolution of DNA sequences into account. The method does not depend on the alignments of orthologous sequences to obtain the candidate motif instances, which avoids the arbitrary alignment score cutoffs to define the candidate functional sites, such as are often encountered in current methods, and allows the flexibility to find similar motif instances in the orthologous sequences even if those motif instances are inverted, translocated, or mutated. Therefore, we can find related sites in species that diverged as much as 250 million years ago. Moreover, the method fully uses the phylogenetic information and tracks the trace of the functional sites during evolution, i.e., the motifs are allowed to evolve, although at a slower rate than the background. Furthermore, the method simultaneously finds similar motif instances not only in many genes but also in orthologous sequences, which enables it to find weak but conserved motifs. Finally, the method automatically chooses the width for motifs.

Methods

Evolution Model. We assume the motif instances evolve more slowly than the nonfunctional background sites. Therefore two 4 × 4 substitution matrices are used to describe the evolution along every branch of the phylogenetic tree for the motif instances and the background sites, respectively. Each row of a matrix gives the probabilities of one type of nucleotide in the ancestor evolving into A, C, G, and T in the descendant, in the order of A, C, G, and T. For instance, the number at the entry (3, 2) in the left matrix in Table 1 tells that the probability for a nucleotide G in the ancestor to evolve into the nucleotide C in the descendant is 0.0347.

Table 1. An example of the substitution matrices for the branch from the common ancestor of S. cerevisiae and S. mikatae to S. cerevisiae in the yeast phylogenetic tree.

Background substitution matrix S. cerevisiae					Motif substitution matrix S. cerevisiae
Ancestor	A	C	G	T	Ancestor	A	C	G	T
A	0.7743	0.0347	0.1329	0.0581	A	0.8730	0.0182	0.0783	0.0305
C	0.0583	0.6791	0.0334	0.2292	C	0.0307	0.8170	0.0176	0.1347
G	0.2320	0.0347	0.6752	0.0581	G	0.1366	0.0182	0.8146	0.0306
T	0.0583	0.1369	0.0334	0.7714	T	0.0307	0.0805	0.0176	0.8712

For background evolution, regions that can be aligned† in the upstream region of orthologous genes are aligned, and the background nucleotide distribution and the branch lengths in the species tree are deduced from the multiple alignments by using maximal-likelihood estimation (11). Then the background substitution matrix for every branch is obtained from the estimated background nucleotide distribution and the branch lengths. Note that here and elsewhere in the paper, the species tree is used as the phylogenetic tree.

To define the motif substitution matrix for a branch, we simply decrease every branch length estimated above by a fixed proportion, say 50%, and then construct the motif substitution matrix for every branch from the decreased branch lengths. This is a primitive way to model the slower evolution of the functional motifs as compared with the background. In the future, with more experimentally verified motif sites available [in the TRANSFAC database (12)], motif substitution matrices may be constructed from them.

Gibbs Sampling. With the two evolution substitution matrices on every branch of the phylogenetic tree defined, we now explain how to implement the Gibbs sampler (6, 13, 14) to infer the model parameters and motif instances under the assumption that there is at most one motif instance for every gene. Gibbs sampler was originally used by Lawrence et al. (13) to find patterns in protein sequences. Later, it was improved to allow zero and multiple occurrences of motifs in one sequence (6) and flexible motif width (14). Here, we further extend the Gibbs sampler framework onto phylogenetic trees to find motifs. We discuss the two-species case in detail first, and the extension to the multiple-species case is briefly outlined at the end of the section.

We assume that the sequences of coregulated genes in the ancestral species at the root of the phylogenetic tree were generated from a mixture model, in which background sequences were generated from the multinomial distribution with parameter 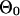, whereas motif instances were generated from the product multinomial distribution with parameter 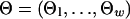, where each 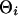is a multinomial distribution and w is the motif width. The background sequences and motif instances evolved according to two different continuous Markov chain models, i.e., at the ith branch of the tree, the background sequences in the parent species evolved according to a background substitution matrix M_0i, whereas the nucleotides in the motif instances evolved according to a motif substitution matrix M_1i. The notations for the model are summarized in Table 2 and some details of the mixture model are in Appendix 2 and Fig. 5, which is published as supporting information on the PNAS web site.

Table 2. Notations in our Gibbs sampler.

Symbol	Definition
	Known parameters
m	Number of current species; there are m – 1 ancestral species.
n	Number of genes in one species.
I	Species set. I = {0, 1,..., 2m – 2}.
S	The set of regulatory sequences from all current species.
	Unknown parameters but can be estimated before applying the Gibbs Sampler
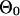	Background site model for species 0.
M0i	Background substitution matrix at the ith branch of the tree, i = 0, 1,..., 2m – 3.
M1i	Motif substitution matrix at the ith branch of the tree, i = 0, 1,..., 2m – 3.
	Unknown parameters that can be estimated from the Gibbs sampling
pi	Probability of a gene containing motif instances in the ith species, i ∈ I.
w	Motif width.
A(i)	Motif instance set in the ith species, i ∈ I.
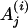	The motif instance in the jth gene of ith species, i ∈ I.
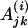	The kth nucleotide in the motif instance in the jth gene of the ith species, i ∈ I.
	Notations that are used for describing the model and no particular interest
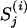	The regulatory sequence of the jth gene in the ith species, i ∈ I.
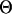	Motif model for species 0, the root species.

There are three main steps in our Gibbs sampler method: initialization, motif instance sampling, and parameter sampling. The last two steps are implemented iteratively after the sampler is initialized. In brief, the three steps are as follows.

Initialization step. p_i, the probability that a gene contains motif instances in the ith species, is sampled from a Beta(1, 1) prior distribution. 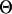is sampled from a Dirichlet prior distribution with parameter 1. w, the motif width, is sampled from a Poisson prior distribution with the mean parameter 6. With the above parameters, motif instances are sampled for the two daughter species and the neighborhood nucleotides around every motif instance are stored. For every orthologous gene group with at least one motif instance in the current species, the ancestral motif instance is assigned randomly to be one of its immediate daughter motif instances and the two neighboring nucleotides of the chosen motif instance are stored as the neighboring nucleotides of the ancestral motif instance. These neighboring nucleotides will be needed subsequently to update the motif width.

Motif instance sampling step. Motif instances at each node of the tree are updated from the root to the leaves for each orthologous gene group, one gene group at a time. This is done based on the parameter values from the previous step.

Parameter sampling step. p_i is sampled from the posterior distribution of p_i; w is updated by using the Metropolis–Hasting algorithm (15) according to the two neighboring nucleotides around the motif instances.

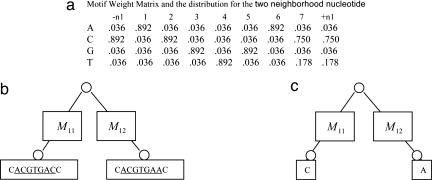
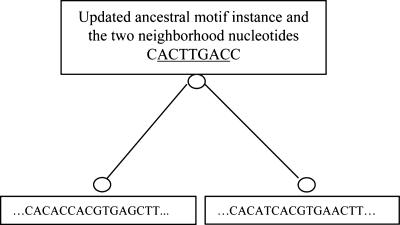
Motif instance sampling step. To describe the details of the Gibbs sampler at the motif instance updating step, we use the orthologous gene group for met10 in two yeast species, S. cerevisiae and S. mikatae, as an example (Fig. 3). First, the ancestral motif weight matrix is calculated by using the ancestral motif instances together with the two neighboring nucleotides from all other orthologous gene groups (Fig. 3a). Every column of the matrix except the first column and the last column is for one position in the motif, and the first column and the last column are for the left and the right neighboring positions of the motif, respectively. Every row of the matrix is for one type of nucleotides, in the order of A, C, G, and T. With the ancestral motif weight matrix, a nucleotide will be drawn for every position in the ancestral motif instance and two neighboring positions in met10. For every position, the conditional probabilities for observing A, C, G, or T at that position which results in the nucleotide(s) at the leaf (or leaves), given the sequences of the offspring motif instances and their neighboring nucleotides, are calculated by using Bayes' theorem. The nucleotides for each position in the ancestral motif instance and at the two neighboring positions are then sampled according to these probabilities. Given this updated ancestral motif instance, we can in turn update the motif instances at the leaf (leaves) where sequences are available. Motif instances for every leaf are sampled independently. We will describe how to sample a motif instance for met10 in S. cerevisiae here; see Fig. 4. First, for every position in the met10 upstream sequence in S. cerevisiae, we calculate the probability that the ancestral motif instance ACTTGAC will evolve into the substring of length w = 7 starting from that position in the sequence. Thus, if the sequence is n base pair long, we will have n - w + 1 such probabilities. From the previous iteration, we also have the probability p_i that there is no motif instance in met10 in S. cerevisiae. Then we sample one of the possibilities according to those n - w + 2 probabilities. Unless the “no motif” case is chosen, we thus obtain a segment in the upstream as the motif instance and its neighboring nucleotides on the left and the right are stored. After the motif instance is sampled for met10 in S. cerevisiae, the same procedure is followed for met10 in S. mikatae, provided the met10 gene sequence in S. mikatae exists. In this way, we can obtain motif instances for all species in the tree. After motif instances for one orthologous gene group are updated, the same procedure for the next orthologous gene group is applied until all orthologous gene groups are considered. At the end, we have updated all of the motif instances for every orthologous gene group.

Fig. 3.

Update ancestor motif instance for gene met10 in yeast. (a) The weight matrix is constructed from all ancestral motif instances except the one in gene met10, which are sampled at the previous step. We also calculate the nucleotide distributions for the two neighboring nucleotides, which are the first and the last column in the weight matrix. (b) We have motif instances ACGTGAC for S. cerevisiae met10 and ACGTGAA for S. mikatae met10 (underlined) and their neighboring nucleotides from the previous sampling cycle. M₁₁ and M₁₂ are the substitution matrices at the corresponding branch. Here both of them are the same as defined in Table 1. (c) For each position, including the two neighboring positions, we calculate the probability that A, C, G, or T will appear there. Then one of the A, C, G, and T is drawn based on those probabilities for that position. For example, the probability that A will appear at the ninth position (the right neighboring position of the motif) is 0.036 × 0.8730 × 0.0182 and divided by some normalization constant, which results in 0.029.

Fig. 4.

Update motif instances at the leaves. We update the motif instance for each species in the current ortholog group, one by one. For each species, the probability that a motif instance starts at each position is calculated. All those probabilities, together with the probability that there is no motif instance in the gene, are used. The sampler will randomly decide whether there is a motif instance and where it is if there is one, according to those probabilities. Note that only the ancestral motif instance that is underlined in the figure contributes to the updating of the motif instance in the current species. If there is a motif instance sampled, the two nucleotides on the left and the right of the motif instance are recorded for future use to decide the motif width.

Parameter sampling step. With the motif instances updated, updating the parameter p_i is straightforward by using its posterior distributions. For the motif width w, the Metropolis–Hasting algorithm (15) is used by proposing to increase or decrease the width by 1 from the left side or the right side. The acceptance or rejection of the change of the current motif width is done according to the joint posterior of w and A⁽⁰⁾ (see Appendix 1) by using the neighboring nucleotides and the ancestral motif instances as the observed data. Note that we limit the motif width to be from 5 to 20 bp, which is the usual range of motif widths. Moreover, we do not sample 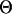anymore because 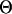is integrated out, which is what the collapsed Gibbs sampler (13) does (see Appendix 2).

Ranking motifs. After sampling for many cycles, our sampler will stay near some local optimal regions in the motif instance space. Calculating the Bayes factors, the ratio of the probability of generating the output motif instances in current species from a motif model to the probability of generating those motif instances from the background model may be the best way to report the significance of the motifs. Unfortunately, we cannot observe the ancestral motif instances, so it is difficult to find an explicit formula for the joint posterior distribution of the motif width and the motif instances in the current species given the sequence data in current species. Another way to report motif significance is to output the most frequent motif instances. However, storing the most frequent motif instances is not practical, given the many genes and the many species. To calculate the motif significance, we output the one with the best log posterior of w and A⁽⁰⁾. The log posterior is some constant plus the value from the following formula (14) (see Appendix 1):

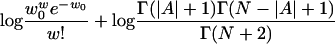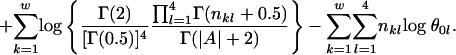In the formula, the first item is from the prior distribution of the motif width and w₀ is the prior width; the second item is from the effect of p₀, the probability that an ancestral gene will contain motif instances, for which Beta(1, 1) is used as the prior distribution; the third and the fourth items are for the motif weight matrix, in which θ_0l is the probability of nucleotide l happening in the background of the root species, and n_kl is the number of nucleotide l on position k in motif instances at the root species. As the parameter of the Dirichlet prior distribution for the parameters in the weight matrix, 0.5 is used.

The above Gibbs sampler for two species can be extended to multiple species. The only change is at the ancestral motif instance updating step. Instead of having an ancestral weight matrix, when we update the motif instance at the inner nodes we have a parent motif instance. At this time, the probability that a nucleotide occurs at a position is the multiplication of two items, the probability that the immediate parent nucleotide updated just now will evolve into this nucleotide and the probability that this nucleotide will evolve into the nucleotides in its immediate daughter instances. Bayes' theorem can again be applied to obtain the desired conditional probabilities.

Results

Harbison et al. (16) provided the target genes for 204 transcription factors in S. cerevisiae. For each transcription factor, the upstream sequences of target genes and their alignments are downloaded from Cliften et al. (17). By manually checking the TRANSFAC database (12), we found that there are a total of 53 transcription factors, for which we have at least 5 target gene sequences in S. cerevisiae and there is no ambiguity on the experimentally verified binding sites. The sampler is tested on those 53 transcription factor target gene sets.

To compare with other multiple species-based methods, we used available software phylocon (8) and compareprospector (7) on the same datasets. Our method not only has much higher sensitivity than the other two but also has higher specificity. See the summary in Table 3 and details in Table 4, which is published as supporting information on the PNAS web site.

Table 3. Comparison of sensitivity and specificity.

	Sensitivity		Specificity
Method	No.	%	No.	%
Gibbs sampler (ours)	41/53	77.4	41/49	83.7
compareprospector	(29 + 1)/53	56.6	(29 + 1)/48	62.5
phylocon	(24 + 1)/53	47.2	(24 + 1)/35	71.4

The + 1s in the second and third rows mean that one motif predicted by compareprospector and one motif predicted by phylocon look similar to the corresponding experimentally verified motif in TRANSFAC, respectively, although they do not satisfy our criteria of correct prediction. The number 41/53 in the first row means Gibbs sampler (ours) correctly made 41 predictions for the total 53 datasets; the numbers (29 + 1)/53 in the second and third rows have similar meaning. The number 41/49 in the first row means Gibbs sampler (ours) correctly made 41 predictions in a total of 49 predictions; the number (29 + 1)/48 in the second row and the number (24 + 1)/35 in the third row have similar meaning.

To investigate whether the incorrect predictions are due to failure of the sampler to search the whole space or due to fundamental inadequacy of our statistical model, we analyzed the incorrect predictions in more detail. Among the eight transcription factors for which we made wrong predictions, our method can identify the correct motif if it starts from a weight matrix constructed from a real motif instance in every case except the cases for RPN1 and SIP4 (we have only seven target gene sequences for the transcription factor RPN1 and SIP4, respectively). Moreover, the six motifs identified by starting from these proper prior distributions have higher scores than the corresponding ones in Table 4. Thus, these false positives are due to failure of the sampler to visit the global optimal region and are not due to inherent limitation of the model. Higher accuracy can be achieved if we improve the mixing of the sampling process.

To test the ability of the method to detect motifs in distant species, we applied it on the 63 ribosomal protein gene pairs from two insect species, fruit fly (Drosophila melanogaster) and mosquito (Anopheles gambiae). These species diverged >250 million years ago, and methods that rely on alignment typically give very poor result in this situation. Our sampler found a pair of motifs with common consensus, ACAGCTGTCAAAA. Moreover, it found motif instances in all 63 gene pairs. If meme (1) is applied on genes in individual species, GCGGTCACACT (fly) and CAGCTGTCAAACGG (mosquito) are identified in 41 and 44 genes, respectively. Although the underlined parts in the motif consensus identified by meme (1) look similar, the instances corresponding to the two motifs in the orthologous gene pairs rarely share >5 nucleotides in the underlined 9-nt parts. The motif instances found by our method share a median 8 bp of 13 positions. Moreover, the motif ACAGCTGTCAAAA identified by our method is similar to an experimentally verified motif CAGTCACA, which was found to regulate 14 ribosomal protein genes in Schizosaccharomyces pombe (17). See the motif instances for every gene in Appendix 3, which is published as supporting information on the PNAS web site.

Although phylocon (8) outputs a motif ACCAGCTGTCAAAGGGG, which contains the one identified by our method, only 7 orthologous pairs are found by phylocon (8) to contain the motif instances. Moreover, the p value of this motif is not significant compared with those of other motifs output by phylocon (8). As to compareprospector (7), there is none in the top 15 output motifs similar to the one identified by our method. Note that 63 motif instance pairs found by our method share 8 bp of 13 positions on average (Appendix 3). This shows that using prealigned sequences as input to find motifs will likely miss many motif instances for distant species, because those alignments in general cannot take the evolutionary distance into account, and many “well” conserved instances are missed.

Discussion

There are other ways to define the evolution mechanism. For background evolution, ancient repeats in the genome or synonymous sites in proteins can be used instead of using the gene upstream regions. As to the motif evolution, the substitution matrix can be specified by users. For example, the evolution mechanism used by phyme (4) can be readily applied here. The only requirement for the motif substitution matrix is that the matrix should have larger diagonal numbers than those in the background evolution matrix. The more similar the matrix is to the identity matrix, the more conserved motifs the users are trying to find. Moreover, our method is very robust to the motif substitution matrices; the motifs found for the 53 yeast transcription factors remain basically the same when using many different motif substitution matrices. More research on the evolution of motif instances (18) should provide better ways to define the evolution mechanisms, which will eventually improve the accuracy of the sampler.

There are a number of complications in directly applying the Gibbs sampler here. First, there may be more than one motif instance in some genes, and it is computationally expensive to explore all of the possible origin relationship of motif instances in orthologous genes. Second, there is no sequence for species at any inner node and the root. Thus, the ancestral motif instances cannot be obtained directly from the ancestral sequences. To resolve the first difficulty, at most one motif instance per gene is sampled, with the aim of picking up the reciprocal “best” matching motif instance pairs. After the motif is found, we can then scan the orthologous sequences to find more motif instances if needed. For the second difficulty, ancestral motif instances are sampled based on the motif instances at leaves from the previous step and the ancestral weight matrix constructed from all other gene groups. This procedure is reasonable because there must be some ancestral motif instances that evolved into the current ones at leaves, given the current ones are real motif instances (i.e., those motif instances are related). See Fig. 3 for details. Note that here we cannot use the alignments to provide good approximations for the whole ancestral sequences in every orthologous gene group, although they are suitable for estimating the background evolution mechanism and the background nucleotide distribution, because many sequence regions in the current species cannot be aligned at all.

Our sampler samples motif instances from scratch instead of from prealigned regions. The motif instances and their counterparts in other species may not be in the prealigned regions when the motif instances are weak. Moreover, with more divergent species, sometimes it is even difficult to find ungapped segments in alignments. Our sampler emphasizes that the motif instances and their counterparts are more similar to each other than motif instances from different orthologous gene groups, which avoids artificially assuming the matching of motif instances and their counterparts.

We do not assume that the motifs in different species are the same or similar. This lack of assumptions makes the model an attractive tool to find different motifs that share the same origin. With the advance of research on the evolution of transcription factor binding sites, we can define a better background evolution model for very divergent species, and distantly related transcription factor binding sites can be discovered.

The current method of calculating motif significance in our sampler is not appealing. The best way to assess the significance is the Bayes factor. Unfortunately, no explicit posterior probabilities can be deduced because the ancestral motif instances are not observed directly. However, approximation based on the em (Expectation Maximization) algorithm (19) can be used. But we have to calculate the significance at every iteration in the sampler. Approximations for calculating Bayes factor are still computationally expensive.

Although the sampler has many appealing aspects, it should be considered as just the first step in modeling motif evolution on phylogenetic trees. With more research on the evolution of transcription factor binding sites, better understanding about the mechanisms of evolution will greatly help the improvement of the sampler. Moreover, the current sampler is often tested on about 1 kb upstream of genes. Many mammalian regulatory elements are still out of this range. Enhancing the sampler should make it applicable to more data.

Appendix 1

Here we are going to show how to find the log posterior for w and A⁽⁰⁾. First we assume that the ancestral gene sequences S are given. Thus, we can think of A⁽⁰⁾ as a set of position indicator functions that track the locations of the motif instances. Then we have

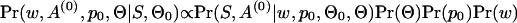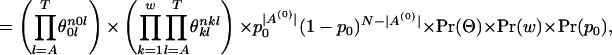where 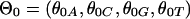is the background nucleotide distribution parameter, 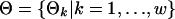and 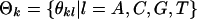are the parameters in the motif weight matrix. Assume a Dirichlet prior D(β_k) for 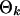(β_k = (β_kA, β_kC, β_kG, β_kT)), a Beta(1, 1) prior for p₀, and a Poisson(w₀) prior for w on the above formula. Now we want to integrate out p₀ and 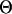. To integrate out p₀, we have

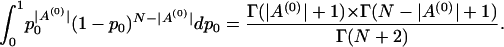To integrate out 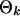, we have

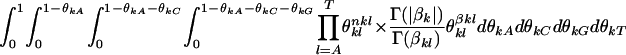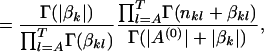where 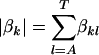. Therefore, the log posterior of w and A⁽⁰⁾ becomes

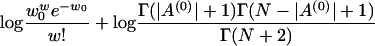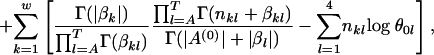where the last term is from the items containing 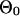, for which we subtract a constant that is the log probability that all sequences are generated from the background model .

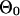Note that we do not actually need the exact sequences S or the locations of the motifs A⁽⁰⁾. All we need is n_kl, which are known from the ancestral motif instances A⁽⁰⁾. Therefore, the above posterior distribution of A⁽⁰⁾ and w is valid even if S is unknown.