A newly custom coordinate system used for preoperative planning of robotic-assisted total knee arthroplasty

Abstract

Purpose

Preoperative planning is critical for total knee arthroplasty (TKA) performed with surgical robots, as it involves establishing a coordinate system to calculate the angle values of the components. This coordinate system serves as a reference during the surgical planning stage. This study aimed to develop a newly custom coordinate system suitable for integration with a surgical robot system.

Methods

The “Skywalker” surgical robot system was used to import computed tomography (CT) images of the entire lower extremities from 50 patients diagnosed with osteoarthritis. Three-dimensional reconstruction was subsequently performed. The TKA component was positioned at a fixed angle using the newly developed custom coordinate system. The angle values of the components, based on the standard CT coordinate system, were then recorded without altering their positioning. These values were analyzed to assess the differences between the two coordinate systems.

Results

The mean and standard deviation values for the coronal, sagittal, and transverse plane positioning of the femoral component (absolute value of error) were 0.004° ± 0.020°, 0.006° ± 0.024°, and 0.158° ± 0.186°, respectively. Similarly, the mean and standard deviation values for the coronal, sagittal, and transverse plane positioning of the tibial component (absolute value of error) were 0.544° ± 0.452°, 0.042° ± 0.076°, and 0.348° ± 0.445°, respectively.

Conclusion

This newly developed custom coordinate system can be employed for preoperative planning in Skywalker surgical robot system-assisted TKA, particularly for patients with significant positional abnormalities in their CT scans.

1. Introduction

Knee osteoarthritis (KOA) predominantly affects the knees, making it the most commonly impacted joint. Individuals with KOA typically suffer from pain, stiffness, and functional impairment. Total knee arthroplasty (TKA) is regarded as the standard treatment for end-stage KOA [1]. While TKA has demonstrated improved implant longevity and positive clinical outcomes, patient dissatisfaction rates remain as high as 12%–20 % [2,3]. To address this issue, surgical robots have been developed and are widely used in TKA, facilitating precise reconstruction of lower extremity alignment and yielding favorable short-term clinical outcomes [[4], [5], [6], [7]]. A key advantage of surgical robot systems is their ability to conduct comprehensive preoperative simulations and simulative component positioning within the TKA preoperative plan, thereby ensuring accurate angles for varus-valgus, eversion–retroversion, and internal-external rotation [8].

Currently, many arthroplasty surgical robots utilize CT for preoperative planning. The standard CT coordinate system is depicted in Fig. 1. Typically, reviewing patient images based on the standard CT coordinate system does not hinder the surgeon's understanding of the patient's anatomical structure. However, in certain special cases, issues may arise when calculating the angles for preoperative component positioning using the standard CT coordinate system. For instance, if the patient's lower extremity is not fully extended when positioned flat on the CT machine, certain angles of internal-external rotation or flexion-extension might occur. Additionally, the presence of lower extremity deformities can result in internal or external rotation. In such cases, using the standard CT coordinate system for surgical robot preoperative planning can lead to significant deviations when projecting the component's simulation angle onto the standard CT coordinate system. As a result, the projected angle may no longer reflect its intended value. Continuing with surgical planning based on a robot system using a deviated angle could lead to improper positioning of the prosthesis, potentially causing postoperative complications such as pain, component instability, malalignment, and ultimately, surgical failure [9]. Therefore, it is essential to establish a precise lower extremity coordinate system.

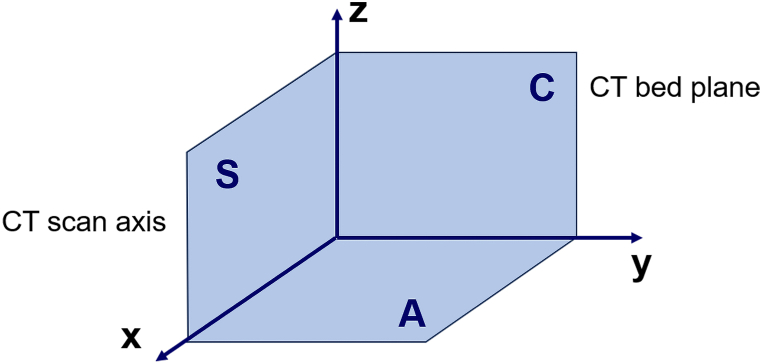
Fig. 1.

The illustration of standard CT coordinate system.

The coordinate system of CT scan takes the bed plane as coronal plane C; the sagittal plane is plane S perpendicular to the coronal plane through the transverse axis of the CT machine; and the plane pairwise perpendicular to both the coronal plane and the sagittal plane is transverse plane A. The intersecting lines of the three planes form the x, y, and z axes with directions.

Several coordinate systems for the lower extremity have been proposed. Sohail et al. [9] developed a femoral coordinate system based on articular surfaces, while Innocenti et al. [10] designed and validated a coordinate system for the human patella using bony landmarks identified through CT scans. Nagle et al. [11] introduced a functional lower extremity coordinate system for biomechanical testing. However, these studies were all conducted utilizing sawbones or cadaver specimens, and lacked clinical patient data to validate their effectiveness. Furthermore, there are no reports of custom coordinate systems specifically designed for robotic-assisted TKA. Therefore, this study aims to: 1) develop a novel custom coordinate system for use in the surgical robot system to address abnormal scenarios, and 2) verify the effectiveness of this new custom coordinate system by comparing it with the standard CT coordinate system.

2. Methods

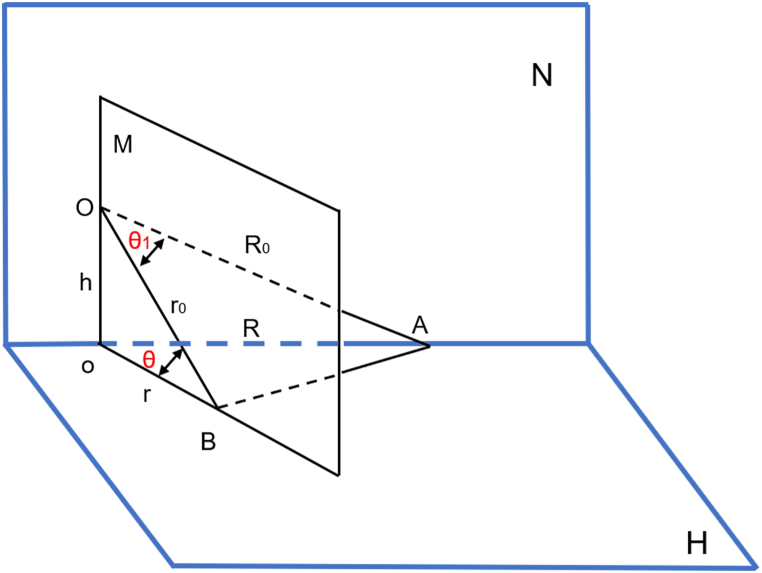
The angles displayed in the robot system are projections on the corresponding plane of the intersection angle between the component axis and the bone axis. For example, the projection angle in the coronal plane between the distal plane of the femoral component and the femoral force line is calculated as the coronal angle of the femoral component. However, the spatial angles may differ when projected onto different planes. As shown in Fig. 2, angle ∠AOB represents a plane angle in space, with points A and B marking the intersection points of the angle and surface H, respectively. Angle ∠AoB is the projection of ∠AOB on surface H. Plane N is formed by points A, o, and O, while plane M is formed by points B, o, and O. Planes N and M are perpendicular to surface H. To explore the projection rule of the plane angle, a mathematical model between the plane angle and its projection was established using the law of cosines. To simplify the model, assuming ∠AOB = θ₁, ∠AoB = θ, OA = R₀, OB = r₀, oA = R, oB = r, Oo = h.

In △AOB, AB² = r₀²+R₀²-2r₀R₀cosθ₁,

while in△AoB, AB² = r²+R²-2rRcosθ.

Because AB = AB, r₀²+R₀²-2r₀R₀cosθ₁ = r²+R²-2rRcosθ , (1)

In △AoO, R₀² = h²+R² (2)

In △BoO, r₀² = h²+r² (3)

Fig. 2.

Projection of the angle in space.

∠AOB is a plane angle in any space, where A and B are the intersection points of both sides of the angle and surface H, respectively. ∠AoB is its projection on surface H. The three points, namely A, o, and O, form plane N. The three points, namely B, o, O, form plane M. Both plane N and plane M are perpendicular to plane H. ∠AOB = θ₁, ∠AoB = θ, OA = R₀, OB = r₀, oA = R, oB = r, Oo = h.

Substituting equations (2), (3) into equation (1) for arrangement, the mathematical model between θ1 and θ can be obtained as equation (4):

$$\mathit{cos}{\mathrm{\theta }}_1=\frac{h^2+\text{rRcos}\mathrm{\theta }}{\sqrt{\left(h^2+R^2\right)\left(h^2+r^2\right)}}$$ (4)

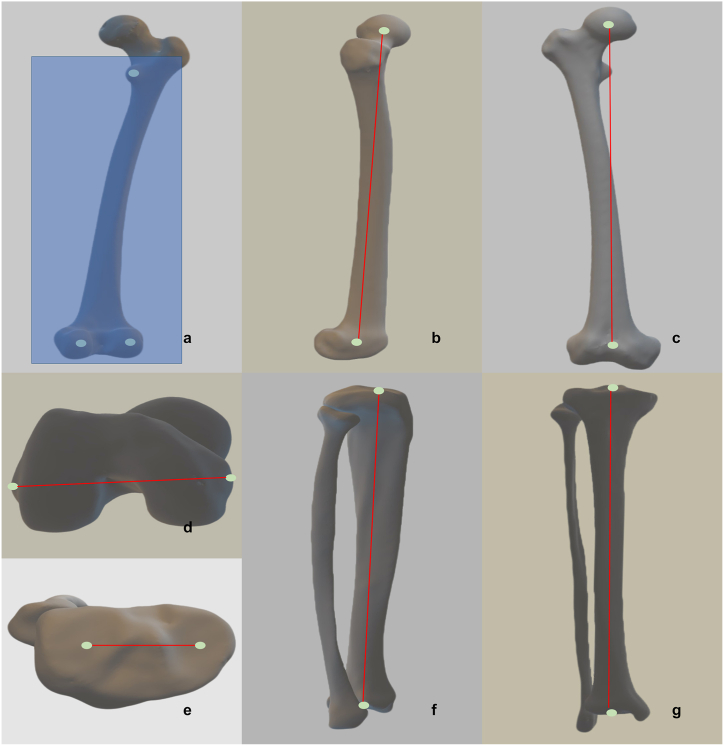
Based on the aforementioned mathematical derivation, we defined the newly developed custom coordinate system for the surgical robot as follows. First, a 3D reconstruction was performed using CT scan data. After segmenting the bone model, specific marker points were selected. These included marker points on the femur and tibia, as illustrated in Fig. 3. The femoral marker points consisted of the center point of the femoral head, the most concave point of the medial epicondyle, the most convex point of the lateral epicondyle, the most convex point of the posterior medial condyle, the most convex point of the lateral posterior condyle, the most convex point of the lesser trochanter, and the center point of the femoral knee joint. The tibial marker points included the center point of the knee joint, the most concave point of the medial tibial plateau, the most concave point of the lateral tibial plateau, and the center point of the ankle joint.

Fig. 3.

The illustration of anatomical point selection.

In Fig. 3a, the most convex point of the lesser trochanter, the most convex point of the medial posterior condyle, and the most convex point of the lateral posterior condyle were selected on the back of the femur, and the coronal plane of the custom coordinate system was constructed with the three points. In Fig. 3b, the center point of the femoral head and the center point of the femoral knee are projected on the sagittal plane of the femur. In Fig. 3c, the center point of the femoral head and the center point of the femoral knee joint are projected on the coronal plane of the femur. In Fig. 3d, the most concave point of the medial epicondyle of the femur and the most convex point of the lateral epicondyle of the femur are connected to form the epicondylar line, which is projected on the transverse plane of the femur. In Fig. 3e, the line between the most concave point of the medial tibial plateau and the most concave point of the lateral tibial plateau is projected on the tibial transverse plane. In Fig. 3f, the center point of the tibial knee and the center point of the ankle joint are projected on the tibial sagittal plane. In Fig. 3g, the center point of the tibial knee joint and the center point of the ankle joint are projected on the tibial coronal plane.

Subsequently, the newly custom coordinate system for the femoral side was developed, as shown in Fig. 4. The coronal plane was defined by passing through three key points: the most convex points of the femoral medial epicondyle, the femoral lateral epicondyle, and the lesser trochanter. The sagittal plane was established by connecting the center point of the femoral head with the center point of the knee joint, which served as the femoral force line axis. This plane was oriented perpendicular to the coronal plane along the femoral force line. The transverse plane was positioned orthogonally to both the coronal and sagittal planes. The intersection of these three planes formed the x-, y-, and z-axes, each with a defined direction. The custom coordinate system for the tibial side is illustrated in Fig. 5. This system was defined by the plane passing through three points: the most concave point of the medial tibial plateau, the point on the lateral tibial plateau, and the center point of the ankle joint, all located in the coronal plane. The sagittal plane was established by connecting the center point of the femoral knee joint with the center point of the ankle joint, serving as the tibial force line axis. This plane was positioned perpendicular to the coronal plane through the tibial force line. Additionally, the transverse plane was positioned orthogonally to both the coronal and sagittal planes. The intersecting lines of the three planes formed the x-, y-, and z-axes, each with a defined direction. Based on these principles, we developed a custom coordinate system that we determined to be anatomically significant.

Fig. 4.

The illustration of femoral coordinate system.

In the custom coordinate system for the femur, the most convex point of the lesser trochanter, the most convex point of the medial posterior condyle, and the most convex point of the lateral posterior condyle were selected on the back side of the femur, and coronal plane C of the custom coordinate system was constructed with the three points. The red line on the figure is the line between the center of the femoral head and the center of the femur knee joint, which forms the mechanical axis of the femur. The sagittal plane is plane S perpendicular to the coronal plane through the mechanical axis, and the plane pairwise perpendicular to the coronal plane and the sagittal plane is transverse plane A. Femoral coordinate system, Z: the intersection line between coronal plane C and the sagittal plane S, point to proximal. Y: the intersection line between sagittal plane S and the transverse plane A, point to anterior. X: the line perpendicular to both Z and Y, point to lateral.

Fig. 5.

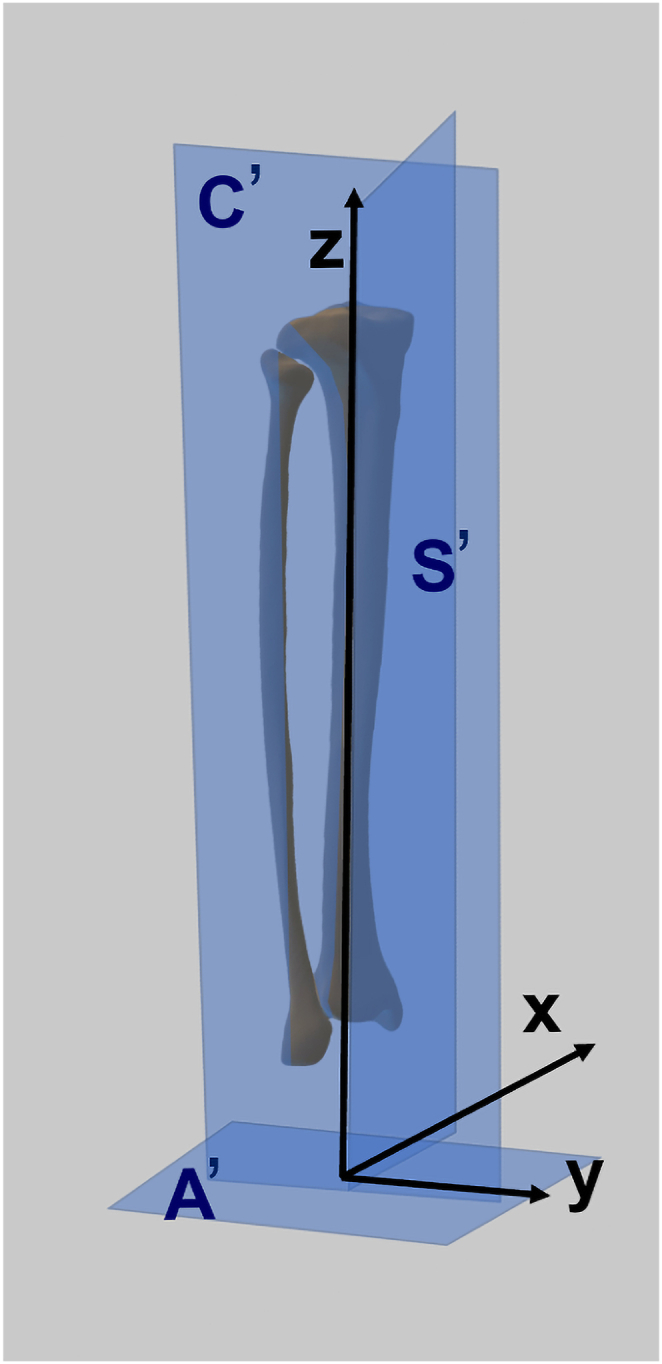
The illustration of tibial coordinate system.

In the custom coordinate system of the tibia, the most concave point on the medial tibial plateau, the most concave point on the lateral tibial plateau, and the center point of the ankle joint were selected to construct coronal plane C′ of the custom coordinate system. The center of the tibial knee joint and the center of the ankle joint connect to form a mechanical axis of the tibia. The sagittal plane is plane S′ perpendicular to the coronal plane through the mechanical axis, and the plane pairwise perpendicular to the coronal plane and the sagittal plane is transverse plane A’. Tibial coordinate system, Z: the line connecting the center point of the tibia knee joint and the center point of the ankle joint, point to proximal. Y: the line perpendicular to the coronal plane C′, point to anterior. X: the line perpendicular to both Z and Y, point to lateral.

Next, we searched the imaging database of Shanghai Ninth People's Hospital for CT images of patients with KOA. The inclusion criteria for selecting images required a diagnosis of KOA (Kellgren-Lawrence grade III or IV), proper positioning during the CT scan, and the absence of osteophytes that could impact the anatomical structure. Exclusion criteria involved cases where osteophyte growth affected the key anatomical structures or where abnormal lower extremity curvature was observed. CT data encompassing the entire lower extremity, including the full femur, tibia, and fibula, were obtained from 25 patients with left knee OA and 25 patients with right knee OA, for a total of 50 patients. The cohort included 15 males and 35 females, with an average age of 68 years (range: 34–80 years). All CT images were acquired using a Philips iCT scanner (Royal Dutch Philips Electronics Ltd., Amsterdam, Netherlands) under a standardized protocol (120 kV, 380 mAs, 1 mm slice collimation, supine position). After obtaining Ethics Committee approval (registration number: SH9H-2019-T212-2), the 50 full-lower-extremity CT scans were imported into the “Skywalker” surgical robot system developed by our team (Microport Inc., Shanghai, China) for 3D reconstruction. Upon importing the CT images, two different colored pens were used to mark the internal contours and external boundaries of the bones. After marking, the CT images were segmented. The segmentation of CT images for both coordinate systems was performed by the same professional image processing engineer and then reviewed by the same experienced orthopedic surgeon. Once the segmented CT images met reconstruction requirements, the three-dimensional bone model was established. Using the segmented and reconstructed bone model, we selected the appropriate type and size for the component and adjusted its position and orientation to achieve optimal varus-valgus angles, anteversion-retroversion, and internal-external rotation. The positioning of the femoral and tibial components (Microport Inc., Shanghai, China) within the newly developed custom coordinate system is shown in Fig. 6. The definition of the component angles is presented in Table 1. The positioning angle of the femoral component in the newly developed custom coordinate system was set as follows: 0° varus in the coronal plane, 0° anteversion in the sagittal plane, and 0° external rotation in the transverse plane. Similarly, the tibial component was positioned in the new custom coordinate system with the following angles: 0° varus in the coronal plane, 5° retroversion in the sagittal plane, and 0° external rotation in the transverse plane. We defined positive values as varus in the coronal plane, anteversion in the sagittal plane, and internal rotation in the transverse plane, while negative values were defined as valgus in the coronal plane, retroversion in the sagittal plane, and external rotation in the transverse plane. Once the component positioning was secured, the angles of the components based on the standard CT coordinate system were recorded. To validate the reliability of this study, the component positioning angles were reviewed by three experienced male orthopedic surgeons, and comparisons were made between their assessments. Interobserver reliability was calculated using the intraclass correlation coefficient (ICC), which ranges from 0 to 1, with values closer to 1 indicating stronger interobserver reliability. Subsequently, the differences in varus-valgus, anteversion-retroversion, and external-internal rotation angles of the femoral and tibial components were calculated separately for the two coordinate systems. Statistical analysis was conducted using SPSS (version 21.0; IBM Corp., Armonk, NY, USA), and a paired t-test was employed to test the null hypothesis. The level of significance (p) was set at 0.05.

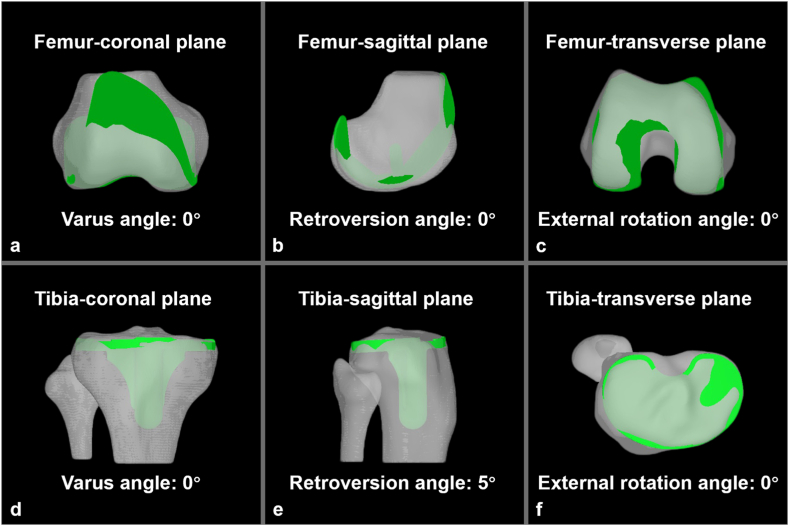
Fig. 6.

Fixed position of the components in custom coordinate system.

Fig. 6a–c shows that in the positioning of the femoral component, varus in the coronal plane is 0°, retroversion in the sagittal plane is 0°, and external rotation in the axial plane is 0°. Fig. 6d–f shows that in the positioning of the tibial component, varus in the coronal plane is 0°, retroversion in the sagittal plane is 5°, and external rotation in the axial plane is 0°.

Table 1.

The definition of the component angle.

CFCA	SFCA	TFCA	CTCA	STCA	TTCA
The projection angle in coronal plane between the distal plane of the femoral component and the femoral force line	The projection angle in sagittal plane between the distal plane of the femoral component and the femoral force line	The projection angle in the transverse plane between the transverse axis of the femoral component and the transepicondylar line	The projection angle in coronal plane between the distal plane of the tibial component and the tibial force line	The projection angle in sagittal plane between the distal plane of the tibial component and the tibial force line	The projection angle in the transverse plane between the proximal plane of the tibial component and the tibial force line

CFCA: coronal femoral component angle SFCA:sagittal femoral component angle TFCA: transverse femoral component angle CTCA: coronal tibial component angle STCA: sagittal tibial component angle TTCA: transverse tibial component angle.

3. Results

Interobserver reliability showed a high level of agreement, with an average ICC of 0.92 (95 % CI [0.88 to 0.97]) for the angle data. After setting the positioning angles of the components in the newly developed custom coordinate system, the corresponding angles in the standard CT coordinate system were obtained. The statistical values are presented in Table 2. By comparing the component angles under the standard CT coordinate system with the fixed angles in the newly custom coordinate system, the following results were observed: The mean and standard deviation of the femoral component positioning (CT minus custom) in the coronal, sagittal, and transverse planes were 0.004° ± 0.020° (range: 0°–0.1°), −0.002° ± 0.025° (range: 0.1°–0.1°), and −0.034° ± 0.243° (range: 0.7°–0.9°), respectively. For the tibial component (CT minus custom), the mean and standard deviation values in the coronal, sagittal, and transverse planes were 0.216° ± 0.677° (range: 1°–1.9°), 0.034° ± 0.080° (range: 0.1°–0.3°), and 0.064° ± 0.564° (range: 1°–2°), respectively. The p values from the paired t-tests comparing the component positioning angles in the standard CT coordinate system and the newly custom coordinate system were as follows: coronal plane positioning of the femoral component, 0.159; sagittal plane positioning of the femoral component, 0.569; transverse plane positioning of the femoral component, 0.327; coronal plane positioning of the tibial component, 0.029; sagittal plane positioning of the tibial component, 0.004; and transverse plane positioning of the tibial component, 0.426.

Table 2.

Statistical results of angle value in the standard CT coordinate system (°).

	Femoral component positioning			Tibial component positioning
	Varus-valgus	Anteversion-retroversion	Internal-external rotation	Varus-valgus	Anteversion-retroversion	Internal-external rotation
The fixed angle value of the newly custom coordinate system	0	0	0	0	−5	0
The average angle value of the standard CT coordinate system	0.004	−0.002	−0.034	0.216	−4.966	0.064
The standard deviation of angle of the standard CT coordinate system	0.020	0.025	0.243	0.677	0.080	0.564
The maximum angle of the standard CT coordinate system	0.1	0.1	0.9	1.9	−4.7	2
The minimum angle of the standard CT coordinate system	0	−0.1	−0.7	−1	−5.1	−1
The median angle of the standard CT coordinate system	0	0	0	0.05	−5	0
t values between the standard CT coordinate system and the newly custom coordinate system	1.429	−0.573	−0.990	2.256	3.012	0.803
P values between the standard CT coordinate system and the newly custom coordinate system	0.159	0.569	0.327	0.029	0.004	0.426

The coronal plane had a positive value in varus and a negative value in valgus; the sagittal plane had a positive value in anteversion and a negative value in retroversion; and the transverse plane had a positive value in internal rotation and a negative value in external rotation.

The absolute value of the difference (CT minus custom) was used to calculate the absolute error between the two coordinate systems. The statistical results are shown in Table 3. The mean and standard deviation of the absolute error for the femoral component positioning in the coronal, sagittal, and transverse planes were 0.004° ± 0.020° (range: 0°–0.1°), 0.006° ± 0.024° (range: 0°–0.1°), and 0.158° ± 0.186° (range: 0°–0.9°), respectively. For the tibial component, the mean and standard deviation of the absolute error in the coronal, sagittal, and transverse planes were 0.544° ± 0.452° (range: 0°–1.9°), 0.042° ± 0.076° (range: 0°–0.3°), and 0.348° ± 0.445° (range: 0°–2°), respectively.

Table 3.

Statistical results of the absolute value of error between the two coordinate systems (°).

Error between the two coordinate systems	Femoral component positioning			Tibial component positioning
	Varus-valgus	Anteversion-retroversion	Internal-external rotation	Varus-valgus	Anteversion-retroversion	Internal-external rotation
The average of the absolute value	0.004	0.006	0.158	0.544	0.042	0.348
The standard deviation of the absolute value	0.020	0.024	0.186	0.452	0.076	0.445
The maximum of the absolute value	0.1	0.1	0.9	1.9	0.3	2
The minimum of the absolute value	0	0	0	0	0	0
The median of the absolute value	0	0	0.1	0.5	0	0.2

4. Discussion

Total knee arthroplasty (TKA) is an effective treatment for relieving pain and restoring joint function in arthritic knees [1]. Achieving precise component alignment is crucial for a successful TKA outcome, as several studies have shown that accurate target alignment is associated with improved clinical results [[12], [13], [14]]. However, with conventional manual instrumentation, identifying key alignment landmarks such as the center of the knee can be challenging. Even the most advanced mechanical instrumentation systems rely on visual inspection to confirm the accuracy of component placement during TKA [15]. The use of more precise 3D imaging techniques, such as CT, may improve the accuracy of component positioning. Since the anatomical coordinate system constructed on a 3D bone model serves as the reference for all calculations, it is essential to establish a well-defined coordinate system. Various approaches have been proposed for defining the bony coordinate system of the lower extremities. Sohail et al. [9] introduced a new definition of the surgical transepicondylar axis (sTEA) for the femoral coordinate system (FCS), based on articular surfaces. They identified the turning points of the lateral and medial fitted arcs as the femoral transverse axis, which were registered on the articular surfaces. The sTEA based on the condyles was experimentally measured on a 3D-printed bone using an Optitrack tracking setup. The angle between the designed sTEA and Whiteside's line was found to be 92.72°, aligning closely with previously reported values in the literature. The authors suggested that the axis defined by this curve-fitting method is parallel to the sTEA and can be used as the transverse axis for the FCS. Nagle et al. [11] introduced a functional lower extremity coordinate system (CS) designed for in vitro biomechanical testing. This functional CS is based on joint motion with low resistance during loading profiles, rather than on anatomical landmark selection. When comparing the kinematics between the functional CS and the anatomical CS, significant improvements in reproducibility were observed: 7.4 mm at the tibia origin (p < 0.001), 3.4 mm at the femur origin (p < 0.001), and 2.9° at the femur FE-axis (p < 0.001). However, these studies have not yet incorporated the lower extremity coordinate system into surgical robotic applications. In this study, we developed a newly custom coordinate system specifically designed for TKA surgical robots. We found that the range of coronal, sagittal, and transverse plane angles (CT vs. custom) for the femoral component positioning was within ±1°, while for the tibial component, it did not exceed 2°. The mean and standard deviation values for the absolute error of the femoral component positioning in the coronal, sagittal, and transverse planes were 0.004° ± 0.020°, 0.006° ± 0.024°, and 0.158° ± 0.186°, respectively. Similarly, for the tibial component, the mean and standard deviation values for the absolute error in the coronal, sagittal, and transverse planes were 0.544° ± 0.452°, 0.042° ± 0.076°, and 0.348° ± 0.445°, respectively. These results demonstrate that our newly developed custom coordinate system exhibits excellent consistency when compared to the angles from the standard CT coordinate system for these 50 lower extremity cases.

Robotic systems for knee arthroplasty can be categorized into image-based and imageless systems [16]. In both approaches, the patient's anatomy must be registered by mapping points on the bone during the registration process, enabling the robot to establish its positional relation to the patient's anatomy. Although numerous studies on image-based surgical robots for TKA have reported favorable outcomes in lower extremity alignment reconstruction and satisfactory short-to medium-term clinical results, they do not discuss the specific coordinate systems utilized by these robots [[17], [18], [19], [20], [21]]. In the case of image-based surgical robot systems, we observed that many patients' CT scans exhibited anatomical or positional abnormalities, leading to notable rotation or curvature in the lower extremities. For such patients, when a surgical robot system is used for preoperative planning, projecting characteristic angles onto the standard CT coordinate system may significantly affect the positioning angle of the component. This could cause the simulated component positioning angles to lose their relevance as a reference. In these situations, our newly developed custom coordinate system can resolve this issue, providing a reliable reference for the component positioning angles. Furthermore, Glowalla et al. [22] discovered a degree of deviation between the position of the component as assessed intraoperatively using the MAKO surgical robot and postoperatively through radiographic evaluation. We hypothesize that this deviation may result from the use of different coordinate systems. By employing the same coordinate system for preoperative planning, intraoperative measurement, and postoperative evaluation, such deviations could potentially be minimized.

In an imageless system, an anatomical model is embedded in the software and refined through registration. The accuracy of this registration depends solely on the data points collected by the surgeon during surgery. Without a preoperative image or plan, the component size, position, and alignment are determined intraoperatively after patient registration. The advantages of the imageless system include reduced costs, as there is no need for CT or MRI scans, no preoperative radiation exposure, and increased convenience for the patient. However, potential disadvantages include the loss of detailed information on bone structure and the absence of preoperative planning. Imageless knee-repositioning robots include systems like Praxim [23] and Navio [24]. Since CT imaging data are not required for imageless surgical robots, a custom coordinate system must be built to serve as a valuable reference for surgical planning. In our case, the maximum error between the newly developed custom coordinate system and the standard CT coordinate system was within 2°, indicating that this custom coordinate system can reliably be used as a reference.

After determining the differences in component positioning angles between the standard CT and our newly developed custom coordinate system, we integrated the custom system into the “Skywalker” total knee arthroplasty robot. We then evaluated the osteotomy performance of the “Skywalker” robot by conducting an osteotomy experiment on 20 femur sawbone models and 20 tibia and fibula sawbone models. We found that the angle deviation between the planned osteotomy plane and the actual osteotomy plane at each osteotomy position did not exceed 1.03° ± 0.55°, and the resection thickness at each osteotomy site was less than 0.78 ± 0.71 mm [25]. Additionally, we conducted a prospective clinical study involving 31 patients who underwent total knee arthroplasty with the assistance of the “Skywalker” surgical robot. The osteotomy accuracy observed in this clinical study was similar to the results of the sawbone experiment, with the resection thickness at each osteotomy site being less than 0.63 ± 1.12 mm. The postoperative lower extremity alignment of all 31 patients fell within 180° ± 3° [26]. As an integral part of the “Skywalker” surgical robot, we believe that the newly developed custom coordinate system plays a significant role in the final osteotomy accuracy. However, further investigation is needed to determine whether more precise osteotomy can lead to improved clinical outcomes, such as reduced intraoperative blood loss, lower postoperative infection rates, and improved range of motion.

One potential limitation of this study is that only simulated component positioning analyses have been performed. Further clinical trials are necessary to validate the effectiveness of the newly developed custom coordinate system in reducing surgical time, blood loss, and improving postoperative outcomes. Additionally, this study was based on the “Skywalker” surgical robot system, and it remains unclear whether the proposed custom coordinate system is applicable to other TKA surgical robot systems. Further testing on other types of TKA surgical robot systems could be conducted to assess its compatibility.

5. Conclusion

Preoperative planning is essential for TKA using surgical robots, as it requires the construction of a coordinate system to determine the component angles in each plane, providing surgeons with a reference for surgical planning. In this study, we developed a custom coordinate system for use in the surgical robot system and compared it with the standard CT coordinate system. Overall, the angle range (CT minus custom) for the three planes of femoral component positioning was significantly smaller than that of the tibial component, indicating that the custom coordinate system showed higher consistency with the standard CT system for the femur compared to the tibia. However, the maximum angle error for tibial component positioning was within ±2°. Moreover, the mean absolute errors for the coronal, sagittal, and transverse plane positioning of both the femoral and tibial components were less than 0.6°. These findings suggest that our newly developed custom coordinate system can be effectively used for preoperative planning in Skywalker surgical robot-assisted TKA, particularly for patients with notable positional abnormalities in their CT scans.

CRediT authorship contribution statement

Hua Qiao: Writing – original draft, Methodology, Conceptualization. Runzhi Xia: Writing – original draft, Methodology, Conceptualization. Yongyun Chang: Software, Project administration, Investigation. Keyu Kong: Methodology, Formal analysis. Minghao Jin: Investigation, Formal analysis. Zanjing Zhai: Software, Data curation. Jingwei Zhang: Visualization, Investigation, Formal analysis. Huiwu Li: Writing – review & editing, Validation, Supervision, Funding acquisition.

Ethics approval

This study was conducted in accordance with the Declaration of Helsinki (revised in 2012), and was approved by the Ethics Committee of the Shanghai Ninth People's Hospital, Shanghai Jiao Tong University School of Medicine. (Registration number: SH9H-2019-T212-2). Informed consent is waived due to it’s an observational study.

Consent for publication

Not applicable.

Data availability statement

Has data associated with your study been deposited into a publicly available repository?

The datasets used during the current study are available from the corresponding author on reasonable request.

Funding

This work was sponsored by program of Shanghai academic/technology research leader [Grant number 22XD1434000].

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.