Abstract
Mechanisms of computation in sensorimotor cortex must be flexible and robust to support skilled motor behavior. Patterns of neuronal coactivity emerge as a result of computational processes. Pairwise spike-time statistical relationships, across the population, can be summarized as a functional network (FN) which retains single-unit properties. We record populations of single-unit neural activity in marmoset forelimb sensorimotor cortex during prey capture and spontaneous behavior and use an encoding model incorporating kinematic trajectories and network features to predict single-unit activity during forelimb movements. The contribution of network features depends on structured connectivity within strongly connected functional groups. We identify a context-specific functional group that is highly tuned to kinematics and reorganizes its connectivity between spontaneous and prey capture movements. In the remaining context-invariant group, interactions are comparatively stable across behaviors and units are less tuned to kinematics. This suggests different roles in producing natural forelimb movements and contextualizes single-unit tuning properties within population dynamics.
Subject terms: Network models, Neural encoding, Motor cortex
By studying cortical activity patterns during prey capture and spontaneous behavior in marmosets, the authors identify distinct subnetworks defined by reliable spike timing correlations. These subnetworks emerge during prey capture, with each potentially playing different roles in controlling reaching movements.
Introduction
The study of the relationship between population activity in primary motor cortex (M1) and upper limb motor behavior has taken one of two diverging approaches. On the one hand, single neuron tuning properties have been characterized and then combined across the population without considering the interactions between neurons1,2. On the other hand, low-dimensional structure in population dynamics has been linked to movement but omits details of single neuron tuning properties3,4. Although these divergent methodologies have each proven useful, comparatively few studies have attempted to place single neuron tuning properties in the context of broader M1 population dynamics. Pairwise spike count correlations provide information about motor behavior beyond what is provided by firing rates alone5 and improve encoding models that predict single-unit activity6. Synchronous activity (measured at a finer timescale) in pairs of motor cortical neurons similarly contains information about movement direction7, while recent work demonstrated that the structure of pairwise spike time correlations across the population carries behaviorally relevant information in M1 that progresses systematically over the course of movement8. A large body of work in mostly primary visual cortex has shown that recurrent interactions within local functional groups can explain single-trial neural activity9, that both tuned and untuned units are essential components of the functional network (FN)10, and suggested that reliable pairwise correlations, rather than first-order statistical features of spike trains, are the building blocks of coding in visual cortex11. Note that we use the term functional group to denote subsets of edges (weighted interactions between a source and target unit) within the FN.
Our understanding of single-unit activity in the context of neuronal interactions has been limited in many cases by the necessity for trial averaging, by restrained and constrained movements due to wired neural recording systems, by the difficulty in quantifying complex kinematics, or by the constraints of analysis methods. Constrained and over-trained behavioral tasks such as center-out reaching or pedaling a wheel12,13 limit the variability in all movement parameters aside from those under investigation and may impose an artificial ceiling on the dimensionality of neural population dynamics14. Even in the case of less stereotyped behaviors like random target pursuit15, reaching around obstacles16, and reach to grasp tasks17, primates are restrained in a chair with head fixation and require weeks of daily training to reliably execute movements. There is evidence to suggest that a significant portion of M1 neurons encode a constrained, well-trained task differently than free behavior18 and that over-training increases synchrony between M1 neurons19. The extent to which findings discovered in the constrained, trained setting will generalize to natural movements remains unclear.
Here we use a wireless neural recording system and computer vision pose estimation tools to study unrestrained and untrained arm movements executed by the common marmoset (Callithrix jacchus) during prey capture of moths20–23. Compared to classical task paradigms, this behavior produces a richer set of movements with variable directions, speeds, and amplitudes and obviates concerns related to overtraining. Instead of assuming a fixed time lag between neural activity and kinematic features12,24–30, we quantify single-unit tuning properties using a temporally extended trajectory tuning model15. At the same time, we incorporate neuronal interactions using a functional network that describes pairwise spike time statistics in the form of a weighted, directed graph. We show that the trajectory tuning model extends to more naturalistic movements and explains neural activity better than a simpler model. We demonstrate that tuning to kinematics depends on the functional interactions between units – particularly on structured strong connections. Finally, we identify a context-specific functional group that reorganizes during natural forelimb movements necessary for prey capture. This context-specific functional group is strongly interconnected and comprises units tightly linked to kinematics with strong, positively correlated preferred trajectories.
Results
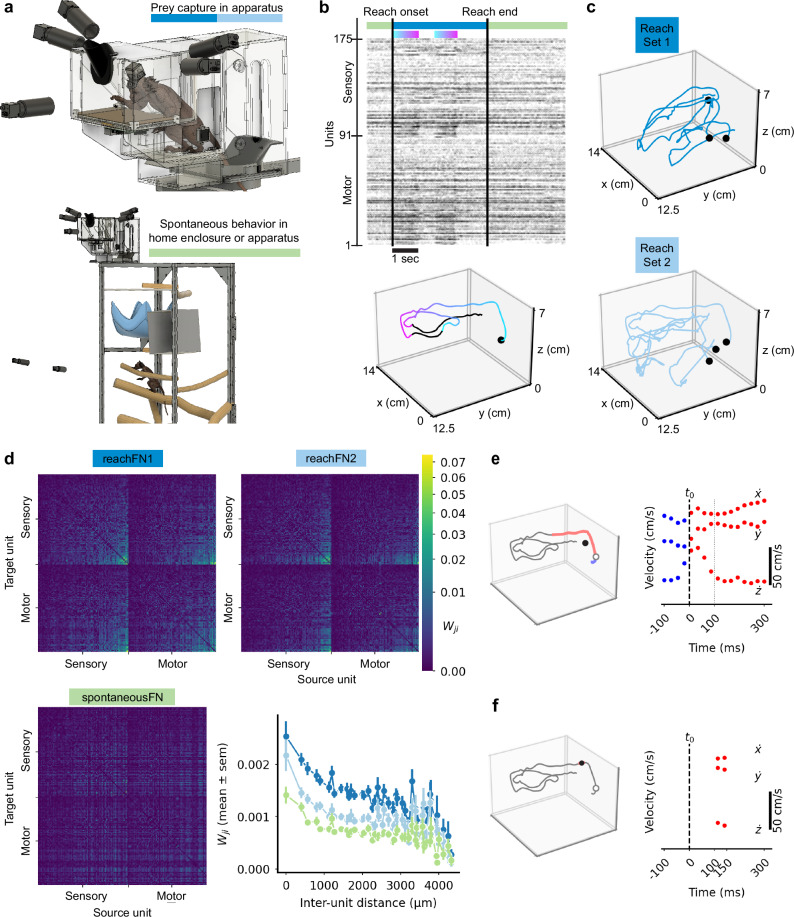
Each marmoset was allowed to voluntarily enter and exit the prey capture apparatus attached to the top of the home enclosure (Fig. 1a). Movement was recorded by high-speed cameras that were automatically triggered using an infrared beam-breaker switch (see Methods). Spontaneous behavior in the home enclosure was recorded continuously by a separate camera system. Spiking activity was recorded throughout the recording session (TY: 175 units, Fig. 1b; MG: 73 units, Supplementary Fig. 1a), during which the monkey was actively reaching for prey (TY: 101 reaches, MG: 56 reaches) or engaged in undirected, spontaneous behavior. We observed clear modulation of M1 and somatosensory cortical (S1) neurons (see Methods for estimation of the boundary between areas); spike rates increased across much of the population during extension of the hand and decreased during movements back toward the partition (Fig. 1b, Supplementary Fig. 1a). Reaches were randomly assigned to reachSet1 or reachSet2 and the corresponding spiking activity during reaches and during spontaneous behavior was used to compute functional networks denoted reachFN1, reachFN2, and spontaneousFN (Fig. 1c, d; Supplementary Fig. 1b, c). Functional networks were computed using the confluent mutual information (conMI) between the binned spike trains of each neuron pair31, which quantifies the information about the spike state of a target unit at time or that is gained from knowledge of the spike state of a source unit at time (Eqs. 3,4). The structures of reachFN1 and reachFN2 were qualitatively indistinguishable in the connection matrices, and both exhibited strong same-electrode connectivity and gradually decreasing weights with increasing inter-electrode distance. Given these similarities, we often refer to them together as reachFN1/2. The structure of connectivity was different in the spontaneousFN for both monkeys with depressed weights at shorter inter-electrode distances – especially for same-electrode functional connections (Fig. 1d, Supplementary Fig. 1c). We built generalized linear models (GLMs) to predict single-sample spiking activity of individual units given a temporally-extended hand velocity trajectory (i.e., velocities that either led or lagged the spike sample) and average position of the hand throughout the trajectory, similar to previous work in macaques15,17,32,33. We refer to these sets of models with and without position terms as the full kinematics and trajectory model, respectively (Fig. 1e). We also built models that approached a time-independent preferred direction representation by sampling brief velocity trajectories and average position between +100 ms and +150 ms with respect to the spike sampling time, which is often treated as the optimal lag between a motor cortical neuron’s firing and velocity27,34. We call these the short kinematics (brief trajectory and average position) and velocity (brief trajectory only) models (Fig. 1f).
Fig. 1. Behavior, data collection and encoding model construction.
a Top: subject capturing prey in the apparatus. Behavioral video data was collected by five (MG) or two (TY) cameras. Bottom: subject behaving freely and spontaneously in the home enclosure. b Top: A raster plot shows the activity of 175 units recorded from TY, from one second before to 3 s after the duration of a reach (reach 3). Units are ordered as in (c). The green and blue bars above the raster indicate times corresponding to spontaneous behavior (green) or prey capture (blue). The gradient bars highlight periods of increased firing rates across the population. Bottom: hand position for reach 3 (black), with reach onset indicated by the black dot and the same gradient indicating neural modulation imposed on the kinematics. c A sample of hand trajectories for six of 101 reaches, separated into reachSet1 (dark blue) and reachSet2 (light blue). d FNs were computed from activity during either reaches in the corresponding reachSet or during spontaneous behavior. Within motor or sensory areas, units are ordered by the average in-weight to the target unit for reachFN1/2. The color scale corresponds to . Lower Right: Functional weights versus inter-electrode distance (mean ± sem), with sample numbers ranging from 4 samples at 4327 µm to 1176 samples at 894 µm (individual sample numbers are available in the Source Data file). e A representative sample for the trajectory and full kinematics models with and . Left: wrist position for a single reach (black) overlaid with the spike sample time (white circle) and corresponding trajectory sample including lead (blue) and lag (red) movements subsampled at 40 Hz. The black dot indicates the average position for the trajectory sample. Right: velocity samples with the spike sample window and trajectory center shown with a vertical black dashed or dotted line, respectively. f The corresponding sample for the velocity and short kinematics models with and . Source data are provided as a Source Data file.
Encoding models incorporating temporally extended velocity trajectories and average position predict single-unit spiking activity
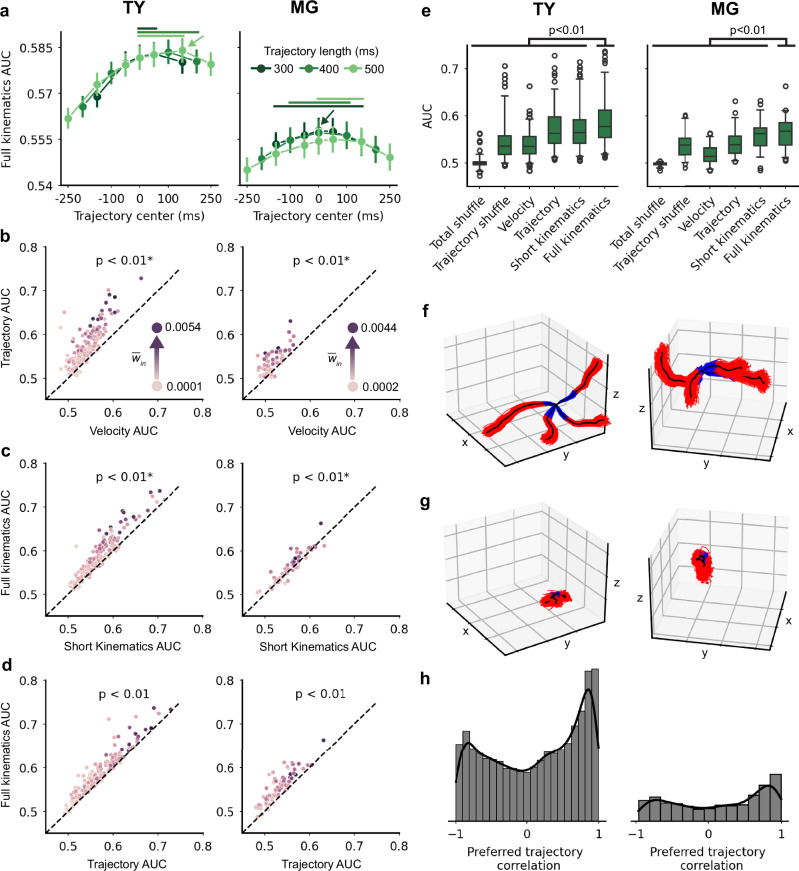
For each unit in the population, we tested each kinematic encoding model across 17 sets of lead and lag times in the trajectory samples – the trajectory samples were 300–500 ms in duration and ranged from entirely lead to entirely lag kinematics (see Supplementary Fig. 2 for summary of full analytical pipeline). For example, the [−300, 0]ms model contained 300 ms trajectories of entirely lead kinematics, the [−250, +250]ms model contained 500 ms trajectories centered on the spike sample window, and the [−100, +300]ms model contained 400 ms trajectories of mostly lag kinematics. For all models, a randomly selected 80% of trajectory samples were used for training and the remaining 20% of samples were used as held-out test data (the train/test split was not related to reachSet1/2). We evaluated each model using the area under the receiver operating characteristic curve (AUC) computed on test data, a metric which ranges from ~0.5 (no predictive power) to 1.0 (perfect prediction). For each model and unit, we fit and tested 500 independent GLMs using a resampled train/test split to obtain a full distribution of results that was not biased by a particular train/test split. We found that the full kinematics model performed best when it incorporated both lead and lag kinematics, particularly for models containing majority lag kinematics (Fig. 2a). We report subsequent results for the [−100, +300]ms model due to its high performance in both monkeys; we confirmed that results match qualitatively across multiple lead-lag sets with similar performance.
Fig. 2. Full kinematics encoding model predicts single-unit activity.
a–h Left: monkey TY. Right: monkey MG. a Mean ± sem AUC for the full kinematics model, all lead-lag sets (n = 500 per set). The trajectory models range from 300 ms to 500 ms in duration, and from lead-heavy samples on the left to lag-heavy samples on the right. The arrow indicates the best-performing lead-lag set. Solid lines above the data denote lead-lag sets for which AUC distributions were not significantly different than the best model (p > 0.05, one-sided sign test with Bonferroni correction). b Scatterplot of the trajectory and velocity model AUC values for each unit, averaged over 500 train/test splits. Each unit’s hue corresponds to average in-weight in the FN, which will be explained in further detail in Fig. 3. Units above the unity line were predicted better by the trajectory model. P-values are the result of a one-sided sign test. The trajectory model predicted activity better than the velocity model (TY: p ≈ 0.0; MG: p = 5.9 × 10−14; one-sided sign test). c The full kinematics model predicted activity better than the short kinematics model (TY: p = 2.1 × 10−24; MG: p = 7.7 × 10−4; one-sided sign test). In (b) and (c), the asterisk indicates that we filtered out units that were not significantly tuned to the trajectory, leaving 163/175 units for TY and 59/73 units for MG. d The full kinematics model outperformed the trajectory model due to the inclusion of average position terms (TY: p = 1.3 × 10−37; MG: p = 2.9 × 10−19; one-sided sign test). e Summary of model performance for 163 units (TY) and 59 units (MG). Center line indicates the median value, whiskers incorporate the middle 95% of data, and circles show the 2.5% of data at each end of the distribution. The full kinematics model produced AUC values significantly higher than all other models (TY: in addition to p-values presented in (c, d), p ≈ 0.0 for full kinematics vs. velocity, p ≈ 0.0 for full kinematics vs. total shuffle and p ≈ 0.0 for full kinematics vs trajectory shuffle; MG: p = 2.8 × 10−19, p = 1.8 × 10−11, and p ≈ 0; one-sided sign test). f The preferred trajectory pathlets for four units with high AUCs. Each of 500 train/test splits is shown in blue and red corresponding to lead and lag movements, and the average pathlet is shown in black. g The pathlets for four units with the lowest AUCs. h Histograms of the Pearson correlation between pathlets for all pairs of units. Source data are provided as a Source Data file.
We created two shuffled models for comparison with real data — total shuffle and trajectory shuffle. For the total shuffle model we permuted the kinematic samples to break the relationship between kinematics and spikes. For the trajectory shuffle model we permuted just the trajectory samples, leaving the relationship between average position and spikes unperturbed. We assessed tuning to kinematics and to the trajectory specifically for individual units by comparing all train/test splits of the full kinematics model to paired total shuffle and trajectory shuffle samples, respectively. For monkey TY, 172 of 175 units were significantly tuned to full kinematics (p < 0.01, one-sided sign test with Bonferroni correction) and 163 units were tuned to the trajectory specifically (p < 0.01). For monkey MG, 71 of 73 units were tuned to full kinematics (p < 0.01) and 59 units were tuned to the trajectory (p < 0.01). For comparisons between models using the brief and full trajectories shown in Fig. 2b, c, we included only the units that were tuned to trajectory details.
Next, we compared model performance at the population level. The trajectory encoding model predicted spikes more accurately than the velocity model (TY: p < 0.01, one-sided sign test; MG: p < 0.01; Fig. 2b) and the full kinematics model was more accurate than short kinematics (TY: p < 0.01; MG: p < 0.01; Fig. 2c), confirming previous studies and showing that activity of individual neurons is more closely related to temporally-extended velocity trajectories than to ballistic velocity at a fixed time. The full kinematics model was significantly more predictive than the trajectory model (TY: p < 0.01; MG: p < 0.01; Fig. 2d), as well as all the other kinematics models we tested (Fig. 2e).
We treated the coefficients of the velocity trajectory terms in the full kinematics model as instantaneous velocities and integrated them to obtain the preferred position trajectory, or pathlet15. Units with high AUC values were tuned to high amplitude preferred pathlets that were consistent across train/test splits, while units with low AUC values had no discernible preferred pathlet (Fig. 2f, g). We computed the Pearson correlation between pathlets for all pairs of units and found that many preferred pathlets tended to be strongly and positively correlated, with a smaller peak of strong negative correlations (Fig. 2h). The population was dominated by tuning to extension of the hand or, to a lesser extent, hand retraction (Supplementary Fig. 3a); this agrees with our observation of modulation related to extension on individual reaches and explains the distribution of correlations shown here. The full kinematics model incorporating a temporally extended hand velocity trajectory and average position over the movement sample was the best predictor of single-unit spiking activity, and individual units exhibited distinct preferred trajectories that tended to be strongly correlated with a preference for positive correlations.
Network features improve the encoding model and strong functional inputs correlate with kinematic tuning
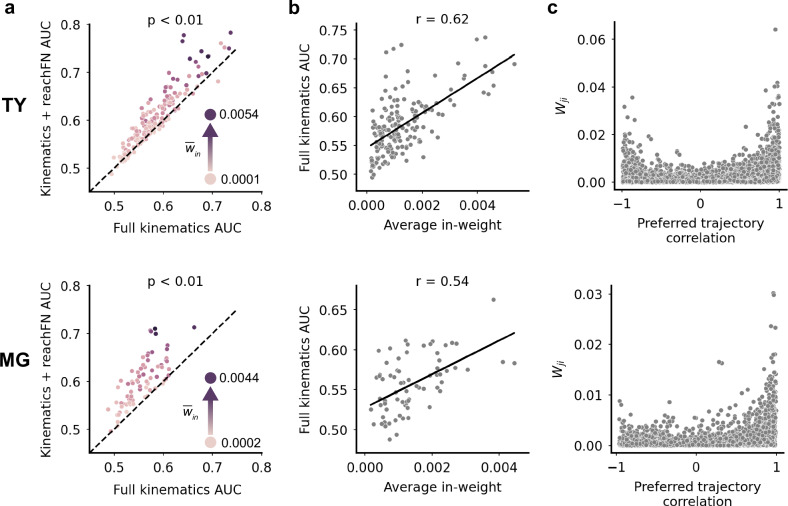
Having established the best models for predicting spiking from kinematics alone across the population of single units, we next incorporated network terms into the best model and evaluated the resulting change in model performance. Specifically, we incorporated the FN in each target unit’s encoding model by taking the dot product of all source unit spikes with the edge weights from the source units to the target unit (Eq. 6) for the leading bin and the coincident bin—this resulted in two network features for each target unit model. Trajectory samples belonging to reachSet1 were paired with network features computed using edge weights from reachFN2, and vice versa. We did this to ensure that trajectory and network features were independent (did not co-vary) within a single sample. We created network features using the computed FN rather than the alternative—fitting all pairwise coupling coefficients in the GLM—for three reasons. First, using conMI values as the coupling coefficients to produce network features constrained the encoding models to strict dependence on finely timed spike-train statistics measured directly from the neural data rather than on maximum likelihood computations. Prior work has shown that couplings taken from an FN approached optimality for most units in a similar model35. Second, our approach allowed us to manipulate the FN directly to observe the effect on model performance and made possible the generalization experiments that we present in a later section. Third, adding just two terms to each target unit model rather than 73 (MG) or 175 (TY) terms reduces the likelihood of overfitting the model. Our final kinematics+reachFN model contained the trajectory features with 48 x–y–z velocity terms, three average position terms, and the coincident and leading network feature terms (Eq. 5).
The inclusion of network activity improved the model significantly across the population (TY: p < 0.01; MG: p < 0.01, one-sided sign test; Fig. 3a). Performance of the full kinematics and kinematics+reachFN models was similar across motor and somatosensory cortical areas (Supplementary Fig. 4a, b). We found that performance of the full kinematics model—which did not include network features—improved with increasing average in-weight (TY: Pearson correlation r = 0.62; MG: r = 0.54; Fig. 3b). Additionally, model improvement from adding network features was positively correlated with average in-weight (TY: r = 0.60; MG: r = 0.62; Supplementary Fig. 4c). While we expected that a model incorporating network activity would exhibit larger performance gains with stronger inputs, it is striking that the units most strongly tuned to the full kinematics model (without network features) also received stronger inputs. Unit pairs with strongly correlated preferred trajectories also tended to have strong functional connections (Fig. 3c). Importantly, the relationship between average full kinematics AUC in a pair of units and their preferred trajectory correlation was weak (Supplementary Fig. 4d), suggesting that even though model performance and trajectory correlation of units may not be strongly linked to each other, the strength of the connections between the units (weights) was independently associated with both better performance and more aligned preferred paths. These findings did not result from variations in unit firing rate or waveform signal-to-noise ratio across the two monkeys, although there was a positive correlation between signal-to-noise ratio and AUC for monkey TY only (Supplementary Fig. 5). Taken together, these results demonstrate that functional interactions influence single-unit activity, that a unit’s tuning to kinematics increases with the degree to which it is interconnected with the surrounding network, and that strongly connected units exhibit similar (or to a lesser extent, opposite) tuning properties.
Fig. 3. Network features improve the encoding model and first order FN structure is linked to kinematic tuning.
a–c Top: monkey TY. Bottom: monkey MG. a Adding the reachFN network features to the full kinematics model improves prediction of single-unit activity (TY: p = 2.24 × 10−16 by one-sided sign-test; MG: p = 1.22 × 10−16). Each unit’s hue corresponds to average in-weight in the FN. b Performance of the full kinematics model (which contains no network feature terms) increases with average in-weight to the unit in the FN (TY: r = 0.62, Pearson correlation; MG: r = 0.54). c A scatterplot of all edge weights versus the pairwise preferred trajectory correlation. Source data are provided as a Source Data file.
We note here that all GLMs were L2-regularized using the penalty weight () that maximized AUC on held-out test data, evaluated for models using lead and lags of [−100, +300]ms and [−200, +300]ms (Supplementary Fig. 6). Based on these results, we trained all kinematics models with and all models incorporating the network with . We note that stronger penalty weights tended to reduce scaling coefficients for network terms in the kinematics+reachFN model and caused performance to drop to the level of the full kinematics model. This lends further evidence that functional interactions provide additional predictive power.
The topology of strong functional interactions underlies accurate prediction of single-sample activity
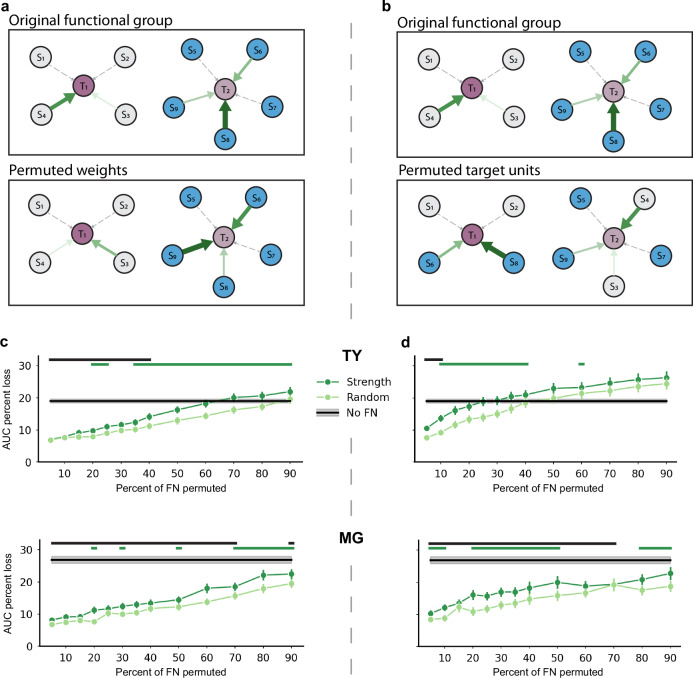
The finding that stronger average inputs correlated with stronger tuning to kinematics and also to greater performance gains provided by network features (Fig. 3b and Supplementary Fig. 4c) could mean that single-unit prediction of activity relies simply on the total strength of functional inputs; alternatively, model performance may depend on the specific structure of the strong connections. Previous work in murine visual cortex has shown that the precise structure of strong connections in the FN are most informative of single-trial activity9,35. Building on the methodology described by Kotekal and MacLean9, we investigated the importance of structured strong connections by selecting functional groups (FGs) comprising N% of the strongest edges and manipulating these FGs in one of two ways—permuting weights or permuting target units. Each edge in the network can be represented by its source unit (Sn in Fig. 4a, b), target unit (Tn), and weight (denoted by arrow size and hue), such that an edge in the N% of strongest edges can be represented by . These edges comprise strong FGs that are unique to each target unit (the set of edges is unique but the set of source units may overlap). Permuting edge weights amongst unchanged source-target pairs leaves the existing FGs intact but alters the weight multiplier applied to each source unit’s activity (Fig. 4a). This permutation can be represented by , where is sampled from the permuted weight values in the FG. This manipulation tests the models’ reliance on the precise relationship between input activity and edge weight. Permuting the target unit, on the other hand, maintains the weight multiplier applied to source unit activity but changes the target unit receiving the input, thus changing the FG of inputs to each single-unit model (Fig. 4b; for example, S4 and its edge weight were originally part of the FG of inputs to T1 but moved into the FG of inputs to T2 after permuting target units). This manipulation, represented as for sampled from permuted target units in the FG, tests the importance of target units receiving input from specific FGs. After each manipulation, network features computed from the permuted FN were substituted into the kinematics+reachFN model. We did not re-train the GLM with manipulated network features, but rather computed the AUC loss on training data compared to the intact kinematics+reachFN model. Re-training the GLM would optimize model coefficients to minimize model error, which would obscure the effect of FN permutations. The AUC loss resulting from each manipulation was compared to the effect of an identical manipulation within a randomly selected FG of matched size. It was also compared to the effect of completely removing network features from the model. This procedure was conducted for 250 resampled train/test splits for each unit, with each model using network terms computed from a resampled permutation of the weights or edges in the FG.
Fig. 4. The topology of strong functional interactions underlies accurate prediction of single-sample activity.
a Diagram of weight permutation. Top: two original functional groups of source units (Sn) and their input edge weights to target units (Tn). Solid green arrows indicate membership in the strongest N% of edge weights, with larger and darker arrows indicating a larger weight. Dashed gray arrows constitute the remaining edges in the FN. Bottom: the strongest edges were permuted freely, even across functional groups, while source-target unit pairs were unchanged within functional groups. Note that for simplicity the diagram does not depict reciprocal connections or the interconnectivity of functional groups. b Top: same original functional group shown in (a). Bottom: source-weight pairs were held constant, but the target unit receiving input from the pair was permuted freely. In other words, source-weight pairs were reassigned to a new target unit, resulting in entirely new functional groups. c Top: percent AUC loss on the original training set (mean ± sem for across 175 units at each percent) resulting from permuting the strongest N% of weights (dark green) or a random N% (light green) versus the size of the permuted functional group for monkey TY. The black line with gray shading indicates the AUC loss due to removal of all network terms (No FN, mean ± sem, 175 units). Green lines above the plot indicate functional group sizes for which permuting the strongest weights resulted in significantly greater loss than permuting random weights (p < 0.01, one-sided sign test, with exact p-values provided in the Source Data file). Black lines indicate group sizes for which the effect of removing the network feature terms entirely was significantly greater than permuting the strong weights (p < 0.01). Bottom: same for monkey MG, showing percent AUC loss due to permutations and with No FN as mean ± sem across 73 units. d Same as (c) for the effect of permuting target units in the original functional groups. Source data are provided as a Source Data file.
For monkey TY, we found that correctly assigned weights in the strongly connected FG carried more information than weights in the random FG for group sizes greater than or equal to 20% of the network, excluding 30% (p < 0.01, one-sided sign test; Fig. 4c, top). Permuting strong weights resulted in partial AUC loss for set sizes up to 40%, beyond which including weaker connections in the manipulation had a similar effect as removing the network features entirely. Consequently, the predictive power resided in the top 40% of strongest weights. For monkey MG, we found that correctly assigned weights in the strongly connected FG carried more information than weights in the random FG for group sizes of 20%, 30%, 50% and 70–90% (p < 0.01; Fig. 4c, bottom). The effect of removing the FN terms from the model significantly exceeded the effect of permuting strong weights for all but one FG size—the 80% permuted FN (p < 0.01, one-sided sign test).
As with permuted weights, permuting target units led to higher AUC loss as group size increased. In contrast with permuted weights, the specific FG of strongly connected inputs to each target unit was particularly important for smaller group sizes. Disruption of strongly connected FGs had a larger effect than random permutation for group sizes of 10–40% and 60% in monkey TY and group sizes of 5–10%, 20–50%, and 80–90% in monkey MG (p < 0.01). The effect of removing FN terms from the model significantly exceeded the effect of permuted target units for FG sizes up to 10% in monkey TY and up to 70% in monkey MG.
A comparison of the results of permuting weights and permuting target units reveals subtle differences in the effect of each manipulation; these differences are present in both monkeys but clearer for monkey TY. Within FGs comprising the strongest 15% of edges, the weights were interchangeable compared to permuting any random 15% of weights in both monkeys. However, permuting strong weights did result in significantly higher loss than random as the group size increased to incorporate successively weaker edges, meaning the weights were no longer interchangeable. In contrast, correct assignment of source-weight pairs to a specific target unit within the original FG was critical for smaller groups of strong edges as compared to randomly selected groups (beginning at 10% of strongest edges for monkey TY and 5% for monkey MG). The loss due to permuting target units plateaued and became non-significant compared to permutations within randomly selected FGs as the group size increased, meaning the specific composition of FGs was interchangeable in these larger groups incorporating successively weaker edges. This suggests that prediction depends more on FG membership than on weights for the most strongly inter-connected FGs, while the precise pairing of input activity and weights becomes more important for larger FG sizes. These results demonstrate that the prediction of single-unit activity depends on the precise topology of strongly connected FGs rather than average in-weight alone. We also showed that disrupting the topology of strongly connected FGs resulted in AUC loss comparable to complete removal of network features, suggesting that most available information was present in a subset of strong connections (this effect was most striking for permuted target units in monkey TY). Taken together, these results provide evidence that the specific structure of interactions captured by the FN are informative of single-unit activity in sensorimotor cortical populations, particularly for strongly connected FGs.
A context-specific functional group reorganizes during prey capture
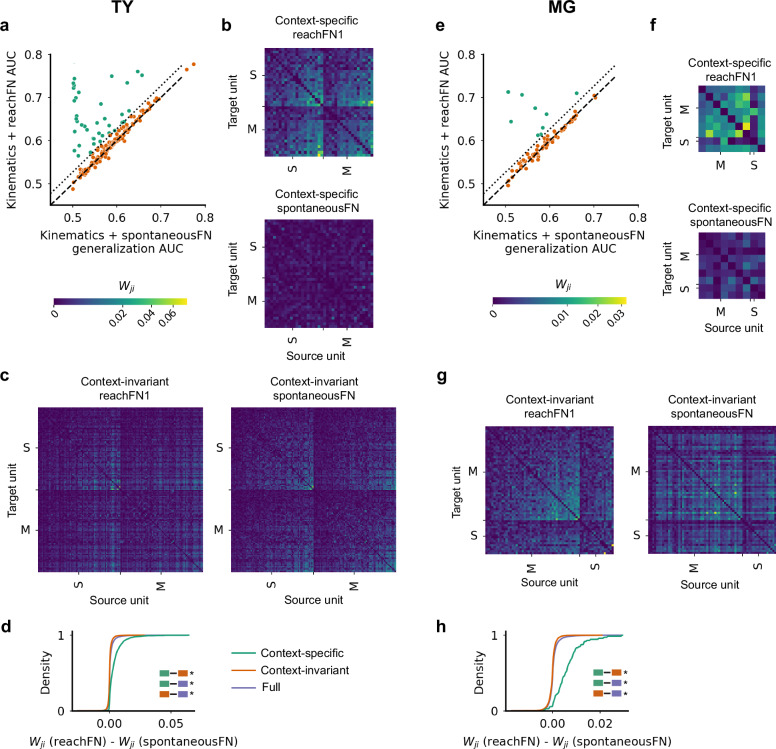
Although these results and prior work demonstrate the importance of strongly connected functional groups in the FN, previous work has also shown that the FN depended on the specific kinematics8. Consequently, we evaluated how specific a FN was to prey capture, which we refer to as reach, as compared to a wide range of non-prey capture behaviors which we refer to as spontaneous. We trained a kinematics+spontaneousFN model by computing network feature terms from the dot product of the spontaneousFN with the spiking activity associated with reach trajectory samples. We then tested this model on network features computed with reachFNs to compare generalization of the kinematics+spontaneousFN model against the performance of the original kinematics+reachFN model. Essentially, we asked whether functional interactions computed during spontaneous behavior were informative during prey capture. We observed that the kinematics+spontaneousFN model generalized well for most units – in fact, there was only a subset of the population for which it clearly could not generalize (TY = 39/175 units, MG = 9/73; Fig. 5a). We call this subset the context-specific functional group and call the remaining units context-invariant. The classifier threshold separating the two groups was selected by identifying the kink in the plot of sorted AUC difference between the models (Supplementary Fig. 7a) which corresponded to the point at which the marginal change in AUC difference was low for all subsequent units.
Fig. 5. A context-specific functional group reorganizes during prey capture.
a–d Monkey TY. a The kinematics + reachFN encoding model versus the network encoding model trained with spontaneousFN network features and tested on reachFN network features. Units above the dotted line are defined as the context-specific functional group (green, 39/175 units), and the remaining are context-invariant units (orange, 136/175 units). b The context-specific functional networks, with reachFN1 on top and spontaneousFN on bottom. The color scale of edge weights is displayed under (a). c The context-invariant reachFN1 and spontaneousFN. d The cumulative distribution of the difference in edge weights between reachFN1 and spontaneousFN for the context-specific, context-invariant, and full (purple) groups. Distribution comparisons are inset as colored pairs of boxes. The * indicates significant differences in the median with p < 0.01 (two-sided median test). All comparisons had p ≈ 0.0. e–h Corresponding results for MG, with 9/73 units in the context-specific functional group. h The * indicates significant differences in the median with p < 0.01 (two-sided median test), as in (d). P-values are 6.9 × 10−14 for context-specific vs. context-invariant, 7.7 × 10−14 for context-specific vs. full, and 5.7 × 10−12 for context-invariant vs. full. Source data are provided as a Source Data file.
We isolated the context-specific and context-invariant functional groups for reachFN1 and spontaneousFN (Fig. 5b, c, f, g). In monkey TY, we found that the edge-wise FN changes from spontaneousFN to reachFN1 were significantly different between the context-specific and context-invariant functional groups and between each functional group and the full FN (p < 0.01 for all comparisons, two-sided median test; Fig. 5d). The context-specific functional group skewed more toward an increase in weights, while the context-invariant group skewed toward decreasing weights. These effects were recapitulated in monkey MG (p < 0.01 for all comparisons; Fig. 5h) with the same directional effects. These and subsequent results are consistent for reachFN2 and are not reported for brevity.
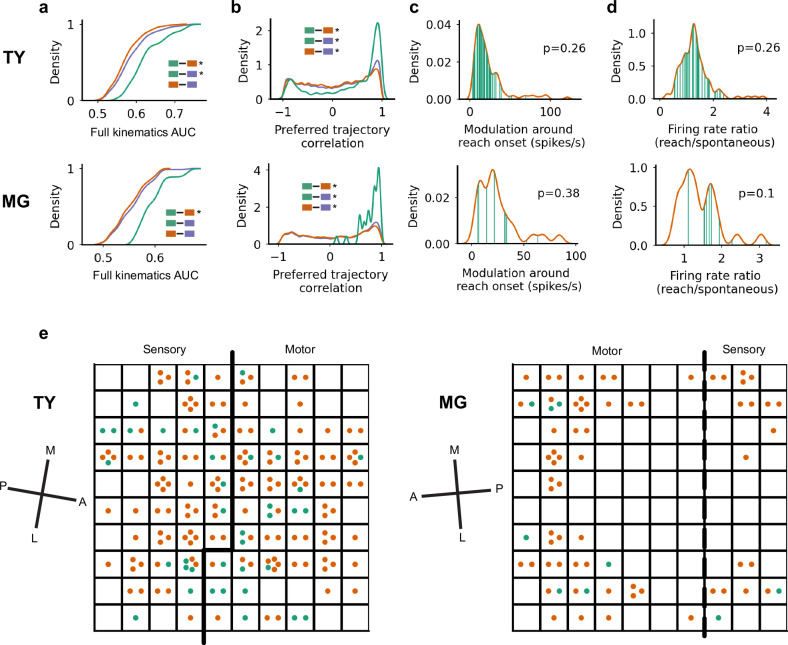
The context-specific functional group (FG) which reorganized during prey capture was also more tightly linked to forelimb movement. We found that the full kinematics model more accurately predicted spiking activity for units in the context-specific FG than for context-invariant units (p < 0.01, TY and MG, two-sided median test; Fig. 6a), as well as the full set of units in monkey TY (p < 0.01) but not MG (p > 0.05). Preferred trajectories were more strongly and positively correlated within the context-specific FG than within the context-invariant or full FNs (p < 0.01; Fig. 6b), while the context-invariant FG skewed toward weaker and negative correlations (p < 0.01 compared to the full FN). The shift toward strong positive trajectory correlations in the context-specific group appears to be due to preferential inclusion of units tuned to extension movements (Supplementary Fig. 3b, c). The results shown in Figs. 5 and 6 were not a result of either increased modulation around reach onset (Fig. 6c) or different ratios of average firing rates during reaching versus spontaneous behavior (Fig. 6d) in the context-specific FG. We note that for Fig. 6c, d we compared AUC-matched FGs, meaning that we used only the units in the context-invariant group with full kinematics AUC exceeding the lowest AUC in the context-specific group. We did this to ensure a fair comparison, given that the modulation and firing rate ratio both correlated weakly with full kinematics AUC (r = 0.13 and r = 0.20, respectively, not shown). Finally, we examined the location of context-specific and context-invariant units on the cortical map and found that members of each FG were spread across estimated motor and somatosensory areas (Fig. 6e). For both monkeys, the majority of units in the context-specific group were recorded from channels which also recorded context-invariant units, confirming that FG membership was not the consequence of channel differences.
Fig. 6. Tuning properties and cortical location of context-specific and context-invariant functional groups.
a Cumulative distribution of AUC values in the full kinematics model for TY (top) and MG (bottom), separated by context-specific vs context-invariant/full groups. Legend and statistics are denoted as in Fig. 5 where * indicates significant differences in the median with p < 0.01 (two-sided median test) and comparisons without * are not significant (p > 0.05). Green, orange, and purple correspond to the context-specific functional group, the context-invariant group, and the full network, respectively. P-values are 5.4 × 10−5 (TY) and 0.0038 (MG) for context-specific vs. context-invariant, 3.9 × 10−4 and 0.14 for context-specific vs. full, and 0.12 and 0.54 for context-invariant vs. full. b Distributions of preferred trajectory correlation, using the same legends and statistical methods as in (a). P-values are ~0.0 (TY and MG) for context-specific vs. context-invariant, ~0.0 (TY and MG) for context-specific vs. full, and 6.0 × 10−26 (TY) and 2.8 × 10−10 (MG) for context-invariant vs. full. c Distribution of unit modulation at reach onset for the context-invariant functional group (orange) overlaid with the context-specific functional group (green), with p-values comparing the medians of the distributions (two-sided median test). d Ratio of unit average firing rates during reaching over rates during spontaneous behavior, with p-values from a two-sided median test. e Cortical location of context-specific and context-invariant units on the array. The dashed-line boundary between motor and sensory areas for monkey MG indicates less confidence in the precise location of the boundary compared to monkey TY (see Methods). The cardinal axes in cortex were estimated from surgical photos and are denoted medial (M), lateral (L), anterior (A) and posterior (P). Source data are provided as a Source Data file.
To rule out the possibility that results from Figs. 5 and 6 might be explained simply by the higher distribution of AUC values in the context-specific FG, we repeated some analyses using AUC-matched sets. To do so, we included all pairs of units within the context-invariant and full FNs for which both units had full kinematics AUCs exceeding the lowest full kinematics AUC in the context-specific FG. AUC-matched comparisons of preferred trajectory correlations (Supplementary Fig. 8a) and edge-wise weight differences (Supplementary Fig. 8b) recapitulate the results shown in Fig. 6a and Fig. 5d, h, respectively, that compared unmatched distributions. Finally, the context-specific FG did not comprise all the units performing well in the full kinematics or kinematics+reachFN model but were intermixed with well-explained context-invariant units (Supplementary Fig. 8c).
Instead of examining just a single broad class of spontaneous behavior, we computed and analyzed functional networks (FNs) for specific behavioral classes from the marmoset’s natural repertoire. We selected and annotated two behaviors, rest and locomotion, which were prominent in the spontaneous behavior recordings, and computed FNs from the associated spike trains. Both the restFN and locomotionFN exhibited qualitatively similar structure to the spontaneousFN, with lower functional weights across many inter-unit distances for the restFN and a weight versus distance relationship for the locomotionFN that resembled reachFN1/2 (Supplementary Fig. 9a and Supplementary Fig. 10a). We also elaborated on the analysis of prey capture by isolating periods of extension and retraction during prey capture reaches. We found that extension periods aligned closely with the periods of firing rate modulation shown in Fig. 1b and Supplementary Fig. 1b, and that the median tangential speed across all moments of extension (TY: 15.9 cm/s, MG: 13.7 cm/s) was significantly greater than the median tangential speed during retraction (TY: 12.9 cm/s, MG: 11.2 cm/s; p < 0.01, median test; Supplementary Fig. 9b and Supplementary Fig. 10b). We compared the FNs computed from these periods to the spontaneous FNs and reachFN1/2 and found that both the retractionFN and extensionFN exhibited similar structure and weight-distance relationships to reachFN1/2, although the retractionFN contained generally lower weights than the extensionFN across all distances (Supplementary Fig. 9c and Supplementary Fig. 10c). We computed the weighted graph alignment score (Eq. 7) between all pairs of FNs and found that the restFN and locomotionFN clustered together with the spontaneousFN while the extensionFN and retractionFN clustered together with reachFN1/2 (Supplementary Fig. 9d and Supplementary Fig. 10d). Finally, we observed lower firing rates in the population during spontaneous behavior and rest, higher rates during locomotion, and the highest rates for reaching periods (Supplementary Fig. 9e and Supplementary Fig. 10e). Importantly, these results indicate that the dynamics underlying reaching are prevalent during both extension and retraction periods of prey capture but are different than the dynamics underlying rest, locomotion, and general spontaneous behavior.
We repeated the generalization experiments discussed in Figs. 5 and 6 by training models with network features computed using the restFN or locomotionFN. These experiments produced similar context-specific FGs which largely overlapped with the context-specific group identified from the general spontaneousFN. For monkey TY, a larger context-specific group was identified using the restFN and comprised most of the context-specific group in Fig. 5a plus additional units (Supplementary Fig. 11a and Supplementary Fig. 7b). The context-specific group was strongly inter-connected during reaching but not during rest, and the graph alignment scores between behaviors revealed an accentuated separation between spontaneous behaviors and reaching behaviors within the context-specific FG (Supplementary Fig. 11b, c). All subsequent qualitative and statistical results presented in Figs. 5 and 6 remained true for this context-specific group – we present a subset of these results in Supplementary Fig. 11d. A smaller context-specific FG was identified using the locomotionFN, which also overlapped with the original group and replicated qualitative and statistical results presented in Figs. 5 and 6 (Supplementary Fig. 11e-h). We found similar results in monkey MG (Supplementary Fig. 12a–h).
Discussion
We have shown that precisely timed single-unit activity during forelimb movements can be predicted accurately by an encoding model incorporating functional interactions, a temporally extended hand velocity trajectory, and the average hand position taken over the trajectory. We also demonstrated that tuning to kinematics depends fundamentally on functional interactions between units – particularly on structured strong connections. This builds on past work in macaque motor cortex demonstrating that movement-related information is present in pairwise spike count correlations5,6, and provides complementary insights to recent work showing that the structure of fine-timing spike correlations in a FN contains movement-related information and evolves systematically over the course of behavior8. Finally, we identified a context-specific functional group within which functional interactions reorganize to produce the natural forelimb movements during prey capture, and a context-invariant functional group within which interactions were preserved across behavioral contexts.
The fact that the functional interactions among most of the neural population remain invariant across a wide range of behavioral contexts is consistent with ex vivo experiments36 and anesthetized studies37,38. However, we also identified a comparatively small subset of neurons whose interactions vary dynamically across contexts, forming a strongly connected functional group during an ethologically relevant behavior (prey-capture). Together this suggests that dynamic elaboration around a stable functional backbone corresponds to the control of natural behavior. Moreover, the context-specific module carries more movement-related information than the context-invariant module. Our work provides evidence for context-invariant and context-specific modules (functional groups) through the study of a wide range of natural behaviors in the marmoset sensorimotor cortex. These distinct functional groups and their relationship to motor control motivate future research leveraging naturalistic behavior across contexts.
Given evidence that neural activity recorded in association with highly constrained and over-trained tasks may not generalize completely to naturalistic, unrestrained behavior14,18,19,29, it was not guaranteed that the results of our full kinematics model would match those from a planar reaching task15. However, as in that study, we found that the trajectory model predicted single-unit activity more accurately than a velocity model and that the full kinematics model was most accurate for trajectories including a range of lead and lag kinematics. In fact, the same [-100, +300]ms model that performed best for M1 units in macaques executing a random-target pursuit task was also amongst the best-performing models here. We show that the model’s accuracy extends beyond M1 to predict units across sensorimotor cortex; this aligns with studies demonstrating similar encoding39 and decoding40 of distal limb movements of the wrist and digits for units in M1 and area 3a. We also found that significantly tuned units exhibited distinct preferred trajectories in addition to average position tuning. Since the trajectory tuning model extended to naturalistic behavior, it served as a useful foundation for investigating the additional information provided by the functional network.
Inclusion of network features in the kinematics+reachFN model significantly increased predictive power over the full kinematics model, and performance of the full kinematics model increased with stronger average functional inputs from other units—despite no direct link built into the full kinematics model. Furthermore, we demonstrated that the prediction of single-unit activity depends on the precise topology of strongly connected functional groups rather than average in-weight alone. This agrees with a similar study in murine visual cortex which demonstrated that the topology of the functional group containing the largest 25% of edge weights was critical to the performance gained by incorporating network features9. We also showed that all the information provided by network features could be eliminated by disruptions to the topology of strongly connected functional groups. For monkey TY, information was concentrated in the strongest 10% of functional inputs and the strongest 40% of strong weights. For monkey MG, information was concentrated in the strongest 70% of both weights and functional inputs.
Work by Levy et al.10 showed that both tuned and untuned units in the visual cortex play essential roles in the FN, and that untuned units were central to the structure of the network. This is in contrast with two results presented here: that strongly interconnected units tended to be more tuned to kinematics, and that members of the context-specific functional group were both more strongly connected to each other and more tightly linked to kinematics. This suggests that untuned units may play a different role in sensorimotor cortex than in visual cortex, which is consistent with the finding that areas and behaviors with different computational constraints exhibit distinct population dynamics41,42. We posit that this difference is related to the generation of temporally smooth population dynamics that are necessary for the production of motor behavior3,4,13.
We identified a subset of the population, the context-specific functional group, for which the kinematics+spontaneousFN model could not generalize to match the kinematics+reachFN model when the animal engaged in prey capture reaching. Surprisingly, the context-specific group comprised less than 25% of the population, while interactions measured during spontaneous behavior generalized well to explain interactions during prey capture for the remaining units. When we compared the context-specific group to the context-invariant and full groups, we discovered that the context-specific functional group was more strongly interconnected in the reachFN, contained pairs of units with more positively correlated preferred trajectories, and reorganized its connectivity patterns significantly between the spontaneousFN and reachFN. The structure of interactions between context-invariant units was comparatively consistent across spontaneous and reaching behavior. Additionally, the context-specific functional group was more strongly tuned to forelimb kinematics than the context-invariant group. Importantly, parallel generalization experiments using the restFN and locomotionFN in place of the spontaneousFN resulted in overlapping context-specific functional groups that replicated the results shown in Figs. 5 and 6, demonstrating that most units are context-invariant even when comparing rest to prey capture and, conversely, that the context-specific functional group captures differences in the underlying dynamics guiding prey capture reaching versus the movements involved in locomotion.
The simplest explanation for the context-specific functional group is that it may play a differential role in extension movements. We showed in Fig. 1b that firing rates modulated across much of the population during extension of the hand into the prey capture workspace and showed in Supplementary Fig. 3b that the context-specific functional group was dominated by units tuned to extension. Interestingly, studies of decorticate human and non-human primate subjects have found hypertonicity of flexion in the upper limbs in the absence of cortical inputs to the spinal cord, suggesting a preferential role for cortex in guiding extension movements43,44. We also found that functional interactions during both the extensionFN and retractionFN were aligned with reachFN1/2 computed from the entire reach, but that the extensionFN was more closely aligned with reachFN1/2 within the context-specific group. Dynamic extensions of the hand – and the muscle activations involved in such movements – are overrepresented during prey capture but comprise a smaller proportion of spontaneous behavior. Movement intensity and grasping may also play a role. Extension movements exhibited significantly higher speeds than retraction movements, suggesting the context-specific functional group’s involvement in producing the most rapid and dynamic movements. Grasping often occurred coincidently with hand extension, raising the possibility that many units including those in the context-specific functional group were tuned to grasp as well as hand extension (although grasp was not quantified by DLC pose estimation in this study). Future work might attempt to elicit experimental behaviors that involve extension and grasp in different contexts. These movements were not common enough in undirected, spontaneous behavior to allow for comparison with prey capture reaching.
Work by Dann et al.45 showed that modularity in the functional network links large groups of interconnected units in a single cortical area to smaller groups in other areas, suggesting a mechanism for information flow between areas. It could be that members of the context-specific functional group described here, which span motor and sensory regions and are tightly coupled by preferred trajectory correlations and strong edge weights, participate in flexible modules to facilitate inter-area communication.
The differences between the context-specific and context-invariant groups aligns with recent work demonstrating that reliable pairwise correlations, rather than first-order statistical features of spike trains, are the building blocks of coding in visual cortex11. The reorganization of the context-specific functional group, which was strongly tuned to kinematics, demonstrates a link between precisely structured interactions and kinematic encoding in sensorimotor cortex.
An alternative (and more speculative) interpretation of the context-specific and context-invariant functional groups is that they might be differentially involved in processes identified by the population dynamics framework. The functional interactions making up the context-invariant group were relatively consistent across reaching and spontaneous motor behaviors in the home enclosure. It is possible that these stable pairwise interaction patterns could preferentially contribute to the generation of low-dimensional and rotational dynamics that evolve in a predictable fashion with low-tangling13. The context-specific group, on the other hand, may contribute to deflections in the neural trajectory correlated with muscle activity13 or to moving the fixed point about which rotational dynamics unfold in neural space46. In that framework, the position of the fixed point determines the angle of rotations – which unfold at a conserved frequency – and varies systematically with direction of movement, suggesting a link between classical tuning and population dynamics. Similarly, the context-specific functional group presented here was strongly tuned to kinematics. It is important to note that no studies in the dynamical systems framework have identified distinct subsets of the population that contribute differentially to separate dimensions or features. This may mean the context-specific and context-invariant functional groups do not, in fact, map directly onto features identified by this approach. On the other hand, previous dynamical systems work studied constrained and over-trained motor behaviors that may exhibit different neural activity patterns than those during naturalistic movements used in the current work18,19. Behaviors in those studies span a smaller and repeated range of speeds, postures, and amplitudes; do not rely on continuous online adjustments to track evasive targets; and are externally cued with instructed delay periods rather than internally cued by ongoing motivation for capture of live prey. Furthermore, prior work did not use neural recordings from rich spontaneous behavior as a comparison with goal-directed behavior. Thus, future work to investigate the impact of the context-specific and context-invariant functional groups on population dynamics requires data suitable for all relevant contexts. This work should span spontaneous behavior, naturalistic forelimb movements, and trial-based reaches, and include simultaneous recordings of muscle activity. It may be that a different functional group is engaged preferentially for each context as well as class of spontaneous behavior; alternatively, structured interactions within the context-invariant group might be conserved across behaviors while the context-specific group reorganizes based on the demands of each behavior. The latter finding might illuminate possible links between the distinct functional groups and dynamical systems features.
Methods
Subjects
These experiments were conducted with two common marmosets, Callithrix jacchus (a 10-year old, 370 g male designated TY and an 8 year old, 350 g female designated MG). All methods were approved by the Institutional Animal Care and Use Committee of the University of Chicago.
Data collection—behavior and cameras
A custom-built, modular apparatus designed for prey capture and other goal-directed tasks47 was attached at the top of the home enclosure. Subjects were allowed to enter the apparatus and engage in prey capture voluntarily. When the subject was prepared and alert, the experimenter dispensed a single moth into the apparatus to initiate a prey capture episode. The next prey was dispensed when the previous prey was either captured and eaten or had escaped the apparatus. Marmoset TY visited the apparatus 49 times (average duration = 31 s, total time = 25.4 min) and completed ~2.1 left-handed extended reaches/visit (101 total extended reaches, average duration = 2.9 s, total time = 4.9 min). An extended reach in some cases included multiple extension/retraction cycles in quick succession that were not separated into individual reaches (e.g. reach 3 in Fig. 1b). The apparatus visits occurred sporadically throughout the 94-minute recording session and reaches/visit were fairly consistent throughout the session. Marmoset MG visited the apparatus 18 times (average duration 98 s, total time = 29.5 min) and completed ~3.1 right-handed extended reaches/visit (56 total extended reaches, average duration = 2.9 s, total time = 2.7 min). The pattern of apparatus visits was similar for MG across the 126-minute recording session, except for a 44-min period lasting from the 42nd minute to the 86th minute during which the entrance to the apparatus was closed (the entrance was closed to give the marmoset a break and increase engagement when prey capture resumed). The subject was engaged in spontaneous behavior in the home enclosure or in the apparatus when not directly alert and responsive to the prey capture task. Spontaneous behavior included but was not limited to leaping, hanging, grooming of self or partner, locomotion or resting in the home enclosure and visual exploration, non-reaching movements, or fine manipulation of prey in between capture episodes in the apparatus. We annotated a subset of these behaviors and present FNs computed from rest and locomotion, as well as subsequent generalization experiments, in the Supplementary Figs. Rest periods—consisting mainly of perched stillness and minor postural adjustments without significant limb motion—were scattered throughout the session and totaled 42.4 min for TY and 66.7 min for MG. Locomotion (which included strict locomotion, brief climbing or leaping between perches in the midst of locomotion, and some postural adjustments within periods of rest) was similarly intermittent across the session and totaled 13.0 min for TY and 4.7 min for MG. A recording session lasted approximately ~1.5 h for TY and ~2.5 h for MG.
High-speed cameras (Blackfly S, 200 frames s−1, 1440 × 1080 resolution; Teledyne FLIR) were used to record video for pose estimation by DLC. For monkey TY, two cameras were positioned to optimize visibility of the left upper limb and recorded at 150 fps. For monkey MG, five cameras recorded at 200 fps—two cameras for each side view and one front-facing camera to improve coverage for reaches occluded in the side views. Image acquisition was triggered by the marmoset activating an infrared beam-break sensor when approaching the partition within the apparatus. Additional cameras were used to record behavior in the home enclosure from a wider angle—two cameras at 30 fps for monkey TY and 4 cameras at 60 fps for monkey MG.
Data collection—neural recording
Each subject was implanted with a 96-channel Utah Array (Blackrock Microsystems, Salt Lake City, UT) using stereotaxic coordinates48 to target the forelimb area of the primary motor cortex in the right (TY) or left (MG) hemisphere. The surgical procedure is described in detail by Walker et al.22 Neural data was collected using a Blackrock Cereplex Exilis, which houses a digital amplifier, wireless transmitter and Li-ion rechargeable battery capable of powering ~90 min of continuous recording in a compact headstage. A quick-connect solution designed in-house facilitated the removal/attachment and charging cycle with minimal experimenter intervention and disruption to the marmosets’ natural behaviors (see Walker et al.22, which describes many of the design concepts which were adapted for the Exilis headstage). Additional battery life was provided in the MG recordings by a detachable external battery circuit designed in-house. Data was transmitted to 8 receiving antennas, then processed by additional products from Blackrock Microsystems. All data was recorded as raw 30 kHz continuous signals.
Data collection—ICMS and receptive field mapping
The extent of motor and sensory areas on the TY array were estimated from results of intra-cortical microstimulation (ICMS) and receptive field mapping of tactile and proprioceptive feedback, which were conducted at night during quiet restfulness. For ICMS, a low current was used to identify muscle groups for which stimulation evoked movement. Then the current was reduced to identify the specific muscle target of the channel and the lowest current that evoked a response. For receptive field mapping, the skin was lightly brushed with a cotton-tipped applicator (tactile) or the muscle body was palpated (proprioceptive). This was repeated 20 or more times for each muscle/body region using a 5 s on/5 s off protocol. Peri-stimulus time histograms were computed from the repetitions and mapped onto the array for manual inspection. Cortical area boundaries were estimated by comparing the composite maps of ICMS and receptive field mapping to prior cortical mapping results in marmosets48–51.
Only receptive field mapping was completed for the MG array. The boundary between motor and sensory areas was estimated based on these results and by comparison to the combined mapping results of the TY array. We have noted the lower degree of confidence in the exact boundary with a dotted line in Supplementary Fig. 4 and Fig. 6. We note that the precise location of the boundary does not affect any results and is only used for display purposes on array maps, raster plots, and functional network connection matrices.
Data processing—spike sorting
Spike sorting was performed on raw neural data at 30 kHz using Spike Interface52. Ironclust (https://github.com/flatironinstitute/ironclust) was the primary sorter, with SpykingCircus53 and waveclus54 used to cross-reference for consistent units that were identified across all sorters. Inter-spike interval and signal-to-noise ratio thresholds (ISI violation rate <0.5, SNR > 5) were applied to automatically pre-classify units as multi-unit activity, then units identified by all three sorters were automatically classified as well-isolated single units. All automatically sorted spikes were manually curated using phy (https://github.com/cortex-lab/phy).
Data processing—kinematics
A DeepLabCut network (DLC)20 with Resnet-50 base architecture was trained on 2343 labeled images from TY and MG recording sessions. Three labels were applied to each side of the wireless headstage housing (for head-tracking in future work), three to the upper limb on each side (shoulder, elbow and wrist), and three to corners of the apparatus to establish a coordinate system — a total of 15 labeled points. The model was iteratively trained and refined until pose estimation was consistent throughout all significant upper-limb movements in the prey capture workspace. Anipose was used to apply the DLC network to videos and to perform subsequent 2D filtering and 3D calibration and triangulation, as described in Moore et al.23 and Karashchuk et al.21
We added multiple steps of post-processing to reduce the effect of brief tracking lapses in outputs from the well-trained DLC network (such as spurious jumps and brief occlusions). Each step was applied independently to all markers and video events. We first filtered out timepoints with reprojection error greater than 20 pixels (35 for MG) and fewer than two cameras tracking the label, leaving only well-tracked segments of kinematic data. We removed very brief segments shorter than 50 ms, then filled tracking data back in for inter-segment gaps shorter than 200 ms (these steps in conjunction eliminated epochs dominated by poor tracking but containing intermittent, brief high-likelihood tracking which often caused problems during interpolation). Most lapses were fixed or removed correctly after these simple steps. Next, we removed any remaining marker jumps using the reprojection error and position data together. Then we replaced any brief inter-segment gaps that remained with either original tracking data – if that data matched a linear interpolation closely—or with the interpolation. Finally, we trimmed long segments with a high percentage of interpolated data at the beginning and end of video events—these segments corresponded to the marmoset maintaining an occluded posture in the back of the apparatus before or after prey capture. The processed data was smoothed with a 3rd order, 70 ms Savitsky-Golay filter. We identified reaching segments by finding y-position peaks that indicated extension of the hand into the prey capture space and assessing when hand speed crossed a threshold before and after each peak.
The continuous position of the shoulder marker was subtracted from hand marker position to isolate hand movements from postural changes, then differentiated to obtain the isolated hand velocity.
Trajectory encoding model
To build the encoding model for each neuron, we used a generalized linear model that estimated the set of coefficients to maximize the likelihood of correctly predicting the spike count within a 10 ms spike sampling window given the corresponding sample of kinematics55. Each kinematic sample was the monkey’s hand velocity trajectory and average position over a kinematic sampling window of length , with the kinematic and paired spike samples centered at . Samples of spikes and kinematics were extracted every 30 ms throughout reaching segments, resulting in around 8000 samples for monkey TY (8149 for the [−100, +300]ms model) and 4000 samples for monkey MG (4250 for the [−100, +300]ms model). Instantaneous velocity trajectories were down-sampled to 40 Hz based on the observation that the power spectrum of velocities mostly fell below 25 Hz. Each velocity sample can be formalized as:
| 1 |
where is the instantaneous 3-dimensional velocity vector at time and . The full kinematics model relates these terms and the average position vector to the conditional spike intensity of target unit :
| 2 |
where is referred to as the preferred velocity trajectory of the neuron and is the vector of coefficients for the average position terms. The preferred path, or pathlet, of the neuron is obtained by integrating in time as if it were a vector of three-dimensional velocities.
GLMs were implemented using the Python statsmodels package and fit with L2-regularization. We trained all kinematics models with penalty weight and all models incorporating the network with .
Area under the receiver operating characteristic curve
To assess the predictive power of each encoding model, we computed receiver operating characteristic (ROC) curves that quantified the relationship between the probability of correctly predicting a spike (hit probability) versus the probability of incorrectly predicting a spike when it was absent (false positive probability). We used 80% of spike-kinematics sample pairs to train the model for each unit and used 20% as held-out test data. We predicted the conditional spike intensity from the encoding model given the 20% of held-out kinematics samples and compared predictions to the held-out spike samples using a set of thresholds to predict spikes when the conditional spike intensity crossed the thresholds. We then computed the area under the ROC curve (AUC), which measures the predictive value of the model and can vary from 0.5 (no predictive power) to 1.0 (perfect prediction). The train/test split was sampled randomly 500 times with replacement, resulting in 500 encoding models for each unit.
Functional network computation
We created weighted, directed FNs by computing pairwise spike time statistics between recorded units. We binned the recorded spike trains into 10 ms bins, assigning a value of 1 if at least one spike occurred in that bin, and 0 otherwise. We then computed the confluent mutual information (conMI) between the binned spike trains31. ConMI quantifies the information about the firing state of target unit at time or that is gained from knowledge of the firing state of a source unit at time :
| 3 |
| 4 |
Incorporating the functional network into the encoding model
We computed reachFN1 from half of the reaching segments chosen at random and reachFN2 from the other half. We paired the kinematics from reachSet1 with the FN computed during reachSet2, and vice versa, to eliminate the concern that kinematics and the FN features might co-vary within a single sample. We also computed the FN during the remainder of the session in which the marmoset was behaving in an undirected, spontaneous manner either in the apparatus or the home enclosure (spontaneousFN). Each FN was represented as a square matrix of directed edge weights (the conMI) between nodes (units), with target units represented along the rows and source units along the columns. Activity in the functional group was incorporated in the encoding model by computing the dot product of weights with spiking activity, represented in sum notation here:
| 5 |
| 6 |
where is the edge weight (the conMI value) from source unit to target unit , and and are spike activity in the source unit at times and , respectively. Thus, and are the coincident and leading network features and , are the corresponding scaling terms fit in the GLM.
Manipulating functional network structure (permutation experiments)
To determine if the topology of the functional group is essential to predictions of single trial activity, we shuffled the functional group in two ways; we identified functional groups comprising either the top N% of strongest connections in the FN or a randomly selected group of the same size. We shuffled the strong weights to determine the importance of strong weights for prediction while preserving the corresponding underlying edges. Formally, we enumerated the edges within the selected functional group as , where a directed edge from source neuron to target neuron exists with weight for . This enumeration contains all tuples such that is in the top N% of strongest weighs (or a randomly selected N% of weights). We then applied a uniformly random permutation (where is the finite symmetric group on points) to act on the weights, furnishing the enumeration . If we let , we have all tuples representing directed edges from neuron to neuron with permuted weights in the functional group.
Similarly, to isolate the importance of the functional edges in prediction, we shuffled the strongest N% (or randomly selected) edges of the functional group. We applied a uniformly random permutation to the list of target neurons, resulting in the enumeration . If we let , we have a new set of tuples representing permuted edges that preserve the weight with respect to the source neuron. This changes the functional group of inputs to target unit and tests the importance of specific functional inputs for prediction.
Weighted graph alignment score
Similarity between two FNs, M and N with k neurons, was measured using a node-identity preserving graph alignment score (GAS), as described in previous work8,10,56:
| 7 |
For an unweighted graph, GAS measures the ratio of overlapping edges to the total number of edges. In the weighted case, the numerator represents the sum of the minimum edge weight between each pair of nodes, and the denominator is the total sum of the edge weights.
Identifying extension and retraction
Extension was defined as any period in which the distance from the shoulder to the wrist was increasing, while retraction referred to periods in which the distance decreased. A Gaussian filter with standard deviation of 11 samples was applied to smooth the distance signal, then the derivative was used to identify periods of extension and retraction.
Statistical tests
We used three statistical tests to evaluate significance of results. We used the sign test for paired tests, including comparisons of unit performances in two encoding models and comparing FN permutations. We used the median test to compare the medians across distributions for context-specific, context-invariant and full FNs. We chose the median test because it is conservative and valid for distributions with different sample sizes and variance. We used the Pearson correlation to quantify preferred trajectory correlations and to evaluate the correlation between pairs of features (for example, full kinematics AUC vs average in-weight). For correlations, we considered |r| <0.2 to be uncorrelated, |r| in [0.2, 0.5] to be weakly or moderately correlated, and |r| > 0.5 to be strongly correlated.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
The authors thank Marina Sundiang for writing and contributing the code to compute confluent mutual information between neurons; Paul Aparicio for developing our spike-sorting pipeline; Daniel Margoliash and Matthew Kaufman for their insight throughout the project; and the veterinary and husbandry staff of the University of Chicago Animal Resources Center for their daily care of our research animals. This work was completed in part with resources provided by the University of Chicago’s Research Computing Center. All work related to experimental preparation, data collection and processing, and initial analyses were supported by the National Institutes of Health through a BRAIN Initiative Grant (R01NS104898) and through an NRSA F31 fellowship (1F31NS118950-01; D.M.). Work involving additional analyses, particularly related to the review process, was supported through another NIH BRAIN Initiative Grant (RF1NS132033).
Author contributions
Dalton D. Moore: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing—original draft, Writing—review & editing, Visualization, Funding acquisition. Jason N. MacLean: Conceptualization, Writing—review & editing, Supervision, Project administration, Funding acquisition. Jeffrey D. Walker: Conceptualization, Methodology, Software, Investigation, Writing—review & editing, Visualization, Supervision, Project administration, Funding acquisition. Nicholas G. Hatsopoulos: Conceptualization, Writing—review & editing, Supervision, Project administration, Funding acquisition.
Peer review
Peer review information
Nature Communications thanks Vikaas Sohal and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. a peer review file is available.
Data availability
The data generated using monkey MG in this study have been deposited in the DANDI Archive under accession code https://dandiarchive.org/dandiset/001062. Data availability for monkey TY is delayed due to the dataset’s use in manuscripts currently in preparation. Source data for figures are provided in the Source Data file. Source data are provided with this paper.
Code availability
Code used for data analysis and visualization is available on Github (https://github.com/hatsopoulos-lab/marmoset-trajectory_and_network_encoding_model), with the version at time of submission archived at 10.5281/zenodo.13840245.
Competing interests
N.H. serves as a consultant for Blackrock Microsystems, Inc. The remaining authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors jointly supervised this work: Jeffrey D. Walker, Nicholas G. Hatsopoulos.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-54343-6.
References
- 1.Georgopoulos, A. P., Schwartz, A. B. & Kettner, R. E. Neuronal population coding of movement direction. Science233, 1416–1419 (1986). [DOI] [PubMed] [Google Scholar]
- 2.Georgopoulos, A. P., Kettner, R. E. & Schwartz, A. B. Primate motor cortex and free arm movements to visual targets in three-dimensional space. II. Coding of the direction of movement by a neuronal population. J. Neurosci.8, 2928–2937 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Churchland, M. M. et al. Neural population dynamics during reaching. Nature487 (2012). [DOI] [PMC free article] [PubMed]
- 4.Shenoy, K. V., Sahani, M. & Churchland, M. M. Cortical control of arm movements: a dynamical systems perspective. Annu. Rev. Neurosci.36, 337–359 (2013). [DOI] [PubMed] [Google Scholar]
- 5.Maynard, E. M. et al. Neuronal interactions improve cortical population coding of movement direction. J. Neurosci.19, 8083–8093 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stevenson, I. H. et al. Functional connectivity and tuning curves in populations of simultaneously recorded neurons. PLoS Comput. Biol.8, e1002775 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hatsopoulos, N. G., Ojakangas, C. L., Paninski, L. & Donoghue, J. P. Information about movement direction obtained from synchronous activity of motor cortical neurons. Proc. Natl Acad. Sci. USA.95, 15706–15711 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sundiang, M., Hatsopoulos, N. G. & MacLean, J. N. Dynamic structure of motor cortical neuron coactivity carries behaviorally relevant information. Netw. Neurosci. 7, 661–678 (2023). [DOI] [PMC free article] [PubMed]
- 9.Kotekal, S. & MacLean, J. N. Recurrent interactions can explain the variance in single trial responses. PLOS Comput. Biol.16, e1007591 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Levy, M., Sporns, O. & MacLean, J. N. Network analysis of murine cortical dynamics implicates untuned neurons in visual stimulus coding. Cell Rep.31, 107483 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Levy, M., Guo, J. K. & MacLean, J. N. A sparse set of spikes corresponding to reliable correlations is highly informative of visual stimulus on single trials. bioRxiv 2022.01, 477564 (2022). [Google Scholar]
- 12.Georgopoulos, A. P., Kalaska, J. F., Caminiti, R. & Massey, J. T. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J. Neurosci.2, 1527–1537 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Russo, A. A. et al. Motor cortex embeds muscle-like commands in an untangled population response. Neuron97, 953–966.e8 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gao, P. & Ganguli, S. On simplicity and complexity in the brave new world of large-scale neuroscience. Curr. Opin. Neurobiol.32, 148–155 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Hatsopoulos, N. G., Xu, Q. & Amit, Y. Encoding of movement fragments in the motor cortex. J. Neurosci.27, 5105–5114 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kaufman, M. T., Churchland, M. M., Ryu, S. I. & Shenoy, K. V. Cortical activity in the null space: permitting preparation without movement. Nat. Neurosci.17, 440–448 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Saleh, M., Takahashi, K. & Hatsopoulos, N. G. Encoding of coordinated reach and grasp trajectories in primary motor cortex. J. Neurosci.32, 1220–1232 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jackson, A., Mavoori, J. & Fetz, E. E. Correlations between the same motor cortex cells and arm muscles during a trained task, free behavior, and natural sleep in the Macaque monkey. J. Neurophysiol.97, 360–374 (2007). [DOI] [PubMed] [Google Scholar]
- 19.Schieber, M. H. Training and synchrony in the motor system. J. Neurosci.22, 5277–5281 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mathis, A. et al. DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci.21, 1281–1289 (2018). [DOI] [PubMed] [Google Scholar]
- 21.Karashchuk, P. et al. Anipose: a toolkit for robust markerless 3D pose estimation. Cell Rep.36, 109730 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Walker, J. D. et al. Chronic wireless neural population recordings with common marmosets. Cell Rep. 36 (2021). [DOI] [PMC free article] [PubMed]
- 23.Moore, D. D., Walker, J. D., MacLean, J. N. & Hatsopoulos, N. G. Validating markerless pose estimation with 3D X-ray radiography. J. Exp. Biol. 225 (2022). [DOI] [PMC free article] [PubMed]
- 24.Evarts, E. V. Relation of pyramidal tract activity to force exerted during voluntary movement. 31 14–27 (1968). [DOI] [PubMed]
- 25.Hocherman, S. & Wise, S. P. Effects of hand movement path on motor cortical activity in awake, behaving rhesus monkeys. Exp. Brain Res.83, 285–302 (1991). [DOI] [PubMed] [Google Scholar]
- 26.Caminiti, R., Johnson, P. B. & Urbano, A. Making arm movements within different parts of space: dynamic aspects in the primate motor cortex. J. Neurosci.10, 2039–2058 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moran, D. W. & Schwartz, A. B. Motor cortical representation of speed and direction during reaching. J. Neurophysiol.82, 2676–2692 (1999). [DOI] [PubMed] [Google Scholar]
- 28.Sergio, L. E. & Kalaska, J. F. Systematic changes in motor cortex cell activity with arm posture during directional isometric force generation. J. Neurophysiol.89, 212–228 (2003). [DOI] [PubMed] [Google Scholar]
- 29.Aflalo, T. N. & Graziano, M. S. A. Relationship between unconstrained arm movements and single-neuron firing in the macaque motor cortex. J. Neurosci.27, 2760–2780 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Aflalo, T. N. & Graziano, M. S. A. Partial tuning of motor cortex neurons to final posture in a free-moving paradigm. Proc. Natl. Acad. Sci.103, 2909–2914 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chambers, B., Levy, M., Dechery, J. B. & MacLean, J. N. Ensemble stacking mitigates biases in inference of synaptic connectivity. Netw. Neurosci.2, 60–85 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hatsopoulos, N. G. & Amit, Y. Synthesizing complex movement fragment representations from motor cortical ensembles. J. Physiol.106, 112–119 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Saleh, M., Takahashi, K., Amit, Y. & Hatsopoulos, N. G. Encoding of coordinated grasp trajectories in primary motor cortex. J. Neurosci.30, 17079–17090 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Paninski, L., Fellows, M. R., Hatsopoulos, N. G. & Donoghue, J. P. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J. Neurophysiol.91, 515–532 (2004). [DOI] [PubMed] [Google Scholar]
- 35.Dechery, J. B. & MacLean, J. N. Functional triplet motifs underlie accurate predictions of single-trial responses in populations of tuned and untuned V1 neurons. PLOS Comput. Biol.14, e1006153 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.MacLean, J. N., Watson, B. O., Aaron, G. B. & Yuste, R. Internal dynamics determine the cortical response to thalamic stimulation. Neuron48, 811–823 (2005). [DOI] [PubMed] [Google Scholar]
- 37.Arieli, A., Sterkin, A., Grinvald, A. & Aertsen, A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science273, 1868–1871 (1996). [DOI] [PubMed] [Google Scholar]
- 38.Luczak, A., Barthó, P. & Harris, K. D. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron62, 413–425 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Goodman, J. M. et al. Postural representations of the hand in the primate sensorimotor cortex. Neuron104, 1000–1009.e7 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Okorokova, E. V., Goodman, J. M., Hatsopoulos, N. G. & Bensmaia, S. J. Decoding hand kinematics from population responses in sensorimotor cortex during grasping. J. Neural Eng.17, 046035 (2020). [DOI] [PubMed] [Google Scholar]
- 41.Suresh, A. K. et al. Neural population dynamics in motor cortex are different for reach and grasp. Elife9, 1–16 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lara, A. H., Cunningham, J. P. & Churchland, M. M. Different population dynamics in the supplementary motor area and motor cortex during reaching. Nat. Commun.9, 2754 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Carey, J. H., Crosby, E. C. & Schnitzlein, H. N. Decorticate versus decerebrate rigidity in subhuman primates and man. Neurology21, 738–744 (1971). [DOI] [PubMed] [Google Scholar]
- 44.Crosby, E. C., Schneider, R. C., de Jonge, B. R. & Szonyi, P. The alterations of tonus and movements through the interplay between the cerebral hemispheres and the cerebellum. J. Comp. Neurol.127, 1–91 (1966). [DOI] [PubMed] [Google Scholar]
- 45.Dann, B., Michaels, J. A., Schaffelhofer, S. & Scherberger, H. Uniting functional network topology and oscillations in the fronto-parietal single unit network of behaving primates. Elife5 (2016). [DOI] [PMC free article] [PubMed]
- 46.Sabatini, D. A. & Kaufman, M. T. Reach-dependent reorientation of rotational dynamics in motor cortex. bioRxiv 2021.09, 459647 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Walker, J. D., Pirschel, F., Gidmark, N., MacLean, J. N. & Hatsopoulos, N. G. A platform for semiautomated voluntary training of common marmosets for behavioral neuroscience. J. Neurophysiol.123, 1420–1426 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Burish, M. J., Stepniewska, I. & Kaas, J. H. Microstimulation and architectonics of frontoparietal cortex in common marmosets (Callithrix jacchus). J. Comp. Neurol.507, 1151–1168 (2008). [DOI] [PubMed] [Google Scholar]
- 49.Burman, K. J., Palmer, S. M., Gamberini, M., Spitzer, M. W. & Rosa, M. G. P. Anatomical and physiological definition of the motor cortex of the marmoset monkey. J. Comp. Neurol.506, 860–876 (2008). [DOI] [PubMed] [Google Scholar]
- 50.Huffman, K. J. & Krubitzer, L. Area 3a: topographic organization and cortical connections in marmoset monkeys. Cereb. Cortex11, 849–867 (2001). [DOI] [PubMed] [Google Scholar]
- 51.Huffman, K. J. & Krubitzer, L. Thalamo-cortical connections of areas 3a and M1 in marmoset monkeys. J. Comp. Neurol.435, 291–310 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Buccino, A. P. et al. Spikeinterface, a unified framework for spike sorting. Elife9, 1–24 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yger, P. et al. A spike sorting toolbox for up to thousands of electrodes validated with ground truth recordings in vitro and in vivo. Elife7 (2018). [DOI] [PMC free article] [PubMed]
- 54.Chaure, F. J., Rey, H. G. & Quian Quiroga, R. A novel and fully automatic spike-sorting implementation with variable number of features. J. Neurophysiol.120, 1859–1871 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Moore, D. D. A dynamic subset of network interactions underlies tuning to natural movements in marmoset sensorimotor cortex. “Hatsopoulos-lab/marmoset-trajectory_and_network_encoding_model: V1.0.0”. Zenodo10.5281/zenodo.13840246 (2024). [DOI] [PMC free article] [PubMed]
- 56.Gemmetto, V., Squartini, T., Picciolo, F., Ruzzenenti, F. & Garlaschelli, D. Multiplexity and multireciprocity in directed multiplexes. Phys. Rev. E94, 042316 (2016). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data generated using monkey MG in this study have been deposited in the DANDI Archive under accession code https://dandiarchive.org/dandiset/001062. Data availability for monkey TY is delayed due to the dataset’s use in manuscripts currently in preparation. Source data for figures are provided in the Source Data file. Source data are provided with this paper.
Code used for data analysis and visualization is available on Github (https://github.com/hatsopoulos-lab/marmoset-trajectory_and_network_encoding_model), with the version at time of submission archived at 10.5281/zenodo.13840245.