Spontaneous snapping-induced jet flows for fast, maneuverable surface and underwater soft flapping swimmer

Abstract

Manta rays use wing-like pectoral fins for intriguing oscillatory swimming. It provides rich inspiration for designing potentially fast, efficient, and maneuverable soft swimming robots, which, however, have yet to be realized. It remains a grand challenge to combine fast speed, high efficiency, and high maneuverability in a single soft swimmer while using simple actuation and control. Here, we report leveraging spontaneous snapping stroke in the monostable flapping wing of a manta-like soft swimmer to address the challenge. The monostable wing is pneumatically actuated to instantaneously snap through to stroke down, and upon deflation, it will spontaneously stroke up by snapping back to its initial state, driven by elastic restoring force, without consuming additional energy. This largely simplifies designs, actuation, and control for achieving a record-high speed of 6.8 body length per second, high energy efficiency, and high maneuverability and collision resilience in navigating through underwater unstructured environments with obstacles by simply tuning single-input actuation frequencies.

Spontaneous snapping enables fast, efficient, and maneuverable manta-like soft swimming robots with high collision resilience.

INTRODUCTION

Marine animals with various swimming modes provide a rich resource for bioinspired soft swimming robots (1–5). Among them, batoid fishes (6) are especially attractive for inspiring the designs of fast-swimming, efficient, and maneuverable robots (2, 7–10), due to their distinctive biological features such as dorsoventrally flattened bodies and extensively expanded pectoral fins. The flapping motions observed in the pectoral fins of batoids (11), known as mobuliform swimming, result in spanwise dorsoventral deformation and chordwise propagating waves. This form of swimming is recognized for its fast speed, high efficiency, and high maneuverability (12), achieved through low-frequency (less than 2 Hz) and high-amplitude fin flapping (fig. S1).

Recent efforts in manta-like soft swimming robots have been devoted to mimicking such a mobuliform swimming form by using soft materials and flapping mechanisms (7, 13, 14), integrated with complex power units and control modules (15–17). However, this goal has yet to be realized. Our recent study on bistable flapping wing–based soft swimmers takes a step toward creating a fast-swimming and efficient soft robot (14). The soft swimmer is composed of a soft pneumatic bidirectional bending actuator as its body and a pair of bistable wings. The bidirectional flexion of its body drives the snapping-induced expedited rotation and stroking of the flapping wings, achieving both a high swimming speed of 3.74 body length per second (BL/s) and high efficiency at a low actuation frequency of 1 Hz (14). It leverages fast snapping instability in bistable wings to achieve rapid response and amplified force via swift energy release. Thus, it provides a promising strategy to effectively overcome the intrinsic limitations in conventional soft swimming robots, including small-amplitude fin flapping, slow-response dynamics, and small propulsive force.

Despite the promise, notable challenges and limitations remain in achieving fast, energy-efficient, and maneuverable soft swimming robots in challenging unstructured underwater environments (7, 18). First, the strategy of bistability is energetically inefficient and complicates both designs and control, especially for periodic motion and locomotion. A bistable structure will stay in either stable state and require additional external actuation energy input to switch between the two stable states reversibly. For example, for the bistable flapping-wing swimmer, upon inflation in the bottom actuation layer, the soft body bends up; consequently, the wing snaps through to stroke up and stays in the upstroke stable state. It will not snap back to stroke down upon deflation unless flexing the soft body downward by inflating another actuation layer on the top. Thus, it needs two actuation inputs and a four-step actuation sequence (inflation-deflation on the top actuator followed by inflation-deflation on the bottom actuator) to achieve one cycle of flapping motion. The dual actuation inputs add additional weight and complexity in terms of design, actuation, and control, limiting both speed and energy efficiency.

Second, the maneuverability of soft swimming robots in unstructured underwater environments with obstacles, especially the swimming capability at different depths and collision resilience, remains largely unexplored. The bistable flapping-wing swimmer is limited to swimming close to the water surface because the bistable design makes it challenging to add extra weight to swim underwater due to its multistep actuation, let alone swimming at different depths (14). To regulate buoyancy underwater, marine animals such as fish often use gas-filled swim bladders. Inspired by the fish, researchers have explored integrating fluid-filled swim bladders with soft swimming robots for buoyancy control (19, 20). However, it needs additional actuation for filling or charging the fluid chambers in the bladders. Moreover, when swimming underwater, how soft swimming robots interact with unstructured underwater environments, especially the capability to tolerate collisions with obstacles for stable swimming, remains to be explored.

Third, the waveform shape of motions has a marked impact on the thrust generation, efficiency, and swimming speed in both marine animals and swimming robots (21). The fin tip motions of manta rays and manta-like robots, including the bistable flapping-wing swimmer, are largely sinusoidal (7, 22). From a fluid mechanics point of view, these sinusoidal motions create conventional reverse von Kármán vortex streets, resulting in a single jet wake responsible for thrust generation. However, previous studies show that nonsinusoidal propulsive motions such as a square waveform can produce up to four times higher thrust than the sinusoidal motions (23, 24). This boost in thrust is achieved by the generation of vortex dipoles produced by the abrupt start-and-stop square wave motions, leading to the formation of bifurcating dual jet wakes (23). Thus, nonsinusoidal motions suggest new strategies for increasing the thrust, swimming speed, and efficiency in soft swimming robots, which remains largely unexplored.

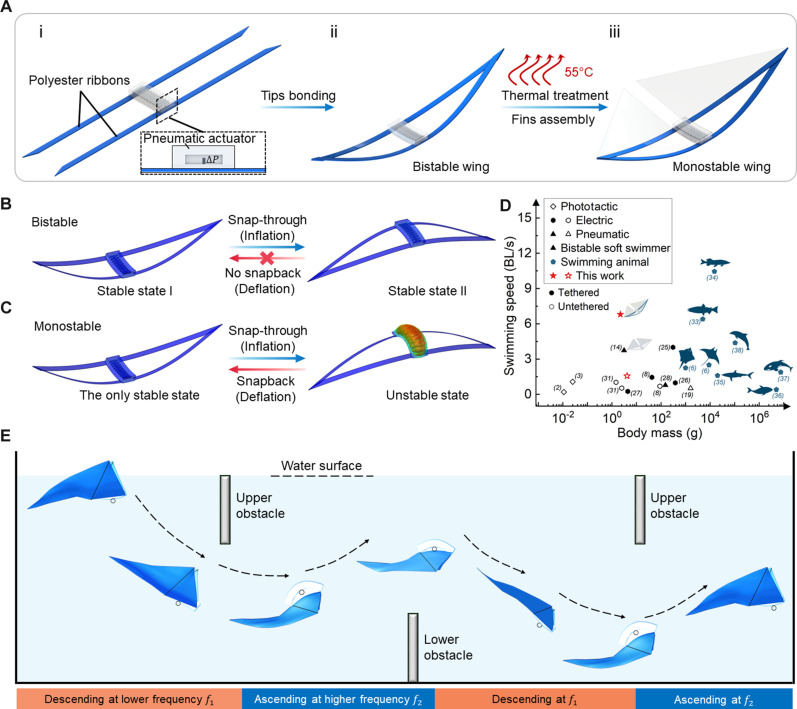
Here, we report a strategy of leveraging monostable instability in soft flapping-wing swimmers to achieve fast speed, high efficiency, and high underwater and underwater-to-surface maneuverability with high collision resilience. The soft swimmer has a monostable wing (Fig. 1A). Compared to bistable designs (14), monostable wing has only one stable state, i.e., it snaps through to an unstable state upon actuation (i.e., stroke down) and spontaneously snaps back to its original sole stable state (i.e., stroke up) upon deactuation without consuming additional energy (Fig. 1, B and C). Thus, it only requires one single actuation input to achieve a periodic flapping motion. This largely simplifies the actuation, design, and control to achieve a record-high speed, close to twice as fast as the swimming speed (~ 6.8 BL/s), while consuming over 1.6 times less energy compared to the bistable design (14) (Fig. 1D). Through combined computational fluid dynamics (CFD) simulation and particle image velocimetry (PIV) measurement, we find that the underlying mechanism for the faster speed resides in the monostability-induced square waveform motion in the wing, which generates bifurcating jet flows for higher thrust. Furthermore, the monostable design also enables the unique capabilities not achievable in bistable designs, including swimming at different depths by simply tuning the actuation frequency without the need for integrating additional swim bladders, navigating through a simple underwater vertical obstacle course with high collision resilience (Fig. 1E), as well as facilitates untethered designs due to its simplified actuation and control.

Fig. 1. Design of leveraging monostability for soft flapping-wing swimmers with high speed and multimodal surface and underwater maneuverability.

(A) Schematic design of the soft flapping-wing swimmer composed of a soft pneumatic bending actuator with a single top layer of air channels as body and a pair of monostable wings. The monostable wings are generated by first bonding the tips of two parallel flexible ribbons to form bistable wings, followed by certain duration of thermal treatment to release the prestress. Thin films and soft extended fins are attached to the soft swimmer to enhance propulsive forces. (B and C) Schematics on the comparison of distinct actuation behaviors between the bistable and monostable flapping-wing soft actuators. (D) Relative speed comparison between this work (tethered and untethered versions) and its bistable counterpart and other soft swimming robots and swimming animals. (E) Schematics of navigation through unstructured underwater environments such as a simple vertical obstacle course by simply tuning the single-input actuation frequencies f of the monostable soft swimmer. The obstacle course is composed of two upper and one lower plates as obstacles. Lowering f makes the swimmer descend, while raising f makes the swimmer ascend with tunable angles of attack. It exhibits a “w”-like swimming path to pass through the obstacle course.

RESULTS

Design of monostable flapping-wing soft swimmer for fast speed and high maneuverability

Figure 1A shows the schematic design and fabrication of monostable flapping-wing soft swimmers (see more details in figs. S2 and S3). It follows the design of our previous bistable flapping-wing soft swimmer (14). Bonding the end tips of two parallel polyester ribbons spontaneously forms a pair of bistable precurved framed wings (Fig. 1A, i and ii). Differently, we use thermal treatment to partially release the prestored elastic strain energy in the framed wing, thus making the bistable wing become monostable (Fig. 1A, ii and iii). Therefore, to drive the flapping of monostable wings, we only need a soft pneumatic bending actuator as its soft body with a single top layer of embedded air channels shown in Fig. 1A, i and figs. S2f and S3, as discussed below.

Figure 1 (B and C) shows the distinct difference between bistable and monostable flapping-wing soft swimmers in terms of actuation behavior. For both bistable and monostable wings before and after thermal treatment, the initial concave configuration of the wing represents one stable state. Inflating the air channels bends the soft body downward, driving the wing to snap through and stroke down. For the bistable case, the wing stays in the convex configuration after deflation and even under negative pressure (Fig. 1B). It cannot be actuated to snap back to its original configuration unless adding another layer of air channels on its bottom like the one in our previous bistable flapping-wing swimmers (14). In sharp contrast, for the monostable case, upon deflation, it will spontaneously snap back and stroke up to return to its original sole stable state driven by the elastic restoring force (Fig. 1C). This is because the convex configuration corresponds to a second stable state in the bistable wing but an unstable state in the monostable wing.

The spontaneous snapback in monostable designs enables quite a few advantages and unique swimming capabilities that are not achievable in bistable ones (14) as summarized below and in table S1 (1). It largely simplifies the design, actuation, and related control because it only requires the control of one single actuation input, which also facilitates the untethered design (2). It reduces the weight of the swimmer without the need for additional actuation layer on the bottom (3). It is more energy efficient because it does not need to consume additional energy to snap back like the bistable swimmer case (4). It can speed up the peak actuation frequency by over 1.6 times of the bistable design (5). It enables square waveform motion of the wing tip for higher thrust and power than the sinusoidal waveform in bistable swimmers and other flapping-wing swimming robots. Thus, it can achieve a close to two times faster swimming speed of 6.8 BL/s at a low actuation frequency of 1.67 Hz than its bistable counterpart but without sacrificing high energy efficiency (Fig. 1D) and consuming 1.6 times less energy (14). This speed is over 1.7 times faster than the fastest high-frequency tunabot (4.0 BL/s at a tail beat frequency of 15 Hz) (25) and other swimming robots (2–4, 8, 9, 14, 19, 25–32) and even comparable to the fast-swimming Atlantic salmon (Fig. 1D and tables S2 to S4) (6, 33–38). It enables extraordinary capabilities compared to its bistable swimmer counterpart (14), including load carrying, high maneuverability of swimming at different depths to navigate through an underwater obstacle course by regulating its buoyancy via simply tuning the actuation frequency (Fig. 1E), as well as collision resilience for stable swimming when colliding into obstacles.

Phase diagram of bistability-to-monostability transition with thermal treatment

Figure 2A shows the phase diagram of the transition from bistable to monostable wings in the flapping-wing soft robots with different wingspan length S after certain duration of thermal treatment T at a temperature of 55°C. The phase diagram is plotted based on the measured force-displacement (F-d) curves for the fabricated bistable wings with different S and T (Fig. 2, B and C, and figs. S4 and S5; see more details in Materials and Methods). It shows that, for any given S, as T increases, the initially bistable wing will gradually transit into a monostable wing due to the prestress release, where its precurved wing shape barely changes before and after transition as shown in Fig. 2B. For the wings with smaller S, it has a much higher prestored elastic energy; thus, it takes longer T to release the energy and transit into monostable.

Fig. 2. Thermal treatment induced bistability-to-monostability transition in the wings.

(A) Phase diagram of the bistability-to-monostability transition for the wings with different wingspan length S and the thermal treatment time T under 55°C. (B) Shape comparisons of the bistable and monostable flapping-wing soft actuators with different S before and after critical thermal treatment, respectively. Scale bar, 10 mm. (C and D) Force-displacement curves (C) and energy landscapes (D) of the bistable and monostable soft actuators with S = 160 mm before and after 20- and 120-min thermal treatment shown in (A), respectively.

Figure 2 (C and D) shows the variation of the measured F-d curves and their corresponding energy landscape U-d curves for an initially bistable wing (S = 160 mm) with different T, respectively (see more details in Materials and Methods). For T = 0 min, as the displacement increases, it shows both a negative slope and negative forces in the F-d curve (Fig. 2C) and two local energy minima in the U-d curve (Fig. 2D), validating its bistability. As T increases to ~20 min, the bistable F-d curve transits to a critical state, where the curve nearly intersects with the horizontal zero force line (Fig. 2C), indicating the transition from a bistable to a monostable state. This corresponds to the transition zone in the phase diagram (Fig. 2A). The corresponding U-d curve shows only one local minimum at d = 0, i.e., the original only stable state (Fig. 2D). As T further increases, the F-d curve is well above the zero force line (Fig. 2C) with only one local minimum energy in the U-d curve from both experiments (Fig. 2D) and analytical modeling (fig. S6; see more details in Materials and Methods), validating its preserved monostability.

High-speed and high energy-efficient monostable flapping-wing swimmer

The phase diagram provides important guidance on the design of a fast-speed monostable flapping-wing robot. Because the power of fast wing strokes is mainly determined by the amount of elastic energy released during snapping in the monostable wings, for any given wingspan length, to achieve the potential fastest swimming speed, we choose the critical thermal treatment time right falling into the transition zone of the phase diagram in Fig. 2A (fig. S4). This is because the monostable wing at the critical state in the transition zone has the highest prestored strain energy for subsequent maximum energy release during actuated snapping because further prolonged thermal treatment will reduce the prestored elastic energy to weaken the power stroke despite its monostability.

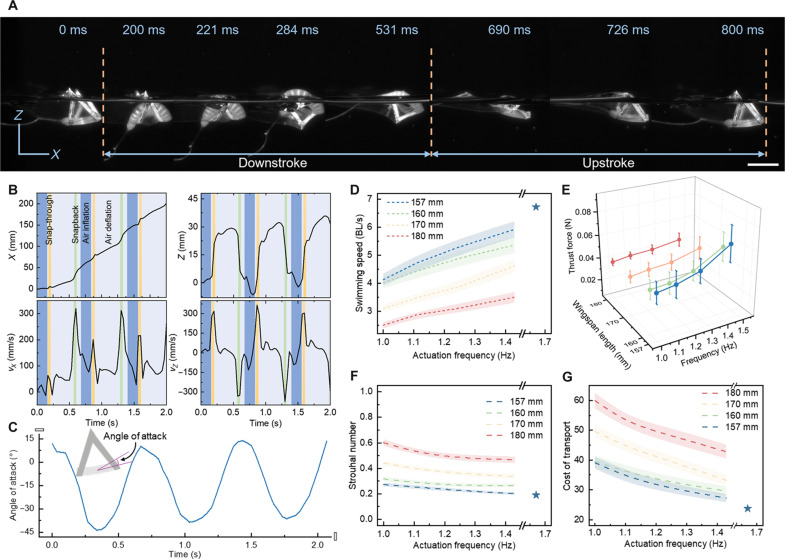
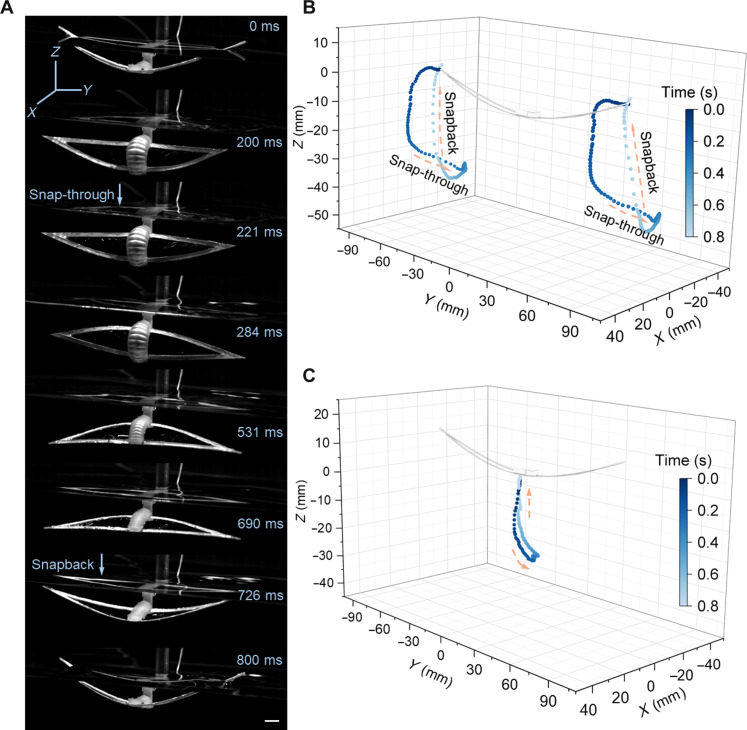
Figures 3A and 4A show the time-lapse free-swimming (side view) and stationary-swimming (isometric view) gait changes of the monostable flapping-wing robot (S = 160 mm, T = 20 min) close to the water surface during one actuation cycle of wing downstroke and upstroke recovery, respectively (fig. S7 and movies S1 and S2). The actuation frequency is f = 1.25 Hz, and the actuation pressure is P = 61 kPa. The wing tip’s motions (e.g., displacement, speed, and acceleration along both horizontal and vertical directions) and trajectories are shown in Figs. 3B (fig. S8) and 4B (figs. S9 to S13), respectively. Upon inflation, the body bends downward to gradually drive both the counterclockwise rotation and downstroke of the wing, followed by a rapid acceleration of the downstroke enabled by fast snap-through in a short duration of 21 ms (Figs. 3, A and B, and 4, A to C) to propel forward. Then, upon deflation, it quickly and spontaneously snaps back to its original configuration by stroking up for further propulsion. The snapback happens within 36 ms. The tracked trajectories of the wing tip and the soft body demonstrate high repeatability and consistency (fig. S14). The trajectory of the wing tip shows a highly asymmetric three-dimensional (3D) 8-like shape (Fig. 4B), while its soft body shows a 2D bending motion (Fig. 4C), indicating the strong deformation and motion asymmetries of the two snap-through and snapback motions. This sharply contrasts the symmetric 8-like shape of the tip trajectory observed in its bistable counterpart (14). Consequently, the tip motion shows an asymmetric square waveform–like motion rather than sinusoidal motions observed in its bistable counterparts and other manta-inspired propulsors and swimming robots, enhancing the thrust as discussed later. During swimming, the angle of attack varies and shows a sinusoidal pattern due to the undulation of its soft body (Fig. 3C and fig. S15).

Fig. 3. Swimming performances of monostable soft flapping-wing swimmers.

(A) Time-lapse side-view optical images depicting the representative surface-swimming gaits of the soft flapping swimmer (S = 160 mm) during one cycle of downstroke and upstroke under an actuation pressure of 61 kPa and a frequency f of 1.25 Hz. Scale bar, 20 mm. (B) Its corresponding displacements and velocities along the horizontal (X axis) and vertical directions (Z axis). (C) Its corresponding angle of attack changes with time. (D to G) Parametric studies on the swimming performances of the soft flapping swimmers with varying wingspan length S and actuation frequency f characterized by the relative swimming speed (D), thrust force (E), St (F), and CoT (G). The blue star in (D), (F), and (G) denotes the optimal design with the highest performances achieved at S = 157 mm and f = 1.67 Hz, showing the peak swimming speed of 6.8 BL/s, St = 0.21, and lowest CoT = 23.7.

Fig. 4. Flapping and rotation motions of the stationary monostable soft flapping-wing swimmer (S = 160 mm and f = 1.25 Hz) at the air-water interface with the rear body end fixed.

(A) Time-lapse images depicting pneumatic-driven motions during a representative downstroke cycle (snap-through, from 200 to 221 ms) and upstroke cycle (snapback, from 690 to 726 ms) of the wing flapping in an isometric view, captured by a high-speed camera. Scale bar, 10 mm. (B) Amplified 3D asymmetric 8-like flapping motion of the monostable wings. (C) 2D bending motion of the soft body.

Parametric studies on the swimming behaviors of monostable flapping-wing robots with different S and actuation frequency f show that it can achieve a high swimming speed yet high energy efficiency at low energy cost. At S = 157 mm and f = 1.67 Hz, it can swim at a peak average speed of ~156.4 mm/s, equivalently ~6.8 BL/s (Fig. 3D and movie S3). This is due to the generation of the highest thrust force (Fig. 3E and figs. S16 and S17). Such a high speed is over 1.8 times faster than its bistable counterpart (~ 3.74 BL/s) (14). We note that it also shows high energy efficiency with low energy consumption. The energy efficiency is evaluated by the Strouhal number St, which is defined as St = fA/U (A is the flapping amplitude and U is forward velocity). The St values of all the swimmers with S = 157 mm under different f fall within the observed naturally selected narrow range of 0.2 < St < 0.4 for high power efficiency (39). The energy consumption is evaluated by the cost of transport (CoT) defined as CoT = E/(mgd) (E is the energy input, m is the mass, g is the standard gravity, and d is the distance traveled). A lower CoT indicates lower energy consumption. The peak speed also shows the lowest CoT = ~23.7 (Fig. 3G), which is over 1.64 times smaller than its bistable counterpart (~39) (14).

Monostability-induced fluid dynamics for high speed and high efficiency

To better understand the underlying mechanism for the observed high-speed and high-efficient monostable swimmer, we combine PIV measurements and CFD simulations to uncover the monostable snapping instability–induced thrust generation mechanism, which remains unexplored in a previous study (14). The detailed setup of experiments and simulation can be found in the Supplementary Materials. The swimmer in the PIV experiment had a Reynolds number (Re_PIV) of 6500 based on the prescribed swimming speed and the wing length. For the CFD simulation, to conserve computational cost, a lower Reynolds number (Re_CFD) of 1500 was used. Many CFD studies of biological organisms and bioinspired applications have found that an Re of over 1000 can eliminate the viscous diffusion effect and is sufficient to reveal the main force-producing flow mechanisms that apply also to higher Re (40–43). Nevertheless, to ensure that the flow physics resolved in the CFD solver is a good reflection of reality, the 2D cross sections of the wake is compared to the PIV images as shown in Fig. 5 (A to F). Despite the difference in Re, PIV measurements (Fig. 5, A to C; fig. S18; and movies S4 and S5) and CFD simulations (Fig. 5, D to F; figs. S19 and S20; and movie S6) demonstrate excellent consistency.

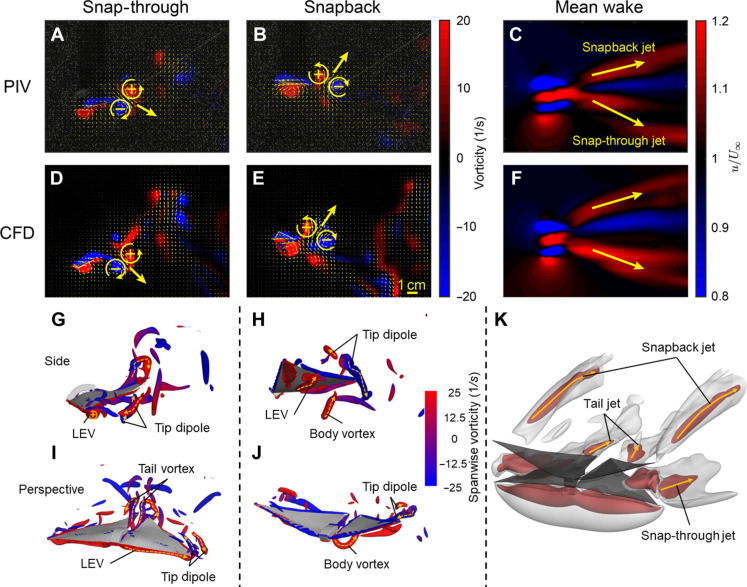
Fig. 5. Monostability-induced fluid dynamics in the monostable flapping-wing swimmer.

(A and B) PIV measurements of the vorticity at the ends of snap-through (A) and snapback motions (B). (C) PIV measurements of the velocity vector fields. (D to F) Corresponding CFD simulation results of the vorticity [(D) and (E)] and velocity vector fields (F). Both snap-through (i.e., stroke down) in (A) and (D) and snapback (i.e., stroke up) motions in (B) and (E) show the thrust-generating vortex pairs and jets. Red regions represent positive counterclockwise vorticity, and blue regions represent negative clockwise vorticity. [(C) and (F)] Cycle-averaged streamwise velocity normalized by the free-stream velocity. Regions with higher velocity than the freestream velocity are shown in red, and regions with lower velocity are shown in blue. All data are taken at the quarter-span position, and free-stream velocity has been subtracted from the velocity vectors. (G to J) CFD-simulated 3D vortex formations corresponding to the ends of snap-through and snapback in (D) and (E). Lateral view [(G) and (H)] and perspective view [(I) and (J)]. The vortices are visualized via Q-criterion isosurfaces colored by lateral vorticity contour. (K) Isosurfaces of high-momentum jets with u/u values of 1.07 (white, transparent) and 1.15 (red). Dashed arrows in (G) to (J) indicate the direction of rotation of the vortices based on the right-hand rule, while solid arrows in (K) indicate directions of high-momentum jets. Scale bar, 10 mm.

The unsteady wake dynamics from both experiments and simulation shown in Fig. 5 unveil its thrust generation mechanism. The soft swimmer sheds one pair of counterrotating vortices at both the downstroke snap-through (Fig. 5, A and D) and the upstroke snapback (Fig. 5, B and E) motions. These vortex dipoles and the resulting jet flows are responsible for the thrust generation. The bifurcating snap-through and the snapback jets are more clearly captured in the mean wake velocity plots (Figs. 5, C and F). When the fin snaps through, the positive leading-edge vortex (LEV) generated under the fin during the upstroke merges with the shed positive trailing-edge vortex (TEV), resulting in stronger TEV dipoles and thus a stronger snap-through jet. However, this vortex merging mechanism is not observed for the snapback. Therefore, the snap-through generates a stronger jet and thus more thrust as compared to the snapback.

Figure 5 (G to K) shows the 3D wake formations of the snap-through and snapback motions (movie S7), with the key vortices labeled. The vortex dipoles found on the quarter-span plane, as shown in Fig. 5 (A to E), corresponding to strong jets, are found here to be concentrated toward the tip region. These tip dipoles form following the snap-through and the snapback and advent high-momentum snap-through and snapback jets, as shown in Fig. 5K. These jets, correspondingly, are strong and concentrated near the tips. In addition, tail vortex loops have been found to form near the trailing tips of the fins. These vortices form semi-loops, as shown in Fig. 5 (G and I), and can also induce high-momentum flow in its center, leading to the formation of tail jets, as shown in Fig. 5K. Another region shown in the mean wake plot (Fig. 5K) with remarkable streamwise momentum is directly beneath the fins. The tip-bound cross section of this high-momentum region is captured in Fig. 5 (C and F). These correspond to the formation of the LEV during the snapback motion. The fast-snapping motion results in the circulation of fluids around the leading edges of the fins forming the LEV, which then detach and roll across the bottom surface of the fin, as shown in both Fig. 5 (A to E) and Fig. 5 (G to J). The increased circulation due to the LEV likely draws the fluid from upstream and thus induces the fast-moving flow downstream. The body vortex (Fig. 5H) and the interaction of the pair of tail vortices (Fig. 5I) induce forward-facing flow, corresponding to the lack of jets directly behind the body.

We note that there are both similarities and differences between the thrust generation mechanism of the monostable soft flapping-wing swimmer and that of fish and batoids. The snapping motion of the wings of the soft swimmer produces LEVs, which is widely observed in biological propulsors, such as bird and insect wings (44–46), fish tails (47, 48), and manta ray fins (22, 49). This LEV-based force production mechanism has been widely recognized as highly efficient (40, 50). Like manta rays, the LEV production of the monostable robot is more prominent near the fin tips than at the fin roots (22, 49). In comparison, during fish swimming, the tails are observed to produce LEV circulations more uniformly distributed along the span of the fish tail (41, 48). The wake of the monostable flapping swimmer near the fin tips consists of two positive-negative vortex pairs (2P) produced per flapping cycle. These vortex pairs induce high-momentum bifurcating jets in the wake, similar to manta rays and manta-like robots (11, 22, 49). This 2P-type wake differs from the reverse von Kármán vortex streets composed of two singular vortices of opposite signs (2S) produced per swimming cycle often observed in the wake of many fish-like and ray-like swimmers with undulatory kinematics (21). The 2P wake is often associated with strong force production both in the streamwise and the lateral directions (21, 51), which helps the monostable swimmer maintain high speed and maneuverability. The snapping motion of the monostable swimmer is less undulatory-like and more oscillatory-like, which makes the 2S-to-2P transition more likely to happen (21).

Another distinction of the current monostable soft swimmer is its square waveform of actuation. Whereas the tip motions of many fish-like and ray-like propulsors are largely sinusoidal, in comparison, the fin tip velocity of the present soft flapping swimmer is closer to a square waveform, featuring two prominent peaks in one cycle due to snapping (see Fig. 3B). Previous studies have demonstrated that a square waveform can produce up to four times more thrust than a sinusoidal waveform for propulsors owing to the generation of stronger thrust jets (23, 24). Therefore, by leveraging this monostable snapping mechanism, the soft flapping swimmer can presumably achieve a higher swimming performance than conventional manta-like robots.

Stable navigation through a simple vertical underwater obstacle course

Next, we explore the underwater and underwater-to-surface maneuverability of the fast and efficient monostable swimmer (S = 157 mm) in both free and unstructured environments without and with obstacles, respectively. To make it swim underwater, we increase its self-weight by attaching a small weight underneath the center of its belly, e.g., a small steel ball with weight of 0.68 g, ~30% of its self-weight (2.2 g), which does not affect its snapping motion. Without actuation, the slightly weighted soft swimmer sinks to the bottom of the water due to its slightly higher mass density than water.

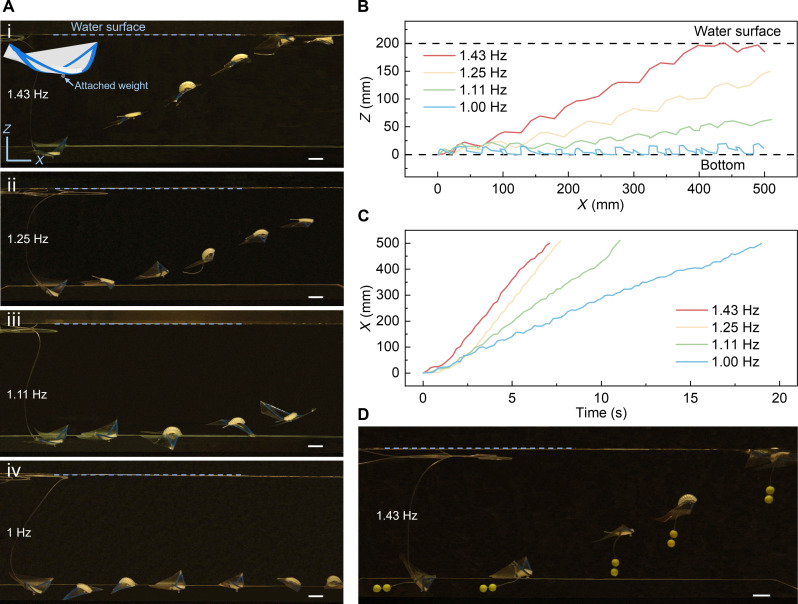
The soft swimmer demonstrates multimodal maneuverable swimming modes by simply tuning the single-input actuation frequency f (Fig. 6A and movie S8). At a relatively high f = 1.43 Hz, it can swiftly swim and ascend from the water bottom to the water surface. Once it reaches the water surface, it swims stably and smoothly transits to the fast surface swimming mode, as shown in the time-lapse images in Fig. 6A, i, the trajectory in Fig. 6B, and movie S8. As f slightly drops, e.g., f = 1.25 Hz, it gradually ascends from the water bottom to a certain depth and transits to a cruising swimming mode at that depth (Fig. 6, A), ii and B. The cruising swimming depth can be lowered by further reducing f, e.g., f = 1.11 Hz (Fig. 6, A), iii and B. The swimming trajectory in Fig. 6B shows that, as f decreases, the ascending angle (approximately the slope) also decreases and approaches to zero when f = 1 Hz. At f = 1 Hz, it transits to a stable crawling-like swimming mode on the bottom of the water despite the interactions between its flapping wings and the bottom surface (Fig. 6, A), iv and B. The variation of its horizontal swimming distance over time is shown in Fig. 6C. Similar to the surface swimming in Fig. 3D, the average underwater swimming speed (slope in Fig. 6C) increases with the increasing f due to the increased thrust and lifting force at a higher f. We note that, when f is fixed, increasing the added weight has the same effect as decreasing f with fixed weight on the multimodal swimming modes (fig. S21 and see detailed discussions in the Supplementary Materials). We further explore its load-carrying capability during swimming. Figure 6D shows that, at a high f = 1.43 Hz, even when carrying a payload of its self-weight, ~2.2 g, the soft swimmer can still rapidly swim and ascend from the water bottom to the water surface (movie S9).

Fig. 6. Tunable underwater swimming of the soft flapping swimmer (S: 157 mm) at different depths by actuation frequencies.

(A) (i to iv) Multimodal underwater and surface swimming behaviors at different actuation frequencies from 1.43 to 1 Hz. Inset in (i) shows the schematic of the swimmer with attached weight at its belly. (B) Corresponding swimming trajectories in the XY plane in (A). (C) Corresponding swimming displacement (in the X direction) over time in (A). (D) Swimming behavior of the soft swimmer carrying a cargo that is equal to its self-weight when actuated at 1.43 Hz. Scale bar, 20 mm.

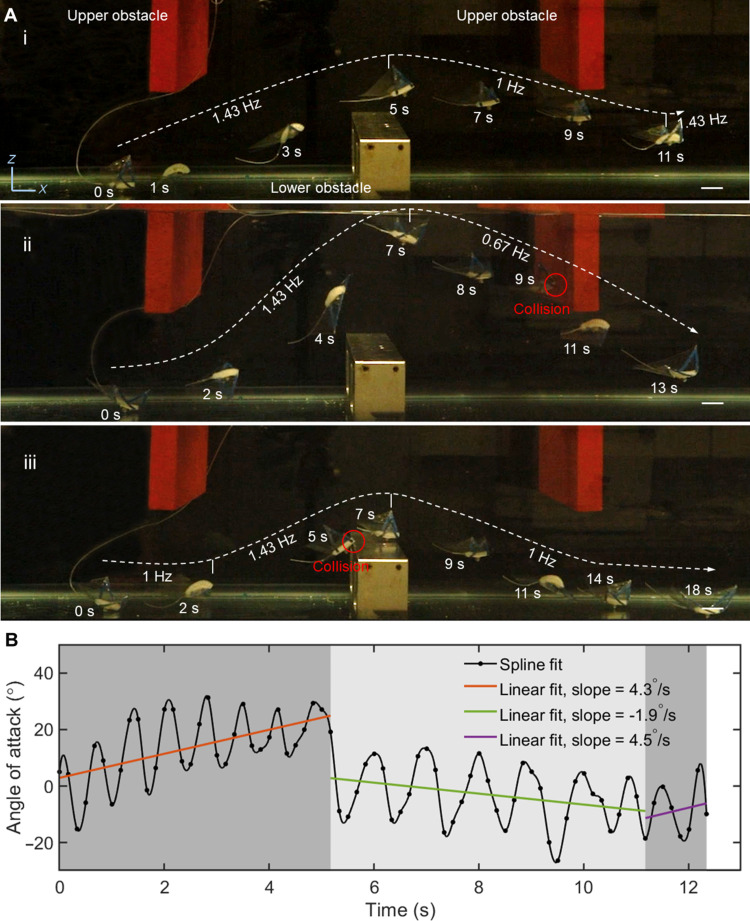
Equipped with the capability of multimodal surface and underwater swimming modes at different depths, the soft swimmer can potentially navigate through more complex unstructured underwater environments with obstacles by simply tuning the single-input actuation frequency. To test it, we designed a simple vertical underwater obstacle course, which is composed of two floating parallel foam plates as upper obstacles on the top and one metal plate as a lower obstacle on the bottom as shown in Fig. 7A, i. It shows that, by tuning f, starting from the bottom of the water, the soft swimmer can adeptly maneuver to first ascend at a relatively higher f (e.g., f = 1.43 Hz), descend by reducing f (e.g., f = 1 Hz), and then ascend again by increasing f (e.g., f = 1.43 Hz) to effectively evade the obstacles and collision-freely navigate through the simple obstacle course via the S-like shape swimming trajectory (Fig. 7A, i and movie S10).

Fig. 7. Navigating through a simple underwater vertical obstacle course with high collision resilience.

(A) Navigation through the underwater obstacle course composed of two foam plates on the top as upper obstacles and one metal plate on the bottom as a lower obstacle without (i) and with collisions (ii) by simply tuning the actuation frequency. The dashed lines show its swimming trajectories. In (ii) and (iii), the soft swimmer collides with the upper and lower obstacle during descending and ascending, respectively. (B) Corresponding angle of attack change with time during its navigation process in [(A), i]. Scale bars, 20 mm.

The ascend and descend maneuver of the soft swimmer is achieved by balancing three vertical forces: weight, buoyancy, and lift. The weight stays constant during the maneuver. The buoyancy force increases when the wing snaps through due to the inflation of the pneumatic chamber (Fig. 3A). The lift force also increases during the snap-through motion because the downward-deflecting snap-through jet is stronger than the upward-deflecting snapback jet (Fig. 5, C and F). This difference in the jet strength presumably results in a positive frequency-dependent lift. Therefore, controlled vertical maneuver can be achieved by tuning the actuation frequency. Figure 7B shows the corresponding angle of attack during the maneuver. At f = 1.43 Hz, the sum of buoyancy and lift exceeds the body weight, and the swimmer experiences a positive vertical force, leading to its ascent (0 s < t < 5 s). By lowering the frequency to f = 1 Hz, we reduce the overall lift of the swimmer, and the swimmer starts to descend due to gravity (5 s < t < 11 s). Last, we tune up the frequency back to 1.43 Hz again and observe another ascending trend (t > 11 s).

Although our soft swimmer is highly maneuverable, collisions are still inevitable in practice. Next, we further explore its resilience to obstacle collisions during navigating through the simple obstacle course. We find that the soft swimmer also shows high collision resilience. To make collisions happen, we intentionally tune different actuation frequencies to hit the obstacles at different descending or ascending stages. For example, Fig. 7A, ii and movie S10 show a scenario that the descending soft swimmer hits the upper obstacle on the right at a relatively lower f = 0.67 Hz. We observe that collision makes the descending soft swimmer momentarily sink vertically due to the interaction-induced reduction of its lift. Benefiting from such swimmer-obstacle interactions, the soft swimmer can lower its attitude to escape the obstacle. When the soft swimmer collides with the obstacle during its ascending stage, e.g., the lower obstacle shown in Fig. 7A, iii, we find that it can keep ascending despite the collision via multiple swimmer-obstacle interactions to cross the obstacle (movie S10). We note that all the collisions happen between the soft body and the rigid obstacles, where the resilience and compliance of its soft body make the safe contact with the obstacles by reducing its impact forces.

In addition to high swimming collision resilience, the soft swimmer also shows high swimming stability when subjected to external perturbations. As a proof of concept, we introduce turbulence by simply agitating the water using a plastic rod to disrupt the flow around and behind the soft swimmer (e.g., breaking the wake structures) during swimming. We find that, even after momentarily sinking upon hitting the boundary, the soft swimmer can efficiently resurface and swiftly resume its surface swimming after a few strokes (movie S11).

Proof-of-concept design and outdoor swimming performance of an untethered soft swimmer

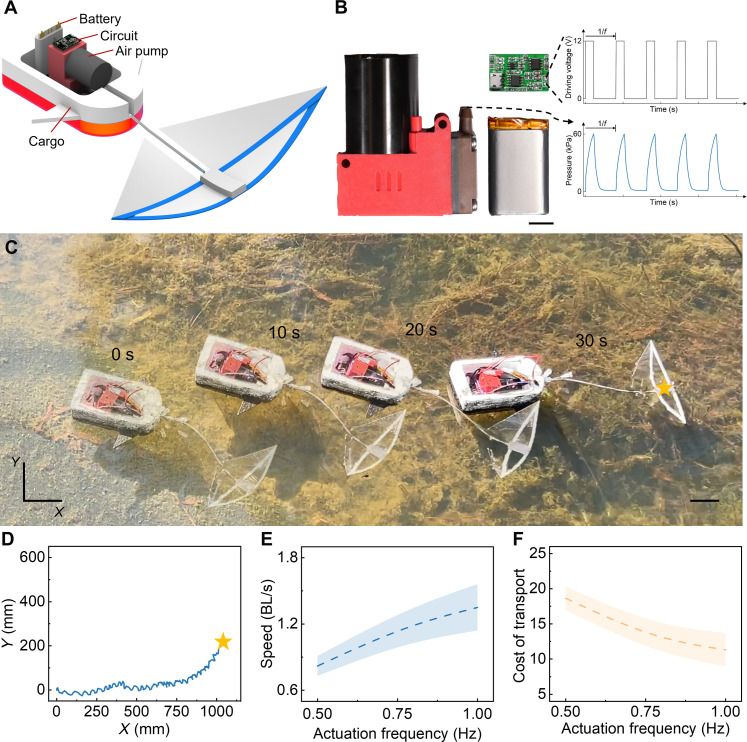
Last, we explore the proof-of-concept design of the untethered monostable soft flapping-wing swimmer due to its simplified single-input actuation. Figure 8A shows the schematics of the untethered design, where a foam cargo containing a circuit board, a battery, and an air pump is integrated on board behind the soft swimmer. The optical image of the untethered unit (circuit board, battery, and air pump) is shown in Fig. 8B and fig. S22. A 12-Vpp (peak-to-peak) voltage is applied to power the air pump to actuate the soft swimmer (details of the circuit board are shown in figs. S23 to S26). The inset displays the output driving signal from the control circuit. To enhance operational efficiency, we slightly increase the sizes of the pneumatic soft bending actuator, the wingspan length, and the ribbon width (see Materials and Methods). The enlarged size also brings down the actuation frequency to 0.77 Hz due to the prolonged inflation and deflation time. Figure 8C shows the time-lapse optical images of the soft swimmer during its untethered swimming in an outdoor natural pond (movie S12). Its corresponding swimming trajectory (in the XY plane) is shown in Fig. 8D. Despite the disturbance of wind and water currents, the untethered soft swimmer demonstrates good stability and agility in the natural environment. It can swim a distance of over 1 m in a short duration of ~30 s, achieving a relative swimming speed U of 1.18 BL/s at f = 0.77 Hz with a low CoT of 12.9. Similar to its tethered version, U increases monotonically with f (Fig. 8E) while CoT decreases with f (Fig. 8F). As f increases from 0.5 to 1 Hz, the average U increases from 0.82 to 1.35 BL/s, while the average CoT decreases from 18.6 to 11.1. Compared to the tethered version, the untethered swimmer shows both markedly reduced speed and CoT due to its onboard integration design. The highest average speed (U = 1.35 BL/s at f = 1 Hz) surpasses most untethered soft swimming robots, as shown in Fig. 1D. Meanwhile, its corresponding CoT (CoT = 11.1) is much lower than other electric untethered soft swimmers based on dielectric elastomer (CoT = 339.7) (52) and hydraulically amplified self-healing electrostatic actuators (CoT = 15.9) (20), which require expensive, high-voltage power supplies (53). This demonstrates the benefit of monostability-enabled energy-efficient design in pneumatic soft swimmers powered by low-cost air pumps.

Fig. 8. Design and swimming performance of a proof-of-concept untethered soft flapping swimmer.

(A) Schematic illustrating the design and assembly of the untethered soft swimmer. (B) Optical images of the air pump, battery, and control unit. Inset: Output driving signal and air pressure signal. Scale bar, 10 mm. (C) Swimming trajectory of the untethered soft swimmer in an outdoor natural pond. Scale bar, 50 mm. (D) Corresponding swimming trajectory in the XY plane. (E and F) Swimming speed (E) and CoT (F) of the untethered soft flapping swimmer as a function of actuation frequency f.

DISCUSSION

In this work, we demonstrate leveraging spontaneous snapback instabilities in monostable wings for achieving unprecedented capabilities in manta-like soft flapping-wing swimmers, including record-high relative swimming speeds at a low energy cost, multimodal surface and underwater swimming modes, high maneuverability and collision resilience in unstructured underwater environments, and stabilized swimming against perturbations. The two vortex pair wake and the bifurcating snap-through and snapback jets account for the generation of high thrust for the fast-swimming and high energy-efficient swimming performance. The frequency-dependent lift makes it highly maneuverable to swim at different depths and navigate through unstructured environments with obstacles by simply tuning the singe-input actuation frequency without the need for additional fish-like swim bladders. The adaptive soft swimmer–obstacle interactions make it capable of enduring and recovering from collisions at different ascending or descending stages.

This work will open an avenue of leveraging monostability for designing fast, efficient, and maneuverable underwater robotic systems not limited to undulatory and oscillatory swimming modes (21). Compared to bistability, monostability can largely simplify designs, actuation, and control for generating fast and powerful periodic motion in varieties of monostable structures (54), which could find broad applications for fast and energy-efficient locomotion in air, on land, and underwater or multimode in soft robotics. This soft flapping swimmer design is suited for real-world applications in complex and unstructured environments, including deep-sea exploration (e.g., ecosystems, underwater surveillance, and detection) and environmental monitoring on surfaces and underwater (e.g., water quality, pollution levels, and environmental changes) (1, 55).

Despite the promise, limitations remain for practical applications, especially in improving the current proof-of-concept bulky untethered design. To use the monostability-induced thrust generation mechanism for real-world applications (1, 55), a highly compact and well-integrated untethered swimmer, featuring wireless control modules, micropumps, and power systems integrated onboard, is needed, allowing for both surface and underwater swimming, which will be explored in the future through design optimization and system integration.

MATERIALS AND METHODS

Fabrication and actuation of monostable soft flapping-wing swimmers

The pneumatic soft bending actuator was fabricated using a conventional manufacturing technique for pneumatic-driven soft actuators, involving molding and demolding processes, as shown in fig. S2. Ecoflex 00-50 from Smooth-On Inc. was chosen as the elastomeric material for constructing the two sections of the soft bending actuator. The molds for the channel layer and bottom layer were produced using VeroClear and 3D printed using a Stratasys Objet260 Connex 3 printer. The two cured Ecoflex layers were then bonded using silicone rubber adhesive (SIL-Poxy, Smooth-On). Flexible ribbons were fashioned from polyester sheets (0.5 mm in thickness; Grafix) and laser cut to the desired shape. These ribbons were integrated into the pneumatic actuator’s edges using super glue. In addition, the two ribbon tips were bonded together using the same super glue to form the bistable structure. Subsequently, the original bistable wings were put in a thermal oven under a controlled temperature of 55°C for a duration of time from minutes to hours to reduce the prestored strain energy and induce their transition into monostable wings.

In the case of the underwater soft swimmer, a stainless steel ball was attached to the bottom of the soft bending actuator using super glue. For untethered soft swimmer, the foam cargo was shaped using a hot wire foam cutter. For the experimental investigation of geometries, dynamic behaviors, and swimming performances of the monostable actuators and soft swimmers across different wingspan lengths (S = 157, 160, 170, and 180 mm), rigorous assessments were conducted.

Analytical model of the buckled precurved wing shape

We construct the analytical model to rationalize the monostable deformation of ribbons and the corresponding elastic energy function $\overline{U}$, which reads

$$\overline{U}=\mathrm{\alpha }{({\mathrm{\kappa }}_1-{\mathrm{\kappa }}_{10})}^2+\mathrm{\beta }{({\mathrm{\kappa }}_2-{\mathrm{\kappa }}_{20})}^2+{(\mathrm{\tau }-{\mathrm{\tau }}_0)}^2$$ (1)

where ${\mathrm{\kappa }}_1$, ${\mathrm{\kappa }}_2$, and $\mathrm{\tau }$ denote the curvature in the principal direction and torsion along the arc length coordinate (56), respectively. ${\mathrm{\kappa }}_{10}$, ${\mathrm{\kappa }}_{20}$, and ${\mathrm{\tau }}_0$ denote the curvature and torsion in the reference state, i.e., after thermal treatment. $\mathrm{\alpha }$ and $\mathrm{\beta }$ are the normalized bending rigidity. The deformation process, as illustrated in fig. S6A, alongside the corresponding energy variations depicted in fig. S6B during deformation, demonstrates how thermal treatment alters the energy profile of ribbons in their reference state.

The governing equations for the ribbons are given by

$$\frac{\mathrm{\partial }\tilde{\mathit{N}}}{\mathrm{\partial }s}+\mathit{f}=0$$ (2)

$$\frac{\mathrm{\partial }\tilde{\mathit{M}}}{\mathrm{\partial }s}+\frac{\mathrm{\partial }\tilde{\mathit{r}}}{\mathrm{\partial }s}\times \tilde{\mathit{N}}+\mathit{l}=0$$ (3)

where vectors $\tilde{\mathit{N}}$ and $\tilde{\mathit{M}}$ denote the resultant force and moment exerted on the cross section by the stress at vector $\tilde{\mathit{r}}(s)$ parameterizing the ribbon’s central curve (56). $\mathit{f}$ and $\mathit{l}$ are the body force and moment per unit length, respectively. Applying this Kirchhoff system to the ribbons generates deformation during actuation.

Force-displacement measurement

We characterized the static mechanical response of both the bistable and monostable soft actuators with precurved wings through quasistatic indentation tests using an Instron 5944 tensile tester. As shown in fig. S5, one end of the pneumatic soft bending actuator, i.e., the soft body, was anchored while the wing tips of the soft body were linked to the vertical indenter. The tests were carried out under load control with a loading rate of 5 mm/min and a loading distance of 30 mm. The forces and displacements during indentation were recorded to create indentation force-displacement curves for the precurved soft actuators with various wingspan lengths S.

Motion capture

The movements of the investigated monostable soft actuators and swimmers were recorded using a high-speed camera (Photron SA-2) operating at a frame rate of 1000 frames/s. The motion analysis was conducted using a Photron FASTCAM Viewer (PFV4).

Aquatic experimental setup

The soft swimmers were placed in aquariums measuring 76 cm by 31 cm by 32 cm and 122 cm by 52 cm by 32 cm for water surface and underwater swimming tests, respectively. These aquariums were filled with 15 and 35 gallons (56.78 and 132.49 liters) of water, respectively. An open-loop pneumatic control system (fig. S27) was connected to the soft swimmers using a 2-m narrow soft rubber tube. The swimming sequences were recorded using a Photron SA-2 camera for both stationary and dynamic in-water testing, in addition to a Canon 6D Mark II camera.

Thrust force measurement of the soft swimmer

As shown in fig. S16, a force sensor (Instron, 2530-5N) and a rigid rope are attached to the tail of the soft swimmer. The soft swimmer is situated in an aquarium (50 cm by 26 cm by 32 cm), which is filled with 9 gallons (34.07 liters) of water. The thrust force is calculated by subtracting the base load from the force peak during the soft swimmer’s swimming motion.

Flow field measurement and simulation

The flow field around the soft swimmer is measured in a recirculating water tunnel using planar PIV with a high-speed camera and two continuous wave lasers. The 3D wake dynamics of the soft swimmer is simulated using direct numerical simulation with an immersed-boundary method (57–59).

Outdoor swimming test

The dimensions of the soft actuators for outdoor testing are increased to 1.3 times their original dimension, and the wingspan length is extended to 190 mm, and the ribbon width is expanded to 2.5 mm.

Supplementary Materials

The PDF file includes:

Supplementary Text

Figs. S1 to S27

Tables S1 to S4

Legends for movies S1 to S12

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S12