Developing a nearly automated open-source pipeline for conducting computational fluid dynamics simulations in anterior brain vasculature: a feasibility study

Abstract

Intracranial aneurysms (IA) pose significant health risks and are often challenging to manage. Computational fluid dynamics (CFD) simulation has emerged as a powerful tool for understanding lesion-specific hemodynamics in and around IAs, aiding in the clinical management of patients with an IA. However, the current workflow of CFD simulations is time-consuming, complex, and labor-intensive and, thus, does not fit the clinical environment. To address these challenges, we have developed a semi-automated pipeline integrating multiple open-source software packages to streamline the CFD simulation process. Specifically, the study utilized medical angiography data from 18 patients. An in-house open-source DL image segmentation model (ARU-Net) was employed to generate 3D computer models of the anterior circulation. The segmented intracranial vasculature models, including IAs, were further refined using the Vascular Modeling Toolkit (VMTK), an open-source Python package. This step involved smoothing the surface of the models and extending the inlet and outlet regions to ensure a realistic representation of the vascular geometry. The refined vascular models were then converted into computational meshes using an open-source mesh generator known as TetGen. This process was nearly automated and required minimal user interaction(s). Blood flow simulations of the cerebral vascular models were performed using established SimVascular solvers (an open-source finite element platform for vascular applications) through an application programming interface (API). The CFD simulation process was also conducted using the manual workflow for comparative purposes. The initial assessment compared the geometries derived from manual and DL-based segmentation. The DL-based segmentation demonstrated reliable performance, closely aligning with manually segmented results, evidenced by excellent Pearson correlation coefficient (PCC) values and low relative difference (RD) values ranging from 3% to 10% between the computed geometrical variables derived from both methods. The statistical analysis of the computed hemodynamic variables, including velocity informatics and WSS-related variables, indicated good to excellent reliability for most parameters (e.g., ICC of 0.85–0.95). Given the data investigated, the proposed automated workflow streamlines the process of conducting CFD simulations. It generates results consistent with the current standard manual CFD protocol while minimizing dependence on user input.

Introduction

Unruptured intracranial aneurysms (UIAs) are prevalent in the adult population (3–6%). These aneurysms are frequently incidental findings from imaging examinations for unrelated medical issues^1,2. With the improving accessibility of state-of-the-art medical imaging technologies, more and more UIAs are detected in an aged society. When UIAs are detected, the primary clinical decision revolves around whether to undertake surgical or endovascular interventions or to adopt a conservative strategy entailing regular imaging surveillance^3–6. Invasive procedures carry significant risks, including procedural complications and extended recovery periods^7–9. However, a UIA generally has a low risk of rupture (e.g., 0.1–1% per year), which could be lower than the risks associated with surgical interventions. Conversely, conservative management (i.e., periodical imaging follow-up) exposes patients to a risk of aneurysm rupture, which can result in catastrophic neurological outcomes (e.g., 50% mortality after IA rupture). As a result, managing patients afflicted with a UIA is a dilemma, and many advocate the need for a refined, individualized treatment paradigm.

Much ongoing research involves personalized risk assessments for patients with a UIA. Outcomes of these personalized risk assessments enable physicians to select patients whose UIA has a high risk of rupture for intervention while confidently leaving other low-risk UIAs for imaging follow-up. Currently, this capability is not available in the clinical workflow. Based on the mechanobiology literature, disturbed flow within an aneurysm is a crucial factor in triggering vascular remodeling^10–12. Over the past two decades, patient-specific computational fluid dynamics (CFD) simulations^13,14 have become a valuable tool for evaluating aneurysmal hemodynamics for individual patients. These “patient-specific” hemodynamic metrics derived from CFD simulations are routinely used in IA research. Many studies have shown that integrating hemodynamic variables into machine learning (ML) models significantly improves the prediction of IA rupture status^15–20. Remarkably, the above-said ML-based methods for rupture status prediction have performed well (e.g., a lot of studies reached the area under the operator receiving curve greater than 0.85). Further developments are still needed to make them clinically useful. The work presented here is an integral part of these translation-driven developments.

The most common workflows used for running “patient-specific” CFD simulations by many research groups^14,19,21,22 are similar. They start with medical imaging data and proceed to the final hemodynamic metrics of interest in three main steps. In the first step, pre-processing involves preparing the medical angiographic data (e.g., CT or MR angiography) for simulations. It includes image segmentation to extract the region of interest (ROI), such as the intracranial vessels, including one or more brain aneurysms, from the angiographic images. Subsequently, a 3D (surface) model is created. Additionally, the pre-processing includes volumetric mesh generation, which entails discretizing the 3D surface model into a volumetric computational mesh composed of grid points or elements that will be used for numerical analysis. The second step (hereafter referred to as the solver step) is to solve the Navier–Stokes equations to compute the time-resolved velocity and pressure fields over the entire volumetric computer mesh. The solver step includes defining the boundary conditions, which are the physical conditions at the boundaries of the computational domain, such as inlet and outlet blood flow rates and pressure conditions. Given the physiological boundary conditions, numerical methods are employed to solve the Navier–Stokes equations governing fluid motion within the computational domain. The last step is known as the (3) post-processing step. Specifically, we analyze and visualize hemodynamic results for each CFD model. Some hemodynamic metrics (e.g., velocity, wall shear stress [WSS], etc.) are standard outputs from a selected CFD solver. The research community is actively developing more advanced parameters (e.g., velocity informatics¹⁹, relative residence time (RRT)²³, vortex core analysis²⁴). Visualization of hemodynamic data has attracted some attention as well^25–27.

The pre-processing step is both time-consuming and labor-intensive. For instance, manually creating a CFD model can take around 1 h and requires a skilled technician or engineer. Such resources are unavailable in a clinical environment, becoming a major hurdle to integrating “patient-specific” CFD simulations into clinical practice.

In this study, capitalizing on the state-of-the-art deep-learning (DL)-based vessel segmentation technologies²⁸, we present a semi-automated pipeline that minimizes user interaction while preserving the accuracy of CFD simulations. The primary objective is to develop a robust semi-automated workflow capable of handling complex geometries with minimal manual interventions. Moreover, in this study, we propose an open-source approach for all three key steps to make our proposed software pipeline accessible to the entire research community. The main thrust of this study is our validation of the proposed pipeline using in vivo angiographic data from 37 human subjects. Our secondary objective is to demonstrate that the proposed pipeline can streamline the evaluation of aneurysmal hemodynamics without compromising simulation fidelity.

The main contribution of this study is our development of an open-source computational hemodynamics simulation platform OpenHemoSim. The proposed OpenHemoSim integrates known open-source packages ARU-Net²⁹, SimVascular³⁰, Vascular Modeling Toolkit (VMTK)³¹, and VTK³² to streamline CFD simulations using patient-specific imaging data. Although this feasibility study focuses on streamlining image-based CFD simulations for IAs, our work contains innovative components. First, the proposed OpenHemoSim connects DL-based segmentation to image-based simulations using open-source packages, as mentioned above. To our knowledge, integrating DL-based image segmentation with image-based CFD simulations for IAs is still relatively new. Second, OpenHemoSim includes both conventional hemodynamic metrics (e.g., wall shear stress and its derivatives) and newly-developed velocity-informatics parameters¹⁹. Notably, velocity-informatics is a novel technology useful for characterizing both the growth status of abdominal aortic aneurysms³³ and the rupture status of IAs²⁵. Making velocity-informatics available augments computerized analysis of IAs.

Related prior work

The most relevant prior work is summarized below, and our review indicates that streamlining the computational hemodynamics workflow has not received sufficient attention. Hence, our review of prior work has been divided into the three most relevant components: (1) DL-based vessel segmentation, (2) neural network-based CFD simulation, and (3) accelerating CFD mesh generation.

DL-based brain vessel segmentation

Recent breakthroughs in DL-based technologies have revolutionized the domain of medical image segmentation. Interested readers are steered to recent survey articles^34,35. Relatively fewer studies^{18,36–39,39–43} have focused on learning hierarchical representations of brain vessels from raw imaging data, as summarized below.

Recall that correct CFD models in and around IAs must meet two requirements: (1) retaining relevant small vessels and (2) eliminating the possibility of unwanted vessel-to-vessel or vessel-to-IA adhesion. Otherwise, incorrect CFD models alter pathways for blood flow, leading to erroneous gross intra-aneurysmal gross hemodynamics. Some early technologies largely adopted existing convolutional neural network (CNN) models (e.g., U-Net or its close variants) developed by the DL community and applied them to brain vessel segmentation or intracranial aneurysm (IA) detection. Thus, most of the DL vessel segmentation methods are not optimized to satisfy these two requirements. Stember et al.⁴⁰ devised a CNN for the automated detection of intracranial aneurysms (IA) utilizing magnetic resonance angiography (MRA) data. However, their reliance solely on 2D maximum intensity projection (MIP) images for model training presents notable limitations, i.e., their method is not suited for creating the 3D vasculature necessary for generating CFD meshes. Jin et al.⁴² introduced an end-to-end spatio-temporal DL neural network tailored for IA segmentation, leveraging both 2D and temporal digital subtraction angiography (DSA) data. Despite its innovation, their model was constrained to 2D image segmentation, reducing its efficacy in distinguishing small aneurysms from vascular accumulations. Patel et al.⁴¹ implemented the DeepMedic architecture³⁷ for IA segmentation utilizing dynamic susceptibility contrast sequences and compared its performance with a 3D U-Net model³⁹. Shahzad et al.⁴⁴ employed a deep learning model to automatically segment aneurysms on computed tomography angiography (CTA) images. Cheng et al.⁴³ tackled IA segmentation using a variant of U-Net CNN architecture⁴⁵, integrating spatial information from 3D rotational angiography (3DRA) images. The network model had difficulties with delineating small structures, e.g., segmenting small-sized IAs, particularly those with dimensions less than 3 mm in height or width.

Some recent work has been devoted to designing DL segmentation methods for creating CFD models/meshes to meet the two requirements mentioned above. Notably, Mu et al.²⁸ added an attention module to improve the depiction of small vessels, which are often needed for the integrity of computational hemodynamics in and around IAs. Also, they developed a post-processing strategy to eliminate unwanted vessel-to-vessel and vessel-to-IA adhesion. Their DL model named ARU-Net was successfully used to create CFD models. However, vessel geometries obtained by ARU-Net often include more distal small vessels (i.e., longer and more distal branches). Of note, extensive small distal vessels add complexity in mesh generation and demand more computational time. In a more recent publication⁴⁶, Mu et al. devised a frequency-domain attention module that selectively tune the inclusion of small vessels. As a result, their latest DL vessel segmentation model, a frequency-domain attention cascade U-Net (FACU-Net) showed promise in automatically creating CFD models with minimal human interventions.

Neural network-based CFD simulations

As described in the introduction, estimating hemodynamic stressors often requires numerically solving Navier–Stokes equations (e.g., using the finite element or finite volume method). Because the numerical solution of Navier–Stokes equations is time-consuming, considerable research has been invested in accelerating the hemodynamic assessments using machine learning (ML) methods in recent years. These ML methods can be largely divided into the following three categories: (1) parameterization and projection methods, (2) point-cloud methods, and (3) mesh-based methods.

Theoretically, parameterization and projection methods involve the transformation of an intricate 3D artery-wall manifold into a simpler Cartesian 1D or 2D domain, aiming to predict one or more hemodynamic variables. In other words, these parameterization and projection methods do not attempt to solve Navier–Stokes equations. For instance, Ilu et al. deployed Multilayer Perceptrons (MLPs) for estimating scalar values like fractional flow reserve (FFR, i.e., a fractional pressure drop after a vessel stenosis) along the artery centerline, leveraging shape descriptors⁴⁷. Su et al.⁴⁸ utilized CNNs to predict scalar magnitudes of WSS through uniform shape sampling techniques. Additionally, Gharleghi et al. employed CNNs for estimating both time-averaged⁴⁹ and transient WSS magnitudes⁵⁰ based on cylindrical parameterizations of the vessel wall. Furthermore, Ferdian et al.⁵¹ employed CNNs to estimate vector-valued WSS, also using a cylindrical parameterization. This approach involved sampling projections of the velocity field at various distances from the aortic wall, reconstructed from 4D flow MRI data. Cylindrical parameterization means that a segment of the artery is projected to an idealized vessel segment, i.e., a cylinder. Although the proposed parameterization mitigated some limitations of early work relying on regularized boundaries (e.g., CFDNet⁵²), these parameterization methods still confront challenges when the vessel segments become complex. It is worth noting that complex artery shapes or vascular abnormalities such as aneurysms or dissections have not been widely tested using this methodology.

3D Point-Cloud Methods have been experimented with to estimate pressure and vector-valued velocity fields for three dimensional (3D) vessels. The 3D vessel geometries are represented by 3D point clouds. Liang et al.⁵³ pioneered the development of deep neural networks (DNNs) to directly infer steady-state distributions of pressure and flow velocity within the thoracic aorta. Similarly, Li et al.⁵⁴ proposed a DL methodology aiming at predicting velocity and pressure fields based on the pre- and post-operative geometric features observed in coronary artery bypass graft surgery. Zhang et al.⁵⁵ proposed a sophisticated analytical framework leveraging multi-attribute point cloud datasets and DL modules augmented by physics-informed neural networks (PINN)⁵⁶. Both studies encoded vessel geometries to include a range of morphological variations in human aorta. For instance, Zhang et al. constructed a set of 110 normal aorta models with and without coronary branches. As a result, their models take into account morphological variations of normal aorta. Consequently, their method showed excellent results, as compared to the results of CFD simulations. However, their methodology may not be easily translatable to vascular aneurysm or dissection applications. After all, vascular aneurysms and dissections are very challenging to geometrically parameterize.

Mesh-Based Approaches utilize Graph Convolutional Network (GCN) architectures to intricately encode detailed information about the artery-wall structure. These methods leverage both the geometric coordinates of mesh vertices and additional local geometric details, such as surface normals and connectivity. For instance, Morales Ferez et al.⁵⁷ utilized surface normal vectors and connectivity as input features for a GCN designed to predict a hemodynamic scalar named endothelial cell activation potential (ECAP) on the surface of the left atrial appendage. Additionally, Suk et al.⁵⁸ utilized Mesh Convolutional Neural Networks to estimate WSS on the coronary artery surface. Although this methodology showed great potential, more work is needed to address whether their successes can be generalized. From the perspective of flow physics, the targeted WSS and its derivatives (e.g., ECAP) depend on the intrinsic vessel shape. However, inputs to mesh CNN and GCN are surface normals, implying WSS and its derivatives are solely dependent on surface normals.

Developments in CFD model/mesh generation

Ghaffari et al.⁵⁹ introduced an advanced technique for automatic parametric mesh generation specifically designed for subject-specific cerebral arterial trees. This method produces high-resolution, anatomically precise computational meshes optimized for rapid blood flow simulations, extending the applicability of 3D vascular modeling to encompass extensive segments of cerebral arterial networks. The parametric meshing framework they developed efficiently decomposes the vascular skeleton, extracts key geometric features, and generates hexahedral meshes. To capitalize on the strengths of both unstructured and parametric meshing, the approach integrates an unstructured mesh for complex, irregular pathologies such as aneurysms with a parametric mesh for the remaining portions of the patient’s arterial tree, achieving a seamless fusion that enhances both accuracy and computational efficiency. However, the method may encounter challenges when handling highly intricate vascular geometries, where the transition between unstructured and parametric meshes could potentially introduce computational artifacts or necessitate additional refinement.

In parallel, prior work on mesh generation for computational simulations has led to the development of several open-source tools that have significantly advanced mesh quality and efficiency, particularly for complex geometries. Gmsh⁶⁰ is recognized as a versatile 3D finite element mesh generator with an integrated CAD engine and post-processor, capable of supporting both structured and unstructured meshes. SALOME⁶¹ extends these capabilities by offering a comprehensive platform for the pre- and post-processing in numerical simulations, excelling in the meshing of intricate geometries and integration with a variety of solvers. TetGen⁶² is notable for its specialization in generating high-quality tetrahedral meshes from 3D point clouds or polyhedral surfaces, making it particularly effective for modeling complex vascular structures. OpenFOAM’s mesh generation tools⁶³, including blockMesh and snappyHexMesh, enhance the meshing process by providing both structured and unstructured mesh options that are seamlessly integrated with the OpenFOAM CFD solver, thereby streamlining the simulation workflow. Netgen⁶⁴ contributes by providing automatic 3D tetrahedral mesh generation from constructive solid geometry (CSG) or boundary representation (BRep), with a strong emphasis on integration with finite element method (FEM) solvers. Additionally, MeshPy⁶⁵ offers a Python-based approach to mesh generation, utilizing the Triangle and TetGen libraries to produce unstructured triangular and tetrahedral meshes, thereby offering flexibility in custom meshing workflows.

Also notably, Xiang and his colleagues developed an open-source CFD simulation platform named AView^66,67. It is worth noting that a user study was successfully conducted for AView. However, there is room for improvement since AView requires a lot of user interactions in the pre-processing step. For instance, an operator needs to click along a centerline to define the scope of vasculture to facilitate CFD model creation. Improving the degree of automation using DL-based image segmentation is one of our goals.

Leveraging the latest DL-based automated image segmentation algorithm, our group has attempted to incorporate DL-based image segmentation into CFD model creation. Particularly, in a recent study by Rezaeitaleshmahalleh et al.⁶⁸, the accuracy and reliability of hemodynamic variables derived from DL-segmented geometries were evaluated. The study systematically compared the geometrical features and hemodynamic parameters of eight 3D rotational angiography (3DRA) datasets containing IA cases using segmented geometries generated by two published DL segmentation models (i.e., MIScnn⁶⁹ and DeepMedic³⁷) and two human raters. Our findings demonstrated almost perfect concordance between human and AI-derived results for most morphological and hemodynamic parameters, suggesting that AI-based segmentation is a promising approach for generating CFD models.

Materials and methods

Study dataset

We identified 23 IAs from our internal database. These patient data were obtained from the Aneurisk open-source repository (http://ecm2.mathcs.emory.edu/aneuriskweb/index). Additionally, we included 14 additional cases from the University of Wisconsin to validate the robustness of our proposed workflow further. Hereafter, we refer to the Aneurisk and UW-Madison datasets to as internal and external datasets, respectively.

Thirty-seven sets of in vivo angiographic data (rotational angiography [RA] or digital subtraction angiography [DSA]) were identified. Specifically, 51% of the dataset images (13 internal and 6 external cases) were used for training, while the remaining 49% (10 internal and 8 external cases) were used for testing. Since the segmented geometries from the 18 testing cases were utilized for CFD simulations, the above-said testing was conducted to evaluate IA morphology and computational hemodynamics.

A description of manual workflow for “patient-specific” CFD simulations

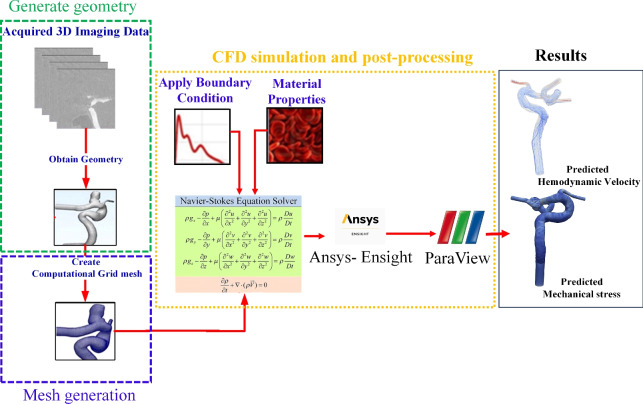
Our current manual CFD simulation workflow follows three steps described in the Introduction. As illustrated in Fig. 1, the manual workflow encompasses four components: reconstruction vasculature from 3D angiographic imaging data (depicted by the green box), mesh generation (indicated by the blue box), and execution of CFD simulations followed by post-processing to convert results into visualizable formats (shown within the orange box) in Paraview (https://www.paraview.org/), an open-source visualization platform.

Fig. 1.

The overall traditional workflow to conduct CFD simulation.

In the initial phase of pre-processing, we employ Mimics Innovation Suite (Version 21, Materialise Inc., Leuven, Belgium), a commercially available segmentation package, to perform image segmentation. An initial mask was established by defining an intensity threshold. Subsequently, manual editing was conducted using a paintbrush tool within the Mimics software. This manual refinement was performed slice by slice; tasks included eliminating small islands, filling holes, trimming downstream vessels, etc. After mask editing, the finalized vessel geometries were extended by six times the vessel diameter at each model’s inlet and outlet(s) using a Python script available in Vascular Modeling ToolKit (VMTK, version 1.4)³¹.

Local smoothing operations were conducted to the above-said extended vessel geometries using commercial software named 3Matics (Version 9, Materialise Inc.,Leuven, Belgium). This pre-processing phase was time-consuming, typically requiring 45–60 min for standard cases with adequate image quality and surface simplicity⁷⁰. However, in scenarios involving complexities such as small vessels near an aneurysm dome, the process may extend to 2–3 h due to increased intricacy and the need for meticulous adjustments.

Subsequently, the smoothed vessel surfaces are fed into in-house Python scripts integrated into the VMTK. Notably, mesh element size optimization is achieved through a radius-adaptive meshing approach. This involves computing the centerline and subsequently generating a mesh based on the distance of each point to the centerline. The final CFD model comprises a 3D volumetric mesh consisting of tetrahedral elements with 3–6 boundary prism layers at the vessel wall. Mesh sizes typically range from 1.5 to 2.0 million elements, achieving an average mesh size of 0.0022 mm.

Finally, in the CFD solution step, we employed the commercial CFD simulation software Fluent (v20.0, Ansys Inc., PA, USA) to solve the unsteady Navier–Stokes equations for laminar flow. Blood was modeled as an incompressible, Newtonian fluid with a dynamic viscosity of 0.004 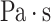and mass density of 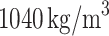. Spatial discretization of pressure and momentum utilized second-order and second-order upwind schemes in Fluent (Ansys Inc., PA, USA), respectively. Temporal discretization was achieved using a second-order implicit scheme in Fluent. The pressure-velocity coupling was resolved using the classic SIMPLE algorithm⁷¹ in Fluent.

In all CFD simulations, the vessel wall was assumed to be rigid, and a no-slip boundary condition was enforced at the vessel wall. Without patient-specific flow waveforms, an averaged pulsatile flow waveform derived from healthy subjects via magnetic resonance imaging served as the inlet boundary condition⁷². Also, the waveform is scaled to a mean physiological flow rate of 280 mL/min at the internal carotid artery. Additionally, zero-pressure boundary conditions were applied at the outlets. The simulations were executed for four cardiac cycles, each comprising 1000 steps, with hemodynamic variables extracted from the results of the fourth cardiac cycle for further hemodynamics analysis.

In the post-processing step, CFD simulation results are converted to VTK data formats compatible with Paraview for subsequent data analysis and visualization.

A description of the proposed nearly automated workflow

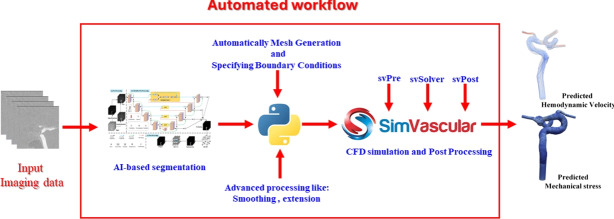
The proposed workflow achieving a nearly automated pipeline is illustrated in Fig. 2. Key components in this workflow, including DL-based image segmentation, generating meshes, performing CFD simulations, and conducting post-processing analysis, and their implementation details are described below.

Fig. 2.

A schematic diagram showing steps in the proposed nearly-automated computational hemodynamic analysis.

Deep-learning-based vessel segmentation

In this step (DL-based segmentation), we utilized 19 cases for training and 18 for testing. We adopted a published DL-based vessel segmentation algorithm named attention residual U-Net (ARU-Net²⁸). ARU-Net was designed to satisfy two major requirements of CFD model creation for intracranial vasculature: (1) retaining small vessels and (2) eliminating unwanted adhesion among adjacent vessels, as mentioned earlier.

In ARU-Net, all angiographic data are pre-processed using a Sobel filter to enhance vessel boundaries. The network configuration of ARU-Net incorporates “attention” mechanisms to steer the focus of the learning to vessels only. Thus, more complete vessel structures, such as small vessels, can be more effectively retained. In the postprocessing stage of the ARU-Net, we utilized a fully connected 3D conditional random field (3DCRF) to eliminate unwanted adhesion between adjacent vessels or between an IA and its neighboring vessels. Subsequently, 3D connected component optimization (3DCCO) was applied to remove noise from the initial segmentation. As a result, accurate intracranial vasculature that is more suitable for CFD simulations can be obtained. Further details can be found elsewhere²⁸.

Vessel truncation

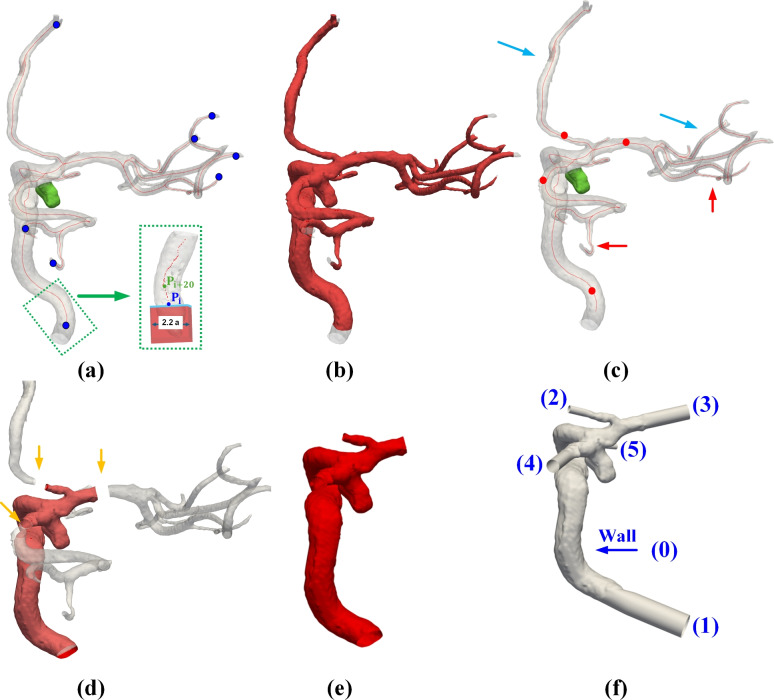
As shown in Fig. 3a, ARU-Net produces an annotated mask representing the vessel geometry of interest. A surface mesh (e.g., an STL or VTP file) can be generated using the ARU-Net-produced mask. Recall that the initial surface is watertight (see Fig. 3a) but considerably longer than a typical CFD model. In other words, we need to truncate a longer watertight surface (see Fig. 3a) to a truncated surface with open ends that are candidates for inlet(s) and outlet(s) of a CFD model (see the red surface in Fig. 3e). Then, these open ends will be assigned as an inlet and one or more outlets, as described below. Recall that removing the downstream small vessels distal to the IA of interest (see the green IA in Fig. 3a) does not impact aneurysmal hemodynamics. But eliminating these downstream small vessels improves the computational efficiency and mitigates the complexity in CFD mesh generation.

Fig. 3.

Illustrations of essential steps involving CFD mesh generation: (a) Detection of terminal points of the vascular structure, (b) Creation of initial open ends for the inlet and outlets, (c) Manual selection of additional cut points, (d) Implementation of new cuts based on manually selected points, (e) Removal of to-be-eliminated regions, and (f) Addition of flow extensions, alongside surface smoothing. In (a), the blue dots denote the locations of endpoints selected automatically, while in (c), the red dots indicate the locations of these manually selected points.

Our procedures start with identifying the terminal points of a vascular structure. Specifically, a skeletonization algorithm⁷³ (i.e., skeletonize-3d function in the skimage.morphology library) was employed to generate centerlines from the mask produced in NIfTI format. Subsequently, points along the centerlines with only one connection were identified as the terminal points of inlet and outlet vessels (see blue points in Fig. 3a).

Centerlines with defined radii were re-calculated from the surface mesh using VMTK by supplying the terminal points as seed points (see blue points in Fig. 3a). VMTK uses a fast marching algorithm to estimate centerlines and provide the maximum inscribed sphere (MIS) radius values along the defined centerlines⁷⁴.

As shown in Fig. 3a, cuts are meticulously crafted using rectangular prisms positioned at the termini of the vessel’s centerlines. The length of each cube (i.e., one for each terminal point) is slightly larger than the respective vessel diameter. Each cube is orientated to align with its centerline; thus, all cuts are normal to their centerlines. As shown in Fig. 3b, IA cases involve small downstream vessels that need to be removed. If the user opts to remove downstream small vessels, they can select additional points along the centerline to define the new cut location (see red dots in Fig. 3c). Using the same approach as for the initial ending points, the MIS and normal direction based on the selected point are utilized to perform these secondary cuts (see Fig. 3d). After completing these cuts, the user retains the vessel of interest (see the red surface in Fig. 3d). Then, they extend the vessel length by adding a flow extension at each open end further to reduce the influence of boundary conditions in CFD simulations. This extension is typically six times the vessel diameter (see numbers 1–5 in Fig. 3f). A longer flow extension (e.g., 15D) is available as well. Since our CFD models contain almost the entire ICA, simulated gross hemodynamic patterns and variables were comparable (e.g., within 5%) to a longer 15D extension.

Automatic mesh generation and vessel boundary assignments

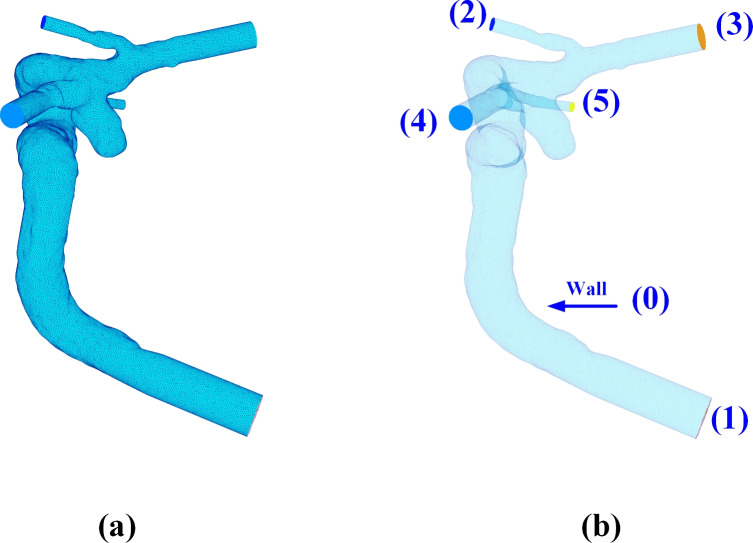
Following the acquisition of the STL file, we employed the VMTK software to generate a volumetric mesh of the reconstructed geometry, utilizing the same parameters and workflow detailed in section.

The volumetric mesh generation process involves enclosing openings (see regions numbered from 1 to 5 in Fig. 3f). Subsequently, all surface regions (one inlet, multiple outlets, and one vessel surface) are identified and labeled, as shown in Fig. 4a. Among these labeled surface regions, the region with the largest surface area is designated as the wall region (see the largest surface numbered 0 in Fig. 4b). In the anterior circulation, the inlet will consistently start at the internal carotid artery (ICA). Recall that LPS (Left, Posterior, Superior) is used in DICOM images. Following the coordinate conversion to a STL file, the proximal end of ICA often has the highest z-coordinates, while distal vessels have lower z-coordinate values. More details can be found in 3D Slicer coordinate definition⁷⁵.

Fig. 4.

A graphic description of surface boundary specification: (a) Identifying the surface regions with distinct region IDs; (b) Determining the largest region as the wall boundary (i.e. wall 0) and the rest (1–5) as the inlet and outlets.

Taking advantage of this convention, the region with the highest z-coordinate at its centroid is assigned to the inlet (see the surface numbered 1 in Fig. 4b). Then, the remaining surfaces are all outlets.

Integration with SimVascular

The CFD simulation and postprocessing analysis in SimVascular software comprise three distinct steps: Presolver (svPre), Flowsolver (svSolver), and Postsolver (svPost). In this study, to streamline the process, programmable Application Programming Interface (API) has been selected to simply pass necessary information from the generated mesh (see subsection named "Automatic mesh generation and vessel boundary assignments") to complete the solution of Navier–Stokes equations.

More specifically, based on a configuration file (i.e., a “.svpre” file), an in-house Python script prompts the svPre application to produce suited files (i.e., “bct.dat”, “geombc.dat.1”, “restart.0.1”, and “numstart.dat”). These files contain essential information representing the computational domain, boundary conditions, and initial state. The geometrical information regarding the computational domain and boundary conditions were extracted from the volumetric mesh and boundary assessments described above in section.

In this study, blood was modeled as an incompressible, Newtonian fluid. We applied an averaged pulsatile flow waveform obtained from healthy subjects via magnetic resonance imaging for the inlet boundary condition⁷². This waveform was uniformly distributed across the inlet region, using a predefined plug profile to ensure consistency. At the outlets, zero-pressure boundary conditions were enforced. Furthermore, the vessel was treated as a rigid wall, aligning with the established protocol for conducting CFD simulations in our recent studies^19,20. Of note, the automated workflow had identical settings to the manual workflow outlined in section.

Post-processing and data analysis

All hemodynamic results obtained through SimVascular were stored in VTK data format (i.e., unstructured vtu format).All data processing was completed by in-house Python scripts.

The quality and reliability of computed results are paramount. Therefore, our data analysis includes: (1) Examining the quality of the extracted surface using AI techniques, and (2) Assessing the consistency of computed hemodynamic parameters using manually segmented geometries or geometries segmented using AI.

Comparison of manually and AI-segmented geometries

The morphological indices of IA cases serve as crucial information in our recent machine learning-based prediction model and related studies focused on predicting ruptured IA cases. Moreover, aneurysm surface quality has a significant effect on aneurysmal flow pattern. Thus, we embarked on a comparison of aneurysm morphology.

To accomplish this, we computed a comprehensive set of IA geometrical features derived from both manual and AI-based segmentation. These features have been extensively discussed in our recent publication¹⁹ and can be found in Supplementary Materials. Subsequently, we employed statistical measures including Pearson correlation coefficient (PCC) and relative difference (RD), and utilized scatter plots to evaluate the consistency and reliability levels between the geometric variables measured using AI- and manually segmented methods.

Comparison of computed hemodynamic variables

A comparative analysis was conducted between the hemodynamic variables computed using our automated workflow and those estimated following manual workflow. We specifically focused on computing the extremities of WSS as well as its spatial average, based on the estimated values at each time step. Furthermore, we calculated the temporally averaged minimum and maximum WSS values along with their spatial averages. Moreover, we calculated the Oscillatory Shear Index (OSI), a dimensionless parameter, at each point along the vessel wall.

Furthermore, we employed Velocity-Informatics (magnitude and directional velocity-informatics; hereafter referred to as MVelocity-informatics and DVeloicity-informatics), the method proposed in our recent publications, to measure general blood flow characteristics^19,33. A brief introduction of velocity informatics variables can be found in Supplementary Materials.

Subsequently, to statistically evaluate the reliability of the computed results derived from different workflows, we utilized a Bland–Altman plot. Additionally, the ICC was employed to assess the consistency and agreement of the hemodynamic parameters. This comparison followed the guidelines presented by Koo⁷⁶ to define the levels of reliability. Based on the 95% confidence interval of the ICC estimate, values less than 0.5 indicate poor reliability, values between 0.5 and 0.75 indicate moderate reliability, values between 0.75 and 0.9 indicate good reliability, and values greater than 0.90 indicate excellent reliability.

Visual assessments

All velocity streamlines and spatial distributions of hemodynamic variables were visually inspected. Three selected cases were included to illustrate subtle differences between the manual and proposed automated workflow.

Ethics approval and consent to participate

This study was approved by the Institutional Review Boards (IRB) of all participating institutions. All imaging data have been de-identified and patient health information was not used. As a result, this was a secondary analysis of existing anonymous imaging data and patient consent requirement was waived by the governing IRBs. All methods were performed in accordance with the relevant guidelines and regulations set up by US National Institutes of Health.

Results

Comparison of geometrical analysis outcomes between DL-based and manual segmentation

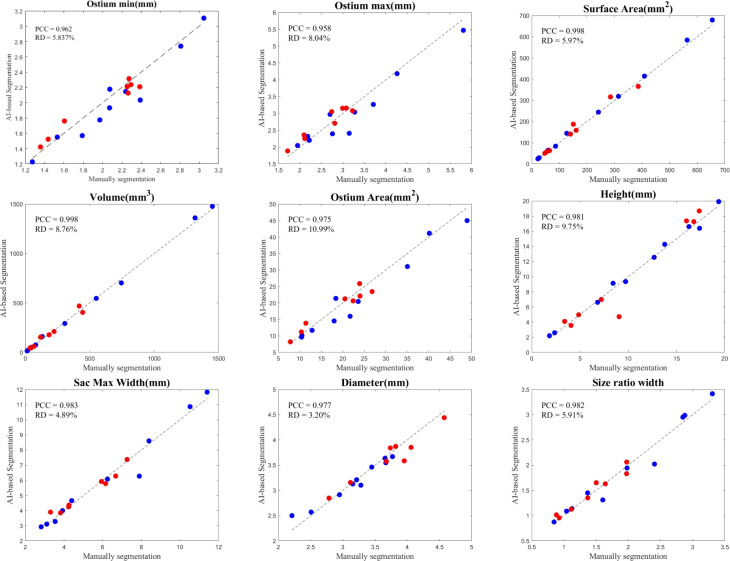
We chose 9 commonly used geometrical features from our recent studies to distinguish between ruptured and unruptured IA cases. We conducted a comparative analysis between the outcomes obtained through manual segmentation and those generated by DL-based segmentation. A summary of this morphological comparison of IAs is illustrated in Fig. 5. PCC and RD were calculated for each geometrical variable. For all nine features, the correlation was high (0.958–0.998), with slightly lower RDs (3–10%).

Fig. 5.

Comparison of measured geometrical features using DL-based and manual segmentation: Blue dots represent internal cases (10), while red dots represent external cases (8). The black dashed line represents the y=x line indicating perfect matching.

It’s noteworthy that while manual segmentation methods typically require an average of 30–45 min to complete any given case, our DL-based model-creation accomplishes the task in a mere 3–5 min (i.e., approximately 1/10 of the time). This reduction in time is substantial and demonstrates the efficiency of our automated workflow.

Qualitative comparisons between results obtained using the manual and proposed automated CFD protocols

CFD simulations were conducted for 18 cases following four distinct protocols. Initially, simulations were performed using manually segmented reconstructed geometries with the SimVascular and Fluent (Ansys Inc., PA, USA) solvers, hereafter referred to as Protocols 1 and 2, respectively. Subsequently, the simulations were repeated for the same cases using DL-segmented geometries, designated as simulation Protocols 3 and 4 for SimVascular and Fluent, respectively. The hemodynamic characteristics computed from these four protocols were then systematically compared across multiple parameters.

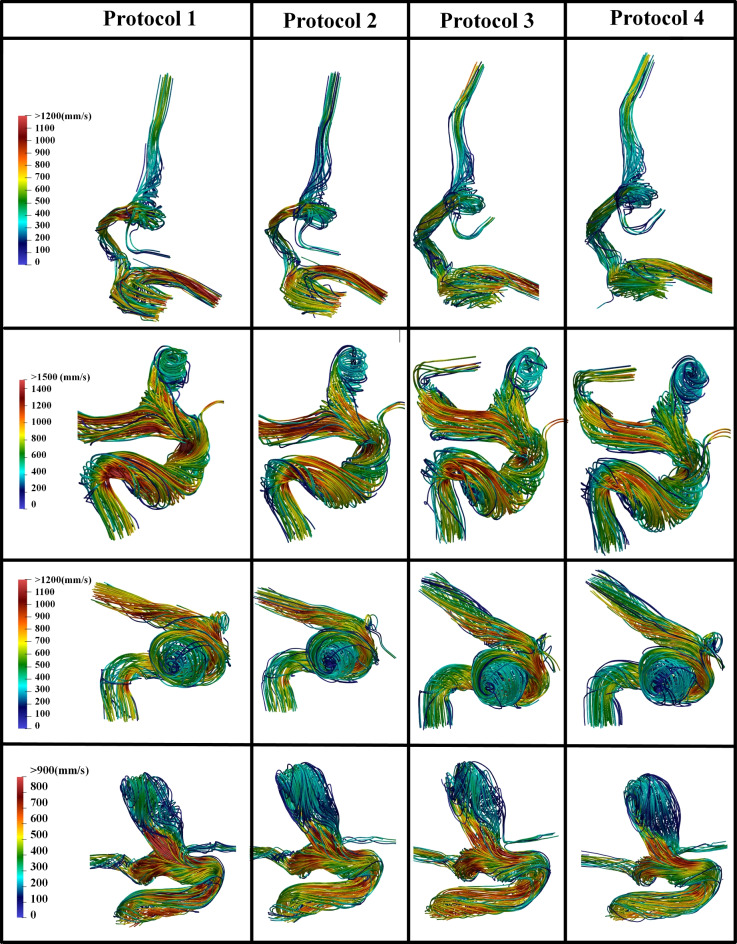
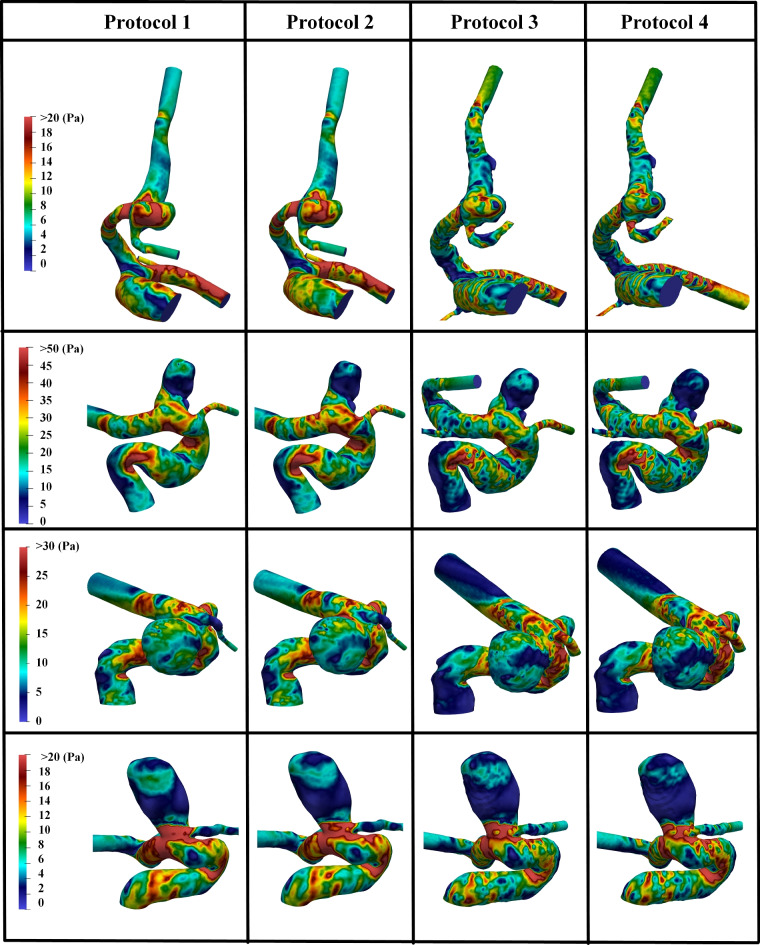
The analysis commenced with a qualitative assessment of flow characteristics, focusing on the general flow patterns visualized through velocity streamlines and WSS distributions within and surrounding the IA at the peak systole. Figs. 6 and 7 present the velocity streamlines and WSS values for four representative cases. These cases were selected to include two randomly chosen from an internal dataset and two from an external dataset ensuring a diverse evaluation of the simulation models.

Fig. 6.

Comparisons of velocity streamlines at peak systole among Protocols 1–4: Protocols 1 and 2 are based on manual segmentation results using SimVascular and Fluent software, respectively, while Protocols 3 and 4 utilize DL-based segmentation and are processed using SimVascular and Fluent software, respectively.

Fig. 7.

Comparisons of computed WSS at peak systole among Protocols 1–4: Protocols 1 and 2 are based on manual segmentation results using SimVascular and Fluent software, respectively, while Protocols 3 and Model 4 utilize DL-based segmentation and are processed using SimVascular and Fluent software, respectively.

Figure 6 presents velocity streamlines for four representative cases across four different simulation protocols, each corresponding to a distinct combination of segmentation method and solver. Each row showcases a different case, providing a detailed visualization of flow patterns at peak systolic conditions. The color scale indicates the velocity in (mm/s), with red representing the highest velocities and blue representing the lowest.

As illustrated in Fig. 6, the consistency in flow patterns and high-velocity regions across different simulation types suggests that DL-based segmentation is a reliable alternative to manual segmentation (see Protocols 3 and 4 versus Protocols 1 and 2). The computed results using SimVascular and Fluent software are comparable (see Protocols 1 and 3 versus Protocols 2 and 4). Minor variations observed are likely due to segmentation differences or different approaches to solving differential equations in the two CFD solvers (Fluent and SimVascular) but do not significantly impact the overall gross hemodynamic patterns represented by velocity streamlines.

The WSS distributions for these same four cases, utilizing the same CFD types as depicted in Fig. 6, are illustrated in Fig. 7. The color scale represents WSS in Pa, with red and blue indicating the highest and lowest WSS values, respectively. Consistent with our expectations, the WSS distributions exhibit similar patterns and high-stress regions across the different simulation protocols. Again, subtle differences observed are likely attributable to variations in segmentation methods or the differential equation handling approaches of the two CFD solvers (SimVascular and Fluent).

Levels of agreement between computed hemodynamic variables

To quantitatively assess the degree of agreement for the computed hemodynamic variables, two methodological approaches were implemented. Initially, ICC analysis was conducted to evaluate the degree of agreement between computed hemodynamic variables using different CFD simulation protocols. In this analysis, the computed variables obtained from the Fluent solver, based on manual segmentation results(i.e., Protocol 2), served as the reference standard. Subsequently, the level of agreement between this reference model and the other three CFD simulation protocols was investigated. This analysis encompassed WSS-related variables and velocity-informatics parameters, specifically Dvelocity- and Mvelocity-informatics (see Tables 1 and 2). These parameters have been identified in recent literature as the most informative variables for machine learning-based classification models^19,20. A brief introduction of these hemodynamic variables can be found in Supplementary Materials.

Table 1.

Intraclass correlation coefficient (ICC) values for computed WSS-related variables using different protocols. This analysis includes CFD simulation results from all 18 cases.

	WSS-related variables
	Protocol 1 vs. 2	Protocol 2 vs. 3	Protocol 2 vs. 4
STA-WSS	0.982	0.941	0.900
TA-WSS-min	0.758	0.792	0.917
TA-WSS-max	0.747	0.424	0.208
SA OSI	0.429	0.501	0.620
Std OSI	0.452	0.426	0.554
LSA	0.757	0.971	0.980

LSA low wall shear area.

Table 2.

Intraclass correlation coefficient values for computed Velocity-Informatics variables using different workflows. This analysis includes CFD simulation results from all 18 cases. 1 to 4 indicate Protocols 1–4. Additionally, Wilcoxon Rank Sum Tests were conducted to compute the p-value between computed variables following Protocol 2 and Protocol 3. RLN RunLengthNonuniformity, GLN GrayLevelNonUniformity, LRHGLE LongRunHighGrayLevelEmphasis, LAHGLE LargeAreaHighGrayLevelEmphasis, STD standard deviation.

	Mvelocity-informatics				Dvelocity-informatics
	ICC (1 vs 2)	ICC (2 vs 3)	ICC (2 vs 4)	p-value (2 vs 3)	ICC (1 vs 2)	ICC (2 vs 3)	ICC (2 vs 4)	p-value (2 vs 3)
DifferenceAverage	0.945	0.935	0.816	0.457	0.941	0.863	0.917	0.248
DifferenceEntropy	0.893	0.912	0.913	0.420	0.928	0.833	0.902	0.169
DifferenceVariance	0.944	0.923	0.737	0.517	0.907	0.584	0.581	0.275
Idm	0.822	0.904	0.899	0.477	0.930	0.923	0.972	0.304
Idmn	0.979	0.966	0.975	0.740	0.934	0.764	0.759	0.200
Idn	0.969	0.961	0.972	0.624	0.946	0.888	0.940	0.235
Imc1	0.879	0.930	0.856	0.169	0.824	0.689	0.936	0.045
JointEnergy	0.333	0.623	0.707	0.304	0.375	0.432	0.575	0.141
JointEntropy	0.727	0.813	0.835	0.304	0.672	0.584	0.890	0.028
MCC	0.926	0.909	0.947	0.275	0.734	0.634	0.853	0.024
SumEntropy	0.746	0.781	0.673	0.862	0.744	0.594	0.673	0.247
GLN	0.989	0.995	0.987	0.987	0.992	0.994	0.987	0.912
LongRunEmphasis	0.695	0.835	0.816	0.537	0.874	0.866	0.977	0.367
LRHGLE	0.931	0.779	0.744	0.912	0.861	0.705	0.841	0.788
RunEntropy	0.757	0.737	0.585	0.887	0.983	0.979	0.979	0.962
RLN	0.998	0.998	0.995	0.837	0.935	0.911	0.992	0.496
RunPercentage	0.796	0.884	0.865	0.580	0.926	0.941	0.984	0.351
RunVariance	0.635	0.804	0.792	0.517	0.879	0.877	0.964	0.402
ShortRunEmphasis	0.846	0.896	0.872	0.537	0.921	0.915	0.987	0.384
LargeAreaEmphasis	0.466	0.507	0.502	0.558	0.718	0.611	0.928	0.558
LAHGLE	0.732	0.334	0.514	0.351	0.736	0.445	0.749	0.537
SizeZoneNonUniformity	0.960	0.975	0.974	0.580	0.696	0.447	0.850	0.018
SmallAreaEmphasis	0.938	0.930	0.915	0.420	0.810	0.631	0.827	0.091
ZoneEntropy	0.911	0.914	0.884	0.580	0.964	0.952	0.976	0.457
ZonePercentage	0.903	0.932	0.939	0.496	0.969	0.937	0.988	0.304
ZoneVariance	0.467	0.503	0.500	0.558	0.726	0.620	0.928	0.580
Average	0.815	0.834	0.816	0.557	0.843	0.755	0.883	0.351

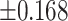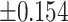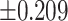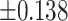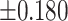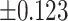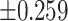As demonstrated in Table 1, the ICC values for STA-WSS consistently exhibit excellent reliability across all workflow comparisons (Protocol 1 vs. Protocol 2, Protocol 2 vs. Protocol 3, and Protocol 2 vs. Protocol 4). Notably, the ICC value for LSA also consistently shows good to excellent reliability across all analyses. . This observation suggests that the computation of STA-WSS is robust across different CFD simulation protocols. In contrast, the ICC values for TA-WSS-min generally indicate good to excellent reliability, particularly between Protocols 2 and 4 workflows. This suggests that the computation of TA-WSS-min is relatively stable across these workflows. However, TA-WSS-max displays significant variability, with ICC values ranging from moderate to poor. This variability is especially pronounced in the comparison between Protocols 2 and 4, indicating that the computation of TA-WSS-max is less reliable and exhibits considerable inconsistency. For SA-OSI and Std-OSI, the ICC values indicate poor to moderate reliability across most workflow comparisons. This relatively low level of consistency suggests noticeable variability in their computation across different protocols.

As indicated in Table 2, several (10 out of the 26 features) Mvelocity-informatics variables demonstrate excellent reliability when comparing Protocol 2 with other protocols. Specifically, the variables DifferenceEntropy, Idmn, Idn, MCC, GLN, RLN, SizeZoneNonUniformity, SmallAreaEmphasis, ZoneEntropy, and ZonePercentage exhibit ICC values greater than 0.9. In contrast, the ICC values for variables such as DiffrenceAverage, DiffrenceVariance, Idm, and Imc1 indicate good to excellent reliability. Notably, only two variables, ZoneVariance and LargeAreaEmphasis, exhibit ICC values in the poor range. For the remaining variables, ICC values range from moderate to good.

Similarly, an Intraclass Correlation Coefficient (ICC) analysis was conducted on the Dvelocity-Informatics variables, with the results summarized in Table 2. As depicted in Table 2, eleven Dvelocity-Informatics (out of 26) variables exhibit excellent reliability, with ICC values exceeding 0.9. This indicates high consistency in the computation of these variables across different workflows. Specifically, the variables DifferenceAverage, Idm, Idn, GLN, RunEntropy, RLN, RunPercentage, ShortRunEmphasis, ZoneEntropy, and ZonePercentage demonstrate high reliability, with ICC values consistently above 0.9 across all protocol comparisons. Furthermore, the variables LAHGLE and SumEntropy display moderate reliability across all protocols. In contrast, the variable JointEnergy shows poor reliability, reflecting lower consistency in its computation across workflows. Interestingly, the remaining features exhibit good to excellent agreement between Protocols 2 and 4, with ICC values ranging from 0.827 to 0.977.

In addition to the ICC analysis, the Bland–Altman plot was utilized as a complementary approach to evaluate the agreement between computed hemodynamic variables. Specifically, computed variables using the Fluent solver based on manual segmentation results were considered as the benchmark, and the reliability of other computed variables was tested against these benchmark variables. The outcomes of the Bland–Altman plot are visualized in Fig. 8 for all WSS-related variables introduced in Table 1. To make the paper concise, the Bland–Altman plots for six selected variables from Mvelocity-informatics and Dvelocity-informatics, introduced in Table 2, are visualized in Figs. 10 and 9, respectively.

Fig. 8.

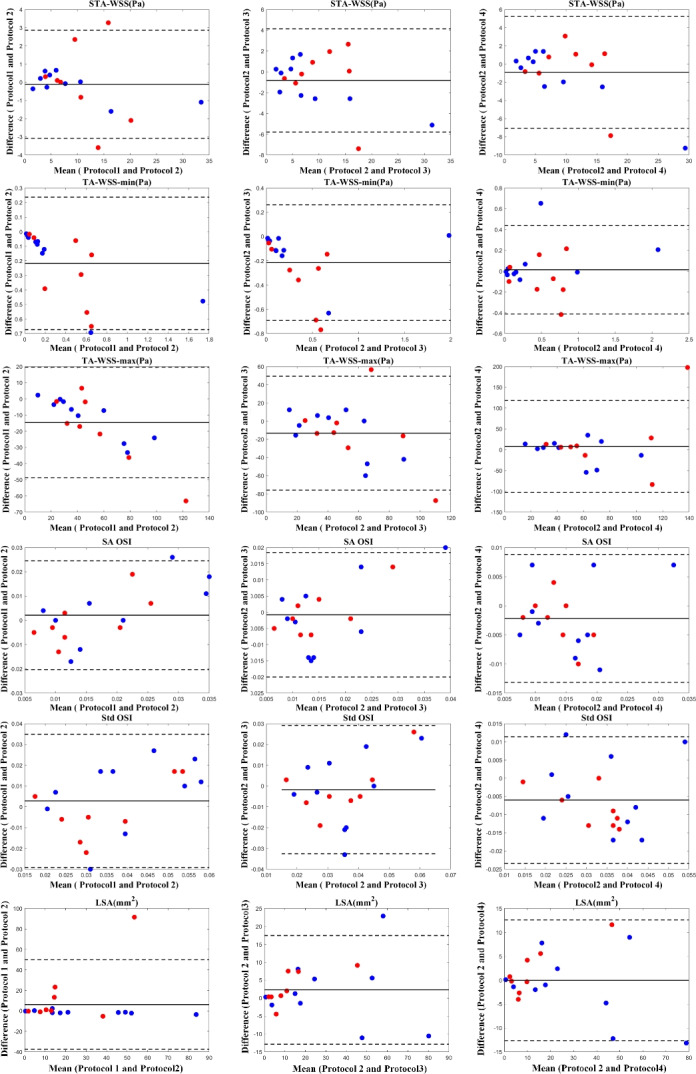
Bland–Altman plots to visualize the degree of agreement between computed WSS-related variables follow the four mentioned protocols: Blue dots represent (10) internal cases, while red dots represent (8) external cases.

Fig. 10.

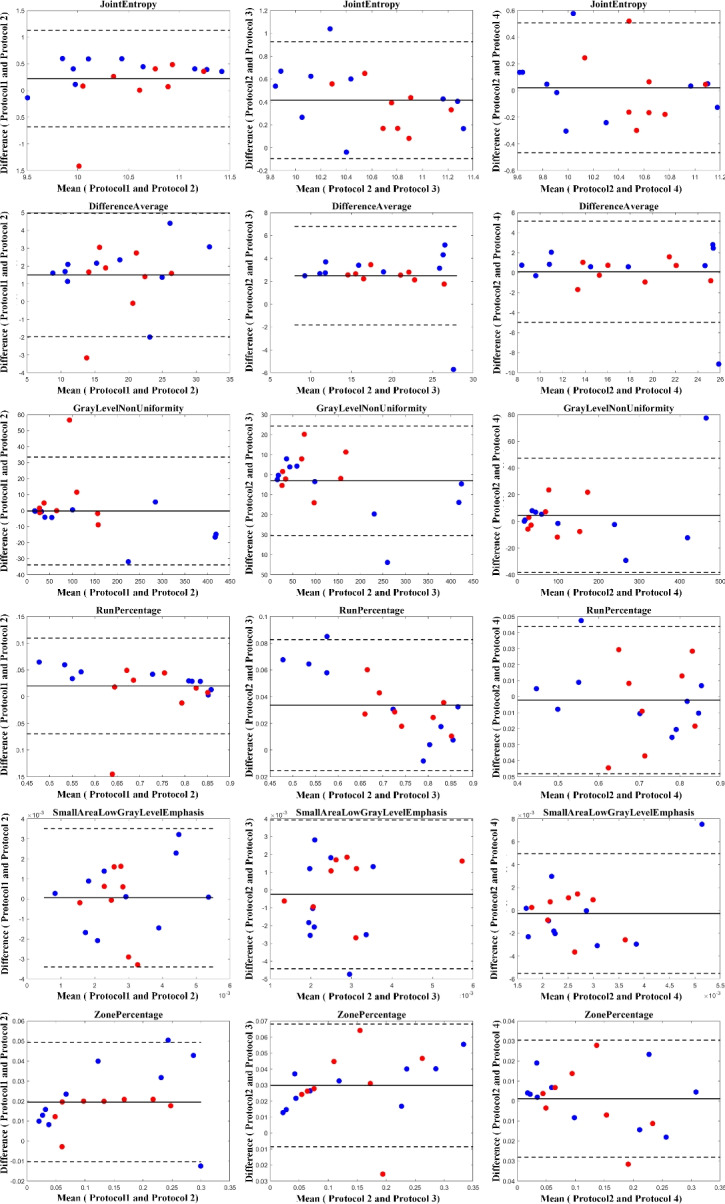
Bland–Altman plots to visualize the degree of agreement between computed Dvelocity-Informatics variables following four mentioned protocols: Blue dots represent (10) internal cases, while red dots represent (8) external cases.

Fig. 9.

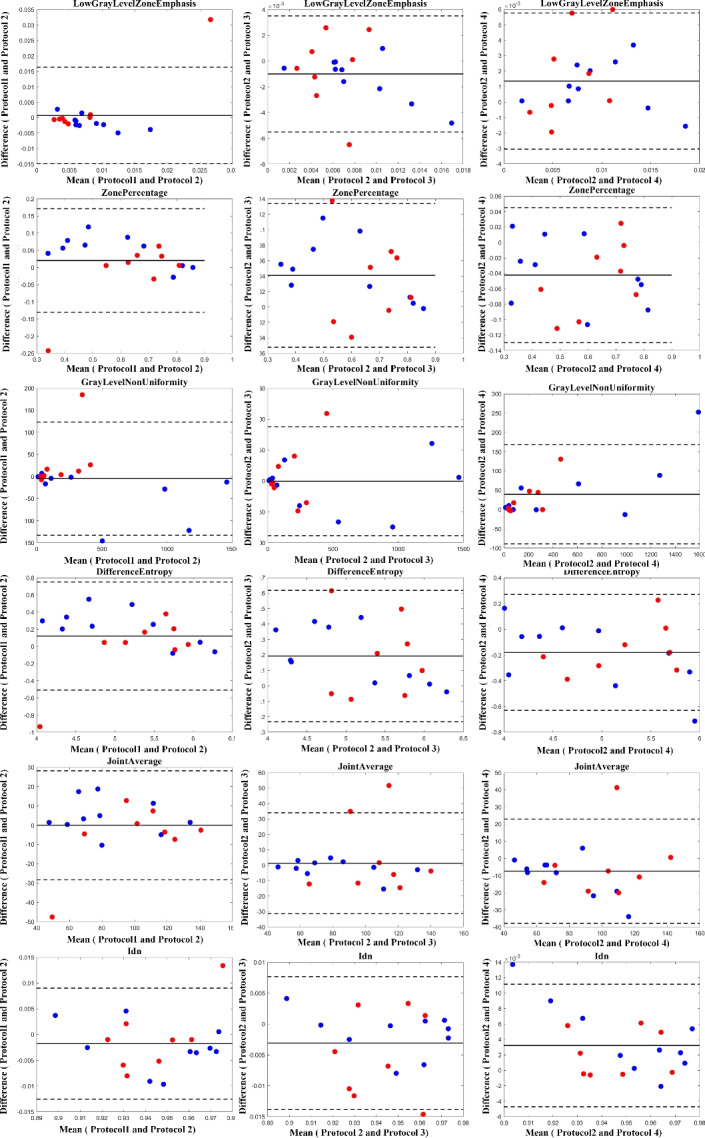
Bland–Altman plots to visualize the degree of agreement between computed Mvelocity-Informatics variables following four mentioned protocols: Blue dots represent (10) internal cases, while red dots represent (8) external cases.

The results illustrated by the Bland–Altman plots are in complete alignment with the computed ICC values presented in Tables 1 and 2. The plots support the high consistency and reliability of variables with high ICC values, as shown by the narrow limits of agreement and low mean differences. Conversely, variables with lower ICC values exhibit broader limits of agreement and greater mean differences, highlighting their variability and reduced reliability across different protocols.

As illustrated in Table 2, comparing Protocols 2 and 3, the consistency of Mvelocity-informatics variables (related to velocity magnitude) is better than that of Dvelocity-informatics variables, though the difference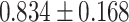s ( vs. 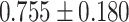) are not statistically significant (p=0.09 using a randsum test). Statistically significant differences between Protocols 2 and 3 were observed for four (4) DVelocity-informatics variables (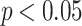): Imcl, JointEntropy, MCC and SizeZoneNonUniformity, as shown by bold fonts in Table 2.

Visual assessments of gross hemodynamics with IAs over a cardiac cycle

The analysis commenced with a qualitative assessment of velocity variations, focusing on the general flow patterns visualized through velocity contours within the IA across five distinct phases of the cardiac cycle. Figure 11 presents one of the four cases illustrated in Fig. 6 as a representative example. This example compares the velocity magnitude values at three different heights of the IA, following Protocol 2 and Protocol 3, thereby providing a comprehensive evaluation of the variations in flow dynamics. The outcomes of the analysis for the remaining three cases are detailed in the Supplementary Materials.

Fig. 11.

Comparison of velocity magnitude: Manual vs. automated workflow across different cardiac phases: (a) IA Geometry and cross-sectional cutting plans, (b) a flow rate waveform, (c) velocity magnitude contour at specific cross-sectional cutting planes (see (a)) and cardiac phases (see (b)).

As illustrated in Fig. 11, the results obtained following Protocols 2 and 3 show a high degree of consistency, with nearly identical velocity-magnitude ranges and distributions. These findings were consistently observed across the other three cases as well. Similar comparisons were conducted for the other three cases listed in Fig. 6. The visualization of the other three cases can be found in Supplementary Materials.

Discussion

This study implemented a nearly automated pipeline (see Fig. 2) for completing the computational hemodynamics for IAs in the anterior circulation. To standardize the process, we intentionally retained long vessel segments starting from the internal carotid artery. Consequently, we could execute CFD simulations with minimal manual intervention.To rigorously evaluate the quality of the computed hemodynamic variables, we performed an in-depth comparison between the results produced by our novel workflow and those obtained through conventional, well-established methodologies. As illustrated in Tables 1, 2, and Figs. 8, 9, and 10, our preliminary analyses demonstrated that a high level of agreement between the key hemodynamic variables computed using our automated pipeline and those obtained through the manual CFD workflow. Specifically, the velocity streamline patterns, which illustrate the gross aneurysmal hemodynamics were consistent across all four protocols, showing similar high-velocity regions. Additionally, the WSS distributions exhibited comparable patterns, ranges, and high WSS regions.

More specifically, we included eight (8) external cases to evaluate the performance of our automated pipeline and validate the robustness of the proposed method for conducting CFD simulations on new cases. This analysis involved two key steps: assessing the quality of the extracted geometry and evaluating the accuracy of the computed CFD simulation results. As depicted in Fig. 5, the blue dots representing external data points are closely aligned with the matching line, indicating the high reliability of the segmentation algorithm employed. Subsequently, the Bland–Altman plots presented in Figs. 8, 9, and 10 further confirm the efficacy of our proposed workflow.

Moreover, we visually assessed gross flow patterns with the IA domes over a cardiac cycle. As illustrated in Fig. 11, aneurysmal velocity contours were analyzed at various cross-sections ascending from the neck of the IA and cardiac phases using both the newly proposed pipeline and manual workflow. The comparative analysis of results, depicted in Fig. 11, shows that the outputs from the proposed pipeline closely align with those obtained from traditional CFD approaches. Although this consistency is generally robust, some visible discrepancies were noted, particularly in the aneurysm neck region. Overall, the gross blood flow patterns shown in Fig. 11 were preserved. This consistency across different spatial heights and temporal steps underscores the overall robustness of the new pipeline in simulating transient blood flow dynamics.

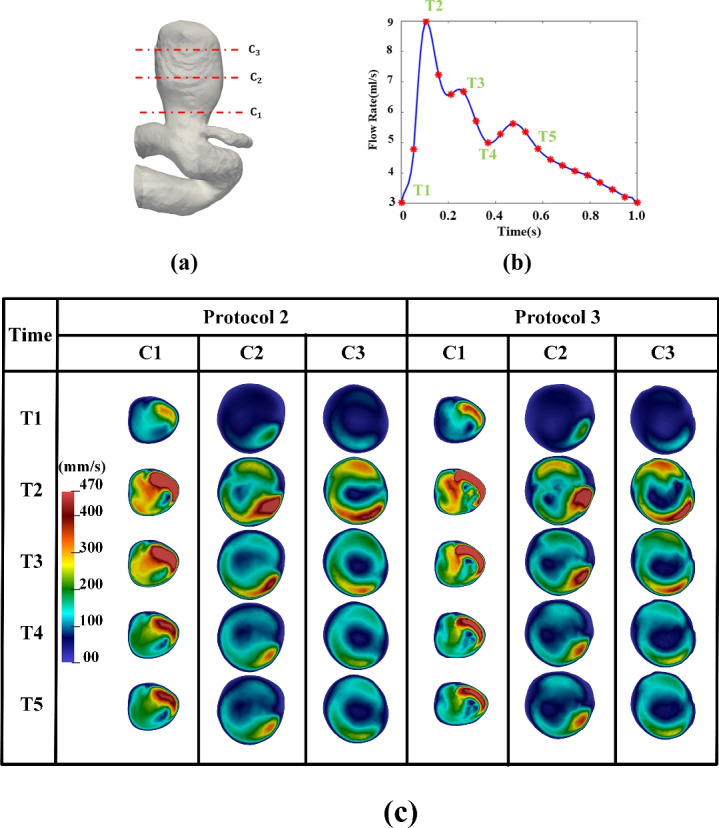
However, it is important to acknowledge that some discrepancies were observed. Visually, discrepancies in velocity contours (between Protocols 2 [manual] and 3 [automated]) are more pronounced in Fig. 12 but are visible in Fig. 11. In Fig. 12, the segmented IA contours differs from human delineated IA contours (e.g., from cross sections C1–C3), while the shape differences from Sections C1 to C3 in Fig. 11 is only slightly visible. In both Figs. 11 and 12, DL-based segmentation produced less smooth contours due to factors such as image resolution and surface complexity, thereby impacting the accuracy of simulated hemodynamic parameters. Our observations serve as examples showing how variations in aneurysm surface affect gross aneurysmal velocity patterns. Perhaps, due to the similar reason (i.e., surface delineation), we also found large discrepancies between Protocols 2 and 3 in some conventional WSS variables (see Table 1) and DVelocity-informatics metrics (see Table 2).

Fig. 12.

Comparison of velocity magnitude: Manual vs. automated workflow across different cardiac phases: (a) IA Geometry and cross-sectional cutting plans, (b) a flow rate waveform, (c) velocity magnitude contour at specific cross-sectional cutting planes (see (a)), and cardiac phases (see (b)).

We also found that the ICC values among conventional WSS variables such as SA OSI and Std OSI were lower across all Protocols. In addition to small IA shape differences due to segmentation as discussed above, differences in the two selected CFD solvers (i.e., Fluent and SimVascular) may also played a role. Specifically, Fluent uses the finite volume method (FVM), whereas SimVascular is finite element method (FEM)-based. It is recognized in the literature⁷⁷ that results of Navier–Stokes equations may be influenced by the numerical scheme selected.

Interestingly, large discrepancies also existed in some DVelocity-informatics variables. Notably, four variables (Imcl, JointEntropy, MCC, and SizeZoneNonUniformity) related to measures of local distributions of velocity vector directions stand out because their variability across Protocols was large (see Table  2). In the low velocity regions with the IA domes, velocity directions are likely more sensitive, as compared with the velocity magnitudes. That probably explains why the discrepancies are greater in DVelcoity-informatics (see Table 2).

Although “patient-specific” CFD simulations have been advocated for around two decades^13,14, labor-intensive and time-consuming processing time has been one of the roadblocks preventing its clinical translation. The proposed workflow streamlines the pre-processing and post-processing stages of CFD simulations, which are traditionally time-consuming and labor-intensive. By minimizing the need for user interactions, this workflow reduces reliance on the user’s experience and makes it more acceptable in a clinical environment. As of now, one simulation takes approximately 2–3 h in a high-end computer workstation equipped with 36 cores and 128 GB memory. Since the vast majority of simulation time was spent by the CFD solver, this workflow can be integrated into High-Performance Computing (HPC) systems to further accelerate the entire process.

Hemodynamics plays a key role in the IA’s natural history^10–12. Thus, a detailed hemodynamic analysis could provide additional insights into the decision-making for unruptured IAs. We project that the proposed system can complete an IA hemodynamic analysis in 1 h on a HPC cluster. Hence, the projected computational efficiency (e.g., 1 h per case) of our automated workflow can produce detailed hemodynamic assessments for unruptured IAs.

To translate computational hemodynamics into the clinical workflow, research must find novel, useful hemodynamic markers that can assist in clinical decision-making. We stipulate that if a less time-intensive computational hemodynamics platform like OpenHemoSim is being actively used in the clinical workflow, there is a greater chance to find these useful hemodynamic markers. One obvious application of the proposed OpenHemoSim is to make it an integral part of a large machine learning (ML)-based risk assessment platform for unruptured IAs. With encouraging results in the literature^15–20, such an ML-based system for predicting the likelihood of IA rupture can impact the clinical management of unruptured IAs. Hence, our ongoing research includes investigating how these discrepancies in simulated aneurysmal hemodynamics influence the outcome of ML-based predictions of IA’s rupture status.

Our study has several limitations. First, the initial validation was only conducted using 18 patients. The number of validation cases limits the generalizability of our findings, though the study plan is still appropriate for a feasibility study of this kind. We are collecting more imaging data (approximately 100 cases) acquired using different imaging protocols (e.g., equipment vendors, resolutions, etc.) to further validate the proposed OepnHemoSim platform. The ongoing validation will also contain more complex IA cases (e.g., complex morphology and multiple closely-spaced IAs). This effort is currently ongoing. Second, the proposed automated pipeline is currently optimized for the anterior brain vasculature, and its applicability to other vascular regions is still under development. Additionally, in reconstructed geometries based on IA-based segmentation, the presence of downstream vessels was noted, which can increase simulation running times and complicate the mesh generation process. Consequently, we often performed additional manual cuts. To make OpenHemoSim fully automated, we plan on adopting a graph-based matching algorithm⁷⁸. More specifically, we plan to match a segmented vasculature to a set of predefined atlases. Using atlases serves dual purposes. On the one hand, we can differentiate IAs in the posterior and anterior circulations and perform CFD simulations correspondingly. On the other hand, by employing the atlases, we will standardize the length of distal vessels that need to be included in the CFD simulations. We are simultaneously exploring the use of DL-based spatial frequency tuning⁴⁶ to control the degree of small vessel retention. By controlling how many small distal vessels will be retained, we anticipate improving the accuracy of the above-mentioned matching between the segmented vessels and atlases. Third, because patient-specific physiology is not available for most patients, we selected an averaged MR flow waveform with zero-pressure outlets. Our ongoing work includes implementing more sophisticated boundary conditions in SimVascular (e.g., Windkessel model and using Murray’s law) and comparing the results to further validate the proposed OpenHemoSim platform.

Conclusions

Overall, the proposed nearly automated platform OpenHemoSim can streamline the execution of CFD simulations for IAs, i.e., eliminating a lot of time-consuming and labor-intensive tasks in the pre- and post-processing steps during hemodynamic analysis of IAs. Our work is a step forward in the right direction for translating computational hemodynamics into the clinical setting. Our preliminary results demonstrate a high degree of concordance between most hemodynamic variables computed using the proposed OpenHemoSim platform (see Fig. 2) and those obtained through manual workflows (see Fig. 1). Overall, we found good agreement exists, suggesting that OpenHemoSim offers acceptable accuracy. Discrepancies in certain hemodynamic metrics exist; we attribute these differences to the variable’s sensitivity to surface quality or the different numerical approaches employed by the software to solve differential equations.

It is also important to note that our findings must be further validated using a large cohort of IA data. Also, our ongoing work is expanding to using results from the proposed workflow to demonstrate its clinical utility (e.g., predicting the rupture risk of an unruptured IA or outcomes of IA’s treatment outcomes).

Author contributions

M.R. wrote the main manuscript and prepared all figures and tables. M.R. also conducted investigations and programming. N. M. contributed to manuscript drafting, programming, and data analytics, and Z. L. was involved in data analytics and investigation. J. G. contributed to data acquisition, study planning, and manuscript revision. A. P. contributed to study planning, project management, and manuscript revision. J. J. contributed to project management, study planning, manuscript revision, and investigation. All authors reviewed the manuscript.

Funding

The study is supported by a research grant from the National Institutes of Health (R01-EB029570A1). Nan Mu is supported by a post-doctoral fellowship from the American Heart Association (23Post1022454). Mostafa Rezaeitaleshmahalleh is supported by a Doctoral Finishing Fellowship at Michigan Technological University. Zonghan Lyu receives partial funding from the Health Research Institute at Michigan Technological University.

Data availability

Prof. Strother from the University of Wisconsin (Madison, WI, USA) supplied partial imaging data and may not be disseminated without approval by the University of Wisconsin. Derived data and source codes supporting this study will be available from the corresponding author (JJ) upon request. We intend to provide source codes through GitHub (https://github.com/jjiang-mtu).

Declarations

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-80891-4.