A study of hybrid deep learning model for stock asset management

Abstract

Crafting a lucrative stock trading strategy is pivotal in the realm of investments. However, the task of devising such a strategy becomes challenging task the intricate and ever-changing situation of the stock market. In recent years, with the development of artificial intelligence (AI), some AI technologies have been proven to be successfully applied in stock price and asset management. For example, long short-term memory networks (LSTM) can be used for predicting stock price variation, reinforcement learning (RL) can be used for control stock trading, however, they are generally used separately and cannot achieve simultaneous prediction and trading. In this study, we propose a hybrid deep learning model to predict stock prices and control stock trading to manage assets. LSTM is responsible for predicting stock prices, while RL is responsible for stock trading based on the predicted price trends. Meanwhile, to reduce uncertainty in the stock market and maximize stock assets, the proposed LSTM model can predict the average directional index (ADX) to comprehend the stock trends in advance and we also propose several constraints to assist assets management, thereby reducing the risk and maximizing the stock assets. In our results, the hybrid model yields an average R² value of 0.94 when predicting price variations. Moreover, employing the proposed approach, which integrates ADX and constraints, the hybrid model augments stock assets to 1.05 times than initial assets.

Introduction

Developing a successful automated stock trading strategy is crucial for investment firms and hedge funds, as it plays a pivotal role in optimizing capital deployment and enhancing investment outcomes, including maximizing expected profits. Achieving profit maximization hinges on accurate assessments of both potential profits and associated risks. Nevertheless, analysts encounter considerable difficulty in comprehensively accounting for all pertinent factors within the intricate and ever-changing landscape of the stock market (Bekiros, 2010; Kim et al., 2017; Zhang & Yang, 2016).

The application of deep learning techniques in forecasting stock prices and trends has garnered significant attention in recent years, driven by the quest for more accurate and efficient investment strategies in the dynamic realm of financial markets (Dong, Wang & Abbas, 2021). Traditional approaches to stock price prediction often rely on statistical models or technical indexes, which may struggle to capture the complexities and non-linearities inherent in market data. In contrast, deep learning offers a powerful framework for automatically learning intricate patterns and relationships from large-scale data, making it well-suited for tackling the challenges of stock market prediction.

LSTM is a type of recurrent neural network (RNN) architecture, it has garnered significant attention for its ability to model temporal dependencies over long sequences of data (Hochreiter & Schmidhuber, 1997; Servan-Schreiber, Cleeremans & McClelland, 1988). This characteristic makes LSTM well-suited for capturing the intricate dynamics and latent patterns present in historical stock price movements. Unlike traditional statistical models, LSTM excels at learning from sequential data with varying time lags, allowing them to adapt to changing market conditions and capture both short-term fluctuations and long-term trends. While LSTM networks have shown advantage in modeling complex temporal dependencies and predicting stock prices, they are not without their limitations. As with any predictive modeling technique, LSTM-based stock price forecasting approaches face several challenges that can impact their accuracy, reliability, and practical utility in real-world trading scenarios (Ma et al., 2024). One of the primary limitations of LSTM-based stock price prediction is the unpredictability of stock markets. While LSTMs excel at capturing patterns within historical data, they may struggle to differentiate between genuine market trends and random fluctuations, leading to suboptimal performance during periods of market volatility or structural shifts.

RL is inspired by principles of behavioral psychology, offers a paradigm shift by enabling agents to learn optimal decision-making policies through interaction with their environment (Williams, 1992). In the context of stock trading, RL algorithms learn to maximize cumulative rewards, such as profit or portfolio by dynamically adjusting buy and sell actions based on market observations and feedback signals. Despite the promising potential of RL in stock trading, challenges such as model interpretability, data efficiency, and the inherent risks associated with algorithmic trading remain significant concerns. Additionally, the deployment of RL-based trading strategies in real-world financial markets necessitates careful consideration of regulatory compliance, market liquidity, and ethical implications.

In response to the aforementioned issues, this paper proposes a hybrid model aimed at maximizing potential total assets. The hybrid model comprises LSTM and RL, with LSTM responsible for predicting variations in stock prices and RL operating stocks for stock trading based on these price variations. To ensure maximum responsiveness to market uncertainty, we propose several constraints and risk indexes to depreciate such uncertainties as much as possible.

The rest of this paper is organized as follows. ‘Related Work’ introduces the related work with literature. ‘Background’ introduces the necessary background knowledge for this paper. ‘Problem Description and Hybrid Deep Learning Model Design’ describes problem details and designs the hybrid deep learning model. ‘Experiment’ introduces several experiments about proposed hybrid deep learning model. ‘Discussion’ discusses the experiment results. ‘Conclusion’ concludes this paper.

Related Work

Seethalakshmi (2018) studied which factor is used to determine specific factors that are providing the most impact on the prediction of the stock closing price. He analyzed with S&P 500 Index using statistical methods in the R environment. Two prediction models have been proposed to predict. The experimental results showed model 1 with all features fitted with R² value 0.997. This indicates open, high, low, volume and adj close are essential for predicting closing value accurately. Model 2 with open, high and low predict close value fitted with R² value 0.992. This indicates prediction of close value is not affected with adj close. This study reveals with open, high, low and volume itself enough for finding approximate prediction of close value.

Panwar et al. (2021), proposed an approach to predict stock price by using support vector machine (SVM) and linear regression. First, they used web scrapping to collect datasets from stock data. Then they plot the data on the graph, from the graph they can analyze the stock prices going high or low. After this, they trained the model to predict stock prices. Their results showed linear regression for stock market analysis is better than the SVM for the same.

Mondal, Shit & Goswami (2014) used the Auto Regressive Integrated Moving Average (ARIMA) model on fifty-six Indian stocks from different sectors. Their results showed accuracy of the ARIMA model in predicting stock prices is above 85%, which indicates that ARIMA gives good accuracy of prediction. For Information Technology sector, the standard deviation is not too low or not too high, whereas they are obtaining an above 90% accuracy in prediction for this sector.

Saud & Shakya (2020) conducted experiments helps in deciding which RNN (recurrent neural network) is best suited for the stock price prediction task. Three variants of RNN are tested. They are VRNN (Vanilla RNN), long short-term memory (LSTM) and gated recurrent unit (GRU). The results showed GRUs, LSTM, recurrent neurall network (RNN) and convolutional neural network (CNN) provide exceptional results in stock price forecasting.

Pothuganti (2021) presented a RNN and LSTM way to deal with anticipated stock market files. Their results showed including the LSTM and artificial neural network (ANN) algorithm LSTM will give better accuracy and here ANN gave an accuracy of 94% yet after performing the LSTM algorithm, they got 97% accuracy.

Lee (2002) presented an innovative method that leverages reinforcement learning to forecast stock prices. The authors conceptualize stock price prediction as a dynamic Markov process and advocate the utilization of the TD(0) algorithm for optimization, benefiting from its ability to learn from experiences. To estimate the values of states representing various stock price trends, an artificial neural network is utilized for function approximation. Through this approach, the authors aim to capture and understand interactions within real-world scenarios, ultimately enhancing the accuracy of stock price predictions.

Gondkar et al. (2021), proposed a novel model for predicting stock price index values. Leveraging data from transportation and traffic departments, the study evaluates and compares the performance of various algorithms. It employs four machine learning techniques: naive Bayes theory, decision trees, random forests, and logistic regression to generate stock price forecasts. Through methods such as constructing confusion matrices, prioritizing data categorization, and comparing against desired accuracy, recall, and F1 score benchmarks, the proposed system undergoes evaluation.

Roobini et al. (2022), mainly focus on predicting either stock price rises or stable states. Additionally, their study scrutinizes the efficacy of diverse machine learning techniques, including logistic regression, random forest, decision trees, and naive Bayes theorem, in producing stock price forecasts. To gauge these methodologies, data from the transportation traffic department is utilized, facilitating a comprehensive comparative examination.

Roy (2019) proposed the Auto-ARIMA and Holt-Winters models are applied for predicting future stock prices. Moreover, linear programming is employed for optimizing portfolios. By continuously updating the model with the latest market data, it becomes adept at capturing the most recent market trends, broadening its applicability across various portfolios over time. The trend analysis obtained can assist in forecasting improved investment strategies in the stock market, empowering investors to make well-informed decisions based on real-time market analysis. This methodology is geared towards maximizing returns and minimizing losses, ultimately supporting investors in making prudent investment selections.

Ilyas et al. (2022) introduces an innovative hybrid model for predicting stock closing prices. This model combines a fully improved Hodrick-Prescott (Hodrick-Prescott) filter to reduce noise in time series data, introduces new features including company returns, changes in opening and closing prices, and applies machine learning algorithms such as SVM, Random Forest, ARIMA, and deep learning techniques such as LSTM and GRUs. The strengths of the model include enhanced predictive accuracy, achieving a prediction accuracy of 70.88% and a root mean square error of 0.04, while reducing the error rate of the model. However, potential drawbacks of the model may include a strong dependence on the length of historical data, challenges with the vanishing gradient problem when dealing with long sequence data in deep learning models, and the high computational complexity of the model, which may require substantial computational resources and time. Overall, this paper proposes a great prediction model and demonstrates excellent prediction results.

Background

Long short-term memory network

LSTM belongs to the family of RNN and excels in capturing long-term dependencies within sequential data (Wikipedia Contributers, 2024). Unlike traditional RNN, LSTM are adept at handling sequential data like time series, text, and speech. They employ a sophisticated architecture comprising memory cells and gates to regulate information flow. This mechanism enables LSTM to selectively retain or discard information as necessary, thereby mitigating the issue of vanishing gradients commonly encountered in conventional RNN. Given these capabilities, LSTM finds extensive applications across various domains, including natural language processing, speech recognition, and time series forecasting.

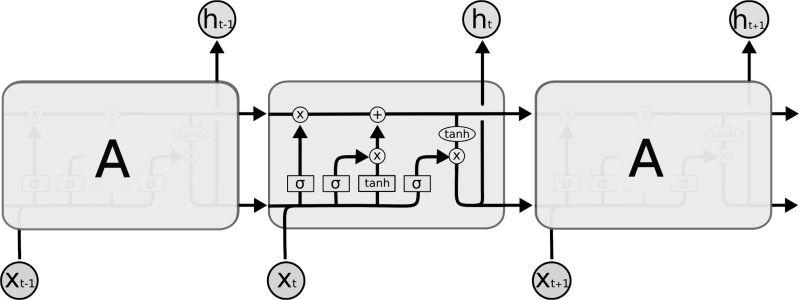
An LSTM network is proficient in managing and analyzing sequential data. LSTM running mechanism is shown in Fig. 1 (Banoula, 2023). Its architecture comprises LSTM cells organized in a sequence, wherein each cell integrates input, output, and forget gates. These gates serve to regulate the information flow within the cell, enabling selective retention or omission of information from previous time steps. This mechanism empowers the LSTM network to preserve long-term dependencies present in the input data, facilitating effective sequential data processing. The LSTM cell also has a memory cell that stores information from previous time steps and uses it to influence the output of the cell at the current time step. The output of each LSTM cell is passed to the next cell in the network, allowing the LSTM to process and analyze sequential data over multiple time steps.

Figure 1. LSTM running mechanism.

Markov decision process

A Markov decision process (MDP) is a mathematical framework used to model decision-making problems where an agent interacts with an environment over a sequence of discrete time steps. The key feature of an MDP is the Markov property, which states that the future state of the system depends only on the current state and action, and not on the sequence of events that preceded them. This property simplifies the modeling of complex systems by focusing on the most recent information (Bellman, 1957). The MDP is defined by the tuple (S, A, P, R) where:

• •S is the set of states.
• •A is the set of actions.
• •P is the state transition probability function: P(s′|s, a) represents the probability of transitioning to state s′ given the current state s and action a.
• •R is the reward function: R(s, a, s′) represents the immediate reward obtained after taking action a in state s and transitioning to state s′.

Reinforcement learning

Reinforcement learning (RL) is a branch of machine learning that focuses on how an agent learns to make a sequence of decisions to maximize cumulative rewards through interaction with an environment. In RL, the agent learns by interacting with the environment, observing its states, taking actions, receiving rewards, and learning how to maximize cumulative rewards over time. RL can be seen as a framework that utilizes MDP to model decision-making problems. MDP provides the formalism for RL problems, defining the structure of the environment, possible actions, and the consequences of those actions. RL algorithms, such as Q-learning and policy gradient methods, operate within the MDP framework to learn the optimal policy. The core concepts in RL as follows (Sutton & Barto, 2005):

• •State (s): Represents a specific configuration or situation in the environment.
• •Action (a): Represents the possible actions the agent can take in a given state. The action set is denoted by A, including all possible actions.
• •Policy (π): Represents the probability distribution of taking specific actions in a given state. Denoted by π, where π(a∣s) is the probability of taking action a in state s.
• •Reward (r): Represents the immediate feedback the agent receives from the environment after taking an action.
• •
  Value function: There are two types of value function. The first type is the state value function (V_π(s)): Represents the expected cumulative reward starting from state s under policy π. The equation is shown as follows.

  $${\displaystyle V_{\pi }\left(s\right)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t\mid s_0=s\right]}$$ (1)

  The second type is action value function (Q_π(s, a)): Represents the expected cumulative reward starting from state s, taking action a under policy π. The equation is shown as follows.

  $${\displaystyle Q_{\pi }\left(s,a\right)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t\mid s_0=s,a_0=a\right]}$$ (2)

The goal of RL is to find an optimal policy π^∗ that maximizes the expected cumulative reward. This is achieved by maximizing the value functions:

$${\displaystyle V^{\ast }\left(s\right)={max}_{\pi }{V}_{\pi }\left(s\right)}$$ (3)

$${\displaystyle Q^{\ast }\left(s,a\right)={max}_{\pi }{Q}_{\pi }\left(s,a\right)}$$ (4)

where V^∗(s) and Q^∗(s, a) represent the optimal state value and action value under the optimal policy.

Problem Description and Hybrid Deep Learning Model Design

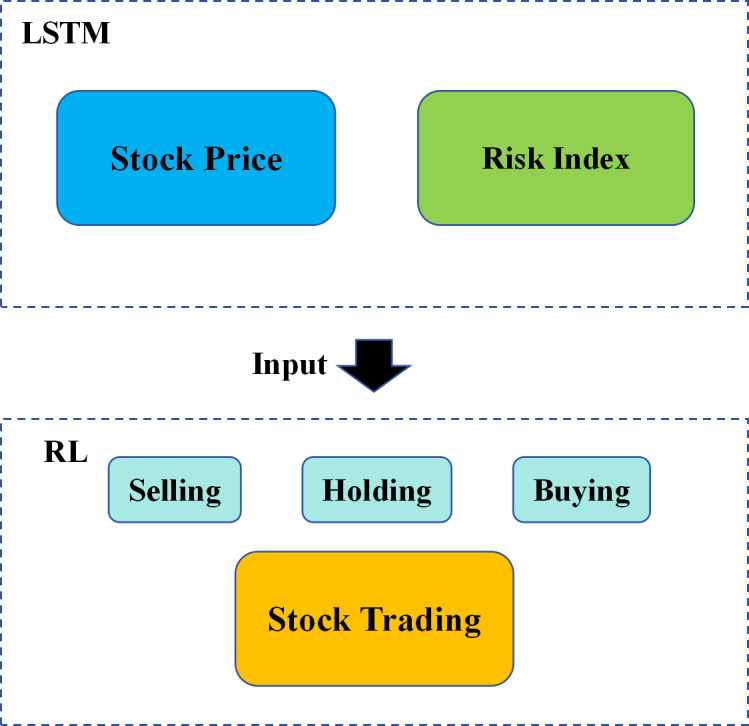
In this section, we propose a hybrid deep learning model designed for stock asset management. This model comprises two parts: LSTM and RL model. The LSTM model focuses on predicting variations in stock prices and risk index, while the RL model is tasked with making decisions regarding stock trading, such as selling, holding, or buying stocks. These two parts work together to build a hybrid deep learning model that can both predict stock prices and operate stock trading.

Problem description and model architecture design

The most difficult and important component of using AI to predict the stock price is Market uncertainty (Connolly, Stivers & Sun, 2005). Stock markets are influenced by various factors, including economic data, political events, natural disasters, and more. These factors are often unpredictable, making stock price prediction very challenging. To address the aforementioned issues, many researchers utilized various technologies to settle them. For instance, LSTM is used to predict stock price variation and RL is used for stock trading, etc. Additionally, to solve market uncertainty, several risk indexes are usually used to describe the degree of market uncertainty, such as Average Directional Index (ADX), Relative Strength Index (RSI), Commodity Channel Index (CCI), and so on (Wang et al., 2018). However, many of research only utilized one type of model to predict stock price variation or operate stock trading, including ADX, RSI and CCI are calculated based on historical data.

In this study, we innovatively propose a hybrid deep learning model that combines the aforementioned models (LSTM and RL), it can predict stock price variation and intelligently opreate stock trading according to price variation, concurrently, the proposed hybrid model can predict risk index to master stock trends in advance that adopt more intelligent policy to operate stock trading. If compared to using one type of deep learning model, the proposed hybrid model offers several potential advantages, such as LSTM can capture long-term dependencies in sequential data, enabling more accurate predictions of stock price changes. By combining with RL, the LSTM’s predictions can be used as inputs to the RL model, enhancing the accuracy and reliability of the trading strategy. Solely relying on an LSTM model may perform poorly in volatile markets or unexpected situations. By combining with RL, a more robust trading strategy can be achieved, as the RL model can adapt to real-time market feedback and exhibit some level of adaptability, etc. The whole architecture of the hybrid deep learning model is shown in Fig. 2. The LSTM model is responsible for stock price and risk index prediction, the RL model is responsible for stock trading by stock price and risk index variation. In terms of different stock prices and risk indexes, the trained agent can adopt the different actions (selling, holding and buying).

Figure 2. Architecture of hybrid deep learning model.

Stock price and risk index prediction using LSTM

In the Introduction, we introduced features of LSTM, It is suitable for handling and predicting time-series data. In stock price prediction, LSTM can be used to analyze historical stock price data, identify patterns and trends within it, and make predictions for future prices. In stock trading, there are four price indexes that people generally pay attention to, which are as follows (Mur, 1999):

• •Open: The first transaction price at the beginning of a trading day.
• •High: The highest price reached during a trading day.
• •Low: The lowest price reached during a trading day.
• •Close: The last transaction price at the end of a trading day.

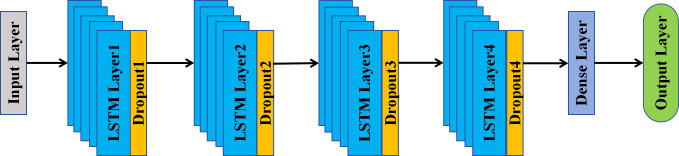
These four different prices each have their own usage. In this study, we mainly focus on Close Price. The close price is widely regarded as one of the most crucial prices for investors because it represents the final transaction price at the end of a trading day. If the close price trend can be predicted in advance, it can reduce unnecessary investment risk. For predicting close price variation, we tend to use LSTM to execute this task. The LSTM architecture is shown in Fig. 3, we plan to adopt a four-layer LSTM architecture and use Dropout layers after each LSTM layer for prediction. The Dropout layer can reduce the complexity of the neural network, decreasing the model’s reliance on the training data and thus reducing the risk of overfitting (Hinton et al., 2012). Meanwhile, the number of LSTM layers should not be utilized too much, because LSTM layers are computationally intensive, especially when the network becomes deeper, having too many LSTM layers can significantly increase the computational cost of training and inference, requiring more memory and processing power.

Figure 3. LSTM architecture.

For the risk index, we mainly focus on ADX (Wilder, 1978). The ADX is a technical indicator used to evaluate the strength of trends in stocks or other financial assets. The value of the ADX index typically ranges from 0 to 100, with higher values indicating stronger trends. Some common ranges and meanings are as follows.

• •0 ∼ 20: Typically considered signals of weakening trends or sideways markets. ADX in this range indicates a lack of clear trend direction, and prices may be in a consolidation phase.
• •20 ∼ 30: This range suggests that the trend in the market is beginning to emerge, but the trend strength is weak. Traders may start to take notice of the emerging trend, but caution is advised as the sustainability of the trend is still uncertain.
• •30 ∼ 40: ADX further increases, indicating an increase in trend strength.
• •40 ∼ 50: Market trends are considered quite strong within this range.

By combining stock price predictions with risk index predictions, it can be made in advance when market uncertainty is high. Meanwhile, in order to verify the robustness of the proposed model, the LSTM architecture in Fig. 3 will be adopted for both stock price prediction and risk index prediction.

Stock trading operating using RL

To leverage RL for operating stock trading, it’s essential to pre-define crucial parameters, with the ultimate objective of maximizing assets through stock transactions. The MDP of stock trading is designed as follows:

• •Environment: We select 10 well-known American companies in different fields around the world, The details are shown in Table 1. These 10 companies cover multiple fields such as technology, finance, and entertainment.
• •State: The state consists of four parts: [A_t, c_t, h_t, X_t]. A_t represents potential total assets in time step t.c_t represents close price of each type of stock in time step t.h_t represents shares owned of each stock. X_t represent ADX.
• •Actions: For each stock, the action spaces are defined as [S_t, H_t, B_t]. Here, S_t represents the action of selling the stock at time step t, H_T represents the action of holding the stock at time step t, and B_t represents the action of buying the stock at time step t.
• •
  Rewards: For maximizing potential total assets, three actions come into play, each influencing the outcome. The selling price of stocks is determined by the closing price, leading to an increase in potential total assets upon selling. Conversely, buying stocks decreases potential total assets. The magnitude of increase/decrease is described in Eqs. (5) and (6). If potential total assets at time step t exceed those at time step t − 1, the reward increases by 1; otherwise, it decreases by 1. However, if potential total assets turn negative, the reward drops by 100. While these equations are straightforward, it’s important to note that increased potential total assets don’t always translate to profit.

  $${\displaystyle A_t=A_{t-1}+h_t{c}_t.}$$ (5)

  $${\displaystyle A_t=A_{t-1}-h_t{c}_t.}$$ (6)

Table 1. Ten well-known American companies.

Ticker symbol (TIC)	Company name	Information
AAPL	Apple	Technology company
AMGN	Amgen	Biotechnology company
BA	Boeing company	Manufacturer of aircraft
DIS	Disney company	Entertainment company
INTC	Intel corporation	Semiconductor design, manufacturing
KO	Coca-cola company	Beverage company
MCD	McDonald corporation	Fast-food restaurant
MSFT	Microsoft corporation	Technology company
TRV	Travelers company	Insurance products and services
V	Visa Inc.	Payment technology

In certain scenarios, stock prices may decline successively, prompting the need to sell off depreciating stocks to limit losses. While this action increases potential total assets, actual profits decrease. To solve this issue, it is imperative to impose constraints. Equations (7) and (8) are proposed in this study to address this concern.

When selling stocks, three constraints are applied. Firstly, the remaining shares after selling must be greater than or equal to 0, denoted by $h_t^{\prime }$ ensuring no overselling. Secondly, the difference between the closing price at time step t and the purchased price c′ should equal or exceed the threshold θ_c1 to ensure profitability. Thirdly, the ADX value must be below the threshold θ_X1, providing insight into trend strength and helping prevent profit decrease. These constraints collectively ensure that stocks are sold under favorable conditions, with the ADX aiding in anticipating trend changes and preserving profits.

When buying stocks, three constraints are also applied. Firstly, the difference between the closing prices at time step t and t − 1 must be greater than or equal to the threshold θc₂, ensuring stocks are purchased during upward trends. Secondly, the number of shares bought should be less than or equal to θs, preventing excessive purchases. Thirdly, the ADX value must exceed θ_X2, indicating strong trend momentum and maximizing profit potential for each stock. These constraints collectively ensure that stocks are acquired during favorable market conditions, with the ADX serving as a preemptive index of trend strength.

$${\displaystyle selling=\left\{\begin{array}{c}{h}_t-h_t^{\prime }\ge 0\hfill \\ c_t-c^{{}^{\prime }}\ge {\theta }_{c_1}\hfill \\ X_t<{\theta }_{X_1}\hfill \end{array}\right..}$$ (7)

$${\displaystyle buying=\left\{\begin{array}{c}{c}_t-c_{t-1}\ge {\theta }_{c_2}\hfill \\ s_t\le {\theta }_s\hfill \\ X_t>{\theta }_{X_2}\hfill \end{array}\right..}$$ (8)

When holding stock, the RL agent refrains from taking any action to actively manage stock trading. Nonetheless, potential total assets may continue to rise during this status, as described by Eq. (9). Even without operating trades, fluctuations in stock prices can still influence potential total assets, leading to changes in their value.

$${\displaystyle holding=A_{t-1}+h_t\left(c_t-c_{t-1}\right).}$$ (9)

Based on Eqs. (7) to (9), RL model can train agent operate stock trading, the critical threshold values from Eqs. (7) to (9) are shown in Table 2, the details about threshold value are as follows:

Table 2. Stock trading thresholds.

Threshold	Value
θ c 1	20
θ X 1	20
θ c 2	10
θ s	500
θ X 2	40

• •For θ_c1, we calculate the difference between the prices of each stock on the first day (2010/07/01) and the last day (2023/10/24), with MSFT having the maximum price difference of 312.77 and INTC having the minimum difference of 21.73. Here we set 20 as the θ_c1 value which is most approximate to the minimum difference. The reason is stocks with the smallest increases may have relatively lower market risk sensitivity. In the stock market, stocks with large price fluctuations are usually associated with high risk. Therefore, selecting the price differential of the stock with the smallest increase as a trading signal implies that the overall market volatility is low, thereby reducing the risk of the investment portfolio.
• •For θ_X1 we set the threshold is 20. As we introduced in ‘Stock Price and Risk Index Prediction using LSTM’, when the ADX is below 20, it typically indicates that the market is in a state of weak trend or lacks a clear trend. The market may be in a sideways or consolidating phase. An ADX value below 20 is generally considered a period of unclear trend, where traders may encounter more oscillations and sideways movements.
• •For θ_c2 we set the threshold is 10. Selling too early may overlook the possibility of the stock continuing to rise, thus potentially forfeiting greater profits in the future. However, waiting for a significant price increase before selling may result in missing the optimal selling opportunity, leading to a price decline and potential loss of profit. So in order to achieve balance, we take a value of 10.
• •For θ_s we set the threshold is 500. Diversifying investments across multiple stocks helps to reduce the risk associated with any single stock. Concentrating all investments in a few stocks may expose the portfolio to significant risks if any of those stocks encounter issues. Setting a maximum limit of 500 shares per stock forces RL agent to diversify investments, thereby reducing concentration risk.
• •For θ_X2 we set the threshold is 40. Also as we introduced in ‘Stock Price and Risk Index Prediction using LSTM’, ADX above 40 suggests a very strong trend in the market, whether it’s an uptrend or downtrend. This indicates that the current trend is likely to continue, combining with the concurrent action of θ_c2, buying stocks at this juncture can significantly enhance the potential for maximizing profits.

Furthermore, in order to maximize the potential total assets obtained and prove threshold values are effective, we conducted preliminary comparative experiments on θ_c1 and θ_c2 with different value ranges. In Table 3, we present the experimental setup and results. The initial values for θ_c1 and θ_c2 are both set to 15, with incremental changes of 1. We compare different combinations of θ_c1 and θ_c2. The first column lists θ_c1 values ranging from 15 to 20, while the second column shows θ_c2 values ranging from 10 to 15. From the results, we observe that when θ_c1 is 20 and θ_c2 is 10, the potential total assets achieve the optimal value, reaching 1, 036, 800.936. This finding aligns with the discussion in ‘Stock Price and Risk Index Prediction using LSTM’, where it corresponds to the universal index used in financial modeling.

Table 3. Experimental results on the potential total assets of different θ_c1 and θ_c2.

θ c 1	θ c 2	Potential total assets
20	10	1,036,800.936
19	11	1,035,848.228
18	12	1,030,829.868
17	13	1,019,809.701
16	14	1,020,766.918
15	15	1,006,301.803

Experiment

Experiment data

In the experiment, the primary foundation lies in the dataset. We select Table 1 data spanning from July 1, 2010, to October 24, 2023, encompassing a comprehensive thirteen-year period (Liu et al., 2020). This dataset is particularly significant as it includes the onset and aftermath of the COVID-19 pandemic, which exerted a profound influence on the stock market (Zhu et al., 2020). Therefore, this dataset serves as a robust choice for training and evaluating the performance of the proposed model. The dataset needs to be partitioned, 70% datasets are used to train and the remaining datasets are used for validation.

Stock price and ADX prediction experiment

Initially, we utilize LSTM to train and predict both stock price and ADX. The LSTM model is implemented using Keras framework (Chollet, 2018). The LSTM architecture is illustrated in Fig. 3. However, to attain the optimal outcome, the number of units for each layer should be dissimilar, their value should be optimized. To achieve this objective, we utilize the Hyperband algorithm to search the optimal hyperparameters for the LSTM model (Li et al., 2017). The optimized hyperparameters of the stock price prediction and the ADX prediction are shown in Tables 4 and 5.

Table 4. Optimized hyperparameters for the stock price prediction model.

Layer	Searching range	Optimal value
LSTM 1	32 ∼ 256	160
Dropout 1	0.1 ∼ 0.5	0.2
LSTM 2	32 ∼ 256	64
Dropout 2	0.1 ∼ 0.5	0.2
LSTM 3	32 ∼ 256	64
Dropout 3	0.1 ∼ 0.5	0.1
LSTM 4	32 ∼ 256	64
Dropout 4	0.1 ∼ 0.5	0.4

Table 5. Optimized hyperparameters for the ADX prediction model.

Layer	Searching range	Optimal value
LSTM 1	32 ∼ 256	224
Dropout 1	0.1 ∼ 0.5	0.3
LSTM 2	32 ∼ 256	192
Dropout 2	0.1 ∼ 0.5	0.1
LSTM 3	32 ∼ 256	96
Dropout 3	0.1 ∼ 0.5	0.1
LSTM 4	32 ∼ 256	160
Dropout 4	0.1 ∼ 0.5	0.5

About the evaluation index for LSTM model, we use the coefficient of determination. The coefficient of determination (R²) is a statistical measure used to assess the goodness of fit of a regression model (Pearson, 2010). R² values range from 0 to 1, where 1 indicates a perfect fit of the model to the data, and 0 indicates that the model does not explain any of the variability in the dependent variable. Its Equation is shown as follows. Where:

$${\displaystyle R^2=1-\frac{\mathrm{SSR}}{\mathrm{SST}}}$$ (10)

• •SSR (Sum of Squared Residuals) represents the total sum of squared differences between the predicted values of the model and the actual observed values.
• •SST (Total Sum of Squares) represents the total sum of squared differences between the target variable and its mean.

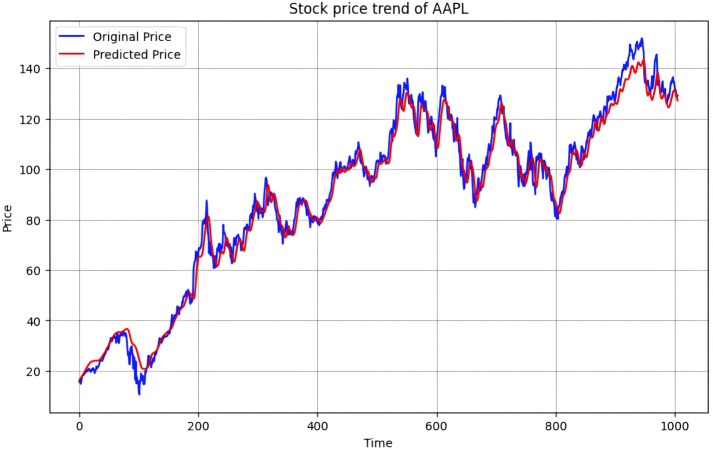
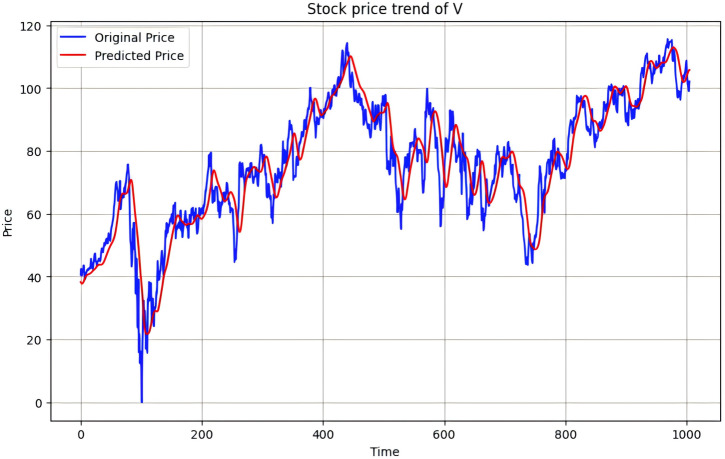
By utilizing Tables 4 and 5 optimized hyperparameters, the R² of stock price prediction results using validation data are shown in Table 6. Based on these results we can clearly know the R² of AAPL stock has impressive performance, achieving a splendid 0.98. The minimal R² is observed for V stock, although it still reaches a respectable 0.83. The price trend of AAPL and V over time is shown in Figs. 4 and 5, this result by using validation data. In Fig. 4, the blue curve represents the original stock price and the red curve represents the predicted price. From these figures, we can perceive the predicted price are not only consistent with the overall trend of the original price, but also predict the subtle changes in prices very well. In Fig. 5, the predicted results are consistent with the overall trend of the original values, but there are still some shortcomings in price fluctuations, especially in peak changes.

Table 6. R₂ of stock price prediction results.

TIC	R 2
AAPL	0.98
AMGN	0.91
BA	0.89
DIS	0.96
INTC	0.95
KO	0.96
MCD	0.96
MSFT	0.96
TRV	0.97
V	0.83
Average	0.94

Figure 4. Stock price trend of AAPL.

Figure 5. Stock price trend of V.

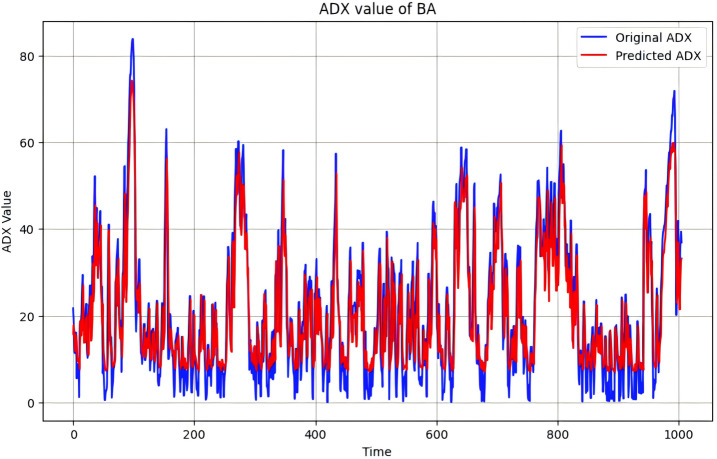
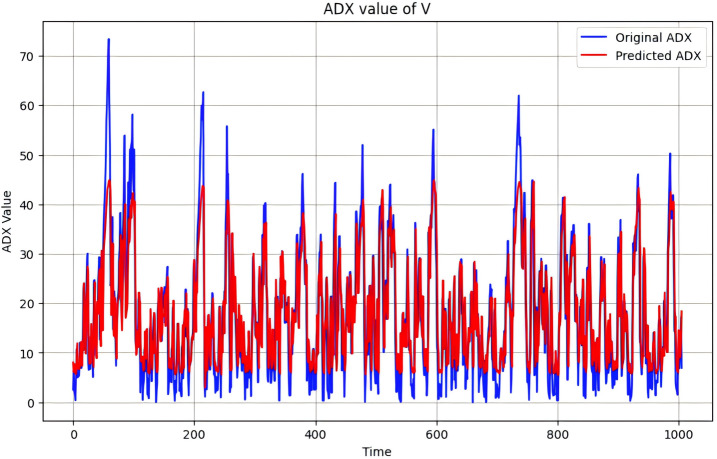
The R² of ADX prediction results are shown in Table 7. The optimal prediction results using validation data in BA, DIS and MCD, their R² can achieve 0.80. On the contrary, The minimal R² is stock V, the result is 0.67. To compare the difference between the optimal and minimal results, the validation result of ADX value of BA and V over time is shown in Figs. 6 and 7. Based on these findings, the prediction results generally exhibit poor performance within the range of low to 10 ADX values. Additionally, accurate predictions are challenging to achieve during peak periods. The reason probably is inadequate model complexity, the proposed LSTM model may hard to capture the complex nonlinear relationships of ADX, requiring a more complex model structure or additional parameters to improve predictive performance, however, the more complex the model, the longer it takes to train it. Fortunately, in ‘Stock Price and Risk Index Prediction using LSTM’, we introduced the several ranges of ADX indicating different trend strengths. Between 0 and 20, the markets show weak trend strength and normally greater than 40, the trend strength is strong. Based on this analysis, we consider it will not have a significant impact on the stock trading by the model, and the ADX values predicted by the model are available.

Table 7. R₂ of ADX prediction results.

TIC	R 2
AAPL	0.77
AMGN	0.74
BA	0.80
DIS	0.80
INTC	0.75
KO	0.72
MCD	0.80
MSFT	0.72
TRV	0.71
V	0.67
Average	0.75

Figure 6. ADX value of BA.

Figure 7. ADX value of V.

To validate the effectiveness of our proposal model, we compared the performance of various loss functions to determine the most suitable one. Specifically, we evaluated the lproposal model using mean squared error (MSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) to analyze their respective results. MSE is a commonly used loss function in regression analysis that measures the average squared difference between predicted and actual values. The equations for the three loss functions are presented below, starting with MSE.

$${\displaystyle MSE=\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2}$$ (11)

where:

• •n is the number of data points.
• •y_i is the actual value.
• •${\hat{y}}_i$ is the predicted value.

MSE penalizes larger errors more heavily than smaller ones, making it sensitive to outliers. A smaller MSE indicates better model performance, with an MSE of 0 representing a perfect fit (James et al., 2013). The second equation is MAE. MAE is a loss function used in regression analysis to measure the average magnitude of errors between predicted and actual values, without considering their direction (Willmott & Matsuura, 2005). It calculates the absolute differences between the predicted and actual values and then averages them. The equation for MAE is:

$${\displaystyle MAE=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|}$$ (12)

where:

• •n is the number of data points.
• •y_i is the actual value.
• •${\hat{y}}_i$ is the predicted value.

MAE is less sensitive to outliers than MSE since it does not square the errors. A lower MAE indicates better model performance, with an MAE of 0 representing a perfect fit. The last loss function we show MAPE equation as follows. MAPE is a loss function commonly used to measure the prediction accuracy of a model in terms of percentage error. It calculates the average absolute percentage difference between predicted and actual values. MAPE is widely used because it expresses the error as a percentage, making it easy to interpret (Armstrong & Collopy, 1992). The equation for MAPE is:

$${\displaystyle MAPE=\frac{100\text{\%}}{n}\sum _{i=1}^n\left|\frac{y_i-{\hat{y}}_i}{y_i}\right|}$$ (13)

where:

• •n is the number of data points.
• •y_i is the actual value.
• •${\hat{y}}_i$ is the predicted value.

MAPE is sensitive to small actual values, which can lead to disproportionately large errors when the actual value is close to 0. A lower MAPE indicates better model performance, with a MAPE of 0% representing a perfect fit.

In Table 8, we compare the R² results for different loss functions when stock price prediction. This Table consists of three columns. The first column presents the MSE results, with an average R² is 0.94 across 10 companies. The optimal performance is achieved by AAPL with an R² is 0.98, while the lowest is by V with 0.83. The second column shows the MAE results, where the average R² remains 0.94, the same as the MSE results. However, the R² values for BA and V are higher under MAE compared to MSE, whereas the result for TRV is lower. The third column contains the MAPE results, where six companies exhibit successful fitting. This limited success may be due to MAPE’s sensitivity to small or 0 values and its lack of robustness to outliers. As MAPE relies on percentage errors, it is particularly vulnerable to unevenly distributed data or outlier effects.

Table 8. R² of stock price prediction results with different loss function.

TIC	R2 (MSE)	R2 (MAE)	R2 (MAPE)
AAPL	0.98	0.97	0.96
AMGN	0.91	0.92	−11.21
BA	0.89	0.93	−4.44
DIS	0.96	0.95	−2.21
INTC	0.95	0.96	0.96
KO	0.96	0.96	0.94
MCD	0.96	0.96	0.95
MSFT	0.96	0.96	0.95
TRV	0.97	0.93	−7.08
V	0.83	0.87	0.89
Average	0.94	0.94	−1.92

In Table 9, we compare the R² results of different loss functions when ADX prediction. Like the previous table, it contains three columns. The first column lists the MSE results, with an average R² is 0.75 across the 10 companies. The optimal R² scores is 0.80 are observed for BA, DIS, and MCD, while V has the minimum at 0.67. The second column reports the MAE results, with an average R² is 0.73, which is slightly lower than the MSE results. Notably, the R² for MSFT is higher under MAE than MSE. The third column shows the MAPE results, where none of the companies demonstrate successful fitting. As with stock price predictions, MAPE’s sensitivity to small or 0 values and its poor handling of outliers likely contribute to these poor results, particularly given its reliance on percentage errors, which makes it less robust in cases of unevenly distributed data. On the basis of the above experimental results, it can be concluded that setting the loss function to MSE and MAE yields outstanding experimental results.

Table 9. R² of ADX prediction results with different loss function.

TIC	R2 (MSE)	R2 (MAE)	R2 (MAPE)
AAPL	0.77	0.77	−2.00
AMGN	0.74	0.73	−2.30
BA	0.80	0.76	−1.80
DIS	0.80	0.76	−1.65
INTC	0.75	0.74	−2.02
KO	0.72	0.71	−1.98
MCD	0.80	0.78	−1.98
MSFT	0.72	0.75	−2.74
TRV	0.71	0.70	−2.34
V	0.67	0.67	−1.83
Average	0.75	0.73	−2.06

Stock price and ADX prediction comparison experiment

In Tables 10 and 11, we present the results of comparison experiments for stock price and ADX prediction using different train-validation split ratios. For stock price prediction, when the validation split ratio is set to 0.2, the R² results of BA, DIS, and INTC are better compared to the results when the validation split ratio is 0.3. However, for KO, the R² score turns negative. Several factors may explain this. First, if the distribution of the validation data differs significantly from the training data, the model may struggle to generalize, performing well on the training set but poorly on the validation set, resulting in a negative R². Second, an overly large proportion of training data can lead to overfitting, where the model learns noise and specific patterns from the training data that do not generalize well. This can also result in a negative R² on the validation data. For the ADX prediction results, when the validation data split ratio is 0.2, the R² result of AMGN is higher than that for a 0.3 split ratio. However, the R² results for other companies are lower when the split ratio is 0.2 compared to 0.3. The average R² result of the 0.2 split ratio is 0.71, which is lower than the 0.75 R² result of the 0.3 split ratio. These results indicate that a 0.3 validation data split ratio offers better overall performance.

Table 10. R² of stock price prediction results using different split ratio.

TIC	Validation data (0.3)	Validation data (0.2)
AAPL	0.98	0.92
AMGN	0.91	0.90
BA	0.89	0.91
DIS	0.96	0.98
INTC	0.95	0.97
KO	0.96	−0.26
MCD	0.96	0.93
MSFT	0.96	0.89
TRV	0.97	0.97
V	0.83	0.76
Average	0.94	0.79

Table 11. R² of ADX prediction results using different split ratio.

TIC	Validation data (0.3)	Validation data (0.2)
AAPL	0.77	0.71
AMGN	0.74	0.75
BA	0.80	0.77
DIS	0.80	0.76
INTC	0.75	0.71
KO	0.72	0.68
MCD	0.80	0.77
MSFT	0.72	0.72
TRV	0.71	0.61
V	0.67	0.62
Average	0.75	0.71

For validating our proposal model performance, we use the traditional ARIMA model and non-linear MLP model to compare. For non-linear MLP model, we choose SRV model. The support regression vector (SRV) model is a machine learning model that is derived from support vector machines (SVM) but adapted for regression tasks (Smola & Schölkopf, 2004). Instead of classifying data points into categories, as in the case of SVM, SRV is used to predict continuous values. The model seeks to find a function that deviates from the true target values by no more than a certain margin, while also being as flat as possible. SRV is particularly useful when dealing with high-dimensional data and has strong theoretical foundations in convex optimization. It aims to minimize the error by balancing the complexity of the model and the precision of predictions. To ensure the consistency of the experiment, we set the ratio of training data to validation data to 0.7 and 0.3 when using the SRV model, the split ratio is same as proposal model training. In Table 12, we show the R² results of stock price and ADX prediction.

Table 12. R² of stock price and ADX prediction results using the SRV model.

TIC	SRV (Stock price)	SRV (ADX)
AAPL	−13.46	0.69
AMGN	−22.60	0.71
BA	−0.14	0.70
DIS	−0.61	0.65
INTC	0.28	0.64
KO	−6.18	0.65
MCD	−7.76	0.67
MSFT	−14.30	0.60
TRV	−2.53	0.57
V	−23.26	0.56
Average	−9.05	0.64

From Table 12, we observe that for stock price prediction using the SRV model, the R² results are significantly worse compared to our propossal model. The SRV model struggles to fit the stock price, showing negative R² values for all 10 companies, with an average accuracy of −9.05. This performance is considerably lower than that of our proposed model. For the ADX prediction results, the SRV model does perform better, successfully fitting the data with positive R² values for all companies. However, when we compare the R² results of the SRV model with those of our proposal model, the SRV model consistently underperforms. The average R² of SRV is 0.64, while the proposal model achieves 0.75. This comparison clearly demonstrates the superior performance of our propossal model. Next we compare traditional ARIMA model results with our proposal model. The autoregressive integrated moving average (ARIMA) model is a popular statistical method used for time series forecasting (Geurts, Box & Jenkins, 1977). ARIMA combines three components:

• •AR (AutoRegressive): The model uses the relationship between an observation and a number of lagged observations (previous values).
• •I (Integrated): This involves differencing the data to make it stationary, which means removing trends or seasonal effects.
• •MA (Moving Average): The model uses the relationship between an observation and a residual error from a moving average model applied to lagged observations.

ARIMA is widely used in forecasting because it can model various types of time series data, including those with trends and seasonality. In the context of stock price prediction, ARIMA can help analyze historical stock prices and project future prices based on patterns observed in the past. However, it is generally most effective when the time series is linear and doesn’t exhibit too much volatility. In Tables 13 and 14, we present the results using the same training and validation data. Each table includes two columns: the first column shows the results based on the training data alone, and it is evident that the traditional ARIMA model struggles to fit both stock prices and the ADX. For stock price predictions, the average R² is negative at −2.87, and for ADX predictions, it is −1.35. These values clearly indicate that the model performs poorly. The second column displays results where the ARIMA model was trained using the entire dataset. While the average R² for stock prices is slightly lower than our proposal model, the ARIMA model performs better for ADX prediction. Specifically, the average R² for stock price predictions reaches 0.98, and for ADX predictions, it reaches 0.74. These results further highlight that the traditional ARIMA model struggles with nonlinear trends and performs poorly when encountering unseen data, reinforcing the effectiveness of our proposal model.

Table 13. R² of stock price prediction results using the ARIMA model.

TIC	ARIMA (Training data only)	ARIMA (Entire data)
AAPL	−4.46	0.99
AMGN	−4.27	0.97
BA	−6.61	0.98
DIS	−2.29	0.99
INTC	−0.08	0.98
KO	−0.51	0.98
MCD	−1.85	0.99
MSFT	−4.27	0.99
TRV	−1.01	0.99
V	−3.42	0.96
Average	−2.87	0.98

Table 14. R² of ADX prediction results using the ARIMA model.

TIC	ARIMA (Training data only)	ARIMA (Entire data)
AAPL	−1.82	0.77
AMGN	−0.49	0.78
BA	−0.003	0.79
DIS	−1.54	0.80
INTC	−0.44	0.73
KO	−0.66	0.72
MCD	−2.43	0.79
MSFT	−0.31	0.75
TRV	−4.79	0.69
V	−1.04	0.67
Average	−1.35	0.74

Stock trading experiment

Experiment setting

For main experiment, we use RL train agent to operate stock trading. For the RL algorithm, we choose the Proximal Policy Optimization (PPO). PPO is an algorithm used for training RL agents, aiming to iteratively optimize the policy while avoiding significant policy updates. PPO achieves this by constraining the relative difference between the new and old policies. There are three concepts of PPO (Schulman et al., 2017):

• 1.Objective: Maximize the expected cumulative reward while limiting the relative difference between new and old policies in each update.
• 2.Surrogate objective: PPO employs a surrogate objective function, the optimization of which ensures that changes to the new policy relative to the old policy are gradual to prevent large updates.
• 3.Importance sampling: Importance sampling is used to adjust the expectation of rewards, considering the differences between the new and old policies.

In PPO, the surrogate objective function is designed to maximize the “clipped surrogate objective” expression:

$${\displaystyle L\left(\theta \right)={\mathbb{E}}_t\left[\min \left(r_t\left(\theta \right){\hat{A}}_t,\mathrm{clip}\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right){\hat{A}}_t\right)\right]}$$ (14)

where:

• •L(θ) is the surrogate objective function.
• •θ represents the policy parameters.
• •${\hat{A}}_t$ is the advantage function, representing the advantage estimate at time step t.
• •
  r_t(θ) is the importance ratio, representing the relative probability between the new and old policies:

  $${\displaystyle r_t\left(\theta \right)=\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{\theta ,old}\left(a_t|s_t\right)}}$$ (15)
• •clip(x, a, b) is a clipping function that restricts x to the interval [a, b].

The update rule of PPO utilizes gradient ascent to update policy parameters by maximizing the surrogate objective function:

$${\displaystyle {\theta }_{\mathrm{new}}={\theta }_{\mathrm{old}}+\alpha {\nabla }_{\theta }L\left(\theta \right)}$$ (16)

where α is the learning rate. Thus, the training process of PPO involves iteratively updating policy parameters to maximize the surrogate objective function, optimizing the agent’s policy.

Stock trading experiment results with original value

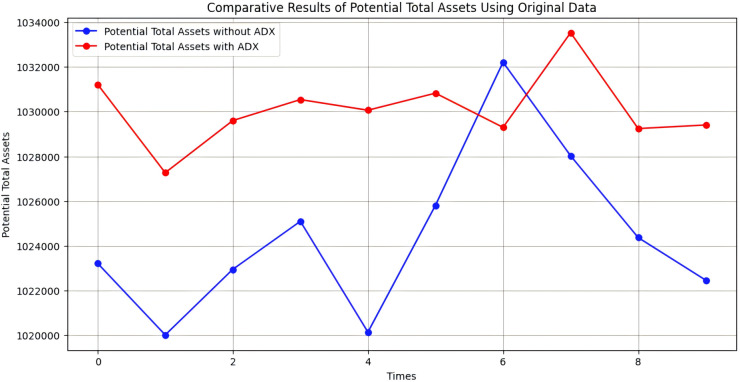
To validate the effectiveness of the risk index ADX, we conducted the experiment in two parts. The first part excluded the use of ADX, while the second part integrated ADX. This approach allowed us to demonstrate the effectiveness of ADX through comparative experiments. We still use the same validation data as ‘Experiment’ and evaluate ten times using RL model. In Fig. 8, the blue curve represents potential total assets without ADX and the red curve represents potential total assets with ADX. The x-axis represents the time step during training and the y-axis represents the potential total assets. The maximum of potential total assets with ADX is 1, 033, 523.43, the minimum of potential total assets with ADX is 1, 027, 267.20 and the average of potential total assets with ADX is 1, 030, 095.29. On the other hand, the maximum of potential total assets without ADX is 1, 032, 204.86, the minimum of potential total assets without ADX is 1, 020, 021.06 and the average of potential total assets without ADX is 1, 024, 431.57. In Fig. 8, only one time the potential total assets without ADX greater than the potential total assets with ADX. it can adequately proves that using ADX is effective and can increase potential reward values.

Figure 8. Comparative results of potential total assets using original data.

Stock trading experiment with hybrid deep learning model

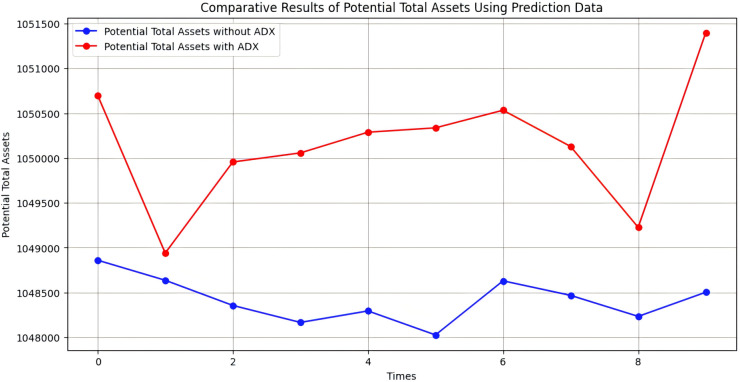
In this experiment, we use predicted stock price and ADX to surrogate original stock price and ADX of data. We also use the same validation data as ‘Experiment’ and evaluate it ten times using the RL model. In Fig. 9, the blue curve represents potential total assets without ADX and the red curve represents potential total assets with ADX. The x-axis represents the time step during training and the y-axis represents the potential total assets. The maximum of potential total assets with ADX is 1, 051, 397.88, the minimum of potential total assets with ADX is 1, 048, 939.57 and the average of potential total assets with ADX is 1, 050, 156.04. On the other hand, The maximum of potential total assets without ADX is 1, 048, 859.81, the minimum of potential total assets without ADX is 1, 048, 026.19 and the average of potential total assets without ADX is 1, 048, 417.05. All the results with ADX greater than results without ADX, it can adequately prove our approach using ADX is effective too with prediction data.

Figure 9. Comparative results of potential total assets using prediction data.

Stock trading experiment with sharp ratio

The Sharpe ratio (S_R) is a measure used to evaluate the risk-adjusted return of an investment or portfolio. It compares the excess return (above a risk-free rate) to the total risk (measured by standard deviation) of the investment (Sharpe, 1966). A higher S_R indicates that the investment offers a better risk-adjusted return.

The equation for the S_R is:

$${\displaystyle S_R=\frac{R_p-R_f}{{\sigma }_p}}$$ (17)

where:

• •R_p is the expected return of the portfolio or investment.
• •R_f is the risk-free rate (often a government bond yield).
• •σ_p is the standard deviation of the portfolio’s excess return, which represents the total risk.

The S_R helps investors understand how much return they are getting per unit of risk. Typically, the higher the S_R, the better the excess return per unit of risk. However, the value can also be negative, indicating that the return of the investment is lower than the risk-free rate. Below are common S_R ranges and their meanings, these ranges based on common knowledge widely used in the finance and investment industries:

• •Negative (S_R < 0): A negative S_R indicates that the investment return is below the risk-free rate, meaning the investment has performed poorly, possibly resulting in losses.
• •Between 0 and 1 (0 ≤S_R < 1): This range suggests that the investment has relatively low returns, while accompanied by some risk, the return is acceptable.
• •Between 1 and 2 (1 ≤S_R < 2): A S_R in this range is generally considered reasonable, indicating a balanced risk-return relationship. Most investors view this range as acceptable.
• •Between 2 and 3 (2 ≤S_R < 3): This range represents very good risk-adjusted returns, meaning that the investment delivers high returns relative to the risk taken. The investment performs excellently.
• •Above 3 (S_R≥ 3): A S_R above 3 is rare and indicates extremely high returns with very low risk. This usually suggests an exceptionally successful investment strategy.

To ensure the integrity and reliability of our experiment, we simulated 500 times stock trading scenarios using 10 companies stock. We calculated the S_R for both the original stock data (with and without ADX) and the predicted stock data (with and without ADX). The results are presented in Table 15. For the original stock data, the results demonstrate that incorporating ADX significantly enhances trading performance. The S_R for the original data with ADX is 0.62, compared to −0.07 without ADX. As noted, a negative S_R signals poor performance and potential losses. This comparison clearly highlights the positive impact of ADX on overall asset growth when applied to the original stock data. Similarly, for the prediction stock data, the results indicate that using ADX improves trading performance. The S_R for the prediction data with ADX is 0.05, whereas it is only 0.0059 without ADX. By comparing the original and prediction data in terms of R² and S_R, we observe that the use of ADX for controlling stock trading, as proposed in this study, leads to a significant improvement in potenial total asset value in both the original and prediction data compared to scenarios where ADX is not utilized.

Table 15. S_R comparison experiment results.

Stock type	ADX	no-ADX
Original data	0.62	−0.07
Prediction data	0.05	0.0059

Stock trading experiment results with Williams R%

The Williams percentage range (Williams R%) is a momentum technical indicator that measures overbought and oversold levels in the market. It was developed by Larry Williams and is used to assess the current closing price relative to the high and low of a specified period, typically 14 days (Mur, 1999). The Williams R% is an oscillator that moves between 0 and −100. A reading above −20 indicates that the stock or asset is overbought, while a reading below −80 signals that the stock or asset is oversold. Traders use this indicator to identify potential reversals in the market, as an overbought condition might signal a potential price drop, while an oversold condition may indicate a potential price increase.

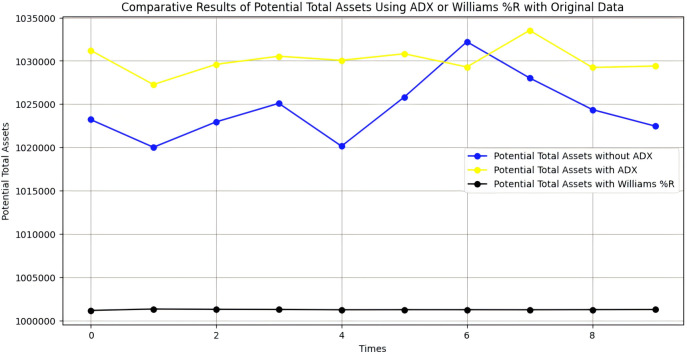
In Fig. 10, we present the average potential total asset values when using Williams R% or ADX to evaluate stock trading performance, applying the same RL algorithm, and comparing the results to our proposal approach. The figure contains three curves: the blue curve represents potential total assets without using ADX, the red curve represents potential total assets with ADX, and the green curve represents potential total assets using Williams R%. From the results, it is evident that using Williams R% as the stock trading evaluation metric results in lower potential total assets compared to using ADX or not using any metric at all. Specifically, the average potential total assets when using Williams R% is 1, 001, 264.96, compared to 1, 024, 431.56 without ADX, and 1, 030, 095.29 with ADX. These findings demonstrate that our proposal approach is more effective, leading to higher potential total assets.

Figure 10. Williams R% comparative experiment results.

Discussion

In our experiments, we used the proposed approach and hybrid deep learning model to maximize the potential total assets. The results showed our approach is effective.

First, we trained an LSTM model to predict stock price variations, utilizing the stocks of ten renowned companies worldwide for prediction. We assessed the model’s performance using the R² score as the evaluation metric. Table 6 presents the results. The average R² across the ten stocks is 0.94, with a maximum of 0.98 achieved for AAPL. These findings underscore the effectiveness of our proposed model in stock price prediction. We also compare our proposal model with other approach, such as traditional ARIMA model, SRV model. The results show our proposal model have great performance. Regarding the ADX prediction model, the average R² across the ten stocks is 0.75, with a maximum of 0.80. While these results exhibit slightly lower accuracy compared to stock price prediction, they still hold superior performance when combined with the insights presented in ‘Stock Price and Risk Index Prediction using LSTM’.

Secondly, we train RL agent to engage in stock trading with the objective of maximizing potential stock assets. This phase of our study comprised two sets of experiments. Firstly, we compared the performance between using the original stock prices with and without the ADX. Secondly, we evaluated the predicted stock prices under the same conditions. Our findings demonstrate the effectiveness of our proposed approach, particularly when incorporating the ADX index. In the experiments utilizing original stock prices, 9 out of 10 results employing the ADX index exhibited superior potential benefits compared to those without it. Similarly, in experiments involving predicted stock prices, all 10 results utilizing the ADX index outperformed those without it. Meanwhile, we use S_R to evaluate our proposal model earn profit or not, all results underscore the efficacy of our approach.

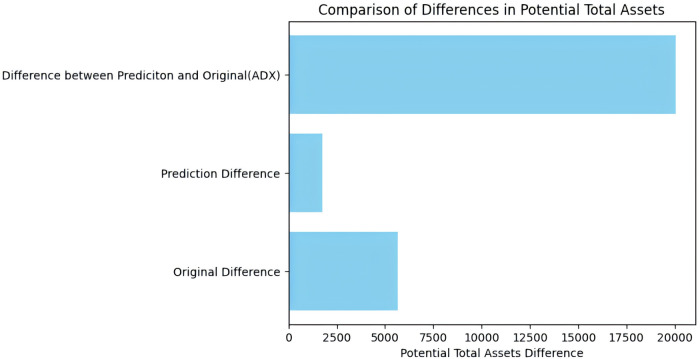
In Fig. 11, we present the results of the comparison of the difference in potential total assets. The initial comparison contrasts the prediction and original outcomes with the utilization of the ADX index. Our findings indicate that our approach exhibits superior performance, yielding greater potential total assets. The subsequent analysis focuses on the predicted results difference between employing the ADX index and not using it, revealing the effectiveness of the ADX index. Lastly, we examine the disparity in the original results between utilizing the ADX index and not using it, reconfirming the effectiveness of the ADX index.

Figure 11. Comparison of difference in potential total assets.

Conclusion

In this paper, we presented a novel hybrid deep learning model that combines LSTM for stock price prediction and RL for stock trading control. Our approach addresses the limitations of using LSTM and RL separately by integrating them into a hybrid model that enables simultaneous prediction and trading. Additionally, we incorporated the ADX prediction from the LSTM model and proposed several constraints to enhance asset management and reduce market uncertainty. Our experiment results demonstrate the effectiveness of the proposed hybrid model, achieving an impressive average R² value of 0.94 in predicting price variations. Moreover, by integrating ADX prediction and applying constraints, our approach significantly increases stock assets to 1.05 times their initial value, underscoring the practical utility and potential profitability of our methodology. Moving forward, further research could explore additional refinements to the hybrid model, investigate its performance across different market conditions, and conduct real-world deployment to validate its effectiveness in practical trading scenarios. Overall, our study contributes to the ongoing advancement of AI-driven approaches in stock trading and asset management, offering valuable insights for investors and practitioners in navigating the complexities of financial markets.

Funding Statement

The authors received no funding for this work.