Abstract
Mixotrophic protists combine photosynthesis with the ingestion of prey to thrive in resource-limited conditions in the ocean. Yet, how they fine-tune resource investments between their two different metabolic strategies remains unclear. Here, we present a modeling framework (Mixotroph Optimal Contributions to Heterotrophy and Autotrophy) that predicts the optimal (growth-maximizing) investments of carbon and nitrogen as a function of environmental conditions. Our model captures a full spectrum of trophic modes, in which the optimal investments reflect zero-waste solutions (i.e., growth is colimited by carbon and nitrogen) and accurately reproduces experimental results. By fitting the model to data for Ochromonas, we were able to predict metabolic strategies at a global scale. We find that high phagotrophic investment is the dominant strategy across different oceanic biomes, used primarily for nitrogen acquisition. Our results therefore support empirical observations of the importance of mixotrophic grazers to upper ocean bacterivory.
Mixotrophic nanoflagellates maximize growth by balancing C and N acquisition via photosynthetic and phagotrophic investments.
INTRODUCTION
Marine microbial mixotrophs combine photosynthesis with the consumption of prey to obtain the energetic and material resources necessary for growth. As our ability to quantify grazing has improved, oceanographers have discovered that mixotrophy is a widespread strategy among eukaryotic phytoplankton, with mixotrophic representatives found in nearly all major lineages (1, 2). Further, both empirical and modeling studies have shown that mixotrophs may have large ecological and biogeochemical impacts (3). By straddling two metabolic niches, mixotrophs can persist in the margins alongside phytoplankton and grazers (4) and tolerate oligotrophic conditions by supplementing their energetic budgets through feeding (5). As a result, mixotrophs are often abundant in oligotrophic regions such as the subtropical gyres, where they may be the dominant grazers (6). Further, accounting for mixotrophy in global ocean models results in predictions of increased mean body size and, as a consequence, increased carbon export through the biological pump (7).
As the recognition of mixotrophy’s importance grows, one major challenge to developing generalizable theory is that mixotrophs are incredibly taxonomically and functionally diverse (8). For example, some mixotrophs are “constitutive”—meaning that they permanently maintain the metabolic machinery for both photosynthesis and heterotrophy—while others are “nonconstitutive” and transiently gain access to photosynthesis either by hosting photosynthetic endosymbionts or through kleptoplasty (theft of functional chloroplasts from photosynthetic prey) (9). Even among the constitutive mixotrophs, metabolic strategies vary: Some “obligate” mixotrophs require both light and food to survive (10), other “inducible” mixotrophs feed only when certain nutrients are limiting (11, 12), and still others are primarily phagotrophic (13). Yet, only by accounting for these different mixotrophic strategies can we accurately model marine ecosystems (14).
One approach to developing a generalizeable model for mixotrophs is to focus on metabolic trade-offs (15). Constitutive mixotrophs lie on a continuum based on the degree to which they invest in photosynthesis and heterotrophy, and the returns on investment they get from these two processes. Previous theory predicts that their growth strategies vary with environmental conditions (16) and cell size (17). However, different growth strategies can be observed even among constitutive mixotrophs of similar size as well as among closely related species (10, 13, 18). Unveiling the trade-offs driving mixotrophic metabolism is critical and can help us to better constrain competition models that predict their ecological dynamics (19).
On the basis of the intersection of these trade-offs with environmental conditions, we might expect different types of mixotrophs across the surface ocean, as suggested by previous global analyses (20, 21). The mechanisms underlying the different biogeographic patterns remain a gap in knowledge, particularly due to the methodological challenges of identifying mixotrophic strategy in situ (22, 23). By developing theory based on optimal resource allocation, and thus avoiding defining a trade-off a priori, we give one step toward unlocking the metabolic trade-offs that mixotrophs experience and apply this model to investigate mixotrophy biogeography at the global scale.
Here, we use a resource-based framework (MOCHA: Mixotroph Optimal Contributions to Heterotrophy and Autotrophy) to account for the trade-offs and synergies that constitutive mixotrophs experience between their two forms of metabolism. We identify what types of mixotroph strategies are favored as a function of environmental conditions, validate our model’s predictions using empirical data from a model genus of mixotrophic nanoflagellates, and use our model to project the distribution of mixotroph types in Earth’s surface oceans. Our results highlight the importance of phagotrophy to constitutive mixotrophs and give insight into how mixotrophs evolving in polar seas might find a different metabolic niche than mixotrophs evolving in the oligotrophic gyres as Earth’s climate warms.
RESULTS
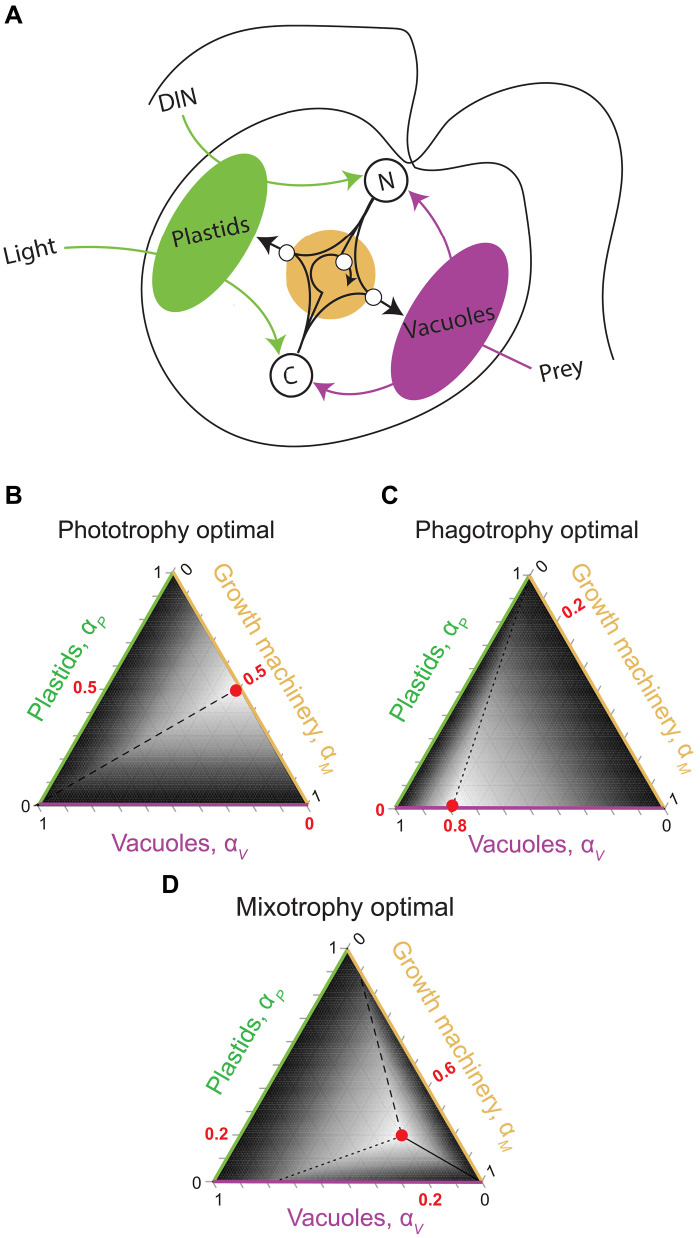
To model a mixotroph’s response to resource supply, we account for how it acquires carbon and nitrogen via prey consumption and photosynthesis, and then uses these resources to build new digestive vacuoles , chloroplasts , and growth machinery (Fig. 1A). The model captures both synergies and trade-offs from mixotrophic strategies: Because carbon and nitrogen are pooled for growth, production of either element by one metabolic strategy can support the other strategy (synergy), but because the organism can only invest the carbon and nitrogen it has available for growth, production of each type of cellular structure comes at the cost of additional investments in the other structure types (trade-off). We consider how a mixotroph balances its vacuoles, chloroplasts, and growth machinery to achieve a growth-maximizing (a.k.a. “optimal”) investment strategy. Our model does not differentiate between enlargement of single cells (or a single multicellular organism) and reproduction (e.g., through cell division) but does assume a constant per-structure resource uptake rate and, therefore, a constant surface area–to–volume ratio for biomass.
Fig. 1. The MOCHA model.
(A) Model schematic illustrating the cell of a constitutive mixotroph that can obtain carbon (C) and nitrogen (N) by investing in phototrophy and/or prey consumption and then use C and N to build three structures: plastids (green), feeding vacuoles (magenta), and growth machinery (gold). The optimal strategies vary with environmental conditions so that (B) phototrophy is optimal if prey is limited but light and external inorganic nitrogen (DIN) are replete, (C) phagotrophy is optimal if prey is abundant but light and DIN are limited, and (D) mixotrophy is optimal if light and prey are replete but DIN is limited. Ternary plots [(B) to (D)] show heatmaps of growth rate as a function of the three-structure investment strategy (dark gray = slow or negative growth; white = fast growth). Lines indicate strategies that produce equivalence of growth components: Solid lines represent C flux = N flux, dashed lines represent C flux = growth flux, and dotted lines represent N flux = growth flux. Note that when strict phagotrophy or strict phototrophy are optimal, only one of these equalities is true. The growth-maximizing strategy (red dot) is at the convergence point of the lines (or, in the cases of strict phagotrophy or phototrophy, where the nonoptimal metabolic investment is set to zero).
First, we explored the spectrum of metabolic outcomes that the MOCHA model can predict. Depending upon resource availability and the acquisition traits that govern an organism’s uptake of these resources, optimal strategies range from strict phototrophy to mixotrophy to strict phagotrophy (Fig. 1, B to D). Mixotrophy is generally favored when the two metabolic strategies are each more effective than the other at obtaining one of the key resources (nitrogen or carbon). For example, if inorganic nutrients are unavailable (because of low supply or inefficient uptake), phagotrophy is obligatory to obtain N. When phototrophy is simultaneously the most efficient source of C (e.g., because bacterial C:N ratios are comparatively low or light is high), then mixotrophy is favored. This is a canonical case in constitutive mixotrophy, in which feeding provides essential nutrients to support photosynthesis. The reverse case—in which phagotrophy is the dominant source of C and phototrophy is the dominant source of N—can also hypothetically arise because MOCHA couples inorganic N uptake to plastids; however, this scenario is unlikely based on studies of extant mixotrophs (and confirmed by our own data analysis; see below).
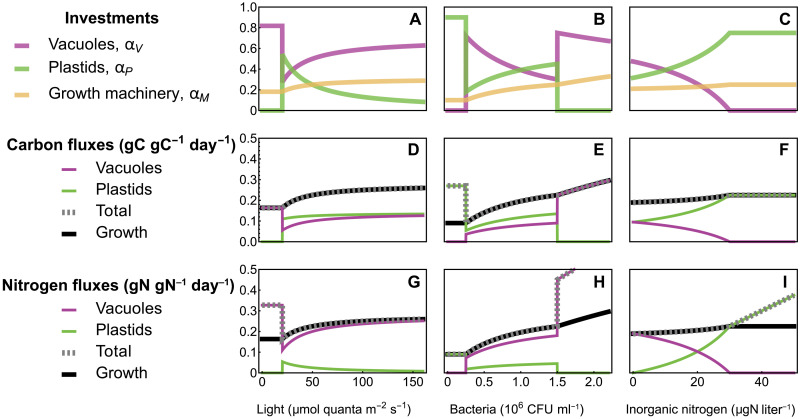
A mixotroph’s optimal investment strategy is sensitive to environmental conditions because the abundance of external resources changes the structure-specific efficiency of C and N uptake (Fig. 2). For example, with increasing light, the optimal strategy switches from pure phagotrophy in darkness to high levels of phototrophy when available light is sufficient to meet C demands (Fig. 2, left column). As light availability continues to increase, each plastid functions more and more efficiently to capture light. To avoid N limitation amidst this surplus of C, the mixotroph “photoacclimates” by down-regulating its plastid investment in favor of investments in digestive vacuoles and growth. In regions of resource space for which the growth-maximizing strategy is mixotrophy, this metabolic strategy is a “zero-waste” strategy, in which the total C and N acquired precisely balance the C and N used for growth (i.e., the gray dashed and black lines overlap in Fig. 2, D to I). In such circumstances, mixotrophs are colimited by C and N. While Fig. 2 provides a generic illustration of the qualitative range of strategies available to a metabolically flexible mixotroph, the existence and precise resource availability thresholds at which strategy transition points occur can only be determined by tuning the model to data from specific mixotrophic taxa (see below).
Fig. 2. Resource dependence of mixotroph strategies.
We computed the mixotroph’s optimal allocation strategy (A to C) and corresponding biomass production normalized fluxes of carbon (D to F) and nitrogen (G to I) as a function of light (left column), bacterial abundance (middle column), and inorganic nitrogen (right column). When the optimal strategy is mixotrophy (i.e., ), the total C (in gC gC−1 day−1) and N (in gN gN−1 day−1) fluxes both converge to the growth rate, indicating a zero-waste strategy. However, in some circumstances, a single metabolic investment is optimal. For example, when light is low or bacterial abundance is high, strict phagotrophy maximizes growth, but bacterial stoichiometric differences produce a surplus of N. In contrast, if bacteria are scarce and strict phototrophy is optimal, the organism produces a surplus of C. This plot shows the qualitative behavior of the model, but the parameter values do not correspond to any specific mixotroph species. The environmental parameters are as follows (when they are not the focal parameter on the x axis): light μmol quanta m−2 s−1, bacteria CFU ml−1, and dissolved nitrogen .
The calculation of the growth-maximizing strategy assumes fixed environmental conditions (i.e., the mixotroph’s metabolic strategy does not change its environment). To assess how growth-maximizing strategies change in response to dynamic feedbacks on resource availability, we extended the MOCHA model to include chemostat-like dynamics. The chemostat model allows the mixotroph to take up inorganic nutrients and bacteria and absorb light as it grows, and thus its strategy evolves alongside its resource environment. Consistent with previous work on phytoplankton growth maximization strategies (24, 25), we found that mixotroph strategies exhibited two distinct phases: an exponential, growth-maximizing phase as the mixotroph asymptotically approached resource limitation, and an equilibrium phase in which the mixotroph’s biomass is constant and its growth rate is equal to the dilution rate (figs. S3 and S4). The MOCHA model is not relevant to this latter phase because organisms in resource-limited environments should shift to competitive, not growth-maximizing, strategies such as those that minimize the equilibrium resource level (24–26). However, mixotroph strategies in the exponential, growth-maximizing phase were constant and identical to the initial MOCHA solutions before any resource feedbacks, indicating that growth-maximizing strategies result in initially balanced drawdown of resources. Thus, we proceeded with the MOCHA algorithm when the assumption of exponential growth was viable.
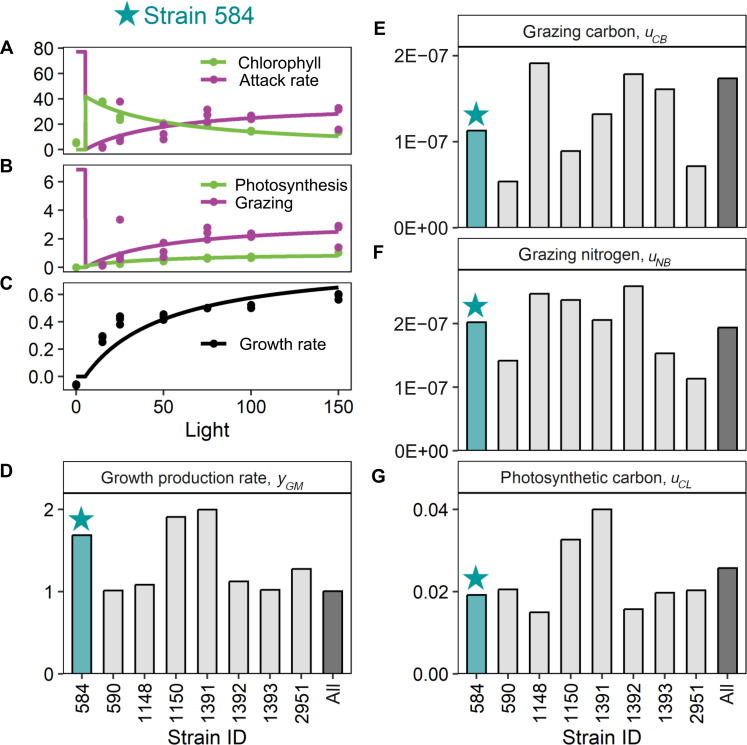
Our model’s qualitative predictions of light-dependent strategies mirrored laboratory measurements of mixotroph exponential growth, photosynthesis, and phagotrophy collected from eight strains of the cosmopolitan constitutive mixotroph genus Ochromonas. Members of this mixotrophic nanoflagellate genus have been collected from both coastal and open ocean ecosystems, are relatively well studied, and are known to exhibit plasticity in their metabolic strategies in response to changing resource availability (10, 13, 27). When we fit the MOCHA model to our published empirical dataset (27), the model recovered the light-saturating dependence of growth, as well as a switch from phagotrophy to phototrophy followed by photoacclimation (reduced chlorophyll per cell) as light levels increased (Fig. 3 and fig. S5 with all strains). Experimental data indicated that while Ochromonas per-carbon photosynthetic rates saturate with increasing light (Fig. 3B and fig. S5), per-chlorophyll photosynthetic rates continued to increase linearly [fig. S6, (27)]. Thus, our model (which assumes a linear relationship between per-plastid carbon fixation rates and light availability) both accurately reflected our experimental data and produced saturating photosynthetic rates as an outcome of reduced investments in photosynthesis (Fig. 2, A and D), as in our experimental system. Our model also captured carbon limitations on growth: when light availability was too low, many of our Ochromonas strains could not achieve positive growth rates because rates of carbon acquisition were less than metabolic costs of respiration (Fig. 2 and fig. S5).
Fig. 3. The MOCHA model reproduces patterns in empirical data.
The MOCHA model reproduces patterns in empirical data. We use data from eight strains of Ochromonas to parameterize our model. Here, we show empirical data (points) and model fits (lines) from strain 584 as an example [(A) to (C)]; data and model fits from all strains are given in fig. S5. Empirical data include the following: (A) photosynthetic investment (chlorophyll content per Ochromonas biomass, mgChl gC−1) and heterotrophic investment (attack rate, a.k.a. “clearance rates,” in units of ml per Ochromonas biomass per day, ml gC−1 day−1), (B) photosynthetic rate (carbon fixed per Ochromonas biomass per day, gC gC−1 day−1) and grazing rate (bacteria per Ochromonas per day, CFU μgC−1 day−1), (C) and growth rate (day−1). On the basis of the model fits, we were able to estimate different parameters in MOCHA [(D) to (G)]. The estimated parameters for strain CCMP 584 (blue bars) were derived from the model fits shown in (A) to (C). The gray bars indicate how variable these parameters were across different strains while the black bar reports the estimated values for an “average Ochromonas cell” based on a global fit to pooled data from all eight strains. Strains varied in their growth factor production rate [, day−1 (D)]; carbon acquisition from bacteria in carbon acquired per carbon vacuole structure, day, and bacteria density [, gC gC−1 day−1 (CFU ml−1)−1 (E)]; nitrogen acquisition from bacteria in nitrogen acquired per carbon vacuole structure, day, and bacteria density [, gN gC−1 day−1 (CFU ml−1)−1 (F)]; and photosynthetic carbon acquisition in carbon acquired per carbon plastid structure, day, and light intensity [, gC gC−1 day−1 (μmol quanta m−2 s−1)−1 (G)].
Our eight Ochromonas strains showed similar capacities for photosynthesis and phagotrophy, though some were relatively more efficient at photosynthetic or phagotrophic resource acquisition (Fig. 3, E to G). Notably, the best-fitting models indicated that these Ochromonas strains were not reliant on inorganic nitrogen uptake for growth, although experiments were conducted using nitrate- and ammonium-containing K media (28). Although we did not experimentally quantify inorganic N uptake in our laboratory experiments, this finding is consistent with our experiments, in which measured grazing rates and bacterial stoichiometry (27, 29) indicated that phagotrophy provided sufficient N to support mixotroph growth without invoking inorganic N uptake.
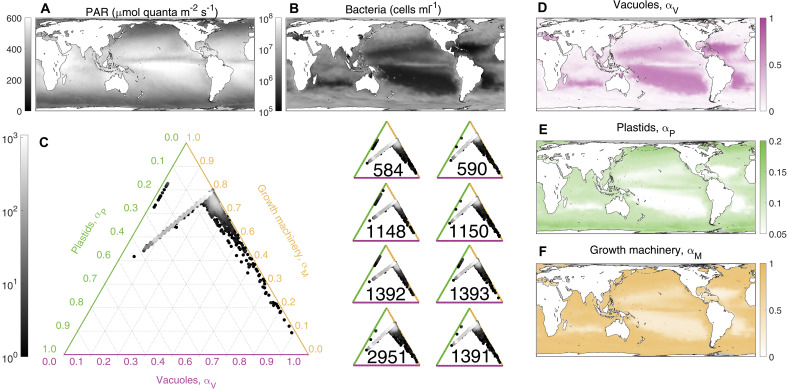
We combined the validated MOCHA model’s estimates of acquisition rates with observed and simulated resource landscapes from Aqua-MODIS satellite missions (30) and output by an ecosystem model (31) to project the optimal strategy of an Ochromonas-like mixotroph at a global scale. The MOCHA model’s projections represent an integration of a complex resource landscape with trade-offs in mixotroph investment strategies (Fig. 4). For example, in the oligotrophic gyres where light is abundant, mixotrophs nonetheless invest substantially (and sometimes exclusively) in phagotrophy to acquire N from bacterial prey. Generally, more photosynthetic strategies are optimal where bacterial abundance is high, such as at higher latitudes and at the equatorial upwelling zone. Growth rates (which are proportional to ) tended to positively correlate with photosynthetic investment, while both and tended to trade off with phagotrophic investment () (Fig. 4). In other words, increasing bacterial abundance allows mixotrophs to reduce investments in phagotrophy and simultaneously increase investments in phototrophy and growth.
Fig. 4. Global distributions of mixotroph strategies.
Light (A) and bacteria (B) resource drivers of the model, interpolated from satellite observations and the output of the Darwin model, respectively. Ternary plots (C) show the global distribution of mixotroph strategies in investment space. Shading represents frequency across the global domain, with brighter points indicating a more widespread strategy. The larger ternary plot (left) shows the simulation assuming an average Ochromonas cell with the strategy for each of the individual Ochromonas strains given by the eight smaller ternary plots (right). Maps of optimal investments in digestive vacuoles [ (D)], plastids [ (E)], and growth machinery [ (F)] are given for a mixotroph with uptake, production, and assimilation traits modeled after an average Ochromonas cell. Note the different axes for the color bar range, chosen to highlight global variability in investment strategy. To generate the bacterial abundance, we assumed a uniform ratio of 10 fg C per bacterial cell.
In general, our projections indicate that Ochromonas-like mixotrophs invest predominantly in producing digestive vacuoles (Fig. 4C), but that strategies can vary substantially at a global scale. Although phagotrophic investments are high, grazing primarily functions to supply N, and most of the mixotroph carbon acquisition is done via photosynthesis (fig. S7); thus, Ochromonas-like mixotrophs truly “mix” two metabolic strategies to obtain two essential resources for growth. The patterns of this variation were broadly consistent across the eight Ochromonas strains for which we parameterized the model, indicating that global within-strain variability is likely to be larger than across-strain variability in this genus.
DISCUSSION
Mixotrophs are increasingly recognized as omnipresent and often substantial components of planktonic communities, where their combination of metabolic strategies allows them to persist when either food or light is limiting. Our modeling approach shows how the combination of phototrophy and phagotrophy can produce both synergies—in which nitrogen obtained via prey consumption supports photosynthesis—and trade-offs—in which investment in one metabolic strategy comes at the cost of maintaining machinery for the other. By fitting the model to empirical data obtained for several Ochromonas strains (27), we find that phagotrophy is the dominant investment strategy among Ochromonas-like mixotrophs across the ocean, used primarily to meet nutrient requirements. We hypothesize that understanding changes in bacterial abundance will be critical to predict mixotrophic metabolisms in a warmer ocean and how their responses might differ between oligotrophic and polar seas.
When mixotrophic (as opposed to strictly phototrophic or strictly phagotrophic) strategies are optimal, growth is “zero-waste,” meaning that mixotrophs are colimited by carbon and nitrogen and investment strategies are balanced to bring in stoichiometrically balanced amounts of carbon and nitrogen. In this way, the MOCHA optimal mixotroph parallels other optimally foraging organisms that must obtain two complementary resources (26, 32). By allowing a mixotroph to obtain carbon and nitrogen from two independent metabolic processes with different acquisition rates, and then synthesize the requisite metabolic machinery, the MOCHA model produces a cell that can demonstrate a wide range of phenotypes as it titrates the relative combination of these two forms of metabolism to match its stoichiometric demands. The model’s general predictions are consistent with studies of mixotroph phenotypic plasticity that show photoacclimation [e.g., reduction of photosynthetic investment at high light (13, 27)], inducible mixotrophy [e.g., investment in phagotrophy when nutrients are limiting (11)], and opportunistic feeding [e.g., up-regulation of bacterivory when prey are abundant (12)].
Our model predicts that, on a global scale, Ochromonas-like mixotrophs tend to invest primarily in phagotrophy, especially in the oligotrophic gyres where mixotrophs are already known to be key grazers (6). This is consistent with observations of robust grazing by Ochromonas species in laboratory experiments (10, 13, 29). In our simulation of the global distribution of mixotroph strategies, the abundance of bacteria was the dominant driver of mixotrophic strategies. However, this played out in a somewhat counterintuitive way: Wherever bacterial abundance was high, mixotroph phagotrophic investment was relatively low. This negative correlation arises through a combination of trade-offs and synergies: First, in our model parameterization, Ochromonas cells are obligate phagotrophs because they must obtain nitrogen through feeding. Second, the more abundant bacteria are, the more efficiently mixotrophic vacuoles can function to obtain this nitrogen. Thus, high rates of bacterivory can be supported by fewer vacuoles, freeing up resources for investment plastids (which have higher C acquisition efficiency) and growth machinery (essential for increasing growth rates) (Fig. 2). Therefore, high-bacteria environments reduce N-limitation, supporting relatively more investment in both plastids and growth machinery, which also allows the mixotrophs to grow more rapidly (Fig. 4F).
With its focus on obligately phagotrophic mixotrophs like Ochromonas, the MOCHA model adds to a growing body of literature describing the environmental circumstances under which mixotrophy is a viable metabolic strategy. Like other studies (16, 17), we model mixotrophs’ simultaneous investment in photosynthesis and phagotrophy to identify growth-maximizing allocation strategies. Our results support prior findings that mixotrophs benefit from synergies between phagotrophic nutrient uptake and phototrophic carbon fixation (16, 17), but do so without invoking constraints on respiratory demand (16) or allometric scaling (17). Unlike Berge et al. (16) and Chakraborty et al.(17), we do not model explicit allocation to nutrient uptake structures. However, because our empirical data indicate that Ochromonas do not need to take up inorganic nitrogen to support their growth, this choice does not affect our results. Thus, in contrast to Berge et al. (16), who modeled an obligately phototrophic mixotroph parameterized after Karlodinium dinoflagellates, our mixotrophs are obligate phagotrophs. Because we were able to parameterize and validate our model with experimental data, we were also able to assess implications for mixotroph metabolic strategies at a global ocean scale. Parameterizing the MOCHA model for other mixotroph types (e.g., that use inorganic nutrients or are obligately phototrophic) would shift the predicted spatial distribution of mixotroph strategies.
Although no large-scale data quantifying mixotroph investment strategies exist to compare directly with MOCHA predictions, there are some parallels with local case studies. For example, mixotrophs are known to be key bacterivores in the oligotrophic gyres (6), the same locations where our model predicts substantial phagotrophic investment. In such regions, prey nutrients may allow mixotrophs to sustain growth when inorganic nutrient supplies are depleted. Edwards (19) combined a metanalysis with a dynamic model to suggest that synergies between metabolic modes may explain mixotroph relative success in the oligotrophic gyres, as well as in coastal regions where the MOCHA model predicts rapid growth by mixotrophs (Fig. 4, yellow panel). These synergies may be important in overcoming trade-offs that mixotrophs experience relative to similarly sized organisms with single metabolic strategies (33). Still, growth maximization does not necessarily correspond to competitive dominance; thus, we caution that the MOCHA model should not be used to project mixotroph absolute (or relative) abundances. However, our approach to identifying growth-maximizing, zero-waste mixotroph allocation strategies could be integrated into a more complex community or ecosystem model [e.g., (4, 19, 34, 35)] to better predict mixotroph persistence alongside specialist trophic strategies.
Here, we have focused on Ochromonas because of its utility as a model organism and the availability of laboratory data with which to validate our model. However, Ochromonas is noteworthy for its heavy reliance on phagotrophy (in comparison to other, inducibly phagotrophic nanoplankton). Further, although Ochromonas lineages have been isolated from numerous marine and freshwater systems, it is unclear how numerically dominant these lineages are because they are not always identified in field studies surveying nanoflagellate diversity (21, 33, 36) or quantifying their activity (6, 37) [including through new isolation techniques, e.g., (38)]. Thus, the MOCHA model should be reparameterized (and its conclusions revisited) for other mixotroph lineages as the necessary experimental data become available.
Nevertheless, our findings have important ramifications given future climate scenarios. Theory and empirical observations have found that warming may drive mixotrophic metabolisms to be more heterotrophic (29, 39, 40). However, warming and shallower mixed layers are expected to decrease bacterial abundance across the ocean with the exception of polar regions (41). In the polar seas, higher light availability can boost primary production, which, in turn, would increase dissolved organic carbon fueling bacterial production (42). According to our model, metabolically plastic mixotrophs may adjust their investment in phagotrophy in response to changing bacterial abundances to meet the N demands of growth. Our model therefore leads to the hypothesis that, in the short term, mixotrophs in polar oceans may reduce phagotrophic investments and grow faster, but need to increase phagotrophic investments (at the expense of photosynthesis and growth) in regions of the ocean where bacterial abundances are expected to decline (e.g., the oligotrophic gyres). However, upper limits on rates of phagotrophy, feedbacks from mixotroph activity on bacterial and other resource availability, and other ecological factors will modulate these responses. Our modeling approach assumes nonequilibrium dynamics during which growth-maximizing strategies should be favored (24, 25); while the dynamic nature of ocean environments (which mix on multiple spatial and temporal scales) may well hold communities in a state of disequilibrium, future applications of this approach would need to consider acquisition-maximizing strategies as well. Nevertheless, our model highlights the importance of changes in bacterial abundance to mixotroph strategies in future oceans.
MATERIALS AND METHODS
General model formulation
The MOCHA model is a special case of a more general model describing the growth of an organism that produces types of structures to obtain distinct components necessary for growth. The model allows for synergies when structures contribute complementary vectors of components for organismal growth, as well as for trade-offs because components are, in turn, invested in the production of structures (and thus investment in one structure requires components that are no longer available for another structure type). Each structure type can take up (or produce) one of the components with a structure- and component-specific efficiency
| (1) |
Structures may also incur maintenance costs, such as via respiration. Costs may be accrued in any component currency at a structure-dependent rate
| (2) |
The -by- matrix accounts for the overall per-structure yields of each component type per unit of structural biomass in the organism. The entries of are
| (3) |
(where and ), and account for the net production (if ) or loss (if ) of the th component type by the th structure type.
If (of length ) is the vector of structure biomasses, then the overall flux of components into the organism is given by a vector of length
| (4) |
After components are obtained and maintenance costs are paid, the organism uses the surplus of components for growth. We assume that all structures have the same stoichiometry, with a per-biomass quota for each component (24, 25). Here, we define , a quotient that determines the amount of biomass that can be produced with one unit of a given resource. This quotient takes into account both the materials needed for biomass and growth efficiency. We assume that growth is limited by the least abundant component. Therefore
| (5) |
The excess production of any nonlimiting components cannot be stored and is immediately lost from the organism.
The organism allocates resources to grow its structures based on an allocation strategy , in which the allocation to each structure determines that structure’s growth rate
| (6) |
To satisfy mass balance, the allocation parameters sum to one
| (7) |
Thus, is the proportion of organismal growth capacity allocated to the th structure.
When growth is positive, organismal structures accumulate exponentially over time. Our model does not differentiate between enlargement of single cells (or a single multicellular organism) and reproduction (e.g., through cell division), except insofar as it specifies that per-structure uptake rates are constant. Thus, surface area and volume must increase proportionately. We find it most convenient to consider growth as representing increases in the structural biomass of a population of organisms of identical stoichiometry and cell size.
A three-structure model for constitutive mixotrophy
To model constitutive mixotrophs, we reduce the dimensionality of the general model to two elemental components—carbon and nitrogen —and three structures—chloroplasts , digestive vacuoles , and growth machinery . The mixotroph obtains and from three types of external resources: bacteria , light , and dissolved inorganic nitrogen . Vacuoles can produce both carbon and nitrogen through digestion of bacteria, and chloroplasts produce carbon through light-dependent photosynthesis. We assume that uptake of inorganic nutrients is also plastid dependent (but note that fitting our model to Ochromonas data suggests that inorganic nitrogen uptake is unnecessary to explain growth in our experiments, so this assumption has limited effects on our analysis).
To assemble these elements for growth, the mixotroph must also produce a third component, growth factors , using its growth machinery . Accounting for the respiration cost of each structure, the yield matrix is
| (8) |
Here, and represent net carbon and nitrogen gained from phagotrophy respectively, and incorporate both bacterial stoichiometry and assimilation efficiencies. Similarly, scales net gain from phototrophy, and scales net gain from inorganic nitrogen. The parameter is the rate of growth factor production per unit of growth machinery .
Note that we have assumed that respiration costs are identical for all three types of structures. Among strictly phototrophic and phagotrophic species, data suggest that the metabolic costs of chloroplasts are lower than those of digestive vacuoles (43, 44). However, these costs have not been quantified for mixotrophs. Absent this information, and because of the value of simplifying assumptions in making model parameterization more tractable (and avoiding overfitting), we have assumed that the metabolic costs associated with chloroplasts, digestive vacuoles, and growth machinery are identical.
The three-structure allocation vector is
| (9) |
where .
Finding optimal growth
Because we are interested in mixotroph optimal allocations, we restrict our analysis to cases of positive growth (). Noting that can never be set to 0 (because growth factors are required for growth), our model allows for three possible outcomes:
1. Strict phagotrophy: When yield from grazing on bacteria exceeds any possible yield from photosynthesis, mixotrophs should set . Thus , and the mixotroph optimizes over a two-dimensional domain. Environments that favor this strategy will have high prey availability and low light and/or inorganic nutrients.
2. Strict phototrophy: When yield from photosynthesis and inorganic nutrient uptake exceeds any possible yield from phagotrophy, mixotrophs should set . Thus, . Environments that favor this strategy will have low prey availability, high light, and high inorganic nutrients.
3. Mixotrophy: Depending on environmental conditions (e.g., resource availability) and organismal traits (e.g., uptake rates, conversion efficiencies, or stoichiometries), mixed investment strategies with can be optimal. These cases typically arise when cellular structures are specialized (e.g., chloroplasts are more effective at acquisition and vacuoles at acquisition), but can also occur if plastids and vacuoles are functionally identical. (Photosynthesis and phagotrophy are unlikely to be functionally identical in nature, so we avoid this case in our analyses.)
We consider all three cases, and mathematically derive their conditions, associated growth rates, and investment strategies in Supplementary Methods. Our analysis reveals that a growth-maximizing strategy is also a waste-minimizing one. Recall that excess (nonlimiting) components are lost because storage is not accounted for in the model. Exact solutions for investments can be derived as a function of acquisition parameters. For an optimally growing mixotroph, maximum growth rate occurs when the mixotroph is balancing investments in C acquisition, N acquisition, and growth factor production such that all three components are equally available to support growth (mathematically: ). For strict phagotrophs or phototrophs, either or is limiting (Fig. 1, B and C).
Finally, we considered the growth-maximizing strategies of a mixotroph in a chemostat-like environment, in which bacterial and inorganic nutrient resources are drawn down by mixotroph growth. Full details of this model are available in Supplementary Methods.
Fitting the model to empirical data
We fit our data to previously published data collected in our laboratory [described in more detail in the Supplemental Materials; for full experimental details, see (27)]. Briefly, we grew eight strains of Ochromonas from the National Center for Marine Algae and Microbiota culture collection in a gradient of light levels (from 0 to 150 μmol quanta m−2 s−1) to stimulate variation in investment in photosynthesis and phagotrophy. From experimental cultures, we obtained measurements of investment in photosynthesis (chlorophyll per carbon biomass) and phagotrophy (bacterial attack rate per carbon), resource flux rates (photosynthetic and grazing rates), and cell growth rates [as described in (27)].
We fit the MOCHA model to these data by maximizing a likelihood function [detailed in (45)]. To do so, we defined relations to convert from experimental data units into the units used by the model. We used the chlorophyll-to-carbon ratio and the photosynthesis rate as proxies for the investment in plastids, , and the attack rate and grazing rate as proxies for investment in vacuoles, . We further use the observed growth rate as a direct proxy for the simulated growth rate under the assumption of growth optimizing investment strategies by the mixotrophs. Details on the model fitting are given in the Supplementary Materials.
We performed fits for each of the eight Ochromonas strains independently to understand strain-by-strain variation within the mixotroph genus (Fig. 3 and fig. S5). We also fit the model to all empirical data simultaneously, to obtain a global mean fit representative of an “average” Ochromonas cell.
Global ocean projections
Using eqs. S30 to S32, we estimated the growth-maximizing mixotroph strategy on a global scale, using light and bacteria abundance as inputs. Light values were obtained from the NASA Aqua-MODIS (Moderate Resolution Imaging Spectroradiometer) ocean color satellite mission (30). These data represent annually averaged measurements of photosynthetically active radiation (PAR) for the year 2021 at a 4 km resolution. Heterotrophic bacterial abundances were obtained from simulations of a coupled physical-biogeochemical-ecosystem model with specific setup following (31) including modifications described in (46). The model data simulate heterotrophic bacterial biomass across a 1° grid with 23 depth bins. We converted biomass to abundance by assuming a fixed bacterial C content of 10 fg per cell. We chose this order of magnitude estimate based on estimates for pelagic bacterial cells [e.g., SAR11; (47, 48)] because the Darwin model is parameterized for pelagic environments and does not resolve near-shore processes, but note that this may result in an overestimate of bacterial abundance (in cells per milliliter) in more coastal regions. The growth-maximizing strategy was calculated using bacterial abundances and PAR values at the sea surface, interpolated to the same 1° grid used by the Darwin model. Global projections were generated using parameters estimated from the empirical data for each Ochromonas strain individually and for all strains combined (Fig. 3).
Acknowledgments
We acknowledge helpful feedback from C. Klausmeier and members of the Moeller Laboratory at UCSB.
Funding: This work was supported by National Science Foundation grants OCE-1851194 and OCE-2237017 (H.V.M.), the Simons Foundation Early Career Fellowship in Marine Microbial Ecology and Evolution (award 689265, H.V.M.), and the Simons Foundation Postdoctoral Fellowship in Marine Microbial Ecology (award 990798, K.M.A.; award 877215, S.G.L.).
Author contributions: All authors contributed equally to the conceptualization, model construction, analysis, writing, and editing of this manuscript. Specifically, according to the CRediT scheme: H.V.M. contributed to writing—original draft, conceptualization, investigation, writing—review and editing, methodology, resources, funding acquisition, data curation, validation, supervision, formal analysis, software, project administration, and visualization. K.M.A. contributed to writing—original draft, conceptualization, writing—review and editing, methodology, formal analysis, software, and visualization. S.G.L. contributed to conceptualization, writing—review and editing, methodology, formal analysis, software, and visualization. F.P. contributed to writing—original draft, conceptualization, investigation, writing—review and editing, methodology, resources, data curation, validation, formal analysis, software, and visualization.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data and code needed to evaluate the conclusions in the paper and reproduce results are present in the paper and/or the Supplementary Materials and at https://zenodo.org/doi/10.5281/zenodo.13826163.
Supplementary Materials
This PDF file includes:
Supplementary Methods
Figs. S1 to S7
Tables S1 to S3
References
REFERENCES AND NOTES
- 1.Worden A. Z., Follows M. J., Giovannoni S. J., Wilken S., Zimmerman A. E., Keeling P. J., Rethinking the marine carbon cycle: Factoring in the multifarious lifestyles of microbes. Science 347, 1257594 (2015). [DOI] [PubMed] [Google Scholar]
- 2.Selosse M.-A., Charpin M., Not F., Mixotrophy everywhere on land and in water: The grand écart hypothesis. Ecol. Lett. 20, 246–263 (2017). [DOI] [PubMed] [Google Scholar]
- 3.Tittel J., Bissinger V., Zippel B., Gaedke U., Bell E., Lorke A., Kamjunke N., Mixotrophs combine resource use to outcompete specialists: Implications for aquatic food webs. Proc. Natl. Acad. Sci. U.S.A. 100, 12776–12781 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Crane K. W., Grover J. P., Coexistence of mixotrophs, autotrophs, and heterotrophs in planktonic microbial communities. J. Theor. Biol. 262, 517–527 (2010). [DOI] [PubMed] [Google Scholar]
- 5.Mitra A., Flynn K. J., Burkholder J. M., Berge T., Calbet A., Raven J. A., Granéli E., Glibert P. M., Hansen P. J., Stoecker D. K., Thingstad F., Tillmann U., Våge S., Wilken S., Zubkov M. V., The role of mixotrophic protists in the biological carbon pump. Biogeosciences 11, 995–1005 (2014). [Google Scholar]
- 6.Hartmann M., Grob C., Tarran G. A., Martin A. P., Burkill P. H., Scanlan D. J., Zubkov M. V., Mixotrophic basis of Atlantic oligotrophic ecosystems. Proc. Natl. Acad. Sci. U.S.A. 109, 5756–5760 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ward B. A., Follows M. J., Marine mixotrophy increases trophic transfer efficiency, mean organism size, and vertical carbon flux. Proc. Natl. Acad. Sci. U.S.A. 113, 2958–2963 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stoecker D. K., Hansen P. J., Caron D. A., Mitra A., Mixotrophy in the marine plankton. Ann. Rev. Mar. Sci. 9, 311–335 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Mitra A., Flynn K. J., Tillmann U., Raven J. A., Caron D., Stoecker D. K., Not F., Hansen P. J., Hallegraeff G., Sanders R., Wilken S., Manus G. M., Johnson M., Pitta P., Våge S., Berge T., Calbet A., Thingstad F., Jeong H. J., Burkholder J. A., Glibert P. M., Granéli E., Lundgren V., Defining planktonic protist functional groups on mechanisms for energy and nutrient acquisition: Incorporation of diverse mixotrophic strategies. Protist 167, 106–120 (2016). [DOI] [PubMed] [Google Scholar]
- 10.Lie A. A., Liu Z., Terrado R., Tatters A. O., Heidelberg K. B., Caron D. A., A tale of two mixotrophic chrysophytes: Insights into the metabolisms of two Ochromonas species (chrysophyceae) through a comparison of gene expression. PLOS ONE 13, e0192439 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Johnson M. D., Inducible mixotrophy in the dinoflagellate Prorocentrum minimum. J. Eukaryot. Microbiol. 62, 431–443 (2015). [DOI] [PubMed] [Google Scholar]
- 12.Sanders R. W., Porter K. G., Caron D. A., Relationship between phototrophy and phagotrophy in the mixotrophic chrysophyte Poterioochromonas malhamensis. Microb. Ecol. 19, 97–109 (1990). [DOI] [PubMed] [Google Scholar]
- 13.Wilken S., Choi C. J., Worden A. Z., Contrasting mixotrophic lifestyles reveal different ecological niches in two closely related marine protists. J. Phycol. 56, 52–67 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leles S. G., Bruggeman J., Polimene L., Blackford J., Flynn K. J., Mitra A., Differences in physiology explain succession of mixoplankton functional types and affect carbon fluxes in temperate seas. Prog. Oceanogr. 190, 102481 (2021). [Google Scholar]
- 15.Andersen K. H., Aksnes D. L., Berge T., Fiksen Ø., Visser A., Modelling emergent trophic strategies in plankton. J. Plankton Res. 37, 862–868 (2015). [Google Scholar]
- 16.Berge T., Chakraborty S., Hansen P. J., Andersen K. H., Modeling succession of key resource-harvesting traits of mixotrophic plankton. ISME J. 11, 212–223 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chakraborty S., Nielsen L. T., Andersen K. H., Trophic strategies of unicellular plankton. Am. Nat. 189, E77–E90 (2017). [DOI] [PubMed] [Google Scholar]
- 18.Calbet A., Bertos M., Fuentes-Grunewald C., Alacid E., Figueroa R., Renom B., Garcés E., Intraspecific variability in Karlodinium veneficum: Growth rates, mixotrophy, and lipid composition. Harmful Algae 10, 654–667 (2011). [Google Scholar]
- 19.Edwards K. F., Mixotrophy in nanoflagellates across environmental gradients in the ocean. Proc. Natl. Acad. Sci. U.S.A. 116, 6211–6220 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leles S. G., Mitra A., Flynn K. J., Stoecker D. K., Hansen P. J., Calbet A., Mc Manus G. B., Sanders R. W., Caron D. A., Not F., Hallegraeff G. M., Pitta P., Raven J. A., Johnson M. D., Glibert P. M., Våge S., Oceanic protists with different forms of acquired phototrophy display contrasting biogeographies and abundance. Proc. Biol. Sci. 284, 20170664 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Faure E., Not F., Benoiston A.-S., Labadie K., Bittner L., Ayata S.-D., Mixotrophic protists display contrasted biogeographies in the global ocean. ISME J. 13, 1072–1083 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wilken S., Yung C. C. M., Hamilton M., Hoadley K., Nzongo J., Eckmann C., Corrochano-Luque M., Poirier C., Worden A. Z., The need to account for cell biology in characterizing predatory mixotrophs in aquatic environments. Philos. Trans. R. Soc. B 374, 20190090 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Millette N. C., Gast R. J., Luo J. Y., Moeller H. V., Stamieszkin K., Andersen K. H., Brownlee E. F., Cohen N. R., Duhamel S., Dutkiewicz S., Glibert P. M., Johnson M. D., Leles S. G., Maloney A. E., Mcmanus G. B., Poulton N., Princiotta S. D., Sanders R. W., Wilken S., Mixoplankton and mixotrophy: Future research priorities. J. Plankton Res. 45, 576–596 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Klausmeier C. A., Litchman E., Daufresne T., Levin S. A., Optimal nitrogen-to-phosphorus stoichiometry of phytoplankton. Nature 429, 171–174 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Klausmeier C. A., Litchman E., Levin S. A., Phytoplankton growth and stoichiometry under multiple nutrient limitation. Limnol. Oceanogr. 49, 1463–1470 (2004). [Google Scholar]
- 26.D. Tilman, Resource Competition and Community Structure (Princeton Univ. Press, 1982), vol. 296. [PubMed] [Google Scholar]
- 27.Barbaglia G. S., Paight C., Honig M., Johnson M. D., Marczak R., Lepori-Bui M., Moeller H. V., Environment-dependent metabolic investments in the mixotrophic chrysophyte Ochromonas. J. Phycol. 60, 170–184 (2024). [DOI] [PubMed] [Google Scholar]
- 28.R. R. Guillard, in Culture of Marine Invertebrate Animals: Proceedings—1st Conference on Culture of Marine Invertebrate Animals Greenport (Springer, 1975), pp. 29–60. [Google Scholar]
- 29.Lepori-Bui M., Paight C., Eberhard E., Mertz C. M., Moeller H. V., Evidence for evolutionary adaptation of mixotrophic nanoflagellates to warmer temperatures. Glob. Chang. Biol. 28, 7094–7107 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.NASA Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group, Moderate-resolution Imaging Spectroradiometer (MODIS) Aqua Level-3 Mapped Photosynthetically Available Radiation Data, version R2022.0, NASA Ocean Biology Distributed Active Archive Center, 2022.
- 31.Follett C. L., Follett C. L., Dutkiewicz S., Ribalet F., Zakem E., Caron D., Armbrust E. V., Follows M. J., Trophic interactions with heterotrophic bacteria limit the range of Prochlorococcus. Proc. Natl. Acad. Sci. U.S.A. 119, e2110993118 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Abrams P., The functional responses of adaptive consumers of two resources. Theor. Popul. Biol. 32, 262–288 (1987). [Google Scholar]
- 33.Edwards K. F., Li Q., McBeain K. A., Schvarcz C. R., Steward G. F., Trophic strategies explain the ocean niches of small eukaryotic phytoplankton. Proc. R. Soc. B 290, 20222021 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Våge S., Castellani M., Giske J., Thingstad T. F., Successful strategies in size structured mixotrophic food webs. Aquat. Ecol. 47, 329–347 (2013). [Google Scholar]
- 35.Ward B. A., Dutkiewicz S., Barton A. D., Follows M. J., Biophysical aspects of resource acquisition and competition in algal mixotrophs. Am. Nat. 178, 98–112 (2011). [DOI] [PubMed] [Google Scholar]
- 36.Choi C. J., Jimenez V., Needham D. M., Poirier C., Bachy C., Alexander H., Wilken S., Chavez F. P., Sudek S., Giovannoni S. J., Worden A. Z., Seasonal and geographical transitions in eukaryotic phytoplankton community structure in the Atlantic and Pacific oceans. Front. Microbiol. 11, 542372 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Frias-Lopez J., Thompson A., Waldbauer J., Chisholm S. W., Use of stable isotope-labelled cells to identify active grazers of picocyanobacteria in ocean surface waters. Environ. Microbiol. 11, 512–525 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li Q., Edwards K. F., Schvarcz C. R., Selph K. E., Steward G. F., Plasticity in the grazing ecophysiology of Florenciella (Dichtyochophyceae), a mixotrophic nanoflagellate that consumes Prochlorococcus and other bacteria. Limnol. Oceanogr. 66, 47–60 (2021). [Google Scholar]
- 39.Wilken S., Huisman J., Naus-Wiezer S., Van Donk E., Mixotrophic organisms become more heterotrophic with rising temperature. Ecol. Lett. 16, 225–233 (2013). [DOI] [PubMed] [Google Scholar]
- 40.Gonzalez L. M., Proulx S. R., Moeller H. V., Modeling the metabolic evolution of mixotrophic phytoplankton in response to rising ocean surface temperatures. BMC Ecol. Evol. 22, 136 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kim H. H., Laufkötter C., Lovato T., Doney S. C., Ducklow H. W., Projected 21st-century changes in marine heterotrophic bacteria under climate change. Front. Microbiol. 14, 1049579 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kirchman D. L., Morán X. A. G., Ducklow H., Microbial growth in the polar oceans—Role of temperature and potential impact of climate change. Nat. Rev. Microbiol. 7, 451–459 (2009). [DOI] [PubMed] [Google Scholar]
- 43.Straile D., Gross growth efficiencies of protozoan and metazoan zooplankton and their dependence on food concentration, predator-prey weight ratio, and taxonomic group. Limnol. Oceanogr. 42, 1375–1385 (1997). [Google Scholar]
- 44.P. G. Falkowski, J. A. Raven, Aquatic Photosynthesis (Princeton Univ. Press, 2013). [Google Scholar]
- 45.T. Jager, R. Ashauer, Modelling survival under chemical stress: A comprehensive guide to the GUTS framework (Toxicodynamics Ltd., 2018).
- 46.Archibald K. M., Dutkiewicz S., Laufkötter C., Moeller H. V., Thermal responses in global marine planktonic food webs are mediated by temperature effects on metabolism. J. Geophys. Res. Oceans 127, e2022JC018932 (2022). [Google Scholar]
- 47.Cermak N., Becker J. W., Knudsen S. M., Chisholm S. W., Manalis S. R., Polz M. F., Direct single-cell biomass estimates for marine bacteria via Archimedes’ principle. ISME J. 11, 825–828 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.White A. E., Giovannoni S. J., Zhao Y., Vergin K., Carlson C. A., Elemental content and stoichiometry of sar11 chemoheterotrophic marine bacteria. Limnol. Oceanogr. Lett. 4, 44–51 (2019). [Google Scholar]
- 49.Sonneborn L. M., Van Vleck F. S., The bang-bang principle for linear control systems. J. Soc. Ind. Appl. Math. Ser. A Control 2, 151–159 (1964). [Google Scholar]
- 50.Holling C. S., Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398 (1959). [Google Scholar]
- 51.Auer M. T., Forrer B., Development and parameterization of a kinetic framework for modeling light-and phosphorus-limited phytoplankton growth in cannonsville reservoir. Lake Reserv. Manag. 14, 290–300 (1998). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Methods
Figs. S1 to S7
Tables S1 to S3
References