DNA tensiometer reveals catch-bond detachment kinetics of kinesin-1, -2 and -3

Abstract

Bidirectional cargo transport by kinesin and dynein is essential for cell viability and defects are linked to neurodegenerative diseases. The competition between motors is described as a tug-of-war, and computational modeling suggests that the load-dependent off-rate is the strongest determinant of which motor ‘wins’. Optical tweezer experiments find that the load-dependent detachment sensitivity of transport kinesins is kinesin-3 > kinesin-2 > kinesin-1. However, when kinesin-dynein pairs were analyzed in vitro, all three kinesin families competed nearly equally well against dynein. One possible explanation is that vertical forces inherent to the large trapping beads enhance motor detachment. Because intracellular cargo range from ~30 nm to > 1000 nm, vertical forces in vivo are expected to range from near zero to larger than the horizontal forces of transport. To investigate detachment rates against loads oriented parallel to the microtubule, we created a DNA tensiometer comprising a DNA entropic spring that is attached to the microtubule on one end and a kinesin motor on the other. Surprisingly, kinesin dissociation rates at stall were slower than detachment rates during unloaded runs, a property termed a catch-bond. A plausible mechanism, supported by stochastic simulations, is that the strong-to-weak transition in the kinesin cycle is slowed with load. We also find evidence that the long run lengths of kinesin-3 (KIF1A) result from the concatenation of multiple short runs connected by diffusive episodes. The finding that kinesins form catch-bonds under horizontal loads necessitates a reevaluation of the role of cargo geometry in kinesin-dynein bidirectional transport.

Introduction

Bidirectional cargo transport by kinesin and dynein is essential for cell viability, and disruptions in transport are linked to neurological diseases including hereditary spastic paraplegia, microencephaly and amyotrophic lateral sclerosis (Bilsland et al., 2010; Brenner et al., 2018; Caballero Oteyza et al., 2014; Makrythanasis et al., 2018; Millecamps & Julien, 2013; Moawia et al., 2017; Nicolas et al., 2018; Pant et al., 2022; Reid et al., 2002; Zhou et al., 2024). It has been established that kinesin and dynein, which move in opposite directions along microtubules, are often bound simultaneously to the same cargo (Encalada et al., 2011; Hendricks et al., 2010; Soppina et al., 2009; Welte, 2004). However, the mechanisms by which the motors compete and coordinate their activities to achieve proper directional transport are still poorly understood.

The prevailing model for bidirectional transport along microtubules is the ‘tug-of-war’ model, which posits that when kinesins and dyneins are both bound to the same cargo, the cargo will be transported in the direction of the strongest motor team (Belyy et al., 2016; Gross, 2004; Hancock, 2014; Hendricks et al., 2010; Muller et al., 2008). Evidence supporting this model includes the elongation of intracellular cargoes just before directional switching (Soppina et al., 2009), and computational modeling that predicts back-and-forth cargo movement similar to the vesicle dynamics observed in cells (Hendricks et al., 2010; Muller et al., 2008). Paradoxically, other studies have shown that knockdown of one motor results in a reduction of transport in both directions, a result not explained by the tug-of-war model (Gross et al., 2002; Hancock, 2014; Kunwar et al., 2011; Martin et al., 1999), and indicating there may be additional regulatory proteins or coordination between the motors either directly or via adaptor proteins.

Intuitively, a motor’s effectiveness in a tug-of-war rests on its ability to remain bound to its microtubule track. Consistent with this, computational simulations have found that the load-dependent off-rate of a motor is the most important determinant of whether it wins or loses in a tug-of-war (Ma et al., 2023; Ohashi et al., 2019). Simply put, motors that remain attached under load beat motors that readily detach under load. Single-bead optical tweezers have found that the transport motors kinesin-1, -2, and -3 all act as slip bonds, defined as load accelerating their detachment rate. Their propensity to detach under load was determined to be: kinesin-3 > kinesin-2 > kinesin-1 (Andreasson, Milic, et al., 2015; Andreasson, Shastry, et al., 2015; Budaitis et al., 2021; Pyrpassopoulos et al., 2023; Tomishige et al., 2002). Based on this slip-bond behavior, it was surprising that when kinesin-1 was linked to dynein, the complex moved at near-zero speeds for up to tens of seconds, much longer than predicted based on previously measured kinesin-1 off-rates (Andreasson, Milic, et al., 2015; Feng et al., 2020; Yildiz et al., 2008). Moreover, a subsequent study found that kinesin-1, -2, and -3 all fared equally well against dynein, contrary to predictions from single-bead optical tweezer measurements that found differing load-dependent detachment rates (Gicking et al., 2022).

A pair of recent theoretical and experimental studies suggested a potential solution to this paradox, namely that the ~micron scale beads used for optical trapping result in significant forces oriented perpendicular to the microtubule as the motor pulls against the force of the trap (Howard & Hancock, 2020; Pyrpassopoulos et al., 2023; Pyrpassopoulos et al., 2020). In support of this, when a three-bead geometry was used (in which the motor is raised up on a pedestal bead and the microtubule was held by beads attached to either end of the microtubule) motors remained bound longer than in the single-bead geometry (Pyrpassopoulos et al., 2023; Pyrpassopoulos et al., 2020). In cells, kinesin and dynein transport cargo that range from tens of nm in diameter (like vesicles), where motor forces are expected to be aligned parallel to the microtubule, up to several microns (like mitochondria and nuclei), where vertical forces are expected to be much larger. Thus, understanding the influence of vertical and horizontal forces on transport motors is important for understanding the mechanics underlying bidirectional transport in cells.

The goal of the present study was to characterize the load-dependent detachment kinetics of kinesin-1, -2 and -3 motors in a geometry that eliminates vertical forces inherent in traditional optical trapping studies. We achieved this by using double stranded DNA (dsDNA), which acts as an entropic spring to resist the pN-level forces generated by the motors (Iwaki et al., 2016; Marko & Siggia, 1995). In this DNA tensiometer, one end of a micron-long (3 kb) strand of dsDNA is bound to the microtubule and the other end to a quantum dot (Qdot)-labeled motor. Motors stretch the DNA spring until reaching stall and remain there until slipping back or detaching from the microtubule. We found that kinesin-1, -2, and -3 all remained at stall for multiple seconds before releasing, which is substantially longer than the unloaded run times for kinesin-1 and -2. This behavior of slower off-rates under load is defined as a ‘catch bond’ and contrasts with the normal ‘slip bond’ behavior load-accelerated off-rates seen previously for kinesin (Thomas et al., 2008).

Results

Constructing a motor-bound DNA tensiometer

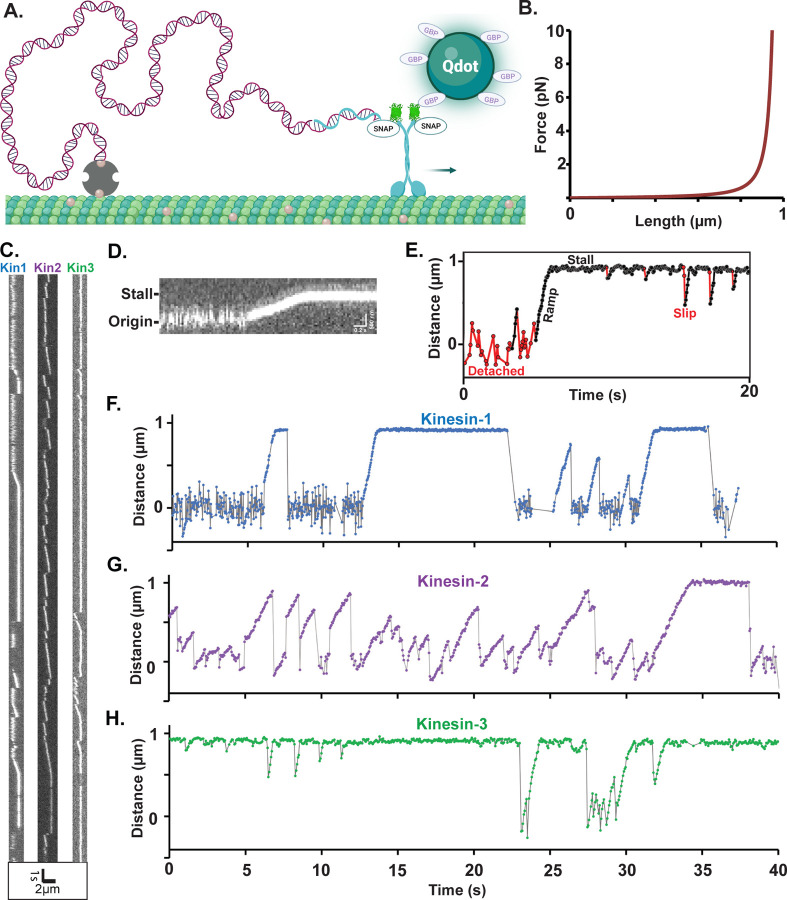
To study motor performance against a resistive load oriented parallel to the microtubule, we constructed a DNA tensiometer consisting of a ~ 1 μm strand of dsDNA attached to the microtubule on one end and a motor on the other (Figure 1A). We used TIRF microscopy to visualize the motor moving against the entropic elasticity of the DNA spring. Due to the nonlinear elasticity of the DNA (Figure 1B) (Iwaki et al., 2016; Marko & Siggia, 1995), the motor moves under minimal load until it stretches the DNA to near its contour length, at which point it stalls (Figure 1C–E).

Figure 1. Experimental Design and Raw Data from Motor-DNA Tensiometers.

(A) Schematic of a motor-DNA tensiometer, consisting of a dsDNA (burgundy) connected on one end to a kinesin motor through a complimentary oligo (blue), and on the other end to the MT using biotin-avidin (tan and gray, respectively). A Qdot functionalized with GFP binding protein nanobodies is attached to the motor’s GFP tag and used to track motor position. (Not to scale; motor and Qdot are both ~20 nm and DNA is ~1 micron) (B) Predicted force extension curve for a worm-like chain 3009 bp dsDNA based on a 50 nm persistence length. (C) Representative kymographs of motor-DNA tensiometers for kinesins-1, -2 and -3. (D) Enlarged kymograph showing diffusion around the origin, ramp, and stall. (E) Example distance vs. time trace (kinesin-3), highlighting detached durations (red), ramps and stalls (black) where the motor has pulled the DNA taut, and transient slips during stall (red). (F-H) Representative distance vs. time plots for kinesin-1 (F), kinesin-2 (G) and kinesin-3 (H), corresponding to the kymographs in (C). Further examples are shown in Figure S3.

Our DNA-motor tensiometer consists of a 3,009 bp (999 nm contour length) dsDNA ‘spring’ that was synthesized by PCR using a biotinylated forward primer for attachment to the microtubule and a reverse primer containing a 3’ overhang for motor attachment (details in Methods). We investigated members of the three dominant families of kinesin transport motors, kinesin-1 (Drosophila melanogaster KHC), kinesin-2 (Mus musculus Kif3A), and kinesin-3 (Rattus norvegicus Kif1A) used in our previous kinesin-dynein study (Gicking et al., 2022). In each case, the motor and neck linker domains were fused to the stable neck-coil domain (residues 345–406) of kinesin-1, followed by EGFP, a SNAP tag, and His₆ tag, as described previously (Gicking et al., 2022). Motors were conjugated to an oligonucleotide complimentary to the 3’ overhang of the dsDNA spring via their C-terminal SNAP tag. The DNA tensiometer complex (Figure 1A) was created in a flow cell by sequentially flowing in biotinylated microtubules, neutravidin, biotinylated dsDNA, and Qdot-functionalized motors containing the complimentary oligo (described fully in Methods).

The resulting dsDNA tensiometer kymographs (Figure 1C) show a reproducible behavior of moving, stalling, and returning to origin multiple times, which contrasts with the singular attachment, unidirectional movement and detachment of motors not bound by DNA (Figure S1). Because motors are tethered to the microtubule by the flexible DNA, large fluctuations around the origin are observed when the motor is detached (Figure 1C–H). Consistent with these fluctuations, initial attachment points were variable and roughly normally distributed with a standard deviation of 145 nm (Figure S2). Upon attachment to the microtubule, the motor walks at a steady velocity, consistent with the expected nonlinear stiffness of the dsDNA tether (Figure 1B), until it either detaches and returns to origin or reaches a stall state. Stalls end in three possible ways: 1) the motor slips a short distance (defined as a minimum distance of 60 nm from the stall point to greater than 400 nm from the origin) and immediately begins moving again; 2) the motor returns to the baseline and rapidly (within 100 ms) begins a new ramp; or 3) the motor returns to the baseline and fluctuates around the origin (generally for a few seconds), before binding and initiating a new ramp (Figure 1E). These three classes of features were seen in all three motors (Figure 1F–H and Figure S3).

Kinesin-1 and -2 act as catch-bonds at stall

The first question we addressed was: what are the detachment rates of kinesin-1, -2 and -3 motors at stall? During a tug-of-war with dynein, kinesins are expected to be at or near their stall force, and the ability of the motor to resist detachment is the major determinant of whether kinesin or dynein prevails in the tug-of-war (Ma et al., 2023; Ohashi et al., 2019). The load-dependence of protein-protein interactions can be described by one of the following mechanisms: a slip-bond (Bell, 1978), defined as a faster off-rate under load; an ideal bond, defined as an off-rate that is independent of load; or a catch-bond, in which the off-rate is slower under load (Thomas et al., 2008). Single-bead optical trapping studies consistently find slip-bond characteristics for kinesin-1, 2 and 3 (Andreasson, Milic, et al., 2015; Andreasson, Shastry, et al., 2015; Budaitis et al., 2021; Rao & Gennerich, 2022), whereas dynein off-rates have been described as a slip-bond or catch-bond (Ezber et al., 2020; Kunwar et al., 2011; Rai et al., 2013; Sanghavi et al., 2021; Soppina et al., 2009).

We define stall duration as the time that a motor stalls against the hindering load of fully extended DNA, without further detectable stepping, before detaching (Figure 1E). We don’t directly measure the stall force, however, based on the predicted force-extension curve of the dsDNA (Figure 1B), the displacements are consistent with the 4–6 pN stall forces for kinesin-1, -2 and -3 measured using optical traps (Blehm et al., 2013; Budaitis et al., 2021; Kojima et al., 1997; Schroeder et al., 2012; Svoboda & Block, 1994; Visscher et al., 1999). Stall durations were compared to the unloaded single-motor run durations determined from TIRF kymograph analysis (Figure S1).

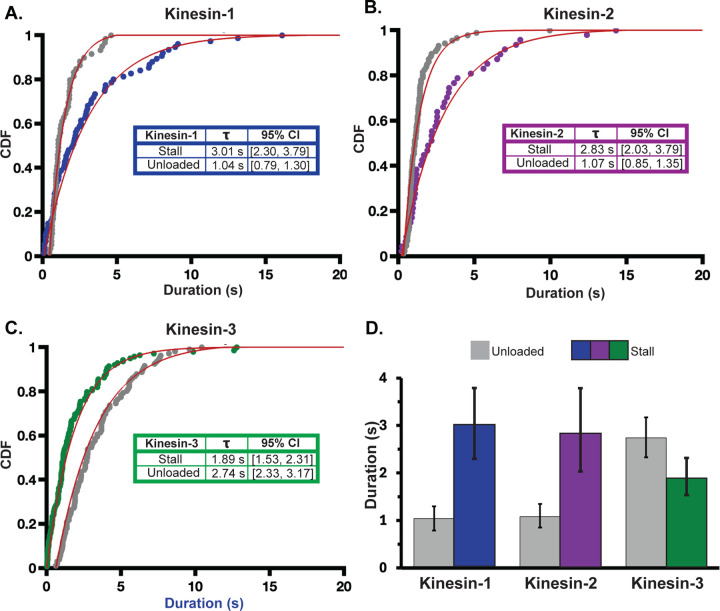
To compare unloaded to stall off-rates, cumulative distributions of the run and stall durations were plotted for each motor and fit with a single exponential function (Figure 2). The kinesin-1 tensiometer stall duration time constant was 3.01 s, with 95% confidence intervals (CI) of 2.30 to 3.79 s determined via bootstrapping in MEMLET with 1000 iterations) (Woody et al., 2016) (N= 78 stalls). In contrast, the kinesin-1 unloaded run duration time constant, measured by a traditional TIRF assay, was 1.04 s, (95% CI of 0.79 to 1.30 s; N= 59) (Figure 2A). Stall durations longer than unloaded run durations indicate that load slows the off-rate, the definition of a catch-bond (Thomas et al., 2008). Similarly, the kinesin-2 tensiometer stall duration time constant of 2.83 s (95% CI of 2.03 to 3.79 s; N= 50) was longer than its unloaded run duration of 1.07 s (95% CI of 0.85 to 1.35 s; N= 87) also indicating a catch-bond. Conversely, the kinesin-3 tensiometer stall duration time constant of 1.89 s (95% CI of 1.53 to 2.31 s; N= 140) was shorter than its unloaded run duration of 2.74 s (95% CI of 2.33 to 3.17 s; N= 106), indicating a slip-bond characteristic by this definition.

Figure 2. Tensiometer Stall Durations Indicate Catch-bond Behavior for Kinesin-1 and -2.

Tensiometer stall durations are plotted for A) kinesin-1 (blue), (B) kinesin-2 (purple), and (C) kinesin-3 (green). Unloaded run durations for each motor are plotted in gray. Distributions were fit with a single exponential function using MEMLET to generate time constants, representing the mean durations, and 95% confidence intervals (CI), given in inset tables. (D) Bar plot indicating the difference between unloaded and stall times for the three motors with error bars indicating 95% CI. Stall durations >20s were excluded from the fit (there were three >20 s stalls for kinesin-1 and two >20 s stalls for kinesin-2). A bi-exponential fit of all data is shown in Figure S6.

In this analysis, we defined transient slips as short as 60 nm as terminations of stall plateaus (Figure 1E). This is a stringent limit because motors rapidly reestablished stall after these slips, and in the context of a tug-of-war, these motors functionally remain attached to the microtubule. Thus, we reanalyzed the stall durations where slips are not defined as terminations of stall plateaus and found that all three motors had substantially longer stall durations (Figure S4). In particular, the kinesin-3 stall duration in this analysis was longer than its unloaded run duration, defining it as a catch-bond by this measure. Finally, to rule out the possibility that the long stall durations were caused by more than one motor binding to the Qdot (despite the 1:10 motor: Qdot mixing ratio), we removed Qdots from the assay entirely and instead incorporated Cy5-dCTP into the dsDNA to visualize tensiometer extensions. This assay produced similarly long stall durations (Figure S5), confirming that the long stalls were caused by single motors.

Kinesin-3 detaches readily under low load

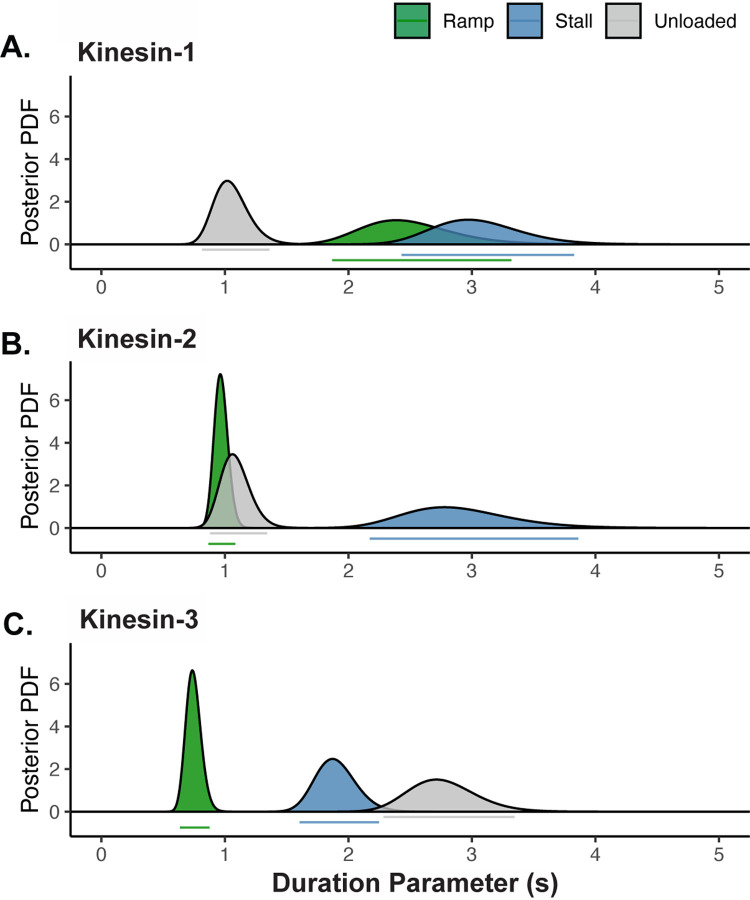
To determine whether sub-stall hindering loads affect motor detachment rates, we compared tensiometer ramp durations to the tensiometer stall and unloaded run durations (Figure 3). Although the dsDNA force extension curve (Figure 1B) predicts negligible loads until the DNA is close to fully extended, there are still non-zero loads imposed during the ramp phase that may affect motor detachment. We defined ramp durations as the time the motor spends walking against the DNA spring, where ‘failed’ ramps are terminated by detachment and ‘successful’ ramps are terminated by reaching stall. To estimate the true detachment rate during the ramp phase in a way that takes into account both the successful and failed ramps, we used a Markov process model, coupled with Bayesian inference methods (detailed in Supplementary Material). In this model, each increment of time is considered to be an independent opportunity to detach while assuming a constant detachment rate. Using the notation $\tau$ for the duration parameter, the probability of staying attached to the microtubule through a segment of duration Δ is $e^{-\Delta /\tau }$. Using this method, ramp duration parameters, $\tau$, were calculated for each motor, along with 95% credible regions. Finally, to allow for proper comparison, we performed a similar analysis to obtain the stall and unloaded duration parameters along with their 95% credible regions (Figure 3). The stall and unloaded durations were similar to estimates from curve fitting in Figure 2 (Table S1).

Figure 3. During Ramps, Kinesin-3 Detaches More Readily Than Under Zero Load.

Unloaded, ramp, and stall duration parameters were estimated using a Markov process model, coupled with Bayesian inference methods. Curves show the posterior probability distributions of the duration parameters for (A) kinesin-1, (B) kinesin-2 and (C) kinesin-3. Bars below each peak indicate the 95% credible regions for the ramp (green), unloaded (gray) and stall (blue) duration parameters. Notably, the estimated ramp durations are larger, the same, and smaller than the unloaded run durations for kinesin-1, -2, and -3, respectively. For the unloaded and stall durations, this estimation method produces almost identical values as the maximum likelihood estimates in Figure 2 (values provided in Table S1).

The simplest prediction is that against the low loads experienced during ramps, the detachment rate should match the unloaded detachment rate. However, each of the three motors had a unique relationship between their unloaded and ramp durations (Figure 3, Tables S3 and S4). The simplest case was kinesin-2, where the ramp duration of 0.97 s was within 95% CI of the unloaded run duration of 1.08 s (Figure 3B). In contrast, the kinesin-1 ramp duration of 2.49 s was much closer to the stall duration (3.05 s) than the unloaded run duration (1.05 s) (Figure 3A). The simplest interpretation is that the catch-bond character of kinesin-1 engages at low loads rather than rising proportionally to load or engaging only near stall (see Discussion).

The most notable ramp behavior was seen in kinesin-3, where the ramp duration of 0.75 s was nearly four-fold shorter than the unloaded run duration (2.76 s) and was more than two-fold shorter than the stall duration (1.90 s) (Figure 3C). As expanded on in the Discussion, the positively charged ‘K-loop’ in the kinesin-3 motor KIF1A is known to interact electrostatically with the negatively charged C-terminal tail of tubulin (Soppina et al., 2022; Zaniewski et al., 2020; Zaniewski & Hancock, 2023); thus, it is reasonable that even the low loads imposed during ramps are sufficient to overcome these weak electrostatic interactions. Notably, by defining the ramp duration as its behavior under low load, kinesin-3 can be classified as a catch bond because high load (stall) durations are longer than low load (ramp) durations.

Kinesin-3 reattaches more rapidly than Kinesin-1 and Kinesin-2

In the cell, motor-microtubule binding events include both the initial attachment of a freely diffusing motor-cargo binding to the microtubule, or it can involve a cargo-bound motor undergoing a constrained diffusion near the microtubule before rebinding to the filament. Our tensiometer geometry roughly encompasses both of these extremes; unbound motors diffusing on a ~1 um long DNA tether mimics free diffusion, whereas transient slips are so short that the motor likely remains weakly associated with the microtubule before reengaging (Figure 1C–H). To compare the behaviors of the three motors, we distinguished three types of reattachment events: 1) slow reattachments in which the motor returns to the baseline and fluctuates diffusively before rebinding to the microtubule; 2) rapid reattachments in which the motor detaches from a ramp or stall, returns to the origin, and immediately (within ~0.1 s) begins walking again from origin; and 3) slips, in which a motor at stall detaches and before it can make it back to origin (>60 nm from the stall plateau and >400 nm from origin), it quickly reattaches within a single frame (~0.04 s) and begins walking again.

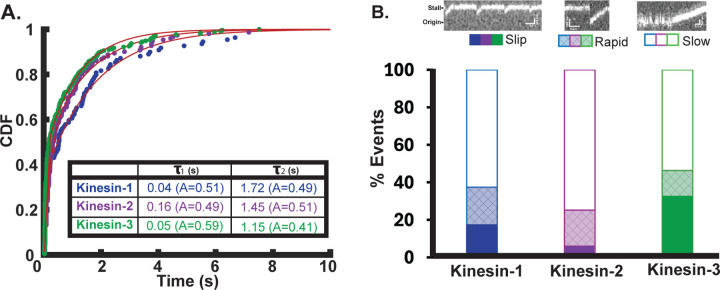
We first plotted all reattachment times as cumulative distributions and fit the data with a bi-exponential to separate out fast from slow events (Figure 4A). All three motors were fit by a fast time constant and a slow time constant with roughly similar amplitudes. One notable feature was that the three motors had different slow durations, with kinesin-1 > kinesin-2 > kinesin-3. This sequence qualitatively matches the relative bimolecular on-rates measured previously by stopped-flow but the quantitative differences here are much more subtle than the >10-fold range measured in solution (Chen et al., 2015; Feng et al., 2018; Zaniewski et al., 2020). Next, we compared the relative fractions of slips and fast and slow reattachments for each motor (Figure 4B with example kymographs of each type of event). The most notable feature is that kinesin-3 had the highest proportion of slip events. This result matches what was seen previously in a three-bead optical trapping assay that had higher time resolution and found that the majority of slip events recovered within 2 ms (Pyrpassopoulos et al., 2023).

Figure 4. Reattachment Rates for Kinesin-1, -2 and -3.

(A) Cumulative distribution of reattachment times for each motor fit to a bi-exponential by least squares. Kinesin-1 (blue) has a fast reattachment time constant of 0.04 s (95% CI [0.03, 0.04]), and a slow time constant of 1.72 s [1.65, 1.79] with (N=109 events). Kinesin-2 (purple) has a fast reattachment time constant of 0.16 s [0.15, 0.18], and a slow time constant of 1.45 s [1.34, 1.56] (N=151). Kinesin-3 (green) has a fast reattachment time constant of 0.05 s [0.04, 0.05]), and a slow time constant of 1.15 s [1.10, 1.20] (N=254). (B) Bar plot showing the fraction of slip, fast, and slow rebinding events for each motor, with example kymographs for each (top). Solid bars indicate slips during stall, where the motor resumes a new ramp within a single frame (~40 ms). Crosshatched shading indicates rapid reattachment events, where the motor falls back to within 400 nm of origin and initiates a new ramp within 100 ms. Open bars indicate slow reattachment events where motors detach from ramp or stall and fluctuate around the origin for >100 ms before rebinding and initiating a new ramp.

Simulating Potential Catch-Bond Mechanisms

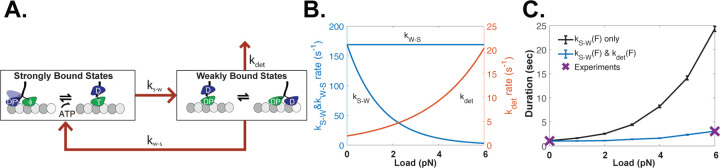
To test potential mechanochemical mechanisms underlying the catch-bond behavior of the three kinesin motor families, we carried out stochastic simulations of load-dependent motor stepping and detachment. For simplicity, we reduced the chemomechanical cycle down to a single strong-binding state (ATP and nucleotide-free states) and a single weak-binding state (ADP and ADP-Pi states). The three rate constants in this model are the strong-to-weak transition, k_s-w, the weak-to-strong transition, k_w-s, and a detachment rate from the weak-binding state, k_det (Figure 5A). Based on backstepping rates observed in optical tweezer experiments, we also incorporated a load-independent backward stepping rate of 3 s⁻¹, meaning that stall is defined as the load at which forward stepping slows to 3 s⁻¹ (Andreasson, Shastry, et al., 2015; Carter & Cross, 2005; Coppin et al., 1997). For simplicity, we set k_s-w = k_w-s, meaning that the motor spends half of its cycle in each state in unloaded condition, and we set k_det to match the unloaded run duration (Figure 5B and Figure S7B).

Figure 5. Chemomechanical Model of Possible Catch-bond Mechanism.

(A) Diagram of kinesin chemomechanical cycle model consisting of a strong-binding state, a weak-binding state, and first-order rate constants for the strong-to-weak transition (k_s-w), the weak-to-strong transition (k_w-s), and detachment from the weak-binding state (k_det). (B) Load-dependent rate constants used to fit the experimental catch-bond behavior for kinesin-1. In this model the strong-to-weak transition (blue curve) slows with load and the detachment rate (red curve) increases with load, while the weak-to-strong transition (blue horizontal line) is independent of load. Model parameters are given in Table S4. (C) Experimental and simulated load-dependent off-rate for kinesin-1. Purple X show the experimental unloaded and stall durations for kinesin-1. Black line shows model in which only the strong-to-weak transition is load-dependent, showing that this model overestimates the stall duration. Blue line shows model using rate constants in (B), where a load-dependent k_s-w and k_det can recapitulate the experimental stall duration for kinesin-1. Simulations for kinesin-2 and -3 and results from other formulations of the model are presented in Figures S7–S10.

Recent work provides strong evidence that the strong-to-weak transition is the load-dependent step in the kinesin-1 mechanochemical cycle (Sudhakar et al., 2021). Sudhakar et al synthesized germanium nanospheres that, due to their high index of refraction, enabled high trapping forces with particle diameters down to 70 nm. The faster response time due to the reduced drag coefficients resolved the 8 nm steps normally observed when motors are labeled through their tail domain into two ~4 nm substeps (Sudhakar et al., 2021). The duration of the first substep was increased both at low ATP and at elevated loads, whereas the second substep was unaffected by ATP or load and was the step from which motor detachments and backward slipping events occurred. These results map well to our two-state model; the strong-to-weak transition is both ATP and load-dependent (and likely involves neck linker docking), and the weak-to-strong transition (involving tethered head attachment to the next binding site) is load-independent.

We implemented these results into our two-state model for kinesin-1 by incorporating an exponential load-dependence into the strong-to-weak transition, such that the motor spends a greater fraction of its cycle in the strong-binding state at elevated loads. However, simulations from this k_s-w(F) model predicted stall durations 10-fold longer than our measured kinesin-1 stall durations (Figure 5C). Thus, to match the experimental stall duration, we introduced an exponential load-dependence into the detachment rate, k_det (Figure 5B and Figure S7B). This model recapitulated both the unloaded run duration and the stall duration (Figure 5C), as well as generating a force-velocity curve that qualitatively matches our experiments (Figure S7C). Importantly, this model generates a catch-bond behavior without requiring a protein-protein interaction with a dissociation rate that decreases with load (Thomas et al., 2008). Instead, detachment from the weak-binding state is a slip bond (the dissociation rate increases with load), but by shifting the fraction of the cycle the motor spends in this vulnerable state, a catch-bond behavior is achieved. We also explored other model formulations, and formulated models to account for the kinesin-2 and -3 behavior, described in Supplementary Information (Figure S7E–S7H).

Discussion

Understanding how motors behave under physiologically relevant loads is crucial to understanding bidirectional transport in cells where cargo are transported by antagonistic kinesin and dynein motors (Cason & Holzbaur, 2022; Hancock, 2014). Optical tweezer experiments have provided many essential details of the kinesin mechanochemical cycle under load; however, the bead diameters needed to achieve substantial trapping forces impose vertical forces on the motors, complicating the interpretation of load-dependent off-rate measurements. Using DNA as a nanospring enables motor protein mechanical experiments using a standard TIRF microscope, which allows for simultaneous monitoring of numerous motor-DNA complexes in a single imaging field (Iwaki et al., 2016; Nick Maleki et al., 2023). In the geometry developed here, a kinesin motor pulls against the elastic force of a stretched DNA solely in a direction parallel to the microtubule, matching the geometry of vesicles measuring a few tens of nanometers. The most striking observation was that members of all three kinesin transport families show catch-bond behavior in which off-rates at stall are slower than those at low or zero loads. These findings necessitate a revised view of how kinesin motors operate against hindering loads and provide important constraints for uncovering the mechanisms that regulate bidirectional transport in cells.

Transport kinesins have a catch-bond behavior under hindering loads

Historically, motors have been studied with single bead assays in which motors are attached to a bead that is roughly 10-fold larger than the extended length of the motor (Andreasson, Shastry, et al., 2015; Block et al., 2003; Schnitzer et al., 2000; Valentine & Block, 2009). From these studies, motors from the kinesin-1, -2, and -3 families were all shown to have faster dissociation rates at increasing loads, with the relative load-dependence kinesin-3 > kinesin-2 > kinesin-1 (Andreasson, Milic, et al., 2015; Andreasson, Shastry, et al., 2015; Budaitis et al., 2021; Kunwar et al., 2011; Pyrpassopoulos et al., 2023; Tomishige et al., 2002). However, using a three-bead optical trap geometry, which minimizes vertical loads, it was found that kinesin-1 engagement times on the microtubule were longer lived than in the single-bead geometry (Pyrpassopoulos et al., 2020). We extend that result here to show that in our geometry, stall durations for kinesin-1 are roughly three-fold longer than unloaded run durations. Kinesin-2, which had previously been shown to detach much more readily under load than kinesin-1 in a single-bead force-clamp geometry (Andreasson, Shastry, et al., 2015), also had a stall duration that was 3-fold longer than the unloaded run duration. The kinesin-3 stall duration was within a factor of two of kinesin-1 and -2.

What is the mechanism of this catch-bond behavior? Cell adhesion proteins such as integrins, selectins, and FimH have been shown to form longer lasting bonds under load, with the proposed mechanisms generally involving an allosteric effect that strengthens the protein:protein interface (Kong et al., 2009; Marshall et al., 2003; Thomas et al., 2002). However, motor proteins are different in that they cycle in a nucleotide-dependent way between strong and weak binding states, offering multiple potential mechanisms for slower dissociation rates under load. For instance, under a few piconewtons of load, Myosin I was shown to dissociate nearly two orders of magnitude slower than in the absence of load, an effect attributed to load-dependent trapping of ADP in the active site that maintained the motor a high-affinity binding state (Laakso et al., 2008). Dynein was also shown to have catch-bond behavior over certain ranges of resisting loads, though the precise mechanism is unclear (Kunwar et al., 2011; Rai et al., 2016; Rai et al., 2013; Sanghavi et al., 2021). Using simulations of the kinesin chemomechanical cycle, we explored different potential mechanisms by which load can both slow the stepping rate and slow the dissociation rate at stall. The simplest modification, introducing load dependence into the strong-to-weak transition, actually predicted significantly longer stall durations than we measured experimentally (Figure 5C). The most straightforward model that could account for our results involved stall force loads slowing the strong-to-weak transition and accelerating the detachment rate from the weak-binding state.

Modeling the mechanochemical cycles enabled estimation of the load-dependence of the detachment rate from the weak-binding state for each motor. Using our modeling approach, where the load-dependent detachment rate $k_{det}\left(F\right)=k_{det}^0{e}^{\frac{F\delta }{k_{B}T}}$, we were able to recapitulate our kinesin-1 experimental results with a slip bond detachment distance parameter, denoting the relative sensitivity to load, of δ = 1.61 nm. The closest experimental comparison comes from kinesin-1 detachment experiments in ADP in which a motor-functionalized bead is dragged at constant velocity along an immobilized microtubule and binding/detachment events are detected by the bead stopping while trap continues to move (Andreasson, Shastry, et al., 2015; Uemura et al., 2002). Our distance parameter of 1.61 nm with an unloaded off-rate $k_{det}^0$ of 1.93 s⁻¹ falls between published values of 1 s⁻¹ / 3 nm from Uemura et al and 11 s⁻¹ / 0.4 nm from Andreasson et al. (Andreasson, Shastry, et al., 2015; Uemura et al., 2002).

Applying the two-state model to the other motors, we found that the load-dependent detachment kinetics of kinesin-2 and kinesin-3 were broadly similar to kinesin-1 (Figure S7E–H). This result was surprising given the strong load-dependence of detachment for these motors seen in single-bead optical tweezer experiments (Andreasson, Shastry, et al., 2015; Uemura et al., 2002). Using the same model we used for interpreting kinesin-1, we found the load dependence of detachment from the weak-binding state was in the order kinesin-3 (2.14 nm) > kinesin-1 (1.6 nm) > kinesin-2 (1.35 nm) (Figure S7B).

The role of vertical forces in motor detachment

We next asked whether by considering the different geometries we could reconcile our catch-bond observations with previous single-bead optical tweezer kinesin-1 slip-bond measurements that found the kinesin-1 off-rate increased from 1.11 s⁻¹ at zero load to 2.67 s⁻¹ at 6 pN (reproduced in Figure S10) (Andreasson, Milic, et al., 2015; Andreasson, Shastry, et al., 2015). Previous modeling work accounted for these off-rates using a two-step detachment process having catch-bond behavior for parallel loads and slip-bond behavior for vertical loads (Khataee & Howard, 2019). Using our two-state model, we instead incorporated both horizontal and vertical loads as accelerating detachment from the weak-binding state:

$$k_{det}\left(F\right)=k_{det}^0{e}^{\frac{\left(F_{\left|\right|}{\delta }_{\left|\right|}+F_{\perp }{\delta }_{\perp }\right)}{k_{B}T}}$$

Here ${\text{F}}_{||}$ and ${\text{F}}_{\perp }$ are the magnitude of the parallel and perpendicular loads and ${\text{δ}}_{||}$ and ${\text{δ}}_{\perp }$ represent the distance parameters in each direction (Figure S10B). Using a 440 nm bead diameter and estimated motor length of 35 nm that results in the force being imposed on the motor at a 60° angle (Figure S10A), it was calculated that a 6 pN force parallel to the microtubule would correspond to a 10 pN force perpendicular to the microtubule (Andreasson, Milic, et al., 2015; Andreasson, Shastry, et al., 2015; Khataee & Howard, 2019). Using ${\text{δ}}_{||}$ = 1.61 from our model in Figure 5, we found that by setting ${\text{δ}}_{\perp }$ = 1.58 nm, we were able to reproduce the slip bond behavior observed in the single-bead optical trap experiments (Figure S10D). Notably, in this model the detachment rate from the weak-binding state has a slip bond character with similar load dependencies in the parallel and perpendicular directions. We stress that this model is a hypothesis that needs further testing, and that the load-dependent off-rate over intermediate loads does not match the experimental data (Figure S10D). Nonetheless, this is a simple formulation that shows that a motor can display either catch bond or slip bond behavior depending on the geometry of the imposed loads.

Ramps reveal detachment behaviors at low loads

In addition to reporting on the detachment properties at stall, our DNA tensiometer provides new insights into fast rebinding that occurs during unloaded runs of kinesin-3. It has long been appreciated that the kinesin-3 motor KIF1A achieves long run lengths due to electrostatic attraction between its positively charged Loop-12 (K-loop) and the negatively charged C-terminal tail of tubulin (Lessard et al., 2019; Okada et al., 2003; Okada & Hirokawa, 1999, 2000; Soppina et al., 2014; Soppina & Verhey, 2014; Zaniewski et al., 2020; Zaniewski & Hancock, 2023). Furthermore, the KIF1A off-rate in ADP, in which the motor diffuses on the microtubule lattice, was found to match the off-rate during processive stepping in ATP (Zaniewski et al., 2020). The relatively high microtubule affinity of this weak-binding state suggests that the motor may be undergoing diffusive episodes between processive runs, while maintaining association with the microtubule. In this way, the observed run length would be a concatenation of a number of shorter runs interspersed by diffusive events.

Our DNA tensiometer offers a way to test the hypothesis that the long, unloaded run lengths of KIF1A are due to a concatenation of shorter runs. Due to the nonlinearity of the dsDNA force-extension curve in our DNA tensiometer, the motor is walking against forces below 1 pN for roughly 90% of the distance to stall (Figure 1B). Consistent with this, motor velocities were nearly constant until they were near the stall force (Figure 1D and S3), and ramp velocities averaged only ~15% slower than unloaded velocities (Table S3), which corresponds to ~1 pN of force if the force-velocity relationship is linear. By developing a Markov Process/Bayesian Inference approach to estimate the KIF1A detachment rate during ramps, we were able to estimate the run duration at low loads. Importantly, this analysis takes into account both motors that dissociate during the ramps and those that complete ramps by achieving stall. We found that the KIF1A ramp duration parameter was nearly four-fold shorter than the unloaded run duration parameter (Figure 3). If, under zero load, the long runs observed were actually a concatenation of a series of shorter runs connected by diffusive weak-binding events, the diffusive state would likely be unable to withstand even the sub-pN forces from the DNA spring (Okada & Hirokawa, 2000). For instance, based on a 0.044 μm²/s diffusion coefficient (equivalent to a ~0.1 pN-s/μm drag coefficient (Howard, 2001; Okada & Hirokawa, 2000)), if the motor were in a weak-binding state for 10 ms, a 1 pN force would pull the motor back 100 nm. Thus, in considering whether KIF1A acts as a catch bond, we used this ramp duration as the best approximation for the true run unloaded length in the absence of diffusive events. The electrostatic interactions that enable KIF1A to be superprocessive do not only act during each step to enhance the probability of completing the step; they also act between runs to maintain association of KIF1A with the microtubule, enabling rebinding and initiation of new runs.

The ramp durations of kinesin-1 and kinesin-2 also provide insights into how load alters their interactions with microtubules. For kinesin-2, the predicted ramp duration was not statistically different from the unloaded run duration, suggesting that unloaded runs do not include short diffusive episodes. This result is somewhat surprising, given previous kinesin-2 force-clamp optical tweezer experiments that found a substantial drop in run length between the unloaded case and the lowest force (1 pN) and a smooth reduction in run length at higher forces ((Andreasson, Shastry, et al., 2015); Figure 4A). However, this discrepancy may be due to vertical forces associated with the single bead geometry accelerating the detachment rate in the optical tweezer study (Khataee & Howard, 2019). Interestingly the predicted ramp duration for kinesin-1 was nearly the same as the stall duration and much longer than the unloaded duration. One possibility for this puzzling result is that the catch-bond effect of hindering load comes into play at low loads and not only at stall where the motor has slowed considerably.

Motor slips and detachments reflect different processes

Because the DNA tensiometer tethers the motor near the microtubule, such that repeated binding and unbinding events occur, it enables comparison of family-dependent differences in kinesin rebinding kinetics. Kinesin-microtubule interactions can be separated into three classes: i) the initial binding from solution, ii) motor rebinding following an attachment/detachment event, and iii) fast motor rebinding seen in slip events during ramps and at stall. Previous stopped-flow studies on these three motors in the same buffer used here found that the solution bi-molecular on-rates were 1.1 μM⁻¹s⁻¹ for kinesin-1, 3.1 μM⁻¹s⁻¹ for kinesin-2, and 17 μM⁻¹s⁻¹ for kinesin-3 (Chen et al., 2015; Feng et al., 2018; Zaniewski et al., 2020). We observed two classes of detachments during stall plateaus, full detachments and slips. Detachment events, which we defined as the motor returning to within 400 nm of the baseline, could be separated into fast events, when a new ramp started within the limit of detection (typically ~0.04 s), and slower events where the motor fluctuated around the origin for multiple seconds. When we fit a bi-exponential to the distribution of all slip and detachment events, the slow phases ranged from 1.72 s for kinesin-3 down to 1.15 s for kinesin-1. Thus, although there were differences between motors, the large variation expected from the stopped-flow studies was not manifested in the slow reattachment durations. Our tentative interpretation is that either the hydrodynamic drag of the DNA and Qdot or the negative charge of the DNA limits the motor on-rate, masking any family-dependent differences.

Slip events were observed for all three motors, with highest frequency for kinesin-3 and lowest frequency for kinesin-1. These slips were first characterized in a 2019 kinesin-1 optical tweezer study from the Cross lab (Toleikis et al., 2020), where at stall, backward displacements could be observed at multiples of 8 nm that were distinct from detachment events. The durations of the plateaus that preceded the slips were longer than the plateaus preceding forward steps, suggesting that the motor transitioned into a different state preceding the slip, such as phosphate dissociation to generate the ADP state. Subsequent higher resolution work, enabled by small Germanium nanoparticles, revealed a staircase pattern during these slips with ~8 nm steps of mean duration 73 μsec, suggesting that the motor was transiently interacting with each tubulin subunit as it slipped backward. Similar slips had been seen earlier for kinesin-2 (Andreasson, Shastry, et al., 2015), and were subsequently seen for two kinesin-3 family members, KIF1A and KIF1C (Pyrpassopoulos et al., 2023; Siddiqui et al., 2022). Using a three-bead optical tweezer geometry, it was found that for KIF1A, ~80% of slip/detachment events lasted less than 10 ms before the motor started a new ramp, whereas for kinesin-1 only ~25% of the slip/detachment events were 10 ms or shorter.

We found that kinesin-3 had roughly twice as many slips as kinesin-1 (Figure 4B). We also found that in the bi-exponential fit to the slip/detachment durations, 34% of the kinesin-1 events were in the fast population, compared to 44% and 46% for kinesin-2 and kinesin-3, respectively. With regard to the catch-bond behavior at stall, perhaps the most informative way to analyze the influence of slips is to compare the stall durations for the three motors when the slip events at stall are ignored. This approach is relevant to tug-of-war events in cells because when kinesin fully detaches, dynein would be able to walk unimpeded until kinesin rebinds; in contrast, kinesin slip events would only lead to a transient elastic recoil of the cargo before the motor regained a footing and continued pulling against dynein. Ignoring slips lead to a 1.5-fold increase in the stall duration for kinesin-1 to 4.4 s, a 2.4-fold increase for kinesin-2 to 6.8 s, and a 3.0-fold increase for kinesin-3 to 5.6 s (Figure S4 and Table S2).

Catch-bond behavior provides insights into tug-of-war with dynein

Consistent with the diversity of intracellular cargo transported by kinesin and dynein, there are many features such as motor number and type, microtubule isotype, and cargo size and geometry that can regulate transport. In previous simulations of kinesin-dynein tug-of-war transport, we found that the strongest determinants of kinesin’s ability to compete against dynein were the load-dependent motor dissociation rate and the motor rebinding rate (Ma et al., 2023; Ohashi et al., 2019). Simply put, if motors detach, then the opposing motor wins, and if they remain attached against strong antagonistic loads, they can at least achieve a stalemate against their opposition. The finding here that all three dominant kinesin transport families display catch-bond behavior at stall necessitates a reevaluation of how motors function during a tug-of-war. There is evidence that dynein forms a catch bond or at least an ideal (load independent) bond (Belyy et al., 2016; Cianfrocco et al., 2015; Kunwar et al., 2011; Rai et al., 2016; Rai et al., 2013; Sanghavi et al., 2021); thus, kinesins and dyneins are primed to strongly oppose on another. Consistent with this, when vesicle motility is quantified during axonal transport, there are often a large fraction of immobile vesicles and even those that move include sustained immobile episodes (Encalada et al., 2011; Fu & Holzbaur, 2013; Gross et al., 2002; Hancock, 2014; Iacobucci et al., 2014). It’s possible that no motors are engaged in these cases, but it’s also possible that the motors are stalled in a tug-of-war with the large antagonistic forces suppressing the kinesin and dynein off-rates.

The catch bond results here help to explain previous in vitro work in which one kinesin and one dynein were connected through a complementary ssDNA (Belyy et al., 2016; Feng et al., 2020; Gicking et al., 2022). It was found that the motor pairs had periods of near-zero velocity that lasted for many seconds, considerably longer than kinesin’s unloaded off-rate. Furthermore, kinesin-2 and kinesin-3 also showed these sustained slow tug-of-war periods despite their reported faster load-dependent off-rates from optical tweezer studies. The functional catch-bond behavior observed here provides a simple explanation for these sustained kinesin-dynein stalemates.

Importantly, the load-dependent off-rates of both kinesins and dynein are expected to depend on the cargo geometry. A 30 nm vesicle would lead to forces on the motor nearly parallel to the microtubule surface, whereas when transporting a micron-scale mitochondria the vertical forces would be larger than the horizontal forces. Cargo geometry and stiffness is also expected to play a role; for instance, deformation of a cargo, either due to compliance of the cargo or to multiple motors pulling on it will tend to reduce vertical force components on the motors. The present work emphasizes that along with motor type, motor number, motor autoinhibition, and the growing list of regulatory proteins, the geometry with kinesin and dynein engage in a tug-of-war can be an important determinant of the speed and direction of cargo transport in cells.

Methods

DNA Tensiometer Construction

For the dsDNA spring, a 5’ biotinylated forward primer (5’-/5Biosg/TGC CTC CGT GTA AGG GGG AT-3’) and a reverse primer with a 5’ overhang (5’-/GGG CCA TCG CCA ATT GGA GTA /idSp/ GTG AGT TAA AGT TGT ACT CGA GTT TGT GTC CAA GAA-3’) were used to create a 3009 bp dsDNA by PCR from plasmid Mus Musculus BicD2-sf-GFP (aa 25–425) in pet28a. The abasic Int 1’,2’-Dideoxyribose spacer (idSp) creates an overhang by terminating the polymerase. All oligonucleotides were purchased from IDT. Each 50 μL PCR reaction contained: 1x Phusion HF buffer, 198 μM dNTPs, 2 μM dCTP-Cy5, 0.5 μM primers, 3 ng template DNA and 1 U/50 μL HF Phusion Polymerase. Fluorescent dsDNA used in Figure S5 had 10μM dCTP-Cy5 and 190μM dNTPs. The PCR reaction was carried out in a thermal cycler with the following procedure: 98°C for 30 s, then 45 cycles of 98°C for 10 s, 58°C for 30 s and 72°C for 1.5 min, then lastly 72°C for 5 min. The product was purified using a NucleoSpin^® PCR clean-up kit and the concentration determined by absorbance on a Nanodrop 2000c Spectrophotometer. DNA bands were visualized on a 1% agarose gel with ethidium bromide staining.

Motor-Microtubule-Tensiometer Assembly

Motors were bacterially expressed, purified and linked through its SNAP tag to an oligonucleotide (5’-/TAC TCC AAT TGG CGA TGG CCC / 3AmMC6T/-3’) complementary to the dsDNA overhang. Details of motor expression, purification and labeling, as well as tubulin biotinylation and polymerization are given in Supplementary Information. The DNA tensiometer was assembled on the microtubule as follows. The following three buffers are made on the same day of the experiment: C2AT (BRB80, 10 μM Taxol, 2 mM MgATP, 2 mg/mL Casein), 2AT (BRB80, 10 μM Taxol, 2 mM MgATP) and Imaging Solution (BRB80, 10 μM Taxol, 2 mg/mL Casein, 2 mM MgATP, 20 mM D-glucose, 0.02 mg/mL Glucose oxidase, 0.008 mg/mL Catalase, 0.5% BME and 2 mg/mL BSA). Full-length rigor kinesin was used to attach microtubules the coverglass (Mickolajczyk et al., 2015). Tensiometers were created in the flow cell using the following work flow: C2AT, 5 min > Rigor kinesin, 5 min> C2AT wash > BioMT, 5 min > 2AT > 8 nM Neutravidin, 5 min> 2AT > 10 nM Bio-dsDNA-Overhang, 5 min> C2AT > 4 nM KinesinMotor + 40nM Qdot-GBP (pre incubated in tube on ice for >15 min) in imaging solution, 10 min > Imaging solution wash. Note that because casein can contain free biotin, casein-free 2AT buffer was used during avidin-biotin binding steps. Following assembly, the Qdot connected to the motor was imaged on a custom-built TIRF microscope, described previously (Nong et al., 2021). Raw data were typically collected at 25 fps (range of 20–40 fps) on a Photometrics Prime 95B camera.

Data Analysis

Movies were uploaded into FIESTA software (Ruhnow et al., 2011) and Qdot intensities were tracked using a symmetric 2-D gaussian function to obtain x,y,t data for each Qdot. When drift correction was needed, TetraSpeck^™ Fluorescent Microspheres (Thermo) and immobile Qdots were used as fiducial markers. The smallest position errors at stall in FIESTA fitting were 3–4 nm, which matched the positional error of Qdot-labeled motors stuck to microtubules in AMPPNP. Points with position errors greater than 20 nm were excluded because they often involved clearly spurrious position estimates. Notably, many tensiometers had small segments of missing data due to the Qdot fluctuating out of the TIRF field or blinking; these occurred most often during periods when the motors were detached from the microtubule.

After obtaining X and Y positions of linear motor tracks in Fiesta, we rotated and translated the data in Excel to generate X versus t traces. The apparent origin was determined by averaging the points where the motor is fluctuating on its tether. In rare instances where no fluctuation was observed, the approximate origin was calculated by averaging the starting positions of all the ramps within the tensiometer (Figure 1). We then measured the ramp time, distance traveled, stall durations, reattachment times and starting positions. Tensiometers occasionally ended with the Qdot signal going dark, denoting either bleaching or failure of the Qdot-motor or motor-DNA connection. Notably, no clear instances of motor-Qdots detaching during stall and continuing walking (denoting the tensiometer breaking) were observed. Stalls that terminated due to the tensiometer going dark or the video ending were excluded from analysis.

Stochastic Modeling

Kinesin run and stall durations were simulated by using a modified version of published stochastic model of kinesin stepping (Gicking et al., 2022; Ma et al., 2023). A motor is either in a strongly-bound state or a weakly-bound state (Figure 5A). At each timepoint, a motor in the strongly bound state can step backward by 8 nm with a constant rate, $k_{back}=3s^{-1}$, or transition into the weakly bound state with a first order transition rate constant, $k_{S-W}$. A motor in the weakly bound state can complete an 8-nm forward step by transitioning back to the strongly-bound state with rate constant, $k_{W-S}$, or it can detach from the microtubule with transition rate, $k_{det}$. All of these transitions are irreversible. The model can be solved analytically. The forward stepping rate and the load-dependent velocity are:

$$k_{forward}={\left(\frac{1}{k_{S-W}}+\frac{1}{k_{W-S}}\right)}^{-1}$$

$$V\left(F\right)=8nm\ast \left(k_{forward}-k_{back}\right)$$

Ignoring relatively slow backstepping rate in stepping cycle, the bound duration is equal to the duration of each step multiplied by the predicted number of steps before detaching:

$$T\left(F\right)={\left(\frac{1}{k_{S-W}}+\frac{1}{k_{W-S}}\right)}^{-1}\ast \left(\frac{k_{W-S}+k_{det}}{k_{W-S}}\right)$$

For simplicity, we set $k_{S-W}=k_{W-S}$ at zero load. Load-dependent transition rates were defined as follows,

$$k\left(F\right)=k^0\ast e^{\frac{F\delta }{k_{B}T}}$$

where $k^0$ is the unloaded transition rate, $\delta$ is the characteristic distance parameter and $k_{B}T$ is the Boltzmann’s constant multiplied by the absolute temperature, equal to 4.1 pN-nm at 25° C. The forward stepping rates for unloaded kinesin-1, -2, -3 simulation were set to 84.5, 53 and 151.5 steps per second, respectively, and set to 3 s⁻¹ (matching the backstepping rate) at the stall force, defined as 6 pN. All simulations were run 1000 times, and each run started from a motor in strongly bound state and continued until detachment or until 50 seconds. The durations of all the runs were averaged and plotted with standard error of mean (SEM).

Significance Statement.

Kinesin and dynein motor proteins transport intracellular cargo bidirectionally along microtubule tracks, with the speed and directionality of transport involving a tug-of-war between the motor teams. We created a ‘DNA tensiometer’ that uses DNA as a spring to measure kinesin performance against loads oriented parallel to the microtubule. We find that dissociation rates paradoxically slow down with imposed loads. Dyneins are also thought to possess this ‘catch-bond’ behavior, meaning that both motors will hang on tightly during a tug-of-war. Previous work showed that combined vertical and horizontal loads cause faster detachment rates under load. Hence, we conclude that the effectiveness of kinesins during bidirectional transport depends strongly on the geometry of their cargo.