Deep representation learning of protein-protein interaction networks for enhanced pattern discovery

Abstract

Protein-protein interaction (PPI) networks, where nodes represent proteins and edges depict myriad interactions among them, are fundamental to understanding the dynamics within biological systems. Despite their pivotal role in modern biology, reliably discerning patterns from these intertwined networks remains a substantial challenge. The essence of the challenge lies in holistically characterizing the relationships of each node with others in the network and effectively using this information for accurate pattern discovery. In this work, we introduce a self-supervised network embedding framework termed discriminative network embedding (DNE). Unlike conventional methods that primarily focus on direct or limited-order node proximity, DNE characterizes a node both locally and globally by harnessing the contrast between representations from neighboring and distant nodes. Our experimental results demonstrate DNE’s superior performance over existing techniques across various critical network analyses, including PPI inference and the identification of protein functional modules. DNE emerges as a robust strategy for node representation in PPI networks, offering promising avenues for diverse biomedical applications.

A strategy preserves complex networks in lower dimensions with discriminative node representation, enhancing PPI network analysis.

INTRODUCTION

Biological networks are instrumental in modeling complex biological systems by providing a detailed blueprint of the myriad interactions among genes, proteins, and other cellular components (1, 2). These networks delineate entities as nodes and their interactions—spanning from physical connections to functional associations—as edges, laying the groundwork for unraveling the complexities of biological systems and processes (3–5). For instance, in protein-protein interaction (PPI) networks, the intricate web of connections contains crucial information for understanding cellular processes and disease mechanisms (6–8). However, deciphering these complex networks to gain biological insights poses a substantial challenge. Network embedding, a process where interconnected nodes within a network are mapped into vectors in a lower dimension while preserving certain network structure properties and node relationships, is a commonly used approach to discern patterns within biological networks (9–11). The accuracy of network embedding critically determines the success of downstream data analysis and applications.

The underlying structure of a biological network is widely recognized to be highly nonlinear because of complex and nonadditive interactions (12–14), and encompasses both local (i.e., immediate connections) and high-order (i.e., clustering) structures (15). Despite extensive efforts to develop network embedding methods capable of coping with such complexity, a practical solution remains elusive. Traditional network embeddings primarily aim to capture node proximity through methods such as matrix factorization (12, 16–18) or shallow models (12, 19, 20). However, these methods often encounter limitations because of their reliance on low-rank approximations or oversimplified network structures, hindering their ability to fully capture the highly nonlinear patterns and resulting in suboptimal embeddings (21). Recently, deep learning–based techniques (22–25) have emerged to tackle the problem by leveraging multiple layers of nonlinear transformations to capture the complex network structure.

For instance, variational graph autoencoder (VGAE) (22) uses graph neural networks to enhance the expressiveness of node embeddings by aggregating information from their neighborhoods. While it preserves certain nonlinear structural aspects within node embeddings, the algorithm solely focuses on patterns within the local neighborhood of each node, thus limiting its capacity to understand the node interrelationships across the wider network. Efforts like Deep Graph Infomax (DGI) aim to mitigate these limitations by preserving global structural information via aligning node embeddings with a global graph summary (23). However, because the focus is on global structure, this approach may overlook fine-grained local details. Deep Graph Contrastive Representation Learning (GRACE) captures global information indirectly by learning embeddings that are invariant to graph corruptions introduced by data augmentation (24). The effectiveness of GRACE may depend on the quality of these data augmentations.

Here, we introduce a general graph representation learning framework that uses deep learning to preserve the nonlinear and multifaceted structure of networks in a lower-dimensional space for high-performance analyses of biological networks. Our proposed method, referred to as discriminative network embedding (DNE), characterizes each node through a nonlinear contrast between the representations of its direct neighbors and nodes that are farther away in the network. Figure 1 illustrates the framework of our proposed DNE method. The proposed approach allows a holistic perspective on the role of each node in the network: It highlights the immediate connections of a node, such as interactions between proteins in PPI networks, and also its community affiliations within the network, such as protein functional modules. We demonstrate that DNE substantially outperforms existing network embedding methods for various networks and multiple downstream tasks, including link prediction (i.e., prediction of PPIs) and node clustering (i.e., identification of functional modules). DNE also offers the flexibility to combine node features with network structures for improved performance. By uniquely incorporating protein sequence features from protein language models, DNE substantially boosts downstream performance compared to traditional methods. Moreover, we demonstrate that DNE can be applied to various network types beyond PPI networks. The proposed method introduces a fresh paradigm for network analysis and promises to broadly advance biomedical data science.

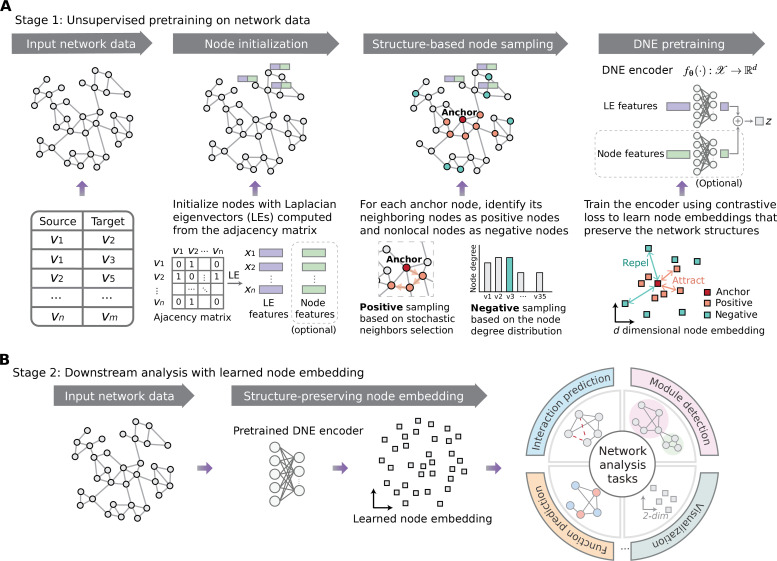
Fig. 1. Overview of DNE.

(A) DNE comprises three main steps: (i) initializing nodes using Laplacian eigenvectors (LEs) of the network’s adjacency matrix, optionally concatenated with node features when available; (ii) identifying node neighbors as positive nodes via stochastic neighbors selection and selecting nodes from other network regions as negative nodes, based on the distribution of node degrees; and (iii) embedding each node through a deep learning encoder, optimizing the encoder’s parameters to ensure the node embeddings preserve discrimination between neighboring and nonlocal nodes. (B) Utilization of the pretrained encoder to generate node representations for versatile downstream analysis tasks.

RESULTS

DNE consistently outperforms existing network embedding methods in link prediction across PPIs

We first demonstrate the efficacy of DNE in link prediction, which predicts the likelihood of edge existence based on the known network structural information. For this purpose, we benchmark our method and conduct a comparative analysis with DNE and other leading algorithms for predicting protein interactions in PPI networks, using the following PPIs: (i) a plant interactome comprising 2774 proteins and 6205 PPIs, from the Arabidopsis thaliana interactome (26); (ii) a worm interactome with 2528 proteins and 3864 PPIs, based on Caenorhabditis elegans (27); (iii) a yeast interactome with 2674 proteins and 7075 PPIs from Saccharomyces cerevisiae (28); (iv) a human interactome consisting of 8272 proteins and 52,548 PPIs, derived from HuRI (29). For each of the four interactomes, a 20% subset of the edges is randomly selected for testing and subsequently removed to form a training network. We then conduct a fivefold cross-validation on the remaining data to obtain optimal performance. This process is repeated for 10 independent runs.

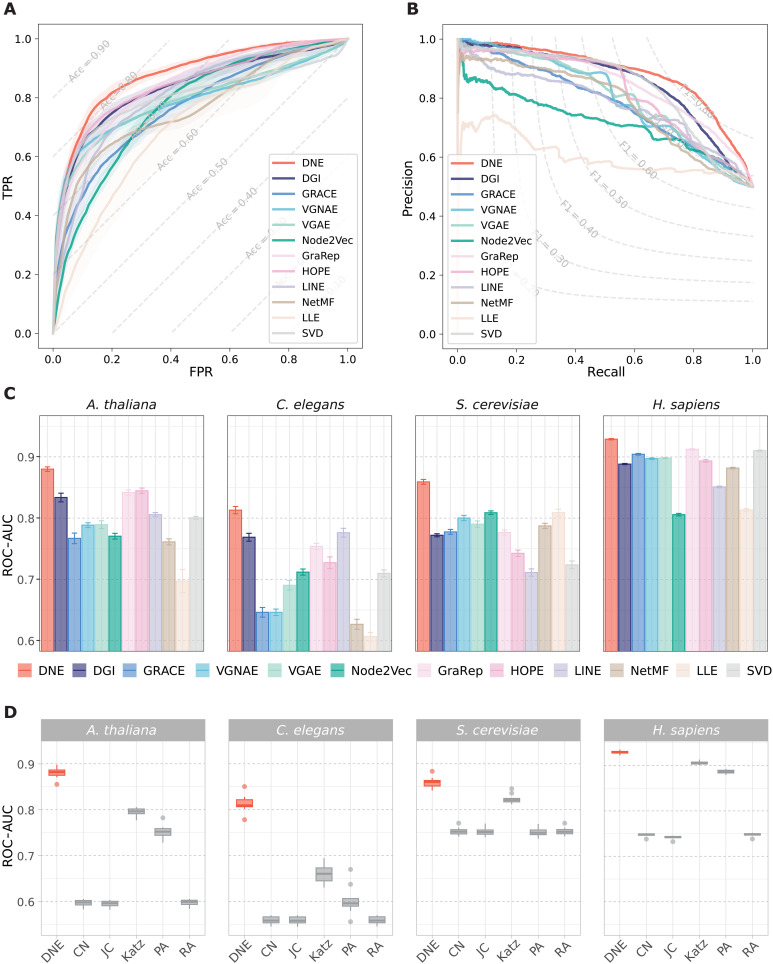
The performance comparison of DNE with 11 other network embedding methods [i.e., DGI (23), GRACE (24), Variational Graph Normalized Autoencoder (VGNAE) (25), VGAE (22), Node2Vec (20), GraRep (16), High-Order Proximity preserved Embedding (HOPE) (17), Large-scale Information Network Embedding (LINE) (19), Network Embedding as Matrix Factorization (NetMF) (18), Locally Linear Embedding (LLE) (12), and Singular Value Decomposition (SVD)] is presented in Fig. 2. In the task of predicting links on the A. thaliana dataset, DNE scores highest in both the area under the precision-recall curve (PR-AUC) and the area under the receiver operating characteristic curve (ROC-AUC) (Fig. 2, A and B). Notably, DNE achieves a mean ROC-AUC of 88.05% across 10 runs, representing approximately a 4% improvement over the results of the next best methods. Moreover, DNE consistently excels across all PPI networks studied (Fig. 2C and figs. S1 to S6), demonstrating its robustness and adaptability to various network characteristics, such as the degree and density in existing PPI networks (see table S1 for detailed network statistics). In contrast, the performance rankings of other methods fluctuate. The observed enhancement in performance and the consistency of its outcomes across various runs underscore DNE’s efficacy in capturing the structural information of the provided PPI networks.

Fig. 2. Performance of different methods for link prediction across four PPI benchmarks.

(A) ROC and (B) PR curves of DNE compared with 11 other network embedding methods for PPI prediction on the A. thaliana dataset. Dashed lines represent level curves for accuracy and F1 score in (A) and (B), respectively. (C) Comparison of DNE with network embedding methods in four PPI benchmarks, presenting mean and SDs of ROC-AUC scores from 10 independent runs. (D) Comparison of DNE with similarity-based link prediction methods in four PPI benchmarks, presenting ROC-AUC scores from 10 runs. The central line within the box denotes the mean, the box edges represent the first and third quartiles, and the whiskers extend to ±1.5 times the interquartile range.

We further compare DNE with five heuristic-based link prediction methods (30), which use heuristic node similarity scores including Common Neighbors (CN), Jaccard Index (JC), Katz Index (Katz), Preferential Attachment (PA), and Resource Allocation Index (RA), for link prediction (Fig. 2D). It is observed that the performance of methods such as Common Neighbors, Jaccard Index, and Resource Allocation Index falls short of expectations. DNE, on the other hand, demonstrates a notable improvement, exceeding over 8% in ROC-AUC scores for the A. thaliana and C. elegans networks over these heuristic approaches. This performance gap highlights the limitations of solely depending on preexisting similarity metrics for predicting new interactions. For example, because of the complex behavior of biological networks, the existence of common neighbors does not necessarily indicate a linkage.

DNE effectively identifies functional modules in PPIs

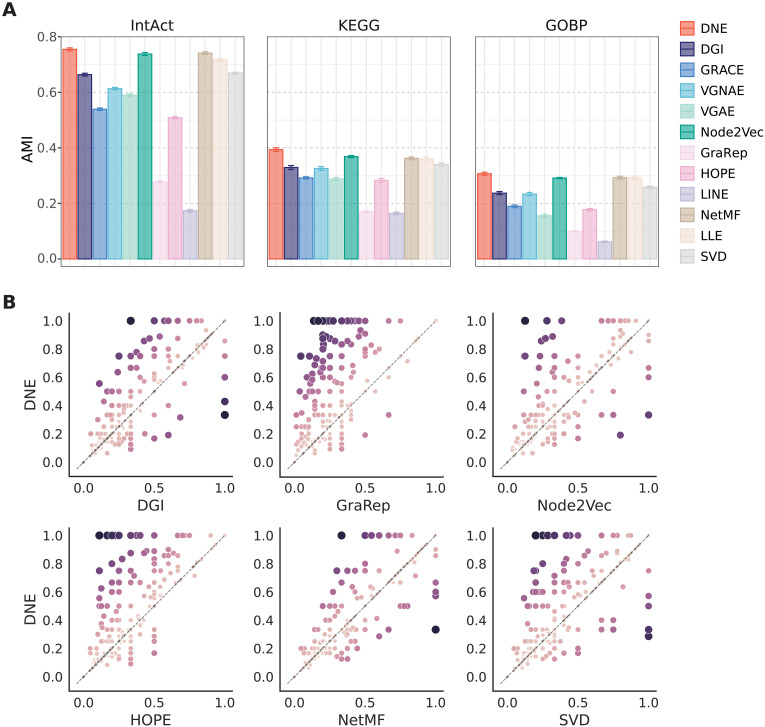
Module detection in PPI and other biological networks is a crucial task aimed at identifying clusters of closely interconnected nodes, where each cluster signifies a group of proteins that share similar functions (31). We evaluate the performance of DNE in module identification using PPI data from S. cerevisiae. The S. cerevisiae offers an excellent testing ground for network clustering due to the extensive knowledge available about its protein complexes. For reference standards, we use IntAct protein complexes (32), Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways (33), and GO Biological Processes (GOBP) (34). Figure 3 compares multiple embedding techniques on these three module detection benchmarks. Different network embedding techniques are used to represent proteins in a continuous vector space. Subsequently, hierarchical agglomerative clustering (35) is applied to these learned embeddings to identify functional modules in PPIs. For evaluation, we compute adjusted mutual information (AMI) score to assess the correspondence between the clusters identified by these methods and the annotated complexes contained in S. cerevisiae.

Fig. 3. Performance of different network embedding methods for module identification.

(A) AMI scores computed from 10 independent runs by using annotated complexes from IntAct, KEGG, and GOBP as reference standards. Mean values are reported, and error bars represent the SDs of the scores. (B) Comparison of per-module Jaccard scores between DNE and six representative baselines. Each point represents a protein complex. The x axis and y axis represent the per-module overlap (Jaccard) scores obtained by the specified baseline method and DNE, respectively. A score of 0 indicates that no members in the complex were captured, and 1 indicates that all members in the complex were captured. The color and size of each point indicate the difference in Jaccard scores between DNE and other baseline methods for the corresponding complex.

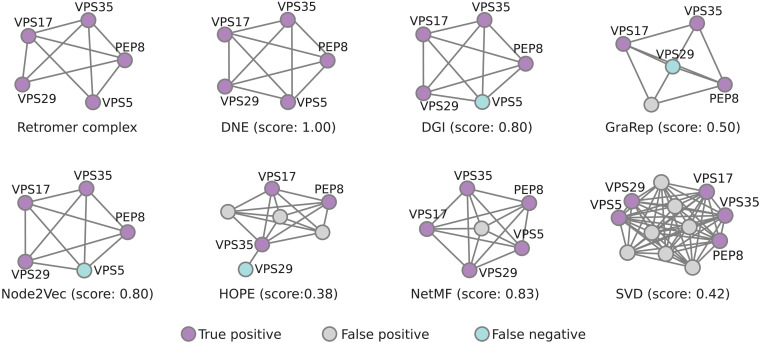
DNE excels in predicting protein complexes, exhibiting a substantially higher mean AMI score than other methods in the benchmarks. Specifically, DNE achieves a 2% improvement in AMI compared to Node2Vec and NetMF and surpasses other baseline methods by a considerable margin, ranging from 10 to 50% (Fig. 3A). Moreover, we evaluate the degree of overlap between known protein complexes and their predicted modules using the Jaccard index. In addition, we compute the disparity in the Jaccard index between DNE and six representative baseline methods for each complex (Fig. 3B). Our observations reveal that DNE not only identifies more complexes but also achieves higher overlap scores. To better understand the performance of DNE in module identification, we scrutinize the Retromer complex (Fig. 4). Comprising genes PEP8, VPS35, VPS29, VPS17, and VPS5, the Retromer complex plays a pivotal role in vacuolar protein sorting (36). DNE successfully captures all members of this complex through its learned embeddings, whereas other methods merely capture a subset of the module or include spurious members. This analysis underscores DNE’s ability to provide biologically meaningful and accurate embeddings for inferring protein functions.

Fig. 4. Evaluation of the overlap between the predicted complex and the standard Retromer complex.

The Retromer complex, as annotated by IntAct, serves as a benchmark to assess the performance of various methods in module identification. This standard complex consists of five members: PEP8, VPS35, VPS29, VPS17, and VPS5. The degree of overlap between the predicted complexes and the standard complex is measured using the Jaccard index. Purple indicates that the predicted member is part of the standard complex, gray indicates that the predicted member is not part of the standard complex, and green denotes that a member from the standard complex has not been captured by the prediction.

DNE offers the flexibility of integrating protein features from protein language models

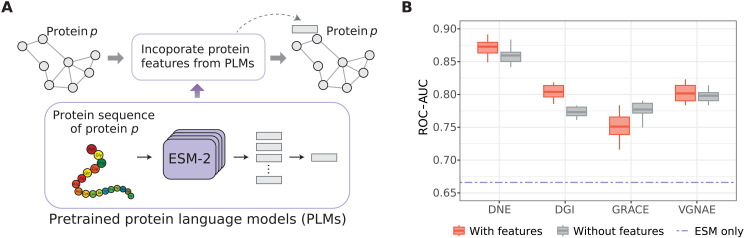
Unlike many network embedding methods that primarily focus on learning network structural information without considering node features, DNE provides the flexibility to incorporate these features into the embedding process. In this study, we enrich the S. cerevisiae network by retrieving its associated protein sequences from the Saccharomyces Genome Database (37) and converting them into protein features using a pretrained protein language model, ESM-2 (38). These features, which contain rich semantic information about proteins, are then integrated into the PPI network as node features (Fig. 5A). We chose this dataset for evaluation because it provides a complete set of protein sequences for each protein in its PPI network, whereas other benchmarks we considered do not offer complete protein sequences.

Fig. 5. Performance comparison of various methods in link prediction incorporating protein features.

(A) Integrating protein features from PLMs as node features in PPI networks for network embedding learning. (B) ROC-AUC scores for DNE and other baseline methods on the Saccharomyces cerevisiae dataset, derived from 10 independent runs. The purple dashed line (ESM only) indicates scenarios using only protein features extracted from ESM-2. Gray boxes indicate cases considering only network structures, while red boxes depict cases incorporating both network structures and node features.

To evaluate the capability of DNE to integrate node features, we explored three distinct scenarios by using the following: (i) only protein features extracted from ESM-2; (ii) network structures alone; (iii) a combination of network structures and ESM-2 protein features. DNE demonstrates a substantial improvement, with over 20% rise in ROC-AUC for PPI prediction on the S. cerevisiae dataset, compared to using solely the protein features (Fig. 5B). Furthermore, DNE consistently outperforms other baseline methods (DGI, GRACE, and VGNAE) in scenarios both with and without node features. DNE also effectively integrates node features, demonstrating a 1.3% increase in ROC-AUC when including features compared to scenarios without them. These results highlight the effectiveness of DNE in improving protein representations by harmonizing protein sequence features with network structure information.

DISCUSSION

We have introduced a network embedding technique named DNE to learn meaningful and discriminative node embeddings from a given network. DNE characterizes each node in terms of the contrast between the representations from its immediate neighbors and farther nodes, in contrast to traditional methods (12, 16–18, 22) that focus primarily on limited-order proximity among nodes. By considering both the local connectivity pattern and interactions with the broader network, DNE allows for a more holistic understanding of node relationships within the network. Our evaluation of DNE on multiple PPI datasets demonstrates its enhanced capability over existing methods in accurately predicting PPIs and identifying functional modules. DNE also exhibits robustness against network perturbations and consistently outperforms other methods across different perturbation ratios (fig. S8). Moreover, DNE effectively captures biologically meaningful signals by reflecting the proximity between proteins in both PPI n-hop distances and Gene Ontology functional similarities via its embeddings (fig. S10).

While DNE has the capability to derive node embeddings solely from the structural information of networks, it also offers the flexibility to incorporate node features into the embedding process when these features are available. In biological networks like PPIs, where each node represents a protein, node (or protein) features can be sourced from diverse sources such as amino acid sequences (39, 40), the three-dimensional (3D) structure of proteins (41), and protein localization (42), providing additional information of proteins beyond their topological function within the network. Our method offers a remarkable approach for predicting PPIs by enhancing the network embedding through the integration of protein sequence features derived from pretrained protein language models. This integration substantially improves PPI prediction accuracy compared to existing methods that rely solely on sequence data.

Overall, DNE offers several advantages for network analysis. First, it generates a more discriminative embedding that captures not only the local connectivity patterns of each node but also distinguishes these patterns from those of other parts of the network. This enables a more accurate representation of each node’s structural role and community membership, reducing the likelihood of overfitting to local network noise. Second, by incorporating data from immediate neighbors as well as other network segments, DNE provides a more holistic view of the entire network. Third, DNE can leverage both the structure of networks and node features to generate more enriched embeddings. In this work, these embeddings are used to infer protein interactions and identify functional modules. Further applications may include disease gene prediction (43), where the embeddings help identify proteins associated with disease mechanisms, and protein function prediction (39) to facilitate the annotation of proteins in newly sequenced genomes. It is worth noting that DNE’s applicability extends beyond PPI networks and is applicable to various domains. Initial findings on diverse network types, such as citation networks (44), power grids (45), and internet service provider networks (46), suggest DNE’s broader applicability (fig. S7). Therefore, our proposed method marks a notable advancement in network embedding and offers an urgently needed solution for high-performance network analysis.

While the proposed method shows promise for network analysis, future enhancements are feasible. First, the method currently prioritizes structural information over node features. While DNE can incorporate node features, they primarily serve to initialize the embeddings so that the final embeddings can reflect these node attributes. This process could be improved by considering the similarity among node features alongside node connections during the sampling of context nodes. Second, the proposed method uses multilayer perceptrons (MLPs) as the encoder. It could also be intriguing to investigate alternative network types for potential use as encoders, such as graph neural networks.

Biological networks such as PPIs serve as a backbone for advancing our understanding of complex biological systems. However, their inherent complexity often poses challenges in analysis and hinders downstream applications. In this study, we presented a self-supervised network embedding technique aimed at providing more discriminative low-dimensional embeddings of high-dimensional network data. The proposed technique uniquely captures the intrinsic characteristics of each node by leveraging insights from both its local environment and the broader network context. Extensive experimental studies across various biological networks demonstrate that this dual perspective offers a comprehensive and robust representation of the network, enabling reliable pattern discovery and accurate downstream network analysis. Thus, DNE promises to be a valuable tool for the fields of bioinformatics and systems biology.

MATERIALS AND METHODS

DNE is proposed to embed network nodes into low-dimensional representations to facilitate downstream biological analysis. The pretraining stage of DNE comprises three key steps (Fig. 1): (i) initializing nodes using node positional encoding obtained from eigenvalue decomposition of the network’s adjacency matrix, optionally concatenated with node features when available; (ii) identifying node neighbors as positive context nodes via stochastic neighbor selection, based on random walks, and selecting nodes from other network regions as negative context nodes, based on the distribution of node degrees; (iii) embedding each node through MLP encoders, where the encoder’s parameters are optimized to reduce distances between embeddings of the anchor node and its positive context nodes, while increasing those between the anchor node and its negative context pairs. The overall framework of DNE is shown in Fig. 1.

Preliminaries

Given an input network $G(V,E)$, where $V$ represents nodes and $E$ represents edges, DNE aims to learn its node representations, such that all nodes ($V=\{v_i\mid i=1,2,\dots ,\mid V\mid \}$) can be converted from high-dimensional space into a set of low-dimensional vectors, denoted as $\{{\mathbf{z}}_i\in {\mathrm{ℝ}}^l\mid i=1,2,\dots ,\mid V\mid \}$, where l is the dimension of the output vectors and $l\ll \mid V\mid$. By learning effective node representations that capture the essential properties of the network, DNE aims to improve the speed and accuracy of graph analytics tasks, as opposed to directly performing such tasks in the complex high-dimensional graph domain.

Node input embedding construction

To construct node input embeddings $x_i$ for nodes $v_i$ ($i=1,2,\dots ,\mid V\mid$), eigenvalue decomposition is performed on the adjacency matrix to obtain node positional encodings. These encodings are then concatenated with node features (optional) to produce the input embeddings.

Positional encoding

Positional encoding involves eigenvalue decomposition on the network’s adjacency matrix A to capture nodes’ positions within the network’s structure. The adjacency matrix A is a square matrix of size $\mid V\mid \times \mid V\mid$, with each element $A_{\mathit{ij}}$ indicating the presence (or absence) of an edge between nodes $v_i$ and $v_j$. Specifically, in an unweighted graph, if nodes $v_i$ and $v_j$ are connected, $A_{\mathit{ij}}=1$ (for weighted graphs, $A_{\mathit{ij}}=w$, where w is the edge weight), otherwise, $A_{\mathit{ij}}=0$. Specifically, DNE implements Laplacian eigenvectors (LEs) for node positional encodings.

Laplacian eigenvectors

LE-based positional encoding performs eigenvalue decomposition (47) of the normalized graph Laplacian matrix $L$, which is given by $L=D^{-1/2}{\mathit{AD}}^{-1/2}$. Here, $D$ is the degree matrix, a diagonal matrix with the nodes’ degrees on its diagonal, and $A$ is the adjacency matrix of the graph

$$L=Q\mathrm{\Lambda }{Q}^T$$

Here, $Q$ represents the matrix of eigenvectors, and $\mathrm{\Lambda }$ is the diagonal matrix of eigenvalues. The k smallest nontrivial eigenvectors from $L$ (excluding the trivial eigenvalue of zero) are then used as positional encoding. This method effectively captures the connectivity and relative distances between nodes in the graph $G$.

Node features

In addition to the adjacency matrix A, a network may also have an associated node feature matrix X, with dimensions $\mid V\mid \times \mid F\mid$, where $\mid F\mid$ represents the number of features of each node. These node features represent the specific characteristics of each node. For instance, in a PPI network, where nodes represent proteins and edges denote protein interactions, node features can be sourced from amino acid sequences (39, 40), the 3D structure of proteins (41), and protein localization (42).

Positive and negative context nodes sampling

For each given node in a network, we treat it as the anchor node and initiate short random walks from this node to its neighbors, selecting nodes that co-occur on these walks as positive context nodes. In addition, an equal number of nodes are randomly sampled from the rest of the graph, following a probability distribution over the nodes where each node’s probability of being sampled is proportional to its degree raised to a specific power (20). These nodes are considered as negative pairs.

Positive context nodes sampling via stochastic neighbors selection based on random walks

Random walks are used to sample a set of neighboring nodes for each node in the training graph $G(V,E)$. In random walks, we start at a chosen node and move to a neighboring node based on a probability distribution, known as the transition probability. This process is similar to a Markov chain, where the next state (or node) we move to depends only on the current state. Each step in the walk is determined by these transition probabilities, which dictate how likely it is to move from one node to its neighbor. A random walk rooted at node $v_i$ (considered as the anchor node) can be represented by ${\mathbf{W}}_{v_i}=(r_0,r_1,\dots ,r_l)$ of length l over the graph from the source node $r_0=v_i$. Specifically, the probability distribution of moving from one node to its neighbors in a random walk can be represented as follows

$${\mathbf{p}}_{t+1}(i)={\displaystyle \sum _{j:(i,j)\in E}}\frac{{\mathbf{p}}_t(j)}{\text{deg}(j)}$$

where ${\mathbf{p}}_t(j)$ is the probability of being at node $v_j$ at step $t$ and $\text{deg}(j)$ is the degree of node $v_j$ (the number of edges connected to $v_j$). The transition probabilities can also be represented in matrix form as

$${\mathbf{p}}_{t+1}=({\mathit{AD}}^{-1}){\mathbf{p}}_t={({\mathit{AD}}^{-1})}^t{\mathbf{p}}_0$$

where ${\mathbf{p}}_0$ is the initial probability distribution across nodes, and ${\mathbf{p}}_t$ is the probability distribution after $t$ steps. The matrix $D$ is the diagonal degree matrix, with $D_{\mathit{ii}}=\text{deg}(i)$ and zeros elsewhere. In our implementation, we initiate a specified number of random walks, denoted by $\mathrm{\gamma }$, each with a length of l, from each node $v_i$. Specifically, we choose l = 10 and = 100 as the default settings. These random walks effectively explore the network, facilitating the sampling of nodes that are representative of the local neighborhood structure of the graph. An ablation study was conducted to evaluate the effects of positive node sampling parameters—walk length (l) and walk number ($\mathrm{\gamma }$)—on link prediction, as shown in fig. S9. Overall, the model demonstrates robustness to variations in these parameters. On the basis of the analysis, increasing the walk length to a certain threshold captures more neighborhood nodes, but further increases can introduce noise by including distant or irrelevant nodes. Similarly, while increasing the walk number initially captures more nodes within the specified walk length, excessive increases may lead to redundancy without adding major improvements.

Negative context nodes sampling based on the distribution of node degrees

Negative context nodes are sampled using the distribution $P_v=\text{deg}{(v)}^{\mathrm{\beta }}$, where $\mathrm{\beta }$ is set to 0.75 on the basis of prior works (48). This distribution is further normalized such that the probabilities sum up to 1. Consequently, nodes with higher degrees are more likely to be sampled as negative context nodes, and vice versa.

Encoder training via contrastive loss

Encoder architecture

DNE leverages MLPs to generate structure-aware representations from node input embeddings. Given $X=({\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_{\mid V\mid })$, where ${\mathbf{x}}_i$ denotes the input embedding of $i$-th node, the DNE encoder learns a function $f_{\mathrm{\theta }}(\cdot ):\mathcal{X}\to {\mathrm{ℝ}}^d$ that encodes ${\mathbf{x}}_i\in \mathcal{X}$ into a fixed-dimension vector representation $f_{\mathrm{\theta }}(x_i)\in {\mathrm{ℝ}}^d$. The encoder comprises two MLP blocks, each containing a fully connected layer, GeLU activation, batch normalization, and a dropout layer. The encoder serves as a nonlinear projection head to map nodes input into fixed-length vector representations

$$\text{MLPBlock}(X)=\text{DropOut}\left\{\text{BN}\left[\text{GeLU}(WX+\mathbf{b})\right]\right\}$$

$$f_{\mathrm{\theta }}(X)=\text{MLPBlock}(\text{MLPBlock}X)$$

Note that when focusing only on network structures, we use a single MLP encoder. However, to integrate node features, we implement a dual encoder approach—one encoder for network structures and another for node features—with their outputs subsequently concatenated (see Fig. 1A).

Encoder training using contrastive loss

For a given set of node inputs $\{{\mathbf{x}}_i\}$, our encoder $f_{\mathrm{\theta }}(\cdot ):\mathcal{X}\to {\mathrm{ℝ}}^d$ maps a node input ${\mathbf{x}}_i$ into a vector of dimension d such that nodes from the same random walks have similar embeddings and vice versa. Our contrastive loss minimizes the embedding distance between a pair of node inputs (${\mathbf{x}}_i$, ${\mathbf{x}}_j$) if they are from the same random walk but maximizes the distance otherwise

$$\begin{array}{c}ℒ({\mathbf{x}}_i,{\mathbf{x}}_j,\mathrm{\theta })=\mathbf{1}[y_i=y_j]{\Vert \left[f_{\mathrm{\theta }}({\mathbf{x}}_i)-f_{\mathrm{\theta }}({\mathbf{x}}_j)\right]\Vert }_1^2\hfill \\ +\mathbf{1}[y_i\ne y_j]\text{max}{\left\{0,\mathrm{ϵ}-{\Vert \left[f_{\mathrm{\theta }}({\mathbf{x}}_i)-f_{\mathrm{\theta }}({\mathbf{x}}_j)\right]\Vert }_1\right\}}^2\hfill \end{array}$$

where $y_i=y_j$ if nodes $v_i$ and $v_j$ are from the same random walks; otherwise, $y_i\ne y_j$. $f_{\mathrm{\theta }}({\mathbf{x}}_i)$ and $f_{\mathrm{\theta }}({\mathbf{x}}_j)$ are outputs of the DNE encoder parameterized by $\mathrm{\theta }$ applied to inputs ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$, respectively. The simplified loss can be written as

$$\begin{array}{c}ℒ(\mathrm{\theta })=\sum _{u\in V}\sum _{v\in N_R(u)}{\mid f_{\mathrm{\theta }}({\mathbf{x}}_u)-f_{\mathrm{\theta }}({\mathbf{x}}_v)\mid }^2\\ +\sum _{i=1}^k\text{max}{\left[0,\mathrm{ϵ}-\mid f_{\mathrm{\theta }}({\mathbf{x}}_u)-f_{\mathrm{\theta }}({\mathbf{x}}_{n_i})\mid \right]}^2,n_i\sim P_v\end{array}$$

where V refers to the entire node set of the input network, $N_R(u)$ represents the sampled neighbors for the source node u using random walks, $n_i$ denotes the negative context nodes drawn from the degree-based probability distribution $P_v=\text{deg}{(v)}^{\mathrm{\beta }}$, k represents the number of negative context nodes, and $\mathrm{ϵ}$ is a constant margin. Here, the first term encourages embeddings of each node u and its neighbors v to be similar by minimizing the squared $L_1$ norm between their embeddings. The second term ensures embeddings of u and a negative sample $n_i$ are at least $\mathrm{ϵ}$ apart by penalizing embeddings that are too close (less than $\mathrm{ϵ}$) with a squared penalty. The loss function $\mathrm{ℒ}(\mathrm{\theta })$ is optimized through Adam. During optimization, the parameters $\mathrm{\theta }$ of the encoder $f_{\mathrm{\theta }}$ are adjusted to minimize $\mathrm{ℒ}(\mathrm{\theta })$.

In the optimal scenario where $\mathrm{ℒ}({\mathrm{\theta }}^{*})$ is minimized, the embeddings of each node $u\in V$ can be expressed as a nonlinear combination of the features of its positive and negative context nodes, as shown by the equation

$$f_{\mathrm{\theta }*}({\mathbf{x}}_u)=\frac{{\displaystyle \sum _{v\in N_R(u)}}{f}_{\mathrm{\theta }*}{({\mathbf{x}}_v)}^2-{\displaystyle \sum _{i=1}^k}{f}_{\mathrm{\theta }*}{({\mathbf{x}}_{n_i})}^2+k\mathrm{ϵ}}{2[{\displaystyle \sum _{v\in N_R(u)}}{f}_{\mathrm{\theta }*}{({\mathbf{x}}_v)}^2-{\displaystyle \sum _{i=1}^k}{f}_{\mathrm{\theta }*}{({\mathbf{x}}_{n_i})}^2]}$$

Here, the presence of positive context nodes contributes positively to the embedding of the anchor node, while its negative context nodes contribute negatively. The weights are determined by the relative importance of positive and negative context nodes, adjusted by $k\mathrm{ϵ}$ and the denominator.

Network datasets

Our study incorporates a collection of interactome networks from various organisms to evaluate the performance of our method compared to existing network embedding techniques for link prediction. These datasets include the following: (i) the A. thaliana interactome, featuring 2774 proteins and 6205 PPIs (26); (ii) the C. elegans interactome, consisting of 2528 proteins and 3864 PPIs (27); (iii) the S. cerevisiae yeast interactome, comprising 2674 proteins and 7075 PPIs (28); and (iv) an extensive human interactome from the HuRI (29) project, which includes 8272 proteins and 52,548 PPIs. These diverse datasets allow us to conduct a comprehensive evaluation across different species and showcase the adaptability of our method.

Benchmark construction for module detection

To assess the effectiveness of our method in identifying functional modules within PPIs, we used data from the S. cerevisiae yeast network. For constructing our benchmarks for module detection, we obtained annotations from several sources: IntAct protein complexes (32), the KEGG pathways (33), and GOBP (34). Modules were identified on the basis of the collection of genes annotated with a particular term from each source. Modules consisting of only one gene were excluded because of their lack of informational value.

Protein sequence features obtained using ESM-2

Our study further enhances the S. cerevisiae PPI by integrating protein sequences from the Saccharomyces Genome Database (http://sgd-archive.yeastgenome.org/sequence/S288C_reference/orf_protein/), alongside features derived from the pretrained protein language model, ESM-2 (38). We selected this dataset for evaluation because it provides complete protein sequences for each protein in its PPI network, unlike other benchmarks we considered. ESM-2 is a transformer-based language model trained on around 65 million unique sequences and learned representations of protein sequences that reflect their biological properties. In this study, we used the pretrained ESM-2 model (esm2_t36_3B_UR50D) to generate protein sequence features, each of length 2560. This was achieved by averaging the last layer outputs of ESM-2 for each amino acid in a protein sequence. The pretrained model is available for public access on HuggingFace.

Downstream prediction models

We developed downstream models for various tasks using node embeddings obtained from network embedding methods as inputs. For link prediction, which was considered as a binary classification task (presence or absence) based on link embeddings, we first constructed link embeddings using four operations: the Hadamard product, absolute difference, squared difference, and averaging of the node embeddings from the start and end nodes of each link. Subsequently, we used logistic regression (https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) as the classifier, with a fivefold cross-validation applied to achieve the best performance of each method under different operators. For module identification, we applied hierarchical agglomerative clustering (35) using the AgglomerativeClustering function from the scikit-learn library (https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html) to cluster the nodes on the basis of their embeddings. We investigated the performance of each method across different linkage methods (single, average, and complete), distance metrics (Euclidean and cosine), and thresholds to obtain the best performance for each method.

Evaluation strategy

To evaluate the methods for link prediction, we randomly selected 20% of the edges E from the input network for testing to create the test edge set $E_{\text{test}}$, while the remaining edges formed the training network and its corresponding training edge set $E_{\text{train}}$. We then conducted a fivefold cross-validation on the remaining data to obtain optimal performance and repeated this process for 10 independent runs. To train our logistic regression classifier with both existing and nonexisting links, we constructed a dataset comprising positive and negative edge examples. Specifically, we selected 10% of edges from $E_{\text{train}}$ as positive examples, and sampled an equal number of nonlinked node pairs from the network as negative examples. The performance of each network embedding method for link prediction was evaluated using the ROC-AUC and the PR-AUC, both widely used metrics for this task (49).

For module identification, we subsampled the module sets to ensure that each gene was assigned to a single cluster, aligning with the assumption behind standard clustering evaluation metrics like the AMI. Subsequently, we assessed our predicted cluster sets against the benchmark module sets using AMI as our primary metric. We report the highest AMI score for each method to ensure the optimal cluster set for each dataset across clustering parameters is used. This evaluation was repeated 10 times to account for score variations due to the cluster subsampling strategy. Moreover, to assess the similarity between the clusters identified by our methods and known IntAct complexes, we used the Jaccard score (ranges from 0 to 1) to quantitatively measure the set overlaps.

Supplementary Materials

This PDF file includes:

Sections S1 to S8

Figs. S1 to S11

Tables S1 and S2